
|
Мулен Э. - Теория игр
БЕСКОНЕЧНЫЕ ИГРЫ
v1?M1v1 = vm(U1).Если ?х принадлежит множеству Л4Х, то вполне смешанный WE-выигрыш игрока 1 совпадает с его гарантированным выигрышем, ?х осторожная смешанная стратегия игрока 1, а рх, вообще говоря, нет.
2) Предположим, что ?х не есть смешанная стратегия (что в силу утверждения 1 эквивалентно ?х ?т (t/x)). Тогда множество Ух отрицательных компонент ?х не пусто.
Скажем, что Хх х Xz матрица Lx есть матрица Ух-потерь, если
?хх € Уі. ^^2) і/г € Xі (Л-іі f/г) ^ ^?хх€^і\Уі, ?^а€^2 М*і. *2) = О-
Покажите, что для любой достаточно малой ненулевой матрицы Ух-потерь L1 игра (Хх, Хг, Ul L1, U2) имеет единственное вполне смешанное равновесие. Соответствующий вектор выигрышей (іх, ?2) удовлетворяет условиям
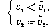
Интерпретация
Игрок 1 несет потери L(xlt - ), если использует стратегию хх € Yv Это наказание в действительности влияет только на его собственный вполне смешанный і?Е-выигрыш, оставляя без изменения выигрыш игрока 2.
3) Рассмотрим игру 2x2, в которой обе функции выигрыша взаимно однозначны (как в рассмотренном выше примере 3). Охарактеризуйте те игры, для которых возникает ситуация из пункта 2. Дайте числовой пример.
3. БЕСКОНЕЧНЫЕ ИГРЫ
Если множества чистых стратегий Х( бесконечны, то даже для игры двух лиц с нулевой суммой нельзя утверждать существование цены в смешанных стратегиях. Тем более не гарантируется существование смешанного ХЕ-исхода.
Пример 4. Китайский покер
Каждый из двух игроков выбирает (неотрицательное) целое число. Игрок, который назвал большее число, выигрывает доллар:
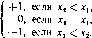
Хх Х2 N, их (хХ1 х2)
Вероятностное распределение на Хг = N принимает вид М/==(Мп))л. где 2 рг(п) = 1, рг(п)0 для всех п$Н.
nsN
Обозначая через Mt множество таких распределений, мы получаем игру (Mit М5, иг), где
(М-і Ма) ^ 2 Мі C^i)' Мг (хі) 2 Иі (^-l) * M's (-^a) -
Xi, X,€ N *1, ATjeN
X, Xt X, Xg
Исходная игра является игрой с нулевой суммой без цены sup inf иг = 1 +1 = inf sup uv
Xt x, xt Xi
На самом деле использование смешанных стратегий совсем не увеличивает гарантированный уровень игроков, поэтому и смешанная игра (Ми Мг, Mj) не имеет цены:
sup inf щ = 1 1 = inf sup (26)
Ді Д* M* Ді
Для доказательства этого неравенства фиксируем вероятностное распределение [аг Тогда для любого е 0 найдется целое число Пе, такое, что
+ 00
2 л (п) 8-
п=пк
Рассмотрим далее (чистую) стратегию Хі пв игрока 2й,(Мі, 6,г) = 2 Mi (ft) + 2 Mi (п) (18) + 8==1 + 2e
Пе H/lg
Поскольку e может быть сколь угодно малым положительным числом, получаем
inf (Ml, Мг) = inf 1 (Ml, 1,
Иг Xt
а значит, справедливо левое равенство в (26). Так как наша игра симметрична (см. упр.
1), то правое равенство также справедливо.
Сложность приведенного выше примера связана с некомпактностью множеств чистых стратегий, а также множеств смешанных стратегий. Когда те и другие множества компактны, непрерывность (исходной) функции выигрыша гарантирует существование равновесия по Нэшу в смешанных стратегиях.
Определение 4. Пусть G (X., up, і ? N) исходная игра [ N лиц в нормальной форме, для которой
для всех і € N.
Х{компактное подмножество некоторого' евклидова пространства Rp щнепрерывная функция на Хд,
Смешанная стратегия ц,- игрока і является вероятностной мерой Радона на X,-; это положительный непрерывный линейный функционал, заданный на множестве непрерывных действительных функций, определенных на X,-, наделенном топологией равномерной сходимости. Значение этого функционала на функции, тождественно равной единице, есть единица. Обозначим через М{ множество всех смешанных стратегий игрока і.
Смешанное расширение игры Gэто игра Gm (М,, up i g N)i
ut(x) = 5 u{(x)dy.(x), где da (x) = 60 dpi(Xi) произведение вероятностных w им мер juf, i?N.
Теорема 5 (Гликсберг [1952]). В условиях определения 3 смешанное расширение Gm игры G имеет по крайней мере одно равновесие по Нэшу.
Доказательство. В силу стандартного результата из функционального анализа (см. например, Данфорд, Шварц [1957], Колмогоров, Фомин [1972]) имеем:
Множество Mt -слабо компактно в пространстве, сопряженном к пространству непрерывных функций на Х{, наделенному топологией равномерной сходимости. Функция и{ линейна относительно переменной р,- и непрерывна на Мд, при условии, что последнее множество наделено произведением -слабых топологий.
Таким образом, теорема Гликсберга следует из теоремы Нэша (теорема 2, гл. III).
Пример 5. Игра размещение магазинов
На одной улице должно быть размещено два магазина спорттоваров. Владельца магазина дешевых товаров назовем игроком 1, а дорогихигроком 2. Если магазины расположены близко друг от друга, то покупатели зачастую предпочитают приобрести дешевый товар. Спрос неэластичен.
Игрок 1 стремится разместить свой магазин как можно ближе к магазину игрока 2, а тот старается по возможности увеличить расстояние между магазинами.
Бояее точно, мы предполагаем, что функции выигрыша имеют следующий вид:Хж = Х, = [0, 1],
u1(xlf хг) 1 X2\t
\xtха, если IX}X,
и2 (*г,
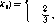
Отметим, что если расстояние между магазинами хотя бы 2/3 (длину улицы мы считаем равной единице), то влияние магазина дешевых товаров прекращается.
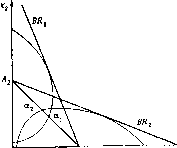
Исходная игра не имеет равновесия по Нэшу. Это показано на рис.
1, где приведены множества наилучших ответов для обоих игроков.
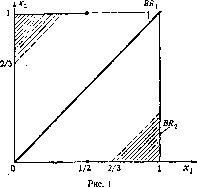
Поскольку множество Xf компактно, а н,непрерывные функции, теорема 5 гарантирует существование по крайней мере одного исхода в смешанных стратегиях равновесия по Нэшу.
Равновесием по Нэшу является следующая пара смешанных стратегий (juf, pf)i
= -g- 60 + -g- Sj. + g S_2_ + gf Si,
3 3
Ни одна из двух смешанных стратегий не является вполне смешанной (определение 2 непосредственно обобщается на случай бесконечных игр на основе понятия носителя меры Радона: см., например, Рудин [1966], Колмогоров, Фомин [1972]). Тем не менее пара (pf, pf) обладает типичным свойством вполне смешанного равновесия, а именно:
WjCpj, pf) = Mx(pf, pf) для всех px6^i. ^7) w2(pf, p2) = M2(pf, pf) для всех р2€М2.
Для проверки первого свойства фиксируем чистую стратегию хх игрока 1 и вычислим
йі(бх„ pf) = 4 (!¦*i) + Y (1 (1*i)) = -j Для всех хг?Хх.
Как и в конечном случае, если функция их{-, pf) постоянна на множестве чистых стратегий, то она постоянна также и на множестве смешанных стратегий (поскольку последние являются пределами выпуклых комбинаций чистых стратегий). Фиксируем далее чистую стратегию х2 игрока 2 и вычислим
. 1 (2+ Т\Т~х*3*2х,3 *2 + 6 (^2 з)+ 6 (з Л'2) + 3 ^ х*)’M2(pf. 8*,) =
1 2 если ух2у.
з'з + б (*2 з ) + 6 (*2 з) + з ^ *)
следовательно,
и*(и*. 8*е) = ц2(pf, р2) = ^ для всех х2?Хг, р2€Ма.
Отметим, что pfоптимальная осторожная стратегия игрока 1 в игре с нулевой суммой (Ми М2, щ). В самом деле, ut (pt, р2) = ¦и (р2, Pj) для всех рп р2, а значит, верхнее уравнение в (27) приводит к тому, что пара (pf, pf) является седловой относительно функции и? Следовательно, цена игры в смешанных стратегиях по функции иг равна 1/2 н совпадает с (??-выиг-рышем игрока 1.
Аналогичными рассуждениями можно показать, что (pf, и*) является (единственной) седловой парой в игре (М,, М2, й2), таким образом, смешанный гарантированный выигрыш игрока 2 равен 7/18 и совпадает с его (?і:-выигрышем.
Заметим, наконец, что наш NE-исход доминируем по Парето.
Вычисление смешанных NE-исходов является чрезвычайно трудной задачей даже в случае, когда исходные множества стратегий являются выпуклыми компактными подмножествами евклидовых пространств. Поэтому мы не будем заниматься дальнейшим изучением этого вопроса, а отошлем читателя к работам Партхасаратхи, Рагхаван [1971], Тийс [1981] и указанной в них литературе.
Два наших следующих примераэто игры, в которых множества стратегий игроков одномерны, а функции выигрыша разрывны. В первой из этих игр выигрыши равномерно ограничены, тем не менее не существует равновесия по Нэшу в смешанных стратегиях.
Этот факт указывает на то, что в условиях теоремы Гликсберга нельзя отбросить требование непрерывности функции выигрыша.
Пример 6. Игра двух лиц в единичном квадрате, не имеющая цены в смешанных стратегиях (Сайон, Вулф [1957])
Положим Хх = Х2 = [0, 1] и
1, если х1х2х1 + ±-,
О, если х% = х2 или х2 = х, -- \
+ 1, если х2 хг или xt + ~ х2.
Утверждается, что смешанное расширение этой игры двух лиц с нулевой суммой не имеет цены. Более точно, выполнено
sup inf и, = -1- inf sup и..
Hi Hi Hi Hi
Докажем правое равенство от противного, предположив, что существует стратегия р,2, для которой*1
Подставляя последовательно в (28) ^=1, ^ = 0, получаем!
где а = [і2(о, у) , ? = р2(^у, і). Далее применяем (28) при *і Т8 и предполагаем, что е стремится к нулю:
(31)
М{0})+М{1})!**({т})+а т*
Суммируя (30) и (31), получаем С другой стороны, [а2это вероятностное распределение, следовательно, Суммируя (33) и (30), имеем Суммируя (34) и (32), получаем противоречие с (29), Следова
тельно, мы доказали, что
inf sup tii j- *
Взяв смешанную стратегию
Р* = у б+ у 61_ + у 6і
4 2
получаем, что она гарантирует игроку 2 проигрыш не больше 3/7.
Упражнение 10 Докажите, что
sup inf! = -i-.
Hi ' Hi d
Указание: осторожная стратегия игрока 1 равна
р?=у бо + у 6j_+y б4.
2
В нашем последнем примере множеством стратегий будет действительная полуось, а функция выигрыша будет разрывна и неограниченна. Тем не менее докажем, что существует вполне смешанный NE-исход.
Пример 7. Игра „аукцион"
Доллар распределяется между п участниками, которые тайно делают ставки. Обозначим эти ставки через xt, ..., хп. Пусть наибольшая ставка принадлежит игроку і0: ш(л;) = {/„}, Где w(x)множество всех игроков, предложивших наивысшую Ставку, а именно
W (X) = {І ? У I х( sup хЛ.
leN
Правило аукциона состоит в том, что игрок і0 выигрывает доллар и должен уплатить вторую из назначенных цен, в то время как каждый из остальных игроков платит то, что он объявил: игрок і, і Ф /0, должен уплатить свою ставку xt.
Если наивысшую ставку предложили одновременно несколько игроков, то для того чтобы определить, кому достанется доллар, эти игроки бросают жребий. Получается следующая игра в нормальной форме:
Эта игра является вариантом игры „война на истощение" (задача 5 гл. Ill), в которой предмет конкуренции имеет одинаковую ценность для всех игроков, а число игроков произвольно.
Анализ исходной игры в нормальной форме (35) аналогичен исследованию игры „война на истощение. Игра (35) имеет п существенно различных /?Е-исходов в чистых стратегиях; все они оптимальны по Парето.
В каждом из таких исходов один игрок делает ставку больше единицы в то время, как остальные не ставят ничего.
Любое равновесие приводит к резкой несимметрии между игроками: для того чтобы сделать равновесие правдоподобным исходом игры, один из игроков должен выступить в качестве лидера, заявив окружающим, что он будет делать ставку больше единицы. Игроки знают о симметричности игры, поэтому вполне возможно, что никто из них не сделает подобного заявления.
В этом случае не может реализоваться исход, в котором какой-либо из игроков является лидером.
Совсем другая картина наблюдается при использовании смешанных стратегий. Здесь уже каждый игрок должен сохранять в тайне чистую стратегию, которая является реализацией смешанной стратегии.
Отсюда вытекает симметричность и вполне смешанность равновесия по Нэшу.
Для того, чтобы доказать это утверждение, мы введем вероятностное распределение ?* на [0, +00). такое, что для всех і€ N
не зависит от х g X,-
Вероятностное распределение ?* выбирается с непрерывной функцией плотности /:
?* (Л) = § f(t)dt для любого измеримого множества Ас[0, -f оо).
А
Обозначим через F функцию распределения:
F(x) = lf(t)dt.
0
Если каждый игрок / из N\{i\ использует смешанную стратегию ?*, то случайная переменная
sup х,
і е N \{і}
имеет функцию распределения Fn_1 с соответствующей плотностью fa~{n\)Fn~1f. Следовательно, мы можем вычислить
X + 00
Щ(6Ж, цТ) = 5(1-0/ (0 dt X I /„ (0 dt = о . *
- (П_ 1) J (1 t)Fn~a (t) f (t) dtx (1 Fn~1(x)).
о
В силу непрерывности / приведенное выше выражение дифференцируемо по х и условие (36) приводит к
О = = (n l)Fn~2(x) f (х) -{-Fn~l (х)-1.
Поэтому G~Fn~l является решением дифференциального уравнения G' (x)-fG(x) = l, и, принимая во внимание, что F(0) = 0, окончательно получаем
1
F(x) = [lе"*]-1 для всех х^О.
Следовательно, в симметричном вполне смешанном NE-исходе каждый игрок использует одну и ту же функцию плотности!
f . 1 е~х
/ (*) „ ! ‘ п-2
Заметим, что для любого сколь угодно большого числа % Вероятность того, что игрок сделает ставку выше X не равна
Кулю (а есть в точности 1(1е_д)п"1) . Отсюда следует, что ваш NE-исход доминируем по Парето. Тем не менее математическое ожидание а наибольшей ставки является конечным:
Заметим, наконец, что, как показывают простые вычисления, /?Е-выигрыш для каждого игрока в точности равен нулю.
Задача 6. Модифицированный китайский покер, имеющий цену
Каждый из двух игроков выбирает натуральное число. Если эти два числа ие равны, то выигрыш равен нулю. Если выбранные числа совпадают хг хг = р, то выигрыш игрока 1 равен ар, где а2 1 ... ^ ар 1 ... неубывающая последовательность
положительных чисел. Таким образом, игрок 2 сталкивается со следующей дилеммой.
Чем больше число, которое он выберет, тем меньше вероятность того, что игрок 1 его угадает, но тем более опасным становится угадывание данного числа. Исходная игра двух лиц с нулевой суммой такова:
G = (Xj, X2, щ),
Ее смешанное расширение может быть определено следующим образом:
S ?(р) = 1 и ?(р) 0 для всех р к р=і I
+ QB
(Их* И.) = 2 арЦі (р) ілг (р)
р=і
(ut может принимать значение -foo).
Возможно и другое определение:
Mt= Mt= /?€Л1 sup[a_-v (/?)] + oo1 , l I pe N f
при этом значения функции щ всегда конечны. При ответе на следующие вопросы можно использовать любой из этих двух вариантов определения смешанного расширения.
1) Докажите, что если
+ OS?± + ржі ар
то смешанное расширение игры G имеет цену, каждый игрок обладает единственной оптимальной стратегией ?, причем стратегия ? вполне смешанная.
2) Докажите, что если
то смешанное расширение G имеет цену, но ни один игрок не имеет оптимальной стратегии.
Кооперативное поведение игроков
В первой части книги мы изучали сообщество, в котором отсутствовал явный обмен информацией между участниками. Это могло быть следствием физических ограничений, юридических барьеров или же результатом взаимного недоверия. Единственным косвенным способом обмена стратегической информацией (см. процедуру нащупывания по Курно, гл. Ill, разд.
3) являлось совместное наблюдение тактических ходов.
Теперь же мы хотим создать поведенческие модели кооперативного сообщества, в котором имеется явный обмен информацией. Структурная неэффективность некооперативных равновесных исходов (присущая большинству примеров игр с ненулевой суммой, рассмотренных в первой части книги) теперь будет интерпретироваться как побудительный мотив к кооперации.
Попытаемся определить ее основные черты.
После этапа переговоров об условиях кооперации, который может включать взаимное выяснение функций выигрыша, торг и различные психологические маневры, игроки приходят к кооперативному соглашению. Соглашения могут быть обязательными (когда несколько игроков подписывают контракт об использовании определенных стратегий и выполнение этого контракта обеспечивается некоторым контролирующим органом, которому подчиняются все игроки) или необязательными (когда такого органа не существует, и поэтому соглашение во многом напоминает международные договоры, которые действуют до тех пор, пока не выгодно их нарушать).
Наш подход состоит в изучении разумных исходов переговоров. При этом не делается никакой попытки дать описание самого процесса переговоров. При рассмотрении необязательных соглашений возникает целый ряд вопросов стабильности, которые могут быть исследованы наилучшим образом при фиксации некоторых информационных предположений (гл.
V и VI). С другой стороны, изучение обязательных соглашений связано с нормативным определением справедливости, которая рассматривается как некая сила, поддерживающая кооперацию.
Обязательные соглашения не будут здесь рассматриваться (см. введение).
СТАБИЛЬНЫЕ СОГЛАШЕНИЯ
Необязательные соглашения определяют исход и, следовательно, конкретную стратегию для каждого игрока. Поскольку мы хотим, чтобы для каждого игрока была сохранена полная суверенность стратегического выбора, то предполагается, что никакого игрока и никакую коалицию игроков нельзя заставить использовать стратегии, рекомендованные соглашением.Таким образом, имеется единственный способ предотвратить возможное невыполнение соглашения отдельными участниками или коалицией участников. Нужно сделать так, чтобы отклонение от соглашения было невыгодно отклоняющимся игрокам.
Это и есть свойство стабильности.
Стабильность является не таким уж простым понятием, как это может показаться на первый взгляд. В самом деле, отклонение некоторых игроков, нарушающих рассматриваемое соглашение, может заставить остальных игроков (которые первоначально не собирались нарушать соглашение) изменить свои стратегии. Эти индуцированные изменения трудно предсказуемы независимо от того, предполагаем ли мы, что первоначальное нарушение соглашения убьет дух кооперации и вынудит игроков придерживаться некооперативного поведения.
В самом деле, единственным бесспорным выводом первой части книги является то, что большинство игр в нормальной форме обладает несколькими различными некооперативными равновесными исходами (см. гл. Ill и IV).
В соответствии с этим необязательные соглашения будут состоять из договоренности об исходе, а также из сценария реагирования каждого игрока і на отступление какой-либо коалиции, не содержащей і. Этот сценарий объявляется заранее. В следующей главе в качестве таких сценариев будут рассмотрены угрозы, которые могут предусматривать различную реакцию на каждое возможное отклонение от соглашения.
На протяжении данной главы мы будем рассматривать очень простой сценарий реагирования, а именно полное отсутствие реакции.
Верность соглашению требует придерживаться условленной стратегии независимо от того, какие стратегии используют остальные игроки. Выше уже было сказано о том, что следует использовать соглашения, которые не выгодно нарушать.
Такие соглашения как бы автоматически, обеспечивают свое выполнение, и в этом смысле мы называем их стабильными.
Основным примером стабильного соглашения является соглашение, базирующееся на равновесии по Нэшу. Его стабильность обеспечивается взаимным незнанием окончательных стратегических выборов.
Мы обобщим концепцию равновесия по Нэшу в двух направлениях. Если игроки-нарушители могут образовывать коалицию, то выполнение соглашения подвергается опасности со стороны потенциальных отклонений любой коалиции. Это приводит к концепции сильного равновесия (разд.
1). Если игроки могут использовать случайный механизм, реализующий коррелированные рандомизированные стратегии и посылающий каждому игроку изолированно сигнал о том, какой стратегии ему придерживаться, то возникает новое понятие стабильного соглашения. Назовем его равновесием в совместных смешанных стратегиях (разд.
2).
I. СИЛЬНОЕ РАВНОВЕСИЕ
Пример 1. Пиратские корабли
Два корабля уходят в один и тот же день на остров сокровищ. Каждый из п пиратов должен принять решение, на каком корабле ему плыть: на корабле А или на корабле В. Если t число пиратов, решивших плыть на корабле А, то путешествие на корабле А затянется на а(() дней, а путешествие на корабле В, на котором (п /) пиратов, продлится Ь(пt) дней.
Каждый игрок стремится минимизировать длительность его собственного путешествия. Данная ситуация описывается следующей игрой:
где t = 2 х,,
І 6 N '
ut (лг) =
Хг = {0, 1} itN а(і), если хг = 1, Ь(пt), если х{ = О,
Х[ = 1 означает, что игрок і плывет на корабле А.
Предположим, что функции а и b строго монотонно возрастают на {0, ..., п] и выполнены условия a(0)6(ft), 6(0) а(/г).
Некооперативным равновесием (МЕ-исходом) в данной игре является любой исход х*, для которого число t* = 2 xt
UN
удовлетворяет следующим условиям:
a(t*)^b(n нет желания переключаться со страте
гии 1 на стратегию О и
b(п1): нет желания переключаться со стратегии 0 на стратегию 1.
Предполагая для простоты, что a{t)^b(nt -f 1) для всех і, получаем, что существует единственное целое число t*, удовлетворяющее двум приведенным выше неравенствам, а именно
f*== sup {t\a(t)^b(n t + 1)} = inf {11 b (n 0 ^ a (/ + 1).
Следовательно, исход x* есть равновесие по Нэшу тогда и
только тогда, когда 2 xf = t*.
le N
Если игроки не могут обмениваться информацией перед выбором стратегии (они должны забронировать место на одном из двух кораблей заранее), то они не смогут скоординировать свои выборы так, чтобы достигнуть равновесия по Нэшу в чистых стратегиях. По-видимому, они будут использовать симметричное вполне смешанное равновесие, которое в действительности доминируемо по Парето любым Л/?-исходом в чистых стратегиях.
Упражнение 1
Докажите существование единственного вполне смешанного /??-исхода, в котором каждый пират выбирает стратегию 1 с одной и той же вероятностью р. Докажите, что этот исход, как правило, доминируем по Парето любым Ni:-исходом в чистых стратегиях.
КЛАССИФИКАЦИЯ ИГР ДВУХ ЛИЦ
Заметим, что стратегия of игрока і в повторяющейся игре является объектом весьма сложной структуры. Эта стратегия на каждом шаге t?N сопоставляет предыстории х1, ...,xt~1 выбор х{ игрока і. В действительности для реализации вектора выигрышей uN(x*) как вектора і?Б'-выигрышей в повторяющейся игре достаточно рассмотреть весьма простой исход о*. Стратегия of игрока і, которую он использует по соглашению, есть чистая стратегия xf до тех пор, пока никакой игрок / не отклонился от xf Если отклонившийся игрок / обнаружен, то стратегия af впредь диктует наказание данного игрока.Поскольку мы интересуемся только равновесиями по Нэшу, то коалиционные отклонения от о* пока не учитываются.
Для того чтобы формально описать данный NE-исход, длякаждого j?N выберем стратегию х\ игроков N\{j], такую,7*ЧТОsup И) = Р/.хі
Для каждого і € N стратегия of игрока і в повторяющейся игре определяется следующим образом:хj = xf: в момент 1 выбирать
если х = х2 ... х~х = х*, то x\ = xf\ в момент t придерживаться условленной стратегии, если все остальные игроки до сих пор делали то же самое;
если х = х2 = ... х~2 Ф х*~г, тогда выбрать /, такое, что х]~гфх*, и далее играть х[ = х[ = х[+і = .. ¦ .
При каких условиях поведение, определяемое по о*, предостерегает игроков от отклонений в одиночку? Краткосрочный доход игрока і от отклонения в момент t (которому нельзя ничего противопоставить до следующей партии) должен перекрываться долгосрочными потерями от наказующего поведения игроков Н\{і} (которые по предположению придерживаются стратегии в моменты времени / + 1, / + 2, ...).
Полагаяи* ixf) = sup ut (х{, х?)xiи сравнивая дисконтированное значение в момент t краткосрочного дохода и* (xf)м,- (х*) с долгосрочными потерями, получаем следующее свойство стабильностиі
и* (xf) U{ (X*) б (щ (X*) 0() + Ь2{Щ (**) fy) Н- . . которое эквивалентно системе неравенств
1б.....и‘ ) для всех i$N, (14)
Таким образом, если б достаточно близко к 1, условия (14) выполнены, и, следовательно, о* является NE-исходом повторяющейся игры (с дисконтированным выигрышем (13) или со средним Чезаро (12)).
Лемма 4. Если система (14) справедлива, то повторенш игры G с дисконтированным выигрышем (13) имеет равновесный по Нэшу исход, которому соответствует последовательность исходов
х* =x = г
Таким образом, NE-выигрьш игрока і равен и{ (х*).
Заметим, что мы не описали полностью множество NE-исходов, возникающих при повторении игры G. Известно (см. Думай [1978]), что множество векторов выигрышей, соответствующих N P-исходам, может разрывным образом зависеть от б.
Приведем пример, который демонстрирует другой подход к повторяющимся играм. В этом примере каждый игрок принимает во внимание только последние наблюденные ходы своих партнеров.
Пример 4. Повторение игры дилемма заключенного (Думай [1978])
Предположим, что игра дилемма заключенного (пример 1, гл. 1) повторяется во времени и каждый игрок использует стационарную стратегию с памятью на один ход). Таким образом, стратегией игрока і является тройка (х(; yit г{), где xit yt, г{ принадлежат множеству {Л, Р} и интерпретируются следующим образом:
1) игрок і выбирает х^х] в первом повторении игры
2) в момент t 2 игрок I выбирает у{, если игрок / вел себя мирно в момент времени t 1, и ведет себя агрессивно, если игрок / был агрессивен, т. е.
х\ * у0 если х\~' = Р, х$ = г{, если х}~' =! А.
Типичной стратегией является стратегия как ты, так и я, а именно (Р; Р, А). После того, как каждый игрок выбрал стратегию {х{\ yt, z{), единственным образом определяется последовательность х, ..., х*, ... и средний выигрыш (12). Следовательно, возникает следующая биматричная игра (8x8)j
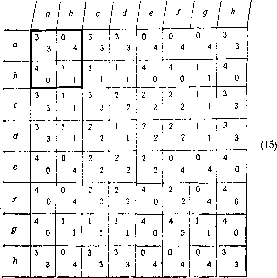
Здесь Ркраткая запись чисто мирной стратегии (Р; Р, Р). Аналогично А = (А; А, А) обозначает чисто агрессивную стратегию. Следовательно, северо-западная 2x2 подматрица (15) является собственно матрицей игры дилемма заключенного.
Отметим, что для удобства вычислений мы слегка изменили числа по сравнению с примером 1 гл. I (см. упр.
4 ниже).
При цикличности последовательности (х*) вектор выигрышей является средним арифметическим соответствующих элементов исходной матрицы 2x2. При этом возможны три варианта:
1) (Р, А) {А, Р)(Р, А)..... например (Р; Р, А) против
(А; Р, А);
2) (Р, Р) (Р, А) {А, А) (А, Р) (Р, Р), .... например (xt; Р, А) против (х2; А, Р) для всех хг, х3;
3) (Р, Р)(А, А)(Р, Р), например (Р; А, Р) против
(Р; а, р).
Во всех других случаях последовательность (х1) становится стационарной после некоторого конечного числа ходов, и соответствующий выигрыш является чистым.
В приведенной выше биматричной игре (8x8) две стратегии каждого игрока сразу же могут быть вычеркнуты, а именно (Р; А, А) кгк эквивалентная А и (Л; Р, Р) как эквивалентная Р.
Таким образом, останется игра (6x6) с двумя равновесными по Нэпу исходами, а именно (Л, Л) (некооперативное равновесие исходной игры) и (Р; Р, Л) (Р; Р, Л) новый NE-исход, в котором оба игрока применяют стратегию как ты, так и я. Интерпретация этого специфического устойчивого соглашения в повторяющейся игре в точности аналогична интерпретации сценария предостережений в примере 1.
Заметим, что в игре (15) стратегия Р (мирная) не доминируется больше стратегией Л (агрессивной). Однако после последовательного исключения доминируемых стратегий мирная стратегия в конце концов окажется отброшенной.
Оптимальный по Парето І?Е-исход (т. е. применение стратегии как ты, так и я обоими игроками) является исходом сложного равновесия игры (15).
Упражнение 4
Докажите, что игра (15) разрешима по доминированию и сложному равновесию соответствует выигрыш (3, 3). Сохранится ли этот результат, если исходная игра будет иметь структуру игры дилемма заключенного, но трем предельным циклам будут соответствовать различные средние выигрыши?
4. КЛАССИФИКАЦИЯ ИГР ДВУХ ЛИЦ
В этом разделе мы ограничимся рассмотрением игр двух лиц. Для таких игр a-ядро совпадает со множеством дележей, а P-ядро и у-ядро (определение 5) являются его подмножествами, причем по крайней мере одно из них непусто (теорема 1).
С этих пор мы предполагаем заданной игру двух лиц G = *= (Х1( Х„ ult и2) с конечными множествами стратегий Xlt Х3 (хотя большинство результатов, приведенных ниже, остается справедливым и для компактов Х( и непрерывных функций и„ t=l, 2).
Лемма 5, а -ядро игры G совпадает со множеством всех дележей
C(G)^/(G).
Р-ядро игры G задается условиями:
( вектор х* оптимален по Парето,** € Ср (G) ф і inf sup и, (у{, (/,),(**), /= 1, 2.I !/i /
Доказательство немедленно следует из определений 3 и 4 И поэтому будет опущено. Отметим, что P-ядро G может быть пустым: рассмотрите, например, игру двух лиц с нулевой сум* мой, не имеющую цены.
Пример 5. Модифицированная координационная игра Два игрока выбирают натуральное число из множества {1, 2, .... 10}.
Пусть выбраны xt, х2 и х1 + х2=10, тогда выигрыш игрока і равен xt. В оставшихся случаях платежный вектор равен (4, 0), если х1-\-х2 четно, и (0, 4), если хг + х2 нечетно. Гарантированный выигрыш игрока i sup inf и{ равенхі х/
Нулю, т. е. совпадает с минимальным возможным выигрышем. Дележи являются оптимальными по Парето исходами, т. е. для них выполнено х1 + х2=Ю.
Тем не менее inf sup и,-= 4, і1, 2, поэтому из леммы 4х/ хі
Следует, что (3-ядро состоит только из трех исходов (4, 6) (5, 5) (6, 4).
Для того чтобы стабилизировать с помощью предостерегающих угроз дележ (2, 8), необходимо, чтобы оба игрока согласились на выбор стратегий в открытую. В противоположность этому реализация дележа из (3-ядра требует более слабого информационного ограничения: нужен лишь сигнал, информирующий игрока об отклонении его партнера. С другой стороны, во многих играх двух лиц a-ядро и (3-ядро совпадают. В частности, это верно для смешанного расширения, поскольку обе игры с нулевой суммой (М„ М2, ых) и (М?
М2, й2) имеют цену.
Рассмотрим подмножество таких дележей, которые могут быть стабилизированы парой предупреждений, т. е. парой угроз, совпадающих с наилучшими ответами игроков.
Определение 5. у-ядро игры G состоит из таких дележей х*, для которых существует сценарий предостережений (х*, ?„),
где угрозы 1;, і=1, 2, суть предупреждения:
Г Uj (хр І; (Xj)) Uj (.x*),
УХ/фх,- j u, (X.y ^ (*,))= sup Ui(xj, Xi).
\ xieXi
Будем использовать обозначение Cy(G) для у-ядра.
Лемма 6. Предположим, что функция ut взаимно однозначная, і=1, 2. Напомним, что S{ обозначает і-выигрыш по Щтакельбергу
S; = sup{M,(x,, xj) I (Xj, X,) € BR,} i = 1, 2,
где BR,множество наилучших ответов игрока j (см. гл. II, разд.
4).
Тогда у-ядро игры G состоит из таких оптимальных по Парето исходов х, для которых
і=1, 2. (16)
Доказательство. Предположим, что я*оптимум Парето, удовлетворяющий (16). Для любого х,фхf обозначим через Xj~\j(xi) наилучший ответ игрока /. ГІо определению S{ имеем
,(*.- ^(x.))S,Mf(x^), І== 1, 2, х{ Фxf.
Следовательно, (я*, g2) является сценарием предостережений, а поэтому исходя* индивидуально рационален (по лемме 1; мы можем также утверждать справедливость неравенства sup inf w; ^ Sj). Таким образом, исход я* является дележом,*1 *7поскольку по предположению он оптимален по Парето.
Докажем обратное утверждение. Пусть я* принадлежит у-ядру игры G. Тогда существует сценарий предостережений (х*, Іг, У, в котором %i(Xj)(единственная в силу предположения о взаимной однозначности) стратегия наилучшего ответа игрока і на яу. Докажем, что я* удовлетворяет (16).
Выберем сначала я, Ф х*. По свойству имеем
щ(х{, ?,(**)
Осталось доказать, что
х, = I, (X*) = и, (xf, х}) щ (я*).
Предположим противное:
щ (я*) щ {xf, xf).
В силу оптимальности по Парето исхода я* получаем sup Uf (я,*, yf) = Uf {xf, Xf) Uf (я*).4f
Полученное противоречие доказывает лемму.
Замечание. Предположение о взаимной однозначности может быть опущено в формулировке леммы 6, если Sf заменить нау, sup inf щ(х{, x,)).X і XjbBRji X;)
Доказательство аналогично предыдущему и оставляется читателю в качестве упражнения.
Предупреждение предполагает выбор игроками своих наилучших ответов и, следовательно, является весьма правдоподобной угрозой. Характерным примером может служить угроза как ты, так и я в игре дилемма заключенного ((1) в примере 1). В противоположность этому любая стабилизирующая угроза, которая отличается от предупреждения, имеет черты запугивания, а именно: Если ты отклонишься, то я пожертвую своими краткосрочными интересами, чтобы наказать тебя и тем самым обеспечить долгосрочную стабильность кооперации.
В работе Шеллинг [1971] содержится замечательный пример такого сорта. В этом примере речь идет об индусском монахе, который без всякого оружия охранял в пути драгоценности одной лишь угрозой покончить с собой, если эти драгоценности будут украдены.
Традиции моральной стойкости оказалось достаточно для убедительности этой угрозы.
Лемма 6 устанавливает связь между осуществимостью стабильности с помощью предупреждений и борьбой за лидерство (гл. Ill, разд. 1.) Она утверждает, что в игре G возникает борьба за лидерство в том и только в том случае, если ее у-ядро пусто.
Таким образом, в игре с пустым у-ядром стабильности любого дележа угрожает возможность захвата лидерства одним из игроков. Вместе с тем, другой игрок в этом случае может использовать угрозу типа машины страшного суда.
Правдоподобность успеха той и другой тактики с точки зрения стороннего наблюдателя конфликта одинакова.
Пример 6. Дуополия с назначением выпуска
Рассмотрим дуопольную игру, аналогичную игре, рассматриваемой в примере 5 гл. III. Две фирмы поставляют некото рый товар на рынок, /-я фирма предлагает товар в объеме xh і'=1, 2. Цена на товар определяется формулой р0(х1 + хг) (для X!-l-x2^p0).
Функции затрат одинаковы у обеих фирм, причем затраты на выпуск единицы продукции линейны относительно количества выпускаемого товара. Затраты на выпуск единицы продукции при увеличении масштабов производства могут быть как возрастающими, так и убывающими.
Хі = Х2 = [0, у/о] ,
?(*!, *а) = 0 х\х{ (c-i-eXi) xt, t=l, 2,
где х х, + х2, а ра, с, ефиксированные параметры, удовлетворяющие условию
О у/70 с /?0.
Предполагается, что е мало по сравнению с р0с.
Случай 1. Постоянные затраты на выпуск единицы продукции Заметим, что
И- и\ [/?„х\хсх хг + (Ро с) х, следовательно, исходы х, такие, что
х ~ ~2 (Ро с)*
являются оптимальными по Парето. Верно и обратное утверждение, т. е. все оптимальные по Парето исходы удовлетворяют условию x = -j(Poс).
Проверку этого утверждения предоставляем читателю ^нужно приравнять нулю определитель матрицы Ь (л;1’ "2 ) ' ^аксимальныи общий доход равен у-(р0с)2.
Гарантированный выигрыш равен 0 (поскольку supinf=\ *1 *2
= sup и] у Po'j'j- Таким образом, дележи представляют
собой произвольное распределение максимального суммарного дохода (при условии, что не получается отрицательных выигрышей). Для вычисления выигрышей по Штакельбергу нам понадобится вычислить наилучший ответ игрока 1:
BR х (х2) = у (р0 с) ^ хг.
Таким образом,
y2 = S2 = sup ul (BR1 (x2), x2) =
0 Xi p0
- sup y[(Poс)хг x22]=S2 (pac)2.
0 * у Po
Симметричными рассуждениями получаем Sj y-(/?0с)2, следовательно, вектор выигрышей (S,, S2) соответствует некотощего максимальный суммарный доход поровну мржду игроками. В этой симметричной игре у-ядро является справедливым кооперативным исходом, реализующим с помощью естественных угроз BRit BR2. Реализация любого несправедливого распределения максимального общего дохода требует применения тактики запугивания.
Такие угрозы выглядят менее убедительно.
Случай 2. Возрастающие или убывающие (е Ф 0) затраты на выпуск единицы продукции
С помощью аналогичных вычислений, использующих аппроксимацию первого порядка (возможную в силу малости е), получаем
Si (е) = S2 (е) ~ -g {pcf (1 + Зв).
Предположим сначала, что е 0. По определению функции и\ имееми? (х) и\ (х) для всех хг 0, х2 0.
Отсюда получаем, что вектор выигрышей (S, (0), S2 (0)), соответствующий некоторому дележу в игре G, не является допустимым в игре G (е), е 0. Тем более вектор выигрышей (S, (е), S2 (е)) не является допустимым, и у-ядро игры G (е) пусто. Аналогичные рассуждения (с учетом S{ (е) S{ (0) и и? и1- для е 0) показывают, что у-ядро игры G (е) непусто при убывающих затратах на выпуск единицы продукции (е 0).
Рисунок 1 показывает разницу между случаями убывающих и возрастающих затрат на единицу выпуска.
е 0 убывающие затраты на единицу выпуска
-ядро есть [а1( а2] Кривые линии определяются условием8 О
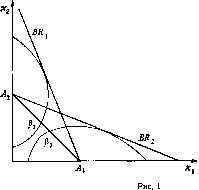
7-ядро пусто на [Рі, Р2] оба игрока используют угрозы типа запугивания.
Упражнение 5
Докажите, что в модифицированной координационной игре (пример 5) множество {ut (х) О S,} пусто. Тем не менее у-ядро не пусто (здесь нужно воспользоваться замечанием 2).
Покажите, что у-ядро состоит из единственного дележа (5, 5), который является справедливым исходом игры.
Упражнение 6
Предположим, что -{ гильбертова норма в ^(порожденная положительно определенной симметричной матрицей 2x2) и і'=1, 2, фиксированы. Рассмотрим игру
f X^X.^R,
I и,{ (х) = II х cLf (I ? 1, 2.
Покажите аналитически и геометрически, что у-ядро не пусто.
Из леммы 6 следует, что у-ядро данной игры G пусто в том (и только том) случае, если в этой игре возникает борьба за лидерство. Из леммы 4 получаем, что (3-ядро игры G пусто тогда (и только тогда), когда вектор выигрышей 3 = (inf sup ut, inf sup u2)
Уг Уі Уі Уг
не является допустимым (т. е. не существует исхода х, для которого было бы выполнено неравенство (3 ^ (ut (х), и2 (%)). Действуя в качестве ведомого, игрок і гарантирует себе результат inf sup щ (поскольку перед выбором у{ он знает у}). ТакимУ; Уіобразом, пустота (3-ядра порождает „борьбу за право второго хода": какой бы дележ ни был выбран, по крайней мере одномуигроку выгоднее подождать пока будет окончательно определена стратегия его партнера, а затем действовать в качестве ведомого:
Vxg Х{і2} Зі € {1, 2} и, (дс) inf sup и,-.
и, Ц
Как показывает следующий результат, эта терминология является корректной, борьба за лидерство (право первого хода) и борьба за право второго хода не могут возникнуть одновременно.
Теорема 1. у-ядро и fi-ядро не могут быть пусты одновременно.
Если у-ядро и fi-ядро не пусты, то они пересекаются.
Следствие. Игры двух лиц распадаются на три класса:
I. Ср = Ф, Су Ф ф: борьба за право второго хода,
II. Су = Ф, Ср Ф ф: борьба за лидерство,
Ш. СрПСуФФ: в этом случае Ср П С? является благоприятной областью для кооперации с использованием угроз.
Доказательство. Пусть х{, і = 1, 2, равновесие по Шта-кельбергу, в котором игрок і является лидером.
Пусть Dt - Множество исходов, удовлетворяющих следующим неравенствам!
Уі Щ (х), р, и, (х).
Поскольку x*j является наилучшим ответом игрока ] на х\, то множество Dt содержит х‘ и поэтому не пусто.
Предположим теперь, что у-ядро и P-ядро пусты. Выберем оптимальный по Парето исход х из Д (например, максимизируя иг-\-щ на Вг). Тогда имеем
Cv(G) = 0±m2(х) у2,
C/3(G) = 0=M*) Pi-
Поскольку хг принадлежит D$, заключаем, что исход хі доминирует по Парето исход х. Получили противоречие.
Предположим теперь, что у-ядро и P-ядро не пусты и докажем, что их пересечение также не пусто. Положим у = (у1( Уа).
Если у^р, то CgcrCy, и все доказано. Аналогично, если Р^у, то Cpf]Cy = Cv. Осталось рассмотреть случаи типа
Рі ^ Ук Уі ^ Pa-
Тогда любой дележ из Dlt например х1, принадлежит Cv f) Ср. Характерным примером игр класса I являются игры с нулевой суммой без цены.
На самом деле игра класса I не имеет равновесий по Нэшу.
Упражнение 7
Если P-ядро игры G пусто, то NE (G) также пусто, и игры е нулевой суммой (Xj, Х2, uj и (Хи Х2, и2) не имеют цены.
Примером игр класса II является игра „перекресток (пример 2 гл. III).
Упражнение 8
Для игры G из класса II выполнено Р/?і- ' = 1.2.
Для любой игры класса III пересечение CvfCp является подходящей областью для кооперации с помощью угроз). Ниже приведены два упражнения и задача.
Они показывают, что типичными примерами игр класса III могут служить игры, имеющие равновесие в доминирующих стратегиях, а также игры с оптимальным по Парето вектором у или (5, как это имеет место в следующих двух упражнениях и задаче.
Упражнение 9
Пусть каждый игрок имеет строго доминирующую стратегию, т. е.
и, (х*, И; (xh Xj) для всех х{ф х? и для всех xJt
тогда игра G принадлежит классу III. Приведите пример, показывающий, что игра G, в которой каждый игрок имеет доминирующую стратегию, может принадлежать классу II.
Упражнение 10
Игра G, для которой вектор у является вектором выигрышей по крайней мере для одного дележа, принадлежит классу III.
Задача 4. Квазинесущественные игры
Скажем, что игра G является квазинесущественной, если р = (inf sup и1( inf sup и2) является вектором выигрышей по
У: У\ Уі Уг
крайней мере для одного оптимального по Парето исхода.
1) Предположим, что функции и1У и2 взаимно однозначны на Х{і2} и что игра G квазинесущественна, Тогда (единственный) исхода;*', для которого (ыДх*), 2(х*)) = Р, является і-равнове-сием по Штакельбергу для /= 1, 2. Этот дележ также является единственным Л^-исходом игры G.
2) Приведите пример квазинесущественной игры, в которой нет /Vf-исхода.
3) Предположим, что игра G квазинесущественна. Докажите, что игра G несущественна в том и только том случае, если игры с нулевой суммой (X,, Х2, ых) и (Хх, Х2, иг) имеют цену.
Приведите пример квазинесущественной игры, не являющейся несущественной, в которой функции и{, І = І, 2, взаимнооднозначны.
Задача 5. Сценарий гарантированных предостережений (Мулен [1977])
Пусть (х*, gj, g2) сценарий предостережений игры G. Назовем угрозу гарантированной, если ее реализация не приносит убытков угрожающему игроку;
ДЛЯ любых Xj, Xj.
(*іі (*і)) ^ (- *¦*) ^ (Іі (%г)і \
и2 (lj (х2), х2) ^ и2 (х*) ^ Ц2 (Xj, ^2 (^і))- I
g-ядром игры G является подмножество, обозначаемое Cg (G), таких исходов х*, для которых существует по крайней *мере один гарантированный сценарий предостережений (х*, х, 2).
1) Докажите следующую эквивалентность:
х€Сг(0)ФФ[х оптимален по Парето и и;(х)^(ЗД
2) Докажите, что g-ядро является подмножеством, возможно пустым, у-ядра:
Cg(G)czCy (G).
3) Приведите примеры игр нз класса I, показывающие, что g-ядро может быть как пустым, так и непустым.
Указание: рассмотрите следующую игру 2x2:и опишите необязательные соглашения в этой игре (включая смешанные Nf-исходЫ и равновесия в совместных смешанных стратегиях).
4) Для игры G, принадлежащей классу III, докажите, что либо ее g-ядро пусто, либо игра G квазинесущественна (задача 4). В последнем случае докажите, что
Cf = Cv = C =(ult 2Г1(Р).
5. ИГРЫ В ХАРАКТЕРИСТИЧЕСКОЙ ФОРМЕ: ЯДРО
Пример 7. Игра „джаз-оркестр" (Янг [1979])
Владелец ночного клуба в Париже обещает 1000 долларов певцу (S), пианисту (Р) и ударнику (D) за совместную игру в его клубе. Выступление дуэта певца и пианиста он расценивает в 800 долларов, ударника и пианиста в 650 долларов и одного пианистав 300 долларов. Другие дуэты и солисты не рассматриваются, поскольку присутствие фортепиано владелец клуба считает обязательным. Дуэт певецударник зарабатывает 500 долларов за вечер в одной удобно расположенной станции метро, певец зарабатывает в среднем 200 долларов за вечер в открытом кафе.
Ударник один ничего не может зара-ботать.
Суммарный доход трех музыкантов максимален (1000) в случае их совместного выступления в ночном клубе. Если певец выступает отдельно от пианиста с ударником, то все втроем они получают 650 -f 200 долларов, если пианист один выступает в ночном клубе, то 300-{-500 долларов.
Наконец, суммарный доход равен 800 долларов, если пианист и певец отказываются от участия ударника. Какое распределение максимального общего дохода следует признать разумным, учитывая описанные возможности игроков в смысле частичной кооперации и индивидуального поведения?
Определение 6. Для данного конечного сообщества N игрой в N -характеристической форме назовем отображение ? из множества непустых коалиций игроков Р (N) в R. Игра (N, ?) называется супераддитивной, если для любых неперееекающихся коалиций Т, S g Р (N) выполнено
v(T) + o(S)^v(T[}S). (17)
Свойство супераддитивности (условие (17)) не является необходимым для большинства результатов, приведенных ниже, однако оно необходимо для интерпретации числа ? (Т) как максимального общего дохода в случае, когда игроки в коалиции Т действуют независимо от дополнительной коалиции Те. Неравенство (17) означает, что коалиция Tl)S имеет не меньше возможностей, чем две независимые непересекающиеся коалиции Т и S,
Из супер аддитивности ? с очевидностью следует, что для любого разбиения Slt ..., Sk множества N выполнено2 v(Sk)^v(N). (18)fe= 1
Следовательно, не существует такого разбиения Sx, .... Sk, которому бы соответствовал суммарный доход, превышающий доход коалиции всех игроков v(N).
Таким образом, кооперация всех игроков является единственным эффективным кооперативным исходом.
Замечание 1. В определении 1 предполагается, что исход кооперации может быть выражен в одних и тех же единицах измерения, т. е.' существует трансферабельный товар, на основе которого могут быть осуществлены побочные платежи между игроками.
Мулен Э. - Теория игр
Книга французского математика, отражающая взаимосвязь между математической экономикой и теорией игр;,в последние годы на стыке этих двух наук получены интересные результаты. Изложение отличается методическими достоинствамиавтор дает возможность читателю самостоятельно разобраться в тщательно подобранных упражнениях.ПРЕДИСЛОВИЕ
Теория игр принадлежит к числу важнейших математических инструментов современных социально-экономических наук. Автор данной книги ставил перед собой две основные цели.1) Предложить неспециалистам замкнутое изложение основных понятий теории стратегических игр. Определения и результаты с математической точки зрения являются совершенно строгими. Вместе с тем обсуждению и сравнению различных понятий равновесия уделено большее место, чем развитию методов их вычисления. Технические детали в большинстве случаев опускаются.
Чтобы стимулировать читателей, предлагается более 75 упражнений и задач, некоторые из них достаточно трудны.
2) Обосновать полезность теоретико-игровых концепций для теоретического анализа социально-экономических ситуаций. Для этой цели были тщательно отобраны 39 ярких примеров.
В основном они почерпнуты из микроэкономических проблем: приведены примеры, относящиеся к теории несовершенной конкуренции, теории общественных благ, рассмотрены модели голосования, методы дележа и т. д. Во многих задачах читателю предлагается развить интерпретацию игровой модели. Для этого было бы полезно некоторое знакомство с логикой экономических рассуждений.
Некоторые важные разделы современных теоретико-игровых исследований в данной книге не рассмотрены. Наибольший пробел исследование игр с неполной информацией, поскольку, по моему мнению, результатам в этой области недостает завершенности и простоты, необходимой для учебника.
Опущено также изложение аксиоматического подхода к решению игр в форме характеристической функции, поскольку я отнес бы их скорее к нестратегическому анализу общественного выбора (см. введение).
Исходным материалом для этой книги послужили лекции курса теории игр, прочитанного в Национальном институте статиста-
ки и экономического управления. Я особенно благодарен Полю Шамсору, который был инициатором этого курса.
Я глубоко признателен Центру математической теории принятия решений Парижского университета, где я начинал изучать теорию игр под руководством Жана-Пьера Обена и Ивара Экланда, а также лаборатории эконометрики Политехнической Школы, поддержка которой обеспечила выход этой монографии в свет, благодаря Вильме де Суза, Мартине Видони и Мари-Элен Понруа, очень хорошо напечатавших рукопись.
Я также благодарен Эндрю Шоттеру, убедившему меня подготовить английский вариант книги, и Институту математических исследований в социальных науках в Стэнфорде, гостеприимство которого позволило мне завершить работу.
Эрве Мулен
ВВЕДЕНИЕ
Игра это идеализированная математическая модель коллек-тивного поведения: несколько индивидуумов (участников, игроков) влияют на ситуацию (исход игры), причем их интересы (их выигрыши при различных возможных ситуациях) различны. Антагонизм интересов рождает конфликт, в то время как совпадение интересов сводит игру к чистой координации, для осуществления которой единственным разумным поведением является кооперация. В большинстве игр, возникающих из анализа социально-экономических ситуаций, интересы не являются ни строго антагонистическими, ни точно совпадающими.Продавец и покупатель согласны, что в их общих интересах договориться о 'продаже, конечно, при условии, что сделка выгодна обоим. Однако они энергично торгуются при выборе конкретной цены в пределах, определяющихся условиями взаимной выгодности сделки. Подобно этому рядовые избиратели, как правило, согласны отвести кандидатов,, представляющих крайние точки зрения. Однако при избрании одного из двух кандидатов, предлагающих различные компромиссные решения, возникает ожесточенная борьба.
Немного поразмыслив, читатель, наверное, согласится с тем, что большинство напоминающих игры ситуаций общественной жизни порождают как конфликтное, так и кооперативное поведение. По нашему мнению, теория игр является полезным логическим аппаратом для анализа мотивов поведения участников в подобных ситуациях. Она располагает целым арсеналом формализованных сценариев поведения, начиная с некооперативного поведения (гл. I) и до кооперативных соглашений с использованием взаимных угроз (гл.
VI). Для каждой игры в нормальной форме использование различных кооперативных и иекооперативиых концепций равновесия, как правило, приводит к различным исходам.
Их сравнение является основным принципом теоретико-игрового анализа и, по-видимому, источником строгих и вместе с тем содержательных рассуждений о побудительных мотивах поведения, вытекающих только из структуры игры в нормальной форме.
Во многих социальных науках имеется большое количество моделей, при анализе которых требуется изучать способы выбора стратегий. Приложения теории игр преимущественно развиваются в связи с исследованием экономики. Это соответствует установкам основоположников теории игр фон Неймана и Мор-генштериа. Однако прочная репутация теоретико-игрового подхода утвердилась только после теоремы Дебре Скарфа, позволяющей рассматривать конкурентное равновесие как результат кооперативных действий.
С тех пор целые разделы экономической теории (такие, как теория несовершенной конкуренции или теория экономического стимулирования) развиваются в тесном контакте с теорией игр (см. обзор Шоттера и Шведиауэра ?1980]).
Начиная с книги Фаркуарсона [1969], анализ процедур голосования, направленный на изучение стратегических возможностей, позволил переосмыслить некоторые традиционные направления политической теории. Хотя используемые при этом Игровые модели по-прежнему вызывают споры, достаточно ясно, jlTO потенциальные возможности теоретико-игрового подхода значительны.
Отсылаем читателя к обзорной работе Брамса [1975] и к последним работам по стратегической реализуемости (Мулен [1981]).
Теоретико-игровой способ мышления является сейчас достаточно общим в социологии (см. Крозье [1977]).
Ясно, что поиск равновесных концепций, являющихся идеализацией целого спектра некооперативных и кооперативных схем поведения, Тесно связан с основами социологии. В частности, наша точка Зрения на кооперацию как на необязательные соглашения (часть II), безусловно, восходит к идеям Руссо об эволюции от естественной свободы к гражданской свободе (см. Руссо [1755]). Тем не менее в современных социологических исследованиях формальные теоретико-игровые модели весьма редки и с математической точки зрения элементарны.
И все-таки влияние теории игр кажется нам уже необратимым, по крайней мере на этапе обучения.
Обзор содержания книги
В части I изучается некооперативное поведение изолированных игроков. Само задание игры в нормальной форме предполагает, что все переменные модели распределены между игроками, которые распоряжаются их выбором по собственному желанию (таким образом, все переменные модели становятся определенными после того, как каждый игрок зафиксирует свою стратегию).
Вначале мы предполагаем, что обмен информацией между игроками невозможен. При этом выдвигается несколько логически обоснованных способов выбора игроком стратегии, которой он должен придерживаться. К таким понятиям следует отнести доминирующие и осторожные стратегии, когда мы предполагаем, что игрок не знает предпочтений остальных игроков (гл. 1), а также сложное поведение, когда мы считаем, что все предпочтения игроков известны каждому участнику игры (гл.
II). Эти стратегии могут быть рассчитаны каждым игроком независимо от поведения других игроков.
Указанные понятия являются статическими. К сожалению, сколь бы привлекательны ни были эти понятия, их математические, свойства являются плохими (в частности, равновесие в доминирующих стратегиях и сложное равновесие, как правило, не существуют). Поэтому мы переходим к рассмотрению концепций некооперативного равновесия второго уровня, а именно, равновесия по Нэшу, которое требует некоторых контактов между игроками хотя бы на уровне совместного наблюдения за происходящим (гл.
III). Предлагается несколько сценариев поведения, обосновывающих определение равновесия по Нэшу; все они требуют перехода к динамике (хотя бы из двух периодов). В отличие от понятий первого уровня, исходы игры, равновесные по Нэшу, обладают хорошими математическими свойствами.
Если игроки используют независимые рандомизированные стратегии, то существование таких исходов можно гарантировать в весьма широких предположениях (гл. IV).
Основная причина перехода от понятий ч. I к понятиям ч. II (кооперативное поведение игроков) состоит в том, что индивидуальная свобода выбора стратегий наносит ущерб общественным интересам. Некооперативное равновесие (является ли оно следствием изолированного поведения, как в гл.
I и II, или удовлетворяет условиям стабильности по Нэшу, как в гл. Ill и IV) может не быть оптимумом Парето. Свободный выбор игроком своей стратегии противоречит требованию эффективности коллективного выбора в том (и только том) случае, когда для каждого оптимального по Парето исхода найдется выгодное с точки зрения какого-либо игрока отклонение.
В этом случае оптимальные по Парето исходы игры нельзя считать правдоподобными. Дилемма заключенного (пример 1 гл.
I) является хорошо известным примером такого противоречия. Это простейший пример противоречия между стабильностью и эффективностью, которое мы считаем главным побудительным мотивом к кооперации.
К сожалению, сами механизмы кооперации являются не столь наглядными.
Для того чтобы получить исходы, лучшие по Парето,, чем некооперативное равновесие, мы предполагаем, что игроки заключают необязательные соглашения. Это такие сценарии поведения, которые не лишают игроков их неотъемлемого права.
придерживаться любой стратегии, находящейся в их распоряжении. Эти соглашения автоматически выполняются благодаря свойству стабильности, которое аналогично свойству, введенному Нэшом: Меня никто не принуждает следовать нашему соглашению, но до тех пор, пока вы, все остальные, ему верны, у меня нет причин его нарушать. На самом деле, понятие равновесия по Нэшу это исторически первый существенный пример кооперативного соглашения такого типа.
Концепции гл. V последовательно развивают различные стороны определения Нэша. Мы сотрудничаем, потому что мы хотим этого, однако добровольная кооперация приводит к обязанностям для нас неожиданным (Дюркгейм [1893]).
Необязательные соглашения полностью признают право свободного выбора игроком своих стратегий. Однако реализуемость таких соглашений требует определенных ограничений на обмен информацией между игроками.
Одна из возможностейзапретить по достижении соглашения дальнейшие переговоры с тем, чтобы участники не могли больше угрожать друг другу. Этот путь приводит к понятиям стабильности гл.
V. Другая возможность состоит в том, чтобы любые отклонения от договоренности (в выборе стратегии) становились известными всем и потому можно было бы своевремен-во привести в исполнение взаимные угрозы. Это приводит к кооперативной точке зрения на предостережения, которым посвящена гл.
VI.
Мы не касаемся обязательных соглашений, поскольку тут Возникает целый круг вопросов, не связанных с выбором стратегий, а скорее относящихся к теории общественного выбора. Под обязательным соглашением мы понимаем договоренность игроков о некотором исходе игры, причем выполнение этой договоренности обеспечивается некоторым контролирующим органом. После подписания такого соглашения игроки фактически лишаются контроля над своими стратегиями. Следовательно, вопросы стабильности соглашений отпадают, поскольку никакие нарушения договоренности ни отдельным игроком, ни коалицией игроков больше не возможны.
Таким образом, все сложные проблемы кооперации снимаются после того, как соглашение подписано, зато все они возникают до подписания. Другими словами, поскольку теперь нет смысла сравнивать соглашения с точки зрения их стабильности, приходится говорить об их большей или меньшей справедливости.
Таким образом, подход к кооперации из описательного (какие соглашения являются стабильными при той или иной информационной структуре?) превращается в нормативный (какие соглашения считать справедливыми при заданных соотношениях сил отдельных игроков и коалиций?). При этом главная аксиома состоит в том, что справедливость это первичный побудительный мотив к кооперации, или, другими словами, несправедливость является решающей причиной разрушения кооперации.
Если хотя бы одному положению суждено остаться неизменным в будущем в теории стратегических игр, то это, по-видимому, будет утверждение о том, что данной игре адекватно несколько, не слишком много, равновесных концепций, в зависимости от условий обмена информацией и кооперации. И значит, игра в нормальной форме, наша основная математическая модель, действительно является богатым источником стратегических сценариев, проясняющих логические связи таких первичных понятий, как кооперативное и эгоистическое поведение, взаимные стратегические ожидания, тактическая неопределенность и ограничение информированности при кооперации, обмен угрозами и обещаниями.
Критика предложенных концепций должна основываться на их приемлемости в приведенных примерах.
Изучение равновесных концепций приводит к ряду теорем существования, а также к некоторым контрпримерам. Однако пустоту, скажем, a-ядра некоторой конкретной игры в нормальной форме не следует интерпретировать как логическое обоснование невозможности кооперации с помощью угроз в этой игре.
Скорее это означает, что сценарий предостережений, который лежит в основе определения a-ядра, не описывает полностью коалиционное поведение, и нужны другие, более сложные схемы (как правило, это двухшаговые концепции, см. гл. VI, разд.
2). Скромность создателя математических моделей требует избегать апокалиптических интерпретаций.
Некооперативное поведение игроков
Основной моделью для анализа некооперативного поведения является игра в нормальной форме.Определение. Пусть N фиксированное конечное сообщество, скажем множество игроков (участников), для обозначения которых используется индекс і.
Игрой в нормальной форме называется совокупность, содержащая для каждого игрока і € N
множество стратегий Х{, элементы которого обозначаются я,-,
функцию выигрыша (функцию полезности) иь являющуюся Отображением из XN = X Х(- в R1’. Элемент х = (xf); е ді из мно-
І € N
жества XN называется исходом игры.
Игрок і выбирает любую стратегию xt € Xt. После того как каждый игрок выбрал свою стратегию, определяются исход х И выигрыш і-го игрока а,- (х).
Отметим, что в описанной выше модели нет ни случайных ходов, ни игрока, который бы моделировал неопределенность, свойственную природе.
*) В книге без пояснений используются общепринятые обозначения! В частности, IR множество вещественных чисел.
Прим, перев.
ГЛАВА I
НЕКООПЕРАТИВНОЕ ПОВЕДЕНИЕ ИЗОЛИРОВАННЫХ ИГРОКОВ
Рассмотрим игру в нормальной форме (Х{, ut\ i$N) и предположим, что игроки в этой игре действуют изолированно, т. е. каждый игрок выбирает свою стратегию независимо, не обращая внимания на то, какие стратегии выбирают другие участники. Игроки не обмениваются информацией. На выборы игроков не оказывает влияния прошлое (предыстория партии игры или начальная позиция).Напротив, все стратегии априори считаются эквивалентными, и их различие должно устанавливаться, исходя из внутренних принципов оптимальности.
На протяжении гл. I будем считать, что каждому игроку известна его собственная функция выигрыша; функций выигрыша остальных игроков он может не знать.
В этих предположениях исследуем по очереди два не противоречащих друг другу сценария поведения изолированных игроков: сначала исключение доминируемых стратегий, а потом осторожное (максиминное) поведение.
1. ДОМИНИРУЮЩИЕ И НЕДОМИНИРУЕМЫЕ СТРАТЕГИИ
Определение 1. Стратегия х{ игрока і в игре в нормальной форме (Х{, ut\ і € X) доминирует стратегию у{, если
Ух, € X, ut(y{, Xi)s^Ui(x(y xt),
Эх, € X, u,(yit xt) щ {xt, xt),
где Xt= X X, и (x,, xt)€XN.
16N\V) '
Обозначим через S)i(ut) множество всех недоминируемых стратегий і-го игрока:
У1$@){(и{) % XjgXp xt доминирует у{.
Стратегия і-го игрока х( доминирует стратегию у{, если независимо от поведения остального мира N\{i} стратегия у{ для него не дает большего выигрыша, чем х(, а для некоторого
допустимого стратегического выбора игроков П\{і\ ему выгоднее выбрать х{, чем у{. Отсюда следует, что игроку і имеет смысл выбирать стратегию только из множества (ut).
Заметим, что t-му игроку для вычисления S){ (ut) достаточно знать множества стратегий Ху своих партнеров; знание их функций выигрыша не требуется.
Определение 2. Стратегия xt игрока і в игре в нормальной форме (Xі, и{\ і ? N) называется доминирующей стратегией), если
VxtZXf. и/(у;, xt),(*„ xt).
Обозначим через множество всех доминирующих стра
тегий і-го игрока.
Исход x = (Xj)t s jv назовем равновесием в доминирующих стратегиях, если х{ является доминирующей стратегией і-го игрока при всех і.
Недоминируемые стратегии существуют при достаточно слабых топологических предположениях, поэтому постулат о том, что при некооперативном поведении игрок исключает доминируемые стратегии, не приводит к логическому противоречию.
Лемма 1. Предположим, что для любого i^N множество X. компактно, а функция и1 непрерывна. Тогда множество (и,) недоминируемых стратегий і-го игрока не пусто.
Доказательство. Для любого / выберем вероятностное распределение ру на Xj таким образом, чтобы каждое непустое открытое подмножество Xj имело положительную меру). Зафиксируем і и рассмотрим функцию ф,-, определенную на Х(:
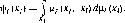
ІФі
Поскольку функция и{ непрерывна, то непрерывна и функция ф/( а следовательно, можно выбрать стратегию xf, максимизирующую функцию ф; на множестве X,-. Покажем, что стратегия xf недоминируема. В самом деле, если существует стратегия X;, доминирующая xf, то в силу непрерывности функции щ найдется открытое подмножество Ot множества Xt, такое, что
?ЛГ/ € Оі U; (xf, Xt) U, (X;, X,).
В силу выбора ру, іфі, получаем
^ и; {xf, xt) dp (х;) jj ut{xh xt) dp? (xt). ot o,
Поскольку неравенство и,- {xf, x!) ^ ut (x{, xt) справедливо на всем множестве Xt, то имеем1)
I U; {xf, xt) d pi (xt) J Uj (xh xi) dp? (xt).
Складывая два неравенства, приходим к противоречию:
^ (xf) ф,- (xt). ¦
В противоположность полученному выше результату доминирующие стратегии могут не существовать даже в топологически тривиальных (конечных) играх.
В самом деле, доминирующая стратегия х{ должна одновременно быть решением задач максимизации
шах іі/ (xh Xt)
х;ех.
при всех значениях параметра хг ? X,-.
Стратегии х,- и у{ і-го игрока будем считать эквивалентными, если они не различимы с его точки зрения:
?Хі € Xi U;{X;, Xt) = ui{y;, Xt).
Лемма 2. Предположим, что в игре в нормальной форме (Xj, up, j g N) множество недоминируемых стратегий і-го игрока непусто'. S). (ц;.) ф 0. Тогда эквивалентны следующие три утверждения:г)
(i) Существует доминирующая стратегия і-го игрокаі Dt (иі) ф 0.
(ii) Все стратегии в множестве S, (и,-) эквивалентны.
(iii) Dt (щ) = й, (и,).
Доказательство леммы 2 оставляется читателю в качестве (элементарного) упражнения.
*) Здесь и далее Асдополнение к множеству Л, Прим, перев.
2) Для того чтобы утверждения (і) (ііі) следовали из (іі), достаточна потребовать компактность множеств Ху и непрерывность функций Uj, j?N. Без этого предположения лемма, вообще говоря, не верна.
Прим, перев.
В лемме 2 говорится о том, что если у игрока есть хотя бы одна доминирующая стратегия, то все доминирующие стратегии эквивалентны и совпадают с его недоминируемыми стратегиями. В этом случае будем считать, что при некооперативном поведении игрок использует одну из них. С другой стороны, если у і'-го игрока нет доминирующей стратегии (наиболее частный случай), то его недоминируемые стратегии не эквивалентны, поэтому его некооперативное поведение не может быть определено однозначно.
Требуются дополнительные предположения об информации, которой располагают игроки (в частности, о функциях выигрыша), чтобы сделать дальнейшие заключения; см. разд, 2 ниже и гл. II.
Равновесие в доминирующих стратегиях постулируется рациональным некооперативным поведением изолированных игроков.
В приведенных ниже примерах 2 и 3 показано, что равновесие в доминирующих стратегиях может быть доминируемым по Парето (см. определение 3), что делает это понятие уязвимым при кооперативном поведении игроков.
Пример I. Дилемма заключенного (Льюс и Райфа [1957]) Каждый из двух игроков располагает двумя стратегиями А и Р, где А обозначает агрессивность, а Рмиролюбие. Предположим, что мир (оба игрока миролюбивы) лучше для обоих игроков, чем война (оба игрока агрессивны), но односторонняя агрессия (один игрок агрессивный, а другой миролюбивый) выгоднее агрессору. Типичная структура выигрышей имеет следующий вид:
| Игрок 1 |
|
||||
| ^2 А2 . Игрок 2 |
Для обоих игроков стратегия А доминирует стратегию Р. Таким образом, единственное равновесие в доминирующих стратегиях имеет вид (Аи Л2), т. е. постулируется, что результатом некооперативного поведения является война. В то же время исход (Pj, Р2) (мир) дает большой выигрыш сразу для обоих игроков. Таким образом, некооперативное эгоистическое рациональное поведение вступает в противоречие с коллективными интересами. Коллективные интересы диктуют выбор мирных стратегий. В то же время, если игроки не обмениваются информацией (так что, например, не могут возникнуть взаимные угрозы типа: Я буду миролюбив, до тех пор пока ты будешь миролюбив; подробнее об этом см. в гл. VI), война является наиболее вероятным исходом: изолированность стратегических выборов может нанести определенный ущерб общественным интересам.
Определение 3. Исход х € XN в игре в нормальной форме (X/, и.;\ i$N) доминирует по Парето исход y?XN, если
I Vi?N ,.(г/Х ,- (*),
\3i?N U; (if) U; (х).
Исход х назовем оптимальным по Парето (или оптимумом Парето), если он не доминируем по Парето.
В следующем примере равновесие в доминирующих стратегиях также доминируемо по Парето.
Пример 2. Аукцион неделимого товара
Товар должен быть куплен одним из п участников. Его ценность для і-го участника измеряется величиной ah причем предполагается, что с ростом і величины а,- не возрастают, т. е.
Будем рассматривать два типа аукционов. На аукционе первого типа каждый участник независимо предлагает цену. Пусть, например, і-й участник выбрал цену х;. Победителем считается тот, кто предложил наиболее высокую цену. Эта цена выплачивается продавцу товара. Обозначим через г начальную цену, назначаемую продавцом, т. е. ценность товара для продавца, и предположим, что г^ап. Складывается следующая игра п лиц:
Х,= ... = Хп = [г, +оо),
ДЛЯ ВСЯКОГО X(;X{1.....п) ПОЛОЖИМ W (х) = {i/Xj = sup дсЛ.
1 / л
Тогда и/(х) = а/хь если i= inf /,
/' € w IX)
и{(х) = 0 в противном случае.
Заметим, что при одинаковых ценах предпочтение отдается тому игроку, для которого ценность товара больше. Покажем, что а,-, т. е. искренняя стратегия і-го игрока, доминирует всякую стратегию X;, для которой выполнено а, хг В самом деле, Щ (Х(, 0 = и; (а,-, Хі) для любого xt. Значит, 3t (и,) = [г, а;].
Тем не менее у і-го игрока нет доминирующей стратегии, если только га,.
Для исключения доминируемых стратегий нужно знать только свою собственную функцию выигрыша.
ОСТОРОЖНЫЕ И ОПТИМАЛЬНЫЕ СТРАТЕГИИ
Если первому игроку известна ценность товара для остальных игроков, то он может исключить стратегии (а2, а,]. Мы разовьем эти соображения в гл. II (см., в частности, упр. 3).В данной главе сосредоточим внимание на изолированном поведении, требующем знания только собственной функции выигрыша.
В аукционе второго типа (аукцион Викри) победителем считается также участник, предложивший наибольшую цену, однако он должен уплатить вторую по величине цену. Возникает следующая игра п лиц:
Хх= ... =Хп = [г, +оо).
Для всех х?Х{1 „} обозначим = sup х,.
1 / п
. І ^ 1
Тогда Uj(x) cijх_і, если і= inf /,
І € to (X)
и, (x) = О в противном случае.
Утверждается, что искренняя стратегия а{ является доминирующей стратегией і-го игрока. В самом деле, фиксируем исход x?Xn и выделим два случая.
Случай 1. Игрок і выигрывает на аукционе при исходе (ait х,).
Отсюда следует Заметим, что иі(х) = аіx_h еслиt-й игрок выигрывает аукцион также и при исходе*, и и((х)=О в противном случае. Следовательно,
;(*,-, х,)^аІх_і = иі(аі, х,).
Случай 2. Игрок і не выигрывает аукциона при исходе (а,-, *?).
Тогда а;^х_1, а значение функции , (*,-, хі) есть либо (,аі*_;), либо 0, поэтомуut(x,, */)0 = Ui(ait xt).
Легко можно убедиться в том, что нет другой доминирующей стратегии і-го игрока, значит, D(- (ие) {а(}, и равновесие в доминирующих стратегиях приводит к победе на аукционе первого игрока, который выплачивает цену а2. Этот исход доминируется по Парето исходом (г, ..., г). Если каждый игрок назначит начальную цену аукциона, то игрок 1 получит товар, заплатив всего лишь г.
Конечно, игроки {2, ..., п) не станут помогать игроку 1, если он не перераспределит часть своего сверхдохода а2-^-г между ними. Такое поведение было бы кооперативным, здесь оно не рассматривается. О нем см. в гл.
VI разд. 5.
Пример 3. Услуга за услугу
Если у одного участника есть несколько доминирующих стратегий, то они для него эквивалентны (см. лемму 2), но возможно не эквивалентны для остальных. Рассмотрим следующую игру двух лиц, в которой стратегии каждого участника влияют только на выигрыш другого, но не на свой собственный:
Игрок 2
Любой исход является равновесием в доминирующих стратегиях, но только один из них оптимален по Парето.
Задача I. Две олигополистические игры (Кейз [1979])
1) Игра с назначением цен в дуополии.
Два дуополиста предлагают на рынок взаимозаменяемую продукцию. Если они установили цены рг и р2, то соответствующий спрос на их продукцию будет равен:
единиц товара, произведенного игроком 1,
dt (у-)** единиц товара, произведенного игроком 2.
Предположим, что затраты на выпуск единицы продукции у обоих производителей не зависят от масштабов производства. Тогда приходим к следующей игре в нормальной форме:
иі(Рь Pt) = (Ptci)di, где С[ постоянная величина,
С{ 0, а, 1, t= 1, 2.
Вычислите равновесие в доминирующих стратегиях для этой игры и проанализируйте выбранную форму функций спроса.
2) Олигополия с назначением выпусков.
Предположим, что цена на некоторый товар с насыщаемым спросом (например, минеральную воду) убывает по экспоненте c-e~s, где Sсовокупное предложение.
Пусть количества минеральной воды, предлагаемой на рынке
п производителями, измеряются величинами хг.....хп, тогда
в предположении нулевых затрат получаем следующую игру;
ut(Xi.....хп) = сх;е-х'+-+Хп.
(Ответьте на те же вопросы, что и в 1.)
Задача 2. Топологические свойства множеств и D{
Пусть для всех i g N множество Х( компактно, а функция и, непрерывна на XN.
1) Докажите, что для любого игрока і единственная недоминируемая стратегия существует тогда и только тогда, когда у него имеется единственная доминирующая стратегия.
2) Покажите на примере, что множества @)t (и,) недоминируемых стратегий и множество исходов, оптимальных по Парето, не обязательно замкнуты. Что можно сказать о множествах D,- (и,) доминирующих стратегий?
Задача 3. Стратегически обоснованное правило голосования с упорядочением (Мулен [1980]))
Пусть (Л, есть (линейно) упорядоченное множество из р кандидатов, среди которых сообщество N {1, 2, ..., п) должно выбрать одного. Для любого нечетного К обозначим через тк следующее отображение из Ак в А: для всех (аь ..., ак) € Л*.
Таким образом, тк(аи ...,ак) является медианой (средним элементом) множества {аг, ..ак\ в соответствии с заданным порядком на Л.
Определим семейство правил голосования на Л. Пусть множество стратегий і-го игрока (множество предложений) есть просто X; = Л, а правило голосования имеет вид
¦. п-1)
Я (Xj, - . - , Хп)
где (xf, . ,.,х„) изменяется на Х{і.....„}, а а*, ...,an_t фик
сированные элементы множества А. В частности, полагая af= ... =ап_г inf а, получаем, что я^, ...,х„)= inf х,-.
аеА Кіл
Или, например, пусть щ=.. .=ay=inf a, aa/+i==...=an_j=sup а.
аеА аъА
Тогда (лгі, ...,*„) есть кандидат ранга / + 1. если только хи ..., расположены в порядке убывания относительно заданного порядка на А. Если для каждого участника і определить полезности и, на А, то правило голосования порождает следующую игру п лиц):
? = (-Xj, - - - і Кп, MjOJt, - .., ипоя).
1) Пусть х{ и Уі два соседних элемента А относительно заданного на этом множестве порядка. Докажите следующие предложения:
{иi (Х;) и, (у;} \x{ доминирует yt для игрока i\,
{и, (х,) = Ui(yt)\ {x, и yj эквивалентны для игрока і].
Выведите отсюда, что ®,(и,) состоит только из локальных максимумов ut, т. е.
Х{ € t (и,) =.[?^ € А {и, (х,) и, (г/,)} =
= Зг, € *г Уд {I (2,) И/ (*/)Н
уни-
2) Докажите, что если функция выигрыша и, игрока модальна на (А, *^), т. е.
За, Р ? А:
на (-, а] и, не убывает, на [а, Р] щ постоянна, на [Р, *¦) и, не возрастает,
то у игрока і есть доминирующая стратегия.
Каково множество D, (и,) в данном случае? Докажите, что равновесие в доминирующих стратегиях в игре g оптимально по Парето.
3) Для произвольных функций выигрыша и, на А докажите, что множество недоминируемых стратегий в играх g, полученных на основе правил голосования я,, . ..,яв_.„ имеет следующий вид;
для я„ . ..,яп_,- 3i(ui) = LM(ut) = {xi?A \х{ локальный максимум щ),
для я,- @i(ui) = {xi€LM(ul)\Vyl€LM(ul) [г/, х,] или ГІ(Уд
Задача 4. Механизм финансирования общественных благ по КларкуГроувзу (Грин, Лафон [1979])
Пусть А множество из р исходов (представляющих различные общественные проекты, кандидатов и т. п.), среди которых сообщество N должно выбрать один. В противоположность предыдущей задаче предположим, что допустимы побочные платежи (денежный обмен) и что участники имеют квазилинейные полезности. Так, если и,- действительная функция на А, представляющая полезность для і-го участника, то совокупная полезность определяется как M;(cz) + ^f, где а ?А является принятым решением, а число t{ (положительное) побочный платеж участнику і.
В механизме Кларка Гроувза каждый участник объявляет свою функцию полезности. Поскольку информация о функции и/ имеется только у і-го участника, он может выбрать любой вектор и утверждать, что это и есть его функция по
лезности. Следовательно, Х; = есть множество стратегий і-го игрока.
После того, как каждый игрок і объявляетх;, складывается исход x$XN. Решение cz* = cz* (х) ? Л выбирается из условия
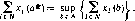
Побочный платеж игроку і есть tt (х):

Следовательно, если (и;);6 nсовокупность истинных функций полезности, то получается следующая игра в нормальной форме:
g = (Xf, uh i?N), где ui(x) = ui(a*(x)) + ti(x).
Отметим, что отображение х а* (х) любое, удовлетворяющее (1).
1) Заметьте, что число tt(x) неположительно, и дайте интерпретацию случаям і,(х) = 0 и іг(х) 0.
2) Докажите, что искренняя стратегия xf = , является единственной (с точностью до аддитивной константы) доминирующей стратегией игрока і.
3) Докажите, что равновесие в доминирующих стратегиях и = (М()іе n оптимально по Парето тогда и только тогда, когда ti (а* (и)) 0 для всех і.
Дайте интерпретацию этому результату.
2. ОСТОРОЖНЫЕ И ОПТИМАЛЬНЫЕ СТРАТЕГИИ
Если у і-го игрока не имеется информации о функциях выигрыша остальных игроков, то он не может исключать из рассмотрения какие-либо допустимые стратегии из Xt (мы предполагаем, что множества стратегий всех игроков известны всем).
Один из способов исключения стратегий на множестве Х{ состоит в удалении доминируемых стратегий. Другой путь соответствует пессимистическому предположению (исключающему риск), что случится худшее.
Определение 4. В игре в нормальной форме (Х{, up i € A/) xi является осторожной стратегией /-го игрока, если выполнено
inf {Xj, Xt) = sup inf ut (у;, x ) = af.
x,sxt *,e X.
Обозначим через Pi(ut) множество осторожных стратегий t-ro игрока. Осторожное поведение реализуемо и совместимо с правилом исключения доминируемых стратегий.
Лемма 3. Предположим, что Х{компакты, а и( непрерывны для всех і ? N. Тогда множество Р{ (,.) осторожных стратегий і-го игрока не пусто, компактно и пересекается с множеством ); (и{) недоминируемых стратегий-
Р1(иі)(\@)і(иі)Ф0.
Доказательство. Фиксируем Поскольку функция и{
непрерывна, то функция ? (yt) inf иДуь хі) полунепрерывнаVsсверху) на Xt и, следовательно, множество ее точек максимума есть непустое компактное множество Р{(и{). Рассмотрим далее игру Н (Ул up у € N), где У; = X, для / Ф і и У, = Р{(и{).
По лемме 1 игрок і имеет по крайней мере одну недоминируемую стратегию хг в игре Н. Предположим, что х{ доминируется стратегией у{ в исходной игре (Xt, up, ig N), т. e.
[Vxf € X u{ (x{, xt) щ (y{, x/)] = f9 (x,) ? (yt)].
Отсюда ?(г/г)= sup ?(гг) и y{ € P{ (ut), что противоречит предположению о недоминируемости х( в игре Н. Значит, xt принадлежит Рг (и,) Л®,-(,-)- В
Н^ке в задаче 5 мы предполагаем другой вариант определения 4, который автоматически выделяет подмножество из множества Р{ (и,-) п @і (щ).
Используя осторожную стратегию, игрок і гарантирует себе выигрыш а;. Назовем аг гарантированным выигрышем.
Если набор (а,- ),¦= л/ гарантированных выигрышей является оптимальным пс) Парето, тогда мы считаем, что осторожные стратегии также могут быть названы оптимальными.
Определение 5. Скажем, что игра в нормальной форме несущественна, если нет исхода г/gX д, для которого
( ?і С N sup inf ,- (л:,-, хі) = сх,- sc; м,- (у)
^ xizxi xteX
[3i?N cti ut (у).
Название несущественные для данного класса игр на интуитивном уровне можно пояснить следующим примером. Имеется единица однородного товара, которая должна быть поделена среди членов сообщества N. Предположим, что игрок і за счет хорошей игры может гарантировать, что его окончательная доля будет не меньше а,{ независимо от поведения остальных игроков.
Допустим, что ? ,= 1. Тогда (a,)i€W есть дележтовара, который должен быть результатом оптимального поведения игроков).. В нашем более общем случае функции выигрыша игроков не являются сравнимыми, а потому их нельзя складывать.
Тем не менее, в несущественной игре осторожные стратегии оптимальны в следующем смысле.
Теорема I. Предположим, что (Х(, up, i ? N)несущественная игра. Пусть осторожная стратегия игрока і для всех і 6 N, и пусть хсоответствующий исход. Тогда
1) и( (х) = а,- ut (х;, у,) для всех i?N и yt? X,-,
2) хоптимальный по Парето исход,
3) для любой коалиции ScN и любого набора стратегий ys 6 Xs одновременное выполнение следующих двух условий невозможно:
iVtgS Ui(x)^Ui(ys, XSc),
\ Зі 6 S щ (х) и(ys, XSc).
Доказательство. Поскольку xtосторожная стратегия і-го игрока, то имеем
а; = inf ut (xt, yt) ^ и, (x). угех.
Данное неравенство выполнено для всех і, а поскольку наша игра несущественна, то а,- = ut (х) для всех і и утверждение 1 теоремы доказано.
Утверждение 2 следует из 3 при S = N. Для доказательства 3 выберем S и ys?Xs, такие, что
VigS а, ut (ys, xSc). (2)
Применяя утверждение 1 к / ? Sc, получаем Vj€Sc а^иДу^ xSc).
Объединяя две системы неравенств, получаем и{ (ys, xsc) = a{ для всех і, поскольку игра несущественна. Следовательно, строгое неравенство в (2) невозможно.
Согласно утверждению 1, если игрок і использует оптимальную (т. е. осторожную) стратегию и ожидает, что остальные игроки сделают то же самое, то он получит выигрыш, равный гарантированному аг. Если некоторые игроки /', Дфі откажутся от использования оптимальных стратегий, то это может быть только выгодно игроку і. Свойство 3 означает, что никакой отдельный игрок и никакая коалиция игроков не имеют причин для одностороннего отхода от осторожных стратегий (мы неявно предполагаем, что побочные платежи внутри коалиции невозможны, т. е. полезности не трансферабельны).
В терминах определения 1 гл. V набор осторожных стратегий является сильным равновесием.
Для того чтобы дать интерпретацию определению 5, рассмотрим также игру (Х;, up і ? N), которая не является несущественной, и заметим, что никакой набор стратегий х не может быть назван оптимальным.
В самом деле, два очевидных требования оптимальности суть а, ^ ti; (х) для всех і и оптимальность по Парето исхода х. По определению 5 эти условия вместе приводят к тому, что для некоторого і ? (V получается
sup inf и, (ус, уі) = а{ и, (х).
?і
Иначе говоря, игрок і не может себе гарантировать выигрыш и,- (х) и может подвергнуться угрозам со стороны дополнительной коалиции N\{i).
Основные примеры несущественных игр следует искать, конечно, среди игр двух лиц с нулевой суммой. Но об этом в следующем разделе.
Упражнение 1. Предположим, что g игра двух лиц, в которой равновесие в доминирующих стратегиях оптимально по Парето. Обязательно ли игра g несущественна?
Задача 5. Лексикографически осторожные стратегии (Му-лен [1981]).
Для каждого элемента г (zlf ..., zt) из IR7 результат переупорядочения его координат по возрастанию обозначим через г*:
г* = (ylt ..., уТ) {ух.....ут[ = {!.....Zt\,
УіУ*---Ут-
Введем далее лексикографический порядок в IRr:
Vt t0 yt = zb У и *t,.
Пусть (X,-, up i?N) игра в нормальной форме, причем множества Х(- конечны. Будем говорить, что стратегия х{ игрока і является лексикографически осторожной, если она максимизирует на множестве X,- по отношению к лексикографическому порядку в IRX? следующее отображение:
х{ = (и, (X;, x,)(xt€Xr)*.
Обозначим через LP(u{) множество лексикографически осторожных стратегий г'-го игрока.
1) Дайте интерпретацию введенного определения.
2) Докажите включение (u;) s Р; (и,) П (г).
3) Докажите, что понятие лексикографически осторожной стратегии обобщает понятие доминирующей стратегии в следующем смысле:
{Рі (,) Ф 0} = {LPi (,.) = D, (ц - ) = (и,)}.
3. ИГРЫ ДВУХ ЛИЦ С НУЛЕВОЙ СУММОЙ
Игры двух лиц с нулевой суммой имеют вид (Хх, Х2; щ, щ), т. е. игроки являются чистыми антагонистами. Обозначим такую игру через G = (Хх, Х2, uj, понимая под (положительный или отрицательный) платеж, который игрок 1 максимизирует, а игрок 2 минимизирует Тогда осторожные стратегии могут быть заданы так:
*і € Л (Щ) inf і(*і, yt) = sup inf ul(ylt y2),
У2€ X2 Уі € X! X2
€ p2 (1Ml) sup Щ (yu x2) = inf sup , (^, y2).
У\ € X, € Л2 г/, € X,
Числа sup inf u, и inf sup u, являются соответственно макси-
Vi Уг Уг Уі
мальным гарантированным выигрышем игрока 1 и минимальным гарантированным проигрышем игрока 2. Они связаны неравенством
sup inf щ sgi inf sup щ. (3)
Vi Уг Уг Vi
Для доказательства (3) фиксируем произвольные XjgXj, хг$Х2 и заметим, что
Фі (*і) = inf Щ (хи уг) щ (хи х2) sup Ui (уь х2) = ср2 (*t).
*/2 У
Отсюда следует
sup Фі (Уі) inf ф2 (y2).
Ух V?
Если выполнено равенство
sup inf щ = nf sup ut = a,
Уі */fi #2 Уі
то будем называть число а ценой игры G1). Если в (3) строгое неравенство, то будем говорить, что игра не имеет цены.
Теорема 2. Пусть G = (X(, Х2, щ) игра двух лиц с нулевой суммой.
Если игра имеет цену, то она несущественна. Обратно, предположим, что Х? Х2 компакты, а , непрерывна, тогда если G несущественна, то она имеет цену.
Ч Наряду с этим термином в отечественной литературе широко используется также термин значение игры. Прим, перев.
Доказательство. Предположим, что G имеет цену, и пусть исход (xt, xJgXj-xXj, таков, что
sup inf щ ^ их (хи х2),
У1 Уг М\
sup inf М, ^ MJ (хи х2) щ (хи х2) ^ inf sup Mj. v '
Уг Уі Уг Уі
Поскольку (3) обращается в равенство, то эти два нера' венства на самом деле тоже равенства, и первое утверждение доказано.
Предположим теперь, что (3) строгое неравенство. В силу сделанных топологических предположений и леммы 3 мы можем выбрать пару (л^, х2) € Рх (их) х Р2 (м2).
Эта пара удовлетворяет системе (4), в которой хотя бы одно из неравенств строгое, и поэтому игра G не может быть несущественной. Ц
Для несущественных игр с нулевой суммой пара оптимальных стратегий является седловой парой.
Определение 6. Седловая пара в игре двух лиц с нулевой суммой (Xt, Х2, Uj) есть такая пара (хи х2)$Х1хХг, что
?(Уіг i^^XfXXj ЧіІУи Хг)^:^і(ХІі Хг) ^:^і(ХІ Уг)-
Обозначим через S множество (возможно пустое) седловых пар.
Теорема 3. Пусть G = (Х{, Х2, их) игра двух лиц с нулевой суммой. Если G имеет цену, то исход является парой оптимальных стратегий тогда и только тогда, когда он является седловой парой: S Px (их) х Р2 (м2).
Если G не имеет цены, то в этой игре нет также и седловой пары.
Доказательство. Предположим сначала, что игра имеет цену и, следовательно, несущественна. По свойству 3 теоремы 1 получаем включение Рх (их) хР2(иг) ? S.
Обратно, выберем седловую пару. Из определения 6 получим
inf sup их sup их (ух, хг) их (хх, х2) inf Mi (xit у2) sup inf иь
Уг У1 Уі Уг Уі Уг
В силу (3) эти четыре неравенства огфащаются в равенство, а значит, хг осторожная стратегия игрока і (і = 1, 2). Ц
Теоремы 2 и 3 показывают, что ключевой характеристикой для игр с нулевой суммой является существование или отсутствие цены игры. Если игра обладает ценой, то оптимальные стратегии существуют и определяются эквивалентно двумя способами: изолированно (как осторожные стратегии) и одновременно обоими игроками (как седловые пары).
Пример 4
Пусть у обоих игроков имеется по 3 стратегии. Функция щ из хХ2 в R задана 3x3 матрицей, в которой строки соответствуют элементам множества Хи а столбцы элементам множества Х2.
Рассмотрим следующую функцию выигрыша.
У игрока 1 одна оптимальная стратегия (+), а у игрока 2 их две. Цена игры равна 1.
С другой стороны, игры без цены обычно порождают несходящуюся последовательность стратегических ожиданий. В самом деле, пусть (Хг, Х2, щ) игра с нулевой суммой, причем
sup inf і = а b = inf sup Uj.
Хх X2 X2 Xj
Скажем, что игрок 1 выигрывает, поднимая финальный платеж выше Ь, а игрок 2 удерживая финальный платеж ниже а. Допустим, что игрок 1 собирается использовать стратегию ас?. Предвидя этот выбор и используя наилучший ответ (стратегию х\), игрок 2 выигрывает:-
(ас?, х\) = inf щ (ас?, у2) а.
Ожидая, что второй игрок выберет хі, и используя наилучший ответ (стратегию ас?), игрок 1 выигрывает:
b sup і (уи хі) = щ (ас?, хі).
У\
И так далее... Для последовательности (асх, Ас?)/ел/, в которой х{ наилучший ответ второго игрока на ас?-’, а ас? наилучший ответ игрока 1 на х{, получаем
! (АС?-1, AC?)af и, (АС?, хі).
Следовательно, ни одна из двух последовательностей (АС?)ел/ и (ас?)6 л/ не сходится?) (в предположении непрерывности щ и компактности X, и Х2).
пример 5
Предположим, что игрок 1 собирается применить свою единственную осторожную стратегию х? Поскольку игроки принимают решения изолированно, то игрок 1, считая, что противник также планирует выбор единственной осторожной стратегии yit может отказаться от осторожной стратегии и применить наилучший ответ хг против стратегии уг и т. д.
Проиллюстрируем сказанное на следующем примере, в котором у каждого игрока имеется по одной оптимальной стратегии.
- хг-х^... -х2п х1=х3=...=х2п+1і
_,У2 = "Уад
-1 Уз=* - - =У2л+і
В заключение приведем пример игр с нулевой суммой без цены и с ценой, а также несколько упражнений и задач.
Пример 6. Раз два три
Каждый игрок выбирает одну из трех стратегий раз, два или три. Выигрыш первого игрока положителен, если он правильно угадал выбор второго игрока, и нуль в противном случае. Выигрыши задаются 3x3 матрицей:
грок 1 ¦
Гарантированный выигрыш игрока 1 равен 0, и любая его стратегия является осторожной, так как гарантирует только 0.
Гарантированный проигрыш игрока 2 равен 1, и у него единственная осторожная стратегия, а именно раз (поскольку два и три могут дать проигрыш величины 2 или 3).
В гл. IV мы будем использовать смешанные (рандомизиро-ваіные) стратегии для расширения рассмотренной выше игры до такой игры, которая имеет цену.
2 тез
Пример 7. Дуэль1)
Каждый из двух игроков может произвести один выстрел. Игроки сходятся с постоянной скоростью.
В момент t = О игроки достаточно далеко друг от друга, а в момент t= 1 сходятся вплотную. Задана действительная функция а( на отрезке [О, 1], измеряющая меткость игрока i, і=1, 2. Значение а,(/) есть вероятность того, что игрок і поразит игрока /, если будет стрелять в момент t. Предположим, что а,- не убывает, непрерывна и удовлетворяет краевым условиям а, (0) = 0 и а,( 1)= 1.
Выигрыш (игрока 1) равен -j-І, если первый игрок поражает второго до того, как сам будет поражен; 1 в симметричном случае и 0, если ни один не поражен, либо оба поражены одновременно.
Множества стратегий суть Х, = Х2 = [0, 1]. Стратегия х; игрока і означает
Я буду стрелять в момент t xb если противник не выстрелит раньше. Если же он выстрелит, но промахнется, то я для надежности буду стрелять в момент t= 1. Следовательно, нормальная форма игры имеет вид (Х„ Х2, и,), где
(5)
Uх (Х,, х2)
2aj (х,) 1, если х, х2, аі (хі) ~ a2 (*і). если х, = х2, 1 2a2 (х2), если х2 х,.
Например, пусть х, = ха. Тогда выигрышу +1 соответствует вероятность a, (х,) (1 a2 (х,)), т. е. игрок 1 попал, а его противник промахнулся.
Выигрышу 1 соответствует вероятность а2 (х2) (1 flj (х,)).
Вычислим осторожные стратегии игрока 1. В силу (5) легко проверить, что для любого х, € [0, 1]
Фі (х,) = inf и, (х„ х2) = inf {2 a, (х,) 1, 1 2a2 (х,)}.
*26[0, 1J
Пусть / есть отрезок, принадлежащий [0, 1] (возможно, и точка), определяемый из условия
/ = {Xj € [0, 1] I 2а, (х,) 1 = 1 2а, (х,)}.
Функция ср, возрастает до /, постоянна на / и убывает после /. Поэтому / = Р,(и,) является множеством осторожных стратегий игрока 1. Гарантированный выигрыш игрока 1 a, = sup inf и, есть общее значение функций 2а,1 и 1 2а„
X, X1
') Этот вид поединка иногда называют шумной дуэлью, чтобы отличить от бесшумной дуэли, когда игрок не слышит выстрела противника (см. упр. 3).
Прим, перев.
на /. Аналогично можно показать, что І Р2(иг) и гарантированный проигрыш второго игрока равен а*. Следовательно, аг есть цена игры, а / множество оптимальных стратегий для обоих игроков.
ПОВЕДЕНИЕ ЛИДЕРА И ВЕДОМОГО
Пусть, например, существует yi?Yit для которогоЩ(Хі, х2)иі(уі, х2). (7)
Положим
Уі{Уі) = {у[ €УіЧуЛУг иіІУи У^щ{у[, у2)).
Мы утверждаем, что Yt (yt) имеет непустое пересечение с Zf. В частности, если гі доставляет максимум функции Ф( на УіІУі), где
Фі(уО= 2 ut(y[, yt),
У г
то можно проверить, что стратегия zf не доминируема в игре (Ух-, У3, и,). Следовательно, zt принадлежит множеству
УіЫПХі, и из (7) получаем
{хі, х2) (zj, х2),
что противоречит нашему предположению о том, что (%j, х2) седловая точка в (Zs, Z2, и^. Итак, доказано, что
S(ZX-, Z,)crS (У, У,).
Повторное применение данного включения приводит к следующей цепочке включений:
S(Xlt X,)^S(X\, X})=...=S(X1, Xi).
Далее, если игра G d-разрешима, то существует целое t, для которого все стратегии из Х\ эквивалентны для игрока і при условии, что стратегии игрока / ограничены множеством X) (определение 1). Для такого t мы, в частности, получаем
S(X(, ХІ) = Х{хХ{ = {сложные равновесия игры G}.
Это завершает доказательство леммы 4.
Следствие из теоремы 1 и леммы 4. Каждая конечная игра двух лиц с нулевой суммой в развернутой форме имеет цену. Каждый игрок имеет по крайней мере одну оптимальную стратегию.
Свойство (3) следует из и2 = иі. Иллюстрацией данного следствия является теорема Цермело\ в шахматах либо белые могут форсированно выиграть, либо черные могут форсированно выиграть, либо при правильной игре обеих сторон партия закончится вничью.
В действительности шахматы являются конечной игрой двух лиц с нулевой суммой в развернутой форме (с тремя значениями функции выигрыша: белые выигрывают, ничья, черные выигрывают), поскольку действует правило, по которому засчитывается ничья, при троекратном повторении на доске одной и той же позицииг).
Пример 3. Игра Ним
Для любого целого числа п^ 1 обозначим G* следующую игру двух лиц с нулевой суммой. Если л = 1, то G}тривиальная игра, в которой выигрывает игрок 1.
Если л 2, то игрок 1 должен выбрать целое число п{і 1. Далее, игрок 2 выбирает либо пи либо л2 = пЛі. Назовем nt выбором игрока 2. Тогда следующий шаг состоит в том, чтобы играть в игру G\. аналог игры Gn., где первый ход делает игрок 2. В частности, если либо пг, либо ла равно 1, игрок 2 выигрывает, выбирая данное число).
Это определяет игру в развернутой форме длины (л1). Из полученного выше следствия получаем, что множество N натуральных чисел разбивается на Н = N1\jN2y где А/,- есть множество тех п, при которых игрок і может гарантировано выиграть в игре G\. Проводя индуктивные по п рассуждения, получаем, что наше разбиение удовлетворяет следующим свойствам: 1 ? и, кроме того,
- I Vn?Nl(n'^s2) Злг, 1^/г^/г 1, и /г/гг€Мг,
\ Vn?N2 Vj 1) или пл1^Л^1.
Предоставляем читателю проверить, что эти условия дают следующий результат:
= \п\1, п Ър или п = Ьр 4 или п = Ьр 1}.
Рассмотрим теперь игры TJ, Г* с теми же правилами, за исключением того, что игрок, выбравший 1, проигрывает, другими словами, в игре Г{ игрок /, / Ф і, выигрывает.
Аналогичные соображения доказывают существование разбиения N = и М2, причем 1 € Л42 и (8) выполнено для Mt вместо Nt, і = 1, 2. Отсюда в свою очередь получается, что iVfjмножество четных чисел.
В качестве упражнения читатель может описать выигрывающие стратегии игрока 1 в G^, n?Niy и в игре Г?, пчетное и выигрывающие стратегии игрока 2 в Gh, п? и в Г?, п нечетное.
Задача 2. Мариенбадская игра
Фиксируем целое число р, р^ 1, и для любого набора п= (nlt ..., tip), где лг, ..., пр целые неотрицательные числа, определим игры Gj, G„ по индукции. Для данного п ^(0, ..., 0) скажем, что п' следует за п, если существует k, \^.k^.p, такое, что
i n'k, = nk, для всех k', 1 ^.k’ 1 р и k’ Ф k,
\ 0 n'ftnA.
Если п = (0.....0), то в игре G„ игрок і выигрывает. Если
п Ф (0, .., 0), то игра G„ разыгрывается следующим образом:
игрок і выбирает п', следующее за п. Если п' = (0, ..., 0), то игрок /, / Ф і, выигрывает партию, в противном случае начинается игра G„', в которой игрок / выбирает п, следующее за п', если п = (0, ..., 0), то игрок і выигрывает, иначе начинается игра Gf,„ и т. д.
Можно себе представить, что имеется р рядов спичек по nit ..., пр штук соответственно и каждый игрок последовательно забирает произвольное ненулевое количество спичек, но только из одного ряда. Игрок, который забирает последнюю спичку из последнего ряда, проигрывает. .
1) Докажите существование разбиения
[HU{0}Y = NiUNv
для которого, если n^N(, то игрок / может гарантированно выиграть в игре G„. Приведите условие, аналогичное (8), характеризующее это разбиение.
2) Для всех п = (п? ..., пр) обозначим через
n4 = a^af_, ... afcjf, 1
двоичное разложение nk, где I есть верхняя граница числа разрядов, необходимых для представления пи ..., пр, (следовательно, некоторые из чисел а\, ..., af могут быть нулевыми, но не все). Обозначим далее
р р
а0 = 2 о, - - - = 2 ar
й=і
Докажите, что N2 = M2U Р2, где
Л42 = {п?/, 0 //, fly четное и 3/, 1 / /, ау 0), /32={п?/, 1^/, fly = 0 и а0 нечетное число).
Задача 3, Топологическая дуэль (Шоке)
Пусть Еметрическое пространство. Обозначим через О множество непустых открытых подмножеств Е. Наша игра устроена так.
На шаге 1 игрок 1 выбирает Аг ? О.
На шаге 2 игрок 2 выбирает Л2^0 с единственным ограничением АісА1... .
На шаге t игрок (1, если t нечетно, и 2, если четно) выбирает At?0 с единственным ограничением Atc:At_1..., и так до бесконечности.
Скажем, что игрок 1 выигрывает, если
П АіФ'0.
t= I
Если это пересечение пусто, то скажем, что выигрывает игрок 2.
1) Докажите, что если Е полное метрическое пространство, то игрок 1 может гарантировать победу.
2) Докажите, что если E = Q, то игрок 2 может гарантировать победу.
3) Для любого ли Е наша игра имеет цену?
4. ПОВЕДЕНИЕ ЛИДЕРА И ВЕДОМОГО
Мы рассмотрели ситуации, в которых все игроки находятся на одном и том же уровне информированности (полное незнание гл, I и полная информация в этой главе). В ряде экономических приложений, в частности при олигополистической, конкуренции с доминирующей фирмой, естественным образом возникает несимметричное распределение информации.
С помощью теоремы Куна мы исследуем простейшую модель такого сорта: поведение типа лидерведомый в игре двух лиц 1).
Для данной игры двух лиц (Х^ Х2, и1г иг) обозначим через BRt график отображения наилучших ответов і-го игрока:
(хь х2) ? BRX ФФ их (xlt xt) = sup их (уи х2)
У\ € Хі
(симметричное определение для BR2).
Определение 5. Назовем {хх, х2) і-равновесием по Штакель-бергу в игре (Х1( Х2, их, и2), если
(AT!, x2)?BR. и U;(xx, xa)= sup і(г/х, y2), (9)
Wи Уг) 6 BRj
где і, / = 1, 2 и іф\.
Можно интерпретировать 1-равновесие по Штакельбергу на основе, следующего сценария: игрок 1 (лидер) знает обе функции выигрыша Uj и и2 и использует эту информацию для предсказания реакции игрока 2. Игрок 2 (ведомый) воспринимает стратегию игрока 1 как заданную экзогенно (обычно он не обращает внимания на функцию выигрыша игрока 1) и максимизирует собственный выигрыш, полагая, что стратегия игрока 1 хх фиксирована. Таким образом, игрок 1, имея первый ход и предвидя, что игрок 2 использует один из своих наилучших ответов на хи найдет оптимальное решение задачи (9).
Заметим, что если игрок 2 имеет несколько наилучших ответов на хи то в (9) предполагается, что он выберет наилуч-ший ответ по отношению к функции их. Это упрощающее предположение не оказывает существенного воздействия на дальнейшее изложение.
Поведение лидера ведомого было впервые рассмотрено экономистом Г. Штакельбергом (в начале этого столетия) при описании стратегий фирм, конкурирующих на одном и том же рынке (в условиях олигополии). В таких ситуациях нередко одна из фирм оказывается сильнее остальных и навязывает им свою цену. Концепция равновесия, описываемая определением 5,
Ч В отечественной литературе поведение этого типа первым исследовал ,Ю. Б. Гермейер (Гермейер [1971]).
Библиографию по играм гермейерского типа см. в (Гермейер [1976]). Соответствующий математический аппарат используется для анализа иерархических систем. Прим, перев, служит для анализа поведения такой фирмы. В гл.
VI мы опишем простую модель дуополии, в которой равновесия по Штакельбергу играют исключительно важную роль (см. пример 6 гл. VI). Принцип поведения, подразумеваемый определением б, весьма напоминает таковой при последовательном исключений доминируемых стратегий.
Следующий результат показывает, что равновесия по Штакельбергу сводятся к сложным равновесиям при надлежащем преобразовании исходной игры.
Лемма 5. Пусть G = (Xiy Х2, и? и2) конечная игра двух лиц, причем функции их и иг взаимно однозначны на Xj х Х2. Тогда существует единственное 1-равновесие по Штакельбергу, которое обозначим (xlt х2). Рассмотрим следующую игру G = (XU X*1, і, и2):
I X*' состоит из отображений т), действующих из Хх в Х2;
I Va:j € Xj, ?т]€Х2х' щ(хи ц) = и;(хи ті (лгг).
Тогда игра G разрешима по доминированию, причем единственное сложное равновесие есть (х? г), где т]стратегия наилучших ответов игрока 2, и Г[{х1) = хі.
Доказательство. Существование и единственность 1-равновесия по Штакельбергу следует из взаимной однозначности ut на XjxX2.
Игра G является нормальной формой игры в развернутой форме, в которой игрок 1 выбирает стратегию из Xf первым, а затем игрок 2, зная выбор игрока 1, выбирает свою стратегию из Х2. В игре G стратегия наилучших ответов т) является доминирующей стратегией игрока 2. В самом деле, для любого xt ? Xt и любой функции ц g Xf' имеем
йг (*і, гГ)=и2 (Хі, л(*і))= SUP *(- !. х*) (хі, ^ (xi))=ut (xt, л)-
Х% 6 А;
Наше предположение о взаимной однозначности полностью определяет тр Перед вторым раундом исключения доминируемых стратегий игрок 1 оказывается участником следующей игры (XJ, {т]}, иІУ н2), в которой его единственная доминирующая стратегия определяется так:
иі (,xf, т)) = Wj (я*, т] (х*)) ^ щ (xj, т] (xj)) = Mj (xj, Я) Для всех Xj.
В силу взаимной однозначности и2 график отображения т) совпадает с BR2. Следовательно, (х*, г) (х*)) есТь_1 -равновесие по Штакельбергу в нашей игре, и поэтому х?=Хі,
Заметим, что существование t-равновесия по Штакельбергу можно гарантировать при обычных топологических предположениях (Х1( Хг компакты, щ, иг непрерывны). Однако лемму 5 непосредственно обобщить не удается.
Пример 4. Процедура голосования по Ролсу Пусть А { 1,2, ...,7} есть множество из 7 кандидатов, среди которых 2 игрока должны выбрать единственного.
Каждый игрок в качестве своего предложения может расставить кандидатов в некотором порядке. Следовательно, стратегия есть взаимно однозначное отображение из А на А, причем если х,(а)=1, то аэто наилучший по мнению игрока кандидат (обман, конечно, разрешен). Обозначим через Z множество стратегий игроков 1 и 2. Для данной пары (х1; x^gZxZ выбирается кандидат n(xit х2), где
J я(хі, x2) = inf {aa€tf (*i, x2)},
S R(xit x2) = {a(E ЛI max [Х (a), x2 (a)] = min шах [х* (b), x2 (?)]}.
v fee A
Очевидно, что R (xf, x2) состоит не более чем из двух кандидатов. Данное правило подобрано так, чтобы выбирался кандидат, чья наихудшая оценка среди двух избирателей является наиболее высокой.
Поскольку игроки могут выбрать любую расстановку кандидатов, то возникает стратегическая игра. Обозначим через ии u2?Z истинные мнения игроков 1 и 2. Тогда избиратели являются участниками следующей игры в нормальной форме:
(Z, Z, ?tj о я, ы2 о я). (10)
(В качестве выигрыша игрока берется ранг избранного кандидата с отрицательным знаком. Напомним, что игроки стремятся к максимизации своих функций выигрыша.)
Вычислим теперь 1-равновесие по Штакельбергу в игре (10). Фиксируем стратегию x^^Z игрока 1. Заметим, что для всех х2 € Z выполнено
я (Xj, х2) = а =ф Xj (а) 4. (И)
Другими словами, предлагая Xf, игрок 1 отводит кандидатов х,_1(7), х,-1 (6), хг'(5). Это справедливо, поскольку по крайней мере один кандидат а в хр1 ({4, 3, 2, 1}) должен быть таким, что х2 (а) ^ 4, поэтому
щах (х} (а), х2 (а)) 4 шах (хг (?), х2 (?))
для всех Ь в хг1 (7, 6, 5}).
Отметим далее, что при данном .Kj игрок 2 может обеспечить избрание любого кандидата из ^({4, 3, 2, 1}):
Vag А [Xj(а)4] =[Зл:2 €Z я^, *,) = а]. (12)
Например, для того чтобы обеспечить избрание хГ1 (4), игрок 2 объявляет свое предпочтение так:
л (xh х2) = а, где и2 (а) = inf {и2 ф) xt ф) 4}. (13)
Отсюда, в частности, следует, что
?(хи х2) ? BR2 и2( п(хи а:2))4
(так как множество {л:1()^4} состоит из 4 элементов).
Следовательно, игрок 1 как лидер может обеспечить избрание кандидата из множества A2 = ujl({ 1, 2, 3, 4}). На самом деле, он может гарантировать выбор любого кандидата из А2 за счет подходящего сообщения. Например, для того чтобы обеспечить выбор а = и^1 (3), игрок 1 объявляет:
Это сообщение вызывает наилучший ответ х2, такой, что в силу (13) я(х*, х,) = а,
Наконец, заключаем, что выигрыш игрока 1 (выраженный в ранге избираемого кандидата) в любом 1-равновесии по Штакельбергу равен
Sx = inf \иг (а) I и2 (а) 4}.
- Если игроки поменяются ролями, то в силу симметрии получаем, что выигрыш (ранг избираемого кандидата) игрока 2 в любом 2-равновесии по Штакельбергу равен
- S2== inf {2 (а) I иі (аХ4Г
Интересное следствие состоит в том, что, вообще говоря, ранги Sj и S2 несовместны в следующем смысле:
не существует такого а, что и1(а)г^,!і и a2(a)^S2. (14)
Более точно, пара (f, и2) либо удовлетворяет (14), либо такова, что
I условия 1 (а*) ^ St и иг (а*) ^ S2 выполнены в точности для \ одного кандидата а*. Тогда = м( (а*) для t = 1, 2.
Если для пары функций (и*, и2) выполнено условие (14), то игра (10) представляет типичную борьбу за лидерство: если игроки информированы о предпочтениях друг друга, то оказывается выгодным иметь первый ход и вынудить другого игрока занять позицию ведомого. Мы детально исследуем этот вид конфликта в гл. VI разд. 4 в связи с анализом угроз.
См. также пример 2 и лемму 2, гл. III.
5. ДРУГИЕ ПРИЛОЖЕНИЯ ТЕОРЕМЫ КУНА
В заключение гл. II рассмотрим несколько примеров и задач, направленных на преодоление технических и концептуальных трудностей, связанных с понятием сложного поведения,
Когда множества стратегий Хг бесконечны при всех і ? N (хотя бы и компактны), то весьма трудно формально определить сложное поведение. Одна из причин состоит в том, что в процессе исключения доминируемых стратегий компактность множеств Х\ не гарантируется (см. задачу 2 гл. I). Далее, сходимость последовательности Xf, t ? N, к подмножеству эквивалентных стратегий может осуществиться только в пределе, отсюда дополнительные топологические трудности...
Наконец, предположение (3) о взаимной однозначности, которое является решающим при доказательстве теоремы Куна, теперь трудно обосновать. Эти трудности демонстрируются в следующем примере, а также в приведенных ниже задачах 4 и 5.
Пример 5. Дележ доллара при инфляции (Дутта, Дживерс [1981])
Участники {1, 2, ..., п\ делят доллар в соответствии со следующим правилом:
Шаг 1. Игрок 1 предлагает дележ л:1 = -{л:!.....л],}, где
П
2 *? = 1, х}^0 при всех i?N. Затем игроки 2, п имеют
= і
право выбора; утвердить х1 или отклонить его. Если все игроки соглашаются на х1, то этот дележ принимается. Если хотя бы один игрок отклоняет лг1, то переходим к шагу 2.
Шаг 2. Игрок 2 предлагает дележ хг на суд остальных игроков. Если они отказываются принять ха, то переходим к шагу 3.
Шаг 3. Игрок 3 делает предложение и т. д. Если дошли до шага п и предложение игрока п отклонено, то вся процедура начинается сначала с предложения игрока 1 и т. д.
Предположим, что доллар обесценивается за каждый период переговоров с коэффициентом дисконтирования т, 0 т 1. Так, во второй период от него остается 6=1 т, в период 3 только 62 подлежит дележу и т. д. Ясно, что если процедура переговоров о дележе будет продолжаться до бесконечности, то выигрыш каждого игрока становится нулем.
Предполагая существование сложного равновесия с исходом х* = {xf, ..., х*) (точное определение и теорему существова-ния см. в работе Рубинштейна [1980]), проведем обычные рассуждения, основанные на анализе стратегических ожиданий для вычисления х*. Предположим, игрок 1 на шаге 1 предлагает х1. Он знает, что игрок і, іфі, рассчитывает с шага 2, если таковой состоится, на равновесный исход (8х*, 8xf, 6xf, ..., 6xJ_i).
В самом деле, игра с шага 2 получается из исходной игры соответствующей перенумерацией игроков. Значит, для того чтобы предложение х1 было принято игроками 2, ..., п, необходимо, чтобы
х\^8х*, бх* - - - Xn^Sxt-i. (15)
Предполагая, что предложение х* будет принято, получаем xf ?8х*, ..., xt^6xt-i. (16)
Выберем теперь х\ так, чтобы
х\ 1 [6xf + 8xf + ... + 6л?_і],
тогда существует допустимый дележ (хі, х\, ..., х„), превращающий все неравенства из (15) в строгие и, следовательно, приемлемый для игроков 2, п. Значит, неравенство
X* 1[8xf 6a:?Li] противоречит оптимальности x+
(сложные равновесия являются равновесиями по Нэшутеорема Д гл. III). Таким образом, получаем
1 ¦- + ... + fix* j] = (1 - б) + Ьх* xf. (17)
Используя (16) и (17), получаем для всех і=1, ..., п xf V-'xt ^ (1 6) б‘"1 + 6‘х* ^ (1 6) 61'-1 + 6 xf,
откуда
* для всех *=1* - - - -
Выражения в правой части в сумме равны 1, поэтому все они суть равенства. Заметим, что когда 6 стремится к 1, предельный дележ становится справедливым (каждый игрок получает 1/п); тем не менее при 6=1 вся стратегическая аргументация оказывается некорректной.
Для того чтобы точно описать в следующем примере некооперативное поведение полностью информированных игроков, требуется уже комбинация концепций решения. А именно, усеченная после исключения доминируемых стратегий игра становится несущественной.
Пример 6. Дележ трога по Штейнгаузу
Пусть отрезок [0, 1] символизирует неоднородный пирог, который должен быть поделен между двумя игроками. Полезность доли А а. [О, 1] оценивается для игрока 1 величиной
?і(А)~ J (дx'jdx,
а полезность доли В с [0, 1] оценивается игроком 2 как
По мере того как время изменяется от t = 0 до t 1, нож двигается со скоростью 1отх = 0кх=1. В любой момент времени каждый из игроков может остановить нож.
Если нож остановлен в момент t игроком і, то этот игрок получает долю [0, /], а другой игрок\t, 1]. Значит, Xf=X2 = [0, 1], где стратегия х1 означает остановку в момент t = x-t игроком і, если другой игрок не остановил нож раньше. Функции выигрыша
определяются так:
щ(хи *2) =
Стратегия th і 1, 2, определяемая из условия
М[0. */]) = МІл-. П).
есть единственная осторожная стратегия игрока і. В самом деле, р(. (*,.)= inf и{(хи х2) inf [?{ ([0, х,]), ,([*„ 1])},
поэтому ф(- достигает максимума, когда доли [0, ^-] и [th 1] равноценны для игрока і.
При нашем специальном выборе о( имеем tt t2. Следовательно, при осторожном поведении игрок 1 получает долю [0, ^], а значит, свой гарантированный выигрыш аі = п,([0, ^]), в то время как игрок 2 оказывается более удачливым: v2§tu 1]) и2([/2, 1]) = а2. На самом деле, при осторожном поведении весь дополнительный по сравнению с гарантированными уровнями (cXj, а2) выигрыш оказывается распределен в пользу игрока 2, а именно:
?г(?и 1]) = max {,(**, хг)\щ(хь Jtr2)af}.
В гл. V мы скажем, что этот исход является наилучшей переговорной точкой для игрока 2.
Первый раунд исключения доминируемых стратегий дает
(н;) = [/,-, 1], поскольку стратегия х{ остановить нож до момента t{ доминируется осторожной стратегией (это легко проверить). Предположим теперь, что игрок 1 знает функцию выигрыша игрока 2 и поэтому может вычислить /2.
При условии, что игрок 2 не остановит нож до момента і2, второй раунд исключения доминируемых стратегий позволяет игроку 1 отбросить стратегии [/t-, t2). В самом деле, при всех х, 6 [^і, Q имеем
?і ([0, xtJ) = tif {х^, x2) C Щ (t2, x2) v ([0, /2]) при всех x2?\t2, 1].
Итак, XJ = [/2, 1] и дальнейшее исключение доминируемых стратегий невозможно, так как
Xl^Xi = [t2, 1] при 1^2.
Поскольку никакие две стратегии в Х‘( не эквивалентны для игрока і на то мы заключаем, что наша игра не раз
решима по доминированию. Тем не менее редуцированная игра ([*2. 1]. [^2.
1]. ии и2) является несущественной. В самом деле, у обоих игроков одинаковые осторожные стратегии = хг = t$
dj inf Mj (/2, x2) v-( ([0, /2]) inf Mj (a^j, л:2) = vj ([л^, 1])
I] I]
При Xf ti,
a2 = inf Ut(xu = 1J) inf u2(лГі, л:2) = v2([л:2, 1])
*,б[г„ i] с, еіб., ij
при л:2 f2.
Более того, (а4, а2) оптимальный по Парето вектор выигрышей (определение 5 гл. I), как это видно из рис. 5. Из теоремы 1 гл.
I заключаем, что хг = л:2 = ігоптимальные стратегии игроков в 2-редуцированной игре. Можно считать исход (t2, t2) соответствующим случаю полной информации игрока 1 о функции выигрыша 2. Заметим, что вектор (а„ а2) = {?г ([0, /2]), н2([*2, І])) оптимален по Парето и в исходной игре, причем перераспределяет весь дополнительный выигрыш в пользу игрока 1і
М[0. ^1) = max {и1 (лГі, х2)\и2(х^, x2)a2}.
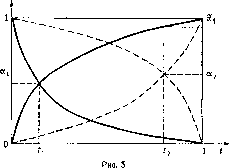
Две кривые, пересекающиеся в (tb aj), суть графики ^ (ГО, Л) и о*([(, 1])- Две пунктирные кривые - графики у2([0, t\) и v2{[t, 1]).
Упражнение 2. Каким будет некооперативное изолированное поведение, если нож двигается от х = 1 к х = 0?
Упражнение 3. Аукцион неделимого товара
Рассмотрим аукцион первого типа из примера 2 гл. I. Проведите последовательное исключение доминируемых стратегий (двух раундов будет достаточно).
Докажите, что эта игра не разрешима по доминированию и что редуцированная игра (после последовательного исключения) не является несущественной. Заметим, однако, что игрок 1 имеет единственную осторожную стратегию в этой игре, что позволяет говорить о естественном некооперативном исходе игры.
Задача 4. Метод деливыбирай
Теперь игрок 1 фиксирует [О, 1J, затем игрок 2 выбирает [0, хх] или [*!, 1] в качестве своей доли (игрок 1 получает оставшееся). Пусть предпочтения игроков описываются теми же полезностями, что и в примере 6.
1) Сформулируйте игру в нормальной форме.
2) Докажите, что каждый игрок имеет по одной осторожной стратегии и осторожное поведение позволяет игроку 2 присвоить весь дополнительный по сравнению с гарантированным выигрыш.
3) Предполагая, что игрок 2 при равенстве для него частей пирога делает благоприятный для игрока 1 выбор, докажите, что игра разрешима по доминированию и исход сложного равновесия отдает весь дополнительный выигрыш игроку 1.
Можете ли вы предложить модификацию определения 1, которая позволила бы ослабить последнее предположение и получить по существу то же поведение?
4) Какими будут t-равновесия по Штакельбергу в этой игре?
Дайте интерпретацию результатов.
Пример 7. Парадоксальный метод дележа
Пираты делят добычу: 100 слитков золота. Процедура дележа устроена следующим образом. Сначала самый старший пират предлагает дележ по своему выбору.
Если хотя бы половина пиратов согласна с этим дележом, то он считается принятым. В противном случае (т. е. если абсолютное большинство пиратов его отвергает) второй по старшинству пират предлагает новый дележ добычи среди оставшихся (п 1) пиратов.
ПОВТОРЯЮЩИЕСЯ ИГРЫ
л:' € / (G), щ (х‘) = sup и,- (х),*6/(0)
что можно эквивалентным образом переписать так:
€ I (G), и; (х) = sup (и; (х) I Uj (х) sup inf Uj (yjt y{)\. (4)
l yj yi )
Более того, любые два дележа, удовлетворяющие условию (4), дают один и тот же выигрыш обоим игрокам:
[х удовлетворяет (4)] =Ф [у (х) = Uj (х‘), } 1, 2].
Доказательство этих двух утверждений оставляем в качестве упражнения читателю.
Лемма 3. Пусть х‘дележ, для которого выполнено условие (4).
Пусть It (агрессивная) угроза игрока і:
( =
Пусть предупреждение игрока /, т. е. угроза вида I/ :) = х), уі
Тогда (х, ?г, ?у)сценарий предостережений.
Доказательство. Из (5) получаем у (г/у, і,-(г//)) sup inf Uj{zf, zt) для всех yf€Xf\{xf}, г/ Zi
Поскольку исход xf индивидуально рационален {х g JR (0)), то получаем
и/ (У/, і( (У/)) у (х) для всех г/у € Ху\{х}.
С другой стороны, из (6) имеем
/(!/(/,). Уі) inf sup (2/, гг) для всех /г€Х;\{*ІЬ
гі г]
Зафиксируем теперь стратегию у{, у{ Ф х\, и предположим Щ (I/ (/,). Уд Щ (х‘).
Последние два неравенства в совокупности с условием х‘ ? € /Я (G) позволяют утверждать, что у = (у{), yt) ? IR (G). В силу наших топологических предположений существует оптимальный по Парето исход г, для которого выполнены неравенстваUi(yXui(z), u/(y)^u/(z).
Таким образом, для дележа г справедливо неравенство щ (х{) tif (2). Получили противоречие.
Итак, мы доказали, что
иі (5/ (/,), Уд Щ (*0 для всех у,-? Х,\{х‘]. Щ
Следуя работе Шеллннг [1971], назовем предупреждением угрозу, которая совпадает с поведением ведомого. Такие ответные действия весьма убедительны.
Все остальные угрозы напоминают машину страшного суда *). В тот момент, когда придется приводить угрозу в исполнение, игрок либо должен отказаться от рационального (с точки зрения краткосрочных интересов) выбора, либо все-таки не осуществить угрозу.
Таким образом, успешное применение угроз в качестве механизма предостережений требует, чтобы угрожающий игрок был обязан приводить угрозу в исполнение или по крайней мере чтобы все в это верили.
Упражнение 1. Метаигры (Ховард [1971], Кукушкин [1974])
Для данной игры двух лиц G (Xit Ха, uit иг) с конечными множествами стратегий обозначим через S(l; G) ее расширение, в котором игрок 1 действует в качестве ведомого (в лемме 5 разд. 4 гл.
II эта игра обозначается G):5(1; G) = (Xfy Х2; 1, й3)2).
Рассмотрите игру
Я = S (2; S( 1, G)).
2) Дайте интерпретацию данной игре.
3) Докажите, что пара (а1г аг) является вектором выигрышей для некоторого NE-исхода игры Н тогда и только тогда, когда выполнены следующие два свойства..
а) (аи а2)допустимый вектор выигрышей в игре G, т. е. для некоторого х*€Х{12}
(ах, а3) = (иХ(х*), иг(х*)).
б) inf sup И, (хх, х2)^.щ(х^),
¦Х2 X,
sup inf и2 (хи х2) sgl и2 (X*).
Ху дг,
4) Докажите, что 1-выигрыш по Штакельбергу в игре 5(1; G) (см. лемму 6 разд. 4 ниже) совпадает с наилучшим выигрышем для первого игрока на множестве дележей в игре G. Вычислите также і-выигрыш по Штакельбергу в игре Н, і= 1, 2.
2. а-ЯДРО
Определение 3. Для данной игры G==(X(., и,-; і 6 N) а-ядром игры G называется подмножество (обозначаемое Ca(G)) таких исходов х*, для которых:
для любой коалиции TcN и любой совместной стратегии Хт?Хт существует совместная стратегия дополнительной коалиции Xtc^Xjc, такая, что не выполнено условие
I и{(хт, хтс)'^иі(х*) для всех і?Т,
\ U;(xt, хтс) м,-(х*) по крайней мере для одного і?Т.
В целях упрощения мы привели формулировку определения 3 без точных ссылок на сценарий предостережений, в котором коалиции реагируют на совместные отклонения дополнительных коалиций. Формально сценарий коалиционных предостережений должен быть такимі
{X*, Sr, Tc=N),
где Iтс такое отображение из Хт в Хтс, что не найдется коалиции TsN и совместной стратегии х? ?Хт, для которых было бы выполнено
j Uj(XT, Sг*(хг))^і(**) лля всех і?Т,
1 и{(хт, Srr (хт)) ut (х*) для некоторого і?7\
Таким образом, х* принадлежит множеству Са (G) тогда и только тогда, когда для любой коалиции TsiV найдется такая угроза коалиции Тс против потенциальных отклонений коалиции Т, что (X*, Sr; Т с= N) коалиционный сценарий предостережений.
По определению 3 исход х* содержится в a-ядре игры G в том случае, если любому отклонению хт коалиции Т может быть противопоставлен ход Хтс дополнительной коалиции Тс, который предостерегает по крайней мере одного члена коалиции Т от принятия стратегии Хт, поскольку в этом случае этот игрок проигрывает: и^хт, хТс) ut (л;*) (или все игроки коалиции Т получают такой же выигрыш, как и раньше
u{(xTt xTc) Ui(x*) для всех і ?Т).
Применяя это свойство последовательно к коалициям Т = М и Т {і\, i$N, получаем, что любой исход в a-ядре является также дележом:Са (G)cl (G).
Отметим, что оптимальный по Парето ME-исход также является дележом (вместе с пассивной угрозой, состоящей в отсутствии реакции, он образует сценарий предостережений). Сильное равновесие содержится в a-ядре (стабилизируется с помощью пассивных угроз):ME (G) п РО (G) с [ (G), SE (G) с Са (G).
Упражнение 3 иллюстрирует эти включения. В частности, приведена простая игра трех лиц, в которой нет сильного равновесия в то время, как a-ядро состоит из двух точек (пункт 2).
В игре двух лиц а-ядро совпадает со множеством дележей и, следовательно, всегда непусто (в топологических предположениях леммы 2). Интересно отметить, что в играх по крайней мере с тремя игроками a-ядро может оказаться пустым.
Пример 3. Парадокс Кондорсе
Пусть М сообщество, состоящее из нечетного числа участников, которые должны из конечного множества кандидатов А выбрать одного. Кандидат выбирается большинством голосов: каждый игрок голосует за одного кандидата, и выигрывает тот, у кого наберется максимальное число голосов.
Для всех і g N обозначим через и; функцию полезности игрока і на А. Полезности любых двух исходов из А считаются различными, поэтому существует ровно р\ отношений предпочтения, где р = Л мощность множества А.
Стратегии игрока і составляют множество Х; = Л. Правилом голосования является любое отображение я из Хц в А, такое, что для всех х^Хці
я (х) = а =Ф I {і € Л/ \xi = a\\^\\i^N\xt = b\\ для всех Ь$А. (7) При фиксированных и{, і?М, возникает следующая игра в нормальной форме:
G = (Xf, и,-ол; 1N).
Найдем в этой игре кооперативно устойчивые исходы. Предположим; что х* ? Хд/ содержится в a-ядре, и обозначим а = я (¦?*). Отметим, что любая коалиция Г, в которую входит более половины участников может обеспечить избраниелюбого кандидата Ь, если все ее члены будут голосовать за b (это следует из (7)):
[хг = b для всех і ?Т]=[я(Хт, Хтс)~Ь Для всех хтс^Хте].
Следовательно, неравенство?і € Т щ ф) и{ (а) (8)
противоречило бы принадлежности исхода х* a-ядру (см. определение 3). Таким образом, для всех коалиций Т, содержащих большинство голосов, и для всех кандидатов Ь, Ьфа свойство (8) не должно быть выполнено. Это утверждение эквивалентным образом может быть переформулировано так:
I {і € NI и{ (а) и,- ф)\\ -іуі для всех Ь, Ьфа. (9)
В силу нечетности N либо сама коалиция содержит большинство игроков, либо ее дополнение. Если выполнено свойство (9), будем говорить, что кандидат а является победителем по Кон-дорсе для порядков предпочтений ,- i?N.
Такой кандидат наносит поражение любому другому кандидату при парном сравнении. Таким образом, мы доказали: .
[х*?Са (6)]=ф[я(х*) является победителем по Кондорсе при
(U;) 1 в Л/ ] -
Обратное утверждение также справедливо мы оставляем его читателю в качестве упражнения.
Данным порядкам предпочтений щ, і € N, соответствует не более одного победителя по Кондорсе (из (9)). Соответственно могут возникнуть только два случая.
Случай 1. Для порядков uh i ? N есть победитель по Кондорсе (а). Тогда a-ядро игры G состоит из всех исходов х, для которых п(х) = а: Са (G) = я~* (а).
Случай 2. Для порядков щ, і ? N, не существует победителя по Кондорсе. Тогда a-ядро игры 0 пусто:
Са(?)=0.
Случай 2 известен под названием парадокса Кондорсе, и возникающая ситуация подробно исследована в обширной литературе по теоріи общественного выбора (см., например, Сен [1970], Мулен [1981] Миркин [1974]). Для того чтобы построить порядки предпочтений, при которых нет победителя по Кондорсе, предположим, что и \N \ = п^Ъ. Выберем далее трехкандидатов с, Ь, с и три натуральных числа пи пг, п3 так, чтобы было ш полнено г)
I + h + ns = n,
\ пк+Ъпт при всех {k, I, т} = { 1, 2, 3}.
Предположим далее, что сообщество N распадается на три однородные щуппы Nk с числом игроков пк, k=\, 2, 3, причемдля всех і € и{ (а) и{ (b) ut (с) и{ (а),
для всех ji ut (b) и{ (с) и{ (а) ц, (а),
для всех і С ?3; ut (с) и,- (а) щ (Ь) и{ (а),
для любого а?А\{а, Ь, с}.
Участники из (j Na кандидата а предпочитают кандидату Ь. Поскольку п -f /г3 пг, то b не может быть победителем по Кондорсе. Аналогично, большинство, состоящее из U Ыг, предпочитает кандидата b кандидату с, а большинство, состоящее из N2 и /?3, предпочитают кандидату а кандидата с.
Упражненіе 2
Докажите, что дележ х из a-ядра игры G не обязательно является сильным равновесием. Тем не менее из пустоты множества SE (G, следует пустота множества Са (G) и наоборот. Более того, ии соответствует избрание одного и того же кандидата
n(SE(G)) = n(Ca(G)).
Что изменится в примере 3 при четном JV ?
В игре с пустым a-ядром кооперативная стабильность не может быть достигнута только за счет предостерегающих угроз. Даже тот факт, что стратегические отклонения могут быть совершены только в открытую, не гарантирует от возможного существования коалиции, для которой отклонение является выгодным, несмотря на соответствующие действия остальных игроков. В этом случае для обеспечения стабильности введем более гибкий сценарий поведения, в котором реакция игроков, поддерживающих соглашение, состоит в том, чтобы подкупить некоторых членов из коалиции отступников, причем таким образом, чтобы остальные члены коалиции отступников понесли существенные потери
і) Напомним, что I Л/1 нечетно .Прим, перед.
Рассмотрим, например, игру выборы большинством голосов (пример 3) с тремя игроками- и тремя кандидатами, в которой порядки предпочтений образуют цикл Кондорсе
щ (а) (Ь) Щ (с),
иг {Ь)иг {с) и2 (а),Щ (с) и* (Ь).
Рассмотрим исход х (Ь, Ь, с), при котором выбирается кандидат Ь. Стабильность, исхода х может быть нарушена коалицией {1, 3}: игроки 1 и 3, выбирая кандидата а, увеличивают свой выигрыш, не боясь каких-либо стратегических действий со стороны игрока 2:
и, (а, хш, а) щ (Ь, Ь, с) для і = 1, 3 и для всех х2?Хг.
Тем не менее игрок 2 может предложить игроку 3 лучший вариант: голосуя вдвоем за кандидата с, они обеспечат его избрание, и тем самым игрок 3 получит наибольший возможный выигрыш. При этом игрок 1 получит наименьший возможный выигрыш.
Предвидя, что игрок 2 может подкупить игрока 3, игрок 1 не станет входить в коалицию [1,3] первоначального отклонения от договора, поскольку иначе его выигрыш в конечном счете может уменьшиться: н1(с)ы1 (Ь).
Двухэтапный сценарий, в котором ход коалиции порождает контрмеры, связанные с подкупом некоторых игроков данной коалиции, для того, чтобы предостеречь остальных игроков из этой коалиции, приводит X концепции стабильности, обобщающей понятие сх-ядра. ПраИДа, изложенный выше сценарий угроз и контругроз достаточно сложен технически. Содержательность такого сценария является спорной, однако это понятие обладает хорошими матек*атическими свойствами, а именно в работе: Лафон, Мулен [$80] доказано, что соответствующее множество равновесных йСхДОв не пусто.
В задаче 3 этот результат приводится для случая трех игроков.
Замечание 1
В литературе по теории игр встречается несколько двух-тапных концепций стабильности: решение НейманаМорген-ітерна (Льюс, Райфа [195?]), сильное решение по Викри [1959], юдрешения и сверхядро (Р0т [1976]) и др. Обзор соответствую-дей литературы см- в Розенталь [1972].
Упражнение 3
1) Дилемма заключенного с тремя игроками.
У каждого игрока есть агрессивная стратегия (Л) и кооперативная стратегия (Q. ИФа симметрична. Ниже перечисленывозможные варианты выигрышей игроков:
Например, пусть игроками являются три конкурирующие фирмы, которые могут назначить обычную цену (С) или использовать политику демпинга (Л). Максимальный суммарный выигрыш равен 6 (достигается, если все игроки придерживаются кооперативного поведения) и уменьшается на единицу при увеличении на единицу агрессивности игроков.
Каждый игрок, переключаясь со стратегии С на стратегию Л, получает дополнительно единицу выигрыша и уменьшает на единицу выигрыш каждого из оставшихся двух игроков.
Докажите, что в этом варианте игры дилемма заключенного равновесие в доминирующих стратегиях доминируемо по Парето и не существует сильного равновесия. Докажите также, что в этой игре ровно четыре дележа и a-ядро совпадает со множеством дележей.
2) Каждый игрок может выбрать одного из трех игроков, в частности самого себя. Таким образом,
а:,={і,2, з).
2, 3, 1) каждый игрок получает ровно по одному голосу.
Докажите, что a-ядро состоит из двух исходов тйпа (2, 3, 1).
Задача 1. Теорема Накамуры (Накамура [1979])
Для данного конечного сообщества N правильная простая игра1) задается подмножеством W множества непустых коалиций из N, для которого выполнены следующие свойства:
I [T?W, Т сГ]#Г eW,
\ T$W=T'$W.
Для данного конечного множества кандидатов А правилом голосования сообщества N по выбору кандидата нз А является отображение л из AN в А (каждый игрок выдвигает ровно одного кандидата). Скажем, что правило голосования я порождено правильной простой игрой W, если выполнено следующее свойство:
?х? AN ?аеА [3TeW ?іет xt = a]^[n(x) = a].
Обозначим через L(A) множество (линейных) порядков на множестве А, а через и е L (A)N совокупность порядков предпочтений на А: для каждого іеН функция ut показывает полезность элемента а для игрока і (равенство полезностей для различных элементов из А недопустимо).
Заданная правильная простая игра W и правило голосования л, порожденное W, определяют для каждой конкретной совокупности порядков предпочтений и игру G (и): множество стратегий Х( = А, функция выигрыша игрока і: щ о л для всех igN.
1) Обозначим через С (и) следующее, возможно пустое, подмножество А:
аеС(и)?ЬеА { g-ЛГ I и j (а) и, (?)} W.
Докажите, что С (и) является образом при отображении я a-ядра игры G (и).
С (ы) = л [Са (G (и))].
В предположении, что простая игра W является сильной, т. е. выполнено условие
T$W=pTeeW,
докажите, что
Са(0()) = я- (С (и)).
2) Предположим, что для некоторой совокупности и мно
жество С (и) пусто. Докажите, что существует р = А не обязательно различных коалиций Тк, k~\, для которых
выполнено
' Тк ? W для всех k= 1, ..., р,
П Тк 0.
3) Предположим, что \N\ = n~^p \A\. Докажите следующую эквивалентность (теорема Накамуры):
[Vu?L(A)K С(и)#0]фф[ ЛI ?(W7)],
где ?(И7) обозначает число Накамуры для простой игры W, которое определяется как минимальное число подмножеств (Та) из W, таких, что
П Та = 0.
а
Дайте интерпретацию.
Задача 2. Выборы с правом вето. Кооперативное поведение (Мулен, Пелег [1982])
Фиксируем сообщество N, множество кандидатов А и предположим, что
IJVI = I ЛI 1. (10)
Отображение я из AN в А называется выборами с правом вето, если Ух ? AN Уі g N я(х)фх{. Из (10) следует, что такие правила существуют.
' 1) Для данных порядков предпочтений u$L(A)A (см. обозначения задачи 1) обозначим через С? (и) следующее подмножество множества А:
a?CV(u)VT=N IТ\ + \Р(Т,а, и)р-1,
где Р (Т, а,и) = {Ь?А\Уі?Т и: (а) щ (Ь)\
множество кандидатов, которых коалиция Т единогласно предпочитает кандидату а.
Докажите, что С? (и) всегда не пусто.
Указаниеі рассмотрите последовательность alt ..., а„, определенную по индукции:
наихудший кандидат по и± среди А, at+1наихудший кандидат по ы+1среди Л\{я1( ..., at\.
Докажите затем, что а = А \{аг.....ап\ принадлежит множе
ству С? (а).
2) Обозначим через G (и) игру со множествами стратегий Х/ = А и функциями полезности о я, і ? N. Докажите, что a-ядро игры G (и) является прообразом множества С? (и) при отображении я:
Ос (с ()) = я-1 (С? (и)).
3) Докажите, что множество С? (и) является образом множества сильных равновесий игры G (и) при отображении я:n(SE(G(u)))=*CV(u).
Указание: Выберем а?С? (и) и обозначимQi = {b€A\ ui(b) Uf (а)}.
Множества Qt являются подмножествами множества Л\{а}, в котором п элементов. Более того, они удовлетворяют условию?Г с N I U QA\T\.I f г I
Таким образом, по лемме о паросочетаниях) элементы множества Л\{а можно занумеровать так, что а1 ? Q. для всех і € N. Докажите теперь, что (ах, .. - , а„) € SE (G (и)).
Задача 3, Возражения и контрвозражения в играх трех лиц) (Лафон, Мулен [1980])
Пусть (Хи Хг, Х3; их, 2, и3) игра трех лиц с конечными множествами стратегий Х{. Для данного исхода х ? Хц, 2.3} обозначим через 012 (х) множество возражений коалиции {1, 2} против хі
[(і/и У г) € Q (х)] [ІШ Uj (Уі, У2, l/j) ^ (xlt Х3, Х3), І 1, 2 J ,
Контрвозражением коалиции ]2, 3) против возражения (уи у2) ? является пара (г2, г8)ёл,хХа, такая, что
' inf иг (ги г„ г) inf и* (ylt yt, у3),г,
sup Mj (2j, г2, z3) E щ (X\ x2, x3). ^ ^г,
Игрок 3 навязывает кооперацию игроку 2: Если ты будешь настаивать на возражении (ух, уг), то я сделаю так, чтобы твой выигрыш был не больше Ыи3{уг, у3, у3). Если же тыV
примкнешь ко мне и мы выберем (z2, z„), то тебе будет обеспечен выигрыш inf w2 (z1( z2, z3). Наконец, нижнее неравенствоz,в (11) предостерегает игрока 1 от внесения возражения (уи у3).
Множество DE (G) в игре G состоит из всех дележей, для которых на каждое возражение со стороны коалиции {і, /} найдется контрвозражение коалиции {г, Щ или коалиции {/, k}. Докажите, что множество DE (G) игры G непусто.
Указание: Предположим сначала, что / (и) = Х{1,2, з}- Скажем, что возражение (yv ya) ? 013 (х) коалиции {1,2} противъ является максимальным, если
1) на него нет контрвозражения;
2) для всех возражений (z1( z2) 4 0la (х) из неравенствinf и{ (г„ z„ г3) inf и, (уг, у„ у3), і = 1, 2,У*
следует, что эти неравенства обращаются в равенства. Предположим далее, что множество DE (G) в игре G пусто. Определим следующую последовательность:
*, (S1, х1), (S2, х2), ..., (S*. х% где
х произвольный элемент множества Х{і23}, х*максимальное возражение коалиции S‘ против х*-1, на которое нет контрвозражения (t ^ 1).
Докажите, что любые два исхода1 х* различны, что противоречит конечности множества Х{!2з}.
3. ПОВТОРЯЮЩИЕСЯ ИГРЫ
Определение 4. 0-ядром игры в нормальной форме G *^(Х{, и{\ і $ N) называется множество Ср (G) исходов х*, обла-дающих следующим свойством.
Для любой коалиции Т, Т с N, существует совместная стратегия дополнительной коалиции хТс € Хт?, такая, что для любой совместной стратегии хт?Хт не может быть выполнена следующая система неравенств:
I и{ (хт, хТс) и{ (х+) для всех і € Т,
\ щ (хт, хТс) иі (х*) по крайней мере для одного і € Т.
Стабильность исхода из 0-ядра является более сильной, чем стабильность исходов из a-ядра: коалиция Тс Может пресечь отклонение коалиции Т, даже если члены коалиции Т выби‘ рают свою совместную стратегию хт тайно. Конечно, сам факт того, что коалиция Т собирается отклониться от согласованной стратегии х*, должен быть известен, иначе игроки коалиции
Тс не узнают о предательстве и не смогут ему ничего противопоставить. Сравнивая определения 3, 4 и определение 1 гл. V, получаем
S?(G)cCf(G)cCa(G).
Для того чтобы дать интерпретацию определению 4, представим, что игра G повторяется во времени. В момент t, t = 1, 2, ..., каждый игрок і, зная предыдущие ходы х1, ..., л;-1, выбирает стратегию х\.
Выборы игроков в момент t могут быть смешанными или коррелированными стратегиями, могут производиться независимо или после некоторого этапа обмена информацией. Важно только, чтобы реализация лотерей, проводимых в момент t, становились известными к моменту t Наконец, выигрыш каждого игрока і есть среднее Чезаро его текущих выигрышей:
t
Ига -т- щ (лг5). (12)
І-+Я s_
В работах Аумана [1978] и Рубинштейна [1979] ) доказано, что все исходы из смешанного 0-ядра игры G могут быть получены как сильные равновесия в повторяющейся игре G (оо). Обратно, выигрыши, соответствующие сильным равновесиям в игре G (оо), покрывают выпуклую оболочку выигрышей, соответствующих смешанному 0-ядру игры G. Таким образом, с помощью повторений исходной игры формализуется весьма существенная черта кооперации с применением угроз.
Отклонения, выгодные в краткосрочном плане, становятся невыгодными в долгосрочном плане, если объявленная угроза приводится в исполнение. Для этого необходимо, чтобы долгосрочные выигрыши всегда перевешивали краткосрочные, как это неявно предполагается в нашей интерпретации сценариев предостережений.
Среднее Чезаро (12) обеспечивает выполнение этого условия.
Мы не будем воспроизводить сложное доказательство этих результатов. Вместо этого разберем более простой вариант повторяющихся игр, в котором общий выигрыш является дисконтированной суммой текущих выигрышей.
Повторяющиеся игры с дисконтированными выигрышами
Предположим, что в исходной игре G = (Xt-, up, t g /V) функции иi равномерно ограничены на множестве XN (например, Xf компактны, а и{ непрерывны при всех i?N). Пусть в момент t = 1 разыгрывается игра G. Исход игры G обозначим через х1. Далее некоторый случайный механизм диктует либо закончить игру с вероятностью (1б), в этом случае общий выигрыш игрока і равен ut{xl), i$N, либо продолжать игру (с вероятностью б), и тогда игра G разыгрывается заново в момент t 2. После каждой партии игры G с вероятностью (1 6) считается, что соответствующий исход является окончательным, а с вероятностью 6 все предыдущие партии аннулируются, и проводится очередная партия игры G.
Другая интерпретация повторяющейся игры, формально эквивалентная приведенной выше, состоит в том, что игра G разыгрывается бесконечное число раз, а общий выигрыш игрока і, соответствующий последовательности исходов х1, х2,... .... х*, ..., равен
(1 б) {и,- (х^-Ь би, (x2)-f- . . (х‘)+ ...} для всех i?N.
(13)
Известно, что при стремлении 6 к 1 значение ряда (13) стремится к среднему Чезаро (12), если предел в (12) существует.
Положим Р,= inf sup и{. Р,-это максимальный выигрыш* X
игрока і, который он может себе обеспечить при условии, что к моменту выбора своей стратегии он знает стратегии всех остальных игроков. Выберем дележ г* так, чтобы выполнялось условие и{ (х*) для всех і € N.
Будем считать, что х* является соглашением, которое игроки хотят сделать стабильным в повторяющейся игре с дисконтированием. Для этого найдем МЕ-тхож о* в повторяющейся игре, который дает каждому игроку выигрыш и{ (х*).
РАВНОВЕСИЕ ПО НЭШУ
Старший пират никакого участия в дальнейшем дележе не принимает. Если новый дележ отвергается большинством голосов, то предложивший его пират устраняется от дальнейшего участия в дележе, и процедура повторяется для (п 2) пиратов.Примем достаточно реалистичное предположение о том, что каждый пират знает функции выигрыша остальных. А именно, каждый пират из двух данных дележей предпочитает тот, в котором его доля золотых слитков больше (дележи, дающие ему одинаковую долю добычи, являются равноприемлемыми независимо от долей остальных игроков).
Дух всеобщего недоверия, царивший, как известно, среди флибустьеров, позволяет предсказать, что их поведение будет некооперативным, а тогда остается только найти окончательный дележ.
Вычислим сложное поведение пиратов. Если осталось только два пирата, то старший из них забирает всю добычу, поскольку младший пират не составляет абсолютного большинства.
Пред-ііоложим, что осталось три пирата. Тогда старший из них может предложить дележ, дающий 99 слитков ему и 1 слиток младшему пирату.
Младший пират вынужден согласиться с таким предложением, поскольку он понимает, что оставшись один на один со средним пиратом, он не получит ничего.
Если пиратов четверо (4, 3, 2, 1), то старший из них (4) будет рассуждать следующим образом: Если мое предложение будет отвергнуто, то три оставшихся пирата поделят добычу так: (99, 0, 1) (см. рассуждения выше). Следовательно, я должен предложить такой дележ, который хотя бы одному из них был
выгоднее этого, а мне давал наибольшую возможную долю. Единственным решением этой задачи является дележ (99, 0, 1, 0), в котором старший пират (4) жертвует всего лишь одним слитком в пользу пирата 2.
Равновесный дележ для произвольного количества пиратов может теперь быть найден по индукции. Выше (с.
63) приведены соответствующие результаты в зависимости от общего числа пиратов.
Итак, если /г = 2р+1 или /г = 2р + 2, то в дележе, соответствующем сложному равновесию, доля старшего пирата равна (100 р) слитков. По одному слитку получают р пиратов, которые имеют номера той же четности, что и старший пират.
Парадоксальность этой процедуры дележа состоит в том, что с виду она весьма демократична, однако добыча делится отнюдь не поровну!
Причина этого парадокса в том, что при последовательном исключении доминируемых стратегий не остается никакой возможности для кооперации. Рассмотрим случай трех пиратов.
Среднему пирату следовало бы поспешить предложить младшему некоторый договор (например, о дележе (50, 50)), чтобы провалить предложение старшего пирата (99, 0, 1). Однако откуда у младшего пирата возьмется уверенность в том, что средний пират, став старейшиной, не отнимет у него всю добычу?
Ведь именно такое поведение вытекает из стремления к максимизации выигрыша.
Другими словами, предложение дележа (50, 50) является для среднего пирата доминируемой стратегией.
Задача 5. Переговоры двух лиц при наличии дисконтирую-щего фактора (Бинмор [1980])
Два игрока договариваются по поводу выбора вектора выигрышей из множества Л с: IR+, которое имеет вид
Л = {(г„ г2) 10 г2 ? (гх), 0гх},
Где ?дифференцируемая на [0, 1] функция, причем
при всех t, 0 t ^ 1.
? (1) = 0, ?'(00 ? (0) = 1, ? (t) 0
Процедура та же, что и в примере 5: на шаге 1 игрок I предлагает исход х3^А. Если игрок II отклоняет х1, то он может предложить х2^6-А, где 6, 0 6 I, есть дисконтирующий фактор. Если игрок I отклоняет хг, то он может предложить х3 ? 62 - А и т. д. Если соглашение наступило на шаге t, то выигрыши игроков в игре суть координаты х*.
Если соглашение не достигнуто ни на одном шаге, то выигрыши равны нулю.
1) Докажите, что исход сложного равновесия соответствует достижению соглашения на шаге 1 и сводится к принятию некоторого оптимального по Парето вектора л:(б) из А. Охарактеризуйте л: (б), используя функцию ?.
2) Докажите, что при б, стремящемся к 1, хг (б) уменьшается, а лга (б) возрастает. Докажите, что предельный исход л;(1) есть арбитражное решение по Нэшу на множестве А, т. е. решение следующей задачи: maxzjz3.
ге А
Задача 6. Общественный механизм принятия решений с побочными платежами (Мулен [1981])
Сообщество N = {1, 2, ..., п} должно принять одно решение из конечного множества А = {а, Ь, с, ...}. Есть один частный товар (деньги), который позволяет осуществлять побочные платежи, а полезность каждого игрока квазилинейна (как в задаче 4 гл.
I). Исходная полезность і-го игрока описывается вектором и{ g Если сообществом принято решение а и игрок і получает денежный платеж tt (он может быть как положительным, так и отрицательным), то окончательно полезность для него описывается величиной
u{(a)-j-t(.
Решение (a; t) состоит из общественного выбора a g А и вектора і = (tu tn) денежных платежей, таких, что
и н* и + - - - +tnО-
Обозначим через ® с Л х R" множество всех таких решений.
1) Мы будем рассматривать два различных механизма. В первом из них игроки последовательно предлагают решения, которые должны быть единогласно утверждены остальными.
Игрок, чье решение отвергнуто, теряет в дальнейшем право вето, и денежный платеж ему больше не выплачивается.
Более точно:
Игрок 1 предлагает сначала решение йх (a1, Р) g 3 для единогласного утверждения остальными участниками. Если каждый из игроков 2, ..., п принимает d1, то это и есть окончательное решение. Если по крайней мере один игрок отклоняет d1, то тогда игрок 2 должен предложить решение dz = (a3, Р) g SD с единственным ограничением: t\ 0.
Решение d2 представляется для единогласного утверждения игроками {3, ..., п}. Если оно отвергается хотя бы одним из этих игроков, то тогда игрок 3 будет предлагать d8 = (а8, Р) ? 3), такое, что t\=t\ = 0, и теперь d3 будет представлено на единогласное утверждение игроков {4, 5, ..., п} и т. д. Если предложения игроков 1, 2 ..., (/г2) последовательно отклоняются, тогда игрок (п1) предлагает dn~1 = (an~1, іп~х), где tn~?
имеет видіп~г (0.....О, іп:\, /Г1)-
Только игрок п имеет право отвергнуть dn~x, и в этом случае он выбирает окончательное решение dn = (an, 0).
Докажите, что предложенный выше механизм определяет разрешимую по доминированию игру (при некоторых дополнительных предположениях, аналогичных принятым в задаче 3).
Вычислите выигрыши, соответствующие сложному равновесию. Любое ли сложное равновесие оптимально по Парето?
2) В нашем втором механизме априори задано некоторое начальное решение (а, I). Приведенная ниже процедура символизирует аукцион за право лидерства:
i) каждый игрок назначает %^0 денег как цену за то, чтобы стать лидером;
ii) один из игроков, предложивший наибольшую цену (например, тот, который имеет наименьший порядковый номер), становится лидером. Пусть это игрок t0;
iii) лидирующий игрок і0 платит каждому из остальных н предлагает решение (a; t)\
і?) это предложение ставится на голосование среди остальных игроков. Следовательно, на шаге (і?):
или предложение игрока і0 (а; () поддерживается всеми остальными игроками, и тогда окончательное решение есть (a; t + s), где
Или (по крайней мере) один игрок отвергает предложение игрока і0 и в этом случае принимается начальное решение (іа?, t). Учитывая денежные платежи, получаем окончательное решение (а, /-М).
Проанализируйте игру, получающуюся из данного механизма на основе каких-либо функций полезности. Рассмотрите сначала игру G(t0), начинающуюся с шага ііі), после того как определен лидирующий игрок і0.
Докажите, что игра G (і0) разрешима по доминированию и найдите выигрыши сложного равновесия. Возвращаясь к шагу і), докажите, что вся игра не разрешима по доминированию, но что после соответствующего исключения доминируемых стратегий, получается несущественная игра (см пример 5).
Вычислите соответствующие равновесные выигрыши.
РАВНОВЕСИЕ ПО НЭШУ
Доминирующая стратегия, осторожное и сложное поведение могут быть определены игроками независимо друг от друга. Каждый игрок самостоятельно, зная только нормальную форму игры, может вычислить стратегию (или стратегии), рекомендованную тем или иным принципом рациональности.Синхронность стратегических выборов в этом случае не требуется.
В противоположность этому равновесие по Нэшу может быть обосновано только динамическим сценарием, в котором стратегические решения, принимаемые сегодня, зависят от предыдущих партий игры или хотя бы от начальной позиции. Таким образом, теперь уже общение игроков становится неизбежным.
Они должны хотя бы наблюдать одни и те же прошлые исходы игры. Приведем определение и обсудим концепцию равновесия по Нэшу прежде, чем подробно исследовать ее привлекательные математические свойства (существование и устойчивость).
1. ОПРЕДЕЛЕНИЕ И ОБСУЖДЕНИЕ
Для данной игры в нормальной форме предположим, что игроки ведут себя так, как будто они не знают о своей стратегической взаимозависимости: когда игрок і рассматривает переключение со стратегии xt на стратегию у{, он не учитывает реакции на свой ход остальных игроков, т. е. он ожидает, что остальные не изменят своей стратегии в ответ на его изменение. Это предположение правдоподобно, если игроков так много, что воздействие, производимое на общий исход одним отклонением, незначительно (см. пример 1). Альтернативная интерпретация предполагает полное незнание игроком і функций выигрыша Uj при / € N\{i}. Игрок і может добывать информацию о функциях Uj, наблюдая реакции игроков из N\{i} на использование им стратегии, выгодной в предположении, что никакой реакции остальных не последует (эта линия рассуждений развивается в разд.
3).
Определение 1. Пусть дана игра в нормальной форме G = (X,-, щ\ i g N). Скажем, что исход x (x;)ieN есть равновесие по Нэшу (кратко NE-нсхоц) игры G, если
?/г€^г иіІУі *-)/(*,- . xt). (1)
Обозначим через ME(G) множество равновесий по Нэшу в игре G.
В равновесии по Нэшу х игрок і рассматривает стратегии Xt как экзогенно заданные и максимизирует функцию м,- на множестве своих стратегий у{. Свойство (1) равновесия по Нэшу состоит в том, что х{это один из наилучших ответов на стратегии xt.
Концепция равновесия по Нэшу не дает конкретных рекомендаций по выбору стратегии, как это было в случае сложного или осторожного поведения. Обычно, если в игре есть два невзаимозаменяемых і??-исхода (см. пример 2 и лемму 2 ниже), то игроки не могут выбрать стратегии, порождающие равновесие по Нэшу, без некоторого механизма координации (на этот счет' см. также гл. V, разд. 2).
Заметим однако, что в играх двух лиц с нулевой суммой Л^Е-исходы суть просто седловые точки (определение 6 гл. I), поэтому ?-стратегии совпадают с осторожными оптимальными стратегиями (теорема 3 ?л.
I).
Представим себе два крайних сценария, мотивирующих Концепцию равновесия по Нэшу:
1) С нормативной точки зрения, предположим, что игроки сообща обсуждают, какой выбрать исход, пока не договариваются до необязательного соглашения. В следующий момент они расходятся, и всякий обмен информацией между ними становится невозможным. Затем каждый игрок тайно выбирает свою настоящую стратегию, не зная действительные стратегические выборы остальных.
Игрок может быть верен достигнутому соглашению, а может и отступить от него, не платя при этом штрафа, и использовать любую, угодную ему стратегию. Тогда (и только тогда), когда согласованный исход есть равновесие по Нэшу получаем стабильное соглашение: Предполагая, что Все остальные лояльны, я тоже лучше буду лоялен (чем более бесспорна моя добродетель, тем больше побудительных мотивов Я дам остальным к тому, чтобы и им быть добродетельными). Этот полукооперативный сценарий исследован в гл.
V как особый способ кооперации: концепция равновесия по Нэшу связана как с некооперативной, так и с кооперативной частью teopHH.
2) С описательной стороны мы ищем устойчивые исходы близоруких процедур нащупывания), в которых каждый игрок придерживается оптимальной стратегии при (постоянно нарушаемом) условии, что остальные не меняют своих стратегий. Когда эта процедура нащупывания по Курно (см. ниже разд.
3) сходится, мы получаем равновесный по Нэшу исход.
Замечание: Метатеоретические соображения, предложенные фон Нейманом и Моргенштерном, дают альтернативный подход к нормативному обоснованию Х?-исходов. Рассмотрим случай полной информации и предположим, что некоторая теория рекомендует в игре G для каждого игрока і оптимальную стратегию Х{.
Поскольку каждый разумный и полностью информированный игрок может сам восстановить всю теоретическую аргументацию и вычислить рекомендованный исход, то необходимо, чтобы наша теория предлагала NE-исход если мы хотим, чтобы эгоистичные игроки, максимизирующие свои функций выигрыша, действительно прислушивались к рекомендациям теории.
Пример 1. Двоичный выбор с взаимным влиянием (Шеллинг [І979])
Пусть имеется много идентичных игроков. Каждый из них должен выбрать одну из двух стратегий: 0 или 1 (скажем, для определенности, использовать собственный автомобиль или общественный транспорт).
Если і(, доля игроков, использующих стратегию
1 (общественный транспорт), то числа a(t) и b(t) обозначают соответственно выигрыши любого игрока, использующего стратегию 1 и стратегию 0 (собственный автомобиль). Таким образом, получается следующая игра в нормальной форме:
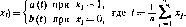
Предположим, что а и b такие, как на рис. 1.
Это означает, что если доля игроков, использующих общественный транспорт, больше то уличное движение настолько свободное, что водитель автомобиля счастливее, чем пассажиры автобуса (учитывая агрегированный показатель затрат и комфорта). Если же доля автомобилистов больше, чем (1 t0), то движение настолько интенсивное (возможно с некоторым приоритетом в правилах для автобусов), что сравнение теперь в пользу пассажиров автобусов. В этой игре равновесиями по
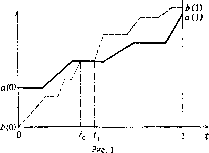
Нэшу являются исходы х*, для которых выполнено условие
П
где t* ~ ^ xf, і = і
означающее, что для каждого отдельно взятого игрока обе допустимые стратегии равноценны.
Пусть величина б обозначает долю игроков, решивших пе-
Гключиться со стратегии 0 на стратегию 1. Заметим, что если настолько велико, что b(t) = a(t) а{і + 6), то выигрыши этих игроков увеличатся при переключении, если бтратегии остальных игроков останутся прежними.
Однако если это переключение произойдет, то у игроков возникнет желание переключиться со стратегии 1 на стратегию 0, поскольку выполнено условие а (t -{- б) b (t -Ь б). Если
П
то желание осуществится, то доля У, х, уменьшится и вновь вернется на отрезок [70, fj.
Аналогично, пусть бдоля игроков, переключившихся по каким-либо причинам (например, из-за случайных ошибок) со стратегии І.на стратегию 0, причем tб /0.
Тогда в силу условия b(tb) a (tб) у игроков появится Желание переключиться обратно на стратегию 1. При овущест-
П
влении этого желания доля х, увеличится и вновь вернется
/-1
йа отрезок [/„, J.
Упражнение 1
Рассмотрим два различных варианта пары функций а (- )(’)-
1) Предположим, что обе функции а и b возрастают по t и a(t) ? (і) для всех t € [0, 1]. Докажите, что соответствующая игра является обобщением дилеммы заключенного (пример 1 гл.
I), в которой единственное равновесие по Нэшу является также равновесием в доминирующих стратегиях.
2) Предположим, что а и b такие, как на рис. 2. Докажите, что соответствующая игра имеет 3 типа і?Е-исходов, один из которых не устойчив по отношению к рассмотренным выше 6-отклонениям.
Отложим до разд. 3 формальный анализ процедуры нащупывания по Курно, который является важным этапом на пути некооперативной интерпретации равновесия по Нэшу.
Определение 2. Исход х игры G = (X{, up, i g N) называется индивидуально рациональным, если
sup inf и{ (уі, г/г) = at и{ (х) для всех і € N.
Уі6 Х( i/;€ Xj
Лемма 1. Все NE-исходы индивидуально рациональны).
Доказательство. Из (1) получаем, что для всех і справедливо неравенство
?/г€*г inf ut(yh уЬЩ(Уі, хг)иг(х).
!/; X/
Взяв супремум по у( в этих неравенствах, получаем (2).
С одной стороны, NE-исход дает каждому игроку по крайней мере его гарантированный выигрыш (индивидуальная рациональность), хотя NE-стратегия может и не быть осторожной (см. пример 2). С другой стороны, NE-исход может не быть оптимальным по Парето (как в примере 1, рассмотренном выше). §олее того, если каждый NE-исход оптимален по Парето, то сосуществование нескольких различных оптимальных по Парето МЕ-исходов порождает обычно борьбу за лидерство (гл. II, разд. 4), что убивает всякую надежду найти оптимальные стратегии.
Это обстоятельство иллюстрируется следующим примером.
Пример 2. Игра перекресток
Два автомобилиста движутся по двум перпендикулярным дорогам и одновременно встречаются на перекрестке. Каждый из них может остановиться или ехать. Следующая игра 2x2 формализует данную ситуацию в предположении, что каждыйигрок предпочитает остановиться, чем пострадать в аварии (исход (ехать, ехать)), и проехать, если другой сделал остановку.
Неотрицательное число е соответствует неудовольствию от созерцания проехавшего, в то время как сам ты вежливо остановился; величина е определяется этическими нормами общества.
Оба AfE-исхода (а именно, (остановиться, ехать) и (ехать, остановиться)) оптимальны по Парето. Тем не менее они не взаимозаменяемы.
Для каждого игрока оптимальной стратегией является остановка, если другой игрок решил проехать перекресток, и наоборот, выгодно проехать, если другой игрок остановился. Высказав решимость придерживаться неосторожной стратегии ехать, игрок выигрывает, поскольку он заставляет другого остановиться и, следовательно, получает максимальный выигрыш, равный 2. Поскольку ни один исход не дает обоим игрокам выигрыш, равный 2, то неизбежна борьба за лидерство.
Каждый игрок будет изображать, что он утратил способность переключиться со стратегии ехать на стратегию остановиться (например, прикидываясь пьяным), и в то же время внимательно наблюдать за своим противником, чтобы выяснить, а вдруг тот и в самом деле не сможет остановиться. Поразительно, что наиболее выгодным оказывается нарочито нерациональное поведение, которое тем самым оказывается вполне разумным.
Симметричность ролей обоих игроков делает невозможным нахождение' арбитражного решения борьбы за лидерство на основе нормальной формы игры. Прекрасные примеры и глубокий анализ читатель найдет в работе Шеллинг [1971], гл.
II.
Выводы предыдущего примера легко обобщить на произвольную игру двух лиц G (XV Х2, и? и2).
Используя обозначения определения 5 гл. II, назовем і-выигрышем по Штакельбергу выигрыш игрока і в любом t-равновесии по Штакельбергу, обозначим его через St:
S; = sup ut(xv х2), где {/, /} = {1, 2}.
(Xux2)tBRj
Таким образом, S(. это выигрыш игрока і, действующего оптимально в качестве лидера. Будем говорить, что в игре G имеет место борьба за лидерство, если не существует такого исхода х, для которого:
Stu,(x), і=1, 2. (3)
Лемма 2. Предположим, что игра G имеет по крайней мере два оптимальных по Парето NE-ucxoda х1, х2 с различными векторами выигрышет
(иДх1), щ (л:1)) ф (,, (л;2), и2(х2)). (4)
Тогда в игре G имеет место борьба за лидерство.
Доказательство. Заметим, что NE (G) = BRl П BR2. Следовательно, по определению St имеем
{х g NE (G)} =Ф {ut (л;) S(, t= 1, 2}.
Если в игре G нет борьбы за лидерство, то найдется исход х, для которого справедливо (3), что означает
Щ (х'Х и, W, і=1, 2, иі (х ) иі (х), = 1, 2-
Поскольку х1 и л;2 оптимальны по Парето, то все четыре неравенства должны обратиться в равенства, что противоречит предположению (4).
В порядке дальнейшего обсуждения NЕ-исходов сравним их с исходами при сложном равновесии.
Теорема I. Предположим, что для всех і С N множества Х( конечны.
-
Если игра G = (Xit up, i ? N) разрешима по доминированию, то любое сложное равновесие является равновесием по Нэшу1).
Доказательство. Доказательство соответствует доказательству леммы 4 гл.
II. Сначала нужно убедиться в том, что для любого прямоугрльного подмножества Y = X Yt множества XN
(6 N
выполнено включение
NE (Z) с NE (Y), где Zf = , (up, Y),
a NE(Y)множество ?-исходов игры (Yh up, i?N).
Пусть X* = X Х\ обозначает множество сложных равнове-
І6 N
сий игры G, тогда
NE(X)z3NE(X1)=...=NE(Xt) = Xt. Щ
Итак, для разрешимых по доминированию игр сложное поведение всегда приводит к /Vf-исходу. Обратное утверждение отнюдь не верно.
NE-стратегия может быть доминируемой стратегией Этот факт является неожиданным. Проиллюстрируем его на примере игры 3x3 (т. е. игры двух лиц в нормальной форме, в которой каждый игрок имеет по три стратегии).
Здесь (Г, L)единственный NE-исход. Тем не менее, для игрока I (выбирающего строки), стратегия Т доминируется стратегией В, а для игрока 2 (выбирающего столбцы), стратегия L доминируется стратегией R. После исключения домини-
!) Из этой теоремы следует существование равновесий по Нэшу в играх в развернутой форме при условии взаимной однозначности (3) разд. 2 гл.
II. В отличие от случая разрешимости по доминированию это условие теперь может быть опущено. Для доказательства существования равновесий по Нэшу в игре в развернутой форме достаточно в алгоритме Куна каждой предфинальной вершине из L (М) приписать ход в финальную вершину с наибольшим выигрышем соответствующего игрока.
Прим, перев, руемых стратегий остается игра с нулевой суммой, в которой нет седловой пары.
Значение этого факта более наглядно для игр в развернутой форме.
Пример 3. Выборы с правом вето (продолжение)
,Із игры трех лиц примера 2 гл. II выделим игру двух лиц, предположив, что игрок 1 наложил вето на исходb (что соответствует его сложному поведению в силу заданных предпочтений). Тогда игроки 2 и 3 участвуют в следующей игре;
\u3(c)u3(a)u3(d)
Рис. 3
Имеется три ?-исхода: (/, R), (р1, L) и (ft, L).
РАВНОВЕСИЕ В СОВМЕСТНЫХ СМЕШАННЫХ СТРАТЕГИЯХ
Имея возможность координировать свои действия, игроки могут договориться о выборе любого М Е -исхода в чистых стратегиях х*. Это соглашение устойчиво не только по отношению к возможным индивидуальным отклонениям (свойство ME-исходов), но также против отклонений коалиций. В самом деле, предположим, что для каждого участника і из некоторой коалиции Т, Т а. М, оказывается выгодным переключиться со стратегии xf на стратегию xt = 1xfUi(xT, xfc)^i Ui(x*) для всех i?T, j
Ц{(хГ, xtc)Ui(x*) по крайней мере для одного І€Т.
Предположим сначала, что число t, определенное формулой
t = 2 хі + 2 xf, равно t*. Тогда по крайней мере для одной іет іетс
пары ja?T выполнено
( х? = 0 лгЛ = 1,
\ *? = 1 Xj, = 0.
Применяя (1) последовательно к /1( /2, получаем
а(/*) ^ Ь(пі*)
I =3a(t*) = b (ni*),
следовательно, щ (xT, х%) = и{ (х*) для всех і € N, что противоречит (1).
Предположим теперь, что t t*. Тогда по крайней мере для одного і € Т имееем
х* = 0, xt = \.
Отсюда в силу (1)
b (п/*) a (t).
Поскольку b (nt*X а (/? + 1), окончательно получаем tt*+l. Полученное противоречие доказывает наше утверждение.
Мы доказали, что любое соглашение, основанное на использовании конкретного М?-исхода, является устойчивым также по отношению к отклонениям коалицией, т. е. любой NE-исход является в данном случае сильным равновесием (см. определение 1 ниже). Если а(і*) и Ь(п1+) достаточно близки, то все игроки в соответствии с соглашением получают приблизительно равные выигрыши, т. е. выбор конкретного WE-исхода не является конфликтной ситуацией. Для реализации одного из этих исходов пираты должны последовательно и открыто выбирать корабль по следующему алгоритму:
*,- = 1 если а(хі + ... +Х;_г + \) b(i[х, + ...+х,._1]), х,- = 0, если Ь (і[х,+ ... +x,_j]) а(х,+ - - +*,-, + !)-
Определение 1. Для данной игры в нормальной форме 0 = (Х/, и,-; і 6 N) скажем, что х*исход сильного равновесия, если не существует коалиции игроков, для которых было бы выгодно отклониться от данного исхода в случае, если дополнительная коалиция не реагирует на отклонение:
?Г с N ?хГ € Хт не выполнено
I ?/^Г u,(xTl xfc) ut (X*),\ 3 І?Т иi (xT, xfc) ut (*?).
Обозначим SE (G) множество сильных равновесий в игре G. Оно может быть пустым.
Полагая T N в формуле (2), получаем, что S?-hcxoa оптимален по Парето. Полагая Т = {і}, і ^ N, получаем, что этот исход является равновесным по Нэшу.
Ясно, что для игр двух лиц SE-исходэто просто оптимальные по Парето й/?-исходы.
Наша интерпретация свойства стабильности (2) основана на двухэтапном процессе принятия решения. На первом этапе игроки приходят к договоренности о некотором конкретном исходе х*. Далее обмен информацией прекращается, и каждый игрок самостоятельно принимает решение о своей окончательной стратегии. Любой игрок і € Л/ может отказаться от использования стратегии xf, но он не может информировать остальных игроков о своем отклонении.
Может также сформироваться любая коалиция Т, отклоняющаяся от хf и выбирающая хг, но игроки вне данной коалиции не могут быть информированы об этом изменении, поэтому ожидается, что они будут придерживаться того поведения, о котором была достигнута договоренность Ur’c). Это ограничение обмена информацией является основным моментом, обосновывающим содержательность определения 1, как показывает от противного приведенный ниже пример 2. См. также определение 1 гл. Ill и следующие за ним комментарии. (Заметим, что для сильных равновесий мы не обсуждаем никаких процедур нащупывания, поскольку близорукое поведение не может быть обосновано при кооперативном способе принятия решений.)
На примере игр двух лиц мы убедились в том, что незыблемость любого ME-исхода разрушается, если возникает борьба за лидерство (см. пример 2 и лемму 2 гл. III).
Аналогичная ситуация возможна и в игре п лиц, что демонстрирует наш следующий пример.
Пример 2. Игра переговоры
п игроков должны поделить доллар. Игроки дают свои заявки арбитру, который удовлетворяет их, если они совместны. В противном случае ни один игрок ничего не получает:
X/ = [0, 1] для всех i?N,
щ (*) =
О, если 2 х/ !-
Мы утверждаем, что
другими словами, исход является сильным равновесием тогда и только тогда, когда соответствующие заявки в сумме дают ровно один доллар. Мы предоставляем читателю проверку этого утверждения.
Заметим, что если коалиция Т, действующая в роли лидера,
выберет некоторый набор стратегий х$ так, что выполнено
условие 2*^=1е (е 0 мало), то коалиция Т, действую-іет
щая как ведомая, выберет в качестве оптимального ответа вектор заявок хтс, такой, чтох, = еи Тс
Следовательно, любой участник или коалиция, присвоив себе право выступать в роли лидера, может забрать почти весь доллар! Поэтому борьба за лидерство в таких переговорах должна быть весьма интенсивной.
Выберем теперь конкретный S?-исход х*, о котором могли бы договориться все игроки, скажем xf = для всех і 6 ЛЛ Для того чтобы сделать это соглашение стабильным, каждый игрок должен решить не обращать никакого внимания на заявки свыше 1/7і со стороны любого игрока, который попытался бы захватить лидерство. Наилучшим образом такая политика глухоты может быть реализована путем разрыва всех каналов обмена информацией между игроками, после чего каждый игрок может изменить свою стратегию, но он не может сделать этого публично.
Решающим моментом, обеспечивающим стабильность соглашения, основанного на конкретном SB-исходе, в рассмотренной игре и аналогичных играх является ограничение обмена информацией между игроками. Это ограничение должно быть законом (как при системе тайного голосования) или физическим ограничением (спутники Одиссея затыкали уши воском). Следовательно, необязательные соглашения требуют некоторых обязательных ограничений в обмене информацией.
Этот момент станет особенно наглядным в концепции равновесия в совместных смешанных стратегиях, которой мы посвятим следующий раздел.
В следующей главе нам потребуются симметричные информационные ограничения для того, чтобы использовать взаимные предостерегающие угрозы как механизм кооперации (см. гл. VI).
Мы уже знаем (гл. Ill, разд. 2), что игра в нормальной форме, у которой множества стратегий являются открытыми подмножествами евклидовых пространств, а функции выигрыша дифференцируемы, в случае общего положения не имеет оптимальных по Парето Л/?-исходов и тем более SB-исходов.
Однако при некоторых очень сильных предположениях о выпуклости существование SE-исхода может быть гарантировано (см. Ауман [1959]).
Упражнение 2. Обобщение примера t
Каждый игрок должен выбрать одно из р общественных благ. Если tkобщее число игроков, выбравших благо с номером k, k=\, ..., р, тогда каждый из tk потребителей получает выигрыш ak(tk), где ак(-) есть неудовлетворение при потреблении блага k, причем это строго возрастающая функция от tk.
Следовательно, получаем игру
X,- = {1, ..., р}, i ?N,
Ui = ak((k), если xs = k и tk = \{i ?N\x; = k}\.
Предположим, что ак(0) = 0 и ак{п)= 1, 6=1, ..., р. Докажите существование по крайней мере одного сильного равновесия в данной игре и приведите условия, при которых все 5Е-исходы приводят к одному и тому же распределению(/j, - - - , tp).
Упражнение 3. Игра размещение магазинов с дополняющими товарами
Два владельца магазинов решают разместить свои магазины на одной улице (на отрезке [0, 1]). Они предлагают дополняющие товары (как, скажем, магазин спортивного оборудования и бюро туристических путешествий), а потому успехи одного оказывают положительное влияние на другого (в противоположность примеру 5 гл.
IV). Кроме того, игрок 1 желает разместить магазин как можно ближе к точке 0, а игрок 2 как можно дальше от точки 0. Таким образом, получается следующая игра:
( х1 = х2 = [0, 1],
I щ{хх, л:2) = а]дг1 I хх х21,
I ut(xv хг) = а2\хг 11 \хх х2\,
[ где ccj 0 а2.
Предположим, что а(^1, 1 = 1, 2.
Докажите, что исход (xlt х2) является сильным равновесием в этой игре тогда и только тогда, когда хх = х%. Разберите остальные случаи,
2. РАВНОВЕСИЕ В СОВМЕСТНЫХ СМЕШАННЫХ СТРАТЕГИЯХ
Смешанные стратегии дают новые равновесные по Нэшу исходы (по теореме 1 гл. IV каждая конечная игра имеет по крайней мере один NE-исход).
С кооперативной точки зрения равновесие по Нэшу в смешанных стратегиях есть необязательное соглашение, которое обеспечивается тайностью проведения лотерей, организуемых игроками для случайного выбора окончательного решения (т. е. чистой стратегии).
Пример 3. Вежливые водители
Модифицируем выигрыши в игре перекресток (пример 1 гл. Ill): если один водитель остановился, то для него предпочтительнее, чтобы другой проехал.
(Этот пример известен в литературе под названием семейный спор, см. Льюс и Райфа [1957].)
В дополнение к двум чистым NE-исходам с векторами выигрышей (l-f-e, 2) и (2, 1+е) соответственно эта игра 2x2 имеет вполне смешанное равновесие, а именно
- j. Этот0+1-с вектором выигрышенсмешанный2 + 8’ ' 2+8j
??-исход доминируется по Парето (любым чистым ??-исходом), поэтому его можно обосновать только тем, что он приносит одинаковые выигрыши идентичным игрокам и в этом смысле является справедливым. Однако в этом смешанном ?/Г-исходе
каждый игрок получает выигрыш 1 +2+і ’ Равный гарантированному выигрышу в смешанных стратегиях. Вместе с тем стратегии р* образующие ?іГ-исход, не являются осторожными, а потому не гарантируют игроку этого выигрыша.
Для проверки этого утверждения заметьте, что цена игры
(Лх, Хг, ut) в смешанных стратегиях равна 1+ггт- и единст-
*4-8
венная седловая пара есть (р, р*), где
бц.
Более того,Ml** бц)=-^-1+2^ = i(pf, pf) = M,(^ бц),
откуда ясно, что смешанная N?-стратегия pf’ является более рискованной, чем осторожная стратегия pj. Единственным стратегическим аргументом в пользу равновесия в смешанных стратегиях можно считать свойство стабильности. Если игроки могут тайно проводить лотереи, то необязательное соглашение о реализации вполне смешанного ?-исхода является стабильным.
Следовательно, для каждого игрока действия остальных вполне предопределены. С этой точки зрения аргументация в пользу осторожных стратегий обманчива, поскольку применение осторожных смешанных стратегий индуцирует последовательность наилучших ответов, что делает окончательный исход совершенно непредсказуемым.
С одной стороны, смешанный ?-исход является разумным, если игрок считает своего партнера столь же рациональным, как и он сам, хотя Л/?-стратегия является более рискованной, чем осторожная стратегия, если партнер может сыграть глупо. С другой стороны, осторожная смешанная стратегия выбирается из соображений минимума риска и, следовательно, безопасна, насколько это возможно.
Тем не менее у рационального игрока возникает желание одностороннего отклонения от исхода, состоящего из пары смешанных осторожных стратегий, поскольку такое отклонение увеличивает выигрыш. Возвращаясь к игре перекресток, построим теперь случайный механизм, который не сводится к независимой рандомизации стратегий, причем этот механизм позволит сделать рановесный исход оптимальным по Парето.
Пример 3'. Игра перекресток со светофором
Игроки сооружают специальный случайный датчик, который показывает (зеленый, красный) и (красный, зеленый) с равной вероятностью. Соглашение состоит в том, что на зеленый свет следует проезжать без остановки, а на красныйостанавливаться.
Это соглашение является стабильным, поскольку при каждом исходе лотереи получается равновесие по Нэшу. Результирующее математическое ожидание выигрыша равно -- + --для каждого игрока, тем самым обеспечивается оптимальность по Парето и справедливость.
Определение 2 (Ауман [1974])
Для игры G = (X(-, и,.; i?N) с конечными множествами стратегии обозначим через L = (L(x))xexN совместную лотерею, т. е. вероятностное распределение на XN. Для всех i g N и для всех X/ € Kt обозначим через LX( условную вероятность реализации х^Хн^у).
_1_
2 у
Vl eXN\{i)
0,
L(xh xt), если знаменатель не равен нулю,
если L (xit уг) = 0 для всех у,?ХN\{i].
Скажем, что L есть равновесие в совместных смешанных стратегиях в игре G, если выполнены следующие неравенства:
Vt g N, ?х0 уi ? X; 2 Щ (xh xt) LX[ (xt)
*:eXN\U)
2 Щ(Уі. x,)LX{(xt). (3)
X!SXN\{C)
Обозначим через CE (G) множество всех равновесий в совместных смешанных стратегиях в игре G.
Кооперативный сценарий, служащий обоснованием определения 2, состоит в следующем. Игроки совместно сооружают случайный датчик, который может производить выбор исходов х ? XN с вероятностью L (х). Если реализовался исход х, то игрок і получает информацию только о компоненте х{.
Далее каждый игрок выбирает свободно и независимо, а также тайно свою настоящую стратегию. Сигнал xt воспринимается игроком і как необязательное предложение сыграть х{. Условия (3) означают, что выполнение соглашения о выборе х{ игроком і обеспечено автоматически при той ограниченной информации, которая доступна каждому игроку.
В самом деле, пусть участнику і предложено использовать стратегию xt. Он выводит из общего распределения L, что с вероятностью Lx. (xf) набор xt будет выбран. Следовательно,
[иі (Уі - ). Ц] = 2 иі(уі, xt)Lx.(xt)
XlSXN\{i)
есть математическое ожидание его выигрыша при применении стратегии у{ € Х{, если все остальные игроки согласны в выборе стратегий следовать сигналу. Таким образом, условие (3) означает, что использование стратегии, предложенной датчиком, есть оптимальный ответ игрока і при заданном уровне инфор-мированности в предположении, что все остальные игроки подчиняются сигналу.
Предположим, что стратегия х{ такова, что L(xt, *f) = 0 для всех xt € т. e. вероятность того, что стратегия х.
будет предложена датчиком, равна нулю. Для такой стратегии х; условие (3) выполняется тривиально, следовательно, мы можем переписать систему (3) в эквивалентном виде
Vi g N Vxit У;Х{ 2 *,) L (xt, x.)
XteXN\{t)
2 U (уi, x,)L(xit X,). (4)
X ... г N\ {i}
Отсюда следует, что лотерея L является равновесием в совместных смешанных стратегиях тогда и только тогда, когда она удовлетворяет системе линейных неравенств (4). Эта система всегда имеет решение, как показывает следующий результат.
Лемма 1. 1) Множество СЕ (G) равновесий в совместных смешанных стратегиях в игре G является непустым выпуклым компактным подмножеством единичного симплекса в R.xw.
3) Если [А = (р,-), 6 n является исходом смешанного ра шире-ния игры G, т. е. исходом игры Gm, то определяемая по этому исходу лотерея L= 0 р.
се/?
L (х) = 0 (X) (5)
(6 N
есть равновесие в совместных смешанных стратегиях в игре G тогда и только тогда, когда уситуация равновесия по Нэшу в игре Gm
Доказательство. Пусть р = (р,-)гл/ исход игры G„ и L соответствующее произведение лотерей, заданное равенством (5). Тогда система (4) примет вид
М*і)-і(6? И,) Р,- (*- ) иі (§? Pf) Для всех і, Х(, Уі. (6)
Это неравенство очевидно, если р; (*,- ) = 0. Следовательно, система (6) эквивалентна системе
Щ(ЬХ., рг) и,-(8У., р?) для всех i%N, х,€[р;1, Уі?Хі- (7)
Предположим теперь, что рсмешанный jVf-исход в игре G. Тогда по теореме 2 гл. IV система условий (7) выполнена. Обратно, из (7) следует, что ы; (6*., pf) не зависит от х{ g [р,]
и, следовательно, равно и, (р). Это завершает доказательство второго утверждения леммы 1.
Далее из теоремы Нэша (теорема 1 гл. IV) следует, что множество NE(Gm) не пусто, откуда получаем непустоту множества СЕ (Gm).
Выпуклость и компактность последнего множества следует из приведенного выше замечания о том, что СЕ (Gm) определяется системой нестрогих линейных неравенств. I
Рассуждения, которые обосновывают стабильность соглашения, базирующегося на равновесии в совместных смешанных стратегиях, во многом аналогичны кооперативному подходу к равновесию по Нэшу. В самом деле, согласно лемме 1 NE-исход как в исходной игре, так и в ее смешанном расширении, отождествляется с равновесием L в совместных смешанных стратегиях, где вероятностное распределение L есть набор независимых случайных индивидуальных стратегий.
В этом случае нет никакой корреляции стратегий различных игроков.
Первый наиболее простой путь получения преимуществ от корреляции индивидуальных стратегий состоит в том, чтобы брать выпуклые комбинации Л?Г-исходов. При этом получается лотерея L типа
р р
L 2 КЬха, 2 ^а = 1. для всех а, (8)
а=І а=1
где Ьжлотерея, в которой исход х выбирается с вероятностью 1, а ХаУ?Е-исход в игре G. Такая лотерея является равновесием в совместных смешанных стратегиях в игре G (заметим, что выпуклая комбинация смешанных NE-исходов также содержится в СЕ (Gm)). Светофор (пример 3') служит примером такого СЕ-исхода. Во многих играх, однако, множество исходов равновесий в совместных смешанных стратегиях шире, чем выпуклая оболочка равновесий по Нэшу.
Это показано в следующем примере.
Пример 4. Музыкальные стулья
Предлагается нестандартная версия игры музыкальные стулья. Имеются два игрока и три стула, помеченные цифрами I, II, III. Стратегия игрока состоит в выборе стула.
Оба игрока несут потери при выборе одного и того же стула. Если же их выборы различны, то тот игрок, скажем і, чей стул сразу следует за стулом игрока /, выигрывает вдвое больше, чем игрок / (предполагается, что I следует за III). Итак, возникает биматричная игра:
В исходной игре нет равновесий по Нэшу. Единственное вполне смешанное равновесие по Нэшу таково:
^ = ^ = Т6і+Тбп+Тбш-
Этот симметричный исход приносит каждому игроку выигрыш, равный единице, и доминируем по Парето. Причина этого в том, что в смешанном исходе (pf, р*) плохой детерминированный исход (і, і) реализуется с вероятностью 1/3. Рассмотрим следующую лотерею L на ХгхХг:
Цх„х%) = ІІ’ *"*.**.- ^ 0, если хх=*хг
Утверждается, что L есть равновесие в совместных смешанных стратегиях в игре (9). Предположим, например, что реализовался детерминированный исход (2, 3) и, следовательно, игроку 1 предлагается использовать стратегию II. При данном L игрок 1 может вывести, что игроку 2 предложено использовать одну из стратегий I или III с одинаковой вероятностью 1/2.
Другими словами, предполагая, что игрок 2 согласен выбирать стратегию, поступающую с датчика, игрок 1 тем самым считает, что игрок 2 использует смешанную стратегию \ б, + ~ бш. Наилучший ответ на эту стратегию и есть стратегия II, поскольку
И] (б[ Ра) Y- 1 Иг) 1 ^ fi2) ~ -
Аналогично игрок 2, которому поступает сигнал применять стратегию III, выводит, что игроку 1 предлагается выбрать стратегию I с вероятностью 1/2 или стратегию II с вероятностью 1/2. В этом случае стратегия 3 является наилучшим ответом игрока 2 на смешанную стратегию р, =у6, + --6И игрока 1.
В силу симметричности нашей игры мы получаем свойство стабильности (3) лотереи L при любых допустимых реализациях.
Заметим, что лотерея L приводит к оптимальным по Парето и справедливым выигрышам (3/2, 3/2), что побуждает игроков вступать в кооперацию на основе использования совместных смешанных стратегий.
Основной чертой необязательного соглашения применять стратегии, вырабатываемые датчиком L, является распределение информации. Оба игрока информированы о лотерее L, которую они выбрали по кооперативному согласию, тем не менее, после того как исход х реализовался как результат применения лотереи, игрок і получает информацию только об t-й компоненте xt. Он не может наблюдать сигнал х{, полученный другим игроком /, а может только вывести из распределения L, что вероятностное распределение х. есть Lx..
Конечно, если L принимает вид (8) при (Х;)аф(Х{)а, для всех і, афа', т. е. распределение L сосредоточено в точках ха, то сигнала xL а достаточно для игрока /, чтобы в точности выяснить сигналы, посылаемые остальным игрокам. В этом случае свойство стабильности (3) требует, чтобы каждый исход был NE-исходом в первоначальной игре (см пример 3').
Пример с музыкальными стульями объясняет, каким образом разумное ограничение возможностей обмена информацией оказывается выгодным с кооперативной точки зрения.
Замечание I
Естественным обобщением определения 2 является рассмотрение возможных отклонений любой коалиции Т с использованием при этом совместной смешанной стратегии L'T на Хт и распространение свойства сильного равновесия на данный рандомизированный случай. Это привело бы к понятию сильного равновесия в совместных смешанных стратегиях, для которого тем не менее нельзя ожидать получения общих условий существования: см., например, игру двух лиц из примера 5 ниже, в которой ни одно равновесие в совместных смешанных стратегиях не является оптимальным по Парето.
В следующем примере в качестве равновесия в совместных вмешанных сратегиях нельзя получить ничего, кроме единственного равновесия по Нэшу. Тем не менее будет приведен новый механизм кооперации, который является более обязательной формой стабильного соглашения, основанного на совместных смешанных стратегиях, и который позволит улучшить по Парето NE-исход.
Пример 5. Конкуренция со специализацией
Два дуополиста снабжают рынок одним товаром, но разного качества. Игра является симметричной. Каждая фирма может выбрать одну из трех стратегий: низкое (L), среднее (УИ), высокое (Я) качество.
Если оба поставят товар низкого качества или обавысокого, то каждый получает нулевую прибыль. Если один игрок выбирает среднее качество, а другой высокое или низкое, то игрок, предложивший среднее качество, получает прибыль 2. Если оба товара среднего качества, прибыль обоих игроков равна 1. Для получения максимальной суммарной прибыли одна фирма должна предложить высокое качество, а другая низкое, при этом игрок, предложивший высокое качество, получает 3, а предложивший низкое качество получает 1.
Заметим, что эта модель может интерпретироваться как известная игра размещение отелей.
Для игроков, придерживающихся некооперативного поведения, эта игра разрешима по доминированию: сначала выбрасываются стратегии L, затем Я. Таким образом, (УИ, УИ) является (единственным1)) NЕ-исходом как самой игры, так и ее смешанного расширения.
Эта игра также имеет единственное равновесие в совместных смешанных стратегиях, которое реализуется на лотерее, выбирающей (М, М) с вероятностью 1 (для проверки этого утверждения заметьте, что С?-лотерея приписывает нулевой вес любой строго доминируемой стратегии, и затем примените это замечание дважды).
Тем не менее оптимальный по Парето выигрыш (2, 2) может быть получен в результате следующего соглашения. Построим лотерею с вероятностным распределением
L = 7Г ®(Н. L) + у 6(L, Я)-
Каждый игрок независимо и тайно выбирает и посылает нейтральному арбитру, который выбран обоими игроками, обязательный сигнал s;, принимающий одно из четырех значений для каждого игрока: три чистых стратегии и сигнал ОВ (согласно лотерее). Получив пару сообщений (s1( s2), арбитр определяет случайный исход (хх, х2) в соответствии с лотереей L. Финальный исход игры определяется по следующему правилу (за этим следит арбитр):
(хи х2), если sx = s2 = OB,
(xlt s2), если s1 = OB, s2 L, M, Я,
1 (si хг)г если si = ^ M, H, s2 = OB,
(sj, s2), если si L, M, H, i 1, 2.
Другими словами, сообщение OB является обязательством применять стратегию, выпавшую по лотерее, причем это обязательство принимается до проведения лотереи.
- ! Без рубрики
- Мулен Э. - Теория игр
- ОСТОРОЖНЫЕ И ОПТИМАЛЬНЫЕ СТРАТЕГИИ
- СЛОЖНОЕ ПОВЕДЕНИЕ
- ПОВЕДЕНИЕ ЛИДЕРА И ВЕДОМОГО
- РАВНОВЕСИЕ ПО НЭШУ
- ТЕОРЕМА НЭША О СУЩЕСТВОВАНИИ РАВНОВЕСИЙ
- СМЕШАННЫЕ СТРАТЕГИИ
- ВЫЧИСЛЕНИЕ РАВНОВЕСИЙ ПО НЭШУ В СМЕШАННЫХ СТРАТЕГИЯХ
- БЕСКОНЕЧНЫЕ ИГРЫ
- РАВНОВЕСИЕ В СОВМЕСТНЫХ СМЕШАННЫХ СТРАТЕГИЯХ
- СТАБИЛЬНОСТЬ НА ОСНОВЕ УГРОЗ
- ПОВТОРЯЮЩИЕСЯ ИГРЫ
- КЛАССИФИКАЦИЯ ИГР ДВУХ ЛИЦ
- Теория игр в нормальной форме
СЛОЖНОЕ ПОВЕДЕНИЕ
Каждый стреляет оптимально, когда і (/) + а2(0= 1.Упражнение 2
Обобщите теоремы 2 и 3 для класса квазиантагонистических игр1) двух лиц (Хь Х2, ии и2), которые определяются следующим образом:
любой исход игры оптимален по Парето, т. е.
Ух, г/€Х,хХ2: [ых (х)и, (у)] ФФ [и2 (/) и2 (х)].
Упражнение 3. Бесшумная дуэль
В этом варианте приведенной выше игры выстрел игрока не слышен для его противника и тот узнает о нем, лишь если он его поражает.
1) Докажите, что соответствующая функция выигрыша имеет вид (Х1 = Х2 = [0, 1]):
если хх х2, если х1 = х2, если х2 xt.
Ч (*і)а2(х2) + аг (xt)-a2 (х2),
(хХ) х2)
1 (%і) ^2
(АГі)а. (х2) о, (хд’й2 (xt),
2) Предположим, что функция аха2 -\-а1-а2 монотонно возрастает по t, a ata2at-a2 монотонно убывает.
Сосчитайте гарантированные выигрыши обоих игроков и докажите, что они не совпадают. Более точно, если ?цена шумной дуэли (пример 7), то докажите, что
sup inf их u inf sup щ.
Х\ Xs Х2 Хі
Упражнение 4
Пусть (Хі, Х„ и,) симметричная игра двух лиц с нулевой суммой, т. е. Хі = Х2; иДхх-, х2)= щ(х2, х4) для всех xit х2. Докажите, что ее цена (если таковая имеется) равна нулю, а множества оптимальных стратегий совпадают.
Задача 6 (Мулен [1976])
Для любых действительных чисел a, b, с, d следующая игра двух лиц с нулевой суммой, в которой у каждого игрока четыре стратегии, имеет цену. Матрица выигрышей для игрока,
!) В отечественной литературе принят термин: игры с противоположными интересами. Прим, перед.
выбирающего строки, имеет вид
b
с
a + ft+e+d 4и a-\rb-{-c-\rd4
Более того, цена val (G) игры G удовлетворяет неравенствам sup {inf (а, b), inf (с, d)} val (G) inf {sup (а, в), sup(b, d)}.
Дайте интерпретацию.
Задача 7 (Шепли)
Пусть G = (Xx, Х2, щ) конечная игра двух лиц о нулевой суммой. Предположим, что для каждого двухэлементного подмножества Y( множества Х(, і= 1, 2, игра (Yt, Y2, щ) имеет цену.
Докажите, что в этом случае игра G также имеет цену.
Задача 8
Пусть (X,, Х2, () игра двух лиц с нулевой суммой. Обозначим через ftj = X* (соответственно R2 = Xf') множество стратегийответов первого игрока (соответственно второго игрока). Докажите следующие равенства:
sup inf Ui(xit х2) = inf sup щ(хи ГД*!)),
*,6Х, xseX, 'teRtxteX,
inf sup Щ (Xf, X2) = sup inf Uf (Гі (x2), x2).
x2€X2x,eX, i.,ex,
Каковы оптимальные стратегии в игре (Rf, Х2, и(), где Щ (гі, xt) = щ (г, (х2), *2)?
2) Предположим, что ХІ( Х3выпуклые компакты. Обозначим через RiczRi (соответственно R2czR2) множество непрерывных функций из Х2 в X, (соответственно из X, в Х2).
Докажите следующие неравенства:
SUp inf Uf ^ SUp inf Uf (rt (xs), xj ^
*t хг r, e R\ x*
inf sup Uf (Xf, r2 (Xf)) inf sup Щ
r,e Rc x *1
(используйте теорему Брауэра: непрерывное отображение выпуклого компакта в себя имеет по крайней мере одну неподвижную точку).
3) Приведите пример, в котгором Х, = Х2 = [0, 1], uf непрерывна и тем не менее
sup inf Ы( = sup inf і inf sup щ inf sup щ.
x, x% rse xi x‘ x
ЛИТЕІРАТУРА
Грин, Лафон (Green J., Laffont J. J.)
[1979] Incentives in public decision making. Studies in public economics, vol.
1, Amsterdam, North-Hollland Publishing Co.
Keih (Case J. H.)
[1979] Economics and the competitive process. New York, University Press.
Льюс, Райфа (Luce R. D., Raiffa H;.)
[1957] Games and decisions, New York,, J. Wiley. [Имеется перевод: Льюс P. Д., Райфа X. Игры и решения.. М.: ИЛ, 1961.]
Мулен (Moulin Н.)
[1976] Prolongement des jeux a deux joueurs de somme nulle. Paris, Bulletin de la Societe Mathematiquie de France, Suppl.
Memoire 45.
[1980] On strategy-proofness and siingle peakedness. Public Choice, 35, 437455.
[1981] Prudence versus sophistication in voting strategies. Journal of Economic Theory, 24, 3, 398412.
СЛОЖНОЕ ПОВЕДЕНИЕ
Осторожное поведение игроков основано на предположении об их полной изолированности, согласно которому каждый игрок ориентируется только на свою собственную функцию выигрыша и не обращает внимания на функции выигрыша остальных игроков. В этой главе исследуем, напротив, случай полной информированности, когда каждый игрок знает все функции выигрыша.При некооперативном поведении игроков это порождает взаимные стратегические ожидания следующего вида: игрок і ожидает, что все другие игроки / исключат свои доминируемые стратегии.
На основе этого ожидания, возможного благодаря полной информированности, у некоторых игроков могут возникнуть новые доминируемые стратегии и т. д.
Сложное поведение будет определено сначала для игр в нормальной форме (разд. 1), затем эквивалентным образом для игр в развернутой форме (разд. 2).
В разделах 3, 4 и 5 демонстри-руются некоторые приложения теоремы Куна.
1. ПОСЛЕДОВАТЕЛЬНОЕ ИСКЛЮЧЕНИЕ ДОМИНИРУЕМЫХ СТРАТЕГИЙ
Пример 1. Выборы большинством голосов с решающим игроком при равном числе голосов (Фаркуареон [1969]).
Сообщество 11, 2, 3} должно выбрать одного из трех кандидатов {а, b, с}. Правило голосования есть правило большинства, при этом голос игрока 1 оказывает решающее влияние при равенстве голосов. Другими словами, множество стратегий (множество предложений) имеет вид Х,= {а, Ь, с} для і =1, 2, 3. Если игроки выдвинули кандидатуры {хи х2, х8}, то выборы происходят по правилу

Предположим, что функции выигрыша игроков при избрании того или иного кандидата имеют следующую структуру (парадокс Кондорсе1)):
Щ (с) щ (Ь) (а),
и2 ф) 2 (а) и2 (с),
з (а) з (с) а Ф).
В игре трех лиц в нормальной форме (Xf, Х2, Х8, щоп, и2ощ ияоп) каждый игрок имеет единственную лексикографически осторожную стратегию (см. задачу 5 гл. I), а именно голосовать за наиболее предпочтительного для себя кандидата.
Следовательно, лексикографически осторожное поведение приведет к избранию кандидата а. При условии полной информированности ситуация будет совершенно другой. Заметим, что стратегия х2 = Ь игрока 2 доминируется (стратегией х\ с) и что стратегии а и с не доминируемые, но и не эквивалентные;
и2ол ф, а, с) = и2 ф) и2 (с) = игоп ф, с, с), и2ол ф, а, а) = и% (а) и2 ф) = и2ол ф, с, а).
Значит, й)2(и2) = {а, с}, и аналогично ?Ds(ua) = {b, с}. С другой стороны, игрок 1, чей голос разрешает спорные ситуации, имеет доминирующую стратегию, а именно а (проверку этого факта оставляем читателю). Таким образом, если считать, что игроки не будут использовать доминируемые стратегии, то множества стратегий сузятся до
Уі = Iй} n = k с), Yt = {b,c}.
При данном усечении множеств стратегий для игрока 2 стратегия а теперь доминируется стратегией с и поэтому может быть исключена:
и2ол (а, а, х3) ы2ол (а, с, х9)
для xa = b, с, и неравенство становится строгим при хя = с.
Аналогично стратегия b игрока 3 теперь доминируется стратегией с:
и3оп(а, х2, b)^.uaon(a, х2, с)
для х2 = а, с, неравенство становится строгим при х2 с.
Следовательно, после двух раундов исключения доминируемых стратегий у каждого игрока останется по одной стратегии и кандидат с будет избран, несмотря на то что он является наихудшим для игрока 1! Следовательно, право первого игрока
!) Классический пример того, что для большинства членов сообщества исход а лучше исхода b, Ь лучше с и с лучше а,Прим, перев.
разрешать спорные ситуации оказывается его слабым пунктом в игре, потому что оно дает возможность сразу предвидеть его стратегический выбор.
Определение 1. Для игры в нормальной форме G = = (Хг, мг; і € N) последовательное исключение доминируемых стратегий означает построение последовательностей X,- = = X^XJz)... zX-zX(+tz... для всех i g N, где Х(+1 = = Ч i?N).
Скажем, что игра G разрешима по доминированию, если существует целое t, такое, что для всех і функция выигрыша и,- не зависит от xt на X‘N:
Уі g X\, VxtZX't Ui(xit xt) = ut(yh xt). (1)
В этом случае назовем Ху множеством сложных равновесий в игре G.
Ясно, что если (1) выполнится для некоторого t (и некоторого tgX), то Х = Х-+1=..., поэтому если игра разрешима по доминированию, то выбор конкретного t не изменит множества X‘N. Следовательно, множество сложных равновесий определено корректно. Для того чтобы получить стратегию, соответствующую сложному равновесию, каждый игрок і должен найти последовательности X), t ? N для всех / ? N, полностью 'использовав таким образом знание функций выигрыша. Эти вычисления производятся независимо каждым игроком в предположении, что остальные игроки делают то оюе самое.
Только в этом ограниченном смысле сложное поведение может быть названо изолированным.
Разрешимость по доминированию игры G, означает, что после конечного числа раундов исключений все стратегии каждого игрока станут для него эквивалентными (ионе для других. См. пример 3, гл.
I). Если функции выигрыша для всех игроков взаимно однозначны на XN, то множество сложных равновесий (если оно существует) состоит из одного элемента.
Следовательно, в таких разрешимых по доминированию играх сложное поведение игроков детерминированно.
Сложное равновесие обобщает равновесие в доминирующих стратегиях в следующем смысле.
Лемма 1. Если в игре G множество D равновьсий в доминирующих стратегиях не пусто, то игра G разрешима по доминированию и D есть множество сложных равными
Доказательство сразу следует из леммы 2, г-л і Если только у одного игрока I есть доминирующ351 стратегия, то, очевидно, D{ (,¦) является і-й компонентой множест.ва сложных равновесий, если последнее существует.
Для игры в нормальной форме не известны достаточные условия разрешимости по доминированию. Для того чтобы получить такие условия, необходимо использовать другое представление игры, а именно развернутую форму.
2. ИГРЫ В РАЗВЕРНУТОЙ ФОРМЕ И ТЕОРЕМА КУНА
Пример 2. Выборы с правом вето
Пусть сообщество N = {1, 2, 3} выбирает одного кандидата из множества А = {а, Ь, с, d}. Правило голосования таково: начиная с игрока 1, каждый игрок последовательно налагает вето на выбор кандидатуры одного из неотведенных кандидатов.
Единственный оставшийся кандидат считается избранным.
Пусть заданы функции выигрыша игроков ии 2, us на множестве А. Возникшая ситуация описывается игрой в нормальной форме:
Множество Хі А\ стратегия игрока 1 состоит в объявлении кандидата, на избрание которого он первым накладывает вето.
Множество Хг состоит из отображений хг из А в А, таких, что х2(а)фа для всех а$А. Стратегия х2 означает, что если игрок 1 уже наложил вето на кандидата а, то игрок 2 после этого накладывает вето на кандидата х2 (а).
Множество Х3 состоит из отображений х3, которые определяют для пары (а, Р), уже отведенных кандидатов, кандидата х3 (а, Р) € Л\{а, РЬ которого отводит игрок 3.
Исход, соответствующий данной тройке (% х2, ха) ? €ХйхХ2 X Х3, определяется так:
Я (Xj, Х2, Х3) = Х2 (Х(), Хд (Х{, Х2 (Xj)).
Нормальная форма игры представима в следующем виде: (Xj, Х2, Ха, ихол, 2ол, ЦдОя). Язык теории графов более удобен; на рис. 1 изображена развернутая форма игры;
Каждой нефинальной вершине этого дерева игры соответст-вуетг некоторый игрок, имеющий право выбирать любую из следующих вершин. Каждая финальная вершина определяет избранного кандидата. Предположим теперь, что функции вц-
игрыша удовлетворяют следующему условию:і (d) щ (с) и, ф) щ (а),
2 Ф) 2 (Ф 2 Ф) 2 (). (2)
з Ф) з И з Ф) 3 ($-
Вначале заметим, что игрок 3 имеет доминирующую стратегию: он отводит менее предпочтительного для себя кандидата из двух еще оставшихся в списке.
Это определяет единственный элемент xf из Х3. Далее отметим, что ни у первого, ни у второго игрока нет доминирующей стратегии.
В самом деле, во множестве Xf ни одна стратегия не доминируется, поэтому (щ) Хі. Для того чтобы проверить это, докажем, например, что стратегия первого игрокаотвести наилучшего для него кандидата ане является доминируемой. Рассмотрим следующие стратегии х2 ? Х2, х3 ? Х2:¦^2 Ф) ^3 Ф* d) ==
- . . , - . . [ Ь, если а, Фа, Ь,
*.( ) = а Для всех а фа, хі (а, а) = і ^ ^ а = {
Тогда иіо%(а, хг, х3) = ф) игоп (а, хг, хя) при а Фа, т. е. xt = aнедоминируемая стратегия игрока 1.
Аналогично можно проверить, что игрок 2 имеет 24 недо минируемых стратегий среди З4 элементов множества Х2: стратегия х2 принадлежит множеству (м2) тогда и только тогда, когда для всех хх € Хі кандидат х2 (хг) не является наилучшим Р9 функции ц, среди кандидатов из множества АХ^}.
Второй раунд исключения доминируемых стратегий позволяет игроку 1 с пользой распорядиться имеющейся у него информацией. А именно, если игрок 1 будет сугубо осторожен и наложит вето на наихудшего для него кандидата d (Р2 (их) = {d}), то произойдет избрание кандидата b (поскольку функции выигрыша игроков 2 и 3 на исходах а, Ь, с определяют один и тот же порядок, то b будет избран при любой паре недоминируемых стратегий: b = n({d}x2(u2)x{x%})).
Однако игрок 1 может надеяться на лучший исход, чем избрание Ь. В самом деле, если на b наложить вето, то для игроков 2 и 3 возникнет следующая игровая ситуация.

Если игрок 2 не обращает внимания на функцию выигрыша игрока 3, он при осторожном поведении наложит вето на с (Р2 (и2) = {х2}, где для всех хх кандидат х2 (лу) является наихудшим по и2 среди ЛХІлу}), тем самым навязывая избрание d, что означает полное поражение игрока 1. Если, напротив, игрок 2 достаточно хорошо информирован, то он имеет возможность предвидеть поведение игрока 3, и в этом случае оптимальным является вето на d, обеспечивающее избрание а.
Возвращаясь к последовательному исключению доминируемых стратегий, мы обнаруживаем, что после двух раундов исключения стратегий игроки 2 и 3 имеют полностью определенные стратегии (xl = {x*}, х = {*?}), а после трех раундов игрок 1 также остается с единственной стратегией, таким образом исход игры при сложном поведении есть избрание кандидата а.
Определение 2. Конечное дерево есть пара Г = (М, о), где Мконечное множество вершин, а а сопоставляет каждой вершине ее ближайшего предшественника, причем:
- Существует единственная вершина т0, такая, что о (m0)=m0. Назовем ее начальной вершиной.
- Существует целое I, такое, что о1 (т) = т0 для всех т$М, Наименьшее такое I назовем длиной дерева Г.
Вершина т, для которой о_1(т) = 0, называется финальной вершиной Г, а множество таких вершин обозначается через
Т (Г). Для нефинальных вершин пг множество о'1 (пг) состоит из преемников пг, т. е. из следующих за m вершин.
Определение 3. Пусть N заданное конечное сообщество. Игрой в развернутой форме со множеством игроков N называется следующая совокупность:
- Конечное дерево Г = (УИ, а).
- Разбиение (М,-),-6д/ множества М\Т (М).
- Для каждого игрока і ? N функция выигрыша и,- из Т{М) в R.
Разбиение (Mfo € n определяет, какой игрок ходит в каждой конкретной нефинальной вершине. Если m0?Mh то игра начинается с того, что игрок і должен выбрать преемника т0, т. е. следующую за т0 вершину, скажем вершину тх из а-1 (т0).
Если тг?Т (М)финальная вершина, то игра окончена и выигрыши игроков суть иД/Пх) при igiV. Если m1(j:T (М) нефинальная вершина, то игрок /, для которого mx € М/, имеет право хода и выбирает следующую за т1 вершину, скажем ma€~l(mi) и т- Д-
Отмеченные вершины являются финальными. Заметьте, что по нашему предположению на каждом шаге игры игрок, делающий ход, имеет полную информацию о текущей вершине и общей структуре игры: это предположение обычно характеризуется как полная информация.
Теорема Куна утверждает, что конечная игра в развернутой форме в общем случае разрешима по доминированию и что в ней легко может быть вычислен исход сложного равновесия. Для того чтобы это продемонстрировать, рассмотрим описанную выше игру: выборы с правом вето (пример 2, рис.
1). Поскольку во всех вершинах, предшествуюш.их финальным, ходит игрок 3, то остальные игроки, зная его функцию выигрыша из (2), могут предвидеть его поведение.
Это позволяет редуцировать игру, изображенную на рис. 1, к следующей:
Поскольку в этом новом дереве во всех вершинах, предшествующих финальным, ходит игрок 2, то игрок 1 может предвидеть результат этих ходов по функции и2, и в итоге получается игра с одним участником первым игроком.
Предлагая отклонить кандидата Ь, игрок 1 реализует стратегию, являющуюся компонентой сложного равновесия.
Приведенная выше попятная процедура может быть обобщена для любой игры в развернутой форме при довольно слабом предположении о взаимной однозначности.
Определение 4. Пусть G = (M, a; M-t, up i?N) игра в развернутой форме, такая, чю для любых т, т' ?Т (М) имеем
[Эі € N Ui (m) = и,- (/n')]=? [V/ € N u,(m) = u/ (m')]. (3)
Пусть L(M) множество вершин, для которых все последующие вершины являются финальными:
m?L (М) (т)аТ (М).
Тогда игре G соответств/ет редуцированная игра G* =s = (M*t о*; Mf, up, i g N), в шторой
- множество вершин определяется равенством М* = =М\Г0(М), где T0(M) = {nitT(M)\e(tn)?L(M)};
- отображение о* есть сужение а на М*\
- финальные вершины дерева (М?, о*) таковы:
T(M*)^L(M)U{T(M)\T0{M)}-
- М* = Mt П { M* \ T (M*)}, значит, (Mf)t е N разбиение М*\Т (М?);
- функция выигрыша и? имеет вид
если пг?Т (М)\Т0 (М), то и? (т) = щ (т),
если m ? L (Af) и mg МЛ то uf (т) иг (mj), где тj оптимальная для игрока / следующая за m вершина; U/(tn,)= sup и,(т').
m'ea-1 (m)
Лемма 2. Если {М, о)дерево длины I, то дерево (М*, а*) имеет длину (I1).
Доказательство леммы 2. Заметим сначала, что множество L (М) не пусто. Если оно пусто, то для каждой нефинальной вершины т множество о-1 (т) содержит хотя бы одну нефинальную вершину, и поэтому мы можем построить бесконечную последовательность различных вершин т0, Ші, .... mt, ..., где mt+i €-1 (Щ)\ это противоречит тому, что длина дерева (М, о) конечна. Выберем далее вершину т, такую, что
о1 (т) = т0, о1~х (т) Ф т0. (4)
Такая вершина существует по определению I. Предположим, что a(m)^L(M). Тогда найдется вершина т'?М\Т(М), такая, что a(m’) = a(m). Выбирая любую вершину m" go-1 (m'), получим о2 (т) = а (т), следовательно, о‘ \т) = а1-1 (т) Ф та.
Получили противоречие. Итак, мы доказали, что a(m)^L(M). Ввиду того что вершина т является финальной, приходим к заключению, что т?Т0(М). Поэтому никакая вершина, удовлетворяющая (4), не может входить в М* и, следовательно, дерево (М*, о*) имеет длину, не превышающую (/1).
Легко показать, что (М*, о*) имеет длину в точности (I1).
Алгоритм Куна состоит из последовательных редукций игры G. После этих / редукций дерево игры (М*1, о*1) имеет длину 0, т. е.'М*1 = {тб), а о*1тождественное отображение. Обозначим через 0(. uf1 (та) (единственное) значение выигрыша игрока і в G*1.
Теорема 1 (Кун). Пусть G = (M, о; МІУ ы;; і ? Ы)игра в развернутой форме, для которой выполнено условие (3). Тогда
игра G, рассматриваемая как игра в нормальной форме, разрешима по доминированию, а выигрыши N, соответствующие сложному равновесию, задаются алгоритмом Куна.
Доказательство. Вначале уточним, что мы понимаем под нормальной формой игры G. Поскольку игрок і должен принять стратегическое решение в каждой вершине множества Mt, то Стратегией х{ будет отображение из Mt в М, причем такое, что
хДт) €т-1 (т) для всех т?М{.
Пусть Х{ множество таких отображений. Заданный набор х(х,)і6л/ порождает партию т0, ..., тк, где
- тв€М1,^ті = Хі'(т0)
- m1^T(M)=^k l
- m1 € Mit =om2 = xtl (mf)
- mt?T (M) = k t
- mt€Mit=$mt+i = xit(mt), и соответствующие выигрыши задаются равенством ui(x)=U;(mk). Мы должны доказать, что игра (Х(, up, i g N) разрешима по доминированию и выигрыши игроков в сложном равновесии определяются алгоритмом Куна. Редукция игры G к игре G* (определение 4) позволяет выкинуть все вершины из Т0(М), превращая вершины из L(M) в финальные и приписывая вершине m из L (М) П Mt вектор выигрышей, который соответствовал'бы оптимальному ходу игрока і в вершине т. Далее, пусть А[ обозначает следующее подмножество множества Хр
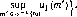
Тогда игра в нормальной форме (А{, up i?N) изоморфна редуцированной игре G* (заметим, что если игрок і безразличен по отношению к двум каким-либо следующим за m € L (М) П М, вершинам, то в силу (3) и все остальные игроки безразличны к выбору из этих вершин, а потому соответствующие стратегии во множестве А{ могут быть отождествлены). Заметим теперь, что стратегия х(-?Х;\Л; является доминируемой стратегией игрока і (в самом деле, xt доминируется стратегией у{ € А{, совпадающей с х, на множестве Mt \ L (М)). Итак, мы имеем
?D{ (u^aAiCzXj.
Теперь мы используем следующую основную лемму,
Лемма 3 (Роше [1980]). Пусть G = (X{, up i?N) конечная игра в нормальной форме, причем для любых двух исходов х, х' ? X выполнено
[i i?N u-t (х) = ut (*')]= [V/ g N /(*) = ,(*')]- (6)
Пусть далее для всех і ? N множество Л, является подмножеством X;, удовлетворяющим условию (5).
Тогда игра G разрешима по доминированию (d-разрешима) в том и только в том случае, если игра Н = (Л;, up, i?N) разрешима по доминированию, а векторы выигрышей, соответствующие сложным равновесиям, совпадают.
Применяя индуктивно лемму 3, получаем G d-разрешима фф G? d-разрешима фф G** d-разрешима ФФ.. и все эти игры имеют одни и те же векторы выигрышей в сложных равновесиях. Поскольку игра G*1, очевидно, d-разрешима и ей соответствуют равновесные выигрыши (РДел/. теорема 1 полностью доказана.
Лемма 3достаточно важный результат: в процессе последовательного исключения доминируемых стратегий некоторые игроки могут оказаться ленивыми и не исключить всех своих доминируемых стратегий или исключение может производиться последовательно (сначала игрок 1 исключит доминируемые стратегии, потом игрок 2 и т. д.), тем не менее разрешимость по доминированию сохранится, а вектор выигрышей в сложных равновесиях не изменится. Этот результат существенно повышает доверие к понятию сложного поведения.
Упражнение 1
Приведите пример игры в развернутой форме, для которой не выполнено предположение (3) об однозначности и соответствующая игра в нормальной форме не разрешима по доминированию.
Задача 1. Доказательство леммы 3 (Гретлейн [1980], Роще [1980])
Пусть игра G = (X{, up, igN)фиксированная конечная игра в нормальной форме с условием (6) и для игры Н = (Л;, up і € N) выполнено условие (5).
Положим XX, = XN), ЛХ= X ?D(u{, AN).
IS N i6 N
1) Если стратегии х{ и у{ игрока і эквивалентны для игрока і в игре G, то в силу (6) получаем
?/€ W, V*,gXf uj {xh xt) = uJ{yi, Xf),
Выведите отсюда, что если отождествить эквивалентные стратегии каждого игрока в игре G, то это не повлияет на d-разре-шимость игры.
2) Отождествляя соответствующим образом стратегии игроков, эквивалентные в игре Я, и используя условие (5), покажите, что
AfcX'icA;, i?N.
3) Завершите доказательство леммы 3, последовательно применяя при построении множеств AlN и X‘N утверждения п. 1 и 2.
3. ИГРЫ ДВУХ ЛИЦ С НУЛЕВОЙ СУММОЙ
Вначале докажем вспомогательный результат.
Лемма 4. Пусть G = (Xit Х2; Uj)игра двух лиц с нулевой Суммой и конечными множествами стратегий. Тогда сложное равновесие в игре G есть седловая точка по функции щ. Следовательно, разрешимые по доминированию игры двух лиц q нулевой суммой имеют цену.
Доказательство. Для данных подмножеств УіСгХ^ У2сгХ2 обозначим через S (Уь У2) множество седловых точек (возможно пустое) в игре (Уь У2, ut). Далее положим
Zi = Si(ui\ Yu У2).
Пусть (xit х2)седловая точка в игре (ZL, Z2, и,), и предположим, что (*1, х2) не является седловой точкой в игре (Уі, У2, щ).
СМЕШАННЫЕ СТРАТЕГИИ
В неравенствах из (13) просто сравниваются модули наклонов касательных к кривым BRt и BR2 в точке х*. Положимs. = д2ы,- /¦ дЧ(
' дх; дХі I дх; дх? ‘
Тогда неравенства (13) можно переписать в следующем виде:
I sj I I s21 = х* локально устойчива,
Sj ) s21 = лг*' не является локально устойчивой.
Для случая б) примера 5 получается неустойчивое равновесие по Нэшу, поскольку I Sj I I s, , причем sx- и s2 одного
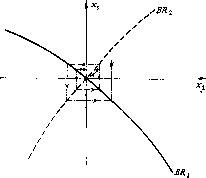
знака. Если s21 и sf, s2 положительны, то получаемобычную нестабильность типа паутины, изображенную на рис. 7.
Если, напротив, Sjs2, то может быть показано, что локально устойчивое равновесие по Нэшу х* является единственным сложным равновесием для усеченной на достаточно малую прямоугольную окрестность х* начальной игры. Проиллюстрируем этот факт на следующем рисунке.
Начинаем с игры ([a*, f)1], [a2, b2], uit u2), выбрав числа a,-, bi так, чтобы ut была вогнута по х{ на [а*, Ь^х[а2хЬ2]. Затем замечаем, что при любом фиксированном х2%[а2, Ь2] выигрыш і (- , х2) возрастает на отрезке от at до гх (х2), затем убывает на [Гі (х2), 6,]. Поскольку rt (x2) ? [cj, df] для всех х2€[а2, Ь2], то отсюда следует, что любая стратегия хг ? [al, cf] игрока 1 доминируется его стратегией си в то время как любая стратегия xf € (df, Ь±] доминируется стратегией d,.
Отбрасывая доминируемые стратегии игрока 1, получаем игру ([cj, dj, [а2, b2], и? и2), в которой в силу аналогичных рассуждений множество недоминируемых стратегий игрока 2отрезок [с2, d2]. Таким образом, получается редуцированная игра ([с4, dj], [с„ d2], ult и2). Если продолжить итеративно эту операцию, то
станет ясно, что множества стратегий стягиваются к устойчивому NE-исходу х, как это видно из рис. 8.
Связь между локальной устойчивостью и локальной разрешимостью по доминированию на самом деле является весьма общей. Скажем, что игра G локально разрешима по доминированию в х?, если существует прямоугольная окрестность Кд, точки х?, такая, что усечение игры G на Кд, обладает следующим свойством: последовательное исключение доминируемых стратегий стягивает Кд, в пределе к х. Тогда в предположении теоремы 3 в работе Габе, Мулен [1980] доказано, что а) Если все собственные числа оператора Т по модулю меньше 1, то игра G локально разрешима по доминированию в х.)
б) Если игра G локально разрешима по доминированию в х*, то абсолютная величина любого собственного числа оператора Т не превосходит I.
Замечание. На рис. 8 мы исключаем доминируемые стратегии последовательно сначала у одного игрока, потом у другого.
По лемме 3 гл. II (обобщенной на данный случай) получается в точности то же самое, что и при одновременном исключении.
Как мы видели в упр. 6, для процедуры нащупывания по Курно это не так.
Упражнение 7.
Для игры трех лиц, в которой множества стратегий всех игроков одномерны, приведите почти совпадающие необходимые и достаточные условия локальной {1, 2, 3}-устойчивости, аналогичные условиям теоремы 3.
Упражнение 8.
В детерминированном варианте войны на истощение (пункт 1 задачи 5) вычислите множества наилучших ответов BR; (в данном случае они не являются кривыми размерности 1) и проанализируйте устойчивость процедуры нащупывания по Курно. Обратите особое внимание на процедуру нащупывания, начинающуюся из (0, 0), и дайте интерпретацию этой процедуре как схеме эскалации.
Далее рассмотрите вариант войны на истощение, в котором каждый игрок не может обнаружить агрессивность противника: стратегия х,- игрока і означает, что игрок і решает раз и навсегда быть агрессивным до момента / = х;. Тогда получаем игру в нормальной форме:
*X
Л._у 2 х*
xz) =
при х3 хь при X, х„
при xt = xt.
Функция и2 определяется аналогично.
Докажите, что в этой игре нет Л^Д-исходов и проанализируйте процедуру нащупывания по Курно. Сравните с игрой Война на истощение.
Задача 5. Устойчивость в олигополии с назначением выпусков
Обобщим пример 4 за счет введения функции затрат с,- (у) на производство у единиц товара производителем і. Тогда возникает игра
Х,. = [0, +оо), иі(х) = хір (х)сі(хі), і ? N.
На функцию р наложим ограничения (7). О функциях с{ мы просто предположим 0.
Значит, затраты на выпуск единицы продукции могут быть возрастающей, убывающей или вообще немонотонной функцией величины у.
Пусть у каждого игрока затраты на выпуск единицы продукции возрастают или не слишком сильно убывают в следующем смысле:
с1(у)2р' (у) + у-р (у) при г/5? 0, і'=1, .... п. (14)
Покажите, что существует по крайней мере один NE-исход.
2) С этого момента предположим существование NE-исхода х?, не требуя обязательного выполнения (14).
Докажите, что исход х* локально устойчив, если выполнены следующие неравенства:
с] (xf) (ft3) I р' (х*) I + (п2) I р (х*) I-xf.
Указание. Полагая
Р'(**)+Р (**)- **
Рі V (**) + р (х*) ¦ xf с\ (xf) ’
докажите, что 0р,-1 при всех t = 1, ..., п (принимая во внимание, что п^ 2). Далее заметьте, что собственное число X оператора Т либо равно р,- для некоторого і = 1, .п, либо является решением уравнения
РІ I I Рп _ I
%-\-Pi Х-\-рп
3) Пусть все игроки идентичны (с{ = с для всех і = 1, п) и х*равновесие по Нэшу на диагонали: xf = xf = г/*. Докажите утверждение, обратное сформулированному в п. 2. Если выполнены неравенства
2р' + у*.р с (п3)р’\ + (п2)¦/*- !р\
(где все р' и р взяты при х* пу*, а с взята в /?), то дг* не является устойчивым NE-исходом. Заметьте, что для NE-исхода г* выполнено неравенство 2р' + у*р с, поскольку функция ut от аргумента х( достигает максимума в точке х*.
Следовательно, устойчивость исхода х? всегда имеет место для п = 2 и требует выполнения все более жестких условий с ростом п.
Задача 6
1) Докажите, что в игре агентов по продаже автомобилей (задача 2) нулевой NE-исход не устойчив.
2) Для ненулевого N ^-исхода докажите, что оператор, опре-деленный по формуле (11), всегда имеет собственное число, равное 1. Используя ту же технику, что и в задаче 5, докажите, что этот исход не является локально устойчивым, если по крайней мере для двух агентов выполнено неравенство
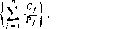
3) В случае п = 2 докажите непосредственно (т. е. найдя BRt и BR2 и нанеся их на рисунок), что ненулевой і?Д-исход устойчив. Аналогично проанализируйте устойчивость Л^Д-исхода в дуополии с назначением выпусков из упражнения 4.
Задача 7. Процедура нащупывания по Курно в непрерывном времени (Мулен [1977])
Пусть G = (л,-, up, і ? N) игра п лиц, в которой каждое множество стратегий одномерно. Пусть рдействительная функция, определенная на R, причем
Ф (0) = 0, ф' (/) 0 при t € R.
Допустим, что функция и{ дважды непрерывно дифференцируема на XN при всех і € Рассмотрим следующее дифференциальное уравнение на XN: dx1
= Ф (ri (xi)X/) для всех i 6 N. (15)
^?устойчивое решение (15) (т. е. найдется окрестность V точки л-*, такая, что система (15) с начальным условием из V порождает траекторию, которая не покидает V и сходится к х?). Докажите, в частности, что если х?локально устойчивый ЛХЕ-исход (определение 3), то он является устойчивым решением (15).
Приведите пример, показывающий, что обратное утверждение не верно.
Задача 8. Локальная дилемма заключенного (Мулен [1979]) 1) Фиксируем пх/г-матрицу Л = /=1.....„ и предполо
жим, что аиФ 0 при всех 7=1, ..., п. Для данных Xt 0, ... Х„ О обозначим через G (Л; X) игру (У, (X,.), и,; і = 1, ..., п), где [hI ^/] Для всех 7=1, п,
В игре G (Л; X) каждый игрок имеет единственную доминирующую стратегию. Обозначим через х (X) ? Yn (X) равновесие в доминирующих стратегиях. Докажите, что следующие четыре утверждения эквивалентны:
1) Для всех К 0 исход х (X) не является оптимальным по Парето в G (Л; X).
2) Для некоторого X 0 исход х (к) не является оптимальным по Парето в G (Л; X).
3) Существует вектор xglR, такой, что
Щ (хі'еі) 01 ,
,*)о; длявсех‘-.......
где в, = (0, О, 1^, 0, .... 0)€RB.
Т
4) Не существует таких р, q ^ 0 (pt, q{ ^ 0 н не равны нулю одновременно), что
П
2 Pfiij = Цфц для всех /= 1, .... п.
Когда все эти условия выполнены, скажем, что линейные платежи А индуцируют дилемму заключенного.
2) Рассмотрим теперь игру в нормальной форме G = (Xh ut; i 1, .... п), где Х[открытые интервалы на действительной прямой, а щнепрерывно дифференцируемая функция, задан*
ная на XN. Пусть дан исход x?XN, такой, что Ф0 для всех і = І, ..п.
Скажем, что игра G имеет локальную дилемму заключенного в точке х, если матрица индуцирует дилемму за-
ключенного. Дайте интерпретацию этому определению на основе результатов первой части задачи.
В олигополии с назначением выпусков из примера 4 найдите исходы, в которых возникает локальная дилемма заключенного.
3) В дополнение к предположениям п, 2 будем считать, что п = 2. Докажите, что игра G обладает локальной дилеммой заключенного в х тогда и только тогда, когда справедлива следующая система неравенств:
(16)
= 2},
дщ_ дщ_ \ п дх2 дхг ) ^ ’
где все производные берутся в точке х.
Докажите, что в случае общего положения любая окрестность NE-исхода или исхода, оптимального по Парето, пересекается с областью (16) (дайте точное определение общего положения).
Изобразив графически область (16) для двух моделей олигополии из примера 5, докажите, что область (16) лежит между І?і:-исходами и границей Парето. До какой степени эта конфигурация является общей? Как условие (16) обобщается на случай п 3? Для произвольного целого п?
СМЕШАННЫЕ СТРАТЕГИИ
В некоторых играх в нормальной форме, хотя каждый игрок может выбирать по желанию любой элемент из своего множества стратегий, тем не менее рациональное поведение заключается в добровольной рандомизации собственного выбора. Это порождает известную неопределенность в выборе стратегии игрока и вызывает реакцию остальных, которая может оказаться ему выгодной.. Рандомизация поведения требует держать в секрете действительно выбранную стратегию (т. е. игроки должны определять стратегии независимо и одновременно). Рандомизация моделирует блеф и отражает идею вездесущности оптимальных стратегий.
Хитрить это значит внушать, что действуешь таким-то образом, или в таком-то месте, в такой-то момент, тогда как в действительности все происходит по-другому. Это, следовательно, своего рода потенциальная вездесущность, как всегда было известно и отмечалось ранними авторами, говорившими о стратегии.
Ксенофонт писал, что знание того, что где-то находится отряд противника без знания его местоположения и сил, разрушает безопасность и все места неизбежно становятся подозрительными (Гильбо [1968]).
Допуская использование смешанных (рандомизированных) стратегий и предполагая, что игроки ориентируются на функции полезности в смысле фон Неймана и Моргенштерна, мы получаем смешанное расширение исходной игры. При этом могут появиться новые равновесные по Нэшу исходы.
Если исходные множества стратегий конечны, то смешанное расширение игры всегда имеет непустое множество равновесий по Нэшу (разд. 2).
Если исходные множества стратегий бесконечны, то возникают определенные топологические трудности. Компактности множеств стратегий и непрерывности функций выигрыша тем не менее оказывается достаточно для того, чтобы гарантировать существование по крайней мере одного NE-исхода (разд.
3).
1. СМЕШАННОЕ РАСШИРЕНИЕ ИГРЫ
Пример 1. Игра де Монмора
В конце 18-го века французский математик Рене де Монмор рассмотрел следующую ситуацию. Для того чтобы сделать подарок своему сыну, отец предлагает: Я возьму золотую монету в правую или левую руку, а ты назовешь одну из них. Если монета у меня в правой руке и твоя догадка правильна, то ты получишь одну золотую монету. Если же монета у меня в левой руке и твоя догадка правильна, то ты получишь две монеты; в противном случае ты не получишь ничего.
Затем Монмор спрашивает, во сколько следует оценить для сына этот подарок, принимая во внимание, что если в этой игре игроки одинаково проницательны и наблюдательны, то нет возможности выработать правило поведения, т. е. не существует оптимальной стратегии в этой игре).
Наша игра 2x2 двух лиц с нулевой суммой такова:
В этой игре нет цены /sup inf и = 0, inf sup и = IV Ни у
одного из игроков нет оптимальной стратегии. Как в любой игре двух лиц с нулевой суммой, не имеющей цены, выяснение, какую стратегию использует противник, позволит добиться хорошего результата за счет использования оптимальных ответов (см. гл.
I, разд. 3). Следовательно, возникает борьба за второй ход, в которой каждый игрок желает скрыть свой окончательный стратегический выбор и в то же время разведать намерения противника.
Но даже глубочайшей секретности недостаточно для того, чтобы не позволить противнику угадать стратегический выбор. Если игрок производит выбор на основе детерминированных дедуктивных рассуждений, то его разумный противник может восстановить саму цепь рассуждений (см. замечание 1 разд.
1 гл. III).
Естественный способ сделать собственный выбор непредсказуемым состоит в том, чтобы сделать его случайным: вместо выбора так называемой чистой стратегии х± из множества {L,R) сын может использовать рандомизированную стратегию рх, выбирающую значения L и R соответственно, с вероятностями ріг 1 pi. Представим себе, например, что сын изготавливает монету, которая с вероятностью рг выпадает на одну сторону, и использует эту монету для выбора своей оптимальной стратегии.
Предположим теперь, что отец не может видеть бросание монеты. Отсюда следует, что стратегия отца, является ли она случайной величиной или нет, не может коррелировать со стратегией сына и, значит, ожидаемый выигрыш, соответствующий так называемой смешанной стратегии р^ не менее inf {2ри
Выбирая рх -j , сын гарантирует себе ожидаемый выигрыш
не менее 2/3. Рассмотрим теперь ситуацию с точки зрения отца. Применяя стратегии L и R соответственно с вероятностями рг, 1р„, он гарантирует себе проигрыш не более величины sup {2ра, 1 Р2}- t
Выбирая р2 = у, отец гарантирует, что ожидаемый проигрыш будет не больше 2/3. Итак, мы заключаем, что внесение тактической неопределенности в стратегический выбор приводит к цене 2/3, которая является разумной оценкой щедрости отца.
Упражнение 1
Используйте аналогичные рассуждения для игры раз дватри (пример 4, гл. I). Докажите, что если игроки используют рандомизированные стратегии, то цена игры равна 6/1 h
Определение 1. Пусть G (X,-, и,.; і ? N) игра в нормальной форме, в которой X,- конечные множества при всех /? Л/.
Смешанной стратегией игрока і называется вероятностное распределение р,- на X,-. Следовательно, множество Mt смешанных стратегий /-го игрока есть единичный симплекс в R*'.
Смешанным расширением игры G называется игра в нормальной форме Gm = (Mf, / g N), где
для всех р € MN ,-(р) = 2 і (х) pf (хг) р2 (хг), .. ., р„ (х„). (1)
хе Xfj
В смешанном расширении Gm игры G стратегия игрока / есть вероятностное распределение р,- на Xt. Под этим подразумевается, что игрок і конструирует собственную лотерею, в которой стратегия х{?Х{ выпадает в соответствии с р,-. То, что лотерея его собственная, означает, что только игрок і знает стратегию х{, которая действительно выпала в лотерее (даже если остальные игроки, возможно, знают вероятностное распределение pf).
Более того, лотерея і'-го игрока стохастически не зависит от лотереи /-го игрока при всех /, /' Ф і (таким образом, игрок / не может получить никакой информации о лотерее t-ro игрока на основе наблюдения своей собственной лотереи).
Поскольку случайные переменные независимы в совокупности, то ы; (р) есть ожидаемый выигрыш игрока і. Принимая и{ за функцию выигрыша игрока і в игре Gm, мы тем самым считаем, что игрок і сравнивает различные лотереи р на р', попросту сопоставляя связанные с ними математические ожидания выигрыша И/ (р) и u-t (р'). Другими словами, и{ есть функция полезности по фон НеймануМоргенштерну, которая распространяет предпочтения игрока і на все возможные лотереи на XN. Дальнейшие обоснования этого предположения относятся к теории статистических решений и здесь не будут рассматриваться (см.
Льюс, Райфа [1957]). Теперь существенно, что функция щ (х) принимает действительные значения, в то время как в предыдущих трех главах важны были только отношения предпочтения, индуцированные функциями ut на Хщ.
Чистая стратегия xt ? X,- игрока і в исходной игре будет отождествляться со смешанной стратегией бxt?Mh выбирающей xt с вероятностью 1:
J 6*, (*[) = 0, х'і^Хі, х'іФх
\6*,(*г)*1.
В самом деле, из формулы (1) сразу следует, что
и1(Ьх) = иі(х) для всех x^XN и bx = (bx.)iiN.
Поэтому будем рассматривать Xt как подмножество Mh а ,- как расширение и{ с XN на MN-
Теорема 1. Если Xtконечное множество для всех i g /V, то множество равновесных по Нэшу исходов в игре Gm является непустым компактным подмножеством множества Мы. Более того, оно содержит множество равновесных по Нэшу исходов в игре G:
W?(G)cW?(GJ^=0. (2)
Доказательство. Выберем любой равновесный по Нэшу исход х в G. Обозначим и заметим, что
sup и, (р„ 6Х) = sup щ (yt, xt),
иееМ( Г ?і^Х{
поскольку Mt выпуклая оболочка Xt (множество Xt отождествлено с подмножеством множества М{) и функция щ линейна по переменной pf.
Теперь в силу того, что исход х есть равновесие по Нэшу, имеем
sup ut (уi, xt) = щ (х) = и{ (Ьх , 8*г).
уі*Хі
Объединяя эти утверждения, получаем, что Ьх есть NE-но ход в игре Gm.
Заметим далее, что игра Gm удовлетворяет предположениям теоремы Нэша (теорема 2, гл. ІИ). А именно, М{ является выпуклым и компактным в RX‘, и{ непрерывна на Мц и линей на относительно переменной р,.
Доказательство теоремы 1 завершено. I
В качестве следствия леммы 1, гл. IV получаем, что все ЛЛЕ-исходы в игре Gm со смешанными стратегиями являются индивидуально рациональными в Gm. На самом деле они также являются индивидуально рациональными в исходной игре G, как показывает следующий результат
Лемма 1. Гарантированный выигрыш игрока і в исходной игре не больше его гарантированного выигрыша в смешанном расширении игрыі
для всех і € N sup inf щ (xt, xt) ^ sup inf ui (py, p,-). m
i(eA( дубМуи(бМ( w
Доказательство. Фиксируем игрока l € V, чистую стратегию xt 6 X; и для каждого / € ?\{і} некоторую смешанную стратегию ру g Му. Тогда щ (6*;, pf) есть математическое ожидание
функции ut{x(, - )g(сужение щ на Xj для фиксированного X.) относительно произведения вероятностных мер ® ру на Хи
/ва?\Ю
Следовательно, имеем
inf щ (xt, xt) й, (6*, р,).
Это неравенство справедливо для всех р, g Mt, поэтому ІШ ut (Xt, Xt) inf Щ фх pt) sup inf щ (py, pi).
*,**1 ^,еМі iiteMt
Поскольку выбор xt произволен, доказательство леммы 1 завершено.
Применяя полученные выше результаты к играм двух лиц с нулевой суммой, сформулируем
Следствие из теоремы 1 и леммы 1. Пусть для данной игры G = (X1( Х2, ых) с нулевой суммой, в которой множества лг, Х2 конечны, игра с нулевой суммой Gm = (M1, Мг, щ) является ее смешанным расширением. Тогда игра Grn имеет по крайней мере одну седловую пару и цену, которую мы назовем ценой игры Gm (или ценой игры в смешанных стратегиях) и обозначим vm(ut).
Более того,
sup inf и1(х1, inf sup (Xj, x2). (4)
JT6 X, x2€ X2 x2€ X2
Предположим сначала, что исходная игра G имеет цену и у каждого игрока имеется оптимальная в игре G стратегия. Тогда смешанное расширение игры G имеет ту же цену и произвольные выпуклые комбинации оптимальных стратегий в игре G являются оптимальными стратегиями игроков в игре Gm (см. задачу 2, п. 1).
Предположим напротив, что игра G не имеет цены и, следовательно, у игроков нет оптимальных стратегий. В игре Gm каждый игрок имеет по крайней мере одну оптимальную смешанную стратегию, и цена игры лежит на отрезке Tsup inf ultL x,
inf sup иЛ. (В общем положении в обеих частях (4) имеют
Хг х, J
место строгие неравенства, см. задачу 1 ниже.) Типичным примером является игра Монмора (пример 1) со смешанной ценой 2/3 и оптимальными осторожными стратегиями обоих игроков
(3-L + -f- R) . См. также разд. 2, в частности упражнения 7, 8.
В качестве еще одной иллюстрации к теореме 1 рассмотрим дилемму заключенного (пример 1 гл. I).
В смешанном расширении этой игры агрессивная стратегия по-прежнему является единственной доминирующей стратегией для каждого игрока, поэтому NE (G) = NE (Gm).
Наш последний пример демонстрирует возможность следующей ситуации:
0 Ф NE (G) cNE (Gm).
Пример 2. Смешанные стратегии в игре перекресток-
В'игре перекресток (пример 2 гл. Ill) имеются два NE-йсхода в чистых стратегиях. В смешанном расширении возни*
кает еще один NE-исход, а именно пара (р*, р*):
где (5)
бі (бц)смешанная стратегия, при которой с вероятностью 1 игрок проезжает перекресток (останавливается).
Имеем
иі Фи Pf) гИТІ* 1 e)=ss 1 ,
t*?)-fex2+dr?xo=i_^.
В силу линейности щ относительно р^получаем i(h- = (р*. р?) для всех
Меняя ролями игроков 1 и 2, в силу симметрии игры получаем и% (Р* Р2) = ы2 (р*, pf) для всех р2?М2.
Отсюда следует, что (р*, \if) NE-исход в смешанном расширении игры перекресток.
СТАБИЛЬНОСТЬ НА ОСНОВЕ УГРОЗ
Сообщение типа М. есть просто обычная чистая стратегия М. Как и в случае равновесия в совместных смешанных стратегиях, выполнение соглашения с проведением лотереи L обеспечено автоматически. В самом деле,щ{ОВ, ОЯ) = -§-их(Я, ^) + yux(l н)йх(Уі, ОВ) =
= L) + T?il^1’ H) для всех У* в М Н}'
ы*(ОВ, OB) = ~u2{L, Я) + ^-и2(Я, L) = 2н2(ОВ, у2) =
= ~и2(Н, y2) + ^u2(L, у2) для всех у2 в {L, М, Я}.
!) В данном случае доминирование является строгим: лг,- строго доминирует уі, если U{{x(, дсг) Ui(jyi, дсг) для любого набора xt?XvПрим, перев.
В противоположность равновесию в совместных смешанных стратегиях решение о согласии с лотереей не может быть отменено после реализации конкретного исхода: это решение должно быть принято раз и навсегда до случайной реализации.
Определение 3 (Мулен, Виал [1978]). Для всех і g N обозначим Lt сужение распределения L на Хд?ч(г}, а именно:
Lt(xt)= 2 ?(*.- хі) для всех xt.
Х{6Х;
Скажем, что лотерея L есть слабое равновесие в совместных смешанных стратегиях в игре G, если выполнены следующие неравенства:
V € N, у*/,- € 2 и* (*) L{x) 2 г (Уь xt) L, (xt).
xeXN xi^xN\{i)
Обозначим через WCE (G) множество слабых равновесий в игре G.
Лемма 2. (1) Множество WCEifi) есть непустое выпуклое компактное подмножество единичного симплекса в RXn. Оно содержит множество СЕ (G) равновесий в совместных смешан-ных стратегиях.
2) Если (хисход игры Gm, то соответствующая лотерея
L= ® р.: является слабым равновесием в совместных смешан-іел/
ных стратегиях в игре G тогда и только тогда, когда исход р есть равновесие по Нэшу в игре Gm.
Доказательство. По определению 3 лотерея L принадлежит множеству WCE(G) тогда и только тогда, когда
V* € N уу{ € X, 2 Щ (х) ? (*) 2 Щ (Уі, xt) L (*).
х 6Хfj * 6 Хдг
Эти неравенства получены из системы (4) суммированием по хі$Х{ при фиксированных і и у;. Итак, окончательно имеем
CE{G)=WCE(G).
Остальные утверждения леммы 2 очевидны.
Определение 3 является последним шагом в развитии концепции стабильных соглашений, основанных на рандомизации и на тайном выборе стратегий. Начав с равновесий по Нэшу в чистых стратегиях, мы сначала допустили независимую рандомизацию индивидуальных стратегий (смешанные стратегии) и установили, что стабильные соглашения существуют, если игроки имеют возможность проводить свои лотереи тайно (теорема 1 гл.
IV). Далее, если игроки могут устраивать совместные лотереи и посылать изолированные сигналы каждому участнику, то множество равновесий становится выпуклым. Из лемм 1 и 2 следует, что
NE (G) а NE (Gm) а СЕ (G) с WCE (G).
Проходя по этой цепочке включений слева направо, мы должны накладывать все больше информационных ограничений для того, чтобы равновесный исход стал стабильным соглашением. Для NE-исхода и для смешанного М?-исхода требуется только соблюдение секретности в выборе индивидуальных стратегий. Для СЕ-исхода мы должны в дополнение к этому потребовать, чтобы отдельные игроки могли наблюдать только свои собственные реализации совместной лотереи.
Для WCE-исхода нужен нейтральный арбитр, который реализует случайный исход лотереи, ничего не сообщая отдельным игрокам. Затем этот арбитр спрашивает независимо и тайно каждого игрока, согласен ли тот вслепую использовать ту стратегию, которая реализовалась при проведении лотереи.
Далее он должен сообщить тем игрокам, которые добровольно согласились с проведением лотереи, выпавший исход и заставить этих игроков действительно использовать рекомендованные стратегии. Короче говоря, арбитр должен иметь возможность пресекать любое стратегическое использование конкретной реализации лотереи.
Общей чертой этих сценариев с усложняющейся информационной структурой является невозможность по достижению договоренности о выборе некоторой совместной стратегии вести прямой обмен информацией между игроками. В случае многократного проведения лотереи кооперация становится неявной, и трудно обнаружить сам факт ее существования. Такая форма молчаливого сговора описана в литературе о поведении фирм в условиях олигополии: Среди соглашений, возможных при олигополии, выделим те, при которых нет явного обмена информацией между участниками.
Одним из примеров такого соглашения является сговор по электрическому оборудованию 1950-х годов (Шерер [1970]), в который были замешаны 29 компаний США, продающих различные виды товаров. Правительство США организовало аукцион, в котором каждая фирма должна была тайно и независимо друг от друга назвать свою цену на некоторый вид электротехнического оборудования.
Однако фирмы провели предварительные секретные переговоры, в которых была определена доля каждой фирмы, участвующей в аукционе. Затем продавцы согласовали свою политику назначения цен на аукционе так, чтобы каждый из них оказался предложившим наименьшую цену (и, следовательно, получил бы заказ от правительства) достаточное число раз для захвата заранее определенной доли рынка. Это было достигнуто за счет раздела рынка на четыре зоны, причем к каждой зоне были приписаны различные продавцы.
Продавцы, прикрепленные к одной зоне, чередовали свои ставки. При определении привилегии назначения наименьшей цены ориентировались на фазы луны.
В результате получился якобы случайный процесс, имитирующий независимое поведение участников (Жерар-Варе, Мулен [1978]).
Упражнение 4
Докажите, что в игре музыкальные стулья (пример 4) все четыре множества ME (G), ME (Gm), СЕ (G) и WCE (G) различны. Докажите, что оптимальные по Парето СЕ-выигрыши покрывают
отрезок [(-- т). (т т)]’ а оптимальные по Парето WCE-выигрыши покрывают отрезок. [(2, 1), (1, 2)].
Упражнение 5
Пусть в игре G = (Xi, i g N) каждое множество Х{ состоит из двух элементов. Докажите, что
CE(G)=WCE{G).
Задача 1
Слабое равновесие в совместных смешанных стратегиях и равновесие по Нэшу (Мулен [1976])
Фиксируем игру двух лиц G = (Xlt Х2, ult м2) с конечными множествами стратегий Xlt Х2 и обозначим через Gm == (Мг, УИ2, и1, иг) ее смешанное расширение. Для совместной лотереи L обозначим через Lv L2 (вместо Lt, Lj) сужение L соответственно на Хи Х2. Заметим, что Li^,Mh t=l, 2. Обозначим, наконец, через [,-, L] математическое ожидание выигрыша игрока i, t'= 1, 2, при лотерее L.
1) Исход (uf, ц*) игры Gm назовем сверхравновесием по Нэшу ((pf, р2) g N+E (Gm)), если не существует такой лотереи L, для которой выполнено
[ и{ (pf, ?,)[,-, L] для і=1, 2, іФ і,
\ причем по крайней мере одно неравенство строгое.
Интерпретация; для любого возможного соглашения L либо у какого-то игрока возникнет желание выбрать стратегию N+E (Gm) (и, (pf, Lj) [и,-, L]), либо для обоих игроков нет разницы между применением стратегии N+E (Gm) и выполнением соглашения при условии, что партнер также выполняет соглашение (, (pf, Lj) =[,-, L1 для t= 1, 2, ІФІ).
Докажите, что М+Е-исход является смешанным XT:-исходом.
2) Обозначим через М+Е (Gm) множество всех У?+^-исходов в игре Gm, а через N^Ei проекцию этого множества на мно.
жество M.t. Докажите, что
N+EiGJczN+EiXN+EtCNEiGJ. (10)
Указание: если (р1( р2) и (vlf ?2) принадлежат множеству N+Е (Gm), то докажите, что
?,) =^(1*,, ?2),
'V2)==U2(M'1i ''’l)-
3) Докажите, что равновесие в доминирующих стратегиях является также і?+?-исходом:
Di (i)xD2 (u2)ciV+?(GJ.
Докажите, что при условии непустоты множества N+E (Gm) множество N+ErxN+Ег содержит доминирующий по Парето элемент р*:
1 +Е1хУ+Ег уі = 1, 2 и,- (р) Щ (р*),
\ V* +ExxN+Ег.
4) Докажите, что исход р* = (р*, pf) является N+E-исходом в игре Gm тогда и только тогда, когда существует действительное число %, 0^ 1, такое, что
V (хі -^г) €X Х2: Хи1(х1, х2)--(1 Х)иг(хj, хг)
kFj (pf, x2) -f (1 Цйг (xlt p*) (11)
(где с некоторым нарушением принятых обозначений и{ (р,-, xj) стоит вместо и{ (р,, б, )).
Выведите отсюда, что множества Л!+E(Gm) и N+Eh і = 1, 2, компактны.
5) Предположим теперь, что функция и{ действительно зависит от х{, t = l, 2, т. е.
3^( € X/ Xj^Xj Uf (Xj, Xj) Ф иi (Xj, Xj). (12)
Обозначим через WCE (Gm) (возможно пустую) внутренность множества WCE (Gm) относительно единичного симплекса в Докажите следующую эквивалентность:
LZWbCEiGJlUiiXi, Lj) [и{, L], і= 1, 2, \фі, х,€Х,.].
(13)
6) В дополнение к (12) предположим, что ни у одного игрока нет доминирующей стратегии в игре Gm.
Докажите следующую эквивалентность:
, WCE^0 N+E = 0.
Указание: Полагая, что Z = X1[)X2 есть объединение множеств Xj и X2, которые считаются непересекающимися, рассмотрите следующую действительную функцию /, определенную на Х{і2}XZ:
?(*і x2)?Xll2} yz?Z f((xlt х2), z) =
M*i, xt)~і(г. х2), если г?Хи и2(хи х2) и2(хг), если г$Х2.
Проверьте, что цена ? игры (Х{12}, Z, /, /) в смешанных стратегиях является неотрицательной.
Покажите, что величина ? равна нулю тогда и только тогда, когда для некоторого %, 0 X 1, выполнено неравенство (11). Покажите далее, что величина ? положительна в том и только в том случае, если существует лотерея L, для которой выполнены неравенства из правой части (13).
СТАБИЛЬНОСТЬ НА ОСНОВЕ УГРОЗ
В этой главе будем предполагать, что игроки по-прежнему стремятся к кооперации, однако, принимая во внимание стратегическую взаимозависимость, присущую игре в нормальной форме, они теперь при выборе собственной стратегии учитывают возможную реакцию остальных. Угрожая друг другу, они могут стабилизировать весьма обширное множество исходов.Поэтому будем рассматривать угрозы как механизм кооперации.
В течение длительного времени кооперация при взаимных предостерегающих угрозах изучалась в экономической литературе, посвященной проблемам олигополии. Так, например, при рассмотрении дуополии по Курно (пример 5 гл. Ill) отмечалось, что исход, реализующий наибольшую суммарную прибыль, не является равновесием по Нэшу, поскольку одностороннее увеличение какой-либо фирмой своего предложения увеличивает ее текущий доход.
Это действие вынуждает другую фирму также увеличивать свое предложение, что в результате приводит к тому, что оба игрока проигрывают по сравнению с исходной ситуацией. Как отмечает Шерер [1970], каждая фирма с большой неохотой идет на такие меры, которые могут в результате реакции других фирм привести к последствиям, нежелательным сразу для всей отрасли (см. также пример 5 ниже).
Предостережение является весьма мощным механизмом кооперации. Для достижения стабильности соглашения игроки угрожают друг другу, т. е. объявляют некоторую схему реагирования на возможные отклонения.
Поскольку отклоняющемуся игроку может стать плохо, если объявленная угроза осуществится, то он поостережется отклоняться, и необязательное соглашение окажется стабильным.
Таким образом, предостережение является разумным использованием потенциальной силы. Успешной является та угроза, которая никогда не реализуется (Шеллинг [1971]).
Стабильные соглашения, рассматриваемые в гл. V, требовали полной секретности принятия стратегических решений. В про-
тивопо$ожность этому угроза является эффективной только в том случае, когда отклонение нельзя скрыть. Следовательно, для достижения стабильности на основе предостережений требуется, чтобы все индивидуальные выборы стратегий производились в открытую. Известны многочисленные военные и экономические примеры ограничения на секретность в выборе стратегий в целях стабилизации кооперативных решений (см. разд.
1).
Основной концепцией равновесия в данной главе является a-ядро, х. е. множество таких исходов, которые при соответствующих угрозах являются стабильными относительно отклонений любых коалиций (разд. 2) Если возможны только индивидуальные отклонения, то с помощью предостерегающих угроз можно-стабилизировать любой дележ игры (разд.
1).
Если a-ядро пусто, то нужны более сложные сценарии предостережений, включающие контругрозы, для того чтобы стабилизировать хотя бы некоторые дележи при возможности коалиционных отклонений (разд 2) Если, напротив, a-ядро не пусто, то при наложении дополнительных условий на предостерегающие угрозы возникают специфические подмножества a-ядра. Одним из таких подмножеств является (3-ядро, которое в особенности полезно при анализе повторяющихся игр (разд. 3).
В разд. 4 для игры двух лиц мы определяем другое подмножество а-ядра, а именно у-ядро; у ядро состоит из тех дележей, которые могут быть стабилизированы при правдоподобных угрозах, т. е. при поведении, основанном на наилучших ответах.
Это приводит к качественной классификации игр двух лиц.
В разд. 5 содержится другая формализация игры, а именно рассматриваются игры в характеристической форме (с побочными платежами).
В качестве стабильного множества для таких игр вводится ядро, которое задается в данном случае конечной системой линейных ограничений, что позволяет получить простые численные результаты.
1. ДЕЛЕЖИ
Пример 1. Кооперативное решение дилеммы заключенного
Некооперативным исходом дилеммы заключенного является война (пример 1 гл. I): (Л^ Л2). Для того чтобы обеспечить мирный исход (Рг, при кооперации, каждый игрок объявляет принцип своего поведения: как ты, так и я, т. е.
если ты будешь вести себя мирно, то я тоже буду вести себя мирно, (1)
если ты будешь агрессивным, то и я буду агрессивным
Приняв во внимание такую угрозу от своего оппонента, каждый игрок предпочтет быть миролюбивым, так как это приводит к миру (исход (Plt Рг)), иначе будет война (исход (Alt Л2)). Так проявляется свойство стабильности' угрозы (1).
Двусторонние угрозы не образуют пару допустимых действий. Для того чтобы реализовать поведение типа (1), игрок должен действовать как ведомый, т. е. знать выбор партнера.
Если игроки выбирают стратегии раз и навсегда, то только один игрок может находиться в положении ведомого. Вместе с тем дилемма заключенного является симметричной игрой, и мы хотим, чтобы кооперативный исход (мир) был обеспечен сценарием предостережений, в котором игроки имели бы симметричные роли. Для преодоления этой трудности можно представлять себе, что игра является повторяющейся и совокупный выигрыш будет, грубо говоря, взвешенной .суммой текущих выигрышей.
Если краткосрочный доход от некооперативного отклонения перекрывается долгосрочными потерями, возникающими в результате реакции типа (1), то сценарий предостережений обеспечивает стабильность мирного кооперативного исхода (см. разд. 3 ниже). Здесь мы приведем наиболее простую с математической точки зрения конструкцию для формализации кооперации на основе угроз.
Игрокам нужно только прийти к договоренности о некотором исходе игры, и для каждого игрока выбрать угрозу, предостерегающую его от отклонения от данного исхода.
Определение 1. Пусть G = (Xh up, i?N) игра в нормальной форме. Назовем сценарием предостережений набор {х, ??; і ? N), где х € XN исход игры G, а г для всех і € N обозначает угрозу игроку і, т. е. отображение из Х{ в Х^^щ, такое, что
(2)
St (* () = *,,
ЩІУі, ЫУі))Щ(*)-
Проиллюстрируем сценарий предостережений, рассматривая игру, разыгрываемую на бесконечном интервале времени. В каждый конкретный момент времени каждый игрок выбирает некоторую стратегию, причем он может поменять свою стратегию в любое время.
Игра происходит в открытую, т. е. стратегии всех игроков всем известны. Это главное информационное предположение, которое делает невозможным тайное нарушение договора.
Игрок, который выполняет соглашение, вначале выбирает согласованную с остальными стратегию х{ и затем наблюдает за текущими стратегиями yt других игроков. Пока уі = Хи игрок і сохраняет стратегию xh как только какой-то игрок, скажем /, переключается на стратегию г/у- ф Xj, игрок і переключается раз и навсегда на t-ю компоненту tiiyj)- Условие стабильности (2) означает, что если все игроки выполняют договор, основанный на сценарии предостережений, то ни у какого игрока не возникает повода для (одностороннего) нарушения соглашения.
В самом деле, выигрыш на бесконечном интервале времени всегда превышает выигрыш на любом промежутке конечной длины.
В определении 1 учитываются только отклонения отдельных игроков. В следующем разделе это определение будет обобщено на случай отклонений коалиций (см. определение 3).
Конечно, иногда трудно выполнить требование вести игру в открытую. Так, в частности, при современном вооружении неожиданное нападение становится все более опасным.
Таким образом, создание демилитаризованных зон, в которых видны все агрессивные действия, или соглашения о взаимной инспекции ядериого оружия вот два примера механизмов обмена информацией типа предостерегающих угроз. Другим примером является бюро открытых цен, которое удерживает конкурирующие фирмы от тайного применения политики скидок покупателям и, следовательно, смягчает общую конкуренцию (Шерер [1970]).
С другой стороны, англо-японское соглашение об ограничении производства военных кораблей не включало в себя специального пункта о контроле за выполнением соглашения, поскольку оно было подписано в то время, когда тайное строительство таких объектов считалось невозможным. (См. Арон [1962].)
Будем придерживаться обозначений, принятых в определении 1.
Лемма 1. 1. Пусть (х, Zt; i?N)сценарий предостережений. Тогда исход х является индивидуально рациональным:
sup ini и f (у;, yf)^ue(x) для всех i?N. (3)
h yt
2. Предположим, что компакт, а щнепрерывная функция, i?N. Тогда в игре G существует по крайней мере один индивидуально рациональный исход. Для каждого такого исхода х при всех существует набор угроз f, такой, что
(х, \й і 6 N) является сценарием предостережений.
Доказательство. Из (2) получаем inf и, (у,-, ytXu;(y{, Ь ІУдХщіх) для всех yt^X{.
Отсюда следует первое утверждение леммы 1. Докажем обратное утверждение. При наших топологических предположениях у каждого игрока есть по крайней мере одна осторожная стратегия, скажем xt (см. лемму 3 гл. I).
Тогда исход * = (*і)і=л/ является индивидуально рациональным.
Далее, для каждого i g N и для любой стратегии у,- g Хь Уіфхі выберем элемент yt ЬІУі) € XN\{i], такой, что
иіІУі, yt)==iniui(yit zt) sup inf щ (zit zt)u,(x).
2! H *f
Это завершает доказательство леммы 1.
Определение 2. Дележом в игре G (X h и;\ i g N) называется оптимальный по Парето индивидуально рациональный исход. Обозначим через / (G) множество дележей в игре G.
Лемма 2. Пусть для любого і g N множество Xкомпактно, а функция U; непрерывна. Тогда в игре G есть по крайней мере один дележ.
Доказательство аналогично доказательству леммы 3 гл. I.
Обозначим через IR(G) непустое компактное подмножество индивидуально рациональных исходов во множестве всех исходов игры G. Выберем далее элемент х из IR(G), который максимизирует 2 иі на 1R (G). Тогда х Является оптимальным по
16 N
Парето исходом. Предположим от противного, что исход у доминирует по Парето исход х. Тогда г/ g //? (G) и 2 ,- (*) 2 ui(y)-
isN is N
Полученное противоречие доказывает лемму.
Дележ является оптимальным по Парето исходом и приносит каждому игроку по крайней мере его гарантированный выигрыш. По лемме 1 любой дележ является исходом оптимального по Парето сценария предостережений, т. е. необязательного соглашения, стабильного относительно индивидуальных отклонений, а также относительно возражений коалиции N всех игроков (оптимальность по Парето).
С другой стороны, двумя минимальными требованиями для кооперативных соглашений как раз и являются индивидуальная рациональность (никакого игрока нельзя заставить получать меньше гарантированного уровня, пока он сам контролирует выбор собственной стратегии) и оптимальность по Парето (поскольку договор заключается при единогласном одобрении всех участников). Следовательно, множество / (G) является максимальной областью переговоров о кооперации. Если игра G несущественна (или почти несущественна, см. задачу 1 гл.
Ill), то множество I (G) одноэлементно и кооперативный исход игры не вызывает сомнения. Но в большинстве игр множество / (G) состоит из большого количества исходов, ч выбор среди них является острой конфликтной ситуацией.
Пример 2. Игра Торг
Игрок 1 продает (неделимый) товар игроку 2. Игрок 1 должен решить, какую назначить цену: высокую или низкую. Для поку--пателя в принципе приемлемы обе цены.
Покупатель не может спорить о цене, он может либо сделать покупку, либо отказаться от нее.
Игрок 1-
Исход (/, /) является равновесием в доминирующих стратегиях, кроме того, он оптимален по Парето. Если игроки не имеют возможности обмениваться информацией, этот исход является, по-видимому, бесспорным итогом игры.
Однако это не единственный дележ игры. Другим дележом является исход (II, /). Для того чтобы выиграть (т. е. продать товар по высокой цене), игрок 1 может объявить, что он будет продавать товар только по высокой цене, т. е. действовать в качестве лидера. С другой стороны, игрок 2 выигрывает, угрожая продавцу: Я буду покупать по низкой цене и откажусь от сделки в случае назначения высокой цены.
Это кажущееся неразумным поведение (поскольку покупатель отказывается от выгодной сделки) оказывается весьма выгодным, если только продавец поверит этой угрозе. С кооперативной точки зрения мы не можем отдать предпочтение ни одному из названных сценариев предостережения или, другими словами, не берем на себя роль арбитра в этом конфликте с двумя антагонистическими угрозами (решимостью продавца назначить высокую цену и отказом покупателя приобретать товар, если не будет назначена низкая цена), которые могут осуществиться одновременно только на исходе, доминируемом по Парето (несостоявшаяся сделка).
В разобранном выше примере покупатель выигрывает, используя радикальную угрозу: На любое твое отклонение я буду реагировать минимизацией твоей функции выигрыша (т. е. я буду применять наихудший для тебя ответ) ‘). Этот радикализм может привести к тому, что выполнение угрозы окажется пагубным для обоих игроков.
Объявление покупателя, что он отказывается от сделки при назначении высокой Цены, является, как он надеется, только предостерегающим сигналом. Однако, для того чтобы угроза произвела впечатление, нужно, чтобы не было сомнений в том, что она будет приведена
!) В отечественной литературе такая угроза получила название стратегии наказания.Прим, перев.
в исполнение. В этом смысле даже наиболее убедительные и успешные угрозы являются рискованными, если объявленная реакция на отклонения не совпадает с наилучшим ответом угрожающего игрока. Сравните, например, агрессивную угрозу и предупреждение в приведенной ниже лемме 3.
Соотношение между убедительностью и рискованностью предостерегающих угроз для игр двух лиц проанализировано в разд. 4.
Ситуация, которая имела место в примере 2, легко обобщается на произвольную игру двух лиц.
Рассмотрим игру двух лиц (Xlt Х2, и,, и2), где множества Xt компактны, а функции и; непрерывны, і= 1, 2. Наилучшим дележом для игрока і является исход х', такой, что
ТЕОРЕМА НЭША О СУЩЕСТВОВАНИИ РАВНОВЕСИЙ
1) При (/, R) игрок 2 отклоняет кандидата d, а игрок 3 всегда выбирает правую дугу. Стратегия R есть доминирующая стратегия игрока 3, а ($, R)сложное равновесие. Выбирается кандидат а.2) В (р1, L) и (ft, L) игрок 2 накладывает вето на с и а, в то время, как игрок 3 использует следующую стратегию L:
j идти направо, если игрок 2 накладывает вето на с или а, \ идти налево, если игрок 2 накладывает вето на d.
Стратегии наилучших ответов игрока 2 на L есть в точности {/, ft}. Более того, L это наилучший ответ как на /, так и на поскольку соответствует избранию наилучшего по иг кандидата d. Следовательно, (р, L) и (ft, L) NE-исходы.
Заметим, что L не только доминируемая (стратегией R) стратегия игрока 3, но также и рискованная (не осторожная) стратегия: применяя L, игрок 3 угрожает избрать с, если только игрок 2 отклонит d, но такой вариант крайне не выгоден обоим игрокам, поскольку снаихудший кандидат как по иг, так
Другой пример NE-исходов, использующих доминируемые стратегии, приведен в нашей простой модели аукциона: см. упражнение 2 ниже.
Заметим, однако, что когда все функции выигрыша взаимно однозначны на XN, то никакой МЕ-исхоя не содержит доминируемой стратегии и концепция равновесия по Нэшу обобщает равновесие в доминирующих стратегиях.
Упражнение 2
Для аукциона второго типа (пример 2 гл. I) докажите, что для каждого игрока і и любой цены р, ограниченной сверху ценностью товара для игрока і (р^а,-), существует Х?-исход, в котором і-й игрок получает товар за цену р.
Напротив, для аукциона первого типа покажите, что любой ХЯ-исход таков, что игрок 1 получает товар по цене между а2 и at.
Задача 1. Почти несущественная игра двух лиц
Пусть G = (Xj, Х2, и? и2)игра двух лиц, в которой Х± и Х2 конечны. Скажем, что G почти несущественна, если всем индивидуально рациональным исходам соответствует один и тот же вектор выигрышей. Другими словами, для любых двух исходов х и у выполнено
{х и у индивидуально рациональны} = {ыг (х) = и,- (у), і = 1, 2}.
1) Приведите пример почти несущественной игры, которая Не является несущественной.
2) Предположим, что игра G почти несущественна и выберем пару (xlt х2)^,Р1(и1)хР2(иг) осторожных стратегий. Покажите, что исход (Xj, х2) является оптимумом Парето, равновесием по Нэшу, t-равновесием по Штакельбергу для і = 1, 2.
3) Всякое ли равновесие по Нэшу в почти несущественной игре является также t-равновесием по Штакельбергу (і=1,2). А что получится, если обе функции выигрыша взаимно однозначны на X^XJ
2. ТЕОРЕМА НЭША О СУЩЕСТВОВАНИИ РАВНОВЕСИЙ
С теоретической точки зрения наиболее привлекательной чертой концепции равновесия по Нэшу являются его хорошие математические свойства.
Теорема Нэша дает достаточные условия существования по крайней мере одного равновесия по Нэшу. Эти условия оказались легко проверяемыми во многих прикладных моделях.
Уже отмечались два различных достаточных условия для того, чтобы игра G имела хотя бы один Х?-исход:
1) если игра G несущественна, тогда по теореме 1 гл. I любой набор осторожных стратегий есть равновесие по Нэшу.
2) если игра G разрешима по доминированию, тогда вступает в силу теорема 1 этой главы.
Однако удобных условий на X,- и иь гарантирующих несущественность или разрешимость по доминированию игры G, не существует. Для игры в нормальной форме обычной является ситуация, в которой и,- построены из элементарных функций (полиномиальных, логарифмических, ...) на основе элементарных операций.
В этом случае оказался весьма полезным результат Нэша.
Напомним, что действительная функция а вогнута, если для всех X, Ог^і^І, и любых t, t' выполнено
Ха (t) -f (1 X) а (t') *^a(Xt + (lX) f).
Теорема 2 (Нэш [1951]). Предположим, что для любого і ? N множество стратегий Х; есть выпуклое и компактное подмножество топологического векторного пространства (вообще говоря, своего для каждого і). Пусть для всех i?N и; непрерывная действительная функция на XN, определенная так, что для всех xi ? Xt функция ut (х;, xt) вогнута по х{ на Хг.
Тогда множество NE(G) равновесий по Нэшу игры G = (X,-, иг; i?N) непусто и компактно.
Доказательство. Доказательство опирается на теорему о неподвижной точке из выпуклого анализа.
Используем следующий результат, который известен как лемма Кнастера Кура-товскогоМазуркевича (ККМ), доказательство которой можно найти в работах: Берж [1957], Партхасаратхи, Рагхаван [1974].
Лемма. Пусть рцелое число и аи ..., арнекоторые точки топологического векторного пространства. П усть далее Ах, ..., Ар некоторые замкнутые подмножества множества СО {а,, ..., ар}, которое является выпуклой оболочкой множества {ах, ..., ар}, причем
?Гс:{1, ..., р} множество (J Ak содержит СО {ak\k^T}.
ks т
р
Тогда пересечение П Ak не пусто
*=і
Следующее короткое доказательство теоремы 2 принадлежит Жоржу Хаддаду.
Определим действительную функцию ф на XNxXNi Ф(х, 0)= 2 [/(*/. Удиі(У)] ПРИ г/СХд,.
іе N
Из вогнутости по Х[ следует вогнутость Ф по х. К тому же Ф непрерывна по у. Определим многозначное отображение Е из XN в себя;
F (x) = {y€XN\4(x, //)0} для всех x?XN.
Поскольку Ф непрерывна по у, то F (х).компакт при всех х. Более того, х g F (х), поэтому F (х) не пустое множество. Фиксируем целое р и р элементов х1, ..., хр из Xn. Утверждается,
ХИ Р
что любая выпуклая комбинация х= 2j Кхк принадлежит U F (хк).
kz=l k-\
В противном случае имеем
??=1, ..., р 0 Ф(х*, х).
Следовательно, мы доказали, что СО {х1, .... хр} с U F (хк).
Поскольку это справедливо для любого р и любых х1, ..., хр,
Р
к= і
то по ККМ лемме П F (хк) не пусто. Так как непустые компактные множества (F(x))xexN таковы, что любое их .конечноесемейство имеет непустое пересечение, то и пересечение всехмножеств п F (х) также не пусто.
Для любого х* из этого xexNпересечения имеемух? XN ф(х, х*)0, что может быть переписано в виде
?і 6 N, ?х,- ? X i ui (xh x?) u- (x*) ^ 0.
Таким образом, П F{x) NE(G) и теорема 2 доказана. Щ xsXn
Следствие из теоремы Нэша (фон Нейман). Пусть Хи Х2 выпуклые компактные подмножества некоторых топологических векторных пространств, и пусть иг непрерывная действительная функция, определенная на XtxX2, причем
1) для всех х2 ? Х2 (Хр х3) вогнута по х,,
2) для всех х1?Х1 и1{х1, х2) выпукла по х2.
Тогда игра двух лиц с нулевой суммой (Хи Х2, иг) имеет по крайней мере одну седловую пару и, следовательно, цену.
Теорема Нэша позволяет утверждать, что множество NE (G) не пусто. Для того чтобы его вычислить, требуется решитьследующую систему уравнений (i?N):
Uj (х*) max ut (хг, xf). (5)
*і€ хі
Если u( вогнута no xf, то приведенная выше задача глобальной оптимизации эквивалентна локальной задаче (как мы знаем из выпуклого программирования). Например, если х{ внутренняя точка множества Х; и функция и,- дифференцируема по х;, то условия (5) эквивалентны условиям
^ (х*) = 0 для всех і ? N. (6)
Поскольку число независимых уравнений равно размерности XN, можно надеяться, что система (6) будет иметь конечное число изолированных решений. По этой же причине для игр гобшріо положения равновесные по Нэшу исходы не оптимальны по Парето (точный результат см.
Грот [1974]).
Проиллюстрируем метод вычисления, который мы описали в общих чертах, на некоторых примерах и задачах.
Пример 4. Олигополия с назначением выпуска
Пусть имеется п производителей с нулевыми затратами, которые регулируют предложение хи ..., х„ некоторого насыщаемого по потреблению товара. Производители поставляют свой товар на рынок.
Общее предложение равно х = хх-}-...
х„, а цена есть р (х), где рубывающая вогнутая функция на положительной полуоси:
Р (0)0, р' (у) 0, р (у) 0 для г/ 0. (7)
Эту ситуацию можно представить как следующую игру:
X,- = [0, +оо), иі(х)=хір(х), і = 1, ..., п.
Из наших условий на р получается, что функция ut вогнута по х,-. Поскольку X, не компактные множества, положим, У, = = [0, S], где S есть предложение, порождающее нулевую цену: p(s) = 0. Для усеченной игры (Y{, иг; і=1, ..., п) применима теорема Нэша, которая позволяет утверждать существование ХЕ-исхода х в усеченной игре.
На самом деле исход х есть равновесие по Нэшу в исходной игре. Действительно, гарантированный выигрыш каждого игрока в усеченной игре есть 0, поэтому по лемме 1
г (х) 0 и, (уі, х,) для y{€[S, +оо).
В силу вогнутости н дифференцируемости и. на множестве X
Л/S'-исход х удовлетворяет системе (6):
xtp'(x)+p(x) = 0.
Таким образом, наша игра имеет единственный Л/Я-исход на диагонали:
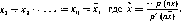
Упражнение 3. Пример 4 (продолжение).
Докажите, что общий выпуск пх при NE-исходе больше выпуска х*, максимизирующего общий доход хр (х).
Докажите, что любая стратегия х{, для которой х* х{, доминируете* стратегией х*. Является ли данная игра разрешимой по доминированию?
Рассмотрим дуополию, которая формализуется как игра двух лиц, в которой множество стратегий каждого игрока есть отрезок [0, 1/2]. Докажите, что функция м,- (х) = x-tp (х) вогнута по х{.
Вычислите функцию наилучших ответов обоих игроков и найдите Л/?-исход. Сравните его с границей Парето.
[1979])
Задача 2. Игра агентов по продаже автомобилей (Кейз
В игре участвуют п игроков, которые являются агентами по продаже автомобилей. Общий спрос фиксирован и равен D. Пусть х,-число автомобилей, которые агент і берет для продажи. Предполагая, что у каждого агента одно и то же число посетителей в единицу времени, получаем, что спрос на машины агента і равен
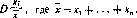
Пусть Р{доход агента с одного проданного автомобиля, а С{ его затраты на хранение одного автомобиля (в единицу времени). Тогда возникает следующая игра в нормальной форме!
1) Найдите недоминируемые стратегии игрока і. Является ли наша игра разрешимой по доминированию?
2) Докажите, что наша игра имеет два Л?Е-исхода и вычислите их. Являются ли они оптимальными по Парето исходами?
3) Сравните соответствующие Wi:-выигрыши в случае, когда
множество агентов разбито на подмножества (1..... nj,
{rtj + l, ..., п}, таких, что для всех і = 1, ...,.пг величина^
С- *
пренебрежимо мала, а для всех і = щ -f 1.....п величина
* І
положительная константа.
Задача 3. Финансирование общественных нужд по добро-вольной подписке
Предположим, что у каждого члена і сообщества N имеется некоторый запас денег М-г
Часть этих денег х) участник может выделить на общественные нужды. Его функция полезности vt (q, /п;) зависит от количества mt оставшихся у него денег, а также от суммы q денег, выделенных всеми участниками на общественные нужды.
Предположим, что функция v-t дифференцируема, строго монотонно возрастает по каждой переменной и вогнута по их совокупности. Таким образом, получается следующая игра в нормальной форме:

1) Докажите, что исход х оптимален по Парето в данной игре тогда и только тогда, когда он удовлетворяет уравнению ЛиндалаСамуэльсона:
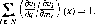
2) Докажите, что функция и; вогнута по переменной xit и выведите существование NE-исхода. Охарактеризуйте NE-исход INI условиями первого порядка.
3) Докажите, что в любом ЛЧ?-исходе количество денег, выделяемых на общественные нужды, меньше оптимального уровня. Более точно, для NE-исхода существует доминирующий его по Парето исход, которому соответствует большее количество средств, выделенных на общественные нужды.
Задача 4. Игра двух лиц с нулевой суммой
Пусть Аь А2две положительно определенные рхр матрицы. Впроизвольная рхр матрица и, наконец, ait
Рассмотрим игру двух лиц с нулевой суммой (Xit Хг, щ), в которой
Xi=Xt = Rr,
^і(.^? *^2) = 2 Хі) + ВХЬ Х2У Ь ~2 {^2Х2 Х2У
+ 1. xt + a2, V-
Докажите, что эта игра имеет единственную седловую пару и вычислите ее.
Задача 5. Война на истощение (Милгром, Вебер [1980])
Каждый из двух игроков стремится завладеть некоторым предметом. Ценность этого предмета для игрока і описывается величиной V;. Победителем является тот, кто дольше остается агрессивным.
Предполагается, что затраты на агрессивность у обоих игроков одинаковы и равны единице. Стратегия х{ игрока і означает: Я буду агрессивным до момента времени t = x{, если только противник не остановится в некоторый момент времени х,- в последнем случае я остановлюсь в момент Лу + e для того, чтобы получить предмет с минимальными издержками.
1) Возникает следующая игра в нормальной форме:(при равенстве для определения победителя бросается монета). Докажите, что наша игра имеет в точности три оптимальных по Парето вектора выигрышей, два из которых соответствуют равновесиям по Нэшу (значит, есть борьба за лидерство).
Докажите, что в любом МЕ-исходе один из игроков использует свою единственную осторожную стратегию и получает гарантированный выигрыш, а другой очень рискованную стратегию.
2) Предположим, что ?і и ?2две независимые равномерно распределенные на [0, 1] случайные величины. Игрок і наблюдает ?{, но не наблюдает vf. Множество его стратегий теперь есть X,-:
Xj € Х(-: X; измеримое отображение из [0, 1] в Х{.
Функции выигрыша определяются так:
Щ fo. *) = $ и, (хг (oj), х2 (oj) dvt dv2.
[О, I]
Докажите существование в игре (Xj, Х2, иь и2) симметричного, доминируемого по Парето Х?-исхода х1 = х2 = х? и вычислите его. Заметьте, что при использовании игроками равновесных стратегий реализуются войны сколь угодно большой протяженности во времени.
Однако математическое ожидание длины войны конечно.
Указание. Предположите, что функция х* возрастающая и дифференцируемая. Докажите тогда, что для всех ?{ € [0, 1] функция
(**) 1 (у)Ф(у)= S (у,x*(t))dtу[\ (я*)-1 (у)]
одолжна достигать максимума на [0, + оо) при y = x*(vt).
3. УСТОЙЧИВЫЕ РАВНОВЕСИЯ
Даже в случае полной информированности (каждый игрок знает составляющие нормальной формы игры, включая функции выигрыша других игроков) концепция равновесия по Нэшу не может быть обоснована, исходя из рассмотрения изолированно принимаемых рациональных решений. Если допустим обмен информацией, то можно использовать сценарий с необязательным соглашением (см. разд. 1). Напротив, в процедурах нащупывания по Курно исследуется динамический процесс принятия близоруких решений, напоминающий механизм совершенной конкуренции.
Каждый игрок максимизирует свой выигрыш, полагая, что стратегии остальных игроков фиксированы. Эта процедура не может быть обоснована соображениями рациональности (поскольку предпосылка о том, что все остальные игроки будут неизменно использовать одну и ту же стратегию, постоянно нарушается).
Тем не менее процедура имеет определенную описательную силу и позволяет разделить /?Е-исходы на устойчивые и неустойчивые. Более того, ее реализация требует минимальной информированности игроков, которую мы будем называть полной неинформированностью (каждый игрок знает только свою собственную функцию выигрыша, а контакты игроков сводятся к совместному наблюдению стратегий)
Пример 5. Устойчивость в дуополии Курно с назначением вып усков
Два игрока поставляют на рынок некоторые количества xt и хг одного и того же товара, цена на который определяется следующим образом:
р(х)=\1с, где х = хг-{-х2.
Рассмотрим два различных предположения о функции затрат:
а) постоянные затраты на выпуск единицы продукции при увеличении масштабов производства: затраты на производство у единиц оцениваются величиной у для обоих игроков;
б) убывающие затраты на выпуск единицы продукции при увеличении масштабов производства: затраты на производство у единиц оцениваются величиной у утУ2 для бих игроков.
Наконец, максимальные производственные возможности обоих игроков равны у (поэтому цена и затраты неотрицательны). В случае а) получаем следующую игру:
*і = ** = [0, 1/2], ui(xi,x2) = xl(\x) ~xi, і=1,2.
Легко вычислить наилучший ответ игрока і на стратегию X/ игрока / (поскольку ,- вогнута по xt).
BRі = дс, = а (*у)/0 */-§}, где а (у) = у~ у
(мы используем обозначения разд. 4 гл.
II).
Единственный /?Е-исход таков:?? = ВЛІПВЛ, = {(, I)}.
Процедура нащупывания по Курно начинается из начальной позиции (Jtj, 4), причем каждый игрок последовательно использует наилучший ответ на текущую стратегию противника:
(4. 4) (4, 4)=(а (4), 4) ? BRt (4,4) = (4, а (4)) € BR** - ,+ (х[, Xt1) = (а (xt1), xt1) € BR1 * (х[, 4) =
= (х\, а (4)) € BR2 (8)
Ha рис. 4 мы изобразили две такие последовательности.
Изобразив самостоятельно еще несколько последовательностей, читатель убедится, что из любой начальной позиции (4.4) последовательности (4, 4) и (4, 4-') сходятся к /?Е-исходу (т т) ¦ ^ качестве упражнения мы оставляем доказательство этого утверждения, а также доказательство геометрической скорости сходимости.) Скажем, что исход (у, у) является устойчивым /ve-исходом.
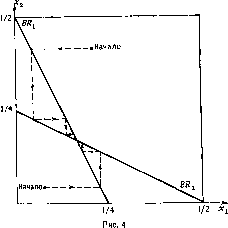
Обратимся теперь к случаю б). Получается следующая игра в нормальной форме:
= [0, 1/2], щ (хи *„) = *,-(I X) (-Jjf,!- *;), 1=1,2.
По-прежнему функция и; вогнута по xt и кривые наилучших ответов имеют вид
В#, = *1 = Р(*,-)0*/-^, где
і г.^- ^ 1
т при 0 у -г-,
Р (//)==S , ,
12у при 2 -
Теперь мы имеем три 1??-исхода
/?? = ??іПВ?2 = {(і, і), (і, О), (О, і-)}.
На рис. 5 мы видим, что, начиная с любого исхода д/ Ф (-І-, -i-J , последовательность (8) всегда сходится к (у, 0) или ^0,
(за конечное число шагов). Это справедливо даже в том случае, когда точка jc сколь угодно близка к точке -М , но не совпадает с ней.
Будем говорить, что (-5-, -^ неустойчивый ME-исход, a (y , О) и ^0, у) (локально) устойчивые.
Упражнение 5
На рис. 6 представлен один из вариантов расположения кривых наилучших ответов BRit і = 1, 2, для игры со множествами стратегий Х, = Х2 = [0, 1]. Проверьте, что все три М?-исхода неустойчивы.
Весьма сложная структура динамической системы (8) в подобной игре проанализирована в работе Рэнд [1978].
Можно дать несколько определений процедуры нащупывания по Курно в играх п лиц: игроки могут изменять свои стратегии последовательно (порядок имеет значение) или одновременно. Соответствующие понятия устойчивости совпадают для игр двух лиц (п 2) и не совпадают в играх по крайней мере с тремя игроками (п 3) (см. упражнение 6 ниже).
Будем придерживаться второго определения.
Определение 2. Пусть множество Xt при всех і С N наделено некоторой топологией. Пусть далее G = (X;, и{; і С М) игра в нормальной форме. Предположим, что каждый игрок имеет единственную стратегию наилучшего ответа на любые стратегии остальных игроков:
для всех і € М и всех xt € X, существует единственная функция Г;(Хі)€Хі, такая, что (гДлу), xt)?BRi. (9)
С любым исходом x?Xn связана процедура (одновременного) нащупывания по Курно, начинающая из х, а именно следующая последовательность х, х\ ..., хі, ... из XN:
хі^ГіІх'Г1), i?N, t= 1,2..... (10)
Скажем, что равновесный по Нэшу исход х* устойчив в игре G, если для любой начальной позиции x??XN процедура нащупывания по Курно, начинающаяся из позиции х, сходится к х*.
Заметим, что устойчивый NE-исход в игре G обязательно является единственным равновесием по Нэшу в игре G, поскольку если начальная позиция есть равновесие по Нэшу, то процедура нащупывания по Курно приводит к стационарной последовательности.
Упражнение 6. Устойчивость процедуры последовательного нащупывания по Курно
Для заданного порядка игроков IV = {1,2, ...,п) процедурой {1, 2.....п)-последовательного нащупывания по Курно,
начинающейся из х, является последовательность
vO yl yt
I /V f f - ^ Л )
4 = r{ (x{,
, где
, 4-i, *m - - - . 4Г1). i € N, t= 1,2.....
Скажем далее, что К S'-исход х* является {1, ..., п\-устойчивым, если для любой начальной позиции х процедура {1, ..., п\-последовательного нащупывания по Курно, начинающаяся из х, сходится к х*.
1) Если п 2, то {1, 2}-устойчивость, ]2, ^-устойчивость и устойчивость согласно определению 2 совпадают.
2) Если 3, то зто разные понятия. Рассмотрим, например, игру трех лиц
f (*) = (Xi x2)2,
X, = Rf t = 1, 2, 3 ,(*) = (*,5-*:s)V
[ m3 (jf) = 3jf2 x3)2.
Единственным /?Е-исходом является точка (0, 0, 0). Докажите, что он не {1, 2, 3}-устойчив, но {2, 1, 3[-устойчнв. Является ли он устойчивым в смысле определения 2?
Достаточные условия устойчивости Ni:-исхода трудно получить, и они оказываются весьма ограничительными (см. Габе, Мулен [1980], Окугучи [1976], Розен [1965]).
Тем не менее если мы ослабим требование устойчивости таким образом, чтобы процедура нащупывания по Курно, начинающаяся около х*, в пределе давала г*, то тогда появится возможность почти полностью описать локально устойчивые У?Е-исходы.
Определение 3 (те же обозначения, что и в определении 1). Скажем, что равновесный по Нэшу исход х* локально устойчив в игре G, если для каждого і € N существует окрестность
К,- точки xf, такая, что на ?дг= X ІЛ выполнено предположе-
iSN
ние (9) и исход х* устойчив в усеченной игре (?;, м(-; і ? N).
Для того чтобы дать вычислимый критерий локальной устойчивости, предположим, что для всех і € N множество Х{ является подмножеством евклидова пространства Е{. Фиксируем равновесие по Нэшу х*, для которого xf есть внутренняя точка Х{ для всех і ? N.
Более того, предположим, что функция полезности м,- дважды непрерывно дифференцируема (С2-дифференцируема) в окрестности xf и что матрица вторых производных задает отри-
дхі
цательно определенный оператор в х* (следовательно, (9) выполнено в подходящей окрестности х*).
Определим линейный оператор Т из EN = X Ej в себя:
іб N
для всех е$Еп! Т,(е)= ? ("ГТ-У*аЖ'е/ (11)
І 6 N\U) ' дхі / ‘ XI
Где все производные посчитаны в х*.
Теорема 3. Предположим, что все собственные числа оператора Т по модулю меньше 1. Тогда х*локально устойчивый NE-ucxod.
Предположим, что х*локально устойчивый NE-ucxod. Тогда все собственные числа оператора Т по модулю меньше либо равны 1.
ди; дх;
в точке
С1дифференЦи-
Доказательство. Поскольку функция д2иі
то по теоне вырожденаруема, а матрицадх\реме о неявной функции г, (локально в X*) есть (^-дифференцируемая функция, действующая из ХЛЧ{,} в Х-. Следовательно, система (10) может быть локально записана какгде f есть С1-дифференцируемое отображение EN в себя.
По предположению х* неподвижная точка отображения /. Значит, из элементарного результата для динамических систем (см., например, Ортега, Рейнбольдт [1970]) получаем, что х* является локально устойчивым решением (12), если все собственные числа оператора f (**) по модулю меньше 1. Обратно, если хотя бы одно собственное число оператора /' (х*) по модулю больше 1, то исход х* не является локально устойчивым. Оставляем читателю проверку справедливости равенства Т f' (х*).
Следствие. Пусть п = 2, а множества Хі и Х2 одномерные. Предположим, что х*NE-ucxod в игре G = (Xit Х2, щ, и2), причем выполнены следующие условияі
1) xfвнутренняя точка Xit
2) функция U; Са-дифференцируема в окрестности х*,
3) (**) -
дх{
Тогда получаем
1 д2и, дги
д2щ д2и2 дх! ’ дх! д2иі д2и2 дх! дх!
=Флг* локально устойчива,
=$х* не является локально устойчивой
дхг дх2 д2и2
I дх і дхз I д2щ
I дхі дх2 дхі дхг
(13)
(все производные взяты в точке X*).
В предположениях следствия множества наилучших ответов BRt являются двумя кривыми класса С1, пересекающимися в х**
Теория игр в нормальной форме
Теория игр в нормальной форме развита в более общих предположениях, индивидуальные функции полезности здесь не предполагаются траисферабельными и даже сравнимыми (см. гл. 1, II, III и VI, разд. 1 4). В данном случае мы ограничиваемся траисферабельными функциями единственно в целях простоты.Ссылки на литературу по играм в характеристической форме без побочных платежей могут быть найдены в работе Аумана [1976].
Следующие два определения аналогичны определениям дележей и а-ядра для игр в нормальной форме.
Определение 8. Дележом в игре ? в ?-характеристической форме называется вектор x=(xt)ieN из Rw, для которого
2 Xi v(N), Х{^?({і}) для всех i?N.
іе л/
Обозначим через I (у) множество дележей игры (V, у).
Применяя итеративно условия супераддитивности (17), получаем
2 о ({/})* (Л).
ібЛ/
Для супераддитивных игр множество дележей I (?) не пусто. о({і})это уровень дохода, который игрок і может себе гарантировать сам. Поэтому ? ({і}) играет роль гарантированного выигрыша для игр в нормальной форме.
Доказательство леммы 2 подчеркивает прямую связь двух понятий дележа.
Если игра {N, ?) такова, что выполнено равенство 2 и ({}) =
ібЛ/
== ? (N), то множество / (у) состоит из одной точки, а игра (N, ?) называется несущественной (см. интерпретацию определения 5 гл. I). В этом случае из супераддитивности ? следует ее я дли-тивность (из (18)):
для всех S^N y(S) = 2 у({*})-
i € 5
(Доказательство этого факта оставляем читателю в качестве упражнения.) Для игр, не являющихся несущественными, ядро это возможно пустое подмножество дележей, стабилизируемых простыми угрозами.
Определение 9. Ядром игры (N, у) называется подмножество таких дележей х g / (у), для которых выполнено:
для всех коалиций S е N
2 ^o(S)- (19)
i€S 4 '
Будем обозначать ядро через С (у).
Пусть игроки договариваются о выборе кооперативного соглашения. Поскольку игра у супераддитивна, такое соглашение предполагает образование коалиции всех игроков N. Обсуждаться может только вопрос о способе дележа общего дохода v(N), т. е. о выборе вектора x?RN, для которого 2 x{ = v(N).
іеЛ/
Минимальным требованием для получения согласия игроков выбрать вектор х является индивидуальная рациональность этого вектора, т. е. условие хг^у({і}), і g N. Таким образом, игроки договариваются о выборе конкретного дележа х. Против выбора дележа х может возражать некоторая коалиция S, требуя для себя более выгодного распределения (например, t/g/(y), для которого у; х{ для всех і ? S). Коалиция S выдвигает это требование, угрожая в противном случае нарушить общую кооперацию (эта угроза вполне реальна, ибо для достижения дохода v(N) требуется единодушное согласие всех игроков). Предположим, что остальные игроки Se реагируют на эту угрозу отказом от всякой кооперации с членами коалиции S. После этого максимальный суммарный доход коалиции S оценивается числом y(S).
Условие (19) означает существование стабилизирующей угрозы коалиции S со стороны коалиции Sc. Таким образом, ядром игры (N, у) является множество устойчивых в смысле коалиционных угроз распределений числа v(N).
Кроме указанной интерпретации ядра с предостерегающими угрозами приведем эквивалентную интерпретацию с нормативной точки зрения.
Лемма 7. Пусть х?І (и)дележ игры (N, у), х принадлежит ядру е том и только том случае, когда для всех коалиций ScN выполнено
Доказательство. Поскольку 2 xi = v(N), то приведенное
Выше неравенство можно переписать так:
0(SC) 2 */¦ ' і е s
Пример 7 (продолжение).
Вектор х = (xs, хр, xD) в игре ,джаз-оркестр" принадлежит ядру тогда и только тогда, когда
Это множество является выпуклой оболочкой следующих трех дележей:
(350, 450, 200) (350, 500, 150) (300, 500, 200).
Таким образом, выигрыши всех игроков определяются с точностью до 50 $. Типичным представителем ядра является центр (среднее арифметическое крайних точек) множества С (?), а именно:
х* (333.3, 483.3, 183.3)
Для дележа х* характерно, что все двухэлементные коалиции имеют одинаковый дополнительный доход: х(-\-х{?({і, /}) = = 16.6 $. Дележ х* является справедливым компромиссом внутри С(?).
Из того, что ядро пусто, не следует невозможность кооперации всех игроков N. Это означает просто, что никакой дележ не может быть стабилизирован с помощью простых, естественных угроз, описанных выше. В этом случае кооперативная устойчивость требует более сложного поведенческого сценария подобно угрозам и контругрозам, описанным в разд.
2 (см., в частности, задачу 3). На этом пути мы придем к концепции переговорного множества, предложенной в работе Аумана, Машлера [1964].
Пустота ядра наблюдается в том случае, когда промежуточные коалиции слишком сильны. Это утверждение проясняется следующим примером.
Пример 8. Симметричные игры
В симметричной игре коалиции с одинаковым числом игроков имеют одинаковый выигрыш. Характеристическая форма о
Гл. ?і. СтабилЬнодМЬ ДО дбнобе ytpM
Имеет следующий вид:
? (S) = ?? (s), где s = I $ I для всех ScAf.
Предположим без потери общности, что у*(1) = 0 и N = { 1, 2, Тогда множеством дележей игры у* является сле
дующий симплекс в Rn:*€ / (?*) ФФ 2 = у* (я), *(0, і = 1, .... п.
; =1
Ядром С (у*) является подмножество / (о*), определенное конечным числом (точнее: 2Пп2) линейных неравенств (19).
Таким образом, ядроэто, возможно, пустой, выпуклый многогранник внутри симплекса / (у*) *). В силу симметричности у ядро С (у*) тоже симметрично, т. е. инвариантно при любой перестановке компонент х? ..., хп.
Учитывая, кроме того, выпуклость С (у*), получаем, что множество С (у*) не пусто в том и только в том случае, когда оно содержит центр х* множества / (у*), а именно xf=*l/n, і 1.....п. Возвращаясь к системе (19), получаем, что
[С(н*)#0]^ для всех s=l, .... п -і- v* (s) ^ v* (п) j .
Таким образом, ядро С (?*) не пусто тогда и только тогда, когда не существует промежуточной коалиции S, в которой средняя доля каждого игрока больше соответствующей величины в коалиции N.
Возвращаясь к общему случаю, охарактеризуем непустоту ядра с помощью линейного программирования.
Определение 10. Для данного множества N обозначим через Р (і) множество коалиций, содержащих игрока і:
Сбалансированным семейством коалиций) назовем отображение б из P(N) в [0, 1], для которого
для всех i?N 2 1.
SeP( о
Наконец, игру в характеристической форме (N, ?) назовем сбалансированной, если
2 бои (S) ? (N) для всех сбалансированных семейств
S6P(N)
коалиций б. (20)
Теорема 2 (Бондарева [1962], Скарф [1967]). Игра (N, ?) имеет непустое ядро тогда и только тогда, когда она сбалансирована.
Доказательство. Пусть xgC(?), а бсбалансированное семейство коалиций, тогда
х (S) ^ ? (S) = ?sx (S) ^ 6so (S) для всех SczN. Суммируя эти неравенства, получаем
2
SeP(A/)2 6sx(S)=2 2 sxi = 2*,-=у(Л0-
SePlN) te N Se p (0 ieN
Ssv (S)
Наоборот, если ядро С (v) пусто, то система линейных неравенств-*(#)a (N),
x(S)^v (S) для всех S с N
не имеет решения. Используя стандартные рассуждения (теорему двойственности), получаем, что для всех S найдется неотрица-
9 Соответствует термину сбалансированное покрытие. Прим, перев.
тельное число 6S, такое, что:
для всех д:$RNy\ Х:= 2 65(2*Л и
іел/ SeP(N) \ies )
2 6so (S) v (N).
SeP(N)
Первое из этих свойств эквивалентно тому, что бсбалансированное семейство коалиций, что и завершает доказательство теоремы 2.
В качестве приложения теоремы 2 рассмотрим игру трех лиц I N I = 3. Каждому разбиению N соответствует тривиальное сбалансированное семейство коалиций:
разбиение N: 6^=1, 6S = 0 для всех S=?N,
разбиение {/}{/?}: б{1} = 1, = 1, 6S = 0 в остальных случаях.
Применяя условие (18) к этим б, получаем условие супе-радднтивности игры ?
?(і) + ! для всех {/, /, 6} = {1, 2, 3}. (21)
Далее, коалиционной структуре {12}, {23}, {31} соответствует сбалансированное семейство коалиций б*6*} = ?2 Для всех *. /. ‘ Ф /,
6* = 0 в остальных случаях.
Применяя (20) к б*, получаем
о(12) + о(23) + о(31)2о(123). (22)
Пусть теперь читатель убедится в том, что все сбалансированные семейства коалиций для N являются выпуклыми комбинациями б^, б‘ !/'* и 6*. Следовательно, непустота множества С(?) характеризуется системой неравенств (21), (22).
Следствие из теоремы 2. Любая супераддитивная игра трех лиц имеет непустое ядро тогда и только тогда, когда выполнено (22).
При увеличении числа игроков проверять сбалансированность игры ? становится все труднее). Например, супераддитивная игра четырех лиц обладает непустым ядром в том и только том случае, когда
? (12) + ? (23) ? (34j -ф ? (41) ^2о(1234), ? (123) + ? (234) + ? (134) + ? (124) З? (1234), о(123) + ? (234) + о (14) 2 (1234),
а также выполнены пять аналогичных неравенств, которые получаются из данных перестановкой игроков.
Упражнение 11. Докажите сформулированное выше утверждение.
Задача 8, приведенная ниже, иллюстрирует типичное приложение теоремы 2 к экономическим моделям.
Задача 6. Ядро в простых играх
Игру (N, ?) назовем простой, если
для всех S^N v(S)~0 или 1.
Обозначим через W множество выигрывающих коалиций, т. е,S€W^y(S) = l
1) Докажите, что игра (N, ?) супераддитивна тогда и только тогда, когда подмножество W множества всех коалиций является монотонным и собственным:
S?W, S=T=bTeW для всех S, Г,
sewzs*$w.
2) Игрока i*?N назовем диктатором W, если {/?} выигрывающая коалиция!{*} € W,
Полагая игру (N, ?) супераддитивной, докажите, что W имеет (единственного) диктатора тогда и только тогда, когда игра несущественна.
3) Пусть W не пусто и не имеет диктатора. Игрока і* назовем вето-игроком, если N\{i*} не является выигрывающей коалицией.
Обозначим через N+ возможно пустое множество вето-игроков.
Докажите, что ядро С (о) не пусто тогда и только тогда, когда не пусто множество N+. В этом случае докажите, что
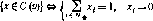
4) Пусть для каждого і голос игрока і имеет вес qt ^ 0. Обозначим через q0 такое число, что
7о 2 q{ 2?о-
і 6 N
Определим взвешенную мажоритарную игру Wq следующим образом:? € Wq фф 2 9; ^ q0.itS
Докажите, что Wq монотонная и собственная простая игра. Докажите, что в этой игре игрок і* является диктатором тогда
и только тогда, когда q0 ^ q.*t и і* является вето-игроком в том и только том случае, если
ItN
5) Сравните полученные результаты с задачей 1 Гл. VI. Задача 7. Выпуклые игры
Пусть (N, ?)выпуклая игра, т. е. такая, для которой справедливо
o(S)-fо(Т);о(SЛТ)-fy(SU'T) для всех S, ГдЛ/.
I) Докажите, что
v(N)v(Sc)= sup {o(SuT’) о (Г)} для всех SczN.
Tc=Sc
Сопоставьте этот факт с утверждением леммы 7.
2) Для любого порядка 1, 2, ..., п в N рассмотрим вектор
*/ = (!, 2.....2, ..., г 1), t= 2.....п.
Докажите, что х принадлежит ядру игры (N, ?).
3) Докажите, что С(?) является выпуклой оболочкой дележей ха, полученных в 2), при условии, что а принимает значение всех возможных порядков в N.
Задача 8. Ядро экономики обмена
Пусть для всех і 6 N ut функция полезности, определенная в неотрицательном ортанте IR?. Мы интерпретируем г ? как вектор потребления, а иг (г) полезность для игрока і вектора г. Обозначим через wt g начальный запас товаров у игрока і.
Игру экономика обмена (с побочными платежами) с функциями (и,, i g N) определим следующим образом:
для всех S^N v (S) = sup J 2 и,- (г,-) 2гг= 2 we, гі€К?і.
(fsS ieS ieS J
1) Предположим сначала, что p=l и N B()S, где для і?В (покупатель) w{ 0, а для igS (продавец) wt= 1.
Пусть функция щ имеет следующий вид:
если і € В
( uf(z) = если /gS
I ujiz) =
( и?(г) = 0 для г 1,
для z 1, U/(z) = S/ ДЛЯ 2 1, О ДЛЯ 2^1.
\ ui(z) = bt
Упорядочим В и S так, что
Ьпь .?J для і'?В = {1, .... пь},
Sj .. ,s, . .smi для j?S = { 1, ..., ms}.
Докажите, что v(N) = ^ (bis;), где t наибольшее целое
1
число, для которого iinf(n6, ms),
Докажите, что если дележ х принадлежит ядру С (у), то должна существовать цена q, такая, что
хі Ь{ q Для і?В, і,
- 0 для i?B, t (?,
*qS/ для jS, //,
= 0 для i?S, / i.
(го)
(23')
Найдите интервал I = [qini, gSUp], обладающий таким свойством: для q ?І дележ (23) принадлежит С (v).
Докажите, что все цены конкурентных равновесий этой экономики обмена принадлежат интервалу /.
2) Пусть теперь рпроизвольное натуральное число и для всех і ? N Uj вогнутая функция, определенная на К?.
Докажите, что игра (N, ?) является сбалансированной и, следовательно, имеет непустое ядро. Докажите, что конкурентное равновесие принадлежит ядру С(?).
ЛИТЕРАТУРА
Арои (Aron R.)
[1962] Paix et guerre entre les nations. Paris, Caiman - Levy Ed. Ауман (Aumann R. J.)
[1976] Lecture on game theory, Stanford, Stanford University, IMSSS
[1978] Survey on repeated games. Stanford, Stanford University, IMSSS. Ауман, Машлер (Aumann R. J-, Maschler M.)
[1964] The bargaining set for cooperative games. Advances in Game Theory, Annals of Math.
Studies n 52, Princeton N. J., Princeton University Press.
- Берж К-
[1962] Теория графов и ее применения. М.: ИЛ.
Бондарева О. Н.
[1962] Теория ядра в игре п лиц. Вестник ЛГУ, сер. мат., мех., астрон., 13, 3, 141142 '- 'Васин А. А.
[1978] Сильные ситуации равновесия в некоторых сверхиграх. Вестник МГУ, сер. мат., мех., 1, 30 40
[1983] Модели процессов с несколькими участниками.М.: Издательство МГУ.
Викри (Vickrey W. S.)
[1959] Self-policing properties of certain imputations sets. Annals of Math.
Studies 40, Princeton, Princeton University Press.
- Гермейер Ю. Б.
[1973] К теории игр трех лиц. ЖВМ и МФ, 13, 6, 14591468.
Термейер Ю. Б., Штильман М. С.
[1975] Некооперативные повторяющиеся игры с произвольным дисконтиро-. ванием. ДАН, 211, 1, 2225 - Кукушкин Н. С.
[1974] Точки равновесия в метаиграх. ЖВМ и МФ, 14, 2, 312320.
Льюс, Райфа (Luce R. D., Raiffa Н.)
[1957] см. литературу гл. I.
- Меньшиков И. С.
[1977] Стационарные стратегии в играх со скользящим дисконтированием.
Вестник МГУ, сер. мат., мех., 4, 1017.
- Меньшикова О. Р.
[1976] Крайние точки С-ядра симметрических игр. Вестник МГУ, серия мат., мех., 5, 6372.
[1977] Методы поиска ядер кооперативных игр и их приложения. Диссертация, Московский университет.
- Миркин Б. Г.
[1977] Cours de theorie des jeux a deux joueurs. Cahier de Mathematiques de la Decision n 7709, Paris, Universite Dauphine.
Мулен, Пелег (Moulin H., Peleg B.)
[1982] Stability and implementation of effectivity functions, Journal of Mathematical Economics 10, 1, 115145.
Мулен (Moulin H.)
[1981] см. литературу к введению Накамура (Nakamura К.)
[1979] The vetoers in a simple game with ordinal preferences. International Journal of Game Theory, 8, 1, 5561,
- Ope O.
[1980] Теория графов. M.: Наука.
- Оуэн Г.
[1971] см. литературу гл. IV. .
Розенталь (Rosenthal R.)
5, 1.
[1972] Cooperative games in effectiveness form. Journal of Economic Theory,
Рот (Roth А.)
[1976] Subsolution and the supercore of cooperative games, Mathematics for Operation Research, 1, 1.
Рубинштейн (Rubinstein A.)
[1979] Equilibrium in supergame with the overtaking criterion, Journal of Economic Theory, 21, 1, 19.
Сен (Sen A.)
[1970] Collective Choice and Social Welfare, San Francisco, Holden Day, Снарф (Scarf H.)
[1967] The core of an N-person game. Econometrics, 35, 5069,
Ховард (Howard N.)
[1971] Paradoxes oi rationality: theory of metagames and political behaviour, Cambridge (USA), M. I. T. Press,
Шеллинг (Schelliig T. C.)
[1971] см. литературу гл. III.
Шерер (Sherer F. M.)
[1970] см. литературу гл. V.
Яиг (Young H. P.)
[1979] The market value of a game, II AS A working paper, Laxenburg,
УКАЗАТЕЛЬ
Арон 155 аукцион 20
Викри 21
второго типа 21, 77
неделимого товара 20, 82
первого типа 20, 82
Ауман 137, НО, 170, 173, 186, 188
агентов по продаже автомобилей 81, 95
аукцион 125
вежливые водители 138
джаз-оркестр 185
китайский покер 119, 128
мариеибадская 51
*¦ музыкальные стулья 142
Ним 50
переговоры 135 * перекресток 139
в смешанных стратегиях 104
пиратские корабли 132
раз-два-игра 33, 101
размещение магазинов 121, 137
с нулевой суммой 3037, 4952, 79, 82. 107, 117
таможенный досмотр 117
торг 156
индивидуально рациональный исход 72, І55
исход игры 15
Берж 67, 78
биматричиые игры 110117 Бинмор 64 блеф 106 Бондарева 190
борьба за лидерство 57, 74, 178, 182
право второго хода 182
первого хода 182 Брамс 14
Брауэр 36
Вебер 83 ведомый 53 Виал 147 Викри 164
война иа истощение 83, 84, 93, 94, 126 Вулф 124
выборы большинством голосов 38 40, 161, 164, 167
- о правом вето 4143, 76 выпуклые игры 194
Кларка Гроувза механизм 24 Кнастера Куратовскоео^т Мазуркееича лемма 78
Кондорсе 9, 161
парадокс 161 контругроза 168 Кун 46
алгоритм 46
теорема 46 Курно 91, 84
-* процедура нащупывания 8495
Габе 89, 92
гарантированный выигрыш 27, 103, 138 Гильбо 99 Гликсбере 121
голосование по Ролсу 5557
Лексикографически осторожная страте гия 29 лидер 53 лидерство 53 лотерея 101
¦ индивидуальная (собственная) 101 совместная 141 Льюс 19, 102. 164
Данфорд 121
двоичный выбор с взаимным влиянием Дележ 156, 175, 186 дерево 43
дилемма^ заключенного 19, 104, 153,
локальная 9697 Дживерс 58
доминирование по Парето 20
стратегий 16 доминирующая стратегия 17 Дутта 58
дуополия 22, 81, 8487, 95, 145, 178 дуаль 34
бесшумная 35
топологическая 52
шумная 34
Машлер 188
Метод дели-выбирай 64 методы дележа 59 парадоксальный 62 Милером 83 Мон мор 100
Ыулен 14, 23, 29. 35, 65,
89, 92, 95,
118. 147. 149, 163. 164.
168. 184
Наилучший ответ 31. 85, 88, 109
отображение 53, 85, 177 Накамура 166
недоминируемая стратегия 16 фон Нейман 79, 164 несущественная игра 27
квази 183 *¦ тт ПОЧТИ 77
Жерар-Варе 149
Игра о нулевой суммой 3037, 4952, 79, 82 107, 117 игра 15
нормальная форма 15
игра в 15
носитель смешанной стратегии 108, 112 Нэш 69
равновесие 69, 87, 90
теорема 78, 102
сильные равновесия 134 смешанное расширение игры 101 смешанные стратегии 101
вполне 108 соглашение 131
необязательное 131 132, 148
стабильное 131, 142, 147149 стратегия 15
стратегическая обоснованность голосования с упорядочением 23 сценарий предостережений 154
Олигополия 2223, 80, 9495 Окугучи 89 Ортега 98
осторожная стратегия 26, 106
Тийс 124 Угрозы 154
устойчивое равновесие 8788 локально 89
Партхаоаратхи 108, 124 Пемг 167
повторяющиеся игры 171 173 полная информация 44 последовательное исключение Доминируемых стратегий 40 почти для всех игр 111 предостережение 154 сценарий 154 предупреждение 158
Фаркуарсон 14, 38
финансирование общественных нужд по добровольной подписке 82
Характеристическая функция 188 игра в форме 185
Равновесие
в доминирующих стратегиях 17
в смешанных стратегиях 102
в совместных смешанных стратегиях 140
по Нэшу 69
по Штакельбергу 53
сильное 134
слабое 147
сложное 40 Рагхаван 108, 124
разрешимость по доминированию 40
локальная 92 Райез 100 Райфа 19, 102, 164 редуцированная игра 45 Рейнбольдт 98
Розен 85 Розенталь 164 Рот 164 Роше 48
Рубинштейн 67, 170 Рудин 123 Рэнд 87
Цена игры 30
--с нулевой суммой 3031
в смешанных стратегиях 79 Цермело 50
Шахматы 50 Шеедиауэр 14 Шеллинг 70, 74, 178 Шварц 121 Шепли 36 Штакельберг 53 Штейнгауя 59 Шоттер 14
Эквивалентные стратегии 18 экономика обмена 193
ос-ядро 160, 175 р-ядро 169, 182 у-ядро 176, 182 Яне 185
Сайон 124
седловая пара (стратегий) 31, 79 Сен 163
ОГЛАВЛЕНИЕ
Предисловие редактора перевода , . .Предисловие......... . , . .
Введение...............
Часть I. Некооперативное поведение игроков 4. Поведение лидера и ведомого ................ со
67 84 6. Другие приложения теоремы Куна
Литература........................
Глава III. Равновесие по Нэшу ...............
1. Определение и обсуждение.................
2. Теорема Нэша о существовании равновесий .........
3. Устойчивые равновесия ..................
Литература ,, ...................... Глава IV. Смешанные стратегии
1. Смешанное расширение игры . ................
2. Вычисление равновесий по Нэшу в смешанных стратегиях , , ,
3. Бесконечные игры
Литература ..9.*...*.........*. Часть II. Кооперативное поведение игроков , 1. Сильное равновесие ...................... Литература.........................
Глава VI. Стабильность иа основе угроз ............
*) В отечественной литературе используется также термин абсолютно оптимальная стратегия, Прим, перев. ) Для существования такой меры достаточно, чтобы в Ху существовало счетное всюду плотное подмножество. Прим, перев. ) Правило голосования называют стратегически обоснованным, если в соответствующей этому правилу игре существует равновесие в доминирующих стратегиях при всех предпочтениях участников из некоторого заданного класса. Прим, перев Функция выигрыша каждого игрока в игре g является суперпозицией отображения я, формализующего правило голосования и функции полезности, заданной на множестве кандидатов А. Прим, перев. ) Функция / (х) называется полунепрерывной сверху, если для любого Я множество {* \ f (x)^ Я) замкнуто. Полунепрерывность сверху функции ? (yt) следует из непрерывности функции к/ (*) в силу равенства
{УХ/1 ? (yt) SS Я) = П {Уі1 ui (Уі xi) ^ M-
КЛХІ
Для случая метрического пространства Лл функция ? (у/,-) является непрерывной. П рим перев. ) Приведем пример несущественной игры. Предположим, что игроки
{1.....п} используют следующую процедуру дележа. Игра проводится в
п этапов. На первом этапе игрок 1 объявляет, что он претендует на некоторую долю *х1.
Игрок 2 можете этим согласиться, а может объявить, что он претендует на некоторую долю х2 л^. Далее игрок 3 может либо принять предложение игрока 2, либо сделать собственную заявку х$ хг и т. д.
На первом этапе игрок і, чья заявка дг,- дг,-_і будет принята игроками і+1, - - - п, получит долю товара дг,- и выйдет из игры. Для остальных игроков повторяется описанная процедура. На этапе п1 остается два игрока.
На последнем этапе п остается один игрок, который и забирает остаток товара. На этом игра кончается.
Нетрудно убедиться в том, что гарантированный выигрыш любого игрока равен 1 /п, а потому игра несущественна и ее исходом является справедливый дележ. Эту игру удобно представлять как игру в развернутой форме.
См. гл. II.
Прим, перев. ) Сходимость последовательностей наилучших ответов подробно исследована в разд. 3 гл.
III. Прим, перев, ) Еще сильнее ограничивает длину партии правило, по которому засчитывается ничья после 50 ходов без продвижения пешки или взятия фигур. Прим, перев. ) Можно представлять себе, что имеется куча из п камешков. В игре G„ игрок 1 произвольно делит кучу на две части, а игрок 2 выбирает одну из них и начинается игра G, и т. д. ... Игрок, выбравший часть, состриг (цую из одного камешка, выигрывает.
Прим, перев. Звездочкой отмечены работы, добавленные при переводе. ) Такие процедуры принятия решений соответствуют гипотезе об ограниченной рациональности участников, не заглядывающих в будущее. Прим, перев. ) Утверждение леммы 1 можно усилить, заменив о,- на 0/ =* *= inf sup щ(уі, у,) а,-. Прим, пврев, Это утверждение неверно, как показывает следующий пример, построенный В. А. Гурвичем. ^Рассмотрим игру четырех лиц с функциями Дайте интерпретацию этого уравнения как непрерывной Версии процедуры нащупывания по Курно. Любой NE-исход х* игры G является неподвижной точкой (15). Найдите почти совпадающие необходимые и достаточные условия (выраженные в терминах оператора Т) того, что 563 - Звездочкой отмечены работы, добавленные при переводе. ) На самом деле, современник Монмора Джеймс Уолдгрейв предложил в аналогичной игре использовать смешанные стратегии. Не ясно, однако имел ли он хотя бы интуитивные представления об оптимальных смешанных стратегиях (см. исторический очерк Райвз [1975]). ) Напомним, что в R существуют замкнутые подмножества без внутренних точек, мера Лебега которых отлична от нуля (и даже такие, дополнение к которым имеет меру не более произвольного е 0). ) К тому же нечетно (см, Харшаньи [1975)). В случае затруднения см. Оуэн [1971] (пример П. 5.9).
Прим, перев. Звездочкой отмечены работы, добавленные при переводе. ) В оригинале doomsday machine.Прим, перев. а) С игрой S из гл. II иа самом деле совпадает игра S (2; 0).~Прим, перев, Правильной простой игрой здесь называется монотонная и суперад-дитнвиая простая игра (см. Оуэн [1971]), Прим, перев. *) См. в Берж {1962], Ope [1980]. Прим, перев. ) Похожий анализ игры трех лиц сі- в работе Гермейера [1973], Прим, перев. По этому вопросу см. также Васин [1978], Васин [1983.] Примй перев. ) Аналогичные условия получены в работе Гермейер, Штильмаи [1976J. В некоторых случаях рассмотрение стационарных стратегий в памятью на один ход не ограничивает общность рассуждений (см. Меньшиков [1977]), Прим, перев. ) Величина у,- характеризует максимальный гарантированный выигрыш лидера (игрока і) без предположения благожелательности ведомого.Прим. перее. ) Из доказательства теоремы 1 следует, что класс III естественным образом разбивается на четыре группы игр.
lllj. CpfCv=Cp. В этом случае, как и для игр класса II, ведомым быть лучше, чем лидером, так как Однако теперь возможен компро
мисс, при котором у лидера нет оснований отказываться от лидерства.
1112. 0^00^= ? Лидером быть лучше (ySsp), но возможен компромисс, устраняющий опасность захвата лидерства ведомым игроком.
1113. СрПС? = Оі = (х I і (x)5s Yi "2 (*) S* p2}- „Естественным лидером в играх этой группы следует считать игрока 1.
1114. Cpf)Cy = D2~ {х I и2 (х) S? уз, j (х) Эг Pi}.
Случай, симметричный ІІІ8. Компромисс фактически сводится к выбору лидером игрока 2. Прим, пере?. ) Крайние точки ядра симметричной игры описаны в работе Меньшикова [1976]. Прим, перев. ) Это объясняется тем, что сбалансированных семейств коалиций (сбалансированных покрытий) становится слишком много. Их полное описание при I /V I С 6 см. в работе Меньшикова [1977].
Прим, перев. Звездочкой отмечены работы, добавленные при переводе.
ВЫЧИСЛЕНИЕ РАВНОВЕСИЙ ПО НЭШУ В СМЕШАННЫХ СТРАТЕГИЯХ
На самом деле мы обнаружили нечто большее: если игрок / использует стратегию ц+, то игроку і безразлично, какую выбрать стратегию. Следовательно, равновесная стратегия игрока і создает как раз такой уровень неопределенности, что все ходы игрока / неразличимы для него по выигрышу.Это свойство рассмотренной игры не является редким. В разд. 2 мы покажем, что это необходимое свойство всех вполне смешанных NE-исходов, т. е. таких исходов, в которых вероятность того, что данный игрок выберет любую данную стратегию, не равна нулю.
Вполне смешанные равновесия не только легко интерпретируются, но и легко вычисляются (см. лемму 3, разд. 2).
Заметим пока, что в отличие от двух WjE-исходов в чистых стратегиях (вполне) смешанный МЕ-исход доминируем по Парето (соответствующий ему вектор выигрышей ^ 1 *
12^ё) вектором выигрышей (1, 1)). Однако
ситуация (р*, р*) симметрична (р* = р*) и равноправна (и* = ?), поэтому она может быть рекомендована с нормативной точки зрения.
На самом деле в симметричных играх всегда существует симметричное равновесие по Нэшу в смешанных стратегиях.
Упражнение 2.
Пусть (Х{, щ\ i?N)симметричная игра:
Xt = X/ для всех (, j € N,
Ui (х{, xN\{L,}, xj) = uf{Xj, xNK[U /}, xt) для всех i, j?N, x?XN.
Докажите, что смешанное расширение имеет по крайней мере один симметричный МЕ-исход у:
Иі ру для всех / ? N.
Указание. Следуйте доказательству теоремы 2 гл. II, положив
Ф(р, ?) = ы1(рІ, ?/)Mj(v) для всех р, \?MN.
Упражнение 3, в котором равновесная по Нэшу стратегия не является осторожной
Мы уже знаем (примеры 2 и 3 гл. Ill), что /??-стратегия может не быть осторожной.
Здесь мы покажем, что то же самое может случиться и в играх со смешанными стратегиями. Рассмотрим игру G 2x2: Докажите, что в смешанном расширении игры G каждый игрок имеет единственную осторожную стратегию ррг и существует единственный М?-исход (р^, рг).
Проверьте следующие соотношения:
"і Р?) р) = (Р?, р?) = і (Рі. РЙ-
Дайте интерпретацию.
Упражнение 4. Пример блефа
Имеются две картыстаршая и младшая. Игрок 1 с равной вероятностью вытаскивает одну из них, причем делает это в тайне от игрока 2. Затем он решает: либо дать доллар второму игроку, либо играть дальше.
В последнем случае игрок 2 принимает решение: либо спасовать, и тогда он дает доллар игроку 1, либо играть дальше. В последнем случае карта игрока 1 открывается и игрок 2 платит 4 доллара игроку 1, если это оказалась старшая карта, в противном случае игрок 1 платит 5 долларов игроку 2.
Смоделируйте эту игру двух лиц с нулевой суммой в нормальной форме и вычислите оптимальные смешанные стратегии обоих игроков и цену игры в смешанных стратегиях.
Упражнение 5. Игра двух лиц с нулевой суммой и линейное программирование
Для игры G = (Xt, Х2, их) докажите, что решение задачи линейного программированияшаха
щ€Л1і. а их (р1( для всех *2€Х2 (6)
относительно переменных (а, рх) дает цену игры в смешанных стратегиях и оптимальную смешанную стратегию игрока 1. Что можно сказать о задаче, двойственной к (6)?
Задача I. Смешанные стратегии в игре двух лиц с нулевой суммой выгодны обоим игрокам
Пусть (Хь Х2, і)игра двух лиц с нулевой суммой без цены:
sup inf ut ах a2 == inf sup uv
Xi Xt Xg X,
1) Предположим, что для любой фиксированной чистой стратегии xt С Xt отображение xf + их взаимно однозначно на Ху ({і, /} = {1, 2}). Докажите, что цена vm(ut) принадлежит открытому интервалу \dt, a2).
2) Приведите пример (с нарушением предположения о взаимной однозначности), в котором
sup inf щ = ?т (Иі) inf sup uv
*1 *i * X,
Задача 2.
1) В предположении, что игра двух лиц G (Xt, Х2, щ) имеет цену, докажите, что любая выпуклая комбинация оптимальных стратегий в игре G является оптимальной стратегией в игре Gm. Приведите пример, показывающий, что обратное утверждение не верно.
2) Пусть теперь G = (X,., щ\ i?N)игра в нормальной фор
ме. ГІокажите на примере, что недоминируемая чистая стратегия хг игрока і в игре G {xt ? (,- )) может быть доминируе
мой в игре Gm.
3) Докажите, что если xtдоминируемая стратегия игрока ? в игре G (Х{ ? S{ (/)), то в игре Gm найдется по крайней мере один NE-исход ц, в котором игрок і не использует стратегию xt:
4) Докажите, что если игрок і имеет доминирующую стратегию р,- в игре Grn (р(- ? Di (М;)), тогда все чистые стратегии xh такие, что р,- (лг() 0, эквивалентны и на самом деле являются доминирующими в игре G (x,?Df (и,)).
Задача 3. Взаимозаменяемость смешанных NE-исходов в играх двух лиц (Партхасаратхи, Рагхаван [1971])
В смешанном расширении йт (Мх, М2, ии и2) игры двух лиц AfjE-исходы, вообще говоря, не являются взаимозаменяемыми:
из р, p'€N?(GjHe следует (pf, р^,), (р[, р2) € W?(GJ.
Такая ситуация имеет место, например, в смешанном расширении игры перекресток (см. пример 2 выше).
1) Докажите, что N Дисходы игры Gm взаимозаменяемы тогда и только тогда, когда множество NE(Gm) является выпуклым подмножеством RXixR*2 (множества Х{ предполагаются конечными).
2) В предположении, что NE(Gm) выпуклое (и, следовательно, в силу 1) прямоугольное) подмножество множества MjXA12, докажите существование по крайней мере одного смешанного NE-исхода р*, который либо доминирует по Парето любой другой смешанный (VjE-исход, либо имеет такой же вектор выигрышей:
Vp $NE(Gm) иДрХиДр*) (=1,2.
2. ВЫЧИСЛЕНИЕ РАВНОВЕСИЙ ПО НЭШУ В СМЕШАННЫХ СТРАТЕГИЯХ
Определение 2. Пусть Xt конечное множество стратегий игрока (, ( € N. Для произвольной смешанной стратегии pf € М{ обозначим через [р,-] носитель р,, т. е. множество чистых стратегий игрока (, которые входят в р, с положительной вероятностью:(хг) 0}.
Скажем, что смешанная стратегия р; является вполне смешанной, если ее носитель есть все множество (чистых) стратегий, т. е. Ы = Xf. Назовем исход р в игре Gm вполне смешанным, если р{вполне смешанная стратегия при всех i?N.
Теорема 2. Предположим, что исходная игра G = (Xit up, i?N) имеет конечные множества стратегий. Пусть р g ? NE (Gm)равновесие по Нэшу в смешанных стратегиях. Тогда справедлива следующая система равенств:
(7)
?і ? N, ?х; € [р,] щ (ЬХ{, р,) = щ (р).
Доказательство. Фиксируем i?N. Тогда по определению ситуации равновесия по Нэшу имеем
и,-(6*., р,-)м;(р) для всех *,€'[р/]. (8)
Предположим, что хотя бы одно из этих неравенств строгое; иі (б*? I*/) иі О4)-
Умножая все неравенства из (8) на р; (xt) и учитывая, что Р/ (х[) 0, получаем
Щ(р) = иі( 2 рЛ= 2 рЛ
і 2 Р,- (xt) I щ (p) = и, (p).
6 ["Л /
Полученное противоречие доказывает, что все неравенства в (8) на самом деле обращаются в равенства. Щ
Согласно теореме 2, равновесие по Нэшу в смешанных стратегиях р обладает следующим свойством: любая смешанная стратегия pj с тем же носителем, что и р,-, является наилучшим ответом игрока і на р;. В частности, если р есть вполне смешанное равновесие, то любая стратегия игрока і является наилучшим ответом на набор рг равновесных стратегий остальных игроков.
Следовательно, в игре двух лиц в состоянии вполне смешанного равновесия игрок і выбирает стратегию, которая уравнивает выигрыши игрока /' при всех его (смешанных) стратегиях. Эта стратегия не зависит от функции выигрыша игрока і. Этот факт проиллюстрирован на разобранном выше примере 2 и в лемме 3 (она будет приведена ниже).
В то же время в игре с тремя по крайней мере игроками стратегии вполне смешанного равновесия должны определяться совместно, причем Иі зависит от платежной функции щ в силу системы (7).
Теорема 2 является основным инструментом, позволяющим вычислять исходы равновесий по Нэшу в смешанных стратегиях. В самом деле, предположим, что мы ищем исход ?NE(Gm), считая носители всех стратегий р,- заданными, т. е,
(9)
Тогда система (7) переписывается в следующем виде;
?( € N ?л:,., у{ ? Y{ ut (6*., pf) = u( (Ьу., p?). (10)
Система (10) дает 2(І^гІ 1) независимых одномерных урав-
І6 N
нений. В силу (9) каждая стратегия pf состоит из ( Yt 1) независимых переменных ^принимая во внимание условие
2 р,- (*,- ) = 1Y Эти простые рассуждения могут быть сущеет-х‘ 6Y‘ /
венно развиты. Они приводят к следующему утверждению.
Фиксируем Хг, i g N; тогда существует открытое всюду плотное подмножество Q из (КЛгл,)Л/ такое, что для всех наборов (и,.); е Л/ из Q и всех прямоугольных подмножеств YN = = X у, из XN система (9), (10) относительно неизвестных pf М;,
f е Л/
і € М, имеет не более одного решения.
Поскольку XN имеет конечное число прямоугольных подмножеств, то отсюда следует, что если (ы,-)гел/ принадлежит Q, то соответствующая игра Gm имеет конечное число ME-исходов: NE(Gm) в общем положении конечно (при (Де д/ из Q), Когда множества стратегий Х{, і ? N, содержат (очень) малое число элементов, то следующий алгоритм позволяет полностью определить NE (Gm). Фиксируем прямоугольное подмножество Yл/ из XN. Решаем систему (9), (10) относительно переменных р, g М{ для всех i g N Для каждого решения р нужно проверить остальные неравенства
V/ € М Vxi?Xi\Yi ы,-(б*., p/)Mf(p„ pf). Биматричные игры
Для игр двух лиц описанные выше вычисления становятся более наглядными при использовании матричного представления, которое мы уже описывали для простых примеров. Выигрыши игрока і теперь заданы матрицей
Ui~ [ні (xt *)]**і*
х% €
где Хгмножество строк, а Х2множество столбцов. Смешанная стратегия р, ? М, есть вектор-строка
Рі= [Рі (Л'і)]^і е х,,
а смешанная стратегия р2 € Mt есть вектор-столбец
Рг = f Рг (^а)1*і е Xs-
Выигрыш игрока і есть обычное матричное произведение Щ (Рі Ра) " Рі^іРг-
Предположим, что (pt, р2)вполне смешанный NE-тхом,. Тогда система (10) принимает вид
(И)
^ 1р2 "
\hUs = vjLx„
где С/,-р2 есть /??-выигрыш игрока t, а fx, (соответст
венно і*,) вектор-столбец (вектор-строка), все компоненты которого равны 1.
Лемма 2. Пусть Хх = Х, и Uv U2две невырожденные XtxXz матрицы. Тогда если игра G = (Xx, Х2, Ult Ut) имеет вполне смешанный NE-ucxod (рх, р2), то он единствен и задается так:
где V; -1, 2.x,Ui х,
Обратно, если векторы р1( р2 удовлетворяют (12) и все их компоненты неотрицательны, то пара (рх, р2) является смешанным NE-исходом в игре G.
Доказательство. Умножая первое уравнение в (11) на 1/р1, получаем р2 = Умножая последнее равенство на і*,,
имеем 1 = іхг-Н'2==уДх!Уі"1:1;с1, следовательно, число ?г отлично от нуля и равно l/i^l^ix,. Обратное утверждение доказывается также легко: из (12) выводим (11), поэтому
I Pit^psj для всех
I = для всех р4€М2-
Заметим, что (р2, р2) вполне смешанный AfjE-исход только при условии, что все его компоненты положительны. Система (12) этого не гарантирует. Для вычислительных целей лучше представлять равновесные выигрыши в (12) следующим образом:
(13)
, det (Up
2 VCi(*u
Х\ € Хі АГд б Xj
где Uc(xu х2) обозначает алгебраическое дополнение элемента (х? х2) в матрице U.
Часто приходится довольствоваться утверждениями для случая общего положения, т. е. верными для почти всех игр.
Определение 3. Пусть множества стратегий игроков Xt и Х2 конечны. Скажем, что некоторое свойство Р выполнено почти для всех игр, определенных на Х1хХ2, если множество
{(и "2)€Кх,хХ*хКх‘х;Чдля игры (Хх, Х2, ии ы2) не выполнено Р)
имеет меру Лебега, равную нулю, и содержится в некотором замкнутом подмножестве без внутренних точек пространства ц?Х,хх2 [rx,xx„ (снабженного обычной топологией) ),
Теорема 3. Пусть Хх и Хгзаданные конечные множества. Почти для всех игр, определенных на X, х Х2, выполнено следующееі
множество равновесий по Нэшу в смешанных стратегиях конечно%) и для любого равновесного по Нэшу исхода игры в смешанных стратегиях (р1) р3) ? N Е (Gm) множества [[хг] и [р3] состоят из одинакового числа элементов.
Доказательство. Напомним, что система из k векторов \еи ек\ пространства R называется аффинно независимой, если система из k 1 векторов (ejек, ..., ек_х ек) линейно независима в IR.
Будем говорить, что игра регулярна, если выполнено следующее условие:
для любых /,сХj и /3сХ3
1) система из /J векторов и[^ (хх) (их (хи х2))Хг6І!(х1^І1) имеет максимальный аффинный ранг в R/z, (14)
2) система из /а векторов и^ (хг) = (и2(хи x2))XiSi,(xs^I2) имее-т максимальный аффинный ранг в IR{.
Ясно, что почти все игры, определенные на XtxX, являются регулярными в смысле условия (14),
Пусть игра (Xj, Х3, и? ы3) регулярна и (р,і( р3) € НЕ (Gm) равновесие по Нэшу в смешанных стратегиях. В силу свойства (7) теоремы 2 для любого фиксированного элемента хі € [р2] выполнено _
?х2 ^ [Ргі ^2 СМ'х ^2г2) ~ П3 (Рі, бд.о ),
ИЛИ /
?Х2 € LmJ 2 4,2{хх, х2) [Aj (Xj) = 2 U2 0^11 Xz) Мт t^l)-
АГ,6[ц,]
Итак, I [p3] I векторов (x3) (x2 € [p3]) лежат в одной и той же гиперплоскости пространства Если бы в [pj содержалось
меньше элементов, чем в [р3], то это противоречило бы регулярности в смысле (14).
Таким образом, [р3] г^[Рх]. Аналогичным образом из теоремы 2 вытекает, что [Р'1]Іг^ІІЛ]- Следовательно, [Рх] = [РаЦ.
Осталось доказать, что множество NE(Gm) конечно. Если бы оно было бесконечно, то нашлись бы две пары по Нэшу смешанных стратегий (ри р2) и (р^, р4), такие, что
[Рі] = [РіІ! [Ра] ~ ІИв]* (Мі M's) (М! И-з)-
Пусть, например, pt Ф р^. Выберем произвольный элемент € [р2]. В силу свойства (7) теоремы 2 имеем
^2 (і^ІІ ^2 (Пі ®л)*2^. б*,)=й2(рь бхо).
(15)
€ [р2]
Однако [р2] векторов и[^ (х2), л;2€[р2] имеют по предположению максимальный аффинный ранг в IRCm.i1, другими словами,
( Ln-a] I !) вектрв {ul/i] (x2) u[ill] (4)), х2 g Ги2] \ хі имеют максимальный линейный ранг, равный) [р2] 1 (напомним, что ІЫЫЫІ)- Между тем рх, м-і€и р,х#рь поэтому векторы pf и р^ линейно независимы.
Итак, в силу условия (15) получаем, что ранг системы векторов {(ы^і] (*2)ы[т3 (4))},2б[(1г] ч х$ не больше ([р2] 2. Полученное противоречие доказывает теорему.
Теорема 4. Пусть Хг и Х2 фиксированные конечные множества. Почти для всех игр, определенных на Xt х Х2, справедливо следующее утверждение:
Равновесные по Нэшу исходы в смешанных стратегиях, которые не являются равновесными в исходной игре, не являются оптимальными по Парето в смешанном расширении игры.
Доказательство. Пусть (рх, р2) (Е НЕ (Gm). Покажем, что исход (р1( р2) не является оптимумом Парето в игре Gm == = (Мг, М2, иь ы2). Пусть игра (Хи Х-2, uit и2) регулярна (т. е. выполнено свойство (14)).
Из доказательства теоремы 3 имеем I [м-і] I = I [м-г] I- Обозначим через И1 и И2 квадратные матрицы порядка I [рх] IXI [р2] , полученные ограничением функций щ и ы2 на [Рі]х[р2]. Обозначим также через р, вектор-строку (pj (я,),
-^і € [м-і]) а чеРез равектор-столбец (р2(л;2), х,€[р2]). Пусть іі (іг) обозначает вектор-строку (столбец) пространства с компонентами, равными единице. Из свойства (7) теоремы 2 получаем
(M-i М-а) * = (М-і М-а)' tfl-i- (16)
Предположим, что матрицы Ut и U 2 не вырождены (напомним, что они квадратные) и удовлетворяют следующему свойству:
I ^€R ±1U^Ui = alii,
\ У2Уг1і. = аа-і2.
В силу (16) имеем
р^ = Ы2 (pj, р2) - H-i ¦ ?72 *; Pg Mj (pj, p2)?/11-H,
Поскольку матрицы Ui и U 2 невырождены, то (^(рх, ц2)ф0 и и, (рх, р2) Ф 0. Итак, свойство (17) эквивалентно следующему:
(18)
(19)
\ 1-7 2 Ш ' -^-2*
Условие (18) можно переписать так:
3?й* = 0 и fc1C/2M-2 0, 362еі?М і3-62 = 0 и ^t/AX).
(Для доказательства эквивалентности (18) и (19) нужно использовать лемму Фаркаша.)
В силу (16) для всех Х0 и Ьи Ь2, удовлетворяющих (19), получаемА + Mi) U і (р* + р1У1р2 =
= * (biU^ + frUA + MJJM = X W^-ЩиА). (20)
Аналогично?Х, 0 (pj + Xfrj) U2 (р2+ М*) = ^ А^гРг 4 Х^И ,2) 4 9l^2P2
Следовательно, в силу (19) для достаточно малой X 0 имеем
Pj?/jP2 (pi 4* Xfx) U j (р2 4 Xf3)i (21)
Рх^гРг (14 4 ^x) (Рг "1" ^г)
Отметим, что по построению рх (хг) 0 при хг ? [р,] и р3 (х2) 0 при х2 ^ [р3]- Следовательно, в силу (19) для достаточно малых X 0 получаем
?*х € [pi] (Pi + Щхг 0 2 (Рх 4 Щ)хг = 1.
(22)*1 е [ц,] ^
? *2 € [р2] (9а 4 Щ)х, . 2 (Рг + ^г)*, = 1 -
*2€[Hs!
Иначе говоря, соответствующие векторам (pi+Xbj) и (р3+лЬ3) смешанные стратегии pJ^Afi с носителем [рх] и р? € М2 с носителем [р3] в силу (21) удовлетворяют условию
/ ui (Рі 9а) иі (91 (^а)' ^23)
\ Ы3 (рх, ра) М3 (рх, рг).
Итак, исход (рі, р3) не является оптимумом Парето в игре (Мл, М2, и2, и2). Чтобы прийти к этому заключению, нам пришлось предположить, что исходная игра регулярна и что ограничения Mj и и2 на [pj х [р2] не вырождены (если их отождествить с квадратными матрицами) и, кроме того, удовлетворяют свойству (17).
Заметим, что свойство (17) заведомо не выполнено, если Ux и U2матрицы 1 х 1, или, другими словами, (М'і. (^а) пара чистых стратегий. Напротив, если Ut и U2 квадратные матрицы с хотя бы двумя строками, почти все пары (Uv U2) состоят из обратимых пар, удовлетворяющих условию (17). (Доказательство оставляем читателю.)
Пусть ймножество регулярных игр, таких, что при /jdXj и /jcXj (I /t (= I /21 1) ограничения их и и2 на /1Х/2 являются невырожденными матрицами, удовлетворяющими условию (17). Тогда множество й открыто и всюду плотно (как конечное пересечение конечных всюду плотных множеств) и его дополнение имеет меру Лебега, равную нулю (поскольку оно является конечным объединением многообразий коразмерности 1). Это доказывает утверждение теоремы 4.
Пример 3, Биматричные игры 2x2 (у каждого игрока по две стратегии: Т, В и L, R, которым на рисунке соответствуют стратегии Верх, Низ и Слева, Справа).
Рассмотрим следующее семейство биматричных игр
Игрок 1
Предположим, что а{, bh c;, d{ четыре различных действительных числа (і=1, 2). Этого достаточно для исключения вырожденных случаев: множество NE (Gm) всегда будет конечно.
Имеется три класса игр.
Случай 1. В исходной игре G по крайней мере один игрок, скажем игрок 1, имеет доминирующую стратегию, скажем Т Тогда игра С и ее смешанное расширение Gm имеют единственную ситуацию равновесия по Нэшу:
{(Г, L)} при йі Cj, {(Т, R)} при аг с2.
NE{G) = NE{Ga)~
В самом деле, неравенства ах bu сх dx приводят к тому, что в игре Gm чистая стратегия Т строго доминирует все остальные смешанные стратегии.
Случай 2. Игра G не имеет равновесия по Нэшу Это может быть следствием выполнения одной из систем неравенств
{Рі ^1 @2 ^2 ^2 ^2}
ИЛИ
{^х С ^1 Сх, С2 ^2 ^2 ^2}
Тогда смешанное расширение Gffl игры G имеет единственный Л/?-исход, а именно вполне смешанное равновесие:
? _ / d2ft2_ а2С2_
(24)
^ \ a2 + d2b2 с2 ’ a2 + d2ft2с2
_ ( rfi~ci сцbj
^ V ai + ^i biCi ’ a1 + d1b1c1
Соответствующие равновесные выигрыши определяются так:
aidjfcxCx ax+dfbiex *
а2Л2b2c2 a2 -\-d2b2c2
(25)
Эти формулы являются непосредственным следствием леммы 3 и уравнения (13): в силу предположений случая 2 либо Ut невырожденная матрица, либо мы можем добавлением константы с к матрице U{ сделать матрицу U(-j-c невырожденной. Эта операция не изменяет множество І?^-исходов и добавляет ту же константу с к І?^-выигрышам.
Случай 3. Игра G имеет два равновесия по Нэшу
Это получается при выполнении одной из систем неравенств
{^х С аи Сх; ^1 ^2 С ^2* ^2 ^2}
или
{af Ь1г dt с2, a2 с2, d2 b2}.
Тогда в игре Gm возникает еще один і?^-исход, а именно вполне смешанное равновесие (p,f, p,f), определяемое из (24):
NE{Gm) = NE{G)U {(м-*. р?)}-
В качестве упражнения оставляем читателю проверить, что случаи 1, 2, 3 есть в точности разбиение семейства биматрич-ных игр 2x2, удовлетворяющих условию о взаимной однозначности.
Упражнение 6
Приведите пример биматричной игры G 2x2, в которой ни у одного игрока нет эквивалентных чистых стратегий, а множество НЕ (GJ бесконечно.
Упражнение 7. Игры 2x2 с нулевой суммой Рассмотрите семейство игр 2x2 с нулевой суммой:
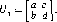
Случай 1. Пересечение [а, d]C\[b, с] не пусто.
Тогда игра G имеет цену. При рассмотрении ее смешанного расширения ничего нового не получается.
Случай 2. Пересечение [a, d] П [b, с] пусто.
Тогда игра G не имеет цены, а в игре Gm существует единственная седловая пара, причем она вполне смешанная. Цена игры Gm определяется так:
ad be a+dbc’vm(G)
Упражнение 8
Дайте геометрический метод вычисления цены игры в смешанных стратегиях и оптимальных смешанных стратегий для любой игры двух лиц с нулевой суммой, в которой хотя бы у одного игрока имеется только две чистые стратегии). Примените этот метод к игре
ГО 3 2 5 3/21[6 2 1 0 2 J-
Упражнение 9
Пусть (Xt, Х5, ?/j) игра двух лиц с нулевой суммой, в смешанном расширении которой нет вполне смешанной седловой пары.
Для всех (лг1( х2) g Xj X Xj обозначим через ?г (х1} х2) цену игры
(Х1\{х1}) Х5\{хг}, иг)
в смешанных стратегиях. Платежная матрица этой игры получается из исходной матрицы U1 зачеркиванием строки х, и столбца х2.
Докажите, что игра (Xlf Xj, ?^) имеет седловую пару в чистых стратегиях и ее цена равна цене игры Gm.
Задача 4. Игра таможенный досмотръ Имеются два игрока таможенник (игрок I) и коммерсант (игрок 2). Коммерсант появляется на таможне несколько раз. Каждый раз он решает взять с собой контрабандный товар
или нет (ему нужно пронести этот товар ровно одни раз). Таможенник при каждом появлении коммерсанта может произвести досмотр. В игре Gn коммерсант появляется на таможне не более п раз.
Игра кончается, если была попытка пронести контрабандный товар независимо от того, удачная она или нет.
Если на шаге п игрок 1 проверяет игрока 2, а у того нет ничего предосудительного, то игрок 1 платит игроку 2 единицу И начинается игра G„_x. Если игрок 1 отказывается от проверки, а игрок 2 проносит контрабанду, то игрок 2 получает с(с1) и игра кончается.
Если игрок 1 обнаруживает контрабандный товар, то он получает награду /(/с) и игра заканчивается. Если проверка не произведена, и контрабанда не пронесена, то никаких платежей не делается и начинается игра G„_j.
1) Предполагая известной цену y„_j игры G„_t в смешанных стратегиях, найдите цену ?п игры Gn в смешанных стратегиях.
2) Вычислите ?п и оптимальные смешанные стратегии обоих игроков.
Задача 5
Зафиксируем конечные множества Xlt Х2 и для любой матрицы Ut обозначим через ?т{і!х) цену игры (с нулевой суммой) (Хи Х2, их) в смешанных стратегиях.
1) Докажите, что ^((/^ непрерывная функция Ux.
2) Докажите, что существует открытое всюду плотное множество Q из R*iX-**, такое, что для любого ?х из Q смешанное расширение игры (Хх, Х2, Ux) имеет единственную седловую пару.
Задача 6. Выгодные потери выигрыша при вполне смешанном равновесии по Нэшу (Мулен [1975])
Пусть G (Xlt Х2, U 1( U2) биматричная игра, в которой множества Хх и Х2 имеют одинаковую мощность, а 1/, и У, невырожденные ХххХ2 матрицы. На протяжении данной задачи предположим, что Gm имеет (обязательно единственное) вполне смешанное равновесие (ц1( р,2), определяемое по лемме 2.
Положим ?1=о1-Их,(/Г1- Таким образом, ?г вектор (строка) из R**. Компоненты этого вектора могут иметь произвольный знак.
Отметим, однако, что Vj-4x, = l и, следовательно, некоторые компоненты ?, неотрицательны.
1) Докажите, что ?х есть смешанная стратегия игрока 1 тогда и только тогда, когда вполне смешанный /V?-выигрыш Oj (заданный в (12)) является ценой игры с нулевой суммой (Х2, Х2, Uj) в смешанных стратегиях:
 Экономика: Знания - Циклы - Макроэкономика
Экономика: Знания - Циклы - Макроэкономика
- Введение в экономику
- Виды экономик
- Экология в экономике
- Экономическая теория
- Экономическая география
- Экономические знания
- Экономика России
- Циклы в экономике
- Макроэкономика
- Макроэкономика в России