Еремеев - Кто Разгадает Загадку Порядка Вэнь-Вана

Среди множества загадок, которые связаны с древнекитайской “Книгой перемен” (И цзин), есть одна очень важная. Она касается последовательности гексаграмм, имеющей название “порядок Вэнь-вана”. Многие исследователи пытались найти принцип расположения гексаграмм в этом порядке. Но их труды оказались в целом безуспешными. Благодаря им были выявлены только некоторые отдельные закономерности. Между тем, разгадка алгоритма построения порядка Вэнь-вана позволила бы вывести изучение “Книги перемен” на качественно новый уровень. Можно было бы, анализируя структурно-математические связи между гексаграммами, сопоставить их со смысловыми связями. Это привело бы к уточнению кодируемых гексаграммами значений, которые, без сомнения, за долгие годы существования “Книги перемен” претерпели ряд существенных искажений. Поэтому, предполагая, что эта задача может быть, в принципе, решена, я обращаюсь ко всем, кто читает данные строки и имеет математические склонности:

Кто разгадает загадку порядка Вэнь-вана?

Исходные данные

В основе символики “Книги перемен” лежат два вида черт (яо). Прерывистая (“сломанная” - чжэ) черта обозначает принцип инь, а сплошная (“одинарная” - дань) - принцип ян (рис. 1).

Рис. 1

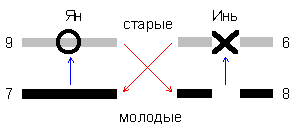
Помимо прерывистой и сплошной черт, в символической системе “Книге перемен” применяются еще два символа. Один из них должен обозначать прерывистую черту, превращающуюся в свою противоположность, т.е. в черту, у которой две половинки соединяются (→ ← ), - “сплетающуюся” (цзяo). А другой обозначает сплошную черту, разрывающуюся на две половинки (← → ), - “раздваивающуюся” (чун). Эти два символа называются “старыми” (лао), в отличие от предыдущих, называемых “молодыми” (шао). “Старый ян” может обозначаться кружочком и числом 9, а “старая инь” - диагональным крестиком и числом 6 (рис. 2). “Молодые” ян и инь имеют числовую символику 7 и 8. Динамика взаимодействий всех четырех принципов выражается следующим образом: “молодые” черты “стареют”, т.е. превращаются в “старые” черты, не меняя знака, а последние уже его меняют, “умирая” и превращаясь в противоположные “молодые” черты, которые вновь “стареют”, и т.д.

Рис. 2

При сочетании сплошной и прерывистой черт в двух позициях образуются четыре диграммы, называемые “сян” (“символы”). Два символа, “большие” (тай) инь и ян, имеют в двух позициях одинаковые черты, а два других, “малые” (шао) инь и ян, - различные (рис. 3).

Рис. 3

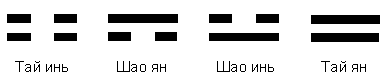
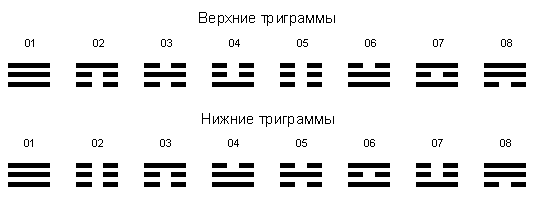
Символы, составленные из комбинирующихся черт, находящихся в трех позициях, называются “гуа”, а в китаеведении их принято называть “триграммами”. Чтобы упростить оперирование триграммами, можно перекодировать их в двоичный код, в котором цифры 0 или 1 при расположении их слева направо (поз. 3, 2, 1) в кодовом знаке (триграммный оператор) соответствуют прерывистой или сплошной чертам в позициях триграмм от верхней до нижней (рис. 4). Следует отметить, что выбор данных цифр не является принципиальным. Можно использовать знаки “-“ и “+”, традиционные обозначения черт цифрами 6 и 9 и проч.

Рис. 4

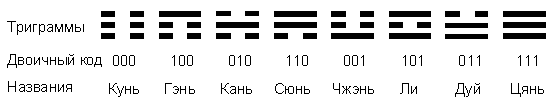
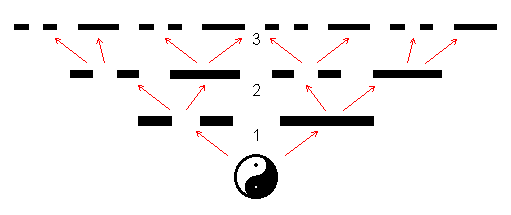
В китайской традиции выделятся несколько последовательностей триграмм. Так, последовательность, представленная на рис. 4, называется “порядком Фуси” (читается справа налево). Принцип построения данного порядка очевиден. Он отражает процесс дихотомического деления некоего единого начала (великий предел - Тай цзи), проходящий в три этапа, которые совпадают со счетом позиций снизу вверх (рис. 5).

Рис. 5

Указанный счет снизу вверх не является обязательным при построении порядков триграмм методом дихотомического деления. В описании этого метода в “Си цы чжуани”, являющемся важнейшим комментарием к “И цзину”, не указывается, что последовательность должна быть именно такой. Чередуя последовательности прохождения позиций, можно получить в общей сложности 6 порядков триграмм, представленных в нижеследующей таблице (табл. 1; порядок Фуси здесь обозначается как В1).

Таблица 1

Серия А	Серия В
A3	A2	A1	B3	B2	B1
Поз. 3-2-1	Поз. 2-1-3	Поз. 1-3-2	Поз. 3-1-2	Поз. 2-3-1	Поз. 1-2-3
111 - М	111 - М	111 - М	111 - М	111 - М	111 - М
110 - Д	011 - М	101 - О	101 - О	110 - Д	011 - М
101 - О	110 - Д	011 - М	110 - Д	011 - М	101 - О
100 - П	010 - В	001 - Д*	100 - П	010 - В	001 - Д*
011 - М	101 - О	110 - Д	011 - М	101 - О	110 - Д
010 - В	001 - Д*	100 - П	001 - Д*	100 - П	010 - В
001 - Д*	100 - П	010 - В	010 - В	001 - Д*	100 - П
000 - П	000 - П	000 - П	000 - П	000 - П	000 - П

В этой таблице также приведена корреляция триграмм и стихий: Цянь и Дуй - металл (М); Кунь и Гэнь - почва (П); Сюнь и Чжэнь - дерево (по корреляциям с этими триграммами будем условно различать “первичное” и “вторичное” дерево - Д и Д*); Кань - вода (В); Ли - огонь (О). В синологии не установлено время ее возникновения. Известно только, что она встречается в сохранившихся письменных источниках, относящихся к сунской эпохе. Так, например, эта корреляция приводится в сочинении неоконфуцианца Шао Юна (1011-1077) “Мэй хуа и шу” (“Числа перемен цветов сливы”). Несмотря на такую позднюю датировку, можно с уверенностью сказать, что происхождение указанной корреляции триграмм и стихий значительно более раннее, поскольку в ней отражены основные закономерности оперирования со стихиями, известные с доханьского времени.

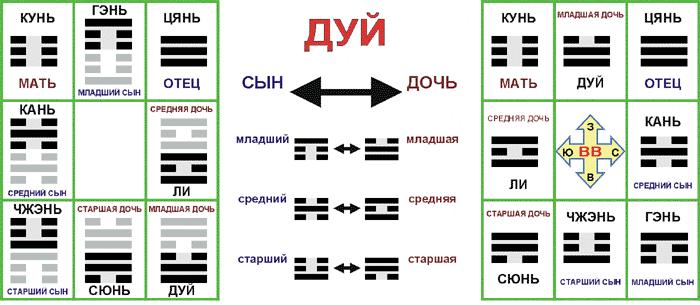
Триграммы, имеющие во всех позициях одинаковые знаки, называются “старшими”. Одна из них, имеющая три янских черт, - это “отец” (111 - Цянь), а другая, имеющая три иньских черт - это “мать” (000 - Кунь). Остальные триграммы называются “младшими”, или “детьми”. Они также подразделяются на янские и иньские, что определяется их структурой. Во всех “младших” триграммах одна черта по знаку противостоит двум другим. “Сыновьями” будут три триграммы, имеющие только одну сплошную черту, а остальные - прерывистые. Сплошная черта в первой позиции - “старший сын” (001 - Чжэнь), во второй позиции - “средний сын” (010 - Кань), в третьей позиции - “младший сын” (100 - Гэнь). “Дочери” имеют только одну прерывистую черту при остальных сплошных: в первой позиции - “старшая дочь” (011 - Сунь); во второй позиции - “средняя дочь” (101 - Ли); в третьей позиции - “младшая дочь” (011 - Дуй).

Триграммы, противоположные по “полу” и одного “возраста”, можно рассматривать как “дополнительные”. У них в одних и тех же позициях имеются различные черты, и эти триграммы можно преобразовывать друг в друга при помощи инверсии черт, или “противоположности” (дуй). Есть еще триграммы, которые образуются одна из другой при помощи “переворачивания” (фань). Это “старшие” и “младшие” триграммы одного “пола” (тр. Чжэнь - Гэнь; Сунь - Дуй). Остальные триграммы при этой операции не модифицируются, так как у них в нижней и верхней позициях имеются одинаковые черты, иначе говоря, они симметричны относительно средней позиции (рис. 6).

Рис. 6

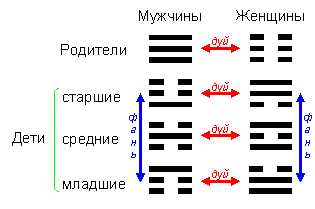
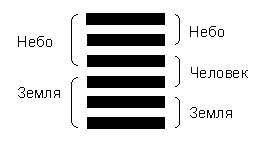
Гексаграммы (гуа), т.е. символы “Книги перемен”, состоящие из шести позиций с прерывистыми и сплошными чертами, можно рассматривать либо как результат процесса дихотомического деления (подобного тому, что представлен на рис. 5), произведенного в шесть этапов, либо как сочетания трех диграмм или двух триграмм. Для определения взаимоотношений диграмм или триграмм, составляющих гексаграммы, применяется маркировка их позиций категориями Небо (тянь), Земля (ди), Человек (жэнь) (рис. 7).

Рис. 7

Комбинации из прерывистой и сплошной черт, записанных в шести позициях, позволяют составить 64 символа. Счет позиций в гексаграммах начинается снизу. Первая позиция (вэй) (или черта-яо) в гексаграммах называется “начальной” (чу), а шестая - “верхней” (шан). Нечетные позиции (“начальная”, 3-я и 5-я) считаются “янскими”, четные (2-я, 4-я и “верхняя”) - “иньскими”.

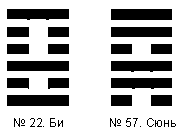
В системе записи в двоичном коде при счете позиций сверху вниз гексаграммы будут записываться слева направо. К этой записи можно добавить цифру после дефиса, которая означает номер гексаграммы в порядке Вэнь-вана. Так, гексаграмма Би обозначится как 100101-22, а Сюнь - как 110110-57 (рис. 8).

Рис. 8

Гексаграммы имеют канонизированные порядки расположения, связанные с именами Вэнь-вана и Фуси. Существуют табличная, или “квадратная” (фан ту фан вэй), и круговая (юань ту фан вэй) запись этих порядков.

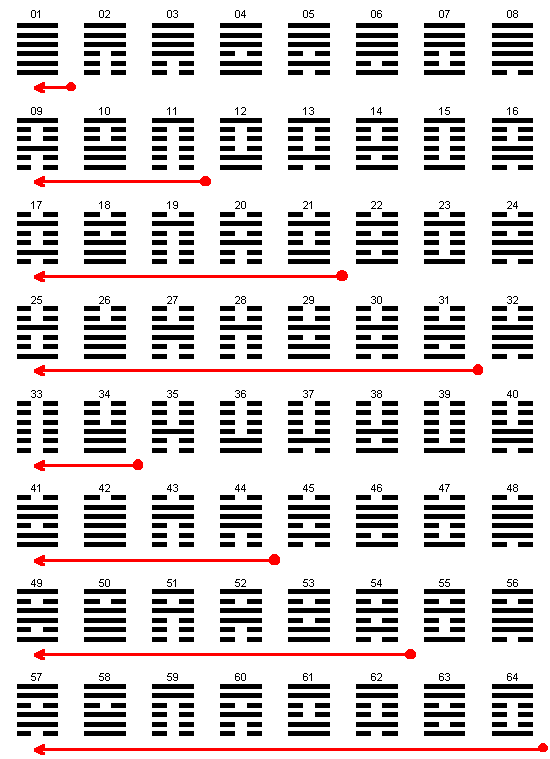
В табличной записи порядок Вэнь-вана читается справа налево и сверху вниз (рис. 9). Единственный и достаточно очевидный принцип связи гексаграмм, обнаруженный пока в этом порядке, заключается в том, что они группируются в пары по принципу переворачивания (фань), а там, где переворачивание приводит к исходной гексаграмме, - по принципу дополнительности (дуй). Пар, составленных только по принципу дополнительности, имеется всего четыре - № 1-2, 27-28, 29-30 и 61-62. Существует также четыре пары, которые совмещают с себе принципы дополнительности и переворачивания: № 11-12, 17-18, 53-54 и 63-64. Остальные пары строятся только по принципу переворачивания.

Рис. 9

Порядок Вэнь-вана в канонической части “Книги перемен” подразделяется на две неравных части, которые состоят соответственно из 30 и 34 гексаграмм (табл. 2).

Таблица 2

1 часть (верхняя)	2 часть (нижняя)
111111-01 000000-02	111101-13 101111-14	111001-25 100111-26	011100-31 001110-32	011111-43 111110-44	001101-55 101100-56
010001-03 100010-04	000100-15 001000-16	100001-27 011110-28	111100-33 001111-34	011000-45 000110-46	110110-57 011011-58
010111-05 111010-06	011001-17 100110-18	010010-29 101101-30	101000-35 000101-36	011010-47 010110-48	110010-59 010011-60
000010-07 010000-08	000011-19 110000-20		110101-37 101011-38	011101-49 101110-50	110011-61 001100-62
110111-09 111011-10	101001-21 100101-22		010100-39 001010-40	001001-51 100100-52	010101-63 101010-64
000111-11 111000-12	100000-23 000001-24		100011-41 110001-42	110100-53 001011-54

Задача нахождения закономерности в расположении гексаграмм в порядке Вэнь-вана может быть разделена на две части. Надо выяснить, по какому правилу выстраиваются в ряд пары гексаграмм и чем определяется очередность гексаграмм внутри пар. При этом можно пользоваться любыми структурно-математическими принципами или основываться на сопоставлении порядка Вэнь-вана с известными нижеследующими порядками гексаграмм, принцип построения которых вполне ясен. Не исключено, что в том или ином месте порядка Вэнь-вана имеются искажения, которые допустимо исправить при наличии соответствующего обоснования.

Порядок Фуси фиксируется в китайской традиции достаточно поздно - в 11 в. В табличной записи он читается справа налево и снизу вверх (рис. 10).

Рис. 10

Порядок Фуси удобно рассматривать как результат комбинирования в составе гексаграмм верхних и нижних триграмм, располагающихся в порядке Фуси (табл. 3, отмечены номера гексаграмм в порядке Вэнь-вана).

Таблица 3

н\в	000	100	010	110	001	101	011	111
000	000000-02	100000-23	010000-08	110000-20	001000-16	101000-35	011000-45	111000-12
100	000100-15	100100-52	010100-39	110100-53	001100-62	101100-56	011100-31	111100-33
010	000010-07	100010-04	010010-29	110010-59	001010-40	101010-64	011010-47	111010-06
110	000110-46	100110-18	010110-48	110110-57	001110-32	101110-50	011110-28	111110-44
001	000001-24	100001-27	010001-03	110001-42	001001-51	101001-21	011001-17	111001-25
101	000101-36	100101-22	010101-63	110101-37	001101-55	101101-30	011101-49	111101-13
011	000011-19	100011-41	010011-60	110011-61	001011-54	101011-38	011011-58	111011-10
111	000111-11	100111-26	010111-05	110111-09	001111-34	101111-14	011111-43	111111-01

Данную таблицу можно преобразовать в другую, у которой нижние триграммы задаются столбцом триграмм не в порядке Фуси, а в порядке А3 из таблицы 1. Это преобразование приводит к формированию диагонали из гексаграмм, которые при переворачивании обращаются сами в себя. Каждая гексаграмма этой диагонали задает столбец и строчку, в которых симметрично располагаются гексаграммы, связанные по принципу “переворачивания” и сгруппированные в порядке Вэнь-вана в пары (табл. 4).

Таблица 4

н\в	000	100	010	110	001	101	011	111
000	000000-02	100000-23	010000-08	110000-20	001000-16	101000-35	011000-45	111000-12
001	000001-24	100001-27	010001-03	110001-42	001001-51	101001-21	011001-17	111001-25
010	000010-07	100010-04	010010-29	110010-59	001010-40	101010-64	011010-47	111010-06
011	000011-19	100011-41	010011-60	110011-61	001011-54	101011-38	011011-58	111011-10
100	000100-15	100100-52	010100-39	110100-53	001100-62	101100-56	011100-31	111100-33
101	000101-36	100101-22	010101-63	110101-37	001101-55	101101-30	011101-49	111101-13
110	000110-46	100110-18	010110-48	110110-57	001110-32	101110-50	011110-28	111110-44
111	000111-11	100111-26	010111-05	110111-09	001111-34	101111-14	011111-43	111111-01

В круговой записи порядка Фуси первая половина всего набора гексаграмм располагается на круге против часовой стрелки, а вторая - по часовой стрелке.

При археологических раскопках, проводившихся в 1973 г. в местечке Мавандуй (рядом с г. Чанша в пров. Хунань), был обнаружен самый древний экземпляр “Книги перемен”, датируемый 180-170 гг. до н.э. В этом тексте гексаграммы располагаются в порядке, который у синологов получил название “мавандуйский” (рис. 11).

Рис. 11

Алгоритм данного порядка достаточно прост. Весь набор гексаграмм подразделяется на восемь серий, в которых имеются одинаковые верхние триграммы. Последовательность смены серий с данными триграммами соответствует их ранжированию по “семейным” характеристикам: отец, младший, средний и старший сыновья, мать, младшая, средняя и старшая дочери. Последовательность нижних триграмм построена по принципу дополнительности, совмещаемому со старшинством: отец и мать, младшие, средние и старшие сын и дочь (рис. 12).

Рис. 12

Сочетания верхних и нижних триграмм в данных последовательностях приводят к образованию восьми серий гексаграмм, в которых затем осуществляется перестановка определенных гексаграмм в начало серии. Для перестановки берутся “чистые” (чунь) гексаграммы, т.е. составленные из одинаковых триграмм и имеющие их названия. В первой серии данная перестановка не требуется или может считаться чисто номинальной, поскольку в ее начале стоит как раз такая гексаграмма.

Еще один способ группировки гексаграмм - по “дворцам” - зафиксирован в сочинении раннеханьского ицзиниста Цзин Фана (77-33) “Цзин-ши и чжуань” (“Комментарий г-на Цзина к [Книге] перемен”). В основе построения системы “дворцов” лежит принцип поочередного изменения черт в позициях. Каждый дворец задается “чистой” гексаграммой. Поскольку таких гексаграмм имеется восемь, то и дворцов тоже будет восемь (рис. 13).



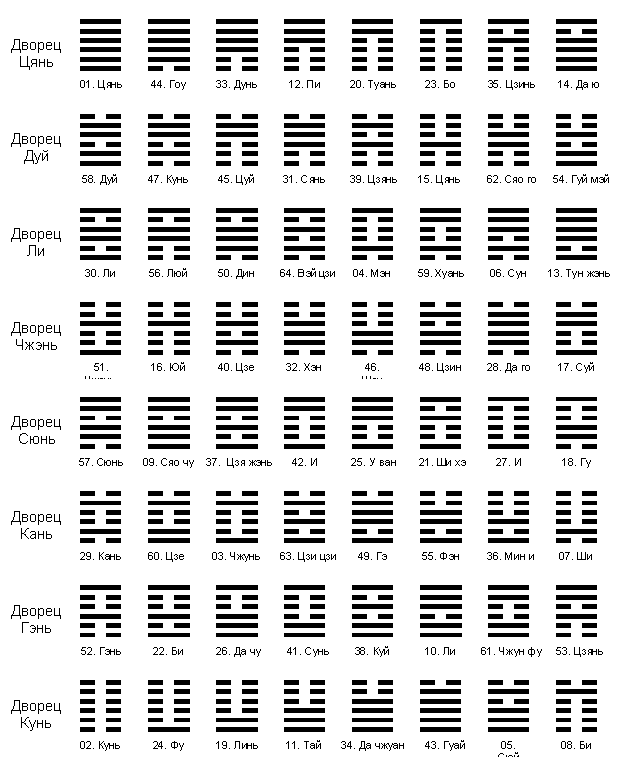
Рис. 13

В каждом “дворце” каждая из пяти гексаграмм, находящихся после “чистой”, отличается от предыдущей только одной чертой, причем изменение черт происходит снизу вверх. Последняя в этом списке гексаграмма совпадает с “чистой” только верхней чертой. Ее изменение привело бы к переходу в другой дворец. Такими сцепленными дворцами, охватывающими в сумме 48 гексаграмм, являются дворцы Цянь и Кунь, Дуй и Гэнь, Ли и Кань, Чжэнь и Сюнь. В них в соответствующих местах стоят инвертные гексаграммы.

Оставшиеся 16 гексаграмм выбиваются из указанных закономерностей. Их нельзя связать между собой посредством последовательно изменения одной черты. К первым шести гексаграммам в каждом дворце они подстраиваются за счет смены одной черты, но при этом нарушается предыдущий порядок переходов от позиции к позиции. При переходе в каждом дворце от шестой к седьмой гексаграмме изменяется четвертая снизу черта. Восьмые гексаграммы отличаются от первых пятой позицией. Между седьмой и восьмой гексаграммами различие образуется за счет инвертирования нижней триграммы.

В заключение можно привести еще одну матрицу гексаграмм, происхождение которой не совсем ясно. Она строится по принципу “магического квадрата”, в котором помимо номеров (чисел) гексаграмм из порядка Фуси учитываются черты гексаграмм. В этом квадрата сумма чисел в каждой строке, столбце и по диагоналям равна 260. В любых одинаковых позициях во всех строках и столбцах располагаются в сумме 4 янских и 4 иньских черт (рис. 14).

Рис. 14

Еремеев В.Е.

Порядок Вэнь-вана и лунные стоянки

Комплекс гексаграмм в порядке Вэнь-вана служил в древнем Китае в качестве символического инструмента для описания различных особенностей движения небесных светил, прежде всего, Луны.

Известно, что каждые сутки Луна перемещается в сторону востока на расстояние, равное 26 своим поперечникам. Такое же число пар гексаграмм получается при исключении из их полного набора четырех пар с “чистыми” и двух пар с инвертными гексаграммами. Если исключить только “чистые” гексаграммы и не удваивать инвертирующиеся гексаграммы № 27, 28, 61, 62, то получится комплекс из 28 “нечистых” пар, который интересен тем, что его можно связать с 28 “лунными стоянками” (сю). Последние представляют собой сектора неба и находящиеся в них определенные созвездия, на фоне которых происходит движение Луны (рис. 1).

Рис. 1

Считалось, что каждый день Луна “гостит” в одной из 28 стоянок. Солнце и известные китайцам пять планет, совершая видимое движение на небесной сфере, находятся в тех или иных стоянках различное время, определяемое их собственными ритмами. Изучая расположение небесных светил в системе координат 28 сю, можно, как писал Чжан Хэн, познать волю Неба:

“Пять планет содержат жизненные первозданные силы пяти стихий (у-син); вся масса звезд расположена в определенном порядке на небе, и все они известны своими духами; имеется пять основных групп [звезд], в которых 35 наименований. Одна группа расположена в центре неба и называется Бэй-доу, она способствует переменам и определяет смысл гаданий, она, по существу, ведает судьбами ванов. С четырех направлений расположены созвездия по семь в каждой стороне, составляя всего 28 зодиакальных созвездий. Солнце и луна движутся кругом и [в ходе своего движения] сулят либо счастье, либо несчастье, а пять планет по своему расположению предупреждают о беде или удаче, таким образом, и проявляется воля Неба” (Чжан Хэн/Вяткин, с. 332).

Гексаграммы “Книги перемен”, подобно астрологическому искусству, должны “предупреждать о беде или удаче”, и поэтому соотнесение их с небесными объектами не выглядит чем-то противоестественным. В цитировавшемся отрывке из “Лин сянь” (“Законы [действия] животворных сил”) говорится о 35 “наименованиях” звезд, которые подразделяются на пять групп. В каждой - по семь наименований. Четыре группы соотнесены с 28 сю. Одна группа находится в центре небесной сферы. Четыре направления и центральная зона небесной сферы назывались у китайцев “дворцами” (гун). “Чистые” гексаграммы у Цзин Фана задают членение всего набора гексаграмм на группы, также называемые этим термином. Если из “чистых” гексаграмм исключить Кунь (000000-02) как относящуюся к Земле, то оставшиеся семь гексаграмм можно связать с семью наименованиями центральных звезд. С другой стороны, “чистые” гексаграммы без Кунь можно связать с семью подвижными светилами - Солнцем, Луной и пятью планетами. Так или иначе, порядок Вэнь-вана при соотнесении гексаграмм с небесами должен описывать прежде всего 28 сю. Тогда местоположение в данном порядке “чистых” гексаграмм либо указывает на пункты влияния центральной звездной зоны на периферию, либо отражает “гороскоп” какого-то судьбоносного для китайской нации события или некоего наиболее уважаемого когда-то правителя, возможно, того, с чьим именем этот порядок связан.

Чтобы установить конкретные корреляции 28 сю и 28 пар “нечистых” гексаграмм, надо просто связать первые в традиционном порядке перечисления с № 1 по № 28 и вторые в порядке Вэнь-вана с № 3-4 по № 63-64 (табл. 1).

Таблица 1

№	Названия стоянок	Код	Названия гексаграмм
Восток
1	Цзюе (“Рог”, “Угол”)	010001-03 100010-04	Тунь (“Стяжательство”) Мэн (“Незрелость”, “Невежество”)
2	Ган (“Шея”)	010111-05 111010-06	Сюй (“Выжидание”) Сун (“Спор”, “Обличение”)
3	Ди (“Основа”)	000010-07 010000-08	Ши (“Войско”) Би (“Близость”)
4	Фан (“Дом”)	110111-09 111011-10	Сяо чу (“Малое воспитание”) Ли (“Поступок”, “Наступление”)
5	Синь (“Сердце”)	000111-11 111000-12	Тай (“Процветание”) Пи (“Упадок”)
6	Вэй (“Хвост”)	111101-13 101111-14	Тун жэнь (“Содружество”, “Союзники”) Да ю (“Большое владение”)
7	Цзи (“Корзина”)	000100-15 001000-16	Цянь (“Уступчивость”, “Кротость”) Юй (“Беспечность”)
Север
8	Доу (“Ковш”)	011001-17 100110-18	Суй (“Следование”) Гу (“Порча”)
9	Ню (“Бык”)	000011-19 110000-20	Линь (“Вторжение”, “Посещение”) Гуань (“Рассматривание”, Наблюдение”)
10	Нюй (“Дева”)	101001-21 100101-22	Ши хо (“Раскусывание”) Би (“Светлость”, “Красота”, “Украшение”)
11	Сюй (“Пустота, дряхлость”)	100000-23 000001-24	Бо (“Разрушение”) Фу (“Возврат”)
12	Вэй (“Кровля, стропила”)	111001-25 100111-26	У ван (“Непроизвольность”) Да чу (“Великое воспитание”)
13	Ши (“Дом”)	100001-27 011110-28	И (“Питание”, “Челюсти”) Да го (“Большой переход”)
14	Би (“Стена, крепость”)	011100-31 001110-32	Сянь (“Взаимодействие”, “Приспосабливание”) Хэн (“Неподвижность”, “Постоянство”)
Запад
15	Куй (“Всадник”, “Скипетр”)	111100-33 001111-34	Дунь (“Уход”, “Бегство”) Да чжуан (“Великая сила”)
16	Лоу (“Оковы”)	101000-35 000101-36	Цзинь (“Выпячивание”, “Восход”) Мин и (“Помрачение”, “Угасание света”)
17	Вэй (“Желудок”)	110101-37 101011-38	Цзя жэнь (“Семья”) Куй (“Отстранение”)
18	Мао (“Гнездо”)	010100-39 001010-40	Цзянь (“Препятствие”) Цзе (“Разнузданность”, “Освобождение”)
19	Би (“Вилы”)	100011-41 110001-42	Сунь (“Убыток”) И (“Прибыль”)
20	Цзуй (“Клюв”)	011111-43 111110-44	Гуай (“Решимость”) Гоу (“Встреча”)
21	Шэнь (“Смесь”, “Толпа”, “Заслуги”)	011000-45 000110-46	Цуй (“Сборище”, “Скопление”) Шэн (“Подъем”)
Юг
22	Цзин (“Колодец”)	011010-47 010110-48	Кунь (““Изнеможение”, “Истощение”) Цзин (“Колодец”)
23	Гуй (“Духи”, “Демоны”)	011101-49 101110-50	Гэ (“Обновление”, “Смена”) Дин (“Треножник”)
24	Лю (“Ива”, “Изгиб”)	110100-53 001011-54	Цзянь (“Неспешность”, “Течение”) Гуй мэй (“Невеста”)
25	Син (“Звезда”)	001101-55 101100-56	Фэн (“Изобилие”) Люй (“Странствие”)
26	Чжан (“Лук”)	110010-59 010011-60	Хуань (“Распад”) Цзе (“Ограничение”)
27	И (“Крыло”)	110011-61 001100-62	Чжун фу (“Верность срединности”) Сяо го (“Малый переход”)
28	Чжэнь (“Колесница”)	010101-63 101010-64	Цзи цзи (“Завершенность”) Вэй цзи (“Незавершенность”)

 

Сразу бросается в глаза, что 22-я сю и гексаграмма № 48 из соответствующей пары называются одинаково - Цзин (“Колодец”). Надо сказать, что некоторые стоянки имеют не одно название, и собрать сведения обо всех вариантах их наименований достаточно проблематично. Однако и среди тех, что широко известны, имеются те или иные смысловые связи с одной из гексаграмм в соответствующей паре. Также иногда та или иная пара задает общую тему, которая созвучна соответствующей стоянке. В подтверждение этому можно привести несколько примеров.

1-я стоянка Цзюе (“Рог”) - это еще и “Ссора”, что сопоставимо с гексаграммой Мэн (“Незрелость”, “Невежество”, “Грубость”). Сыма Цянь в своих “Исторических записках” (“Ши цзи”) в трактате “Тянь гуань шу” (“Трактат о небесных явлениях”) указывал, что “левая звезда созвездия Цзюе (“Рог”) управляет законами, правая звезда созвездия Цзюе управляет войсками” (Сыма Цянь/Вяткин, 1986, с. 117). Видимо, данная гексаграмма “родилась” под правой звездой.

Название 11-й стоянки Сюй (“Пустота”) может быть переведено как “Дряхлость” и тем самым сближено с соответствующей гексаграммой Бо (“Разрушение”, “Разложение”). Об этой стоянке в “Тянь гуань шу” написано, что она “ведает делами, [сопровождаемыми] плачем и слезами” (Сыма Цянь/Вяткин, 1986, с. 120).

Там же отмечается, что стоянка № 13, Ши “(Дом”), имеет еще названия Ли гун (“Дворец расставаний”) и Гэ дао (“Подвесная дорога”) (Сыма Цянь/Вяткин, 1986, с. 121). Данная стоянка коррелирует с гексаграммой Да го (“Большой переход”), название которой перекликается с идеей дороги. В ее “изречениях” (цы) упоминаются “перекладины, поперечные балки” (дун), которые могут рассматриваться в качестве частей либо крыши дома, либо подвесного моста.

Название 14-й сю Би (“Стена”), как образ чего-то крепкого и препятствующего внешним воздействиям, соотносимо по смыслу с гексаграммой Хэн (“Неподвижность”, “Постоянство”) и, также как и последняя, находится в оппозиции с гексаграммой Сянь (“Взаимодействие”, “Приспосабливание”).

Стоянка № 15, Куй (“Всадник”, Скипетр”), может ассоциироваться по величавости связанных с ней образов с “Великой силой”, как переводится название одной из соответствующей ей гексаграмм (Да чжуан), или, по связи с идеей движения, с “Бегством, Уходом” (Дунь), которое входит в пару с ней.

Сыма Цянь в “Люй шу” (“Трактат о музыкальных звуках и трубках”) писал, что название созвездия Шэнь (сю № 21) “означает, что все существующее и произрастающее может смешиваться, отсюда и название шэнь или цань - “смешать”” (Сыма Цянь/Вяткин, 1986, с. 104). М.Е. Кравцова перевела иероглиф этого созвездия как “Толпа” (Кравцова, 1999, с. 415). Ему соответствует пара с гексаграммой Цуй (“Сборище”, “Скопление”, “Куча”), что близко по значению.

Стоянка № 23, Гуй (“Духи”, “Демоны”), о которой в трактате “Тянь гуань шу” написано, что она “связана с делами по приношениям духам предков” (Сыма Цянь/Вяткин, 1986, с. 118), коррелирует с гексаграммой Дин (“Треножник”), обозначающей ритуальный сосуд, использовавшийся в жертвоприношениях.

24-я стоянка Лю (“Ива”), имеющая еще название Чжу (“Течение”), соответствует паре, в которой есть гексаграмма Цзянь (“Течение”, “Неспешность”, “Постепенность”).

Стоянка № 25 под названием Син (“Звезда”) коррелирует с гексаграммой Фэн (“Изобилие”), являющейся единственной гексаграммой, в которой говорится о звездах, точнее, о неяркой звезде Мэй (Алькор), расположенной рядом с Дзетой созвездия Большая Медведица, и о самом этом созвездии - Доу (Ковш).

27-я сю - И (“Крыло, Крылья”) - соответствует паре, в которой имеется гексаграмма Сяо го (“Малый переход”). Форма этой гексаграммы ассоциировалась китайцами с летящей птицей, распростершей крылья (рис. 2). Туловищу соответствуют две янские черты внутри гексаграммы. Две иньские черты вверху и две внизу можно рассматривать как символ крыльев.

Рис. 2

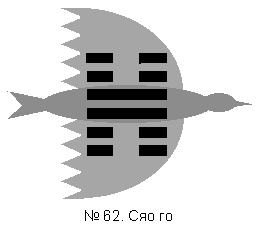
Стоянка № 28, Чжэнь (“Колесница”), сочетается с парой гексаграмм, собранных вокруг темы передвижения - Цзи цзи (“Завершенность”, “Конец переправы”) и Вэй цзи (“Незавершенность”, “Перед переправой”). И т.д. и т.п.

В.А. Сазонов указывал на отражение в названиях некоторых гексаграмм того, что они являются символами лунных и солнечных циклов. Так, в частности, ряд гексаграмм в усеченном порядке Вэнь-вана начинается с пары Чжунь (“[Начальные] трудности” - тот же иероглиф, что и Тунь - “Стяжательство”. - В.Е.) и Мэн (“Незрелость”), а заканчивается гексаграммами Цзи цзи (“Завершенность”) и Вэй цзи (“Незавершенность”) (Сазонов, 1985, с. 69). При вышеуказанном счете стоянок начало и конец их списка совпадают с данными парами. Однако в традиции имеются и другие способы перечисления сю. Например, их считают, начиная с 7-й сю, Цзи (“Корзина”), в обратном направлении (Жэнь Инцю/Богачихин, с. 37-38). Сыма Цянь дал описание “28 остановок” (эр ши ба шэ) и их коррелятов как в прямом порядке, начиная с 1-й сю, Цзюе (“Рог”), так и в обратном направлении, начиная с № 14 - Би (“Стена”) (Сыма Цянь/Вяткин, 1986, с. 138, 102).

Эти варианты счета определяются тем, что стоянки использовались не только в качестве описания местоположений Луны, но и в качестве универсальной системы координат, по которой определялись месячные, годовые и другие ритмы различных небесных явлений. Проследить отражение всех этих ритмов в названиях гексаграмм при этом оказывается достаточно трудно ввиду их неопределенного количества. Кроме того, при интерпретации связей гексаграмм и стоянок следовало бы учитывать эффект прецессии и проходившие в древнем Китае изменения календарных систем.

Велико было значение системы стоянок в древнекитайской астрологии, без обращения к которой не совершалось ни одно крупное начинание. С помощью астрологии проводился также анализ исторических событий. Так, в “Го юй” (“Речи царств”) в записи, относящейся к 522 г. до н.э. (чжан 31), приводится астрологическая карта, приуроченная ко времени нападения родоначальника династии Чжоу У-вана на династию Инь. Частично ее можно проинтерпретировать с помощью рассмотренной выше корреляции стоянок и гексаграмм.

“В прошлом, когда У-ван напал на династию Инь, планета Юпитер находилась в созвездии Чуньхо, Луна в созвездии Тяньсы, Солнце - на Млечном пути у созвездия Симу, место встречи Солнца и Луны было у рукояти Большой Медведицы, Меркурий находился в созвездии Тянь-юань, Меркурий, Солнце и место встречи Солнца и Луны лежали в северном углу неба...” (Го юй/Таскин, с. 75).

Местонахождение Юпитера, Солнца и Меркурия определяются здесь по нескольким сю, объединенным по принадлежности к циклическим знакам и имеющим специфические названия: Чуньхо - цикл. знак у (7), объединяющий сю Чжан, Син, Лю; Симу - цикл. знак инь (3) - Цзи, Вэй; Тяньюань - цикл. знак цзы (1) - Вэй, Сюй, Нюй. Место встречи Солнца и Луны также связывается с подобной группой: Синцзи - цикл. знак чоу (2) - Ню, Доу. Ввиду указания на связи с двумя или тремя сю, все эти астрологические приметы расшифровать с привлечением гексаграмм невозможно. Однако Луна связана здесь с одним созвездием - Тяньсы. Переводчик “Го юя” В.С. Таскин (Го юй/Таскин, с. 340) указывает в комментариях, что Тяньсы - одно из названий созвездия Фан (сю № 4). Тогда данный астрологический прогноз можно связать с гексаграммой Ли (“Поступок”, “Наступление”, “Попрание”) из соответствующей пары. Эта гексаграмма символизирует настойчивость и дееспособность, позволяющие, по образному выражению из ее описания, не бояться “наступить на хвост тигра”, что и сделал У-ван, покорив династию Инь.

Корреляция пар гексаграмм с кругом 28 стоянок имеет некоторые структурные особенности (рис. 3). Пары с инвертными гексаграммами - №№ 27, 28 и №№ 61, 62 - являются диаметрально противоположными и соседствуют с так называемыми “небесными” и “земными вратами” (тянь мэнь и ди мэнь), охватывающими соответственно стоянки Би (14) и Куй (15) и стоянки Цзюе (1) и Чжэнь (28). Две пары “чистых” гексаграмм - №№ 1, 2 и №№ 29, 30 - по их местоположению в порядке Вэнь-вана также прилегают к данным стоянкам, но не имеют четкой диаметральной противопоставленности.

Рис. 3

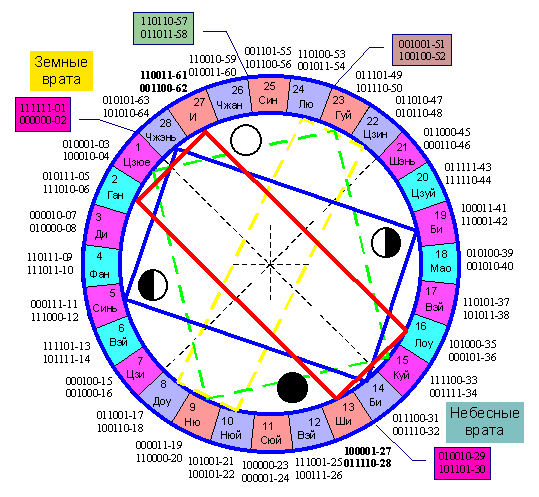
Если сравнить данную схему со схемой месяца из 30 дней, то можно увидеть, что семантика некоторых гексаграмм и их положение оказываются в некоторой степени связанными с лунным циклом. В этом случае счет дней производится по часовой стрелке с пары гексаграмм под №№ 25 и 26, соответствующей дню новой луны. Названия данных пар - У ван (“Непроизвольность”) и Да чу (“Великое воспитание”), возможно, и отражают процесс появления на небосводе узкого, почти незаметного лунного серпа. Более четкие очертания серпа появятся только на следующий день, которому приписана гексаграмма № 24, Фу (“Возврат”). Вхождение во вторую четверть месяца будет соответствовать дню с гексаграммами № 11, Тай (“Процветание”), и № 12, Пи (“Упадок”), своей структурой символизирующими форму полумесяца. Появление полной луны, которая уже несет в себе первые признаки ущербности, коррелирует с парой №№ 59-60 - Хуань (“Распад”) и Цзе (“Ограничение”). Последняя четверть месяца начинается с дня, которому ставится в соответствие пара №№ 41-42 - Сунь (“Убыток”) и И (“Прибыль”), семантически близкая паре №№ 11-12 - Тай (“Процветание”) и Пи (“Упадок”), но по структуре гексаграмм уже не отражающая форму обратного полумесяца.

Пары с инвертными гексаграммами - №№ 27, 28 и №№ 61, 62 -располагаются в концах соответственно второй и первой половин месячного цикла. Если месяц считается состоящим из 30 дней, то каждой из этих гексаграмм будет соответствовать свой день. Если устанавливается 29-дневный месяц, то гексаграмма № 28, Да го (“Большой переход”), либо убирается, либо присоединяется к соседнему дню с гексаграммой № 27 - И (“Питание”, “Челюсти”). В 29-дневном месяце гексаграмма № 61, Чжун фу (“Верность срединности”), оказывается ровно посередине цикла (15-й день). При переходе к 28-дневному месяцу инвертная ей гексаграмма Сяо го (“Малый переход”) либо связывается с ней, обозначая в таком случае 14-й день, либо изымается из цикла.

В комплексе всех 28 пар “нечистых” гексаграмм выделяется четыре группы, в которых пары объединены таким образом, что на круговой схеме образуют прямоугольники. Принципы этого объединения базируются на системе “дворцов” Цзин Фана. Для того, чтобы сделать их наглядными, надо попарно связать между собой те “дворцы”, в которых под “дворцовыми” номерами с 2-го по 6-й содержатся перевернутые гексаграммы. Получится четыре группы “дворцов”: Цянь и Кунь, Дуй и Чжэнь, Гэнь и Сюнь, Ли и Кань. При табличной записи этих “дворцов” следует расположить друг против друга перевернутые гексаграммы под указанными выше номерами. Тогда в каждой группе “дворцы” выстоятся в противоположных друг другу направлениях, и весь набор 64-х гексаграмм разделится на девять строк с некой формой симметричности относительно четвертой строки (табл. 2). При такой записи гексаграммы под оставшимися “дворцовыми” номерами 1, 7 и 8 будут образовывать пары по перевернутости не в одной группе, а в разных, находясь при этом в одной или в симметричных строках. Инвертные пары тех гексаграмм, которые при переворачивании обращаются в самих себя, также окажутся в одной или в симметричных строках. В целом получается достаточно стройная система расположения гексаграмм, допускающая некоторые вариации, о которых не имеет смысла здесь говорить.

Таблица 2

№		Цянь	Кунь		Дуй	Чжэнь		Гэнь	Сюнь		Ли	Кань
0-8			010000-08			011001-17			100110-18			000010-07
1-7		111111-01	010111-05		011011-58	011110-28		100100-52	100001-27		101101-30	000101-36
2-6		111110-44	011111-43		011010-47	010110-48		100101-22	101001-21		101100-56	001101-55
3-5		111100-33	001111-34		011000-45	000110-46		100111-26	111001-25		101110-50	011101-49
4-4		111000-12	000111-11		011100-31	001110-32		100011-41	110001-42		101010-64	010101-63
5-3		110000-20	000011-19		010100-39	001010-40		101011-38	110101-37		100010-04	010001-03
6-2		100000-23	000001-24		000100-15	001000-16		111011-10	110111-09		110010-59	010011-60
7-1		101000-35	000000-02		001100-62	001001-51		110011-61	110110-57		111010-06	010010-29
8-0		101111-14			001011-54			110100-53			111101-13

 

Указанные выше прямоугольники представлены в данной системе двояким образом. Два из них пронизывают все группы сдвоенных “дворцов” - это ряд пар гексаграмм под 4-ми “дворцовыми” номерами и два ряда 1-7, 7-1. Два других прямоугольника (на рис. 2 изображены пунктиром) занимают каждый по два ряда пар гексаграмм в двух группах: в рядах 3-5 и 5-3 охватываются группы Цянь-Кунь и Ли-Кань, а в рядах 2-6 и 8 - группы Дуй-Чжэнь и Гэнь-Сюнь. Какой за всеми этими закономерностями стоит смысл - не ясно, но чисто формально тот факт, что через посредство гексаграмм комплекс 28 сю, пусть и частично, также подразделяется неким упорядоченным образом на “дворцы”, является достаточно примечательным.

Оставшиеся 12 пар гексаграмм из набора, сопоставленного с 28 сю, не образуют подобные прямоугольники на круговой схеме, из чего можно сделать выводы, что либо в последовательности гексаграмм в порядке Вэнь-вана нет и не было никаких более глубоких закономерностей по сравнению с обмеченными, либо они основываются не на системе “дворцов” Цзин Фана, а на чем-то ином, либо в данной последовательности имеются случайно внесенные туда искажения, внешне не приметные и поэтому не поддающиеся исправлению, либо в ней имеется несколько срезов, для каждого из которых существуют свои фрагментарные закономерности.

Что здесь подразумевается под срезами? Например, от 28 пар “нечистых” гексаграмм можно перейти к набору из 26 пар без инвертных гексаграмм, а от них к 22 парам без перевернуто-инвертных. Последнее число соответствует сочетанию 10 “небесных стволов” (тянь гань) и 12 “земных ветвей” (ди чжи). Или можно из 28 пар исключить четыре пары гексаграмм, которые содержат инвертные гексаграммы и в таблице с дворцами (см. табл. 2) охватывают полную строку (1-7; 7-1). Из получившихся 24 пар гексаграмм, совпадающих по числу с набором сезонов китайского календаря, также можно исключить четвертку пар, которые в данной таблице охватывают вторую полную строку (4-4). Оставшиеся 20 пар гексаграмм соотносятся с числом 40, возникающим при суммировании чисел в “магическом квадрате” Ло шу без учета центрального числа 5 (подробнее см. Еремеев, 2002, с. 313-315).

Используя другие принципы классификации, можно найти и более дробные наборы пар гексаграмм из порядка Вэнь-вана, предположив, что один из них является базовым и в нем заложена первичная закономерность, на которую накладываются все остальные при добавлении гексаграмм и переходе к более массивному срезу. Однако при этом возникает множественность не поддающихся селекции вариантов, и вопрос о природе этого порядка гексаграмм приходится оставить открытым.

Литература

1. Го юй/Таскин. - Го юй (“Речи царств”). Пер. В.С. Таскина. М., 1987.

2. Еремеев, 2002. - Еремеев В.Е. Символы и числа “Книги перемен”. 1-е изд. М.: АСМ, 2002.

3. Жэнь Инцю/Богачихин. - Жэнь Инцю. Базовая теория китайской медицины: пять вращений, шесть энергий. Пер. М.М. Богачихина. М., 1994.

4. Кравцова, 1999. - Кравцова М.Е. История культуры Китая. СПб., 1999.

5. Сазонов, 1985. - Сазонов В.А. Солнечные и лунные циклы в интерпретации “И цзина”. - “Общество и государство в Китае”. 16-я научная конференция. Тезисы докладов. Ч. 1. М., 1985.

6. Сыма Цянь/Вяткин, 1986. - Сыма Цянь. “Исторические записки” (“Ши цзи”), т. IV. Пер. с кит., предисл. и коммент. Р.В. Вяткина. М., 1986.

7. Чжан Хэн/Вяткин. - Чжан Хэн. Лин сянь ("Законы [действия] животворных сил"). Пер. Р.В. Вяткина. - Древнекитайская философия. Эпоха Хань. М., 1990.



Еремеев В.Е.

Система 36 пар гексаграмм

В “Книге перемен” все 64 гексаграммы связаны в 32 пары, из которых в четырех парах гексаграммы объединены по принципу “противоположности” (дуй), поскольку при переворачивании они обращаются сами в себя.

Если эти инвертные пары преобразовать, удвоив находящиеся в них гексаграммы и рассматривая новообразованные пары строящимися по принципу “переворачивания” (фань), то в целом порядок Вэнь-вана будет состоять из 36 пар, построенных по принципу “переворачивания” (табл. 1).

Таблица 1

1 часть (верхняя)	2 часть (нижняя)
111111-01 111111-01	000111-11 111000-12	100000-23 000001-24	011100-31 001110-32	011111-43 111110-44	001101-55 101100-56
000000-02 000000-02	111101-13 101111-14	111001-25 100111-26	111100-33 001111-34	011000-45 000110-46	110110-57 011011-58
010001-03 100010-04	000100-15 001000-16	100001-27 100001-27	101000-35 000101-36	011010-47 010110-48	110010-59 010011-60
010111-05 111010-06	011001-17 100110-18	011110-28 011110-28	110101-37 101011-38	011101-49 101110-50	110011-61 110011-61
000010-07 010000-08	000011-19 110000-20	010010-29 010010-29	010100-39 001010-40	001001-51 100100-52	001100-62 001100-62
110111-09 111011-10	101001-21 100101-22	101101-30 101101-30	100011-41 110001-42	110100-53 001011-54	010101-63 101010-64

Традиционно основной текст “Книги перемен” подразделяется на две неравномерные части: первая часть состоит из 30, а вторая - из 34 гексаграмм. При введении дополнительных гексаграмм (в первую часть - 6, во вторую - 2) весь их комплекс разделится на две равные части, состоящие каждая из 18 пар или 36 гексаграмм. В целом получится 72 гексаграммы. Все эти числа с нумерологической точки зрения достаточно интересные, а главное, они кратны числу шесть, соответствующему количеству черт в гексаграмме. 36 пар гексаграмм вписываются в матрицу 6 на 6. Кроме того, их можно связать с 36-ю десятидневками года. Каждой десятидневке будет соответствовать 12 черт, получаемых при сложении соответствующих пар гексаграмм.

При дальнейшем анализе преобразованного порядка Вэнь-вана следует исходить из того, что “малое является ценным в многочисленном; единое является главным во многом”. Данная формулировка известного ицзинистского правила была высказана ученым Ван Би (226-249) в его трактате “Чжоу и люэ ли” (“Основные принципы “Чжоу и””), где он указывает и на возможность его применения в отношении к структуре гексаграмм:

“Если в данной гексаграмме пять [линий] Света и одна линия Тьмы, то одна [линия] Тьмы является в ней главным; если же пять [линий] Тьмы и одна - Света, то [линия] света является в ней главным” (Ван Би. Основные принципы “Книги перемен”. - Петров А.А. Ван Би. М., 1936, с.100).

Для триграмм одна черта (линия), противопоставленная двум другим, должна считаться главной. В гексаграммах не только одна противопоставленная черта, но и две будут главенствовать и определять полярность всего символа. Так, символ 001 будет янским, поскольку в нем имеется одна янская черта, а символы 101111 или 001111 будут иньскими, поскольку в них присутствуют соответственно одна и две иньских черт. Символы с одинаковым количеством янских и иньских черт будут равновесными. Символы, состоящие только из одного типа черт, триграммы и гексаграммы Цянь и Кунь, имеют соответственно полярности ян и инь.

Всего в набор 64 гексаграмм входят:

1. 2 гексаграммы, составленные из 6-и знаков одного типа (прерывистые или сплошные черты);

2. 12 гексаграмм - 5-и одного типа и 1-го - другого;

3. 30 гексаграмм - 4-х одного типа и 2-х - другого;

4. 20 гексаграмм - 3-х одного типа и 3-х - другого.

Произведенное выше удвоение симметричных гексаграмм приводит к тому, что увеличивается до 4-х количество гексаграмм, состоящих из 6-ти черт одного типа, и до 36-ти - из 4-х черт одного типа и 2-х - другого типа.

При трансформации порядка Вэнь-вана в комплекс из 36 пар обратных гексаграмм в нем образуется некоторая избыточность. Действительно, зная первую гексаграмму в паре, ее можно автоматически, методом перевертывания, преобразовать во вторую гексаграмму. Само собой, вторая гексаграмма будет в той же степени янской или иньской, что и первая.

Введем “цену” каждой пары гексаграмм, выразив любую входящую в нее гексаграмму положительным или отрицательным числом, составляющим число янских или иньских главных линий (табл. 2). Так, например, гексаграмма 111111-01 будет иметь число “+6”, 010000-08 - число “+1”, 110011-61 - число “-2”, и т.д. Равновесные гексаграммы определяются числом [3], которое можно рассматривать и как положительное, и как отрицательное в зависимости от конкретного местоположения этих гексаграмм в порядке Вэнь-вана.

Таблица 2

1 часть (верхняя)	2 часть (нижняя)
01	111111-01 +6	07	000111-11 +3	13	100000-23 +1	19	011100-31 +3	25	011111-43 [-1]	31	001101-55 +3
02	000000-02 -6	08	111101-13 -1	14	111001-25 -2	20	111100-33 -2	26	011000-45 [+2]	32	110110-57 -2
03	010001-03 +2	09	000100-15 +1	15	100001-27 +2	21	101000-35 +2	27	011010-47 +3	33	110010-59 +3
04	010111-05 -2	10	011001-17 -3	16	011110-28 -2	22	110101-37 -2	28	011101-49 -2	34	110011-61 -2
05	000010-07 +1	11	000011-19 +2	17	010010-29 +2	23	010100-39 +2	29	001001-51 +2	35	001100-62 +2
06	110111-09 -1	12	101001-21 -3	18	101101-30 -2	24	100011-41 -3	30	110100-53 -3	36	010101-63 -3

Последнее требует разъяснения. Дело в том, что другие пары гексаграмм располагаются так, что их цены чередуются по своей полярности. Например, гексаграммы №№ 3-4 имеют цену “+2”, №№ 5-6 - цену “-2”, №№ 7-8 - цену “+1” и т.д. Исключение составляют пары №№ 43-44 и 45-46, которые имеют противоположные знаки, по сравнению с тем, что требовалось бы на их месте. Чтобы не нарушить ритм чередования янских и иньских пар, равновесным парам гексаграмм как раз и приписывается подходящая для их места полярность (рис. 1).

Рис. 1

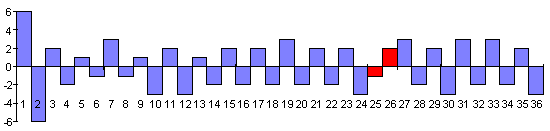
Разумеется, подобная “ценовая” перекодировка пар гексаграмм выхолащивает их значения, поскольку при ней не учитываются различия в структуре тех или иных гексаграмм (например, гексаграммы 110110-57 и 011110-28 имеют одинаковую цену “-2”). Однако она позволяет выявить в порядке Вэнь-вана некоторые интересные закономерности (табл. 3).

Таблица 3

1 часть (верхняя)	2 часть (нижняя)	Σ 1	Σ 2
+6 (01,01)	+3 (11,12)	+1 (23,24)	+3 (31,32)	-1 (43,44)	+3 (55,56)	+15
-6 (02,02)	-1 (13,14)	-2 (25,25)	-2 (33,34)	+2 (45,45)	-2 (57,58)	-11	+17
+2 (03,04)	+1 (15,16)	+2 (27,27)	+2 (35,36)	+3 (47,48)	+3 (59,60)	+13
-2 (05,06)	-3 (17,18)	-2 (28,28)	-2 (37,38)	-2 (49,50)	-2 (61,61)	-13
+1 (07,08)	+2 (19,20)	+2 (29,29)	+2 (39,40)	+2 (51,52)	+2 (62,62)	+11	-17
-1 (09,10)	-3 (21,22)	-2 (30,29)	-3 (41,42)	-3 (53,54)	-3 (63,64)	-15
0	-1	-1	0	+1	+1	0
	-2			+2

Оказывается, что первая и вторая части таблицы симметричны по суммам цен как в целом, так и по отдельным столбцам. При этом первая ее часть является иньской, а вторая - янской по знаку. Также своеобразная симметрия по суммам цен наблюдается и в строках таблицы. На этот раз верхняя часть из трех строк является янской, а нижняя - иньской. Общие суммы цен как по столбцам, так и по строкам равны нулю. Подобного рода симметрии наблюдаются еще при размещении 36 пар гексаграмм в таблицах 18 × 2, 9 × 4 и 3 × 12. Таким образом, порядок Вэнь-вана предстает как сложносбалансированная система.

Игорь Бурдонов

 

Доклад на конференции

" Междисциплинарные исследования китайской классической "Книги Перемен" (в аспектах изучения духовных традиций Востока и Запада) "

 

25 марта, Дом Композиторов

 

Введение

Мой доклад посвящен проблеме порядка Вэнь-вана. Но сначала несколько слов о том, что это такое.

Самый ранний слой Книги Перемен составляют 64 гексаграммы, по-китайски - гуа-образы. Последующие слои - это названия гексаграмм и, так называемые, афоризмы к ним. Все вместе называется "И цзин" - "Книга Перемен" или, более точно, "Канон Перемен". После этого идут "И чжуань" - "Комментарии к Переменам", или "Ши и" - Десять Крыльев - древнейшие комментарии, авторство которых традиция приписывает Конфуцию. Все вместе называется также "Чжоу И" - "Чжоуские Перемены", то есть, "Канон Перемен эпохи Чжоу" или, в зависимости от перевода слова "чжоу", "Всеохватно-круговые Перемены". Этих слоев я касаться почти не буду. Во-первых, потому что мало времени. Во-вторых, потому что их связь с гексаграммами сама по себе представляет отдельную проблему. В-третьих, потому что сами китайцы всегда подчеркивали, что основа Книги Перемен - это именно гексаграммы, и для того, чтобы Книгу Перемен понимать и применять на практике, нужно понимание устройства самих образов-гуа, то есть гексаграмм. Наконец, в-четвертых, потому что мне, как математику, интересно исследовать систему 64 гексаграмм саму по себе, поскольку она представляет собой вполне формальную систему и ее можно исследовать чисто математическими методами.

Итак, 64 гексаграммы. Каждая гексаграмма состоит из 6 черт, читаемых снизу вверх. А каждая черта может быть двух видов: целая черта - символизирует ЯН, и прерванная черта - символизирует ИНЬ. Всего теоретически возможно 2**6=64 таких гексаграмм, и вся эта совокупность образует базовый слой Книги Перемен без пропусков и добавлений. Каждую гексаграмму можно представить не только как последовательность 6 черт ЯН-ИНЬ, но и как последовательность двух триграмм - нижней и верхней. Триграмма - это последовательность из трех черт ЯН-ИНЬ. Триграмм, очевидно, 2**3=8. А их упорядоченных пар 8**2, то есть, как и следовало ожидать, 64.

Традиция приписывает изобретение триграмм полумифическому императору Фуси, демиургу китайской цивилизации, жившему в 28-27 веках до н.э. А вот гексаграммы методом "удвоения триграмм" создал Вэнь-ван - Царь Просвещенный - родоначальник династии Чжоу (12 век до н.э.). Он же расположил гексаграммы в определенном порядке, который и называется порядком Вэнь-вана. Именно этот порядок зафиксирован в Книге Перемен.

Кроме порядка Вэнь-вана известны и другие расположения гексаграмм. Например, так называемый порядок Фуси, или порядок Мавандуйской версии Книги Перемен, обнаруженной при раскопках уже в XX веке. Однако, все эти порядки, во-первых, не столь "каноничны", если можно так выразиться. Во-вторых, все они легко объяснимы - каждый порядок строится по известному легко понимаемому закону, или алгоритму.

Среди Десяти Крыльев Книги Перемен есть трактат "Сюйгуа чжуань", который как раз и предназначен для объяснения порядка Вэнь-вана. Однако никакого удовлетворительного для нас объяснения мы там не обнаружим. То ли автор трактата уже и сам не вполне понимал, почему Вэнь-ван расположил гексаграммы так, а не иначе, и дал свою собственную субъективную и достаточно произвольную интерпретацию этого порядка. То ли мы как-то не так этот трактат читаем, что, правда, маловероятно. В любом случае никакого Закона Вэнь-вана, который полностью объяснял бы этот порядок, до сих пор не обнаружено.

Между тем, найти такой закон очень важно. Ведь Книга Перемен по праву считается фундаментом китайской философии и научной, или, если кому-то так больше нравится, донаучной, методологии, самой техники китайского способа мышления. Последовательность гексаграмм претендует на то, чтобы служить моделью, архетипом мирового процесса развития, космического цикла бытия. И тому подобное. С этой точки зрения совсем не все равно, в каком порядке идут гексаграммы в И-цзине.

Вот почему так много усилий тратиться на, казалось бы, вполне частную и, можно сказать, схоластическую проблему порядка Вэнь-вана. При этом многие исследователи, изучая и применяя Книгу Перемен в более широком констексте, устанавливают связи гексаграмм с самыми разными явлениями. Здесь и генетический код, и календарный цикл, и шахматы, и арифметика, и формальная логика. Перечислять - не хватит времени на мой доклад. С одной стороны, здесь нет ничего удивительного в свете того, что я говорил о гексаграммах как методологической основе всего и вся, как своеобразной универсальной матрице. С другой стороны, каждое такое сопоставление есть, говоря языком математики, сопоставление абстрактной модели и конкретной интерпретации. Расчет на то, что при этом будет найден Закон Вэнь-вана, скорее всего неверен. Не все ли равно, пытаться объяснить порядок гексаграмм, или соответствующую последовательность годов календарного цикла? Скорее уж наоборот, если мы отгадаем загадку И-цзина, мы можем рассчитывать на какие-то открытия в иных областях, как следствие их сопоставления с гексаграммами.

Итак, существует ли и в чем заключается Закона Вэнь-вана? Почему гексаграммы перечислены именно в таком порядке?

По этому поводу есть несколько версий.

Версия 1. Никакого Закона Вэнь-вана не существует, гексаграммы расположены в случайном порядке. Эта версия привлекательна тем, что снимает саму проблему и освобождает силы и время исследователей для других дел. Однако, у нее есть существенный недостаток - она противоречит фактам. А факты таковы, что порядок Вэнь-вана не может быть полностью случайным. Известны несколько закономерностей, которые невозможно игнорировать.

Версия 2. Другая крайность - закон Вэнь-вана безусловно существует, но мы его еще не нашли. Именно эта версия привлекает исследователей к данной проблеме. Против этой версии говорят годы, века и даже тысячелетия безрезультатной работы сотен исследователей. Впрочем, наука знает примеры такого рода, когда решение в конце концов находилось. Правда, как правило, не там, где его искали.

Версия 3. Эта компромиссная версия возникла, по-видимому, из-за отчаяния исследователей. Раз никакие вроде бы обнаруживаемые закономерности в порядке Вэнь-вана не объясняют его целиком, потому что постоянно где-то что-то оказывается расположенным не так, как нам хотелось бы, значит что-то не в порядке с самим порядком Вэнь-вана. Это значит, что закон Вэнь-вана существует и мы даже догадываемся, в чем он заключается, но только этот закон - не для того порядка, который мы называем порядком Вэнь-вана. Настоящий, истинный порядок Вэнь-вана был немного другим, а то, что до нас дошло, есть проявление стандартного закона Истории под названием "Ошибка переписчика". Здесь, конечно, лед тонок, потому что ни доказать, ни опровергнуть подобные теории невозможно. Каждый раз время жизни мифического переписчика отодвигается в те времена, из которых до нас не дошло достоверных письменных свидетельств. Тем не менее, эта теория весьма популярна. Ищут идеальный порядок гексаграмм, подходящий для любимой авторами закономерности, а потом смотрят, насколько он отличается от порядка Вэнь-вана. Если совсем чуть-чуть, то, может быть, и правда виноват переписчик?

Версия 4. Эта версия также компромиссна и основана на идее, которую, насколько я знаю, впервые высказал Давыдов больше 10 лет назад, а я с тех пор повторяю и развиваю. Я думаю, Давыдов меня простит, если я ее выскажу в форме анекдота. Вэнь-ван был очень просвещенным человеком. У него было много идей, и всех их он хотел символически воплотить в Книге Перемен в виде соответствующих закономерностей расположения гексаграмм. Однако, идеи эти, как это обычно и бывает с хорошими идеями, часто друг другу противоречили, поэтому, воплощение идей шло с некоторым трудом. Когда очередная идея не влезала в прокрустово ложе уже имеющей последовательности гексаграмм, Вэнь-вану приходилось слегка поднажать, в результате чего закономерности уже воплощенных идей слегка подламывались. Вэнь-ван был упорным человеком, и, в конце концов, все его идеи были втиснуты в Книгу Перемен. Однако, почти все реализующие их закономерности расположения гексаграмм оказались слегка подпорченными. В результате, как, наверное, замечали многие исследователи Книги Перемен, в порядке Вэнь-вана можно обнаружить много всяких закономерностей, но почему-то почти все они оказываются с единичными нарушениями.

Если же говорить серьезно, то, как выразился в частной беседе Давыдов, в Книге Перемен - все как жизни: нет ни Первозданного Хаоса, ни Божественного Порядка. Все здесь "почти", все "на грани". Вот, казалось бы, мы почти нашли великий Закон Вэнь-вана, вот мы рисуем красивые симметричные картинки, которые должны все объяснить. И вдруг - выражаясь в терминах Книги Перемен - происходит "переразвитие". И наш закон оказывается не всеобщим: он, конечно, выполняется, но "почти", то есть, не везде и не всегда. И-цзин словно играет с нами в салочки, постоянно увиливая от наших так ловко расставленных сетей логики, симметрии и гармонии.

Версия 5. Эта версия является развитием предыдущей. Суть ее в том, что вся совокупность частичных закономерностей, которым удовлетворяет порядок Вэнь-вана, как раз и объявляется искомым Законом Вэнь-вана. Расчет на то, что никакой другой порядок, кроме порядка Вэнь-вана, не удовлетворяет столь же "почти" всем этим закономерностям.

Это можно формализовать, если на множестве всех возможных порядков определить метрику. Например, если один порядок получается из другого с помощью всего лишь одной транспозиции, то есть, перемены местами двух соседних гексаграмм, то расстояние между этими порядками равно 1. Если нужны две транспозиции, то расстояние равно 2. И так далее. После этого введем понятие "достаточно близких" порядков как порядков, расстояние между которыми меньше некоторой "мировой константы". Как определить эту константу - вопрос отдельный. Далее, для каждой закономерности можно найти тот идеальный порядок, где она реализуется стопроцентно, безо всяких нарушений. И если порядок Вэнь-вана "достаточно близок" по нашей метрике к этому идеальному порядку, то будем говорить, что закономерность почти реализуется на порядке Вэнь-вана. Тогда Закон Вэнь-вана гласит: порядок Вэнь-вана - это единственный порядок, на котором почти реализуются все закономерности из некоторой совокупности их. Вот такая программа исследований получается. Нужно только найти эту совокупность закономерностей и правильно выбрать мировую константу минимального расстояния.

Наконец, последняя, шестая версия ставит философский вопрос: а что, собственно говоря, мы имеем в виду, когда говорим о закономерном или случайном расположении гексаграмм? Эта версия доводит известную амбивалентность случайности и закономерности до логического конца, или до абсурда. И утверждает, что один порядок гексаграмм ничуть не лучше другого просто потому, что у нас нет надежных критериев различения хаоса и порядка. Это, конечно, от большого скепсиса и нежелания разбираться с трактатами по проблеме Вэнь-вана, которые и правда в последние годы стали напоминать известные трактаты с доказательствами Великой Теоремы Ферма.

Тем не менее, в исследовании порядка Вэнь-вана действительно есть опасности, связанные с самим понятием закономерности. Это понятие я бы назвал эстетически-статистическим. Если в порядке Вэнь-вана мы нашли какую-то закономерность, то, по крайней мере, мы должны убедиться, что хотя бы большинство остальных порядков этой закономерностью не обладают. Иными словами, вероятность того, что при случайном бросании монет получится порядок гексаграмм с такой закономерностью, должна быть достаточно мала. Однако, с точки зрения теории вероятностей все порядки гексаграмм одинаковы. Поэтому мы должны еще каким-то образом отличать закономерные порядки от случайных. Закономерный порядок - это порядок симметричный, красивый, простой, ясный, легко объяснимый и т.п. Это уже вопрос эстетический.

Я хотел бы указать на три конкретные опасности.

Первая опасность. Приведу пример. Закономерен ли порядок, в котором реализуется такое свойство: при чтении гексаграмм черта за чертой нигде в последовательности 6*64=384 черт не идут подряд более 16 одинаковых черт? Казалось бы, замечательная закономерность! Можно даже придумать соответствующее философское обоснование и найти цитату из китайской классики - что-нибудь вроде "большой ветер не продержится весь день".

К сожалению, такая закономерность реализуется в любом порядке следования гексаграмм. Дело в том, что само множество 64 гексаграмм безотносительно к их порядку обладает целым рядом регулярных свойств и подчиняется целому ряду закономерностей. Естественно, что эти свойства и закономерности как-то проявляются в каждом из порядков гексаграмм. Велика опасность выдать общее свойство множества за особенность именно этого порядка, что и происходит в моем примере.

Вторая опасность связана с малым числом вариантов. Число порядков 64 гексаграмм чрезвычайно велико - 64! Естественно, что среди этих вариантов какие-то мы можем считать построенными по тому или иному закону, алгоритму, а остальные - случайными. Однако, если вы изучаете порядок следования трех гексаграмм, то здесь лед тонок. Число вариантов всего 6 - можно ли разделить их на случайные и закономерные?

Третья опасность - это попытка выдать желаемое за действительное, и частную закономерность - за всеобщий закон. Вообще, чувство порядка - это такое интуитивное, эстетическое чувство. Например, симметричное кажется нам красивым (тщательно выверенная, рассчитанная асимметрия китайского и японского искусства - частный случай такой симметрии). В тоже время симметрия играет большую роль, скажем, в таких точных науках, как физика и математика. В эвристике красота вообще, и симметрия в частности, являются одним из критериев истины. При исследовании И-цзина очень часто получаются разного рода красивые симметричные картинки, целые мозаики и своеобразные хитросплетенные ковры из цифр, значков, иероглифов.

Все это очень хорошо, но рискованно. Симметрия по определению является не полным, а частичным объяснением, поскольку основана всего лишь на сопоставлении: левого и правого, верха и низа, через центр и т.п. Симметрия часто создает всего лишь иллюзию идеального порядка, в основе которого оказывается полный хаос.

Есть даже такая детская игрушка, наглядно демонстрирующая всю коварность симметрии. Называется калейдоскоп. Смотришь в трубочку - вот какая красивая симметричная картинка. Повернешь - другая кратинка, тоже красивая и симметричная. А на самом-то деле, если игрушку разобрать, там всего лишь кучка цветных камушков, случайной формы, случайных размеров. Зато очень ловко расставлены зеркала. Вот и Вэнь-ван бросил в случайном порядке восемь триграмм, а потом хитрыми зеркалами их удвоил и получился И-цзин. Но, скорее, наоборот, восемь триграмм - это зеркала, а камушки - даже не знаю что. Но симметричные картинки получаются.

И вот сейчас, чтобы не быть голословным, я хочу продемонстрировать серию таких картинок.

 

 

 

Плакат 01: Первая Дихотомия

Как известно, для гексаграмм определены две важные операции:

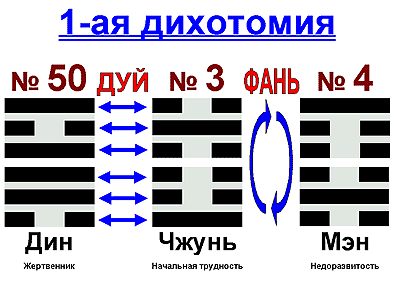
●операция переворота гексаграммы на 180о - операция ФАНЬ; результат операции - "перевернутая" или "обратная" гексаграмма

●операция инверсии черт гексаграммы (когда ЯН превращается в ИНЬ, а ИНЬ - в ЯН) - операция ДУЙ; результат операции - "инвертированная" гексаграмма.

Как пишет Кобзев в предисловии к изданию "Книги Перемен" 1993 года:

"Эти два вида противопоставления в традиционной китайской методологии охватывают все контрарные и контрадикторные отношения, т.е., и противоположность и противоречие. Кроме того, они выражают два универсальных закона мироздания, синтезируемых в понятии дао. Сам исходный смысл иероглифа дао - "путь" - двуедин: путь - это и статический объект, дорога, и динамический процесс, движение по дороге. Соответственно, наиболее общие определения дао выделяют в нем и универсальную статическую структуру "супротивности" [то, что я называю "инверсией"] в виде бинарной оппозиции сил инь и ян, и универсальный процесс "обращения вспять" [то, что я называю "переворотом"]""

Известно, что в расположении Вэнь-вана гексаграммы объединяются в пары: гексаграмма с нечетным номером и следующая за ней гексаграмма с четным номером. Гексаграммы одной пары получаются друг из друга с помощью операции переворота - ФАНЬ. Исключение составляют симметричные гексаграммы, которые при перевороте не меняются. В этих случаях гексаграммы пары получаются друг из друга с помощью операции инверсии - ДУЙ. Имеется 4 таких пары типа ДУЙ; остальные 28 пар гексаграмм - типа ФАНЬ.

Эту хорошо известную парность гексаграмм я назвал ПЕРВОЙ ДИХОТОМИЕЙ И-цзина.

Плакат 02: Вторая Дихотомия

ВТОРОЙ ДИХОТОМИЕЙ И-цзина я называю традиционное деление И-цзина на две части: первые 30 гексаграмм и следующие 34 гексаграммы.

На первый взгляд такое деление вызывает недоумение. Почему в первой части именно 30 гексаграмм? Если уж делить И-цзин на две части, то почему не поровну - по 32 гексаграммы?

На помощь приходит первая дихотомия И-цзина. Представим себе, что каждая гексаграмма записывается на отдельной табличке. Однако, для пары гексаграмм типа ФАНЬ достаточно одной таблички: вторая гексаграмма пары получается при перевороте таблички на 180о. Таким образом, читая на табличке, например, гексаграмму #3, мы можем, перевернув табличку, прочесть и следующую гексаграмму #4. В то же время для пары гексаграмм типа ДУЙ нам потребуются две таблички. Таким образом, можно "сэкономить" дефицитные таблички и для записи всех 64 гексаграмм использовать всего 36 табличек. При этом оказывается, что первая и вторая части И-цзина записываются на равном числе табличек - по 18 табличек. В этом смысле можно считать, что вторая дихотомия делит И-цзин как раз на две равные части.

Плакат 03: Третья Дихотомия

10 лет назад я делал доклад на XXI конференции "Общество и государство в Китае" в Институте Востоковедения, в котором рассказывал о найденной мною закономерности в расположении гексаграмм по Вэнь-вану. Эту закономерность я назвал ТРЕТЬЕЙ ДИХОТОМИЕЙ И-цзина.

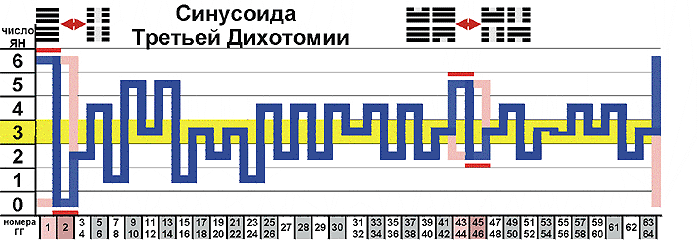
Коротко ее суть заключается в следующем: если для каждой таблички с нарисованной на ней гексаграммой подсчитать число черт ЯН, то при движении по И-цзину это число будет попеременно то увеличиваться, то уменьшаться. Это можно изобразить на графике, где по вертикальной оси отложено число черт ЯН на табличке, а по горизонтали - номер таблички или номера изображенных на табличке гексаграмм. Получится вот такая синусоидальная линия, отображающая волновой процесс увеличения и уменьшения "света", то есть, светлых черт ЯН, или, если угодно, процесс уменьшения и увеличения "тьмы", то есть, темных черт ИНЬ. Этот процесс является замкнутым - после последней таблички с гексаграммами #63-64 снова читается первая табличка с гексаграммой #1.

Как видим, имеются два нарушения общего правила: в двух местах графика идут подряд два увеличения числа черт ЯН. Каждое из этих нарушений можно было бы устранить, если бы поменять местами две соседние таблички. В первом случае меняем местами таблички с первыми двумя гексаграммами ЦЯНЬ и КУНЬ, а во втором случае - табличку с парой гексаграмм #43-44 и табличку с парой гексаграмм #45-46.

10 лет назад я показывал аналогичный плакат в несколько ином виде. Тогда я по горизонтальной оси откладывал не таблички, а пары гексаграмм; соответственно, по вертикали откладывалось общее число черт ЯН в паре гексаграмм. В этом случае первое нарушение, связанное с гексаграммами ЦЯНЬ и КУНЬ, не наблюдается. Это говорит о том, что первое нарушение как бы несущественно. Оно зависит, так сказать, от точки зрения. Однако, второе нарушение имеется в обоих случаях. Оно связано с положением пары гексаграмм #43-44. Запомним эту пару гексаграмм. Мы будем еще неоднократно к ней возвращаться.

Этот волновой процесс частично объясняется тем, что сами таблички гексаграмм подразделяются на две группы: четные и нечетные по их положению в И-цзине. Поэтому-то я и назвал эту закономерность третьей дихотомией. В нечетных табличках, как правило, преобладает ИНЬ, а в четных табличках - ЯН. Казалось бы, это нарушает традиционную ассоциацию нечета с ЯН и чета - с ИНЬ. В этом смысле график, основанный не на табличках, а на парах гексаграмм, кажется логичнее, поскольку там в нечетных парах преобладает как раз ЯН, а в четных - ИНЬ. Однако, на самом деле в традиции связь с ЯН вовсе не означает преобладание черт ЯН. Дело обстоит скорее наоборот.

Рассмотрим, например, традиционную семейную символику триграмм. Старшие триграммы ЦЯНЬ и КУНЬ - это отец и мать. Отец, действительно, содержит все три черты ЯН, а мать - все три черты ИНЬ. Однако, их дети - младшие триграммы - делятся на сыновей и дочерей по той черте, которая оказывается в меньшинстве. Сыновья содержат по одной черте ЯН, а дочери - по одной черте ИНЬ.

Вообще, в символике "Книги Перемен" то, что в меньшинстве, - это молодое, растущее, развивающееся и, в конечном итоге, побеждающее. А то, что в большинстве, - это старое, перерастающее само себя, "переразвивающееся" и, в конечном итоге, переходящее в свою противоположность.

Плакат 04: Три Дихотомии - 4 квадранта И-Цзина

На этом плакате наглядно изображены три дихотомии И-цзина, о которых шла речь. Оси координат показывают три направления, по которым происходит деление гексаграмм по каждой из дихотомий. Желтые квадратики - это таблички с номерами гексаграмм. На белых квадратиках написаны номера соответствующих перевернутых гексаграмм. Вторая дихотомия делит И-цзин на две части, которые будем называть верхней и нижней частями по их расположению на этом плакате. Соответственно, третья дихотомия делит И-цзин на левую и правую части. Вместе обе дихотомии делят И-цзин на 4 квадранта, обозначенных числами 1,2,3,4.

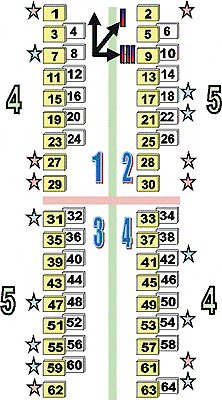
Сегодня моя задача - показать глубокую внутреннюю связь всех трех дихотомий И-цзина и все закономерности, о которых я буду говорить, так или иначе с этим связаны.

Одну из таких закономерностей можно увидеть уже на этом плакате. Здесь синими звездочками отмечены таблички с гексаграммами, у которых равное число черт ЯН и ИНЬ. Каждой такой табличке соответствует пара гексаграмм типа ФАНЬ, и общее число черт ЯН (также как ИНЬ) равно 6. Это число черт свойственно также кажой паре гексаграмм типа ДУЙ; гексаграммы, входящие в такие пары отмечены красными звездочками. Мы видим, что 1-ый и 4-ый квадранты содержат по 4 звездочки, а 2-ой и 3-ий - по 5 звездочек. Поэтому 2-ая и 3-я дихотомии каждая делит И-цзин на две части, в которых одинаковое число звездочек - 9.

Плакат 05: ХУ ГУА - Взаимопроникающие триграммы.

4 терминальные гексаграммы

В гексаграмме выделяют две взаимопроникающие триграммы - ХУ ГУА, - которые образуются, соответственно, из 3,4,5 и 2,3,4 черт гексаграммы. Они могут использоваться как, соответственно, верхняя и нижняя триграммы новой, производной, гексаграммы. Считается, что эта производная гексаграмма характеризует более глубокое состояние ситуации, описываемой исходной гексаграммой. На мой взгляд, точнее следовало бы говорить не о более глубоком, а о более обобщенном, более абстрактном состоянии.

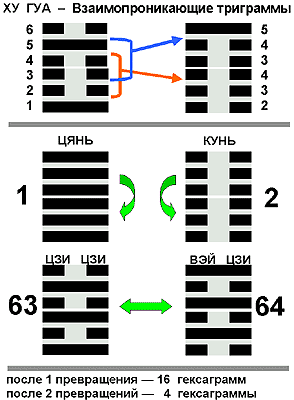
Дело в том, что после одно такого преобразования 64 гексаграммы переходят в 16 гексаграмм, а после второго остается всего 4 гексаграммы. Происходит как бы процесс обобщения, абстрагирования, в котором нескольким гексаграммам ставится в соответствие одна гексаграмма, отражающая некое общее своейство исходных гексаграмм.

На этом плакате изображены все 4 гексаграммы, которыми заканчивается процесс обобщения. Это две первые и две последние гексаграммы И-цзина. При этом первые гексаграммы ЦЯНЬ и КУНЬ в результате преобразования ХУ ГУА не изменяются, а последние гексаграммы ЦЗИ ЦЗИ и ВЭЙ ЦЗИ переходят друг в друга. В бесконечном процессе превращений ХУ ГУА выстраиваются три линии: линия ЦЯНЬ, линия КУНЬ и линия взаимопревращающихся, как бы осциллирующих, гексаграмм ЦЗИ ЦЗИ и ВЭЙ ЦЗИ.

Эти три линии можно соотнести с известной триадой китайской методологии и философии: НЕБО, ЗЕМЛЯ и ЧЕЛОВЕК. НЕБО - ЦЯНЬ - это абсолютное светлое начало, все 6 черт ЯН; ЗЕМЛЯ - КУНЬ - это абсолютное темное начало, все 6 черт ИНЬ. Гексаграммы ЦЗИ ЦЗИ и ВЭЙ ЦЗИ содержат равное число света и тьмы, черт ЯН и ИНЬ; более того, в этих гексаграммах они строго чередуются: "то ЯН, то ИНЬ". Человек - это существо, в котором светлое и темное начало как бы перемешаны в равных пропорциях и чередуются друг с другом. Разделение на две гексаграммы - ЦЗИ ЦЗИ и ВЭЙ ЦЗИ - соответствует разделению на два пола - мужчину и женщину. Их постоянное взаимопревращение изображает процесс жизни, цепь поколений людей, постоянно рождающихся и умирающих. Характерны в этой связи названия гексаграмм: ЦЗИ ЦЗИ означает УЖЕ КОНЕЦ, ВЭЙ ЦЗИ - ЕЩЕ НЕ КОНЕЦ.

Плакат 06:ХУ ГУА - Взаимопроникающие триграммы.

16 гексаграмм первого уровня

Таким образом гексаграммы можно разделить на три категории: небесные, земные и человеческие, - в зависимости от того, во что они переходят двойным применением операции ХУ ГУА. В целом распределение этих категорий по расположению Вэнь-вана не имеет явно просматриваемой закономерности. В каждом из квадрантов есть гексаграммы каждой категории в различных пропорциях:

квадрант	гексаграммы	таблички
ЦЯНЬ	КУНЬ	ЦЗИ ЦЗИ - ВЭЙ ЦЗИ	ЦЯНЬ	КУНЬ	ЦЗИ ЦЗИ - ВЭЙ ЦЗИ
1	1	10	4	1	6	2
2	4	1	10	3	1	5
3	7	2	8	4	1	4
4	4	3	10	2	2	5

 

Однако, если рассматривать не все 64 гексаграммы, а 16 промежуточных, в которые превращаются эти 64 гексаграммы однократным применением операции ХУ ГУА, то здесь ситуация более ясная.

На этом плакате видно, что левая и правая части И-цзина (соответствующие 3-ей дихотомии) содержат равное число гексаграмм - 8. Гексаграммы из левой части помечены желтым цветом, а гексаграммы из правой части - белым.

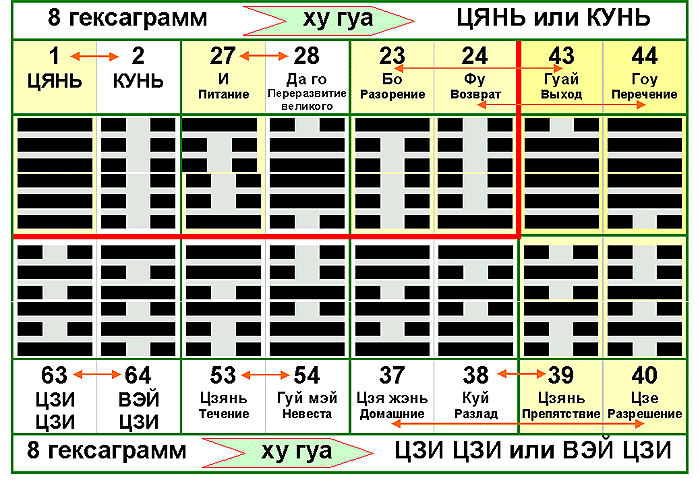
Верхняя и нижняя части И-цзина (соответствующие 2-ой дихотомии) разделены на плакате красной линией. Верхняя часть содержит только земные и небесные гексаграммы, а все человеческие гексаграммы относятся к нижней части. Однако к нижней части относятся также две небесные гексаграммы с #43-44. Если бы эта пара также относилась к верхней части, то обе части содержали бы равное число гексаграмм, причем все земные и небесные принадлежали бы верхней части, а все человеческие - нижней. Отметим, пара гексаграмм #43-44 - это та самая пара, из-за которой в одном месте нарушается волновой процесс 3-ей дихотомии.

Стрелками соединены взаимно-инвертированные по операции ДУЙ гексаграммы.

Плакат 07: 4 симметричные триграммы и 8 гексаграмм ##43-50

А теперь я хочу напомнить одну хорошо известную закономерность, которая имеет прямое отношение к нашим дихотомиям И-цзина.

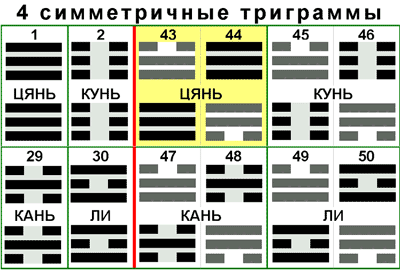
На этом плакате изображены слева от красной линии все четыре симметричные гексаграммы, составленные из симметричных триграмм. Верхняя пара гекаграмм начинает верхнюю часть И-цзина, а нижняя пара - заканчивает ее. Соответственно, левые две гексаграммы начинают и заканчивают 1-ый квадрант И-цзина, правые две гексаграммы - 2-ой квадрант.

Справа от красной линии изображена последовательность из 8 подряд идущих гексаграмм из нижней части И-цзина. Левые четыре гексаграммы относятся к 3-му квадранту, правые четыре - к 4-му квадранту. Каждая из этих 4-х пар гексаграмм устроена по одному образцу. Внутренние триграммы во всех парах одни и те же: верхняя триграмма первой гексаграммы - триграмма СЮНЬ, нижняя триграмма второй гексаграммы - обратная ей (по правилу ФАНЬ) триграмма ДУЙ. Внешние триграммы (нижняя триграмма первой и верхняя триграмма второй гексаграммы) одинаковы - это симметричные триграммы. И эти симметричные триграммы идут в той же последовательности, что и в верхней части И-цзина.

Можно обратить внимание на то, что эта последовательность из 8 гексаграмм начинается двумя уже знакомыми нам гексаграммами #43-44. Возможно, именно для того, чтобы создать такую последовательность из 8 гексаграмм, пара гексаграмм #43-44 и была помещена на свое место. Иными словами, здесь имеется как бы перекрещивание нескольких закономерностей, из-за чего в некоторых из них возникают единичные нарушения.

12 лет назад С.Д. Давыдов при исследовании порядка гексаграмм внутри пар 1-ой дихотомии, обнаружил интересную закономерность, частично объясняющую, по какому принципу гексаграммы одной пары идут в том или ином порядке. Однако, у этой закономерности есть одно-единственное нарушение: гексаграммы #49-50 идут "не в том порядке". Весьма показательно, что рассмотренная нами последовательность из 8 гексаграмм начинается с гексаграмм #43-44, нарушающих 3-ю дихотомию, а заканчивается гексаграммами #49-50, нарушающими закономерность Давыдова. Так что эта последовательность вносит единичные нарушения уже в две известные закономерности.

Это позволяет сделать вывод о более позднем происхождении этой последовательности внутри расположения Вэнь-вана; иными словами, она представляет собой как бы "заплатку" на некоем исходном расположении. Цель такой заплатки заключалась, может быть, в желании добавить в И-цзин какую-то новую идею, какой-то новый процесс, описываемый последовательностью из 8 подобранных гексаграмм. Для этого, конечно, потребовалось изъять эти гексаграммы из тех мест, где они были ранее, что и нанесло ущерб уже имевшимся ранее закономерностям. Впрочем, возможно весь И-цзин складывался таким образом: методом добавления закономерностей с возможными единичными нарушениями уже имеющихся.

Плакат 08: Последние 4 гексаграммы верхней и нижней частей

На этом плакате отражена еще одна частная закономерность, относящаяся ко второй дихотомии. Здесь сверху изображены 4 последних гексаграммы верхней части И-цзина, а снизу - 4 последних гексаграммы нижней части.

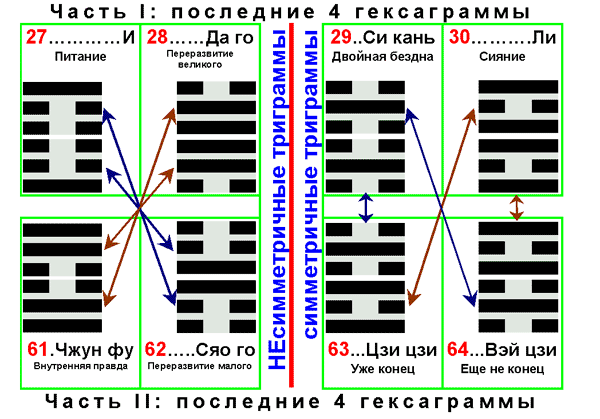
Можно заметить, что каждый набор из 4-х гексаграмм не содержит старших триграмм (ЦЯНЬ и КУНЬ) и содержит все 6 младших триграмм. Симметричные триграммы КАНЬ и ЛИ в соответствии с правилом парности гексаграмм по первой дихотомии методом ФАНЬ или ДУЙ встречаются в каждом наборе по 2 раза. Поэтому 8 триграмм из набора 4-х гексаграмм - это все 4 несимметричные триграммы (по одному разу) и обе симметричные триграммы (по 2 раза).

Последняя пара гексаграмм как сверху, так и снизу содержит только симметричные триграммы, а первая пара - только несимметричные.

Наконец, в этот набор из 4-х пар гексаграмм входят все симметричные гексаграммы, составленные только из младших триграмм. Таких гексаграмм - 6, и они образуют 3 пары типа ДУЙ; 4-ая пара - это последняя пара гексаграмм И-цзина.

Плакат 09: Вероятность выпадения при гадании гексаграммы как гексаграммы возможного будущего

Поскольку "Книга Перемен" возникла и использовалась как гадательная книга, было бы правильно учитывать существовавшие мантические процедуры при иссследовании расположения гексаграмм.

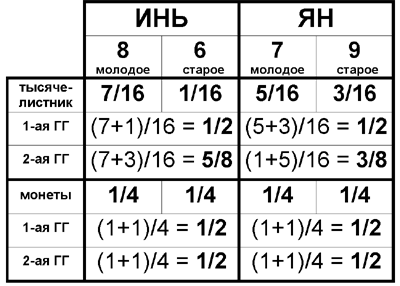
Как известно, основная такая процедура заключается в последовательном определении значения каждой из 6 позиций гексаграммы. При этом для каждой позиции возможно не два значения - ЯН и ИНЬ, которые в самом И-цзине обозначаются числами 9 и 6, - а 4 значения. Добавляются еще два числа - 7 и 8, которые обозначают неподвижные или молодые черты ЯН и ИНЬ. Числа же 9 и 6 обозначают подвижные или старые черты ЯН или ИНЬ.

Таким образом, в результате гадания получается пара гексаграмм: гексаграмма, описывающая текущую ситуацию, и гексаграмма, описывающая возможное будущее. Эта вторая гексаграмма получается из первой, когда все подвижные черты переходят в свою противоположность: старая черта ЯН превращается в ИНЬ, а старая черта ИНЬ - в ЯН.

Классическим способом такого гадания является гадание на стеблях тысячелистника. Этот способ существенно отличается от применяемого иногда гадания на монетах. Вероятности выпадения чисел 6,7,8,9 для обоих способов показаны на этом плакате.

В обоих случаях вероятности получения ЯН и ИНЬ для первой гексаграммы одинаковы (1/2), соответственно, вероятность выпадения гексаграммы в качестве первой одна и та же для всех 64 гексаграмм (1/64). Однако, вероятности получения ЯН и ИНЬ для второй гексаграммы при гадании по тысячелистнику уже различны: ИНЬ выпадает с большей вероятностью, чем ЯН. Соответственно, вероятность выпадения гексаграммы как второй при гадании по тысячелистнику для разных гексаграмм разная. Большую вероятность имеет та гексаграмма, в которой больше черт ИНЬ и меньше черт ЯН. В целом имеется 7 таких разных вероятностей и, соответственно, 7 классов гексаграмм - по числу черт ЯН (или ИНЬ).

Плакат 10: 7 классов гексаграмм по их вероятностям (по числу ЯН)

На этом плакате все 64 гексаграммы распределены по 7 этим классам. Каждому классу соответствует столбец таблицы. Таблица заполнялась в соответствии с последовательностью Вэнь-вана сверху вниз, то есть, когда очередную гексаграмму нужно было поместить в соответствующий столбец, выбиралась самая верхняя свободная ячейка в этом столбце.

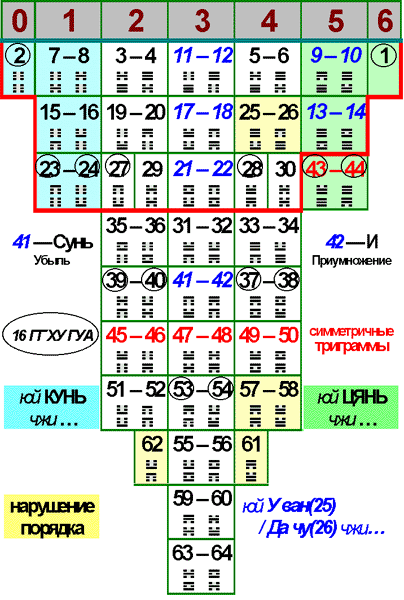
Как правило, переход на следующую, более нижнюю, строку происходил тогда, когда текущая строка и все более верхние строки уже заняты полностью. Исключений всего 4 - они отмечены желтым цветом.

Прежде всего, обратим внимание на то, что верхняя часть И-цзина (первые 30 гексаграмм) занимает целиком верхние три строки таблицы. Исключение составляет только уже знакомая нам пара гексаграмм #43-44.

С этой таблицей тесно связано известное преобразование гексаграмм, при котором выделяется одна из шести черт и меняется на противоположную (ЯН-ИНЬ). Это описывается формулой чжи A юй B, где A - это исходная гексаграмма, а B - производная гексаграмма, отличающаяся от A только одной чертой. Очевидно, от каждой гексаграммы можно получить 6 таких производных гексаграмм. Добавляя саму исходную гексаграмму, а также инвертированную (по правилу ДУЙ) гексаграмму, получаем набор из 8 гексаграмм, который, по предположению Кобзева, назывался термином БА ГУА.

На плакате зеленым цветом изображены гексаграмма #1-ЦЯНЬ и все 6 производных из нее по правилу ЧЖИ ЮЙ гексаграмм. Соответственно, синим цветом изображены инвертированная гексаграмма #2-КУНЬ и все 6 производных из нее по правилу ЧЖИ ЮЙ гексаграмм. Как видим, все эти 14 гексаграмм относятся к верхней части И-цзина.

Теперь возьмем пару гексаграмм #25-26, которая является единственной парой верхней части И-цзина, нарушающей порядок заполнения таблицы. Номера 12 производных гексаграмм написаны синим цветом и подчеркнуты. Из них 10 гексаграмм относятся к верхней части И-цзина и заполняют целиком столбцы 3 и 5. В некотором смысле это можно считать объяснением того, какие именно 6 из 20 гексаграмм 3-го столбца попадают в верхнюю часть И-цзина. Более важно то, что таким образом осуществляется отбор для верхней части И-цзина 4-х из 6 гексаграмм 5-го столбца. Отсеиваемая пара гексаграмм - та самая пара #43-44.

Две гексаграммы, получающиеся из пары гексаграмм #25-26 по правилу ЧЖИ ЮЙ, и относящиеся к нижней части И-цзина, - это гексаграмма #41-СЮНЬ-Убыль и гексаграммы #42-И-Приумножение. Названия этих гексаграмм являются важнейшими терминами китайской философии. Кроме того, непосредственно за ними следует последовательность из 8 гексаграмм с симметричными внутренними триграмммами, рассмотренная нами выше. На этом плакате номера этих 8 гексаграмм записаны красным цветом. Наконец, операция инверсии ДУЙ соотносит эту пару с парой #31-32 -первой парой гексаграмм нижней части И-цзина.

На этом плакате показаны также 16 гексаграмм, к которым сводятся все гексаграммы однократным применением правила ХУ ГУА, - их номера обведены кружками.

Плакат 11: Распределение триграмм по квадрантам И-цзина

На этом плакате изображено распределение триграмм по квадрантам И-цзина. При этом учитывается положение триграммы как нижней или верхней в гексаграмме. В силу первой дихотомии для симметричных триграмм это не имеет значения, а для несимметричных триграмм распределение триграммы как верхней совпадает с распределением соответствующей перевернутой триграммы как нижней. В центральном квадрате указаны именно верхние триграммы.

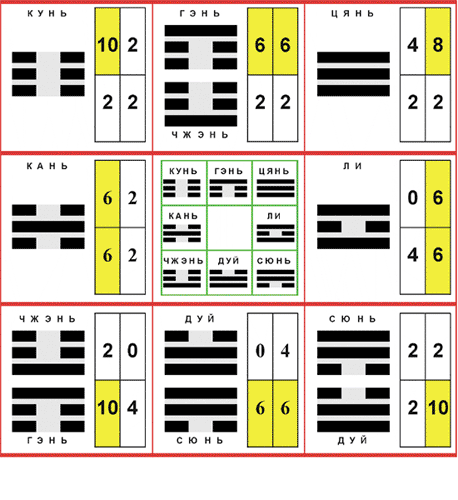
Мы видим, что четыре триграммы КУНЬ, ЦЯНЬ, ЧЖЭНЬ, СЮНЬ тяготеют к квадрантам 1,2,3,4. Четыре остальные триграммы КАНЬ, ЛИ, ГЭНЬ, ДУЙ тяготеют к одной стороне: левой, правой, верхней и нижней.

Таким образом, получается девятиклеточный квадрат, 4 угла которого соответствуют квадрантам И-цзина, а 4 средние клетки сторон - соответствующим частям И-цзина: верхней, нижней, левой и правой, то есть, паре соседних квадрантов. Этим 8 клеткам соответствуют 8 триграмм, тяготеющих к ним по расположению в И-цзине.

Получившемуся пространственному расположению восьми триграмм соответствует круговая последовательность триграмм, которая получается при считывании триграмм в девятиклеточном квадрате по часовой стрелке. Соответственно, эта круговая последовательность порождает восемь линейных последовательностей - в зависимости от выбора начала отсчета.

Плакат 12: Новое расположение триграмм и расположение Вэнь-вана

Эти пространственное расположение и линейные последовательности триграмм не совпадают ни с одним из известных порядков триграмм. Во всяком случае, они не совпадает ни с одной из 11 последовательностей, выделенных Карапетьянцем 15 лет назад:

o6 последовательностей из "Шогуачжуань",

oпоследовательность Фуси,

oпоследовательность Вэнь-вана,

oпоследовательность, соответствующая последовательности гексаграмм в расположении Вэнь-вана, у которых верхняя и нижняя триграмма совпадают,

oпоследовательности нижних и верхних триграмм в Мавандуйской версии И-цзина.

Вместе с тем это расположение триграмм обладает довольно хорошей симметрией. В углах находятся две симметричные и две несимметричные взаимно-инвертированные триграммы: ЦЯНЬ-КУНЬ и ЧЖЭНЬ-СЮНЬ. Взаимно-инвертированные триграммы расположены симметрично относительно вертикальной оси. На сторонах также имеются две симметричные и две несимметричные взаимно-инвертированные триграммы: КАНЬ-ЛИ и ГЭНЬ-ДУЙ. Взаимно-инвертированные триграммы расположены симметрично относительно центра.

Кроме того, после некоторых естественных преобразований это расположение триграмм легко привести к расположению Вэнь-вана. На этом плакате в левом девятиклеточном квадрате изображено наше расположение триграмм с указанием их семейной символики. Для несимметричных триграмм здесь выбираются не верхние триграммы, а с учетом семейной символики: у сыновей выбираются верхние триграммя, а у дочерей - нижние. В результате получается расположение триграмм, которое превращается в расположение Вэнь-вана инверсией черт младших триграмм, которое в семейной символике интерпретируется как взаимопревращение сыновей и дочерей.

Плакат 13: Матрица Второй Дихотомии

На этом плакате изображена матрица, столбцы которой соответствуют верхним триграммам гексаграмм, строки - нижним триграммам, а клетки - соответствующим гексаграммам. Последовательность верхних триграмм соответствует полученной нами круговой последовательности верхних триграмм. В качестве начала отсчета здесь выбрана триграмма КАНЬ. Последний столбец - снова первая триграмма КАНЬ - добавлен для наглядности. Последовательность нижних триграмм (строки матрицы) - это последовательность перевернутых верхних триграмм.

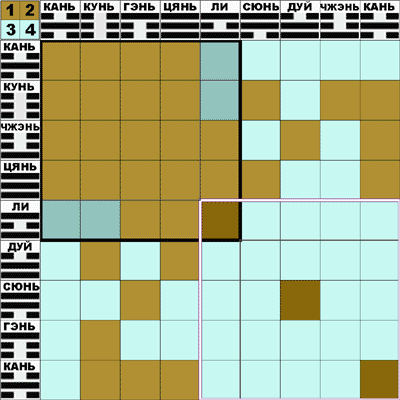
Темно-желтым цветом помечены гексаграммы верхней части И-цзина, а светло-синим - нижней части.

Мы можем увидеть две пересекающиеся в одной клетке подматрицы 5х5. Левая верхняя подматрица почти полностью составлена из верхних гексаграмм (84%), а правая нижняя подматрица - из нижних гексаграмм (88%). Это означает, что в верхнюю часть И-цзина входит 84% гексаграмм, верхние триграммы которых - это все симметричные триграммы (КАНЬ, КУНЬ, ЦЯНЬ, ЛИ), плюс триграмма ГЭНЬ, а нижние триграммы - соответствующие перевернутые триграммы. Соответственно, в нижнюю часть И-цзина входит 88% всех гексаграмм, верхние триграммы которых - это все младшие триграммы, кроме ГЭНЬ, а нижние триграммы - соответствующие перевернутые триграммы.

Плакат 14: Матрица Третьей Дихотомии

На этом плакате изображена аналогичная матрица, составленная исходя из той же последовательности верхних триграмм, но с другой точкой отсчета - триграммой ГЭНЬ.

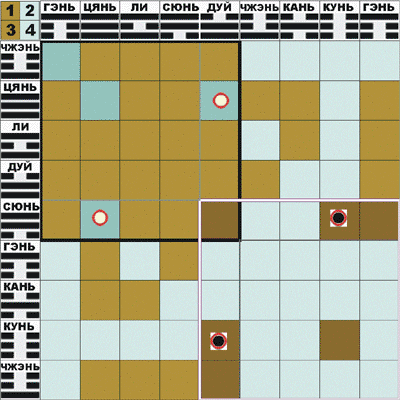
Здесь уже темно-желтым цветом помечены гексаграммы левой части И-цзина, а светло-синим - правой части.

Мы опять видим две пересекающиеся в одной клетке подматрицы 5х5. Левая верхняя подматрица почти полностью составлена из левых гексаграмм (84%), а правая нижняя подматрица - из правых гексаграмм (76%).

Светлыми кружками отмечена знакомая нам пара гексаграмм #43-44, а темными кружками - следующая пара гексаграмм #45-46. Если их поменять местами ("исправление" 3-ей дихотомии), то левая верхняя подматрица будет уже на 92% заполнена левыми гексаграммами, а правая нижняя подматрица - на 84% правыми гексаграммами.

Идея этих матриц гексаграмм с выделением соответствующих подматриц пришла мне в голову еще 10 лет назад, хотя я тогда и не рассказывал об этом на конференции. Правда, я использовал немного другие последовательности триграмм. Та последовательность триграмм, которая использована здесь, дает возможность более детально исследовать распределение гексаграмм в И-цзине.

Плакат 15: Матрица четырех квадрантов

На этом плакате изображена матрица, в которой каждый из квадрантов обозначен своим цветом. Здесь по главной диагонали выделено 8 девятиклеточных квадратов: 4 квадрата обведены черной рамкой и 4 квадрата - белой рамкой.

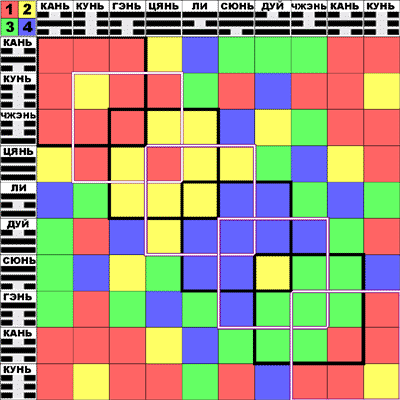
Каждый из этих квадратов содержит 9 гексаграмм, образованных всеми сочетаниями трех триграмм. Эти три триграммы последовательно выбираются из нашей последовательности триграмм: КАНЬ, КУНЬ, ГЭНЬ, ЦЯНЬ, ЛИ, СЮНЬ, ДУЙ, ЧЖЭНЬ.

Четыре квадрата в черной рамке соответствуют четырем триграммам из углов нашего пространственного расположения триграмм: КУНЬ, ЦЯНЬ, СЮНЬ, ЧЖЭНЬ. Можно увидеть, что каждый из этих квадратов содержит не менее семи из девяти клеток, окрашенных в один цвет, то есть, относящихся к соответствующему квадранту И-цзина.

Четыре квадрата в белой рамке соответствуют четырем триграммам из середин сторон нашего пространственного расположения триграмм: ГЭНЬ, ЛИ, ДУЙ, КАНЬ. Можно увидеть, что каждый из этих квадратов содержит не менее семи из девяти клеток, окрашенных в два цвета, то есть, относящихся к соответствующей части И-цзина: верхней, правой, нижней и левой, то есть, паре квадрантов.

Плакат 16: Восемь 9-клеточных квадратов

Эти восемь девятиклеточных квадратов частично пересекаются. Для того, чтобы они были видны более наглядно, я их изобразил отдельно на этом плакате.

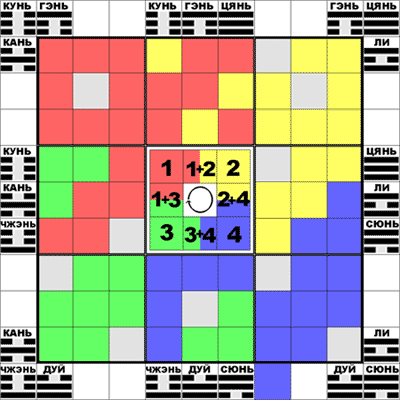
Здесь уже хорошо видно, что в 1-ом квадранте И-цзина (красный цвет) находятся почти все гексаграммы, образованные тройкой триграмм КАНЬ, КУНЬ, ГЭНЬ. Соответственно, 2-му квадранту (желтый цвет) соответствует тройка триграмм ГЭНЬ, ЦЯНЬ, ЛИ. И так далее.

Также верхняя часть И-цзина (красный и желтый цвета) содержит почти все гексаграммы, образованные тройкой триграмм КУНЬ, ГЭНЬ, ЦЯНЬ. Аналогично, нижняя, левая и правая части И-цзина.

Плакат 17: Квадрат 6х6

На этом плакате изображены все 36 табличек с гексаграммами, распределенные по четырем квадрантам И-цзина в соответствии с порядком Вэнь-вана. Порядок табличек внутри каждого квадранта я подобрал таким образом, чтобы были нагляднее видны закономерности, о которых пойдет речь. Этот порядок, тем не менее, как мы увидим ниже, все же закономерным образом связан с реальным порядком Вэнь-вана.

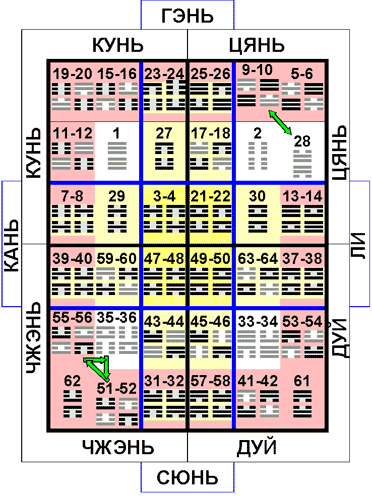
Здесь видны наше пространственное расположение триграмм и их соответствие периферийным клеткам девятиклеточного квадрата, на который разбивается И-цзин, и которые образуются из четырех частей И-цзина (верхняя, нижняя, левая, правая) и четырех квадрантов (левый верхний угол, правый верхний угол, левый нижний угол, и правый нижний угол).

Каждая гексаграмма попадает в три клетки этого большого девятиклеточного квадрата: в один из четырех квадрантов, в верхнюю или нижнюю части И-цзина, и в левую или правую части И-цзина. Тем самым каждой гексаграмме соответствуют три триграммы, что было видно и на предыдущем плакате и здесь. Эти триграммы будем называть значимыми триграммами. В изображении гексаграмм значимые триграммы выделены черным цветом, а незначимые - серым цветом. Напомню, что соответствие триграмм клеткам девятиклеточного квадрата И-цзина устанавливается по верхним триграммам гексаграмм. Поэтому для несимметричных триграмм значимая триграмма является верхней, а нижняя триграмма значима, если это перевернутая значимая триграмма.

Каждый квадрант И-цзина содержит 9 табличек, занимающих также девятиклеточный квадрат. Оказывается, что все эти четыре малых девятиклеточных квадрата устроены аналогичным образом.

Красным фоном обозначены таблички, содержащие значимую триграмму соответствующего квадранта (угловая клетка большого девятиклеточного квадрата). Как видим, каждый квадрант содержит 5 таких табличек из 8-ми возможных. Исключение составляет 2-ой квадрант, соответствующий триграмме ЦЯНЬ. Он содержит только 4 таблички с триграммой ЦЯНЬ. Об этом исключении мы еще поговорим чуть позже.

Желтым фоном обозначены таблички, содержащие значимые триграммы соответствующей части И-цзина (средняя клетка одной из сторон большого девятиклеточного квадрата). Как видим, каждый квадрант содержит 5 таких табличек: по три таблички для каждой части, в которую входит этот квадрант, и при этом одна табличка - общая. Например, в квадранте 1 имеются три таблички с триграммой ГЭНЬ и три таблички с триграммой КАНЬ. При этом одна табличка содержит обе эти триграммы.

Рассмотрим, как устроена эта тройка табличек каждого квадранта, содержащая триграммы соответствующей части И-цзина. Одна табличка общая с другой тройкой. Такая табличка состоит, очевидно, только из значимых триграмм. Эти таблички располагаются в центре - их четыре (по числу квадрантов) - и выделены более темным желтым фоном. Еще одна табличка содержит значимую триграмму этого квадранта. Такая табличка, очевидно, также содержит только значимые триграммы. Эти таблички располагаются в середине сторон матрицы и обозначены желтым цветом на красном фоне. Наконец, третья табличка тройки не содержит других значимых триграмм, то есть, если в ней есть другие триграммы, то они не значимы.

Наконец, каждый квадрант содержит одну табличку без значимых триграмм. Такая табличка располагается в центре квадранта на белом фоне.

Таким образом, в устройстве каждого квадранта мы наблюдаем нумерологически значимые числа 1, 2, 3, 5, 6, 8, 9, 10 и 11 и нумерологически значимую взаимосвязь этих чисел. Число 9 - это число квадрата ЛО ШУ, и это число табличек в квадранте. Число 1 - это символ ДАО как единства, и это одна центральная табличка без значимых триграмм. Число 3 - это триада НЕБО-ЗЕМЛЯ-ЧЕЛОВЕК, и это число табличек со значимыми триграммами одной части И-цзина. Число 2 - это ЯН и ИНЬ, и это число частей И-цзина, в которые входит квадрант, и, соответственно, число троек табличек, относящихся к этим частям. 3*2=6, однако, поскольку одна табличка общая в этих двух тройках, то общее число табличек со значимыми триграммами частей И-цзина равно 5. Также число 5 - это число табличек со значимыми триграммами квадранта. 6+5=11, а 5+5=10, но, с учетом общих табличек, получается 8. Число 10 - это число креста ХЭ ТУ, а число 11 является символом единства Неба (число 6) и Земли (число 5).

При более внимательном изучении этого квадрата можно сформулировать общее правило:

oВыделяются 8 областей, которые будем называть "домами" по 6 табличек в каждой:

o4 прямоугольных треугольника с катетами из 3-х табличек расположены в углах квадрата;

o4 прямоугольника 2х3 расположены по сторонам квадрата: меньшая сторона (2) примыкает к стороне квадрата.

oКаждому дому своя триграмма.

oКаждая гексаграмма располагается либо в доме своей верхней триграммы, либо в доме перевернутой нижней триграммы. Очевидно, симметричная гексаграмме принадлежит одному дому.

Следует особо подчеркнуть: это правило объясняет, правда не всегда однозначно, распределение гексаграмм по квадрантам И-цзина, однако оно не объясняет порядок гексаграмм в каждом квадранте.

Из этого глобального правила есть 7 исключений (3 из 8 симметричных гексаграмм и 4 из 56 несимметричных гексаграмм):

1.симметричная гексаграмм #1 - 77

2.симметричная гексаграмма #2 - 00

3.симметричная гексаграмм #28 - 36

4.пара несимметричных гексаграмм #33-34 - 74-17

5.пара несимметричных гексаграмм #35-36 - 5005

Вообще говоря, существует порядок гексаграмм, полностью удовлетворяющий этому правилу. Но оно отличается от порядка Вэнь-вана.

Это правило можно изменить, потребовав, чтобы угловые дома содержали по 5 табличек, а центральная табличка каждого квадранта не содержала триграмм, соответствующих трем домам этого квадранта (угловому дому, входящему в квадрант, и двум прямоугольным домам, пересекающимся с квадрантом). Тогда у нас будет только одно исключение:

1.симметричная гексаграмм #28 - 36

Правда, правило перестает быть глобальным: оно не объясняет, какие гексаграммы должны попадать в центральные клетки квадрантов. В порядке Вэнь-вана это гексаграммы:

oквадрант 1 - #1 - 77

oквадрант 2 - #2 - 00

oквадрант 3 - пара #35-36 - 50-05

oквадрант 4 - пара #33-34 - 74-17

Здесь есть своя закономерность: это первые две гексаграммы И-цзина и первые две пары гексаграмм второй части И-цзина, если бы делить на две равные по числу гексаграмм части - по 32 гексаграммы.

Плакат 18: Гексаграммы, расположенные не в своих областях

Итак, мы видим, что в каждом квадранте располагаются 5 (или 4 - для квадранта 2) из 8-ми табличек, содержащих соответствующую значимую триграмму. Также в каждой части И-цзина, объединяющей два соседних квадранта, располагаются 6 из 8-ми табличек, содержащих соответствующую значимую триграмму. Возникает вопрос: где расположены остальные таблички со значимыми триграммами?

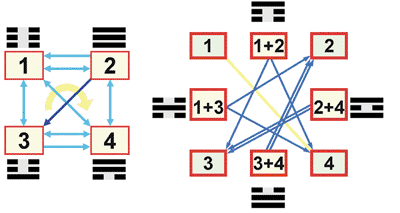
На этом плакате цифрами в прямоугольниках обозначены квадранты и части И-цзина, то есть клетки большого девятиклеточного квадрата И-цзина. Рядом с ними нарисованы соответствующие значимые триграммы. Слева изображены триграммы угловых клеток, а справа - триграммы средних клеток сторон квадрата.

Стрелка ведет из клетки, которой соответствует нарисованная значимая триграмма, в клетку, в которой имеется табличка с этой триграммой. Мы видим, что правая картинка симметрична относительно главной диагонали, нарисованной желтой линией. Левая картинка переходит сама в себя при повороте на 180о. Однако, здесь есть одно нарушение: стрелка обозначенная более темным цветом при повороте меняет свое направление. Это нарушение непосредственно связано с тем, что во 2-ом квадранте не 5, как в остальных квадрантах, а 4 таблички со значимыми триграммами.

В конечном счете эти нарушения также связаны с парой гексаграмм #43-44, содержащими значимую для 2-го квадранта триграмму ЦЯНЬ. Если поменять местами табличку с этой парой гексаграмм и табличку с гексаграммой #28, то нарушения исчезнут. Однако, для исправления нарушения 3-ей дихотомии пару #43-44 нужно поменять местами с парой #45-46. Таким образом, все эти нарушения вместе можно исправить циклической заменой: #43-44 > #36 > #45-46 > #43-44.

Я не призываю исправлять И-цзин. Эта мысленное исправление просто позволяет лучше узнать структуру порядка Вэнь-вана.

Плакат 19: Граф инверсии для квадрата 6х6

При таком расположении табличек с гексаграммами можно обнаружить еще одну закономерность, связанную с операцией инверсии черт ДУЙ. На этом плакате изображена та же матрица, только табличка обозначена кружком, в котором написан относительный номер этой таблички в соответствующем квадранте для порядка Вэнь-вана. Линии соединяют таблички, содержащие взаимно-инвертированные гексаграммы. Пунктирная линия соединяет таблички с парами гексаграмм, переходящих друг в друга операцией ДУЙ. Таких табличек всего 4. Как видим, получается картинка симметричная относительно вертикальной оси.

20 Плакат 19 Граф 6х6 Номера ГГ

До сих пор я в основном говорил о распределении гексаграмм и, соответственно, табличек с гексаграммами по квадрантам И-цзина. При этом мы исследовали устройство множества табличек, попадающих в тот или иной квадрант. Однако, вопрос о том, почему в порядке Вэнь-вана это множество таблички внутри каждого квадранта упорядочено так, а не иначе, остается в открытым. Здесь имеется только несколько частных наблюдений. Об одних мы уже говорили: это первые и последние две гексаграммы И-цзина, это последние четыре гексаграммы верхней и нижней частей И-цзина, это последовательность из восьми гексаграмм с симметричными внутренними триграмми из второй части И-цзина.

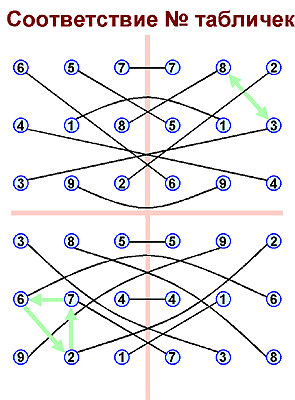
Еще об одной такой частной закономерности я хочу сказать сейчас. Вот на этом плакате можно попытаться соединить линиями таблички с одинаковыми номерами, расположенные в одной верхней или в одной нижней части И-цзина. Таким образом, мы увидим некоторую связь между тем расположением табличек внутри квадрантов, которое я выбрал для наглядности, исходя из особенностей устройства множества табличек квадранта, и тем, которое соответствует порядку Вэнь-вана.

Однако, если это сделать на этом плакате, то симметричной картины не получится. Точнее, получится картина как бы наполовину симметричная: какая-то часть ее действительно симметрична, но в другой имеется ряд нарушений. Тем не менее, для того, чтобы картина получилась полностью симметрична, достаточно сделать небольшое число локальных изменений расположения табличек внутри квадрантов.

На этом плакате зелеными стрелками обозначены требуемые изменения (точнее, обратные изменения, которые возвращают к предыдущему расположению). Две таблички из 2-го квадранта меняются местами и три таблички из 3-го квадранта меняются местами по циклу. Эти изменения затрагивают 5 из 36 табличек, то есть, примерно 14%. Конечно, в результате таких изменений исказится плакат с инверсией черт - картинка перестанет быть полностью симметричной. Зато картинка с линиями, соединяющими таблички с одинаковыми номерами, станет полностью симметричной.

Мы видим, что некоторые одинаковые номера табличек расположены симметрично относительно вертикальной оси, делящей И-цзин по 3-ей дихотомии на левую и правую части. Для верхней части это три номера 1,7 и 9, а для нижней - тоже три, но других, номера 4,5 и 6. Остальные номера объединяются в пары так, что первый номер левой пары симметричен второму номеру правой пары, а, соответственно, второй номер левой пары симметричен первому номеру правой пары. Для верхней части И-цзина это три пары номеров 2-6, 3-4 и 5-8, а для нижней части - тоже три, но других, пары номеров 1-7, 2-3 и 8-9.

Таким образом, оказывается, что реальное расположение табличек внутри квадрантов по Вэнь-вану имеет довольно близко, хотя и не совпадает, с тем расположением, в котором проявляется структура связей между табличками по инверсии ДУЙ.

 

Возвращаюсь к Плакату Плакат 15 Таблица 6 на 6

При более внимательном изучении этого квадрата можно сформулировать общее правило:

oВыделяются 8 областей, которые будем называть "домами" по 6 табличек в каждой:



o4 прямоугольных треугольника с катетами из 3-х табличек расположены в углах квадрата;

o4 прямоугольника 2х3 расположены по сторонам квадрата: меньшая сторона (2) примыкает к стороне квадрата.

oКаждому дому своя триграмма.

oКаждая гексаграмма располагается либо в доме своей верхней триграммы, либо в доме перевернутой нижней триграммы. Очевидно, симметричная гексаграмме принадлежит одному дому.

Следует особо подчеркнуть: это правило объясняет, правда не всегда однозначно, распределение гексаграмм по квадрантам И-цзина, однако оно не объясняет порядок гексаграмм в каждом квадранте.

Из этого глобального правила есть 7 исключений (3 из 8 симметричных гексаграмм и 4 из 56 несимметричных гексаграмм):

1.симметричная гексаграмм #1 - 77

2.симметричная гексаграмма #2 - 00

3.симметричная гексаграмм #28 - 36

4.пара несимметричных гексаграмм #33-34 - 74-17

5.пара несимметричных гексаграмм #35-36 - 5005

Вообще говоря, существует порядок гексаграмм, полностью удовлетворяющий этому правилу. Но оно отличается от порядка Вэнь-вана.

Это правило можно изменить, потребовав, чтобы угловые дома содержали по 5 табличек, а центральная табличка каждого квадранта не содержала триграмм, соответствующих трем домам этого квадранта (угловому дому, входящему в квадрант, и двум прямоугольным домам, пересекающимся с квадрантом). Тогда у нас будет только одно исключение:

1.симметричная гексаграмм #28 - 36

Правда, правило перестает быть глобальным: оно не объясняет, какие гексаграммы должны попадать в центральные клетки квадрантов. В порядке Вэнь-вана это гексаграммы:

oквадрант 1 - #1 - 77

oквадрант 2 - #2 - 00

oквадрант 3 - пара #35-36 - 50-05

oквадрант 4 - пара #33-34 - 74-17

Здесь есть своя закономерность: это первые две гексаграммы И-цзина и первые две пары гексаграмм второй части И-цзина, если бы делить на две равные по числу гексаграмм части - по 32 гексаграммы.

 

Литература

Книги

Еремеев В.Е. Арифмосемиотика “Книги перемен”. М., 2001.

Еремеев В.Е. Символы и числа “Книги перемен”. М., 2002.

Еремеев В.Е. Чертеж антропокосмоса. М., 1993.

Кобзев А.И. Учение о символах и числах в китайской классической философии. М., 1993.

Лукьянов А.Е. Дао “Книги перемен”. М., 1993.

У Цзинь, Ван Юншэн. Сто ответов на вопросы о “Чжоу и”: “Чжоу и”, китайская медицина и цигун. Киев, 2001.

Чжоу Цзунхуа. Дао И-Цзина. Киев, 1996.

Щуцкий Ю.К. Китайская классическая “Книга перемен. М., 1993.

Статьи в сборниках научной конференции “Общество и государство в Китае” (далее НКОГК)

Блюмхен С.И. Некоторые особенности распределения триграмм в гексаграммах “Книги перемен”. - 18-я НКОГК. Ч. 1. М., 1987.

Блюмхен С.И. Опыт реконструкции семантики “Книги перемен”. - 19-я НКОГК. Ч. 1. М., 1988.

Богачихин М.М. Математическая модель гексаграмм. - 19-я НКОГК. Ч. 1. М., 1988.

Бурдонов И.Б. Третья дихотомия “И цзина”. - 21-я НКОГК. Ч. 1. М., 1990.

Бытев В.О. Об одном способ структурализации “Книги перемен”. - 21-я НКОГК. Ч. 1. М., 1990.

Давыдов С.Д. Еще раз о порядке гексаграмм в Книге перемен”. - 20-я НКОГК. Ч. 1. М., 1989.

Давыдов С.Д. О мавандуйских порядках триграмм. - 21-я НКОГК. Ч. 1. М., 1990.

Давыдов С.Д. О порядке гексаграмм в “Книге перемен”. - 19-я НКОГК. Ч. 1. М., 1988.

Давыдов С.Д. Пять элементов и восемь триграмм. - 18-я НКОГК. Ч. 1. М., 1987.

Емельянов С.С. К реконструкции пространственной композиции гексаграмм. - 20-я НКОГК. Ч. 1. М., 1989.

Еремеев В.Е. Ло шу, принцип “сань у” и “схема изменчивости”. - 17-я НКОГК. Ч. 1. М., 1986.

Еремеев В.Е. Гармонические структуры в традиционной китайской науке. - 18-я НКОГК. Ч. 1. М., 1987.

Еремеев В.Е. Еще раз о эннеаграмме. - 22-я НКОГК. Ч. 1. М., 1991.

Еремеев В.Е. К реконструкции схемы изменчивости “И цзина”. - 16-я НКОГК. Ч. 1. М. 1985.

Еремеев В.Е. Космологические представления “Тай цзи ту шо” и их типологические аналоги. 19-я НКОГК. Ч. 1. М., 1988.

Еремеев В.Е. Логико-семантический конструктор “Книги перемен”. - 21-я НКОГК. Ч. 1. М., 1990.

Еремеев В.Е. О древнекитайской пространственно-временной модели мира. - 20-я НКОГК. Ч. 1. М., 1989.

Зинин С.В. К проблеме построения гексаграмм “И цзина”. - 13-я НКОГК Ч. 1. М., 1982.

Карапетьянц А.М. “Ба гуа” как классификационная схема. - 13-я НКОГК Ч. 1. М., 1982.

Карапетьянц А.М. Двоично-четвертичное кодирование в “И цзине”. - 16-я НКОГК Ч. 1. М., 1985.

Карапетьянц А.М. Древнекитайская системология и ее материальная основа. - 19-я НКОГК Ч. 1. М., 1988.

Кобзев А.И. Гексаграммная мантика в эпоху Чуньцю. - 20-я НКОГК. Ч. 1. М., 1989.

Кобзев А.И. Пространственно-числовые модели китайской нумерологии. - 19-я НКОГК Ч. 1. М., 1986.

Сазонов В.А. Интерпретация схем Хэ ту и Ло шу. - 18-я НКОГК Ч. 1. М., 1987.

Сазонов В.А. Солнечные и лунные циклы в интерпретации “И цзина”. - 16-я НКОГК Ч. 1. М., 1985.

Спирин В.С. О значении древнего порядка триграмм. - 17-я НКОГК Ч. 1. М., 1986.

Фалев А.И. Методологические принципы поддержания баланса в организме в традиционной китайской медицине (Историко-медицинский обзор). - 19-я НКОГК. Ч. 1. М., 1988

Хорошилов Г.А. О принципах фань и дуй в связи с последовательностями гексаграмм по Фуси и Вэнь-вану. - 18-я НКОГК. Ч. 1. М., 1987.

Хорошилов Г.А. О принципе “переворачивания в “Книге перемен” в связи с порядком гексаграмм по Вэнь-вану. - 19-я НКОГК. Ч. 1. М., 1988.

Швырев Ю.А. О гексаграммах мавандуйского “И цзина”. - 17-я НКОГК. Ч. 1. М., 1986.

    Эзотерика: Применение - Практики - Религии

• Эзотерика
  
• Религии
  
• Мировая эзотерика
  
• Индийская эзотерика
  
• Восточная эзотерика
  
  
• Западная эзотерика
  
• Русская эзотерика
  
• Эзотерические практики
  
• Аcтрология
  
• Астрал
  
  
• Тайны эзотерики
  

---

---