История алгоритмических языков, насчитывающая немногим
Три богатыря на рубеже столетий
История алгоритмических языков, насчитывающая немногим менее полувека, успела зафиксировать создание и разрушение своеобразной Вавилонской башни, в стенах которой было погребено более 3000 оригинальных и не очень оригинальных версий универсальных и специализированных языков программирования.
Почти одновременно с появлением первых ЭВМ системные программисты стремились переложить на плечи ЭВМ наиболее рутинную работу, сопровождавшуюся многочисленными ошибками и описками. Первые элементы автоматизации процесса написания программ были связаны с заменой числовых кодов машинных операций их мнемоническими символьными обозначениями. Например, команда сложения содержимого двух ячеек памяти вместо сугубо числового кода 01 0100 0101 0102 превращалась в более осмысленное действие типа ADD 0100,0101,0102. Почти сразу же стало ясно, что использование естественной числовой нумерации ячеек памяти становится неразумной преградой между обозначениями переменных решаемой задачи и их эквивалентами в виде числовых адресов. Почему бы не возложить на специальную программу чисто механическую работу по замене символьных обозначений исходных и промежуточных данных задачи на их машинные адреса? И тогда очередной пункт алгоритма, выражавшийся простой формулой z = х + у, превращался в достаточно наглядную и близкую по смыслу команду ADD X,Y,Z. На первом этапе развитие этих идей сдерживало отсутствие устройств ввода/вывода, которые могли бы обрабатывать алфавитно-цифровую информацию. Как только аппаратные средства позволили преодолеть это препятствие, неотъемлемой частью программного обеспечения ЭВМ стали системы, получившие название Автокодов или Ассемблеров.
Следующий бастион, который был взят сторонниками автоматизации тяжелого ручного труда по составлению программ, — укрупнение и стандартизация операций, встречавшихся при решении различных задач. Операции, входившие в состав машинных команд, представляли собой слишком микроскопические действия, на которые приходилось разлагать более понятные человеку процедуры. Так появились алгоритмические языки, каждая строка которых могла быть автоматически трансформирована в цепочку эквивалентных машинных команд. И этот труд по сию пору с честью выполняют многочисленные "переводчики" (трансляторы, компиляторы) и "исполнители" (интерпретаторы).
К числу первых алгоритмических языков, получивших достаточно широкое распространение, относятся Фортран (FORTRAN — от FORmula TRANslation, "трансляция формул") и Алгол (ALGOL — от ALGOrthmic Language, "алгоритмический язык"). Первый из них родился в недрах фирмы IBM в 1954 г. и активно поддерживался этим наиболее могущественным концерном по производству средств вычислительной техники. В нашей стране он стал широко известен в связи с переходом на выпуск ЭВМ Единой Системы (ЕС ЭВМ), программно совместимых с ранее появившимися моделями IBM/360, IBM/370. История развития Фортрана насчитывает довольно много версий и диалектов, среди которых наиболее известны Fortran-II, Fortran-IV, Fortran-77 и Fortran-90.
Алгол-60 появился как противовес Фортрану в результате объединенных усилий европейских ученых, представлявших, по большей части, академическую и вузовскую науку. Первые сведения о нем были опубликованы в 1958 г., но как стандарт языка он был утвержден в 1960 г. Алгол получил довольно широкое признание в нашей стране. Для него отечественными учеными были разработаны несколько систем программирования — ТА-1М (Вычислительный центр фирмы С. П. Королева), ТА-2М (Институт прикладной математики АН СССР), Альфа (Вычислительный центр СО АН СССР). Однако следующий стандарт языка Алгол-68 практически остался академическим проектом и большого распространения не получил, т. к. в срочном порядке был вытеснен Фортраном.
Несмотря на совершенно разную структуру и наличие несоизмеримых по финансовой мощи спонсоров, оба языка оказали существенное влияние на последующее развитие систем программирования. Так, например, язык Бейсик многое заимствовал из Фортрана, тогда как Паскаль продолжил линию алголоподобных языков. Несколько особняком стоит язык Си, впитавший в себя элементы как низкоуровневого программирования (наследие от языков типа Ассемблер), так и типы данных и синтаксические конструкции алгоритмических языков высокого уровня. Он не только объединил эти две кажущиеся противоположными компоненты, но и внес значительный вклад в развитие объектно-ориентированного программирования.
Далеко немногие алгоритмические языки выдержали испытание временем. Однако языки Бейсик, Си и Паскаль, включенные в нашу книгу, сродни трем былинным богатырям. Их возраст либо приближается к заветному сказочному рубежу в 33 года, либо уже превысил его, что мы и постарались отметить в названии первой главы. На сегодняшний день они являются наиболее популярными как у начинающих, так и у профессиональных программистов.
Самый почтенный среди них — Бейсик, днем рождения которого считается 1 мая 1964 г. В этот день в Дартмутском колледже (США) проявил первые признаки жизни интерпретатор, созданный студенческим коллективом во главе с профессорами Джоном Кемени (J. G. Kemeny) и Томасом Куртцем (Т. Е. Kurtz). Своим названием BASIC обязан сокращению фразы Beginner's All-purpose Symbolic Instruction Code, которая дословно переводится как "многоцелевой код (язык) символических инструкций для начинающих".
Бейсик открыл эру диалогового программирования. До него культивировался пакетный режим, при котором бумажные или магнитные носители с программами сдавались дежурному оператору и упорядочивались в соответствии с приоритетами их владельцев. Составленный таким образом пакет программ поступал в ЭВМ на последовательную обработку. При этом достигалась максимальная загрузка оборудования, но каждая программа выполнялась либо до первой автоматически обнаруженной ошибки, либо до истечения лимита заказанного времени. Информация о результатах прохождения программ выдавалась их авторам 2—3 раза в сутки. Поэтому календарные сроки создания программ затягивались на многие месяцы.
Системы коллективного доступа, работавшие в диалоговом режиме, обеспечивали одновременное обслуживание нескольких пользователей, запускавших свои программы с электромеханических или электронных терминалов. Оперативно получив сообщение об очередной ошибке, пользователь имел возможность тут же исправить текст исходной программы и снова выполнить ее.
Диалоговый режим, естественно, был связан с дополнительными накладными расходами на многотерминальное обслуживание. Загрузка ЭВМ при этом снижалась, но оперативность в отладке программ приводила к существенному сокращению календарных сроков их разработки.
Бейсик был одним из первых алгоритмических языков, в составе которого изначально присутствовали операторы общения пользователя с пошагово выполняющейся программой. Одновременно с текстом сообщения об ошибке Бейсик-система сообщала номер строки программы, нарушившей синтаксис языка или приведшей к аварийной ситуации. Первые Бейсик-системы, совмещавшие в себе возможности ввода, редактирования, исполнения и отладки программ, послужили прототипами современных интегрированных сред.
Вторая особенность, привлекающая массового потребителя к Бейсику, кроется в простоте начального освоения и краткости его изобразительных средств. Попробуйте найти хотя бы еще один язык, на котором программа, отвечающая на вопрос, чему равно дважды два, состоит всего из четырех символов:
?2*2
Аналогичная программа на Паскале содержит, минимум, три строки, а ее длина превышает 20 символов:
begin
(writeln 2 *2);
end.
Примерно вдвое большего по числу символов требует ее аналог на Си:
#include
main()
{ printf ("%d",2*2); }
Становлению и распространению Бейсика в нашей стране способствовали первые в мире пошаговые компиляторы с этого языка, созданные в 1969 г. для отечественных ЭВМ типа М-20 в Горьковском университете под руководством одного из авторов этой книги.
Второе поколение Бейсик-систем ведет свой отсчет от появления первых ПК на базе 8-разрядных микропроцессоров Intel-8080 и Z-80, для которых в середине 70-х годов был разработан компактный интерпретатор BASIC-80. Именно с него началась карьера самого молодого американского миллиардера Билла Гейтса, основавшего корпорацию Microsoft.
Появление 16-разрядных IBM-совместимых ПК ознаменовалось конкурентной борьбой между компаниями Borland International и Microsoft Corp. Первая из них выпустила на рынок удобную интегрированную среду с компилятором Turbo BASIC, которая быстро привлекла на свою сторону многочисленных любителей Бейсика. Однако более мощная компания, постоянный президент которой не упускает случая прибавить к своей профессии приставку "программист Бейсика", не могла смириться с таким положением. На смену тихоходному интерпретатору GW-BASIC пришла целая серия скоростных систем Quick BASIC, в составе которых наряду с интегрированной средой поставлялись автономные компиляторы и достаточно мощные библиотеки программ. Соревнование Бейсик-систем третьего поколения закончилось поражением фирмы Borland, прекратившей сопровождение своей разработки и передавшей права на Turbo BASIC одному из авторов, вышедшему из состава компании. Одна из последующих его разработок известна под названием Power Basic (Мощный Бейсик).
А фирма Microsoft совершенствовала свое любимое детище и выпустила в конце 80-х годов мощные системы для профессиональных разработок (Professional Development System) BASIC PDS-6 и PDS-7.
Авторы языка Кемени и Куртц спустя 25 лет попытались разработать новую версию под названием True Basic (Истинный Бейсик), однако из-за отсутствия серьезной поддержки со стороны крупных производителей программного обеспечения эта попытка, кроме издания книги и выпуска пробной версии системы, продолжения не получила.
Наконец, четвертое поколение Бейсика мы связываем с появлением в 1991 г. системы визуального программирования Visual Basic и ее последующим совершенствованием сотрудниками Microsoft. На момент выпуска нашей книги в эксплуатации находится версия VB-6.0. До версии 3.0 включительно Visual Basic был построен по схеме интерпретатора, однако последние его версии позволяют получать готовые к исполнению модули. Кроме полноценной системы программирования, фирма Microsoft с 1993 г. выпускает версии YBA (Visual Basic for Application -- система для разработки программируемых процедур в пакете MS Office) и VBScript (ограниченная версия для разработки Web-приложений).
Алгоритмический язык Паскаль был придуман в 1968 г. профессором Института информатики при Швейцарской высшей технической школе Ник-лаусом Виртом. В 1970 г. под его руководством был разработан первый компилятор, а в следующем году появилась и первая публикация. Свое название язык получил в честь известного французского математика Блеза Паскаля, который в 19-летнем возрасте изобрел первую суммирующую машину.
Новый язык, являясь продолжателем традиций алгоритмического языка Алгол-60, был ориентирован, главным образом, на обучение курсу систематического программирования. В Паскале были представлены наиболее распространенные типы данных и средства для создания пользовательских структур. К числу элементов, способствующих созданию надежных программ, относились блочные конструкции и требование обязательного описания (объявления) всех объектов — типов данных, констант, переменных, меток, функций и процедур.
Заметную роль в разработке стандарта языка Паскаль и совершенствовании его средств ввода/вывода сыграла рабочая группа Британского института стандартов во главе с А. Эддиманом. Британский стандарт был принят в 1982 г., а несколько позднее его утвердила международная организация ISO. Однако к этому времени Н. Вирт, недовольный предложениями рабочей группы, отказался от сотрудничества по совершенствованию Паскаля и переключился на новый проект Модула.
Паскаль довольно долго оставался средством для изучения программирования в университетах, т. к. ни одна серьезная компьютерная фирма его не поддерживала. Перелом в отношении к этому языку наметился в 1984 г., когда молодой француз Филипп Кан привез в США необычайно скоростной компилятор Turbo Pascal для IBM-совместимых ПК и начал торговать им по смехотворно низкой цене 49 долларов 95 центов (для сравнения напомним, что первые версии Бейсик-интепретатора распространялись по цене порядка 500 долларов). Удачная реклама и бросовая цена позволили Кану продать за первый месяц более 3000 копий системы и заложить основы фирмы Borland International. Последующие восемь лет Turbo Pascal оставался наиболее опекаемым продуктом фирмы, которая сумела выпустить девять различных версий. Самая последняя из них (7.0, 1992 г.) включает две системы — Turbo Pascal, функционирующую под управлением MS-DOS, и расширенную версию Borland Pascal, работающую в среде Windows. Несмотря на то, что в январе 1995 г. Ф. Кан покинул пост президента и ушел из компании, фирма Borland на базе языка Object Pascal выпустила одну из наиболее популярных сред визуального программирования — Delphi и продолжает поддерживать ее версии в современных операционных системах. На сегодня наибольшей популярностью пользуется версия Delphi 5.O.
Язык Си был придуман в 1972 г. сотрудником Bell Laboratories (отделение известной телефонной компании AT&T) Деннисом Ритчи, одним из первых пользователей операционной системы Unix. Задумывался он не как универсальный алгоритмический язык, а, скорее, как инструмент для развития операционной системы и создания новых обслуживающих программ (утилит). Такой подход характерен для большинства системных программистов, разрабатывающих сложные проекты и придумывающих для облегчения своего труда различные сервисные процедуры, макрокоманды и т. п. По завершении разработки, как правило, эти инструментальные наборы предаются забвению или, в лучшем случае, остаются в личных архивах авторов. Язык Си эта участь миновала. Вполне возможно, что его становлению способствовало последующее всемирное признание операционной системы Unix.
Как алгоритмический язык сравнительно низкого уровня, т. е. достаточно близкий к Ассемблеру, Си имел предшественников в лице аналогичных инструментальных средств — языков CPL, BCPL (Basic Combined Programming Language — базовый комбинированный язык программирования) и В. Два первых разрабатывались в конце 70-х годов в Кембриджском университете в качестве машинно-независимых языков для создания трансляторов. Последний был придуман Кеном Томпсоном — сотрудником Bell Laboratories и автором операционной системы Unix. В отличие от своих предшественников Д. Ритчи наряду с машинно-ориентированными типами данных (байт, слово) ввел в состав Си объекты и операторы, присущие универсальным языкам (числовые и символьные переменные, структурные блоки), сохранив при этом элементы, характерные для макроассемблера MACRO-11 (логические операции над битами, сдвиги, работа с адресами и регистрами).
Первым программным продуктом, написанным почти полностью на Си, был компилятор с языка Си в код машинных команд компьютера PDP-11/20 (прототип мини-ЭВМ СМ-4). В 1973 г. Д. Ритчи и К. Томпсон переписали на Си большую часть операционной системы Unix. Из 13 000 машинных команд для PDP-7, на которой появилась первая версия Unix, только 800 пришлось вручную перевести в ассемблер PDP-11. В процессе перевода Unix из однопользовательской операционной системы, ориентированной на работу в конкретной ЭВМ, превратилась в мобильную операционную систему коллективного пользования. Успех этой операции в значительной мере предопределил популярность новой операционной системы и ее базового инструмента — языка Си. В 1976 г. Д. Ритчи и К. Томпсон перенесли Unix с ЭВМ фирмы DEC на компьютеры другой архитектуры (Interdata 8/32), практически ничего не изменив в ядре операционной системы, написанном на Си. Точно таким же образом система Unix распространялась на десятки машин различных типов.
В 1978 г. появилась первая книга, посвященная описанию Си и технике Программирования на этом языке, которая с большим запозданием была переведена на русский язык (Б. Керниган, Д. Ритчи, Л. Фьюэр. "Язык программирования Си. Задачи на языке Си". — М.: Финансы и статистика, 1985). От фамилий двух первых авторов произошло сокращенное обозначение первого, никем не утверждавшегося, но принятого всеми программистами стандарта языка Си — K&R.
Дальнейшая работа по совершенствованию языка Си и принятию в 1987 г. первого настоящего стандарта ANSI С была выполнена на общественных началах рабочей группой при Американском национальном институте стандартов. Возглавлял эту работу Лэрри Рослер — сотрудник Bell Labs. Наиболее серьезный вклад в развитие языка Си за последние годы внес еще один представитель той же лаборатории Бьерн Страуструп, который ввел в обращение новые объекты — классы, объединяющие данные, и обрабатывающие их функции. С 1983 г. за расширенной версией языка Си с классами закрепилось название C++.
Первые версии Си подвергались серьезной критике за отсутствие достаточной строгости, приводившей к многочисленным ошибкам из-за работы с неинициализированными переменными, отсутствия контроля за выходом индексов у элементов массивов из установленных пределов, несоответствия типов формальных и фактических параметров функций и т. п. Перед системными программистами Bell Labs эти проблемы остро не стояли, т. к. они пользовались специальной программой Lint, которая проводила тщательный анализ программ, написанных на Си, перед их трансляцией и выполнением.
Для рядовых пользователей ситуация изменилась с появлением интегрированных сред, из которых наибольшую популярность приобрели Турбо-системы фирмы Borland. Первая версия Turbo С, работавшая в среде MS-DOS, была выпущена в 1987 г. Совсем недавно фирма Borland выпустила на рынок версию 5.0, предназначенную для работы под управлением Windows. На базе этого компилятора компания Borland (новое название — Inprise Corp.) разработала серию систем визуального программирования — Borland C++ Builder.
Известны и другие реализации языка Си на IBM-совместимых ПК -Microsoft С, Lattice С, Zortech С, Symantec С. В нашей стране продукция фирмы Borland получила наибольшее распространение, хотя за последнее время намечается тенденция к более широкому использованию среды Visual C++, разработанной фирмой Microsoft. В основном, это диктуется требованиями зарубежных фирм, размещающих свои заказы у отечественных производителей программных продуктов.
Современные версии трех наиболее устоявшихся алгоритмических языков обладают примерно равными функциональными возможностями. Подтверждению именно этого фундаментального свойства универсальных систем программирования посвящена наша книга. Завершая краткий исторический экскурс, остановимся еще раз на мотивах, объясняющих наш выбор языков и систем программирования.
Бейсик — один из наиболее распространенных в мире алгоритмических языков, используемых, как правило, непрофессиональными программистами. По данным из пяти миллионов программирующих пользователей ЭВМ Бейсиком пользуется не менее двух миллионов человек. Большая часть учащихся средних школ начинает освоение информатики с изучения Бейсика, т. к. он доступен на самой допотопной вычислительной технике, которой, к сожалению, еще до сих пор укомплектовано большинство школ России. Несмотря на то, что Бейсик является старожилом по сравнению с Си и Паскалем, в последние годы он переживает вторую молодость в связи с появлением модных систем визуального программирования и массовым использованием Microsoft Office.
Паскаль —алгоритмический язык, созданный специально для изучения программирования и широко используемый в высших учебных заведениях. Вслед за Бейсиком он тоже вступил на тропу визуального программирования, и система Delphi считается одним из лучших инструментальных средств для создания приложений, функционирующих под управлением Windows 95/98/NT.
Си —язык профессионалов, на котором сегодня написано большинство программных систем. Большая часть высших учебных заведений, особенно технического профиля, использует Си в качестве основного языка преподавания программирования. Такие среды визуального программирования, как Borland C++ Builder и Microsoft Visual C++ являются несомненными лидерами в разработках современного программного обеспечения.
В связи с тем, что книга ориентирована на начальное знакомство с перечисленными алгоритмическими языками, в качестве сред программирования нами выбраны самые непритязательные по требованиям к оборудованию системы — QBasic, Turbo С 2.0 или Borland C++ 3.1 и Turbo Pascal 7.0. Все они могут функционировать на самых примитивных IBM-совместимых ПК с оперативной памятью от 1 Мб, занимая на винчестере от 1 до 25 Мб. Кроме того, система QBasic является составной частью операционной системы MS-DOS и представлена там всего двумя небольшими файлами — интерпретатором qbasic.eхe и файлом помощи qbasic.hlp.
Что такое "хорошая" программа?
Если отвлечься от конкретного содержания той или иной задачи, то основные этапы ее решения с помощью компьютера, преобразующего исходные данные в выходные, приведены в таблице ниже.
Номер этапа | Содержание | Исполнитель | |||||
1 | Формулировка задачи | Человек | |||||
2 | Выбор алгоритма | Человек | |||||
3 | Составление исходной программы на алгоритмическом языке | Человек | |||||
4 | Перевод исходной программы в коды машинных команд | Компьютер | |||||
5 | Исполнение машинной программы | Компьютер | |||||
Эта схема достаточно условна. В ней скрыты довольно важные моменты, связанные с использованием готовых к употреблению библиотечных программ, с устранением синтаксических и алгоритмических ошибок в тексте исходной программы. В некоторых системах программирования (к ним, в частности, относится и QBasic) этапы 4 и 5 совмещены.
Каждому из этапов присущи свои особенности. Формулировка задачи должна исключать какую-либо неопределенность в задании исходных данных и устанавливать область их допустимых значений. Состав исходной информации должен быть достаточен для решения поставленной задачи. Так, например, нельзя построить треугольник, зная только два его параметра. Задание трех его углов тоже не позволяет найти однозначное решение. Алгоритм, как правило, должен приводить к решению задачи за конечное чис-
ло шагов или предусматривать прекращение бесконечных циклов при выполнении определенных условий. Программа на алгоритмическом языке .должна иметь четко выраженную структуру и быть понятной не только ее автору. В случае необходимости она должна допускать участие человека в процессе принятия решений. Машинная программа должна располагать удобным интерфейсом и предоставлять в распоряжение пользователя интуитивно понятные средства ввода, управления вычислительным процессом, визуализации промежуточных и окончательных результатов. Это — далеко не полный перечень требований, выработанных многолетней практикой. Но остановимся чуть подробнее на деталях, связанных с организацией исходной программы на алгоритмическом языке.
Во-первых, программа должна выполнять свое главное функциональное назначение — правильно решать поставленную задачу при любом допустимом наборе исходных данных. Без этого любая программа теряет свой смысл.
Во-вторых, программа должна быть, по возможности, эффективной и не тратить на решение задачи лишнее время и ресурсы компьютера. Это особенно важно, когда предполагается многократное использование программы или ее включение в состав более сложного программного комплекса. Конечно, эффективность программы в первую очередь зависит от выбранного алгоритма. Но и реализация последнего может внести свою лепту. Профамма может быть идеальной с точки зрения использования конструкций алгоритмического языка, но далеко не самой эффективной из-за неудачного алгоритма. Представим себе, что потребовалось сложить натуральные числа от kl до R2. Такая процедура реализуется простым циклом, например, на Паскале:
s:=0;
for j:=k1 to k2 do s:=s+j;
Однако сумму членов арифметической прогрессии можно найти вспомнив или элементарно получив нужную формулу. Выпишем друг под другом ее элементы в прямом и обратном порядках:
kl kl+1 kl+2 ........ kl+(k2-kl)
kl+(k2-kl) k2-l k2-2 ........ kl
Сумма каждой пары равна (kl+k2), и таких пар (k2—kl+1). Поэтому искомая сумма может быть найдена по формуле
s:=(kl+k2)*(k2-kl+l)/2;
И для ее нахождения потребуется всего пять операций, независимо от числа слагаемых. Из этого примера можно сделать довольно тривиальный вывод -знание техники программирования является необходимым, но не всегда достаточным фактором для эффективного решения задачи.
В-третьих, программа не должна быть очень замысловатой по своей реализации и не должна допускать модификацию или расширение возможностей другими программистами. Поэтому такие моменты, как простота и наличие полноценного комментария способствуют продлению жизненного цикла программы. Очень вредит простоте программы неумеренное использование оператора безусловного перехода. Приводимый ниже пример программы-
спагетти на языке Бейсик предназначен для поиска максимального среди значений трех переменных — max (a,b,c).
10 INPUT А,В,С
20 IF А>В THEN GOTO 80
30 IF B>C THEN GOTO 60
40 PRINT "Наибольшее число = "; С
50 GOTO 100
60 PRINT "Наибольшее число = "; В
70 GOTO 100
80 IF A
90 PRINT "Наибольшее число = "; A
100 END
Представляете, как разрастется подобный монстр, если количество переменных, среди которых ищется максимум, достигнет 10. Насколько изящнее выглядит следующая программа:
10 INPUT А,В,С
20 МАХ=А
30 IF MAX
40 IF MAX
50 PRINT "Наибольшее число = ";МАХ
Эта программа значительно короче, и в ней нет ни одного оператора перехода. Кроме того, она допускает простое обобщение на поиск максимума среди элементов массива:
МАХ=А(1)
FOR K=2 TO N
IF MAX
Красивую программу можно сравнить со скульптурой, гениальный творец которой отсек от камня все лишнее.
Для кого написана эта книга?
Для тех, кто начинает изучение основ информатики и пытается освоить технику программирования на примерах сравнительно несложных задач. Для их понимания вполне достаточно элементов математики, изучаемых в средней школе.
Для тех, кто хочет научиться отличать хорошую программу от плохой и не собирается ограничивать свои познания техникой программирования. Последнее подразумевает знание допустимых типов данных и их внутреннего представления в памяти ЭВМ, умение использовать конструкции алгоритмического языка, функциональные возможности системы программирования и операционной системы.
Для тех, кто владеет основами программирования на одном из алгоритмических языков и хочет познакомиться со спецификой других достаточно распространенных алгоритмических языков. Современное общее образование вряд ли может считаться полноценным без изучения хотя бы одного иностранного языка. Точно так же профессиональное образование программиста не может ограничиваться рамками единственного алгоритмического языка. Мы постарались донести до читателей идею о том, что все достаточно универсальные алгоритмические языки очень похожи друг на друга и хорошее знание одного из них позволяет сравнительно просто разобраться с изобразительными средствами другого.
Для начинающих преподавателей информатики, которые хотели бы быстро пополнить арсенал своих учебных программ. Мы были бы крайне признательны вам за любые предложения по совершенствованию предлагаемых программ и расширение состава полезных задач.
Почему была написана эта книга?
Сегодня грех жаловаться на недостаток литературы по компьютерной тематике. Однако полки в специализированных отделах книжных магазинов заполнены, в основном, многочисленными руководствами, обещающими в немыслимо короткие сроки обучить пользователя навыкам работы с наиболее популярными программными продуктами. На фоне этого довольно поверхностного изобилия не так часто встречаются хорошие книги, посвященные глубокому изучению алгоритмических языков и методам их использования для решения различных задач.
Столь же безрадостная участь постигла и серию книг по практике программирования. Во-первых, таких книг просто мало. Во-вторых, набор рассмотренных в них программ обычно относится к двум противоположным полюсам. Это либо тексты программ, занимающих 5—10 строк и демонстрирующих самые поверхностные возможности того или иного алгоритмического языка, либо задачи повышенной сложности, входившие в программы международных олимпиад по информатике, где наиболее важным моментом является выбор оптимального алгоритма, а вопросы конструирования, оформления и тестирования программ отходят на второй план или просто не рассматриваются. Наконец, нам кажется абсолютно непродуктивной идея многочисленных курсов по информатике, базирующихся на последовательном изучении двух-трех универсальных языков программирования. Такие алгоритмические языки имеют слишком много общего и просто нерационально отводить дефицитные учебные часы на изучение каждого из них с самого начала по стандартной схеме. Параллельное изучение эквивалентных конструкций в разных алгоритмических языках позволяет выработать навыки автоматического преобразования программ, что может оказаться полезным в практической работе.
Внешнее и внутреннее представление числовых данных
Практика программирования (Бейсик, Си, Паскаль)
Работа с числовыми данными
Современные представления о числовых данных базируются на так называемых позиционных системах счисления. Для этих систем характерно основание системы р, степень которого определяет вес цифры а (а = о, 1, 2.....P-I) в зависимости от занимаемой позиции:
ak ak-1 . . . a1a0, b-1b-2 ... b-m = ak*pk + ak-1*pk-1 + . . . + a1*p1 + a0*p0 + b-1p-1 + + b-2*p-2 + . . . + b-m*p-m
Главенствующую роль в человеческом общении играет десятичная система счисления (р = 10; а =0, 1, ..., 9). Однако ЭВМ используют более рациональную двоичную систему (р = 2; а = 0,1). Единственным ее недостатком является большая длина чисел. Количество разрядов (цифр) в двоичном представлении числа примерно в три раза превышает количество десятичных цифр. Для преодоления этого неудобства программисты прибегают к более компактной записи двоичных кодов в виде восьмеричных или шест-надцатеричных чисел. При этом три или четыре смежные двоичные цифры заменяют одной восьмеричной или шестнадцатеричной цифрой. Например:
19210 - 110000002,
110000002 = 3003,
110000002 = C016.
Внешнее и внутреннее представление числовых данных
Под внешним представлением числовой информации подразумеваются способы записи данных, используемые в текстах программ, при наборе чисел, вводимых в ЭВМ по запросу программы, при отображении результатов на экране дисплея или на принтере. Кроме естественного представления числовых констант в виде целого или вещественного числа, языки программирования допускают различные добавки в начале ("префиксы") или конце ("суффиксы") числа, определяющие способы преобразования и хранения данных в памяти компьютера.
Во входном языке системы QBasic такого рода добавки представлены одним из символов %, !, & или #, приписываемым вслед за числом, и одной из двухсимвольных комбинаций &в, &о или &н, располагаемой перед числом:
В Си к аналогичным суффиксам относятся указания об удвоенной длине целых чисел (буквы L или l), указания о вещественном формате числа, не содержащего в своей записи десятичной точки или десятичного порядка (буква F или f), указания об использовании беззнакового представления целых чисел (буква и или и). Префиксы в Си используются для записи восьмеричных (число начинается с о) или шестнадцатеричных (числу предшествует одна из комбинаций Ох или ох) констант:
В Паскале используется единственный префикс — символ $, предшествующий шестнадцатеричному числу:
$ОА, $FOA5, $FF00140D.
Наличие в естественной записи числа точки (3.1415) или указателя десятичного порядка (314.1592б5е-02) означает, что соответствующее значение представлено в ЭВМ в виде вещественного числа с плавающей запятой.
Машинные форматы представления чисел мы будем называть внутренними, и из приведенных ранее примеров следует, что машинные числа бывают целыми и вещественными. В свою очередь, каждый из этих типов данных допускает несколько представлений) отличающихся диапазоном допустимых чисел. Остановимся более подробно на машинных форматах числовых данных, соответствующих их аналогам в алгоритмических языках.
Самые короткие числа со знаком представлены в памяти ЭВМ одним байтом, в котором может разместиться любое число из диапазона от —128 до + 127. В Си для описания данных такого типа используется спецификатор char, а в Паскале — shortint.
В одном же байте может быть расположено и самое короткое целое число без знака. В Си для описания таких данных служит спецификатор unsigned char, в Паскале — byte, диапазон допустимых данных при этом смещается вправо и равен [0, 255]. QBasic не располагает языковыми средствами для работы с однобайтовыми целыми числами.
Вторая категория целых чисел представлена двухбайтовыми данными. В варианте со знаком они предлагают диапазон от —32 768 до +32 767, в варианте без знака — от 0 до 65 535.
QBasic обеспечивает работу с двухбайтовыми числами со знаком для переменных, описанных как AS INTEGER или устаревшее DEFINT,. и переменных, чьи имена заканчиваются символом %. Двухбайтовые целые без знака в QBasic записываются в виде двоичных, восьмеричных или шестнадцатерич-ных констант. Однако арифметические операции над такими данными иногда выполняются некорректно.
Си использует для описания двухбайтовых целочисленных данных спецификаторы int и unsigned int. В Паскале для этой же цели служат спецификаторы integer и word. Оба языка корректно выполняют арифметические операции и с беззнаковыми данными при условии, что результат не выходит за пределы разрешенного диапазона.
Третья категория целых чисел в IBM PC представлена четырехбайтовыми данными. В варианте со знаком они перекрывают диапазон от —2 147 483 648 до +2 147 483 647, в варианте без знака — от 0 до 4 294 967 295.
В QBasic допустимы только данные со знаком и имена переменных такого типа описываются как AS LONG или DEFLNG. К ним же относятся и переменные, чьи имена заканчиваются символом &.
Для описания четырехбайтовых данных целого типа в Си используются спецификаторы long (эквивалент long int) и unsigned long. В Паскале работа с длинными целыми без знака не предусмотрена. Там можно оперировать с четырехбайтовыми данными только типа longint.
Следует помнить, что для хранения любых целых чисел со знаком в IBM PC используется дополнительный код, что сказывается на представлении отрицательных чисел:
+5 0 0000101 0 000000000000101
-5 1 1111011 1 111111111111011
Наиболее часто применяемые типы вещественных чисел представлены короткими (4 байта) и длинными (8 байт) данными.
В QBasic им соответствуют описания AS SINGLE (устаревшее — DEFSNG) и AS DOUBLE (устаревшее — DEFDBL). Си использует для этой же цели спецификаторы float И double, Паскаль — single И double.
Короткий вещественный формат по модулю обеспечивает представление чисел в диапазоне от 10-38 до 10+38 примерно с 7—8 значащими цифрами. Для 8-байтового формата диапазон существенно расширяется — от 10-308 до 10+308, а количество значащих цифр увеличивается до 15—16.
Сопроцессор IBM PC предлагает еще два формата данных, занимающих соответственно 8 и 10 байт. Первый из них допускает работу с целыми числами из диапазона от —263 до 263-1. Второй формат перекрывает диапазон данных (по модулю) от 10-4932 до 10+4932, сохраняя 19—20 значащих цифр. Расширенный формат вещественных данных можно использовать в программах на Си (long double) и на Паскале (extended). А формат сверхдлинных целых чисел используется только в Паскале, но там они почему-то отнесены к вещественным данным типа сотр.
В Паскале по традиции сохранился еще один тип вещественных данных -real, занимающий в памяти 6 байт. Его диапазон совпадает с типом single, однако количество значащих цифр несколько больше — 10—12. Формат real не поддерживается аппаратными средствами IBM PC, поэтому операции над такими данными выполняются с помощью подпрограмм, что существенно увеличивает время решения задачи.
В машинном представлении вещественных данных разного типа на IBM PC не выдержана какая-то общая идеология. Объясняется это, по всей вероятности, разными наслоениями на прежние аппаратные решения, которые принимались при разработке процессоров в разных отделениях фирмы Intel. Поэтому здесь имеют место такие нюансы, как сохранение или не сохранение старшего бита мантиссы, представление мантиссы в виде чисто дробного (0,5 < < m < i) или смешанного (1 < m < 2) числа и т. п. Прикладных программистов эти детали мало интересуют, однако при создании специальных системных компонент с точным представлением данных приходится считаться.
Ввод числовой информации
Каких-либо особых проблем с вводом числовой информации в программах не возникает. Но на некоторые детали в том или ином алгоритмическом языке надо обратить внимание.
В QBasic можно натолкнуться на неприятности при вводе нескольких числовых значений в одном операторе. Например:
INPUT А,В,С
Числовые данные, набираемые пользователем, должны быть разделены пробелом. Если в наборе второго или третьего значения вы допустите ошибку, то последует сообщение Redo from start, которое заставит вас повторить
ввод всех трех чисел с самого начала. Некоторые программисты даже предпочитают вводить одним оператором только одно значение. Несоответствие между типом переменной и вводимым значением приводит к ошибке при попытке ввести вещественное значение в целочисленную переменную или при наборе недопустимого символа в числе.
В Си основные неприятности форматного ввода (функция scant) связаны с попыткой указать в списке ввода не адрес переменной, а ее имя:
scanf("%d",x); //правильно было бы scanf("%d",&x);
Компилятор ТС/ВС такую ошибку, к сожалению, не замечает и преобразует имя х в какой-то фантастический адрес. Последующую работу программы в этом случае предсказать трудно. Не обращает внимания компилятор Си и на несоответствие между спецификатором формата и типом переменной из списка ввода. Всего этого можно избежать, используя потоковый ввод:
cin » х;
Самый тщательный .контроль за соответствием между типами вводимых значений и типами соответствующих переменных в списке параметров процедур read и readin обеспечивает Паскаль. Однако здесь при попытке ввести непредусмотренный символ в числе вслед за сообщением об ошибке задача снимается, если программист не смог предвидеть заранее обход системной реакции на особые ситуации.
Вывод числовых результатов
Наиболее приятный вид имеет числовая информация, организованная по табличному типу — в виде колонок фиксированной ширины, в которых одноименные числовые разряды располагаются друг под другом (единицы -под единицами, десятки — под десятками, сотни — под сотнями и т. д.). При этом, в частности, более рационально используется площадь экрана, что достигается за счет управления форматами выводимых данных.
В QBasic для этой цели служит оператор PRINT USING, совмещающий в себе и строку с описанием формата и список выводимых значений:
PRINT USING "А=##.## B=### С=#.####^^^^"; А,В,С
Аналогичные средства имеются и в Си:
printf ("A=%6.3f B=%3d С=%10.4е",А,В,С);
При выводе в поток, когда к Си-программе подключаются заголовочные файлы iostream.h и iomanip.h, тоже существует возможность управлять форматом выводимых данных:
cout << "А=" << setw(6) << setprecision(5) << А;
Несколько скромнее выглядит управление форматом в Паскале:
write('А=',А:6:3,"В=',В:3,'С=',С:10);
Среди форматных спецификаторов в Си есть дополнительные возможности, отсутствующие в QBasic и Паскале. Например:
printf("%4x %6о",х,у);
Приведенные здесь спецификаторы позволяют вывести значения целочисленных переменных х и у соответственно в виде шестнадцатеричного числа с четырьмя цифрами и восьмеричного числа с шестью цифрами.
В Си можно прижимать выводимое число к левой границе отведенного поля (по умолчанию действует правый прижим), печатать знак "+" у положительных чисел, подавлять или разрешать вывод незначащих нулей и др. Подробную информацию о структуре форматного описателя можно найти в файлах помощи.
Задачи,советы и ответы
Задание 2.01. Ввод и вывод целочисленных данных
Ввести 20 целых чисел. Вывести их компактно (в одну или несколько строк), размещая перед каждым числом его порядковый номер. После нажатия какой-либо клавиши вывести числа столбиком, располагая одноименные разряды друг под другом, подвести под столбиком черту и напечатать сумму введенных чисел.
Совет 1
Совет 2
А$=""
М10 : A$=INKEY$ ; IF А$="" THEN GOTO M10
Можно воспользоваться и другим приемом — включить в программу оператор ввода в какую-либо переменную символьного типа. Такая переменная предпочтительнее числовой, т. к. в нее можно ввести пустое значение, нажав только клавишу
В Си временный приостанов до нажатия какой-либо клавиши организуют с помощью функции getch.
В Паскале можно организовать бесконечный цикл, аналогичный приведенному выше варианту для QBasic, с помощью логической функции KeyPressed:
while not KeyPressed;
Аналогом ввода пустого значения INPUT А$ в QBasic в Паскале является использование процедуры read/readln без параметров. В этом случае для проталкивания программы потребуется нажать клавишу
Программа 2_01.bas
RЕМ Ввод, вывод и суммирование 20 целых чисел
DIM A(20)
F$="##:###### "
PRINT "Введите 20 чисел, по одному в строке"
FOR 1=0 ТО 19: INPUT A(I): S=S+A(I): NEXT I
FOR 1=0 TO 19: PRINT USING F$;I+1;A(I); : NEXT I
INPUT A$
FOR 1=0 TO 19: PRINT USING F$;I+1;A(I): NEXT I
PRINT " —
PRINT USING " ######"; S
END
Программа 2_01.с
/* Ввод, вывод и суммирование 20 целых чисел */
#include
#include
main() {
int j,s=0,a[20];
clrscr();
printf("Введите 20 чисел, по одному в строке\n"
for(j=0; j<20; j++) { scanf("%d",&a[j]); s+=a[j]; }
for(j=0;j<20;
printf("%2d:%-6d ",j+l,a[j]>; for(j=0;j<20; j++)
printf("\n%2d:%6d ",j+l,a[j]) ; printf("\n -------\n%9d",s);
getch();
Программа 2_01.pas
program io_numbers;
{ Ввод, вывод и суммирование 20 целых чисел }
uses Crt;
var
j, s:integer;
a:array [1..20] of integer; begin
s: =0 ;
clrscr;
writeln('Введите 20 чисел, по одному в строке"!
for j:=1 to 20 do
begin readln(a[j]); s:=s+a[j]; end;
for j:=l to 20 do write(j:2,':',a[j]:6,' ');
writeln('Нажмите любую клавишу';
readkey; clrscr;
for j:=l to 20 do writeln(j:2,':',a[j]:6,' ');
writeln(' --------');
writeln (s: 9).;
readln; end.
Задание 2.02. Ввод и вывод вещественных данных
Самостоятельно выполнить задание 2.01 в предположении, что вводимые числа вещественные и имеют две значащие цифры в дробной части.
Задание 2.03. Преобразование десятичного числа в системы С основанием 2, 8, 16
Ввести длинное неотрицательное число. Вывести его в двоичном, восьмеричном и шестнадцатеричном представлении.
Совет 1 (QBasic)
Совет 2 (Си)
Совет 3 (Паскаль)
Программа 2_03.bas
REM Перевод числа в системы с основаниями 2, 8 и 16
CLS
INPUT "Введите положительное число : ",N&
А$=ОСТ$(N&)
PRINT "В двоичном представлении ";N&;"= ";
FOR k=l TO LEN(A$)
B$=MID$(A$,k,1) : ' Выделение очередной восьмеричной цифры
SELECT CASE B$
CASE "О": IF k=l THEN PRINT ""; ELSE PRINT "000";
CASE "1": IF k=l THEN PRINT "1"; ELSE PRINT "001";
CASE "2": IF k=l THEN PRINT "10"; ELSE PRINT "010";
CASE "3": IF k=l THEN PRINT "11"; ELSE PRINT "01l";
CASE "4": PRINT "100";
CASE "5": PRINT "101";
CASE "6": PRINT "111";
CASE "7": PRINT "111";
END SELECT
NEXT k
PRINT "В восьмеричном представлении ";N&;"= ";OCT$(N&)
PRINT "В шестнадцатеричном представлении ";N&;"=";HEX$(N&)
END
Программа 2_03a.bas
REM Перевод числа в системы с основаниями 2, 8 и 16
CLS
INPUT "Введите положительное число : ",n&
а$=ОСТ$(п&) : ' Перевод в восьмеричную систему
IF n&=0 THEN
PRINT "Это число в любой системе равно 0" STOP END IF PRINT "В двоичном представлении ";п&;"= ";
B$=LEFT$(а$,1}: : ' Выделение очередной восьмеричной цифры SELECT CASE B$
SELECT CASE B$
CASE "0": PRINT "";
CASE "1": PRINT "1";
CASE "2": PRINT "10";
CASE "3": PRINT "11";
CASE "4": PRINT "100";
CASE "5": PRINT "101";
CASE "6": PRINT "111";
CASE "7": PRINT "111";
END SELECT
FOR K = 2 TO LEN(a$)
B$ = MID$(a$, K, 1)
SELECT CASE B$
CASE "0": PRINT "000";
CASE "1": PRINT "001";
CASE "2": PRINT "010";
CASE "3": PRINT "011";
CASE "4": PRINT "100";
CASE "5": PRINT "101";
CASE "6": PRINT "111";
CASE "7": PRINT "111";
END SELECT
NEXT K
PRINT "В восьмеричном представлении ";n&;"= ";OCT$(n&)
PRINT "В шестнадцатеричном представлении ";n&;"= ";HEX$(n&) END
END
Программа 2_03.с
/* Перевод числа в системы счисления с основаниями 2, 8 и 16 */
#include
#include
#include
main()
{
long N;
char a[33];
clrscr();
printf("Введите положительное число : ") ;
scanf("%ld",&N);
if(N==0) {
printf("\n Такое число в любой системе = 0") ;
exit(1);
}
ltoa(N,a,2);
/* перевод в двоичную систему */
printf("\n B двоичном представлении %ld = %s",N,a);
ltoa(N,a,8);
/* перевод в восьмеричную систему */
printf("\nВ восьмеричном представлении %ld = %s",N,a);
ltoa(N,a,16);
/* перевод в шестнадцатеричную систему */
printf("\n В шестнадцатеричном представлении %ld = %s",N,a);
getch();
}
Программа 2_03.pas
program _2_8__16;
{ Перевод числа в системы с основаниями 2, 8 и 16 }
uses crt; var
N1,N:longint;
a:array [0..31] of byte;
j,k:byte;
s:char; begin
clrscr;
write('Введите положительное число : ');
readln(N);
if N=0 then begin
writeln('Такое число в любой системе = 0');
exit;
end;
N1:=N;
for j:=0 to 31 do
a[j]:=0;
while Nl<>O do
begin
a[j]:=N1 mod 2; {цикл выделения двоичных цифр}
dec(j);
N1:=N1 div 2;
end;
write('В двоичном представлении ',N,'=');
for k:=j+l to 31
do write(a[k]:1);
writeln;
N1:=N;
for j:=0 to 10 do a[j]:=0;
while N1<>0 do begin
a[j]:=Nl mod 8; {цикл выделения восьмеричных цифр)
dec(j);
N1:=N1 div 8;
end;
write (' В восьмеричном представлении ',N,'=');
for k:=j+l to 10
do write(a[K]:i);
writeln; N1:=N;
for j:=0 to т 7 do a[j];=0;
while N1<>0 do begin
a[j]:=N1 mod 16;
dec(j);
N1:=N1 div 16;{ цикл выделения шестнадцатеричных цифр}
end; write('В шестнадцатеричном представлении ',N,'=');
for k:=j+l to 7 do begin
if a[k]<10
then s:=chr(ord('0')+a[k]}
else s:=chr(ord('A')+a[k]-10);
write (s) ;
end;
readln;
end.
Задание 2.04. Преобразование десятичного числа в Систему с основанием r
Составить функцию num_to_str (пшп, г), возвращающую в качестве своего значения строку с представлением натурального числа num в системе счисления с основанием г. Предполагается, что число num в памяти компьютера представлено 4-байтовым целым, а основание r принадлежит диапазону |2, 16]. Для обозначения цифр, превосходящих 9, рекомендуется воспользоваться латинскими буквами А, в, ... , F.
Совет 1 (общий)
Совет 2 (QBasic)
описанных как AS LONG, AS STRING, AS INTEGER, или более старомодный с добавками %, &, $ в конце имени переменной. Возможность "складывать" символьные значения в любом порядке позволяет избежать инвертирования результирующей строки. Для этого вместо оператора А$ = A$ + CIF$ удобнее воспользоваться левосторонней конкатенацией А$ = CIF$+A$.
Совет 3 (Си)
Программа 2_04.bas
REM Перевод числа в систему с основанием r
DECLARE FUNCTION NToStr$(NUM&,R%)
CLS
INPUT "Введите натуральное число : ",N&
PRINT "Его представление в разных системах счисления таково : "
FOR J%=2 TO 16
PRINT "по основанию ";
J%,N&;"= ";NToStr$(N&,J%) NEXT J% END
FUNCTION NToStr$(NUM&,R%) A$="": MS=NUM& DO
CIF=M& MOD R% : ' Выделение очередной цифры
IF CIF<10 THEN
A$=CHR$(ASC("0")+CIF)+A$ : ' Замена цифры кодом ASCII ELSE
A$=CHR$(ASC("A")+CIF-10)+A$ END IF
М&=(М&-CIF)/R% : ' Исключение обработанной цифры
LOOP UNTIL M&=0 NToStr$=A$ END FUNCTION
Программа 2_04.с
/* Перевод числа в систему с основанием r */
#include
# include
char *num_to_str (long num, char r) ;
void main (void) {
long N;
char j ;
printf ("\n Введите натуральное число ");
scanf ("%ld",&N);
printf ("Его представление в разных системах счисления таково :\n")
for(j=2; j<17; j++)
printf ("\n по основанию %2d = %s", j ,num_to_str (N, j ) ) ;
getch ( ) ;
}
char *num_to_str(long num, char r) {
static char a[33];
char cif, k, count=0; do {
cif=num % r;
/* Выделение очередной цифры */
if(cif<10) a[count++]='0'+cif;
/* Замена цифры кодом ASCII, если цифра меньше 10 */
else a[count++]='A'+cif-10;
/* Замена цифры кодом ASCII, если цифра больше 9 */
num=num/r;
/* Исключение обработанной цифры */ }
/* Цикл изменения порядка цифр в массиве а */
while (num != 0);
a[count--]=0х0;
for(k=0; k<=count/2; k++)
{ cif=a[count-k]; a[count-k]=a[k]; a[k]=cif; } return a; }
Программа 2_04.pas
program num to pos;
{ Перевод числа в систему с основанием г }
var
N:longint;
j:byte;
function num_to_str(num: longint;r:byte):string; var
a:string[33];
cif,k:byte; begin
a:='';
repeat
cif:=num mod r; { Выделение очередной цифры }
if (cif<10) then a:=chr(48+cif)+a
{ Замена цифры кодом ASCII, если цифра меньше 10 }
else a:=chr(65+cif-lO)+a;
{ Замена цифры кодом ASCII, если цифра больше 9 }
num:=num div r; { Исключение обработанной цифры }
until (num=0);
num_to_str:=а; end; begin
write('Введите натуральное число - ');
readln(N);
writelnf'Ero представление в разных системах счисления таково :']
for j :=2 to 16 do
writeln('no основанию ',j:2,' = ',num_to_str(N,j));
readln; end.
Задание 2.05. Симметричное разложение с наименьшим основанием
Дано натуральное число N (N < зоооо). Найти систему счисления с наименьшим основанием Pmin, в которой N имеет симметричное представление. Например,
ДЛЯ N=0 Pmin-2 (910 = 10012),
ДЛЯ N-1000 Emin=S (100010 - 13319)
Программа должна запрашивать число N, выдавать Pmin и значения
цифр в представлении числа N в этой системе (цифры можно выводить в виде обычных десятичных чиселл).
Cовет 1(oбщий)
Второй очевидный факт заключается в том, что всегда найдется такая система счисления, в которой разложение любого числа N будет симметричным. Такой системой, в частности, является система с основанием N-1, т. к. в ней число N выглядит как 11. Поэтому остается только организовать цикл по основаниям систем от 2 до N-I и, как только будет найдено симметричное разложение, прекратить перебор.
Совет 2 (общий)
Совет 3 (QBasic)
Программа 2_05.bas
RЕМ Поиск симметричного разложения числа
DECLARE FUNCTION perevod!(n%,p%,a%())
DECLARE FUNCTION proba! (a%(),k%)
DIM a%(16)
CLS
INPUT "Введите число из диапазона [0,30000] : ",n%
FOR p%=2 TO n%-l
k%=perevod(n%,p%,a%()) : ' Перевод в р-ричную систему
IF proba(a%(), k%) о 0 THEN
PRINT "Симметричное разложение с минимальным основанием
FOR i = 0 ТО k% - 1
PRINT TAB(0);а%(i);"*";р%; "^";k%-i;"+";
NEXT i
PRINT :
PRINT a% (0);"*";p%;"^";0
END
END IF
NEXT p%
END
FUNCTION perevod (n%,p%,a%())
REM Перевод числа n в систему с основанием р
RЕМ Цифры р-ричного числа запоминаются в массиве а
m%=n%
FOR i=0 TO 15
a%(i)=m% MOD p%
m%=(m%-a%(i))/p%
IF m%=0 THEN perevod=i: EXIT FUNCTION
NEXT i
END FUNCTION
FUNCTION proba (a%(),k%)
REM Анализ числа, представленного k цифрами в массиве а
REM Если число - палиндром, то proba=l
proba=l
FOR i=0 TO k%/2
IF a% (i)0a% (k%-i) THEN proba=0: EXIT FUNCTION
NEXT i
END FUNCTION
Программа 2_05.с
/* Поиск симметричного разложения числа */
#include
#include
int perevod( int n, int p, int *a);
int proba(int *a, int k);
int i ;
main() {
int k,p,N,a[16];
clrscr () ;
scanf("%d",&N);
for (p=2; p
k=perevod(N, p, a); /* Перевод в р-ричную систему */
if (proba(a,k)==0) continue;
printf("Хпминимальное основание = %d\n",p);
for(i=0; i<=k; i++)
printf("%d ",a[i]);
break;
getch(); }
int perevod(int n,int p,int *a) /* Перевод числа п в систему с основанием р
Цифры р-ричного числа запоминаются в массиве а */
for(1=0; 1<1б; 1++)
a[i]=n % р; n=n/р;
if(n==0) return i;
}
int proba (int *a, int k)
/* Анализ числа, представленного k цифрами в массиве а
Если число - палиндром, то proba=l */ {
for(i = 0; i <= k/2; 1++)
if(a[i] != a[k-i]) return 0; return 1 ;
Программа 2_05.pas
program min_base;
{ Поиск симметричного разложения числа }
uses Crt;
var
i, k, p,N: integer;
a:array [0..15] of integer;
function perevod(n,p:integer) :integer;
{ Перевод числа n в систему с основанием р
Цифры р-ричного числа запоминаются в массиве а}
begin
for i:=0 to 15 do
begin
a[i]:=n mod p;
n:=n div p;
if n=0 then
begin perevod:=i;
exit;
end;
end;
end;
function proba(k:integer):integer;
{ Анализ числа, представленного k цифрами в массиве а
Если число - палиндром, то proba=l }
begin
for i:=0 to k div 2 do
if a[i]<>a[k-i] then
begin proba:=0;
exit;
end;
proba:=1;
end;
begin clrscr;
writeln('Поиск симметричного разложения с минимальным основанием');
writeln('Введите число');
readln(N);
for p:=2 to N do
begin
k:=perevod(N,p);
if proba(k)=0 then continue;
writeln('минимальное основание = ',p);
for i:=0 to k do writeln(a[i]);
break;
end;
readln;
end.
Задание 2.06. Суммирование десятичных цифр
Составить функцию sum_dig(n), аргументом которой является длинное целое число. Возвращаемое значение должно быть равно сумме десятичных цифр числа n.
Совет 1 (общий)
Совет 2 (OBasic)
Совет 3 (Си, Паскаль)
Программа 2_06.bas
RЕМ Суммирование десятичных цифр числа
DECLARE FUNCTION SUMDIG (N&)
CLS
INPUT "Введите целое число";М&
K=SUMDIG(M&)
PRINT "Сумма его цифр = ";К
END
FUNCTION SUMDIG(N&)
IF N&<0 THEN N&=-N& : ' Смена знака у отрицательного числа
RESULT=0
DO
RESULT=RESULT+(N& MOD 10&) : ' Накопление суммы цифр
N&=(N&-(N& MOD 10&))/10& : ' Удаление обработанной цифры
LOOP WHILE N&<>O
SUMDIG=RESULT
END FUNCTION
Программа 2_06.с
/* Суммирование десятичных цифр числа */
#include
int sum_digits(long N);
main()
}
long M;
printf ("\n Введите целое число: ");
scanf ("%ld", &M) ;
printf ("\n Сумма его цифр = %d", sum_digits (M) ) ;
getch ( ) ; }
int sum_digits (long N) {
int Result=0;
N=labs (N) ; /* Смена знака у отрицательного числа */
do {
Result=Result+N%10; /* Накопление суммы цифр */
N=N/10; /* Удаление обработанной цифры */ }
while (N != 0) ;
return Result;
}
Программа 2_06.pas
program sumdigits;
{ Суммирование десятичных цифр числа }
var
M:longint;
function sum_digits (N: longint) : integer;
const
Result : integer=0 ;
begin
if N<0 then N:=-N;
{ Смена знака у отрицательного числа } repeat
Result :=Result+N mod 10; { Накопление суммы цифр }
N:=N div 10; { Удаление обработанной цифры }
until N=0;
sum_digits : =Result;
end;
begin
write ( ' Введите целое число : ' ) ;
readln (M) ;
writeln('Сумма его цифр =',sum_digits(M)! readln;
end.
Задание 2.07. "Счастливый" Сияет
Составить логическую функцию luck(n), аргументом которой является число п из диапазона [0, 999999]. Функция должна возвращать значение true (Паскаль) или i (Си, QBasic), если ее аргумент представлен "счастливым" числом, у которого суммы трех старших и трех младших цифр совпадают.
Программа 2_07.bas
REM Анализ "счастливого" билета
DECLARE FUNCTION LUCK(M AS LONG)
INPUT "Введите номер билета ";N& IF LUCK(N&)=1 THEN
PRINT "Радуйтесь - счастливый" ELSE
PRINT "Нет счастья в жизни" END IF END
FUNCTION LUCK(M AS LONG)
REM Подсчет и сравнение сумм старших и младших цифр М
REM Если суммы совпадают LUCK=1
DIM A(6)
LUCK=0
IF M<0 OR M>999999 THEN
PRINT "luck : недопустимый аргумент":
EXIT FUNCTION
END IF
FOR i=0 TO 5
A(I)=M MOD 10 : ' Выделение очередной цифры
M=(M-A(I))/10 : ' Удаление обработанной цифры
NEXT I
IF (A(0)+A(1)+A(2)=A(3)+A(4)+A(5)) THEN LUCK=1
END FUNCTION
Программа 2_07.с
/* Анализ "счастливого" билета */
#include
int luck(long M);
main() {
long N;
printf("\n Введите номер билета ");
scanf("%ld",&N);
if (luck(N)==l)
printf("\n Радуйтесь - счастливый");
else
printf("\n Нет счастья в жизни"); getch(); }
int luck(long M)
/* Подсчет и сравнение сумм старших и младших цифр М
Если суммы совпадают luck=l*/ {
int i ; char a[6];
if((M<0) || (M>999999)) {
printf("\nluck : недопустимый аргумент");
exit(0); }
for(i=0; i<6;.i++) {
a[i]=M % 10; /* Вьщеление очередной цифры */
M=M/10; /* Удаление обработанной цифры */
}
if(a[0]+a[l]+a[2]=a[3]+a[4]+a[5]> return 1;
return 0; }
Программа 2_07.pas
program lucky_ticket;
{ Анализ "счастливого" билета
var
N:longint;
function luck(M:longint):boolean;
{ Подсчет и сравнение сумм старших и младших цифр М
Если суммы совпадают luck=true }
var
i:integer;
a:array [1..6] of byte;
begin
if (M<0) or (M>999999) then begin
writeln('luck : недопустимый аргумент');
exit;
end;
for i:=l to 6 do
begin
a[i]:=M mod 10; { Выделение очередной цифры }
M:=M div 10; { Удаление обработанной цифры }
end;
luck:=(a[l]+a[2]+a[3])=(а[4]+а[5]+а[6]);
end;
begin
writeln('Введите номер билета');
readln(N);
if luck(N) then
writeln('Радуйтесь - счастливый') else
writelnt'HeT счастья в жизни');
readln;
end.
Задание 2.08. Количество различных цифр в десятичном числе
Составить функцию num_digits (n), аргументом которой является длинное целое число. Возвращаемое значение должно быть равно количеству различных цифр в десятичной записи п. Например: num_digits (1998) =3.
Совет 1 (общий)
единицы и т. д. Вначале массив счетчиков обнуляется, а после выделения всех цифр числа проверяется, сколько счетчиков хранят ненулевые значения. Вообще говоря, можно не заниматься подсчетом количества появлений каждой цифры —достаточно фиксировать сам факт появления той или иной цифры.
Совет 2 (Си, Паскаль)
Программа 2_08.bas
RЕМ Определение количества различных цифр в числе
DECLARE FUNCTION NumDig!(N&)
CLS
INPUT "Введите число : ", N&
PRINT "Количество разных цифр в его записи = ";NumDig(N&)
END
FUNCTION NumDig(N&)
REM Выделение и подсчет количества разных цифр в числе N
DIM d(10) : ' Массив для фиксации обнаруженных цифр
КЕМ При вызове функции d(i)=0
IF N&<10 THEN NumDig=l: EXIT FUNCTION
DO
k%=N& MOD 10 : ' Выделение очередной цифры
d(k%)=d(k%)+l : ' Подсчет количества цифр, равных k
N&=(NS-k%)/10 : ' Удаление обработанной цифры
LOOP UNTIL N&=0
FOR k%=0 TO 9 : ' Цикл подсчета количества обнаруженных цифр
IF d(k%)<>0 THEN s=s+l : ' Если d(i)=0, цифры i не было
NEXT k%
NumDig=s
END FUNCTION
Программа 2_08.с
/* Определение количества различных цифр в числе */
#include
#include
int num_digits(long N);
main() {
long N;
printf("\n Введите число - ");
scanf("%ld",&N);
printf("\Количество разных цифр в его записи = %d ",
num_digits(N));
getch(); }
int num_digits(long N)
/* Выделение и подсчет количества разных цифр в числе N */ {
char d[10]={0,0,0,0,0,0,0,0,0,0}; /* Массив счетчиков цифр */
int k,s=0;
if(N<10) return 1;
while (N) {
d[N % 10]++; /* Выделение и учет очередной цифры */
N=N/10; /* Удаление обработанной цифры */ }
/* Цикл подсчета количества обнаруженных цифр */
for(k=0; k<10; k++)
if(d[k]) s++;
return s; }
Программа 2_08.pas
program NumDigits;
{ Определение количества различных цифр в числе }
var
N:longint;
function num_digits(N:longint):byte;
{ Выделение и подсчет количества разных цифр в числе N } var
d:array [0..9] of byte; { Массив счетчиков }
s,k:byte;
begin
if N<10 then num_digits:=1
else begin
for k:=0 to 9 do d[k]=0; { Сброс счетчиков }
s: =0 ;
while N<> 0 do begin
inc(d[N mod 10]); { Выделение и учет очередной цифры }
N := N div 10; { Удаление обработанной цифры }
end;
{ Цикл подсчета количества обнаруженных цифр }
for k:=0 to 9 do
if(d[k]<>0) then inc(s);
num_digits:=s;
end;
end;
begin
write('Введите число : ');
readln(N);
writeln('Количество разных цифр в его записи = ',num_digits(N));
readln;
end.
Задание 2.09. Определение цифры в заданной позиции
Составить функцию digit_in_pos (n,i), аргументами которой являются длинное целое число n и номер i позиции цифры в десятичном представлении n. Отсчет номеров позиций ведется справа налево от 0 и соответствует "весу" цифры (степени основания), с которым цифра входит в число. Например:
n=1985
в 0-й позиции находится цифра 5;
в 1-й позиции находится цифра 8;
во 2-й позиции находится цифра 9;
в 3-й позиции находится цифра 1;
Функция digit_in_pos должна возвращать цифру, расположенную в 1-й позиции числа п.
Программа 2_09.bas
RЕМ Анализ цифр в каждой позиции заданного числа
DECLARE FUNCTION DIGINPOS(N AS LONG,J AS INTEGER)
INPUT "Введите целое число: ";М&
FOR K%=0 ТО 9
DIGIT=DIGINPOS(M&,К%)
PRINT "В позиции ";К%;" находится ",DIGIT NEXT K%
END
FUNCTION DIGINPOS(N AS LONG,J AS INTEGER)
REM Определение десятичной цифры числа N в позиции j
N1&=N
FOR K%=0 TO J
RESULT=N1& MOD 10
N1&=N1&-RESULT)/10 NEXT K%
DIGINPOS=RESULT
END FUNCTION
Программа 2_09.с
/* Анализ цифр в каждой позиции заданного числа */
#include
int digit_in_pos(long N,int j);
main () {
long M;
int k;
printf("ХпВведите целое число: ");
scanf("%ld",&M);
for(k=0; k<10; k++)
printf("\nB позиции %d находится %d",k,digit_in_pos(M, k)) ;
getch(); }
int digit_in_pos(long N,int j)
/* Определение десятичной цифры числа N в позиции j */ {
int Result,k;
for (k=0; k<=j; k++) {
Result=N % 10; N=N/10;
}
return Result; }
Программа 2 09.pas
program DigitlnPos;
{ Анализ цифр в каждой позиции заданного числа }
var
M:longint;
k:integer;
function digit_in_pos(N:longint;j:integer):integer;
{ Определение десятичной цифры числа N в позиции j }
var
Result,k:integer;
begin
for k:=0 to j do
begin
Result:=N mod 10;
N:=N div 10;
end;
digit_in_pos:=Result;
end;
begin
writeln('Введите целое число:');
readln(M);
for k:=0 to 9 do
writeln('В позиции ',k,' находится ',digit_in_pos(M,k));
readln;
end.
Задание 2.10. Генерация чисел с заданной суммой цифр
Составить программу, которая выдает все числа из диапазона [0, 999], сумма цифр которых равна вводимому числу N (о < N < 27).
Программа 2_10.bas
REM Генерация чисел с заданной суммой цифр
INPUT "Введите число в диапазоне от 0 до 27 : ",n
PRINT "Список чисел, сумма цифр которых равна ";n;" :"
FOR a2%=0 ТО 9
FOR a1%=0 TO 9
FOR a0%=0 TO 9
IF a2%tal%+aO%=n THEN
PRINT USING "####";100*a2%+10*al%+a0%;
END IF
NEXT a0%,al%,a2%
END
Программа 2_10.c
/* Генерация чисел с заданной суммой цифр */
#include
#include
main () {
int a2,al,a0,n;
printf("\n Введите число в диапазоне от 0 до 27 : ");
scanf("%d",&n);
printf("\n Список чисел, сумма цифр которых равна %d :\n",n);
for(a2=0; a2<10; а2++)
for(al=0; al<10; al++)
for(a0=0; a0<10; a0++)
if(a2+al+a0==n) printf("%4d",100*a2+10*al+a0);
getch(); }
Программа 2_10.pas
program numbers;
{ Генерация чисел с заданной суммой цифр }
var
а2,al,aO,n:integer; begin
write('Введите число в диапазоне от 0 до 27 : ');
readln(n);
writeln(' Список чисел, сумма цифр которых равна ',n, ' :');
for a2:=0 to 9 do
for al:=0 to 9 do
for a0:=0 to 9 do
if (a2+al+a0)=n then write(100*a2+10*al+a0:4);
readln;
end.
Задание 2.11. Вывод числа словами
Составить строковую функцию num_to_3tr(n), аргументом которой является целое число (|n| < 1000). Возвращаемое значение должно быть строкой, в которой величина п представлена словами. Например:
num_to_str(-87) = "минус восемьдесят семь".
Совет 1 (общий)
Совет 2 (Си)
Совет 3 (QBasic)
Совет 4 (Паскаль)
num1. num2 и num3 предлагается поместить соответствующие описания в раздел типизированных "констант".
Программа 2_11.bas
RЕМ Формирование словесного описания числа
DECLARE FUNCTION NumToStr$(m%,numl$(),num2$(),num3$())
CLS
DATA "ноль","один","два","три","четыре","пять","шесть","семь"
DATA "восемь","девять","десять","одиннадцать","двенадцать" .
DATA "тринадцать","четырнадцать","пятнадцать","шестнадцать"
DATA "семнадцать","восемнадцать","девятнадцать"
DIM numl$ (20)
FOR k=0 TO 19: READ numl$(k): NEXT k
DATA "двадцать ","тридцать ","сорок ","пятьдесят "
DATA "шестьдесят ","семьдесят "("восемьдесят ","девяносто "
DIM num2$(8)
FOR k=0 TO 7: READ num2$(k): NEXT k
DATA "","CTO ","двести ","триста ","четыреста ","пятьсот "
DATA "шестьсот ","семьсот ","восемьсот ","девятьсот "
DIM num3$(10)
FOR k=0 TO 9: READ num3$(k): NEXT k
INPUT "Введите целое число от -999 до 999: ",n%
PRINT n%;"= ";NumToStr$(n%,numl$(),num2$(),num3$())
END
FUNCTION NumToStr$(m%,numl$(),num2$() , num3$())
IF m%=0 THEN NumToStr$=numl$(0): EXIT FUNCTION
IF m%<0 THEN m%=-m%: Res$="минус " : 'Учет знака числа
dlg100%=m%\100 : ' Вьщеление сотен
Res$=Res$+num3$(dig100%) /Приклеили обозначение сотен
m%=m%-100*dig100% : "Удаление обработанных сотен
IF m%=0 THEN NumToStr$=Res$: EXIT FUNCTION
IF m%<20 THEN NumToStr$=Res$+numl$ (m%) : EXIT FUNCTION
dig10%=m%\10 :' Вьщелеыие десятков, если dig10 >=20
Res$=Res; +num2$ (diglO%-2)
digl%=m% MOD 10 :' Приклеили обозначение десятков
КЕМ Если в числе присутствуют ненулевые разряды единиц
IF digl%<>0 THEN Res$=Res$+numl$(digl%)
NumToStr$=Res$
END FUNCTION
Программа 2_11a.bas
RЕМ Формирование словесного описания числа
DECLARE FUNCTION NumToStr$(m%)
CLS
DATA "нуль","один","два","три","четыре","пять","шесть", "семь"
DATA "восемь","девять","десять","одиннадцать","двенадцать"
DATA "тринадцать","четырнадцать","пятнадцать","шестнадцать"
DATA "семнадцать","восемнадцать","девятнадцать"
DIM SHARED numl$(20)
FOR k=0 TO 19: READ numl$(k): NEXT k
DATA "двадцать ","тридцать ","сорок "," пятьдесят "
DATA "шестьдесят ","семьдесят ","восемьдесят ","девяносто "
DIM SHARED num2$(8)
FOR k=0 TO 7: READ num2$(k): NEXT k
DATA "","сто ","двести ","триста ","четыреста ","пятьсот "
DATA "шестьсот ","семьсот ","восемьсот ","девятьсот "
DIM SHARED num3$(10)
FOR k=0 TO 9: READ num3$(k): NEXT k
INPUT "Введите целое число от -999 до 999: ",n%
PRINT n%;"= ";NumToStr$(n%) '
END
FUNCTION NumToStr$(m%)
IF m%=0 THEN NumToStr$=numl$(0): EXIT FUNCTION
IF m%<0 THEN m%=-m%: ResS-''мииус " : 'Учет знака имела
dig100%=m%\100 : 'Выделение сотен
Res$=Res$+num3$(dig!00%) :' Приклеили обозначение сотен
m%=m%-100*diglOO% : ' Удаление обработанных сотен
IF m%=0 THEN NumToStr$=Res$: EXIT FUNCTION
IF m%<20 THEN NumToStr$-Res$-t-numl$ (m%) : EXIT FUNCTION diglO%=m%\10 :
' Выделение десятков, если
dig10>=20 R@s$=R.es$-l-num2$ (diglO%-2) :' Приклеили обозначение десятков
diglS-^m* MOD 10
КЕМ Если в числе присутствуют ненулевые разряды единиц
IF digl%<>0 THEN Res$=Res$+numl$(digll)
NumToStr$=Res$ END FUNCTION
Программа 2_11.с
/* Формирование словесного описания числа */
#include
#include
#include
char *num_to_str(long m) ;
main() {
long n;
clrscr() ; m:
printf("ХпВведите целое число : ");
scanf("%ld",&n);
printf("\n%ld = %s",n,num_to_str(n));
goto m;
getch(); }
char *num_to_str(long m)
/* Преобразование числа в словесное описание */ {
char *numl[]={"ноль","один","два","три",
"четыре","пять","шесть","семь","восемь","девять",
"десять","одиннадцать","двенадцать",
"тринадцать","четырнадцать",
"пятнадцать","шестнадцать","семнадцать", "восемнадцать",
"девятнадцать " }';
char *num2[]=1
"двадцать ","тридцать ","сорок ",
"пятьдесят ","шестьдесят ",
"семьдесят ","восемьдесят ","девяносто "};
char *num3[]=("",
"сто ","двести ","триста ","четыреста ",
"пятьсот ", "шестьсот ","семьсот "/'восемьсот "/'девятьсот "} ;
static char Result[50]="";
int digl,dig10,dig100;
if(m==0) return numl[0]; Result[0]=0x0;
if(m<0) /* Учет знака числа */ {
m=-m;
strcpy(Result,"минус ") ; }
diglOO=m/100; /* Выделение сотен */
strcat(Result,num3[diglOO]);
/* Приклеили обозначение сотен */
m=m-100*dig100;
/* Удаление обработанных сотен */
if (m=0) return Result;
/* Если две оставшиеся цифры - нули */
if(m<20) /* Если две младшие цифры меньше 20 */
{
strcat(Result,numl[m]);
return Result; }
diglO=m/10;
/* Выделение десятков, если diglO >=20 */
strcat(Result,num2[diglO-2]);
digl=m % 10;
/* Если в числе присутствуют ненулевые разряды единиц */
if(digl != 0)
strcat(Result,numl[digl]);
return Result; }
Программа 2_11.pas
program nd_10;
{ Формирование словесного описания числа )
uses Crt;
var
n:longint;
function num_to_str(m:longint):string;
{ Преобразование числа в словесное описание }
label ret;
"const
numl :array [0. .19] o£ string= (
1 ноль', 'один', 'два', 'три', 'четыре', 'пять', 'шесть', 'семь','восемь','девять','десять','одиннадцать', 'двенадцать','тринадцать','четырнадцать', 'пятнадцать','шестнадцать','семнадцать', 'восемнадцать','девятнадцать');
num2:array [2..9] of string=(
'двадцать ','тридцать ','сорок ','пятьдесят ', 'шестьдесят ','семьдесят ','восемьдесят ','девяносто ');
num3:array [0..9] of string = ('',
'сто ','двести ','триста ','четыреста ','пятьсот ', 'шестьсот ','семьсот ','восемьсот ','девятьсот ');
var
digl,diglO,diglOO: byte;
Result:string;
begin
if m=0 then begin
Result:=numl[0];
goto ret;
end;
Result:='';
if m<0 then { Учет знака числа }
begin
m:=-m;
Result:='минус '; end;
diglOO:=m div 100; { Выделение сотен }
Result:=Result + num3[diglOO];
{ Приклеили обозначение сотен }
m:=m-100*diglOO;
{ Удаление обработанных сотен }
if m=0 then goto ret;
{ Если две оставшиеся цифры - нули }
if m<20 then begin
{ Если две младшие цифры меньше 20 }
Result:=Result+numl [m] ;
goto ret;
end;
dig10:=m div 10;
{ Выделение десятков, если diqlO >=20 }
Result:=Result+num2[dig10] ;
digl:=m mod 10; { Если в числе присутствуют ненулевые разряды единиц }
if dig100 then Result:=Result + numl[digl];
ret:
num_to_str:=Result;
end;
begin
clrscr;
write{'Введите целое число : ');
readln (n) ;
writeln(n, ' = ' ,num_to__str (n) ) ;
readln; end.
Задание 2.12. Суммирование двоичных цифр
Составить функцию sum_bits(n), аргументом которой является длинное целое число. Возвращаемое значение должно быть равно количеству единиц в двоичном представлении числа п.
Совет 1 (общий)
Совет 2 (QBasic)
Программа 2_12.bas
RЕМ Суммирование двоичных цифр введенного числа
INPUT "Вводи N"/ N&
Js=&H40000000
RESULT=0
IF N&<0 THEN RESULT=1 : ' Учет 1 в знаке отрицательного числа
FOR K=31 TO I STEP -1
IF N& AND J& THEN RESULT=RESULT+1 : ' Учет k-того разряда
J&=J&/2 : ' Сдвиг шкалы на разряд вправо NEXT К PRINT RESULT END
Программа 2_12.с
/* Суммирование двоичных цифр введенного числа */
#include
int sum_bits(long N) ;
main () {
long M;
printf("ХпВведите целое число: ");
scanf("%ld",&M);
printf("\n Сумма его цифр = %d",sum_bits(M));
getch(); }
int sum_bits(long N)
/* Подсчет единиц в двоичном представлении N */
{
int Result=0,k;
unsigned long j=0x80000000;
for(k=31; k >= 0; k--) {
if(j & N) Result++;
/* Учет k-того разряда */
j=j >> 1; }
return Result;
}
Программа 2_12.pas
program sumbits;
{ Суммирование двоичных цифр введенного числа }
var
M:longint;
function sum bits(N:longint):integer;
const
Result:integer=0;
j:longint=$80000000; var
k:integer; begin
for k:=31 downto 0 do
begin
if (N and j)<>0 then inc(Result);
{ Учет k-того разряда }
j:=j shr 1;
end;
sum_bits:=Result;
end;
begin
write('Введите целое число: ');
readln(M);
writeln('Сумма его цифр = ',sum_bits(M));
readln; end.
Задание 2.13. Позиция старшей единицы
Составить функцию lef t_bit (n), аргументом которой является длинное целое положительное число. Возвращаемое значение должно совпадать с номером старшей единицы в двоичном представлении п. Нумерация двоичных разрядов ведется справа налево от 0 до 31.
Совет 1 (общий)
Программа 2_13.oas
RЕМ Определение позиции старшей единицы в двоичном числе
DECLARE FUNCTION LeftBit!(N&)
INPUT "Введите целое число: "/Ms
IF M&=0 THEN PRINT "D этом числе единиц нет" : END
PRINT "Старший разряд находится в позиции номер ";
LeftBit(M£)
END
FUNCTION LertBil(N&)
REM Определение позиции старшей единицы в числе N
КЕМ Если N=0, то LeftBit=-l
LeftBit=-l
j&=&H40000000
FOR k=30 TO 0 STEP -1
IF (j& AND N&) THEN ' Анализ k-го разряда LeftBit-k EXIT FUNCTION
END IF
j&=j&/2 NEXT k
END FUNCTION
Программа 2_13.с
/* Определение позиции старшей единицы в двоичном числе */
#include
int left_bit(long N) ;
main() {
long M;
printf("\n Введите целое число: ");
scanf("%ld",&M);
if(M==0) {
printf("\n B этом числе единиц нет");
exit(0); }
printf("\n Старший разряд находится в позиции номер %d", left__bit(M));
getch(); }
int left_bit(long N)
/* Определение позиции старшей единицы в числе N
Если N=0, функция возвращает -1 */ {
int k;
long j=0x80000000;
for(k=31; k >= 0; k--) {
if(j & N) return k;
j=j >> 1;
}
return -1; }
Программа 2_13.pas
program LeftBit;
{ Определение позиции старшей единицы в двоичном числе }
var
M:longint;
function left_bit(N:longint):byte;
{Определение позиции старшей единицы в числе N Если N=0, функция возвращает -1 }
var
k:byte; const
j:longint=$80000000;
begin
left_bit:=-l;
for k:=31 downto 0 do
begin
if (j and N)<> 0 then begin
left_bit:=k;
exit;
end;
j:=j shr 1;
end;
end;
begin
write('Введите целое число: ');
readln(M);
if M=0 then writeln('B этом числе единиц нет')
else
writelnf'Старший разряд находится в позиции номер ', left_bit(M));
readln; end.
Задание 2.14. Максимальное количество подряд стоящих единиц
Составить функцию max_bits(n), аргументом которой является длинное целое положительное число. Возвращаемое значение должно быть равно максимальному числу подряд расположенных единиц в двоичном представлении п. Например:
n = 3310 = 100012 max_bits (33) =1
n = 2810 = 111002 max_bits(28) =3
Совет 1 (общий)
Совет 2 (QBasic)
Совет 3 (Си)
Программа 2_14.bas
RЕМ Определение максимальной группы единиц в двоичном числе
DECLARE FUNCTION MaxBitS!(N&,s$)
CLS
INPUT "Введите целое число : ",М&
k%=MaxBits(M&,a$)
PRINT "Двоичное представление этого числа :"
PRINT a$
PRINT "Максимальное число подряд стоящих единиц = "; k%
END
FUNCTION MaxBits(NS,s$)
REM Перевод числа N в двоичное символьное представление
REM Поиск самой длинной группы единиц (MaxBits = длина)
IF N&=0 THEN MaxBits=0: s$="0": EXIT FUNCTION
FOR j=0 TO 31 : ' Формирование двоичного числа в строке s$
IF N& AND &H1 THEN
kBits=kBits+l : ' Подсчет подряд идущих единиц
IF kBits>max THEN max=kBits : ' Запомнили максимум
s$="l"+s$ : ' Приписали очередную единицу ELSE
kBits=0 : ' Сброс счетчика при встрече нуля
s$="0"+s$ : ' Приписали очередной ноль END IF
N&=(N&-k)/2 : ' Сдвиг на один разряд вправо
NEXT j
MaxBits=max
END FUNCTION
Программа 2_14.с
/* Определение максимальной группы единиц в двоичном числе */
#include
#include
#include
int max_bits(long N);
main ()
{
long M;
char str[33];
clrscr () ;
printf("\nВведите целое число : ");
scanf("%ld",&M);
printf("Двоичное представление этого числа :");
ltoa(M,str,2);
printf("\n%32s",str);
printf("\ n Максимальное число подряд стоящих единиц = %d",
max_bits(M));
getch(); }
int max_bits(long N)
/* Перевод числа N в двоичное символьное представление
Поиск самой длинной группы единиц (max_bits = длина) */
{
int k_bits=0,max=0;
char s[33];
if(N==0) return 0;
while (N) /* Формирование двоичного числа в строке s$ */
{
if(N & 0x80000000) /* если очередной разряд равен 1 */
{
/* подсчет подряд идущих единиц */
k_bits++;
if(k_bits>max) max=k_bits; /* запоминание максимума */
}
else
k_bits=0; /* сброс счетчика, если очередной разряд = 0 */
N=N << 1 ; /* сдвиг на 1 разряд влево */
}
return max; }
Программа 2_14.pas
program MaxBits;
{ Определение максимальной группы единиц в двоичном числе }
uses Crt;
var
M:longint;
str:string[33];
function max_bits(N:longint)rshortint;
{ Перевод числа N в двоичное символьное представление
Поиск самой длинной группы единиц (max_bits = длина) }
var
k bits, max:byte;
begin
k_bits:=0;
max:=0;
if N=0 then
begin
max_bits:=0;
exit;
end;
while N<>0 do { Формирование двоичного числа в строке s$ }
begin
if (N and $00000001)00 then { если разряд равен 1 }
begin
str:='l'+str;
inc(k_bits); { подсчет подряд идущих единиц }
if k_bits>max then max:=k_bits end else begin
str:='0'+str;
k_bits:=0; { сброс счетчика, если очередной разряд = 0 }
end;
N:= N shr 1; { сдвиг на 1 разряд вправо }
end;
max_bits:=max; end;
begin clrscr;
write('Введите целое число : ') ;
readln(M);
writeln('Максимальное число подряд стоящих единиц = ',max_bits(M));
readln;
end.
Задание 2.15. Расстояние между двоичными кодами
Под "расстоянием" между двумя n- разрядными двоичными кодами понимают количество несовпадений в каждой из п позиций. Например:
01011010
00101110
-------------
=***=*== "расстояние"=4
Составить функцию rasst (ni,n2), аргументами которой являются два длинных положительных числа, рассматриваемые как 32-разрядные двоичные коды. Возвращаемое функцией значение должно совпадать с "расстоянием" между nl и п2.
Совет 1 (общий)
Программа 2_15.bas
REM Определение расстояния между двоичными кодами
DECLARE FUNCTION NumToBin$(N&)
DECLARE FUNCTION SumBits!(N&)
CLS
INPUT "Введи первое число :",N1&
INPUT "Введи второе число :",N2&
PRINT "Двоичное представление этих чисел :"
PRINT NumToBin$(N1&) : ' Двоичное разложение N1
PRINT NumToBin$(N2&) : ' Двоичное разложение N2
PRINT "Расстояние между этими кодами = "; SumBits(N1& XOR N2&)
END
FUNCTION NumToBin$(N&)
REM Формирование в строке двоичного представления числа N
а$="": К=&Н1
IF N&=0 THEN NumToBin$="0": EXIT FUNCTION
FOR J=0 TO 30
IF N& AND К THEN s$="l"+S$ ELSE s$="0"+s$
K=K*2 : ' Сдвиг шкалы на 1 разряд влево
NEXT J
IF N&<0 THEN s$="l"+s$ : ' Учет единицу в знаковом разряде
NumToBin$=s$
END FUNCTION
FUNCTION SumBits (N&)
КЕМ Подсчет количества единиц в двоичном числе
J&=&H40000000
RESULT=0
IF N&<0 THEN RESULT=1
FOR K=31 TO 1 STEP -1
IF N& AND J& THEN RESULT=RESULT+1
J&=J&/2 NEXT К
SumBits=RESULT END FUNCTION
Программа 2_15.c
/* Определение расстояния между двоичными кодами */
#include
int rasst(long nl, long n2);
char s [ 4 0];
main() {
long M1,M2;
printf("\ n Введите два целых числа : ");
scanf("%ld %ld",&Ml,&M2);
printf("\nMl =%32s",ltoa(Ml,s,2)); /* Двоичное разложение N1*/
printf("\nM2 =%32s",ltoa(M2,s,2)); /* Двоичное разложение N2*/
printf("\nXOR=%32s",ltoa(MlAM2,s,2));
printf("\nРасстояние между этим кодами = %5d",rasst(M1,M2));
getch();
}
int rasst(long nl,long n2)
{
int Result=0,k;
long j=0x00000001;
for(k=0; k <32; k++)
{
/* Сравнение одноименных двоичных разрядов */
if((j & nl)!=(j & n2)) Result++;
j=j « 1; /* сдвиг шкалы на разряд влево */
}
return Result; }
Программа 2_15.pas
program distance;
{ Определение расстояния между двоичными кодами }
var
Ml,M2:longint;
function rasst(nl,n2:longint):byte;
const
Result:byte=0 ;
j:longint=$00000001;
var
k:byte;
n3:longint;
begin
n3:=nl xor n2;
for k:=0 to 31 do { цикл подсчета единиц в двоичном числе }
begin
if (j and n3)<>0 then inc(Result);
j:=j shl 1;
{ сдвиг шкалы на разряд влево }
end;
rasst:=Result; end; begin
write('Введите два целых числа : ');
readln(Ml,M2);
writeln('Расстояние между этим кодами = ',rasst(Ml,M2));
readln; end.
Задание 2.16. Чтение числа справа налево
Составить функцию invert (n), аргументом которой является длинное целое число. Возвращаемое значение должно быть равно числу, полученному из n перестановкой цифр в обратном порядке. Знак числа при этом сохраняется на прежнем месте. Например:
invert(314159) =951413
invert(-2718) = -8172
Совет 1 (общий)
Программа 2_16.bas
RЕМ Перестановка старших и младших разрядов в числе
DECLARE FUNCTION invert!(N&)
CLS
INPUT "Введите целое число : ",М&
PRINT " Справа налево оно выглядит так ";invert(MS)
END
FUNCTION invert(N&)
Res&=0: sign=SGN(N&) : ' Учет знака числа
IF N&<0 THEN N&=-N& '
DO
k%=(N& MOD 10) : ' очередная цифра справа
Res&=Res&*10+k% : ' формирование перевернутого результата
N&=(Ns-k%)/10 : ' удаление обработанной цифры
LOOP UNTIL N&=0
invert=Res&*sign : ' приклеили знак
END FUNCTION
Программа 2_16.с
/* Перестановка старших и младших разрядов в числе */
#include
long invert(long N);
main()
{
' long M;
printf("\nВведите целое число : ");
scanf("%ld",&M);
printf("\nСправа налево оно выглядит так %ld",invert(M));
getch();
}
long invert(long N) {/* инвертирование числа */
long Result=0, sign=l;
/* Учет знака числа */
if(N<0)
{ N=-N; sign=-l;}
while (N!=0) {
Result=Result*10 + (N % 10);
/* формирование результата */
N=N/10;
/* удаление обработанной цифры */
}
return Result*sign; /* приклеили знак */ }
Программа 2._16.pas
program rotate;
{ Перестановка старших и младших разрядов в числе }
var
N:longint;
function invert(N:longint):longint; const
Result:longint=0; sign:shortint=l;
begin
if N<0 then { Учет знака числа }
begin N:=-N;
sign:=-l;
end;
while (N<>0) do begin
Result:=Result*10+(N mod 10);{ формирование результата }
N:=N div 10; { удаление обработанной цифры }
end;
invert:=Result*sign; { приклеили знак }
end;
begin
write('Введите целое число : ');
readln(N);
writeln('Справа налево оно выглядит так : ',invert(N));
readln;
end.
Задание 2.17. Числовые палиндромы
Натуральное число N = a1a2... ak называют палиндромом, если его величина совпадает со значением, прочитанным справа налево, NI ak...a2a1. При этом предполагается, что a1> о. Например, 1881 — палиндром, а 1812 — нет. Составить функцию paiindrom(n), аргументом которой является длинное положительное целое число. Функция должна возвращать значение true (Паскаль) или 1 (QBasic, Си), если ее аргумент является числовым палиндромом.
Совет 1 (общий)
Совет 2 (общий)
Совет 3 (QBasic)
иметь в виду, что функция STR$ выдает результат с пробелом в первой позиции для положительных чисел. Поэтому сравнение цифр начинается со второй позиции. Для выделения симметрично расположенных цифр использована функция MID$, второй аргумент которой определяет начальную позицию в строке, а третий — количество выделяемых символов.
Программа 2_17.bas
REM Является ли введенное число палиндромом?
DECLARE FUNCTION palindrom!(NS)
СLS
DIM noyes$(2)
noyes$(0)="не"
INPUT "Введите целое число: ",М&
PRINT "Это - "; noyes$(palindrom(M&));" палиндром"
END
FUNCTION palindrom(N&)
REM Если N - палиндром, то palindrom = 1
palindrom=l
IF N&<10 THEN EXIT FUNCTION : ' Одноразрядное - всегда палиндром
s$=STR$(N&) : ' Перевод числа в строку
k%=LEN(s$)
FOR j=2 TO l+k%/2 : ' Цикл проверки симметрии цифр
IF MID$ (s$, j,l)OMID$ (s$,k%+2-j,l) THEN palindrom=0
NEXT j
END FUNCTION
Программа 2_17.с
/* Является ли введенное число палиндромом? */
#include
#include
int palindrom(long N);
main () {
long M;
printf("\n Введите целое число: ");
scanf("%ld",&M);
if (palindrom(M)) printf("\n Это - палиндром");
else printf("\пЭто - не палиндром");
getch(); }
int palindrom(long N)
{
/* Если N - палиндром, то palindrom = 1 */
int j,k=l;
char digit[10];
if(N<10) return 1; /* Одноразрядное - всегда палиндром */
for(j=0; j<10; j++)
{
/* цикл выделения десятичных цифр */
digit[j]=N%10;
N=N/10; /* удаление обработанной цифры */
if(N!=0) k++;
}
for(j=0; j<=k/2; j++) /* Цикл проверки симметрии цифр */
if(digit[j]!=digit[k-j-1]) return 0;
return 1;
}
Программа 2_17.pas
program Palindroms;
{ Является ли введенное число палиндромом ? }
var
М: longint; function
palindrom(N:longint):boolean;
{ Если N - палиндром, то palindrom = true }
var
j,k:integer;
digit:array [0..9] of byte;
begin
palindr om: =t rue ;
if N<10 then exit; { Одноразрядное - всегда палиндром }
k:=0;
for j:=0 to 9 do { цикл выделения десятичных цифр }
begin
digit[j]:=N mod 10; { очередная цифра числа N }
N:=N div 10; { удаление обработанной цифры }
if(N<>0) then k:=k+l; { счетчик цифр в числе N }
end;
for j:=1 to (k div 2) do { Цикл проверки симметрии цифр }
if digit[j]odigit[k-j] then palindrom:=false;
end;
begin
write('Введите целое число: ');
readln(M);
if palindrom(M) then
writeln('Это - палиндром') else
writeln('Это не палиндром');
readln;
end.
Программа 2_17a.pas
program Palindroms;
{ Является ли введенное число палиндромом? }
var
М: longint; const
noyes:array [false..true] of string=('не', '');
function palindrom(N:longint):boolean;
{ Если N - палиндром, то palindrom = true }
var
j,k:byte ;
s:string[16];
begin
palindrom:=true;
if N<10 then exit; { Одноразрядное - всегда палиндром }
str(N,s); { перевод числа в символьную строку }
k:=length(s) ;
for j:=l to (k div 2) do { Цикл проверки симметрии цифр }
if s[j]<>s[k+l-j] then palindrom:=false; end; begin
write('Введите целое число: ');
readln(М);
writeln('Это - ',noyes[palindrom(М)],' палиндром');
readln;
end.
Задание 2.18. Генерация палиндромов с заданным свойством
Составить программу, выводящую на экран все четырехзначные палиндромы, квадраты которых тоже являются палиндромами. Задачу можно несколько усложнить, если считать количество цифр в исходном палиндроме параметром k (k < 5).
Совет 1 (общий)
Программа 2_18.bas
RЕМ Генерация палиндромов, квадраты которых тоже палиндромы
DECLARE FUNCTION palindrom!(N&)
CLS
FOR Al=l TO 9: FOR A2=0 TO 9
M&=(((A1*10)+A2)*10+A2)*10+A1
M2&=M&*M&
IF palindrom(M2&) THEN PRINT M&,M2& NEXT A2, A1 END
FUNCTION palindrom (N&)
REM Если N - палиндром, то palindrom = 1
palindrom=l
IF N&<10 THEN EXIT FUNCTION : ' Одноразрядное - всегда палиндром
s$=STR$(N&) : ' перевод числа в символьную строку
k%=LEN(s$)
FOR j=2 TO l+k%/2 : ' Цикл проверки симметрии цифр
IF MID$ (s$, j,l)OMID$(s$,k%+2-j,l) THEN palindrom=0 NEXT j
END FUNCTION
Программа 2_18.с
/* Генерация палиндромов, квадраты которых тоже палиндромы */
#include
#include
int palindrom (long N);
ma in ()
{
long M,M2;
int al,a2;
for(al=l; al<10; al++)
for(a2=0; a2<10; a2++)
{
M=(((al*10)+a2)*10+a2)*10+a1;
M2=M*M;
if(palindrom(M2))
printf ("\пчисло=%1d квадрат=%1d",М,М2) ; }
getch();
int palindromflong N)
{/* Если N - палиндром, то palindrom = 1 */
int j,k=l;
char digit[10];
if(N<10) return 1; /* Одноразрядное - всегда палиндром */
for(j=0; j<10; j++) /* Цикл выделения цифр числа N */
{
digit[j]=N % 10; N=N/10;
if(N!=0) k++;
}
for(j=0; j <= k/2; j++) /* Цикл проверки симметрии цифр */
if(digit[j]!=digit[k-j-1])
return 0;
return 1; }
Программа 2_18.pas
program sqr_pal;
{ Генерация палиндромов, квадраты которых тоже палиндромы }
var
M,M2:longint;
al,a2:integer;
function palindrom(N:longint):boolean; { Если N - палиндром, то palindrom = true }
var
j,k:integer;
digit:array [0..9] of byte; begin k:=l;
palindrom:=true;
if N < 10 then exit; { Одноразрядное - всегда палиндром } for j : =0 to 9 do { Цикл выделения цифр числа^ N }
begin
digit[j]:=N mod 10; N:=N div 10;
if N00 then inc(k);
end;
for j:=0 to k div 2 do { Цикл проверки симметрии цифр }
if digit[j]odigit[k-j-1] then palindrom:=false; end;
begin
for al:=l to 9 do
for a2:=0 to 9 do begin
M:=(((al*10)+a2)*10+a2)*10+al;
M2:=M*M;
if palindrom(M2) then
writeln('число=',M,' квадрат=',М2);
end;
readln; end.
Задание 2.19. Числовые преобразования до обнаружения зацикливания
Составить программу, которая вводит длинное целое число N и подвергает его многократному преобразованию по следующей схеме:
N1+i = a(i,k)3+ a(i,k-l)3+ ... + a(i,0}3
Здесь через a (i,k), a(i,k-i),... , a(i,0) обозначены цифры числа NL Обработка прекращается при обнаружении зацикливания (N! = N-J, i > j).
Совет 1 (общий)
Совет 2 (QBasic)
Совет 3 (общий)
Попробуйте модифицировать программу таким образом, чтобы обнаружить все числовые последовательности, образующие цикл с самого первого шага. В качестве примера приведем некоторые из них:
1 —> 1 (одношаговый цикл),
136 -> 244 —> -136 (двухшаговый цикл),
55 -> 250 -> 133 -> (трехшаговый цикл).
Программа 2_19.bas
RЕМ Поиск циклов при суммировании кубов цифр
DECLARE FUNCTION nkub& (N&)
DIM MASS(100) : ' Массив для последовательности чисел
CLS
INPUT "Введите число - ", N&
К=0: MAS&(0)=N& ml: К=К+1 : ' Счетчик числа шагов
MASS(K)=nkub&(MASS(K-l))
PRINT "Шаг =";К," N =";MAS&(K)
FOR 1=0 ТО К-1 : ' Поиск совпадения с предыдущими числами
IF MAS&(I)=MASS(K) THEN GOTO m2
NEXT I
GOTO ml m2: PRINT "Обнаружен цикл": PRINT "Начало цикла шаг ";1
PRINT "Конец цикла шаг ";К-1
END
FUNCTION nkub&(N&)
КЕМ Преобразование числа в сумму кубов его цифр
DIM S AS INTEGER, M AS LONG S=0: M=N& WHILE M<>0
D=M MOD 10: M=(M-D)/10 : ' Выделение очередной цифры
S=S+D*D*D : ' Накопление суммы кубов
WEND nkub&=S
END FUNCTION
Программа 2_19.c
/* Поиск циклов при суммировании кубов цифр */
#include
#include
long n_kub(long N);
long N;
int i=l,Q[6562];
main ()
{
clrscr();
printf("\nВведите число ");
scanf("%ld",&N); Q[N-l]=i; ml:
printf ("\n Шaг=%2d N=%ld", i,N) ;
N=n_kub(N);
if(Q[N-1]!=0) /* He было ли раньше такого же числа ?*/ {
printf("\nHa %d шаге обнаружен цикл N=%ld",i+l,N);
getch ();
exit(0) ;
}
Q[N-l]=i++; /* Фиксация очередного числа в массиве Q*/
goto ml;
}
/ *-------------------------------------* /
long n_kub(long N)
{
/* Преобразование числа в сумму кубов его цифр */
int k;
long s=0; while (N)
{
k=N%10;
N=N/10; /* Выделение очередной цифры */
s+=k*k*k; /* Накопление суммы кубов */
}
return s;
}
Программа 2_19.pas
program loop cub
{ Поиск циклов при суммировании кубов цифр }
uses Crt; label ml; var
N:longint;
Q:array [1..6562] of integer; i:integer;
function n_kub(N:longint):integer;
{ Преобразование числа в -сумму кубов его цифр }
var
s,k:integer; begin s:=0;
while (N<>0) do begin
k:=N mod 10;
N:=N div 10; { Выделение очередной цифры }
s:=s+k*k*k; { Накопление суммы кубов }
end;
n kub:=s;
end;
begin clrscr;
write('Введите число');
readln(N);
for i:=l to 6562 do Q[i]:=0;
{ Очистка массива Q}
i:=l;
Q[N]:=1;
ml:
writeln('Шar=',i:2, ' N=',N);
N:=n_kub{N);
if Q[N]<>0 then { He было ли раньше такого же числа ?}
begin
writeln('Ha шаге ',1+1:2,' обнаружен цикл');
readln;
halt;
end;
inc(1); { Счетчик числа шагов )
Q[N]:=i; { Запоминание счетчика в массиве Q }
goto ml;
end.
Задание 2.20. Разложение числа на простые множители
Составить программу, которая выдает разложение заданного целого числа N на простые множители. Например:
128 = 2*2*2*2*2*2*2 17 = простое число
Совет 1 (общий)
Программа 2_20.bas
RЕМ Разложение числа на простые множители
CLS
К& = 2: J% = 0
INPUT "Введите целое число: ", М&: М1& = Ms / 2
PRINT M&; "=";
Ml:
IF MS MOD K&=0 THEN
J=l: M&=M&/K&: PRINT K&;
IF M&<>l THEN PRINT "*";
ELSE K&=K&+1
END IF
IF K&<=M1& THEN GOTO Ml
IF J=0 THEN PRINT " простое число"
END
Программа 2_20.с
/* Разложение числа на простые множители */
#include
#include
main() {
long M,M1,k=2;
char j=l;
printf("\n Введите целое число: ");
scanf("%ld",&M);
Ml=M/2;
printf("\n%ld=",M);
ml:
if (M % k=0) {
j=0;
M=M/k;
printf("%ld",k) ;
if(M!=l)printf("*"); }
else k++;
if(k<=Ml) goto ml;
if(j==l)
printf("простое число");
getch(); }
Программа 2_20.pas
program razlojenie;
{ Разложение числа на простые множители }
var
M,Ml,k:longint ;
j:boolean;
IF K&<=Ml& THEN GOTO Ml
IF J=0 THEN PRINT " простое число"
END
Программа 2_20,с
/* Разложение числа на простые множители */
#include
#include
main ()
{
long M,M1,k=2;
char j=l;
printf("\n Введите целое число: ");
scanf("%ld",&M);
Ml=M/2;
printf("\n%ld=",M);
ml:
if(M % k==0)
{
j=0; M=M/k;
printf("%ld",k) ;
if(M!=l) printf("*"); }
else k++;
if(k<=Ml) goto ml;
if(j==l) printf ("простое число");
getch();
}
Программа 2_20.pas
program razlojenie;
{
Разложение числа на простые множители }
var
М,М1,k:longint;
j:boolean;
label 1;
begin
j:=true; k: =2 ;
write('Введите целое число: ');
readln(M);
M1:=M div 2;
write(M,' = ');
1:
if(M mod k)=0 then begin
j:=false;
M:=M div k;
write (k) ;
if Mol then write ('*');
end
else k:=k+l; if k<=Ml then goto 1;
if j then write('простое число'};
readln; end.
Задание 2.21. Проверка числа на "простоту"
Составить функцию prime (п), аргументом которой является длинное целое положительное число. Функция должна возвращать значение true (Паскаль) или 1 (Си, QBasic), если ее аргумент является простым числом. В противном случае функция должна возвращать значение false или о.
Совет 1 (общий)
Программа 2_21.bas
DECLARE FUNCTION prime!(N&)
REM Проверка числа на простоту
CLS
INPUT "Введите целое число: ", М&
IF prime (M&)=1 THEN
PRINT "Это число - простое " ELSE
PRINT "Это число - составное"
END IF
END
FUNCTION prime(N&)
REM Если N - простое, то prime = 1
DIM j AS LONG
IF N&<4 THEN GOTO Ml : ' Числа 2, 3 - простые
IF N& MOD 2=0 THEN GOTO MO : ' Четные числа - составные
REM Проверка делимости на нечетные числа
FOR j=3 TO SQR(N&)+1 STEP 2
IF N& MOD j=0 THEN GOTO MO NEXT j
Ml: prime=l: EXIT FUNCTION M0: prime=0 END FUNCTION
Программа 2_21.с
/* Проверка числа на простоту */
#include
#include
int prime(long N) ;
main() {
long M;
char *a[]={"составное","простое"};
printf("\n Введите целое число: ");
scanf("%ld",SM);
printf("\n Это число - %s", a[prime(M)]);
getch(); }
int prime(long N)
{
/* Если N - простое, то prime = 1 */
long kmax,j;
if(N<4) return 1; /* Числа 2, 3 - простые */
if(N % 2==0) return 0; /* Четные числа - составные */
/* Проверка делимости на нечетные числа */
for(j=3; j*j<=N; j+=2)
if( N % j==0) return 0; return 1;
Программа 2_21.pas
program prostota;
{ Проверка числа на простоту }
var
М:longint; const
a:array [0..1] of string=('составное','простое');
function prime(N:longint}:byte;
{ Если N - простое, то prime = 1 }
var
j:longint; label ml;
begin
prime:=1;
if N<4 then exit; { Числа 2, 3 - простые }
prime:=0;
if N mod 2=0 then exit; { Четные числа - составные }
j:=3;
{ Проверка делимости на нечетные числа }
ml:
if N mod j=0 then exit;
j:=j+2;
if j*j<=N then goto ml;
prime:=1; end; begin
writeln ('Введите целое число: ');
readln(М);
writeln('Это число - ', a[prime(М)]);
readln; end.
Задание 2.22. Решето Эратосфена
История сохранила память о древнегреческом математике Эратосфене Кипренском, который применил оригинальный алгоритм нахождения всех
простых чисел. На длинном папирусе он выписал числа 2, 3, 4, ... , 1000. Затем, сохранив первое число 2, он проколол каждое второе число, т. е. все четные числа, делящиеся на 2. В следующий раз, пропустив второе, не проколотое число 3, удалил после него каждое третье число, т. е. все числа, делящиеся на 3. Такая же участь постигла и каждое пятое число после 5, каждое седьмое число после 7 и т. д. К концу эксперимента на папирусе остались не проколотыми только простые числа. Возможно, что Эратосфен не догадался вдвое облегчить свою работу и использовать вдвое более короткий папирус, изначально выписав на нем только нечетные, числа. Зато сейчас мы составим программу, которая использует идею Эратосфена и находит все простые числа среди первых maxk нечетных чисел.
Совет 1 (общий)
Совет 2 (Паскаль)
Программа 2_22.bas
DEFINT A-Z CLS
МАХК=500 DIM ISI(MAXK+1)
FOR I=0 ТО МАХК-1: IS1(I)=1: NEXT I
FOR I= 0 TO MAXK IF ISI(I)=l THEN
'если число еще не "проколото"
PRIME=I+I+3: ' сформировали очередное простое число
N=N+1: ' увеличили счетчик простых чисел
PRINT USING "#####";
PRIME; : ' вывод очередного простого числа
K=I+PRIME: ' индекс для первого "прокола"
WHILE К<=МAХК
REM "проколы" чисел, делящихся на
PRIME IS1(K)=0: K=K+PRIME
WEND
END IF
NEXT I
PRINT "Среди первых ";МАХК+1; " нечетных чисел";
PRINT " найдено "; N; " простых"
END
Программа 2_22.с
#include
#include
#define maxk 500
main() {
int pr_num,n=0;
char is[maxk+1];
register int i,k;
clrscr () ;
for(i=0; i<=maxk; i++) is[i]=l; /* все числа "на папирусе" */
for(i=0; i<=maxk; i++)
{if(is[i]==l) /* если число еще не "проколото" */
{ pr_num=i+i+3; /* сформировали очередное простое число */
n++; /* увеличили счетчик простых чисел */
printf("%5d",pr_num); /* вывод очередного простого имела */
k=i+pr num; /* индекс для первого "прокола" */
while (К<:=mахk)
{
/* "проколы" чисел, делящихся на pr_num */
is[k]=0; k+=pr_num;
}
}
}
printf("\nСреди первых %d нечетных чисел", maxk+1);
printf("найдено %d простых", n);
getch();
}
Программа 2_22.pas
program sievel;
uses Crt;
const
maxk=500;
n:integer=0;
var
is: array [0..maxk] of byte;
i,k,prime:integer;
begin clrscr;
for i:=0 to maxk do is[i]:=1; { все числа "на папирусе" }
for i:=0 to maxk do
begin
if is[i]=l then { если число еще не "проколото" }
begin
prime:=i+i+3; { сформировали очередное простое число }
inc(n); { увеличили счетчик простых чисел }
write(prime:5); { вывод очередного простого числа }
k:=i+prime; { индекс для первого "прокола" }
while k<=maxk do
begin { "проколы" чисел, делящихся на pr_num }
is[k]:=0; inc(k,prime); end end; end;
writeln;
write(' Среди первых ',maxk+l, ' нечетных чисел ');
writeln(' найдено ',n,' простых');
readln;
end.
Программа 2_22a.pas
program sieve; uses Crt; const
maxN=255; (не более 255} var
primes: set of 2..maxN;
i,j:integer;
begin clrscr;
primes:=[2..maxN]; { первоначальная роспись папируса }
for i:=2 to maxN do
if i in primes then { если i принадлежит множеству }
begin
write (i:5); { вывод очередного простого числа }
for j : =1 to maxN div i do
primes:=primes-[i*j]; { удаление чисел, кратных i}
end;
readln;
end.
Задание 2.23. Разложение четного числа на сумму простых чисел
В 1742 г. Христиан Гольдбах высказал предположение, что любое четное число можно представить в виде суммы двух простых чисел, а любое нечетное — в виде суммы трех простых чисел. На самом деле, вторая часть утверждения Гольдбаха является следствием первой. Если из нечетного числа вычесть подходящее простое, то остаток будет четным, и как только его удастся разложить на сумму двух простых, первоначальное нечетное число будет равно сумме трех простых чисел. Несмотря на кажущуюся простоту проблемы Гольдбаха, до сих пор ее справедливость ни доказана, ни опровергнута. Более того, в начале 2000 г. английский книгоиздатель Фейбер предложил награду в размере 1 миллиона долларов тому, кто сумеет доказать или опровергнуть предположение Гольдбаха.
Предлагается провести численный эксперимент, который, к сожалению, не претендует на получение объявленной награды. Составим программу, которая находит все возможные разложения числа п на сумму двух простых чисел.
Совет 1 (общий)
разложение найдено. Анализ слагаемых можно организовать с помощью функции prime, построенной в одном из предыдущих заданий. Естественно, что начать перебор можно с k = 2, а затем в качестве первого слагаемого пробовать все нечетные числа, не превосходящие п/2.
Программа 2_23.bas
DECLARE FUNCTION prime!(N&)
REM Разложение четного числа на сумму двух простых CLS
INPUT "Введите четное число: ",М& IF prime (M&-2)=1 THEN
PRINT M&; "=2-f ";M&-2
FOR j&=l TO M&/2 STEP 2
IF prime(j&)=l AND prime (M&-J&)=1 THEN
PRINT M&;"=";j&;"+";M&-j&
END IF
NEXT j& END
FUNCTION prime (N&)
DIM j AS LONG
IF N&<4 THEN GOTO Ml
IF N& MOD 2=0 THEN GOTO MO
FOR j=3 TO SQR(N&)+1 STEP 2
IF N& MOD j=0 THEN GOTO MO
NEXT j
Ml: prime=l: EXIT FUNCTION MO: prime=0
END FUNCTION
Программа 2_23.с
/* Разложение четного числа на сумму двух простых */ tinclude
{
long M,j;
clrscr () ;
printf("\n Введите четное число: ");
scanf("%ld",&M);
if (prime(M-2) ) printf ("%ld== 2+%ld\t",M,M-2) ;
for(j=l; j <= M/2; j+=2)
if(prime(j) && prime(M-j)) printf("!ld=l31d+%ld\t",
M, j, M-j);
getch(); }
int prime(long N) {
long kmax,j;
if(N<4) return 1;
if(N%2==0) return 0;
kmax=sqrt(N)+0.5;
for(j=3; j<=kmax; j+=2)
if(N%j==0) return 0; return 1; }
Программа 2_23.pas
program razlojenie;
{ Разложение четного числа на сумму двух простых }
var
M:longint;
j:integer; label m2;
function prime(N:longint):byte; var
j:longint; label ml; begin
prime:=l;
if N<4 then exit;
prime:=0;
if N mod 2=0 then exit; j:=3;
ml: if N mod j=0 then exit;
J:=J+2;
if j*j<=N then goto ml;
prime:=1; end; begin
write ('Введите четное число: ');
readln(M);
if prime(M-2)=l then writeln(M,'+',M-2);
j:=3; m2:
if (prime(j)=l) and (prime(M-j)=1) then writeln(M,'=',j,'+',M-j);
j:=j+2;
if j< M div 2 then goto m2;
readln; end.
Задание 2.24. Генерация чисел Хэмминга
Числами Хэмминга называются натуральные числа, которые среди своих делителей имеют только степени чисел 2, 3 и 5. Первые 10 упорядоченных по возрастанию чисел Хэмминга образует последовательность 1, 2, 3, 4, 5, 6, 8, 9, 10 и 12. Первому числу этого ряда соответствуют нулевые степени всех сомножителей. Составить программу, которая генерирует первые 1000 чисел Хэмминга.
Совет 1 (общий)
Гораздо более эффективный алгоритм базируется на определении следующего числа Хэмминга по уже построенной последовательности. При этом приходится запоминать, какое из ранее найденных чисел необходимо домножить на 2, какое — на 3 и какое — на 5. Из трех возможных вариантов следует выбирать минимальное произведение. На первом шаге мы знаем единственное число Хэмминга, равное 1, и именно оно может быть умножено на следующем шаге на один из трех возмож-
ных множителей. Минимальное произведение равно 2, и это — второе число Хэмминга. Теперь умножению на 2 должно быть подвергнуто второе число, а умножению на 3 и 5 — пока еще первое. Поэтому на втором шаге минимальное произведение равно 3. После этого умножению на 2 и 3 может быть подвергнуто второе число, а на 5 — пока еще только первое. Одним словом, когда определено минимальное произведение, использованный множитель должен "переместиться" на следующее, уже найденное число Хэмминга.
Совет 2 (общий)
Программа 2_24.bas (оптимальный вариант)
DEFLNG A-Z
DIM Xam(1000)
CLS
Xam(0)=l
PRINT 1,1
FOR J=l TO 999
x2=Xam(k2)*2
x3=Xam(k3)*3
x5=Xam(k5)*5
IF x2<=x3 AND x2<=x5 THEN Xam(J)=x2: k2=k2+l
IF x3<=x2 AND x3<=x5 THEN Xam(J)=x3: k3=k3+l
IF x5<=x2 AND x5<=x3 THEN Xam(J)=x5: k5=k5+l
PRINT USING "###:########## "; J,Xam(J) ;
REM Приостанов после заполнения экрана
IF J MOD 20=0 THEN INPUT A$
NEXT J
END
Программа 2_24.с (оптимальный вариант)
#include
#include
main() (
long Xam[1000], н2, хЗ, к5;
int j;
int k2=0,k3=0,k5=0;
clrscr(); -
Xam[0]-l,-
printf("%4d %9d",l,l);
for(i=i; j<1000; j++) {
x2=Xam[k2]*2; x3=Xam[k3]*3;
x5=Xam[k5]*5;
if(x2<=x3 && x2<=x5)
{Xam[j]=x2; k2++;}
if(x3<=x2 && x3<=x5)
{Xam[j]=x3; k3++;}
if(x5<=x2 && x5<=x3)
{Xam[j]=x5; k5++;}
printf("\n%4d %91d",j,Xam[j]);
if(j % 20==0)
getch(); }
getch (); }
Программа 2_24.pas (оптимальный вариант)
program Hamming;
uses crt;
var
Xam:array[i..1000] of longint;
x2,x3,x5 : longint;
j:integer; const
k2:integer=l;
k3:integer=l;
k5:integer=l; begin
Xam[l]:=1;
writeln(l:4,' ',1:10);
for j:=2 to 1000 do
begin
x2:=Xam[k2]*2;
x3:=Xam[k3]*3;
x5:=Xam[k5]*5;
if(x2<=x3) and (x2<=x5) then
begin
Xam [ j ] : =x2;
inc(k2);
end;
if(x3<=x2) and (x3<=x5) then
begin Xam[j] := x3; inc(k3);
end;
if (x5 <= x2) and (x5 <= x3) then begin Xam[j] := x5; inc(k5);
end;
writeln(j:4,' ',Xam[j]:10);
if (j mod 20)= 0 then readln; end; readln; end.
Программа 2_24a.pas (полный перебор)
program Hammingl;
uses crt,WinDos;
var
j,Hour,Hourl,min,mini,sec,seel,hsec,hsecl : word; i,k : longint;
begin clrscr;
gettime(Hour,min,sec,hsec); i:=l; j:=0; repeat k:=i;
while (k mod 2)=0 do k:=k div 2;
while (k mod 3)=0 do k:=k div 3;
while (k mod 5)=0 do k:=k div 5;
if k=l then begin
{ write(i:10); } {отключение вывода } inc(j);
end; inc(i);
until j>=1000;
gettime (Hourl,min1,secl,hsecl) ;
writeln;
writeln(Hour,':',min,':',sec,'.',hsec);
writeln(Hourl,':',minl,':',seel,'.',hsecl); readln; end.
Задание 2.25. Генерация неправильно сокращаемых дробей
Существует очень мало правильных дробей вида m/n, которые можно привести к несократимой дроби "незаконным" образом — зачеркнув одинаковые цифры в числителе и знаменателе. Например:
26/65 = 2/5.
Построить программу, которая использует заданное ограничение (п < юо) и выводит все дроби, обладающие указанным выше свойством. Тривиальные дроби типа 10/20, 10/30, ... , 20/30, ... , 80/90, ... желательно не генерировать.
Совет 1 (общий)
Программа 2_25.bas
RЕМ Генерация неправильно сокращаемых дробей CLS
RЕМ Двойной цикл по перебору дробей от 10/11 до 98/99
FOR N=11 TO 99 FOR M=10 TO N-1
T=M/N : ' Настоящее значение дроби
Nlo=N MOD 10 : ' Младшая цифра знаменателя
Nhi=(N-Nlo)\10 : ' Старшая цифра знаменателя
Mlo=M MOD 10 : ' Младшая цифра числителя
Mhi=(M-Mlo)\10 : ' Старшая цифра числителя
IF Mlo=0 THEN GOTO 100
КЕМ Анализ различных сочетаний "зачеркиваемых" цифр
IF Nlo=Mlo AND ABS(T-Mhi/Nhi)<.001 THEN PRINT M;"/";N;"=";Mhi;"/";Nhi
END IF
IF Nlo=Mhi AND ABS(T-Mlo/Nhi)<.001 THEN
PRINT M;"/";N;"=";Mlo;"/";Nhi
END IF
IF Nlo<>0 THEN
IF Nhi=Mlo AND ABS(T-Mhi/Nlo)<.001 THEN
PRINT M;"/";N;"=";Mhi;"/";Nlo
END IF
IF Nhi=Mhi AND ABS(T-M1o/Nlo)<.001 THEN
PRINT M;"/";N;"=";Mlo;"/";Nlo
END IF
END IF
100 :
NEXT M NEXT N END
Программа 2_25.с
/* Генерация неправильно сокращаемых дробей */
#include
#include
#include
main() !
char n,m,n_lo,n_hi,m_lo,m_hi; float t; clrscr();
/* Двойной цикл до перебору дробей от 10/11 до 98/99 */ for(n=ll; n<100; п++) for(m=10; m
t=(float)m/n; /* Настоящее значение дроби */
n_lo=n % 10; /* Младшая цифра знаменателя */
n__hi=n/10; /* Старшая цифра знаменателя */
m_lo=m % 10; /* Младшая цифра числителя */
m_hi=m/10; /* Старшая цифра числителя */
if(m % 10 == 0) continue;
/* Анализ различных сочетаний "зачеркиваемых" цифр */
i£(n lo==m lo && n_hi!=0 && fabs (t-m_hi/n_hi) <1.e-3)
printf("\n%d/%d=ld/id",m,n,m_hi,n_hi);
if(n_lo==m_hi && n_hi!=0 && fabs(t-m_lo/n_hi)
printf ("\n%d/%d=%d/%d",m,n,m_lo,n__ni) ;
i£(n hi==m_lo ££ n__lo!=0 ££ fabs(t-m_hi/n_lo)
printf("\n%d/%d=ld/ld",m,n,m_hi,n_lo);
if(n_hi==m_hi && n_lo!=0 && fabs(t-m_lo/n_lo)
printf("\n%d/%d=%d/%d",m,n,m_lo,n_lo); }
getch{); }
Программа 2_25.pas
program drobi;
{Генерация неправильно сокращаемых дробей}
uses crt;
var
n, m, n_lo, n__hi, m_lo, m_hi: byte ; t:real; begin
clrscr;
{ Двойной цикл по перебору дробей от 10/11 до 98/99 } for n:=ll to 99 do for m:=10 to n-1 do begin
t:=m/n; { Настоящее значение дроби }
n_lo:=n mod 10; { Младшая цифра знаменателя }
n_hi:=n div 10; { Старшая цифра знаменателя }
m_lo:=m mod 10; { Младшая цифра числителя }
m_hi:=m div 10; { Старшая цифра числителя }
if m_lo=0 then continue;
{ Анализ различных сочетаний "зачеркиваемых" цифр }
if (n_lo=m_lo) and (n_hi<>0) and (abs(t-m_hi/n_hi)
writeln(m:3, '/',n:2, ' = ',m_hi:l, '/',n_hi) ;
if (n_lo=m_hi) and (n_hi<>0) and (abs(t-m_lo/n_hi)
writeln(m:3,'/',n:2,'=',m_1о:1,'/',njii);
if (n_hi=m_lo) and (n_lo<>0) and (abs(t-m_hi/n_lo)
writeln(m:3,'/',n:2,'=',m_hi:l,'/',n_lo);
if (n_hi=m_hi) and (n__lo<>0) and (abs(t-m_lo/n_lo)
writeln(m:3,'/',n:2,'=',m_lo:1,'/',n_lo); end; readln;
end.
Задание 2.26. Разложение натурального числа на сумму квадратов
Утверждение, принадлежащее Лагранжу, гласит, что любое натуральное число N можно представить в виде суммы не более чем четырех квадратов целых чисел (N = а2 + ь2 + с2 + d2). Составить программу, которая вводит длинное целое число N и находит хотя бы одно такое разложение. О неединственности результата свидетельствует пример: 4 = 22 = 12 + 12 + 12 + 12. Кроме того, существует довольно много прямоугольных треугольников с целочисленными сторонами, которые позволяют заменить сумму квадратов катетов квадратом гипотенузы, а сумму четырех квадратов, следовательно, -суммой трех.
Совет 1 (общий)
a
Совет 2 (общий)
Программа 2_26.bas
RЕМ Разложение числа на сумму квадратов
DECLARE SUB PROBA (Al AS INTEGER, Bl AS INTEGER,Cl AS INTEGER, Dl AS INTEGER,N AS LONG)
INPUT "Введите натуральное число - ", N& IF (N& MOD 2)=0 THEN
REM Если число N - четное
PROBA 0,0,1,1,N&
PROBA 0, 0,0,0,N&
PROBA 1,1,1,1,N& ELBE
REM Если число N - нечетное
PROBA 0,0,0,1,N&
PROBA 0,1,1,1,N& END IF END
SUB PROBA (Al AS INTEGER,Bl AS INTEGER,Cl AS INTEGER,Dl AS INTEGER,N AS LONG)
'Подпрограмма перебора вариантов
Q=INT(SQR{N)+.5) : ' Определение верхней границы
FOR A%=A1 TO Q STEP 2: S1=A%*A%
FOR B%=B1 TO Q STEP 2: S2=S1+B%*B%
FOR C%=C1 TO Q STEP 2: S3=S2+C%*C%
FOR D%=D1 TO Q STEP 2
IF S3+D%*D%=N THEN
PRINT "Искомые слагаемые :"
PRINT "a=";A%,"b=";B%,"c=";C%,"d=";D% END
END IF
NEXT D%: NEXT C%: NEXT B%: NEXT A% END SUB
Программа 2_26.с
/* Разложение числа на сумму квадратов */
#include
#include
#include
void proba(int al,int bl,int cl,int dl,long N) ;
main() {
long N;
printf("\n Введите натуральное число - ");
scanf("%ld",&N);
if((N % 2)==0) /* Если число N - четное */
{
proba(0,0,l,l,N);
proba(0,0,0,0,N);
proba(1,1,1,1,N) ;
}
else /* Если число N - нечетное */
{ proba(0,0,0,l,N);
proba(0,l,l,l,N); } }
void proba(int al,int bl,int cl,int dl,long N)
/* Подпрограмма перебора вариантов */
{ int a,b,c,d,q; long sl,s2,s3;
q=floor(sqrt(N)+.5);
/* Определение верхней границы */
for(a=al; a<=q; a+=2)
{
sl=a*a;
for(b=bl; b<=q; b+=2)
{
s2=sl+b*b;
for(c=cl; c<=q; c+=2)
{
s3=s2+c*c;
for(d=dl; d<=q; d+=2)
if (s3+d*d=N)
{
printf("\n Искомые слагаемые :");
printf("\n a=%d b=%d c=%d d=%d",a,b,c,d);
getch();
exit(0);
}
}
}
}
return;
}
Программа 2_26.pas
program razlojenie;
{ Разложение числаг на сумму квадратов }
var
N:longint;
procedure proba(al,bl,cl,d1:integer; N:longint);
{ Подпрограмма перебора вариантов }
var
a,b,с,d,q:integer; s1,s2,s3:longint;
begin
q:=round(sqrt(N)); {Определение верхней границы }
a:=al;
while a<=q do begin
sl:-a*a,- b:-b1;
while b<=q do begin s2:=sl+b*b;
c:=cl;
while c<=q do begin s3:=s2+c*c;
d:=dl; while d<=q do begin
if(s3+d*d=N) then begin
writeln('Искомые слагаемые :');
writeln('а=',а,' b=',b,' c=',c,' d=',d);
readln;
exit;
end;
inc(d,2);
end; inc(c,2);
end;
inc(b,2);
end; inc(a,2);
end;
end;
begin
write('Введите натуральное число - ');
readln(N);
if odd(N) then begin { Если число N - нечетное }
proba(0,0,0,l,N);
proba(0,1,1,1,N);
end else begin { Если число N - четное }
proba (0, 0,1,1,N) ;
proba(0,0,0,0,N);
proba(1,1,1,1,N);
end;
end.
Задание 2.27. Анализ взаимного расположения точки и треугольника
Составить программу, которая определяет, лежит ли точка с заданными координатами внутри или вне треугольника. В реальности возможны три ситуации: либо точка принадлежит хотя бы одной из сторон (то есть находится на границе треугольника), либо она расположена строго внутри, либо -строго снаружи.
Совет 1 (общий)
Поэтому, если точка р находится строго внутри треугольника две, то точки А и Р находятся в одной полуплоскости по отношению к прямой вс, точки В И Р — в одной полуплоскости по отношению к прямой АС, точки С И Р - в одной полуплоскости по отношению к прямой АВ.
Программа 2_27.bas
RЕМ Анализ взаимного расположения точки и треугольника
DECLARE FUNCTION R!(U!,V!,Ul!,VI!,U2!,V2!)
PRINT "Введи координаты вершин треугольника"
INPUT X1,Y1,X2,Y2,X3,Y3
'XI = 0: Yl = 0: X2 = 0: Y2 = 1: X3 = 1: Y3 = 0
PRINT "Введи координаты точки" INPUT X, Y
IF (R(X,Y,X1,Y1,X2,Y2)*R(X3,Y3,XI,Yl,X2,Y2)>0 AND R(X,Y,X2,Y2,X3,Y3)*R(X1,Y1,X2,Y2,X3,Y3)>0
AND R(X,Y,X1,Y1,X3,Y3)*R(X2,Y2,X1,Y1,X3 Y3)>0) THEN
PRINT "Точка находится внутри треугольника": END
END IF
IF (R(X,Y,X1,Y1,X2,Y2)*R(X3,Y3,X1,Y1,X2,Y2)<0
OR R(X,Y,X2,Y2,X3,Y3)*R(X1,Y1,X2,Y2,X3,Y3)<0
OR R(X,Y,X1,Y1,X3,Y3) *R(X2,Y2,X1.,Y1,X3,Y3)<0) THEN
PRINT "Точка находится вне треугольника": END
END IF
PRINT "Точка принадлежит границе" END
FUNCTION R(U,V,U1,V1,U2,V2)
REM Анализ взаимного расположения точки (U,V) и прямой,
RЕМ проходящей через точки (U1,V1) и (U2,V2)
R=0
IF ((U-U1)*(V2-V1)-(V-V1)*(U2-U1)>0) THENR=1
IF ((U-U1)*(V2-V1)-(V-V1)*(U2-U1)<0) THENR=-1
END FUNCTION
Программа 2_27.c
/* Анализ взаимного расположения точки и треугольника */
#inclucte
#include
int r(float u,float v,float ul,float vl, float u2,float v2);
main () {
float X0,y0,xl,yl,x2,y2,x3,y3;
float k012,k012, k023, k123, K312, k213;
printf("\n Введи координаты вершин треугольника\п");
scanf("%f %f %f %f %f %f",&xl,&yl,&x2,&y2,&x3,&y3);
printf{"\n Введи координаты точки\n");
scanf("%f %f",&x0,&y0);
k012=r(x0,y0,xl,yl,x2,y2);
k312=r(x3,y3,xl,yl,x2,y2);
k023=r(x0,y0,x2,y2,x3,y3);
k123=r(xl,yl,x2,y2,x3,y3);
k013=r(x0,y0,xl,yl,x3,y3);
k213=r(x2,y2,xl,yl,x3,y3);
if(k012*k312>0 && k023*k!23>0 SS k013*k213>0)
{
puts("Точка находится внутри треугольника");
getch();
exit(0);
} if(k012*k312<0 || k023*k123<0 || k013*k213<0)
{
puts("Точка находится вне треугольника"); getch(); exit(O);
}
puts("Точка находится на границе"); getch();
}
/*--------------------------------------*/
int r(float u,float v,float ul,float vl, float u2,float v2)
/* Анализ взаимного расположения точки (U,V) и прямой,
проходящей через точки (U1,V1) и (U2,V2) */
{
float s=(u-ul)*(v2-vl)-(v-vl)*(u2-ul);
if(s>0) return 1;
if(s<0) return -1;
return 0;
}
Программа 2_27.pas
program triangle;
( Анализ взаимного расположения точки и треугольника }
var
Xd,y0,xl,yl,x2,y2,x3,y3:real;
k012, k312,k023,k!23,k013,k213:integer;
function r(u, v,ul, vl,u2, v2:real) :integer;
{ Анализ взаимного расположения точки (U,V) и прямой,
проходящей через точки (U1,V1) и (U2,V2) }
var
s:real;
begin
s: = (u-ul) * (v2-vl)- (v-vl) * (u2-ul) ;
r:=0;
if s>0 then r:=l;
if s<0 then r:=-l;
end;
begin
writeln('Введи координаты вершин треугольника');' readln(xl,yl,х2,у2,хЗ,уЗ);
writeln('Введи координаты точки');
readln(x,у);
k012:=r(x0,y0,xl,yl,x2,y2);
k312:=r(x3,y3,xl,yl,x2,y2);
k023:=r(х0,у0,х2,у2,хЗ,уЗ);
k123:=r(xl,yl,x2,y2,x3,y3);
k013:=r(x0,y0,xl,yl,x3,y3);
k213:=r(х2,у2,х!,у!,хЗ,уЗ);
if (k012*k312>0) and (k023*k!23>0) and (k013*k213>0) then begin
write('Точка находится внутри треугольника');
halt;
end;
if (k012*k312<0) or (k023*k!23<0) or (k013*k213<0) then begin
write ('Точка находится вне треугольника'),' halt; end;
write ('Точка в треугольнике' ) ;
readln;
end.
Задание 2.28. Игра на вычитание
И фа заключается в последовательном вычитании партнерами из числа, находящегося на кону. Программа генерирует случайное число от 50 до 100 и передает ход человеку. Ходят по очереди. За один ход можно вычесть из оставшегося числа от 1 до 9 (в общем случае от 1 до м). Побеждает тот, кто сумеет оставить на кону нулевое число.
Совет 1 (общий)
Программа 2_28.bas
RЕМ Программа игры на вычитание до нуля
DEFINT A-Z
ml:
CLS
RANDOMIZE 32767
N = INT(RND * 25) + 26
PRINT "На кону - "; N; " Брать можно от 1 до 5"
m2:
PRINT "Ваш ход. Сколько берем? - "
m4:
a$ = INKEY$: IF a$ = "" THEN GOTO m4
k = ASC(a$) - 48
IF 1 > k OR k > 5 THEN PRINT "Так ходить нельзя!": GOTO m2
N = N - k
PRINT "После Вашего хода осталось "; N
IF N = О THEN PRINT "Поздравляю! Вы выиграли!": GOTO ex
IF (N MOD 6) = 0 THEN k = 1 ELSE k = N MOD 6
N = N - k
PRINT "Я беру "; k; " остается "; N
IF N = 0 THEN
PRINT "К сожалению, Вы проиграли!": GOTO ex
ELSE
GOTO m2
END IF ex: .,
PRINT "Хотите еще? - (y/n) : "
m3:
a$ = INKEY$: IF a$ = "" THEN GOTO m3
IF a$ = "y" THEN GOTO ml
END
Программа 2_28.с
// Программа игры на вычитание до нуля
#include
#include
#include
void main() { int N,k,j; ml:
clrscr();
randomize();
N=random(25)+26;
printf("Ha кону - %d. Брать можно от 1 до 5.\n",N);
m2:
printf("\n Ваш ход. Сколько берем? - ");
k=getche()-48;
if(l>k || k>5) {printf("\n Так ходить нельзя!"); goto m2;}
N=N-k;
printf("\n После Вашего хода осталось %d",N);
if(N==0){printf("\n Поздравляю! Вы выиграли!");
goto ex;}
k=(N%6=0)?l:N%6;
printf ("\n Я беру %d остается %d",k,N);
if(N==0){printf("\n K сожалению, Вы проиграли!");
goto ex;
}
goto m2;
ex:
printf("ХпХотите еще? - (y/n) : ");
if(getch()=='y') goto ml; )
Программа 2_28.pas
{Программа игры на вычитание до нуля}
program game_mun;
uses Crt;
var
N,k,j:integer; label
ml,m2,ex;
begin ml:
clrscr;
randomize;
N:=random(25)+26;
writeln('Ha кону - ',N,'. Брать можно от 1 до 5.');
m2:
writeln('Bain ход. Сколько берем? - ');
k:=Ord(ReadKey)-48;
if(l>k) or (k>5) then
begin
writeln('TaK ходить нельзя!1); goto m2; end;
N:=N-k;
writeln('После Вашего хода осталось ',N);
if N=0 then
begin writeln('Поздравляю! Вы выиграли!'}; goto ex; end;
if (N mod 6)=0 then k:=l else k:=N mod 6;
N:=N-k;
writeln('Я беру ',k,' остается ',N);
if N=0 then
begin writeln('К сожалению, Вы проиграли!'); goto ex; end;
goto m2; ex:
writeln('Хотите еще? - (y/n) : ');
if ReadKey ='y' then goto ml; end.
Задания 2.29—2.31. Путешествия по узлам целочисленной решетки
Существует довольно много задач, связанных с нумерацией узлов целочисленной решетки. Одна из них известна под названием "скатерти Улама" (Ulam S. М.). Развлекаясь на одном из скучных собраний, Улам пронумеровал по спирали клетки тетрадного листа. Когда он обвел номера клеток, соответствующие простым числам, на листе возник довольно занятный узор, который мог оказаться полезным для изучения закономерностей в числовых последовательностях.
В отличие от Улама мы будем нумеровать не клеточки, а узлы целочисленной решетки, начав эту процедуру с нулевого узла в начале системы координат (рис. 2.1).
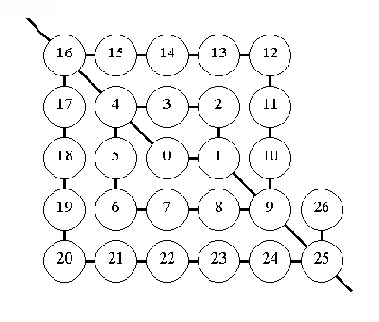
Рис. 2.1. Нумерация точек на скатерти Улама
Одна из наиболее естественных задач заключается в определении координат точки по ее номеру-ы. Конечно, ее решение можно построить на базе прямого перебора всех точек спирали до узла с заданным номером. При этом движение, начинающееся из точки с номером о, состоит сначала из одного шага вправо (x=x+1) и вверх (у=у+1), затем из двух последовательных шагов влево (x=x-1) и вниз (y=y-l), из трех последовательных шагов вправо и вверх, из четырех последовательных шагов влево и вниз и т. д. Однако при достаточно больших значениях N такая процедура требует слишком много времени.
Гораздо интереснее построить более эффективный алгоритм решения задачи. Одна из идей заключается в определении координат угловой точки, расположенной на общей с нашей точкой горизонтальной или вертикальной ветви спирали. Заметим, что на луче, проведенном из начала координат через узлы с координатами (-п,п), располагаются точки с номерами (2*n)2.
На аналогичном луче, начинающемся из первой точки и проходящем через точки с координатами (n,-n+l), расположены точки с номерами (2*n-1)2. Поэтому нам достаточно обнаружить ближайший к N квадрат числа q, чтобы сообразить, на какой из четырех ветвей "спирали" находится точка с номером N. Если q -- четное, то в зависимости от разности qz-N интересующая нас точка находится на верхней или левой ветви. И для вычисления координат достаточно откорректировать одну из координат угловой точки (-q,q) на величину разности. Если q оказалось нечетным, то ветвь, содержащая точку с номером N, находится либо внизу, либо справа. И тогда коррекции надо подвергнуть одну из координат точки (q, -q+1).
Аналогичная идея может быть использована и для обратного преобразования координат заданной точки (х,у) в ее порядковый номер на спирали. Достаточно определить ближайшую угловую точку с коррдинатами (-q, q) или (q,-q+i) и произвести соответствующую коррекцию номера выбранной угловой точки. Несмотря на кажущуюся простоту идеи, ее реализация требует тщательной проверки многочисленных условий.
Обратим внимание на то, что диагональ у=х делит узлы нашей решетки на два множества. Для всех узлов, расположенных слева от диагонали, выполняется условие х > у. Пусть точка с координатами (х,у) расположена либо на горизонтальном витке спирали, находящемся в левой полуплоскости, либо на вертикальном витке, спускающемся до диагонали. Разобьем каждый из этих витков на две части и пронумеруем их следующим образом:
На каждом из этих участков справедливы следующие соотношения:
1 : х > 0, у > 0
2 : х < 0, у > 0, у > |х|
3 : х < 0, у > 0, у < |х|
4 : х < 0, у < 0
Определив принадлежность точки тому или иному участку, мы можем вычислить координаты левого верхнего угла поворота (х0,у0) и найти порядковый номер этого узла N =(2*х0)2. Далее, в зависимости от номера участка, уже не сложно найти номер точки с координатами (х, у).
Аналогичные рассуждения можно повторить и для участков горизонтальной и вертикальной ветвей, принадлежащих правой полуплоскости. В программе для обозначения соответствующих четырех частей использованы буквенные обозначения — а, b, с, d. Для вычисления номера нашей точки здесь используется правый нижний угол поворота.
Ниже приводятся тексты программ, демонстрирующие работу процедуры
coord_to_n.
Программа 2_29.bas
DECiARF, FUNCTION CoordToN! (Х&, Y&)
REM Вычисление номера узла по его координатам
INPUT "Введите координаты узла : ", Х&, Y&
М& = CoordToN(X&, Y&)
PRINT "Его номер = "; М&
END
FUNCTION CoordToN (XS, Y&)
IF X& <= Y& THEN 'если узел в левой полуплоскости
IF Х& >= 0 AND Y& > 0 THEN GOTO m12 'случай 1
IF Х& < 0 AND Y& >= 0 AND Y& >= ABS(X&) THEN 'случай 2
'обработка случаев 1 и 2
m12:
х0 = -Y&: у0 = Y&: N& = (2 * х0)^2'координаты и номер угла
CoordToN = N& + х0 - Х&: EXIT FUNCTION
ELSE
'обработка случаев 3 и 4
х0 = Х&: у0 = -XS: N& = (2 * х0)^2 CoordToN = N& + у0 - Y&:
EXIT FUNCTION
END IF
END IF ' если узел в правой полуплоскости
IF X& <= 0 AND Y& < 0 THEN GOTO mab' случай а
IF x& >= 0 AND'YS < 0 AND ABS
mab: х0 = -Y& +1: Y0 = -Y&: N& = (2 * хО - 1) ^2
CoordToN = N& - хО + Х&: EXIT
FUNCTION ELSE
'обработка случаев с, d
х0 = Х&: у0 = -Х& + 1: N& = (2 * х0 - 1) ^ 2
CoordToN = N& + YS - у0
END IF
END FUNCTION
Программа 2_29.с
#include
#include
#include
long sqr(long x);
long coord_to_n(long x,long y);
void main() { long x,y,M;
printf("\n Введите координаты узла : ");
scanf("%ld %ld",Sx,&y);
M=coord to n(x,y); .
printf("\nEro номер = %ld",M);
getch(); }
long coord_to_n(long x,long y) { long N,x0,y0;
if(x<=y) //если узел в левой полуплоскости
{
if(х>=0 && у>0) goto m12; //случай 1
if(x<0 && y>=0 && y>=labs(x)) //случай 2 {//обработка случаев 1 и 2
ml2:
х0=-у;
у0=у;
N=sqr(2*хО); //координаты и номер угла
return N+x0-x; } //обработка случаев 3 и 4
х0=х; у0=-х; N=sqr(2*х0); return N+y0-y; }
//если узел в правой полуплоскости
if(х<=0 && у<0) goto mab; //случай 2
if(x>=0 && у<0 && labs(y)>=x) //случай 3
{//обработка случаев 1, 2
mab:
x0=-y+l;
y0=-y;
N=sqr(2*х0-1);
return N-x0+x;
} //обработка случаев 3, 4
х0=х;
у0=-х+1;
N=sqr(2*x0-l);
return N+y-y0;
long sqr(long x)
{ return x*x; }
Программа 2_29.pas
program CoordToN;
var
M,x,y:longint;
function coord_to_n(x,y:longint}:longint;
var
x0,y0,N:longint;
label ml2,mab;
begin
if x<=y then { если узел в левой полуплоскости }
begin if (x>=0) and(y>0) then goto m!2; { случай 1 }
if (x<0) and (y>=0) and (y>=abs(x)) then { случай 2 }
begin { обработка случаев 1 и 2 }
m12: x0:=-y; y0:=y; N:=sqr(2*x0); { координаты и номер угла }
coord__to_n: = N+xO-x; exit;
end;
{ обработка случаев З и 4 }
x0:=x; y0:=-x; N:=sqr(2*x0);
coord_to_n:=N+yO-y; exit;
end;
{ если узел в правой полуплоскости }
if(x<=0) and (y<0) then goto mab; { случай а }
if(x>=0) and (y<0) and (abs(y)>=x) then { случай b }
begin { обработка случаев a, b }
mab: x0:=-y+l; y0:=-y; N:=sqr(2*x0-l);
coord_to_n:= N-xO+x; exit;
end;
{ обработка случаев с, d }
x0:=x; y0:=-x+l; N:=sqr(2*xO-l);
coord_to_n:= N+y-y0;
end;
begin
writeln('Введите координаты узла : ');
readln(x,у);
м.=toord_to_a(x,y);
writeln ('Его номер = \М);
readln;
end.
На базе процедур n_to_coord и coord_to_N можно построить Программы определения расстояния между точками с номерами NI и N2, нахождения номеров ближайших соседей к точке с номером N и т. п.
Программа 2_30.bas
DECLARE SUB NtoCoord (N&, X&, YS)
REM Определение расстояния между двумя точками
INPUT "Введи номер первой точки : ", N&
NtoCoord N&, xl&, yl&
INPUT "Введи номер второй точки : ", N&
NtoCoord N&, х2&, у2&
dx = xl& - x2&: dy = yl& - у2&
PRINT "Расстояние = ", SQR(dx * dx + dy * dy)
END
SUB NtoCoord (N&, X&, Y&)
DIM k AS LONG, j AS LONG, d AS LONG
j = INT(SQR(N&) + .5)
d = N& - j * j
k = j \ 2
PRINT "j="; j, "d="; d, "k="; k
IF (j MOD 2) О О THEN
IF d > 0 THEN
X& = k + 1: Y& = -k + d
ELSE
X& = k + 1 + d: Y& = -k
END IF
ELSE
IF d > 0 THEN
X& = -k: Y& = k - d
ELSE
X& = -k - d: Y& = k
END IF
END IF
END SUB
Программа 2_30.с
//Определение расстояния между двумя точками
#include
#include
#include
void n_to_coord(long N, long *x, long *y) ;
void main()
{ long N,xl,yl,x2,y2;
double dx,dy;
printf("\ n Введи номер первой точки : ");
scanf("%ld",&N);
n_to_coord(N,Sxl, &yl);
printf("\n Введи номер второй точки : ");
scanf("%ld",&N);
n_to_coord(N,&x2,&y2) ;
dx=xl-x2; dy=yl-y2;
printf("ХпРасстояние = %f",sqrt(dx*dx + dy*dy));
getch();
}
void n_to_coord(long N,long *x,long *y)
( long k,j,d;
j=floor(sqrt(N)+0.5);
d=N-j*j; k=j / 2;
if (j % 2)
{ if (d>0) { *x=k+l; *y=-k+d; }
else { *x=k+l+d;*y=-k; }
}
else
{ if (d>0) { *x=-k; *y=k-d; }
else { *x=-k-d; *y=k; )
}
}
Программа 2_30.pas
program spiral;
var
xl, yl, x2,y2,N:longint;
dx, dy: double;
procedure n_to_coord(N:longint;var x,y:longint);
var
k,j,d:longint;
begin
}
j:=trunc(sqrt(NJ+0.5) ;
d:=N-sqr(j);
k:=j div 2; if odd(j) then begin
if d>0 then begin x:=k+l; y:=-k+d;end else begin x:=k+l+d; y:=-k; end; end
else if d>0 then begin x:=-k; y:=k-d; end else begin x:=-k-d; y:=k; end; end; begin
writeln('Введи номер первой точки'); readln(N);
n_to_coord(N,xl,yl); writeln('Введи номер второй точки'); readln(N);
n_to_coord(N,x2, у2); dx:=xl-x2; dy:=yl-y2;
writeln('Расстояние = ',sqrt(dx*dx + dy*dy)); readln; end.
Вторая схема нумерации точек целочисленной решетки, расположенной в первом квадранте, заключается в движении по раскручивающейся диагонали (рис. 2.2).
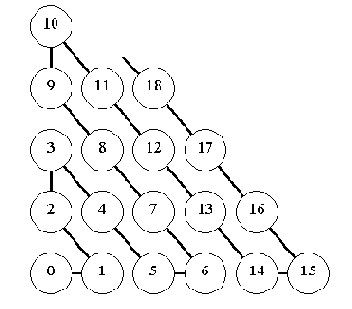
Рис. 2.2. Нумерация точек по диагоналям
Базовые процедуры по-прежнему сводятся к установлению прямых и обратных связей между координатами точек и их номерами. Пронумеруем диагонали в порядке их удаления от начала координат — 0, 1, 2, ... В качестве нулевой "диагонали" будем рассматривать вырожденный отрезок, содержащий единственную точку с номером о. Очевидно, что на диагонали с номером k находится k+1 точек, удовлетворяющих уравнению соответствующей прямой:
X + у = b(k) .
Заметим, что на диагоналях с нечетными номерами номера точек возрастают при движении снизу вверх, а на диагоналях с четными номерами — при движении сверху вниз. Осталось только подметить закономерность между номером диагонали, ее уравнением и координатами начальной и конечной точек. В этом нам поможет анализ табл. 2.1.
Таблица 2.1. Закономерность между номером диагонали, ее уравнением
и координатами начальной и конечной точек
Номер Номера начальной диагонали и конечной точек |
Координаты начальной и конечной точек |
|||||
nDiag |
nBeg |
nEnd |
(хВеg, уВеg) |
(xEnd, yEnd) |
||
0 |
0 |
0 |
(0,0) |
(0,0) |
||
1 |
1 |
2 |
(1,0) |
(0,1) |
||
2 |
3 |
5 |
(0,2) |
(2,0) |
||
3 |
6 |
9 |
(3,0) |
(0,3) |
||
4 |
10 |
14 |
(0,4) |
(4,0) |
||
5 |
15 |
20 |
(5,0) |
(0,5) |
||
6 |
21 |
27 |
(0,6) |
(6,0) |
||
7 |
28 |
35 |
(7,0) |
(0,7) |
||
8 |
36 |
44 |
(0,8) |
(8,0) |
||
9 |
45 |
54 |
(9,0) |
(0,9) |
||
10 |
55 |
65 |
(0,10) |
(10,0) |
||
По содержимому табл. 2.1 можно установить следующие факты:
nEnd = nBeg + nDiag nBeg(nDiag-t-l) = nEnd(nDiag) + 1
Если nDiag -- четное, то координаты начальной точки — (0, nDiag) и при перемещении по диагонали х уменьшается, а у возрастает. В противном случае начальная точка имеет координаты (noiag, 0) и при перемещении по диагонали х возрастает, а у уменьшается.
Ниже приводятся тексты программ, определяющие номера смежных точек для точки с заданным номером. Для уменьшения количества передаваемых параметров характеристики диагонали вынесены в глобальные переменные.
Массивы dx и dy предназначены для определения координат смежных точек, количество которых может варьироваться от трех (для точки с номером 0) или пяти (для начальной и конечной точек диагонали) до восьми (в случае внутренних точек). Анализ того, какая из восьми возможных точек является допустимой, вынесен в процедуру nextpoint. Она проверяет принадлежность точки первому квадранту, восстанавливает по координатам порядковый номер допустимой точки и выводит его на экран.
Программа 2_31.bas
DECLARE SUB NEXTPOINT (X&, Y&)
DIM nDiag AS LONG 'номер диагонали
DIM xBeg AS LONG, yBeg AS LONG 'начальная точка на диагонали
DIM nPoints AS LONG 'количество точек на диагонали
DIM nBeg AS LONG 'номер начальной точки на диагонали
DIM dx(8), dy(S)
DATA -1,-1,-1,0,1,1/ 1/ 0
FOR J = 0 TO 7: READ dx(J): NEXT J
DATA -1, 0, 1,1,1,0,-1,-1
FOR J = 0 TO 7: READ dy(J): NEXT J
ml:
CLS
INPUT "Введите номер точки: ", N КЕМ Определение параметров диагонали
nBeg = 0: М = N: хВед = 0: уВеg = 0
FOR k = 0 ТО 200000000
М = М - k
IF М < 0 THEN EXIT FOR
nBeg = nBeg + k NEXT k
nDiag = k - 1: nPoints = k
IF (nDiag MOD 2) = 0 THEN 'диагональ с четным номером
yBeg = nDiag xN = xBeg + (N - nBeg) yN = yBeg - (N - nBeg)
ELSE 'диагональ с нечетным номером
xBeg = nDiag
xN = xBeg - (N - nBeg)
yN = yBeg + (N - nBeg) END IF
PRINT "Номера смежных точек: "
FOR k = 0 ТО 7
X& = xN + dx(k)
Y& = yN + dy(k)
NEXTPOINT X&, Y& NEXT k PRINT
PRINT "Хотите повторить - (y/n) : ";
m2:
A$ = INKEY$: IF A$ = "" THEN GOTO m2
IF A$ = "y" THEN GOTO m1 END
SUB NEXTPOINT (X&, Y&)
SHARED nDiag AS LONG, xBeg AS LONG, yBeg AS LONG, nPoints AS LONG
DIM N AS LONG, J AS INTEGER
IF X& < 0 OR Y& < 0 THEN EXIT SUB
nBeg = 0: nDiag = X& + Y&: xBeg = yBeg = 0
nPoints = nDiag + 1
FOR J = 0 TO nPoints - 1: nBeg = nBeg + J: NEXT J
IF (nDiag MOD 2) = 0 THEN
yBeg = nDiag: N = nBeg + yBeg - Y&
ELSE
xBeg = nDiag: N = nBeg + xBeg - X&
END IF
PRINT N; ",";
END SUB
Программа 2_31.с
#include
#include
void nextpoint(long x,long y) ;
int dx[8]={-l,-l,-l,0,l,l, 1, 0};
int dy[8]={-l, 0, 1,1,1,0,-!,-!};
long nDiag, //номер диагонали
xBeg,yBeg, //координаты начальной точки на диагонали nPoints, //количество точек на диагонали nBeg; //номер начальной точки на диагонали
void main() { long N,M,
xN,yN, //координаты введенной точки x,y,k; clrscr (); m:
printf("\n\n Введите номер точки: "} ; scanf("%ld",&N);
//Определение параметров диагонали nBeg=0; M=N;
хВед=уВед=0;
for(k=0;;k++)
{ M=M-k;
if(M<0) break; nBeg=nBeg+k; }
nDiag=k-l; nPoints=k;
if((nDiag % 2)=0) //диагональ с четным номером { yBeg= nDiag; xN=xBeg+(N-nBeg); yN=yBeg-(N-nBeg);
)
else //диагональ с нечетным номером
{ xBeg=nDiag;
xN=xBeg-(N-nBeg); yN=yBeg+(N-nBeg); }
printf("Номера смежных точек:\n" ); for(k=0;k<8;k++) { x = xN + dx[k]; у = yN + dy [k] ; nextpoint(x,y); }
printf("ХпХотите повторить - (y/n) : ");
if(getch(}=='у'} goto m; }
void nextpoint(long x,long y) { long N;
if(x<0||y<0) return;
nBeg=0;
nDiag=x+y;
xBeg=yBeg=0;
nPoints=nDiag+l;
for fint j=0;j
if((nDiag % 2)==0) { yBeg=nDiag; N=nBeg+yBeg-y;}
else { xBeg=nDiag; N=nBeg+xBeg-x; }
printf("%ld ",N);
}
Программа 2_31.pas
program spirall;
uses Crt;
label ml;
var
nDiag, {номер диагонали}
xBeg,yBeg, ( координаты начальной точки на диагонали}
nPoints, {количество точек на диагонали}
nBeg, {номер начальной точки на диагонали}
N,M,
xN,yN, {координаты введенной точки}
х,у,k: longint; const
dx : array [0..7] of integer =(-1,-1,-1,0,1,1, 1, 0);
dy : array [0..7] of integer =(-1, 0, 1,1,1,0,-1,-1);
procedure nextpoint(x,y:longint);
var
N: longint ,-
j. integer/" begin
if (x>=0)and(y>=0) then
bey in nBeg:=0; nDiag;=x+y; xseg:=0;
yBeg:=0;
nPoints:=nDiag+l;
for j:=0 to nPoints-1 do nBeg:=nBeg+j;
if ((nDiag mod 2)=0) then begin
yBeg:=nDiag; N:=nBeg+yBeg-y; end
else begin
xBeg:=nDiag; N:=nBeg+xBeg-x; end;
write(N,', ') ; end; end; begin
clrscr; ml:
write('Введите номер точки: ');
readln(N);
{ Определение параметров диагонали }
nBeg:=0;
M:=N;
xBeg:=0;
yBeg:=0;
k:=0;
repeat
M:=M-k;
if M<0 then break; nBeg:---nBeg+k;
k:=k+l;
until k<0; nDiag:=k-l;
nPoints:=k;
if(nDiag mod 2)=0 then {диагональ с четным номером} begin
yBeg:=nDiag;
xN:=xBeg+(N-nBeg) ;
yN:=yBeg-(N-nBeg) ; end
else {диагональ с нечетным номером}
begin
xBeg:=nDiag; xN:=xBeg-(N-nBeg) ;
yN:=yBeg+(N-nBeg) ; end;
writeln('Номера смежных точек : ');
for k:=0 to 7 do begin
x := xN + dx[k]; у := yN + dy[k]; nextpoint(x,y);
end;
writeln;
writeln('Хотите повторить - (y/n) : ');
if ReadKey='y' then goto ml;
end.
Символьные данные и их внутреннее представление
Обработка фрагментов строк
Под фрагментом строки понимают цепочку символов заданной длины, выделенную из исходной строки, начиная с указанной позиции. В частности, выделяемый фрагмент может состоять и из единственного символа. Кроме выделения фрагмента тем или иным способом к числу наиболее распространенных операций относятся действия по определению длины строки, объединению (конкатенации) символьных цепочек и поиску вхождения одной строки в другую.
В QBasic для выделения фрагментов используют системные функции LEFT? (выделение левой подстроки), RIGHTS (выделение правой подстроки) и MID$ (выделение внутренней подстроки). Последняя функция может выступать и в роли оператора, заменяющего старый фрагмент новым значением. Например:
LЕFТ$("Вася",1) 'выделяет "В"
LЕFТ$("Вася",2) 'выделяет "Ва"
RIGHT$("Вася",1) 'выделяет "я"
RIGHT?("Вася",2) 'выделяет "ся"
MID$("Вася",2,2) 'выделяет "ас"
MID$("Вася",3)="илиса" 'заменяет на "Василиса"
Функция (оператор) MID$ позволяет опустить третий аргумент, и тогда в соответствующей операции участвуют все конечные символы, начиная с ука-занного. В операторе MID$ присваиваемое значение может быть пустым, что эквивалентно удалению фрагмента.
В Паскале для выделения подстроки используется функция сору, аналогичная функции мю$:
s2 := copy('Вася',2,3); {выделяется 'ася'}
Для удаления или вставки фрагмента здесь используются процедуры delete
И insert: delete(s1,start,len);{удаляется len символов, начиная с позиции start} insert(s1,s2,start);{в строку s2, начиная с позиции start, вставляется строка s1}
Функции работы со строками в Си включены в состав заголовочного файла string.h. Для копирования строки или ее части в другую здесь можно воспользоваться одной из следующих функций:
strcpy(s1,s2); //копирует строку s2 в строку s1
strncpy(s1,s2,n); //копирует первые п символов из строки s2 в s1
Задавая аргумент-источник не ссылкой на начало символьного массива, а адресом любого его элемента, мы можем скопировать либо правую, либо среднюю подстроку:
strcpy(s1, &s2[k]); // копирует правую подстроку из s2 в s1
strncpy(s1, &s[2],n); //копирует среднюю подстроку из s2 в s1
Длина строк в рассматриваемых системах программирования определяется одной из системных функций LEN (QBasic), Length (Паскаль) или strlen (Си). Единственным аргументом у каждой из них является анализируемая строка.
Для конкатенации (объединения) строк в Паскале и QBasic используется довольно естественная операция сложения:
А$="Здравствуй, "+NAME$+"!" s1:='3дравствуй, '+nаmе+'!'
В Си эта операция реализуется с помощью одной из следующих функций:
strcat(s1, s2); //добавляет s2 к s1
strncat(s1, s2, n); //добавляет и первых символов из s2 к s1
Поиск вхождения одной строки в другую дает ответ на вопрос, содержится ли значение одного текста в другом и с какой позиции обнаружено это вхождение. Нулевая позиция в качестве результата такой операции соответствует отрицательному ответу.
Функция, определяющая в QBasic, входит ли значение строки А2$ в строку А1$, имеет вид:
INTSR(A1$,A2$) или INSTR(k,Al$,А2$)
В первом случае анализ вхождения ведется с начала строки AI$, во втором случае — начиная с k-й позиции строки AI$. Последний вариант позволяет последовательно определить все вхождения искомого образца.
Примерно такими же возможностями обладает функция pos(si,s2) в Паскале. Для поиска повторного вхождения можно удалить уже исследованный фрагмент и снова обратиться к функции роз.
Гораздо более разнообразные варианты поиска вхождений предлагает Си:
strstr (s1,s2); //ищет вхождение строки s2 в s1
strchr(s1,с); //ищет вхождение символа "с" с начала строки s1
strrchr(s1,с); //ищет вхождение символа "с" с конца строки s1
strpbrk(s1,s2); //ищет вхождение любого символа из s2 в s1
strspn(s1,s2); //ищет вхождение любого фрагмента, составленного
//из символов s2 в s1
Символьные данные и их внутреннее представление
Символьная (текстовая) информация — самый простой тип данных с точки зрения его представления в памяти ЭВМ. Каждому символу текста в памяти соответствует байт с 8-разрядным кодом этого символа в том или ином стандарте. Буквам латинского алфавита, цифрам, знакам операций и различным разделителям (скобки, точки, запятые и т. п.) в некотором смысле повезло больше, т. к. их кодировка практически универсальна. Она предложена фирмой IBM и составляет первую половину большинства 8-разрядных кодировочных таблиц, используемых в разных странах. В терминологии IBM PC такие таблицы принято называть кодовыми страницами. Вторая половина кодовых страниц отведена под национальную символику.
В отечественной практике чаще всего приходится иметь дело либо с символикой MS-DOS в стандарте ASCII (American Standard Code for Information Interchange), либо с одной из кодовых страниц ANSI (American National Standard Institute), применяемых в среде Windows. Между этими таблицами существует принципиальное различие, связанное с кодировкой букв русского алфавита.
В таблице ASCII (кодовая страница 866) заглавные русские буквы начинаются со 128-й позиции. Вплотную вслед за ними располагается цепочка строчных букв от буквы а (код — 160) до буквы п (код — 175). Далее следуют символы псевдографики, используемые для формирования таблиц с одинарными и двойными линиями (диапазон кодов от 176 до 223). Начиная с 224-й позиции располагаются остальные буквы от р до я. И наконец, вслед за ними, выбиваясь из алфавитного порядка, размещены буквы Ё (код -240) и ё (код — 241).
В таблице ANSI (кодовая страница 1251) коды русских букв начинаются с позиции 192 (код буквы А) и расположены сплошным интервалом до 255-й позиции (код буквы я). Символы псевдографики в графической оболочке Windows смысла не имеют и поэтому в таблице ANSI отсутствуют. Буквы Ё и ё здесь тоже не включены в общепринятую алфавитную последовательность и имеют, соответственно, коды 168 и 184. Более того, их обозначение на большинстве русифицированных клавиатур отсутствует, и для включения таких букв в набираемый текст приходится нажимать самую левую клавишу в верхнем ряду (на латинском регистре этой клавише соответствует символ "~").
Все достаточно развитые алгоритмические языки включают серию процедур по обработке символьных (каждый объект — отдельный символ) и строковых (цепочки символов) данных. В системе QBasic текстовые данные находятся в символьных переменных, имена которых либо заканчиваются знаком $, либо начинаются с одной из букв, упомянутых в объявлении вида DEFSTR c-J, либо описаны в операторе DIM сочетанием ...AS STRING. Базовым текстовым элементом в Си являются объекты типа char, значением каждого их которых является единственный символ. Объединение таких объектов в одномерный массив позволяет работать с цепочками символов. Паскаль обеспечивает работу как с одиночными символами (данные типа char), так и с их последовательностями (данные типа string).
Каждый из рассматриваемых языков обеспечивает возможность доступа к отдельному символу строки.
В Си это вытекает из способа представления текстовой информации. Начальное присвоение (char name [5]="Вася";) или копирование одной строки в другую (strcpy (name, "Вася");) эквивалентно 5 обычным операторам присваивания:
name[0] = 'B' ;
name[1]='а';
name[ 2 ] ='с' ;
name[ 3 ] ='я' ;
name[4]='\0';
Паскаль позволяет одновременно обращаться и к переменной типа string целиком и к отдельным ее символам как к значениям элементов одномерного массива:
const
name : string[4]='Вася';
writeln(name[l], name);
Байт с нулевым индексом используется в Паскале для хранения информации о длине текущего значения.
С точки зрения внутреннего представления текстовых данных в памяти ЭВМ в языках программирования преобладают два похода. В первом случае перед цепочкой символов располагается один (Паскаль) или два (QBasic) байта, в которых хранится общее количество символов — длина цепочки. Для неинициированных данных она обычно равна 0. Во втором случае (Си) вслед за цепочкой символов располагается байт с признаком конца текста (обычно это — нулевой код). Первый подход более прост с точки зрения программирования соответствующих процедур обработки строк. Однако он накладывает ограничение на максимальную длину строкового объекта, например, в Паскале длина строки не должна превышать 255 символов. Для преодоления этого недостатка и обеспечения совместимости по данным с другими системами программирования в последних версиях Паскаля были введены объекты типа pchar.
Сравнение и сортировка текстовых данных
Операции сравнения отдельных символов или строк основаны на последовательном анализе отношений числовых значений соответствующих кодов. В кодовых страницах символы букв упорядочены в соответствии с их расположением в латинском или национальном алфавитах. Поэтому код буквы А меньше кода буквы F, код буквы г меньше кода буквы ю и т. д.
Некоторое неудобство вызывает тот факт, что одноименные заглавные и строчные буквы имеют разные коды — в одной клетке кодировочной таблицы можно разместить только один символ, кроме того, заглавные и строчные буквы имеют разный смысл. Это не позволяет напрямую упорядочить слова в соответствии с их лексикографическим расположением в словарях. Поэтому приходится предварительно заменять коды всех малых букв в тексте на коды больших (или наоборот) и только после этого выполнять операцию сравнения. Такая замена для букв латинского алфавита особых проблем не представляет, т. к. смещение между кодами соответствующих заглавных и строчных букв — величина постоянная. А ьот с русскими буквами приходится поооэнтьсл — D кодировке ASCII цепочка строчной буко между пир разорвана символами псевдографики, а буквы вне вообще находятся "не на своих местах.
Учитывая эту специфику, следует достаточно внимательно использовать языковые средства, связанные с преобразованием или игнорированием разницы в кодировке заглавных и строчных букв. Для русскоязычных текстов их применять нельзя.
QBasic позволяет преобразовывать содержимое символьных строк к верхнему (UCASE$(A$>) или нижнему (LCASE$(A$)) регистру. В Паскале имеется только одна функция upCase (с), заменяющая строчную букву заглавной. Но коды символов, не принадлежащих множеству букв латинского алфавита, она оставляет без изменения. Такая же оговорка распространяется на функции strupr(s) Hstrlwr(s) В Си.
В Паскале и QBasic операции сравнения символьных данных ничем не отличаются от аналогичных операций над числовыми величинами:
RЕМ Упорядочение слов по "возрастанию"
IF A$>B$ THEN
ТМР$=А$ : A$=BS : В$=ТМР$
END IF
или
{Упорядочение слов по "убыванию"}
if s1
begin
tmp:=sl;
sl:=s2;
s2:=tmp;
end;
Для сравнения строк Си предлагает довольно много системных функций, но не забывайте, что их действие не всегда допустимо над русскими словами. Каждая из описываемых ниже функций принимает положительное значение, если ее первый операнд строго "больше" второго, нулевое значение при "равенстве" операндов, и отрицательное значение, если первый операнд оказался "меньше".
strcmp(s1,s2); //сравнивает строки s1 и s2
strcmpi(s1,s2); //сравнивает s1 и s2 с игнорированием
//разницы между большими и малыми буквами
stricmp(s1,s2); //эквивалентна функции strcmpi
strncmp(s1,s2,k); //сравнивает первые k символов в s1 и s2
strncmpi(s1,s2,k); //сравнивает первые k символов в s1 и s2
//с игнорированием разницы между большими
//и малыми буквами
strnicmp(s1,s2,k); //эквивалентна функции strncmpi
Управление цветом в текстовом режиме
Наиболее важная информация, которую можно почерпнуть из многочисленных источников (книги, руководства по системам программирования, файлы помощи), сводится к трем следующим фактам:
Самый распространенный текстовый режим допускает отображение в цвете 25 строк, каждая из которых содержит по 80 символов. При этом объем соответствующей страницы видеопамяти равен 4000 байт и каждый символ, отображаемый на экране, в принципе, может иметь индивидуальные цветовые характеристики, не зависящие от цветовой гаммы в соседних позициях.
В любом руководстве приводится следующее описание формата байта цветовых атрибутов:
7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | ||||||||||
В | b | b | b | I | f | f | f | ||||||||||
Самый старший бит управляет режимом мерцания символа, которое осуществляется аппаратным способом примерно с частотой 1 раз в секунду при B=1. Три следующих бита (ььь) представляют код цветности фона, который должен принадлежать интервалу [0, 7]. Четверка младших битов (Ifff) определяет код цветности переднего плана. Среди них особо выделяют бит I, единичное значение которого обычно соответствует повышенной яркости, т. е. цвету, сопровождаемому приставкой "ярко" или "светло".
Из сказанного выше следует, что стандартный текстовый режим на цветном мониторе позволяет задавать для каждого символа один из 8-ми фоновых оттенков и один из 16-ти цветов, выделяющих контур символа. А если вы хотите вывести мерцающий текст, то байты атрибутов соответствующих символов должны быть увеличены на 128.
Управление содержимым байта цветовых атрибутов осуществляется с помощью одной или нескольких системных процедур (операторов), действие которых распространяется на все последующие операции вывода до новой переустановки характеристик цветности.
В Си и Паскале код цветности символов задается с помощью процедуры textcoior (fc). Значение фонового цвета изменяется процедурой textbackground(bc). В этих же системах программирования существует и более универсальная процедура textattr, позволяющая за одно обращение изменить оба цвета и установить признак мерцания:
textattr(В + bc*16 + fc);
Следует отметить, что при работе с мониторами SVGA сравнительно давно разработанные системы Borland C++ 3.1 и Turbo Pascal 7.0 не очень точно следуют ограничениям, вытекающим из структуры байта цветовых атрибутов. В указанных выше процедурах вы можете задавать цвет фона из диапазона [0, 15], а эффект мерцания символов может и не наблюдаться.
Кроме того, в Си для вывода разноцветного текста следует использовать не стандартную функцию вывода printf, а функцию cprintf, использующую "прямое" обращение к видеопамяти.
Система QBasic абсолютно точно придерживается описанного выше формата цветовых атрибутов и управляет значениями соответствующих характеристик с помощью оператора COLOR:
COLOR fc, be
Для вывода мерцающего текста к коду цветности символа fc (o
Ввод и вывод текстовой информации
Наиболее простые средства ввода символьных и строковых данных предлагают Паскаль и QBasic. Здесь достаточно указать в списке ввода имя переменной соответствующего типа:
INPUT A$
ИЛИ
var
c1:char;
s1:string;
readln(cl);
readln(s1);
В Си имеется довольно много возможностей для ввода одиночных символов и цепочек строк. Форматный ввод с помощью функции scanf использует для этой цели два спецификатора:
"%s" - при вводе строковых значений в массив типа char; "%с" - при вводе одиночных символов в переменную типа char. Например:
char c1,s1l[80];
scanf("%c",&c1l); // не забывайте указывать адрес переменной
scanf("%s",s1); // имя массива одновременно является адресом
Ввод символьных и строковых данных завершается после нажатия клавиши
Конечно, такой способ ввода может доставить неприятности и привести к непредусмотренному продолжению работы программы. Понятно также, что для ввода одного символа не хочется нажимать две клавиши, а вводимые строки могут состоять и из нескольких слов. Поэтому ввод символьных данных лучше выполнять с помощью других процедур:
int c1;
c1=getch(); //Ввод кода нажатой клавиши без отображения
//соответствующего символа на экране
c1=getche(); //Ввод кода нажатой клавиши с соответствующего
//символа на экране
c1=getchar(); // Ввод кода нажатой клавиши вслед за нажатием
//клавиши Enter
Обратите внимание на то, что вводимый символ передается не в переменную типа char, а в двухбайтовую целочисленную переменную. Именно такие значения возвращают указанные выше функции. Вторая особенность их применения связана с разбиением клавиатуры на две категории клавиш — отображаемые и управляющие. Окраска клавиш не совсем точно передает принадлежность клавиши той или иной группе. Например, функциональные клавиши
Дело в том, что при нажатии обычной клавиши в буфер входного потока (stdin) поступает единственный байт с ненулевым кодом. Именно он и извлекается при первом же обращении к одной из функций getch, getchar или getche. От нажатия управляющих клавиш в буфер stdin поступают два байта, первый из которых содержит нулевой код, а второй представляет уже собственно числовой код, соответствующий выбранной клавише. Для извлечения второго байта к этим функциям приходится обращаться повторно, и таким образом программа может проанализировать сложившуюся ситуацию.
Есть некоторые нюансы и при нажатии клавиши
одном случае, что поступил признак конца файла (end-of-file) с кодом 26, а в другом — что встретился признак EOF, которому соответствует числовой код — 1. Функция getchar не позволяет ввести код клавиши
Зато с функций gets, осуществляющей ввод строки, у вас никаких проблем не возникнет:
gets (s);
Вы можете набирать любые предложения, содержащие любое количество пробелов, и все они будут введены в строку s. Однако длина вводимой строки ограничена емкостью буфера (128 байт).
Дополнительные возможности по вводу текстовых данных связаны с использованием потоков:
#include
char c1, s1[80];
cin >> c1;
cin >> s1;
С выводом символьных и строковых значений все обстоит гораздо проще. В Паскале и QBasic достаточно в списке выводимых значений указать данные соответствующего типа:
PRINT А$,"Вася"
или
var
cl:char;
si:string;
writeln (c1, s1, .'Вася') ;
Форматный вывод в Си при помощи функции printf использует указанные выше спецификаторы, однако константные текстовые данные, которыми перемежаются выводимые значения, здесь располагаются между спецификаторами формата:
printf("%с Вася %s",c1,s1);
Вывод отдельного символа или одиночной строки в Си можно выполнить и c помощью
putchar (c1)
и
puts (s1)
Выводимое значение обычно располагается на экране, начиная с текущей позиции курсора. Если необходимо разместить текст в заранее предусмотренном месте, следует прибегнуть к одной из служебных процедур предварительного перемещения курсора в заданную позицию:
LOCATE col, row 'Так это выглядит на QBasicgotoxy(col,row);
// А так делается на Си и Паскале
Параметр col задает номер колонки в диапазоне от 1 до 80, а второй аргумент (row) определяет номер строки в диапазоне от 1 до 25.
Еще один способ управления по размещению текста связан с заданием ширины поля, отведенного под выводимое значение. Отображаемый текст, при этом прижимается к правой границе поля. Ширина поля в Паскале задается числовым выражением, которое записывается в операторе вывода через" двоеточие вслед за выводимым текстовым значением:
writelnt'Вася':10,c1:k+5,s1:7);
В QBasic для указания ширины поля используется оператор PRINT USING:
PRINT USING "##### ### #######";"Вася",А$,В$
В Си ширина поля включается в спецификатор формата ("%3с %10s"). Однако здесь имеется дополнительная возможность указать, что выводимое значение требуется прижать к левой границе выделенного поля ("%-Зс" %-10s").
Сформировать на экране таблицу ASCII
Задание 3.01. Формирование таблицы ASCII
Сформировать на экране таблицу ASCII таким образом, чтобы в ней были представлены все отображаемые символы 866-й кодовой страницы и их числовые коды. Один из возможных вариантов заполнения экрана такой таблицей представлен на рис. 3.1.
Совет 1 (общий)

Рис. 3.1. Таблица ASCII
Программа 3_01.bas
RЕМ Вывод таблицы ASCII
CLS : PRINT TAB(31); "Таблица ASCII"
FOR I=32 TO 52: LOCATE I-29,1
FOR J=I TO 255 STEP 21
PRINT USING "! ### ";CHR$(J);J;
NEXT J
NEXT I
Программа 3_01.с
/* Вывод таблицы ASCII */
#include
main() {
int i,j;
clrscr ();
gotoxy(31,1);
printf("Таблица ASCII");
for (i=32; i<=52; i++) {
gotoxy(1,i —2 9) ;
for (j=i; j<=255; j+=21)
printf("%c %3d ",j,j);
} getch();
}
Программа 3_01.pas
program ASCII; {Вывод таблицы ASCII} uses Crt; var
i,j:word; begin clrscr;
gotoxy(31,1);
write('Таблица ASCII');
for i:=32 to 52 do
begin
gotoxy(l,i-29);
j:=i;
repeat
write(chr(j) :l,j:4, ' ');
j:=j+21;
until j>255;
end;
readln;
end.
Задание 3.02. Преобразование строк к верхнему регистру
Составить подпрограмму (функцию) up (s), которая заменяет в строке s коды малых букв кодами аналогичных больших букв с учетом их расположения в таблице ASCII.
Совет 1 (общий)
По этой же таблице можно установить, что смещения в кодах между выделенными группами малых букв и их прописными эквивалентами, соответственно, равны 32, 32, 80 и 1 позициям.
Совет 2 (QBasic)
В приводимых ниже двух вариантах программы преобразование к верхнему регистру выполнено в виде подпрограммы UP и функции UP$. Чтобы не портить аргумент функции и другие глобальные переменные головной программы, в теле функции объявлены свои локальные переменные в и j.
Совет 3 (Си)
Совет 4 (Паскаль)
Программа 3_02.bas
REM Замена малых русских букв большими
DECLARE SUB UP (A$)
PRINT "Введите строку, содержащую малые и большие буквы"
INPUT "",A$
UP A$
PRINT A$ END
SUB UP(A$)
FOR j=l TO LEN(A$)
SELECT CASE MID$(A$,j,l)
CASE "a" TO "z": MID$(A$,j,1)=CHR$(ASC(MID$(A$, j , 1) )-32)
CASE "a" TO "n": MID$(A$,j,l)=CHR$(ASC(MID$(A$,j,l))-32)
CASE "p" TO "я": MID$(A$,j,1)=CHR$(ASC(MID$(A$,j,1))-90)
CASE "e": MID$(A$,j,l)="E"
END SELECT
NEXT j
END SUB
Программа 3_02a.bas
RЕМ Замена малых русских букв большими
DECLARE FUNCTION UP$(A$)
PRINT "Введите строку, содержащую малые и большие буквы"
INPUT "",A$
B$=UP$(A$)
PRINT A$
PRINT B$
END
FUNCTION UP$(A$)
'Чтобы не испортить аргумент А$, введена локальная переменная
DIM В AS STRING
В=А$
FOR J=l TO LEN(A$)
SELECT CASE MID$(В,J,1)
CASE "a" TO "z": MID$ (B, J, 1) =CHR$ (ASC (MID$ (B, J, 1) )-32)
CASE "a" TO "n": MID$ (B, J, 1)=CHR$ (ASC (MID$ (B, J, 1) ) -32)
CASE "p" TO "я": MID$(B,J,1)=CHR$(ASC(MID$(B,J,1))-80)
CASE "e": MID$(B,J,1)="E"
END SELECT
NEXT J
UP$=B
END FUNCTION
Программа 3_02.с
/* Замена малых русских букв большими */
# include
#include
#include
char *up(char *a);
void main() {
char a[80],*b;
printf("\n Введите строку, содержащую малые и большие буквы\n");
gets(a);
b=up(а);
printf("\na=%s",a);
printf("\nb=%s",b);
getch (); }
char *up(char *a) {
unsigned char b[80]; int j ;
strcpy(b,a);
for(j=0; j
if ( 97<=b[j] && b[j]<=122) b[j]-=32;
if (160<=b[j] && b[j]<=175) b[j]-=32;
if (224<=b[j] && b[j]<=239) b[j]-=80;
if (241==b[j]) b[j]— ; }
return b; }
Программа 3_02.pas
program UperCase;
{ Замена малых русских букв большими }
var
a,b>:string[80] ; function up(a:string):string; var
j:integer;
begin
for j:=1 to length(a) do
case a[j] of
'a1..'z': a[j] :=chr (ord (a [ j ] )-32) ;
'a'.,'n'; a[j]:=chr(ord(a[j])-32);
'р'.'я': a[j]:=chr(ord(a[j])-80);
'ё': a[j]:='Ё'; end;
up:=a; end; begin
writeln('Введите строку, содержащую малые и большие буквы ');
readln(a);
b:=uр(а);
writeln(a);
writeln(b);
readln;
end.
Задание 3.03. Сортировка-фамилий
Составить программу, которая запрашивает у пользователя 10 фамилий, сортирует их по алфавиту и выводит отсортированный список. Пока сортируемый массив мал, мы не будем обращать внимание на эффективность алгоритма сортировки. Один из следующих разделов специально будет посвящен этому достаточно сложному и важному вопросу.
Так как программа должна сортировать фамилии, то следует установить правила их набора на клавиатуре, исключающие неоднозначность результатов сравнений:
Такие правила позволят вам не обращать внимания на различие между кодами больших и малых букв, т. к. сравниваться между собой, как правило, будут буквы одного регистра, коды которых соответствуют лексикографическому порядку. Коды инициалов и символы-разделители (точки, пробелы, тире) в таблице ASCII расположены раныпе кодов малых букв и поэтому на результаты сравнений не повлияют.
Совет 1 (общий)
Совет 2 (QBasic)
Совет 3 (Си)
В программе 3_03а. с для размещения фамилий использованы динамически запрашиваемые строки, на начало которых "смотрят" элементы массива указателей типа char (см. обращение к функции malloc). Вместо перестановки фамилий, расположенных не в алфавитном порядке, меняются местами соответствующие 4-байтовые указатели.
Перевод курсора в начало очередной строки списка осуществляется функцией gotoxy (col, row), последовательность параметров которой прямо противоположна соответствующему оператору QBasic.
Программа 3_03b!с построена менее замысловато. В ней использован двумерный массив для хранения фамилий, да и вывод результатов оформлен попроще.
Программа 3_03.bas
RЕМ Сортировка фамилий DIM NAMES(10)
N=10
CLS
FOR J=l TO 10
INPUT "Введи очередную фамилию - ", NAMES(J)
NEXT J CLS
PRINT "Фамилии до упорядочения : " FOR J=l TO N
LOCATE J+2,1: PRINT NAMES(J)
NEXT J
FOR J=l TO N-l
FOR K=J+1 TO N
IF NAME$(J)>NAME$(K) THEN
TMP$=NAME$(J)
NAME$(J)=NAME$(K)
NAMES(K)=TMP$
END IF
NEXT К
NEXT J
LOCATE 1,40
PRINT "Фамилии после упорядочения :"
FOR J=l TO N
LOCATE J+2,40: PRINT NAME$(J)
NEXT J
END
Программа 3_03а.с
/* Сортировка фамилий */
#include
#include
#include
#include
main()
{
#define n_max 10
#define len_max 20
int j,k;
char tmp[len_max], *names[n_max], *p;
clrscr();
for(j=0; j< n_max; j++) {
printf("\n Введи очередную фамилию - ");
scanf("%s",tmp);
names[j]=(char *)malloc(len_max);
strcpy(names[j],tmp); }
clrscr () ;
printf("Фамилии до упорядочения :");
for(j=0; j
gotoxyd, j+2) ;
printf("%s",names[j]); }
for(j=0; j
if (strcmp(names[j],names[k]) > 0} {
p=names[j];
names[j]=names[k] ;
names[k]=p; } }
gotoxy(40,1);
printf("Фамилии после упорядочения :");
for(j=0; j
gotoxy(40,j+2);
printf("%s",names[j]) ; }
getch(); }
Программа 3_03b.c
/* Сортировка фамилий */
#include
#include
#include
#define N 10
main () {
cnar a[N][20],tmp[20];
int i,j; Clrscr () ;
puts(" Введите 10 фамилий по одной в строке");
for(i=0; i
gets(&a[i][0]);
for(1=0; i
if(strcmp(&a[i] [0], &a[j] [0])>0) {
strcpy(tmp,&a[i][0]);
strcpy(&a[i][0],&a[j][0]);
strcpy(&a[j][0],tmp); }
puts("А теперь они же по алфавиту");
for (1=0; i
puts(&a[i][0]);
getch(); }
Программа 3_03.pas
program sort;
{ Сортировка фамилий }
uses crt;
const
n=10; var
j,k:integer; tmp:string[20];
name:array [l..n] of string[20];
begin cirscr;
for j:=1 to n do begin
writeln('Введи очередную фамилию');
readln(name[j]); end;
clrscr;
writeln('Фамилии до упорядочения :');
for j :=1 to n do
begin
gotoxy(1,j+2);
write(name[j]);
end;
for j:=1 to n-1 do
{
for k:=j+l to n do
begin
if name[j]>name[k] then
begin
tmp:=name [j];
name[j]:=name[k];
name[k]:=tmp;
end
end;
gotoxy(40,l);
writeln('Фамилии после упорядочения :');
for j:=1 to n do
begin
gotoxy (40,j+2);
write(name[j]);
end;
readln;
end.
Задание 3.04. Подсчет числа слов в строке
Предполагая, что вводимая строка содержит не более 80-ти символов и состоит из "слов", разделенных одним или более пробелами, подсчитать количество слов в строке. Обратите внимание на критические ситуации — строка пуста, строка состоит из одних пробелов, строка содержит единственное слово, слова могут содержать единственный символ, отличный от пробела.
Совет 1 (общий)
Программа 3_04.bas
RЕМ Подсчет числа слов в строке
CLS
SPACE=1: WORDS=0
PRINT "Введите строку"
INPUT "",S$
LENS=LEN(S$)
IF LENS=0 THEN GOTO RET
IF LEFT$(S$,1)<>" " THEN SPACE=0: WORDS=1
FOR J=2 TO LENS
IF SPACE=1 AND MID$(S$,J,1)<>" " THEN SPACE=0: WORDS=WORDS+1
IF SPACE=0 AND MID$(S$,J,1)=" " THEN SPACE=1
NEXT J
RET:
PRINT "Число слов в строке = "; WORDS
END
Программа 3_04.с
/* Подсчет числа слов в строке */
#include
#include
#include
main() {
char s[81], space=l, words=0, i,len;
clrscr ();
puts("Введите строку");
gets (s) ;
len=strlen(s);
if (len=0) goto ret;
if (s[0]!=' ') {
space=0;
words=l; }
for(i=l; i
if (space==l &&, s[i]! = ' ') {
space=0; words++; }
if (space==0 && s[i]==' ')space=l; } ret:
printf("\n Число слов в строке = %d",words);
getch () ; }
Программа 3_04.pas
program num_words;
{ Подсчет числа слов в строке }
label ret;
var
s:string[81];
space:boolean;
words:byte;
i,len:byte; begin
writeln('Введите строку');
readln(s);
len:=length(s);
if len=0 then goto ret;
space:=(s[1]=' ');
if not space then words:=1;
for i:=2 to len do
begin
if (not space)and(s[i]=' ') then space:=true;
if (space)and(s[i]<>' ') then
Degin
space;=false; inc(words);
end;
end;
ret:
writeln('Число слов в строке = ',words);
readln;
end.
Задание 3.05. Анализ нажатой клавиши
Составить программу, которая анализирует код нажатой клавиши и выводит его на экран. Программа должна завершать свою работу после нажатия клавиши
Совет 1 (общий)
Совет 2 (QBasic)
Совет 3 (Си)
Совет 4 (Паскаль)
Программа 3_05.bas
RЕМ Анализ кода нажатой клавиши CLS
GETKEY: A$=INKEY$: IF A$="" THEN GOTO GETKEY
IF ASC(A$)=27 THEN STOP
IF LEN(A$)=1 THEN
IF ASC(A$)=13 THEN
PRINT "Нажата клавиша Enter с кодом = 13": GOTO GETKEY
END IF
PRINT "Нажата обычная клавиша ' "; A$; " ' с кодом ="; ASC(A$)
ELSE
PRINT "Нажата управляющая клавиша с кодом ";ASC(RIGHT$(A$,1))
END IF
GOTO GETKEY
Программа 3_05.с
/* Анализ кода нажатой клавиши */ #include
main() { unsigned char ch;
clrscr(); getkey:
ch=getch();
if(ch==27) exit(0);
if(ch==13) {
printf("\n Нажата клавиша Enter с кодом = 13");
goto getkey; }
if(ch==0) {
ch=getch();
printf("\n Нажата управляющая клавиша с кодом = %d",ch); }
else printf("\n Нажата обычная клавиша %с с кодом=%d",ch,ch);
goto getkey;
}
Программа 3_05.pas
program keyboard;
( Анализ кода нажатой клавиши }
uses Crt;
label getkey;
var
ch:char;
begin
clrscr; getkey:
ch:=readkey;
if ord(ch)=27 then exit;
if ord(ch)=13 then
begin
writeln('Нажата обычная клавиша Enter с кодом = 13');
goto getkey;
end;
if ord(ch)=0 then
begin
ch:=readkey;
writeln('Нажата управляющая клавиша с кодом = ',ord(ch));
end else
writeln('Нажата обычная клавиша "',ch,'" с кодом=',ord(ch));
goto getkey; end.
Программа 3_05a.pas
program keyboard;
{ Анализ кода нажатой клавиши }
uses Crt;
var
ch:char; begin clrscr; repeat
ch:=readkey;
if ord(ch)=13 then
writeln('Нажата обычная клавиша Enter с кодом =13') else
if ord(ch)=0 then
begin
ch:=readkey;
writeln { 'Нажата управляющая клавиша с кодом = ' ,ord(ch) } ;
end else
writeln('Нажата обычная клавиша "',ch,'" с кодом = ',ord(ch});
until ord(ch)=27;
end.
Задание 3.06. Три цвета радуги
Мнемоническая фраза " Каждый охотник желает знать, где сидят фазаны" используется для запоминания последовательности цветовых оттенков радуги — красный, оранжевый, желтый, зеленый, голубой, синий, фиолетовый. Составить программу, которая вводит три слова, представляющие разные цвета радуги, и выводит их на экран в том порядке, в каком они должны быть расположены в описанной выше цветовой гамме. Например, введены слова желтый, красный и синий. На экран их следует вывести в "правильном" порядке — красный, желтый, синий.
Совет 1 (общий)
Программа 3_06.bas
REM Упорядочение цветов радуги
DATA "красный","оранжевый","желтый","зеленый"
DATA "голубой","синий","фиолетовый"
DIM А$ (7) , В$ (3)
FOR I=0 ТО 6: READ A$(I): NEXT I
PRINT "Введите по одному в строке 3 цвета радуги"
FOR I=0 ТО 2: INPUT B$ (I): NEXT I
PRINT "В радуге эти цвета следуют в таком порядке:"
FOR J=0 TO 6: FOR I=0 TO 2
IF A$(J)=B$(I) THEN PRINT A$(J)
NEXT I: NEXT J
END
Программа 3_06.c
/* Упорядочение цветов радуги */
#include
#include
#include
{
char a[7][11]={"красный","оранжевый",
"желтый","зеленый","голубой","синий","фиолетовый"};
char b[3][11]; int i,j;
printf("\n Введите по одному в строке 3 цвета радуги\n");
for (i=0; КЗ; i++) gets (&b[i] [0] ) ;
printf("\ nB радуге эти цвета следуют в таком порядке:\n");
for(j=0; j<7; j++) for(i=0; i<3; i++)
if(strcmp(&a[j][0],&b[i][0])==0)
puts(&a[j][0]); getch(); }
Программа 3_06.pas
program raduga;
{ Упорядочение цветов радуги }
const
a:array [1..7] of string[10]=('красный','оранжевый',
' желтый', ' зеленый', ' голубой', ' синий', ' фиолетовый') ;
var
b:array [1..3] of string[10];
i,j:byte; begin
writeln('Введите по одному в строке 3 цвета радуги');
for i:=l to 3 do readln(b[i]);
writeln('В радуге эти цвета следуют в таком порядке:');
for j:=1 to 7 do
for i:=l to 3 do
if a[j]=b[i] then writeln(a[j]);
readln;
end.
Задание 3.07. Левый и правый прижим, центрирование текста при выводе
Составить программу, которая запрашивает у пользователя текст, содержащий не более 20-ти символов, и выводит его в рамках колонки, расположенной с 10-й по 50-ю позиции с разными вариантами прижима. Для контроля правильности работы программы можно ограничиться вводом единственного символа и выдачей на экран строки, маркирующей номера колонок.
Совет 1 (QBasic)
Совет 2 (Си, Паскаль)
Программа 3_07.bas
CLS
PRINT "Введите строку, содержащую не более 20 символов"
FOR I = 1 ТО 8: PRINT "1234567890"; : NEXT I
INPUT "", A$
PRINT "Вывод, начиная с 10-й позиции :"
FOR I = 1 ТО 8: PRINT "1234567890"; : NEXT I
PRINT TAB(10); A$
PRINT "Вывод по центру между 10-й и 50-й позициями :"
FOR I = 1 ТО 8: PRINT "1234567890"; : NEXT I
PRINT TAB(10 + (50 - 10) / 2 - LEN(A$) / 2); A$
PRINT "Вывод с прижимом к 50-й позиции :"
FOR I = 1 ТО 8: PRINT "1234567890"; : NEXT I
PRINT TAB(51 - LEN(A$)); A$
END
Программа 3_07.с
#include
#include
#include
main()
{
char str[20], rule [] ="1234567890";
int i;
clrscr () ;
puts(" Введите строку, содержащую не более 20 символов");
for(i=0; i<8; i++)
printf("%s",rule);
gets (str) ;
puts("Вывод, начиная с 10-й позиции :");
for(i=0; i<8; i++) printf("%s",rule);
gotoxy(10,wherey()); puts (str) ;
puts("Вывод по центру между 10-й и 50-й позициями :");
for(i=0; i<8; i++) printf("%s",rule);
gotoxy(10+(50-10)/2-strlen(str)/2,wherey());
puts(str);
puts("Вывод с прижимом к 50-й позиции :");
for (i=0; i<8; i++) printf("%s", rule);
gotoxy(51-strlen(str),wherey());
puts(str);
getch(); }
Программа 3_07.pas
program text_justify;
uses Crt;
const
rule:string='1234567890'; var
s:string[20];
i:integer; begin
clrscr;
writeln('Введите строку, содержащую не более 20 символов');
for i:=0 to 7 do write(rule);
readln(s);
writeln('Вывод, начиная с 10-й позиции :');
for i:=0 to 7 do write(rule);
gotoxy(10,wherey); writeln(s);
writeln('Вывод по центру между 10-й и 50-й позициями :');
for i:=0 to 7 do write(rule);
#include
main() {
char str[20], rule[]="1234567890";
int i ;
clrscr();
puts("Введите строку, содержащую не более 20 символов");
for(i=0; i<8; i++)
printf("%s",rule);
gets (str) ;
puts("Вывод, начиная с 10-й позиции :");
for(i=0; i<8; i++) printf("%s",rule);
gotoxy(10,wherey()); puts (str) ;
puts("Вывод по центру между 10-й и 50-й позициями :");
for (i=0; i<8; i++) printf("%s",rule);
gotoxy(10+(50-10)/2-strlen(str)/2,wherey());
puts(str); puts("Вывод с прижимом к 50-й позиции :");
for (i=0; i<8; i++)
printf("%s",rule);
gotoxy(51-strlen(str),wherey());
puts(str);
getch(); }
Программа 3_07.pas
program text justify;
uses Crt;
const
rule:string='1234567890'; var
s:string[20];
i:integer; begin
clrscr;
writeln(' Введите строку, содержащую не более 20 символов');
for i:=0 to 7 do write(rule);
readln(s);
writeln('Вывод, начиная с 10-й позиции :');
for i:=0 to 7 do write(rule);
gotoxy(10,wherey); writeln(s);
writeln('Вывод по центру между 10-й и 50-й позициями :');
for i:=0 to 7 do write(rule);
gotoxy(10+(50-10) div 2 - length(s) div 2,wherey);
writeln(s); writeln{'Вывод с прижимом к 50-й позиции :');
for i:=0 to 7 do write(rule);
gotoxy(51-length(s),wherey);
writeln(s);
readln; end.
Задание 3.08. Сравнение строк с игнорированием пробелов
Написать подпрограмму-функцию compare, имеющую своими аргументами две строки, которая сравнивает их, игнорируя пробелы между словами и разницу между кодами больших и малых букв. Функция должна возвращать следующие значения: 1, если первая строка "больше" второй; -1, если первая строка "меньше" второй; о, если обе строки равны.
Совет 1 (общий)
Программа 3_08.bas
REM Сравнение строк с игнорированием пробелов
DECLARE SUB UP(A$)
DECLARE FUNCTION COMPARE(B$, C$)
PRINT "Введите первую строку"
INPUT "",A1$
PRINT "Введите вторую строку"
INPUT "", A2$
K=COMPARE(A1$,A2$)
IF K=l THEN PRINT "Первая строка 'больше'"
IF K=-l THEN PRINT "Первая строка 'меньше'"
IF K=G THEN PRINT "Обе строки равны"
END
FUNCTION COMPARE(B$,C$) DIM B1$,C1$
UP B$: UP C$
FOR J=l TO LEN(B$)
IF MID$ (B$, J, 1)<>" " THEN B1$=B1$+MID$ (B$,J, 1 )
NEXT J
FOR J=l TO LEN(C$)
IF MID$(C$,J,1)<>" " THEN C1$=C1$+MID$(C$,J,1) NEXT J
IF B1$>C1$ THEN COMPARE=1 IF B1$=C1$ THEN COMPARE=0
IF B1$
SUB UP(A$)
FOR J=l TO LEN(A$)
SELECT CASE MID$(A$,J,1)
CASE "a" TO "z": MID$ (A$, J, 1) =CHR$ (ASC (MID$ (A$, J, 1) )-32)
CASE "a" TO "n": MID$(A$,J,1)=CHR$(ASC(MID$(A$,J,1))-32)
CASE "p" TO "я": MID$(A$,J,1)=CHR$(ASC(MID$(A$,J,1))-80)
CASE "ё": MID$(A$,J,1)="Ё" END SELECT
NEXT J
END SUB
Программа 3_08.с
/* Сравнение строк с игнорированием пробелов */
#include
#include
#include
char *up(char *a);
int compare(char *s1, char *s2);
void main() {
char s1[80],s2[80];
puts("Введите первую строку");
gets (s1);
puts("Введите вторую строку");
gets(s2);
switch(compare(s1,s2)) {
case 1: puts("Первая строка 'больше'");break;
case -1: puts("Первая строка 'меньше'");break;
case 0: puts("Обе строки равны");
}
getch(); }
char *up(char *a)
{
/* Замена кодов малых букв кодами больших */
static unsigned char b[80]; int j ;
strcpy (b, a) ;
for(j=0; j
if(97<=b[j] && b[j]<=122) b[j]-=32;
if(160<=b[j] && b[j]<=175) b[j]-=32;
if (224<=b[j] && b[j]<=239) b[j]-=80;
if (241==b[j]) b[j]—; }
return b; }
int compare(char *s1,char *s2) {
char ssl[80],ss2[80]; char j,k;
strcpy(s1,up(s1)};
/* Замена малых букв большими */
strcpy (s2*, up (s2) );
/* с записью на то же место */
for(j=0,k=0; j
if (sl[j] != ' ') ssl[k++]=sl[j];
/* Извлекаем непробелы */
ssl[k]=0x0; /* Добавили признак конца */
for(j=0,k=0;
j
if(s2[j]!=' ') ss2[k++]=s2[j];
ss2[k]=0x0;
k=atrcmp(ss1.ss2) /* Cравнили преобразованные строки */
if(k>0)return 1;
if(k<0)return 1;
return 0;
}
Программа 3_08.pas
program comp_string;
{ Сравнение строк с игнорированием пробелов }
var
s1,s2:string;
function up (a:string):string; var
j:integer; begin
for j:=l to length(a) do
case a[j] of
'a'..'z': a[j] :=chr(ord(a[j])-32) ;
'a'..'n': a[j]:= chr(ord(a[j])-32} ;
'р'..'я': a[j]:= chr(ord(a[j])-80} ;
'ё': a[j]:='E'; end; up:=a; end;
function compare(s1,s2:string):integer;
var
ssl,ss2:string; j:byte;
begin
sl:=up(s1);
s2:=up(s2);
ssl:=' ';
for j:=l to length(s1) do
if sl[j]<>' ' then ssl:=ssl+sl[j];
ss2:=' ';
for j:=l to length(s2) do
if s2[j]<>' ' then ss2:=ss2+s2[j];
compare:=0;
if ssl>ss2 then compare:=1;
if ssl
begin
writeln('Введите первую строку');
readln(s1);
writeln('Введите вторую строку');
readln(s2);
case compare(s1,s2) of
1: writeln('Первая строка "больше"');
-1: writeln('Первая строка "меньше"');
0: writeln('06e строки равны');
end;
readln;
end.
Задание 3.09. Разноцветный текст
Написать программу, которая выводит на экран текст, меняя цвет букв и цвет фона.
Совет 1 (общий)
Программа 3_09.bas
RЕМ Разноцветный текст А$ = "ПРОГРАММИРОВАНИЕ"
CLS
' Отображение разноцветных букв на допустимой фоновой гамме
FOR CF=0 TO 7
FOR CS=0 TO 15
COLOR CS,CF LOCATE CF+1,2*CF+CS+1
PRINT MID$(A$,CS+1,1)
NEXT CS
NEXT CF
'Отображение мигающих разноцветных букв
FOR CF=0 TO 7
FOR CS=0 TO 15
COLOR CS+16,CF
LOCATE CF+1,2*CF+CS+41
PRINT MID$(A$,CS+1,1)
NEXT CS
NEXT CF
Программа 3_09.с
/* Разноцветный текст */
#include
main() {
int i ;
textbackground(0);
clrscr () ;
for(i=0; i<24; i++) {
gotoxy(2*i+l,i+l);
textcolor(128+i);
textbackground(i+2);
cprintf("Цветовая гамма в текстовом режиме"); }
getch(); }
Программа 3_09а.с
/* Разноцветный текст */
#include
main() {
int i;
textbackground(0) ;
clrscr();
for(i=0; i<24; i++) {
gotoxy(2*i+l,i+1);
textattr(128+i + ((i+1) « 4));
cprintf("Цветовая гамма в текстовом режиме");
}
getch (); }
Программа 3_09.pas
program colorl;
{ Разноцветный текст }
uses crt;
var
i:integer; begin
textbackground(0); clrscr;
for i:=0 to 23 do
begin
gotoxy(2*i+l,i+l);
textcolor(128+i);
textbackground(i+l);
writeln('Тест цветовой гаммы ');
end;
readln;
end.
Задание 3.10. Преобразование обычной дроби в десятичную
Составить функцию символьного (строкового) типа, преобразующую два своих целочисленных аргумента — числитель m и знаменатель п правильной дроби (m < n < 100) в строку, представляющую запись десятичной дроби. Для бесконечной дроби период следует заключить в круглые скобки. Например:
m=3 n=5 значение функции - "0.6"
m=1 n=6 значение функции - "0.1(6)"
Совет 1 (общий)
Совет 2 (Си)
Программа 3_10.bas
RЕМ Преобразование обычной дроби в десятичную
DECLARE FUNCTION FRAC2STR$(M%, N%)
CLS : DEFINT A-Z
INPUT "Введите числитель и знаменатель дроби : ",M,N
PRINT M;"/";N;"= ";FRAC2STR$(M,N)
END
DEFSNG A-Z
FUNCTION FRAC2STR$(M AS INTEGER,N AS INTEGER)
DIM S AS STRING, REST(100) AS INTEGER
DEFINT A-Z
I=3: S="0."
DO
Q=M*10\N : P=M*10 MOD N: REST(I)=P
IF P=0 THEN
FRAC2STR=S+CHR$(Q+48) EXIT FUNCTION
END IF
FOR J=3 TO 1-1
IF REST(J)=P THEN
FRAC2STR=LEFT$(S, J-l}+"("+RIGHT$(S,LEN(S)-J+l)+")"
EXIT FUNCTION
END IF
NEXT J
S=S+CHR$(Q+48): I=1+1: M=P LOOP UNTIL P=0
END FUNCTION
Программа 3_10.с
/* Преобразование обычной дроби в десятичную */
#include
#include
char *frac_to_str(char m,char n);
main() {
char m,n;
printf("\n Введите числитель и знаменатель дроби : ");
scanf("%d %d",sm,&n) ;
printf("\n%d/%d=%s",m,n,frac_to_str(m,n));
getch();
}
/ *-----------------------------------------------* /
char *frac_to_str(char m,char n) {
int i=2,j,p,q;
char rest[100];
static char s [100]="0.";
do {
q=m*10/n; p=m*10%n; rest[i]=p;
if(p==0) { s[i]=q+48;
s[i+l]=0x0;
return s; }
for(j=2; j
for(p=i; p>=j; p--)
s[p+l]=s[p];
s[j]='(';
s[i+l]=')';
s [i+2]=0x0 ;
return s ; }
s[i]=q+48;
i++;
m=p; }
while (p!=0); }
Программа 3_10.pas
program drobi;
{ Преобразование обычной дроби в десятичную }
var
m, n:byte;
function frac_to_str(m,n:byte):string;
var
i,j,p,q:word;
s:string;
rest:array [1..100] of byte;
begin
s:='0.';
i:=l;
repeat
q:=m*10 div n;
p:=m*10 mod n;
rest[i]:=p;
if p=0 then begin
frac_to_str:==s+chr (q+48) ;
exit;
end;
for j:=l to i-1 do
if p=rest[j] then
begin insert(' (',s,j+2); frac_to_str:=s+')';
exit;
end;
inc(i);
s:=s+chr(q+48);
m:=p;
until p=0;
end;
begin
writeln('Введите числитель и знаменатель дроби :');
readln(m,n);
writeln(m,'/',n, ' = ', frac_to_str(m,n));
readln; end.
Задание 3.11. Перевод чисел в римскую систему счисления
Составить функцию символьного (строкового) типа, аргументом которой является натуральное число из интервала [1, 3999]. Функция должна возвращать строку с эквивалентным значением в формате римской системы счисления. Напомним, что в римской системе счисления используются большие латинские буквы — M(1000), O (500), C(100), L (50), X(10), V(5) и I(1). Если меньшая "цифра" находится левее "большей", то она вычитается (например: IV == V-I = 4, IX= X- I= 9, XL = L - X- 40). Если меньшая "цифра" расположена правее, то она прибавляется (например: VI = = V+ I= б, XI = X+ I= I I, LX = L + X = 60). Для некоторых "цифр" римская система допускает наличие до трех идущих подряд одинаковых
цифр —
I I= I + I = 2,
I I I = I + I+ I= 3,
XXX = X + X + X = 30,
ССС == C+ C+ C= 300,
MMM = M+ M+ M + 3000.
Совет 1 (общий)
Таблица 3.1. Расположение массива в порядке убывания числовых названий
Индекс элемента |
Символьный массив |
Числовой массив |
||
0 |
M |
1000 |
||
1 |
CM |
900 |
||
2 |
D |
500 |
||
3 |
CD |
400 |
||
4 |
С |
100 |
||
5 |
ХС |
90 |
||
6 |
L |
50 |
||
7 |
XL |
40 |
||
8 |
X |
10 |
||
9 |
IX |
9 |
||
10 |
V |
5 |
||
11 |
IV |
4 |
||
12 |
I |
1 |
||
Начинаем вычитать из переводимого числа первый элемент числового массива и вычитаем до тех пор, пока результат остается положительным. Каждый раз, когда вычитание возможно, к результирующей строке присоединяем соответствующее символьное значение. И так продолжаем экспериментировать с каждым элементом числового массива. Кстати, сумма всех элементов равна 3999, чем и объясняется ограничение на допустимый диапазон обрабатываемых чисел.
Программа 3_11.bas
RЕМ Перевод чисел в римскую систему
DECLARE FUNCTION torome$ (M%)
КЕМ Перевод арабских чисел в римскую систему счисления
DEFINT A-Z
COMMON SHARED ND()
COMMON SHARED SD$()
DATA 1,4,5,9,10,40,50., 90,100,400,500,900,1000
DIM ND(13)
FOR J=0 TO 12: READ ND(J): NEXT J
DATA I, IV, V, IX, X, XL, L, XC, C, CD, D, CM, M
DIM SD$(13)
FOR J=0 TO 12: READ SD$(J): NEXT J
INPUT "Введите целое число от 1 до 3999 : ", N
IF N<1 OR N>3999 THEN PRINT "Число вне диапазона":
END
PRINT "В римской системе счисления "; N;" = ";torome$(N)
END
FUNCTION torome$ (M)
SHARED ND(), SD$()
S$=""
FOR K=12 TO 0 STEP -1
WHILE ND(K)<=M
M=M-ND(K): S$=S$+SD$(K)
IF M=0 THEN EXIT FOR
WEND
NEXT К
torome$=S$
END FUNCTION
Программа 3_11.с
/* Перевод чисел в римскую систему счисления */
#include
#include
#include
char *to_rome(int n) ;
main() {
int N;
printf("\n Введите целое число от 1 до 3999 : ");
scanf("%d",&N); if (N<0 | | N>3999) {
printf("\n Число вне диапазона");
getch();
exit(0); }
printf("\n B римской системе счисления %d = %s",N,to_rome(N));
getch();
}
/*-------------------------------*/
char *to_rome(int n) {
int k;
static char s[20]="";
int nd[13]={l,4,5,9,10,40,50,90,100,400,_500,900,1000};
char *sd[13]={"I","IV","V","IX","X","XL",
"L","XC","C","CD","D","CM","M"}; for(k=12; k>=0; k—) {
while(nd[k]<=n) {
n=n-nd[k]; strcat(s,sd[k]);
if(n==0) break;
} }
return s; }
Программа 3_11.pas
program in_rome;
{Перевод чисел в римскую систему счисления}
var
N:1..3999;
function to_rome(n:integer): string;
const
nd:array [1..13] of integer=
(1,4,5,9,10,40,50,90,100,400,500,900,1000) ;
sd:array [1..13] of string=
( 'I', 'IV, 'V, 'IХ', 'X', 'XL',
'L', 'XC', 'C','CD','D','CM', 'M');
var
k:integer;
s:string;
begin s : = " ;
for k:=13 downto 1 do
while nd[k]<=n do begin
n:=n-nd[k];
s:=s+sd[k];
if n=0 then break;
end;
to_rome:=s;
end; begin
write ('Введите целое число от 1 до 3999 : ' ).; readln(N);
writeln('B римской системе счисления ',N, ' = ', to_rome (N) ) ;
readln;
end.
Задание 3.12. Перевод чисел из римской системы счисления
Составить программу обратного преобразования из строки с записью числа в римской системе счисления в обычное число.
Программа 3_12.bas
REM Перевод чисел из римской системы счисления в арабскую
DEFINT A-Z
DATA 1,4,5,9,10,40,50,90,100,400,500,900,1000
DIM ND(13)
FOR J=0 TO 12: READ ND(J): NEXT J
DATA I,IV,V,IX,X,XL,L,XC,C,CD,D,CM,M
DIM SD$(13)
FOR J=0 TO 12: READ SD$(J): NEXT J
INPUT "Введите число в римской системе счисления : ", R$
J=l: M=0
100 :
FOR К=12 ТО 0 STEP -1
N=LEN(SD$(К))
IF MID$(R$,J,N)=SD$(К) THEN M=M+ND(K): J=J+N: GOTO 100
END IF
IF J>LEN(R$) THEN EXIT FOR
NEXT К
PRINT "В арабской системе счисления ";R$;" = ";M
END
Программа 3_12a.bas
REM Перевод чисел из римской системы счисления в арабскую
DATA 1000,900,500,400,100,90,50,40,10,9,5,4,1
DIM ND(13):
FOR J=0 TO 12: READ ND(J): NEXT J
DATA M,CM,D,CD,C,XC,L,XL,X,IX,V,IV,I
DIM SD$(13): FOR J=0 TO 12: READ SD$(J): NEXT J
INPUT "Введите число в римской системе счисления : ",R$
FOR J=l TO LEN(R$)
FOR K=0 TO 12
N=LEN(SD$(K))
IF MID$(R$,J,N)=SD$(К) THEN M=M+ND(K): J=J+1: K=K-1
END IF NEXT К NEXT J
PRINT "В арабской системе счисления ";R$;" = ";M
END
Программа 3_12.с
/* Перевод чисел из римской системы счисления в арабскую */
#include
#include
#include
main() {
int nd[13]={1000,900,500,400,100,90,50,40,10,9,5,4,1};
char *sd[13]={"M","CM","D","CD","C","XC","L","XL","X",
"IX","V","IV","I"}; char r[20],s[3]; int j,k,n,m=0;
printf("ХпВведите число в римской системе счисления : ");
scanf("%s", r);
for(j=0; j
n=strlen(sd[k]);
strncpyfs, &r.[j] ,n) ;
s[n]=0;
if(strcmp(s,sd[k])==0)
{ m += nd[k]; j++; k—; } }
printf("\nB арабской системе счисления %s = %d",r,m);
getch(); }
Программа 3_12.pas
{ Перевод чисел из римской системы счисления в арабскую }
program from rome;
const
nd:array [1..13] of integer=(1000,900,500,400,100,
90,50,40,10,9,5,4,1);
sd:array [1..13] of string=('M','CM','D','CD','C',
'XC' , 'L', 'XL', 'X', 'IX1, 'V, 'IV, 'I' ) ; var
r,s:string;
j,k,n,m: integer; begin
m:=0;
write('Введите число в римской системе счисления : ');
readln(r);
J:=l;
while j<=length(r) do begin k:=l;
while k<=13 do begin
n:=length(sd[k]);
s:=copy(r,j,n);
if s=sd[k] then begin
inc(m,nd[k]); inc(j);
dec(k);
end;
inc(k);
end;
inc(j);
end;
writeln('B арабской системе счисления ',r,' = ',m);
readln;
end.
Задание 3.13. Вхождение строки с разрядкой
Строка S2 может входить в более длинную строку S1 в общепринятом смысле, когда непрерывная подпоследовательность символов строки S1совпадает с цепочкой символов S2. Однако возможна и другая ситуация, когда строка S2 входит в строку S1 с разрядкой. При этом символы S2 с равномерным шагом через 1, 2, 3 или более символов встречаются в строке S1.
Например, для строк S1="ABCBEEC" и S2="ABC" имеют место обычное (с нулевым шагом разрядки) вхождение (символы 1, 2 и 3 в строке si) и вхождение с разрядкой в 2 символа (символы 1, 4 и 7 в строке S1).
Составить программу, которая:
Задача программы — определить все возможные варианты вхождения S2 в S1.
Совет 1 (общий)
сравнение надо с символа S1[I], совпадающего с первым символом S2. Однако реализация этой идеи может быть разной. Например, из строки si можно извлечь с заданной разрядкой нужное число символов и результат сравнить с S2. Более эффективно совместить эти две операции и сравнивать извлекаемый из S1 символ с очередным символом S2, прекращая выборку при первом несовпадении. Указанный подход был реализован победителем областной студенческой олимпиады В. Мартьяновым (апрель 2000 г.), на базе программы которого и построены приведенные ниже примеры. Наиболее оригинальной, на наш взгляд, является проверка условия (h=l) или (L2>1). Здесь L2—длина второй строки.
Программа 3_13.bas
RЕМ Поиск вхождения S2 в S1 с разрядкой
CLS
INPUT "Введите S1: ", Sl$: L1=LEN(S1$)
INPUT "Введите S2: ", 32$: L2=LEN(S2$)
FOR H=l TO L1
IF (H=l) OR (L2>1) THEN
FOR I=1 TO Ll-(L2-l)*H
IF MID$(S1$,I,1)=MID$(S2$,l,l) THEN
FOR J=2 TO L2,
IF MID$(S1$,I+(J-1)*H,1)<>MID$(32$,J,1) THEN GOTO ml
NEXT J
PRINT "Шаг: ";Н-1,"Позиции: ";I;
FOR К = 1 TO L2 - 1: PRINT "-"; I + К * H; : NEXT K: PRINT
К = 1 ml:
END IF
NEXT I
END IF
NEXT H
IF К = 0 THEN PRINT "Строка S2 не входит в S1"
END
Программа 3_13.с
/* Поиск вхождения S2 в S1 с разрядкой */
#include
#include
#include
{
char s1 [80],s2[80];
int i,j,k=0,h,Ll,L2;
clrscr();
printf("Введите S1: ");
scanf("%s",s1);
Ll=strlen(s1);
printf("Введите S2: ");
scanf("%s",s2);
L2=strlen(s2);
for(h=l; h<=Ll; h++)
{
if(h==l || L2>1
}
{
for(i=0; i
if (sl[i]=s2[0])
{
for(j=l; j
if(si[i+j*h]!=s2[j]) goto ml;
printf("\n Шаг: %2d Позиции: %d",h-l,i+1);
for(k=l; k
ml:;
}
} } }
if(k==0) printf(" Строка S2 не входит в S1");
getch () ; }
Программа 3_13.pas
program red_str;
(Поиск вхождения S2 в S1 с разрядкой}
uses crt;
var
s1,s2:string;
i,j,k,h,L1,L2:integer;
label 1;
begin
clrscr;
write('Введите S1: ');
readln (si);
Ll:=length(sl);
write('Введите S2: ');
readln (s2);
L2:=length(s2);
k:=0;
for h:=l to L1 do
if (h=l)or(L2>1) then
for i:=l to L1-(L2-1)*h do
if s1[i]=s2[l] then begin
for j:=2 to L2 do
if s1[i+(j-l)*h]os2[j] then goto 1;
write ('Шаг: ',h-l:2,' Позиции: ',i);
for k:=l to L2-1 do
write('-',i+k*h);
writeln;
k:=l;
1:
end;
if k=0 then writeln('Строка 32 не входит в S1');
readln;
end.
Объявление массивов
Как правило, массив представляет собой
Работа с массивами
Как правило, массив представляет собой набор однотипных данных, расположенных в оперативной памяти таким образом, чтобы по индексам элементов можно было легко вычислить адрес соответствующего значения. Например, пусть одномерный массив А состоит из элементов, расположенных в памяти подряд по возрастанию индексов и каждый элемент занимает по k байт. Тогда адрес 1-го элемента вычисляется по формуле:
адрес(A[i]) = адрес(А[0]) + i * k
Если мы имеем дело с двумерным массивом в размерности MXN, расположенным в памяти по строкам, то адрес элемента в [i, j ] вычисляется по формуле:
адрес(В[i,j]) = адрес(В[0,0]) + (i * N + j) * k
Приведенные выше формулы незначительно усложняются в тех случаях, когда начальные индексы отсчитываются не от нуля, что характерно для Паскаля.
Использование массивов позволяет заменить большое количество индивидуальных имен каждого объекта одним групповым именем набора данных, вслед за которым в круглых (QBasic) или квадратных (Си, Паскаль) скобках задаются один или несколько индексов, определяющих местоположение требуемого значения. Естественно, что такая возможность упрощает и массовую обработку данных в соответствующих циклах программы.
В большинстве задач приходится иметь дело с массивами, элементами которых являются числа того или иного типа, символы и строки фиксированной длины. Однако приходится обрабатывать и битовые массивы, каждый элемент которых представлен одним или несколькими двоичными разрядами, соответствующими кодам цветности пикселов графических изображений. Некоторые системы программирования позволяют работать с массивами, состоящими из неоднородных элементов. Например, с одномерными массивами, каждый элемент которых представлен строкой переменной длины.
Инициализация массивов
Термином "инициализация" обозначают возможность задать начальные значения элементов массива без программирования соответствующих действий. Например, не прибегая к программным средствам типа присвоения значений в цикле или считывания данных из внешнего источника (файл, клавиатура, блок данных).
Средства такого рода имеются только в Си и Паскале. Здесь одновременно с объявлением массива можно задать начальные значения всех элементов массива или только нескольких первых его компонент:
char а[7]="Привет";
char b[7]={'П','р','и','в','е','т',0x00};
char с[]="Привет";
int d[10] = {1,2,3,4};
int f[2][3]={{1,2,3}, {4,5,6}};
В символьном массиве а формируются значения семи компонент, первые шесть из которых соответствуют кодам отображаемых символов заданной строки. Признак конца строки — байт с нулевым кодом — заносится в элемент а [6] автоматически. В отличие от этого в массиве ь, где значения элементов формируются посимвольно, такой признак конца программист должен задавать сам. Обратите внимание на третью строку, в которой отсутствует указание о размере массива. Компилятор Си сам сформирует нужное значение по количеству инициализирующих данных. В нашем случае под массив с будет отведено 7 байт, включая последний байт с нулевым кодом, завершающий каждую строку.
В Паскале инициализация производится в разделе const: const
a:string[7]='Привет';
d:array [1..10] of integer=(1,2,3,4);
f:array [1..2,1..3] of integer=((1,2,3),(4,5,6));
Инициализация глобальных и статических массивов в Си производится один раз при загрузке программы. Локальные массивы в функциях языка Си инициализируются при каждом обращении к функции.
Массивы в качестве параметров процедур и функций
Программисты, работавшие на Фортране, с грустью вспоминают времена, когда передача массива любой размерности в подпрограмму или функцию никаких забот не вызывала. Достаточно было написать нечто похожее на:
SUBROUTINE MATMULT(A,B,C,N)
REAL A(N,N),B(N,N),C(N,N),D
DO 1 J=1,N
DO 1 K=1,N D=0
DO 2 L=1,N
2 D=D+A(J,L)*B(L,K)
1 C(J,K)=D
END
И дальше работать с элементами массивов, ни о чем не задумываясь. Подпрограмма такого вида позволяет перемножать квадратные матрицы любого размера.
Массивы-параметры в подпрограммах и функциях QBasic
Ближе всего к идеологии Фортрана оказался QBasic. В нем довольно похожим образом можно передать массив в подпрограмму или функцию. Продемонстрируем эту возможность на примере подпрограммы сложения целочисленных квадратных матриц:
Программа 4_01.bas
DECLARE SUB ADDMAT(A%(),B%(),C%(),N%) DEFINT A-Z CLS
DIM A1(2,2), A2(2,2),A3{2,2)
DIM Bl(3,3),B2(3,3),B3(3,3)
FOR J=0 TO 2 : FOR K=0 TO 2
A1(J,K)=J+K : A2(J,K)=J*K
NEXT К : NEXT J
CALL ADDMAT(Al(),A2(),A3() ,2) 'Так можно обратиться к подпрограмме
FOR J=0 TO 3 : FOR K=0 TO 3 B1(J,K)=J+K :
B2(J,K)=J*K
NEXT К : NEXT J
ADDMAT Bl(),B2(),B3(),3 'И так можно обратиться к подпрограмме END
SUB ADDMAT (A%(),В%(),С%(),N%)
DEFINT A-Z
FOR Q=0 TO N : FOR S=0 ТО N
C(Q,S)=A(Q,S)+B(Q,S)
NEXT S : NEXT Q
END SUB
Как в заголовке подпрограммы, так и в операторах обращения к ней массив-параметр сопровождается пустыми круглыми скобками, независимо от числа индексов, приписанных фактически передаваемым массивам. Никаких переобъявлений типа DIM A(N,N) в теле подпрограммы не нужно. Более того, попытка вставить такой оператор приведет к фиксации ошибки, сопровождаемой сообщением о повторном объявлении массива. Обратите внимание на то, что в заголовке подпрограммы использованы имена А%, B%, C%, N%, а в тексте подпрограммы вместо них выступают имена А, в, с, N. Своей эквивалентностью они обязаны оператору DEFINT A-Z, объявляющему все переменные внутри подпрограммы целочисленными.
Немного сложнее приходится поступать в программах на Си и Паскале, особенно если речь идет о передаче в качестве параметров двумерных массивов переменного размера.
Массивы-параметры в процедурах и функциях Паскаля
Первое ограничение, с которым сталкиваются программисты в Паскале, звучит следующим образом — если формальным параметром является массив, то его нельзя описать явным образом. Например, ошибочным является заголовок:
function Max(a:array [1..100] of integer):integer;
Правильным считается предварительное объявление типа в головной программе и его использование в заголовке функции:
type
mas100=array [1..100] of integer;
function Max(a:mas100):integer;
Однако такая функция обрекает нас на определение максимального элемента только в массиве типа masioo. А если в нашей программе понадобится обрабатывать массивы и с другим количеством элементов? Конечно, можно добавить еще один параметр — количество обрабатываемых элементов:
function Max(a:mas100; n:integer):integer;
Это позволит ограничиться первыми n элементами массива, но размерность фактического параметра может быть только mas100.
Первый выход из столь неприятного положения заключается в том, чтобы передать массив как адрес параметра без типа:
function Max(var a; n:integer):integer;
type
b=array [1.. Maxlnt] of integer;
var
m,k:integer;
begin
m:=b(a}[1];
for k:=2 to n do
if m
Max:=m;
end;
Несколько необычная запись b(а) означает, что нетипизированный параметр а приводится к типу целочисленного массива, каковым он на самом деле и является. Только функция мах об этом "не знает". Может показаться немного странным выбор верхней границы индекса в типе "b". Однако он позволяет избежать неприятностей, когда фактическое значение параметра n достаточно велико (при этом может возникнуть аварийная ситуация, вызванная выходом индекса за границы диапазона). Каким бы большим не было значение п, оно не может превысить величину Maxint, ибо массивы в Паскале не могут быть более 64 Кбайт.
Второй подход является модернизацией предыдущего с той лишь разницей, что не потребуются никакие преобразования типов:
function Max(var a; n:integer):integer;
var
c:array[l.. Maxlnt] of integer absolute a;
m,k:integer;
begin
m:=c[l];
for k:=2 to n do
if m
Max:=m;
end;
Конструкция с использованием служебного слова absolute означает, что массив с, под который дополнительное место не выделяется, расположен в памяти, начиная с того же адреса, что и массив а.
Третья идея заключается в том, чтобы передать нетипизированный указатель на массив а:
function Max(pa:pointer; n:integer):integer;
var
m,k:integer;
pb:^integer;
begin
pb:=ptr(зед(ра^) , ofs(ра^) ) ;
m:=рb^;
for k:=2 to n do
begin
pb:=ptr(seg(ра^),ofs(ра^)+k*2);
if m < рb^ then m:=рb^;
end;
Max:=m;
end;
Для вызова такой функции при определении максимального элемента в массиве q необходимо задавать адрес аргумента:
max_q:=Max(&q,100);
Этот пример демонстрирует работу с адресами и указателями в Паскале. В нем использована функция ptr, вычисляющая адрес элемента данных по сегменту (seg) и смещению (ofs). Адрес сегмента, задающий начало массива, у локачьного указателя ь совпадает с адресом массива a (seg(pb^)=seg(pa^)), а смещение очередного элемента вычисляется в цикле путем прибавления к смещению начального элемента ofs (ра^) приращения 2*k.
Наверное, все эти три подхода блекнут перед новинкой в лице открытых массивов, появившихся в последних версиях Паскаля. В качестве открытого массива может выступать любой одномерный массив, индексы в котором отсчитываются от 0. Признаком открытого массива является его описание в укороченном виде — без задания индексных границ:
function Max(a:array of integer):integer;
var
m,k:integer;
begin
m:=a[0];
for k:=l to High(a) do
if m < a[k] then m:=a[k];
Max:=m; end;
Для открытых массивов появилась системная функция High, позволяющая узнать максимальный индекс. При использовании открытых массивов вы должны включить соответствующее указание компилятору — {$P+}.
Несмотря на всю привлекательность последней версии функции поиска максимума, предыдущие варианты сбрасывать со счетов не стоит. Во-первых, открытые массивы могут быть только одномерными. Во-вторых, их элементы передаются через стек, что замедляет работу программы и может послужить причиной переполнения стека.
Распространим некоторые идеи передачи параметров на двумерные массивы в задаче суммирования квадратных матриц. Первый пример использует нетипизированные переменные:
procedure sum+mat(var a,b,c; n:integer);
var
x:array [0..0] of integer absolute a;
y:array [0..0] of integer absolute b;
z:array [0..0] of integer absolute c;
j,k:integer;
begin {$R-}
for j :=0 to n-1 do
for k:=0 to n-1 do
z[j*n+k]:=x[j*n+k]+y[j*n+k];
{$R+} end;
В этом примере в качестве элементов суммируемых массивов в теле процедуры выступают одномерные массивы, начало которых совпадает с началом соответствующих двумерных массивов, а индексы пересчитываются по ранее приводившимся формулам. Несколько непривычный диапазон индексов от 0 до 0 компенсируется отключением контроля за выходом индексов из установленного диапазона на время работы циклов по суммированию.
Второй пример использует вариант с указателями:
procedure sum_mat(pa, pb, pc:pointer; n:integer);
var
a,b,с:^integer;
j,k:integer;
begin
for j:=0 to n-1 do
for k:=0 to n-1 do
begin
a:=ptr(seg(ра^),ofs(ра^)+(j*n+k)*2) ;
b:=ptr(seg(pb^),ofs(рb^)+(j*n+k)*2);
c:=ptr(seg(рс^),ofs(рс^)+(j*n+k)*2);
с^:=а^+b^;
end;
end;
Массивы-параметры в функциях Си
В отличие от Паскаля язык Си располагает более широкими возможностями по части адресной арифметики. Здесь можно прибавлять смещение к указателям, не заботясь о длине адресуемых операндов. Однако двумерные массивы все равно доставляют хлопоты в тех случаях, когда мы хотим построить универсальную функцию для обработки массивов разного размера.
Продемонстрируем технику программирования на тех же задачах, что и в предыдущем разделе.
int Max(int *a, int n) {
int m, k;
m=a[0];
for(k=l; k
if (m < a[k]) m=a[k];
return m; }
Предлагаемый вариант очень напоминает работу с открытым массивом с той лишь разницей, что функции типа High в Си нет. Поэтому список параметров дополнен еще и количеством элементов в массиве а.
Абсолютно эквивалентным является вариант с использованием арифметики указателей:
int Max(int *a, int n) {
int m,k;
m=*a;
for(k=l; k
if (m < *(a+k) m=*(a+k);
return m; }
Следующий пример демонстрирует сложение квадратных матриц с приведением адресов элементов двумерного массива к их одномерным аналогам:
void sum_mat(int *a, int *b, int *c, int n) {
int j,k,m;
for(j=0; j < n; j++)
for(k=0; k < n; k++) {
m=j*n+k;
* (c+m)=* (a+m) + *(b+m) ; } }
Объявление массивов
В QBasic для объявления массивов и одновременного отведения памяти под хранение их элементов используется оператор DIM:
DIM А(10),В(2 ТО 8,3 ТО 5),С(3,2,6)
В простом объявлении указывается максимальный индекс и, поскольку минимальный индекс по умолчанию равен 0, то в массиве А, например, содержится не 10, а 11 элементов. Конструкция "qq то kk" позволяет одновременно задать и минимальный, и максимальный индексы.
Интерпретатор QBasic существенно отличается от многих других систем программирования, где операторы объявления относятся к разряду невыполняемых и обрабатываются только на стадии компиляции программы. Здесь вполне возможны фрагменты следующего типа:
INPUT "Введите размерность массива F", N DIM F(N)
После работы с этим массивом в программе может встретиться следующая пара операторов:
INPUT "Введите новую размерность массива F",M REDIM F(M)
И новое значение верхней границы может быть как меньше предыдущего, так и больше. Массивы подобного рода в QBasic принято называть динамическими. В отличие от этого оператор DIM с конкретными числовыми границами формирует статические массивы, значения элементов которых сохраняются и после завершения работы программы.
Ни Си, ни Паскаль таких "вольностей" не позволяют. В них, конечно, можно определить массив достаточно большого размера и использовать только его часть. Но память будет выделена под весь массив, включая и неиспользуемый в конкретном варианте остаток.
Объявление массивов в Си чем-то особым не отличается от других алгоритмических языков. Разве что в задании многомерных массивов каждый индекс записывается в отдельных квадратных скобках:
#define N_max 50
char a1[20], a2[5][80];
int b1[25],b2[N_max];
Индексы в Си всегда отсчитываются от 0, так что, например, в массиве b1 можно манипулировать с элементами b1[0], b1[1], ..., b1[24]. Элемент b1[25] массиву ы уже не принадлежит и попытка записи в него может привести к непредсказуемым последствиям.
В Паскале существует несколько вариантов для объявления многомерных массивов. Например, целочисленная матрица f, содержащая q строк и k столбцов (значения q и k предварительно должны быть объявлены константами), может быть включена в текст программы одним из следующих описаний:
type
mat_q_k=array [l..q,l..k] of integer;
var
f :mat_q__k;
ИЛИ
var
f:array [l..q,l..k] of integer;
ИЛИ
var
f:array [l..q][l..k] of integer;
ИЛИ
var
f:array [l..q] of array [l..k] of integer;
Еще одна дополнительная особенность Паскаля заключается в том, что в качестве индексов могут использоваться не только числа, но и любые данные интервального или перечислимого типов. Например, буквы:
var
ch:array ['A'..'Z'] of integer;
str:string;
begin
.....................
inc(ch[str[j]]) ;
....................
Приведенный фрагмент наиболее простым способом позволяет подсчитать частоту появления тех или иных букв в обрабатываемом тексте.
Поиск
Алгоритмические и математические аспекты поиска достаточно сложны и их исследованию посвящены многочисленные работы. Наиболее полно эти вопросы рассматриваются в ранее упоминавшейся трилогии Д. Кнута. Мы же ограничимся самыми простыми алгоритмами и программами, позволяющими понять суть проблемы и познакомиться с некоторыми подходами к повышению эффективности поиска.
В достаточно общих чертах задача поиска формулируется следующим образом. Имеется массив а, содержащий п однородных объектов (чисел, строк, записей), и нужно установить, содержится ли в нем заданный объект q. При положительном ответе следует дополнительно сообщить порядковый номер (индекс) j найденного объекта (a[j] = q).
Последовательный поиск
Если исходный массив а не упорядочен, то единственно разумным способом является последовательный перебор всех элементов массива и сравнение их с заданным значением. В лучшем случае мы можем получить ответ на первом же шаге, если q = а [ 1 ]. В худшем случае придется перебрать все п элементов и только после этого дать положительный или отрицательный ответ. В среднем количество проверок может оказаться порядка п/2.
Классический алгоритм последовательного поиска включает следующие шаги:
Большинству программистов кажется, что приведенный алгоритм является оптимальным и ничего сократить в нем нельзя. Однако это — очень распространенное заблуждение. Д. Кнут приводит модификацию алгоритма последовательного поиска, в которой цикл содержит не две логические проверки (шаги S2 и S4), а всего одну. В нашем случае это довольно существенно, т. к. описанный выше цикл реализуется пятью-шестью машинными командами и исключение из него даже одной команды эквивалентно повышению производительности на 15—20%.
Модификация состоит в том, что к массиву а добавляется еще один элемент, в который до начала цикла заносится q. Теперь цикл повторяется до тех пор, пока не будет встречен элемент а [ j ], равный q, и необходимость в проверке j < n + 1 отпадает. Конечно, перед возвратом из процедуры надо удостовериться в том, что найденный индекс j не равен n + l. Но такая проверка выполняется за пределами цикла.
Для программистов, имеющих дело с языком ассемблера, известен и более простой прием, не требующий расширения исходного массива. Очевидно, цикл поиска можно организовать как в прямом (j меняется от 1 до n), так и в обратном (j меняется от n до i) направлении. Обратный цикл на ассемблере реализуется с помощью команды LOOP, организующей возврат в начало цикла с одновременным вычитанием 1 из счетчика сх. Цикл повторяется до тех пор, пока содержимое регистра сх не станет равным 0. Таким образом, дополнительного сравнения (j < n + 1) здесь не требуется.
В приводимых ниже программах последовательного поиска возвращаемое соответствующей функцией значение либо равно индексу найденного элемента, либо равно — 1, если искомая величина в массиве не обнаружена.
Функция ssearch.bas
FUNCTION SSEARCH(Q,A(),N)
FOR J=0 TO N-l
IF Q=A(J) THEN SSEARCH=J: EXIT FUNCTION
NEXT J
SSEARCH=-1
END FUNCTION
Функция ssearch.c
int ssearch(int q, int *a, int n)
}
register int j;
for(j=0; j
if(q==a[j]) return j;
return -1;
}
Функция ssearch.pas
function ssearch(q:integer;a:array of integer;n:integer):integer;
var
j:integer; begin
for j:=0 to n-1 do
if q=a[j] then
begin
ssearch:=j;
exit;
end;
ssearch:=-l;
end;
Бинарный поиск
Бинарный поиск, суть которого была раскрыта выше на примере поимки льва в пустыне, применяется только для предварительно упорядоченных массивов. Несмотря на абсолютную прозрачность идеи деления пополам, ее программная реализация требует большой аккуратности как в использовании сравнений, так и в выборе очередного интервала поиска.
Исключим тривиальный случай, когда искомое значение g выходит за пределы интервала [а[1],а[n]]. Обозначим через left и right индексы элементов массива, определяющие текущий диапазон поиска. В начальный момент left = 1 и right = n. Сравним значение q с величиной среднего элемента a [mid] в диапазоне поиска (mid = (left + right)/2). Если значение q строго меньше a [mid], то заменим правую границу диапазона поиска на mid - 1. Если значение q строго больше a [mid], то заменим левую границу диапазона поиска на mid + 1. Если оба строгие неравенства не выполнены, то имеет место равенство q = a [mid], и в этом случае процедура поиска завершена успешно.
Поиск следует продолжать до тех пор, пока значение индекса left не превосходит значения индекса right. А нарушиться это условие может только в случае, когда диапазон поиска сведен к минимальному (right = left + l) и имеют место неравенства:
a[left] < q < a[right]
Это означает, что значение q в массиве а не содержится.
Функция bsearch.bas
FUNCTION BSEARCH(Q,A() ,N) LEFT=0: RIGHT=N-1
WHILE LEFT <= RIGHT
MIDDLE=(LEFT+RIGHT)\2
IF Q < A(MIDDLE) THEN RIGHT=MIDDLE-1: GOTO M
IF Q > A(MIDDLE) THEN LEFT=MIDDLE+1: GOTO M
BSERACH=MIDDLE : EXIT FUNCTION M:WEND
BSEARCH=-1 END FUNCTION
Функция bsearch.c
int bsearch(int q,int *a,int n)
{
register int left,right,mid;
left=0; right=n-l;
for(;left <= right;)
{
mid=(left+right)12;
if(q < a[mid]) right=mid-l;
else if(q > a[mid]) left=mid+l;
else
return mid; }
return -1; }
Функция bsearch.pas
function bsearch(q:integer;a:array of integer;n:integer):integer;
var
left,right,mid:integer;
begin
left:=0; right:=n-l;
until left <= right do
begin
mid:=(left+right) div 2;
if q < a[mid] then right=mid-l
else if q > a[mid] then left=mid+l
else
begin
bsearch:=mid;
exit;
end;
end;
bsearch:=-l;
end;
Идея бинарного поиска может быть с успехом реализована в игре с отгадыванием задуманного целого числа из заранее установленного диапазона [O,N]. В ответ на число, предложенное угадывающим, его партнер может дать один из трех ответов:
Оптимальное поведение отгадывающего в точности повторяет схему бинарного поиска. Сначала надо предложить число, расположенное в середине интервала, т. е. N/2. Затем, сузив интервал поиска вдвое, повторить аналогичный маневр. Попадание в цель произойдет не более чем через log2N шагов.
Приведенные ниже тексты программ реализуют оптимальную тактику отгадывания чисел из диапазона [0,100], затрачивая на это не более 7 шагов. На вопросы программы загадавший должен нажимать клавишу Y или у (в случае положительного ответа) или любую другую клавишу, если вопрос программы не соответствует загаданному числу.
Программа 4_02.bas
'Программа угадывания задуманного числа в интервале [0,100]
DEFINT A-Z
CLS
LEFT=0: RIGHT=100:
DO
MIDDLE=(LEFT+RIGHT)\2
PRINT "Задуманное Вами число больше, чем"; MIDDLE; " (Y/N) - ";
INPUT "",A$
IF RIGHT-LEFT <= 1 THEN
IF A$="Y" OR A$="y" THEN
PRINT "Вы задумали ";RIGHT: END
ELSE
PRINT "Вы задумали ";LEFT: END
END IF
END IF
IF A$="Y" OR A$="y" THEN LEFT=MIDDLE+1 ELSE RIGHT=MIDDLE
LOOP
END
Программа 4_02.с
/* Программа угадывания задуманного числа в интервале [0,100] */
#include
#include
main ()
{
int left=0, right=100, middle, ok;
char ch;
clrscr();
for (;;)
{
middle={left+right)/2;
printf("\n Задуманное Вами число больше, чем % d (Y/N) - ", middle);
ch=getche();
if(right-left <= 1)
if (ch=='Y' || ch == 'y') { ok=right; break; }
else { ok=left; break;}
if(ch=='Y' II ch== 'y') left=middle+l;
else right=middle; }
printf("\пВы задумали %d",ok); getch(); }
Программа 4_02.pas
{ Программа угадывания задуманного числа в интервале [0,100] }
uses Crt;
var
ch: char;
left, right, middle, ok: byte;
begin
left:=0;
right:=100;
clrscr;
repeat
middle := (left + right) div 2;
write('Задуманное Вами число больше, чем ',middle,' (Y/N) - ');
ch:=readkey;
writeln(ch);
if (right-left <= 1) then
if (ch='Y') or (ch = 'y') then begin ok:=right;
break;
end else begin ok:=left;
break;
end; if(ch='Y') or (ch='y') then left := middle + 1
else right := middle;
until false;
writeln('Вы задумали ',ok);
readln;
end.
Сортировка больших массивов
Говорят, и это подтверждается многочисленными примерами, что 90% времени работы программы.приходится на так называемые узкие места, занимающие в общем объеме программы не более 10% команд. Поиск таких мест и улучшение их временных характеристик — один из основных методов совершенствования программ.
К числу таких узких мест относятся фрагменты программ, занимающиеся упорядочением достаточно объемной информации, поиском данных в больших массивах и т. п. Ниже приводится описание нескольких довольно популярных методов упорядочения числовых массивов и тексты реализующих их процедур. Схемы программ на Си заимствованы из [12], однако в их тексты внесены небольшие изменения. Желающим познакомиться более подробно с другими методами сортировки и возникающими при этом серьезными математическими проблемами мы рекомендуем книгу Д. Кнута "Искусство программирования для ЭВМ", т. 3.
Пузырьковая сортировка (bubble)
Идея этого метода заключается в сравнении двух соседних элементов массива, в результате которого меньшее число (более легкий пузырек) перемещается на одну позицию влево. Обычно такой просмотр организуют с конца массива и после первого прохода самое маленькое число перемещается на первое место. Затем все повторяется от конца массива до второго элемента и т. д.
Известна и другая разновидность обменной сортировки (bubble1), при которой также сравниваются два соседа и, если хотя бы одна из смежных пар была переставлена, просмотр начинают с самого начала. Так продолжают до тех пор, пока очередной просмотр не закончится без перестановок.
С целью повышения быстродействия программ на Си наиболее активно используемые переменные i и j распределяются в регистровой памяти.
Подпрограмма bubble.bas
SUB BUBBLE(X(),N)
FOR 1=1 TO N-l
FOR J=N-1 TO I STEP -1
IF X(J-l) > X(J) THEN
TMP=X(J-1): X(J-l) =X(J): X(J)=TMP
END IF
NEXT J
NEXT I
END SUB
Подпрограмма bubbiei.bas
SUB BUBBLE1(X(),N) M:Q=0
FOR 1=1 TO N-l
IF X(I-l) > X(I) THEN
TMP=X(I-1): X(I-1)=X(I): X(I)=TMP: Q=l
END IF
NEXT I
IF Q=l THEN GOTO *M
END SUB
Функция bubble.с
void bubble(int *x, int n) {
register int i,j;
int tmp;
for(i=l; i
for(j=n-l; j>=i; j—)
if
{
tmp=x[j-1] ;
x[j-l] = x[j];
x[j ] = tmp; } }
Функция bubblel.c
void bubblel(int *x, int n) {
register int i,j;
int tmp,q; m:q=0;
for(i=0; i
if(x[i] > x[i+l]) {
tmp=x[i];
x[i]=x[i+l];
x[i+l]=tmp;
q=l; }
if(q!=0) goto m; }
Процедура bubble.pas
procedure bubble(var x:array of integer;n:integer);
var
i,j,tmp:integer;
begin
for i:=l to n-1 do
for j:=n-l downto i do
if x[j]
tmp:=x[j-l]; x[j-l]:=x[j];
x[j]:=tmp;
end;
end;
Процедура bubblel.pas
procedure bubblel(var x:array of integer;n:integer);
label m;
var
i,tmp,q:integer;
begin m:q:=0
for i:=0 to n-2 do
if x[i] > x[i+l] then begin
tmp:=x[i];
x[i]:=x[i+l];
x [i+1] :=tmp;
q:=l; end;
if q=l then goto m;
end;
Сортировка методом отбора (select)
Идея метода отбора заключается в следующем. Находится элемент с наименьшим значением и меняется местами с первым элементом. Среди оставшихся ищется наименьший, который меняется со вторым, и т. д.
Подпрограмма select.bas
SUB SELECT(X(),N)
FOR I=0 TO N-2
Q=0: K=I: TMP=X(I)
FOR J=I+1 TO N-l
IF X(J)
IF Q=l THEN X(K)=X(I): X(I)=TMP NEXT I
END SUB
Функция select.с
void select(int *x, int n) {
register int i,j,k;
int q,tmp;
for(i=0; i
q=0;
k=i;
tmp=x[ i ] ;
for(j=i+l; j
if(x[j] < tmp) {
k=j;
tmp=x[ j ] ;
q=l; } } if (q)
{x[k]=x[i];
x[i]=tmp;} } }
Процедура select.pas
procedure select(var x:array of integer;n:integer);
var
i,j,k,q,tmp:integer;
begin
for i:=0 to n-2 do begin
q:=0;
k:=i;
tmp:=x[i];
for j:=i+l to n-1 do
if x[j]
k:=j;
tmp:=x[j];
q:=l;
end;
if q=l then begin
x[k]:=x[i];
x[i]:=tmp;
end;
end;
end;
Сортировка методом вставки (insert)
Идея этого метода базируется на последовательном пополнении ранее упорядоченных элементов. На первом шаге сортируются первые два элемента. Затем на свое место среди них вставляется третий элемент. К трем упорядоченным элементам добавляется четвертый, который занимает свое место в новой четверке. И так продолжается до тех пор, пока к n-1 ранее упорядоченным элементам не присоединится последний. Примерно таким способом игроки упорядочивают свои карты при сдаче их по одной.
Подпрограмма insert.bas
SUB INSERT(X%(),N%) DIM I,J,TMP
FOR I=1 TO N-l TMP=X(I)
FOR J=I-1 TO 0 STEP -1
IF TMP > X(J) THEN EXIT FOR
X(J+1)=X(J)
NEXT В X(J+1)=TMP
NEXT I
END SUB
Функция insert.c
void insert(int *x,int n) {
register int i,j; int trnp;
for(i=l; i
tmp=x[ i ] ;
for(j=i-l;j>=0 && tmp < x[j]; j--)
x[j+l]=x[j];
x[j+l]=tmp;
} }
Процедура insert.pas
procedure insert(var x:array of integer;n:integer);
var
i,j,tmp:integer;
begin
for i:=l to n-1 do
begin
tmp:=x[i];
j:=i-l;
while (j>=0) and (tmp
begin .
x[j+l]:=x[j]; j:=j-l;
end;
x [ j+1] :=tmp;
end;
end;
Сортировка методом Шелла (shell)
Метод Д. Л. Шелла, опубликованный в 1959 г., предлагает сортировать массив в несколько этапов. На первом этапе в сортировке участвуют достаточно далекие элементы, например, отстоящие друг от друга на восемь позиций. На втором проходе сортируются элементы, расстояние между которыми уменьшено, например до четырех. Затем упорядочиваются каждые вторые элементы и, наконец, на последнем этапе сравниваются смежные элементы. Выбор последовательно уменьшающихся шагов в методе Шелла представляет довольно сложную математическую задачу. На практике чаще всего применяют пятизвенную схему 9—>5—>3—>2—>1.
Подпрограмма shell.bas
SUB SHELLSORT (X%"() , N% )
DIM I, J,GAP,K,XX,A(5) A(0)=9: A(l)=5: A(2)=3: A(3)=2: A(4)=l
FOR K=0 TO 4 GAP=A(K)
FOR I=GAP TO N-1 XX=X(I)
FOR J=I-GAP TO 0 STEP -GAP
IF XX >= X(J) THEN EXIT FOR
X(J+GAP)=X(J)
NEXT J X(J+GAP)=XX
NEXT I
NEXT К
END SUB
Функция shell.с
void shell(int *x,int n) {
register int i,j,gap,k; int xx;
char a[5]={9,5,3,2,l};
for(k=0; k<5; k++) {
gap=a[k];
for(i=gap; i
xx=x[i];
for(j=i-gap; xx < x[j] && j >= 0; j=j-gap)
x[j+gap]=x[j); x[j+gap]=xx; } } }
Процедура shell.pas
procedure shell(var x:array of integer;n:integer) ;
var
i,j,k,gap,xx:integer;
const
a:array [0..4] of byte=(9,5,3,2,1};
begin
for k:=0 to 4 do
begin
gap:=a[k];
for i:=gap to n-1 do begin
xx:=x[i];
j:=i-gap;
while (j >= 0) and (xx < x[j]) do
begin
x[j+gap]:=x[j];
j:=j-gap;
end;
x[j+gap]:=xx;
end;
end;
end;
Сортировка методом Хоара (quicksort)
Метод Ч. Э. Р. Хоара, опубликованный в 1962 г., издалека напоминает способ ловли льва в пустыне "методом Вейерштрасса". Сначала пустыню делят пополам и выбирают ту половину, в которой находится лев. Затем эту половину снова делят пополам и так продолжают до тех пор, пока область, содержащая льва, не помещается в клетку. В математике подобный метод применяют для нахождения корня функции, принимающей на концах отрезка разные знаки. Это и есть метод Вейерштрасса, более известный под названием "метода деления пополам".
Хоар применил подобный подход к сортировке и предложил следующий алгоритм. Выберем какой-то средний элемент последовательности хх (обычно в качестве такового выбирают средний элемент). Если он стоит на своем месте (имеется в виду ситуация, когда последовательность упорядочена), то все элементы, расположенные левее, не больше хх, а элементы, находящиеся правее, — не меньше хх. Поэтому первый шаг быстрой сортировки заключается в том, чтобы перенести в левую часть массива те элементы правой половины, которые меньше хх, а в правую часть — те элементы из левой половины, которые больше хх. Обычно при этом поиск ведут в обе стороны от хх и как только обнаруживают пару, нарушающую порядок, производят обмен.
Затем аналогичный прием применяют к каждой из полученных половин. В каждой из них выбирается свой средний элемент и относительно него осуществляются необходимые перестановки. Как следует из описания, алгоритм Хоара очень хорошо укладывается в понятие рекурсивной процедуры. Для единообразия в обращении процедура быстрой сортировки представлена в виде двух процедур — внешней hoar, к которой обращается пользователь, и внутренней — quick. Последняя выполняет рекурсивную обработку подмассива, заданного граничными значениями индексов — left и right.
Подпрограмма hoare.bas
SUB HOARE(X% (),N%)
QUICK X%(),0,N%-1
END SUB
SUB QUICK(X%(),LEFT%,RIGHT%)
DIM I,J,XX,YY
I=LEFT%: J=RIGHT%
XX=X((LEFT%+RIGHT%)\2)
DO
WHILE X%(I) < XX AND I < RIGHT%: I=I+1: WEND
WHILE XX < X%(J) AND J > LEFT%: J=J-1: WEND
IF I <= J THEN
YY=X%(I): X%(I)=X%(J): X%(J)=YY: 1=1+1: J=J-1
END IF
LOOP WHILE I <= J
IF LEFT% < J THEN QUICK X%(),LEFT%,J
IF I < RIGHT% THEN QUICK X%(),I,RIGHT%
END SUB
Функция hoare.c
void hoare(int *x,int n) {
quick(x,0,n-1);
return;
}
/*--------------------------------*/
void quick(int *x, int left, int right) {
register int i,j;
int xx,tmp;
i=left;
j=right;
xx=x[(left+right)/2];
do
{
while (x[i] < xx && i < right) i++;
while (xx < x[j] && j > left) j--;
if (i<=j)
{
tmp=x[ i ] ;
x[i]=x[j];
x[j]=tmp;
i++; j-- ;
}
}
while(i<=j);
if(left < j) quick(x,left,j);
if(i < right) quick(x,i,right);
}
Процедура hoare.pas
procedure quick(var x:array of integer;left,right:integer);
var
i,j,xx,tmp:integer;
begin
i:=left; j:=right;
xx:=x[(left+right) div 2];
repeat
while (x[i] < xx) and (i < right) do i:=i+l;
while (xx < x[j]) and (j > left) do j:=j-l;
if i<=j then
begin
tmp:=x[i];
x[i]:=x [j];
x[j]:=tmp;
i:=i+l;
j:=j-i;
end;
until i>j;
if left < j then quick(x,left,j);
if i < right then quick(x,i,right);
end;
procedure hoare(var x:array of integer;n:integer);
begin
quick(x,0,n-l);
end;
Статические и динамические массивы
Статическим массивом называют набор данных, для хранения которого перед началом функционирования программы выделяется фиксированное место в памяти, освобождаемое после завершения работы программы.
QBasic трактует это понятие несколько шире, сохраняя значения статических массивов и после останова или полного завершения работы программы. Не выходя из интегрированной среды, можно посмотреть значения элементов статических массивов. В отличие от этого, место для хранения динамических массивов выделяется и освобождается в процессе выполнения программы. В одних случаях эти операции осуществляются системой автоматически. Например, когда отводится память для хранения локальных массивов в процедурах и функциях. В других случаях пользователю предоставляется возможность запросить участок памяти нужного размера и в дальнейшем — освободить его. Только таким способом в программах на Си и Паскале можно завести массив переменного размера.
В системе QBasic по умолчанию массивы с конкретными числовыми границами считаются статическими, а с переменными границами —динамическими. Однако, если первой строкой программы задана метакоманда вида КЕМ $STATIC или REM $DYNAMIC, то все массивы в программе будут заводиться либо как статические, либо как динамические. По оператору ERASE v1,v2, ... статические массивы "чистятся", а динамические массивы освобождают занимаемую память. Чистка массивов подразумевает засылку нулевых значений во все элементы числовых массивов и засылку "пустых" (нулевых) строк в элементы массива символьного типа. Оператор REDIM позволяет переопределить размеры ранее объявленных динамических массивов, не изменяя количество приписанных им индексов. Одновременно с этим происходит чистка переобъявляемых массивов.
В Си для запроса и освобождения памяти используются следующие системные функции:
q=(тип_q *)calloc(n_el,s_el); //запрос памяти с очисткой;
q=(тип q *)farcalloc(n_el,s_el); //запрос памяти с очисткой;
q=(тип_q *)malloc(n_byte); //запрос памяти в ближней "куче"
q=(тип_q *)farmalloc(n_byte); //запрос памяти в дальней "куче"
q new=realloc(q_old,n_byte); //изменение размера блока
q_new=farrealloc(q_old,n_byte); //изменение размера блока
free(q); //освобождение памяти
farfree(q); //освобождение памяти
В приведенных выше обращениях q обозначает указатель на тип данных элементов массива, заменяющий имя массива. Параметры n_el и s_el задают соответственно количество элементов в массиве и длину каждого элемента в байтах. Параметр n_byte определяет количество запрашиваемых байтов.
Максимальный размер сегмента памяти, предоставляемого в ближней "куче", равен 65 521 байт. Добавка far означает, что программа использует дальние указатели типа far или huge, которые позволяют адресоваться к дальней "куче" и использовать сегменты размером более 64 Кбайт. Любая функция выделения памяти возвращает начальный адрес или "нулевой" указатель (NULL) в случае отсутствия свободной памяти запрашиваемого размера. Для того чтобы нормально работать с предоставленным фрагментом памяти, возвращаемый адрес обязательно должен быть приведен к типу указателя q.
Функция realloc (farreallioc) позволяет перераспределить ранее выделенную память. При этом новый размер массива может быть как меньше предыдущего, так и больше. Если система выделит память в новом месте, то все предыдущие значения, к которым программа обращалась по указателю q_old, будут переписаны на новое место автоматически.
В новых версиях Borland C++ появились две более удобные процедуры для запроса и освобождения памяти, не нуждающиеся в дополнительном указании о приведении типа возвращаемого адреса:
q=new тип[n_е1]; //запрос памяти под массив из n_e1 элементов;
q=new тип; //запрос памяти под скалярную переменную;
delete q[n_e1]; //освобождение памяти, занятой массивом;
delete q; //освобождение памяти, занятой массивом или
//скалярной переменной;.
Для формирования в Паскале динамического массива с элементами определенного типа с таким массивом надо связать соответствующий указатель и обратиться к процедуре New:
type
mas=array [1..200] of integer;
point=^mas; var
p:point;
j:integer;
..................
begin New(p);
for j :=1 to 200 do
readln(p^[j]);
...................
Запрошенная таким образом память освобождается процедурой Dispose (р). Для запроса и освобождения памяти под разнородные данные в Паскале можно использовать процедуры GetMem(q,n_byte) и FreeMem(q,n_byte). Указатель я, которому присваивается начальный адрес выделенного сегмента, в данном случае представлен нетипизированным указателем (q:pointer;).
Как в Си, так и в Паскале, процедура освобождения памяти не чистит указатель, "смотревший" на начало возвращаемого сегмента. Запись по такому указателю после возврата памяти приводит к трудно обнаруживаемым ошибкам. Поэтому к правилам "хорошего тона" в программировании относится и сброс указателей после возврата динамически запрашивавшейся памяти:
q=NULL; //так это делается в Си
p:=nil; //так это делается на Паскале
Не менее хорошее правило заключается и в проверке, выделена ли запрашиваемая память после обращения к соответствующей процедуре. Например, в Си, не контролирующем запись по нулевому адресу, после стирания нескольких первых элементов несуществующего массива происходит зависание операционной системы.
Составить процедуру инвертирования целочисленного массива,
Задание 4.03. Перестановка элементов одномерного массива в обратном порядке
Составить процедуру инвертирования целочисленного массива, которая меняет местами первый элемент с последним, второй — с предпоследним и т. д. Процедура должна обрабатывать массивы любой длины.
Совет 1 (общий)
Программа 4_03.bas
DECLARE SUB INVERT (A%(), N%)
DEFINT A-Z
CLS
N = 20
DIM A(N)
PRINT "Массив до перестановки :"
FOR I=0 ТО N-l: A(I)=I+1: PRINT A(I); : NEXT I
INVERT A(), N
PRINT "Массив после перестановки :"
FOR I=0 ТО N-l: PRINT A(I); : NEXT I
END
SUB INVERT (A%(), N%)
DEFINT A-Z
FOR I = 0 TO (N-l)\2
TMP = A(I): A(I) = A(N-I-l): A(N-I-1) = TMP
NEXT I
END SUB
Программа 4_03.с
#include
#include
void invert(int *a, int n) ;
void main(void)
{
#define N 20
int i,a[N];
clrscr ();
printf("Массив до перестановки :\n");
for(i=0; i < N; i++)
fa[i]=i+l; printf("%3d",a[i]); }
invert(a,N);
printf("\n Массив после перестановки :\n");
for(i=0; i < N; i++)
printf("%3d",a[i]);
getch(); } void invert(int *a, int n)
int j,tmp;
for(j=0; j < n/2; j++)
{ tmp=a[j];
a[j]=a[n-j-1];
a[n-j-l]=tmp; } }
головной и хвостовой частях. Основным препятствием для реализации процедуры является запрет на использование вспомогательного массива.
Совет 1 (общий)
Конечно, можно принять предложенный алгоритм на веру и убедиться на нескольких примерах, что он работает правильно. Но это не может дать абсолютной уверенности в том, что также произойдет на любых сочетаниях исходных данных. Поэтому можно попытаться доказать правильность алгоритма, проследив за местоположением (индексом) каждого элемента после указанных перестановок.
Если элемент с исходным индексом i принадлежал голове массива (i < i < k), то инвертирование головы перемещает:
1-й элемент в позицию с индексом k, 2-й элемент в позицию с индексом k-l,
k-й элемент в позицию с индексом 1.
Сумма индексов элементов, меняющихся своими местами, при этом равна k+l. Поэтому 1-й элемент из головной части после инвертирования головы массива окажется на месте с индексом k-i+1. При последующем инвертировании всего массива сумма индексов взаимных пар меняющихся элементов равна п+1. Следовательно, элемент с первоначальным индексом i из головной части окажется на месте элемента с индексом (n+l) - (k-i+l)=n-k+i. Таким образом:
1-й элемент окончательно окажется в позиции n-k+l, 2-й элемент окончательно окажется в позиции n-k+2,
k-й элемент окончательно окажется в позиции n-k+k.
Это означает, что прежняя голова массива переместится в его хвост, сохранив взаимное расположение элементов.
Теперь рассмотрим поведение 1-го элемента из хвостовой части (k + i < i < n). После инвертирования хвоста:
элемент с индексом k+l окажется в позиции п, элемент с индексом k+2 окажется в позиции n-1,
элемент с индексом п окажется в позиции k+l.
Сумма индексов пар, меняющихся при этом местами, равна n+k+i. Поэтому 1-й элемент из хвостовой части после инвертирования хвоста перемещается в по-
зицию n+k+l-i. При последующем инвертировании полного массива, когда сумма индексов соответствующих пар равна n+1, произойдет следующее:
элемент с индексом k+l, предварительно перемещенный в позицию n, займет место элемента с номером (n+l)-n=l;
элемент с индексом k+2, предварительно перемещенный в позицию п-1, займет место элемента с номером (n+1)-(n-1)=2;
элемент с индексом п, предварительно перемещенный в позицию k+l, займет место элемента с номером (n+l)-(k+l)=n-k.
Таким образом, хвостовые элементы, сохраняя взаимное расположение, перейдут в голову нового массива и будут находиться вплотную перед его прежней головой.
Совет 2 (общий)
Программа 4_04.bas
DECLARE SUB INVERT1 (A%(), J%, N%)
DEFINT A-Z
CLS
N=20: K=15
DIM A(N)
PRINT "Массив до перестановки :"
FOR I=0 TO N-l: A(I)=I+1: PRINT A(I); : NEXT I
INVERT1 A(),0,K
PRINT "После перестановки в головной части :"
FOR I=0 ТО N-l: PRINT A(I); : NEXT I: PRINT
INVERT1 A(),K,N-K
PRINT "После перестановки в хвостовой части :"
FOR I=0 ТО N-l: PRINT A(I); : NEXT I: PRINT
INVERT1 A(),0,N
PRINT "После полной перестановки :"
FOR I=0 TO N-l: PRINT A(I); : NEXT I
END
SUB INVERT1 (A%(), J%, N%)
DEFINT A-Z
FOR I = J TO J+(N-1)\2
TMP=A(I): A(I)=A(2*J+N-1-I): A(2*J+N-l-I)=TMP
NEXT I
END SUB
Программа 4_04.с
#include
#include
void invertl(int *a, int j , int k) ;
void main(void) {
#define N 20
#define К 15
int i,a[N];
clrscr () ;
printf("Массив до перестановки :\n");
for(i=0; i < N; 1++)
{
a[i] = 1 + 1;
printf("%3d",a[i]); }
invertl(a,0,K);
printf("\n После перестановки в головной части :\n");
for(i=0; i < N; i++)
printf("%3d",a[i]);
invertl(a,K,N-K);
printf("\n После перестановки в хвостовой части :\n");
for(i=0; i < N; i++)
printf("%3d",a[i]);
invertl(a,0,K);
printf("\n После полной перестановки :\n");
for(i=0; i < N; i++)
printf("%3d",a[i]);
getch(); }
void invertl(int *a, int j, int k) {
int m,tmp;
for(m=j; m < j+k/2; m++)
{
tmp=a[m]; a[m] = a[2*j+k-m-1];
a[2*j+k-m-l]=tmp; }
}
Программа 4_04,pas
program pearl; uses crt; const
N=20; K=15; var
a:array [1..N] of integer;
i:integer;
procedure invertl(var a; j,k:integer);
var
m,tmp:integer;
aa:array [1..1] of integer absolute a;
begin {$R-}
for m:=j to j + k div 2 do begin
tmp:=aa[m];
aa[m]:=aa[2*j+k-m-1];
aa[2*j+k-m-l]:=tmp;
end;
{$R+} end;
begin clrscr;
writeln('Массив до перестановки : ') ;
for i:=l to N do
begin a[i]:=i;
write(a[i]:3);
end;
writeln;
invertl(a,1,K);
writeln('После перестановки в головной части :');
for i:=l to N do
write(a[i]:3);
writeln;
invertl(a,K+l,N-K);
writeln('После перестановки в хвостовой части :');
for i:=l to N do write(a[i]:3);
writeln; invertl(a,l,N);
writeln('После полной перестановки :');
for i:=l to N do
write(a[i]:3);
readln;
end.
Задание 4.05. Вывод массивов
Составить процедуру (функцию) вывода небольших целочисленных матриц размерности m x n с управлением по ширине колонок (w) и по местоположению на экране (row — строка, col — столбец, определяющие левый верхний угол матрицы). Предполагается, что матрица целиком помещается на экране и что ширина ее колонок не превосходит девяти позиций.
Совет 1 (общий)
Совет 2 (QBasic)
Совет 3 (Си)
Совет 4 (Паскаль)
Программа 4_05.bas
DECLARE SUB PRINTA (ROW%, COL%, W%, C% (-) , N%, M%)
DEFINT A-Z
CLS
DIM A(2, 3) , B(3, 3)
FOR J = 0 ТО 2: FOR К = 0 TO 3
A(J, K) = J + К * К NEXT К: NEXT J PRINTA 5, 5, 3, A() , 3, 4
FOR J = 0 TO 3: FOR К = 0 ТО 3
B(J, K) = J * 10 + К * 25 NEXT K: NEXT J PRINTA 5, 40, 5, B() , 4, 4
END
SUB PRINTA (ROW%, COL%, W%, C%(), N%, M%) DEFINT A-Z
F$ = LEFT$("##########", W)
FOR J = 0 TO N - 1: FOR К = 0 TO M - 1
LOCATE ROW + J, COL + K*W
PRINT USING F$; C(J, K) NEXT K: NEXT J
END SUB
Программа 4_05.с
#include
#include
void printa(int row,int col,int w,int *c,int n,int m) ;
void main(void) {
int a[3] [4] = {{!,2,3,4),{10,20,30,40},{100,200, 300, 400}};
int b[4][4]={{l,2,3,4},{5,6,7,8},{9,10,ll,12},{13,14,15,16}};
clrscr();
printa (5,5,4, (int *)a,3,4);
printa(5,40,5,(int *)b,4,4);
getch(); }
void printa(int row,int col,int w,int *c,int n,int m) {
int j,k;
char f[4]="%0d";
f[1] += w;
for(j=0; j
for(k=0; k
{
gotoxy(col+k*w,row+j);
printf(f,c[k+j*m]); }
}
Программа 4_05.pas
program mat_print;
uses crt;
const
a:array [1..3,1..4] of integer = ((1,2,3,4), (10,20,30,40), (100,200,300,400));
b:array [1..4,1..4] of integer = ((1,2,3,4), (5,6,7,8), (9,10,11,12), (13,14,15,16));
procedure printa(row,col,w:integer,-var с;n,m:integer);
var
j,k:integer;
d:array [0..MaxInt-l] of integer absolute c;
begin
for j:=0 to n-1 do
for k:=0 to m-1 do
begin
gotoxy(col+k*w,row+j); write(d[k+m*j]:w);
end;
end;
begin clrscr;
printa(5, 5, 4, a, 3, 4);
printa(5, 40, 5, b, 4, 4);
readln;
end.
Задание 4.06. Ход конем
Существует довольно много комбинаторных задач, связанных с шахматным полем. Это и задача о расстановке восьми ферзей, которые бы не угрожали друг другу, т. е. чтобы ни одна из пар не находилась на общей вертикали, горизонтали и диагонали. Это и различные путешествия коня по шахматному полю. Среди них — построение траектории ходов, при которых конь, начиная из заданной позиции, обходит все клетки поля, не заходя повторно в уже пройденные. Или — заданы начальная и конечная позиции, и нужно построить одну или все траектории между указанными клетками, содержащие минимальное число ходов. Самая простая среди "лошадиных" задач заключается в определении минимального количества ходов, за которое конь может добраться из начальной позиции в конечную. Именно ей и посвящено очередное задание.
Говорят, что конь ходит буквой "Г". Это не совсем точно, т. к. допустимые ходы этой фигуры образуются перемещениями на две клетки по горизонтали (вертикали) с последующим поворотом на 90 градусов по или против часовой стрелки и сдвигом по вертикали (горизонтали) еще на одну клетку. Если сопоставить с шахматной доской матрицу 8x8, то из позиции a[i,j] возможны максимум 8 ходов в клетки со следующими индексами:
1. a[i-2,j-1] 5. a[i+l,j-2]
2. a[i-2,j+l] 6. a[i+l,j+2]
3. a[i-l,j-2] 7. a[i+2,j-1]
4. a [i-1,j+2] 8. a[i + 2,j + 1]
По мере приближения к границам поля какие-то из этих перемещений становятся недопустимыми из-за выхода некоторых индексов за пределы установленного диапазона. Минимальным числом ходов, равным 2, обладают угловые клетки шахматной доски.
Для определения минимального количества ходов, соединяющих клетки a[i1,j1] и a[i2,j2], предлагается следующий алгоритм. Сначала все элементы массива расписываются каким-то кодом, например числом — 1, означающим, что все клетки шахматного поля свободны. Затем в начальную позицию a[i1,j1] заносится 0 и делаются попытки определить все клетки, достижимые за один ход. В каждую из них заносим 1. Для каждой клетки, достигаемой после первого хода, делается попытка совершить следующий ход, и все вновь достигаемые позиции метятся кодом 2. Естественно, что среди них исключаются ходы, возвращающие нас в начальную позицию, т. е. ходить надо только по свободным клеткам. Из каждой клетки, достигаемой за два хода, делается попытка совершить следующий ход в еще не занятые позиции и пометить все допустимые элементы массива числом 3. Числовую метку, которую мы заносим на очередном шаге охвата клеток шахматного поля, можно назвать уровнем досягаемости.
Расстановка уровней досягаемости продолжается до тех пор, пока мы не попадем в конечную позицию а [12, j2]. А еще лучше — до тех пор, пока не будет заполнена вся матрица, и тогда мы получим ответ, за сколько ходов можно переместиться из позиции a [i1, j1] в любую другую клетку шахматного поля.
Наряду с матрицей а можно ввести еще один массив ь и заполнять его аналогичным образом, начиная из конечной позиции b[i2,j2]. Если n-минимальное число ходов, переводящих коня из клетки a[i1, j1] в клетку а [i2, j2], то обратное путешествие по минимальной траектории займет тоже п шагов. Кроме того, можно заметить, что в каждой клетке любой минимальной траектории имеет место равенство
a[i,j] + b[i,j] = n.
Оно означает, что число промежуточных ходов из начальной позиции в клетку a [i, j ] и число встречных ходов по этой же траектории из конечной точки в сумме составляют длину минимальной траектории. Этот факт позволяет отсечь все недопустимые позиции и, тем самым, выделить клетки, принадлежащие только минимальным траекториям.
В качестве программы, доведенной до конца, мы ограничимся формированием всех уровней досягаемости из заданной позиции и по результатам ее работы узнаем, что любая клетка шахматного поля может быть достигнута не более чем за шесть ходов.
Совет 1 (общий)
Программа 4_06.bas
DIM A(8,8)
FOR I=0 ТО 7 : FOR J=0 TO 7
A(I,J)=-l NEXT J: NEXT I
CLS : INPUT "Задайте начальную позицию :",I,J A(I,J)=0 : K=0 M:NEWLEVEL
IF XOD = 1 THEN GOTO M
FOR I=0 TO 7 : FOR J=0 TO 7
PRINT A(I,J) NEXT J: PRINT : NEXT I END
SUB NEWLEVEL XOD=0
FOR I=0 TO 7 : FOR J=0 TO 7
IF A(I,J)=K THEN
TRY(I-2,J-l): TRY(I-2,J+1)
TRY(I-1,J-2): TRY(I-l,J+2)
TRY(I+1,J-2): TRY(I+1,J+2)
TRY(I+2,J-l): TRY(I+2,J+1)
END IF NEXT J: NEXT I
K=K+1
END SUB
SUB TRY(P,Q)
IF P>=0 AND P<8 AND Q>=0 AND Q<8 AND A(P,Q)<0 THEN A(P,Q)=K+1 : XOD=1
END IF
END SUB
Программа 4_06.с
#include
#include
char newlevel(void);
void try(int p,int q);
char a[8][8],i,j,k=0,xod;
void main(void) {
clrscr();
for(i=0; i<8; i++)
for(j=0; j<8; j++)
a[i][j]=-l;
puts("Задайте начальную позицию :");
scanf("%d %d",&i,&j);
a[i][j]=0; m:newlevel();
if(xod==l) goto m;
for(i=0; i<8; i++) {
for(j=0; j<8; j++)
printf("%3d",a[i] [j]) = —1;
printf("\n");
}
getch(); )
char newlevel(void) {
char di[8]={-2,-2,-l,-l, 1,1, 2,2};
char dj[8]={-l, l,-2, 2,-2,2,-1,1};
char f;
xod=0;
for(i=0; i<8; i++)
for(j=0; j<8; j++)
if (a[i] [j]==k)
for(f=0; f<8; f++)
try(i+di[f],j+dj[f]);
k++;
return xod; }
void tryfint p,int q) {
if(p>=0 && p<8 && q>=0 && q<8 && a[p][q]<0)
{ a[p][q]=k+l;
xod=l;} }
Программа 4_06.pas
program horst;
{=======================================
Построение полей досягаемости ходом коня из заданной позиции.
Индексы позиций задаются от 0 до 7. Поле, из которого конь начинает, помечается уровнем 0. Поля, достигаемые после первого хода, помечаются уровнем 1, после второго хода - уровнем 2 и т. д.
=====================================}
uses Crt;
label m;
var
i,j,k,xod:byte;
a:array [0..7,0..7] of shortint;
procedure try(p,q:integer);
{=================================
Попытка совершить ход уровня k+1 в позицию (p,q). При возможности хода в а[р,q] заносится номер уровня, а в переменную xod - значение 1. В противном случае переменная xod остается равной 0.
==================================}
begin
if (p>=0) and (p<8) and (q>=0) and (q<8) and (a[p,q]<0) then
begin a[p,q]:=k+l; xod:=l; end; end;
procedure newlevel;
{================================
Поиск всех ходов уровня k+1 из клеток, достигнутых за k ходов
================================}
const
{смещения по индексам i,j для 8 возможных ходов коня}
di:array [0..7] of integer = (-2,-2,-1,-1, 1,1, 2,2);
dj:array [0..7] of integer = (-1, l,-2, 2,-2,2,-1,1); var
f:byte; begin
xod:=0; {Гашение признака возможности совершить ход}
{Поиск полей, достигаемых на k-том уровне)
for i:=0 to 7 do
for j:=0 to 7 do
if a[i,j]=k then
{Если поле найдено, из него делаются попытки сходить по 8 возможным направлениям}
for f:=0 to 7 do try(i+di[f],j+dj[f]);
k:=k+l;
{Повышение уровня хода}
end;
begin
k:=0; {Уровень хода} clrscr;
for i:=0 to 7 do
for j:=0 to 7 do
a[i,j]:=-1; {Начальная роспись матрицы позиций}
write('Задайте начальную позицию : '};
readln(i,j);
a[i,j]:=0; (Отметка начальной позиции)
m: newlevel;
{На поиск ходов следующего уровня}
if xod=l then goto m; {Если поиск был завершен успешно} {Цикл вывода заполненной матрицы с уровнями ходов}
for i:=0 to 7 do
begin
for j:=0 to 7 do
write (a[i,j]:3);
writeln;
end;
readln;
end.
Задание 4.07. Сравнение методов сортировки
Составить программу тестирования методов сортировки, приведенных выше. Предполагается, что тестовая программа будет генерировать случайным образом целочисленный массив достаточно большого размера, например содержащий 15 000 элементов. Для чистоты эксперимента каждому методу должен задаваться один и тот же исходный массив, т. е. не надо прибегать к процедуре randomize. В начале и конце работы программы сортировки необходимо зафиксировать показания системных часов, по разности которых можно судить о быстродействии того или иного алгоритма на данном компьютере.
Совет 1 (общий)
Совет 2 (общий)
Программа 4_07.bas
DECLARE SUB BUBBLE(X%(),N%)
DECLARE SUB INSERT(X%(),N%)
DECLARE SUB SELECT1(X%(},N%)
DECLARE SUB SHELLSORT(X%(),N%)
DECLARE SUB HOARE(X%(),N%)
DECLARE SUB QUICK(X%(),LEFT%,RIGHT%)
DEFINT A-Z
CLS
CONST N=5000
DIM A(N)
FOR J=0 TO N
A(J)=INT(N*RND) 'PRINT USING "#### "; A(J); NEXT J
PRINT T1#=TIMER BUBBLE A() , N ' INSERT A (),N 'SELECT1 A(),N 'SHELLSORT A(),N 'HOARE A{},N T2#=TIMER
PRINT T2#-T1#; "сек"
'FOR J=0 TO N: PRINT USING "#### ";A(J); : NEXT J END
REM Тексты подпрограмм сортировки
Программа 4_07.с
#include
#include
#include
#include
#define MAX 15000
void bubble(int *x, int n) ;
void select(int *x, int n) ;
void insert(int *x, int n);
void shell(int *x, int n);
void hoare(int *x, int n);
void quick(int *x, int left, int right);
main( ) {
int num[MAX];
int i ;
struct time w;
clrscr();
//cout << "До сортировки" << endl;
for(i=0; i < MAX; i++) // {
num[i]=random(MAX);
// cout << num[i] << " ";}
// cout << endl; // getch();
// cout << "После сортировки" « endl;
gettime (&w);
cout << (unsigned int)w.ti_sec <<".";
cout << (unsigned int)w.ti_hund << endl;
bubble(num,MAX);
//select(num,MAX);
//insert(num,MAX);
//shell(num,MAX);
//hoare(num,MAX);
gettime(&w);
cout << (unsigned int)w.ti_sec <<".";
cout << (unsigned int)w.ti_hund << endl;
//cout << "Кончили";
getch();
//for(i=0; i
//getch();
return 0; }
/*==== тестируемые процедуры ========*/
Программа 4_07.pas
program all_sort; uses crt,WinDos; const
MAX=15000; type
xarr=array [0..MAX-1] of integer; var
x:xarr;
i:integer;
hour,minute,second,sec100:word;
{===== тестируемые процедуры ======}
begin
clrscr;
for i:=0 to MAX-1 do
begin
x[i]:=random(MAX); {write(x[i],' ');}
end;
writeln;
write('До сортировки - ');
gettime(hour,minute,second,sec100);
write(minute:2,' мин ',second:2,'.',sec100:2, ' сек');
writeln;
{Вызов метода}
{ bubble(x,MAX);}
{ select(x,MAX);}
{ insert(x,MAX);}
shell(x,MAX);
{ hoare(x,MAX);}
gettime(hour,minute,second,sec100};
write('После сортировки - ');
write(minute:2,' мин ',second:2,'.',seclOO:2,' сек');
writeln;
{ for i:=0 to MAX-1 do write(x[i],' ');}
readln; end.
Задание 4.08. Счастливый билет
Билет с шестизначным цифровым номером считается "счастливым", если сумма трех старших цифр совпадает с суммой трех младших цифр. В предположении, что в билетной кассе находится миллион билетов с номерами от 000000 до 999999, надо определить количество потенциально осчастливленных пассажиров.
Совет 1 (общий)
N = S[0] * S[0] + S[l] * S[l] + ... + S[27] * S[27].
Программа 4_08.bas
DIM S(28)
FOR Al=0 TO 9: FOR A2=0 TO 9: FOR A3=0 TO 9
S(A1+A2+A3)=S(A1+A2+A3)+ 1 NEXT A3: NEXT A2: NEXT A1
FOR K=0 TO 27: N=N+S(K)*S(K) : NEXT К
PRINT "Количество счастливых билетов = ";N
END
Программа 4_08.с
#include
#include
main()
{
int s[28],al,a2,a3,k;
long N;
clrscr();
for(k=0; k<28; k++)
s[k]=0;
for(al=0; al<10; al++)
for(a2=0; a2<10; a2++)
for(a3=0; аЗ<10; а3++)
s[al+a2+a3]++;
for(k=0,N=0; k<28; k++)
N += s[k] *s [k] ;
printf("\n Количество счастливых билетов = %ld",N);
getch(); }
Программа 4_08.pas
program lucky_ticket;
var
al,a2,a3,k:integer;
N:longint;
s:array [0..27] of integer;
begin
for al:=0 to 9 do
for a2:=0 to 9 do
for a3:=0 to 9 do
inc(s[al+a2+a3]);
for k:=0 to 27
N:=N+s [k] *s["k] ;
writeln('Количество счастливых билетов = ',N);
readln;
end.
Задание 4.09. Количество разных элементов в целочисленном массиве
Составить подпрограмму подсчета количества разных чисел в массиве, элементами которого являются неотрицательные двухбайтовые значения. Эта задача интересна не своей практической ценностью, а возможностью продемонстрировать несколько разных подходов к ее решению.
Совет 1 (общий)
Совет 2 (общий)
Совет 3 (общий)
Совет 4 (Си)
Программа 4_09a.bas
DECLARE SUB SORT (A() AS INTEGER, N%)
DECLARE FUNCTION DIFFERENCE% (A() AS INTEGER, N%)
DEFINT A-Z
DIM A(5)
DATA 0,0,0,0,0
DATA 1,1,1,1,1
DATA 0,1,1,1,1
DATA 0,0,1,1,2
DATA 0,1,2,3,4
DATA 1,2,3,4,5
CLS
FOR k=1 TO 5
FOR I=0 TO 4: READ A(I): NEXT I
PRINT "Количество разных чисел в массиве ";k;" = ";
PRINT DIFFERENCE(A(), 5} NEXT k END
FUNCTION DIFFERENCE (A() AS INTEGER, N%)
SORT A(),N%
M=l
FOR I=0 TO N%-2
IF A(I)<>A(I+1) THEN M=M+1
NEXT I
DIFFERENCE=M
END FUNCTION
SUB SORT(A() AS INTEGER,N%)
REM тело любой процедуры сортировки
END SUB
Программа 4_09b.bas
DECLARE SUB SORT (A() AS INTEGER, N%)
DECLARE FUNCTION DIFFERENCE% (A() AS INTEGER, N%)
DEFINT A-Z
DIM A0(5),A1{5),A2(5),A3(5},A4(5),A5(5)
DATA 0,0,0,0,0
FOR I=0 TO 4: READ А0(I): NEXT I
DATA 1,1,1,1,1
FOR I=0 TO 4: READ A1(I): NEXT I
DATA 0, 1,1, 1, 1
FOR I=0 TO 4: READ A2(I): NEXT I
DATA 0,0, 1, 1,2
FOR I= 0 TO 4: READ A3(I): NEXT I
DATA 0,1,2,3,4
FOR I=0 TO 4: READ A4(I): NEXT I
DATA 1,2,3,4,5
FOR I=0 TO 4: READ A5(I): NEXT I
PRINT "Количество разных чисел в массиве А0 = ";
PRINT DIFFERENCE(А0(),5)
PRINT "Количество разных чисел в массиве А1 = ";
PRINT DIFFERENCE(A1(),5)
PRINT "Количество разных чисел в массиве А2 = ";
PRINT DIFFERENCE(A2(),5)
PRINT "Количество разных чисел в массиве A3 = ";
PRINT DIFFERENCE(A3() ,5)
PRINT "Количество разных чисел в массиве А4 = ";
PRINT DIFFERENCE(A4(),5)
PRINT "Количество разных чисел в массиве А5 = ";
PRINT DIFFERENCE(A5(), 5)
END
FUNCTION DIFFERENCE (АО AS INTEGER-,N%) DEFINT A-Z
FOR I=0 TO N%-1
IF A(I)=0 THEN K0=l: EXIT FOR NEXT I
FOR I=0 TO N%-1 IF A(I)<>0 THEN
FOR J=I+1 TO N%-1
IF A(I)=A(J) THEN A(I)=0: EXIT FOR NEXT J END IF NEXT I
FOR I=0 TO N%-1
IF A(I)<>0 THEN M=M+1 NEXT I
DIFFERENCE=M+K0
END FUNCTION
Программа 4_09а.с
#include
#include
void sort(int *a,int n);
int difference(int *a,int n);
main() {
int a0[5]={0,0,0,0,0};
int a1[5]={l,l,l,l,l};
int a2[5]={0,l,l,l,l);
int a3[5]={0,0,l,l,2};
int a4[5]={0,l,2,3,4};
int a5[5]={l,2,3,4,5};
printf("\n Количество разных чисел в этом массиве равно ");
printf("%d",difference(a0,5));
getch(); }
void sort(int *a,int n) {
/* тело любой процедуры сортировки */
return; }
int difference(int *a, int n) {
int i,m;
sort(a,n);
for(i=0,m=l; i
return m; }
Программа 4_09b.c
#include
#include
int difference(int *a,int n);
main() {
int a0[5]={0,0,0,0,0};
int al[5] = {l,l,l,l,1};
int а2[5]={0,1,1,1,1};
int a3[5]={0,0,l,l,2};
int a4[5]={0,l,2,3,4};
int a5[5]={l,2,3,4,5};
printf("\n Количество разных чисел в этом массиве равно ");
printf("%d",difference(a0,5));
getch (); }
int difference(int *a,int n) {
int i,j,k0,m;
for(i=k0=0; i
if(a[i] == 0) { k0=1; break; }
for(i=0; i
{ if(a[i]==0) continue;
for(j=i+l; j
if(a[i]==a[j]) { a[i]=0; break; } }
for(i=m=0; i
if(a[i] !=0)m++;
return m+k0; }
Программа 4_09с.с
#include
#include
#include
int difference(int *a,int n);
main() {
int a0[5]={0,0,0,0,0};
int a1[5]={l,l,l,l,l};
int a2[5]={0,l,l,l,l};
int a3[5]={0,0,l,l,2);
int a4[5]={0,l,2,3,4);
int a5[5]={l,2,3,4,5};
printf("\ n Количество разных чисел в этом массиве равно ");
printf("%d",difference(a5, 5)) ;
getch(); }
int difference(int *a, int n) {
char *b;
char mask[8]={128,64,32,16,8,4,2,1};
int bit,byte,i,m;
b=calloc(4096,1);
for(i=m=0; i
byte = a[i]/8; bit = a[i]%8;
if ((b [byte] & mask [bit] )=0)
{ m++; b[byte] | = mask[bit]; } }
free(b); return m; }
Программа 4_09a.pas
program dif;
const
a0:array [0..4] of integer=(0,0,0,0, 0)
al:array [0..4] of integer=(l,1,1,1,1)
a2:array [0..4] of integer=(0,1,1,1,1)
a3:array [0..4] of integer=(0,0,1,1, 2)
a4:array [0..4] of integer=(0,1,2,3,4)
a5:array [0..4] of integer=(1,2, 3, 4, 5)
procedure sort(var a:array of integer);
begin end;
function difference(a:array of integer):integer;
var i,m: integer;
begin
sort(a);
m:=l;
for i:=0 to High(a)-1 do
if a[i] <> a[i+l] then inc(m);
difference:=m;
end;
begin
write('Количество разных чисел в этом массиве равно ');
write(difference(a5));
readln; end.
Программа 4_09b.pas
program difl; const
a0:array [0..4J of integer=(0,0,0,0,0)
a1:array [0..4] of integer= (1,1,1,1,1)
a2:array [0..4] of integer=(0,1,1,1,1)
a3:array [0..4] of integer=(0,0,1,1,2)
a4:array [0..4] of integer=(0,1,2,3,4)
a5:array [0..4] of integer=(1,2,3,4,5)
function difference(a:array of integer):integer;
var
i,j,k0,m,n:integer;
begin
k0:=0; n:=High(a);
for i:=0 to n do
if a[i]=0 then begin k0:=l;
break;
end;
for i:=0 to n-1 do begin
if a[i]=0 then continue; for j:=i+l to n do
if a[i]=a[j] then begin a[i]:=0;
break; end; end ;
m:=0; for i:=0 to n do
if a[i]<>0 then inc(m);
difference:= m+k0;
end;
begin
write(' Количество разных чисел в этом массиве равно ');
write(difference(a5)};
readln;
end.
Задание 4.10. Перемешивание "колоды карт"
Практически все карточные игры нуждаются в процедуре тасования колоды карт.
Совет 1 (общий)
Совет 2 (общий)
Совет 3 (общий)
Совет 4 (общий)
Программа 4_10.bas
DECLARE SUB MIXER(В() AS INTEGER)
DEFINT A-Z
DIM A(36)
CLS
PRINT "Упорядоченная колода:"
FOR K=0 TO 35: A(K)=K: PRINT USING "####";A(K); : NEXT К
FOR J=0 TO 4
MIXER A()
PRINT "Перетасованная колода:"
FOR K= 0 TO 35: PRINT USING "####";A(K); : NEXT К NEXT J END
SUB MIXER(B() AS INTEGER) DEFINT A-Z
RANDOMIZE INT(32767*RND)
FOR J=0 TO 10000
I=INT(35*RND+.5)
TMP=B(0)
B(0)=B(I)
B(I)=TMP
NEXT J
END SUB
Программа 4_10.с
#include
#include
void mixer(char *b);
main()
{
char j,k, a[36];
clrscr();
printf("\n Упорядоченная колода:\n");
for (k=0; k<36; k++) {
a[k]=k;
printf("%4d",a[k]); }
for(j=0; j<5; j++) {
mixer(a);
printf("\n Перетасованная колода:\n");
for(k=0; k<36; k++)
printf("%4d",a[k]);
begin clrscr;
writeln('Упорядоченная колода:') ;
for k:=0 to 35 do begin
a[k]:=k; write(a[k]:4);
end;
writeln;
for j:=0 to 4 do begin
mixer(a);
writeln('Перетасованная колода:');
for k:=0 to 35 do
write(a[k]:4);
writeln;
end;
readln;
end.
Задание 4.11. Игра в НИМ
Правила игры:
Совет 1 (общий)
Совет 2 (общий)
Совет 3 (общий)
Программа 4_11.bas
DECLARE SUB USER()
DECLARE SUB START{)
DECLARE SUB COMPUTER()
DECLARE SUB PRINTXOD(col%,msg$)
DEFINT A-Z
DIM SHARED N
DIM SHARED В AS INTEGER,S AS INTEGER,M AS INTEGER,Q AS INTEGER
N=5: Q=12
DIM SHARED A(N) AS INTEGER,I AS INTEGER,J AS INTEGER,К AS INTEGER
M=l
START m1:
USER
COMPUTER
GOTO ml END
SUB COMPUTER S=0
FOR I=0 TO K-1: S=S XOR A(I): NEXT I
IF s=o THEN
J=0: S=A(0)
FOR I=1 TO K-1
IF S
B=l
NEXT I ELSE
FOR J=0 TO K-1
B=A(J)-(A(J) XOR S)
IF B>=0 THEN EXIT FOR NEXT J END IF
A(J)=A(J)-B
PRINTXOD 4, "Победил компьютер"
END SUB
SUB PRINTXOD(col%,msg$) COLOR col%, 0 FOR I=0 TO K-1
LOCATE M+l,3*I+1: PRINT USING "###";A(I)
NEXT I
M=M+1: IF M>23 THEN M=2: CLS: PRINTXOD col%, msg$'
S=0
FOR J=0 TO K-l: S=S+A(J): NEXT J
IF S<>0 THEN EXIT SUB LOCATE M,2: PRINT msg$ SLEEP STOP
END SUB
SUB START
CLS : RANDOMIZE (VAL(RIGHTS(TIME$, 2)))
K=INT(RND*(N-3))+3: ' число кучек
FOR I=0 TO K-l
A(I)=INT(RND*Q)+1
NEXT I
LOCATE 1,2 : PRINT "Начало игры"
PRINTXOD 4,"" END SUB
SUB USER COLOR 2,0
LOCATE M, 20
PRINT "Ваш ход (кучка - сколько берем):"
М2:
LOCATE M, 33: PRINT ""
LOCATE M,33: INPUT J
IF (J<1) OR (J>K) OR (A(J-1)=0) THEN GOTO M2
m3:
LOCATE M, 35: PRINT "-"
LOCATE M, 37: INPUT В
IF (B<1) OR (B>A(J-1J) THEN GOTO m3
A(J-1)=A(J-1)-B SLEEP
PRINTXOD 2, "Вы победили"
END SUB
Программа 4_11.c
#include
#include
#include
void print_xod(int color,char *msg);
void start(void);
void user(void);
void computer(void);
#define N 5
#define Q 12
int i,j,k,b,s,m=l;
int a[N];
main() {
start(); ml:
user () ;
computer() ;
goto ml; }
void start(void) {
clrscr();
randomize();
k=random(N-3)+3; /* число кучек */
for(i=0; i
print_xod(RED,"Начало игры"); }
void user(void) {
textcolor(GREEN);
gotoxy(20,m-l); cprintf("Ваш ход (кучка - сколько берем):");
m2:
gotoxy(33,m);
cprintf(" ") ;
gotoxy(33,m);
scanf("%d",&j);
if((j
m3:
gotoxy(35,m); cprintf("- ") ;
gotoxy(37,m); scanf("%d",&b);
if((b
a[j-l]-=b;
print_xod(GREEN,"Вы победили");
return; }
void computer(void) {
for(s=0, i=0; i
if(s==0) {
for(i=l,j=0,s=a[0]; i
else
for(j=0; j
if(b>=0) break;}
a[j]-=b;
print_xod(RED,"Победил компьютер");
return; }
void print_xod(int color,char *msg) (
textcolor(color);
for(i=0; i
gotoxy(3*i+l,m) ;
cprintf("%3d",a[i]);}
m++;
if(m>23)
{
m=2;
clrscr();
print_xod( color, msg) ;
}
for(j=0,s=0; j
if(s!=0) return;
gotoxy(l,m);
cprintf("%s",msg);
getch();
exit(0); }
Программа 4_11.pas
program nim; uses Crt; const
n=5; q=12; var
i,j,k,b,s,m:integer; a:array [l..n] of byte; label ml;
procedure print_xod(color:integer);
begin textcolor(color);
for i:=l to k do begin
gotoxy(3*i,m);
write(a[i]:2);
end;
m:=m+l;
if m > 23 then begin clrscr;
m:= 2;
print_xod(color);
end;
end;
procedure start;
begin
clrscr; randomize;
k:=random(n-3)+3; {число кучек}
m:=1;
if m>23 then begin clrscr;
m:=2;
print_xod(color);
end;
for i:=l to k do
a[i]:=random(q)+1;
print_xod(RED);
end;
procedure user;
label m2,m3;
begin
textcolor (GREEN) ;
gotoxy(20,m-1);
write('Ваш ход (кучка - сколько берем):');
m2:
gotoxy(33,m); write(' ');
gotoxy(33,m) ; read(j);
if(j
m3:
gotoxy(35,m);
write('- ');
gotoxy(37,m);
read(b);
if(b
a[j]:=a[j]-b;
print_xod(GREEN);
end;
procedure computer;
begin s:=0;
for i:=l to k do s:=s xor a[i];
if s=0 then begin s:=a[l];
j:=l;
for i:=2 to k do
if s
s:=a[i];
j:=i;
end;
b:=l;
end
else
for j:=l to k do begin b:=a[j]-(a[j] xor s) ;
if b>=0 then break; end;
a[j]:=a[j]-b;
print_xod(RED);
end;
begin
start;
ml : user;
s:=0;
for j:=l to k do s:=s+a[j];
if s=0 then begin
gotoxy(1,m);
write('Вы победили');
readln; readln;
exit; end;
computer; s:=0;
for j:=l to k do s:=s+a[j];
if s<>0 then goto ml;
gotoxy(l,m);
write('Победил компьютер');
readln;
readln;
end.
Задание 4.12. Игра "крестики-нолики"
Составить программу для игры в крестики- нолики на поле размером 3x3. Правила игры: играют двое, делая последовательные ходы в клетках игрового поля. Первый игрок ставит крестики, второй — нолики. Выигрывает тот, кому первому удастся разместить три своих символа на одной из восьми игровых линий (три горизонтали, три вертикали, две диагонали). Если на поле после девятого хода выигрышная ситуация не выстроена, то считается, что игра закончилась вничью. Многими докомпьютерными поколениями подтверждено, что при "правильном" поведении обоих игроков, каждому из них обеспечена, как минимум, ничья. И только при явной ошибке партнера создается выигрышная ситуация для его оппонента.
Беспроигрышная тактика для первого игрока заключается в соблюдении трех следующих правил:
a) если обнаружена линия, на которой расположены два крестика и есть свободное поле (выигрышная ситуация), заполните его;
b) если ситуация а) не обнаружена, но имеет место выигрышная позиция для противника, воспрепятствуйте этому;
c) если не обнаружена ни ситуация а), ни ситуация Ь), то поставьте крестик на любое свободное поле.
Для второго игрока беспроигрышная тактика заключается в соблюдении следующих правил:
a) если обнаружена линия, ведущая к победе, сделайте решающий ход;
b) если своего выигрышного хода нет, воспрепятствуйте выигрышу первого игрока;
c) если не обнаружена ни ситуация а), ни ситуация b), то ставьте нолик на любое свободное поле.
Совет 1 (общий)
Выбор конфигурации рабочего поля. Не будем усложнять программу графическими процедурами, остановимся лишь на работе дисплея в текстовом режиме. Для того чтобы приблизить конфигурацию рабочего поля к квадрату, разумно выбрать соотношение сторон клетки 5 (по горизонтали) к 3 (по вертикали) и размещать символ в центральной позиции такого прямоугольника.
Нумерация позиций игрового поля, привязка к экрану и хранение информации о ходах. Пронумеруем клетки рабочего поля слева направо и сверху вниз от 1 до 9 и сопоставим содержимое центра каждой клетки с элементом целочисленного массива а:
Центры клеток в относительных номерах столбцов (х) и строк (у) имеют следующие координаты:
В программе массив роз заполнен элементами, соответствующими экранным координатам позиций игрового поля.
Нумерация игровых линий.
Пронумеруем линии числами от 1 до 8 следующим образом:
Обратите внимание на массив lines, каждая тройка элементов которого соответствует одной из игровых линий.
Отображение игрового поля. Воспроизведение контуров игрового поля осуществляется выводом семи строковых констант, состоящих из нужной цепочки символов псевдографики. Для отображения сделанных ходов организуем цикл перебора элементов массива а и выводим в центрах каждой клетки символ, соответствующий значению элемента a[j]. В программе для этой цели использована процедура show(j, k), которая совмещает описанные выше действия с предварительной засылкой числа k в элемент а [ j ] (параметр k может принимать значения +2 или -2, в зависимости от того, кем был сделан текущий ход). После отображения игрового поля курсор переводится в центр, т. к. из него можно добраться до любой игровой клетки самым быстрым способом.
Ввод хода игрока. Для индикации хода человека используется процедура input (в программе на QBasic—USER, т. к. слово INPUT является служебным). Она предоставляет возможность перемещать курсор по центральным позициям игрового поля с помощью стрелок на клавиатуре. В выбранной позиции человек должен нажать клавишу
Выполнение первого хода программы (в приводимых ниже программах первый ход делает компьютер, реализация второго варианта вносит очень небольшие изменения в текст головной программы). Реализуется непосредственным обращением к процедуре show (5, 2).
Выполнение второго хода компьютера. На любой из возможных восьми ходов человека предусмотрен фиксированный ответ — если человек выбрал клетку с номером j (j = l, 2, 3, 4, б, 7, 8 или 9), то второй ход программы определяется значением элемента массива b [ j ].
Выполнение последующих ходов компьютера. Осуществляется процедурой step345, действия которой сводятся к следующим акциям:
Определение выигрышной ситуации. Организуем цикл перебора игровых линий с суммированием элементов a[j], соответствующих клеткам, через которые проходит линия. Если полученная сумма равна 4, то на данной линии находятся два крестика и имеется свободное поле. В него и надо поставить очередной крестик, чтобы победить. Этот анализ выполняется с помощью функции xod(k1 = 2, k2 = 2). Она пытается найти линию, в которой сумма элементов а [ j ] равна 2*k1, и, если таковая находится, заносит в "свободный" элемент линии число k2. Функция xod принимает значение "истина", если победный ход был сделан.
Определение угрожающей ситуации со стороны второго игрока. Организуем аналогичный цикл и, если получена сумма, равная -4, то найдена линия, в которой находится два нолика и имеется свободная позиция. В нее и нужно поставить очередной крестик, чтобы воспрепятствовать выигрышу соперника. Этот анализ тоже выполняет функция xod, но теперь ее аргументы k1 = -2 и k2 = 2. Если угрожающую линию удалось закрыть, то функция xod принимает значение "истина".
Определение свободного поля. Если речь идет о линии, то номера перебираемых элементов определяются соответствующей тройкой из массива lines. Если нужно сделать несущественный ход, то можно перебирать элементы массива а подряд.
Определение результата игры. В случае обнаружения выигрышной позиции надо зафиксировать победный ход и сообщить о победе компьютера. Для обнаружения ничейной ситуации можно ограничиться подсчетом абсолютных значений элементов а [ j ]. После девятого хода, заполняющего рабочее поле, там находится пять величин, соответствующих ходам программы (+2), и четыре величины, фиксировавших ходы человека (-2). Так что общая сумма элементов (по модулю) будет равна 18. Конечно, о ничейном результате можно было бы догадаться и раньше, но такой анализ несколько утяжелил бы программу.
Совет 2 (QBasic)
Совет 3 (Си, Паскаль)
Программа 4_12.bas
DECLARE SUB STEP345()
DECLARE SUB RESULT(s$)
DECLARE SUB CURIND(cur%,porog%,dcur%,dind%)
DECLARE SUB SHOW(k%,c%)
DECLARE SUB USER()
Обратите внимание на массив lines, каждая тройка элементов которого соответствует одной из игровых линий.
Отображение игрового поля. Воспроизведение контуров игрового поля осуществляется выводом семи строковых констант, состоящих из нужной цепочки символов псевдографики. Для отображения сделанных ходов организуем цикл перебора элементов массива а и выводим в центрах каждой клетки символ, соответствующий значению элемента a[j]. В программе для этой цели использована процедура show(j, k), которая совмещает описанные выше действия с предварительной засылкой числа k в элемент а [ j ] (параметр k может принимать значения +2 или -2, в зависимости от того, кем был сделан текущий ход). После отображения игрового поля курсор переводится в центр, т. к. из него можно добраться до любой игровой клетки самым быстрым способом.
Ввод хода игрока. Для индикации хода человека используется процедура input (в программе на QBasic — USER, т. к. слово INPUT является служебным). Она предоставляет возможность перемещать курсор по центральным позициям игрового поля с помощью стрелок на клавиатуре. В выбранной позиции человек должен нажать клавишу
Выполнение первого хода программы (в приводимых ниже программах первый ход делает компьютер, реализация второго варианта вносит очень небольшие изменения в текст головной программы). Реализуется непосредственным обращением к процедуре show(5, 2).
Выполнение второго хода компьютера. На любой из возможных восьми ходов человека предусмотрен фиксированный ответ — если человек выбрал клетку с номером j (j =l, 2, 3, 4, б, 7, 8 или 9), то второй ход программы определяется значением элемента массива b [ j ].
Выполнение последующих ходов компьютера. Осуществляется процедурой step345, действия которой сводятся к следующим акциям:
Определение выигрышной ситуации. Организуем цикл перебора игровых линий с суммированием элементов a[j], соответствующих клеткам, через которые проходит линия. Если полученная сумма равна 4, то на данной линии находятся два крестика и имеется свободное поле. В него и надо поставить очередной крестик, чтобы победить. Этот анализ выполняется с помощью функции xod(k1 = 2, k2 = 2). Она пытается найти линию, в которой сумма элементов а [ j ] равна 2*k1, и, если таковая находится, заносит в "свободный" элемент линии число k2. Функция xod принимает значение "истина", если победный ход был сделан.
Определение угрожающей ситуации со стороны второго игрока. Организуем аналогичный цикл и, если получена сумма, равная -4, то найдена линия, в которой находится два нолика и имеется свободная позиция. В нее и нужно поставить очередной крестик, чтобы воспрепятствовать выигрышу соперника. Этот анализ тоже выполняет функция xod, но теперь ее аргументы kl = -2 и k2 = 2. Если угрожающую линию удалось закрыть, то функция xod принимает значение "истина".
Определение свободного поля. Если речь идет о линии, то номера перебираемых элементов определяются соответствующей тройкой из массива lines. Если нужно сделать несущественный ход, то можно перебирать элементы массива а подряд.
Определение результата игры. В случае обнаружения выигрышной позиции надо зафиксировать победный ход и сообщить о победе компьютера. Для обнаружения ничейной ситуации можно ограничиться подсчетом абсолютных значений элементов а [ j ]. После девятого хода, заполняющего рабочее поле, там находится пять величин, соответствующих ходам программы (+2), и четыре величины, фиксировавших ходы человека (-2). Так что общая сумма элементов (по модулю) будет равна 18. Конечно, о ничейном результате можно было бы догадаться и.раньше, но такой анализ несколько утяжелил бы программу.
Совет 2 (QBasic)
Совет 3 (Си, Паскаль)
Программа 4_12.bas
DECLARE SUB STEP3450
DECLARE SUB RESULT(s$)
DECLARE SUB CURIND(cur%,porog%,dcur%,dind%)
DECLARE SUB SHOW(k%,c%)
DECLARE SUB USER()
DECLARE FUNCTION XOD!(k%,kl%)
DEFINT A-Z
DIM SHARED POS1(1 TO 18) AS INTEGER,lines(0 TO 23) AS INTEGER
DIM SHARED A(l TO 9) AS INTEGER,b(l TO 9) AS INTEGER
DIM SHARED x0 AS INTEGER,у0 AS INTEGER
DIM SHARED Ind AS INTEGER,CurX AS INTEGER,CurY AS INTEGER
FOR k=l TO 9: A(k)=0: NEXT k
DATA 3,1,1,1,5,3,1,7,3
FOR k=l TO 9: READ b(k): NEXT k x0=l: y0=l
DATA 3,2, 7, 2, 11, 2, 3,4,
7, 4, 11, 4,3, 6, 7, 6, 11, 6
FOR k=l TO 18: READ POSl(k): NEXT k
DATA 1,2,3,4,5,6,7,8,9,1,4,7,
2,5,8,3,6,9,1,5,9,3,5,7
FOR k=0 TO 23: READ lines(k): NEXT k
CLS
SHOW 5,2 ' Первый ход программы
USER ' Ввод 1-го хода игрока
FOR J=l TO 9 ' Второй ход программы
IF A(J)=-2 THEN SHOW b(J),2: EXIT FOR NEXT J
m2: USER ' Ввод последующих ходов игрока
STEP345 ' Последующие ходы программы
GOTO m2 END
DEFSNG A-Z
SUB CURIND(cur%,porog%,dcur%,dind%)
IF curoporog THEN cur=cur+dcur: Ind=Ind+dind END SUB
DEFSNG A-Z SUB RESULT(s$)
LOCATE 1,40: PRINT s$: END END SUB
DEFINT A-Z
SUB SHOW(k%,C%) DEFINT A-Z CLS
LOCATE x0,y0: PRINT "+-------------------+"
LOCATE x0+l,y0: PRINT "| | | |"
LOCATE x0+2, y0: PRINT " |-----|-----|-----| "
LOCATE x0+3,y0: PRINT "| | | |"
LOCATE x0+4,y0: PRINT "|-----|-----|-----|"
LOCATE x0+5,y0: PRINT "| | | |"
LOCATE x0+6,y0: PRINT "+-----+-----+-----+"
A(k%)=c% FOR J=l TO 9
LOCATE y0-l+POSl(J*2),x0-1+POSl(J*2-l)
IF A(J)=2 THEN PRINT "X"
IF A(J)=-2 THEN PRINT "0" NEXT J
CurX=xO+6: CurY=y0+3: Ind=5 LOCATE CurY,CurX,l END SUB
SUB STEPS45 DEFINT A-Z
IF XOD(2,2)=1 THEN RESULT "Победа компьютера": END
IF XOD(-2,2)=1 THEN EXIT SUB
FOR J=l TO 9
IF A(J)=0 THEN SHOW J,2: EXIT FOR
NEXT J END SUB
DEFSNG A-Z
SUB USER
DEFINT A-Z
Left=75: Right=77: Up=72: Down=80: Enter=13 k=0:
FOR J=l TO 9: k=k+ABS(A(J)): NEXT J IF k=18 THEN RESULT "Боевая ничья": END
m: ch$=INKEY$:
IF LEN(ch$)=0 THEN GOTO m
SELECT CASE ASC(RIGHTS(ch$,1))
CASE Left: CURIND CurX,3,-4,-l
CASE Right: CURIND CurX,ll,4/l
CASE Up: CURIND CurY,2,-2,-3
CASE Down: CURIND CurY,6,2,3
CASE Enter:
IF A(Ind)=0 THEN SHOW Ind,-2:
EXIT SUB
CASE ELSE: BEEP END SELECT
LOCATE y0-l+CurY,x0-l+CurX,l USER END SUB
DEFINT A-Z FUNCTION XOD(k%,kl%)
DIM J AS INTEGER,m AS INTEGER,p AS INTEGER XOD=0
FOR J=0 TO 7 m=J*3
IF A(lines(m))+A(lines(m+1))+A(lines(m+2))=2*k% THEN XOD=1
FOR p=m TO m+2
IF A(lines(p))=0 THEN SHOW lines(p),kl% EXIT FUNCTION END IF NEXT p
END IF NEXT J END FUNCTION
Программа 4_12.с
#include
#include
void input(void);
void cur_ind(int *cur,int porog,int dcur,int dind);
void step345(void);
int xod(int k, int kl);
void showfint k, int c);
void result(char *s);
int a[9]={0,0,0,0,0,0,0,0,0}, b[9]={3,l,l,l,5,3,l,7,3},
х0=1, у0=1, j, CurX, CurY, Ind; main()
{
clrscr();
window(x0,y0,x0+13,y0+7);
show(5,2); /* Первый ход программы */
input(); /* Ввод 1-го хода игрока */
for(j=0; j<9; j++) /* Второй ход программы */
if (a[j]==-2) { show(b[j],2); break; }
m2:
input(); . /* Ввод последующих ходов игрока */
step345(); /* Последующие ходы программы */
goto m2;
}
/*--------------------------------*/
void result(char *s) {
window(40,l,60,2);
puts(s);
getch () ;
exit(0);
}
/*-------------------------------*/
void show(int k,int c) {
char pos[18]=(3,2,7,2,11,2,3,4,7,4,11,4,3,6,7,6,11,6};
char j;
clrscr ();
printf("+-----------+\n");
printf("| | | |\n");
printf ( "|----|----|----| \n") ;
printf("| | | |\n");
printf (" |----|----|----| \n"} ;
printf("| | | |\n");
printf ("+----------------+") ;
a[k-l]=c;
for(j=0; j<9; j++) {
gotoxy(x0-l+pos[j*2],y0-l+pos[j*2+l]);
if(a[j]==+2) printf("X");
if(a[j]==-2) printf("0"); }
CurX=x0+6; CurY=y0+3; Ind=5; gotoxy(CurX,CurY);
}
/*-------------------------------*/
int xod(int k, int k1) {
char line[24]={1,2,3,4,5,6,7,8,9,1,
4,7,2,5,8,3,6,9,1,5,9,3,5,7},
j,m,p;
for(j=0; j<8; j++)
{
m=j*3;
if(a[line[m]-1)+a[line[m+1]-1]+a[line[m+2]-1]==2*k)
{
printf ("\nm=%d",m) ; for(p=m; p
show(line[p],kl); return 1; } } } return 0;
}
/*-------------------------------------* /
void step345(void)
{
if(xod( 2,2)) result("Победа компьютера");
if(xod(-2,2)) return;
for(j=0; j<9; j++)
if(a[j]==0) {
show(j+l,2); break;
} }
/*----------------------------*/
void cur_ind(int *cur, int porog, int dcur, int dind) {
if( *cur != porog) {
*cur += dcur;
Ind += dind; }
}
/*----------------------------*/
void input(void) {
int ch, j, k;
for(k=0, j=0; j<9; j++) k+=abs(a[j]);
if(k==18) result("Боевая ничья");
ch=getch(); if(ch==0) ch=getch();
switch (ch)
{
case 75: cur_ind(&CurX, 3,-4,-l);break; /*Left*/
case 77: cur_ind(&CurX,11, 4, 1); break; /*Right*/
case 72: cur_ind(&CurY, 2,-2,-3); break; /*Up*/
case 80: cur_ind(&CurY, 6, 2, 3); break; /*Down*/ case 13:
printf("\nInd=%d",Ind); /*Enter*/
if(a[Ind-l]==0)
{ show(Ind,-2); return;}
else
printf("%c",0x7);
break;
default: printf("%c",0x7); }
gotoxy(x0-l+CurX,y0-l+CurY);
input(); }
Программа 4_12.pas
program krestiki;
uses Crt;
label m2;
const
a-.array [1..9] of integer = (0,0,0,0,0,0,0,0,0);
b:array [1..9] of byte = (3,1,1,1,5,3,1,7,3);
x0=5; y0=5;
var
j, CurX, CurY, Ind : word; procedure result(s:string);
begin
window(40,1,60,2);
write(s);
readln; halt; end;
procedure show(k,с:integer) ;
const
pos:array [1..18] of byte = (3,2,7,2,11,2,3,4,7,4,11,4,3,6,7,6,11,6);
var
j:byte;
x,у:word;
begin
clrscr;
writeln (' +----+----+----+')
writeln('| | | |')
writeln (' |----|----|----| ')
writeln('| | | |')
writeln(' |----|-----|-----|')
writeln('| | | |')
write (' +----+----+----+')
a[k]:=c;
for j:=1 to 9 do begin
x:=pos[(j-l)*2+l]; y:=pos[(j-1)*2+2];
gotoxy(x,y);
if a[j]=+2 then write('X');
if a[j]=-2 then write('0');
end;
CurX:=7; CurY:=4; Ind:=5;
gotoxy(CurX,CurY); end;
function xod(k,kl:integer):boolean;
const
line:array [0..23] of byte=
(1, 2, 3,4, 5, б, 7, 8, 9,1,4, 7, 2, 5, 8, 3,6, 9,1,5, 9, 3,5,7) ;
var
j,m,p:byte; begin
xod:=false; for j:=0 to 7 do begin m:=j*3;
if a[line[m]]+a[line[m+1]]+a[line[m+2]]=2*k then begin
xod:=true;
for p:=m to m+2 do
if a[line[p]]=0 then
begin
show(line[p],kl);
exit;
end;
end;
end;
end;
procedure step345; begin
if xod( 2,2) then result('Победа компьютера');
if xod(-2,2) then exit;
for j :=1 to 9 do if a[j]=0 then begin
show(j,2);
break;
end;
end;
procedure input; const
Left=#75;
Right=#77;
Up=#72;
Down=#80;
Enter=#13; var
ch:char;
j,k:byte;
procedure cur_ind(var cur:word;porog,dcur,dind:integer) ;
begin
if cur <> porog then begin
cur:=cur+dcur;
Ind:=Ind+dind; end;
end; begin
k:=0;
for j:=l to 9 do
k:=k+abs(a[j]);
if k=18 then result('Боевая ничья');
ch:=readkey;
if ch=#0 then ch:=readkey;
case ch of
Left: cur_ind(CurX, 3,-4,-l);
Right: cur_ind(CurX,11, 4, 1);
Up: cur_ind(CurY, 2,-2,-3);
Down: cur_ind(CurY, 6, 2, 3);
Enter: if a[Ind]=0 then begin
show(Ind,-2);
exit;
end
else write(tt7);
else write(#7); end;
gotoxy(CurX,Cury);
input; end; begin
clrscr;
window(x0,y0,x0+13,y0+7);
show(5,2);
{ Первый ход программы }
input; { Ввод 1-го хода игрока }
for j:=1 to 9 do { Второй ход программы }
if a[j]=-2 then
begin show(b[j],2);
break;
end;
m2: input; { Ввод последующих ходов игрока }
step345; { Последующие ходы программы }
goto m2;
end.
Задание 4.13. Слияние массивов
Составить процедуру, которая объединяет два предварительно упорядоченных по возрастанию массива, получая в результате массив с возрастающими по величине элементами.
Совет 1 (общий)
текущий указатель в массиве, из которого на предыдущем шаге был выбран минимальный элемент. Однако предварительно разумно проверить, не исчерпан ли уже один из массивов.
Программа 4_13.bas
DECLARE SUB MERGE (A%(),NA%,B%(),NB%,C%())
DEFINT A-Z
CLS
NA=3:
DIM A(NA)
DATA 0,2,4
FOR K=0 TO NA-1: READ A(K): PRINT A(K); : NEXT K: PRINT
NB=4
DIM B(NB)
DATA 1,3,5,7
FOR K=0 TO NB-1: READ B(K): PRINT B(K); : NEXT K: PRINT
DIM C(NA+NB)
MERGE A(),NA,B(),NB,C()
FOR K=0 TO NA+NB-1: PRINT C(K); : NEXT К
END
SUB MERGE(A(),NA,В(),NB,С())
JA=0: JB=0
FOR JC=0 TO NA+NB-1
IF JA=NA THEN GOTO MB
IF JB=NB THEN GOTO MA
IF A(JA)
NEXT JC
END SUB
Программа 4_13.с
#include
#include
void merge(int *a,int ka,int *b,int kb,int *c);
main() {
#define na 3
#define nb 4
int j,a[na]={0,2,4},b[nb]={l,3,5,7},c[na+nb];
clrscr();
for(j=0; j
printf("\n");
for(j=0; j
printf("\n");
merge(a,na,b,nb,c);
for(j=0; j
getch(); }
void merge(int *a,int ka,int *b,int kb,int *c) {
int ja=0,jb=0,jc;
for(jc=0; jc
if (ja==ka) goto mb;
if (jb==kb) goto ma;
if (a[ja]
c[jc]=b[jb];
jb++;
continue;
ma:
c[jc]=a[ja];
ja++;
} }
Программа 4_13.pas
program merge2;
uses Crt;
const
na=3 ;
nb=2 ;
a:array [0..na] of integer = (0,2,4,6);
b:array [0..nb] of integer = (1,3,5);
var
c:array [0..na+nb+l] of integer;
j:integer;
procedure merge(a,b:array of integer;var c:array of integer);
var
ja,jb,jc,na,nb,nc:integer;
label ma, mb;
begin
na:=High(a); ja:=0;
nb:=High(b);
jb:=0;
nc:=High(c);
if nc < na+nb+1 then begin
writeln('Массив с слишком мал');
exit;
end;
for jc:=0 to na+nb+1 do begin
if ja > na then goto mb;
if jb > nb then goto ma;
if a[ja] < b[jb] then goto ma;
mb:
с[jc]:=b[jb]; inc(jb);
continue;
ma:
с[j с]:=a[j a];
inc(j a};
end;
end;
begin clrscr;
for j:=0 to na do
write(a[j]:4);
writeln;
for j:=0 to nb do
write(b[j]:4) ;
writeln; merge(a,b,c);
for j:=0 to na+nb+1 do
write(c[j]:4) ;
readln; end.
Задачи,советы и ответы
Глава 5.Задачи,советы и ответы
Инфляция
Персонаж без которого невозможно представить не один разговор "за экономику". По мне, так это слова братья. Без экономики не бывает инфляции, а без инфляции не живет экономика. Они зачем-то нужны дружка дружке. Зачем? Я кажется знаю ответ - чтобы был повод поднимать цены.Анализ инфляции
Антиинфляция и инфляция
Инфляция и банки
Инфляция в России
Управление инфляцией
Сущность инфляции
Теория инфляции
Оформление и вызов программных единиц в системе QBasic
считается рекурсивной, если она пытается
Рекурсивные функции и процедуры
В простейшем варианте процедура (функция) считается рекурсивной, если она пытается вызвать сама себя. Математики нередко прибегают к рекурсивному определению функций:
n! = n*(n-1)!
Естественно, что при таком хождении "по кругу" должно быть предусмотрено условие выхода, иначе вычислительный процесс может продолжаться бесконечно долго. В примере с факториалом тело процедуры на Паскале может выглядеть следующим образом:
if n < 2 then fact:=l else fact:=n*fact(n-1);
В более сложных вариантах рекурсивная процедура входит в состав двух или более процедур, последняя из которых вновь обращается к начальной:
А -> В -> А -> В -> А ...
В язык Паскаль, требующий описать любой объект до его использования, пришлось включить специальное опережающее объявление рекурсивных процедур, сопровождаемое служебным словом forward:
{ Опережающее объявление первой в цепочке процедуры А }
procedure А(<список параметров>);
forward; { Описание последней в цепочке рекурсивной процедуры В }
procedure В(<список параметров>);
begin
А(...); { Вызов рекурсивной процедуры А }
end; { Описание первой в цепочке рекурсивной процедуры А }
procedure A; { Здесь можно не повторять список аргументов } begin
В (...); { Вызов рекурсивной процедуры В } end;
Несмотря на все изящество рекурсивных программ, их работа сопряжена с повышенными затратами машинного времени и ресурсов по памяти. При каждом новом вызове рекурсивной процедуры приходится сохранять значения всех ее локальных переменных и выделять новые участки памяти для очередной порции локальных данных. Как правило, рекуррентный алгоритм с большими или меньшими усилиями можно превратить в обычный циклический процесс. Например, фрагмент программы, вычисляющей n!, может выглядеть следующим образом:
Р = =1;
for i:=l to n do p:=p*i;
fact:=p;
Однако, как бы ни относились разные программисты к рекурсии, следует признать, что некоторые рекурсивные программы выглядят очень эффектно и их алгоритмы оказываются намного более прозрачными (см., например, процедуру быстрой сортировки quicksort илиигровую программу "Ханойские башни").
когда итальянский математик Леонардо Пизанский
Задание 5.01. Числа Фибоначчи
История чисел Фибоначчи восходит к началу XIII в., когда итальянский математик Леонардо Пизанский нашел изящное решение задачи о размножении кроликов. Пусть в начале эксперимента имеется единственная пара -самец и самка, которые приносят каждый месяц приплод, состоящий также из самца и самки. Дети включаются в цикл продолжения рода через два месяца. Требуется определить количество пар, спустя k месяцев после начала эксперимента. Ситуация не так уж и сложна:
Леонардо догадался, что числа указанной последовательности связаны рекуррентным соотношением:
fk = fk-2 + fk-1
В разных учебниках последовательность чисел Фибоначчи дополняют либо еще одной единицей, либо нулем и единицей:
1,1,2,3,5,8,13,21,34,55,...
0,1,1,2,3,5,8,13,21,34,.....
Последний вариант принят в приводимых ниже программах, отсчет порядковых номеров чисел Фибоначчи ведется от 0. Диапазон действия этих программ не так уж велик: fit>(22)=17711, fib(23) =28657 и уже 24-е число выходит за пределы предусмотренного диапазона. Если вас заинтересуют числа с большими номерами, то можно изменить тип функции fib или воспользоваться формулой Бинэ:
f ib (k) = ( ( (1+sqrt (5) ) /2)*k- ( (1-sqrt (5) ) /2} ^k) /sqrt (5)
Наиболее известное применение чисел Фибоначчи — оптимальный выбор точек при поиске экстремума унимодальной функции на заданном отрезке. Рекурсивная реализация нахождения чисел Фибоначчи абсолютно неэффективна, т. к. в теле процедуры при каждой итерации происходит два обращения к этой же процедуре и объем вычислений с ростом k возрастает почти в геометрической профессии.
Программа 5_01.bas
DECLARE FUNCTION FIB%(N%)
INPUT " Задайте порядковый номер числа Фибоначчи - ",N%
PRINT "Число Фибоначчи с номером ";N%;" равно ";FIB%(N%)
END
FUNCTION FIB%(N%)
IF N% < 2 THEN
FIB%=N% ELSE
FIB%=FIB%(N%-2)+FIB%(N%-1)
END IF
END FUNCTION
Программа 5_01.с
#include
