Введение в схемы, автоматы и алгоритмы
Введение в схемы, автоматы и алгоритмы
Автоматическое зарядное устройство для автомобиля
Автоматическое зарядное устройство для автомобильных свинцово-кислотных аккумуляторов.
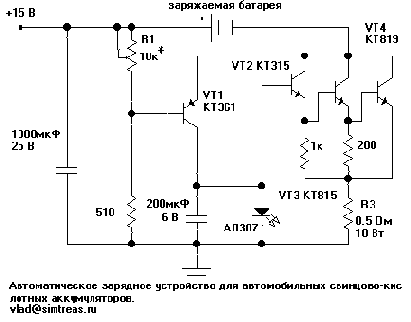
Данная схема позволяет автоматически заряжать автомобильные аккумуляторы.
Зарядный ток через батарею в зависимости от напряжения на ней (прикладываемого к Б-Э переходу VT1), регулируется транзистором VT1, коллекторным напряжением которого управляется индикатор заряда на светодиоде (по мере зарядки ток заряда уменьшается и светодиод постепенно гаснет) и мощный составной транзистор, содержащий VT2, VT3, VT4.
Резистор R3 ограничивает максимальный зарядный ток, поэтому он должен быть достаточно мощным, не менее 10 Вт, наверное лучше проволочным.
Момент полного заряда батареи (и уменьшение зарядного тока до нуля) определяет необходимое напряжение на ней - обычно достаточно 12.5 В (!). Konstantin (RK1NA) утверждает (и ,похоже, меня он тоже убедил), что электро-химические потенциалы используемых материалов свинцовых аккумуляторов позволяют обеспечить ПОЛНУЮ зарядку батареи лишь при напряжении в 13.8 В (!).
Т.е. необходимо устанавливать порог заряда чуть больше 13.8 В, например 13.9 В, при котором обеспечивается зарядка "до отказа", на полную емкость батареи.
Этот порог устанавливается резистором R1, порог зависит от типа применяемых транзисторов
Булевы функции от 1-ой и 2-х переменных
Перечислим вначале все булевы функции от 1-ой переменной
. Как мы знаем, их всего четыре.
- - константа 0;
- - константа 1;
- - тождественная функция;
- Эта функция называется отрицанием
и обозначается (используется также обозначение , а в языках программирования эта функция часто обозначается как ).
В следующей таблице представлены наиболее используемые 12 (из 16) функций от 2-х переменных.
Таблица 1.2. Булевы функции от 2-х переменных| | | | | | | | | | | | | |
0 0
0 1
1 0
1 1 | |
0
0
0
0 | |
1
1
1
1 | |
0
0
1
1
| |
1
1
0
0 | |
0
1
0
1 | |
1
0
1
0 | |
0
0
0
1 | |
0
1
1
1 | |
1
1
0
1 | |
0
1
1
0 | |
1
0
0
1 | |
1
1
1
0 | |
Многие из этих функций часто считаются "элементарными" и имеют собственные обозначения.
- - константа 0;
- - константа 1;
- - функция, равная 1-му аргументу;
- - отрицание ;
- - функция, равная 2-му аргументу;
- - отрицание ;
- - конъюнкция, читается " и " (используются также обозначения , , и AND ));
- - дизъюнкция, читается " или " (используются также обозначения , и OR ));
- - импликация, читается " влечет " или "из следует " (используются также обозначения , и ( IF THEN ));
- - сложение по модулю 2, читается " плюс " (используется также обозначение );
- - эквивалентность, читается " эквивалентно (равносильно) " (используется также обозначение );
- - штрих Шеффера (антиконъюнкция), иногда читается как "не и ".
В качестве элементарных функций будем также рассматривать 0-местные функции-константы 0 и 1.
Отметим, что функции
и
фактически не зависят от значений обоих аргументов, функции
и
не зависят от значений аргумента
, а функции
и
не зависят от значений аргумента
.
Определение 1.1. Функция
не зависит от аргумента , если для любого набора значений
остальных аргументов
имеет место равенство
. Такой аргумент
называется
фиктивным. Аргументы, не являющиеся фиктивными, называются
существенными.
Функции
и
называются равными, если функцию
можно получить из функции
путем добавления и удаления фиктивных аргументов.
Например, равными являются одноместная функция
и двухместная функция
, так как вторая получается из первой добавлением фиктивного аргумента
. Мы не будем различать равные функции и, как правило, будем использовать для обозначения равных функций одно и то же имя функции. В частности, это позволяет считать, что во всяком конечном множестве функций все функции зависят от одного и того же множества переменных.
Булевы функции от n переменных
Булевы функции1) названы в честь английского математика ХIХ века Дж. Буля, который впервые применил алгебраические методы для решения логических задач. Они образуют самый простой нетривиальный класс дискретных функций - их аргументы и значения могут принимать всего два значения. С другой стороны, этот класс достаточно богат и его функции имеют много интересных свойств. Булевы функции находят применение в логике, электротехнике, многих разделах информатики.
Обозначим через
двухэлементное множество
. Тогда
- это множество всех
двоичных последовательностей (наборов, векторов) длины
. Булевой функцией
от
переменных (аргументов) называется любая функция
. Каждый из ее аргументов
может принимать одно из двух значений 0 или 1 и значением функции на любом наборе из
также может быть 0 или 1. Обозначим через
множество всех булевых функций от
переменных. Нетрудно подсчитать их число:
Имеется несколько различных способов представления и интерпретации булевых функций. В этом разделе мы рассмотрим табличное представление, а также представление с помощью логических формул. В лекциях 2 и 3 будет рассмотрено еще два способа представления булевых функций: логические схемы и упорядоченные бинарные диаграммы решений.
Деревья
Деревья являются одним из интереснейших классов графов, используемых для представления различного рода иерахических структур.
Определение 1.10. Граф
называется деревом, если
- в нем есть одна вершина , в которую не входят ребра; она называется корнем дерева;
- в каждую из остальных вершин входит ровно по одному ребру;
- все вершины достижимы из корня.
На рисунке 2 показан пример дерева
С ориентированными деревьями связана богатая терминология, пришедшая из двух источников: ботаники и области семейных отношений.
Корень - это единственная вершина, в которую не входят ребра, листья - это вершины, из которых не выходят ребра. Путь из корня в лист называется ветвью дерева. Высота дерева - это максимальная из длин его ветвей. Глубина вершины - это длина пути из корня в эту вершину. Для вершины
, подграф дерева
, включающий все достижимые из
вершины и соединяющие их ребра из
, образует поддерево
дерева
с корнем
.
Высота вершины - это высота дерева
. Граф, являющийся объединением нескольких непересекающихся деревьев, называется лесом.
Рис. 1.2. Дерево G1
Если из вершины
ведет ребро в вершину
, то
называется
отцом , а
-
сыном (в последнее время в ангоязычной литературе употребляется асексульная пара терминов: родитель - ребенок). Из определения дерева непосредственно следует, что у каждой вершины кроме корня имеется единственный отец. Если из вершины
ведет путь в вершину
, то
называется
предком , а
-
потомком . Вершины, у которых общий отец, называются
братьями
или
сестрами.
Пример 1.4. В дереве на рис. 1.2
вершина
является корнем, вершины
- листья. Путь
- одна из ветвей дерева
. Вершина
является отцом (родителем) вершин
и
а каждая из этих вершин - ее сыном (ребенком). Между собой вершины
и
являются братьями (сестрами). Глубина
равна 1, а высота - 2. Высота всего дерева
равна 3.
Для деревьев часто удобно использовать следующее индуктивное определение.
Определение 1.11. Определим по индукции класс графов
, называемых деревьями. Одновременно для каждого из них определим выделенную вершину - корень.
- Граф , с единственной вершиной и пустым множеством ребер является деревом (входит в ).
Вершина называется корнем этого дерева. - Пусть графы с корнями принадлежат , а - новая вершина, т.е. . Тогда классу принадлежит также следующий граф , где , . Корнем этого дерева является вершина .
- Других графов в классенет.
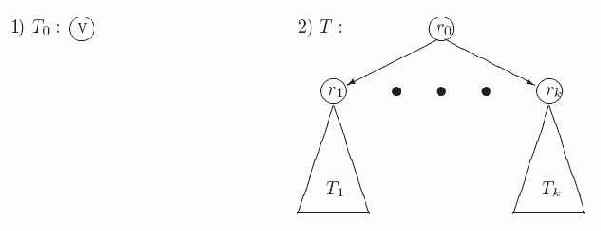
Рисунок 1.3 иллюстрирует это определение.
Рис. 1.3. Индуктивное определение ориентированных деревьев
Определения ориентированных деревьев 1.10 и 1.11 эквивалентны.
Выделим еще один класс графов, обобщающий деревья,
ациклические графы. Два вида таких размеченных графов будут использованы далее для представления булевых функций. У этих графов может быть несколько корней - вершин, в которые не входят ребра, и в каждую вершину может входить несколько ребер, а не одно, как у деревьев.
Дерево называется бинарным или двоичным , если у каждой его внутренней вершины имеется не более двух сыновей, причем ребра, ведущие к ним помечены двумя разными метками (обычно используются метки из пар: "левый" - "правый", 0 - 1,
- и т.п.)
Бинарное дерево называется
полным, если у каждой его внутренней вершины имеется два сына и все его ветви имеют одинаковую длину.
Дизъюнктивные и конъюнктивные нормальные формы
Имеется ряд специальных подклассов формул, позволяющих задавать все булевы функции. В этом разделе мы определим два таких подкласса функций, использующих только операции
и
.
Пусть
- это множество пропозициональных переменных. Введем для каждого
обозначения:
и
. Формула
(
), в которой
и все переменные разные, т.е.
при
, называется
элементарной конъюнкцией (элементарной дизъюнкцией).
Определение 1.4.Формула
называется дизъюнктивной нормальной формой (ДНФ), если она является дизъюнкцией элементарных конъюнкций, т.е. имеет вид
где каждая формула
- это элементарная конъюнкция.
называется совершенной ДНФ, если в каждую из ее конъюнкций
входят все
переменных из
Аналогично, формула
называется конъюнктивной нормальной формой (КНФ), если она является конъюнкцией элементарных дизъюнкций, т.е.
где каждая формула
- это элементарная дизъюнкция. Она является совершенной КНФ, если в каждую
входят все
переменных из
Рассмотрим произвольную булеву функцию
, зависящую от переменных из
. Oбозначим через
множество наборов значений переменных, на которых
принимает значение 1, а через
множество наборов, на которых
принимает значение 0, т.е.
и
Определим по этим множествам две формулы:
и
Теорема 1.1.
(1) Если функция
не равна тождественно 0, то формула
- это совершенная ДНФ, задающая функцию
.
(2) Если функция
не равна тождественно 1, то формула
- это совершенная КНФ, задающая функцию
.
Пример 1.2. Например, для функции
, представленной в таблице 1.1
совершенная ДНФ равна
, а ее совершенная КНФ:
Отметим, что совершенные ДНФ и КНФ часто являются чересчур сложными и длинными представлениями булевых функций. В нашем примере
может быть задана более простой ДНФ:
.
Формулы
Как мы видели, табличное представление булевых функций подходит лишь для функций с небольшим числом аргументов. Формулы позволяют удобно представлять многие функции от большего числа аргументов и оперировать различными представлениями одной и той же функции.
Мы будем рассматривать формулы, построенные над множеством элементарных функций
. Все эти функции, кроме констант, называются
логическими связками или
логическими операциями. При этом для 2-местных функций из этого списка будем использовать
инфиксную запись, в которой имя логической связки помещается между 1-ым и 2-ым аргументами.
Зафиксируем некоторое счетное множество переменных
. Определим по индукции
множество формул над с переменными из
. Одновременно будем определять числовую характеристику
формулы
, называемую ее глубиной, и множество ее подформул.
Определение 1.2.
а)
Базис индукции. 0, 1 и каждая переменная
является формулой глубины 0, т.е.
. Множество ее подформул состоит из нее самой.
б)
Шаг индукции. Пусть
и
- формулы,
. Тогда выражения
и
являются формулами. При этом
, а
. Множество подформул
включает саму формулу
и для
все подформулы формулы
, а для
все подформулы формул
и
Каждой формуле
сопоставим булеву функцию, которую эта формула задает, используя индукцию по глубине формулы.
Базис индукции. Пусть
. Тогда
или
В первом случае
задает функцию
, во втором - функцию, тождественно равную константе
.
Шаг индукции. Пусть
- произвольная формула глубины
. Тогда
или
для некоторой булевой связки
. Так как
то формулам
и
соответствующие функции
и
уже сопоставлены. Тогда формула
задает функцию
, а формула
задает функцию
.
Для определения функции, задаваемой небольшой формулой, удобно использовать таблицу, строки которой сответствуют наборам значений переменных, а в столбце под знаком каждой логической связки стоят значения функции, задаваемой соответствующей подформулой.
Пример 1.1. Например, для формулы
функция
задается выделенным столбцом
следующей таблицы.
Таблица 1.3. Функция | | | |
|
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
| |
0 0 0 1 0
0 0 0 1 0
0 1 1 0 1
0 1 1 0 1
1 1 0 1 0
1 1 0 1 0
1 1 1 0 1
1 1 1 0 1
| |
1
1
0
1
1
0
0
1
| |
0 0 0 0 1 0
1 1 0 0 1 0
0 0 0 0 0 1
1 1 0 0 0 1
0 1 1 1 1 0
1 0 1 1 1 0
0 0 1 0 0 1
1 1 1 0 0 1
| |
Каждая строка этой таблицы задает процесс вычисления функции
на соответствующих аргументах изнутри-наружу: вместо каждого вхождения переменной в формулу подставляется ее значение, затем в полученной формуле, состоящей из констант и булевых связок, последовательно вычисляются значения самых внутренних функций (подформул), для которых уже определены значения их аргументов, до тех пор, пока не будет получено значение всей формулы.
Графы
Мы часто сталкиваемся с задачами, в условиях которых заданы некоторые объекты и между некоторыми их парами имеются определенные связи. Если объекты изобразить точками (вершинами), а связи - линиями (ребрами), соединяющими соответствующие пары точек, то получится рисунок, называемый графом. Приведем основные определения.
Граф (ориентированный) - это пара
, где
- конечное множество вершин (узлов, точек) графа, а
- некоторое множество пар вершин, т.е. подмножество множества
или бинарное отношение на
. Элементы
называют ребрами (дугами, стрелками, связями). Для ребра
вершина
называется началом
, а вершина
- концом
, говорят, что ребро
ведет из
в
.
В графе полустепень исхода вершины - это число исходящих из нее ребер, а полустепень захода - это число входящих в данную вершину ребер.
Заметим, что в графе может быть ребро вида
, называемое
петлей.
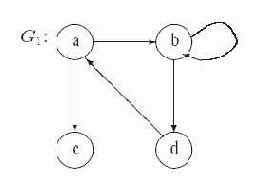
Пример 1.3. На рис. 1.1 приведен пример графа
. Здесь
, В графе
ребро
является петлей, полустепень исхода вершины
равна 2, а полустепень захода для нее равна 1.
Рис. 1.1. Граф G1
Во многих приложениях с вершинами и ребрами графов связывается некоторая дополнительная информация. Обычно она представляется с помощью функций разметки вершин и ребер.
Определение 1.6.
Размеченный граф - это граф
, снабженный одной или двумя функциями разметки вида:
и
, где
и
- множества меток вершин и ребер, соответственно.
Упорядоченный граф - это размеченный граф
, в котором ребра, выходящие из каждой вершины
, упорядочены, т.е. помечены номерами
, где
- полустепень исхода
, т.е.
.
Упорядоченный граф с полустепенью исхода вершин
называется бинарным.
В качестве множества меток ребер
часто выступают числа, задающие "веса", "длины", "стоимости" ребер. Графы с такой разметкой часто называют
взвешенными.
Часто на одном множестве объектов определено несколько различных бинарных отношений. Для представления такой ситуации служат мультиграфы.
Определение 1.7. Мультиграф
состоит из конечного множества вершин
и мультимножества ребер
состоящего из пар вершин
в которое эти пары могут входить по нескольку раз.
Обычно несколько ребер, соединяющих одну и ту же пару вершин, различаются метками - именами соответствующих бинарных отношений. В лекциях 4-6 мультиграфы будут использоваться для представления диаграмм конечных автоматов.
Во многих случаях естественно не различать графы, отличающиеся лишь именами (порядком) вершин.
Определение 1.8. Изоморфизм графов. Два графа
и
называются изоморфными, если между их вершинами существует взаимно однозначное соответствие
такое, что для любой пары вершин
из
ребро
ребро
.
Для изоморфизма размеченных графов требуется также совпадение меток соответствующих вершин :
и/или ребер:
.
Многие приложения графов связаны с изучением путей между их вершинами.
Определение 1.9.
Путь в (мульти)графе - это последовательность ребер вида
. Этот путь ведет из начальной вершины
в конечную вершину
и имеет длину
. В этом случае будем говорить, что
достижима из
. Будем считать, что каждая вершина достижима сама из себя путем длины 0. Путь в графе (не мультиграфе!) можно также определять как соответствующую последовательность вершин:
где
при
.
Путь назывется
простым, если все ребра и все вершины на нем, кроме, быть может, первой и последней, различны.
Циклом в графе называется путь, в котором начальная вершина совпадает с конечной и который содержит хотя бы одно ребро. Цикл
называется простым, если в нем нет одинаковых вершин, кроме первой и последней, т.е. если все вершины
различны.
Если в графе нет циклов, то он называется
ациклическим.
Следующее утверждение непосредственно следует из определений.
Лемма 1.1.Если в графе
имеется путь из вершины
в вершину
, то в нем имеется и простой путь из
в
.
Эквивалентность булевых формул
Определение 1.3.Булевы формулы
и
называются эквивалентными, если соответствующие им функции
и
равны.
Обозначение:
. Эквивалентные формулы называют также тождественно равными, а выражения вида
логическими тождествами.
Таким образом, эквивалентные формулы являются различными заданиями одной и той же булевой функции. Ниже мы приводим ряд пар эквивалентных формул (тождеств), отражающих существенные свойства логических операций и важные соотношения между различными операциями. Они часто позволяют находить для булевых функций по одним задающим их формулам более простые формулы. Большинство из приводимых тождеств имеют собственные имена. Часто их называют законами логики.
Пусть
- это одна из функций
. Для этих трех функций выполнены следующие две эквивалентности (законы ассоциативности и коммутативности).
(1) Ассоциативность:
(2) Коммутативность:
(3) Дистрибутивные законы:
(4) Двойное отрицание:
(5) Законы де Моргана (внесение отрицания внутрь скобок):
(6) Законы упрощения:
Некоторые законы упрощения имеют собственные названия: эквивалентности в первой строке называются
законами идемпотентности,
- это
закон противоречия,
- это
закон исключенного третьего.
Следующие две эквивалентности позволяют выразить импликацию и сложение по модулю 2 через дизъюнкцию, конъюкцию и отрицание.
Правильность этих эквивалентностей легко устанавливается прямым вычислением функций для их левых и правых частей.
Соглашения об упрощенной записи формул. Законы ассоциативности показывают, что значения формул, составленных из переменных и одних операций конъюнкции, не зависят от расстановки скобок. Поэтому вместо формул
и
мы будем для упрощения писать
Аналогично, будем использовать выражения
и
для сокращения формул, состоящих из одних дизъюнкций или одних сложений по модулю 2, соответственно. Будем также опускать внешние скобки в записи формулы, если ее внешней функцией является одна из функций
.
Таким образом, с использованием этих соглашений формула
может быть записана как
Табличное представление
Булевы функции от небольшого числа аргументов удобно представлять с помощью таблиц. Таблица для функции
имеет
столбец. В первых
столбцах указываются значения аргументов
, а в
-ом столбце значение функции на этих аргументах -
.
Таблица 1.1. Табличное представление функции | . . . | |
. . .
. . .
. . .
. . . . . .
. . .
| |
| |
Наборы аргументов в строках обычно располагаются в
лексикографическом порядке:
существует такое
, что при
а
. Если эти наборы рассматривать как записи чисел в двоичной системе счисления, то 1-ая строка представляет число 0, 2-ая - 1, 3-я - 2, ... , а последняя -
.
При больших
табличное представление становится громоздким, например, для функции от 10 переменных потребуется таблица с 1024 строками. Но для малых
оно достаточно наглядно.
Введение в схемы, автоматы и алгоритмы
Логические схемы (схемы из функциональных элементов)
Многие элементы в современной электронике являются устройствами, преобразующими некоторые входные сигналы (данные) в выходные. Логические схемы, в отечественной литературе чаще называемые схемами из функциональных элементов, представляют собой математическую модель таких устройств, в которых временем выполнения преобразования входов в выходы можно пренебречь.
Чтобы не усложнять определение, зафиксируем конкретный базис B0={
,
, ¬} и определим схемы в этом базисе.
Определение 2.1. Логической схемой (схемой из функциональных элементов) в базисе B0 называется размеченный ориентированный граф без циклов S=(V,E), в котором
- вершины, в которые не входят ребра, называются входами схемы, и каждая из них помечена некоторой переменной (разным вершинам соответствуют разные переменные);
- в каждую из остальных вершин входит одно или два ребра; вершины, в которые входит одно ребро помечены функцией ¬, а вершины, в которые входят по два ребра, - одной из функций или . Такие вершины называются функциональными элементами.
Как и для деревьев, для ориентированных графов без циклов можно естественным образом ввести понятие глубины.
Определение 2.2. Глубина вершины v
V в схеме S=(V,E) - это максимальная длина пути из входов S в v .
Глубиной D(S) схемы S назовем максимальную из глубин ее вершин.
Пусть входы схемы S помечены переменными x1, … , xn. С каждой вершиной v
V схемы S свяжем булеву функцию fv(x1,… , xn), реализуемую в этой вершине. Определим fv индукцией по глубине v .
Определение 2.3.Базис: v имеет глубину 0. Тогда это входная вершина, которая помечена некоторой переменной xi. Положим fv(x1,… , xn) = xi.
Шаг индукции. Пусть всем вершинам w глубины
k уже сопоставлены функции fw и пусть v - произвольная вершина глубины k+1. Тогда
если v помечена ¬ и в нее входит ребро (w,v) , то положим
если v помечена и в нее входят два ребра (w1,v) и (w2,v), то положим
если v помечена и в нее входят два ребра (w1,v) и (w2,v), то положим
Нетрудно понять, что шаг индукции в этом определении корректен, так как, если в схеме S имеется ребро (w,v) и глубина вершины v равна k+1, то глубина вершины w не превосходит k и для нее fw уже определена по индукционному предположению.
Определение 2.4. Схема S реализует набор булевых функций g1, g2, … , gm, если для каждого i
[1,m] в схеме существует такая вершина vi, что
.
Замечание. Определение логических схем естественным образом можно распространить и на другие базисы. При этом, однако, для вершин, помеченных несимметричными функциями ( например, импликацией), нужно явно нумеровать входящие в них ребра, указывая, каким аргументам они соответствуют.
Определение 2.5. Сложность L(S) схемы S - это число функциональных элементов в S. Сложность L(f) булевой функции f(x1, …, xn) - это наименьшая из сложностей схем, реализующих эту функцию.
Отношения между булевыми функциями и схемами естественно приводят к двум следующим основным проблемам.
Проблема анализа: по заданной схеме из функциональных элементов и выделенному подмножеству ее выходных вершин определить булевы функции, реализуемые в этих вершинах.
Проблема синтеза: по некоторому описанию булевой функции построить схему из функциональных элементов, реализующую эту функцию. При решении проблемы синтеза для исходной функции часто стараются построить схему минимальной или почти минимальной сложности.
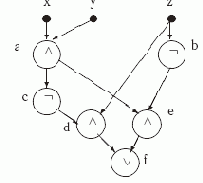
Пример 2.1. Рассмотрим схему S1
с тремя входными переменными x, y и z, изображенную на рис. 2.1 и решим для нее проблему анализа.
Рис. 2.1. Схема S1
В соответствии с данным выше определением вершины схемы S1 реализуют следующие функции:
fa(x,y,z) = x
y, fb(x,y,z) = ¬ z, fc(x,y,z) = ¬ fa(x,y,z)=¬( x
y), fd(x,y,z) = fc(x,y,z)
z = ¬( x
y)
z, fe(x,y,z) =fa(x,y,z)
fb(x,y,z)= x
y
¬ z и, наконец, ff(x,y,z) =fd(x,y,z)
fe(x,y,z) = (¬( x
y)
z)
((x
y )
¬ z).
Глубина этой схемы D(S1)= 4, а ее сложность L(S1)=6. В то же время формула для результирующей функции ff содержит 7 функциональных знаков. За счет чего достигнута экономия? За счет того, что функция (x
y) в схеме S1 вычисляется один раз в вершине a, а в формуле приходится вычислять ее дважды.
В этом и состоит основное преимущество вычислений булевых функций схемами:
каждую подформулу (подфункцию) достаточно вычислить один раз, а затем полученное значение можно использовать сколько угодно раз в качестве аргумента для других подфункций.
Схемы и линейные программы
Указанное выше свойство характерно и для программ, в которых один раз вычисленное значение выражения можно использовать неоднократно. Рассмотрим один из простейших классов программ -
линейные или неветвящиеся программы. Такие программы представляют последовательности присваиваний вида:
где X, X1, … , Xk - переменные, F - имя k-местной базисной функции.
В случае нашего базиса B0={
,
, ¬} линейная программа состоит из присваиваний вида: Z = X
Y, Z = X
Y и Z = ¬ X.
Линейная программа P с выделенными входными переменными X1, … , Xn
порождает для каждого набора ?1, …, ?n значений входных переменных естественный процесс вычисления: вначале переменным X1, … , Xn присваиваются значения ?1, …, ?n, соответственно, а каждой из остальных переменных присваивается значение 0. Затем последовательно выполняются присваивания программы P, в результате чего каждая из переменных Z программы получит заключительное значение PZ(?1, …, ?n).
Определение 2.6.
Скажем, что программа P со входными переменными X1, … , Xn
вычисляет в выходной переменной Z функцию F(X1, …, Xn), если для любого набора значений входов ?1, …, ?n после завершения работы PZ(?1, …, ?n)=F(?1, …, ?n) .
Между схемами и линейными программами имеется тесная связь.
Теорема 2.1.- По каждой логической схеме S со входами x1, … , xn и функциональными элементами v1, …, vm можно эффективно построить линейную программу PS со входными переменными x1, … , xn и рабочими переменными v1, …, vm, которая в любой переменной vi, i=1,…,m, вычисляет функцию .
- По каждой линейной программе P со входными переменными X1, … , Xn, вычисляющей в выходной переменной Z некоторую функцию F(X1, …, Xn) можно эффективно построить логическую схему SP со входами X1, … , Xn, в которой имеется вершина v такая, что fv((X1, …, Xn) = F(X1, …, Xn).
Доказательство. (1) Пусть S - схема со входами x1, … , xn и функциональными элементами v1, …, vm. Построим по ней линейную программу PS со входными переменными x1, … , xn следующим образом. Упорядочим все входные и функциональные вершины S по глубине (вершины одной глубины в любом порядке): u1, …, un+m.
Программа PS будет последовательностью m присваиваний.
- Пусть вершина un+i помечена ¬ и в нее входит
- ребро из uj. Тогда в качестве i-ой команды поместим в PS присваивание un+i= ¬ uj.
- Пусть вершина un+i помечена \circ {, } и в нее входят ребра из uj и uk. Тогда в качестве i-ой команды поместим в PS присваивание un+i= uj ? uk.
Упорядочение вершин по глубине гарантирует, что j

.
Доказательство пункта (2) проведите самостоятельно (см. задачу 2.1).
Пример 2.1.
Применим конструкцию теоремы к схеме S1, представленной на рис.2.1. Ее вершины можно упорядочить по глубине так: x, y, z, a, b, c, d, e, f. Порождая команды по описанным выше правилам, получим следующую линейную программу P_{S1}:
Замечание. Число команд в линейной программе PS, т.е. время ее выполнения, совпадает со сложностью L(S) схемы S. Глубина схемы D(S) также имеет смысл с точки зрения времени вычисления. Именно, D(S) - это время выполнения PS на многопроцессорной системе. Действительно, все команды, соответствующие вершинам одинаковой глубины, можно выполнять параллельно на разных процессорах, так как результаты любой из них не используются в качестве аргументов другой.
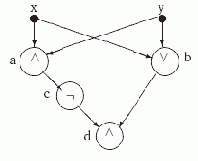
Рассмотрим схему S+ на рис.
Рассмотрим схему S+ на рис. 2.2.
Рис. 2.2. Схема S+ для функции x+y
В соответствии с определением вершины этой схемы реализуют следующие функции:
fa(x,y) = x
y, fb(x,y) = x
y, fc(x,y) = ¬ fa(x,y)=¬( x
y), fd(x,y) = fc(x,y)
fb(x,y) = ¬( x
y)
( x
y) = x +y.
Таким образом, схема S+ реализует (в вершине d) функцию + сложения по модулю 2.
Из приведенного выше примера следует, что L(S+)=4 и L(+)
4.
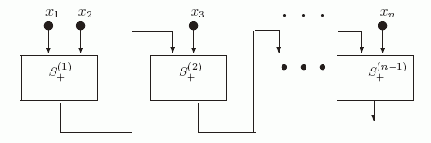
Используя схему S+, нетрудно построить схему Sodd для реализации линейной функции-суммы n аргументов по модулю 2 odd(X1,X2,…, Xn)= X1 +X2 +… + Xn (см. рис. 2.3).
Рис. 2.3. Схема Sodd
На этой схеме прямоугольники S+(1), S+(2), … ,S+(n) содержат копии схемы S+. При этом входами S+(1) являются переменные x1 и x2, а входами S+(i+1) являются выход схемы S+(i) и переменная xi+1. По индукции легко показать, что вершина d в S+(i) реализует функцию (x1 + x2 + … + xi+1). Таким образом, нами установлена
Теорема 2.2.
Существует схема Sodd, реализующая функцию odd(X1,X2,…, Xn)= X1 +X2 +… + Xn
со сложностью L(Sodd)= 4 (n-1).
Сумматор
Сумматором порядка n называют схему, вычисляющую результат сложения двух n-разрядных двоичных чисел
и
. Пусть
( здесь ai, bi, ci
{0, 1} - соответствующие двоичные разряды этих чисел).
Сумматор должен вычислять набор из (n+1)-ой результирующей функции:
задающих соответствующие разряды суммы c.
Обозначим через pi бит переноса из (i-1)-го разряда в i-ый. Тогда нетрудно видеть, что при i =0
c0 = a0 + b0 и p1 = a0
b0,
а при 1
i
n-1
ci= pi + ai + bi и pi+1 = (ai
bi)
(pi
ai)
(pi
bi).
Старший разряд c совпадает с последним переносом: cn=pn.
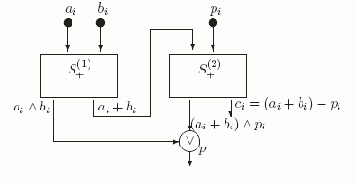
Рассмотрим теперь построенную выше схему S+ как схему, вычисляющую набор из двух функций: x
y (в вершине a) и x+y (в вершине d). Используя два экземпляра этой схемы S+(1) и S+(2), можно легко реализовать схему одноразрядного сумматора SUM1 (см. рис. 2.4) , которая имеет три входа ai, b_ i и pi (1
i
n-1) и вычисляет ci и pi+1.
Рис. 2.4. Схема SUM1
Действительно, из построения следует, что в вершине p этой схемы вычисляется функция fp = (ai
bi)
((ai + bi)
pi) = (ai
bi)
(pi
ai)
(pi
bi) = pi+1. Из представленной схемы видно, что сложность одноразрядного сумматора L(SUM1)= 9.
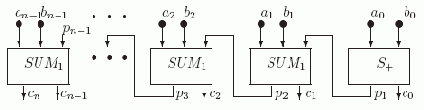
Теперь из S+ и одноразрядных сумматоров SUM1 соберем схему SUMn для n-разрядного сумматора.
Рис. 2.5. Схема cумматора SUMn
Таким образом мы установили следующее утверждение.
Теорема 2.3.Для каждого n
1 cуществует схема SUM, реализующая операцию суммирования двух n-разрядных двоичных чисел и имеющая сложность L(SUMn)= 9n -5.
Замечание Логические схемы интенсивно исследовались 50-х-70-х годах прошлого столетия. В частности, К. Шеннон и О.Б. Лупанов установили оценки сложности схем для булевых функций от n аргументов. Оказалось, что любую такую функцию можно реализовать со сложностью не большей (по порядку) 2n/n и что "почти все" они имеют не меньшую сложность. При этом до сих пор не известна ни одна последовательность "конкретных" функций fn, сложность которых по порядку превосходила бы линейную функцию.
что минимальная схема для сложения
Задача 2.1. Докажите пункт (2) теоремы 2.1.
Задача 2.2. Докажите, что минимальная схема для сложения имеет сложность L(+) = 4.
Задача 2.3. Используя схему SUMn, постройте схему, реализующую операцию вычитания двух n-разрядных двоичных чисел: d =a - b (при условии, что a
b). Оцените сложность полученной схемы.
Задача 2.4. Определите глубину схем S+, Sodd, SUM1 и SUMn.
Задача 2.5. Два игрока независимо выбирают одно из четырех чисел от 0 до 3. Первый игрок выигрывает, если выбранные числа совпадают. Постройте схему, определяющую выигрыш 1-го игрока. Ее входы x1,x2 представляют число, выбранное 1-ым игроком, а y1,y2 - число, выбранное 2-ым игроком. Реализуемая функция F(x1,x2,y1,y2) равна 1 тогда и только тогда, когда x1=y1 и x2 =y2.
Задача 2.6. Постройте схему, определяющую результат голосования в комитете, состоящем из трех членов и председателя. В случае равенства голосов, голос председателя является решающим.
Задача 2.7. Пусть наборы аргументов булевой функции от трех аргументов упорядочены лексикографически, а ее значения задаются последовательностью 8 нулей и единиц. Постройте схемы, реализующие следующие функции.
- f1=(1111 1011),
- f2=(1001 1001),
- f3 =(0011 1001).
Введение в схемы, автоматы и алгоритмы
Основные определения
Одним из предшественников УБДР являются бинарные деревья решений.
Определение 3.1.
Бинарное дерево решений (БДР) - это бинарное дерево T=(V,E), все внутренние вершины которого помечены переменными, а листья - значениями 0 или 1. Из каждой внутренней вершины v выходят 2 ребра, одно помечено 0, другое - 1; вершина w0, в которую ведет ребро, помеченное 0, называется 0-сыном v, а вершина w1, в которую ведет ребро, помеченное 1, называется 1-сыном v.
Такое дерево, вершины которого помечены переменными x1, …, xn реализует булеву функцию f(x1, …, xn), если для каждого набора значений переменных ?1, ?2, …, ?n ветвь в дереве, соответствующая этому набору (из вершины xi идем по ребру, помеченному ?i), завершается листом с меткой f(?1, ?2, …, ?n).
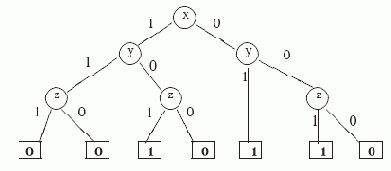
Пример 3.1. Например, рассмотрим изображенное ниже БДР T1 (на всех рисунках предполагается, что ребра направлены сверху вниз).
Рис. 3.1. По определению T1 реализует функцию f1(x,y,z), представленную в таблице 3.1.
Таблица 3.1. Функция f1(x, y,z), реализуемая БДР T1 на рис.3.1xyzf(x,y,z)
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1. | 1 | 0 |
Нетрудно построить ДНФ этой функции: f(x, y, z) = (¬ x
y)
(¬ y
z).
УБДР являются модификацией БДР, в которой все листья с одной меткой представлены одной вершиной, в каждую вершину может входить несколько ребер, возможен выбор порядка появления переменных на ветвях.
Определение 3.2. Пусть зафиксирован некоторый порядок n переменных
: x
(1), …, x
(n).
Упорядоченная бинарная диаграмма решений относительно порядка переменных
- это ориентированный граф без циклов с одним корнем, в котором
- существует лишь две вершины, из которых не выходят ребра; они помечены константами 0 и 1 и называются стоками;
- остальные (внутренние) вершины помечены переменными и из каждой из них выходят два ребра, одно помечено 0, другое - 1;
- порядок, в котором переменные встречаются на любом пути из корня в сток, совместим с , т.е. если из вершины, помеченной x(i), есть путь в вершину, помеченную x(j), то i < j.
Как и в случае БДР, УБДР реализует булеву функцию f(x1, …, xn), если для каждого набора значений переменных ?1, ?2, …, ?n путь в диаграмме, начинающийся в корне и соответствующий этому набору (из вершины xi идем по ребру, помеченному ?i), завершается стоком с меткой f(?1, ?2, …, ?n).
Из этого определения непосредственно следует, что каждая внутренняя вершина диаграммы v, помеченная переменной x
(k), является корнем поддиаграммы, которая включает все вершины диаграммы, достижимые из v, и реализует некоторую функцию fv( x
(k),x
(k+1), …, x
(n)) от (n -k +1) переменных x
(k),x
(k+1), …, x
(n). При этом ее 0-сын w0 является корнем поддиаграммы, реализующей функцию fw0(x
(k+1), …, x
(n)) =fv( 0, x
(k+1), …, x
(n)), а 1-сын w1 - корень поддиаграммы, реализующей функцию fw1(x
(k+1), …, x
(n)) =fv( 1, x
(k+1), …, x
(n)). Пусть диаграмма реализует функцию f(x1, … , xn) = f'(x
(1), …, x
(n)) и ?
(1),… , ?
(k-1) - это набор значений переменных x
(1), …, x
(k-1), который соответствует пути из корня в вершину v (таких наборов может быть несколько). Тогда fv( x
(k), …, x
(n))= f'(?
(1),… , ?
(k-1),x
(k), …, x
(n)).
Пример 3.2. Реализуем с помощью УБДР функцию f1(x,y,z), представленную выше в примере 3.1, с помощью БДР T1 и таблицы 3.1.
Вначале зафиксируем порядок переменных: x < y < z. Объединив листья с одинаковыми метками и две z- вершины с одинаковыми потомками, получим УБДР D1, приведенную на рис.3.2.
Рис. 3.2. Ясно, что реализация функции f1(x,y,z) с помощью УБДР D1 намного компактнее, чем с помощью БДР T1.
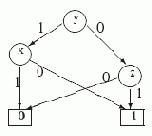
Под сложностью L(D) УБДР D будем понимать число внутренних вершин в D. Например, L(D1)=4. Может ли сложность диаграммы для некоторой функции зависеть от порядка переменных? Да! Рассмотрим порядок переменных y < x < z. Как показывает следующий рисунок, относительно этого порядка функцию f(x,y,z) можно реализовать УБДР D2 со сложностью L(D2)=3.
Рис. 3.3.
Построение сокращенных УБДР по формулам
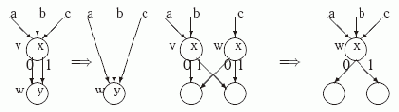
Алгоритм СОКРАЩЕНИЕ-УБДР позволяет построить сокращенную УБДР для функции f, по любой другой ее УБДР. Но как построить УБДР, если f задана, например, с помощью формулы? Можно, конечно, попытаться построить полное бинарное дерево решений, объединить в нем все листья с меткой 0 в один сток, а листья с меткой 1 - в другой. Затем применить к получившейся УБДР алгоритм СОКРАЩЕНИЕ-УБДР. Но этот подход годится только для функций от небольшого числа переменных, так как полное БДР для f(x1, …, xn) будет содержать 2n листьев.
Другой подход связан с построением УБДР "сверху-вниз". Объясним его для естественного порядка переменных: x1< x2 < … < xn.
Начнем построение с корня, помеченного x1. Рассмотрим две остаточные функции: f0(x1, …, xn)=f(0, x2, …, xn) и f1(x2, …, xn)=f(1, x2, …, xn). Если они одинаковы, то f не зависит от x1 и тогда изменим метку у корня на x2. Если обе функции f0 и f1 существенно зависят от x2, то для каждой из них добавляем вершину, помеченную x2, и далее реализуем по индукции. Если fk (k

{0, 1}) не зависит от переменных x2,… , xj, но зависит существенно от xj+1, то добавляем вершину, помеченную xj+1, и проводим в нее ребро с меткой k из вершины, соответствующей f . Пусть для некоторого i уже построены вершины для всех различных остаточных функций вида f?1 … ?i}(xi+1, … , xn)= f(?1… ?i, xi+1, … , xn), существенно зависящих от xi. Для каждой из них получим две остаточные функции f_{?1… ?i 0}( xi+2, … , xn)= f(?1… ?i, 0, xi+2, … , xn) и f_{?1… ?i 1}( xi+2, … , xn)= f(?1… ?i, 1, xi+2, … , xn). Затем выберем из множества этих функций разные, для каждой из них добавим в диаграмму вершину, помеченную xi+1, и проведем в них соответствующие ребра из вершин, помеченных x_{i}. Продолжая построение, дойдем до функций от 1-ой переменной xn и до констант, для которых минимальные реализации очевидны.
Пример 3.2. Рассмотрим, например, функцию f(x1, x2, x3, x4), заданную формулой (x1
x2
x4)
(¬ x1
x2
¬ x4)
(¬ x2
x3)
(¬ x2
x4), и построим для нее УБДР относительно порядка x1 < x2 < x3
Вначале создадим корень, помеченный x1, и рассмотрим остаточные функции, получающиеся при x1=0 и x1 =1. Имеем
Они разные и обе существенно зависят от x2. Поэтому добавим для каждой из них вершину, помеченную x2. Затем для каждой из них определим остаточные функции, получающиеся при x2=0 и x2 =1. Получим
Так как f00=f10, а f01 и f11 от x3 не зависят, то нам потребуется только одна вершина, помеченая x3. Она будет представлять функцию f00=f10=(x3 x4). При x3=0 она превращается в x4, а при x3=1 равна константе 1. В результате получается УБДР Df, показанная на рис.3.6.
Рис. 3.6.
Сокращенные УБДР
Когда порядок переменных зафиксирован, то достаточно просто можно по произвольной УБДР для функции построить минимальную УБДР, реализующую данную функцию.
Определение 3.3. УБДР называется сокращенной, если
- из любой внутренней вершины v ее 0-сын и 1-сын не совпадают;
- нет такой пары внутренних вершин u и v, для которых поддиаграммы с корнями u и v являются изоморфными (т.е. взаимно однозначно отображаются друг на друга с сохранением всех меток).
Смысл этого определения понятен: если из некоторой вершины v оба ребра ведут в одну вершину, то такая вершина v не нужна, а если имеются две вершины с одинаковыми поддиаграммами, то их можно слить. Определим два типа эквивалентных преобразований УБДР.
Правило сокращения: если 0-сын и 1-сын вершины v совпадают и равны w, то удалить v, перенаправив все входящие в нее ребра в вершину w.
Правило слияния: если вершины v и w помечены одной переменной и имеют одинаковых 0-сыновей и 1-сыновей, то удалить вершину v, перенаправив все входящие в нее ребра в вершину w.
На следующем рисунке показаны преобразования по этим правилам.
Рис. 3.4. Правило сокращения Правило слияния
Следующая простая теорема показывает, что применимость этих двух правил является критерием несокращаемости УБДР.
Теорема 3.1.
УБДР D является сокращенной тогда и только тогда, когда к ней не применимо ни правило слияния, ни правило сокращения.
Доказательство. Если к D применимо правило сокращения, то не выполнено условие (1) из определения сокращенной УБДР, а если к D применимо правило слияния, то поддиаграммы с корнями v и w являются изоморфными и не выполнено условие (2).
? Пусть к УБДР D нельзя применить правило сокращения. Тогда в ней нет вершин с совпадающими 0- и 1-сыновьями и выполнено условие (1). Пусть к УБДР D нельзя применить правило слияния. Тогда из следующей леммы можно заключить, что в D нет пары вершин, поддиаграммы которых являются изоморфными, и следовательно, выполнено условие (2).
Лемма 3.2. Если в D есть такая пара вершин u и v, для которых поддиаграммы с корнями v и w являются изоморфными, то в D имеется и пара вершин v', w' с попарно одинаковыми 0- и 1-сыновьями и, следовательно, к D применимо правило слияния.
Доказательство леммы проведем индукцией по высоте h поддиаграмм Dv и Dw с корнями v и w, соответственно (так как Dv и Dw изоморфны, то их высоты, т.е. длины максимальных путей из корней до стоков, одинаковы).
Базис: h=1. В этом случае 0- и 1-сыновьями вершин v и w являются одинаковые стоки.
Шаг индукции. Предположим, что утверждение верно для h=k. Пусть Dv и Dw - поддиаграммы высоты h=k+1. Пусть v0 и w0 - это 0-сыновья вершин v и w, соответственно, а v1 и w1 - их 1-сыновья. Если v0=w0 и v1=w1, то в качестве v', w' подходят сами v и w. Если же для некоторого i {0,1} vi wi, то поддиаграммы и с корнями vi и wi являются изоморфными и имеют высоту k. Тогда по предположению индукции утверждение леммы выполнено.
Из теоремы 3.1 непосредственно следует, что, применяя к произвольной УБДР правила сокращения и слияния, мы, в конце концов, получим сокращенную УБДР. Чтобы эта процедура работала эффективо, нужно применять правила в порядке "снизу-вверх". Мы опишем этот алгоритм для "естественного" порядка переменных: x1, … , xn.
Алгоритм СОКРАЩЕНИЕ-УБДР
Вход: УБДР D для функции f(x1, … , xn).
Выход: сокращенная УБДР для .
1. Занумеруем множество вершин D: V = {v1, v2, …, vm}; 2. ДЛЯ i = n, n-1, …, 1 ВЫПОЛНЯТЬ 3. { 4. V(i) = { v | v помечена переменной xi }; /* Применение правила сокращения: 5. ДЛЯ КАЖДОЙ v V(i) ВЫПОЛНЯТЬ 6. ЕСЛИ (0-сын v) = (1-сын v) = w ТО} 7. { удалить v из V(i); 8. перенаправить все ребра, входящие в v, в вершину w; 9. удалить v из D } 10. ИНАЧЕ key(v) = (j, k), где vj - это 0-сын v, а vk - 1-сын v; /* Применение правила слияния: 11. Отсортировать V(i) по ключу key(v): пусть в этом порядке V(i)={ u1, …, uki}; 12. тек_ключ=(0, 0); 13. ДЛЯ j = 1, …, ki ВЫПОЛНЯТЬ 14. ЕСЛИ тек_ключ=key(uj) ТО 15. { удалить uj из V(i); 16. перенаправить все ребра, входящие в uj, в тек_вершина; 17. удалить uj из D } 18. ИНАЧЕ} {тек_вершина= uj; тек_ключ=key(uj)} 19. }
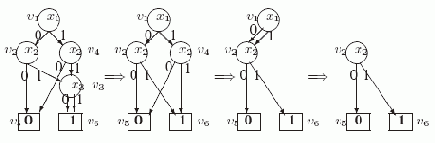
Пример 3.1. Рассмотрим пример применения алгоритма СОКРАЩЕНИЕ-УБДР, показанный на следующем рисунке.
Рис. 3.5. Применение алгоритма СОКРАЩЕНИЕ-УБДР
На исходной УБДР слева все вершины уже занумерованы. Стрелки разделяют УБДР, получаемые после очередных итераций основного цикла в строках 2 - 19. При первом исполнении цикла i=3, V(3) = {v3}. Для вершины v3 условие в строке 6 выполнено (w= v6), поэтому применяется правило сокращения и эта вершина удаляется, а ее входы направляются в v6. При следующем исполнении цикла i=2, V(2) = {v2, v4}. После цикла в строках 5 - 10 key(v2)= {5, 6} и key(v4)= {5, 6}. После сортировки u1=v2, u2 = v4. В цикле в строках 13-18 для u2 выполнено условие в строке 14. Поэтому применяется правило слияния и вершина v4 удаляется, а ее вход передаeтся вершине v2. При третьем исполнении цикла i=1, V(1) = {v1}. Для вершины v1 условие в строке 6 выполнено (w= v2), поэтому применяется правило сокращения и эта вершина удаляется.
Оказывается, что построенная алгоритмом УБДР является единственной и минимальной для заданного порядка.
Теорема 3.2.
- Алгоритм СОКРАЩЕНИЕ-УБДР строит сокращенную УБДР, эквивалентную исходной УБДР D.
- Эта сокращенная УБДР является при данном порядке переменных единственной (с точностью до изоморфизма) и минимальной.
Доказательство первого пункта непосредственно следует из выполнения критерия теоремы 3.1, так как к результирующей диаграмме никакое правило сокращения или слияния неприменимо.
Доказательство второго пункта основано на следующем индуктивном утверждении:
Лемма 3.1.
После выполнения i-ой итерации алгоритма в полученной диаграмме для каждой подфункции f(?1, ?2, …, ?_{i-1},xi, …, xn) (?k {0, 1} при k=1,2,…, i-1), существенно зависящей от xi, имеется ровно одна вершина - корень поддиаграммы, реализующей эту подфункцию.
Напомним, что функция f(x1, x2, …, xi, …, xn) существенно зависит от переменной xi, если существуют такие два набора значений аргументов (?1, …, ?i-1, 0, ?i+1,…, ?n) и (?1, …, ?i-1, 1, ?i+1,…, ?n), различающиеся только значением xi, на которых f принимает разные значения: f(?1, …, ?i-1, 0,?i+1, …, ?n) f(?1, …, ?i-1, 1,?i+1, …, ?n) .
Доказательство этой леммы и вывод из нее утверждения 2 теоремы 3.2 оставляем в качестве задач 3.2 и 3.3.
Задача 3.1. Докажите, что совершенная, сокращенная и минимальная ДНФ функции odd(X1,X2,…, Xn) совпадают и состоят из 2n-1 элементарных конъюнкций длины n.
Задача 3.2. Докажите лемму 3.2 возвратной индукцией по i.
Задача 3.3. Используя лемму 3.2, докажите утверждение 2 теоремы 3.2.
Задача 3.4. Постройте минимальные УБДР для двуместных функций: x y, x y, x + y, x y, x|y.
Задача 3.5. Постройте минимальные УБДР для функции
относительно двух упорядочений переменных:
- x1 < x2 < x3 < x4 < x5 < x6 и
- x1 < x3 < x5 < x2 < x4 < x6.
Задача 3.6. Пороговая функция Tnk от n переменных с порогом k выдает 1, если во входном наборе имеется не менее k единиц: Tnk(x1,x2, …, xn) = 1 x1 + x2 + … + xn k.
- Постройте минимальные УБДР для пороговых функций T32, T42, T53.
- Зависит ли сложность минимальной УБДР для пороговых функций от порядка переменных?
- Оцените сложность минимальной УБДР для пороговой функции Tnk.
Задача 3.7. Выберите подходящий порядок переменных и постройте для него минимальные УБДР, реализующие функции из задач 12.5 и 12.6.
Задача 3.8. Как мы видели, логические схемы естественным образом реализуются в виде неветвящихся программ. Наоборот, для деревьев решений и УБДР естественным программным представлением являются ветвящиеся программы, включающие лишь условные операторы вида if ... then ... else ... с тестами вида "x = 0?" и "x = 1?" (они соответствуют внутренним вершинам диаграмм) и операторы присвоения значения 0 или 1 результату (они соответствуют вершинам-стокам).
Напишите ветвящиеся программы, вычисляющие функции, представляемые УБДР D2 на рис. 3.3 и Df на рис.3.6.
Введение в схемы, автоматы и алгоритмы
Детерминированные конечные автоматы (ДКА) и автоматные языки
Пусть ?={a1, …, am} - это алфавит, который состоит из конечного множества элементов, называемых символами (буквами).
Слово в алфавите ? - это конечная последовательность символов этого алфавита: w =w1… wn, wi ? при i=1, …, n. Число букв в этой последовательности называется длиной слова и обозначается |w|. Имеется одно специальное "пустое" слово длины 0. Будем обозначать его через ?. На словах определена операция приписывания одного слова после другого, называемая конкатенацией: если слово w =w1… wn, а слово v =v1… vm, то их конкатенация w ? v - это слово w1… wnv1… vm длины n+m. Обычно знак конкатенации ? будем опускать и писать просто w v (по аналогии со знаком умножения в алгебре). Пустое слово - это единственное слово такое, что для любого слова w справедливо равенство w ?= ? w = w. Операция конкатенации ассоциативна: для любых трех слов w, v и u, очевидно, имеет место равенство: (w v)u = w(v u). Поэтому скобки при записи конкатенации нескольких слов будем опускать. Для представления нескольких конкатенаций одного и того же слова используют сокращенную "степенную форму" записи: w0 = ?, w1= w,…, wi+1 = wiw. Например, a3b4c2 - это сокращенная запись слова aaabbbbcc.
Языком в алфавите ? называется произвольное множество слов этого алфавита . Язык, включающий все слова в алфавите ? ( в том числе и пустое слово ?), будем обозначать через ?*.
Конечные автоматы часто используются для определения тех или иных свойств слов, т.е. для распознавания языков: автомат, распознающий некоторый язык L должен по произвольному слову w ответить на вопрос " w L? ". Для решения такой задачи функция выходов может быть заменена на проверку того, в какое состояние переходит автомат после получения входного слова w - "принимающее" или "отвергающее".
Определение 4.3. Детерминированный конечный автомат (ДКА) - распознаватель - это система вида
включающая следующие компоненты:
- ? ={a1, … , am} (m 1) - конечное множество - входной алфавит;
- Q={q0, … , qn-1} (n 1) - конечное множество - алфавит внутренних состояний;
- q0 Q - начальное состояние автомата;
- F Q - множество принимающих (допускающих, заключительных) состояний;
- ?: Q ? ? Q - функция переходов,
- ?(q, a) - это состояние, в которое переходит автомат из состояния q, когда получает на вход символ a.
Функцию ? называют программой автомата A и задают как список из m n команд вида qiaj ?(qi,aj) .
Удобно также задавать функцию ? с помощью описанной выше таблицы размера n ? m, строки которой соответствуют состояниям из Q, а столбцы - символам из входного алфавита ?, и в которой на пересечении строки qi и столбца aj стоит состояние ?(qi,aj).
Как и автоматы-преобразователи, автоматы-распознаватели можно представлять с помощью размеченных ориентированных графов, называемых диаграммами.
Определение 4.4.
Диаграмма ДКА A = - это ориентированный (мульти)граф DA=(Q, E) с помеченными ребрами, в котором выделена вершина-начальное состояние q0 из каждой вершины q Q выходит |?X| ребер, помеченных символами a ? так, что для каждой q Q и каждого символа a ? имеется единственное ребро из q в вершину q' =?(q,a) с меткой a .
Скажем, что представленный последовательностью ребер путь p=e1e2 … et в диаграмме несет слово w=w1w2 … wt, если wi - это метка ребра ei (1 i t). Если q - начальная вершина (состояние) этого пути, а q' - его заключительная вершина, то будем говорить, что слово w переводит q в q'.
Работа конечного автомата-распознавателя состоит в чтении входного слова и изменению состояний в зависимости от его символов.
Определение 4.5. Назовем конфигурацией ДКА A = произвольную пару вида (q, w), в которой q Q и w ?*.
На множестве конфигураций введем отношение перехода за один шаг :
Если w=?, то положим для каждого q Q: (q, ?) (q, ?).
Через обозначим рефлексивное и транзитивное замыкание .
Содержательно, означает, что автомат A, начав работу в состоянии q на слове w=w1 … wl, через некоторое конечное число шагов 0 k l прочтет первые k символов слова w и перейдет в состояние q', а w' =wk+1 … wl - это непрочтенный остаток слова w.
Определение 4.6.
ДКА A распознает (допускает, принимает) слово w, если для некоторого q F
, т.е. после обработки слова w автомат переходит в принимающее состояние.
Язык LA, распознаваемый (допускаемый, принимаемый) автоматом A, состоит из всех слов, распознаваемых этим автоматом:
Язык называется конечно автоматным, если он распознается некоторым ДКА.
Из этого определения, в частности, следует, что ? LA q0 F. Один и тот же язык может распознаваться разными автоматами.
Определение 4.7.
Автоматы A и B называются эквивалентными, если совпадают распознаваемые ими языки, т.е. LA = LB.
Определение распознавания слова и языка можно легко перевести на язык диаграмм.
Лемма 4.3. Автомат A распознает (допускает, принимает) слово w, если для некоторого q F в диаграмме DA имеется путь из q0 в q, который несет слово w, т.е. w переводит q0 в заключительное состояние q.
Доказательство можно провести индукцией по длине слова w (см. задачу 4.3).
Tаким образом, язык LA, распознаваемый автоматом A, состоит из всех слов, которые переводят в его диаграмме DA начальное состояние q0 в заключительные состояния из F.
Наша цель теперь состоит в изучении класса конечно автоматных языков.
Во многих случаях удается доказать, что язык L конечно автоматный, непосредственно построив распознающий его автомат. Для этого нужно постараться разбить множество всех входных слов на конечное число классов "однородных", "эквивалентных" слов, т.е. слов, получение которых на входе одинаково влияет на возможность их продолжения до слов распознавемого языка. Затем для каждого такого класса создать состояние автомата и определить переходы между этими состояниями. Часто полезно бывает выделить одно состояние для представления "ошибочных" слов, для которых ни они сами, ни любые их продолжения не входят в язык.
Недетерминированные конечные автоматы и их детерминизация
Недетерминированные конечные автоматы, рассматриваемые в этом параграфе, являются обобщениями детерминированных: они при чтении очередного символа на входе могут выбрать в качестве следующего одно из нескольких состояний, а кроме того, могут изменить состояние без чтения входа. Основной результат, который мы установим, утверждает, что это обощение не существенно: недетерминированные и детерминированные конечные автоматы распознают одни и те же языки.
Определение 4.8. Недетерминированный конечный автомат (НКА) - распознаватель - это система вида
включающая следующие компоненты:
- ? ={a1, … , am} (m 1) - конечное множество - входной алфавит;
- Q={q0, … , qn-1} (n 1) - конечное множество - алфавит внутренних состояний;
- q0 Q - начальное состояние автомата;
- F Q - множество принимающих (допускающих, заключительных) состояний;
- ?: Q ? (? {?}) 2Q - функция переходов.
Для a ? значение ?(q, a) - это множество состояний в каждое из которых может перейти автомат из состояния q, когда получает на вход символ a. ?(q, ?) - это множество состояний в каждое из которых может перейти автомат из состояния q без чтения символа на входе.
Как и для детерминированных автоматов, функцию переходов можно представить с помощью набора команд-программы: для каждой пары q Q и a ? и каждого состояния q' ?(q, a) в программу помещается команда q a q', и для каждого состояния q' ?(q, ?) в программу помещается команда q q'. Отличие от детерминированного случая состоит в том, что для одной пары q Q и a ? в программе может быть несколько команд вида q a q' или не быть ни одной такой команды. Кроме того, могут появиться ?-команды (пустые переходы) вида q q', означающие возможность непосредственного перехода из q в q' без чтения символа на входе.
При табличном задании функции ? в таблице появляется (m+1)-ый столбец, соответствующий пустому символу ? и на пересечении строки q и столбца a (? {?}) стоит множество состояний ?(q,a).
Для недетерминированного автомата M = в диаграмме DM=(Q, E) с выделенной начальной вершиной q0 и множеством заключительных вершин F ребра взаимно-однозначно соответствуют командам: команде вида q a q' (a ?) соответствует ребро (q,q'), с меткой a , а команде вида q q' соответствует ребро (q,q'), с меткой ?.
Скажем, что заданный последовательностью ребер путь p=e1e2 … eT в диаграмме DM несет слово w=w1w2 … wt (t T), если после удаления из него "пустых" ребер (т.е. ребер с метками ?) остается последовательность из t ребер , метки которых образуют слово w , т.е. wi - это метка ребра . Очевидно, это эквивалентно тому, что последовательность меток на ребрах пути p имеет вид , где kj 0 (j=1,2, … , t+1) и .
Слово w переводит q в q' в диаграмме DM, если в ней имеется путь из q в q' который несет w .
На недетерминированные автоматы естественным образом переносится определение конфигураций и отношения перехода между ними.
Определение 4.9. Назовем конфигурацией НКА M = произвольную пару вида (q, w), в которой q Q и w ?*. Определим отношение перехода из одной конфигурации в другую за один шаг:
или
Как и для ДКА, через обозначим рефлексивное и транзитивное замыкание отношения .
Внешне определение распознавания слов НКА совпадает с определением для ДКА.
Определение 4.10. НКА M распознает (допускает, принимает) слово w, если для некоторого \ .
Язык LM, распознаваемый НКА M, состоит из всех слов, распознаваемых автоматом:
Отличие состоит в том, что у НКА может быть несколько различных способов работы (путей вычисления) на одном и том же входном слове w. Считаем, что НКА распознает (допускает, принимает) это слово, если хотя бы один из этих способов приводит в заключительное состояние из F.
Из определения диаграммы DM непосредственно следует, что НКА M распознает слово w, тогда и только тогда, когда существует такое заключительное состояние q F, что в диаграмме DM слово w переводит q0 в q. Иными словами, в DM имеется путь из q0 в q, на ребрах которого написано слово w (с точностью до меток ?).
Пример 4.1. Рассмотрим НКА N1 = < {a, b}, {0,1,2,3, 4}, 0, {3}, ?>, где
?:Q\?Xab?
| 0 | {0,1} | {0} | |
| 1 | | | {4} |
| 2 | {3} | | |
| 3 | | | {1} |
| 4 | | {2} | |
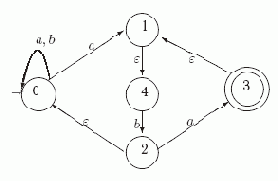
Его диаграмма представлена ниже на рис. 4.3.
Рис. 4.3. Диаграмма автомата N1
Рассмотрим работу этого автомата на слове ababa:
Так как 3 - заключительное состояние, то ababa LN1. Заметим, что у автомата N1 имеются и другие способы работы на этом слове, не ведущие к заключительному состоянию. Например, он может после чтения каждого символа оставаться в состоянии 0. Но чтобы слово допускалось, достаточно существовать хотя бы одному "хорошему" способу.
Очевидно, что детерминированные конечные автоматы являются частными случаями недетерминированных. Естественно спросить, распознают ли недетерминированные конечные автоматы больший класс языков чем детерминированные? Следующая теорема показывает, что классы языков, распознаваемых НКА и ДКА совпадают.
Теорема 4.2. (Детерминизация НКА)
Для каждого НКА M можно эффективно построить такой ДКА A, что LA = LM.
Доказательство Пусть M= - НКА. Процедура построения по нему эквивалентного ДКА состоит из двух этапов: на первом по M строится эквивалентный ему НКА M1, в программе которого отсутствуют переходы по ?, а на втором этапе по M1 строится эквивалентный ДКА A.
Переработка информации с помощью конечных автоматов
Конечные автоматы являются математической моделью устройств, перерабатывающих дискретную входную информацию в режиме "реального времени", т.е. в темпе ее поступления.
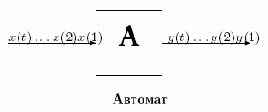
Автомат
На такие устройства в последовательные дискретные моменты времени 1,2, …, t, t+1,… поступают входные сигналы x(1),x(2), …, x(t),x(t+1),… и в ответ на них автомат A вырабатывает выходные сигналы y(1) y(2), …, y(t), y(t+1),…. Конечные автоматы характеризуются двумя особенностями.
- Отсутствие предвосхищения: выходной сигнал y(t), выдаваемый автоматом в момент t, зависит лишь от полученных к этому времени входов x(1),x(2), …, x(t), т.е. автомат не может предвосхитить будущие входы и заранее на них отреагировать. Таким образом, имеется некоторая функция выходов (x(1),x(2), …, x(t))= y(t), определяющая очередной выход по предшествующему входу.
- Конечная память: в каждый момент t информация в автомате о полученном к этому моменту входе x(1),x(2), …, x(t) конечна. Это свойство удобно интерпретировать следующим образом: автомат имеет конечное множество состояний Q и в каждый момент находится в одном из этих состояний. При получении очередного входа состояние может измениться. Таким образом, состояние q Q, в котором находится автомат после получения входной последовательности x(1),x(2), …, x(t), и представляет информацию об этой последовательности, используемую в дальнейшей работе автомата при определении следующего состояния и выхода.
Наше обсуждение приводит к следующему определению конечного автомата с выходом.
Определение 4.1. Конечный автомат - преобразователь - это система вида
включающая следующие компоненты:
- ?X={a1, … , am} (m 1) - конечное множество - входной алфавит;
- ?Y={b1, … , br} (r 1) - конечное множество - выходной алфавит;
- Q={q0, … , qn-1} (n 1) - конечное множество - алфавит внутренних состояний;
- q0 Q - начальное состояние автомата;
- ?: Q ? ?X Q - функция переходов, ?(q, a) - это состояние, в которое переходит автомат из состояния q, когда получает на вход символ a;
- : Q ? ?X ?Y - функция выходов, (q, a) - это символ из ?Y, который выдает на выход автомат в состоянии q, когда получает на вход символ a.
Иногда пару функций ?, называют программой автомата A и задают как список из m n команд вида qiaj ?(qi,aj) / (qi,aj).
Другой удобный способ задания функций ? и - табличный. Каждая из них определяется таблицей (матрицей) размера n ? m, строки которой соответствуют состояниям из Q, а столбцы - символам из входного алфавита ?X. В первой из них на пересечении строки qi и столбца aj стоит состояние ?(qi,aj), а во второй - выходной символ (qi,aj).
Еще один способ представления конечного автомата основан на использовании ориентированных размеченных графов.
Определение 4.2. Диаграмма автомата A = 
> - это ориентированный (мульти) граф DA=(Q, E) с помеченными ребрами, в котором выделена вершина-начальное состояние q0 и из каждой вершины q
?Y). Таким образом, для каждой q
(q,a) из q в вершину q' =?(q,a).
Как автомат A перерабатывает входное слово x1x2 … xt? Он начинает работу в состоянии q(0)=q0. Затем, получив (прочитав) входной символ x1, переходит в состояние q(1)= ?(q0,x1) и выдает символ y(1)=
(q0,x1). Далее, получив x2 A переходит в состояние q(2)= ?(q(1),x2) и выдает символ y(2)=
(q(1),x2) и т.д. Таким образом, работа автомата, характеризуется последовательностью проходимых им состояний q(0), q(1), … , q(t), … и последовательностью выходных символов y(1), … , y(t), … . Они определяются следующими реккурентными соотношениями:
Рассмотрим несколько примеров автоматов-преобразователей.
Мы уже строили схему из функциональных элементов SUMn, реализующую для фиксированного n суммирование двух n-разрядных двоичных чисел. Построим теперь конечный автомат SUM, который сможет складывать два двоичных числа произвольной разрядности. На вход этого автомата будут последовательно подаваться пары x(i)= (x1(i),x2(i)) соответствующих i-ых (1
r) разрядов двух двоичных чисел x1=x1(r) … x1(2) x1(1) и x2=x2(r) … x2(2) x2(1), а признаком завершения чисел будет служить символ x(r+1)= * (если одно из слагаемых короче другого, то будем считать, что недостающие разряды - нули).
Выходом автомата должна быть последовательность (r+1) двоичных разрядов суммы y = x1 + x2:
Таким образом, входной алфавит автомата: ?X ={ (00), (01), (10), (11), *}, а выходной алфавит: ?Y={ 0, 1}. Что нужно знать автомату SUM о первых i разрядах x1 и x2, чтобы получив их (i+1)-ые разряды (x1(i+1),x2(i+1)), верно определить выход y(i+1)? Ясно, что для этого достаточно знать, был ли перенос в i-ый разряд. Поэтому можно зафиксировать множество состояний Q = {q0, q1}, в котором q0 означает, что переноса не было, а q1 - что перенос был. Теперь легко построить таблицы, представляющие функции переходов и выходов автомата SUM.
Заметим, что после получения символа * автомат SUM переходит в начальное состояние q0 и готов выполнять сложение следующей пары чисел.
На диаграмме автомата у вершины q0 четыре петли, а у вершины q1 - три, объединены в одну с четырьмя и тремя метками, соответственно. Точно так же слиты два ребра из q1 в q0. Стрелкой указано начальное состояние.
Рассмотрим одну важную конструкцию конечного автомата по двум другим, называемую произведением автоматов, которая позволит установить замкнутость класса конечно автоматных языков относительно теоретико множественных операций.
Пусть M1 = и M2 = - два конечных автомата с общим входным алфавитом ?, распознающих языки L1 и L2, соответственно. Определим по ним автомат M= , называемый произведением M1 и M2 (M= M1 ? M2), следующим образом. Q= Q1 ? Q2 ={ (q, p) | q
Q2}, т.е. состояния нового автомата - это пары, первый элемент которых - состояние первого автомата, а второй - состояние второго автомата. Для каждой такой пары (q,p) и входного символа a
? определим функцию переходов: ?((q,p), a) = (?1(q,a), ?2(p,a)). Начальным состоянием M является пара q0= (q01, q02), состоящая из начальных состояний автоматов-множителей. Что касается множества заключительных состояний, то оно определяется в зависимости от операции над языками L1 и L2, которую должен реализовать M.







 , а в языках программирования эта функция часто обозначается как
, а в языках программирования эта функция часто обозначается как ).
).

















 ;
;

 ;
;
 и
и " (используются также обозначения
" (используются также обозначения ,
, ,
, и
и AND
AND ));
));
 или
или " (используются также обозначения
" (используются также обозначения ,
, и
и OR
OR ));
));
 влечет
влечет " или "из
" или "из следует
следует " (используются также обозначения
" (используются также обозначения , и ( IF
, и ( IF THEN
THEN ));
));
 плюс
плюс " (используется также обозначение
" (используется также обозначение );
);
 эквивалентно (равносильно)
эквивалентно (равносильно) " (используется также обозначение
" (используется также обозначение );
);
 и
и ".
".





































































 и пустым множеством ребер
и пустым множеством ребер является деревом (входит в
является деревом (входит в ).
).

 принадлежат
принадлежат , а
, а - новая вершина, т.е.
- новая вершина, т.е. . Тогда классу
. Тогда классу принадлежит также следующий граф
принадлежит также следующий граф , где
, где ,
, . Корнем этого дерева является вершина
. Корнем этого дерева является вершина .
.

















































































































































































































































 . Такие вершины называются функциональными элементами.
. Такие вершины называются функциональными элементами.































 ,
, } и в нее входят ребра из uj и uk. Тогда в качестве i-ой команды поместим в PS присваивание un+i= uj ? uk.
} и в нее входят ребра из uj и uk. Тогда в качестве i-ой команды поместим в PS присваивание un+i= uj ? uk.













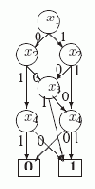




































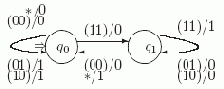





























































































































































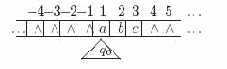







































































































 Учет: Делопроизводство - Автоматизация - Софт
Учет: Делопроизводство - Автоматизация - Софт