
|
А.А. Мельников, А.В. Ушаков - Двоичные динамические системы дискретной автоматики
В монографии освещены вопросы анализа и синтеза двоичных динамических систем, используемых в современной дискретной автоматике «четкой логики». Монография отражает современные достижения в области теории двоичных динамических систем (ДДС) с использованием возможностей алгебраических методов, которые опираются на матричный формализм метода пространства состояния с учетом специфики свойств матриц над простым двоичным полем Галуа, образующих класс линейных ДДС (ЛДДС), а также формализм автоматной логики, разрабатываемый в рамках теории конечных автоматов (КА), именуемых в монографии в рамках общесистемных представлений нелинейными ДДС (НДДС). В этой связи авторами решается задача взаимной трансформируемости НДДС в ЛДДС и наоборот. Особняком в монографии стоят проблемы анализа и синтеза двоичных динамических систем, которые сочетают в себе элементы автоматной логики и линейных векторно-матричных представлений, в силу чего авторами выделенные в особый класс гибридных ДДС (ГДДС).
Монография рассчитана на широкий круг специалистов в области дискретной автоматики, отраслевой телемеханики, аспирантов специальности 05.13.05.-«элементы и устройства вычислительной техники и систем управления», а также студентов старших курсов, обучающихся по направлению 6519.00- «автоматизация и управление» бакалаврской и магистерской подготовки и специальности 2101.00-«управление и информатика в технических системах» подготовки специалиста-инженера.
ПРИНЯТЫЕ СОКРАЩЕНИЯ И ОБОЗНАЧЕНИЯ
| АА - | абстрактный автомат |
| БП - | блок памяти |
| БФ - | булева функция |
| ВА - | время «аппаратурное» |
| ВВ - | модель «вход-выход» |
| ВК - | время «канальное» |
| ВМП - | векторно-матричное представление |
| ВНН - | вектор невязки наблюдения |
| ВПС - | векторный показатель сложности |
| ВС - | модель «вход-состояние» |
| ВСВ - | векторно-матричное линейное описание «вход-состояние-выход» |
| ГДДС - | гибридная двоичная динамическая система |
| ГСА - | граф-схема алгоритма |
| ДА - | дискретная автоматика |
| ДДС - | двоичная динамическая система |
| ДКП - | двоичная кодовая последовательность |
| ДКУ - | декодирующее устройство |
| ДНУ - | двоичное динамическое наблюдающее устройство |
| ДПВ - | диаграмма переходов и выхода |
| ДСНФ - | дизъюнктивная совершенная нормальная форма |
| ДУПК - | дивидендное устройство помехозащитного кодопреоб-разования |
| ИВП - | источник входной последовательности |
| ИЧК - | информационная часть кода |
| КА - | конечный автомат |
| КПР - | кодовое пространство |
| КС - | канал связи |
| КУ - | кодирующее устройство |
| ЛДДС - | линейная двоичная динамическая система |
| ЛУ - | линейное устройство |
| ММ - | модулярный многочлен |
| МС - | модельная среда |
| НДДС - | нелинейная двоичная динамическая система |
| ОПВ - | относительная оценка приведенной востребованности |
| ОСВ - | оценка степени востребованности |
| ПЗК - | помехозащищенный код |
| ПЗКА - | помехозащищенный конечный автомат |
| ПНЗК - | помехонезащищенный код |
РКС
СД
СДБФ
УДА
УДММ
УК
УКК
УПЗК
УС
УФСК
ХММ
ХП
ЦДУ
ЦКУ
ЦПЗК
ЧПС
ЭЗ
ЭП
аппарат селлерсовского дифференцирования булевых функций
устройство дискретной автоматики устройство деления модулярных многочленов устройство коммутации устройство коррекции кода укороченный помехозащищенный код уравнение Сильвестра
устройство формирования сигнала коррекции характеристический модулярный многочлен характеристический полином циклическое декодирующее устройство циклическое кодирующее устройство циклический помехозащищенный код частная производная Селлерса элемент задержки элемент памяти
Г - гипотеза;
К - концепция; ПМ - примечание; Пр. - пример;
ПС - постулат;
С - следствие;
СВ - свойство;
Т - теорема;
У - утверждение;
¦ - знак завершения доказательства утверждения, решения примера, завершения алгоритма;
? - знак завершения формулировки утверждения, определения, примечания, следствия, свойства, постулата, гипотезы;
A, A1, A j - матрица, i -я строка, j -й столбец матрицы A;
col {ai, i = 1, n} - столбцовая матричная структура с элементами аг в
столбце;
D {(•)(*)} - прямое D-преобразование кодовой последовательности (•) над простым полем Галуа;
EM - оператор округления величины (•) до ближайшего большего целого;
F (d )=D {f (к)} - D-образ последовательности f (к);
f (к )=D-1ff (d )} - оригинал D-образа последовательности f (к);
GF(p) = {0,1,2,...,p -1},p e N - простое поле Галуа;
GF(pn), p, n e N - расширенное поле Галуа;
к - дискретное время (к = 0,1,2,К ), выраженное в числе тактов длительностью a t процессов кодопреобразования; row fai,i = 1,n} - строчная матричная структура с элементами аі в строке;
и(к) - входная кодовая последовательность ДДС; х(к) - вектор исходного состояния ДДС; х(к + 1) - вектор состояния перехода ДДС;
У(к) - выходная кодовая последовательность ДДС;
& - союз «И» предикатов; ? - союз «ИЛИ» предикатов.
ВВЕДЕНИЕ
Вниманию проблемно ориентированного читателя предлагается монография «Двоичные динамические системы дискретной автоматики», которая содержит три тематически замкнутых раздела.
Первый раздел, посвященный проблемам анализа и синтеза линейных двоичных динамических систем (ЛДДС) дискретной автоматики (ДА), инструментально строится на результатах процесса алгебраи-зации общей теории систем. Алгебраизация методов исследования устройств дискретной автоматики (УДА), которые составляют обширный класс динамических систем над конечными простым и расширенным полями Галуа, стала проникать в практику разработчиков этих устройств в последней трети XX в. На первом этапе она проявилась в использовании векторно-матричных модельных представлений линейных УДА над конечными полями с основанием (характеристикой) два. Процесс алгебраизации, опираясь на возможности матричного формализма, позволил решить проблемы анализа свойств линейных УДА на основе исследования структуры пространств матриц состояния, управляемости и наблюдаемости и их пересечения, что особенно эффективно проявило себя при анализе структуры неподвижных состояний ЛДДС, их замкнутых циклов, а также при редуцировании размерности УДА. В задачах синтеза ЛДДС устройств ДА применение принципа векторного и матричного подобия позволило конструктивно использовать возможности формализма матричного уравнения Сильвестра (УС) над конечным полем для расширения банка реализаций линейных УДА. Более того, алгебраизация обнаружила свои возможности в переносе идей динамического наблюдения, разработанных в недрах теории систем над бесконечными полями, на УДА и двоичные каналы связи с целью оценки их состояния. Причем в случае постановки задачи оценки начального состояния «регистра помехи» в двоичном канале связи удается по-новому сформулировать задачу помехоустойчивости передачи кодированных сигналов в фазе декодирования, которая также решается с помощью матричного уравнения Сильвестра. Последнее обстоятельство позволило разработать алгоритмическое обеспечение конструирования проверочных и образующих матриц помехозащищенных кодов, также опирающееся на возможности матричного уравнения Сильвестра. В случае неконтролируемой кодовой систематики эта задача может быть решена с помощью SVD-процедуры сингулярного разложения матриц с использованием программной оболочки MATLAB, адаптированной к модулярной арифметике.
Второй раздел, посвященный проблемам анализа и синтеза нелинейных двоичных систем (НДДС) дискретной автоматики, инструментально опирается на результаты в области теории и практики конечных автоматов, которые с точки зрения общей теории систем образуют класс НДДС. В разделе проблемы синтеза и анализа устройств дискретной автоматики в рамках существующих версий автоматной логики рассматриваются как в канонической «автоматной» постановке, так и с использованием граф-схем алгоритмов (ГСА) описания функционирования УДА, при этом разработка методов погружения ГСА в автоматную среду позволила построить алгоритмы синтеза УДА в различных типах автоматной и триггерной логики.
Возможности автоматных представлений УДА распространяются на реализацию циклических дивидендных кодирующих и декодирующих устройств в произвольной триггерной логике, а также устройств коррекции искаженных при передаче по двоичным каналам связи кодовых комбинаций с использованием синдромов и квазисиндромов искажений. Автоматные представления ДДС обнаруживают свои возможности и при построении циклических кодирующих и декодирующих дивидендных устройств укороченных кодов с управляемым циклом деления путем коммутации структуры устройств оптимальных кодов. Богатые возможности в теории и практике автоматных описаний обнаруживает аппарат Селлерса дифференцирования булевых функций. Эти возможности в монографии используются для контроля корректности выбора булевых переменных, оценки их востребованности в процессе функционирования УДА, а также сравнительной оценки «степени нелинейности» и сложности альтернативных реализаций комбинационных схем по числу членов разложения булевых функций в ряд по селлерсовским производным.
Третий раздел монографии посвящен проблемам анализа и синтеза гибридных двоичных динамических систем (ГДДС) дискретной автоматики, сочетающей в себе элементы линейных и нелинейных модельных представлений. Первым признаком гибридности ДДС является размерность ее блока памяти, которая занимает промежуточное положение между размерностью автоматной реализации и линейной при решении одной и той же задачи кодопреобразования. В этой связи важной концептуальной задачей синтеза ГДДС являются проблема «кодового пространства» и формирование способов его заполнения. В монографии указанные проблемы решаются путем редуцирования линейных ДДС и введением избыточности при кодировании состоянии ДДС, синтезируемых в автоматной логике, с целью приданию им помехозащищенности. Причем последняя задача решается в постановке рационального использования ресурсов помехозащиты, в качестве критерия которого используется фактор востребованности булевых переменных кодов состояний на всех наборах переменных. Еще одним эффективным способом решения проблемы «кодового пространства» на паре НДДС-ЛДДС является обмен аппаратурного пространства на временные затраты. Гибридные ДДС образуют достаточно новый класс двоичных динамических систем, разработка теории которых является весьма актуальной.
Авторы отдают себе отчет в том, что предлагаемая вниманию читателей монография является скромным вкладом в теорию двоичных динамических систем устройств дискретной автоматики, основы которой заложены фундаментальными работами Буля Дж. (Boole G.), К. Шеннона (C.Shannon), Э. Мура (E. Moore), А. Гилла (A. Gill), М. Арбиба (M. Arbib), У. Питерсона (W. Peterson), Ф. Селлерса (F. Sellers), Д. Бохманна (D. Bochmann), Х. Постхофа (C. Posthoff), Р. Хэмминга (R.Hamming), В. М. Глушкова, Ю. Т. Медведева, Р. Г. Фа-раджева, С. И. Баранова, В. В. Сапожникова, Вл. В. Сапожникова, В. А. Горбатова, Ю. Л. Сагаловича, А. А. Шалыто, Н. С. Щербакова и многих других зарубежных и отечественных ученых.
Основу монографии составили результаты научных исследований в лаборатории телемеханики кафедры систем управления и информатики (бывшей кафедры автоматики и телемеханики) университета, проводившихся под руководством доктора технических наук, профессора А. В. Ушакова. Результаты последних лет авторами получены при разработке теоретических проблем, к решению которых во исполнение региональной комплексной целевой программы «ТЕЛЕМЕХАНИКА -2000» в инициативном порядке подключилась лаборатория телемеханики. Монография в предложенном виде содержит в основном результаты последних лет, имеющие как научный, так и методикопознавательный характер. Последнее позволяет рекомендовать ее специалистам в области дискретной автоматики, а также аспирантам специальности 05.13.05.- «элементы и устройства вычислительной техники и систем управления», студентам старших курсов направления 6519.00- «автоматизация и управление» и специальности 2101.00-«управление и информатика в технических системах».
Замысел монографии возник у авторов в результате постоянных научных контактов и обмена научными идеями, в результате чего основной текст монографии авторы написали совместно. В написании параграфов 1.6, 1.7 и 2.4 приняла участие Е.В. Рукуйжа.
Конструктивную критику по существу структуры и содержания монографии просим направлять авторам:
почтовый адрес - 197101, Санкт-Петербург, Кронверкский пр., 49,
Санкт-Петербургский государственный университет информационных технологий, механика и оптики (СПбГУ ИТМО);
телефон 595-41-28;
электронная почта - и .
1 ЛИНЕЙНЫЕ ДВОИЧНЫЕ ДИНАМИЧЕСКИЕ СИСТЕМЫ ДИСКРЕТНОЙ АВТОМАТИКИ
1.2. Аппарат передаточных функций в задаче модельного представления линейных двоичных динамических систем
Двоичные динамические системы (ДДС), интегрированные в некоторую техническую среду приема, хранения, обработки и передачи двоичной информации, при выполнении конкретных функций решают в основном задачи преобразования кодов, элементы которых принадлежат простому полю Галуа GF(p)={о,1,2,К ,p -1 }, которое при
p = 2 принимает вид GF(2)={0,і} [15, 29, 42, 55]. Преобразуемые коды могут быть представлены тремя основными способами: в виде вектора, не параметризованного дискретным временем; в виде кодовой последовательности (скалярной или векторной), параметризованной дискретным временем, и в виде модулярных многочленов (ММ) [15, 55]. Если процесс преобразования кода, поданного на вход ДДС, в код, наблюдаемый на ее выходе, осуществляется с помощью линейной композиции результатов линейных операций умножения и суммирования по модулю два, то такая двоичная динамическая система является линейной (ЛДДС). Если при этом основной результат преобразования кодов с помощью ЛДДС фиксируется на ее выходе и входе, то описание функционирования такой ЛДДС может быть задано в классе модельных представлений «вход - выход».
Одним из конструктивных средств задания модельного представления «вход - выход» над бесконечными и конечными полями является аппарат передаточных функций (матриц). В основе методологии аппарата передаточных функций (матриц) лежит алгебраизация отношения «вход - выход», которое для непрерывных систем над бесконечным полем осуществляется с помощью преобразования Лапласа, для дискретных систем над бесконечным полем - с помощью Z -преобразования, а для дискретных систем над конечным простым полем Галуа GF(p), частным случаем которых при p = 2 являются
ЛДДС, - с помощью D-преобразования кодовых последовательностей и модулярных многочленов (см. Приложение).
Передаточная функция, записанная в виде отношения двух полиномов, представляет собой решение графа [46], к которому может быть применено правило Мейсона некасающихся контуров в инверсной постановке. Суть инверсного использования правила Мейсона [25, 46] состоит в воссоздании класса графов с вложенными (касающимися) контурами минимальной размерности, эквивалентных в смысле решений этих графов в форме передаточной функции отношения «вход -выход». Построенный класс графов образует множество возможных структурных представлений ЛДДС, которые могут быть положены в основу схемотехнических реализаций двоичных динамических систем, решающих заданную задачу преобразования кодов.
Возможности аппарата передаточных функций (матриц) в задаче модельного представления ЛДДС рассмотрим, опираясь на систему определений и утверждений.
Определение 1.1 (О1.1). Х-мерной двоичной кодовой последовательностью
f(k): f( 0 ),f( 1), f( 2), К ,f(k), К (1.1)
будем называть параметризованный дискретным временем k, выраженным в числе k тактов длительностью at, векторный кортеж
[29], компоненты которого /(k) для Vk представляют собой Х-мерные векторы, элементы которых принадлежат простому полю Галуа GF(p)|p_2 = {0,1}. ?
Если в (1.1) размерность Х компонентов равна единице, то последовательность f (k) является скалярной или одномерной.
Кодовая последовательность (1.1) может быть конечной по времени и периодической, если выполняется равенство
f(k)= f(k + T), (1.2)
где T - период периодической последовательности.
Определение 1.2 (О1.2). D-образом F(d) двоичной кодовой последовательности (1.1) в силу прямого D-преобразования (см. Приложение) называется сходящаяся бесконечная сумма
<х>
F(d) = D{f(k)}=Z.f(k)dk .? (1.3)
k=0
Введем теперь в рассмотрение передаточные матрицы и функции линейной ДДС.
Определение 1.3 (О1.3). Пусть ЛДДС преобразует r-мерную входную двоичную кодовую последовательность (ДКП) u(k) в m-мерную выходную ДКП y (k), тогда передаточной матрицей ф( d) этой ЛДДС называется матрица, связывающая D-образ Y(d) выходной ДКП y (k) с D-образом U (d) входной ДКП u (k) при нулевом
начальном состоянии ЛДДС в силу соотношения
Ф(d)= arg {Y(d)=Ф(d)U(d), Y(d),U(d)-fix }? (1.4) Введем в рассмотрение (i, j)-й сепаратный канал ДДС, который связывает ее i-й выход Y (k) с j-м входом Uj (k) (i = l,m;j = l,r ). Тогда (i, j )-й сепаратный канал ЛДДС может быть описан передаточной функцией Фу (d), задаваемой определением.
Определение 1.4 (О1.4). Передаточной функцией (i,j)-го сепаратного канала Фф(d) ЛДДС называется отношение Y (d) - D-образа выходной ДКП yi(k), наблюдаемой на i-м выходе системы и
U} (d) - D-образа входной двоичной кодовой последовательности Uj(k), поданной на j-й вход линейной ДДС, полученное при нулевом начальном состоянии ЛДДС:
ФИ (d ) = . ?
(1.5)
Uj (d)
Нетрудно видеть, что Ф(d) является (i, j)-м компонентом передаточной матрицы Ф(d) (1.4). Таким образом становится справедливым положение следующего утверждения.
Утверждение 1.1 (У1.1). Передаточная матрица Ф(d) (1.4) линейной ДДС, осуществляющей преобразование r -мерной кодовой последовательности u(k) в m-мерную кодовую последовательность
y(k I имеющих представление
u(k)= col {Uj (k),j = 1,r }; y(k)= col {y, (k),i = 1,m }, (1.6)
представляет собой (m xr)-матрицу, составленную из передаточных функций Фу (d) (1.5) всех (m xr) ее (i, j)-х сепаратных каналов так, что становится справедливым представление
Ф(d)= row {col\фу (d); i = 1,m]; j = 1,r }. ? (1.7)
Если ЛДДС преобразует скалярную входную кодовую последовательность u(k) в скалярную кодовую последовательность y(k) так, что r = m = 1, то передаточная матрица (1.4) ЛДДС вырождается в передаточную функцию, задаваемую дивидендным выражением
ф(й)
y (d)=m (d) = Ъаа
U (d) N (d) ? fijdj
j=0
во = 1, ?
(1.8)
где M (d), N (d) — модулярные многочлены (ММ) относительно переменной d, соответственно степеней X и т .
Выделим теперь случай, когда входной и выходной коды задаются в форме модулярных многочленов
u( x) = uXxХ + u X-1 x + К + u1 x + u0, (1.9)
У(х )= ymxm + Ут-1xm-1 + К + Уіx + У0, (1-10)
где Хит именуются степенями ММ u(x) и y(x); uv(v = 1, х), y^(p = 1,m ) принадлежат простому полю Галуа GF(p)|р=2 = {0,1},
при этом приведение подобных при сложении и умножении модулярных многочленов производится по правилам сложения и умножения по модулю p = 2 ( modp = mod2 ).
Процесс преобразования входного кода u, задаваемый ММ u (x) (1.9) в выходной вектор у, задаваемый модулярным многочленом у (x) (1.10), может быть так же описан с помощью передаточной функции 0(d) вида (1.8), если будут сконструированы D-образы U(d) и
Y (d) модулярных многочленов u (x) и у (x) соответственно. D-образ
модулярного многочлена зависит от того, каким разрядом вперед организована в среде линейных ДДС передача (преобразование) модулярных многочленов.
Утверждение 1.2 (У1.2). D-образ модулярного многочлена
f (x ) = t fx = fx + fn-1 x"-1 + к + f x + fo, (1.11)
k=n
F (d ) = D{f (x )} при его передаче младшим разрядом вперед задается выражением
F(d) = D{f(x)} = f{x)\xd = f + f,x + К + f^d’- + f„d" ? (1.12)
Доказательство утверждения состоит в формировании последовательности
f( k): fo.fi К ,f"-i,f", (1.13)
с последующим применением к (1.13) прямого D-преобразования. ¦ Утверждение 1.3 (У1.3). D-образ модулярного многочлена
f (x )= t fk
(1.14)
kx
k=0
F(d)= D{f (x)} при его передаче старшим разрядом вперед задается выражением
F(d) = D{f(x)}= f(x_1 ^ _! d =
= fn + f„-id + K+ ftdn-' + fd ; f(x) = x-nf(x) ? (1.15)
Доказательство утверждения строится на формировании последовательности
7 (к) •• f„.fn-,.K J,Jo, (1.16)
с последующим применением к (1.16) прямого D-преобразования. ¦
Заметим, что в современных устройствах дискретной автоматики (УДА) преобразование кодов, заданных с помощью модулярных многочленов, осуществляется старшим разрядом вперед.
Отмеченное выше позволяет ввести следующее определение.
Определение 1.5 (О1.5). ЛДДС, осуществляющая преобразование входного кода, заданного с помощью модулярного многочлена u (x) (1.9), в выходной код, заданного с помощью модулярного многочлена У (x) (1.10), может быть описана передаточной функцией вида (1.8),
в которой D-образы Y(d) и U(d) вычисляются в силу (1.15). ?
Отдельного рассмотрения требует вопрос конструирования передаточной функции ДДС в случае, если ставится задача синтеза устройства умножения или деления модулярных многочленов. В данной постановке передаточная функция ф( d) ДДС, осуществляющей умножение ММ a (x) и b (x), будет определяться в силу правила
ф(d )= arg {(a(d )v b(d ))°ф(d )=
= min {ega(d ),degb (d)}} (1.17)
В случае, когда ставится задача конструирования ДДС, осуществляющей деление модулярного многочлена a (x) и ММ b (x) в форме
a (x I, то передаточная функция ф( d) ДДС будет иметь вид b (x)
1
b(d) .
Ф(d )
(1.18)
Представленные положения своей целью имеют получение структурного представления ЛДДС для последующей ее технической реализации или структурно-функционального анализа. Получить структурное представление ЛДДС с использованием понятия передаточной функции (матрицы) позволяют положения следующего утверждения.
Утверждение 1.4 (У 1.4). Структура модельного представления ЛДДС, описываемой передаточной функцией вида (1.8) с единичным свободным членом знаменателя, может быть построена с использованием правила некасающихся контуров метода Мейсона, в соответствии с которым она выразится в форме касающихся (вложенных друг в друга) контуров, передаточные функции которых заданы мультипликативной структурой из постоянного коэффициента а, и соответствующей степени i переменной d знаменателя передаточной функции так, что их число не превышает m, а число прямых ветвей от входа к выходу этой реализации определяется числом ненулевых элементов числителя передаточной функции с передаточными функциями ветвей Pidl, число которых не превышает m + 1. ?
Доказательство утверждения можно найти в литературе по теории графов, например, в [25]. ¦
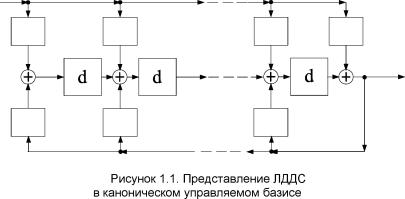
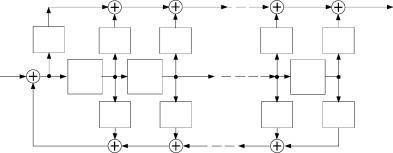 |
| Рисунок 1.2. Представление ЛДДС в каноническом наблюдаемом базисе |
Элементы d модельных представлений, показанных на рисунке 1.1
^юкр^5а^_по^
ожения следующего ут-
и 1.2, имеют смысл, который верждения.
Утверждение 1.5 (У 1.5). Элемент памяти, передаточная функция ФЭП (d) которого имеет представление
Фэп (d ) = d, (1.19)
является D-триггером. ?
Доказательство утверждения строится на понятии D-триггера и
свойстве D-преобразования для сдвинутой ДКП (см. Приложение). Из
теории элементов дискретной автоматики известно, что D-триггер представляет собой элемент памяти (ЭП), реализующий задержку выходной у(к) ДКП на один такт относительно входной и(к) ДКП так,
что и(к) = y(k +1). Если теперь воспользоваться свойством D-преобразования для сдвинутой ДКП, то получим:
d ~lY (d ) = U (d),
откуда для ФЭП (d) будем иметь:
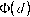
= Y(d) = Y (d) = _
U(d) d~'Y(d) d ' '
Положения раздела позволяют сформировать следующий алгоритм конструирования передаточной функции и построения структурного представления соответствующей ЛДДС.
Алгоритм 1.1 (А 1.1)
0. Классифицировать задачу кодопреобразования: в форме ЛДДС, преобразующей входную последовательность в выходную, или в форме ЛДДС, осуществляющей умножение/деление ММ. Если рассматриваемая задача соответствует первому случаю, то продолжить выполнение алгоритма с п.1, если второму - с п.6 алгоритма.
1. Задать преобразуемый (входной) двоичный код в форме двоичной кодовой последовательности и (к) или модулярного многочлена и (х).
2. Задать выходной двоичный код в форме ДКП y(k) или ММ У(х).
3. Вычислить U (d) D-образ и( к) или и (х).
4. Вычислить Y(d) D-образ y(к) или у(х).
5. Сконструировать передаточную функцию Ф( d) синтезируемой ЛДДС в форме (1.8) и перейти к выполнению п.7 алгоритма.
6. В случае конструирования ЛДДС, осуществляющую умножение ММ, вычислить ее передаточную функцию ф( d) в силу (1.17).
В случае конструирования ЛДДС, осуществляющую деление ММ, то вычислить ее передаточную функцию 0(d) в силу
(1.18).
7. С помощью правила Мейсона некасающихся контуров построить структурные представления передаточной функции 0(d) в канонических структурных формах [25].
8. Сравнить реализации по векторному показателю сложности (ВПС) с компонентами, учитывающими число элементов памяти с передаточной функцией ФЭП (d) = d, число элементов двухвходового суммирования по mod 2, число точек ветвления распространения сигналов, число ветвей.
9. Принять к реализации одну из структур (с меньшей нормой ВПС). Осуществить схемотехническую реализацию принятой версии ЛДДС. ¦
Пример 1.1 (Пр1.1)
В качестве примера рассматривается линейная ДДС, преобразующая входную единичную последовательность и (к )= 1( к) в периодическую периода T = 7, обеспечивающую размещение в регистре хранения информационных разрядов кода Хэмминга (7,4).
0. Выполним п.0 алгоритма 1.1, в соответствии с которым продолжим выполнение алгоритма с п.1.
1. Зададим преобразуемый (входной) двоичный код в форме двоичной кодовой последовательности и( к):
и (к )= 1( к ) = 11111111111111К
2. В соответствии с расположением информационных разрядов в кодах Хэмминга (7,4) зададим выходной двоичный код в форме ДКП у( к):
y(k) = 1110100\1110100К 1110100К .
3. Используя прямое D-преобразование (П1.1), вычислим
U (d) D-образ преобразуемой (входной) кодовой последовательности и(к) в результате чего получим:
и (d )=D{и (к )}=.
1 + d
4. Аналогично п.3 вычислим Y(d) D-образ выходной ДКП У(к):
С помощью правила Мейсона некасающихся контуров построим структурные представления передаточной функции Ф(d ) в канонических структурных формах (рисунок 1.3, ри
Y (d )=D {y (k)}
1 + d7
Сконструируем передаточную функцию синтезируемой ЛДДС в форме (1.8) и перейдем к выполнению п.7 алгоритма.
Y (d) = ( 1 + d + d2 + d4)(1 + d) = 1 + d3 + d4 + d5
Ф(d ) =
U (d)
1 + d7
1 + d7
7.
| сунок 1.4). |
 |
| Рисунок 1.3 |
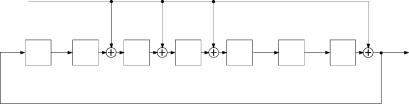 |
| Рисунок 1.4 |
Пример 1.2 (Пр1.2)
Рассматривается задача конструирования линейной ДДС, осуществляющей деление произвольной входной ДКП (задаваемой в виде ММ
и (х)) на неприводимый многочлен в(х ) = х3 + x + 1 с учетом передачи ДКП старшим разрядом вперед.
0. Выполним п.0 алгоритма 1.1, в соответствии с которым продолжим выполнение алгоритма с п.6.
6. Сконструируем передаточную функцию синтезируемой ЛДДС в форме (1.17) с учетом передачи ДКП старшим разрядом вперед:
f (х )= х3 (1 + x ~2 + x ~3);
J3(d) = D{e(x)}=/~ (х -1 )| _1 = 1 + d2 + d3;
0(d)= 1^= 1 -.
J3(d) 1 + d2 + d3
7. С помощью правила Мейсона некасающихся контуров построим структурные представления полученной передаточной функции 0(d) в канонических структурных формах (см. рисунок 1.5, рисунок 1.6):
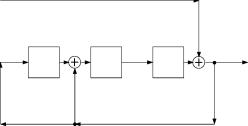 |
| Рисунок 1.5 |
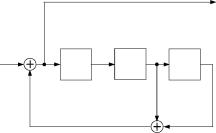 |
| Рисунок 1.6 |
Общесистемные тенденции к расширению банка модельных представлений динамических систем над бесконечными и конечными полями [3, 9, 15, 29] привели разработчиков теории систем к достаточно универсальной модельной среде (МС), которая опирается на триаду «вход-состояние-выход» (ВСВ). Применительно к двоичным динамическим системам модель ВСВ последних имеет вид
ДДС: { u,x,y,k, А,8 } (1.20)
где u - r -мерный вектор входной последовательности; x - n -мерный вектор состояния ДДС; y - m -мерный вектор выходной последовательности; k - счетное множество моментов кодопреобразования, осуществляемого ДДС; А - правило перехода ДДС из исходного состояния x( k) в состояние перехода x( k +1) под действием вектора
входной последовательности u(k); 8 - правило выхода, описывающее процесс формирования элементов выходной последовательности y( k) на переходе из состояния x (k) под действием u (k) или как функции только состояния x(k).
Введем в рассмотрение следующее определение.
Определение 1.6 (О1.6). Каноническим представлением «вход- состояние-выход» произвольной двоичной динамической системы (1.20) называется ее представление в виде двух векторных выражений
x(k + і) = А[ x( k),u( k)], (1.21)
y(k)=8[x(k),u(k)]. ? (1.22)
Векторное модельное описание ВСВ (1.21), (1.22) произвольной ДДС имеет структурное представление, приведенное на рисунке 1.7.
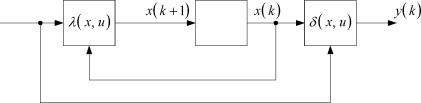 |
| Рисунок 1.7. Структурное представление произвольной ДДС |
Определение 1.7 (О1.7). Если правило перехода Л(x,u) и правило
выхода S(x,u) ДДС (1.21), (1.22) допускают представление в виде композиции линейных операций умножения матрицы на вектор и суммирования в рамках правил модулярной арифметики по модулю p = 2
так, что (1.21) и (1.22) принимают вид
x(k +1) = Ax(k) + Bu(k), x(0); (1-23)
y (k)= C x (k)+ H u (k), (1-24)
то такая ДДС называется линейной. В (1.21), (1.22) A - (n х п)-матрица состояния, B - (n х r)-матрица входа, C - (п х т)-
матрица выхода, H - (т х r~)-матрица вход-выход ДДС, x (0 ) - начальное состояние ДДС. ?
Краткости ради представление (1.23), (1.24) ЛДДС будем называть ее (,B,C,H )-матричным представлением.
Линейное векторно-матричное представление (1.23), (1.24) двоичной динамической системы имеет структурный графический аналог, приведенный на рисунке 1.8. На рисунке 1.8 ЭЗ - элемент задержки, который образует БП ЛДДС, а блоки с матричными коэффициентами передачи B,A,C,H и сумматоры по модулю p = 2 образуют комбинационную схему линейной ДДС.
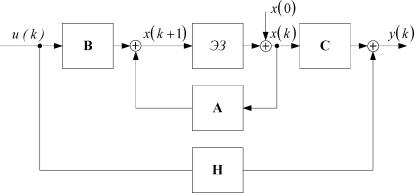 |
| Рисунок 1.8. Структурное представление векторно-матричной модели (1.23), (1.24) ЛДДС |
Утверждение 1.6 (У1.6). Суммарное векторно-матричное представление ЛДДС (1.23), (1.24) задается соотношениями
x(k) = Akx(0)+X Ak-1-iBu(i), (1.25)
i=0
y (k ) = CA kx (0)+X CA k-1-i B u(i) + u (k) ? (1.26)
i=0
Доказательство утверждения строится с использованием рекуррентного соотношения (1.23), которое для первых трех тактов позволяет записать
x (1) = A x (0) + B u (0);
x (2) = A x (1)+ B u (1)= A2 x (0)+ AB u (0)+ B u (1);
x (3)= A x (2)+ B u (2)= A3 x (0)+ A2 B u (0)+ AB u (1)+ B u (2);
Полученная база индукции для любого момента k делает справедливым представление
x(k) = Akx(0)+XAk-1-iBu(i), (1.27)
i=0
Второе соотношение суммарной ВМП ЛДДС в форме (1.26) получается подстановкой (1.27) в (1.24). ¦
Соотношение (1.27) допускает модификацию, обнаруживающую динамическое преимущество моделей ВСВ над моделями «вход-выход», коими являются передаточные функции двоичных динамических систем. Модифицированное представление суммарной ДДС зададим с помощью утверждения.
Утверждение 1.7 (У 1.7). Суммарная модель (1.27) процессов по вектору состояния линейной ДДС допускает представление
x(k) = Akx(0) = Wy (k) U(k), (1.28)
где
U (k)=[uT (k - l),uT (k - 2),К ,uT (l),uT (0)] (1.29)
Wy (k) = [B\AB !К ! Ak-1 B^ (1.30)
при этом U(k) именуется «вектором стратегии» перевода ЛДДС из начального состояния x(0) в желаемое состояние x(k) за k-тактов, а матрица Wy (k) (1.30) именуется матрицей управляемости линейной двоичной динамической системы за k -тактов. ?
Доказательство утверждения строится на представления выражения (1.27) в форме
x(k)+ Akx(0) = Bu(k -1)+ ABu(k - 2)+ A3Bu(k - 3) + К
К+ A k-2B u (1)+ A k-1B u (0) (1.31)
Выражение (1.31) путем введения агрегированных матрицы и вектора в правой части позволяет записать
х (к)+ A kx (0 ) =
= [в\ЛБ |К |Aк-B ][ (к - 1),ит (к - 2 ),К ,uT (1),ит (0 ) (1.32) Введение обозначений (1.29), (1.30) приводит (1.32) к виду (1.28). ¦
Представление (1.28) позволяет сформулировать критерий управляемости линейной ДДС с индексом управляемости, равным к.
Утверждение 1.8 (У1.8). Для того чтобы линейная ДДС (1.23),
(1.24) была полностью управляемой с индексом управляемости [29] равным к, то есть за к тактов линейная двоичная система могла быть переведена из любого начального состояния х(0) в любое конечное состояние необходимо и достаточно, чтобы выполнялось условие
гапк Wy (к) = n = dimx. ? (1.33)
Доказательство утверждения строится на том, что выполнение равенства (1.33) является необходимым условием обратимости матрицы Wy (к), то есть существование W— (к). Но если это так, то это условие
становится достаточным для вычисления «вектора стратегии» управления U (к) на основе (1.28), записываемого в форме
U (к )= W-1 (к)(x (к) + A kx (0)) (1.34)
для любых x (к) и x (0). ¦
Условие полной управляемости с индексом к < n = dimx является достаточно жестким, более мягкой формой является условие полной управляемости с индексом n = dim x, которое принимает вид
rank Wy (n) = rank[b j AB |k |An-1 B]= n = dimx. ? (1.35)
Соотношение (1.35) является условием полной управляемости, то есть управляемости за n тактов, при этом используется обозначение Wy (n) = Wy, где матрица
Wy =[ b\ab ! К ! An-1 B ] (1.36)
именуется матрицей управляемости ЛДДС (1.23), (1.24).
По аналогии с (1.32) может быть сконструировано векторноматричное соотношение, позволяющее по результатам измерений на первых к тактах выходной последовательности y( к) и входной последовательности и (к) восстановить начальное состояние x(0) линейной ДДС.
Утверждение 1.9 (У1.9). Для того чтобы линейная ДДС (1.23),
(1.24) была бы полностью наблюдаемой с индексом наблюдаемости к, то есть чтобы имелась возможность восстановить начальное состояние x(0) за первые к тактов, необходимо и достаточно, чтобы
матрица наблюдаемости WH (к) с индексом наблюдаемости к обладала рангом, равным n = dimx, иначе чтобы выполнялось условие
rank {w н (n)= col [CAC i = 0,к -1]=
dimx •?
(1.37)
Доказательство утверждения строится на формировании измерений на первых к тактах в силу (1.24) и (1.27) у (0 ) = C x (0 )+ H и (0)
(1.38)
у (l)= C x (l)+ H и (1)= CAx (0) + CB и (0)+ H и (l) у (2 )= C x (2)+ H и (2)= CA 2x (0) + CAB и (0) + CB и (l)+ H и (2)
M
у (к -1)= C x (k -1)+ H и (к -1)= CA k-1x (0)+ CA k-2 B и (0) +
+ CA k-3B и (l) + K + H и (к -1)
Сформируем на основе (1.38) вектор измерения z(к) с компонентами у (0)+ H и (0)
| z | 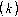 |
у (l)+ CB и (0)+ H и (l)
у (2)+ CAB и (0)+ CB и (l)+ H и (2)
M
у (к -1)+ CAк-2 B и (0)+ CAk-3 B и (l) + K + H и (к -1)
Совместное использование представлений (1.38) и (1.39) позволяет записать
z(к) = col [al; i = 0,к - 1\x(0) = Wн (к)x(0). (1-40)
Выполнение условия (1.37) является необходимым для обратимости матрицы наблюдаемости с индексом к Wн (к), а существование
матрицы W- (к) является достаточным для вычисления вектора начального состояния ЛДДС x( 0) в силу (1.40) в форме
x( 0)= Wn1 ( к) z( к) • ¦
Нетрудно видеть, что условие (1.37) для матрицы наблюдаемости с индексом к является сильным, более слабым является выполнение этого условия для к = n = dim x, тогда матрица наблюдаемости с индексом n W (n) называется просто матрицей наблюдаемости ЛДДС
(1.23), (1.24) или пары матриц (A,C) и обозначается следующим образом
WH =WH (n )= col {CAI: i = 0,n -1}. ? (1.41)
Векторно-матричная модель ВСВ линейной ДДС (1.23), (1.24) позволяет сконструировать модель «вход-выход» (ВВ) в форме передаточной
функции (матрицы), а также в форме рекуррентного уравнения ВВ с матричными коэффициентами.
Утверждение 1.10 (У1.10). Линейная ДДС (1.23), (1.24) может быть описана передаточной функцией (матрицей) ф( d), связывающей D-образ Y(d) выходной последовательности y( к) и D-образ U(d) входной последовательности и(к) в мультипликативной форме
Y(d)=ф(d) U(d) (1.42)
где ф(d) задается в виде
ф^) = C (d—I + A)- B + H. ? (1.43)
Доказательство утверждения строится на применении к (1.23),
(1.24) прямого D-преобразования, которое дает выражения
d ~'x( d) + d ~'x( 0) = Ax( d) + BU (d) (1.44)
Y (d ) = Cx( d) + HU( d) (1.45)
Если исключить из (1.44) и (1.45) x( d) и разрешить их с использованием модальной арифметики относительно D-образа Y (d), то получим Y(d)={c(d-1 + A)-1 B + H }u(d) + C(d-1 + A)~1d~1x(0). (1.46) Положив в (1.46) нулевое начальное состояние ЛДДС в форме x (0)=0,
запишем для D-образа Y (d) выходной последовательности
Y(d)={C(d-11 + A)'1 B + H }u(d). (1.47)
Сравнение (1.47) с (1.42) позволяет записать (1.43). ¦
Из выражения (1.43) становится корректным вычисление Ф(d) -
передаточной функции (i, j)-сепаратного канала ЛДДС, связывающего І -й выход yt ( к) с j -м входом Uj (к) в виде
Фц (d) = c) d I + a)-' Bj + Hij, (1.48)
где Ci - i -я строка матрицы C, Bj - j -й столбец матрицы B и Hj -(i, j)-й элемент матрицы H.
С целью дальнейших исследований воспользуемся разложением Д. К. Фаддеева [25] резольвенты (d—I + А)- ЛДДС (1.23), (1.24). Разложение построим в силу положений следующего утверждения.
Утверждение 1.11 (У1.11). Резольвента (d—I + А)- ЛДДС (1.23),
(1.24) может быть представлена в форме
(I + А) = det(d(I + A) )(d"^ + L1 (d"^ + L(F +Л Л+ Ln-2 (d- )+ L„-t ] (1.49)
где матричные компоненты Lx (X= 1,n -1) определяются в силу рекуррентной процедуры Д. К. Фаддеева [25]
Lx = axI + ALX-1, X= 1,n -1; L0 = I (1-50)
где элементы ax, X= 1,n суть коэффициенты характеристического полинома det(( 11 + a)= )d 1) + a1 (d 1) 1 + a2(d 1) 2 + Л + an-1 (d 1)+ an?(1.51)
Доказательство утверждения строится на последовательном умножении слева выражения (1.49) на характеристическую матрицу
(d- I + а) ЛДДС (1.23), (1.24), затем на характеристический полином det (d- I + а), записанный в форме (1.51), и приравнивании матричных коэффициентов при скалярных степенях (d_1 ^, X= 0,n -1 слева и справа. Выполнение указанных действий приводит к (1.49) с матричными коэффициентами (1.50). ¦
Утверждение 1.12 (У 1.12). Линейная двоичная динамическая система (1.23), (1.24) может быть модельно представлена рекуррентным уравнением ВВ с матричными коэффициентами, которое имеет вид
y(k + n) + a1y(k + n -1) + a2y(k + n - 2)+K + an-1y(k +1)+ any(k) =
= Hu(k + n) + (CL0B + a1 H) u(k + n - 1)+K
K+(CL„_2B + a„_,H)u(k + 1)+{CL„_,B + a„H)u{k) ? (1.52)
Доказательство утверждения строится на подстановке резольвенты (d-11 + A)-1, записанной в форме (1.49), с характеристическим полиномом вида (1.50) в выражение (1.47), что позволяет записать d ~ny(d) + ad ~(n-1)y(d) + a2d ~(n~2)y(d)+К + an-1d ~1y(d) + any(d) =
= Hd-nu( d) + (CL0 B + a2 H) d -(n-1)u( d)+К
К +(CLn_2B + an-1H) d~1u(d)+(CLn-1 B + anH) u(d) (L53)
Если теперь к левой и правой частям (1.53) применить обратное D-преобразование, памятуя о том, что при нулевых начальных условиях в силу свойств прямого D-преобразования выполняется соотношение
D{D[f ( + p)]}= D{d-pF(d) }=f (k + p) (1.54)
то становится понятным переход от (1.53) к (1.52). ¦
Нетрудно видеть, что в структуре доказательств утверждений У1.11 и У1.12 содержится доказательство следующего утверждения.
Утверждение 1.13 (У 1.13). Если передаточная функция ф(й) линейной ДДС (1.23), (1.24) задана в форме отношения модулярных многочленов по положительным степеням переменной d
^d )=MM.
V ' D (d)
(1.55)
где M (d) и D(d) соответственно степеней degM (d ) =
deg D(d ) = n, то характеристический полином det(d 11 + a) матрицы состояния A ЛДДС с передаточной функцией (1.55) определится выражением
det(d~l I + a)= D(d~l), (1.56)
где D (d_1) - модулярный полином по отрицательным степеням переменной d, вычисляется в силу соотношения
D(d )= dnD(d_1). ? (1.57)
Теперь поставим обратную задачу конструирования (,B,С,H) представления линейной ДДС в форме (1.23), (1.24) по ее передаточной функции ф(d) отношения «вход-выход». Возможности решения поставленной задачи заложены в параграфе 1.1 структурными представлениями в виде рисунков 1.1 и 1.2 передаточных функций, а также тем обстоятельством, что элемент памяти с передаточной функцией ФЭП(d) = d реализует задержку на один такт двоичного кодового преобразования произвольной переменной ж( k +1), наблюдаемой на его входе, в переменную №(k), наблюдаемую на его выходе. Решение поставленной задачи представим в виде алгоритма.
Алгоритм 1.2 (А 1.2)
конструирования (A,B,C,H) представления ЛДДС по ее передаточной функции ф( d)
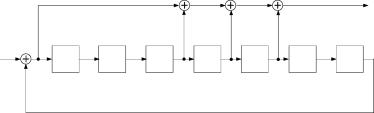
Для приведенных на рисунке 1.1 и рисунке 1.2 структурных реализаций заданной в форме отношения двух модулярных много
членов (1.55), размеченных переменными состояния (к) и xt (к +1)
слева направо (рисунок 1.9) и справа налево (рисунок 1.10) конструирование матриц A, B,С и H дает для последних представления
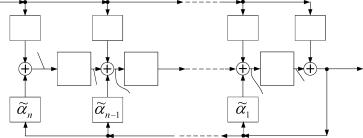 |
| Рисунок 1.9. Представление ЛДДС в каноническом управляемом базисе |
| i | l |
| _1 | l_ |
|
/V OC . n-1 |
| i | L |
| _1 | ' |
| «2 |
ос.
—«—-0^-—I
^^ле/ие ід[с J
шаемом базисе /Рисунок 1.10. Пред в каноническом наблюдаемо
|
O T —O(_n-u__ 1 n-1 )x( n-1) |
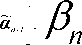 | (1.58) |
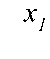
(k+1)


Pn +Po On Pn-1 + Po an-1 Л ~
Pi + Po ai
C =[n-i) \i] _[Po ],
(1.59)
2) в каноническом наблюдаемом базисе (рисунок 1.10)
| ¦ o | ! 1 | o | o" | O(n-1) ] 1 (n-1 )x(n-1) | ||
| o | o | 1 | o | |||
| o | o | o | Л | o | _ | |
| o | o | o | 1 | |||
| a1 | \d2 | a3 | Л | an _ | _ aanx1 _ |
(nrll
1
H = [Po ]
,C _ [n + Po an I Pn-1 + Po an-1 I K I Pi + Po ai ]
(1.61)
Пример 1.3 (Пр1.3)
Сконструировать (A,B,C,H)-представление ЛДДС по ее передаточной функции ф(й), обеспечивающую размещение в регистре хранения информационных разрядов кода Хэмминга (7,4).
1. Выполним алгоритм 1.1, в результате чего получим передаточную функцию ЛДДС
1 + d3 + d4 + d5
1 + d7
и структурные представления, приведенные на рисунке 1.3 и рисунке 1.4.
2. Разметим соответствующим образом структурные реализации (см. рисунок 1.11, рисунок 1.12).
CN
К
ГГі
X
'О
X
*1(A + Or*
-©
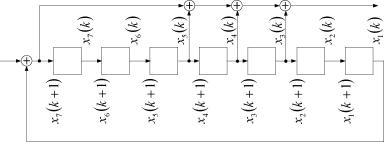 |
| Рисунок 1.12 |
(1.24)
1) в каноническом управляемом базисе (рисунок 1.1
} = [от6\і\н = [і]
О '
O6
бхб
|
с = \о2 \і3 \о2\н = [1 ] |
В параграфах 1.1 и 1.2 рассмотрены возможности модельных представлений линейных двоичных динамических систем в классе отношений «вход-выход» в форме передаточных функций (матриц) и рекуррентного уравнения ВВ n-го порядка, а также в классе отношений «вход-состояние-выход» в форме векторно-матричных представлений правил перехода и выхода рекуррентной и суммарной версий. Однако в одном из вариантов модельных представлений ЛДДС пока не затронута проблема их минимального модельного представления. Тем не менее, проблема построения минимальной схемотехнической реализации линейных ДДС ставит задачу редуцирования их первичных модельных представлений. Очевидно, эта задача может быть решена двумя способами. Первый способ опирается на формализм модулярных многочленов, использующий фактор делимости модулярных многочленов числителя и знаменателя передаточной функции [15, 38, 55]. Второй способ использует свойства пространств управляемости и наблюдаемости, конструируемых на матричных компонентах модельного ВСВ-представления линейных двоичных динамических систем [38].
1.4.1 Редуцирование линейных двоичных динамических систем на основе делимости модулярных многочлена числителя и знаменателя передаточной функции
Рассмотрение данного способа редуцирования начнем с исследования некоторых основных свойств квадратных (n х n)-матриц, часть из которых носит общесистемный характер, то есть выполняется для матрицы над любым полем, а часть имеет силу над простым полем Галуа GF (p) при p = 2. Заявленные свойства зададим с помощью утверждений.
Г0 10 0"
А= 0010 А=0001-1 0 0 1 _
Зададим матрицу выхода ЛДДС в форме C = [ 1 0 0 0], матрицу входа
B не задается так, как задача решается в классе автономных представлений.
Дальнейшее конструирование НДДС осуществим в три этапа. На первом этапе воспользуемся моделью
x(k +1)= А x(k );y(k )= C x(k) и сформируем таблицу 3.4 переходов и выхода устройства.
| |||||||||||||||||||||||||||
| xT (к + l) = ( A x(k ))T |
| Таблица 3.4 (продолжение) | |||||||||||||||||||||||||||
| |||||||||||||||||||||||||||
| xT (к + l) = ( A x(k ))T |
На третьем этапе с использованием полученных результатов формируем таблицу 3.5 переходов и выхода НДДС для условия и(к ) = 0 и
исходного состояния x(0) = [1000J, в которое НДДС можно перевести из нулевого начального состояния x( 0 )= [ 0000]T с помощью сигнала начальной установки и = x1x2x3x4, подаваемый на вход первого триггера.
| |||||||||||||||||||||||||||
| xT (k + 1) = ( Л[ x[k), u(k)] )T |
| Таблица 3.5(продолжение) | |||||||||||||||||||||||
| |||||||||||||||||||||||
| xT(к + І)=(/i[x(k), u(k)])T |
триггеров и формирования выхода у устройства при движении по заданному в постановочной части примера циклу примут вид:
U = ХгХ2Х3Х4 V XiX2X3X4 V Х1Х2Х3Х4 V Х1Х2Х3Х4 V
V ХіХ2Х3Х4\/ ХуХуХзХ^/ ХуХуХзХ^/ Х1Х2Х3Х4
U2
= ХгХ2Х3Х4 V Х1Х2Х3Х4 V Х1Х2Х3Х4 V Х1Х2Х3Х4 V
V ХгХ2Х3Х4 V Х1Х2Х3Х4 V Х1Х2Х3Х4 V Х1Х2Х3Х4
JU3 = Х1Х2Х3Х4 V Х1Х2Х3Х4 V Х1Х2Х3Х4 V Х1Х2Х3Х4 V V Х1Х2Х3Х4 V Х1Х2Х3Х4 V Х1Х2Х3Х4 V Х1Х2Х3Х4 ; U4 = Х1Х2Х3Х4 V Х1Х2Х3Х4 V Х1Х2Х3Х4 V Х1Х2Х3Х4 V
V Х1Х2Х3Х4 V Х1Х2Х3Х4 V Х1Х2Х3Х4 V Х1Х2Х3Х4
у = Х1
С учетом сигнала и начальной установки НДДС функция возбуждения первого триггера принимает вид
Xi X2 X3 X4 Xi X2 X3 X4
Mi = XjX2X3X4 V ( XjX2X3X4 V XjX2X3X4
|
V XjX2X3X4 V XjX2X3X4 ). X,X2X3X4 X,X2X3X4 |
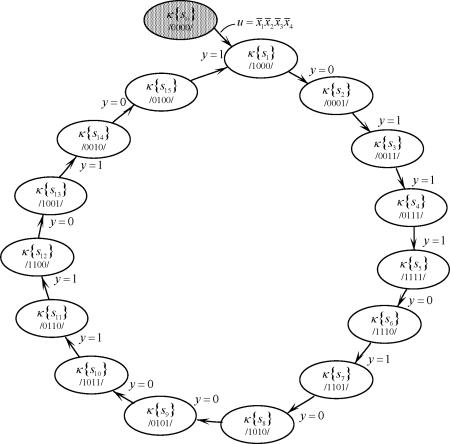 |
| Рисунок 3.4. Диаграмма переходов и выхода ГДДС |
Mi = Mi У = Xi •
M2 = M2 = X3; M3 = M3
M4 =M4
Xi + x4 ;
Если теперь составить БФ ju'i, i = 1,4 возбуждения информационных входов vi, i = 1,4 D-триггеров для модели х(к + l)= A х(к) с полученной матрицей A вида
Г0 10 0"
A = 0 0 10 A=0001’
1 0 0 1_
то получим тождества
f1 = ц! = fij; ц2 = ц*2= ц'2; ц3 = ц*3 = ц'3; ц4 = ц*4= ц4. Так как матрица выхода имеет вид C = [1 0 0 0], то для БФ у *, формирующей в силу матрицы C выход устройства, можно записать, что у = у * = х1.
Построим теперь реализацию конструируемой ГДДС в структурной форме рисунок 3.5.
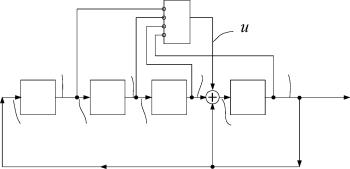 |
| Рисунок 3.5. Структурное представление ГДДС |
3.2. фактор востребованности переменных булевых описаний двоичных динамических систем
В разделе 2 показано, что аппарат селлерсовского дифференцирования булевых функций (СДБФ) является достаточно удачным инструментом для исследования булевого описания ДДС, позволяющим уже на стадии аналитического конструирования ДДС контролировать ее булево описание на предмет наличия в нем избыточных компонентов. Целью настоящего параграфа является распространение возможностей аппарата СДБФ на решение задачи оценки степени востребованности переменных булевых описаний комбинационной схемы ДДС.
Решение указанной задачи будем осуществлять памятуя о том, что среда ДДС состоит (см. §1.2) из двух компонентов: комбинационной схемы и блока памяти, каждый из которых характеризуется своей коммутационной способностью, что и обнаруживает аппарат СДБФ. Следует заметить, что реализация блока памяти ДДС предполагает использование того или иного типа триггера, правило X перехода которых для выбранного типа является фиксированным и не зависит от задачи кодопреобразования, решаемой ДДС. В этой связи задача состоит в исследовании компонента ДДС - комбинационной схемы и формировании оценок ее коммутационной способности, понятие которой введем с помощью следующего определения.
Определение 3.5 (О3.5). Под коммутационной способностью комбинационной схемы ДДС будем понимать способность булевых функций ju(x,и) вида (2.12) возбуждения информационных входов триггеров, составляющих блок памяти ДДС, изменять (коммутировать) свое значение на кодовых переходах. ?
С учетом введенного понятия решение поставленной задачи будем осуществлять в предположении справедливости следующей гипотезы.
Гипотеза 3.1 (Г3.1). Коммутационная способность комбинационной схемы ДДС, представленной булевыми функциями цi(х,и), i = 1,n
возбуждения, количественно оценивается показателем
|
(2.86) n n = ZZ P i=1 k=1 | 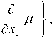 |
m=ZZZ
d?L
d xk
(3.9)
i=1 k=1 j=1
выраженным в числе кодовых переходов, на которых ДДС осуществляет требуемое кодопреобразование, где n - число переменных xk со-
dMi
col\xk, k = 1,n } ДДС,
значение первой частной
стояния x
Jj
селлерсовской производной БФ jul(x,u), i = 1,n возбуждения информационного входа i -го триггера по переменной xk на j -м кодовом наборе, составляющим алфавит состояния X представления НДДС в форме КА в виде кортежа (2.5). ?
Величина (3.9), как нетрудно заметить, характеризует совокупную величину коммутационной способности КСХ произвольной ДДС. В силу О3.5 и положений Г3.1 можно сказать, что коммутационная способность КСХ, представленной БФ — (x,u), i = 1,n возбуждения, обнаруживает, что аргументы указанных БФ оказываются «разновостребованными» на кодовых переходах, на которых эти БФ изменяют свое значение. В связи с тем, что БФ —(x,u), i = 1,n имеют своими аргументами переменные xt, і = 1,n состояния и переменные ux, Х= 1,r входа, то решение задачи будем проводить в два этапа: при рассмотрении ДДС как автономной системы, в которой ux = 0, Х= 1,r, и при рассмотрении общего случая, при котором ихФ 0, Х= 1,r.
Рассмотрим первый этап решения задачи (случай автономной ДДС, для которой uj = 0, j = 1,r), для чего введем следующие понятия.
Определение 3.6 (О3.6). Под абсолютной оценкой востребованности I булевой переменной xi произвольной автономной ДДС, то есть такой ДДС, функционирование которой определяется только переменными xk, k = 1,n ее состояния, будем понимать величину
д—
d xk
(2.86) n
шт n 2n
r=zz
k=1J=1
f P\)x— I.: n < I<„2", (3.10)
k=1
-‘J
определяющую число кодовых переходов, на которых соответствующая частная производная —— меняет свое значение. ?
a xk
Определение 3.7 (О3.7). Под относительной оценкой приведенной востребованности [ (ОПВ) булевой переменной xt произвольной автономной ДДС будем понимать величину
(2.86) 1 n |д
1 -f P\^ —
д —
д xk
1 n 2n
— ff
п2пЬм
[П=
2~n < I< 1. ? (3.11)
n2n
д xk
k=1 ^ -Л-k
Рассмотрим теперь случай, когда функционирование ДДС определяется кроме переменных состояния xk, k = 1,n также и набором вход
ных переменных ux, Х= 1,r. В этом случае выражения (3.9) - (3.11) необходимо уточнить. С этой целью опираясь на О3.6, О3.7 сформулируем понятие обобщенной относительной оценки приведенной востребованности некоторой выбранной булевой переменной произвольной ДДС.
Определение 3.8 (О3.8). Обобщенной относительной оценкой приведенной востребованности [Г] булевой переменной xi произвольной
ДДС будем называть величину, имеющую два эквивалентных представления:
d?L
д xk
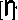 |
1 ш2ш |
| + | ||||||
|
r 2п +ZZ k=1 j=1 |
| ш = n + r, |
1
п2ш
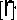
|
z p k=1 | 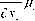 |
|
+ Z P k=1 | 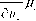 |
где uk, k = 1,r - булевы переменные входа ДДС. ?
Нетрудно видеть, что введенные О3.7 и О3.8 дают количественную оценку востребованности соответствующих булевых переменных в процедуру динамического кодопреобразования, при этом оценка вычисляется с приведением ее к мощности полного множества кодовых переходов ДДС так, что для выражения (3.10) она определяется нормирующим коэффициентом
(3.13)
к =_
/? авт у\п 5
n2
а для выражений (3.12а), (3.12б) - нормирующим коэффициентом
(3.14)
1
пр
п2ш
Разница в коэффициентах обуславливается тем, что значения переменных uk, k = 1,r входа ДДС на кодовых переходах не формируются непосредственно средой ДДС так, как формируются значения переменных состояния посредством БФ ці(x,u), i = 1,п возбуждения (2.12), а лишь принимают участие в процедуре кодопреобразования.
Приведенные соображения уже являются достаточными для решения поставленной задачи, однако процедура решения становится много удобнее, если воспользоваться следующими понятиями.
Определение 3.9 (О3.9). Матрицей Sf чувствительности Селлерса векторной булевой функции f (j = ^)= col{f(xt), j = 1,ш} к вариациям булевых переменных xt называется такая матрица Sf,
dff
д xi
строки sJf которой образованы частными производными s (ff )=
Селлерса булевых функций fj(x1 ,x2,...,xn) по булевым переменным xt так, что матрица Sf принимает вид
(3.15)
Sf = col {), i = 1,n , j = 1,m }•
Определение 3.10 (О3.10). Матрицей SДДС чувствительности Селлерса произвольной ДДС к вариациям ее переменных xt, i = 1,n состояния и переменных uk, к = 1,r входа называется матрица
| S ДДС = co1 |
| у ¦> |
строки sj которой образованы первыми частными производными
дЦ, djUj
д x.
и -- Селлерса БФ цг(x,u), i = 1,n возбуждения (2.12) по соот-
¦Р д ик
ветствующим булевым переменным. ?
Определение 3.11 (О3.11). Под матрицей весов PS матрицы SДДС
(3.16) чувствительности Селлерса будем понимать матрицу
дЦ
д ик
дЦ
д xp
i,p=1 n , k = 1,r
, j = 1,n
PS = col
row*
ji+r
(3.17)
с весовыми элементами pSji, вычисленными на множестве полной мощности равной 2m кодовых переходов так, что 0 < pS < 2m. ?
С учетом О3.11 и Г3.1 обобщенная относительная оценка коммутационной способности [ПТ комбинационной схемы ДДС с учетом (3.9) характеризуется нормой, которая имеет вид:
n m 2 г -I
= n--K\k, sj e SДДС, (3Л8а)
[пт
n m 2
S ДДС
i=1 -=1к=1
или с учетом (3.20) в эквивалентной форме
[пт
(3.18б)
n" К TZ Ps,i , Ps-1 e PS ,
S ДДС
i=1 j=1
где к * - нормирующий коэффициент, определяемый спецификой решаемой задачи конструирования ДДС
Введенные определения позволяют сформулировать понятие степени востребованности произвольной переменной булевого описания ДДС, использование которой (как будет показано в параграфе 3.3) оказывается весьма эффективным при выборе рационального ресурса по-мехозащиты процесса динамического кодопреобразования в среде
ДДС.
Определение 3.12 (О3.12). Степенью востребованности некоторой булевой переменной xi кода состояния ДДС будем называть величину
Psj е Ps ¦ ? (3Л9)
sij е S ДДС >
R 1 1 ] ] 1 psj ’ ДДС’ t'Sji
j=1k=1 j=1
Определение 3.13 (О3.13). Обобщенной (совокупной) степенью R востребованности переменных xi,i = 1,n булевого описания ДДС будем называть норму вектор-столбца
| ij ik |
| , (3.20) | |||||||||||||||
| вычисляемую на множестве полной мощности кодовых переходов ДДС, имеющую вид |
j=1 k=1
(3.21)
II К 11 = п ^!rС Г е R
i=1
Смысл величины степени востребованности, вычисляемой в силу (3.21), состоит в том, что эта величина уточняет величину обобщенной ОПВ для каждой переменной в силу специфики конкретной структуры ДДС, выраженной числом ее переменных состояния xt,i = 1,п , а также числом экзогенных переменных uk,k = 1,r. Процедура вычисления степени востребованности переменных булевого описания ДДС может быть осуществлена выполнением следующего алгоритма.
Алгоритм 3.3 (А.3.3)
вычисления обобщенной степени востребованности переменных булевого описания ДДС (ГДДС)
3. Вычислить с использованием (3.21) величину обобщенной степени востребованности переменных xi,i = 1,n булевого описания
ДДС в форме нормы || R 11. ¦
Пример 3.3 (Пр.3.3)
Требуется оценить степень востребованности в процессе функционирования ДДС булевых переменных ее описания, полученного при конструировании устройства, формирующего из унитарной экзогенной последовательности u(k) = 1(k) выходную периодическую последовательность y(k) = y(k +12) = 101001011100 ... при обеспечении простоты ее технической реализации.
Конструирование устройства в силу положений алгоритма 2.1 с учетом требования минимальной сложности его технической реализации приводит к выбору соседних кодов для осуществления кодирования в форме X = } алфавита S состояния ДДС и дает граф перехо
дов (рисунок 3.6). При этом совмещенное представление правил перехода и выхода принимает вид таблицы 3.6, в соответствии с которой и назначением D-триггеров для технической реализации ячеек памяти конструируются булевы функции, аналитически реализующие правило перехода Л(х, и) и выхода S( x) устройства.
| Таблица 3.6 | ||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||
| xT (k +1)= ([(k), и(k)])T |
| ||||||||||||||||||||||||||||
| xT(к + і)=(л[х(к), и(к)])T |
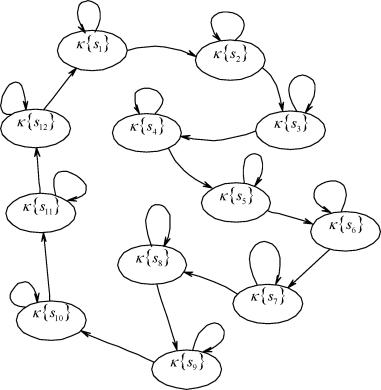 |
| Рисунок 3.6. Граф переходов ДДС |
И = u {xlx2x3x4 V x(2x3x4 V XjX2X3X4 V XjX2X3X4 V XjX2X3X4 V XjX2X3X4 )v
V u ( X3X2X3X4 V X1X2X3X4 V X1X2X3X4 V XjX2X3X4 V XjX2X3X4 V XjX2X3X4 ) ;
U2 = u (x1x2x3x4 V X1X2X3X4 V X1X2X3X4 V X1X2X3X4 V X1X2X3X4 V X1X2X3X4 ) V
V U ( XjX2X3X4 V X1X2X3X4 V X1X2X3X4 V X1X2X3X4 V X1X2X3X4 V x1x2x3x4);
U3 = u ( X1X2X3X4 V X1X2X3X4 V XjX2X3X4 V X1X2X3X4 V X1X2X3X4 V X1X2X3X4 V X1X2X3X4 V x1x2x3x4 )v
V u ( XjX2X3X4 V X1X2X3X4 V XjX2X3X4 V X1X2X3X4 V XjX2X3X4 V X1X2X3X4 V X1X2X3X4 V XjX2X3X4 ) ;
U4 = u ( X1X2X3X4 V X1X2X3X4 V X1X2X3X4 V X1X2X3X4 V X1X2X3X4 V X1X2X3X4 V X1X2X3X4 V x1x2x3x4 )v v u (X1X2X3X4 V X1X2X3X4 V X1X2X3X4 V X1X2X3X4 V X1X2X3X4 V X1X2X3X4 V X1X2X3X4 V x1x2x3x4) ;
= XjX2X3X4 V XjX2X3X4 V XjX2X3X4 V XjX2X3X4 V XjX2X3X4 V XjX2X3X4 .
Вычислим далее с использованием алгоритма 3.3 оценку степени востребованности булевых переменных полученного аналитического описания ДДС, в соответствии с которым:
1. конструирование матрицы S (3.16) чувствительности булевого описания ДДС к вариациям переменных xi, i = 1,4 ее состояния
и ее экзогенной булевой переменной u дает матрицу S в форме (поэлементно):
|
*-~1 =3. i_ |
1- *-~i =3. fO fo fo *-~1 fo | ||
| d u | d Xj \ d x2 \ d x3 \ d x4 | ||
| s.. s2 s„ s.4 s5 | du2 | d u2 \ d u2 \ d U2 \ d u2 | |
| S 21 s 22 s 23 s 24 s 25 | d u | d x4 1 d x2 1 d x3 1 d x4 | |
|
sssss 31 32 33 34 35 | dUs | d 1 d 1 d Из 1 d | |
| s 41 s 42 s43 s 44 s 45 J | d u | d Xj j d x2 j d x3 j d x4 | |
| d U4 | dju4 ! du ! du4 ! du4 | ||
| d u | d x} \ d x2 [ d x3 ] d x4 |
S11 = (U (XjX2X3X4 V xlx2x3x4 V xlx2x3x4 V XjX2X3X4 v x1x2x3x4 v x1x2x3x4 )v
V U( XjX2X3X4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4) )©
© (U(x1x2x3x4 v x1X2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4)v
V u (x1x2x3x4 v x1X2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4) ),
s2 = (u(x1x2x3x4 v x1X2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4)v
V U( X1X2X3X4 V X1X2X3X4 V XjX2X3X4 V X1X2X3X4 V X1X2X3X4 V x1x2x3x4) )©
© (u(x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4)v
v U(x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4))
s13 = (u(x1x2x3x4 v x1X2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v xIx2x3x4)v
V U (x1x2x3x4 V XjX2X3X4 V XjX2X3X4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4) )©
© (u{x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4)v
v U(x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4)),
s4 = (u(x1x2x3x4 v x1X2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4)v
V U (x1x2x3x4 V XjX2X3X4 V XjX2X3X4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4) )©
© (U (x1x2x3x4 V XjX2X3X4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 )v
V U( x1x2x3x4 x x1x2x3x4 v x3x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4) ),
s15 = (u (x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4~)v
V U (x1x2x3x4 X XjX2X3X4 V XjX2X3X4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4) )©
© (u(x1x2x3x4 V X1X2X3X4 V X1X2X3X4 V X1X2X3X4 V X1X2X3X4 V x1x2x3x4)v
v U(x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4))
s21 = (U ( X1X2X3X4 X X1X2X3X4 V X1X2X3X4 V X1X2X3X4 V XjX2X3X4 v x1x2x3x4 ~)v
V U( x1x2x3x4 x X1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4) )©
© (U{x1x2x3x4 x X1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4~)v
V u ( x1x2x3x4 x X1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4) ),
s22 = (u(x1x2x3x4 v X1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4~)v
V U (x1x2x3x4 X XjX2X3X4 V X1X2X3X4 V XjX2X3X4 V X1X2X3X4 V XjX2X3X4) )©
© (u ( x1x2x3x4 x x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4~)v
V U( x1x2x3x4 x x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4))
s23 = (u ( x1x2x3x4 v X1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4~)v V U (x1x2x3x4 X X1X2X3X4 V XjX2X3X4 V X1X2X3X4 V XjX2X3X4 V XjX2X3X4) )©
© (u(x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4~)v v U(x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4))
s24 = (u (XjX2X3X4 v (1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 )v v u (XjX2x3x4 v X1x2x3X4 v x1X2x3x4 v x1X2x3X4 v x1x2x3X4 v x1x2x3x4))©
© (u (X1x2x3x4 v X1x2X3x4 v x1X2x3x4 v x1X2X3x4 v x1X2X3X4 v x1x2X3X4)v
v u (x1x2x3x4 v X1x2X3X4 v x1X2X3x4 v x1X2X3X4 v x1x2x3x4 v x3x2X3x4)),
s21 = (u (X1x2X3x4 v (1x2x3x4 v x1X2X3x4 v x1X2x3x4 v x1X2x3X4 v x1x2x3X4)v
v u (X1x2x3x4 v (Ix2x3x4 v x1X2x3x4 v x1X2x3X4 v x1x2x3X4 v x1x2x3x4))©
© (u(X1x2X3x4 v X1x2x3X4 v x1X2X3X4 v x1X2x3X4 v x1X2x3x4 v x1x2x3x4)v
v u (X1x2x3X4 v (1x2x3x4 v x1X2x3X4 v x1X2x3x4 v x1x2x3x4 v x1x2x3X4))
s31 = (u(X1x2x3x4 v X1x2x3X4 v XjX2X3X4 v x1X2x3X4 v x1x2x3X4 v x1x2x3x4 v x1x2X3x4 v X1x2X3x4)v
v u (X1x2x3x4 v XjX2x3X4 v X1x2X3X4 v xIX2x3X4 v x1x2x3X4 v x1x2x3x4 v x1x2X3x4 v X1x2X3x4))©
234
v u ( x1x2x3x4 v x1x2x3x4 v xIx2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4)),
© (u (x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4)v
s32 = (u(x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4)v v u (x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4))© © ( u ( X1X2X3X4 v XjX2X3X4 v XjX2X3X4 v X1X2X3X4 v XjX2X3X4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 )v v u ( x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4)),
s33 = (u ( x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 ~)v v u (x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4))© © (u ( XjX2X3X4 v XjX2X3X4 v X1X2X3X4 v XjX2X3X4 v X1X2X3X4 v XjX2X3X4 v x1x2x3x4 v x1x2x3x4 ~)v v u ( x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4)),
SM = (u ( x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 ~)v v u (x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4))©
© (u (x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4)
v u ( x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4)),
s5 = (u ( x1x2x3x4 v xIx2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4~)v
v u (x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4))©
© (u(x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4)v v u ( X1X2X3X4 v XjX2X3X4 v X1X2X3X4 v XjX2X3X4 v X1X2X3X4 v XjX2X3X4 v x1x2x3x4 v x1x2x3x4)),
s4i = (u (xIx2x3x4 v x1x2x3x4 v xIx2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4~)v
v u (x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4))©
234
v u ( x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4)),
© (u ( xIx2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 ~)v
s42 = ( u ( xlx2x3x4 V xlx2x3x4 V xlx2x3x4 V xlx2x3x4 V xlx2x3x4 V xlx2x3x4 V XjX2X3X4 v xIx2x3x4 )v
v u (xIx2x3x4 V x1x2x3x4 V x1x2x3x4 V x3x2x3x4 V xIx2x3x4 V xIx2x3x4 V xIx2x3x4 V xIx2x3x4))©
© (u (xIx2x3x4 V xIx2x3x4 V xIx2x3x4 V xIx2x3x4 V xIx2x3x4 V xIx2x3x4 V xIx2x3x4 V xIx2x3x4)
V u ( xIx2x3x4 V xIx2x3x4 V xIx2x3x4 V xIx2x3x4 V xIx2x3x4 V xIx2x3x4 V xIx2x3x4 V xIx2x3x4)),
s43 = (u(xIx2x3x4 V xIx2x3x4 V xIx2x3x4 V xIx2x3x4 V xIx2x3x4 V xIx2x3x4 V xIx2x3x4 V xIx2x3x4)v v u (xIx2x3x4 V xIx2x3x4 V xIx2x3x4 V xIx2x3x4 V xIx2x3x4 V xIx2x3x4 V xIx2x3x4 V xIx2x3x4))© © (u(xIx2x3x4 v xIx2x3x4 v xIx2x3x4 v xIx2x3x4 v xIx2x3x4 v xIx2x3x4 v xIx2x3x4 v xIx2x3x4)v v u (xIx2x3x4 v xIx2x3x4 v xIx2x3x4 v xIx2x3x4 v xIx2x3x4 v xIx2x3x4 v xIx2x3x4 v xIx2x3x4)),
Stt = (u ( xIx2x3x4 v xIx2x3x4 v xIx2x3x4 v xIx2x3x4 v xIx2x3x4 v xIx2x3x4 v xIx2x3x4 v xIx2x3x4 )v
v u (xIx2x3x4 v xIx2x3x4 v xIx2x3x4 v x3x2x3x4 v xIx2x3x4 v x3x2x3x4 v xIx2x3x4 v xIx2x3x4))©
234
v u ( xIx2x3x4 v xIx2x3x4 v xIx2x3x4 v xIx2x3x4 v xIx2x3x4 v xIx2x3x4 v xIx2x3x4 v xIx2x3x4)),
© (u (xIx2x3x4 v xIx2x3x4 v xIx2x3x4 v xIx2x3x4 v xIx2x3x4 v xIx2x3x4 v xIx2x3x4 v xIx2x3x4)v
s5 = (u(xIx2x3x4 v xIx2x3x4 v xIx2x3x4 v xIx2x3x4 v xIx2x3x4 v xIx2x3x4 v xIx2x3x4 v xIx2x3x4)v v u (xIx2x3x4 v xIx2x3x4 v xIx2x3x4 v xIx2x3x4 v xIx2x3x4 v xIx2x3x4 v xIx2x3x4 v xIx2x3x4))© © (u(xIx2x3x4 v x3x2x3x4 v xIx2x3x4 v xIx2x3x4 v xIx2x3x4 v xIx2x3x4 v xIx2x3x4 v xIx2x3x4)v v u ( xIx2x3x4 v xIx2x3x4 v xIx2x3x4 v xIx2x3x4 v xIx2x3x4 v xIx2x3x4 v xIx2x3x4 v xIx2x3x4)).
2. выполнение п.2 алгоритма с использованием вычислительных средств дает матрицу весов PS матрицы S (3.16) чувствительности Селлерса
| S |
|
= [56 [ 60 ! 56 ! 56]T ;
R = соі Л ; Psiе ps }1;i =1,n
j=I
при выборе нормирующего коэффициента К * = (m2m)1 дает Rl| = /K *? Тг =(nm2m )-1? Г = 0,00I6-(56 + 60 + 56 + 56 )= 0,36
i=I
i=I
3.3. Использование фактора востребованности булевых переменных кодов состояний НДДС для рационального использования ресурса помехозащиты
Ставится и решается задача обеспечения гарантированной информационной надежности [11] функционирования УДА, порождаемая общей проблемой [56, 57] обеспечения надежности функционирования УДА, средствами использования при кодировании состояний их автоматного представления помехозащищенных кодов. Концептуальной особенностью параграфа является его направленность на рациональное использование ресурса помехозащиты, выражающейся в использовании фактора востребованности булевых переменных кодов состояния ДДС УДА в соответствии с правилом: более востребованной булевой переменной хр состояния ДДС УДА - больший ресурс X помехозащиты.
#( к)
у(к )
' f( к ) = У( к )+#( к)
#( к)
| V |
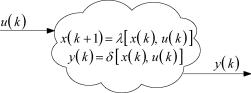 |
| Рисунок 3.7. Структурное представление среды КС и ДДС |
Рассмотрим далее процедуру построения ДДС гарантированной информационной надежности с использованием процедуры помехоустойчивого кодирования, применяемой для обеспечения помехозащищенности кодовых посылок, передаваемых по двоичным КС. Эта процедура опирается на гипотезу равновостребованности булевых переменных кодов состояния устройств в процессе их функционирования, а также на информацию о значении вероятности p элементарного
сбоя в функционировании ДДС, представляющего собой искажение произвольного двоичного элемента кода вектора x ее состояния, определяемой путем симметрирования с помощью выражения
Р = max( PonPio ), (3.22)
где p01,p10 - соответственно вероятность трансформации (искажения)
значения произвольного элемента кода вектора x ее состояния из нуля в единицу и наоборот. Задача обеспечения информационной надежности при этом состоит в обеспечении в среде ДДС выполнения неравенства
Pc6 Z Рдоп, (3.23)
где Рсб - вероятность сбоя в формировании кода вектора состояния
ДДС на кодовых переходах, которая не должна превосходить заданной допустимой [22 - 24] вероятности Рдоп сбоя, средствами сформированного ресурса помехозащиты. Концептуально ресурс помехозащиты в среде ДДС зададим в следующей форме.
Концепция 3.1 (К3.1). Ресурс X помехозащиты ДДС выражается числом вводимых в ее среду - в вектор ее состояния, избыточных разрядов (переменных), что наделяет его коды корректирующей способностью. ?
Выбор X ресурса помехозащиты и соответствующего ему (n, n) помехозащищенного кода осуществляется выбором избыточности Хизб = n - n помехонезащищенных кодов в силу соотношения
п+Хизб
= arg\ Рсб = ? С^р-(1 -рГк-‘-‘ <Р„ \ (3.24)
i=s+1
при реализации корректирующей способности в форме исправления сбоев кратности s, и решением
П+Кзб
i=r+1
^Кзб = arg\ Рсб = ? Cn+ХизбР(1 -р)<Рдоп \ (3.25)
при реализации корректирующей способности в форме обнаружения сбоев кратности r. С учетом того, что процесс декодирования помехозащищенных кодов состояния ДДС обладает минимальной аппаратурной сложностью, когда коды помехозащищенного УДА обладают полной блоковой систематикой [11], то образующую матрицу G помехозащищенного кода выберем [42, 51] в форме
G = [I \G] (3-26)
где I - n х n -единичная матрица, G - n х( n - n)-матрица проверочных частей кодов, с учетом чего вектор X состояния ДДС будет иметь вид
(3.27)
x I xG
Таким образом, в форме выполнения условия (3.23) помехозащищенную ДДС на этапе своего конструирования будем называть помехозащищенным КА (ПЗКА), задаваемым в силу автоматного представления (2.7)-(2.12), а также представлений (3.26), (3.27) в форме макровектора
ПЗКА: [и, X, Y, X, S,G } (3.28)
с элементами
G: x(k )= [ x(k)\ x(k)G ], (3.29)
X: x( k + l)=X [ x( k), u (k)], (3.30)
S: y(k) = ?[x(k),u(k)], (3.31)
//: v(k )=// [x (k ),X [x(k), u (k )]]=// [x(k), u (k)] (3.32)
при этом с учетом представлений (3.24), (3.25), используемых для выбора ресурса помехозащиты, саму помехозащищенную ДДС будем называть двоичной динамической системой гарантированной информационной надежности с номинальным ресурсом помехозащиты.
Для рационального использования ресурса помехозащиты, что проявляется в минимальной избыточности кодовых реализаций вектора состояния ДДС, введем определение, опирающееся на О3.12 степени Rxi востребованности булевой переменной xi кода состояния ДДС, вычисляемой в силу (3.19).
Определение 3.14 (О3.14). Оценкой степени востребованности (ОСВ) булевой переменной xt ДДС в силу (3.24) будем называть величину
m |—ч (Ъ.22) ¦—ь
Prq = к *Ё Psp = к * R« = к * Г ; Psp е PS , ri е R , (3.33)
І=1
где к * - нормирующий коэффициент, определяемый спецификой решаемой задачи конструирования ДДС. ?
Вычисленную с помощью (3.33) величину ОСВ для булевых переменных xi, i = 1,n, образующих вектор состояния ДДС, необходимо учесть в (3.22) при выборе ресурса помехозащиты с использованием
(3.24), (3.25). Из выражения (3.33), нетрудно видеть, что значение оценки prqi удовлетворяет неравенству
О < Pq < 1, (3.34)
в силу чего эта оценка справедливо может быть использована для уточнения величины (3.22) вероятности p элементарного сбоя в форме
pi = P Prqi . (3.35)
Введем в рассмотрение следующие определения.
Определение 3.15 (О3.15). Под глобально-мажорантным ресурсом помехозащиты Хгл max будем понимать число \зб = n -n избыточных
разрядов кода (p, n), параметры n, n которого связаны соотношением (3.24) или (3.25) так, что Дл max = \зб. ?
Определение 3.16 (О3.16). Под локально-мажорантным ресурсом помехозащиты XLmax будем понимать число Хизб = nL - n избыточных
разрядов кода (pL, n), параметры nL,n которого связаны соотношением (3.24) или (3.25), где вероятность p является решением уравне
ния ( . -— \. ?
P=argjmax p^, i = 1, n j
Понятие минорантного ресурса помехозащиты введем с помощью следующего определения.
ОпРеделение 3Л7 (О3.17). Пусть pBmn = arg{minprqi,i = 1,n }
представляет собой минимальное значение оценки востребованности булевых переменных кода состояния, тогда Хтт ='kmin (~,n), где n, n удовлетворяют неравенствам (3.24) или (3.25), при подстановке в них вместо р вероятности ртп = pрвтп будем называть минорантным ресурсом помехозащиты. ?
Определение 3.18 (О3.18). Под двоичной динамической системой гарантированной информационной надежности с эффективным использованием ресурса помехозащиты понимается такая ДДС, булевы переменные xt которой разбиты на подмножества Gk, k = 1,? такие, что их мощности удовлетворяют условию
SG ]=n, (3.36)
к=1
при этом локальные ресурсы помехозащиты Xk, выделенные каждому из подмножеств Gk , удовлетворяют оценочным неравенствам
X . <Хк <Х . ? (3.37)
Определение 3.19 (О3.19). Помехозащищенную ДДС, в которой X положено равным Хлmax для всех k = 1,?, будем называть двоичной динамической системой гарантированной информационной надежности с рациональным использованием ресурса помехозащиты. ?
Примечание 3.3 (ПМ3.3). Заметим, что в случае если ОСВ prqi = 1,і = 1,n, то выражения (3.22), (3.24) и (3.25) для выбора ресурса
помехозащиты ДДС имеют тот же смысл и вид, что и для обеспечения помехозащищенности кодовых комбинаций, передаваемых по КС. Различная востребованность переменных булевого описания ДДС приводит к тому, что ресурс помехозащиты, требуемый для обеспечения выполнения неравенства (3.23) для ДДС, оказывается меньшим, чем для обеспечения той же помехозащищенности кодовых комбинаций, передаваемых по КС. ?
Вышеизложенные положения позволяют сформировать алгоритм, которому присвоим номер 3.3.
Алгоритм 3.4 (А3.4) конструирования ГДДС
гарантированной информационной надежности с рациональным использованием ресурса помехозащиты
4. Выполнить алгоритм 3.3.
5. В силу положений определения 3.16, заданной в виде (3.22) вероятности р элементарного сбоя в функционировании ДДС, допустимой вероятности Рдоп сбоя в функционировании ДДС и в
зависимости от требуемого способа реализации корректирующей способности помехозащищенного кода, вычислить в силу соотношений (3.24) (3.25) величину локально-мажорантного ресурса помехозащиты XLmax и образующую матрицу (3.26) помехозащищенного кода.
6. Построить формализованное описание конструируемой ГДДС в форме (3.28) - (3.31).
7. Получить с использованием полученного в результате выполнения п.3 алгоритма правила Л(X,и) перехода и правила 8(X,и) выхода ГДДС аналитическое представление булевых функций, описывающих выход ГДДС в форме у = 8 (X, и) и правило (3.32) возбуждения информационных входов триггеров в векторной форме ? = р(Х,и), i = 1,n.
8. Построить с использованием полученных в результате выполнения п.4 алгоритма схемотехническую реализацию ГДДС. ¦
Пример 3.4 (Пр3.4)
Требуется на базе ДДС, сконструированной в примере 3.3, построить ГДДС гарантированной информационной надежности при рациональном использовании ресурса помехозащиты при вероятности Рсб < 1 х 10— и вероятности элементарных сбоев p = 1 х 10~4, а также
при реализации корректирующей способности в форме исправления сбоев.
В соответствии с постановкой задачи конструирования ГДДС:
1. выполнение алгоритма 3.3 дает
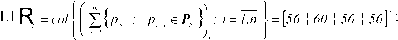
| 1.2оценки степени востребованности для переменных xi} i = 1,4, вычисленные в силу (3.33) |
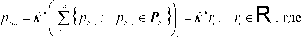 |
|
^ * = (m2m ) =((dim{X }+ dm{U })2{dim{X }+dim{U}) = |
160’
форме вектор-столбца [p
rqi h=1,n'
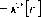 |
T i=1,n |
j=1
i=1,n
= — [56 \60 \ 56 ! 56]T = [0,35 [ 0,38 \ 0,35 ! 0,35 ]T *
160
«[0,4 ! 0,4 ! 0,4 ! 0,4TT.
2. Вычисление в силу (3.24) оценки локально-мажорантного ресурса помехозащиты XLmax для исправления сбоев первой крат
ности дает
р = p arg{maxprqi, i = 1,4 }= 0,4• 1 • 10~4 = 0,4• 10“4.
2n—n - 1 > C
Nсиндромов > Nсбоев :
n+X436
(1 — p 'у+Кзб-i
^ XL max 3
n+X...
arg
1Lmax
Кб = arg\ P6 = ± Сп+Хшбp
I i=s+1
доп
что приводит к выбору образующей матрицы
1 0 1 111 1 1 0 0 1 1
G7,4 =
10 0 0 0 10 0 0 0 10 0 0 0 1
(7,4)
помехозащищенного
кода.
3. Построение формализованного описания конструируемой ГДДС в форме (3.28) - (3.31) приводит с учетом проверочных частей кодов состояния ГДДС и представления для соответствующих разрядов помехозащищенного кода вида к{х} = {x4 \x3 \x2 \x1 \m3\m2\m1 };
x1\111 x2\001 x3\100 x4\010 x5\001 x6\111
x7\010 x8\101 x9\110 x10\000 x11\011 x12\100
для сепаратной информационной части x вектора состояния X ГДДС агрегированное табличное (таблица 3.7) представление правила X [ x(k), u(k)] и правила S [ x( k), и( к)]. Справедливость таких действий основывается на том, что сепаратная проверочная часть xG вектора X состояния ГДДС образуется в силу проверочных равенств, аргументы которых представляют собой исключительно компоненты сепаратной информационной части x вектора x состояния ГДДС.
| Таблица 3.7 | ||||||||||||||||||||||||||||
|
Таблица 3.7 (продолжение)
| Вход и | Выход у( к) выхода устройства | |||||
| 0 | 1 1 | 1 | 0 | 0 | ||
| Вектор хт (к) состояния устройства | ||||||
| 1100 | 1000 | 1001 | 1011 | 1010 | 1110 | |
| 0 | 1100 | 1000 | 1001 | 1011 | 1010 | 1110 |
| 1 | 1000 | 1001 | 1011 | 1010 | 1110 | 1111 |
4. Формирование булевых функций возбуждения информационных входов триггеров, реализующих сепаратную информационную часть х вектора X состояния ГДДС, дает
jl1 = и ( х1х2х3х4 ? х1х2х3х4 ? х1х2х3х4 ? х1х2х3х4 ? х1х2х3х4 ? х1х2х3х4) ? и (х1х2х3х4 ? х1Х2х3х4 ? х1х2х3х4 ? х1х2х3х4 ? х1х2х3х4 ? х1х2Х3х4 fi2 = и(х3х2х3х4 ? х1х2х3х4 ? х1х2х3х4 ? х1х2х3х4 ? х1х2х3х4 ? х1х2х3х4)? ? и (х1х2х3х4 ? х1х2х3Х4 ? х1х2х3х4 ? х1Х2х3х4 ? х1х2х3х4 ? х1х2х3х4) ;
р,3 = и ( х1х2х3х4 ? х1х2х3х4 ? х1х2х3х4 ? х1х2х3х4 ? х1х2х3х4 ? х1х2х3х4 ? х1х2х3х4 ? х1х2х3х4 )? ? и (х1х2х3х4 ? х1х2х3Х4 ? х1х2Х3Х4 ? х1Х2х3х4 ? х1х2х3х4 ? х1х2х3х4 ? х1х2х3х4 ? х1х2Х3х4) .
jd4 = и ( х1х2х3х4 ? х1х2х3х4 ? х1х2х3х4 ? х1х2х3х4 ? х1х2х3х4 ? х1х2х3х4 ? х1х2х3х4 ? х1х2х3х4 )? ? и (х1х2Х3х4 ? х1Х2Х3х4 ? х1Х2х3х4 ? х1х2х3х4 ? х1Х2х3х4 ? х1х2х3х4 ? х1х2х3х4 ? х1х2х3х4),
а булевы функции возбуждения информационных входов триггеров, реализующих сепаратную (избыточную) часть xG вектора x состояния ГДДС, с учетом проверочных равенств
m3 = х4 0 x3 0 x2, m2 = х3 © x2 © x1, m1 = x4 © x3 © x1, получаемых из выбранной образующей матрицы G 7 4, дает
Mm3 = М4 ©Мз ©М2 ,
Mm2 =Мз ©М2 © Мі ,
Мті = м4 © Мз © Мі;
и булева функция выхода у = x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4.
Полученное аналитическое описание ГДДС является достаточным для построения схемотехнической реализации ГДДС.
Следует заметить, что процедура конструирования ГДДС гарантированной информационной надежности с рациональным использованием ресурса помехозащиты в форме А3.4 обнаружила сокращение использованного ресурса помехозащиты. Без учета степени востребованности условию Рсб < 1 х 10— удовлетворяет код (11,4). Этот эффект будет проявляться особенно заметно с ростом числа состояний ГДДС, обнаруживая преимущества в схемотехнической реализации перед широко используемыми методами, такими, как «двойная память» [8]. ¦
а булевы функции возбуждения информационных входов триггеров, реализующих сепаратную (избыточную) часть xG вектора x состояния ГДДС, с учетом проверочных равенств
m3 = х4 0 x3 0 x2, m2 = х3 © x2 © x1, m1 = x4 © x3 © x1, получаемых из выбранной образующей матрицы G 7 4, дает
Mm3 = М4 ©Мз ©М2 ,
Mm2 =Мз ©М2 © Мі ,
Мті = м4 © Мз © Мі;
и булева функция выхода
x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4 v x1x2x3x4.
Полученное аналитическое описание ГДДС является достаточным для построения схемотехнической реализации ГДДС.
Следует заметить, что процедура конструирования ГДДС гарантированной информационной надежности с рациональным использованием ресурса помехозащиты в форме А3.4 обнаружила сокращение использованного ресурса помехозащиты. Без учета степени востребованности условию Рсб < 1 х 10— удовлетворяет код (11,4). Этот эффект будет проявляться особенно заметно с ростом числа состояний ГДДС, обнаруживая преимущества в схемотехнической реализации перед широко используемыми методами, такими, как «двойная память» [8]. ¦
3.4. Построение эквивалентного линейного
векторно-матричного представления НДДС на основе принципа агрегирования переменных булевых описаний
Цель настоящего параграфа - решить задачу расширения модельного ряда гибридных ДДС построением эквивалентного линейного векторно-матричного представления НДДС. Решение этой задачи позволит конструировать ГДДС не как гибридную версию соответствующей НДДС в рамках тех же нелинейных представлений, а уже как гибридную версию этой ДДС в классе линейных моделей. В свою очередь это даст возможность использовать большой потенциал линейных векторно-матричных описаний для исследования ГДДС, который с позиции отношения «вход-состояние-выход» соответствующего модельного представления ДДС позволит, например, исследовать вопросы управляемости-наблюдаемости, структуры неподвижных состояний и замкнутых циклов.
Решение поставленной задачи в концептуальной постановке использует принцип агрегирования переменных булевых описаний НДДС. Рассмотрение предложенного подхода предварим формулировкой следующей гипотезы.
Гипотеза 3.2 (Г3.2). (О возможности построения эквивалентного линейного векторно-матричного представления НДДС). Возможность построения эквивалентного векторно-матричного представления НДДС обусловливается представимостью произвольной булевой функции над простым полем Галуа GF(2) композицией линейных операций,
определяющих базис [17] (0, ®, 1) Жегалкина, при этом следует заметить, что функция «®» умножения двух переменных по модулю два совпадает с логической функцией «& » конъюнкции этих переменных. В общесистемной постановке такой переход возможен в силу свойств модулярной арифметики над простым полем Галуа GF(2). ?
Справедливость положений гипотезы нетрудно обнаружить, если рассмотреть в общем виде представление полиномов Жегалкина, которые строятся на композиции линейных операций умножения (или операции конъюнкции «&») и суммирования по модулю два. Вопрос лишь в способе представления в таких полиномах булевых термов, представляющих собой конъюнкцию набора булевых переменных. ¦
Задача приведения нелинейного (автоматного) представления ДДС (2.7) - (2.12) к линейному векторно-матричному виду состоит в получении описания функционирования исходной нелинейной ДДС в векторно-матричной форме
x(k + l)= Ax (k) + Bu (k); (3.38)
y (k )= CX (k)+ Hu (k), (3.39)
где X (k) - вектор состояния, dim X = n'; u (k) - вектор входной последовательности, dimu = r; y (k) - вектор выходной последовательности, dim y = m; A - матрица состояния, dim A = n'xn'; B - матрица входов, dim B = n'xr; C - матрица выходов, dim C = m x n'; H - матрица вход-выход УДА, при этом действия в описаниях (3.38), (3.39) осуществляются линейными операциями умножения матрицы на вектор и сложения по модулю p = 2.
Для очевидности предлагаемой методологии приведения автоматного представления ДДС (2.7) - (2.12) к линейному векторноматричному виду сформулируем следующее утверждение.
Утверждение 3.2 (У3.2). Пара матриц (A,B) линейного векторноматричного описания (3.38), (3.39) ДДСразмерности n задает булевы функции ц(, i = 1,n возбуждения информационного входа соответствующих D-триггеров в форме (2.12). ?
Доказательство. Для доказательства утверждения выделим переменные состояния xi из выражения (3.38) векторно-матричного описания ДДС и сопоставим их с аналитическим представлением функции возбуждения информационного входа ?( триггера, которое для D-триггера имеет общий вид:
vdi (k )= xi (k + 4 (3.40)
где xt - переменная состояния D-триггера.
Выделим в общем виде переменную xi состояния ДДС в парамет-ризированной дискретным временем форме
(k + l)= Sanixi(k)© b u(k)
(3.41)
i=1
где an i, bt - элементы матриц A и B, соответствующие переменной xi векторно-матричного описания (3.38), (3.39). Здесь и далее по тексту S( • ) - суммирование по модулю два элементов (• ). i
Подставим в выражение для функции (3.40) возбуждения информационного входа vi триггера значение переменной xi(k + l) состояния из соотношения (3.41):
V (k )= xi (k + 1)= І an,,x, (k )© b,u (k) . (3 .42)
i=1
Сопоставление выражения (3.42) с выражением (2.12) показывает справедливость положений, постулируемых утверждением. ¦
Зафиксируем значения входных переменных, соответствующие условию переходов в ДДС. Очевидно, что для решения задачи необходимо свести аналитическое описание БФ возбуждения информационного входа ? триггера, имеющее вид
i<2n n * ч
/i(x1,x2...xn)=\ (УС(xj), (3.43)
где ?(;) - дизъюнкция элементов (•i), &(•,) - конъюнкция эле-
i і
ментов (• j), а переменная xjJ (здесь и далее по тексту) определяется следующим образом:
=ixJ, pj=1
(3.44)xj, p = 0
к линейному виду:
ц(x1,x2...xn) = a0 ? Za,x,,
(3.45)
где a, - логическая константа, принимающая значение 0 или 1.
Свести представление (3.43) булевых функций возбуждения к виду (3.45) позволяют положения теоремы Т2.1 в силу представления (2.95) (см. §2.5):
n d 2 f
=0 ¦ x, ? Z-L
x 0 jidxt dx
i* j
f (x )=f (0 )?і df
i=i d x,
x=0 ' x,xj ?К
d mf
x = 0 ¦ x,ix,2 К x im ? К
dx,,d xi2 К d x,
І1І2 К m = i UX,iUX,2
дп f
d x, d x 2 К d x
12 n
л • x,x 2 К x
x = 0 12 n
откуда видно, что в результате преобразования выражения (3.43) будем иметь линеаризованную булеву функцию, аргументы которой представляют собой сочетания переменных состояния в форме их произведения. Однако последнее обстоятельство не позволяет напрямую получить линейное векторно-матричное описание из системы полученных булевых функций. Решить эту проблему позволяют положения следующего утверждения.
Утверждение 3.3 (У3.3). Произвольная НДДС представима линейной версией с векторно-матричным описанием в форме (3.38), (3.39) агрегированием конъюнкций булевых переменных булевого описания НДДС в форме полиномов Жегалкина в переменные ~ состояния, расширяющие исходный вектор x, dimx = n, состояния НДДС в форме
|
xT = \xT'aT ] (3-46) при этом матрица A размерности dim A = n'x n' состояния имеет вид | ||||||||
| ||||||||
| ж |
ва P {р,,р2,К ,pz}: р, е {0,l},i = 1,%, образующее по классическому
n!
Cm
n =
«композици-
множество
m! (n - m)!
онных» параметров в форме произведения параметров из множества P мощности ^ = [Р ]; вх - коэффициент, значение которого принадлежит множеству {0,1}, а агрегирование переменных x осуществляется с использованием следующей рекуррентной процедуры (3.48) -(3.53):
(k + 1) = fi ((k + 1))= ao © а1}х} (k) © К © an_}Xn_j (k) © К
к© ainxn(k )©к © Z a Cx (k)
%=i & =i
?
i,j =1,n; a0,ai},ax :f (pi,p2,K ,pJ = rvCPn
n=i
а,у = {0,1},п = 1, ?
(3.48)
a Cx&(k )ф0
№ = 1
, X= 1,v; k = {xx ф 0 }
| к |
|
(k + 1)=П ^ (k + 1)=П f№ (x№ (k + 1)
(k + 1)= f (xi (k + 1)) = a0 © a1jxj (k)© К © a
К © a1nxn (k)©K ©Zaxxx(k), i,j = 1,
1=1
(k + 1) = fx(xx(k + 1) = a0 © a1,xj(k)©K ©
0 w ^1jpj-
К © a1nxn(k)©К © Z a\ Cx№(k), i,j = 1,
1=1 № = 1
a'x Cx№ (k )ф 0
№=1
xx(k )= arg
Доказательство. Из выражения (3.48) видно, что на каждом шаге выполнения рекуррентной процедуры формируются агрегированные переменные ~х, представленные сочетаниями булевых переменных xi состояния ДДС в форме соответствующих конъюнкций. Начальный шаг рекурсии характеризуется мощностью алфавита
? = [x ] = 2” - n -1 (3.54)
всех возможных сочетаний булевых переменных х, без повторений,
кроме случая, когда элемент сочетания представлен одной переменной. Из выражения (3.53) видно, что на очередном шаге выполнения рекуррентной процедуры алфавит агрегированных переменных пополнится новыми сочетаниями из числа ?-к оставшихся. В этой связи предельный переход при к ^ 2п - n -1 дает
?= lim ?-к= lim [(2n - n - і)-к]= 0. (3.55)
к^-2п —n—1 к^-2”-n-1L ' ' J
пустое множество (3.54) всех оставшихся возможных сочетаний булевых переменных xi без повторений. Таким образом, рекуррентная процедура (3.48) - (3.53) всегда будет завершаться за конечное число шагов, число которых не превысит значения, определяемого выражением
(3.54), а полученные агрегированные переменные образуют вектор (3.46) состояния, что в итоге позволяет по результатам рекурсии получить матрицу состояния линейной версии ДДС в форме (3.47). ¦
Примечание 3.4 (ПМ3.4). Получаемое с использованием рекуррентной процедуры (3.48) - (3.53) векторно-матричное представление (3.38), (3.39) линейной версии НДДСразмерности n по сути представляет собой векторно-матричное представление ГДДС с вектором состояния (3.46), при этом агрегированные переменные х1, i = 0,n' - n состояния синтезированной линейной ДДС являются так называемыми линейными эквивалентами переменных состояния исходной НДДС. ?
Примечание 3.5 (ПМ3.5). Появление агрегированных переменных xi, i = 0,n' - n состояния эквивалентной гибридной линейной ДДС при выполнении рекуррентной процедуры (3.48) - (3.53) опирается на то, что аналитическое представление в форме полиномов Жегалкина БФ возбуждения информационных входов триггеров НДДС в общем случае включает в себя компоненты, представляющие конъюнкцию нескольких переменных хх ее состояния, так, что для таких БФ можно записать
д 2М,
д xt д xj
am
,К
}*0.
д x1 д x2 К д xn
1 2 n
дхпдx2К дхш
i,j=1,n
i* i
x=0
i1 ’i2 К im.
x=0
=1,n
x=0
(3.56)
Запись (3.56) означает, что для указанного случая множество R не является пустым, что, в свою очередь, с использованием аппарата селлерсовского дифференцирования может быть использовано при проверке соответствующих булевых описаний ГДДС на корректность их составления. ?
Примечание 3.6 (ПМ3.6). Следует заметить, что при конструировании эквивалентной гибридной ДДС нелинейной ДДС, построенной как ЦКУ или ЦДУ (см. §2.2), множество (3.56) будет пустым, то есть R = 0, что приведет при выполнении рекуррентной процедуры (3.48) - (3.53) и к пустому множеству {~} агрегированных переменных булевого описания эквивалентной гибридной ДДС. Очевидность приведенных положений проистекает из того, что булевы функции возбуждения информационных входов триггеров ЛДДС имеют вид полиномов Жегалкина, в которых отсутствуют термы, представляющие собой конъюнкцию переменных ее состояния. ?
Примечание 3.7 (ПМ3.7). В силу нелинейности среды кодопреоб-разования исходной НДДС, ее линейная версия в форме (3.38), (3.39) не всегда характеризуется свойствами полной управляемости и наблюдаемости. ?
Выдвинутые положения параграфа позволяют сформировать
Алгоритм 3.5 (А3.5)
конструирования эквивалентного линейного векторно-матричного представления НДДС на основе принципа агрегирования переменных булевых описаний
9. В соответствии с задачей кодопреобразования средствами НДДС получить путем выполнения п.п.1-6 алгоритма 2.1 или алгоритма 2.2 ее описание в форме системы булевых функций ju (2.12) возбуждения информационных входов триггеров и выхода, которые представить в базисе Жегалкина.
10. Выполнить рекуррентную процедуру (3.48) - (3.53) с целью формирования составного вектора X (3.46) состояния эквивалентной ЛДДС.
11. Построить покоординатное представление переменных вектора X(k +l) состояния перехода эквивалентной ЛДДС.
12. Опираясь на результаты п.3 алгоритма сформировать матричные А, 13,(2,H компоненты описания эквивалентной линейной ДДС.
¦
Пример 3.5 (Пр3.5)
Проиллюстрируем процесс построения линейной ДДС эквивалентной в смысле отношения «вход-выход» в некоторой задаче кодопреоб-разования, реализуемой заданной нелинейной ДДС, при помощи алгоритма 3.5.
Тогда следуя алгоритму 3.5:
1. Получим булево описание процесса кодопреобразования средствами НДДС в виде системы булевых функций ju (2.12) возбуждения информационных входов D-триггеров и выхода, имеющих представление
у,І = uxIx2 v xIx2 v uxIx2; fi2 = uxI vxIx2 v uxIx2; y = xIx2,
которые в базисе Жегалкина записываются в форме
ц1 = xI 0 x2 0 ux2; ц2 = u © xI © uxI © xIx2 © uxIx2, y = xIx2.
2. Выполним рекуррентную процедуру (3.48) - (3.53), в результате чего образуем агрегированную переменную х3:
x3 = xI x2 ,
которая совместно с переменными xi , x2 задает составной вектор x = [xI x2 х3 ] состояния конструируемой эквивалентной линейной ДДС.
3. Составим выражения для переменных xI (к + I) , x2 (к +1), ~3(к + і) состояния перехода эквивалентной ЛДДС в покоординатной форме:
xI(к + і)= xI ©x2 ©ux2(к);
x2(к +1) = u © xI(к)© uxI(к)© ~3(к)© ux3(к);
x3(к + l) = xI(к)© x3(к)© ux3(к).
4. Опираясь на результаты п.3 алгоритма формируем матричные A, B,C,H компоненты описания эквивалентной линейной ДДС, которые получают представления: в виде четверки матриц { A(u),B,C, H }, где
| C = x о I ], H = [0 ]; |
{A,B(x),C,H }, где
| а так же в виде четверки матриц | |||||||||||||||
|
Проанализируем полученные результаты решения примера. Нелинейная природа исходной НДДС при построении эквивалентной линейной ДДС проявилась в параметризации матричных компонентов линейного представления правил перехода Л(x,u) и выхода S(x,u) несмотря на расширение размерности вектора состояния эквивалентной ЛДДС. Тем не менее, отмеченная параметризация не лишает разработчика возможности анализировать с использованием линейного аналога НДДС ее структурные свойства: управляемость, наблюдаемость, а так же структуру неподвижных состояний и замкнутых циклов с привлечением возможностей матричного формализма. Заметим, что
пара матриц (A,B(х)) несмотря на то что матрица A обладает рангом равным двум - меньшим размерности пространства эквивалентной ЛДДС, пара матриц является управляемой. Так, в случае нулевого начального состояния Х(0)=[000 ] матрица управляемости этой пары матриц в указанной точке пространства состояния принимает вид
Wy =[в (0[ A B (0 )• A2 B (0 )]= row{[010 ]T ,[100 ],[111 ]T }
и обладает рангом равным трем, то есть размерности пространства состояния эквивалентной ЛДДС. Таким образом, эквивалентная ЛДДС с помощью входного сигнала равного единице выводится из нулевого начального состояния. Аналогичным образом может быть исследована любая точка пространства эквивалентной ЛДДС на всех наборах переменных ее вектора состояния. ¦
Примечание 3.8 (ПМ3.8). При исследовании исходной НДДС средствами векторно-матричного инструментария линейных ДДС встает задача достаточно «тонкой» природы переноса результатов анализа структурных свойств (управляемости и наблюдаемости) эквивалентной ЛДДС на структуру пространства исходной НДДС. Эта же проблема возникает при межсистемном переносе результатов анализа неподвижных состояний и замкнутых циклов. Принципиально алгебраическими методами эта проблема решаема, для чего вектор состояния эквивалентной ЛДДС и вектор состояния исходной НДДС необходимо связать матрицей преобразования подобия в общем случае -вырожденного, которое от исследователя требует элементарной «матричной аккуратности», причем матричные процедуры при переносе результатов с эквивалентной ЛДДС на НДДС могут потребовать использование псевдообращения матриц над конечным полем.
Дополнительной проблемой является фактор «параметризирован-ности» матричных компонентов эквивалентного линейного модельного описания. Представляется, что более удобной с целью исследования структуры пространств управляемости и наблюдаемости является версия линейной модели с непараметризированной матрицей состояния и параметризированной матрицей входа эквивалентной ЛДДС. В этом случае пространство наблюдаемости ЛДДС оказывается стационарным и не зависящим от текущих значений переменных состояния и входа. Фактор «параметризированности» матрицы входа требует по-новому взглянуть на проблему анализа пространства управляемости. Очевидно возникает необходимость во введении понятия пространства гарантированной управляемости, которое представляет собой пересечение подпространств управляемости, полученных на всех наборах переменных состояния эквивалентной ЛДДС, параметризирующих матрицу входа.
И последнее что хотелось бы отметить в заключение. В силу использования в составе эквивалентной ЛДДС агрегированных переменных вектора состояния, которые в своей основе представляют собой конъюнкции переменных вектора состояния исходной НДДС, эквивалентная ЛДДС оказывается линейной в основном по форме записи. По-существу она является гибридной ДДС. Таким образом алгоритм 3.5 представляет собой эффективный способ конструирования гибридных ДДС на основе исходной нелинейной ДДС. Причем в алгоритме заложена возможность управления размерностью вектора состояния эквивалентной ЛДДС. Следует ожидать интересных результатов при построении агрегированных переменных использованием дизъюнкций конъюнкций. ?
3.5. Проблема обмена на паре
«аппаратурное пространство - временные затраты» в задачах помехозащитного кодопреобразования
Проблема обмена аппаратурного пространства на временные затраты и наоборот в теории и практике двоичных динамических систем устройств дискретной автоматики имеет более широкий постановочный характер, чем тот, что вынесен в заголовок параграфа. Эта проблема возникает всякий раз, когда в составе аппаратуры УДА есть функциональные компоненты, в которых процесс кодопреобразования носит векторный характер, не параметризованный дискретным временем. При этом с указанными компонентами соседствуют другие, в которых процессы кодопреобразования имеют скалярный характер, параметризованный дискретный временем.
Тем не менее наиболее наглядно проблема обмена аппаратурного пространства на временные затраты обнаруживается в задачах именно помехозащитного кодопреобразования. Таким образом, поставленная задача будет решаться на четырехфазном процессе помехозащитного кодопреобразования: «помехозащитное кодирование - передача ПЗК по каналу связи, сопровождающаяся искажением помехозащищенного кода, - декодирование принятого из КС ПЗК с искажениями с целью формирования синдрома ошибки - исправление ошибки в принятом из КС коде».
При решении поставленной проблемы постулируем следующие положения.
Постулат 3.3 (ПС3.3). Помехонезащищенный код (ПНЗК) может поступать на узел помехозащиты в скалярной параметризованной дискретным временем форме, то есть в виде последовательного кода старшим разрядом вперед. ?
Постулат 3.4 (ПС3.4). ПНЗК может подаваться на узел помехо-защиты в векторной не параметризованной дискретным временем форме, то есть в виде параллельного кода (старшимразрядом вниз). ?
Постулат 3.5 (ПС3.5). Двоичный КС передачи ПЗК от узла помехозащиты к узлу декодирования и коррекции кода при всех реализациях процесса помехозащитного кодирования и декодирования является скалярный параметризованный дискретным временем так, что по нему передается последовательный двоичный код. ?
Постулат 3.6 (ПС3.6). Процесс кодопреобразования характеризуется «канальным» временем (ВК), если он происходит в форме ввода двоичной кодовой последовательности в канальную среду при передаче или вывода из канальной среды при приеме. ?
Постулат 3.7 (ПС3.7). Процесс кодопреобразования характеризуется «аппаратурным» временем (ВА), если его осуществление непосредственно не связано с каналом связи. ?
Примерами процессов кодопреобразования, осуществляемых в темпе канального времени являются: дивидендное помехозащитное кодирование; преобразование вектора ПЗК, сформированного матричным не параметризованным дискретным временем методом, в последовательный код; дивидендное помехозащитное декодирование с целью формирования синдрома ошибок; размещение искаженного ПЗК, принятого из КС, в сдвиговом регистре хранения и т.д.
Примерами процессов кодопреобразования, осуществляемых в темпе аппаратурного времени являются: преобразование последовательного ПНЗК в параллельный при матричном методе формирования ПЗК; процесс деления в дивидендном декодирующем устройстве при повторных циклах деления и т.д.
Следует заметить, что канальное время, определяемое длительностью элементарного сигнала кода и числом разрядов этого кода, не модифицируемо в силу требований используемого протокола канального уровня. Аппаратурное время, напротив, является модифицируемым, при этом выбором делителей частоты генераторов тактовых импульсов можно осуществить такое соотношение между канальным и аппаратурным временем, при котором процессы преобразования последовательного кода в параллельный при матричном методе помехозащитного кодирования можно осуществить за один такт канального времени; за один такт канального времени можно также осуществить каждый повторный цикл деления при дивидендном декодировании.
Модифицируемость аппаратурного времени является основным резервом сокращения временных затрат при помехозащитном кодировании и декодировании.
Определение 3.20 (О3.20). Мера аппаратурного пространства, занимаемого функциональным компонентом, задействованном в процессе помехозащитного линейного кодопреобразования, осуществляемого векторно-матричным способом, не параметризованным дискретным временем, определяется размерностью матрицы линейного кодового преобразования. ?
Определение 3.21 (О3.21). Мера аппаратурного пространства, занимаемого функциональным компонентом, задействованном в процессе помехозащитного нелинейного кодопреобразования, осуществляемого в силу булева описания процесса, определяется размерностью нелинейного кодового преобразователя, задаваемой мультипликативным образом на числе булевых переменных на входе и числе булевых функций на выходе. ?
Примечание 3.9 (ПМ3.9). Нетрудно видеть, что введенные меры обладают заметной достаточностью так, как они в линейном случае не учитывают число нулевых элементов матриц, а в нелинейном - число основных конъюнкций в дизъюнкции конъюнкций. ?
Определение 3.22 (О3.22). Функционалом размещения в аппаратурном пространстве и времени функционального компонента, задействованного в процессе помехозащитного преобразования, называется мультипликативная скалярная характеристика, элементами которой является мера аппаратурного пространства и временные затраты, выраженные в числе тактов канального времени. ?
Определение 3.23 (О3.23). Будем считать размещение функционального компонента, задействованного в процессе помехозащитного преобразования, в аппаратурном пространстве и времени оптимальным, если это размещение характеризуется минимальным значением функционала размещения. ?
Утверждение 3.4 (У3.4). Пусть процесс кодопреобразования характеризуется числом фаз этого процесса, равным q, тогда совокупный функционал размещения Jz многофазного процесса в аппаратурном пространстве и времени обладает аддитивным свойством так, что выполняется соотношение
(3.57)
j=i
Доказательство утверждения использует тот факт, что естественным аддитивным свойством обладают время и аппаратурное пространство. ¦
Теперь может быть сформулирован принцип проектирования устройств помехозащитного кодопреобразования, использующего возможности обмена аппаратурного пространства на временные затраты и наоборот - с целью достижения оптимального размещения устройства в аппаратурном пространстве и времени. Этот принцип формально может быть записан в виде
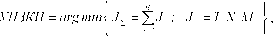 |
| j=і |
где УПЗКП - устройство помехозащитного кодопреобразования; Tj -длительность осуществления j -ой фазы помехозащитного кодопреоб-разования; Nj, M - компоненты меры аппаратурного пространства, в котором размещено устройство, реализующее j -ю фазу кодопреобра-зования, и характеризующееся мерой Sj = Nj Mj.
ЗАКЛЮЧЕНИЕ
В монографии сделана попытка объединить исследования двух ветвей двоичных динамических систем устройств дискретной автоматики под «одной обложкой».
В современной теории ДДС ветвь линейных двоичных динамических систем и ветвь двоичных динамических систем, построенных в одной из автоматных логик, обычно рассматриваются порознь. Совместное рассмотрение линейной и автоматной версий двоичных динамических систем привело авторов к необходимости введение третьего класса ДДС, объединяющих возможности линейных и автоматных версий этих систем, названного авторами гибридными двоичными динамическими системами. Следует ожидать, что класс гибридных ДДС в ближайшее время обнаружит дополнительные интересные возможности и поставит новые проблемы, с результатами разработок которых авторы обязательно познакомят научную общественность.
приложение D-преобразование двоичных
ПОСЛЕДОВАТЕЛЬНОСТЕЙ
Определение П1.1 (ОП1.1). Прямым D-преобразованием F(d) двоичной последовательности f (к), где к - дискретное время, выраженное в числе тактов длительности A t, над простым полем Галуа GF( p)= = {0,1,2,К ,Р - 4-где p = 2 называется бесконечная сумма
F(d) = D{f (к)}=І/(к)dk, (П1.1)
к=0
при условии, что она сходится. ?
Функция F(d) называется D-образом двоичной последовательности
/ (к).
Определение П1.2 (ОП1.2). Обратным D-преобразованием D-1 {F (d)}
D-образа F(d) двоичной последовательности f (к) называется преобразование, позволяющее по D-образу F(d) двоичной последовательности /(к) восстановить исходную последовательность /( к) в силу соотношения
D -1 { F ( d )}= /( к ). ? (П1.2)
Последовательность / (к) именуется оригиналом D-преобра-зования. Таким образом / (к) и F ( d) представляет собой взаимные D-трансформанты.
Канонически сложившегося аналитического обратного D-преобразования
D-1 {f (d)} пока не существует, но имеются способы их вычисления, которые опираются на определение прямого
D-преобразования. Для иллюстрации этих способов запишем (П1.1) в развернутой форме
F (d )= / (0) + f (1)d + f (2)d2 + f (3)d3 +К + f( к )dк +К (П1.3)
Первый способ вычисления обратного D-преобразования, записываемого в форме
D{F(d)}=[f(0)\f(1)d\f(2)d2 |к IДкК |к] = ] (Пі.4)
на основе (П1.3) позволяет с учетом модальной арифметики записать:
f (0 ) = limF (d);
d ^0
f (1)= lmFMf ;
f (2) = lmF(d)+f{0)+fil)l;
d ^0 d2
M
(П1.5)
k-1
F (d )+Z f (i У
f (k ) = lim-
i=0
dk
Второй способ вычисления обратного D -преобразования, записываемого в
форме (П1.4) на основе (П1.3) позволяет использованием операции дифференцирования по переменной d записать:
f (0 ) = lmF (d);
d ^0
f (1)=lm ;
d d 1 d2F(d);
(П1.6)
f (2) = lim d 2 d -+0 2! d d
1 d kF (d)
f (k ) = lim
d -+0k! d d
Третий способ вычисления обратного D-преобразования для случая, когда F (d) представим в виде отношения двух модулярных многочленов, записанных по степеням переменной d ,
M (d) N (d)
b0 + bid + b2d + b3d + К + byd a0 + a,d + a2d + a3d +К + ad
0 12 3 n
F (d)
(П1.7)
позволяет путем деления ММ «уголком» с учетом модулярной (по mod 2 ) арифметики
a0 + a,d + a2d2 + a3d3 +K + a dn
0 12 3
bg + bd + b2d + b3d +K + bxd
bo , ai +Ad + ai(ai + bi) + (a2 + b2)d2 +K
a0 + a,d + a2d + a3d +K + a dn
0 12 3
ar,
ar,
an
((%i + bi )d + ( сі2 + b2 )d + ( CI3 + b3 )d + К
an
(ai + bi )d + — (ai + bi )d2 +—(ai + bi )3 +К
an
(a1 + b1 )(a3 + b3)
a,
(C1 + b1 )+(a2 + b 2 )
d3 +К
d2 +
V ao
V ao
для двоичной последовательности записать
f (k ):f (0 )= Kf (1)= C b
an
an
(П1.8)
f (2 ) = a1 (a1 + b1)+(a2 + b2) j (3) = К
a02
Рассмотрим теперь основные свойства прямого D-преобразования.
Свойство П1.1 (СП1.1). Прямое D -преобразование является
линейным так, что выполняются условия:
(П1.9)
(П1.10)
і D{j(k)+ g(k)}=D{j(k)}+D{g(k)}= f(d)+g(d)
p=2'
2. D {a f (k)}=aD {f (k)}=aF (d), где a e GF( p)|
Свойство СП1.1 линейности D-преобразования строится на линейности операции суммирования в (П1.1).
Свойство П1.2 (СП1.2). (Свойство сдвига в области действительной переменной k) Пусть D {f (k)} = F ( d), тогда
m-1
D {f (k + m)}= d~mF(d)+ d~m ? f (i(d1 .
(П1.11)
i=0
Доказательство справедливости свойства опирается на определение прямого
D-преобразования смещенной на m тактов последовательности f (k + m), которое в силу (П1.1) позволяет записать
D {f (k + m )} = f (m)+ f (m + 1)d + f (m + 2)d2 +К
К+ f (m + k) dk +К (П1.12)
Если путем умножения с одновременным делением правой части (П1.12) на dm и
т-1
суммирования дважды по mod2 линейной комбинации ^ f (i)d1 обеспечить
i=0
равенство индексов А компонентов f (А) и степеней мультипликативного члена dА в (П1.12), то получим (П1.11). ¦
Свойство П1.3 (СП1.3). (Свойство изменения масштаба в области переменной d). Пусть D { f (к)} = F (d), тогда
D {a f (к )}= F (ad). ? (П1.13)
Доказательство справедливости свойства строится на непосредственном использовании прямого D-преобразования к последовательности ак f (к), которое в силу (П1.1) дает
D {ак f (к)}=a0f (о) + а}f (l)d + а2f (2)d2 + К +akf (к(dk +К =
= f (0)+ f (l)(ad) + f (2 )(ad )2 +К + f (к )(ad )к +К = = F (ad). ¦
Рассмотрим теперь D-преобразование типовых двоичных последовательностей.
1. Последовательность
f( к) = 8( к): 1,0,0К ,0,К (П1.14)
именуемая одиночным импульсом или дискретной 8 -функцией над простым полем Галуа GF ( p )| p=2. Если к (П1.14) применить (П1.1), то получим
D {f ( к )=8( к )}=F8{ d )= 1. ¦ (П1.15)
2. Последовательность
f (к) = 1 (к): 1,1,1,К ,1,К (П1.16)
именуется унитарным кодом или единичной последовательностью. Если к (П1.16) применить (П1.1), то получим
D {f (к )= 1(к)}=F (d ) = 1 + d + d1 +К + dli +К (П1.17)
Если к (П1.17) применить формулу суммы членов бесконечной геометрической прогрессии с показателем d с учетом специфики модулярной арифметики по mod 2 для (П1.17) можно записать
(П1.18)
D {(к )= 1(к )}=f ()=1-
1 + d
3. Периодическая последовательность с целочисленным периодом Т
f (к )= f (к + Т):
f^f^f^ , f (Т -1), f (0), f (1) f (2 ),К , f(T-1,) (П1.19)
f(0), f(1), f(2 ),К , f(T-1), f(0), f(1), f (2 ),К , АТ-1),К
Если к периодической последовательности f ( к )= f ( к + Т), записанной в форме (П1.19), применить прямое D-преобразование, то в силу (П1.1) можно записать
F (d ) = D {f (k ) = f (k + T )}=
=(f(0) + f(l)d + f(2)d2 +K +f(T-l)dT-‘ )(l + dT + ( + d3T +k)
(П1.20)
Если к выражению (П1.20) применить формулу суммы членов геометрической
прогрессии с показателем dT , то получим для периодической последовательности с учетом специфики модулярной арифметики по mod 2
F (d ) = D {f (k + T )} =
T-l
(П1.21)
= f(0)+f(l)d +f( 2 )d2 +K + f( T-l)d
1 + dT
Если встает задача преобразования модулярных многочленов над простым полем Галуа GF(p) при p = 2 с привлечением возможностей аппарата ID-
преобразования, то возникает необходимость ввести в рассмотрение прямого D-преобразования ММ
f ( х )= a0xn + a1xn-1 + a2xn-2 +K + an-1x + an, (П1.22)
где ai e GF(p)|p=2, i = 0,n; с целью вычисления его образа F (d) =
= D {f ( x)}. Вычисление D-образа ММ f (x) зависит от того, каким разрядом вперед ММ f (x) передается в канальной среде: младшим или старшим, в силу
чего модулярный многочлен имеет два D-образа F (d). Способы вычисления
D-образов ММ f ( x) (П1.22) зададим с помощью утверждений.
Утверждение П1.1 (УП1.1). D-образ F ( d) модулярного многочлена f ( x) (П1.22) при его передаче младшим разрядом вперед задается соотношением
F (d )= D {f(x)} = f{x\=d =
= an + an-1d + an_2d +K + a2d + a0d . ? (П1.23)
Доказательство утверждения строится на формировании последовательности f (к) из коэффициентов ММ f (X) с учетом его передачи младшим разрядом вперед
f (к): an, an_i, an_2 ,К ,an a0,0,0,0,K (П1.24)
с последующим применением к (П1.24) D-преобразования (П1.1). ¦
Утверждение П1.2 (УП1.2). D-образ F ( d) модулярного многочлена f ( X) (П1.22) при его передаче старшим разрядом вперед задается соотношением
F (d )= D {f( x)} = f ^ \_1=d =
= a0 + aid + a2d +K + an_d + and , (П1.25)
где f (x 1) - полином по отрицательным степеням X 1 задается в силу представления
f (x )=x"7(x _ )=
= x (a0 + ajX + a2x +K + an_1X ( ) + and ) ? (П1.26)
Доказательство утверждения строится на формировании последовательности f (к) из коэффициентов ММ f ( X) с учетом его передачи старшим разрядом вперед
(П1.27)
f (к)•• a0,a1,a2,K ,an_1,an,0,0,0,K
с последующим применением к последовательности (П1.27) прямого D-преобразования (П1.1) и констатацией факта совпадения порядка следования коэффициентов ai (i = 0,n) в последовательности (П1.27) и в ММ f (x 1) (П1.26). ¦
ЛИТЕРАТУРА
| 1 |
Автоматизация проектирования цифровых устройств/ С. И. Баранов, С. А. Майоров, Ю. П. Сахаров, В. А. Селютин. - Л.: Судостроение, 1979. |
| 2 |
Автоматы//Сборник статей под ред. К.Э. Шеннона и Дж. Маккарти - М.: ИЛ, 1956. |
| 3 | Акунов Т.А., Алишеров С., Оморов Р.О., Ушаков А.В. Матричные уравнения в исследовании дискретных процессов над бесконечными и конечными полями. Бишкек: Илим, 1993. |
| 4 | Алгебраические методы в теории устройств дискретной автоматики и телемеханики//Труды лаборатории телемеханики кафедры автоматики и телемеханики. -СПб.: СПбГИТМО(ТУ), 2001. |
| 5 | Андреев Ю.Н. Управление конечномерными линейными объектами. М.: Наука, 1976. |
| 6 |
АрбибМ. Теория автоматов: в кн. Калман Р., Фалб П., Арбиб М. Очерки по математической теории систем. -М.: Мир, 1971. |
| 7 |
Баев А.П., Салмыгин И.П., Ушаков А.В. Автоматный синтез циклических кодирующих и декодирующих устройств. //Изв. вузов. Приборостроение, 1998. Т.41. №7. |
| 8 |
Баранов С. И. Синтез микропрограммных автоматов. -Л.: “Энергия”, 1979. |
| 9 | Бохман Д., Постхофф Х. Двоичные динамические системы. - М.: Энер-гоатомиздат, 1986. |
| 10 | Букреев И.Н., Манеуров Б.М., Горячев В.И. Микроэлектронные схемы цифровых автоматов. - М.: Советское радио, 1975. |
| 11 | Буханова Г. В. Высоконадежные оперативные запоминающие устройства, тенденции развития//Автоматика и телемеханика. 1993. №2. |
| 12 | Воеводин В.В., Кузнецов Ю.А. Матрицы и вычисления. -М.: Наука, 1984. |
| 13 | Гантмахер Ф. Р. Теория матриц. - М.: «Наука», 1967. |
| 14 | Гилл А. Введение в теорию конечных автоматов. -М.: Наука, 1965. |
| 15 | Гилл А. Линейные последовательностные машины. -М.: Наука, 1974. |
| 16 |
Голуб Дж., Ван Лоун Ч. Матричные вычисления: Пер. с англ. - М.: «Мир», 1999. |
| 17 | Горбатов В. А. Фундаментальные основы дискретной автоматики. Информационная математика. - М.: «Наука». Физматлит, 1999. |
| 18 | ГОСТ 14422 - 72 Системы передачи данных. |
| 19 | ГОСТ 17422 - 82 Система передачи данных и основные параметры помехоустойчивых циклических кодов. |
| 20 | ГОСТ20687 - 75 Коды помехоустойчивые итеративные. Структура кода. |
| 21 | ГОСТ24734 - 81 Устройство защиты от ошибок аппаратуры передачи данных. Типы и основные параметры. |
| 22 | ГОСТ 26.205-88Е Комплексы и устройства телемеханики. |
| 23 |
ГОСТ Р МЭК 870-5-101-2001 Устройства и системы телемеханики. Часть 5. Протоколы передачи. Раздел 101. Обобщающий стандарт по основным функциям телемеханики. |
| 24 |
ГОСТРМЭК 870-5-104-2004 Аппаратура и системы телеуправления. Часть 5-104. Протоколы передачи данных. Доступ к сетям, использующим стандартные профили по МЭК 60870-5-101. |
| 25 |
Заде. Л., Дезоер Ч. Теория линейных систем/Пер. с англ. М.: Наука, 1970. |
| 26 |
Золотарев В.В., Овечкин Г.В. Помехоустойчивое кодирование. Методы и алгоритмы: Справочник/Под ред. чл.-кор. РАН Ю.Б. Зубарова. - М.: Горячая линия - Телеком, 2004. |
| 27 |
Интегральные микросхемы: Справочник / Б.В. Тарабрин, Л.Ф. Лунин, Ю.Н. Смирнов и др.; под ред. Б.В. Тарабрина. -М.: Радио и связь, 1984. |
| 28 | Ирвин Дж., Харль Д. Передача данных в сетях: инженерный подход: Пер. с англ. - СПб.: БХВ-Питер, 2003. |
| 29 |
Калман Р., Фалб П., АрбибМ. Очерки по математической теории систем. - М.: Мир, 1971. |
| 30 | Калужнин Л. А. Введение в общую алгебру. М.: «Наука», 1973. |
| 31 | Квакерпаак Х., Сиван Р. Линейные оптимальные системы управления / Пер. с англ. М.: Мир, 1977. |
| 32 |
Кирюшин А.А., Рассветалова Л.А., Ушаков А.В. Модальное управление в задаче синтеза двоичных динамических систем в логике линейных триг-геров//Автоматика и телемеханика, 1993 №8. |
| 33 | Компьютерные сети. Принципы, технологии, протоколы: Учебник для вузов. 2-е изд. / В.Г. Олифер, Н.А. Олифер. - СПб.: Питер, 2004. |
| 34 |
Крутько П.Д. Обратные задачи теории управления. М.: Наука, 1987. |
| 35 | Кузовков Н. Т. Модальное управление и наблюдающие устройства. М.: Машиностроение, 1976. |
| 36 | Лазарев В. Г., Пийль Е. И. Синтез управляющих автоматов. - М.: Энергия, 1978. |
| 37 | Мельников А. А., Рукуйжа Е. В., Ушаков А. В. Использование свойств матриц для обнаружения неустойчивых циклов и неподвижных состояний двоичных динамических систем / Научно-технический вестник СПбГИТ-МО(ТУ). 2002. Выпуск 6. |
| 38 | Мельников А. А., Ушаков А. В. Алгебраические структурные свойства матричных компонентов модельных представлений линейных УДАТ в задаче редуцирования их размерности//Алгебраические методы в теории устройств дискретной автоматики и телемеханики. -СПб.: СПбГИТМО(ТУ), 2001. |
| 39 | Мельников А. А., Ушаков А. В. Устройства дискретной автоматики гарантированной информационной надежности с редуцированным ресурсом помехозащиты.//Изв. вузов. Приборостроение, 2001. Т.44. №2. |
| 40 | Никифоров В. О., Ушаков А. В. Управление в условиях неопределенности: чувствительность, адаптация, робастность. СПб.: СПбГИТМО(ТУ), 2002. |
| 41 | Оре О. Теория графов. — М.: Наука, 1980. |
| 42 | Питерсон У., Уэлдон Э. Коды, исправляющие ошибки. -Пер. с англ. М.: «Мир», 1976. |
| 43 | Рассветалова Л. А., Ушаков А. В. Двоичное динамическое наблюдение в задаче помехоустойчивого кодирования. // Автоматика и телемеханика. 1993. №6. |
| 44 |
Рукуйжа Е.В., Ушаков А.В. Сравнительный анализ матричных и дивидендных представлений процессов кодирования и декодирования в задачах защиты информации // Совр. Технологии: Сборник научных статей / Под. ред. С. А. Козлова и В.О. Никифорова. - СПб.: СПбГИТМО(ТУ), 2002. |
| 45 |
Сапожников В. В., Сапожников Вл. В., Гессель М. Самодвойственные дискретные устройства. СПб.: Энергоатомиздат. Санкт-Петербургское отд-ние, 2001. |
| 46 |
Свами М., Тхуласираман К. Графы, сети, алгоритмы. / Пер. с англ. М.: Мир, 1976 |
| 47 | Селлерс Ф. Методы обнаружения ошибок в работе ЭЦВМ, - М.: «Мир», 1972. |
| 48 |
Синтез дискретных регуляторов при помощи ЭВМ / В.В. Григорьев, В. Н. Дроздов, В. В. Лаврентьев, А. В. Ушаков. Л.: Машиностроение, 1983. |
| 49 | Согомонян Е. С. Слабаков Е.В. Самопроверяемые устройства и отказоустойчивые системы. - М.: Радио и связь, 1989. |
| 50 | Темников Ф. Е., Афонин В. А., Дмитриев В. И. Теоретические основы информационной техники. - М.: Энергия, 1979. |
| 51 | Тутевивич В. Н. Телемеханика. М.: «Высшая школа», 1985. |
| 52 | УонемМ. Линейные многомерные системы: геометрический подход. М.: Наука, 1980. |
| 53 | Ушаков А.В. Обобщенное модельное управление. // Изв. вузов. Приборостроение. 2000. т.43. №3. |
| 54 | Ушаков А. В. Синтез циклических кодирующих и декодирующих устройств в логике произвольных триггеров//Автоматика и телемеханика. 1997. №11. |
| 55 | Фараджев Р. Г. Линейные последовательностные машины. - М.: Сов. радио, 1975. |
| 56 | Щербаков Н.С. Достоверность работы цифровых устройств. - М.: Машиностроение, 1989. |
| 57 | Hadjicostis C.N. “Nonconcurrent Error Detection and Correction in Fault- |
| Tolerant Linear Finite-State Machines”, IEEE Trans. Automat. Contr., vol.48, no.12, pp.2133-2140, Dec. 2003. | |
| 58 |
Massey J.L. and SainM.K., “Codes, automata and continuous systems: Explicit interconnections”, IEEE Trans. Automat. Contr., vol.AC-12, pp.644650, Dec. 1967. |
| 59 |
Massey J.L. and Sain M.K., “Inverses of linear sequential circuits”, IEEE Trans. Comp., vol.C-17, pp.330-337, Apr. 1968. |
| 60 |
Rosenthal J. “Some interesting problems in systems theory which are of fundamental importance in coding theory”. in Proc. 36 Conf. Decision Control, vol.5, San Diego, CA, 1997, pp. 4574-4579. |
| 61 | Rosenthal J. and Marcus B., Eds., Codes, Systems and Graphical Models. ser IMA Volumes in Mathematics and its Applications. New York: Springer-Verlag, 2001, vol.123. |
| 62 | Rosenthal J. and Smarandache R., “Maximum distance separable convolutional codes”, Appl. Alg. Eng., Commun. Comput., vol.10, no1, pp.1532, 1999. |
| 63 | Rosenthal J. and York F.V. “BCH convolutional codes”, IEEE Trans. Inform. Theory, vol.45, pp.1833-1844, Sept.1999. |
| 64 |
Rosenthal J. , York F.V. and Schumacher J.M. “On the relationship between algebraic systems theory and coding theory: Representations of codes”, in Proc. 34 Conf. Decision Control, vol.3, New Orleans, LA, 1995, pp.32713276. |
| 65 | Sellers F., Hsio M. Y., Bearson L. W. Analyzing errors with Boolean difference //IEEE Trans. Comp. C-17. 1968. pp. 676-683. |
Автомат
- абстрактный 102
- конечный 57, 102 Автоматика дискретная 10 Алгоритм
- автоматного синтеза канонический 102
- по граф-схеме алгоритма 109
- синтеза линейных двоичных динамических систем 19, 30 Алфавит
- входа 102, 121
- выхода 102, 121
- высокого уровня 102
- состояния 102, 121 Анализ
- структуры замкнутых циклов 74
- неподвижных состояний 74 Аппарат
- передаточных функций 13
- селлерсовского дифференцирования 142
Базис
- Жегалкина 189
- канонический наблюдаемый 31, 32
- управляемый 31, 32 Блок памяти 24
Вектор
- входа 23
- выхода 23
- состояния 23, 38, 43, 47, 56 Вес
- производной булевой функции 145
Время
- аппаратурное 199
- канальное 198 Вычисление
- производной Селлерса булевой функции 143
- степени образующего модулярного многочлена помехозащищенного кода 99, 118
Граф переходов и выходов 106 Граф-схема алгоритма (ГСА) 11, 101, 109
Декодирование
— помехозащитное векторно-матричное 59
— дивидендное 93,99, 199
---укороченных циклических кодов 135, 137, 138
— на основе концепции наблюдения состояния канала связи 56 Деление модулярных многочленов 17
Дешифратор синдрома ошибки 129, 139 Достоверность передачи 135
Код
- Грея 157
- двоичный 157
- Джонсона 157
- искаженный 51, 59
- помехозащищенный 51, 53, 59, 61, 62, 68
- - укороченный 135
- помехонезащищенный 59, 61, 66, 198
- циклический 54, 57, 66, 69 Кодирование
- помехозащитное векторно-матричное 60
- дивидендное 99, 199
---укороченных циклических кодов 135
- кодов состояния конечного автомата 181
- на основе концепции наблюдения состояния канала связи 51
Галуа GF ( p) 102
- элементами простого поля
- элементов алфавитов абстрактного автомата 102 Кодопреобразование
- линейное 24
- нелинейное 24 Код
- помехи в канале связи 59
- синдрома ошибки 59
- Хэмминга помехозащищенный 20, 104 Коды
- линейные 62
- систематические 61
- с полной блоковой систематикой 62, 69
- соседние 103 Концепция подобия 43, 44 Критерий
- наблюдаемости линейных двоичных динамических систем 26, 27
- управляемости линейных двоичных динамических систем 26, 27
Матрица
- входа 24
- выхода 24
- наблюдаемости 27, 36
- нильпотентная 44, 47, 51
- образующая 53, 60 - 62, 66, 136
- передаточная 15, 28, 34
- проверочная 54, 61, 62, 65, 136
- остатков 69
- принадлежащая показателю 47, 51, 53, 96
- состояния 24, 30, 47
- преобразования подобия 43, 46
- управляемости 25, 26, 40 Многочлен
- модулярный 13, 16, 19, 21, 29, 30, 34 - 36, 41, 66
- неприводимый 36, 66, 118
- образующий 54, 69, 136
- помехозащищенного кода 96, 118
- принадлежащий показателю 35, 37, 136
- характеристический 30, 35, 44, 83
Наблюдаемость линейных двоичных динамических систем 38 Наблюдатель
- состояния регистра канала связи 52 Надежность информационная 180, 181 Нуль-пространство матрицы 63, 68, 80
Опознаватель (синдром) ошибки (искажения) в коде 59 - 61, 64 Ошибка
- исправляемая 62, 182
- обнаруживаемая 63, 182
Памяти элемент 19, 20, 30, 51 Полином (см. многочлен)
Последовательность
- кодовая 15, 20, 51
- периодическая 20, 36, 37
- скремблирующая 164
Проблема заполнения кодового пространства 155 Производная Селлерса булевой функции 143 Пространство
- аппаратурное 198 - 200
- кодовое 101
- вырожденное 156
- невырожденное 156
Ранг 26, 27
Расстояние кодовое 73, 99 Регистр сдвига 47, 51 Редуцирование 34, 38
Синдром
(см. опознавателъ) ошибки Система
- двоичная динамическая 13, 15, 17, 23
- гибридная двоичная динамическая 11, 155
- линейная двоичная динамическая 13, 15, 17, 21, 24, 26, 27, 29, 30
- нелинейная двоичная динамическая 10, 101
- динамическая над бесконечным полем 13, 39
- над конечным полем 13, 39 Скремблирование 164
Сходимость процессов над двоичным полем 44
Тип триггера 55, 56, 103 Триггер 19, 55, 56, 117
Управляемость системы линейной двоичной динамической 38 Устройство
- дискретной автоматики 10, 11, 17
- кодирующее 51, 117
- декодирующее 54, 76, 117
Функция
- булева возбуждения входа триггера 103, 104
— формирования выхода 104
Цикл замкнутый 74, 85
Число
- ошибок 73, 99
- проверочных разрядов 66, 73, 135, 136
- синдромов 73, 99
Ядро (см.нуль-пространство) матрицы
ИЗ ИСТОРИИ

ЛАБОРАТОРИИ ТЕЛЕМЕХАНИКИ
Лаборатория телемеханики, как проблемное подразделение кафедры систем управления и информатики (до 2001 года кафедры автоматики и телемеханики) Санкт-Петербургского государственного университета информационных технологий, механики и оптики (ИТМО), организована в ее составе в 1945-м году одновременно с основанием кафедры в структуре факультета электроприборостроения, со временем переименованным в радиотехнический. Основание кафедры и лаборатории телемеханики связано с именем ее первого заведующего и одновременно первого декана факультета электроприборостроения профессора Марка Львовича Цуккермана. На кафедру автоматики и телемеханики (ИТМО), в отличие от существовавших к тому времени кафедр аналогичного профиля в ЛПИ им. М. И. Калинина (ныне СПбГТУ) и ЛЭТИ им. В. И. Ульянова (Ленина) (ныне СПбГЭТУ («ЛЭТИ»)), была возложена задача по подготовке специалистов в области автоматизации и телемеханизации приборостроительной, оптической и оборонной промышленности.
Профессор Цуккерман М. Л. в 1910-м году закончил Санкт-Петербургский государственный политехнический институт им. Петра Великого. В 20-е годы XX в. он организовал в Ленинграде (ныне Санкт-Петербург) отраслевую лабораторию электроизмерений (ОЛИЗ) и был известен в стране как крупный специалист в области телеизмерения. Научные интересы профессора Цуккермана М. Л. и персонала новой кафедры и лаборатории телемеханики на многие годы определили основные направления научной, учебной и методической деятельности лаборатории, проблемным куратором которой профессор Цуккерман М. Л. оставался вплоть до своей кончины в 1959-м году. В этот период основное направление научноисследовательской работы лаборатории составили задачи автоматизации и телемеханизации измерения и регистрации параметров кораблей во время их ходовых испытаний, выполнявшихся по заданию ВМФ. Учебный процесс лаборатория проводила для студентов специальности 0606 — приборы и устройства автоматики и телемеханики по программам дисциплин «Телемеханические приборы и устройства» и «Телеизмерение», причем лекции по последней из них читал проф. Цуккерман М. Л., которому ассистировал ассистент Шпаков А. М. Курсы лекций по дисциплине «Телемеханические приборы и устройства» были поставлены и читались доцентом Юргенсоном Р. И. и старшим преподавателем Соколовым В.В., которым в лабораторном практикуме ассистировала выпускница кафедры ассистент Никифорова Л. Т. Основу лабораторного оборудования в это время составляли устройства дистанционного управления тренажеров специального назначения, промышленные устройства релейно-контактной телемеханики типа РВКБ, а также макеты релейно-контактной телемеханики, изготовленные силами сотрудников лаборатории и экспериментально-производственных мастерских (ЭПМ) ИТМО.
С 1959-го года по 1970-й год кафедру возглавляет ученик профессора Цуккермана М. Л., выпускник кафедры автоматики и телемеханики ЛЭТИ им. В. И. Ульянова (Ленина) 1936-го года доцент
Танский Е.А. За этот период по разным причинам кафедру покидают Юргенсон Р.
И. и Шпаков А. М., дисциплина «Телеизмерение» входит в качестве содержательного компонента в дисциплину «Телемеханические приборы и устройства», обучение по которой в рамках всех видов учебной деятельности дневного и вечернего образования легло на плечи сотрудников лаборатории старших преподавателей Никифоровой Л.Т. и Соколова В. В. Содержание дисциплины заметным образом модернизируется: в нем появляются разделы по алгебраическому синтезу дискретных устройств телемеханики, использующему возможности булевой алгебры, а также элементы современной теории помехозащитного кодирования дискретной информации при ее передаче.
Устанавливаются творческие связи с Ленинградским научно-производственным предприятием «Электропульт», в результате которых в лаборатории телемеханики для нужд учебного процесса появляются образцы телемеханической аппаратуры заводского изготовления типа ТНЧ-2. В рамках научно-технического сотрудничества с НИИЭТУ (г. Ленинград) лаборатория принимает участие в разработке фототелеграфной аппаратуры комплекса 'Тазета-2". Теоретические исследования в лаборатории в это время сосредоточены на обеспечении помехоустойчивости процесса фазирования фототелеграфной аппаратуры передающего и приемного полу-комплектов комплекса, а также эффективной буферизации передаваемой информации.
В 1970-м году по результатам конкурса заведующим кафедрой становится известный в стране специалист в области автоматизированного электропривода и фотоэлектрических следящих систем выпускник ЛИИ им. М. И. Калинина 1938-го года профессор Сабинин Ю. А., который руководил кафедрой до мая 1990-го года. Ироисходят изменения в составе сотрудников лаборатории телемеханика, на смену старшему преподавателю Соколову В. В. приходит выпускник кафедры доцент (ныне профессор) Ушаков А. В., позднее состав лаборатории пополняется выпускниками кафедры ассистентом (ныне старшим преподавателем) Салмыгиным И. И. и лаборантом (позднее инженером)
Рукуйжей Е. В., а также доцентом Баевым А. И.
В учебном плане специальности 0606 — автоматика и телемеханика дисциплина «Телемеханические приборы и устройства» получает название «Телемеханика», появляется дисциплина «Теоретические основы кибернетики» (ТОК), в программу которой включается раздел по прикладной теории информации, проблемно ориентированный на теоретические основы канализации информации и кодопре-образования в задачах телемеханики; по дисциплине вводится курсовая работа. В составе лабораторного оборудования появляются отечественные ИЭВМ типа Т3-16, ДВК-3М, а к 1986-му году благодаря усилиям и инициативе старшего преподавателя Никифоровой Л. Т. и заведующего кафедрой Сабинина Ю. А. лабораторная база была подвергнута полной модернизации, в результате чего лаборатория телемеханики была оснащена лабораторными макетами типа ЛАТ-01 и ЛАТ-011, разработанными с участием сотрудников лаборатории и изготовленными на предприятии Союзвузприбора. Лабораторная база нового поколения позволила осуществить фронтальный метод проведения лабораторного практикума. Лаборатория установила научные контакты с предприятиями и НИИ телемеханической проблемной ориентации НИО
им. Коминтерна и НИО «Дальняя связь» (г. Ленинград), три сотрудника которых Яковлев А. А., Кирюшин А. А. и Рассветалова Л. А. по программе аспирантского обучения выполнили диссертационные исследования на соискание ученой степени кандидата технических наук по проблематике своих организаций под научным руководством профессора Ушакова А. В. В рамках хоздоговорных отношений с ОКБ МЭИ (г. Москва) во исполнение Комплексной целевой программы «Излучение» по созданию высокоточной аппаратуры для контроля деформаций металлоконструкций больших полноповоротных радиотелескопов с диаметром раскрыва главного рефлектора 32, 64 и более метров типа ТНА-400 и ТНА-1500 в процессе юстировки перед вводом их в эксплуатацию и в процессе эксплуатации разработана уникальная локальная сеть с использованием волоконно-оптических линий связи (ВОЛС) МС-8201, ППЗ-структур и ПК для комплексных телеизмерения и телесигнализации с целью введения поправок на деформацию элементов радиотелескопа при его наведении на объект радиоастрономического наблюдения. Теоретическая работа лаборатории направлена на использование алгебраических методов в теории устройств дискретной автоматики и телемеханики, опирающихся на теорию микропрограммных автоматов и результаты алгебраизации общей теории систем над бесконечными и конечными полями, как следствие этой работы заметно выросло число публикаций сотрудников и аспирантов лаборатории. В этот период кафедра, а вместе с ней лаборатория телемеханики, пережила две реорганизации структуры факультетом института. С 1970-го года по 1980-й год кафедра была в составе факультета оптико-электронного приборостроения, c 1980-го по 1993-й - точной механики и вычислительной техники.
С 1990-го года кафедрой руководит ее воспитанник профессор Григорьев В. В. На время его руководства кафедрой пришлись реформы высшей школы России, кафедра входит в состав факультета компьютерных технологий и управления. На кафедру помимо традиционной подготовки инженеров электриков по специальности 2101.00. — управление и информатика в технических системах возлагается подготовка бакалавров и магистров по направлению 5502.00. — управление и автоматизация. В образовательный стандарт указанных специальности и направления вводится отдельной строкой дисциплина «Прикладная теория информации». Происходит изменение в кадровом составе лаборатории телемеханики, учебный процесс в лаборатории во всей его полноте возлагается на старшего преподавателя Салмыгина И. П. и профессора Ушакова А. В. Лаборатория телемеханики в этот период осваивает возможности программных оболочек ELECTRONICS WORKBENCH 3.0 (EWB 3.0) и EWB 5.0, позволяющих моделировать аналоговые и цифровые устройства автоматики и телемеханики, цифроаналоговые и аналого-цифровые преобразования электрических сигналов, все виды кодовых преобразований, триггеров в любой логике, автоматное представление устройств кодопреобразования в логике Мура и Мили и линейное в любом базисе представления устройств дискретной автоматики и телемеханики и многое другое, для целей адаптации их к задачам дипломного и курсового проектирования, а также перевода лабораторного практикума на технические средства нового компьютерного поколения. Лаборатория в инициативном порядке включается в проведение научных исследований по разработке устройств дискретной автоматики и телемеханики гарантированной информационной надежности с гибким использованием ресурса помехозащиты по Региональной комплексной целевой программе (РКЦП) «ТЕЛЕМЕХАНИКА - 2000», возложенной на НИИ Точной механики (НИИ ТМ) (г. Санкт-Петербург) для модернизации управления стрелочным и инженерным хозяйством метрополитена. В рамках инициативного участия в РКЦП «ТЕЛЕМЕХАНИКА - 2000» в лаборатории под руководством профессора Ушакова А. В. ведутся теоретические разработки проблем анализа и синтеза устройств дискретной автоматики и телемеханики и завершаются диссертационные исследования по проблеме «устройства дискретной автоматики с гибким использованием ресурса помехозащиты» аспирантом кафедры Мельниковым А. А. на соискание ученой степени кандидата технических наук, которые получили одобрение диссертационного совета университета, выразившегося в присуждении советом в 2001-м году ученой степени кандидата технических наук по специальности 05.13.05.-«элементы и устройства вычислительной техники и систем управления» автору исследований.
В 2001-м году сотрудники лаборатории телемеханики предприняли попытку обобщить полученные за последние годы научные достижения, в результате чего свет увидел сборник трудов лаборатории телемеханики под редакцией профессора А.В.Ушакова, объединенных названием «Алгебраические методы в теории устройств дискретной автоматики и телемеханики». Авторами сборника были бывшие и нынешние сотрудники лаборатории: профессор Ушаков А.В., доцент Баев А.П., старшие преподаватели Никифорова Л.Т. и Салмыгин И.П., заведующая лабораториями кафедры Рукуйжа Е.В., а также аспиранты Белоконев Г.В., Мельников А.А., Рассветалова Л. А..
В 2001-м году кафедра автоматики и телемеханики под воздействием сложившихся в научно-техническом сообществе тенденций в модификации терминологии сменила свое название, в результате чего она стала называться кафедрой систем управления и информатики. Одновременно произошли изменения в нумерации направления подготовки бакалавров так, что студенты бакалавриата кафедры систем управления и информатики стали обучаться по направлению 651900 - «автоматизация и управление». Произошли изменения в министерских учебных планах в части распределения дисциплин между подготовкой по «направлению» и «специальности», а также в содержании некоторых дисциплин. Так в учебном плане подготовки специалиста-инженера исчезла дисциплина «Телемеханика» цикла специальных дисциплин СД, но при этом в учебных планах подготовки как бакалавра техники и технологии по направлению 651900, так и специалиста-инженера по специальности 210100 появилась дисциплина «Информационные сети и телекоммуникации (в задачах диспетчерского управления техническими объектами)» цикла федеральных специальных дисциплин СД.Ф. В этой связи кафедра и лаборатория устанавливают творческие связи с Санкт-Петербургской фирмой - «Закрытое акционерное общество: Системы связи и телемеханики (ЗАО ССТМ)», которая появилась на рынке телемеханической продукции в 1994-м году и заявила о себе целой гаммой систем телемеханики и диспетчерского управления, созданной на основе базового комплекта «Телеканал-М», удачно агрегируя телемеханическую аппаратуру прежних поколений с сетевыми телекоммуникационными технологиями типа Ethernet различных скоростных модификаций.
Продолжается научная работа в области анализа и синтеза двоичных динамических систем в составе аппаратуры устройств дискретной автоматики, разработки декодирующих устройств дивидендного типа с коммутируемыми входными цепями, гибридных двоичных динамических систем УДА, обобщением которой является предлагаемая вниманию читателей монография «Двоичные динамические системы устройств дискретной автоматики».
В рамках программы подготовки специалистов высшей научной квалификации успешно ведутся диссертационные исследования докторантом кафедры Мельниковым А.А. по научной проблеме «Концепция гибридности в теории устройств дискретной автоматики», а также аспирантом кафедры Осипцевой О.С. по теме «Синтез законов цифрового дистанционного управления с учетом фактора канальной среды» и соискателем Е. В. Рукуйжей по теме «Дивидендные кодирующие и декодирующие устройства помехозащищенных кодов с коммутируемыми структурами».
Лаборатория телемеханики на настоящий момент представляет собой компактный активный коллектив, полный творческих планов. Лаборатория телемеханики приглашает желающих в аспирантуру и открыта для научного сотрудничества.
220
Выполнить алгоритм 1.1.
Разметить выбранную структурную реализацию передаточной функции Ф(d), для чего выходам элементов памяти с передаточной функцией ФЭП (d) = d в определенном порядке присвоить переменную xt (k), а их непосредственным входам - переменную X(k +.
Из размеченной структурной реализации передаточной функции
ф(d) сконструировать матрицы A,B,С и H векторно
матричного представления линейной ДДС в форме (1.23), (1.24).
¦
Выполнить А1.1, получив передаточную функцию ЛДДС в фор-
^ л M(d) ме Ф(d )=—.
? ' D(d)
Выполнить А1.2, получив матричные компоненты (A, B,C, H) представления ВСВ (1.72).
Выполнить А1.3, получив оценку пynH размерности пересече
ния пространств управляемости и наблюдаемости.
Сформировать k -разрядный ПНЗК на основе мощности [ Q] = Nu заданного массива Q передаваемой или хранимой информации так, что
k = arg{2k >Nu =[Q]} (1.167)
2. Сформировать число m проверочных разрядов, удовлетворяющих требованием к достоверности передачи или хранения информации и к способу реализации корректирующей способности синтезируемого ПЗК.
3. Выбрать неприводимый модулярный многочлен g(X) степени degg(X) = m, удовлетворяющий всем требованиям к корректирующей способности кода [28, 42, 51].
4. Задать m х m -матрицу Г в произвольном базисе
Г = arg {det {X + Г ) = g (X) (1-168)
так, чтобы она обладала характеристическим полиномом g {X).
5. Выбрать матрицу L размерности m х 1, образующую с матрицей Г полностью управляемую пару {Г, L).
В соответствии с постановочной частью задачи конструирования назначаем элементы алфавита Z входа, S состояния и W выхода описания устройства в форме АА и составляем формальную его модель в логике абстрактных автоматов Мура (рисунок 2.1) и автоматов Мили (рисунок 2.2). При этом соответствующие им таблицы правила X перехода и правила 8 выхода запишутся в виде таблиц 2.1 и 2.2.
Сформулировать постановку задачи кодопреобразования, решаемой конструируемой ДДС.
2. Построить вербальную ГСА функционирования ДДС на основе ее словесного описания или анализа временной диаграммы с учетом того обстоятельства, что ГСА является направленным графом [8], использующим вершины трех типов: начальную/конечную операторную, рабочие операторные и условные.
Выполнить п.п.1-2 алгоритма 2.3.
Сконструировать передаточную матрицу-столбец ФЦДУ (d),
описывающую функционирование конструируемой ДДС в форме УДММ, вида
Выполнение п.п. 1-7 алгоритма 2.3, которое дает структурное представление ЦКУ, приведенное на рисунке 2.10
На основе проверочной матрицы H (канонической или модифицированной путем перестановки столбцов или циклической перестановки строк исходной канонической) помехозащищенного кода построить в силу второго уравнения (2.23) с учетом (2.27) таблицу истинности для формирования компонентов П = row{nj; j = n,1 j векторного сигнала п коррекции искажений с ошибками только первой кратности на наборах булевых переменных, определяемых синдромами e = \_Em [Em 1К \E1 ] однократных ошибок.
Памятуя о том, что при формировании проверочной матрицы H ПЗК, способного исправлять искажения с ошибками в s разрядах так, чтобы выполнялось второе векторно-матричное соотношение (2.23) и при этом формировался синдром E (s) равный сумме по mod 2 s синдромов однократных ошибок, сформировать на основе таблицы истинности БФ r/j = nj (E), полученной
выполнением п.1 алгоритма, полную таблицу истинности путем суммирования на все сочетания синдромов однократных ошибок
Сформировать параметр к1 информационной части ПЗК в силу соотношения
Без учета переменных входа UІ = 1,Г.
Выполнить в силу (3.4) кодирование элементов алфавита высокого уровня S состояния АА, для чего воспользоваться п.1 алгоритма 1.11 при выборе образующего многочлена g(х) помехо-
Выполнить п.п.1, 2 алгоритма 2.1 и получить описание функционирования ДДС в форме АА (2.1).
Выполнить кодирование элементов алфавитов высокого уровня Z входа и W выхода АА, полученного в п.1 алгоритма, элементами простого поля Галуа GF (2) так, чтобы размерности кодов получаемого при этом конечного автомата (2.5) и мощности алфавитов Z и W были связаны неравенствами (2.6).
В силу (3.16) и положений определения 3.10 сконструировать матрицу SДДС чувствительности Селлерса булевого описания
произвольной ДДС ее переменных xi, i = 1,п состояния и переменных uk, k = 1,r входа к их вариациям на кодовых переходах.
Вычислить в силу (3.20) и положений определения 3.11 матрицу весов Ps матрицы чувствительности SДДС, сконструированную
выполнением п.1 алгоритма.
в каноническом управляемом базисе (рисунок 1.9)
Рисунок 1.11
Утверждение 1.14 (У 1.14). (Теорема Гамильтона-Кэли). Произвольная квадратная (п х n)-матрица A над простым полем Галуа GF (p) при p = 2 обнуляет свой характеристический модулярный многочлен (ХММ) так, что выполняется равенство
det ( (I + A))=a = О-g A + a.j A + К + am_j A + am I = O ? (1.62)
Доказательство утверждения строится по той же схеме, что и над бесконечным полем F = R действительных чисел [12, 13]. ¦
Утверждение 1.15 (У 1.15). Если характеристический полином матрицы A D(Х) = det (XI + A) степени n входит в разложение дву-
л , л .Г хл +1 п,
члена X + 1, где л= тт< л, : rest--г = 0 1, то матрица A
j [ J det(XI + A)
принадлежит показателю /л в том смысле, что
AM = I. ? (1.63)
Доказательство утверждения строится на факте делимости без остатка двучлена Хл +1 на ХММ D(x) = det (XI + A), который позволяет записать
Хл + 1 = Q(X) det (XI + A) = Q(X) D(x) (1.64)
Выражение (1.64) делает справедливым соотношение
A>‘+1 = Q( A) D( A) = Q( A)det (XI + A)x=a, (1.65)
в котором в силу У 1.14 член det (XI + A)x= A оказывается равным нулю, что доказывает справедливость У 1.15. ¦
Приведем еще одно утверждение, положения которого будут востребованы при решении задачи редуцирования модельного представления линейной ДДС.
Утверждение 1.16 (У 1.16). Любой модулярный многочлен f (x) над простым полем Галуа GF(p) при p = 2 с ненулевым свободным членом, то есть неделящийся без остатка на x, является при некотором целом числе л делителем двучлена 1 + x11, при этом минимальное значение л называется показателем, которому принадлежит f (x). ?
Доказательство утверждения можно найти в [15]. ¦
Нетрудно видеть, что объединение положений У1.15 и У1.16 позволяет сформулировать утверждение, использование которого дает возможность сформировать простую технологию оценки показателя л, которому принадлежит ММ f( x).
Утверждение 1.17 (У1.17). Если сконструировать некоторую квадратную (n х n) матрицу P, где n = degf (x) в сопровождающей
f (x) форме так, что
f(X)= det (XI + P) = D(X), (1.66)
то оценка
Л = arg {pл = I } (L67)
для случая минимального значения л представляет собой показатель, которому принадлежит ММ f (x). ?
Доказательство утверждения строится на непосредственном вычислении р, при котором выполняется равенство Pр = I. ¦
Вернемся к решению проблемы редуцируемости передаточной функции Ф^ )=M (d)/ D(d) на основе сокращаемости ММ числителя M (d) и знаменателя D(d). Математической основой возможной сокращаемости модулярных многочленов над простым полем Галуа является основная теорема арифметики [30] о представлении отличного от нуля целого числа произведением степеней простых чисел. Над конечным полем GF(p) при p = 2 свойствами простого числа обладают
неприводимые многочлены. В этой связи весьма важным является следующее утверждение.
Утверждение 1.18 (У1.18). Если степень р бинома хр +1 представима в форме
р = 2п -1, (1.68)
где р и п положительные целые числа, то в разложении бинома
хр +1 входят все без исключения неприводимые ММ, степени которых, начиная с единицы, являются делителями числа п. ?
Доказательство утверждения можно найти в [15]. ¦
Утверждение 1.18 является эффективным инструментом при редуцировании передаточных функций ф( d) линейных ДДС, решающих
задачи кодопреобразования, в результате которого на выходе ДДС формируется периодическая последовательность y( к) с периодом T. В этом случае в знаменателе передаточной функции ф( d) появляется
бином dT +1, который в силу У1.18 представим произведением неприводимых ММ, что порождает возможность редуцирования Ф(d).
Приведем еще одно утверждение, положения которого могут быть так же полезны в решении задачи редуцирования модельного представления ЛДДС.
Утверждение 1.19 (У1.19). Если степень р бинома хр +1 представима в форме р = 2?, где ? - целое положительное число, то бином хр +1 над простым полем Галуа GF(2) при p = 2 может быть записан в форме
хр + 1 = х2?+1 = ( х? + 1)2. ? (1.69)
Доказательство утверждения сводится к непосредственному вычислению правой части (1.69) с учетом специфики модулярной арифметики по modp = mod2. ¦
Как следствие из У 1.19 становится справедливым положение следующего утверждения.
Утверждение 1.20 (У 1.20). Если степень ц бинома хц +1 представима в форме ц = 2?, где ?- целое положительное число, то этот бином над простым полем Галуа GF(2) при p = 2 может быть записан в виде
хц + 1 = х2 +1 = (х2?І +1)(х2?-2 + і)к (х2 +1). ? (1.70)
Доказательство утверждения строится на использовании У 1.19, позволяющее записать
| ||||||
| V У\ |
Пример 1.4 (Пр1.4)
В качестве примера рассматривается линейная ДДС, преобразующая входную импульсивную последовательность и(k)=д(к) в периодическую последовательность у (к): 11110000 \ 11110000К периода T = 8.
Следуя А1.4 получим передаточную функцию проектируемой ЛДДС в силу определения
ф( d) Y (d) 1 + d + d2 + d3 M (d)
Ф( ) = U(d)= \+d* = Dd)
Задачу редуцирования размерности ф( d) решим с использованием делимости модулярных многочленов, то есть полинома наибольшего
общего делителя M(d)= 1 + d + d2 + d3 и D(d)= 1 + d8 =(1 + d4). С этой целью проверим: не принадлежит ли M(d) показателю ц = 4.
Следуя У 1.17, сформируем матрицу P сопровождающую модулярный многочлен M(d) = 1 + d + d2 + d3 так, что
0 10 0 0 1 111
с целью решения задачи
ц = arg {p ц = I},
которая в своем решении дает ц = 4.
dц +1 = d4 +1
форме
Представим
полином
d4 +1 = (d + 1)M (d) и осуществим редуцирование передаточной функции ф(d) с помощью цепочки равенств
ф(d ) =
M(d)= M(d)
D(d) (1 + d4 ) + d4) (1 + d )M (d) + d4)
Сконструируем структурное представление редуцированной версии проектируемой ЛДДС, которое приведено на рисунке 1.13.
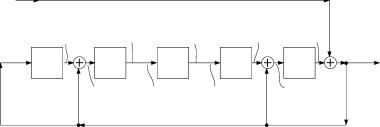 |
| Рисунок 1.13 |
Рассмотрим векторно-матричное В СВ представление ЛДДС х(& + І) = Ах(к) + Ви(к), х(о); у(к)= Сх(к)+Ни(к). (1-72)
В предыдущем разделе исследованы вопросы управляемости и наблюдаемости ЛДДС, записанной в форме (1.23), (1.24) или (1.72) за n тактов ее функционирования, где n = dimx. В случае неполной управляемости и наблюдаемости структура пространства ЛДДС (1.72) разбивается на четыре части, так что вектор состояния линейной ДДС предста-
вим в форме
T I T I T I T
X IX IX IX
ун унн нун нунн
(1.73)
где хуи - управляемая и наблюдавшая чріср, [веупрра состояния х;
унн
управляемая, но ненаблюдаемаі^
( Л-ГІУ‘
[асть х: х,
нун
Heyn^ajj
но наблюдаемая часть х; хиуии - неуправляемая и ненаблюдаемая часть
вектора х. ЛДДС (1.72) с вектором состояния (1.73) структурно представим схемой (рисунок 1Л4).
|
рі ляемая. |  |

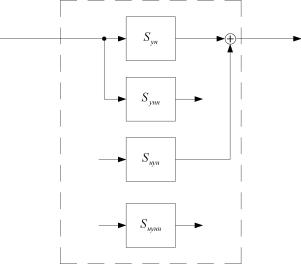 |
| Рисунок 1.14. Структурная схема ЛДДС (1.72) с вектором состояния (1.73) |
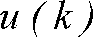
Структурное представление, приведенное на рисунке 1.14, системы, характеризующееся четырьмя перечисленными компонентами вектора состояния, справедливо для систем над бесконечными и конечными полями предложено Р. Калманом [29] и носит название «каноническое представление Р. Калмана». Из приведенного представления видно, что передаточная функция ф( d), как модель «вход-выход» описывает только полностью управляемую и полностью наблюдаемую часть ЛДДС. При вычислении передаточной функции ЛДДС (1.72) в силу соотношения
ф^) = C ( dI + A)-1 B + H (1.74)
должно происходить сокращение сомножителей числителя и знаменателя ММ, которые задействованы для описания неуправляемых и ненаблюдаемых частей ЛДДС. Таким образом размерность передаточной функции ЛДДС в целом, которая совпадает с передаточной функцией ее полностью управляемой и полностью наблюдаемой части, в ее минимизированной после сокращения сомножителей форме определится размерностью пересечения пространства управляемости пары матриц AB ) и пространства наблюдаемости пары матриц (A,C). Для вычисления размерности этого пересечения может быть использован следующий алгоритм.
Алгоритм 1.3 (А 1.3)
4. Построить матрицу Wy управляемости пары матриц (A, B) модели ЛДДС (1.71) в форме
wy = [в|ав|а2 в |а |аП-1 в]. (1.75)
5. Составить матрицу WH наблюдаемости пары матриц (A,C) модели ЛДДС (1.72)
іТ \ ^ л\Т \ I ^ л2 Т Іа і / гілп-1
Wh =
CT i(CA)T j(CA2J \ A j(CAn-1 f] . (1.76)
6. Вычислить размерности пространств L {Wy} управляемости
наблюдаемости L {w T } с помощью соотношений
пу = dim L {Wy }= rank Wy ; nH = dim L {wh }= rank WH (1.77)
7. Вычислить размерность ny^H объединения L {Wy }u L {wht } пространств управляемости и наблюдаемости ЛДДС в силу вы-
Wy! wht
y I H
ражения
rank
yuH
8. Вычислить размерность nynH пересечения пространств управляемости и наблюдаемости L { Wy} n L {wht }
dim {L {Wy } n L {WhT }}= ny + Пн - ny
lynH (¦- (w yV 1 ¦- w H ))~ ,ly^ ,lH ~ ,lyyjH ¦ (1.78)
Практика построения редуцированных модельных представлений линейных ДДС показывает, что наилучший результат решения задачи редуцирования имеет место при комбинировании двух рассмотренных подходов. Это комбинирование позволило сконструировать следующий алгоритм синтеза линейных ДДС редуцированной размерности.
Алгоритм 1.4 (А 1.4)
4. Проанализировать полученное значение nупН, при этом если n, то перейти к выполнению п.9 алгоритма, иначе - к
упН
выполнению п.5.
5. Оценить порядок np = nупН
степень ее редуцируемости np
редуцированной модели ЛДДС и
= n - n у п Н .
6. На множестве ММ степени np найти такой, который входит в разложение полинома числителя M (d) и знаменателя D (d) передаточной функции ф( d) синтезируемой ЛДДС, с целью конструирования Фр (d) передаточной функции ЛДДС размерности
np.
7. Построить структурное представление передаточной функции 4>p, (d) в одном из канонических базисов и разметить его переменными Xj (k) и Xj (k + 1).
8. Построить векторно-матричное ВСВ-представление редуцированной ЛДДС
xp (k +1) = Apxp(k) + Bpu(k)- xp(0);
y(k )= CpXp(k) + H u (k) (I.79)
9. Построить техническую реализацию редуцированной ЛДДС в схемотехнической версии в соответствии со структурным представлением Фр (d) или в программной версии в соответствии с
(1.79). ¦
Пример 1.4 (продолжение)
В продолжение примера 1.4 решим задачу редуцирования с использованием оценки nупН размерности пересечения пространств управляемости и наблюдаемости исходной (A, B ,C, H) модели синтезируемой ЛДДС.
Ф(d ) =
Имеем передаточную функцию устройства
)= Y (d ) = 1 + d + d2 + d3 = M (d)
U(d) = 1 + d8 = D(d) ‘
Выполняем А 1.4 с пункта 2.
2. Строим структурное представление передаточной функции устройства и размечаем ее. В результате указанных действий получаем структурную схему, представленную на рисунке 1.15.
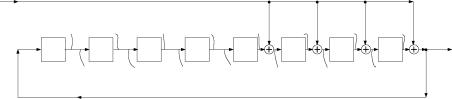 |
| Рисунок 1.15 |
A = O
| По отмеченной А,В,С,Н | |
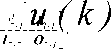 | В = |
C = \oL \I 1x1 ]
Н = [1].
3. Выполняем А1.3 с использованием пакета Matlab 6.5. В резуль
тате находим np = n
у^н
4. Выполняем п.п.4,5 и находим, что величина уменьшения раз-
мерности пр оказывается равной трем, то есть .
5. Находим общий делитель/ jd^dj)j= 1 + d + d2 + d3, что приводит к редуцированной передаточной функции ЛДЬС вида
0p(d) = (l + d + d4 + а5У^
6. Строим структурную схему полученной передаточной функции
и осуществляем ее разметку (рисунок 1.13). X ( k^~ 1)
7. Строим по размеченной структурной схеме (рисунок І.ЬІувек- 7 торно-матричное В СВ-представление (1.79) редуцированной ЛДДС, матрицы которой принимают вид

| ар = |
|
в теории линейных двоичных динамических систем
Концепция подобия в теории динамических систем над бесконечными полями получила в последнее время заметное распространение при решении широкого круга задач управления [5, 35, 40, 48, 53]. В рамках векторно-матричного формализма метода пространства состояний в непараметризованной временем форме концепция подобия сводится к выполнению соотношения
П = M х. (1.80)
В параметризованном временем виде соотношение (1.80) достигается в асимптотике так, что
П(Т) = Mх(т)-?(т), (1-81)
при этом
Ііт?(т)= 0 ?х(0\ц(0). (1.82)
Т——х>
В (1.80) - (1.82) х - вектор состояния некоторого эталонного динамического процесса, п - вектор состояния конструируемой динамической среды, dimn = m, dimх = Х, M - (m x X) - матрица в общем случае
особого [12] преобразования подобия; т - принимает смысл непрерывного времени t ( т = t) в непрерывных по времени процессах и смысл
дискретного времени к (т = к), выраженного в числе интервалов дискретности длительности д t так, что t = к д t, в дискретных по времени процессах, ? - вектор невязки выполнения векторно-матричного подобия, задаваемого в форме
П(т) = M х(т); ?Х( 0 \п( 0), (1.83)
Если на асимптотически сходящемся процессе (1.82) можно указать т* такое, что при т>т* соотношение (1.83) выполняется «почти точно»,
то т* следует называть временем установления векторно-матричного подобия (1.83). В технической среде достижение векторно-матричного подобия (1.83), обеспечиваемого путем выполнения условия (1.82), реализуется в виде связей по вектору состояния п и части компонентов вектора состояния х так, что математическая модель по вектору невязки ? представляет собой автономную систему, которая для непрерывного времени имеет вид
?&і)= Л??(і); ?(0)= Mх(т)- п(0), (1.84)
и
?(к +1) = Л??(к); ?(0)= Mх(т)- п(0), (1.85)
для дискретного времени. Указанные связи должны быть выбраны так, чтобы процессы в (1.84) и (1.85)
0(t)= eА?1в(0); ?(к)= А?к ?(0), (1.86)
сходились за назначенное время т*. Для процессов с непрерывным временем матрица А? должна быть гурвицевой, для процессов с дискретным временем матрица А? должна иметь собственные значения в единичном круге [5, 48].
К схеме (1.81), (1.84), (1.85) сводится задача регулирования [31] в форме модального управления [48, 53], задача слежения за конечномерным экзогенным воздействием [5, 48, 31, 52], задача динамического наблюдения [5, 35, 48]. К этой же схеме сводятся задачи адаптивного управления [40]. Для случая единичной матрицы преобразования подобия (М = I), когда отношение подобия превращается в отношение
тождественного равенства, разработаны методы решения обратных задач динамики [34].
Следует ожидать, что перенос концепции подобия на динамические системы над конечными полями, частным случаем которых являются двоичные динамические системы, заметно обогатит алгоритмическое обеспечение синтеза как линейных, так и нелинейных ДДС (конечных автоматов). Следует заметить при этом, что обеспечение условия вида (1.82) опирается на особые свойства матриц над конечным полем Галуа GF(p) при p = 2 [37]. Часть этих свойств представлены в разделе 1.3.1. Этими свойствами являются: свойство обнуления произвольной квадратной m х m -матрицей с элементами из конечного поля Галуа GF(p) при p = 2 своего характеристического полинома (Теорема Гамильтона-Кэли над конечным полем Галуа GF(p) при p = 2) в форме (1.62); свойство принадлежности квадратной m х m -матрицы с элементами из конечного поля Галуа GF(2) показателю р в форме (1.63).
Для целей дальнейших исследований введем в рассмотрение еще одно свойство матриц над конечным полем Галуа GF (2).
Свойство 1.1 (СВ1.1). (Нильпотентность индекса ?матрицы А). Квадратная (m х m) -матрица А с элементами из GF(2) обладает
свойством нильпотентности индекса ? если выполняется условие
А = O. ? (1.87)
Утверждение 1.21 (У1.21). Для того чтобы (m х m)-матрица А с элементами из конечного поля Галуа GF(2) обладала свойством СВ1.1 достаточно, чтобы матрица А обладала нулевым корнем кратности ? при этом ее каноническое представление имело вид
Доказательство утверждения строится на свойстве матричной функции от матрицы сохранять отношение подобия. Действительно, если существует (m х m)- неособая матрица М преобразования подобия такая, что выполняется матричное соотношение
A = MAV M-1, (1.89)
тогда по указанному свойству выполняется и соотношение
f( A)= M f ( A,.)M. (1.90)
Если в качестве f(A) выбрана функция от матрицы f(A)= Av, то соотношение (1.90) примет вид
AX = MAVM-1, (1.91)
но AV при X=v в силу представления (1.88) обнуляется:
O(y-j)x(m-v+l) ! I(v-1)x(v-1)
(1.88)
Av =
O,
(.m-v+1)x(1.92)
AV = O,
что приводит к выполнению (1.87) в силу (1.91). ¦
1.5.1 Концепция подобия в задаче динамического наблюдения состояния произвольной линейной ДДС
Пусть линейная ДДС, состояние которой подлежит наблюдению, имеет векторно-матричное описание
Х(к + j)= A х(к) + Bu (к), x(0)=Xo, ;(k)= C x(k), (ОЗ) где х,иД - соответственно n-мерный вектор состояния, r-мерный вектор входной последовательности и X -мерный вектор выходной последовательности, матрицы A ,B ,C согласованы по размерности с векторами х, и и ; . Элементы векторов и матриц принадлежат двоичному простому полю Галуа GF (2).
Двоичное динамическое наблюдающее устройство (ДНУ), использующее всю доступную для непосредственного измерения информацию об ДДС (1.93) в виде входной последовательности и (к) и выходной - у (к), строится в форме
z (к +1)= Г z (к) + L;( к) + G и( к), z (0)= z0, (1.94) где z - m -вектор состояния ДНУ, матрица Г определяет динамику процесса наблюдения в форме (1.82), а пара матриц (L,G) обладает свойствами
L = arg {contr(Г,L)}, G = arg {contr(r,G)}, (1.95)
где contr {(*),(•)} - предикат наличия полной управляемости пары матриц {(*),(•)}.
Задачу наблюдения вектора х состояния системы (1.93) в среде ДНУ (1.94) сформулируем в форме (1.81), записываемой в виде
z(k) = T х(к) + ?(к), V к, (1.96)
где T - матрица преобразования подобия (в общем случае - особого). Уравнение (1.96) позволяет построить модель процесса наблюдения по вектору невязки наблюдения, которое принимает вид
?(к + ]) = T х( к + ]) + z (к + ]). (1.97)
Структурная модель процесса двоичного динамического наблюдения в форме (1.97) в соответствии с моделями (1.93) и (1.94) представлена на рисунке 1.16.
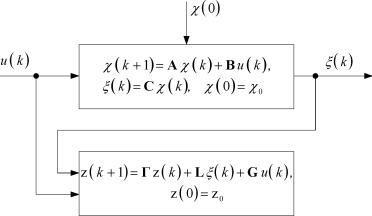 |
| Рисунок 1.16. Модель процесса двоичного динамического наблюдения состояния произвольной ЛДДС |
Утверждение 1.22 (У 1.22). Если матрицы T, L,G удовлетворяют матричным соотношениям
ГТ +TA = LC, G = TB, (1.98)
то процесс по вектору невязки наблюдения (ВНН) ?( к) описывается рекуррентным векторно-матричным уравнением
?(к + ]) = Г ?( к), ?( 0) = Tx( 0)+ z (0). ? (1.99)
Доказательство утверждения строится на подстановке в (1.99) векторно-матричных соотношений (1.93) и (1.94), в результате чего получим
?(к + ]) = Г?(к)+(TA + ГT + LC)х(к)+(TB + G)и(к). (1.100) Если в (1.100) подставить (1.98), то приходим к (1.99). ¦
Модель процесса двоичного динамического наблюдения в форме процесса по ВНН (1.99) позволяет сформулировать требования к матричным компонентам наблюдаемой ДДС (1.93) и ДНУ (1.94), которые позволят обеспечить все возможные задачи наблюдения.
Так если ставится задача наблюдения вектора х(к) текущего состояния ДДС (1.93), то следует воспользоваться явным (показательным) решением (1.99), записываемым в форме
?(к)= Гк ?(0); ?(0) = Тх(0)+ z(0). (1.101)
Следует заметить, что при нормальном использовании ДНУ его состояние при запуске обнуляется так, что z (0)= 0 . С учетом этого обстоятельства (1.101) принимает вид
?(к) = Гк Tх(0). (1.102)
В свою очередь подстановка (1.102) в (1.96) дает
z(k)= Тх(к)+ Гк ?(0). (1.103)
Потребуем от матрицы Г состояния ДНУ обладания свойством нильпотентности с индексом ?, тогда при к >? устанавливается равенство
z (к )= Т х( к), к >?. (1.104)
Таким образом, вектор z (к) состояния ДНУ с точностью до матрицы преобразования подобия Т задает текущее состояние вектора х(к) наблюдаемой ДДС (1.93). Заметим, что подобие (1.104) можно
преобразовать в тождество, если в матричное уравнение Сильвестра
(1.98) положить Т = I, где I - единичная матрица, и решить уравнение (1.100) относительно матрицы L.
Поставим теперь задачу наблюдения вектора Х( 0) начального состояния наблюдаемой ДДС (1.93). Для этого потребуем, чтобы матрица Г принадлежала показателю ц так, что Гц = I. В этом случае при к = ц соотношение (1.102) примет вид
z (ц)= Т х(ц) + ?( 0 ) = Т х(ц)+ Т х( 0). (1.105)
Дополним ситуацию еще одним условием, для чего предположим, что наблюдаемая ДДС (1.93) представляет собой регистр сдвига, функционирующий при и (к ) = 0 и х( 0 )^ 0. Если учесть, что показатель ц удовлетворяет неравенствам
п <ц< 2п -1, (1.106)
то к моменту к = ц (1.105) примет вид
z (ц)= Т х( 0). (1.107)
Таким образом (1.107) обнаруживает результат, который не достигается над бесконечными полями. Если наблюдаемая ДДС (1.93) представляет собой регистр сдвига размерности п с нулевой входной последовательностью и (к)= 0 и ненулевым начальным состоянием х(о), а двоичное наблюдающее устройство (1.94) таково, что его матрица Г состояния принадлежит показателю ц, то в силу выполнения (1.107) состояние z(к) ДНУ при к = ц является синдромом состояния Х(о )•
Выделим еще одну постановочную версию задачи наблюдения состояния ДДС (1.93), предположив, что входная последовательность и (к) формируется с помощью конечномерной автономной ДДС.
%(к +і) = R?( к); ?( 0) = &; и( к)= S?( к). (1.108)
Соотношения (1.108) задают источник входной последовательности (ИВП) и (к).
Объединим системные компоненты - наблюдаемая ДДС (1.93), ДНУ (1.94) и ИВП (1.108), - процесса наблюдения, охарактеризовав
его агрегированным вектором состояния X = \ zT, ХТ ,%T ^ . Тогда динамика системы с агрегированным вектором X описывается автономной ДДС
Х(к + і)= А х(к), Х(о )=\?Т (о ),XT (о),?(о ^
(1.109)
(1.110)
где матрица A имеет представление
Г LC GS О A BS
О О R
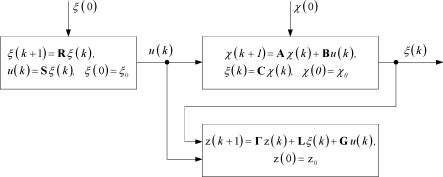 |
| Рисунок 1.17. Структурное представление модели (1.109) процесса двоичного динамического наблюдения |
Для системы (1.109) явное решение х( k) в показательной форме
принимает вид
x(k) = A х(0). (1.111)
С целью покомпонентного вычисления (1.111) сформулируем утверждение.
T ( nR k + А k П )
ЖЯk + Ak П
Rk
Утверждение 1.23 (У 1.23). Показательная матричная функция Л1 матрицы Л вида (1.110) представима в форме
гk гk 'г + 'г_/A.k
(1.112)
0 Аk
0 0
где матрица T удовлетворяет матричному уравнению Сильвестра
(1.98) , а матрица Л - матричному уравнению Сильвестра
ПR + ЛП = BS . ? (1.113)
Доказательство утверждения осуществляется на замене матричных членов LC и BS в представлении (1.108) матрицы Л, являющихся правыми частями уравнений Сильвестра (1.98) и (1.113), на их левые части, а так же подстановке второго матричного соотношения
(1.98) в (1.108) так, что становится справедливым матричное равенство
GS =TBS. (1.114)
После проведенной модернизации представления (1.108) матрицы Л осуществляется конструирование базы индукции степеней матрицы Л , что приводит к (1.112). ¦
Если теперь в агрегированном векторе х выделить векторный компонент z, представляющий собой вектор состояния ДНУ, то в силу (1.111) и (1.112) для него можно записать
z (k) = Г kz (0)+(rk T + ТЛk )х( 0)+ T (л Rk + Л k л)^(0). (1.115) Выражение (1.115) обнаруживает все богатство решений задач двоичного динамического наблюдения, рассмотренных выше на основе частных композиций начальных состояний и свойств матричных компонентов.
Пример 1.5 (Пр1.5)
Пусть требуется синтезировать ДНУ для наблюдения вектора состояния ДДС, Л, B ,C, H -описание которой имеют вид
| "0 1 0 | "0" | ||
| Л = | 0 0 1 | , B = | 0 |
| 1 1 0 | 1 |
H = [ 0].
С целью решения поставленной задачи в соответствии с (1.103) и (1.104) выберем в качестве модели ДНУ регистр сдвига третьего порядка, матрица Г ВМ описания которого будет иметь следующий вид
0 1 0 0 0 1 000
к >?, для чего
Решим поставленную задачу в форме z (к )= х( к),
в силу (1.104) выберем матрицу T в форме T = I. Решение уравнения Сильвестра (1.98) относительно матрицы L и вычисление матрицы G дает
L = [001], G = [001] .
В силу (1.104) и того, что матрица Г имеет индекс нильпотентности, равный трем, то, очевидно, что начиная с момента к > 3 вектор состояния z ДНУ должен будет совпасть с вектором состояния х исходной ДДС. Покажем это, полагая, что входная последовательность и (к) ДДС на первых семи тактах имеет вид и (к): 1001010 , а начальное состояние х(0) ДДС определяется вектором х(0)= [011] .
Таблица 1.1
| к | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| и (к) | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 |
| хт (к) | 011 | 110 | 100 | 001 | 011 | 111 | 111 | 110 |
| zT (к) | 000 | 000 | 000 | 001 | 011 | 111 | 111 | 110 |
| и | 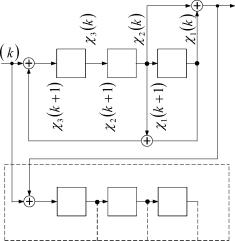 |
|
і і і z3(к) Z2(к) z1(к) Рисунок 1.18. Структурное представление процесса двоичного динамического наблюдения |
Из таблицы 1.1 видно, что начиная с третьего такта, то есть с выполнением условия к = 3, вектор состояния z синтезированного ДНУ повторяет в форме z(к) = х(к) состояние х(0) наблюдаемой ДДС.С использованием полученных результатов структурно-функциональная схема процесса двоичного динамического наблюдения вектора состояния заданной ДДС примет вид, как показано на рисунке 1.18.
Из таблицы 1.1 видно, что начиная с третьего такта, то есть с выполнением условия к = 3 , вектор состояния z синтезированного ДНУ повторяет в форме z(к) = х(к) состояние х(0) наблюдаемой ДДС.С использованием полученных результатов структурно-функциональная схема процесса двоичного динамического наблюдения вектора состояния заданной ДДС примет вид, как показано на рисунке 1.18.
1.5.2 Концепция подобия в задаче декодирования систематических помехозащищенных кодов
Задачу декодирования систематических помехозащищенных кодов, подвергшихся воздействию на функциональном и модельном уровнях, зададим следующим образом. Кодирующее устройство (КУ) на выходе которого формируется (n, к)-помехозащищенный код у, выводимый в
канал связи в виде двоичной кодовой последовательности у(к), старшим разрядом вперед, представляется n -разрядным регистром сдвига, начальное состояние которого х( 0) представляет собой передаваемую
помехозащищенную кодовую посылку. Векторно-матричное модельное представление КУ имеет вид
х(к + 1)= Fх(к); x(в); у(к) = Px(к), (1.116)
где F - матрица размерности (n х n) является нильпотентной с индексом нильпотентности ? равным n так, что ? = n. Формирователь импульсной помехи f, которая в канале связи (КС) искажает передаваемую кодовую посылку у, также представим n -разрядным регистром сдвига, который будем именовать регистром канала связи (РКС). РКС характеризуется нулевой входной последовательностью и вектором начального состояния х(0), который представляет собой n -разрядный вектор помехи f, выводимый в КС в виде последовательности f( к) старшим разрядом вперед. Векторно-матричное описание РКС имеет вид
х(к +1)=Ах(к);х(0); f(к)=Cх(к). (1.117)
Матрица A совпадает с матрицей F и так же является нильпотентной с индексом нильпотентности ? = n .
Процесс искажения кодовой последовательности у( к), при передаче по КС представим суммированием в простом двоичном поле GF (2), в результате чего формируется искаженная кодовая комбинация f = у + ?, в виде кодовой последовательности
/(k) = У( k) + Z{k). (1.118)
Процесс декодирования реализуем в форме построения ДНУ, формирующего к моменту к = n состояние z(n), которое с точностью до
матрицы преобразования подобия представляло бы собой вектор х( 0) начального состояния РКС. Векторно-матричное описание ДНУ - декодирующего устройства (ДКУ) принимает вид
z (к + 1) = Г z ( k)+ L / ( к); z ( 0), (1.119)
а структурное представление процесса декодирования - так, как показано на рисунке 1.19.
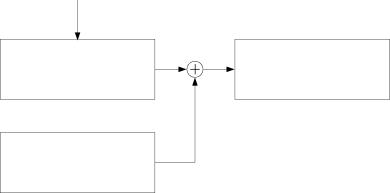 |
| Рисунок 1.19. Структурное представление двоичного динамического наблюдения начального состояния регистра канала связи |
Утверждение 1.24 (У1.24). Вектор z(к) состояния ДКУ, построенного по структуре двоичного наблюдающего устройства для наблюдения векторов x(0) и х(0), задается соотношением
z (к )= Г kz (0)+(rx A к + Гк Tx)z( 0)+(tx Fк + Гk Tx )x (0), (1.120) где матричные компоненты Тх и Tx вычисляются как решение матричных уравнений Сильвестра
Тх A + ГТХ= LC, Tx F + ГТХ = LP. ? (1.121)
Доказательство утверждения ведется по той же схеме, что и доказательство У 1.23. В рассмотрение вводится агрегированный вектор
z = [zT,zT.xT f. (1.122)
Вектор (1.122) подчиняется рекуррентному векторно-матричному уравнению
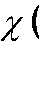
(1.123)
|
z(к + l) = Гz(к); z(0)=[zT (0),xT (0),xT (0)f, явное решение которого в показательной форме имеет вид z (к ) = Г к z (0). В (1.123) и (1.124) матрицы Г и Гк имеют вид | |||||||||||||||||||||
| (1.125) |
Подстановка Гк из (1.125) в (1.124) и выделение из z(к) компонента z(k) приводит к (1.120). ¦
В стандартной постановке задачи декодирования [51] сформированный ДКУ синдром ошибки представляет собой образ вектора начального состояния х(0) РКС, формируемого с помощью матрицы преобразования подобия Т?. В этой связи выясним при каких условиях
А
и свойствах матричных компонентов соотношения (1.120) последнее вырождается в соотношение вида (1.107), записываемое в форме
1 к •)= Tzx( 0). (1.126)
Решение поставленной задачи получим с использованием положений следующего утверждения.
Утверждение 1.25 (У1.25). Если ДНУ начального состояния х(0) функционирует так, что всегда z (0 ) = 0, то есть перед запуском его состояние обнуляется, матрица Г принадлежит показателю ц = п,
матрицы A и F обладают индексом нильпотентности ? = п, матрица преобразования подобия Tx обладает свойством
Tx GТ = O. (1.127)
где G - образующая матрица систематического кода [51], то выполняется соотношение векторно-матричного подобия
z ( п ) = Тгх( 0). ? (1.128)
Доказательство утверждения строится на определениях свойств нильпотентности матрицы и принадлежности матрицы показателю, а так же на использовании условия z( 0) = 0, что приводит (1.120) к виду
z(n)= Тх х(0)+ Т,ж(0). (1.129)
Напомним, что вектор x(0) формируется из информационной части хи (0) систематического помехозащищенного кода с помощью образующей матрицы G кода в силу соотношения
х(0)= G ТХи (0). (1.130)
Если (1.130) подставить в (1.129) и учесть (1.127), то получим (1.128). ¦
Следует заметить, что в силу (1.127) матрица Tx как решение матричного уравнения Сильвестра (1.121) является проверочной матрицей [51 ] систематического кода.
Пример 1.6 (Пр1.6)
В качестве примера рассмотрим аналитику решения в виде (1.130) задачи конструирования декодирующего устройства в форме ДНУ
циклического кода с образующим многочленом g (x) = x3 + x +1.
Сконструируем ДКУ в форме ДНУ и кодирующее устройство в виде модельных представлений «вход-состояние-выход» с матричными компонентами
6x6
T
O7
C = P =[l jO6T]
соответственно.
Решение относительно матрицы T матричного уравнения (1.97) дает
1110 10 0 0 1110 10 110 10 0 1
Следует заметить тождественность результата для вычисленной матрицы T каноническому [51] представлению проверочной матрицы H циклического кода, который в рассматриваемом примере соответствует образующему многочлену g (x )= x3 + x + 1, которая имеет вид
| H = |
| T |
матрицы TT на вектор начального состояния х( 0) РКС. Нетрудно видеть, что в силу равенств матриц T и H T , процесс декодирования циклических кодов полностью совпадает с классическим его представлением. Структурная схема процесса декодирования циклического кода с образующим многочленом g(x) = x3 + x + 1 представлена на рисунке 1.20. ¦
X 7 (0) Хб (о) X 5 (0) X 4 (0) Хз (о) X 2 (0) X! (о)
|
1 X2 (0) 1 |  |
x(0)
| T | |||||||
|
X5 (0) 4 | ||||||
| d |
X3 (0)
-•Ф* d ¦*0-» d -*©-*¦ d ¦*©¦•> d -*©-•> d -*©-*- d -*©¦
ДНУ
Z3 (k)
Z2(k) Zi (k)
f (k)
¦€>
*©-
Рисунок 1.20. Структурное представление процесса декодирования
циклического кода
1.5.3 Концепция подобия в задаче синтеза двоичных динамических систем в логике произвольных линейных триггеров
Решая поставленную задачу, следует отметить, что банк линейных триггеров состоит из D- и T- триггеров при этом так, как передаточная функция элемента памяти (ЭП), выполненного в виде D- триггера, характеризуется передаточной функцией
Фв эп( d) = d, (1.131)
а в виде T- триггера - характеризуется передаточной функцией
Фт эп (d ) = 1Ld, (1.132)
1 + d
то векторы состояний ДДС, имеющих D- и T- триггерную реализацию, оказываются связанными отношениями подобия
xT (к)= M xD (к), Vк . (1.133)
Пусть в результате синтеза ДДС, решающей задачу преобразования входной последовательности и (к) в выходную у (к), получена D-триггерная реализация системы, имеющая векторно-матричное представление
xD (к + 1) = ADxD (к) + BDu (к), yD (к )= CDxD (к)+ Н и (к). (1.134) Требуется, опираясь на условие векторно-матричного подобия (1.133), построить T- триггерную реализацию системы
xT (к + 1) = AT xT (к)+ BTu(к), ут (к )= CTxT (к)+ Ни (к), (1.135)
решающую ту же задачу кодопреобразования. Поставленную задачу решим, опираясь на следующие утверждения.
Утверждение 1.26 (У 1.26). Матричные компоненты векторноматричных представлений (1.134) и (1.135) ДДС, решающих одну и ту же задачу кодопреобразования входной последовательности и (к) в выходную у (к), связаны соотношениями
AT = MAd M-1, (1.136)
BT = MBD, CT = CD M-1. ? (1.137)
Доказательство утверждения строится на использовании (1.133), которое должно выполняться для ?к, а потому оказывается справедливой запись
xT (к + l)= M xD (к + l), Vк . (1.138)
Подстановка в (1.138) соотношений (1.134) и (1.135) приводит к справедливости (1.136) и первого соотношения в (1.137). Второе соотношение в (1.137) получается после подстановки (1.133) в выражение для выходной последовательности у (к) в (1.135). ¦
Утверждение 1.27 (У1.27). Матричное условие подобия (1.136), записанное в форме
MAd = ATM, (1.139)
представимо в виде неоднородного матричного уравнения Сильвестра
M Ad + AT M = BT Ld , (1.140)
где dim AD = dim AT, (AD, Ld) - полностью наблюдаемая пара матриц [4], (AT, BT) - полностью управляемая пара матриц, алгебраические спектры собственных значений матриц AD и AT не пересе-
каются, то есть c{Ad At }=0, размерности матриц BT, LD
согласованы в силу соотношения dim BT = dim LD. ?
Доказательство утверждения строится на представлении матрицы At в форме
At = At + BT NT, (1.141)
где матрица NT допускает представление
NT = Ld M-1. (1.142)
Выражение (1.142) допускает эквивалентное представление
Ld = NT M. (1.143)
Подстановка (1.143) в (1.140) с учетом (1.141) приводит к (1.139). ¦
Утверждение (У 1.27) является основой следующего алгоритма синтеза ДДС в логике T- триггеров.
Алгоритм 1.5 (А 1.5)
конструирования двоичных динамических систем в логике произвольных линейных триггеров
10. Выполнить А1.2, получив представление линейной ДДС в форме (1.138).
11. Назначить произвольные матрицы At, Bt и LD, удовлетворяющие условиям У 1.30.
12. Решить матричное уравнение Сильвестра (1.140) относительно матрицы подобия M и вычислить матрицу M_1.
13. Сконструировать матричные компоненты T-триггерной реализации линейной ДДС (1.138) с помощью соотношений (1.136) и (1.137). ¦
Следует отметить, что так как нелинейные ДДС, именуемые конечными автоматами, имеют линейные аналоги, то, как представляется авторам, концепция подобия может быть распространена и на этот класс ДДС.
Пример 1.7 (Пр1.7)
Построить для декодирующего устройства циклического кода с образующим многочленом g(x) = x3 + x +1 модельное представление ДДС в логике линейных T-триггеров.
1. Выполнение п.1 А1.5 формирует модельное «вход-состояние-выход» представление декодирующего устройства с матричными компонентами
CD =[1 0 0], H = [1].
| "0 1 0" | "0" | |
| 1 0 1 | , BD = | 1 |
| 1 0 0 | 1 |
| "1 | 1 | 0" | "0" | |
| 0 | 1 | 1 | , BT = | 0 |
| 0 | 0 | 1 | 1 |
3. Выполнение п.3 алгоритма, состоящее в решении матричного уравнения Сильвестра (1.138) относительно матрицы подобия M, приводит к матрице
| соответственно. |
| "1 | 1 | 0" | "0" | |
| 0 | 1 | 1 |
; Bt = | 1 |
| 1 | 0 | 0 | 0 |
Структурное представление векторно-матричного описания искомой ДДС с полученными компонентами AT ,BT ,CT имеет вид, как показано на рисунке 1.21. ¦
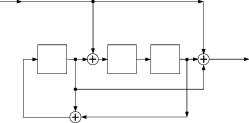 |
| Рисунок 1.21 |
линейного помехозащитного кодопреобразования,
непараметризованное дискретным временем.
Методы формирования матриц помехозащищенных кодов
Процесс линейного помехозащитного кодопреобразования как в фазе кодирования, так и в фазе декодирования [15, 42, 55, 51] как частный случай линейного кодопреобразования имеет три модельных представления, приведенных в параграфе 1.1. В данном параграфе используется векторно-матричное представление линейного помехозащитного кодопреобразования, непараметризованное дискретным временем, при этом особое внимание обращается на методы формирования образующей и проверочной матриц помехозащищенного кода (ПЗК).
Полная схема, описывающая процесс кодирования, состоящий в преобразовании исходного помехонезащищенного кода в помехозащищенный, его передачу по двоичному каналу связи, сопровождающуюся искажением помехозащищенного кода, и процесс декодирования принятого из КС кода с целью формирования кода синдрома (опо-знавателя) внесенной при передаче ошибки (искажения), приведена на рисунке 1.22.
| - | f=у+4, | E ( | |
На рисунке 1.22: КУ - кодирующее устройство; КС - канал связи, искажение в котором моделируется сумматором по модулю два помехозащищенного кода и кода ошибки; ДКУ - декодирующее устройство, формирующее синдром ошибки; a - вектор-строка исходного помехонезащищенного кода, dim a = к; у - вектор-строка помехозащищенного (n, к)-кода, наблюдаемого на выходе КУ, dim у = n, n > к, m = n - к - число вводимых избыточных разрядов кода у; 4 - вектор-строка помехи, воздействующей на КС, dim 4 = n ; f = у + 4 - вектор-строка искаженного кода, принимаемого из КС; E - вектор-строка синдрома ошибки (искажения) в принятой из КС кодовой комбинации, dim E = m .
Процесс формирования вектор-строки помехозащищенного кода у из вектор-строки помехонезащищенного кода a, осуществляемый в КУ, может быть описан линейным векторно-матричным соотношением
у = aG, (1.144)
где G - (к х п)-матрица, именуемая образующей матрицей [42, 51] помехозащищенного линейного кода у .
Процесс искажения передаваемой кодовой комбинации у в канале связи под действием помехи % такой, что на выходе КС формируется вектор-строка искаженного кода f, может быть представлен операцией суммирования
f = У + %, (1-145)
соответствующих вектор-строк.
И, наконец, процесс декодирования, состоящий в формировании вектор-строки синдрома (опознавателя) E из вектор-строки принятого из КС искаженного кода f может быть описан векторно-матричным соотношением
E = fH, (1.146)
где H - (к х п)-матрица, именуемая проверочной [42, 51] матрицей помехозащищенного кода у .
Заметим, что все операции умножения и суммирования в соотношениях (1.144) - (1.146) и ниже осуществляются по правилам модулярной арифметики с модулем два (mod 2).
Выясним: какими свойствами должна обладать пара матриц (G, H)
с тем, чтобы она порождала помехозащищенный код?
С этой целью сформулируем утверждение.
Утверждение 1.28 (У1.28). Матрица G, принятая за образующую матрицу, и матрица H, принятая за проверочную матрицу, порождают помехозащищенный код, если они удовлетворяют матричному соотношению
GH = O. ? (1.147)
Доказательство утверждения строится [42] на использовании соотношений (1.146), (1.145) и (1.144). Если в (1.146) подставить (1.145), в котором учесть (1.144), то получим цепочку равенств
E = f H = (у + %)H = ( a G + %) H = a GH + %H. (1.148)
Напомним, что декодирующие устройства помехозащищенных кодов, построенные в прямой логике, функционируют так, что при отсутствии ошибки в принятой кодовой комбинации декодирующее устройство формирует нулевой синдром, а в случае наличия ошибок, для обнаружения или исправления которых осуществлено помехозащитное
кодирование, ДКУ формирует соответствующий ненулевой синдром. Таким образом ДКУ реализует соотношение
E = E(#)|{_ = O, E = E({)\(t0 *O. (1.149)
Если теперь в (1.148) положить ? = 0, то в силу первого из соотношений (1.149) получим векторно-матричное равенство
E = aGH = O, (1.150)
выполняемое при любых вектор-строках исходного кода a, что доказывает справедливость утверждения. ¦
Примечание 1.1 (ПМ1.1). Следует заметить, что характеристическое свойство (1.147) матриц ПЗК не нарушается при перестановке строк образующей матрицы G и столбцов проверочной матрицы H. При перестановке столбцов матрицы G для сохранения (1.147) необходима согласованная перестановка строк матрицы H . ?
Нетрудно видеть, что соотношения (1.147) - (1.149) содержат доказательство следующего утверждения.
Утверждение 1.29 (У1.29). Процедура формирования синдрома E имеет два эквивалентных представления (1.145) и
E = ?H . ¦ (1.151)
Следует заметить, что векторно-матричные представления (1.146) и (1.149) имеют различную нагрузку и среду реализацию. Первое используется в аппаратурной среде, а второе - в аналитической при формировании проверочной матрицы H помехозащищенного кода.
Заметим так же, что доказательство У 1.28 делает справедливым положения следующего утверждения.
Утверждение 1.30 (У 1.30). Пара матриц (G,H) размерности
dim G = к х n и dim H = n х m, удовлетворяющие матричному соотношению (1.147), принятые соответственно за образующую и проверочную матрицы кода, порождают помехозащищенный (n, к)-код, характеризующийся корректирующей способностью, определяемой мощностью [{E}] множества {E} ненулевых синдромов, задаваемой в силу (1.149) соотношением
[{E}]= 2m - 1. ¦ (1.152)
Поставим теперь задачу конструирования алгоритмов формирования образующей G и проверочной H матриц помехозащищенного кода. Эта задача не инвариантна относительно требований к блоковой систематике формируемого помехозащищенного кода. В связи с этим введем следующие определения.
Определение 1.8 (О1.8). Систематическим помехозащищенным кодом называется код, элементы которого представляют собой комбинации элементов исходного помехонезащищенного кода. При этом ПЗК называется линейным, если эти комбинации строятся на основе линейных бинарных операций модулярной арифметики, и нелинейным, если комбинации строятся на основе нелинейных бинарных операций модулярной арифметики. ?
Нетрудно видеть, что ПЗК, сформированные в силу правила (1.144), являются систематическими и линейными, при этом вся систематика помехозащищенного линейного кода у заложена в образующей матрице G.
Определение 1.9 (О1.9). Систематический ПЗК называется систематическим помехозащищенным кодом с полной блоковой систематикой, если проверочные разряды кода, вводимые в структуру ПЗК процедурой кодирования, и информационные разряды, образованные исходным помехонезащищенным кодом (ПНЗК) а, представляют собой отдельные монолитные блоки. ?
Следует заметить, что в современной телекоммуникационной технике, в которой преобладает передача кодов «старшим разрядом вперед», в ПЗК с полной блоковой систематикой исходный ПНЗК образует старшие разряды кода, а блок проверочных разрядов - младшие его разряды.
Определение 1.10 (О1.10). Систематический ПЗК называется кодом с неполной блоковой систематикой, если разряды исходного ПНЗК и проверочные разряды ПЗК перемежаются, не образуя монолитные блоки. ?
С целью конструирования алгоритмов формирования матриц G и H ПЗК сформулируем дополнительно следующее утверждение.
Утверждение 1.31 (У1.31). Если помехозащищенный код исправляет ошибки кратности у = 1,s, то синдром E jY ошибки ;jY в у разрядах для j -ой их комбинации j = 1,С% равен сумме по модулю два у строк И1 ,i = 1,n проверочной матрицы H однократных ошибок, сумма которых образует данную ошибку ;jY. ?
Доказательство утверждения строится на использовании соотношения (1.149), в котором вектор-строку синдрома E, вектор-строку ошибки ; следует писать в поэлементной форме
E = row{Ex, Х= 1,m }, ; = row[;,i = 1,n }, (1.153)
а проверочную матрицу H записать в столбцовой форме
H = col [и1 ,i = 1n }, (1.154)
где И i - i -я строка матрицы H . Подстановка компонентов соотношения (1.149), представленных в форме (1.153), (1.154), в соотношение (1.152) доказывает справедливость утверждения. ¦
Примечание 1.2 (ПМ1.2). Нетрудно видеть, что если при кодировке векторов ошибок % векторами-синдромами E при построении ПЗК, исправляющего ошибки кратности s > 1 или обнаруживающего ошибки кратности r > 2, учтены условия У1.31, то достаточно иметь таблицу кодировок ошибок % только первой кратности. Ниже
при построении алгоритмов формирования матриц G и H кода предполагается, что условия У1.31 выполняются. ?
Утверждение 1.32 (У1.32). Столбцы Hx, Х = 1,m матрицы H принадлежат ядру матрицы G так, что выполняются соотношения
Hxe kerG v GHX = O; (1.155)
в свою очередь столбцы GTj , j = 1,k транспонированной GT образующей матрицы принадлежат ядру транспонированной HT проверочной матрицы кода так, что выполняются соотношения
GT е ker HT v HTGT = O. ? (1.156)
Доказательство утверждения строится на представлении матричного соотношения (1.147) в векторно-матричной форме с использованием правых вектор-столбцов
G\H,\ H2 ІК !H,.!K \H„,]= O, (1.157)
что позволяет записать
GHX = O ,X= 1,m v Hxe ker G.
в свою очередь матричное соотношение (1.147) в транспонированной форме по аналогии с (1.157) может быть записано в виде
HTGT = HT
GT і Gt ІК
ІК i GT
'G T
I j
что позволяет записать
HTGT = O,j = 1,k v GT е kerHT. ¦
Утверждение 1.33 (У 1.33). Матрицы G и H, сформированные в виде
| G = \l„ \ G ] H = | 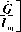 |
где Ik - k x k -единичная матрица, Im - m x m -единичная матрица, G - k x m -матрица синдромов однократных ошибок вида
~ % = \%!Om]. (1-159)
где % - k-мерный вектор-строка, содержащий одну единицу, Om -
m-мерная нулевая вектор-строка, порождают помехозащищенный код, обладающий полной блоковой систематикой. ?
Доказательство утверждения в первой части состоит в непосредственной подстановке матриц G и H вида (1.158) в (1.147), которая приводит к
| GH = |
| = G + G = O. |
(1.160)
aG = a
I\G
a\aG
что обнаруживает полную блоковую систематику ПЗК у. ¦
Алгоритмы формирования матриц G и H ПЗК различаются последовательностью этой процедуры. Сначала рассмотрим процедуры формирования матриц помехозащищенного кода, в которых сперва конструируется проверочная матрица H, а затем на основе сформулированных утверждений вычисляется образующая матрица G ПЗК. Вторую группу алгоритмов составляют процедуры, в которые на первом этапе формируется матрица G кода, а затем формируется проверочная матрица H ПЗК.
1.6.1 Формирование матриц ПЗК
с помощью проверочных равенств при декодировании и кодировании
Процедура формирования матриц H и G ПЗК, основанная на использовании проверочных равенств при декодировании и кодировании, инвариантна относительно требований к блоковой систематике кода. По существу уровень блоковой систематики в структуре проверочной матрицы H кода закладывается в силу (1.146) и У1.31 на первом шаге процедуры, состоящем в кодировке векторов-строк ошибок векторами-строками синдромов Ej. Следует заметить, что на этапе кодировок ошибок синдромами Ej может быть так же заложен [42, 51]
способ технической реализации исправления ошибки(ок) в принятой кодовой комбинации. Так кодировкой ошибок синдромами Ej по
схеме Р. Хэмминга [42, 51] закладывается возможность технической реализации исправления однократных ошибок с использованием стандартных дешифраторов [27, 51].
Алгоритм 1.6 (А 1.6)
формирования матриц ПЗК с помощью проверочных равенств при кодировании и декодировании
14. Составить таблицу кодировок векторов-строк однократных ошибок ^ векторами-строками синдромов Ej, начиная с ошибки в старшем разряде ^ , = [і! о..-і ] и заканчивая ошибкой в
младшем разряде ^ = [о,.-і! 1] , где On-1 - (n -1) -мерная нулевая вектор-строка, так, что E} удовлетворяют условиям У 1.31 и
принятым техническим соображениям относительно процедуры коррекции искаженного кода.
15. Сформировать проверочную матрицу H на основании составленной таблицы кодировок и соотношения (1.151), которая построчно должна удовлетворять условию
нj = En+1-j; j = In. (1.161)
16. На основании составленной проверочной матрицы H кода и соотношения (1.146), описывающего процесс формирования синдрома в аппаратурной среде ДКУ, составить аналитические выражения для каждого разряда Ex, Х= m, 1 синдрома как функции принятой из КС искаженной кодовой комбинации f = row{fn+1-j;j =1,n } в силу соотношения
E, = f Hm+1-X, X= 1m, (1.162)
где Hm+1-x - (m + 1 - А)-ый столбец матрицы H .
17. Сформировать аналитические выражения для помехозащитного кодирования помехонезащищенного кода a = row\at,i = k,1}, для чего записать соотношения (1.162) в предположении, что в КС отсутствует помеха (% = 0), положив, тем самым, справедливость выполнения условий
EX = 0 ,fn+1-j = Уn+1-j > J = 1,n , (1.163)
порождающих систему равенств
0 = У Hm+1-X = У n+1- j , b= 1,m , (1.164)
допускающих явное разрешение относительно разрядов yj ПЗК как функций разрядов ai помехонезащищенного кода в форме
Уз = У} (a,, i = 1,k ),j = 1,n. (1.165)
18. Сформировать образующую матрицу
G = row{Gj,j = 1,n } коДа
на основании соотношения (1.144) в силу условия
Gj = arg{ = a Gj = {(ax ,i = 1,k) ;j = 1, n }, (1 •166)
в котором известны вектор-строка помехонезащищенного кода a, а также линейная связь у. и at в форме (1.165). ¦ 1.6.2 Формирование матриц ПЗК
с использованием матричного уравнения Сильвестра
На возможность использования матричного уравнения Сильвестра для формирования проверочной матрицы циклического помехозащищенного кода (ЦПЗК) указано в параграфе 1.4. Эти возможности в систематизированном виде являются основой алгоритма 1.7 формирования указанной матрицы ЦПЗК.
Алгоритм 1.7 (А 1.7)
формирования проверочной матрицы ЦПЗК на основе использования матричного уравнения Сильвестра
6. Задать матрицу A размерности n х n, где n = к + m, с индексом нильпотентности ? равным ? = n в канонической Жордановой [12, 13] форме
A = J[Л = 0 }. (1.169)
7. Выбрать матрицу P размерности 1 х n, образующую с матрицей A полностью наблюдаемую пару (A, P) матриц.
8. Найти решение матричного уравнения Сильвестра
TA + ГТ = LP (1.170)
относительно матрицы Т.
9. Сформировать проверочную матрицу H помехозащищенного (n, к )-кода в силу соотношения
H = Тт . ¦ (1.171)
Примечание 1.3 (ПМ.1.3). Множество формируемых матриц H с помощью приведенного алгоритма (А1.7) может бытъ существенно расширено, если в матрицах L и P допуститъ отличное от единицы соответственно число столбцов и строк, но при этом они всякий раз должны бытъ согласованы с тем, чтобы существовало их произведение LP. ?
1.6.3 Использование сингулярного разложения матриц в задаче формирования матриц ПЗК
Рассмотрим теперь алгоритм конструирования образующей матрицы G ПЗК по известной проверочной матрице H, который основан на положениях У 1.32 и использующий возможности сингулярного разложения (SVD-процедуры) матриц [12, 16]. С этой целью сделаем некоторые пояснения.
Определение 1.11 (О1.11). Сингулярным разложением [12, 16] ?х /л матрицы N над произвольным полем называется ее представление в форме
N = UZVT, (1.172)
где U - ?х? -матрица левого сингулярного базиса, V - лх л -матрица правого сингулярного базиса, обладающие свойством над этим полем
UUт = UT U = І?, VVт = V TV = Іл, (1.173)
Z - ? х л-квазидиагоналъная матрица сингулярных чисел, размещаемых на главной диагонали, при этом их число равно min {?,л }• ?
Если с помощью (1.172) сконструировать матрицы NNT и NTN, то в силу (1.173 получим
NNT = UNNTUT; NTN = VNTNVT, (1.174)
при этом оказывается, что сингулярные числа совпадают с арифметическими значениями корней из собственных значений матриц NNT и NT N. Элементы левого сингулярного базиса U являются нормированными собственными векторами матрицы NNT, а элементы правого сингулярного базиса V являются нормированными собственными векторами матрицы N T N.
Выделим случай реализации ?хц -матрицы N, которая характеризуется выполнением условия
ц<?, (1.175)
тогда [12, 16] ц-? последних столбцов матрицы V правого сингулярного базиса будут принадлежать ядру матрицы N, что записывается в форме
V е kerN,i = ? + 1,ц . (1.176)
Для построения алгоритма формирования образующей матрицы G
ПЗК по известной проверочной матрице H, необходимо положить N = HT.
Если с помощью (1.172) сконструировать матрицы NNT и NTN, то в силу (1.173 получим
NNT = UZZTUT; NTN = VZTZVT, (1.174)
при этом оказывается, что сингулярные числа совпадают с арифметическими значениями корней из собственных значений матриц NNT и NT N . Элементы левого сингулярного базиса U являются нормированными собственными векторами матрицы NNT, а элементы правого сингулярного базиса V являются нормированными собственными векторами матрицы N T N.
Выделим случай реализации ?хц -матрицы N, которая характеризуется выполнением условия
ц<?, (1.175)
тогда [12, 16] ц-? последних столбцов матрицы Vправого сингулярного базиса будут принадлежать ядру матрицы N, что записывается в форме
V е kerN,i = ? + 1,ц . (1.176)
Для построения алгоритма формирования образующей матрицы G ПЗК по известной проверочной матрице H, необходимо положить N = Hт.
Алгоритм 1.8 (А 1.8)
формирования образующей матрицы G ПЗК по известной проверочной матрице H с использованием SVD-процедуры
1. Сформировать проверочную n х m -матрицу H помехозащищенного (n, к )-кода с помощью приведенных А1.6 и А1.7.
2. Построить сингулярное разложение m х n -матрицы Hт в форме
Hт = UHІн?, (1.177)
где dim Uн = m х m , dim Ін = m х n, dim ?н = n х n .
3. Сконструировать ядро матрицы HT в форме
kerHт = row{v e(kerHT), i = m + 1,n}. (1.178)
4. В силу соотношений (1.156) сформировать образующую матрицу G помехозащищенного (n, к)-кода в форме
G = (kerHт J. ¦ (1.179)
1.6.4 Формирование матриц ПЗК с полной блоковой систематикой
Рассмотрим проблемы формирования матриц G и H ПЗК с полной блоковой систематикой. Если формирование матриц кода осуществляется с помощью алгоритма 1.6, то блоковая систематика закладывается на этапе кодировке вектор-строк однократных ошибок ^ в m
младших разрядах помехозащищенного (n, к )-кода векторами-строками синдромов Ej так, чтобы последние m синдромов в таблице кодировок образовывали m х m -единичную матрицу Im . При этом проверочная матрица H (n,к)-кода примет вид (1.158), который в силу положений утверждения У.1.33 является основой для формирования образующей матрицы G ПЗК в форме (1.158).
Завершим рассмотрение поставленной проблемы формирования матриц (G,H) помехозащищенного (n,к)-кода случаем циклических
ПЗК, матрицы которых обладают полной блоковой систематикой. Приводимый ниже алгоритм строится на базе работ [42, 44].
Алгоритм 1.9 (А 1.9)
конструирования матриц циклического ПЗК с полной блоковой систематикой
Пример 1.8 (Пр1.8)
Решается задача формирования матриц G и H ПЗК (15,7), исправляющего ошибки кратности s = 2 и обладающего синдромами однократных ошибок, удовлетворяющих условиям У 1.31.
Формирование матриц требуется осуществлять с помощью проверочных равенств при декодировании и кодировании. Тогда, следуя алгоритму 1.6:
1. Составим таблицу 1.2 однократных ошибок, используя синдромы группового кода [50], исправляющие ошибки кратности s=2.
2. Составим проверочную матрицу H , используя соотношение (1.158), в результате чего получим
H = соі{н< = Н„+н; j = 1,15 }
110 110 11 10 110 10 1 10 0 10 110 1 0 0 0 0 0 0 0 0 110 10 10 01010101 01000000 0 0 1 1 0 0 1 1 00100000 00010000 0 0 0 0 1 1 1 1 00001000 00000100 00000010 00000001
71
| Номер искаженного разряда |
Синдром Е = [E8 E7 Ee E5 E4 Ез E2 E1 ] | Номер искаженного разряда |
Синдром E = [E8 E7 E6 E5 E4 E3 E2 E1 ] |
| 15 | 110 110 11 | 7 | 00100000 |
| 14 | 10 110 10 1 | 6 | 00010000 |
| 13 | 10010110 | 5 | 00001111 |
| 12 | 10000000 | 4 | 00001000 |
| 11 | 0 110 10 10 | 3 | 00000100 |
| 10 | 0 10 10 10 1 | 2 | 00000010 |
| 9 | 01000000 | 1 | 0 0 0 0 0 0 0 1 |
| 8 | 0 0 1 1 0 0 1 1 |
| мут вид | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4. Сформируем аналитические выражения для помехозащитного кодирования, используя соотношения (1.163), в результате чего |
|
получим Уі2 = У lS | + | У l4 | + | УіЗ | ||||
| У 9 = У lS | + | Уіі | + | Уі0 | ||||
| У 7 = Уі4 | + | Уіі | + | У s | ||||
| Уб = У lS | + | У14 | + | У13 | + | У10 | + | Уs |
| У 4 = Уі5 | + | Уіі | + | У 5 | ||||
| У3 = У l4 | + | УіЗ | + | У10 | + | У 5 | ||
| У 2 = УіЗ | + | У15 | + | Уіі | + | У s | + | У 5 |
| Уі = Уі5 | + | У14 | + | Уі0 | + | У s | + | У 5 |
[ [15 [14 [13 [12 [11 У10 У9 У8 У7 У6 У5 У4 У3 У У, ] = ’
a7 a6 a5 a4 a3 a2 a1
где
| У15 = | a. |
| Уі4 = | a |
| УіЗ = | a |
| У12 = | a |
| Уіі = | a |
| У10 = | a |
| У 9 = | a |
то образующая матрица кода (15,7) принимает вид
100100100101011
010100001100101
001100000100110
000010101001010
000001100100101
000000011100011
000000000011111
Примечание 1.4 (ПМ1.4). Рассмотренный ПЗК ((5,1), исправляющий ошибки кратности s = 2 имеет избыточное число проверочных разрядов. Действительно, число синдромов
Nc = 2m -1 = 28 -1 = 255, а число ошибок первой и второй кратности
Nош = СІ + С2 = n(n +1)/2 = 120. Складывается впечатление, что соотношение Nc > Nош сохранится, если число m проверочных разрядов сократить с 8 до 7. Действительно, в этом случае код (15,7) трансформировался бы в код (14,7), для которого было бы справедливо неравенство
Nc = 2m -1 = 27 -1 = 127 > N ош = Сі + С 2 = 105.
Но в этом случае необходимо было бы приведенные в таблице 1.1 синдромы укоротить на один старший разряд. Однако при этом нарушается условие [42, 51] и корректирующая способность ПЗК, исправляющего ошибки кратности s = 2, что вызывается появлением нулевого синдрома (для ошибки в двенадцатом разряде в рамках рассмотренного примера) и сокращением кодового расстояния между синдромами до dmin = 3. ?
Пример 1.9 (Пр1.9)
Иллюстрируется процедура формирования проверочной матрицы H ПЗК (7,4), исправляющего ошибки кратности s = 1.
Читателю предлагается убедиться, что проверочная матрица H вида
| " G ~ | ||
| H= | _ I і _ | , где G = |
011_
получена решением уравнения Сильвестра (1.170) относительно матрицы Т = Hт с матричными компонентами
| ||||||||||||
| Матрица H обнаруживает полную блоковую систематику ПЗК (7,4), поэтому образующая матрица кода принимает вид q = [і4 ! G]• |
Пример 1.9 (Пр1.9)
Иллюстрируется процедура формирования проверочной матрицы H ПЗК (7,4), исправляющего ошибки кратности s = 1 .
Читателю предлагается убедиться, что проверочная матрица H
вида
| H= |
|
| получена решением уравнения Сильвестра (1.170) относительно матрицы Т = Hт с матричными компонентами | ||||||||||||
| ||||||||||||
| Матрица H обнаруживает полную блоковую систематику ПЗК (7,4), поэтому образующая матрица кода принимает вид q = [і4 \ G] |
1.7. Анализ структуры неподвижных состояний
и замкнутых циклов линейных двоичных динамических систем
В данном параграфе рассматриваются проблемы, связанные со спецификой структуры пространства состояния линейных двоичных динамических систем, характеризующихся наличием неподвижных состояний и замкнутых циклов при отсутствии (и (к ) = 0) и наличии (и (к0) экзогенной задающей последовательности на входе ЛДДС.
Решаемая задача связана с особенностью структуры алгебраического спектра собственных значений а{ A } = {Лг- : D(A) = det(AI + A) = 0 }
матрицы A состояния линейной ДДС, особенностями структуры геометрического спектра собственных векторов {? : А?г- = <Е!І;i = 1,n } той же матрицы, с фактом, когда этот спектр имеет своими элементами вектор начального x(0) (в общем случае исходного x (к )) состояния системы и столбцы матрицы B входа ЛДДС. Для случая, когда и (к )^ 0 решаемая задача связана с проблемой управляемости пары матриц (A, B). И, наконец, решение задачи в значительной степени зависит от показателя ju, которому принадлежит матрица A.
Рассматриваемая проблема решается с использованием моделей «вход-состояние» линейных ДДС, задаваемых в рекуррентной
x(к + 1) = Ax(к)+ Bи(к), x(0); (1.183)
и суммарной
x(к)= Aк x(0)+Х Aк-1-іBи(i) (1.184)
і=0
формах.
Анализ структуры пространства состояния ЛДДС, задаваемой моделями (1.183), (1.184) проведем для случая, когда (n х r) матрица B входа представляет собой n -мерный вектор-столбец так, что r = 1.
1.7.1 Неподвижные состояния
линейной двоичной динамической системы
Рассмотрение проблемы начнем с определения неподвижного состояния.
Определение 1.12 (О1.12). Состояние x(к) ЛДДС (1.182), (1.183)
называется неподвижным, если оно удовлетворяет условию
x(к + 1) = x(к), Vк. ? (1.185)
Анализ структуры неподвижных состояний начнем со случая, когда экзогенная последовательность и (к) на входе ЛДДС отсутствует. Для этого случая и (к )= 0, поэтому модели (1.183), (1.184) принимают вид
х(к + l)= Аx(к), x(0); (1.186)
х(к) = Акх(0). (1.187)
Утверждение 1.34 (У1.34). ЛДДС (1.186), (1.187) при любой (п х п)-реализации матрицы А состояния всегда имеет в качестве неподвижного состояния нулевое
х (к) = 0 . ? (1.188)
Доказательство утверждения использует рекуррентную модель (1.186), подстановка в которую (1.188) дает цепочку равенств
х (к + 1) = А х (к)=А • O = O = х (к). ¦
Утверждение 1.35 (У1.35). ЛДДС (1.186), (1.187) при реализации матрицы А состояния в форме единичной (п х п)-матрицы так, что
А = I, имеет неподвижными все 2п состояния двоичной системы. ?
Доказательство утверждения, как и выше, использует рекуррентную модель (1.186) ЛДДС, в которой следует положить A = I так, что (1.186) принимает вид
х(к + 1) = Ax(к) =Ix(к) = x(к); Vx(k). ¦
Выделим теперь класс матриц состояния ЛДДС (1.186), (1.187), при которых двоичная система обладает неподвижным состоянием x (к)ф О , отличным от нуля.
Утверждение 1.36 (У 1.36). Если состояние x (к) является собственным вектором % матрицы A, соответствующим ее собственному значению равному единице (Л = і), то состояние
x(k) = % (1.189)
является неподвижным. ?
Доказательство утверждения использует рекуррентную модель ЛДДС (1.186) и определение собственного вектора % матрицы
А? = Л?. (1.190)
Для собственного значения Л = 1 соотношение (1.190) принимает вид
А% = %. (1.191)
Если x (к) выбран в форме (1.189), тогда используя (1.186) получим цепочку равенств
x (к + 1)= A x (к) = А% = % = x (к). ¦ (1.192)
Выделим класс матриц состояния ЛДДС, которые не порождают ненулевые неподвижные состояния x (к)ф 0. Очевидно, что в этот класс входят все (n х п)-матрицы A, обладающие индексом ? нильпотентности, удовлетворяющим неравенствам
1 <?< п. (1.193)
Это вызвано тем, что нильпотентная (п х п)-матрица A с индексом нильпотентности (1.193) имеет все п собственных значений, равных нулю (Л = 0), что делает невозможным переход от (1.190) к (1.191).
В этот класс также входит (п х п)-матрица A, принадлежащая максимальному показателю ц = 2п -1, что имеет место, когда характеристический полином матрицы A D(X)= det(Л + A) представляет собой неприводимый полином степени п (degD(X) = п). В этом случае матрица A не имеет собственных значений в простом двоичном поле Галуа gf(2)={0,і}, как следствие матрица A не имеет собственных
векторов, в силу чего не выполняется соотношение (1.191). Таким образом неподвижным ненулевым состоянием обладает ЛДДС, (п х п)-матрица A состояния которая принадлежит показателю ц, удовлетворяющему неравенствам
n <ц< 2n -1. (1.194)
Рассмотрим теперь структуру неподвижных состояний для случая отличной от нуля экзогенной последовательности на входе ЛДДС так, что выполняются соотношения
и(к)ф 0;u(к) = 1, Vк. (1.195)
Утверждение 1.37 (У 1.37). Нулевое состояние x (к ) = О не принадлежит множеству неподвижных состояний ЛДДС при ненулевой экзогенной последовательности, удовлетворяющей условиям (1.195). ? Доказательство утверждения строится на подстановке x (k ) = 0 и (1.195) в модель (1.183) ЛДДС, что приводит к соотношению
x (k +1) = B и (к). (1.196)
В случае если dimB =(n х 1) и Bф O соотношение
x (к + 1)= O = x (к) при и (к ) = 1 не выполняется. ¦
Утверждение 1.38 (У 1.38). Ненулевое неподвижное состояние ЛДДС (1.183) вычисляется в силу соотношения
x(к)= (I + A)'1 B. ? (1.197)
Доказательство утверждения строится на непосредственном вычислении неподвижного состояния, опирающегося на его определение (1.185), и соотношение (1.183) с учетом (1.195), из которых получаем
x (к )= A x (к) + B,
что записывается в форме
(I + A)x (к) = B, (1.198)
приводящей к выражению (1.197), если матрица (I + A) обратима. ¦ Выделим случай, когда матрица (I + A) не является обратимой.
С этой целью воспользуемся свойством спектра собственных значений матричной функции от матрицы. В соответствии с этим свойством спектр <j{i + A}= {4 ;i = 1,n } состоит из элементов
4 = 1 + A, i = Tn, (1.199)
где A - элемент алгебраического спектра
j{a}= A : det(AI + A) = 0; i = 1,n }
собственных значений матрицы A . В силу соотношения (1.199) матрица (l + A) является обратимой, а следовательно линейная ДДС (1.183), (1.184) имеет при u (к )= 1 неподвижное состояние, определяемое в силу (1.198), если матрица A является нильпотентной с любым индексом ? нильпотентности или если матрица A имеет своим характеристическим полиномом любой неприводимый полином степени n , принадлежащий показателю ц, удовлетворяющему условию (1.194).
Необратимой матрица (/ + Л) является для ЛДДС, матрица Л состояния которой имеет в своем алгебраическом спектре собственных значений с{л} = {Xi: det(XX + Л)= 0; i = l,n* } элемент Xj = 1 так, что X} в силу (1.200) обращается в ноль (Xj = 0). В этом случае линейная ДДС
(1.183), (1.184) не имеет неподвижных состояний отличных от нулевого. Следует, однако, заметить, что сказанное выше справедливо, если иметь в виду произвольную реализацию матрицы B. Если же матрица входа такова, что она принадлежит пространству столбцов матрицы B, то есть выполняется условие B е Jm(I + Л), то вектор x(к) ищется из условия
X(к)= argjB = Х(І + A)ixi (к)
1.7.2 Замкнутые циклы линейных ДДС
Вынесенную в название параграфа проблему как для случая исследования неподвижных состояний будем решать с использованием модельных представлений ЛДДС в форме (1.186), (1.187) при отсутствии на входе двоичной динамической системы экзогенной последовательности ( и(к)=0 ) и в форме (1.183), (1.184) при наличии на входе системы экзогенной последовательности ( и (к0 ).
Предварим исследование важным для решения проблемы утверждением.
Утверждение 1.39 (У1.39). Пусть (n х n)-матричная функция f (Л) от (п х п)-матрицы Л задана над простым полем Галуа GF(p) при p = 2 в степенной форме
f( Л)= Лq (1.200)
где q - целое положительное число. Пусть матрица Л обладает алгебраическим спектром с{Л }={Xi : det(XU + Л) = 0; Xя е GF(2)} собственных значений и геометрическим спектром
Afj =4i;j = ИЛ}
собственных векторов. Пусть матричная функция f( Л ) от матрицы Л обладает алгебраическим спектром
c{f (A)}={Xfi = f (U ):det[xf1+f (a)=0;1 =1,n}
собственных значений и геометрическим спектром JX: f (A)x = ?f }• Тогда геометрический спектр \%fX; X= 1,r } собственных векторов f (a) включает в себя геометрический спектр \gj-; j = 1,nA } собственных векторов матрицы A, при этом они могут не совпадать так, что выполняется соотношение
\%f X; X= 1,rf }^ \%J-; j = 1,r } (1.201)
rf > r. ? (1.202)
Доказательство. Очевидно сформулированное утверждение справедливо для матрицы A, не являющейся нильпотентной матрицей любого значения индекса ? нильпотентности, которая обладает алгебраическим спектром собственных значений, составленным из нулей так, что <г\А }= \х = 0; i = 1,n }, а также для матрицы A, имеющей своим характеристическим полиномом D(X) = det(XI + A) неприводимый полином степени n, который не имеет корней в простом поле Галуа GF (2) так, что <г\А }=\А g GF(2)}. Таким образом утверждение имеет дело со случаем, когда характеристический полином матрицы A разложим в произведение двучленов
D(X) = det (Я/ + А) = П(а + А^. ) (1.203)
j=1
и который характеризуется кратными единичными собственными значениями Я. = 1 (j = 1,n ). Известно [13], что число rA различных собственных векторов матрицы A, имеющей кратные корни, меньше n = dim x и определяется из соотношения
rA = dim{Ker (Х/ + A)} n - dimJm (X. / + a)}= n - rank (i + A) (1.204) В свою очередь число rf собственных векторов ^fX матричной функции f (A) от матрицы A определяется из соотношения
rf = dim\er( / + f (a))}=
= n - dimJm\XfX/ + f ( a)}= n - ran k( + f(A)) (1.205)
Причем так как по свойству спектра собственных значений матричной функции f (A) от матрицы A оказывается справедливым соотношение
Хх= f(Xj) : j,X= , (1.206)
то с учетом степенного характера f (A)= Aq спектр кратных единичных значений матрицы A \х. = 1: j = 1,n } сохраняется и для матричной функции f (A) \XfX = ХХ = 1: Х= 1,n }. Если к этому добавить, что матричная функция f(А) в общем случае не сохраняет базис представления исходной матрицы A, то размерности ядер (нуль-пространств) матриц (XjI + A)= (I + А) и (XJ + f(A))=(/ + f(())
могут быть различными так, что выполняется неравенство
rf > rA. ¦ (1.207)
Пример 1.10 (Пр1.10)
Для иллюстрации положений утверждения рассмотрим матрицу
01
A=
00
11
и матричную функцию от матрицы
| f (А)= А 2 = А ¦ А = |
|
1 \ 1 \ X + 1
= Xf +X2 +X +1 = (X + 1)3.
det (ЛІ + А) = det
v{A} = {Xl =Xa = Xf = 1}.
XA 0 ! 1 1 !"1 + xA 1
___1_____j_±___
1 \ 0 Uf
= X3f +X2f +Xf +1 = ( +1)
det (I + f (А))= det\
a{f(А)= А }= {xj1 = Xf2 = Xff =1}-Вычислим
| ¦¦ n - dim{jm(ЛІ + А) | ||||||||||||
| 110 0 1 1 110 |
rA = dim<
= n - rank(I + А) = f - rank
Размерность rA ядра Ker(X + А), определяющая число собственных векторов ^, составляет rA = 1. Таким образом, матрица А имеет единственный собственный вектор
| ||||||||||||||||||||||||||||
| Оценим теперь размерность rf ядра Ker (Лf I + f (A)), определяющую число собственных векторов ) |
| Ker (I + f (A) |
|
01
= 3 - rank 1
101
Таким образом f (A) = A2 имеет следующие собственные вектора:
¦ ) 1 = ) по свойству матричной функции от матрицы сохра
нять геометрический спектр собственных векторов в форме f (A) = A2 ) = = A) = ) = )f1. Действительно
4
| f (A) |
| |||||||||||||||
| ¦ )2 и )3, вычисленные из соотношения |
что
|
f = f = |
|
=) f2 = ) /3- | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| Заметим, что собственные векторы ) 1, )2, )3 матричной функции f (A) = A2 оказались линейно зависимыми. Действительно |
|
ff1 =ff2 +ff3 = f3 ff3 =ff1 + f = f2 |
| и т.д. |
Введем понятие замкнутый цикл в структуре пространства матрицы состояния линейной ДДС с помощью следующего определения.
Определение 1.13 (О1.13). Пусть множество ~ мощности
[х ] = N = 2n -1 состояний линейной ДДС (1.186), (1.187), не включающее в себя нулевое неподвижное состояние, тогда подмножество множества ~, содержащее T состояний, на котором выполняется соотношение
х( к )= х( к + T), (1.208)
называется замкнутым циклом длинной T , составленным из векторов состояния
{х(к));х(к +1)= Ах(к );х( к + 2 )= Ax( к +1)= A2x( к) ,К
К ,х(к + T -1) = АТ-1х(к)}. ? (1.209)
Рассмотрим факторы, определяющие длину Т замкнутых циклов на множестве состояний ЛДДС при отсутствии экзогенной последовательности (и (к ) = 0) на ее входе. С этой целью соотношение (1.208) запишем в форме (1.187)
х( к ) = АТ х( к). (1.210)
Сформулируем следующее утверждение.
Утверждение 1.40 (У1.40). При х(к)ф 0 соотношение (1.210) выполняется в случаях, когда:
- матрица А принадлежит показателю Т;
- х(к) является собственным вектором матрицы АТ. ?
Доказательство справедливости первой части утверждения строится на определении показателя ц, которому принадлежит матрица А, в соответствии с которым выполняется матричное равенство
Ац= I, (1.211)
подстановка ц = Т делает справедливым (1.210). Доказательство справедливости второй части утверждения строится на определении собственного вектора с учетом специфики простого поля Галуа GF (p) при
p = 2. ¦
Нетрудно видеть, что длина Т замкнутых циклов удовлетворяет неравенствам
1 < Т < n -1. (1.212)
Очевидно, что в структуре пространства (n х n) -матрицы А состояния ЛДДС (1.186), (1.187) имеется цикл длины Т = 1, когда х(к) является собственным вектором матрицы А. Иначе говоря, ненулевое неподвижное состояние образует цикл длительностью Т = 1. Максимальная длительность Т = 2n -1 имеет место, когда (n х n) -матрица А и ее характеристический полином D(X)= det(AI + A) принадлежат показателю ц = 2п -1.
Наложим на неравенства (1.212), определяющие возможные по длине T циклы на множестве ненулевых состояний ~ мощности
[х]= N = 2п -1, неравенства, оценивающие возможные показатели ц, которым могут принадлежать (п х п) -матрица состояния ЛДДС и ее характеристический полином D( Л)
п <ц< 2п -1. (1.213)
В результате этого наложения, а также с использованием положений У1.39 и У1.40 можно предложить следующий алгоритм анализа структуры замкнутых циклов линейных ДДС (1.186), (1.187), которому придадим номер 1.10.
Алгоритм 1.10 (А 1.10)
6. Построить векторно-матричное представление линейной двоичной динамической системы в форме (1.183), (1.184).
7. Перейти от представления ЛДДС (1.183), (1.184) к ее представлению в форме (1.186), (1.187), положив в (1.183), (1.184) и (к) = 0.
8. Вычислить характеристический полином D(A) матрицы A состояния ЛДДС в силу соотношения D(A) = det (ЛІ + A).
9. Определить показатель ц которому принадлежит характеристический полином D(A) и матрица A состояния ЛДДС с использованием таблиц полиномов, принадлежащих конкретному ц или возведением матрицы A в степень над полем Галуа GF(2) до момента выполнения равенства AM = I.
10. Проанализировать полученное значение ц: если ц = 2п -1, то осуществить переход к п.11 алгоритма, в противном случае - к п.6 алгоритма.
11. Найти корни характеристического полинома D(A), после чего его записать в форме
D(X)= ?(Л)ПЛ' +1), (1.214)
j=1
где g(Л) - неприводимый модулярный многочлен,
п1 = 1 < п2 <К < nj < п-+1 <К < п% (1.215)
degD(X)= п = degg (Л)+^ п- (1.216)
j=1
12. Вычислить величину rE, определяющую сумму размерностей ядер матриц (I + Лп]) в силу соотношений
2й -1 = п,и + rZt (1.217)
где п,, - число циклов длины T = и .
И- 1
13. Вычислить размерности rj ядер Ker(I + Лnj) матриц I + Лп],
определяющих число собственных векторов матриц Лп], а, следовательно, длину Tj = rj соответствующих им замкнутых циклов.
14. Вычислить собственные векторы %fj матриц Лп].
15. Определить состав и очередность изменения состояний в замкнутых циклах длиной Tj = rj, порожденных собственными векторами f матриц Лп], используя для этого представление циклов в форме (1.209).
16. Определить состав и очередность изменения состояний в замкнутых циклах длиной T, = и, порожденных фактом принадлежности матрицы Л состояния ЛДДС показателю и, используя представление циклов в форме (1.209), в котором за исходное состояние х(к) цикла взять любое состояние множества ~, не принадлежащее циклам, сформированным в п.10.
17. Сформировать структуру замкнутых циклов и неподвижных состояний линейной ДДС (1.186), (1.187) (при и( к )= 0) путем объединения циклов в п.п. 10 и 11, дополнив их нулевым неподвижным состоянием. ¦
Пример 1.10 (Пр1.10) (Продолжение)
1. Выполним п.п.1-3 А1.10, в результате чего ЛДДС будет иметь матрицу Л состояния и характеристический полином
D( Я) = det (ЯІ + Л)
010 0 0 1 111
d(x) = X +X + Я + 1; п = 3
Л=
| 4. Путем возведения матрицы A в степень получим | ||||||||||||||||||||||||||||||||||||||||||
| Л2 = Л ¦ Л = |
| |||||||||||||||||||||||||||||||||||||||||
| что показатель и , которому принадлежит матрица Л, равен четырем (и = 4) |
в результате чего необходимо перейти к п.6 А1.10.
6. Выполнение п.6 алгоритма дает Л1 = л2 = лз = 1 и О(л) представим в форме
п(л)=л3 + л2 + л + 1 = (л2 + 1)(л + 1),
где g (л) = 1;п1 = 1;п2 = 2.
7. Выполнение п.7 алгоритма дает 2п -1 = 7 = 1 • 4 + 3 так, что в структуре пространства матрицы A состояния ЛДДС имеется один замкнутый цикл длиной T = и = 4.
8. Вычисление размерности rj ядер матриц
| (і + An1)=(I + A)) |
|
9. Вычисление собственных векторов матриц Anj приводит к результату
{4f1 }= arg {A n1?f1 =4f1 }= arg { A4 = 4} =
| arg |
|
|
"11 1 | II |
"11 0 | f |
"01 1 |
| 1 | 1 | 0 |
4}
11. Определение состава и очередность смены состояния ЛДДС в замкнутом цикле длины Tu = ju = 4, порожденным фактом принадлежности матрицы A показателю ц = 4, если за x(k) принять x(k)= [001] , не принадлежащий {4 1} ^ {%f2}, и воспользоваться (1.208), дает замкнутый цикл| "01 | "01 | "11 | "11 | "01 | ||||||
| 0 | f | 1 | f | 1 | f | 0 | f | 0 | ||
| 1 | 1 | 0 | 0 | 1 |
| 0 |
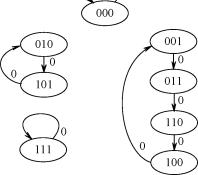 |
| Рисунок 1.23. Структура замкнутых циклов и неподвижных состояний ЛДДС |
в рекуррентной форме
x(k +1)= Ax(k)+ B ; x(0) (1.218)
и в суммарной форме
x(k + 1)= Akx(0) + Ak-1 B + Ak-2B + K + AB + B; x(0). (1.219)
Следует заметить, что введенное с помощью О1.13 определение замкнутого цикла длинной T сохраняется, однако структура этих циклов не только зависит от показателя ц, которому принадлежит матрица A, структуры собственных векторов {к} степенных матричных
функций f (A)= Aq от (n х n)-матрицы A состояния ЛДДС, но и от матрицы B. Последняя может принадлежать пространству столбцов матрицы A, то есть ее образу
B с Jm A, (1.220)
тогда пара матриц (A,B) оказывается не полностью управляемой, простейший случай такой ситуации является случай, когда матрица B является собственным вектором матрицы A .
В этой связи сформулируем утверждение.
Утверждение 1.41 (У1.41). Если матрица B векторно
матричного описания ЛДДС является собственным вектором матрицы A, то ЛДДС с такой парой матриц (A,B) не является полностью
управляемой, при этом размерность подпространства управляемости равна единице. ?
Доказательство. Тот факт, что матрица B суть собственный вектор матрицы A состояния ЛДДС над простым полем Галуа GF(2), позволяет записать
AB = B . (1.221)
Составим матрицу управляемости пары (A, B)
Wy(A,B)=[b \ab\A2B I К I An-1 B]• (1-222)
Для элементов Wy (A,B) можно записать
AB = B ; A2 B = AB = BК , An-1 B = a( An-2 B)=К = B. Подстановка полученных матричных равенств в (1.222) дает для матрицы управляемости
rank Wy (A, B) = rank \b\b \b !k \b] = rank B = 1 < n • ¦
Следует заметить, что рекуррентная форма (1.218) представления ЛДДС при u (k )= 1 содержит конструктивный алгоритм формирования структуры замкнутых циклов путем простого суммирования состояния перехода с матрицей B , так что в цикле происходит аддитивный сдвиг на векторный компонент B. Однако это впечатление обманчиво. Структура замкнутых циклов может измениться так, что в них могут полностью исчезнуть неподвижные состояния. Напомним, что выше было доказано, что при u(k )= 1 нулевое состояние перестает быть неподвижным, а ненулевое неподвижное состояние существует, когда матрица (/ + A) обратима или когда матрица B принадлежит ее образу. Но возможны ситуации, когда ни одно из этих условий не выполняется. Проиллюстрируем сказанное на примере.
Пример 1.11 (Пр1.11)
Рассмотрим ЛДДС с матрицей A состояния из Пр1.9 в сочетании с двумя версиями матрицы входа B:
| B1 = |
|
| Для поиска ненулевого неподвижного состояния x(k): x(k + 1)= x( k) в силу (1.198) сконструируем матрицу | |||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||
| Ранг матрицы (A +1) меньше n = 3, действительно rank (A +1) = rank |
=2.
Матрица (A +1) является необратимой, а потому использование соотношения (1.197) для поиска ненулевого неподвижного состояния оказывается некорректным. Однако проверим принадлежат ли матрицы BJ и В2 в силу (1.198)
(A +i) x( к) = В
образу (A +1). Для первой версии матрицы B = B1 имеет место соотношение
| "J | J | О" | т | |
| О | J | J | х(к ) = | J |
| J | J | О | J |
x(к)= [О J О] и х(к)= [j О J] .
Для второй версии имеем
| 'J | J | О" | 'О" | |
| О | J | J | х(к ) = | О |
| J | J | О | J |
следствие следует ожидать объединения «коротких» замкнутых циклов. На рисунке 1.24 приведена структура циклов ЛДДС с парой матриц (A, Bj), построенная в силу (1.217).
 |
| Рисунок 1.24. Структура циклов ЛДДС с парой матриц (A, Bj) |
На рисунке 1.25 приведена структура циклов ЛДДС с парой матриц (A,B2) - полностью управляемой, так как
00
0j
jj
rank Wy (A, B2) = rank
Рисунок 1.25. Структура циклов ЛДДС с парой матриц (A, B2)
Неподвижные состояния в случае и(к)= J в ЛДДС с парой матриц (A,B2) «исчезли», структура пространства состояний распалась на два замкнутых цикла длиной T = ц = 4. В силу полной управляемости пары (A,B2 ) существует последовательность и (к) , которая позволяет обойти все состояния ЛДДС. Примером такой последовательности является и(к)= JJ0JJJ0JIJJ0JJJ0J! ... ¦
В заключение следует остановиться на проблеме вычисления состояния, из которого ЛДДС переходит в нулевое состояние. Нетрудно видеть, если в левой части (1.218) положить для состояния перехода х(к + j)= 0, то х(к), из которого происходит под действием и(к) переход в нулевое состояние, определится выражением
х( к)= A-B. (1.223)
Оценка состояния (1.223) особенно важна в задачах помехозащитного декодирования.
Следует также заметить, что структура замкнутых циклов претерпевает минимальную модификацию для случая, когда матрица A состояния ЛДДС принадлежит показателю и = 2п -1. В этом случае нулевое состояние перестает быть неподвижным, существует единственное ненулевое неподвижное состояние х( к) = (A +1) 1B и единственный замкнутый цикл длиной T = 2п -1. Пара матриц (A,B) при любой
реализации матрицы B является управляемой так как матрица A с неприводимым характеристическим полиномом D(X) = det(XI + A) не
имеет над GF(2) собственных векторов.
В заключение приведем в форме таблицы 1.3 результаты исследования всех 28 возможных вариантов реализаций пар (A, B) матриц, задающих соответствующие ЛДДС при размерности dimx вектора x их состояния равной трем, что является широко распространенным случаем конструирования ДДС. Для компактности записи в таблицах использованы представления матриц, циклов, последовательностей в виде их десятичных эквивалентов, причем величина периодичности представлена скобочной записью с указанием длительности периода в виде нижнего индекса у правой скобки.
91
| Таблица 1.3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Таблица 1.3 (продолжение) | ||||||||||||||||||||||||||||||||||||||||||||||||
|
Примечания.
1. Матрица Ат представлена построчно: в таблице указаны десятичные эквиваленты строк матрицы.
2. Матрица Bт представлена десятичным эквивалентом ее столбца.
3. Запись вида (^)о означает цикл длины (о) с последовательностью кодов состояния (•), каждый из которых задан в
десятичном эквиваленте.
1.8. Линейные двоичные динамических системы
в задачах дивидендного помехозащитного кодирования
Дивидендное представление процессов помехозащитного кодопре-образования в фазе кодирования и декодирования использует векторно-матричное описание, параметризованное дискретным временем к этих процессов в форме линейных двоичных динамических систем, опирающиеся на модели «вход-состояние» (ВС) вида (1.23), (1.25)
х(к + 1) = Аx(к)+ Ви(к), x(в)= 0, (1.224)
к-1
(к )=| Ак x (0 ) + Х Ак-1-1 В и (i)
= x Ak~1-B u (i). (1.225)
i=0
x ( 0 )=0 i=0
Форма модели ВС (1.224), как указано в параграфе 1.2, именуется рекуррентной формой, форма (1.225) - суммарной. В (1.224), (1.225) х (к) - вектор состояния ЛДДС, осуществляющей помехозащитное ко-допреобразование; и (к) - входная кодовая последовательность; dimx = m, dimu = 1, dim A =( m x m), dim B = ( m x 1). В зависимости от задачи помехозащитного кодопреобразования u ( к) принимает смысл помехонезащищенного информационного кода и(к)= а(к) при формировании помехозащищенного кода у (к) и смысл принятого из канала связи искаженного кода f(к )= У(к )+Н к) так, что и (к) = f (к) в
задаче декодирования. Характерной особенностью модельных представлений (1.224) и (1.225) является то, что матрица Аку состояния кодирующего устройства и матрица Адку состояния декодирующего устройства совпадают так, что выполняется равенство
АкУ = Адку = А . (1.226)
Матрица A состояния КУ и ДКУ задается в одном базисе, при этом чаще всего в сопровождающей характеристический полином (ХП) форме, причем ХП D(A) = det(AI + А) совпадает с образующим ПЗК модулярным многочленом g (x) так, что выполняется соотношение
D(A)= g( x )| x=a (1.227)
Матрицы входа для устройств кодирования и декодирования чаще всего не совпадают так что для КУ и ДКУ модель (1.224) соответственно получает представление
x (к + 1) = А x (к)+ Ву и (к); x (к + 1) = А x (к)+ Вдку и (к). (1.228)
Если при формировании ПЗК предполагается возможность перехода от их матричного задания, не параметризованного дискретным временем к, с помощью образующей матрицы G и проверочной матрицы
H, то следует иметь в виду следующее. Необходимое условие реализуемости матричного представления ПЗК (1.144), (1.146) дивидендным способом, осуществляемым средствами ЛДДС (1.228), является однозначное соответствие строк проверочной матрицы H ПЗК с точностью до процедуры транспонирования с матрицей входа Бдку устройства декодирования и строк матрицы G при представлении образующей матрицы ПЗК в форме (1.158) с матрицей входа Бку (1.228) устройства кодирования.
Высказанные соображения подтвердим следующими утверждениями.
Утверждение 1.42 (У1.42). Матрица Бку ЛДДС дивидендного
кодирующего устройства с точностью до операции транспонирования совпадает с последней строкой (к-ой) строкой Gк образующей матрицы G так, что выполняется соотношение
Бку = G“ = к{ g( x) + x" }, (1.229)
где *¦{(•)}- код модулярного многочлена (•). ?
Доказательство. Рассмотрим процесс кодирования для случая u (k)= a(x) = 1, то есть для случая к -элементной входной последовательности
u (k)=[u (0) = 0,u (1) = 0К , u (к - 2 ) = 0, u (к -1) = 1 ]. (1.230) В течение первых (к -1)-тактов ЛДДС КУ будет находится в нулевом неподвижном состоянии. При приеме элемента u (к -1)= 1 ЛДДС КУ (1.228) перейдет в состояние
x(к) = Бку u(к -1)|u(1-) = Бку. (1.231)
Состояние (1.231) определяет код остатка, выводимый из КУ, для a(x)= 1, задаваемый последней строкой матрицы G кодов остатков так, что выполняется цепочка равенств
xT (к ) = БТКу = Gк =к{ g ( x) + x" }. ¦ (1.232)
Утверждение 1.43 (У1.43). Матрица Бдку входа ЛДДС (1.228) дивидендного декодирующего устройства с точностью до процедуры транспонирования совпадает с последней строкой проверочной матрицы H ПЗК так, что выполняется равенство
БТдку = Hп. ? (1.233)
Доказательство. В силу идентичности результатов процедур формирования синдрома E при декодировании в форме (1.146), (1.151) с целью анализа процессов в ЛДДС (1.228) при декодировании рассмотрим последний при входной последовательности u(к~) = ^(к). Как и выше, ограничимся ситуацией, когда последовательность %(к) содержит единицу только в младшем разряде
и (к) = %(к)=[ и (0) = 0, и (1) = 0,К , и (к - 2) = 0, и (к -1) = 1 ]. (1.234) При входной последовательности вида (1.234) ЛДДС (1.228) устройства декодирования в течение первых (n -1) -тактов, характеризующихся и (к) = 0 остается в нулевом неподвижном состоянии, а на последнем n -м такте перейдет в состояние, совпадающее с матрицей Бдку. Однако в силу правил декодирования это состояние представляет
собой синдром ошибки в младшем разряде, который в силу правил формирования проверочной матрицы H ПЗК является ее последней строкой, что приводит к цепочке равенств
E = xT (n) = ВТку = Hn. ¦ (1.235)
Поставим задачу: матрица A ЛДДС устройств кодирования и декодирования (1.228) фиксирована, матрица входа ЛДДС кодирующего устройства фиксирована в форме (1.232), модифицируема ли матрица входа ЛДДС устройства декодирования при сохранении матричного характеристического свойства ПЗК (1.146) GH = O ?
С целью решения поставленной задачи сформулируем утверждение, предварив его следующим определением.
Определение 1.14 (О1.14). Матрицей циклического сдвига на один шаг «вниз» строк произвольной (n х т)-матрицы H называется (п х n)матрица Pc вида
O1 х(т-1)-1 х 1___
1 (n-l)x (n-1)\O( n—1) х 1
(1.236)
Pc =
Определение 1.15 (О1.15). Матрицей циклического сдвига на один шаг «вверх» произвольной (n х т)-матрицы H называется (n х n)-матрица Pc-1 вида
| P- |
| ? | ||||||
| Из (1.236) и (1.237) видно, что матрицы циклического сдвига «вниз» и «вверх» строк произвольной (n х т) -матрицы H связаны соотноше- |
ниями
P1 = PT, P PT = PTP = I. (1.238)
Определение 1.16 (О1.16). Матрицей циклического сдвига на ? шагов «вниз» строк произвольной (n х т)-матрицы H называется
(n х n~)-матрица Рс? вида
p; =
:(n-?)
(1.239)
1 (п-?)х (n-?)0(t
Определение 1.17 (О1.17). Матрицей H(у) размерности (n х m), полученной из (п х m)-матрицы H путем сдвига на у шагов ее строк
«вниз», называется матрица, вычисленная в силу матричного соотношения
H(у) = РуН. ? (1.240)
Утверждение 1.44 (У 1.44). Характеристическое свойство (1.147) матриц (G,Н) помехозащищенного кода сохраняется для матриц
(,Н(у)) так, что
GH(у) = GPyH. ? (1.241)
Доказательство утверждения строится на использовании матрицы G, записанной в каноническом виде (1.158)
| G= |  |
H = [а [ Вд«у\А [ Вдку К\АВдкГ \Вдку ]. (1.242)
При этом используются свойства (m х т)-матрицы А принадлежности показателю п = 2т -1, в силу чего выполняется равенство
Ап = I, (1.243)
а также справедливости теоремы Гамильтона-Кэли позволяющей записать
oWL = D( А) = O. (1.244)
Если записать (1.241) в транспонированной форме
H T (Ру) GT, (1.245)
подставить в нее матрицу H в форме (1.242), Ру в форме (1.239) и матрицу G в форме (1.158), учесть (1.243) и (1.244), тогда получим матричное соотношение
HT (pyjGT = гт{Ар 0(А)Вд„,; i = U,\p,\ = 0,1,2,К,т }= O. ¦ (1.246)
Пример 1.12 (Пр1.12).
Проиллюстрируем положения У 1.44 на примере циклического ПЗК с образующим ММ g(x)= x3 + x + 1, который характеризуется матрицами G и H
1 0 1 111 1 1 0 0 1 1
10 0 0 0 10 0 0 0 10 0 0 0 1
1110100 0 1110 10 110 10 0 1
(1.247)
G=
Матрица Рс циклического сдвига «вниз» строк матрицы H на один шаг (1.236) имеет вид
Oi i V—
I7 7 o7 ,
7 x 7 I 7 x]
(1.248)
Pc =
Тогда для матриц (1.245) для v = 0,v = 3, v = 6 получим
1000
0100
0010
000]
]]]0
0]]]
]]0]
H T G G = [ Вд„, I А1 Вдку I А4 Вдку j A3 B^ \ A 2 Вдку \ АВд„у ^j
(1.249)
H2 (P3 )g 2
]000 0]00 00 ]0 000] ]]]0 0]]] ]]0]
= [A 2 Вдку ! АВдку Вдку В А6 В^ \ А1В ^ \ В В^ ! А3 В ^ ]
(1.250)
H т (P6 )g 2
]000 0]00 00 ]0 000] ]]]0 0] ]] ]]0]
= [В3 Вду I AG Agj В3 Вду В А2 ^дуу j АВ^ ^^ \ А6 В^
(1.251)
Раскрытие произведений матриц позволяет для (1.248) - (1.250) записать
H2 Gт =[( + А2 + і) '(А3 + А2 + А + і)Вд,:у
(а4 + А2 + А)ВдКу U3 + А + і)Вд,у ] (1-252)
H2 (Pc3 )g 2 = [(а3 + А3 + А2 )Вдку !(а 1 + А4 + А3 + А)Вду
(А1 + А4 + і) |(а6 + А4 + А3 ']Вдк>, ] (1-253)
H2 (р G = [(а6 + А3 + а)в7у КА6 + А4 + А + 1)Вдуу
(а3 + А + і)Вдуу U + А2 + 1)Вд,у ] (1-254)
Если в (1.252) - (1.254) учесть (1.243) и (1.244), записываемые для рассматриваемого примера в форме
A7 = I, D(A) = A3 + A +1 = O, (1.255)
то (1.252) - (1.254) примут вид
H T G T =[A ~'D(A)BdKy A !D(A)Bm
AD(A)B„k, \D( A)BgKy ] = O (1-256)
H T (P )T = [a 2 D( A)Bg,T; AD( A)B„V
A~3D( A)Bk I A3D( A)Bk ] = O (1 -257)
H T (p6 )g t = [A-2D(A)Bdv j A3D( A)Bdv
d( A)BdKy A ~3d( a)b0i!;, ]=O (1-258)
Общее представление результатов (1.256) - (1.258) имеет вид (1.246). ?
Утверждение (У1.44) и Пр1.11 по существу содержат доказательство следующего утверждения.
Утверждение 1.45 (У 1.45). В качестве матрицы Вдку входа устройства дивидендного декодирования, реализованного в форме линейной ДДС (1.228), может быть принята любая строка проверочной матрицы H помехозащищенного кода в транспонированном виде так, что
Вдку = HT, i = П1, (1.259)
при этом образующая и проверочная матрицы ПЗК, сформированного средствами ЛДДС (1.228) с матрицей входа (1.259) устройства декодирования сохраняют свое характеристическое свойство (1.147). ?
Таким образом пользователь аппаратуры дивидендного помехозащитного кодирования - декодирования без изменения ее кодирующей части может модифицировать декодирующую часть путем изменения матрицы Вдку входа декодирующего устройства. Количество вариантов
модификации матрицы Вдку составляет Ns = n, где n - полное число разрядов помехозащищенного (n, к )-кода. При этом опасность получения неуправляемой пары матриц (A, Вдку) на указанном наборе отсутствует, так как матрица Вдку при всех ее версиях не является собственным вектором матрицы A. Последнее объясняется тем, что матрица A состояния ЛДДС кодирующих и декодирующих устройств (1.228) имеет своим характеристическим полиномом неприводимый модулярный многочлен, который не имеет корней в простом поле Галуа GF (2), что гарантирует и отсутствие собственных векторов.
Полученные в параграфе результаты позволяют сформировать алгоритм синтеза линейных ДДС дивидендного помехозащитного кодирования и декодирования.
Алгоритм 1.11 (А1.11)
синтеза ЛДДС дивидендного помехозащитного кодирования и декодирования
18. По заданному информационному массиву Q мощности [q] = Nи
определить размерность к помехозащищенного кода в силу соотношения
к = arg {2 > N и =[ Q]}.
19. По заданной корректирующей способности помехозащищенного (n,к)-кода определить степень m = n - к его образующего модулярного многочлена g (x) в силу соотношения
(k+m)
m = arg\NC = 2m -1 > Nош =? C(
i=1
где Nc - число синдромов, Nош - число ошибок, s - кратность исправляемой ошибки. Выбрать или сформировать реализацию образующего ММ g(x) степени m в классе неприводимых, гарантирующих минимальное кодовое расстояние dmin на используемых кодовых комбинациях ПЗК
dmin > 2s + 1.
20. Вычислить D-образ ММ g (x) в форме
g(d )= D{ g(x )}= ~(x - )| x-1=d, где ~(x'1): g(x)= xm~(x-).
21. Сконструировать передаточную функцию устройства деления модулярных многочленов в форме
Md '=іи ¦
22. Пользуясь правилом Мейсона некасающихся контуров построить структурную реализацию ф( d) на элементах памяти (ЭП) с
передаточной функцией Ф ЭП (d) = d.
23. Произвести отметку входов и выходов ЭП переменными xi(к + 1) на входе и xi(к) на выходе и сформировать векторноматричное описание автономной версии УДММ
x( к +1)= Ax( к).
24. Сформировать матрицу входа Вку дивидендного кодирующего
устройства (1.228) в силу соотношения (1.229).
25. Сформировать проверочную матрицу H ПЗК и матрицу Вдку
входа дивидендного декодирующего устройства (1.228) в силу соотношения (1.259).
26. Проверить правильность функционирования устройств кодирования и декодирования (1.228) сформированными парами мат-
рщ (A, ВкУ) и (A,Вдку).
27. Построить техническую реализацию устройств дивидендного кодирования и декодирования:
a. в схемотехнической форме на базе структурных представлений;
b. в программной форме на базе рекуррентных процедур (1.228).
¦
2. НЕЛИНЕЙНЫЕ ДВОИЧНЫЕ ДИНАМИЧЕСКИЕ СИСТЕМЫ (НДДС) ДИСКРЕТНОЙ АВТОМАТИКИ
Рассматриваются проблемы, связанные с использованием нелинейных двоичных динамических систем (НДДС) в составе устройств дискретной автоматики. Причем первоочередной проблемой является разработка методологии и алгоритмического обеспечения конструирования нелинейных модельных представлений ДДС. В связи с тем, что «нелинейность» в общесистемной постановке суть разновидность статической «памяти», то следует ожидать при использовании НДДС в составе устройств дискретной автоматики для решения задач кодопре-образования заметного сокращения размерности кода состояния ДДС, что влечет за собой системологическую проблему «кодового пространства» на классе ЛДДС-НДДС реализаций проектируемых двоичных систем. При этом разработчик УДА должен помнить, что априорным преимуществом НДДС перед ЛДДС является возможность использования всего банка существующей триггерной логики, что существенно расширяет класс схемотехнических реализаций ДДС.
2.1. Построение модельного представления НДДС с использованием средств автоматной логики
В настоящем параграфе в развитие положений параграфа 1.2, в котором в классе моделей «вход-состояние-выход» (ВСВ) (1.20) построены линейные представления правил (функций) X перехода и 8 выхода в форме (1.23) и (1.24), ставится задача конструирования их нелинейных аналогов. Для целей построения нелинейных модельных представлений правил X и 8 при описании ДДС используются возможности автоматной логики [6, 7, 8, 14, 39] в двух ее реализациях. Одна из этих реализаций опирается на процедуру канонического автоматного синтеза ДДС, а другая - на процедуру автоматного синтеза ДДС с использованием граф-схем алгоритмов (ГСА) ее функционирования.
Первая из отмеченных процедур конструирования нелинейного модельного представления в форме НДДС реализуется в виде следующего алгоритма.
Алгоритм 2.1 (А2.1)
конструирования модельного ВСВ представления НДДС на основе канонического автоматного синтеза
1. Сформулировать постановку задачи кодопреобразования, решаемой конструируемой ДДС.
2. Формализовать задачу кодопреобразования в виде абстрактного автомата (АА), задаваемого в виде пятиэлементного макровектора
АА: { Z,S,W,A,S }, (2.1)
где Z - алфавит высокого уровня (с возможным использованием вербальных описаний) входов абстрактного автомата мощности [z] = rz, S - алфавит высокого уровня его состояния мощности [S] = ns, W - алфавит высокого уровня выходов АА мощности [W] = mW, Л - правило (функция) перехода АА
8 - правило (функция) выхода, задаваемое функциональными соотношениями соответственно
в логике абстрактного автомата Мура и
в логике абстрактного автомата Мили. В (2.2) - (2.4) s(0), s( к), s(к +1) - соответственно начальное состояние, исходное состояние и состояние перехода АА, к - дискретное время, выраженное в числе тактов длительностью а t. При этом основным математическим средством описания правил (функций) Л, 8 на первом этапе конструирования являются графы переходов и выходов, на втором - таблицы переходов и выходов.
3. Осуществить переход от абстрактного автомата (2.1) к конечному автомату (КА)
КА: { U,X,Y,Л,8 } (2.5)
над простым полем Галуа GF(p) при p=2, путем кодирования элементов алфавитов высокого уровня АА (2.1) кодами, составленными из элементов поля GF (p). В выражении (2.5) U = h{Z}, X = h{s}, Y = h{W}, где к{(^)} - код (вектор-строка) элемента алфавита (•) размерности dimк{(^)}. Раз-
мерности кодов конечного автомата (2.5) и мощности алфавитов абстрактного автомата (2.1) связаны соотношениями dimU = r = argmin{pr > rZ }, dimX = n = argmin{pn > nS }, dimW = m = argmin{pm > mW } (2.6)
Коды алфавитов входа и выхода могут строиться в рамках требований (2.6) достаточно произвольно. Коды элементов алфавита состояния с тем чтобы избежать начальную установку КА должны использовать нулевую комбинацию, а так же учитывать специфику графа переходов АА. Так, если в графе переходов АА явно обнаруживается некоторая его цикличность, то из соображений простоты технической реализации НДДС коды ее состояний, соседние по графу, должны быть максимально приближены к соседним) [8], то есть должны характеризоваться минимальным кодовым расстоянием (см. параграф 3.2).
Представить правила X, 8 (2.2) - (2.4) КА после процедуры кодирования соответствующих алфавитов АА, соответственно в виде
и
при использовании автоматной логики Мура и
при использовании автоматной логики Мили, где x(0), x(k), x(k + l) - соответственно коды начального состояния, исходного состояния и состояния перехода.
4. Выбрать тип автоматной логики (Мура или Мили) функционирования конечного автомата на основе анализа требований, предъявляемых к НДДС по быстродействию и информационной надежности, таблиц переходов и выходов КА, полученных в результате выполнения п.3 алгоритма.
5. Выбрать тип используемых при построении НДДС триггеров, число которых не зависит от выбранного их типа и определяется размерностью n кода состояния автоматного представления НДДС. Учесть, что выбор конкретного типа триггера вводит в рассмотрение дополнительную функцию описания КА - функцию ju возбуждения информационного входа v триггера, задаваемую в форме
v(k ) = p[x(k )x(k + l)]. (2.10)
6. Построить аналитическое представление функционирования НДДС в виде двух систем булевых функций, описывающих процесс:
формирования выхода у в форме
у = у [ x( к ) и (к)], (2.11)
и формирования сигналов возбуждения информационных входов триггеров в форме
?(к )= ju\_x(k [,Х\_х(к к), и (к )]]= ц [х(к), и (к )]• (2-12)
Булеву функцию (БФ) (2.11) составить непосредственно на основе табличного представления правила 8 функции выхода КА, являющейся таблицей истинности на всем множестве наборов переменных, представленных кодами исходных состояний и входов. Для построения БФ (2.12) сконструировать таблицу возбуждения входов всех триггеров выбранного типа на основе представления (2.10) и таблицы переходов КА. Построенную таблицу использовать для построения БФ (2.12) в качестве таблицы истинности.
7.Привязать аналитические описания (2.11), (2.12) к элементной базе и построить схемотехническую реализацию НДДС. ¦
Примечание 2.1 (ПМ.2.1) Из приведенного алгоритма нетрудно видеть, что автоматный синтез существенно расширяет банк схемотехнических реализаций ДДС за счет снятия ограничений на логику функционирования триггеров, которое имело место в линейном синтезе ДДС. ?
Пример 2.1 (Пр.2.1)
В качестве примера рассматривается конструирование НДДС, преобразующая входную последовательность и(к)=8(к) в периодическую последовательность, обеспечивающую размещение информационных разрядов в кодах Хэмминга (7,4) (см. Пр1.1).
Для решения поставленной задачи конструирования ДДС воспользуемся алгоритмом 2.1.
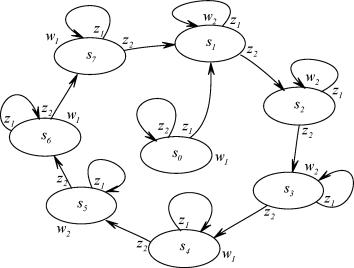 |
| Рисунок 2.1. Модель НДДС в логике абстрактного автомата Мура |
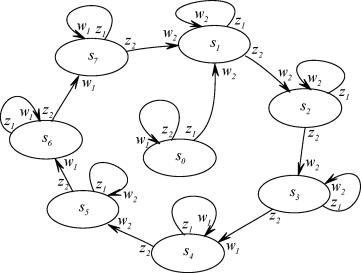 |
| Рисунок 2.2. Модель НДДС в виде абстрактного автомата Мили |
| Условие перехода | Состояния Sj | |||||||
| zi | S0 | S1 | S2 | S3 | S4 | S5 | S6 | S7 |
| zi | S1 | S1 | S2 | S3 | S4 | S5 | S6 | S7 |
| z2 | S0 | S2 | S3 | S4 | S5 | S6 | S7 | S1 |
| Таблица 2.2 | ||||||||||||||||||||||||||||||||||||||||||
|
| Таблица 2.3 | ||||||
|
| Состояния sk |
к Коды состояний КА sk x}x2x3 )k |
| S0 | 000 |
| s1 | 001 |
| s2 | 010 |
| s3 | 011 |
| s4 | 100 |
| S5 | 101 |
| s6 | 110 |
| S7 | 111 |
| Таблица 2.5 | ||||||
|
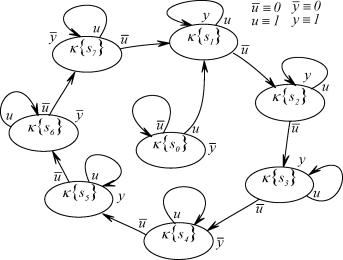 |
| Рисунок 2.3. Модель НДДС в виде конечного автомата Мура |
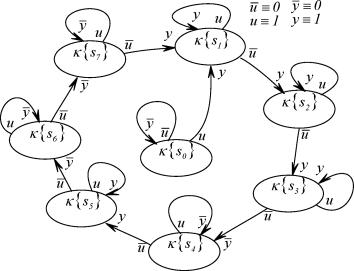 |
| Рисунок 2.4. Модель НДДС в виде конечного автомата Мили |
| Таблица 2.6 | ||||||||||||||||||||||||||||
|
| Таблица 2.7 | ||||||||||||||||||||||||||||||||||||||||||
|
формироваться сигнал по длительности кратный длЛ|0|ЫІо- Л / сти тактов работы устройства) выбираем для роежзации I / НДДС конечный автомат, функционирующий в автоматной логике Мура (рисунок 2.3).
4. Выбираем для реализации переменных состояния НДДС (рисунок 2.3) JK-триггеры.
5. Конструируем системы булевых функций:
- функции ц возбуждения, формирующие сигналы vJг и vK t
возбуждения информационных входов триггеров в форме
- U( XjX2X3 V XjX2X3 V XjX2X3 V XjX2X3 ) V
)
);
vj i
VJ 2
VJ 3
U\XjX2X3 V XjX2X3 V XjX2X3 V X1X2X3
= U ( XjX2X3 V XjX2X3 V XjX2X3 V XjX2X3 ) V
и(xjX2x3 v X1x2x3 V x1x2X3 V x1x2x3);
= U( X1x2X3 v x1X2X3 v x1x2X3 v x1x2x3 ) v
и(x1X2X3 v x1X2X3 v X1x2x3 v x1x2x3 v x1x2x3
);
Vk 1 - U X1X2X2 ;
vK2 - u (x1x2x3 v X1X2X3);
vK3 - и (x1x2x3 v X1X2X3 v X1X2X3);
и функции выхода в форме
- X1X2X3 V X}X2X3 V X1X2X3 V X1X2X3
Полученные в результате выполнения п.6 алгоритма булевы функции являются основой для схемотехнической реализации устройства. ¦ Рассмотрим теперь возможности автоматного конструирования с использованием граф-схем алгоритмов функционирования ДДС, для построения ее нелинейного модельного представления «вход-состояние выход» (ВСВ).
Алгоритм 2.2 (А2.2)
автоматного конструирования модельного представления (ВСВ) НДДС с использованием ГСА описаний
В операторные вершины вписать вербальные конструкции в виде инфинитивов или отглагольных существительных, несущих информацию о необходимости выполнения конкретного действия, с учетом того, что начальная и конечная вершины имеют соответственно только выход или только вход, а рабочая операторная вершина имеет один вход и один выход;
В условные вершины вписать словесные логические условия, с помощью которых осуществляется управление последовательностью действий проектируемой НДДС. Условные вершины имеют один вход и два выхода, причем если вершина моделирует процесс (состояние) ожидания выполнения условия, то один из ее выходов соединяется с ее входом.
Проконтролировать корректность составленной ГСА путем проверки наличия хотя бы одной ветви с выхода произвольной вершины, ведущей к входу конечной вершины, и проверки отсутствия ветвей с выхода вершины графа к входам более чем одной вершины. При контроле дополнительно учесть, что ГСА допускает размещение одного и того же условия в различных условных вершинах графа и разрешает выполнение одного и того же действия в различных операторных вершинах графа.
3. Составить формальную версию ГСА путем замены вербальных конструкций операторных вершин на элементы алфавита высокого уровня wj, j = 0, mW -1 символьного представления действий (операций, команд), и вербальных конструкций, вписанных в условные вершины, на элементы ,i = 1,rZ , алфавита символьного представления условий, имеющих бинарную реализацию.
4. «Погрузить» сформированную в п.3 алгоритма формальную версию ГСА конструируемой ДДС в среду абстрактных автоматов с учетом следующих обстоятельств.
Если АА строится в автоматной логике абстрактного автомата Мура, то всем операторным вершинам Wj присваиваются состояния sk+1, причем начальная w0 и конечная wk=mw-1
вершины объединены в одну, которой присваивается состояние s1 .
Если АА строится в автоматной логике абстрактного автомата Мили, то состояние s1 присваивается входу первой условной вершины, непосредственно следующей за начальной операторной вершиной. Это же состояние присваивается конечной операторной вершине. Остальные состояния sk, к = 2, nS присваиваются входам всех условных вершин, непосредственно следующих за операторными вершинами графа.
Обратить внимание на то, что АА, реализующий ГСА в логике автоматов Мура, характеризуется числом состояний nS , совпадающим с числом операторных вершин, в то время как АА, реализуемый в логики Мили, характеризуется числом состояний nS , в общем случае не совпадающим с числом операторных вершин, причем возможны такие ГСА, где число состояний меньше числа операторных вершин. На этапе погружения формальной ГСА в автоматную среду на паре автоматных логик Мили/Мура осуществить начальную минимизацию автоматной реализации НДДС. Зафиксировать результат погружения формальной версии ГСА в автоматную среду в форме АА, задаваемого с помощью макровектора (2.1) с функциями перехода и выхода в форме (2.2) - (2.4).
5. Выбрать автоматную логику функционирования АА и построить в выбранной логике граф переходов АА, в среду которого погружена формальная ГСА.
6. Выполнить п.п.3-7 алгоритма 2.1 применительно к АА в выбранной логике. ¦
Примечание 2.2 (ПМ2.2). При выполнении п. 5 А2.2 в фазе кодирования следует отметить, что кодирование алфавитов состояния и выхода осуществляется в полном соответствии с п. 2 А2.1. Кодирование элементов алфавита Z следует осуществлять путем переобозначения в форме ut = zt ,i = 1,rZ , причем rZ и r связываются условием тождественного равенства, если указанный способ кодирования неосуществим, то следует воспользоваться схемой п.2 алгоритма 2.1.
Данное примечание вызвано тем обстоятельством, что при построении формальной версии ГСА логические переменные zt в большинстве случаев имеют бинарную реализацию, то есть принадлежат полю Галуа GF(2). ?
Примечание 2.3 (ПМ2.3). При составлении БФ, предусмотренных п.5 алгоритма 2.1 применительно к конструированию функций возбуждения триггеров, они строятся в виде дизъюнкций основных конъюнкций, которые формируются на кодах исходных состояний x(k) и управляющих сигналов, считываемых с условных вершин и связывающих исходное состояние с состоянием перехода x( к +1). БФ формирования выходов, в случае использования логики абстрактных автоматов Мура, конструируются посредством дизъюнкций основных конъюнкций, представляющих собой исходные состояния автомата. В случае использования абстрактных автоматов Мили булевы функции строятся по той же схеме, что и булевы функции возбуждения. ?
Пример 2.2 (Пр2.2)
Конструируется нелинейная ДДС, которая решает задачу кодопре-образования, отмеченные ГСА- описания которой для абстрактных автоматов Мили и Мура представлены на рисунках 2.5 и 2.6 соответственно. При этом требуется обеспечить максимальное быстродействие устройства.
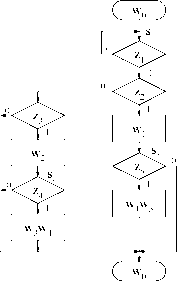 |
| Рисунок 2.5 |
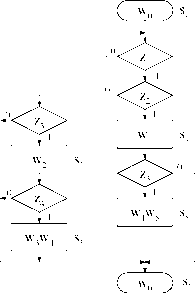 |
| Рисунок 2.6 |
1. Строим графы переходов и выхода описания функционирования устройства: для абстрактного автомата Мили - как показано на рисунке 2.7, для абстрактного автомата Мура - как показано на рисунке 2.8, при этом соответствующие им таблицы правила X перехода и правила 8 выхода запишутся в виде таблицы 2.8 и 2.9. В силу того, что характер решаемой задачи накладывают требование повышенного быстродействия на данное устройство, то принимаем логику функционирования конструируемого устройства в форме абстрактного автомата Мили.
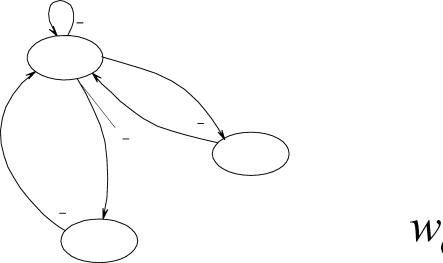 |
| Рисунок 2.7. Модель НДДС в логике абстрактного автомата Мили |
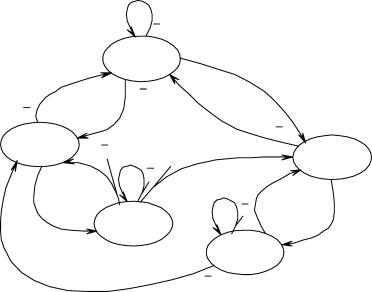 |
| Рисунок 2.8. Модель НДДС в логике абстрактного автомата Мура |
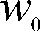



|
Структура АА |
Условие перехода zi | Состояния si | ||||
| s1 | s2 | s3 | s4 | s5 | ||
| Рисунок 2.7 | zi | s1 | — | — | — | — |
| z1z 2 | s3 | — | — | — | — | |
| z1z2 z3 | s2 | — | — | — | — | |
| z4 | — | s1 | — | — | — | |
| z4 | — | s1 | — | — | — | |
| z5 | — | — | s1 | — | — | |
| z5 | — | — | s1 | — | — | |
| Рисунок 2.8 | z1 | s1 | — | s3 | — | s5 |
| z1z 2 | s4 | — | s4 | — | s4 | |
| z1z2 z3 | s2 | — | s2 | — | s2 | |
| z4 | — | s3 | — | — | — | |
| z4 | — | s1 | — | — | — | |
| z5 | — | — | — | s5 | — | |
| z5 | — | — | — | s1 | — |
| Таблица 2.9 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| к{(к )} | к{( к +1)} | k{z (к)}, и. | k{w( к)} |
Возбуждаемые входы D триггеров | |
| (к)} 00 | 00 | U1 | 000 | ||
| 01 | Uj u2 | 001 | A | ||
| 11 | u1 U2u3 | 010 | A | A | |
| к{3 (k )} 01 | 00 | U5 | 000 | ||
| U5 | 100 | ||||
| 01 | — | — | — | — | |
| 11 | — | — | — | — | |
| k{s2 (k )} 11 | 00 | u4 | 000 | ||
| u4 | 011 | ||||
| 01 | — | — | — | — | |
| 11 | — | — | — | — |
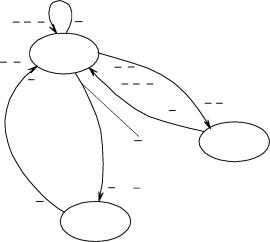 |
| Рисунок 2.9. Модель НДДС в виде конечного автомата Мили |
конструируемого устройства в виде КА, для чего выполняем кодирование указанных алфавитов и строим совмещенную таблицу 2.10 правила X перехода и правила 8 выхода. В соответствии c полученной таблицей строим граф (рисунок 2.9) переходов конструируемого устройства в виде КА.
Для реализации ячеек памяти устройства будем использовать D-триггеры. В этой связи булевы функции ju возбуждения входов vt триггеров и формирования выхода у устройства примут вид:
Uj - Uj U2U3 XjX 2 ;
U2 — {uju2 v uj u2u3)xjx2;
yj — u5x4x2;
y2 — uju2u3 xj x2 v u4 xj x2;
y3 — uju2 Xj x2 v u4 xj x2.
Полученные булевы функции могут быть положены в основу схемотехнической реализации конструируемого устройства. ¦
В заключение следует отметить, что банк модельных описаний устройств дискретной автоматики и телемеханики с использованием средств автоматной логики, конструируемых на триаде «{каноническое автоматное представление с помощью ГСА} - {автоматная логика Мили/Мура} - {триггерная логика}», предоставляет разработчику широкие возможности минимизации сложности схемотехнической реализации структурного представления «блок памяти - комбинационная схема» ДДС.
конструируемого устройства в виде КА, для чего выполняем кодирование указанных алфавитов и строим совмещенную таблицу 2.10 правила X перехода и правила 8 выхода. В соответствии c полученной таблицей строим граф (рисунок 2.9) переходов конструируемого устройства в виде КА.
Для реализации ячеек памяти устройства будем использовать D-триггеры. В этой связи булевы функции ц возбуждения входов vt триггеров и формирования выхода у устройства примут вид:
Uj - uj u2u3 XJX2 ;
ц2 — (ju2 v uj u2u3 )xjx2;
yj — u5 XjX2 ;
y2 — uju2u3 xj x2 v u4 xj x2;
y3 — uju2 xj x2 v u4 xj x2.
Полученные булевы функции могут быть положены в основу схемотехнической реализации конструируемого устройства. ¦
В заключение следует отметить, что банк модельных описаний устройств дискретной автоматики и телемеханики с использованием средств автоматной логики, конструируемых на триаде «{каноническое автоматное представление с помощью ГСА} - {автоматная логика Мили/Мура} - {триггерная логика}», предоставляет разработчику широкие возможности минимизации сложности схемотехнической реализации структурного представления «блок памяти - комбинационная схема» ДДС.
2.2. Построение дивидендных устройств помехозащитного кодопреобразования с помощью НДДС в логике произвольных триггеров
Рассмотренная в разделе 1 процедура конструирования линейных дивидендных устройств помехозащитного кодопреобразования (ДУПК) в форме ЛДДС опирается на векторно-матричный аппарат и имеет две фазы: кодирование и декодирование. Погружение в аппаратурную среду векторно-матричных описаний этих фаз в форме соответствующих ЛДДС дает для последних базовое представление в логике линейных D-триггеров [7, 42, 51], которое на основе концепции подобия (см. §1.4) может быть дополнено использованием линейных T-триггеров. Таким образом ДУПК в виде кодирующих и декодирующих устройств, реализованных в форме линейных ДДС, не выводит получаемые схемотехнические решения за пределы возможностей логики линейных триггеров.
Решение задачи конструирования указанных устройств с использованием возможностей нелинейных ДДС в логике произвольных триггеров является предметом данного параграфа. Задача решается погружением линейного дивидендного кодирующего и декодирующего устройств в фазе, когда получено векторно-матричное представление правил перехода и выхода устройств, в автоматную среду, свободную от ограничения на тип используемой триггерной логики. Таким образом решение задачи достигается агрегированием алгоритмов линейного и автоматного синтеза ДДС помехозащитного кодирования и декодирования.
Алгоритм 2.3 (А2.3)
линейного синтеза дивидендного кодирующего устройствах помехозащитного кодопреобразования
1. Сформировать параметр k информационной части (n,к)-ПЗК на основании мощности [ Q] = Nu передаваемого информационного массива Q в силу соотношения
к = arg{2к > Nu = [q]}.
2. Сформировать по заданной корректирующей способности (в виде выполнения условия Рош < Рдоп при вероятности
p = max [p01,p10 ] искажения элементарного сигнала кода) помехозащищенного кода и способу ее реализации число m проверочных разрядов (n, к )-ПЗК с помощью соотношения
Z C(+m )
i=1
т = arg\ Nc = Т -1 > N0ш
где Nc - число синдромов, Nош - число ошибок, s - кратность исправляемой ошибки и выбрать неприводимый модулярный многочлен степени m в силу соотношения
g(x)= arg{deg[g(x)]= m & dmin[g(x)] = 2s + 1} в качестве образующего многочлена ПЗК.
3. Найти D - образ g (d) выбранного в п.2 алгоритма образующего ММ g(x) с учетом того, что все передачи кодов и модулярных многочленов в аппаратуре кодопреобразования ведутся старшим разрядом вперед, в силу соотношений
(2.13)
x~=d :
g(d )=D {g(x )}= ~(x -)
где
g(x-): g(x) = xmg(x-) . (2.14)
4. Вычислить передаточную функцию ФЦКУ (d) устройства деления
модулярных многочленов (УДММ), в котором делителем является ММ g (x) так, что
Фцку ( d )= g( d). (2.15)
5. Построить структурную реализацию передаточной функции (2.15) в одном из канонических базисов с использованием правила некасающихся контуров Мейсона [41] на m элементах памяти 1-го порядка с передаточной функцией ФЭП (d)= d так, чтобы матрица B входа УДММ определялась соотношением
BT = K{xm + g( x)}.
6. Разработать устройство коммутации (УК) цепей проектируемого циклического кодирующего устройства и агрегировать его с УДММ, источником помехонезащищенного кода и линейным устройством (ЛУ) канала связи, с тем, чтобы в течение первых к тактов с помощью УК информационная часть кода направлялась
(x)
где
g(x)
в КС, а в УДММ формировался остаток r(x)= rest
a(x) - ММ помехонезащищенного кода, с которым совпадает информационная часть формируемого помехозащищенного кода, а в течение последних m тактов ЛУ канала связи подключалось к выходу УДММ, который с помощью УК на (к + і)-м такте преобразуется в регистр сдвига, хранящий остаток, выводимый через ЛУ в канал связи.
7. Присвоить, соблюдая порядок индексации, выходам элементов памяти состояния xi (к )> i = 1,m, а их входам - x,(k +1), что позволяет построить векторно-матричное описание функционирования циклического кодирующего устройства (ЦКУ), в течение первых к тактов записываемое как
x(k +1)= Ax(к)+ Bu(к); y(к)= Hu(к), (2.16)
и в течение последних m тактов как
x(k +1)= Ax(к); x(0)= x(к);y(к)= Cx(к), (2.17)
где A, A - матрицы состояния размерности m х m, B - матрица входа, C - матрица выхода, H - матрица «вход-выход» УДММ.
8. Проверить правильность функционирования кодирующего устройства с помощью векторно-матричных описаний (2.16), (2.17).¦
Процедура линейного синтеза устройства дивидендного декодирования представлена алгоритмом 2.4, особенность которого состоит в том, что синдром ошибки представляет собой вектор состояния циклического декодирующего устройства (ЦДУ), формируемый на последнем n -ом такте цикла деления.
Алгоритм 2.4 (А2.4)
линейного синтеза дивидендного декодирующего устройствах помехозащитного кодопреобразования
ФЦДУ(d)= col{dm+I-'g-1 (d); i = l,m}, (2.18)
принимая во внимание то обстоятельство, что выходом УДММ устройства декодирования является его вектор состояния.
3. Выполнить п.5 алгоритма 2.2 так, чтобы матрица B входа УДММ удовлетворяла равенству BT = Hп, Hп - последняя строка проверочной матрицы кода.
4. Следуя п.7 алгоритма 2.2, построить векторно-матричное описание ЦДУ в форме
x(k + l) = Ax( к)+ B f (к), (2.19)
где f(к)= y(k)+<^(к) - кодовая последовательность, поступающая в декодирующее устройство из канала связи, в котором вектор состояния x по принятии п разрядов кода f (к) принимает значение синдрома E ошибки <^( к).
5. Спроектировать устройство формирования сигнала п коррекции (УФСК) искажений принятого из канала связи кода f (к) в
зависимости от способа реализации корректирующей способности кода.
6. Проверить правильность функционирования декодирующего устройства с помощью векторно-матричного соотношения (2.19).¦
С целью решения поставленной задачи построения дивидендных кодирующих и декодирующих устройств в логике произвольных триггеров выполним «погружение» векторно-матричных моделей (2.16), (2.17) и (2.19), задающих соответственно функции перехода и выхода ЦКУ и функцию перехода ДКУ, в автоматную среду. Содержательной базой такого погружения в автоматную среду является то обстоятельство, что кодирование алфавитов входа, состояния и выхода уже произведено при построении линейных векторно-матричных представлений (2.16), (2.17) и (2.19). Если эти векторно-матричные соотношения использовать для формирования таблиц функций перехода и выхода ЦКУ и ДКУ, то конструирование автоматного представления устройств циклического кодирования и декодирования получит форму конечного автомата (КА).
Для случая помехозащитного кодирования в среде НДДС макровектор НДДС-ЦКУ автоматного описания ЦКУ принимает вид
НДДС - ЦКУ: {U,X,Y,X,S}, (2.20)
где двухразрядный код U = [ u, и у ] имеет элементами старшего разряда
элементы помехонезащищенного кода так, что u = uu, а младший разряд uу принимает значение «0» в течение первых k тактов работы ЦКУ, и значение «1» - в течение последних m тактов, при этом реали-
зация кода U в форме U = [ 11] невозможна; X = row{xl,i = 1,m}, Y = [y] имеют тот же смысл, что и в (2.16), (2.17); правила перехода Л и выхода 8 определяются в силу (2.16) и (2.17). Следует заметить, что в силу (2.16), (2.17) макровектор (2.20) задает ЦКУ как конечный автомат в логике автоматов Мили.
Макровектор НДДС-ЦДУ, описывающий циклическое декодирующее устройство в автоматной канонической форме, принимает вид
НДДС - ЦДУ: {F,X,H ,Л,8}, (2.21)_
где одноразрядный код F = [f], m-разрядный код X = row{xl,i = 1,m} имеют тот же смысл, что и в (2.16), код H имеет разрядность l сигнала (кода) коррекции, которая равна единице (l = 1) в режиме обнаружения ошибок и s (l = s) в режиме исправления ошибок информационной части кода; правило Л перехода определяется в силу (2.19), правило 8 выхода задается в форме булевой l-мерной функции
П = 8( x), (2.22)
что определяет ЦДУ как конечный автомат, функционирующий в автоматной логике Мура.
Погружение процедуры помехозащитного кодопреобразования в автоматную среду в фазе кодирования в форме НДДС-ЦКУ (2.20) и в фазе декодирования НДДС-ЦДУ (2.21) может быть выполнено с использованием представленных ниже алгоритма 2.5 и алгоритма 2.6 соответственно.
Алгоритм 2.5 (А2.5)
синтеза ЦКУ в форме НДДС в логике произвольных триггеров
1. Выполнить п.п.1-7 алгоритма 2.3.
2. Сформировать код входного алфавита КА (2.20) U = [и,иу ].
3. Выполнить п.2 алгоритма 2.1 и получить таблицу реализации функции перехода Я вида Я: x( k)х U(kx(k +1) НДДС-ЦКУ (2.20) для наборов U = [0М]; U = [ім] с использованием (2.16), для набора U = [0Щ - с помощью (2.17).
4. Выполнить п.2 алгоритма 2.1 и построить таблицу реализации функции выхода 8 : x( k)х U(k)^ y( k) НДДС-ЦКУ (2.20) для наборов U = [о\о ] и U = [ 1\ о ] с использованием (2.16), для набора U = [оМ] - с помощью (2.17).
5. Выполнить п.п. 4-6 алгоритма 2.1. ¦
Алгоритм 2.6 (А2.6)
синтеза ЦДУ в форме НДДС в логике произвольных триггеров
1. Выполнить п.п.1-4 алгоритма 2.4.
2. Выполнить п.2 алгоритма 2.1 и построить совмещенную таблицу реализации функций перехода Я: x(k)х F(k)^ x(k +1) и выхода 8 : x(k)^ n(k) НДДС-ЦДУ (2.21) с помощью (2.19) и (2.22).
3. Выполнить п.п. 4-6 алгоритма 2.1. ¦
Проиллюстрируем на примере процедуры синтеза двоичных устройств помехозащитного кодопреобразования в логике произвольных триггеров
Пример 2.3 (Пр2.3)
Просинтезировать циклическое кодирующее устройство, формирующее помехозащищенный код (7,4) с образующим многочленом
g (x )= x3 + x + 1 в форме НДДС в логике произвольных триггеров.
Решение поставленной задачи осуществляем с использованием алгоритма 2.5, в соответствии с которым осуществим:
123
| xT (k ) | xT (k + 1) | U = [u, uy ] | y( k) | Возбуждаемые входы триггеров | |||||||||||
| D | T | RS | JK | ||||||||||||
| 000 | 000 | 00 | 0 | ||||||||||||
| 011 | 10 | 1 | A | A | T |
T 13 | S 2 | S 3 | J 2 | J 3 | |||||
| 000 | 01 | 0 | |||||||||||||
| 001 | 010 | 00 | 0 | A |
T 1 2 |
T 13 | S 2 | A | J 2 | * 3 | |||||
| 001 | 10 | 1 | A | ||||||||||||
| 010 | 01 | 0 | A |
T J 2 |
T 13 | S 2 | A | J 2 | * 3 | ||||||
| 010 | 100 | 00 | 0 | A | T1 |
T 1 2 | A | A | J1 | * 2 | |||||
| 111 | 10 | 1 | A | A | A | T1 |
T 13 | A | S 3 | J1 | J 3 | ||||
| 100 | 01 | 0 | T1 | T | A | A | J1 | * 2 | |||||||
| 011 | 110 | 00 | 0 | A | A | T1 |
T 13 | A | A | J1 | * 3 | ||||
| 101 | 10 | 1 | A | A | T1 | T ^ 2 | A | A | J1 | * 2 | |||||
| 110 | 01 | 0 | A | A | T1 |
T 13 | A | A | J1 | * 3 |
| xT (k ) | xT (k + 1) | U = [u, uy ] | y( k) | Возбуждаемые входы триггеров | |||||||||||
| D | T | RS | JK | ||||||||||||
| 100 | 011 | 00 | 0 | A | A | T1 |
T J 2 |
T 13 | R1 | S 2 | S 3 | A | j 2 | J 3 | |
| 000 | 10 | 1 | T1 | R1 | A | ||||||||||
| 000 | 01 | 1 | T1 | R1 | A | ||||||||||
| 101 | 001 | 00 | 0 | A | T1 | R1 | A | ||||||||
| 010 | 10 | 1 | T1 |
T 1 2 |
T 13 | R | S 2 | R3 | A | j 2 | K 3 | ||||
| 010 | 01 | 1 | T1 | T |
T 13 | R1 | S 2 | R3 | A | j 2 | K 3 | ||||
| 110 | 111 | 00 | 0 | A | A | A | T | S 3 | J 3 | ||||||
| 100 | 10 | 1 | A |
T 1 2 | R2 | K 2 | |||||||||
| 100 | 01 | 1 | A |
T J 2 | R2 | K 2 | |||||||||
| 111 | 101 | 00 | 0 | A | A | T ^ 2 | R2 | K 2 | |||||||
| 110 | 10 | 1 | A | A | T | R3 | K 3 | ||||||||
| 110 | 01 | 1 | A | A | T | R3 | K 3 |
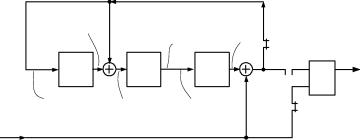 |
| Рисунок 2.10 |
| |||||||||||||||
| для последних m тактов |
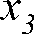
A
2.
3.
4.
0 10 0 0 1 0 0 0
C = [ 1 0 0].
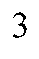
Выполнение п.2 алгоритма, которое устанавливает соответствие иу = 0 при [K1,K2,K3\=[101] и иу = 1 при
[К1,К2,КЗ]=[010\-Выполнение п.п.З, 4 алгоритма, которое дает совмещенную таблицу 2.11 реализации функций перехода Я : x(k)хU(к)^ х(к +1) х(А)х и(к)=> у(к)
НДДС-ЦКУ (2.20) для наборов U = [ 0 \ 6\ и U = [ 7_]Л с ж/ 7 і 7 пользованием (2.16), для набора t/ = [0|7] - с іАмордь^) А? ' J.
(2.17), а также - возбуждения ?(к)= ^[х(к),х(к +1)] информационных входов D-, Т-, RS- и ЛС-триіТерІув.
Выполнение п.п.4-6 алгоритма ^/с/учершугаблицы 2.11 для триггеров JK- типа, возбуждаемые входьтжоторых указаны в последних трех столбцах таблицы 2.11, которое дает систему булевых функций для формирования сигналов vJ? и ?к/ воз
буждения информационных входов триггеров, а также - для выхода ЦКУ, задаваемых в форме:
(и у V и у и),
Vj} = х}х^иу V иу и vJ 2 = иу их2 ((1х3 v х1х3) V иу их2 х3 V и у их2 ( ? х1х3)
Vj3 = х1х3 иу и ? х1х3 иу и ,
(и у V и у и ),
?К1 = хіх2 \иу V иу и,
?к2 = иу их2 ( х}х3 V х,х3 ) V иу и х2х3 V иу и х2 ((1х3 V х1х3)
?К3 = х1х3 и V х1х3 уиу и V иу и
)>
у = и у и V иу их1 ¦ ¦
(и у V и у и ),
VJ1 = х1х2\иу V иу и
VJ 2 = иу их2 (1х3 V х1х3) V иу их2 х3 V и у их2 (х V х1х3)
vJ 3 = х1х3 иу и V х1х3 иу и ,
(и у V и у и ),
?К1 = х1х2 \иу V иу и,
?К2 = иу их2 ( х1х3 V х1х3) V иу и х2х3 V иу и х2 ((1х3 V х1х3
?к3 = х1х3 и V х1х3 уиу и V иу и
)>
у = и и V и их, ¦ ¦
У у у 1
2.3. НДДС в задачах коррекции искажений помехозащищенных кодов
Коррекция принятых из канала связи помехозащищенных средствами помехозащитного кодирования кодовых комбинаций является финальной фазой помехозащитного кодопреобразования перед передачей принятой информации в техническую среду получателя информации. Организация коррекции искажений принятой из КС кодовой комбинации определяется многими факторами, основными из которых являются:
— метод формирования оценки искажения (матричный, не параметризованный дискретным временем, рассмотренный в параграфе 1.5, или дивидендный, построенный на линейных ДДС, рассмотренный в параграфах 1.7 и 2.2);
— форма представления оценки искажения (в виде синдрома ошибки, характерного для обоих методов формирования оценки искажения, и квазисиндрома, характерного только для дивидендного метода формирования оценки искажения);
— способ реализации корректирующей способности кода (в форме режима обнаружения ошибок или в форме режима исправления их);
— кратность обнаруживаемой и исправленной ошибки. Указанные факторы, определяющие характер алгоритмической и технической реализации процесса коррекции искажения принятых из КС искаженных, прошедших помехозащитное кодопреобразование на передающей стороне, кодовых комбинаций, сведены в таблицу 2.12.
127
| Метод формирования | Форма представления | Способ реализации корректирующей способности кода | ||
| оценки искажения кода | оценки искажения кода | Обнаружение ошибок | Исправление ошибок | |
| Матричный | с канонической проверочной матрицей | Синдром ошибки | Произвольной кратности r | Произвольной кратности s |
| с модифицированной проверочной матрицей | Синдром ошибки | Произвольной кратности r | Произвольной кратности s | |
| с канонической матрицей | Синдром ошибки | Произвольной кратности r | Произвольной кратности s | |
| Дивидендный | входа | Квазисиндром ошибки | — | Произвольной кратности s |
| с модифицированной | Синдром ошибки | Произвольной кратности r | Произвольной кратности s | |
| матрицей входа | Квазисиндром ошибки | — | Произвольной кратности s |
E = f H, E = fH. (2.23)
Если корректирующие способности ПЗК реализуются в форме режима обнаружения ошибок, то независимо от их кратности r сигнал п коррекции является скалярным и формируется как дизъюнкция элементов синдрома
E = [ ! Ет-} |К \ Е} ] = row{Ei; i = m,1}, (2.24)
который сформирован с помощью системы проверочных равенств, построенных в силу первого векторно-матричного соотношения (2.23) так, что для сигнала п можно записать
П = V Ei. (2.25)
i=m
Для режима обнаружения сигнал п коррекции искаженного ПЗК представляет собой квитанцию, которая используется для обнуления состояния сдвигового регистра хранения принятого из КС искаженного ПЗК и формирования запроса на передающую сторону на повторение передачи кодовой комбинации. Синдром E и сигнал п коррекции формируются на n -ом такте приема ПЗК из КС, где n - число разрядов помехозащищенного (n, к )-кода так, что отмеченное обстоятельство приводит к представлению сигнала п в форме
(2.26)
С і
п =
где
синхросигнал, подаваемый на вход конъюнктора на n -ом
такте; v , & - символы дизъюнкции и конъюнкции соответственно.
Если корректирующие способности ПЗК реализуются в форме режима исправления, то сигнал п коррекции становится векторным и представляет собой n -мерную вектор-строку, который содержит s единиц так, что при правильно сформированных параметрах (n,к) ПЗК для помеховой обстановки в КС выполняется соотношение
n = f. (2.27)
Математически векторный сигнал п коррекции искажений в принятом ПЗК в силу (2.26) и (2.23) может быть сформирован в силу соотношения
П = E H + (2.28)
где H + - матрица псевдообратная проверочной матрице H . На практике, как и в случае формирования синдрома E, при котором от векторно-матричного соотношения E = f H переходят к системе проверочных равенств, являющихся аналитической основой построения линейного шифратора, на выходе которого образуется синдром, при формировании векторного сигнала п коррекции принятого ПЗК приходится использовать тот же прием. В результате полученной системы Ч, =п,{E = [E,„!E„w ік\E,]} j = П1, (2.29)
конструируется синдромный дешифратор, на вход которого подается синдром E , а на его выходной шине - наблюдается векторный сигнал коррекции п = row{nj; j = n,1 j. Алгоритм формирования сигналов
коррекции (2.29) для случая произвольной кратности s исправляемого искажения принимает вид
Алгоритм 2.7 (А2.7)
формирования векторного сигнала коррекции искажения произвольной кратности s принятого из КС ПЗК
и векторов f помех по mod 2 с тем, чтобы мощность каждой суммы составила величину
No, = Nc = IСП. (2.30)
i=1
3. Пользуясь таблицей истинности, сформированной в п.2 алгоритма, составить систему булевых функций в дизъюнктивной совершенной нормальной форме (ДСНФ) тех синдромов, на которых j -й компонент j вектора п = row\pj; j = п,1} сигнала коррекции принимает единичное значение
С 1 _
(2.31)
П, = ?
&Ег\; j = п,,
V i=m J
где символ ~ принимает смысл символа инверсии ( - ), если Ei = 0 , и смысл пустого символа, если Ei = 1.
4. Пользуясь системой булевых аналитических выражений (2.31) построить схемотехническую реализацию синдромного дешифратора (СД) E = \EjEm-1 К E1 ] формирующего на выходной шине векторный сигнал п = [j! Пп-1 іК j ] коррекции принятого
из КС ПЗК. ¦
При этом следует иметь в виду, что если осуществлять коррекцию только информационной части ПЗК, то синдромный дешифратор может быть сокращен в схемотехнической реализации, где выходная шина СД будет иметь только к линий, на которых будет сформирован к -разрядный сигнал коррекции информационной части ПЗК
Г с 1 \ _1
(2.32)
& Ei
V i=m J
j = n,n - m
П = row
Следует заметить, что формы (2.31) и (2.32) являются нелинейным представлением линейного векторно-матричного соотношения (2.28).
Для осуществления коррекции информационной части (ИЧК) принятого из КС ПЗК сдвиговый регистр хранения последнего должен быть дополнен устройством коррекции кода (УКК). Это устройство представляет собой линейку сумматоров по модулю два, входы которых подключены к выходам триггеров регистра хранения принятого из КС ПЗК, находящихся в состоянии fr j = 1,п, и к выходным шинам синдромного дешифратора, на которых формируется сигнал п j , j = 1,п коррекции. Откорректированная информационная часть кода
y = row{yj = fj + пj; j = 1,п - m} (2.33)
переписывается в рабочий регистр хранения пользовательской технической среды для дальнейшего использования содержащейся в ИЧК информации.
Необходимо отметить, что формирование сигнала (2.32) принятого из КС ПЗК осуществляется как в случае обнаружения на n -ом такте, в силу чего реализационная версия сигналов коррекции (2.31) и (2.32) принимают вид
& (&C( n))
(2.34)
8 = row \ц = ?
= n,n
При формировании сигналов коррекции в форме (2.34) учитывается то обстоятельство, что m < n = к + m .
Пример 2.4 (Пр2.4)
Проиллюстрируем процедуру формирования сигнала коррекции информационной части ПЗК на примере кода (8,2), исправляющий ошибки кратности s = 1 и s = 2. Тогда следуя А2.7:
1. Составим таблицу истинности для формирования сигналов коррекции ошибок первой кратности на основании проверочной матрицы кода (8,2), имеющей представление
~1 1 0 0 1 Г 1 0 0 0 0 0 0 1 0 0 0 0 H= 001111 H= 0 0 1 0 0 0 .
000100
000010
000001
Сформируем синдромы однократных ошибок в силу второго соотношения (2.23), принимающего вид
[E E5 E4 В3 E2 E, ] = ] & 6 6 & 6 6 & ] H. Сигналы коррекции ошибок первой кратности получим, положив nJ = 6J; J = 8,1. Эта таблица истинности составляет первые восемь строк таблицы 2.13.
2. Образуем двукратные ошибки путем суммирования по модулю два двух однократных ошибок и сформируем соответствующие им синдромы путем суммирования по модулю два двух синдромов однократных ошибок. Результаты выполнения п.п.1,2 алгоритма сведены в таблицу 2.13.
3. На основе таблицы 2.13 оставим булевы представления сигналов П8 и Пь коррекции искажений в информационных (8-м и 5-м) разрядах кода (8,2), которые принимают вид
П8 = E6E5E4E3E2E1 V E6E5E4E3E2E1 V E6E5E4E3E2E1 ? E6E5E4E3E2E1 ? E6E5E4E3E2E1 ? E6E5E4E3E2E1 ? E6E5E4E3E2E1l
|
E6E5E4E3E2E1 V E6E5E4E3E2E1 V E6E5E4E3E2E1 V ¦ E6E5E4E3E2E1 V E6E5E4E3E2E1 Таблица 2.13 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Таблица 2.13 (Продолжение) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Утверждение 2.1 (У2.1). Пусть процесс дивидендного декодирования ПЗК, принятого из КС, осуществляется декодирующем устройством, имеющим векторно-матричное описание, параметризованное дискретным временем к, записываемое в форме
x(к + l)= Ax(k)+ Bu(к), x(0) = 0, (2.35)
где dimx = m, dimu = 1, dim A =(m x m), dimB =( m x 1), причем характеристический полином матрицы A состояния (2.35) удовлетворяет цепочке равенств
D(X) = det(AI + A) = g( x) I x=x, (2.36)
где g(x) - образующий модулярный многочлен ПЗК, degg(x) = m, при
этом степень m выбрана из условия исправления ошибок кратности s так, что
m = arg{ Nc = 2m -1 > Now = ±C(+„,}, (2.37)
где Nc, Nom - соответственно число синдромов и ошибок вплоть до
кратности s, тогда синдром однократной ошибки в X-ом разряде в помехозащищенном (n,к)-коде формируется на n-ом такте процесса деления в форме
Е = xT(n)=(Ak~1 B). ? (2.38)
Доказательство. Для доказательства утверждения рассмотрим случай, когда по КС передается нулевой ПЗК у (к )= 0 так, что из КС
принимается кодовая последовательность
і(к) = у( к ) + ?( к ) = ?( к). (2.39)
В силу того, что n -мерный вектор искажения по условиям утверждения имеет единицу только в X-ом разряде, то он имеет представление = 0;[ = 0;К ;tn-ui = 0;tn-x = 1;^ = 0;к ;i = о]. (2.40)
Вектор (2.40), записанный в виде кодовой последовательности 4(k) имеет вид
4(k): 4(0) = 0;4(1) = 0;К ;4(n-X-1) = 0;4(n- X) = 1;
4(n -X+1) = 0;К ;4(n -1)= 0. (2.41)
Рассмотрим суммарную версию ЛДДС (2.35) при входной последовательности и(к )=4(к), тогда на основании (1.25) с учетом x(0)= 0, а также вида (2.41) входной последовательности получим x(n)= An-1 Bи(0) + An-2Bи(1) + К + An-1-(n-X)Bu(n - X) + К
К+ Bи(n -1)= AnXB. ¦ (2.42)
Выражение (2.42) по существу содержит доказательство следующего утверждения.
Утверждение 2.2 (У2.2). Если принятый из КС ПЗК характеризуется искажениями в /л -ом и ?-ом и т.д. р-ом разрядах, то сформированный на n -ом такте деления синдром E ошибки 4 имеет вид
ET = (n) = Ал-1 B + Av-1 B +К + Ap-1 B). ¦ (2.43)
С целью дальнейших исследований сформулируем и докажем следующее утверждение.
Утверждение 2.3 (У2.3). Пусть процесс деления в дивидендном декодирующем устройстве (2.35) продолжается в течение (t +1) циклов
длительностью n тактов, тогда, если принятый из КС ПЗК f = у + 4 характеризуется искажением в р-ом и ?-ом и т.д. р-ом разрядах, то на каждом цикле деления на каждом такте кратном n = dim f будут формировать синдром E ошибок 4 в форме
ET =(x(nt)= Ал-1 B + Av-1 B +К + Ap-1 B). ? (2.44)
Доказательство утверждения строится на том, что при k > n u(k)= f (k) = 0, поэтому процессы при k > n в ЛДДС (2.34) декодирующего устройства будут описываться векторно-матричным выражением
x(k + 1) = Ax(k); x(n) = Ap1B + Av1B +К + Ap1B, (2.45) что для k = nt позволяет записать
x (k = nt )= A( t-1) nx (n). (2.46)
Если теперь учесть, что матрица A с характеристическим полиномом D(X)= g(x)| , принадлежащим показателю n, принадлежит показа
телю n так, что для нее можно записать
An = I, (2.47)
откуда следует и выполнение матричного равенства
A(t-1)n = I. (2.48)
Соотношение (2.48) совместно с (2.46) и (2.45) приводят к (2.44). ¦
И, наконец, сформулируем и докажем еще одно утверждение. Утверждение 2.4 (У2.4). Пусть принятый из КС ПЗК f = у + % характеризуется искажением в X-ом разряде, тогда, если в дивидендном декодирующем устройстве (2.35) процесс деления продолжается в течение (t +1) циклов длительностью n тактов, тогда при
k = nt + №, где № = n -X+ 1 будет формироваться квазисиндром E ошибки % в форме
E = BT . ? (2.49)
Доказательство. Учтем, что при k > n ЛДДС (2.35) дивидендного декодирующего устройства описывается векторно-матричным соотношением
х(k + l)= Ax(k), x(n), (2.50)
где x(n) для случая однократной ошибки в X-ом разряде имеет вид (2.42). Тогда для момента k = nt + №, где № = n -X+ 1 можно записать х (k = nt + № ) = A( t-1) n+№x (n ) = A№ Ak~1 B. (2.51)
Тогда равенство x(nt + №) = B выполняется при № = n - X + 1. ¦
Возвращаясь к проблеме коррекции искажений ПЗК, принятого из КС, с использованием синдромов E, которые формируются в моменты k = nt следует заметить, что организация коррекции как в режиме обнаружения, так и в режиме исправления полностью совпадает со случаем матричного метода формирования оценки искажения ПЗК. Так в случае реализации корректирующей способности циклического ПЗК скалярный сигнал ц коррекции, который представляет собой квитанцию, формируется на n -ом такте размещения ПЗК в сдвиговом регистре деления и процесса деления в регистре деления дивидендного ДКУ, формируется в силу (2.25).
В случае реализации корректирующей способности циклического ПЗК векторный сигнал ц = row{nj; j = n,1} коррекции формируется в
соответствии с алгоритмом 2.7, который следует модифицировать с учетом специфики формирования проверочной матрицы H кода. Тогда процесс формирования векторного сигнала rj = row{nj; j = n,1}
коррекции для дивидендного метода его формирования может быть представлен следующим алгоритмом.
Алгоритм 2.8 (А2.8)
формирования векторного сигнала коррекции искажения произвольной кратности s принятого из КС ПЗК
1. Построить проверочную матрицу H ПЗК, исправляющего искажения кратности s в форме
H = [a п-1В\Л n2B |К\AB\b] (2.52)
2. Выполнить п.п. 1-4 А2.7. ¦
Как и в случае матричного метода формирования оценки искажения ПЗК целесообразно ограничиться коррекцией искажений только в ИЧК, при этом сигнал коррекции формируется нелинейным способом в форме (2.33).
Особняком в дивидендном методе формирования оценки искажения ПЗК стоит задача коррекции кода с помощью квазисиндрома E вида (2.49). Квазисиндром может быть использован только в режиме исправления. При его использовании скалярный сигнал коррекции ц формируется в силу соотношения
n(k = (t + l)n -Х+ 1 ) = &Et = & BT; t = 1,2,К (2.53)
i=m i=m
Коррекция искажений с помощью сигнала коррекции (2.53) требует организации сдвигового вывода ПЗК из сдвигового регистра хранения кода в дополнительный регистр сдвига или перевода приемного регистра в режим кольцевого регистра сдвига на n -ом такте деления. На выходе приемного регистра сдвига должен быть включен сумматор по модулю два, выполняющий функции устройства коррекции ПЗК, на один вход которого подается искаженный ПЗК, а на другой - сигнал коррекции (2.53), на выходе которого наблюдается откорректированный код.
Алгоритм 2.8 (А2.8)
формирования векторного сигнала коррекции искажения произвольной кратности s принятого из КС ПЗК
3. Построить проверочную матрицу H ПЗК, исправляющего искажения кратности s в форме
H = [a n-1B\A n-2B |К !ab|b]T (2.52)
4. Выполнить п.п. 1-4 А2.7. ¦
Как и в случае матричного метода формирования оценки искажения ПЗК целесообразно ограничиться коррекцией искажений только в
ИЧК, при этом сигнал коррекции формируется нелинейным способом в форме (2.33).
Особняком в дивидендном методе формирования оценки искажения ПЗК стоит задача коррекции кода с помощью квазисиндрома E вида (2.49). Квазисиндром может быть использован только в режиме исправления. При его использовании скалярный сигнал коррекции п формируется в силу соотношения
n(k = (t + 1)п -Х + 1 ) = &Ег = & B f ; t = 1,2,К (2.53)
i=m i=m
Коррекция искажений с помощью сигнала коррекции (2.53) требует организации сдвигового вывода ПЗК из сдвигового регистра хранения кода в дополнительный регистр сдвига или перевода приемного регистра в режим кольцевого регистра сдвига на п -ом такте деления. На выходе приемного регистра сдвига должен быть включен сумматор по модулю два, выполняющий функции устройства коррекции ПЗК, на один вход которого подается искаженный ПЗК, а на другой - сигнал коррекции (2.53), на выходе которого наблюдается откорректированный код.
2.4. Дивидендные кодирующие и декодирующие устройства укороченных циклических кодов с коммутируемой структурой
Проблема укороченных кодов состоит в реализации возможности сокращения аппаратурных затрат при использовании матричного метода помехозащитного кодирования и декодирования, не параметризованных дискретным временем, и сокращения временных затрат при использовании для тех же целей дивидендного метода. Проблема укороченных кодов возникает, когда в силу целочисленности числа m проверочных разрядов это число оказывается одним и тем же для числа разрядов k помехозащищенного кода а и для случая числа разрядов k1 < k кода а. Это означает, что два соотношения при заданных помеховой среде в КС и требованиях к достоверности передачи соотношения
n=m+k
(2.54)
i=1
i
п 1=m 1+k 1
Nc = 2m1
(2.55)
m1
arg
ош
i=1
дают один и тот же результат так, что выполняется равенство
m1 = m . (2.56)
Как следствие в случае решения задачи помехозащитного кодопреоб-разования средствами циклического кодирования и декодирования укороченный помехозащищенный (n1, к1 )-код, где n1 = к1 + m, будет иметь тот же образующий ММ g(x) с degg(x)= m, что и (n, к)-ПЗК, где n = к + m, при этом g(x) принадлежит показателю n .
Если задача помехозащитного кодопреобразования укороченного (n1, к1)-ПЗК решается матричными методами, то помехозащитное ко-
допреобразование может быть осуществлено с использованием редуцированной образующей матрицы G, а помехозащитное декодирование может быть осуществлено с использованием редуцированной проверочной матрицы H (n, к)-помехозащищенного кода. Редуцирование
образующей матрицы G осуществляется вычеркиванием (к - к1) первых столбцов и первых строк этой матрицы, в результате чего формируется образующая ( х (щ = к1 + m )) -матрица G(n,ki) ПЗК (nl5 к1) с
тем же числом проверочных разрядов, что и код (n, к). Редуцирование матрицы H осуществляется вычеркиванием ( к - к1 ) первых строк этой матрицы, в результате чего формируется проверочная (n1, m)-матрица H(п,кі) ПЗК (n1, к1), которая при декодировании будет формировать синдромы той же размерности m , что и в случае декодирования (n, к)-ПЗК с помощью матрицы H . В связи с тем, что при практической реализации матричного метода помехозащитных процедур кодирования и декодирования от матриц ПЗК переходят к системе линейных скалярных соотношений для кодирования и проверочных соотношений для декодирования редуцирование матриц G и H не приводит к уменьшению числа этих соотношений. Сокращается лишь число аддитивных членов в них, что в итоге приводит к уменьшению аппаратурного состава устройств кодирования и декодирования на число (к - к1) сумматоров по модулю два.
При дивидендном методе помехозащитного кодопреобразования укороченных кодов имеет место следующая картина. Аппаратурно в кодирующем устройстве с точностью до изменения момента коммутации в устройстве деления модулярных многочленов, когда оно переводится в режим регистра сдвига для вывода в КС остатка от деления, ничего не меняется. В декодирующем устройстве, если не предпринять специальных структурных мер, появляется временная избыточность, состоящая в том, что при nj < n так, как образующий ММ g(x) укороченного (nj, к1 )-кода и (n, к)-ПЗК один и тот же, причем он принадлежит показателю п, а не nj, то есть она оказывается большей длины укороченного (nj, к )-кода. Более того, «квазисиндром» искаженного укороченного кода по своему положению на временной оси на повторных циклах деления перестает быть согласованным с искаженным разрядом укороченного кода (УПЗК). Таким образом корректирующие возможности (nj, к)-ПЗК оказываются представленными только синдромом, квазисиндром перестает быть опознавателем ошибки. Однако корректирующие возможности (n^ к)-ПЗК могут быть расширены до возможностей (n, к)-ПЗК, если сделать цикл деления равный длительности nj (nj, к )-ПЗК. Эта задача решается, если базовую векторноматричную модель ДКУ
x(к + 1)= Ax(к) + Ви(к), x(0) = 0, (2.57)
дополнить цепями коммутации структуры цикла деления так, что векторно-матричная модель ДКУ укороченного (nj, к )-ПЗК принимает
вид
(к + l)= Ax(к) + Bu(к)+ BK1 ик1 + Вк2 ик2, x(0)= 0. (2.58)
В (2.58) сигналы коммутации принимают значение ик 1 = 1,ик2 = 0 когда и(к )= f (к) - принимаемая из КС искаженная кодовая комбинация в момент коммутации характеризуется равенством и (к )= 0, и и к 1 = 0,и к 2 = 1 - когда и (к) в момент коммутации характеризуется равенством и(к) = 1. В связи со сказанным матрицы Вк 1 и Вк2 можно сформировать, опираясь на положения следующего утверждения.
Утверждение 2.5 (У2.5). Для того, чтобы цикл деления при декодировании укороченного (nj, к )-ПЗК дивидендным методом был бы
согласован с редуцированной на (n - nj) первых строк проверочной матрицей достаточно, чтобы матрицы входа Вк 1 и Вк2 для коммутирующих сигналов ик1 и и к2 имели вид
Вк 1 = ( I + A)в , (2.59)
Вк2 = AnВ . ? (2.60)
Доказательство утверждения начнем со случая, когда и(к )= О, ик1 = 1 и ик2 = 0 . Для этого случая модельное представление (2.58) примет вид
_х (к + l) = A x (к)+ BK1,_(2.61)
где х(к) и х(к +1) с точностью до транспонирования должна совпадать соответственно с первой и последней строками редуцированной проверочной матрицей (n1, к1 )-ПЗК так, что выполняются равенства
_X ( к ) = Ит{п.п,+1), (2.62)
но
_Н(П1+11) = Aп- B ; HI = B ._(263)
Подстановка (2.62) в (2.61) с учетом (2.63) приводит к (2.59). Рассмотрим теперь случай, когда и( к)= 1, иK1 = 0 и ик2 = 1. В этом случае модель ДКУ (2.58) принимает вид
_х(к + 1) = Aх(к) + B + BK2._(264)
Подстановка в (2.64) соотношений (2.62) с учетом (2.63) приводит к (2.60). ¦
Следует заметить, что сигналы и к1 и ик 2 коммутации дивидендного декодирующего устройства формируются в форме конъюнкций
и к1 = и к и (к), и к 2 = и к и (к), (2.65)
где сигнал ик формируется, как основная конъюнкция набора переменных, задаваемых элементами вектора х состояния ДКУ, удовлетворяющего соотношению
_х = An1 -1B ._(266)
Дивидендное декодирующее устройство (2.58) для декодирования укороченных (п1, к1 )-ПЗК формирует синдромы E ошибок в моменты к = n1 (t + 1)+(п1 + 1 - А) при искажении ПЗК в X-ом разряде при передаче по каналу связи при (t +1)-циклах деления длительностью п1.
Полученные результаты по синтезу дивидендного декодирующего устройства УПЗК с коммутируемой структурой цикла деления, обеспечивающей корректирующие возможности помехозащищенного кода в форме синдромов и квазисиндромов искажений можно представить в виде следующего алгоритма.
Алгоритм 2.9 (А2.9)
конструирования дивидендного декодирующего устройства с коммутируемой структурой
k1 = arg {2l Q] = Nu }
где [Q] = Nu - мощность информационного массива Q .
2. Сформировать параметр m проверочной части ПЗК в силу
(2.54)-(2.56).
3. Выбрать образующий модулярный многочлен g(х) степени deg g(х)= m и определить показатель n, к которому принадлежит g (х).
r (х)= rest Х i = 1,n -1 сформировать g(х)
4.
С помощью остатков проверочную H и
образующую G матрицы (n,k
)-
помехозащищенного кода.
5. Построить редуцированные проверочную и образующую матрицы (n, k = n - m ) -УПЗК.
6. Вычислить D-образ g (d) образующего ММ g (х).
7. Вычислить передаточную функцию ф( d) устройства деления модулярных многочленов в форме
ф( d )= g-1 (d) •
8. Построить структурное представление передаточной функции
ф(d ) = g _1 (d ) в таком сопровождающем базисе, в котором матрица информационного входа В удовлетворяла второму условию в (2.63).
9. Построить векторно-матричное представление ДКУ в форме
(2.57).
10. Построить векторно-матричное представление ДКУ с коммутируемой структурой в форме (2.58), сформировав матрицы Вк 1 и
Вк2 коммутирующих входов в форме (2.59), (2.60).
11. Дополнить ДКУ с векторно-матричным представлением (2.58) цепями формирования сигналов коммутации ик1 и ик2 с помощью булевых функций (2.65).
12. Сформировать цепи вывода из ДКУ синдрома E и квазисиндрома E. ¦
Пример 2.5 (Пр2.5)
Для иллюстрации полученных результатов рассмотрим процедуру синтеза ДКУ с коммутируемой структурой на примере укороченного (n1, k1 )= (5, 2)-кода, построенного на базе (n, k)-кода (7, 4), сформированного с помощью образующего ММ g (х) = х3 + х + 1 и обладающего образующей и проверочной матрицами
| u | 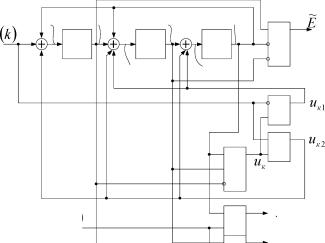 |
| C (n, )= C ( 5) |
x2(k )C (ni )= E23
x3( k )C (ni )= El
(k+1)
ET =E E2 E, J
Рисунок 2.11. Структурная схема ДКУ
| G = |
| 1110 10 0 0 1110 10 110 10 0 1 |
Следуя А2.9 получим: редуцированные о<
рицы (5, 2)-УПЗК в форме
— редуцированные образующую G и проверочную H мат-
(5,2) (5,2)

| 10100 110 10 0 10 0 1 |
|
G = (S.2) | |||||||||||||||
|
— векторно-матричное представление ДКУ укороченного (5,2)-УПЗК с коммутируемой структурой в форме (2.58) с матрицами коммутирующих входов
| B + A5 B |
|
BK 2 = AП1B = A5 B =
— сигналы коммутации
u к 1 = u к u (k )= x1x2x3u ( k ), u к 2 = u к u( k )= x1x2x3u( k )
На рисунке 2.11 приведена сконструированная структурная схема ДКУ (5, 2)-УПЗК с коммутируемой структурой.
— векторно-матричное представление ДКУ укороченного (5, 2)-УПЗК с коммутируемой структурой в форме (2.58) с матрицами коммутирующих входов
| 0 | 1 | 1 | ||
| 0 | I | 1 | = | 1 |
| 1 | 1 | 0 |
BK 2 = An1 B = A5 B =
— сигналы коммутации
uK1 = uKu ( k)= x1x2x3u ( k), u K 2 = u K u( k )= x1x2x3u( k )
На рисунке 2.11 приведена сконструированная структурная схема ДКУ (5, 2)-УПЗК с коммутируемой структурой.
2.5. Аппарат селлерсовского дифференцирования в задачах анализа булевого описаний НДДС дискретной автоматики
В своей работе [65] Ф. Селлерс ввел в практику использование производных (разностей) булевых функций на предмет обнаружения ошибок в функционировании дискретных устройств, аналитическое представление которых задается с помощью аппарата БФ. В своей монографии [47] Ф. Селлерс переносит предложенный аппарат на задачу обнаружения ошибок в работе ЭВМ. Однако аппарат селлерсовского дифференцирования, за некоторым исключением [1, 9, 17], остается за пределами массовой технической литературы, проблемно ориентированной на разработки устройств дискретной автоматики.
Задача параграфа - привлечь внимание разработчиков УДА к возможностям аппарата селлерсовского дифференцирования и предложить инструментарий для исследования аналитических описаний УДА в классе НДДС представлений. С этой целью сформулируем основные положения аппарата селлерсовского дифференцирования.
Определение 2.1 (О2.1). Частной производной Селлерса (ЧПС) 1-го порядка [1, 9, 17, 47, 65] булевой функции
д x
д f (x)
д x,
f (x) = f (x1,x2,K ,x,,K xn) по булевой переменной x, называется булева функция df (x), задаваемая выражением
Л
=f (xnx2,K ,x,,K xn)© f(xnx2,K ,x,,K xn). ? (2.67)
Вычисление частной производной Селлерса от БФ
f (x) = f (x1 ,x2,K , x, ,K xn)
по переменной x, может быть произведено несколькими способами. Первый способ основан на определении ЧПС (2.67).
Второй способ использует метод карт Карно [47], в соответствии с которым строятся две карты Карно для булевых функций f (, x2,K , x, ,К xn) и f (x1, x2,K , x, ,K xn), которые суммируются по модулю два, что приводит к карте Карно для частной производной. Этот способ позволяет получать минимальное представление ЧПС.
Третий способ использует разложение К. Шеннона [1], которое для (2.66) позволяет записать
д f (x)
д x,
.)• (2.68)
, x,-1,1
-1,0,x1+1,K xtx^x2,K
xi+1,K x,
x^x2,K
Четвертый способ, в развитие третьего способа, использует представление БФ f (x1, x2,K , x, ,K xn) с помощью таблицы истинности, наборы переменных в которой представлены в форме, имеющей x, в качестве переменной младшего разряда набора. В этом случае смена значения с xі на xi, приводящая к смене значения БФ, свидетельствует о единичном значении ЧПС на этом наборе, а отсутствие смены значения БФ - о нулевом значении ЧПС. Следует заметить, что последний способ позволяет оценивать значимость переменной x, в БФ, определяемую весом ЧПС на всех наборах переменных.
Для вычисления частных производных Селлерса от БФ полезно использовать их свойства, которые могут быть установлены [1] непосредственно из определения.
Свойство 2.1 (СВ2.1). (Инвариантность ЧПС относительно инверсии)
(2.69)
f = f = f =д? дxi дxi д x, дx,
Свойство 2.2 (СВ2.2). (Правило дифференцирования констант)
— = — = 0. ? (2.70)
дxi дxi
Свойство 2.3 (СВ2.3). («Тривиальные свойства» дифференцирования)
dx, dx, dx, dx,
= 7. ? (2.71)
dx, dx, dx, dx,
Свойство 2.4 (СВ2.4). Если БФ f (x7,x2K ,x,,K xn) представима в форме конъюнкции функций, одна из которых не зависит от x f {xj,x2K ,x,,K xn) =
= f1 (xj , j = 7,n,j * І )¦ І2 ( x!,x2 ,K ,x, ,K xn )= f1 (x) ¦ f2 (x)-
то
df (x)=d{ fl ( x )f2 ( xD = f (x )d f2 ( x) ?
(2.72)
dx, dx, dx,
Свойство 2.5 (СВ2.5). Если БФ f (x) представима в виде конъюнкции БФ (p1 (x) и (р2(x):
f ( x )= (Pi ( x )^2 ( x ) ,
то
fl = p) P( (X)9P( (x)S?H e^PH .%№. ? (2.73)
dx, dx, dx, dx, dx,
Свойство 2.6 (СВ2.6). Если БФ f (x) представима в виде дизъюнкции БФ р7(x) и р2(x):
f ( x )=Pi( x )vp2( x ), (2.74)
то
sjUJpM P (x)e-p (^^pH e^pH .%№. ? (2.75)
d x,
d x,
d x,
d x,
d x,
Свойство 2.7 (СВ2.7). Если БФ f( x) представима в виде суммы по модулю два БФ р7 (x) и p2 (x):
f ( x )=p7 ( x )e p2 ( x ), то
d f ( x) =dPl ( x) edP2 ( x) ? dx, dx, dx,
•-Ч r( \
(2.76)
x)
Свойство 2.8 (СВ2.8). Если БФ f (x) представима в форме конъюнкции ее переменных:
| д f ( x ) = д x, |
|
Свойство 2.9 (СВ2.9). Если БФ f (x) представима в форме дизъюнкции ее переменных:
|
* : II * | (2.79) |
|
дf ( x) n - -= & x J. ? д x, J&1 J | (2.80) |
j * i
Свойство 2.10 (СВ2.10). Если f (x) является сложной БФ, задаваемой в форме
f ( x )= f ( x,V( x )), (2.81)
то
= f (x1,x2,K , x, ,K xn,^(x1,x2,K , x, ,K xn ))©
д f ( x )
© f (x1,x2,K ,xt,K xn,v(xnx2,K ,xt,K xn)).? (2.82) Рассмотрим далее понятие частных смешанных производных Селлерса высокого порядка БФ и их свойства.
Определение 2.2 (О2.2). Двукратной смешанной производной Селлерса булевой функции f (x)= f (xl5 x2,K , x, ,K , xj ,K , xn) от n булевых
переменных называется БФ, задаваемая [9, 17] выражением
| dxj dxt dxj dxt dxt |
|
Определение 2.3 (О2.3). m-кратной смешанной производной Селлерса по m переменным xn, x,2,K , xim булевой функции
f (x) = f (x1,K , xi1,K , xi2 ,K,xim,K,xn) называется БФ, задаваемая [9, 17] выражением
д mf (x) = д
д xl
дxt1дxi2K дxit
V д^2
V V im ))) f
\Y\
д f (x )
(2.84)
д x„
V дxi(m-1)
V дxi1 JJ)
Введем в рассмотрение еще одну m-кратную производную по вектору из m элементов.
Свойство 2.11 (СВ2.11). (Равенство нулю частной селлерсовской производной порядка к > 1 произвольной БФ)
(2.85)
д xk
к >1
Доказательство. Свойство является следствием определения О2.1, примененного к булевой функции типа ЧПС первого порядка от исходной БФ по той же переменной. ¦
Определение 2.4 (О2.4). Производная m-го порядка
от булевой функции f (x) = f (.x]tx2,K ,xn) по кортежу переменных (xi1xi2 К xim) определяет условия, при которых функция f (x) изменяет
свое значение при одновременном изменении значений переменных кортежа. ?
Для вычисления введенной с помощью О2.4 производной воспользуемся теоремой Д. Бохманна, доказательство которой можно найти в
[9].
д mf (x)
3(Xi1Xi2 К Xjm )
Теорема Д. Бохманна. (Теорема Т.2.1)
зmf(x)
по кортежу (xi1xi2 К xjm) от скалярной
Производная
3 (xj1Xj2 К Xim )
булевой функции f (x) = f (x1,x2K ,xn) представима суммой по модулю два всех ее переменных порядка к от 1 до n:
з mf (x) . Z f ©z д 2f
3(XUXi2 К Xim ) Vi 3x,
i.j dXi»dXjv
iM* Jv
д 3f
д mf
(2.86)
©К ©-
.¦
дxi13xi2 К дxn
д x,,,d xjvd x
i,j,l
Jv^lp
ip
jv
i,
Сформулированную задачу решим в нескольких постановках. В первой постановке контроль корректности булевых описаний с помощью аппарата частных производных Селлерса 1-го порядка осуществим инвариантным относительно его конкретного использования способом с помощью веса ЧПС на всех наборах переменных. В этой постановке задача решается использованием следующих определений и утверждений.
f (x )
Определение 2.5 (О2.5). Весом P
частной производной
f (x) Селлерса 1-го порядка от булевой функции f (x) по перемен-
ной xt называется сумма значений БФ -f (x) на всех 2п наборах
д Xi
x = row{xi,i = 1,п}:
{x} булевых переменных
(2.87)
д xi
h=1
{ x}=X
Введенное определение позволяет на основе свойств частной производной Селлерса (ЧПС) 1-го порядка сформулировать следующее утверждение.
д
Утверждение 2.6 (У2.6). Если вес ЧПС -f (х) на всех 2п набо-
д X;
\хг,і = 1,п}
рах х = row\xi,i = і,піравен нулю так, что
P(х )1 =
(2.88)
то в дизъюнктивной форме представления булевой функции f (х) происходит полное «склеивание» по переменной xt. ?
Доказательство утверждения строится на том, что
P1-^ f(х)! = 0 означает, что дf(X) = 0 на всех наборах переменных, [д х, J дхг
в том числе и на тех ц наборах, где f (х) принимает единичное значение так, что для этих наборов становится в силу (2.67) справедлива запись:
f (х^Д ,х,,К хп) = 1; f (хпх2К ,х,,К хп) = 1. (2.89)
Тогда (2.89) позволяет для дизъюнктивной нормальной формы БФ f (х) записать
Г \
Ц п
V & х
l=1 j=1
V j *1
(хі V хі ) = V &
(2.90)
a
где хі
1 = хj при a = 0 и хj1 = хj при a = 1. ¦
Утверждение 2.7 (У2.7). Если вес ЧПС
на всех 2п наборах
переменных х = row{хІ,і = 1,п}равен 2п так, что
д
д х,
f (х )
2п
(2.91)
то при конструировании множества пар наборов булевых переменных полной мощности равной 2п~1, на которых эта БФ меняет свое значение, не найдется такой пары, на которой эта БФ сохраняет свое значение. ?
Доказательство утверждения содержит в себе определение ЧПС д f (х), которое фиксирует изменение значения БФ f (х) при измене-
д хі
нии переменной х, на ее инверсию х(, что соответствует своей паре наборов булевых переменных. ¦
Утверждение 2.8 (У2.8). Вес P{-^ f (х)} ЧПС дf (х) на всех 2П
[д xt \ д xt
наборах переменных в простом поле Галуа GF(2) всегда представляет собой величину кратную двум. ?
Доказательство утверждения строится на том факте, что для каждого набора переменных вес P f (х) I может принимать значение
[д х, J
нуль или единица, а любая смена значения функции f (х) всегда подразумевает два набора переменных, на которых БФ f (х) переключается по схеме 0 ^ 1 и 1 ^ 0, а, следовательно, исключительно на которых P{dj^f(х)} = 1' ¦
Следствие 2.1 (С2.1) из У2.7 и У2.8.
i = 1,n, позволяет проранжировать переменные
дх
Вес P{—^— f (х)},i = 1,n,
хг,і = 1,n по степени их значимости в булевой функции f(х), при этом, чем больше значение веса P{-^ f (х)}, і = 1,n, тем значимее
I дх, I
переменная хі. ?
Вторая постановка задачи предполагает «встроенность» булевых функций в структуру аналитического описания комбинационной схемы (КСХ) УДА. Здесь основными БФ являются булевы функции возбуждения входов используемых триггеров и булевы функции формирования выхода процесса кодопреобразования в УДА. Причем задачу в этой постановке решим с использованием канонических автоматных представлений и ГСА-описаний функционирования УДА.
Выполнить контроль корректности составления ГСА-описания функционирования НДДС на фазе перехода от «вербальной» версии ГСА к ее формальной версии позволяют положения У2.6 и У2.7. Здесь оказываются полезными положения следующего утверждения.
Утверждение 2.9 (У2.9). Пусть fms(х) - БФ перехода от операторной вершины Ym к операторной вершине Ys, тогда fms (х) оказывается составленной корректно, если ни по одной из переменных х, на наборах, на которых эта функция принимает единичное значение,
д fms (х)
производная этой функции
і = 1,n не принимает нулевое
значение, то есть
ф 0, i = 1,n. ? (2.92)
d xi
Доказательство утверждения не приводится в силу того, что данное утверждение можно рассматривать как следствие из У2.7 применительно к формальной версии ГСА-описаний НДДС. ¦
Как уже упоминалось выше, в общем случае произвольная НДДС включает в свой состав БФ, реализующие правило ц (2.12) формирования сигнала ? возбуждения информационных входов триггеров, а также БФ, реализующие правило 8 (2.8), (2.9) формирования выхода. Таким образом, применив к (2.8), (2.9), (2.12) аппарат частных производных Селлерса 1-го порядка, получим оценки структурных свойств НДДС в форме детектируемости и достижимости, описываемых каноническими конечными автоматами.
Утверждение 2.10 (У2.10). Состояние Sl НДДС с кодом состояния к {S,} = row{xj,j = 1,n} является недетектируемым по переменной xi относительно р-го компонента выхода НДДС если ЧПС от р-го компонента функции выхода (2.16) по этой переменной удовлетворяет условию
д8р( x)
д xi
(2.93)
=0. ?
x=к {s, }
Доказательство утверждения использует содержательное определение ЧПС 1-го порядка. ¦
Очевидно, становится справедливым положение следующего утверждения.
Утверждение 2.11 (У2.11). Переменная xi кодов состояния НДДС оказывается полностью недетектируемой относительно р-го ком-
д8р( )
0 на
понента выхода НДДС, если по выходу St вес ЧПС P \ —р
{ dx
всех 2п наборах переменных x = row{xj,j = 1,n}. ?
Доказательство утверждения опирается на положения У2.7 и содержательную часть У2.10 о детектируемости состояний конечного автомата. ¦
Утверждение 2.12 (У2.12). Состояние Sl УДАТ с кодом состояния к {S,} = row{xj,j = 1,п} является недостижимым по входной переменной uv ,v = 1,r, если ЧПС от функции возбуждения (2.12) для этого состояния удовлетворяет условию
dju (x,u) . —
col{ —--; ] = 1,n
ди
д~ (x,u )
0. ? (2.94)
Is, I
ди?
Доказательство. Справедливость положений утверждения обнаруживают свойства ЧПС 1-го порядка и аналитическое представление функции возбуждения триггеров. ¦
Примечание 2.4 (ПМ2.4). Нетрудно видеть, что У2.12 содержит в себе потенциал развития мысли в направлении введения понятия полной недостижимости состояния Sl, когда условие (2.94) выполняется для всех v = 1,r входных переменных и?. ?
Примечание 2.5 (ПМ2.5). Положения У2.11 являются эффективным средством контроля булевого описаний НДДС на предмет достижимости неопределенных описанием НДДС состояний. Такая ситуация имеет место в НДДС, если при ее заданном функционировании используются не все кодовые комбинации вектора x ее состояния размерности dimx = n при мощности 2п полного их множества. ? Воспользуемся теперь смешанными производными Селлерса для разложения булевой функции в заданной точке пространства над двоичным полем Галуа GF(2). Конструктивный результат решения этой
задачи содержится в теореме Горбатова В. А. [17, теорема 2.3].
Теорема В. А. Горбатова (Теорема Т2.1) Любая булева функция
f (x) = f (xl, x2,K > xn )
представима своим значением в точке x = (00K 0) и значениями всех
д д f д 2f K д nf ее производных ——,---,К
в этой точке в виде
д xi
д xi1д xi2
дx1 д x2 K дxn
n д 2 f
¦ xt © Z-—
~= 1 д xi д x ¦ x=0 iij i j
f (x ) = f (0
¦ xixj 0K
1 J
д x;
i=1
x=0
x i 1 x i 2 K x im ©K
=i дx41 д xi2 K д x4
4.,2K im = lV*ilV*i2
(2.95)
¦ x1 x 2 K x n .
1 2 n
д nf
д x1 д x 2 K д x
12
где i1,i2,K im e (1,n) и попарно не равны друг другу, © - сложение по
модулю два. ?
В заключение необходимо сделать примечание к разложению (2.95) произвольной булевой функции f (x). Очевидно, что число членов разложения в (2.95) определяет степень близости f (x) к ее линейной
версии, а произведение числа членов разложения на размерность блока памяти определяет функционал размещения данной задачи кодопреоб-разования в диаде «комбинационная схема - блок памяти».
Полученные результаты исследований позволяют предложить следующий алгоритм контроля булевого описаний нелинейных ДДС дискретной автоматики.
Алгоритм 2.10 (А2.10)
контроля булевого описаний НДДС дискретной автоматики в фазе их аналитического конструирования
1. Выполнить в зависимости от формального описания НДДС: в случае ГСА-описаний при контроле корректности ее составленной в силу У2.9 - п.п. 1-5 А2.2,а затем - п.п. 2-6 А2.1; в случае использования канонического автоматного синтеза - п.п. 1-6
А2.1.
2. Проверить с использованием положений У2.6, У2.7 и У2.8 факт избыточности переменных булевого описаний БФ, задающих функции ц (2.12) возбуждения информационных входов ? триггеров, и в случае обнаружения такового выполнить соответствующее приведение этих переменных.
3. Проверить с использованием положений У2.6, У2.7 и У2.8 факт избыточности переменных булевого описаний БФ, задающих функцию у (2.11) выхода НДДС, и в случае обнаружения такового выполнить соответствующее приведение этих переменных.
4. Выполнить с использованием положений У2.10 и У2.12 контроль постановочного описания в форме диаграмм переходов и выхода (ДПВ) или ГСА нелинейной ДДС с полученным его аналитическим представлением, определяемым соответствующими БФ.
5. Выполнить п.6 А2.1. ¦
Примечание 2.6 (ПМ2.6). Следует заметить, что предложенный алгоритм контроля булевого описаний НДДС достаточно просто реализуем в программной среде, что позволит разработчикам существенно сэкономить время при разработке НДДС. ?
Для иллюстрации приведенных положений рассмотрим два примера, в первом из которых рассмотрим использования аппарата селлер-совского дифференцирования применительно к произвольным БФ.
152
| Таблица 2.14 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Таблица 2.15
| x: | x2 | x3 | f (x) |
d f d x3 | x3 | x: | x2 | f (x) |
d f d x2 | x2 | x3 | x: | f (x) |
d f d xx |
| 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 |
Рассматривается переключательная функция 3-х переменных f(x )= f (хъ x2 , x3) = (x:x2 v x3) —— (x2x3 0 Xj) на предмет вычисления частных производных Селлерса 1-го порядка по всем переменным и оценки их веса. Для вычисления производной дf /дxt используется 4-й способ (см. выше способы вычисления ЧПС). Результаты вычисления сведены в две таблицы: таблица 2.14 представляет собой таблицу истинности, а таблица 2.15 - иллюстрирует 4-й способ вычисления ЧПС.
д f
Из таблицы 2.15 нетрудно видеть, что все ЧПС -,i = 1,2,3, при-
д xi
нимают единичные значения на 4-х переменных. Таким образом, все
>,i = 1,2,3 всех ЧПС характеризуются одной величиной
веса P-
д f
д xi
P \ г = 4. Иначе говоря, все переменные в БФ f (x1, x2, x3) обладают
l д xi J
равной значимостью. ¦
Пример 2.7 (Пр2.7)
Рассматривается процедура контроля булевого описаний НДДС в составе:
— БФ возбуждения информационных входов D-триггеров в виде
U = u (x1x2 v x1x2) = u (x1 0 x2), ju2 = u x1x2;
— БФ формирования выхода НДДС в форме У = x2x2.
Выполняем алгоритм 2.10 с п.2.
2. Контроль факта избыточности переменных булевого описаний БФ, задающих функции и возбуждения информационных входов триггеров, на кодовых переходах дает
ди
p\u\ = P{ux2 }= 2; p\^1l 1 = P{ux1 }= 2;
д x2
дU2
P\ди L = P{x1x2 }= 2; P\^\ = P{ux2 }= 2;
д x1
д u
ди2
P\^l V = P{ux1 }= 2; P\u\ = P{x1x2 }= 2,
что свидетельствует об отсутствии избыточности переменных булевого описаний соответствующих БФ, кроме этого полученные веса имеют значения кратные двум, что подтверждает корректность их вычисления.
3. Контроль факта избыточности переменных булевого описаний БФ, задающую функцию у выхода НДДС, на кодовых переходах дает
P\тт ) = P}= 2; P\тт 1 = P{X }= 2 ’
1дхі J ldx2 J
что свидетельствует об отсутствии избыточности переменных булевого описаний функции у выхода, кроме этого полученные веса имеют значения кратные двум, что подтверждает корректность их вычисления.
4.
Контроль постановочного описания ННДС в форме ДПВ с полученным его аналитическим представлением, определяемым со-ответ-ствующими БФ, в форме
— проверки детектируемости состояний НДДС по соответствующим булевым переменным дает
д у п д у - п
-= х2 ф 0;-= х, ф 0,
дх, 2 дх2 1
что свидетельствует о детектируемости состояний НДДС по этим переменным;
— проверки достижимости состояний НДДС по соответствующим булевым переменным дает
дц _ _ л dju2 _
—1 = х,х2 ф 0; —- = х,х2 ф 0, ди ди
что свидетельствует о достижимости состояний НДДС по входной переменной и .
Выполнение п.5 алгоритма авторы сочли возможным опустить. ¦ Примечание 2.7 (ПМ2.7). Следует заметить, что при решении задач минимизации БФ использование аппарата селлерсовского дифференцирования, в отличие от соответствующих методов минимизации БФ, при своей простоте позволяет одновременно исследовать среду БФ: определять и ранжировать ее переменные по степени их значимости, проверять корректность БФ; в рамках ДДС - производить анализ детектируемости и достижимости состояний, а также корректности составления ГСА-описания ее функционирования в фазе перехода от «вербальной» версии ГСА к ее формальной версии. ?
103
3. ГИБРИДНЫЕ ДВОИЧНЫЕ ДИНАМИЧЕСКИЕ СИСТЕМЫ ДИСКРЕТНОЙ АВТОМАТИКИ
Положения разделов 1 и 2 содержат инструментарий, позволяющий решать требуемую задачу кодопреобразования как в классе линейных двоичных динамических систем, модельное представление которых опирается на аппарат передаточных функций или векторноматричных описаний, так и в классе нелинейных ДДС, модельное представление которых формируется с использованием возможностей автоматной логики в двух ее версиях.
В настоящем разделе рассматривается класс ДДС, построенных на композиции двух указанных выше математических модельных представлений. Класс таких систем назван классом гибридных двоичных динамических систем (ГДДС). Класс гибридных ДДС достаточно нов и теоретически мало разработан, он имеет пока скромное библиографическое обеспечение. Ниже приводятся избранные результаты по исследованию класса гибридных ДДС, известные на настоящий момент.
3.1. Проблема заполнения кодового пространства
классом гибридных двоичных динамических систем
Процедуры конструирования ДДС в классе линейных представлений приводит к размерности dim x вектора x ее состояния равной пл.
Решение той же задачи кодопреобразования в классе нелинейных представлений приводит к вектору состояния размерности пн, причем в общем случае размерности пл и пн связаны отношением порядка в виде неравенства
п л ^ Пн = E { log2nS К (3-1)
где п8 - мощность алфавита состояний абстрактного автомата, погружаемого в двоичную динамическую среду, E {(•)} - оператор округления величины (•) до ближайшего большего целого.
Возникают естественные системные вопросы: какими свойствами обладает ДДС, размерность пг вектора состояния которой удовлетворяет отношениям порядка в виде неравенств
пл > пг > Пн , (3.2)
и как ее сконструировать, если при этом она решает ту же задачу кодопреобразования? Следует ожидать, что реализация ДДС с размерностью пг вида (3.2) вектора ее состояния строится в классе гибридных двоичных динамических систем (ГДДС), обладающих свойствами как линейных, так и нелинейных двоичных динамических систем. Этому классу двоичных динамических систем посвящен данный параграф, который начнем с формулировки следующих определений.
Определение 3.1 (О3.1). Мощность множества реализаций ДДС, размерность пг вектора состояния которых удовлетворяет неравенствам (3.2), образует кодовое пространство (КПР). ?
Определение 3.2 (О3.2). Гибридными двоичными динамическими системами устройств дискретной автоматики будем называть ДДС, размерности векторов состояний которых принадлежат кодовому пространству, сформированному в смысле определения 3.1. ?
Определение 3.3 (О3.3). Кодовое пространство называется невырожденным, если размерности пн и пл удовлетворяют условию
пн - пл ^1. ?
Определение 3.4 (О3.4). Кодовое пространство называется вырожденным, если размерности пн и пл удовлетворяют условию
пн - пл = 0. ?
Рисунок 3.1
Понятие «кодовое пространство» позволяет рассматривать гибридные ДДС как некоторую динамическую среду, осуществляющую двоичное кодопреобразование и заполняющую невырожденное КПР. С этой точки зрения линейные ДДС, построенные с использованием аппарата передаточных функций или векторно-матричного описания, а также нелинейные ДДС, где в качестве кодов состояния используются двоичные коды на все сочетания, образуют «полярные» реализации решения задачи конструирования ДДС, формируя тем самым проблему заполнения возникающего между ними кодового пространства классом гибридных ДДС. Решение проблемы заполнения КПР классом ГДДС можно осуществить двумя путями. Первый путь решения проблемы состоит в редуцировании размерности вектора состояния линейных ДДС. Механизмы редуцирования размерности вектора состояния линейных ДДС, опирающиеся на результаты первого раздела, представимы в форме диаграммы, приведенной на рисунке 3.1.
Второй путь заполнения КПР гибридными ДДС формируется в классе нелинейных версий двоичных динамических систем и направлен на увеличение размерности вектора их состояния. С этой целью выбор двоичного кода при кодировании состояний абстрактного автоматного представления синтезируемой НДДС осуществляется с нарушением условия (2.6), то есть
пг > пн : dimX = пн ф argmin{рПн > ns}, (3.3)
что исключает использование для этой цели двоичных кодов на все сочетания. Указанная проблема удовлетворения условию (3.3) при выборе способа кодирования элементов алфавита S, мощности ns, состояния АА приводит к использованию таких кодов как, например, кодов Джонсона, кодов Грея, соседних кодов или, например, кодов с минимальным кодовым расстоянием не меньшим двух, то есть помехозащищенных кодов.
Следует заметить, что использование кодов Джонсона, кодов Грея или соседних кодов приводит к ситуации, при которой на соседних кодовых переходах х(к),х(к + і) происходит изменение значения лишь
одного элемента вектора х состояния НДДС, своего для каждого перехода. Это может быть использовано как для решения проблемы борьбы с «гонками» в среде НДДС, так и для обеспечения простоты комбинационной схемы (КСХ) и быстродействия НДДС, жертвуя при этом размерностью вектора состояния.
Особый интерес представляет использование помехозащищенных кодов для кодирования алфавита S состояния АА при его погружении в среду КА с целью обеспечения помехозащищенности процесса кодо-преобразования, осуществляемого средствами НДДС. Решение этой задачи приводит к непосредственному назначению помехозащищенных кодов в качестве кодов состояния ДДС. Однако такой подход влечет за собой модификацию А2.1 и решение вопросов согласования в (2.6) мощностей соответствующих алфавитов и формирования модифицированных правил A,S, что без учета специфики формирования проверочной части ПЗК неоправданно увеличивает сложность комбинационной схемы НДДС.
Решение вопроса заполнения КПР с использованием ПЗК получим конструированием в силу (1.159) агрегированного вектора XГДДС состояния ГДДС в форме
I Т
НДДС \ ХНДДС
I ~ Т !x НДДС
\Т
ГДДС
G = к ir. (x )= rest——; i = 1,k\ (-4)
I g(x) J
что позволяет на стадии конструирования НДДС использовать алгоритм 2.1 без каких-либо изменений, после чего вектор состояния x НДДС агрегируется в указанной в (3.4) форме.
Использование такого подхода разбивает КСХ на две сепаратные части, одна из которых формирует на кодовых переходах значение Xнддc (k + 1), а другая - значение ~НДДС (k + l). Из выражения (3.4) видно, что для формирования значений xHMC(k + 1) и хНДДС(k +1) достаточно значения xHMC (k) , что и обеспечивает простоту КСХ в отличие от конструирования последней с использованием значения x,rMC (k) большей размерности.
Выдвинутые соображения показывают, что заполнение невырожденного КПР гибридными ДДС осуществимо «движением» по нему слева направо или справа налево в неравенствах (3.2). Следует заметить, что при заполнении КПР возможно и возвратно-поступательное движение в неравенствах (3.2). Так, например, с целью обеспечения быстродействия НДДС и ее помехозащищенности движением по КПР справа налево производится кодирование двоичными кодами элементов алфавита S состояния АА, задающего логику функционирования НДДС, после чего в силу (3.4) конструируется вектор xГДДС состояния
ГДДС, обладающий свойством помехозащищенности. Затем с целью снижения сложности технической реализации ГДДС движением по КПР слева направо осуществляется редуцирование размерности вектора xГДДС (см. параграф 3.3). Аналогично решается задача заполнения
КПР, если те же требования предъявляются и к линейной ДДС.
Результаты исследований настоящего параграфа, а также разделов 1 и 2 показывают, что заполнение КПР при движении по нему в неравенствах (3.2) слева направо удобно осуществлять выполнением алгоритмов 1.3 и 1.4. Заполнение КПР при движении по нему в неравенствах (3.2) справа налево при решении задач повышения быстродействия НДДС, обеспечение простоты ее комбинационной схемы, борьбы с «гонками» в ее среде, осуществимо с использованием положений следующего алгоритма.
Алгоритм 3.1 (А3.1)
заполнения кодового пространства ГДДС, конструируемых с использованием возможностей автоматных представлений
1. Выполнить п.п.1, 2 алгоритма 2.1 и получить описание функционирования ДДС в форме абстрактного автомата (2.1).
2. Выполнить первый этап перехода от абстрактного автомата к конечному автомату путем кодирования алфавитов высокого уровня Z входа и W выхода АА, полученного в п.1 алгоритма, элементами простого поля Галуа GF (2) так, чтобы размерности
кодов конечного автомата (2.5) и мощности алфавитов Z и W были связаны неравенствами (2.6).
3. Завершить переход от АА к КА, закодировав с учетом (3.3) элементы алфавита высокого уровня S состояния АА:
— двоичными кодами Грея, если число nS элементов алфавита состояний АА удовлетворяет равенству
ns = 2q, q е I +;
— двоичными кодами Джонсона или соседними кодами с обеспечением минимальной избыточности кодовых реализаций элементов алфавита S АА.
4. Выполнить п.п.4-7 алгоритма 2.1. ¦
Заполнение КПР при движении по нему справа налево при решении задач наделения свойством помехозащищенности процедуры ко-допреобразования в среде НДДС достижимо выполнением следующего алгоритма.
Алгоритм 3.2 (А3.2) заполнения кодового пространства помехозащищенными гибридными ДДС
защищенного кода, и получить кодовые вектора хГДДС состояния
ГДДС.
4. Модифицировать правила X, 8 (2.7) -форме
(2.9) с учетом (3.4) в (к), u(k)] (3.5)
(к +1):
X ,xГДДС
гддс
(3.6)
8: У(к )=8 [ гддс (k)]
при использовании автоматной логики Мура и
8: У(кЬ8[ХГДДС(к\ u(k)] при использовании автоматной логики Мили.
5. Выбрать тип триггера, реализующий компоненты вектора xГДДС
состояния ГДДС, и сконструировать функции ці, i = 1, dimxГДДС возбуждения информационного входа vt триггеров в форме
Vi (к )= А і (к )Д ДГДДС і (к )’ u(k )]]^^^^ [ ХГДДС i (к ~)> u(k )] (3.8)
6. Проверить правильность функционирования полученной ГДДС в соответствии с ее аналитическим описанием на множестве полной мощности ее кодовых переходов. ¦
Пример 3.1 (Пр3.1)
Рассматривается задача заполнения КПР конструированием гибридной версии устройства, функционирование которого описывается диаграммой рисунок 3.2 переходов и выхода. При этом требуется обеспечить выявление однократных сбоев в кодах вектора состояния ГДДС в форме их обнаружения.
Для решения поставленной задачи в силу А3.2 осуществляем:
1. Кодирование в силу (3.4) элементов алфавита S состояния АА при образующем многочлене g (x )= x + 1, полученным в
соответствии с п.1 алгоритма 1.11, дает кодовые вектора xГДДС состояния ГДДС - представленные в таблице 3.1.
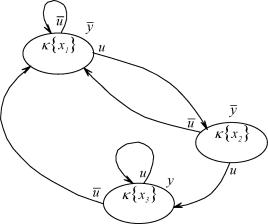 |
| Рисунок 3.2. Диаграмма переходов и выхода исходного устройства |
| Таблица 3.1 | |||||||||||||||||||||||||
|
Таблица 3.2
| |||||||||||||
| xT (к + l)= X([ х(к), и(к)] ] |
| |||||||||||
| y(k )= S [(к), u (k)] |
 |
| Рисунок 3.3. Диаграмма переходов и выхода ГДДС |
jui, i = 1,dimxГДДС возбуждения их информационного входа
V вида
ju1 = и (((Х2 ? x1x2) = u ((1 0 x2) ju2 = ux1x2,
jd3 = и((1x2 ? x1x2) = и(x1 0 x2) = v1 ¦
5.Конструирование булевой функции формирования выхода ГДДС, которое дает аналитическое представление
У = xi x2 •
Полученное булево описание ГДДС является аналитической базой для построения схемотехнической реализации устройства. ¦
Примечание 3.1 (ПМ3.1). Следует заметить, что реализация корректирующей способности в рассмотренном примере 3.1 для случая использования автоматной Мили осуществляется посредством формирования синдрома E сбоя в кодах вектора состояния ГДДС с помощью БФ E = у 0 Xj, в свою очередь для ГДДС, использующей автоматную логику Мура, синдром формируется в силу БФ E = х3 0 х2 0 xj. ?
Примечание 3.2 (ПМ3.2). С использованием аппарата селлерсов-ского дифференцирования нетрудно убедиться, что в рамках примера 3.1 при составлении соответствующих БФ возбуждения информационных входов D-триггеров /л1, i = 1,dimXГДДС как функций четырех аргументов {u,xj,x2,x3} происходит их минимизация склеиванием термов по переменной x3, что приводит БФ к функции трех аргументов {u,xj,x2}. ?
В заключение рассмотрим ситуацию, когда кодовое пространство оказывается вырожденным, что имеет место в силу определения 3.4 при выполнении условия пн = пл. Охарактеризуем ситуацию следующими постулатами.
Постулат 3.1 (ПС.3.1). Задача кодопреобразования, решаемая средствами ЛДДС, векторно-матричное описание которой имеет (п х п)-матрицу A состояния с характеристическим неприводимым
полиномом D(X)= det (А! + A), принадлежащим показателю ц = 2n -1, характеризуется минимальной размерностью вектора состояния на множестве линейных ДДС, формирующих на своем выходе периодическую последовательность периода T = ^. ?
Постулат 3.2 (ПС.3.2). Задача кодопреобразования, формализуемая на уровне абстрактного автомата в виде графа переходов, образующего замкнутый цикл с числом состояний nS, равным 2п -1, и решаемая средствами НДДС-КА, характеризуется размерностью пг = пн = E { log2 nS }= п вектора состояния этой ДДС.
Следует заметить, что ПС3.1 и ПС3.2 обнаруживают ситуацию, характеризующуюся вырождением кодового пространства. Этот факт делает справедливыми положения следующего утверждения.
Утверждение 3.1 (У.3.1). Для того чтобы сконструировать НДДС с минимальной размерностью п вектора состояния и сложностью КСХ, генерирующую произвольную кодовую последовательность максимального периода T = 2п -1 достаточно на этапе перехода от формализованной в форме АА версии устройства к его версии в форме
КА осуществить кодирование алфавита состояния АА так, чтобы в качестве кодов были использованы коды, получаемые в силу соотношения (1.209) вида x(k + 1) = Aqx(0), x( 0) Ф O, q e [l,2n -1], в котором матрица A имеет характеристический неприводимый полиномом D(X)= det(Л + А), принадлежащий показателю /л = 2п -1 так, что
Ац = I, а также в качестве ячеек памяти НДДС были использованы D-триггеры, при этом степень q и номер кодируемого состояния АА должны быть согласованы. ¦
Проиллюстрируем на примере положения утверждения 3.1.
Пример 3.2 (Пр3.2)
Требуется сконструировать автономную (u (k ) = 0) НДДС при условии минимальной сложности ее технической реализации, которая генерирует скремблирующую [28, 33] периодическую последовательность с периодом T = 15, имеющую вид
y(k ) = y(k + T )= 10 00 11 110 10 1100\1000К В соответствии с утверждением 3.1 выбираем в качестве характеристического полинома D(X) = det(ЛІ + А) матрицы А неприводимый
многочлен степени n = 4 D(X) = Л + Л3 + 1, который принадлежит показателю ц = 15.
Матрицу А зададим в сопровождающей выбранный характеристический полином форме:
 Учет: Делопроизводство - Автоматизация - Софт
Учет: Делопроизводство - Автоматизация - Софт
- Управленческий учет
- Технологии управленческого учета
- Делопроизводство
- Стандарты делопроизводства
- Делопроизводство предприятия
- Секретарь и делопроизводство
- Автоматизация делопроизводства
- Документооборот
- Автоматизация
- Автоматизация управления
- Практика автоматизации
- Софт для автоматизации