
|
Савельев А. Я. - Прикладная теория цифровых автоматов
В книге излагаются способы представления информации в цифровых автоматах, методы выполнения арифметических и логических операций в них, а также методы логического описания и основанные на них методы логического проектировании цифровых устройств. Уделяется внимание разработке способов контроля нраоилыюсти функционирования цифровых автоматов при выполнении различных операций, методам минимизации логических выражений. Теоретический материал иллюстрируется примерами и сопровождается вопросами для самоконтроля.
«Прикладная теория цифровых автоматов» как учебный предмет вводится впервые в подготовку специалистов. При формировании 4 гой дисциплины необходимо было:
1) представить минимум вопросов, отражающих состояние теории и практики цифровых автоматов;
2) учесть тот полезный и важный материал, который уже сложился в курсе «Арифметические и логические основы цифровых Ійтоматов»;
3) ввести в программу вопросы из теории прикладной информации.
В типовом учебном плане данный предмет является одним из Первых спецкурсов, которые формируют существо и содержание специальности «Электронные вычислительные машины». Этот предмет дает теоретическую базу для изложения в последующем Специальных дисциплин, таких, как «Схемотехника ЭВМ», «Теория и проектирование ЭВМ и систем», «Периферийные устройства ЭВМ, систем и сетей», «Основы автоматизации проектирования ЭВМ», является продолжением разделов «Математики» и должен знакомить студента с прикладными задачами разработки алгоритмов функционирования устройств электронных вычислительных машин. Поэтому в учебнике выделены теоретические вопросы анализа и синтеза цифровых автоматов (гл. 2, 11, 12); информационные основы (гл. 1, 8, 9); арифметические (гл. 3, 4, 5, 6, 7) и логические (гл. 2, 10, 11) основы анализа и синтеза цифровых автоматов. Изложить это в книге оказалось нелегкой задачей, которая усложнилась многообразием терминологии и различием толкований терминов.
Одним из главных понятий является понятие цифрового автомата. Здесь автор придерживается определения, которое было ввезено акад. В. М. Глушковым: «Электронные цифровые машины с программным управлением представляют собой пример одного из наиболее распространенных в настоящее время типов преобразова-іелей дискретной информации, называемых дискретными или цифровыми автоматами. Поэтому задача синтеза схем электронных цифровых машин с программным управлением входит в качестве частного случая в более общую задачу синтеза схем цифровых автоматов». В свете данного определения термин «автомат» в тексте учебника используется в двух аспектах: 1) автомат как устройство, выполняющее все действия без участия человека; 2) автомат как математическая модель, описывающая реальные технические автоматы.
B. М. Глушкова, Д. фон Неймана, Э. Поста, А. Тьюринга, С. В. Яблонского, В. Г. Лазарева и др. При этом автор старался изложить те теоретические вопросы, которые необходимы для понимания прикладных задач, имея в виду, что читатель, интересующийся более глубоко вопросами анализа и синтеза автоматов, найдет эти сведения в специальной литературе.
Основными вопросами гл. 1, 8, 9 являются вопросы информации и ее кодирования. В основу этого материала положены результаты работ, опубликованных К. Шенноном, В. А. Котельниковым, Р. Хэ-мингом и др. Большое внимание уделено методам контроля правильности функционирования цифрового автомата и выбору методов кодирования.
Гл. 4—7 учебника содержат наиболее отработанный и сложившийся материал, вошедший в книгу «Арифметические и логические основы цифровых автоматов» (Высшая школа, 1980); в них изложены методы представления числовой информации и алгоритмы выполнения арифметических операций в двоичной и десятичной системах счисления. Основой этого раздела послужили также работы
C. А. Лебедева, В. А. Мельникова, М. С. Шура-Бура, Р. К. Ричардса, А. Н. Тихонова, Л. Н. Королева и др. Изложение материала построено таким образом, чтобы достичь максимальной общности при сохранении непосредственного практического применения теории. С целью облегчения изложения теоретических вопросов разработки алгоритмов выполнения отдельных операций рассматривается некая гипотетическая ЭВМ, обладающая определенной структурой,-которая оговаривается в практических примерах.
Наконец, гл. 2, 10, 11 посвящены логическим основам анализа и синтеза цифровых автоматов. Расположение гл. 10 и 11 в конце учебника не снижает необходимости его знания при чтении других глав учебника. Автор разместил материал подобным образом именно в силу сложившейся практики чтения курса лекций по этому предмету в МВТУ им. Баумана, четко отдавая себе отчет в том, что возможны различные методики изложения подобной информации. Материал этого раздела' основан на трудах Д. Буля, Э. МакКласки, В. И. Шестакова, С. А. Лебедева, В. М. Глушкова и др.
При подборе и изложении материала автор стремился к тому, чтобы дать возможность широкому кругу лиц, не знакомых с глубинными вопросами электроники и функционирования различных электронных схем, понять суть проблем, возникающих при проектировании алгоритмов функционирования отдельных устройств ЭВМ
Автор выражает благодарность рецензентам: проф. Г. Н. Соловьеву (Московский инженерно-физический институт) и коллективу кафедры «Электронные вычислительные машины» Московского лесотехнического института (зав. кафедрой проф. Б. И. Зобов) за ценные замечания, позволившие улучшить содержание учебника. Автор также заранее благодарит читателей за все замечания, кото: рыс помогут в дальнейшем улучшить материал книги и просит присылать их по адресу: 101430, Москва, ГСП-4, Неглинная ул., д, 29/14, издательство «Высшая школа».
Автор
Уровень внедрения вычислительной техники в экономику нашей страны становится в настоящее время одним из решающих факторов ускорения научно-технического прогресса и экономического развития всех отраслей народного хозяйства.
В Основных направлениях экономического и социального развития СССР на 1986—1990 гг. и на период до 2000 г. поставлены задачи развивать теоретическую и прикладную математику, информатику и кибернетику, широко внедрять машины и оборудование с встроенными средствами микропроцессорной техники, ускоренно развивать выпуск средств автоматизации управленческого и инженерного труда, малых электронных вычислительных машин высокой производительности, персональных электронных вычислительных машин.
Сегодня трудно себе представить деятельность человека без электронных вычислительных машин (ЭВМ). Появившись около 40 лет назад, ЭВМ открыли новую страницу в истории человеческих знаний и возможностей, высвободили тысячи вычислителей, значительно облегчили труд ученых, дали возможность изучать сложнейшие процессы. Сейчас нет ни одной отрасли народного хозяйства, где нельзя было бы применить ЭВМ; более того, целые разделы науки и техники не смогут существовать без них.
Появление ЭВМ было подготовлено историческим развитием средств вычислений. Древнейшим счетным инструментом, который дала сама природа человеку, была его собственная рука. От пальцевого счета берут свое начало пятиричная (одна рука) и десятичная (две руки) системы счисления. Издревле употреблялся еще один вид инструментального счета — деревянные палочки с зарубками (бирки) и веревки с узелками. Но с ростом и расширением торговли они не смогли удовлетворить потребности в средствах вычислений. И вскоре появился специальный счетный прибор, известный в древности под названием «абак», представляющий собой доску с вертикальными желобками, в которых передвигались камешки. Русский абак — счеты — появились на рубеже XVI— XVII вв. Главное их отличие — десятичный принцип счисления. Форма счетов, установленная более 250 лет назад, в настоящее время почти не изменилась. В XVII в. появились и первые логарифмические линейки.
В России первое суммирующее устройство было изобретено и изготовлено в 1770 г. Е. Якобсоном часовым мастером и механиком в г. Несвиже. Суммирующие устройства, создаваемые в то время, не имели применения, они скорее выставлялись напоказ, чем использовались по назначению. Это объяснялось их ненадежностью, неудобством в эксплуатации, серьезными конструктивными недостатками из-за отсутствия необходимой материально-технической и технологической базы. Процессы ввода чисел и выполнения операций в этих устройствах были медленными.
Коренной перелом в создании счетных устройств произошел в середине XIX в., когда появилась необходимая технологическая база, обеспечивающая требуемую для них точность изготовления деталей. Кроме того, общественно-экономическая обстановка (бурный рост промышленности, развитие банков и железных дорог) требовала создания надежных и быстродействующих счетных устройств. Для этого необходимо было в первую очередь изменить «медленную установку» чисел. Приближенно эту задачу решило изобретение клавишного ввода. Принципиально решена проблема была лишь с появлением радиоэлектроники. Тем не менее благодаря клавишному механическому вводу в середине 80-х годов XIX в. удалось организовать промышленный выпуск суммирующих устройств, получивших широкое распространение в первой половине нашего столетия. Начиная с 50-х годов в клавишных устройствах стали использовать электропривод, а затем и электронику.
Параллельно с развитием счетных суммирующих устройств создавались арифмометры. Первым в мире арифмометром стала «арифметическая машина» Г. Лейбница, появившаяся в конце XVII в. Сначала Лейбниц пытался лишь улучшить машину Паскаля, но выяснилось, что для выполнения операций умножения и деления необходим совершенно новый принцип. Лейбниц блестяще разрешил эту задачу, предложив использовать цилиндр, на боковой поверхности которого, параллельно образующей, было расположено девять ступенек различной длины. Этот цилиндр впоследствии назвали ступенчатым валиком. Машина не получила широкого распространения, но основная идея Лейбница — идея ступенчатого валика — осталась действенной и плодотворной даже в XX в. На принципе ступенчатого валика был построен и арифмометр Томаса — первое в мире счетное устройство, изготовляемое промышленностью. Создавались арифмометры и другой конструкции. Основным их элементом было зубчатое колесо Однера с переменным числом зубьев.
Существенным недостатком суммирующих устройств и арифмометров считается невозможность значительного увеличения скорости вычислений. Производительность устройств определяется быстротой рук человека. Поэтому ввод информации и управление операциями необходимо передать в ведение машины. Впервые автоматизировал вычислительный процесс в XIX в. английский ученый
Ч. Бэббедж, создав проект арифметической машины — прообраз современных компьютеров. Машина состояла из «склада» для хранения чисел (памяти); «мельницы» — для производства арифметических операций (арифметического устройства); устройства, управляющего в определенной последовательности операциями машины (устройства управления); устройства ввода и вывода данных. Для ввода данных предполагалось использовать перфорированную карту. Время на производство арифметических операций оценивалось Ч. Бэббеджем так: сложение и вычитание— 1 с; умножение и деление — 1 мин. Идеи Ч. Бэббеджа не были поддержаны современниками. К ним обратились только в 40-х годах XX столетия при создании автоматической универсальной вычислительной машины «Марк-2».
Первая действующая счетно-аналитическая машина была создана Г. Холлеритом для автоматизации длительной, однообразной и утомительной работы по обработке данных переписи населения в США в 1880 г. Как и в машине Ч. Бэббеджа, в качестве носителей информации использовались перфокарты, но все остальное оборудование: простой пробойник (перфоратор), сложный пробойник, сортировальная машина и табулятор — было оригинально.
Конец XIX в. и начало XX в. характеризуются бурным развитием электротехники, телефонии, радиотехники, а позднее электроники. Большой материал, накопленный в этой области, позволил создать вычислительную машину немеханического типа.
В 1947 г. была закончена работа над релейной вычислительной машиной «Марк-2», в которой впервые использовалась двоичная система исчисления, а для запоминания чисел, выполнения арифметических операций и операций управления — электромеханические реле (13 тыс. шт.), обладающие двумя устойчивыми состояниями. В машине операции сложения и вычитания занимали примерно 0,125 с, умножения — 0,25 с.
В 1943 г. в Гарвардском университете под руководством американских ученых Д. Моучли и Д. Эккерта приступили к созданию электронной вычислительной машины (ЭВМ). К этому времени уже были известны и построены диод (1904), триод (1905), триггер (1918). Машина создавалась по заказу артиллерийского управления и предназначалась для расчета баллистических таблиц. Завершенная в конце 1945 г. машина, получившая название ЭНИАК, имела громадные размеры: содержала 18 тыс. электронных ламп и 1,5 тыс. реле, потребляла около 150 кВт электроэнергии — мощность, достаточная для работы небольшого завода. Использование электронных ламп позволило резко повысить скорость выполнения машинных операций: сложение — 0,0002 с, умножение — 0,0028 с. Управление счетом осуществлялось с помощью программ, набираемых вручную на многочисленных коммутационных досках и переключателях. Несоответствие между временем решения задачи и временем ее подготовки вручную было настолько большим, что выигрыш от скорости вычисления почти полностью покрывался проигрышем во времени на подготовительных операциях.
Создание вычислительной машины ЭНИАК положило начало бурному развитию ЭВМ первого поколения.
В СССР первая малая электронная счетная машина (МЭСМ) — прототип современных ЭВМ — была создана в 1951 г. под руководством С. А. Лебедева. Для МЭСМ характерно наличие универсального арифметического устройства, выполнявшего 50 арифметических или логических операций в секунду. Связанное с универсальным арифметическим устройством оперативное запоминающее устройство в свою очередь могло быть соединено с долговременным запоминающим устройством, на котором осуществлялся ввод и хранение команд. В случае математической ошибки или переполнения разрядной сетки машина останавливалась. Потребляемая ею мощность составляла 25 кВт. По сравнению со специализированной машиной ЭНИАК созданная С. А. Лебедевым машина имела принципиально новое решение.
Одной из первых в мире ЭВМ с параллельной обработкой кодов была МЭСМ. Эта машина стала базовым прототипом для мирового цифрового математического машиностроения и обусловила переход к новому периоду развития искусства программирования. Появление МЭСМ послужило мощным толчком для разработки широкого круга вопросов вычислительной математики: на машине было решено большое количество задач ядерной физики, осуществлен расчет линии электропередачи Куйбышев — Москва, решены задачи ракетной баллистики и др., решение которых вручную надолго задержало бы развитие некоторых важных направлений отечественной науки и техники. Разработка МЭСМ носила экспериментальный характер и явилась необходимым этапом создания первой быстродействующей электронной счетной машины.
В течение нескольких последующих лет БЭСМ с быстродействием 8 ты.с. опер./с была самой быстродействующей машиной в Европе. На ней были решены многие задачи, считавшиеся ранее неразрешимыми из-за большого объема вычислений. Весьма примечательным было то, что ряд технических решений, воплощенных в БЭСМ, предвосхитил идеи ЭВМ второго поколения. Так, в состав машины входило специальное устройство контроля, а независимое подключение к памяти арифметического устройства и устройств ввода и вывода соответствовало структуре мультипрограммных машин. Особо важное значение имел схемный метод обращения к подпрограмме и возможность модификации команд с помощью систем местного и центрального управления командами, что открыло новые возможности в развитии искусства программирования. Структура и основные схемы БЭСМ стали классическими; они были прложены в основу быстродействующих машин БЭСМ-2, М-2 и др.
В 1953 г. под руководствомЮ. А. Базилевского была создана цифровая вычислительная машина (ЦВМ) «Стрела», в 1954 г. под руководством Б. И. Рамеева — ЭВМ «Урал». Почти одновременно с этими машинами появились такие ЭВМ, как М-3, «Минск-1» и др., которые составили семейство отечественных ЭВМ первого поколения.
Характерными чертами ЭВМ первого поколения можно считать не только использование электронных ламп в основных и вспомогательных схемах, но и наличие параллельного арифметического устройства, разделение памяти машины на быстродействующую оперативную ограниченного объема (выполненную на электроннолучевой трубке или на ферритовых сердечниках) и медленную внешнюю большого объема (использовавшую накопители на магнитных барабанах и лентах), применение полупроводниковых диодов и магнитных сердечников в логических элементах машины, перфолент и перфокарт как носителей информации при вводе и выводе данных. Среднее быстродействие ЭВМ первого поколения достигало десятка тысяч арифметических операций в секунду. ?
Поиск структур, обеспечивающих максимальную загрузку всех устройств за счет совмещения их работы во времени, привел к появлению ЭВМ второго поколения, в которых на смену ламповым схемам пришли транзисторные. Основу технической базы ЭВМ второго поколения составили полупроводниковые диоды и транзисторы.
Наиболее мощная отечественная ЭВМ второго поколения — БЭСМ-6, созданная под руководством С. А. Лебедева. Трудно переоценить то значение и влияние на развитие вычислительной техники и других областей науки, которое оказало создание этой высокопроизводительной оригинальной по архитектуре и структуре отечественной вычислительной машины.
В нашей стране на основе БЭСМ-6 были созданы центры коллективного пользования, управления, координационно-вычислительные и др. До настоящего времени БЭСМ-6 широко используется в системе проектирования для разработки математического обеспечения новых ЭВМ, моделирования сложных физических процессов и процессов управления.
Архитектуру и структуру семейства ЭВМ БЭСМ-1, БЭСМ-2, М-20, БЭСМ-ЗМ, БЭСМ-4 характеризуют целостность концепции и изящные инженерные решения. Наиболее полно это проявилось в БЭСМ-6; несмотря на то что машина — сложная система, механизмы функционирования ее устройств, их функциональные связи легко понимаются, четко интерпретируются и, следовательно, машина БЭСМ-6 эксплуатируется легко. Элементная база БЭСМ-6 совершенно новая. Все связи в машине записаны формулами булевой алгебры. Машины семейства БЭСМ ни по системе команд, ни по внутренней структурной организации не являются копией какой-либо отечественной или зарубежной установки. В создании и развитии этих машин принимал активное участие акад. В. А. Мельников.
Для ЭВМ второго поколения характерен параллелизм в работе отдельных блоков, начиная от «перекрытия» времени выполнения отдельных команд и кончая параллельным выполнением двух команд или более из одной или из разных программ, что позволило достичь быстродействия до миллиона операций в секунду. Дальнейшее увеличение быстродействия ЭВМ тормозилось конструктивным выполнением электронных схем, собираемых из отдельных элементов — резисторов, конденсаторов, диодов, транзисторов.
Миниатюризация конструктивных элементов затруднялась необходимостью работы с каждым элементом в отдельности. Выходом из этих затруднений явилась интегральная технология. Малые интегральные схемы (МИС) стали базой машин третьего поколения.
В интегральных схемах роль электронных приборов и элементов выполняют небольшие группы молекул. Основой для таких схем служат полупроводниковые материалы, чаще всего кремний. Специально выращенные большие кристаллы кремния, имеющие очень высокую степень химической чистоты, разрезаются на отдельные пластины, на поверхности которых или внутри специальным способом формируются участки, обладающие свойствами конденсаторов, сопротивлений, диодов, транзисторов и т. д. Достаточно тончайшим металлическим выводом или просто «каналом связи» внутри кристалла соединить один его участок с другими, выполняющими ту или иную функцию, и интегральная схема готова. Одна интегральная схема заменяет большое число различных деталей и позволяет избавиться от многих недостатков полупроводниковых схем. , Переход на интегральные схемы способствовал повышению качества ЭВМ, уменьшению их габаритов и потребляемой ими энергии.
В чем же основное отличие ЭВМ третьего поколения от ее предшественников?
1. ЭВМ третьего поколения оперируют произвольной буквенноцифровой информацией. В них фактически соединились два направления предыдущих поколений машин: ЭВМ для делового, коммерческого применения с обработкой алфавитной информации и ЭВМ, предназначенные для научных учреждений и обработки цифровой информации.
2. Изменился порядок работы ЭВМ третьего поколения; эти машины построены по принципу независимой параллельной работы различных их устройств: процессоров, средств внешней памяти. Независимую работу устройств обеспечивают каналы, управляемые специальным устройством, куда поступает информация от пользователей ЭВМ. Это устройство и осуществляет первичную переработку информации, освобождая основное устройство от непроизводительной работы. Благодаря параллельной работе отдельных устройств ЭВМ может выполнять серию операций: переписывать информацию для очередной задачи с магнитной ленты или магнитного диска, выводить информацию для соответствующего устройства, вводить информацию и т. д.
Типичные представители ЭВМ третьего поколения — машины единой системы (ЕС ЭВМ) — семейство машин, предназначенных для решения научно-технических, экономических и управленческих задач, применения в различного рода АСУ и -системах обработки данных. Они созданы совместными усилиями коллективов ученых, инженеров и рабочих НРБ, ВНР, ГДР, ПНР, СССР и ЧССР. Промышленный выпуск первых моделей ЕС ЭВМ был начат в 1972 г. Высокое быстродействие (миллионы операций в секунду) и широкие возможности являются базой для эффективного использования моделей ЕС ЭВМ.
По мере развития ЭВМ стабильно проявляется тенденция к увеличению их быстродействия. Это объясняется следующими обстоятельствами. Так как основной узел ЭВМ — сумматор, производящий только операцию сложения, то, с одной стороны, решение любой задачи должно быть сведено к выполнению какого-то количества простых действий. Например, при умножении числа 241 на число 358 фактически необходимо число 241 сложить 16 раз. Аналогичным образом выполняются и другие арифметические операции. С другой стороны, предположим, что требуется решить задачу, объем вычислений в которой составляет ІО13 операций сложения.
Если вычислительная машина работает со скоростью ІО6 опер./с, то решение задачи займет ІО7 с, что составит примерно 3000 ч. Работать бесперебойно такой длительный срок ЭВМ не всегда могут. Поэтому естественно стремление пользователя решать даже самые сложные задачи за короткий промежуток времени, чтобы неисправности в работе ЭВМ не влияли на результат решения.
Производительность традиционных вычислительных систем повышалась двумя путями: развитием элементной базы и развитием архитектуры самих систем.
Если в первом направлении достигнут практически уже предел (достигнута максимально возможная скорость переключения, определяемая скоростью света), то по второму направлению имеются большие резервы, которые открываются в связи с использованием методов параллельной обработки информации. Сюда можно отнести конвейерные методы, или же системы (машины) потока данных.
Системы пятого поколения в структурном аспекте будут отличаться именно применением таких параллельных структур. Второй отличительной чертой вычислительных систем пятого поколения будет способность производить не только числовые расчеты (как это делают современные машины), но и обработку смысловой информации с выполнением операции анализа и вывода. Необходимость в подобных системах определяется расширением областей применения ЭВМ в таких нетрадиционных сферах, как образование, услуги населению и т. п. Здесь речь идет о возможностях создания искусственного интеллекта. Третьей особенностью систем пятого поколения станет элементная база. Это будет не только сверхбольшие интегральные схемы (СБИС), но и созданные на их основе ЭВМ, имеющие некоторое сходство по структуре с искусственным интеллектом, а также оптоэлектроника с использованием когерентного излучения. А так как скорость света значительно выше скорости электронов, то повысится как быстродействие машины, так и пропускная способность линий связи, по которым информация должна поступать в ЭВМ. Для решения этой задачи сделано уже немало. Созданы световоды с малыми потерями — на расстоянии в 1 км интенсивность света в них уменьшается всего в 2 раза.
Поиск новых принципов построения ЭВМ, совершенствование уже известных алгоритмов выполнения арифметических и логических операций — главнейшие задачи для специалиста в области проектирования и создания ЭВМ. Весь дальнейший материал учебника посвящен принципам построения алгоритмов функционирования машин и методам формального описания их работы, используемых при проектировании цифровых вычислительных машин.
ИНФОРМАЦИОННЫЕ ОСНОВЫ РАБОТЫ ВЫЧИСЛИТЕЛЬНЫХ МАШИН
§ 1.1. ОБЩИЕ СВЕДЕНИЯ ОБ ИНФОРМАЦИИПрежде всего определим, что такое вычислительная машина. Интуитивно понятно, что это — средство для автоматизации вычислений. Однако вычислительные машины используются настолько широко и для решения такого обширного круга задач (от вычислений до составления меню в ресторане и даже сочинения музыки), что поневоле возникает сомнение в правильности интуитивного определения.
В «Энциклопедии кибернетики» [20] приведено следующее определение: «Вычислительная машина (ВМ)—физическая система (устройство или комплекс устройств), предназначенная для механизации или автоматизации процесса алгоритмической обработки информации и вычислений». Таким образом, понятие «вычислительная машина» самым тесным образом связано с понятиями «информация» и «алгоритмическая обработка».
Объект передачи и преобразования в вычислительных системах (машинах) — информация. В этом смысле вычислительную машину (систему) можно называть информационной, в отличие, например, от энергетической системы, где объект передачи и преобразования — энергия. Все процессы, происходящие в вычислительной системе, связаны непосредственно с различными физическими носителями информационных сообщений и все узлы и блоки этой системы являются физической средой, в которой осуществляются информационные процессы. Специфика информационных процессов состоит не только в передаче информационных сообщений посредством заданной физической среды, но и в преобразовании, переработке и хранении информации. Все это составляет предмет науки информатики. Информатика представляет собой неразрывное единство трех составных частей: теории передачи и преобразования информации; алгоритмических средств обработки информации и вычислительных средств.
Информация определяет многие процессы в вычислительной машине. В самой общей форме процесс решения задачи на вычислительной машине проходит через следующие этапы:
ввод информации или установка исходных данных;
Информация
/,Предметный \ Язык
язык Алгоритмический программирования язык
определение результатов и вывод переработанной информации.
Вычислительная машина получает информацию, запоминает ее, обрабатывает по заданным алгоритмам и направляет потребителю (пользователю) или в другие системы обработки (рис. 1.1).
Термин «информация» имеет много определений. В широком смысле информация — отражение реального мира. Существует определение термина в узком смысле: информация — любые сведения, являющиеся объектом хранения, передачи и преобразования. И то, и другое определение важны для понимания процессов функционирования вычислительной машины.
Важный вопрос теории передачи и преобразования информации — установление меры, количества и качества информации.
Информационные меры, как правило, рассматриваются в трех аспектах: структурном, статистическом и семантическом.
В структурном аспекте рассматривается строение массивов информации и их изменение простым подсчетом информационных элементов или комбинаторным методом. Структурный подход применяется для оценки возможностей информационных систем вне зависимости от условий их применения.
При статистическом подходе используется понятие энтропии как меры неопределенности, учитывающей вероятность появления и информативность того или иного сообщения. Статистический подход учитывает конкретные условия применения информационных систем.
Семантический подход позволяет выделить полезность или ценность информационного сообщения.
§ 1.2. СТРУКТУРНАЯ МЕРА ИНФОРМАЦИИ
Информация всегда представляется в виде сообщения. Элементарная единица сообщений — символ. Символы, собранные в группы, — слова. Сообщение, оформленное в виде слов или отдельных символов, всегда передается в материально-энергетической форме (электрический, световой, звуковой сигналы и т. д.).
Различают информацию непрерывную и дискретную.
При использовании структурных мер информации учитывается только дискретное строение сообщения, количество содержащихся в нем информационных элементов, связей между ними. При структурном подходе различаются геометрическая, комбинаторная и аддитивная меры информации.
Геометрическая мера предполагает измерение параметра геометрической модели информационного сообщения (длина, площадь, объем и т. п.) в дискретных единицах. Например, геометрической моделью информации может быть линия единичной длины (рис. 1.3, а — одноразрядное слово, принимающее значение 0 или 1). квадрат (рис. 1.3, б — двухразрядное слово) или куб (рис. 1.3, в — трехразряднбе слово). Максимально возможное количество информации в заданных структурах определяет информационную емкость модели (системы), которая определяется как сумма дискретных значений по всем измерениям (координатам).
В комбинаторной мере количество информации определяется как число комбинаций элементов (символов). Возможное количество информации совпадает с числом возможных сочетаний, перестановок и размещений элементов. Комбинирование символов в словах, состоящих только из О и 1, меняет значения слов.
Рассмотрим две пары слов 100110 и 001101, 011101 и
111010. В них произведена перестановка крайних разрядов (изменено местоположение знакового разряда в числе — перенесен слева направо).
Аддитивная мера (мера Хартли), в соответствии с которой количество информации измеряется в двоичных единицах — битах, — наиболее распространена. Вводятся понятия глубины <7 числа и длины п числа.
Длина п числа — количество позиций, необходимых и достаточных для представления чисел заданной величины.
В гл. 3 понятие глубины числа будет трансформировано в понятие основания системы счисления. При заданных глубине и длине числа количество чисел, которое можно представить, N — qn. Величина N не удобна для оценки информационной емкости. Введем логарифмическую меру, позволяющую вычислять количество информации, — бит:
I(q) — log2iV = nlog2<7. (1.1)
Следовательно, 1 бит информации соответствует одному элементарному событию, которое может произойти или не произойти. Такая мера количества информации удобна тем, что она обеспечивает возможность оперировать мерой как числом. Количество информации при этом эквивалентно количеству двоичных символов 0 или 1. При наличии нескольких источников информации общее количество информации
I(Qi,q2,-.,qk) = І(Я\) + Ду7г) + ••• + І(Як), 0-2)
где I(qk) — количество информации от источника k.
Логарифмическая мера информации позволяет измерять количество информации и используется на практике.
$ 1.3. СТАТИСТИЧЕСКАЯ МЕРА ИНФОРМАЦИИ
В статистической теории информации вводится более общая мера количества информации, в соответствии с которой рассматривается не само событие, а информация о нем. Этот вопрос глубоко проработан К. Шенноном в работе «Избранные труды по теории информации». Если появляется сообщение о часто встречающемся событии, вероятность появления которого близка к единице, то такое сообщение для получателя малоинформативно. Столь же малоинформативны сообщения о событиях, вероятность появления которых близка к нулю.
События можно рассматривать как возможные исходы некоторого опыта, причем все исходы этого опыта составляют ансамбль, или полную группу событий. К- Шеннон ввел понятие неопределенности ситуации, возникающей в процессе опыта, назвав ее энтропией. Энтропия ансамбля есть количественная мера его неопределенности и, следовательно, информативности, количественно выражается как средняя функция множества вероятностей каждого из возможных исходов опыта.
Пусть имеется N возможных исходов опыта, из них k разных типов и г-й исход повторяется и,- раз и вносит информацию, количество которой оценивается как /,. Тогда средняя информация, доставляемая одним опытом,
Но количество информации в каждом исходе связано с его вероятностью р\ и выражается в двоичных единицах (битах) как /,= = log2 (1 /Рі)— —l°g2 pi. Тогда
Выражение (1.4) можно записать также в виде
Но отношения n/N представляют собой частоты повторения исходов, а следовательно, могут быть заменены их вероятностями: п,/Л?=р,; поэтому средняя информация в битах:
/сР = Рі(—log2Pi)+ - + Pk(—log2 рк),
' ИЛИ k
/ср = — log3pfc = tf. (1.6)
i= 1
Полученную величину называют энтропией и обозначают обычно буквой Н. Энтропия обладает следующими свойствами.
1. Энтропия всегда неотрицательна, так как значения вероятностей выражаются величинами, не превосходящими единицу, а их логарифмы — отрицательными числами или нулем, так что члены суммы (1.6) —неотрицательны.
2. Энтропия равна нулю в том крайнем случае, когда одно из рі равно единице, а все остальное — нулю. Это тот случай, когда об опыте или величине все известно заранее и результат не дает новую информацию.
3. Энтропия имеет наибольшее значение, когда все вероятности равны между собой: pi = p2 — ...=pk = l/k. При этом
Н = — log2(l/fe)=log2fe.
4. Энтропия объекта А В, состояния которого образуются совместной реализацией состояний А и В, равна сумме энтропий исходных объектов А и В, т. е. Н(АВ)=Н(А)-{- Н(В).
Если все события равновероятны и статистически независимы, то оценки количества информации, по Хартли и Шеннону, совпадают. Это свидетельствует о полном использовании информационной емкости системы. В случае неравных вероятностей количество информации, по Шеннону, меньше информационной емкости системы. Максимальное значение энтропии достигается при р — 0,5, когда два состояния равновероятны. При вероятностях р — 0 или р = 1, что соответствует полной невозможности или полной достоверности события, энтропия равна нулю.
Количество информации только тогда равно энтропии, когда не определенность ситуации снимается полностью. В общем случае нужно считать, что количество информации есть уменьшение энтропии вследствие опыта или какого-либо другого акта познания. Если неопределенность снимается полностью, то информация равна энтропии: / = Н.
Наибольшее количество информации получается тогда, когда полностью снимается неопределенность, причем эта неопределенность была наибольшей — вероятности всех событий были одинаковы. Это соответствует максимально возможному количеству информации /', оцениваемому мерой Хартли:
/' = log2yV = log2 (1/p) = — log2p,
где N — число событий; р — вероятность их реализации в условиях равной вероятности событий.
Таким образом, /‘ = Ятах.
Абсолютная избыточность информации ?)а6с представляет собой разность между максимально возможным количеством информации и энтропией: ?)а6с = /' —Я, или Яабс = Ятах — Я.
Пользуются также понятием относительной избыточности
0= (Ятах-Я)/Ягаах. (1.7)
§ 1.4. СЕМАНТИЧЕСКАЯ МЕРА ИНФОРМАЦИИ
Вычислительные маійины обрабатывают и преобразуют информацию разного содержания — от числовых данных до сочинения музыки и стихов. Вся эта информация изображается соответствующими символами. Оценка содержания разнохарактерной информации — весьма сложная проблема.
Среди семантических мер наиболее распространены содержательность, логическое количество, целесообразность и существенность информации.
Содержательность события і выражается через функцию меры т(і) — содержательности его отрицания. Оценка содержательности основана на математической логике, в которой логические функции истинности т(і) и ложности т(і) имеют формальное сходство с функциями вероятностей события р(і) и антисобытия q{i) в теории вероятностей.
Как и вероятность, содержательность события изменяется в пределах 0^т(і)^1.
Логическое количество информации Inj, сходное со статистическим количеством информации, вычисляется по выражению
¦ /nf= log2(l/m(0)= — log2m(/).
Отличие статистической оценки от логической состоит в том, что в первом случае учитываются вероятности реализации тех или иных событий, что приближает к оценке смысла информации.
Мера целесообразности информации определяется как изменение вероятности достижения цели при получении дополнительной информации. Полученная информация может быть пустой, т. е. не изменять вероятности достижения цели, и в этом случае ее мера равна нулю. В других случаях полученная информация может изменять положение дела в худшую сторону, т. е. уменьшить вероятность достижения цели, и тогда она будет дезинформацией, которая измеряется отрицательным значением количества информации. Наконец, в благоприятном случае получается добротная информация, которая увеличивает вероятность достижения цели и измеряется положительной величиной количества информации.
Мера целесообразности в общем виде может быть аналитически выражена в виде соотношения
/цел= log2Pl — log2/?0 = lOg2-?4 (1.8)
Ра
где ро и рі — начальная (до получения информации) и конечная (после получения информации) вероятности достижения цели.
Следует различать существенность самого события; существенность времени совершения события или его наблюдения (рано — поздно — момент); существенность координаты совершения события.
Измерение некоторого параметра X можно характеризовать несколькими функциями величины х\ вероятностью р(х), погрешностью измерения е(х) и существенностью с(х). Каждой из этих функций можно поставить в соответствие определенную меру информации. Мерой Хартли оценивается функция погрешности е при фиксированных значениях функции вероятности (р = const) и существенности (c = const). Мерой Шеннона оценивается функция вероятности (р = ?аг) при фиксированных значениях функций погрешности (e = const) и существенности (c = const). Мера существенности относится к ситуации с фиксированными функциями погрешности (e = const) и вероятности (p = const). Можно ввести функции существенности: сх, зависящие от х; ст, ?>, зависящие от времени Т и пространства (канала) N.
§ 1.5. ПРЕОБРАЗОВАНИЕ ИНФОРМАЦИИ
Информационное сообщение всегда связано с источником информации, приемником информации и каналом передачи.
Дискретные сообщения состоят из конечного множества элементов, создаваемых источником последовательно во времени. Набор элементов (символов) составляет алфавит источника.
Непрерывные сообщения задаются какой-либо физической величиной, изменяющейся во времени. Получение конечного множества сообщений за конечный промежуток времени достигается путем
лов приходится решать вопрос о том, как часто следует производить отсчеты функции, т. е. каков должен быть шаг дискретизации Ati=ti — ti-1. При малых шагах дискретизации количество отсчетов функции на отрезке обработки будет большим и точность воспроизведения — высокой. При больших шагах дискретизации количество отсчетов уменьшается, но при этом, как правило, снижается точность восстановления. Оптимальной является такая дискретизация, которая обеспечивает представление исходного сигнала с заданной точностью при минимальном количестве отсчетов.
Методы дискретизации и восстановления информации классифицируются в зависимости от регулярности отсчета, критерия оценки точности дискретизации и восстановления, вида базисной функции, принципа приближения.
Регулярность отсчета определяется равномерностью дискрети
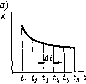

дискретизации (во времени) и квантования (по уровню) (см. рис. 1.2).
В большинстве случаев информация о протекании того или иного физического процесса вырабатывается соответствующими датчиками в виде сигналов, непрерывно изменяющихся во времени. Переход от аналогового представления сигнала к цифровому дает в ряде случаев значительные преимущества при передаче, хранении и обработке информации. Преобразование осуществляется с помощью специальных устройств — преобразователей непрерывных сигналов и может быть выполнено дискретизацией во времени и квантованием по уровню.
Рассмотрим разновидности сигналов, которые описываются функцией x(t).
1. Непрерывная функция непрерывного аргумента. Значения, которые могут принимать функция x(t) и аргумент /, заполняют промежутки (хгпіп, дгщах) и (—7", Т) соответственно.
2. Непрерывная функция дискретного аргумента. Значения функции х(7) определяются лишь на дискретном множестве значений аргумента U, г = 0± 1 ±2, ... Величина х(/,) может принимать любое значение в интервале (xmin, х,тіах).
3. Дискретная функция непрерывного аргумента. Значения, которые может принимать функция x(t), образуют дискретный ряд чисел х), х'2, ..., Xk. Значение аргумента t может быть любым в интервале (—7\ 7’).
4. Дискретная функция дискретного аргумента. Значения, которые могут принимать функция x(t) и аргумент t, образуют дискретные ряды чисел х\, хч, ..., xk и tь fa, ..., tk, заполняющие интервалы (xmirl, лещах) и (—Т, Т) соответственно.
Первая из рассмотренных разновидностей принадлежит непрерывным сигналам, вторая и третья — дискретно-непрерывным, а четвертая — дискретным сигналам.
Операцию, переводящую информацию непрерывного вида в информацию дискретного вида, называют квантованием по времени или дискретизацией. Следовательно, дискретизация состоит в преобразовании сигнала x(t) непрерывного аргумента t в сигнал x(ti) дискретного аргумента U.
Квантование по уровню состоит в преобразовании непрерывного множества значений сигнала х(1,) в дискретное множество значений х*, k = 0, 1, ... (m — 1); х*е(хп,іп, xmax) (третий вид сигнала).
Совместное применение операций дискретизации и квантования по уровню позволяет преобразовать непрерывный сигнал x(t) в дискретный по координатам хи t (четвертая разновидность).
В результате дискретизации исходная функция x(t) заменяется совокупностью отдельных значений x(ti). По значениям функции х{и) можно восстановить исходную функцию х(і) с некоторой погрешностью. Функцию, полученную в результате восстановления (интерполяции) по значениям x(f,-), будем называть воспроизводящей и обозначать К(7).
зации.
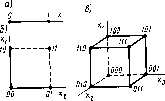
Дискретизация называется равномерной (рис. 1.4, а), если длительность интервалов A^=const на всем отрезке обработки сигнала. Методы равномерной дискретизации широко применяют, так как алгоритмы и аппаратура для их реализации достаточно просты. Однако при этом возможна значительная избыточность отсчетов.
Дискретизация называется неравномерной (рис. 1.4,6), если длительность интервалов между ответами Л7, различна, т. е. Af,=var. Выделяют две группы неравномерных методов: адаптивные и программируемые. При адаптивных методах интервалы Д7, изменяются в зависимости от текущего изменения параметров сигналов. При программируемых методах интервалы Ді; изменяются либо оператором на основе анализа поступающей информации, либо в соответствии с заранее установленной программой работы.
Критерии оценки точности дискретизации сигнала выбираются получателем информации и зависят от целевого использования сигнала и возможностей аппаратной (программной) реализации. Чаще других используются критерий наибольшего отклонения, среднеквадратический, интегральный и вероятностный критерий.
Тип базисных (приближающих, воспроизводящих) функций в основном определяется требованиями ограничения сложности устройств (программ) дискретизации и восстановления сигналов.
Воспроизводящие функции v(t) обычно совпадают с приближающими функциями р(і), хотя в общем случае они могут отличаться друг от друга. Чаще всего для дискретизации и восстановления используют ряды Фурье и Котельникова, полиномы Чебышева и Лежандра, степенные полиномы, функции Уолша и Хаара, гипергеометрические функции.
П
номы вида V{t)= 2 atf, где п — степень полинома, а, — действи-
;=о
тельные коэффициенты. Из этого класса функций наиболее полно исследовано применение полиномов нулевой и первой степени. Алгебраические полиномы удобны для программирования и обработки на ЭВМ.
Выбор оптимальной системы функции представляет определенные трудности, так как при решении задачи минимизации числа дискретных характеристик для описания сигнала с заданной точностью должны учитывать сложность аппаратуры (программ), допустимое время задержки в выдаче информации и другие факторы.
Метод дискретизации при преобразовании непрерывной информации в дискретную влияет на количество информации, которое надо хранить или преобразовывать в ЭВМ. Важна теорема Котельникова, согласно которой функция, имеющая ограниченный спектр частот, полностью определяется дискретным множеством своих значений, взятых с частотой отсчетов:
F0 = 2fm, (1.9)
где /« =2яи)т — максимальная частота в спектре частот S(/w) сигнала x(t); ш,„ — угловая скорость; функция x(t) воспроизводится без погрешностей по точным значениям х(/<) в виде ряда Котельникова:
(1.10)
где At — шаг дискретизации.
Теорема Котельникова справедлива для сигналов с ограниченным спектром. Реальные сигналы — носители информации — имеют конечную длительность. Спектр таких сигналов не ограничен, т. е. реальные сигналы не соответствуют в точности модели сигнала с ограниченным спектром, и применение теоремы Котельникова к реальным сигналам связано с погрешностями при восстановлении сигналов по формуле (1.10) и неопределенностью выбора шага дискретизации или частоты отсчетов.
Для практических задач, однако, идеально точное восстановление функций не требуется, необходимо лишь восстановление с заданной точностью. Поэтому теорему Котельникова можно рассматривать как приближенную для функций с неограниченным спектром. На практике частоту отсчетов часто определяют по формуле
Ko=2fmaxfe3, (Ml)
где к3— коэффициент запаса (обычно 1,5<?3<6); fmax — максимальная допустимая частота в спектре сигнала x(t), например, с учетом доли полной энергии, сосредоточенной в ограниченном частотой спектре сигнала.
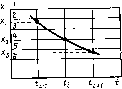
Квантование по уровню состоит в преобразовании непрерывных значений сигнала x(t,) в моменты отсчета U в дискретные значения (рис. 1.5). В соответствии с графиком изменения функции x(t) ее истинные значения представляются в виде заранее заданных дискретных уровней 1, 2, 3, 4, 5 или 6. Функция в моменты отсчета может задаваться или точно (значение xs— уровень 4), или с некоторой погрешностью (значение Х'з — уровень 2, значение хз — уровень 6).
Квантование по уровню может быть равномерным и неравномерным в зависимости от величины шага квантования. Под шагом (интервалом) квантования 8т понимается разность 8т — хт — хт-\, где Хот, Хот—1 — соседние уровни квантования.
Уровень квантования для заданного значения сигнала x(t) можно выразить двумя способами:
1) сигнал x(ti) отождествляется с ближайшим уровнем квантования;
2) сигнал x(ti) отождествляется с ближайшим меньшим (или большим) уровнем квантования.
Так как в процессе преобразования значение сигнала x(t) отображается уровнем квантования хт, а каждому уровню т может быть поставлен в соответствие свой номер (число), то при передаче или хранении информации можно вместо истинного значения величины х'т использовать соответствующее число т. Истинное значение уровня квантования легко восстановить, зная масштаб по шкале х. Для представления т уровней квантования с помощью неизбыточного равномерного кода потребуется n = log2m разрядов. Такое преобразование сопровождается шумами, или погрешностью квантования. Погрешность квантования связана с заменой истинного значения сигнала х(/,) значением, соответствующим уровню квантования хт. Максимальная погрешность квантования зависит от способа отождествления сигнала с уровнем квантования. Для первого из рассмотренных способов она равна 0,56т, для второго — б™.
Чем меньше шаг квантования, тем меньше погрешность квантования. Можно принять, что погрешность квантования в пределах шага квантования имеет равновероятный закон распределения, т. е. любое значение функции в пределах шага будет равновероятным.
25


Квантование и дискретизация находят широкое применение в преобразователях информации, используемых при связи ЭВМ с конкретными объектами (процессами).
§ 1.6. ФОРМЫ ПРЕДСТАВЛЕНИЯ ИНФОРМАЦИИ
Информация всегда представляется в виде сообщения, которое передается некоторой физической средой. Носителем информации может быть любая предметная среда, которая меняет состояние в зависимости от передаваемой информации. Это может быть бумага, на которой информация изображается либо знаками, либо специальными отметками (например, перфорация); магнитный материал (лента, диск и т. п.), состояние которого меняется с помощью магнита; электрический сигнал, у которого изменяется какой-либо параметр (частота, амплитуда).
Различают две формы представления информации: статическую /с (рис. 1.6, а) и динамическую /д (рис. 1.6,6). Возможность передачи сообщения посредством электрического сигнала реализуется с помощью канала связи, соединяющего источник и приемник информации (рис. 1.7). Чтобы передать информацию, необходимо ее предварительно преобразовать.

Декодирование — операция восстановления принятого сообщения. В систему связи необходимо ввести устройства для кодирования и декодирования информации (рис. 1.8). Теоретическое обоснование таких систем дал в своих работах К- Шеннон. Рядом теорем он показал эффективность введения кодирующих и декодирующих устройств, назначение которых состоит в согласовании свойств источника информации со свойствами канала связи. Одно
Целесообразность устранения избыточности сообщения методами эффективного кодирования с последующим перекодированием помехоустойчивым кодом обусловлена тем, что избыточность источника сообщения в большинстве случаев не согласована со статистическими закономерностями помехи в канале связи и поэтому не может быть полностью использована для повышения достоверности принимаемого сообщения. Кроме того, избыточность источника сообщений иногда является следствием ряда причин.
Если избыточность источника сообщений мала и помехи в канале связи практически отсутствуют, то введение как кодера источника, так и кодера канала нецелесообразно. Если избыточность источника сообщений высока, а помехи весьма малы, то целесообразно ввести кодер источника. Если избыточность источника мала, а помехи велики, то целесообразно ввести кодер канала. При большой избыточности и высоком уровне помех целесообразно ввести оба дополнительных кодирующих (и декодирующих) устройств. Большинство кодов, используемых при кодировании информации без учета статистических свойств источника и помехи в канале связи, основано на системах счисления.
§ 1.7. ПЕРЕДАЧА ИНФОРМАЦИИ
Современные вычислительные средства (персональные ЭВМ, микро-, мини- и максиЭВМ) часто используются в составе вычислительных систем или сетей. В этих случаях необходимо решать вопросы не только эффективного представления информации, но также вопросы передачи информации по каналам связи без иска-

связь НС пользователя вычислительными средствами, телефонный канал ТлК, телеграфный канал ТгК, радиоканал РК, телевизионный канал ТвК, другие виды связи.
Вид канала определяет характер и величину помех, которые при этом появляются. Поэтому инженер-проектировщик ЭВМ должен учитывать эти обстоятельства при разработке технических, математических и программных средств.
Рассмотрим некоторые общие вопросы, возникающие при передаче информации.
Передача информации по каналу без помех. Если через канал связи без помех передается последовательность дискретных сообщений длительностью Т, то скорость передачи информации по каналу связи (бит/с),
?— Пт (1/Т), (1.12)
Т -*¦ ос
где / — количество информации, содержащейся в последовательности сообщений.
Предельное значение скорости передачи информации называется пропускной способностью канала связи без помех с = утах.
Количество информации в сообщениях максимально при равной вероятности состояний. Тогда
с= lim log2 k/T. (1.13)
7 -> оо
Скорость передачи информации в общем случае зависит от статистических свойств сообщений и параметров канала связи.
Пропускная способность — характеристика канала связи, которая не зависит от скорости передачи информации. Количественно пропускная способность канала связи выражается максимальным количеством двоичных единиц информации, которое данный канал связи может передать за одну секунду.
Для наиболее эффективного использования канала связи необходимо, чтобы скорость передачи информации была как можно ближе к пропускной способности канала связи. Если скорость поступления информации на вход канала связи превышает пропускную способность канала, то по каналу будет передана не вся информация. Основное условие согласования источника информации и канала связи
Согласование осуществляется путем соответствующего кодирования сообщений. Доказано, что если скорость информации, вырабатываемой источником сообщений ?И, достаточно близка к пропускной способности канала с, т. е. ?„ = с — е, где е — сколь угодно малая величина, то всегда можно найти такой способ кодирования, который обеспечит передачу сообщений, вырабатываемых источником, причем скорость передачи информации будет весьма близка к пропускной способности канала.
Верно и обратное утверждение: невозможно обеспечить длительную передачу всех сообщений, если поток информации, вырабатываемый источником, превышает пропускную способность канала.
Если ко входу канала подключен источник сообщений с энтропией, равной пропускной способности канала связи, то считается, что источник согласован с каналом. Если энтропия источника меньше пропускной способности канала, что может быть в случае неравновероятности состояний источника, то источник не согласован с каналом, т. е. канал используется не полностью.
Согласование в статистическом смысле достигается с помощью статистического кодирования. Оно позволяет повысить энтропию передаваемых сообщений до величины, которая получается, если символы новой последовательности равновероятны. При этом число символов в последовательности будет сокращено. В результате источник информации согласуется с каналом связи.
Передача информации по каналу с помехами. При передаче информации через канал с помехами сообщения искажаются и на приемной стороне нет уверенности в том, что принято именно то сообщение, которое передавалось. Следовательно, сообщение недостоверно, вероятность правильности его после приема не равна единице. В этом случае количество получаемой информации уменьшается на величину неопределенности, вносимой помехами, т. е. вычисляется как разность энтропии сообщения до и после приема: I' — H(i) — Hj(i), где Н{і) — энтропия источника сообщений; Hj(i) — энтропия сообщений на приемной стороне.
Таким образом, скорость передачи по каналу связи с помехами
v'= lim ¦—1. (1-15)
7 —> оо *
Пропускной способностью канала с шумами называется максимальная скорость передачи информации при условии, что канал связи без помех согласован с источником информации:
с — lim
оо 1
Если энтропия источника информации не превышает пропускной способности канала (Я<!с), то существует код, обеспечивающий
c=Fmlog2(l + WJWm), (1.16)
где Fm — полоса частот канала (Гц); Wc — средняя мощность сигнала; Wm — средняя мощность помех (равномерный спектр) с нормальным законом распределения амплитуд в полосе частот канала связи.
Следовательно, можно передавать информацию по каналу с помехами без ошибок, если скорость передачи информации меньше пропускной способности канала, определяемой формулой (1.16). Для скорости ?>с при любой системе кодирования частота ошибок принимает конечное значение, причем оно растет с увеличением значения ?. Из выражения (1.16) следует, что для канала с весьма высоким уровнем шумов (1^Ш>Ц7С) максимальная скорость передачи близка к нулю.
Задание для самоконтроля
1. Являются ли словами следующие комбинации:
¦л) корабль; б) аааа; в) 12345; г) 1а25АВС.
2. Что такое «бит»?
3. Какое количество информации можно изобразить с помощью двадцатиразрядных десятичных чисел?
4. В каких случаях статистическая мера информации совпадает с аддитивной мерой?
5. Определите пропускную способность канала связи, в котором отношение полезного сигнала к сигналу помехи составляет:
а) 1, 2; б) 0,2.
Полоса частот канала — 1 МГц.
ЭЛЕКТРОННЫЕ ВЫЧИСЛИТЕЛЬНЫЕ МАШИНЫ
§ 2.1. ЭЛЕКТРОННЫЕ ЦИФРОВЫЕ ВЫЧИСЛИТЕЛЬНЫЕ МАШИНЫ
Вид перерабатываемой информации влияет на структуру вычислительных машин (ВМ), которые в зависимости от этого делят на два основных класса [20]: аналоговые и цифровые (рис. 2.1).
Аналоговая вычислительная машина (АВМ) — машина, оперирующая информацией, представленной в виде непрерывно изменяющихся физических величин. В качестве физических переменных могут быть использованы сила тока в электрической цепи, изменение скорости или ускорения движения тела и т. п.
Многие явления в природе математически описываются одними и теми же уравнениями. Следовательно, с помощью одного физического процесса можно моделировать различные процессы, имеющие одно и то же математическое описание.
Цифровая вычислительная машина (ЦВМ) — машина, оперирующая информацией, представленной в дискретном виде.
В настоящее время в математике разработаны методы численного решения многих видов уравнений. Следовательно, появилась возможность решать различные уравнения и задачи с помощью набора простых арифметических и логических операций. Поэтому любая ЦВМ, как правило, является универсальным вычислительным средством. В противоположность этому АВМ по своему характеру предназначены для решения каких-то классов задач.
Существуют вычислительные машины, в которых совмещены положительные качества ЦВМ (высокая точность и универсальность в отношении классов задач) и АВМ (оперативность ввода информации и быстродействие в выполнении операций). Такие машины получили название комбинированных или гибридных ВМ.
По принципу действия основных узлов АВМ и ЦВМ разделяют на механические, смешанные (гидромеханические, электромеханические, пневмомеханические и т. п), электронные и оптоэлектронные.
В настоящее время наиболее распространены электронные вычислительные машины (ЭВМ), выполненные на основе применения новейших достижений электроники (полупроводники, интегральные схемы различной степени интеграции). Основная задача данной книги — изложение принципов построения алгоритмов функционирования электронных ЦВМ.
Универсальная ЭВМ — машина, обладающая широкими возможностями в решении задач для различных отраслей науки, техники и народного хозяйства. Универсальные ЭВМ характеризуются быстродействием. Ранее по классификации, принятой в стране, ЭВМ делились на малые (до 5 тыс. опер./с), средние (до 200 тыс. опер./с) и большие машины (более 200 тыс. опер./с). За последние годы вычислительная техника достигла такого уровня развития, что деление ЭВМ по быстродействию не характерно. Условно считают, что машины, которые разрабатываются и выпускаются в странах СЭВ, относятся к большим машинам. Краткие характеристики некоторых моделей ЕС ЭВМ приведены в табл. 2.L
Среди проблемно-ориентированных машин целесообразно выделить вычислительные машины настольного типа, персональные и управляющие ЭВМ. Проблемно-ориентированные машины отличаются от универсальных ЭВМ тем, что путем сужения возможностей ЭВМ в отношении классов решаемых задач удается существенно упростить структуру самой машины. В машинах настольного типа [2, 5], персональных ЭВМ реализован заранее заданный набор программ (достаточно широкий, но все же ограниченный). Ограничения касаются так же набора языков программирования, трансляторы для которых выполняются схемным способом и поставляются в виде дополнительных модулей расширения возможностей. В качестве примера таких ЭВМ можно назвать машины типа «Искра-226», «Электроника ДЗ-28», «Электроника С5-31» и ряд других.
Существуют проблемно-ориентированные машины, предназначенные для управления реальными процессами или объектами. Отличительной особенностью этих машин является то, что они должны работать в реальном масштабе времени и обрабатывать информацию непрерывного вида. Поэтому в состав таких машин должны входить аналого-цифровые и цифроаналоговые преобразователи. К таким проблемно-ориентированным машинам относятся бортовые машины для управления движением самолета (ракеты), технологическими процессами, металлургическими объектами и т. п.

(СССР)
2
11
200
1500
(СССР)
2
6
ПО
1500
(ГДР)
2
4
40
1500
1
6
110
1300
(СССР)
1
5
40
1300
1
6
25
1300
1
4
40
1500
1
4
40
740
(ЧССР)
1
1
24
800
(ВНР)
1
1
20
240
стика
ОЗУ,
К байт Количество каналов: мультиплексных селекторных
Скорость передачи информации по каналам,
К байт/с: мультиплексному
селектор
ному
і
стика
память»
бит
С точки зрения пользователя вычислительная машина — «черный ящик». Параметры его раскрываются при тщательном анализе процессов представления и переработки информации. Излагаемый далее материал относится к универсальным вычислительным машинам.
Для автоматического решения задач универсальная ЭВМ должна включать в себя следующие устройства. Ввод данных в ЭВМ

Входная информация — информация (числовая, текстовая, графическая, электрические сигналы и т. п.), представленная в символах входного алфавита. Она записывается в память ЭВМ.
Память ЭВМ — функциональная часть ЭВМ,, предназначенная для запоминания и (или) выдачи входной информации, промежуточных и окончательных результатов, вспомогательной информации. В памяти машины находятся также программы решения задач, через команды которой осуществляется управление работой всей машины. Вся информация в памяти ЭВМ представляется символами внутреннего алфавита, выбор которого влияет на многие характеристики ЭВМ.
Основные параметры, характеризующие память, — емкость и время обращения к памяти.
Емкость памяти — количество слов информации, которое можно записать в памяти. При этом словом является упорядоченная последовательность символов алфавита конечной длины. Ячейка памяти — часть памяти, содержащая слово.
Емкость памяти можно выразить количеством содержащихся в ней слов или количеством ячеек. Длина ячейки памяти измеряется количеством битов (один бит равен одному двоичному разряду) или байтов (один байт равен восьми битам). Ячейка памяти может вмещать информацию разной длины или разного формата. Формат измеряется словом, двойным словом или полусловом в зависимости от принятого для данной ЭВМ способа представления информации.
Время обращения — интервал времени между началом и окончанием ввода (вывода) информации в память (из памяти). Оно характеризует затраты времени на поиск места и запись (чтение) слова в память.
Для построения запоминающих устройств в качестве физических элементов используют электронные схемы, ферритовые магнитные материалы, магнитные ленты и диски, барабаны с магнитным покрытием, оптические запоминающие элементы и т. д.
Арифметико-логическое устройство (АЛУ) — функциональная 'шсть ЭВМ, выполняющая логические и арифметические действия, необходимые для переработки информации, хранящейся в памяти. Оно характеризуется: временем выполнения элементарных операций; средним быстродействием, т. е. количеством арифметических или логических действий (операций), выполняемых в единицу времени (секунду); набором элементарных действий, которые оно
вита или системы счисле- л
ния, в которой производятся все действия (выбор системы счисления оказывает влияние на все технические характеристики АЛУ).
Быстродействие АЛУ современных ЭВМ лежит в довольно широких пределах — от сотен тысяч
до десятков миллионов операций в секунду. АЛУ выполняет такие элементарные действия, как сравнение, сложение, вычитание, умножение, деление и целый набор логических операций.
Устройство управления (УУ) — функциональная часть ЭВМ, предназначенная для автоматического управления ходом вычислительного процесса, обеспечивающая взаимодействие всех частей машины в соответствии с программой решения задачи. УУ обращается в память машины, выбирает очередную команду, расшифровывает ее и вырабатывает сигналы, указывающие другим устройствам, что им надлежит делать. Управление от программы решения задач, которая хранится в памяти ЭВМ, обеспечивает полную автоматизацию процесса решения. Поэтому универсальные ЭВМ называют программно-управляемыми автоматами. Оператор может вмешаться в ход решения задачи через пульт, соединенный с устройством управления.
Выводные устройства (ВУ) — устройства, осуществляющие преобразование результатов решения задачи, представленных в символах внутреннего алфавита, в выходную информацию, представленную символами выходного алфавита и выдачи информации из машины. В зависимости от вида выходной информации различают устройства выходные печатающие, графические, отображающие и т.д.
Универсальные ЭВМ, как правило, выдают информацию в виде, удобном для человека. Специальные ЭВМ могут выдавать на выходе электрические управляющие сигналы или другую информацию, что определяется характером системы, в которой работает машина.
Рассмотренный состав структурной схемы ЭВМ (рис. 2.2) можно назвать классическим.
Комплекс устройств, охватывающий АЛУ, часть оперативной памяти и УУ, называется процессором. Процессор — самостоятельная функциональная часть ЭВМ, непосредственно осуществляющая процесс преобразования информации и управления ею.
Скорость работы внешних устройств ЭВМ, включающих устройства ввода и вывода информации, значительно меньше скорости работы процессора. Поэтому для более эффективного использования возможностей процессора к нему через входной и выходной
Вычислительные машины, построенные на основе микропроцессора, называются микроЭВМ [15] и отличаются тем, что обычно имеют два вида памяти: RAM (Random — Access — Memory)—¦ память с произвольной выборкой (ППВ) и ROM (READ — ONLY — Memory) —постоянную память (ПП) на интегральных схемах. В постоянную память можно вложить уже готовый транслятор с алгоритмического языка или готовый пакет программ, выполняющий определенную функцию. Это позволяет расширить возможности микроЭВМ путем изготовления модулей расширения, в виде ROM. Структурная схема микроЭВМ представлена на рис. 2.5.
каналы подключают несколько одновременно обслуживаемых внешних устройств. Такая схема организации работы ЭВМ характерна для машин третьего поколения (рис. 2.3).
Успехи современной технологии и микроэлектроники в части производства интегральных схем большой и сверхбольшой плотности позволили изготовлять процессоры и готовые микроЭВМ на одном кристалле [8]. Это привело к изменению структуры вычислительной машины.
Микропроцессор — функционально законченное, программно управляемое устройство обработки данных, состоящее из арифметико-логического устройства, памяти и устройства управления. В микропроцессорах важную роль играют шины данных и адресные шины или адресные и числовые магистрали. Структурная схема микропроцессора представлена на рис. 2.4. Числа в скобках указывают разрядность шин и устройств.
цу
.ВЗУ
ГТ“
on
Г Вывод
і _а_
'Ввод'—?-п
ЙЙ j і і ЙЙ
! r-j-H-jЙЙ
L_g_^p
ЙЙ

Рис. 2.3.
Структурная схема третьего поколения
ЭВМ

Характеристики некоторых микроЭВМ приведены в табл. 2.3.
Понятие «вычислительные системы» пока не определено достаточно четко. Наиболее часто под вычислительной системой (ВС) понимается совокупность средств вычислительной техники, включающая в себя не менее двух процессоров или вычислительных машин, из которых роль основного процессора выполняет одна машина. В таком понимании различают разделимые и неразделимые вычислительные системы. Как правило, разделимые вычислительные системы (рис. 2.6) состоят из нескольких вычислительных машин, каждая из которых может работать самостоятельно. Неразделимые

Рис. 2.6. Структурная схема вычислительной системы

системы (многопроцессорные или мультипроцессорные) состоят из нескольких процессоров, которые могут выполнять свои функции только в составе системы.
Изложенный выше материал касался в основном технических средств ЭВМ и ВС, обеспечивающих функционирование машины.
Чтобы эти технические средства выполняли предписанные функции, необходимы программные средства, обеспечивающие управление работой ЭВМ. В современных ЭВМ или ВС эту роль отводят операционным системам (ОС).
Развитие электронной вычислительной техники идет не только в направлении усложнений структур технических средств, но и в направлении аппаратной реализации многих функций, которые раньше реализовывались с помощью программных средств.
§ 2.3. АБСТРАКТНЫЕ АВТОМАТЫ И ПОНЯТИЕ АЛГОРИТМА
Классические примеры абстрактных автоматов — машины Тьюринга или машины Поста. Как правило, такая машина содержит бесконечную ленту, разделенную на отдельные секции (ячейки), в которые можно либо заносить метку, либо считывать метку с помощью записывающей или считывающей головки (рис. 2.7). Лента (или головка) может передвигаться в левую или правую стороны на один шаг в зависимости от команды. Лента всегда останавливается так, чтобы напротив, головки находилась секция (ячейка). Команды абстрактного автомата обычно включают в себя одно из следующих действий (на примере машины Поста): движение головки вправо, движение головки влево, запись метки, стирание метки, передача управления, остановка (стоп).
Каждая команда имеет свой номер і. Стрелка указывает направление движения. Второе число /, стоящее в конце команды, называется отсылкой. У команды передачи управления может быть две отсылки. Поэтому программа абстрактного автомата должна обладать двумя свойствами:
Поста

1
4

I ІтНтМ-
Ў Ў Ў ЎЎ
Рис. 2.9. Автоматное изображение чисел
1) на первом месте в списке всегда стоит команда с номером 1, на втором месте — с номером 2 и т. д.;
2) отсылка любой из команд всегда находится в списке команд программы.
После передвижения ленты влево или вправо головка считывает состояние секции (пустая или записана метка). Информация о том, какие секции пусты, а какие отмечены, образует состояние ленты или состояние автомата. Таким образом, обладая указанным выше набором команд, автомат может осуществлять определенные действия, которые будут задаваться программой. Программой абстрактного автомата будем называть конечный непустой список команд.
Для «работы» абстрактного автомата необходимо задать программу и начальное состояние, т. е. положение головки и состояние ячеек ленты. После этого автомат приступает к выполнению команды номер 1. Все секции (ячейки) ленты нумеруются в определенном порядке. Порядок нумерации ячеек может совпадать с порядком, в котором расположены натуральные целые числа.
Каждая команда выполняется за один шаг, после чего начинается выполнение команды, номер которой указан в отсылке. Если эта команда имеет две отсылки, то команда с номером верхней отсылки выполняется, если под головкой находится пустая ячейка. Если же под головкой находится ячейка с меткой, то выполняется команда с номером нижней отсылки. Выполнение команды передачи управления не изменяет состояния автомата (ни одна из меток не уничтожается и не ставится, и лента остается неподвижной). При запуске автомата может возникнуть одна из следующих ситуаций:
автомат дошел до выполнения невыполнимой команды (запись метки в занятую ячейку, стирание метки в пустой ячейке); выполнение программы прекращается, автомат останавливается (назовем это состояние поломкой автомата), происходит безрезультатная остановка;
автомат дошел до команды стоп; программа считается выполненной; происходит результатная остановка;
автомат не доходит ни до результатной, ни до безрезультатной остановки; происходит бесконечная работа (автомат «завис»).
Рассмотрим работу автомата, начальное состояние которого задано рис. 2.8 при выполнении следующей программы:
2. 4
3. V 2
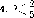
С другой стороны, различные программы, примененные к одному и тому же начальному состоянию, дают разный результат.
На таких элементарных автоматах, как машина Поста или машина Тьюринга, можно производить различные действия над числами. Для этого необходимо представлять числа в абстрактном автомате.
Назовем последовательность секций (ячеек), содержащих метку, массивом, а число секций в нем — длиной массива. Условимся число п представлять на ленте массивом длины п+1. Тогда этот массив будем называть автоматным изображением числа. Например, числа 6, 3 и 2 представлены соответственно на рис. 2.9 автоматными изображениями.
Представим себе, что на машине Поста надо прибавить 1 к любому числу. Для этого требуется написать программу для машины Поста, обладающую следующим свойством: для любого числа п, записанного на ленте, программа должна дать результатную остановку с записью числа п-\-1 в произвольном месте ленты.
Программа может выглядеть следующим образом: 2-й вариант
1. 2;
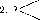
3. V
4. стоп.
В качестве начального состояния может быть выбрано любое состояние, при котором головка находится над одной из отмеченных ячеек ленты (т.е. над набором числа). Если же головка будет находиться в произвольном месте ленты, то программа усложнится. Читателю предлагается самостоятельно написать такую программу.
С помощью абстрактного автомата можно реализовать и другие преобразования числовой информации. Рассмотрим, например, сложение двух чисел. В самой общей постановке эта задача формулируется так: составить программу сложения двух чисел П\ и п2, записанных на ленте на произвольном расстоянии друг от друга. Начальное состояние автомата показано на рис. 2.10.
пг + 1
МтМ?І?МтІ ПтЫтЫ ІтМтІ
Рис! 2.10. Начальное состояние автомата для программы сложения чисел
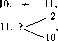
1. з 2; 4. з 5; 7. V 8;
2. 3; 5. 6; 8. -> 9;

Представленные примеры программ машины Поста не исчерпывают всех ее возможностей. Можно составить программы для умножения, деления чисел. Есть ли ограничения на вычисления, производимые на машине Поста? Ответ на этот вопрос был сформулирован самим Э. Постом в следующем виде: «Задача на составление программы, приводящей от исходного данного к результирующему числу, тогда и только тогда имеет решение, когда имеется какой-нибудь общий способ, позволяющий по произвольному и одному данному выписать результирующее число».
Формулировка постулата Поста подводит к понятию алгоритма. Существует много определений термина «алгоритм». Например, по определению акад. А. Н. Колмогорова, алгоритм или алгорифм— это всякая система вычислений, выполняемых по строго определенным правилам, которая после какого-либо числа шагов заведомо приводит к решению поставленной задачи.
В инженерной практике часто используется следующее определение: алгоритм — конечная совокупность точно сформулированных правил решения какой-то задачи [1].
По форме задания алгоритмы могут быть словесными и математическими. Пример словесной формы алгоритма — алгоритм Евклида для нахождения наибольшего общего делителя двух чисел а и Ь.
1. Обозревая два числа а и Ь, переходи к следующему пункту.
2. Сравни обозреваемые числа (а равно Ь, а меньше, больше Ь)' и переходи к следующему пункту.
3. Если а и Ь равны, то прекрати вычисление: каждое из чисел дает искомый результат. Если числа не равны, то переходи к следующему пункту.
5. Вычитай второе число из первого, обозревай два числа: вычитаемое и остаток; переходи к п. 2.
По указаниям этого алгоритма можно найти наибольший общий делитель для любой пары целых чисел.
Массовость — одна из главных черт словесного алгоритма, позволяющего применять его для решения широкого круга задач.
Пример алгебраической формы алгоритма — любая математическая формула для нахождения какой-то величины. Например, значение корней уравнения вида ахг-\-Ьх-\-с— 0 можно найти по формуле xj.2= [ — b± f/b2—4ac] /2а, которая представляет собой алгоритм нахождения этих корней. Однако для того, чтобы реализовать математическую форму алгоритма, требуется дать еще ряд словесных указаний, указать область применения алгоритма.
Детерминированный алгоритм — алгоритм, имеющий место при четкой и ясной системе правил и указаний и однозначных действиях.
Случайный алгоритм — алгоритм, предусматривающий возможность случайного выбора тех или иных правил.
Алгоритм должен обеспечить получение результата через конечное число шагов для любой задачи определенного класса. В противном случае задача неразрешима.
Таким образом, алгоритм дает возможность ответить на вопрос «что делать?» в каждый момент времени. Однако создать алгоритм не всегда возможно. Это подтверждается, например, следующей алгоритмически неразрешимой ситуацией [9]. В городе живет парикмахер, который бреет только тех, кто не бреется сам. Спрашивается, что делать парикмахеру с самим собой? Построить алгоритм решения подобной ситуации невозможно, так как не существует непротиворечивой последовательности правил, следуя которой можно было бы выйти из положения парикмахера.
Численный алгоритм — алгоритм, соответствующий решению поставленной задачи с помощью арифметических действий.
Логический алгоритм — алгоритм, используемый в случае, если при решении задачи приходится применять некоторые логические действия.
Процесс решения задачи на ЭВМ прежде всего должен быть выражен каким-то алгоритмом. Разработка алгоритмов решения задач — задача программиста, а разработка алгоритмов функционирования цифрового автомата для решения поставленных задач — задача инженера-разработчика.
Задание для самоконтроля
1. В чем состоит отличие аналоговой вычислительной машины от цифровой?
2. Чем отличается процессор от арифметико-логического устройства?
3. Есть ли разница между быстродействием и производительностью ЭВМ?
4. Что такое программа для автомата?
5. Что такое автоматное изображение числа?
ПРЕДСТАВЛЕНИЕ ЧИСЛОВОЙ ИНФОРМАЦИИ В ЦИФРОВЫХ АВТОМАТАХ
§ 3.1. ВЫБОР СИСТЕМЫ СЧИСЛЕНИЯ ДЛЯ ПРЕДСТАВЛЕНИЯ ЧИСЛОВОЙ ИНФОРМАЦИИ
Информация во внешнем по отношению к ЭВМ мире представляется в непрерывном или дискретном виде. Внутри ЭВМ информация всегда представляется в виде чисел, записанных в той или иной системе счисления. Если же речь идет о текстовой информации, то обычно она кодируется также с помощью чисел. Вопрос о выборе системы счисления для цифрового автомата — один из важнейших вопросов проектирования как алгоритмов функционирования отдельных устройств, так и расчет технических характеристик этого автомата [11, 12].
Система счисления — совокупность приемов и правил для записи чисел цифровыми знаками. Наиболее известна десятичная система счисления, в которой для записи чисел используются цифры О, 1, ..., 9. Способов записи чисел цифровыми знаками существует бесчисленное множество. Любая предназначенная для практического применения система счисления должна обеспечивать:
возможность представления любого числа в рассматриваемом диапазоне величин;
единственность представления (каждой комбинации символов должна соответствовать одна и только одна величина);
простоту оперирования числами.
Все системы представления чисел делят на позиционные и непозиционные. Самый простой способ записи чисел может быть описан выражением
Ad = D, + D2 + ... + D*= 2 Д-,
і=і
где А0 — запись числа А в системе счисления ?>; D, — символы системы, образующие базу D={D\, D2, ..., Z+}.
По этому принципу построены непозиционные системы счисления.
Непозиционная система счисления — система, для которой значение символа не зависит от его положения в числе.
В общем случае системы счисления можно построить по следующему принципу:
Ад — а\В\ + а2В2 + ... + апВп, (3.1)
где Ад — запись числа А в системе счисления с основанием В,-; а, — цифра (символ) системы счисления с основанием В,; В, — база, или основание, системы.
Если предположить, что Bt=ql, то с учетом (3.1)
В,= <7іД-і. (3.2)
Позиционная система счисления — система, удовлетворяющая равенству (3.2).
Естественная позиционная система счисления имеет место, если q — целое, положительное число.
В позиционной системе счисления значение цифры определяется ее положением в числе: один и тот же знак принимает различное значение. Например, в десятичном числе 222 первая цифра справа означает две единицы, соседняя с ней — два десятка, а левая — две сотни.
Любая позиционная система счисления характеризуется основанием. Основание (базис) q естественной позиционной системы счисления — количество знаков или символов, используемых для изображения числа в данной системе. Возможно бесчисленное множество позиционных систем, так как, приняв за основание любое число, можно образовать новую систему. Например, запись числа в шестнадцатиричной системе может производиться с помощью следующих знаков (цифр): 0, 1, ..., 9, ABCDEF ^вместо А, ... F можно записать любые другие символы, например 1, 2, ..., 5).
Для позиционной системы счисления справедливо равенство
А„ = 's a,q‘, (3.3)
і — —m
ир Ая = апцп + ... + а^'-\-а0ц0 + а-\ц-' + ... + а„ш</~т, где Aq — Произвольное число, записанное в системе счисления с основанием Щ н+ 1, m — количество целых и дробных разрядов. і; На практике используют сокращенную запись чисел:
Aq = anan- 1 ... aia0a_i ... a_m.
цифра
В двоичной системе счисления используют цифры 0, 1. Например, 1001,11012= 1 •23+0-22+0-2‘ +1 -2°+1 - 2~1Н-1 •2-2+0-2~3 + +1 -2~\
Для записи чисел в троичной системе берут цифры 0, 1,2. Например, 21223=2-33+1.32+2-3‘+2-3°.
В табл. 3.1 приведены эквиваленты десятичных цифр в различных системах счисления.
Для любой позиционной системы счисления справедливо, что основание изображается символом 10 в своей системе, т. е. любое число можно записать в виде
Aq = ап • 10п -J- ... -j-йі • 10* -f- do • 10° -f- о,—1*10 1 -|- ... а~т *10 т.
(3.4)
В ЭВМ используют в основном позиционные системы счисления. В дальнейшем для простоты изложения будем употреблять термин «система счисления», имея в виду позиционные системы.
Вес разряда pt числа в позиционной системе счисления выражается соотношением
р, = ^79° = ?. (3.5)
где і — номер разряда при отсчете справа налево.
Если разряд иуіеет вес р,= 10А, то следующий старший разряд будет иметь вес рі + і=10*+1, а соседний младший разряд — вес Рі—\=10* 1 ? Такая взаимосвязь разрядов приводит к необходимости передачи информации между ними.
Если в данном разряде накопилось значение единиц, равное или большее q, то должна происходить передача единицы в соседний старший разряд. При сложении такие передачи информации называют переносами, а при вычитании — заемами. Передача переносов или заемов происходит последовательно от разряда к разряду.
Для разных систем счисления характерна разная длина разрядной сетки, необходимая для записи одного и того же числа. Например, 96= 140g= 10120з = 1IOOOOO2. Здесь одно и то же число, записанное в разных базисах, имеет разную длину разрядной сетки. Чем меньше основание системы, тем больше длина числа.
Если длина разрядной сетки задана, то это ограничивает максимальное (или минимальное) по абсолютному значению число, которое может быть записано.
Пусть длина разрядной сетки равна любому положительному числу, например п. Тогда AQmax=qn— 1; Aqmm=—(qn— 1).
Диапазон представления (ДП) чисел в заданной системе счисления — интервал числовой оси, заключенный между максимальным и минимальным числами, представленными длиной разрядной сетки:
^„тах>ДП>Л,тіп. (3.6)
Правильный выбор системы счисления — важный практический Івопрос, поскольку от его решения зависят такие технические ха-(рактеристики проектируемой ЭВМ, как скорость вычислений, объем памяти, сложность алгоритмов выполнения арифметических операций. При выборе системы счисления для ЭВМ необходимо учитывать следующее:
основание системы счисления определяет количество устойчивых состояний, которые должен иметь функциональный элемент, выбранный для изображения разрядов числа;
длина числа существенно зависит от основания системы счисления;
система счисления должна обеспечить простые алгоритмы выполнения арифметических и логических операций.
Десятичная система, столь привычная в повседневной жизни, не является наилучшей с точки зрения ее технической реализации в ЭВМ. Известные в настоящее время элементы, обладающие десятью устойчивыми состояниями (элементы на основе сегнетокера-мики, декатроны и др.), имеют невысокую скорость переключения, а следовательно, не могут обеспечить соответствующее быстродействие машины.
Подавляющее большинство компонентов электронных схем, применяемых для построения ВМ, — двухпозиционные. С этой точки зрения для ЭВМ наиболее подходит двоичная система счисления. Но рационально ли использование’этой системы с точки зрения затрат оборудования? Для ответа на этот вопрос введем показатель экономичности системы — произведение основания системы на длину разрядной сетки, выбранную для записи чисел в этой системе:
C = qN, (3.7)
где q — основание системы счисления; N — количество разрядов.
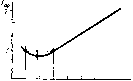
23 q 5 6 7 8 q
Рис. 3.1. Зависимость относительного показателя экономичности от основания системы счисления
Максимальное число, которое можно изобразить в системе с основанием q,
A4mn=qN-\. (3.8)
Из (3.8) можно найти требуемую длину разрядной сетки:
/V=log4(A,max + l). (3,9)
Тогда для любой системы счисления C—q log,(Л, max + l).
Представим, что величина q принимает любые значения (целочисленные и дробные), т. е. является непрерывной величиной. Это необходимо для того, чтобы рассматривать величину С как функцию от величины q. Данное допущение не является строгим, однако позволяет получить интересный вывод: если за единицу измерения оборудования принят условный элемент с одним устойчивым состоянием, то для сравнения двух систем счисления можно ввести относительный показатель экономичности
F=q log q{Aq max + l)/[2 log2 (A 2 max +1)], (3- 1 0)
позволяющий сравнить любую систему счисления с двоичной.
Если функция F непрерывна, то, как видно из приведенного ниже соотношения, она имеет минимум.
</... 2 з 4 6 8 ю
F.... 1,000. 0,946 1,000 1,148 1,333 1,505
На рис. 3.1 представлена зависимость величины F от основания системы счисления q. Нижняя точка графика соответствует минимуму функции F, определяемому из условия dF/dq—О, что соответствует значению ц = е. Следовательно, с точки зрения минимальных затрат условного оборудования, наиболее экономичной является система счисления с основанием, равным е « 2,72.
Используя (3.10), можно доказать, что троичная система счисления экономичнее двоичной. В подавляющем большинстве ЭВМ используют двоичную систему счисления, однако для ЭВМ это связано с преодолением дополнительных трудностей, возникающих при переводе входной информации в двоичную систему счисления и двоичной информации в выходную информацию.
В процессе преобразования информации в цифровом автомате возникает необходимость перевода чисел из одной позиционной системы счисления в другую. Это обусловлено тем, что в качестве внутреннего алфавита наиболее целесообразно использовать двоичный алфавит с символами 0 и 1.
Рассмотрим задачу перевода чисел в общей постановке.
В соответствии с (3.3) числа в разных системах счисления можно представить следующим образом:
Ап= 2 aiqі= 2 bjq^A^. (3.11)
/'= —m j ——s
В общем виде задачу перевода числа из системы счисления с основанием q\ в систему счисления с основанием q2 можно представить как задачу определения коэффициентов bj нового ряда, изображающего число в системе с основанием q2- Решить эту задачу можно подбором коэффициентов Ь(. Основная трудность при этом заключается в выборе максимальной степени, которая еще содержится в числе Aq . Все действия должны выполняться по правилам q\-арифметики, т. е. по правилам исходной системы счисления.
После нахождения максимальной степени основания проверяют «вхождение» в заданное число всех степеней нового основания, меньших максимального. Каждая из отмеченных степеней может «входить» в ряд не более q2—1 раз, так как для любого коэффициента ряда накладывается ограничение:
1; 0<й/<<72—1. (3.12)
Пример 3.1. Перевести десятичное число А =96 в троичную систему счисления (92 = 3).
Решение. 96 = 0-З5 + 1 -З4 +0-З3 + 1 -З2 + 2-3' + 0-3°= 101203.
Ответ: Аз= 10120.
Рассмотренный в примере 3.1 прием может быть использован только при ручном переводе. Для реализации машинных алгоритмов перевода применяют следующие методы.
Перевод целых чисел делением на основание q2 новой системы счисления. Целое число Aqi в системе с основанием q2 записывается в виде
Аь = bkqk2 + bk -1q2 _ 1 + ...+ bxq2 + b0qi
Переписав это выражение по схеме Горнера, получим
Aq^ = (...((bkq2~F Ьк—\) <?2+ + Ь\) <72 + бо- (3.13)
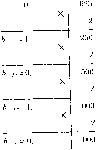
1101001
1010
001100
1010
1010
1010
*2=1
X
1010
II
1
о
1010
1010
1010
Правую часть выражения (3.13) разделим на величину основания </2- В результате определим первый остаток Ьо и целую часть (... ((bkq2+bk-i)q2+ ...)+М- Разделив целую часть на q2, найдем второй остаток Ь\. Повторяя процесс деления fe+І раз, получим последнее целое частное bk, которое, по условию, меньше основания системы <7г и является старшей цифрой числа, представленного в системе с основанием q2.
Пример 3.2. Перевести десятичное число Л = 98 в двоичную систему счисления (№ = 2).
Решение.
_98 98 49
*о = 0 48 24 JJ2_
6, = 1 24 12 |J2^
62 = 0 12 6 [2_
*з = 0 6 3 |^2_
64 = 0 2 1=*„
*5=1
Ответ: Л2 = 1100010.
Пример 3.3. Перевести двоичное число Л2= 1101001 в десятичную систему счисления (</2=І0). Основание q2 изображается в двоичной системе эквивалентом </2 = = 10102.
Решение.
11010 1010
*1=0000
*0 = 0101
Ответ: на основании табл. 3.1 можно записать: 60 = ОЮІ2 = *2 = 00012= 1. Л = 105.
Этот способ применяют только для перевода целых чисел.
Перевод правильных дробей умножением на основание q2 новой системы счисления. Пусть исходное число, записанное в системе счисления с основанием q\, имеет вид
Aqi —a-iqi 1-f- ... + a~mq\ m-
Тогда в новой системе с основанием q2 это число будет изображено как 0, Ь-і, ... bs, или
Aq2 = b — \q2l b-sq2s.
¦ Ап = д2\Ь-, + Ч21(Ь-2+...+Ч2ХЬ-гу). (3.14)
Если правую часть выражения (3.14) умножить на q2, то получится новая неправильная дробь, в целой части которой будет число Ь-\. Умножив затем оставшуюся дробную часть на величину основания q2, получим дробь, в целой части которой будет Ь~2, и т. д. Повторяя процесс умножения s раз, найдем все s цифр числа в новой системе счисления. При этом все действия должны выполняться по правилам ^-арифметики, и следовательно, в целой части получающихся дробей будут проявляться эквиваленты цифр новой системы счисления, записанные в исходной системе счисления.
Пример 3.4. Перевести десятичную дробь Л = 0,625 в двоичную систему счисления ((/2 = 2).
Решение.
Ответ: Л2 = 0,10102.
Пример 3.5. Перевести двоичную дробь Л2 = 0,1101 в десятичную систему счисления (Cj2~ Ю102).
Решение.
Ответ: Л =0,8125.
в десятичную систему счис-
00001 00010
2°=1 2'= 2.
01000 10000
23 = 8 24= 16
16+1.8 + 0-4
+ 0-2
-М-1 + 1-0,5 = 25,5.
При переводе правильных дробей из одной системы счисления в другую можно получить дробь в виде бесконечного или расходящегося ряда. Процесс перевода можно закончить, если появится дробная часть, имеющая во всех разрядах нули, или будет достигнута заданная точность перевода (получено требуемое количество разрядов результата). Последнее означает, что при переводе дроби необходимо указать количество разрядов числа в новой системе счисления. Естественно, что при этом возникает погрешность перевода чисел, которую надо оценивать.
Для перевода неправильных дробей из одной системы счисления в другую необходим раздельный перевод целой и дробной частей по правилам, описанным выше. Полученные результаты записывают в виде новой дроби в системе с основанием q2-
Пример 3.6. Перевести десятичную дробь Л =98,625 в двоичную систему счисления (<7г = 2).
Решение. Результаты перевода соответственно целой и дробной частей возьмем из примеров 3.2 и 3.4.
Ответ: Л2 = 1100010, 1010.
Табличный метод перевода. В простейшем виде табличный метод заключается в следующем: имеется таблица всех чисел одной системы с соответствующими эквивалентами из другой системы; задача перевода сводится к нахождению соответствующей строки таблицы и выбору из нее эквивалента. Такая таблица очень громоздка и требует большой емкости памяти для хранения.
Другой вид табличного метода заключается в том, что имеются таблицы эквивалентов в каждой системе только для цифр этих систем и степеней основания (положительных и отрицательных); задача перевода сводится к тому, что в выражение ряда (3.3) для исходной системы счисления надо подставить эквиваленты из новой системы для всех цифр и степеней основания и произвести соответствующие действия (умножения и сложения) по правилам </г-ариф-метики. Полученный результат этих действий будет изображать число в новой системе счисления.
Пример 3.7. Перевести десятичное число Л = 113 в двоичную систему счисления, используя следующее соотношение эквивалентов цифр и степени основания:
Десятичное число........ ІО2 10’ ІО2
Двоичный эквивалент....... 0 001 1010 1 100 110
Решение. Подставив значения двоичных эквивалентов десятичных цифр и степеней основания в (3.11), получим
А = 113= 1 • І02+ I • 10' + 3-10° = 001-1100100 + 0001 -1010 + 0011 -0001 = 111000І2-Ответ: 111000І2-
ления:
Двоичное число...... 0,1
Десятичный эквивалент . . . 2"'=0,5
Двоичное число...... 00100
Десятичный эквивалент ... 22 = 4
Решение. А — Ответ: А = 25 5
Рассмотрим примеры, в которых перевод одного и того же числа в разные системы счисления осуществляется методом деления на основание новой системы. Запись будем вести в столбик, где справа от вертикальной черты записываются остатки деления на каждом шаге, а слева — целая часть частного.
Пример 3.9. Перевести десятичное число Л = 121 в двоичную систему счисления, используя в качестве промежуточной восьмеричную систему счисления.
Решение.
Сравнивая эти примеры, видим, что при переводе числа из десятичной системы в восьмеричную требуется в два с лишним раза меньше шагов, чем при переводе в двоичную систему. Если при этом учесть, что восьмеричная система связана с двоичной соотношением 8*=(23)fe, то перевод из восьмеричной системы в двоичную, и наоборот, можно осуществить простой заменой восьмеричных цифр их двоичными эквивалентами. Триада — двоичный эквивалент восьмеричных цифр.
Пример 3.10. Перевести двоичное число Л2 = 1011,0111 в восьмеричную систему счисления.
Решение. Исходное число условно разбиваем на триады справа налево для целых чисел и слева направо для правильной дроби. Затем заменяем каждую триаду в соответствии с нижеприведенным соответствием.
Восьмеричная цифра ..0 1 2 3 4 5 6 7
Двоичный эквивалент . . 000 001 010 011 100 101 ПО 111
Л2 = 001 011,011 100,
Л8= 1 3,3 4 .
Ответ: Л = 13,34.
В качестве промежуточных систем счисления целесообразно использовать системы с основанием q=2k. При этом существенно упрощается преобразование информации из системы счисления с основанием q=2k в двоичную систему и наоборот. Преобразование фактически сводится к тому, что символы первоначальной информации, заданной в системе с основанием q—2k, заменяются соответствующими двоичными эквивалентами (см. табл. 3.1). Обратное
дробей); эти группы (диады, триады, тетрады (табл. 3.2) и т. д.) заменяются соответствующими символами исходной системы счисления.
Системы счисления с основанием q=2k широко используют для записи программ решения задач, а также в машинах ЕС ЭВМ для ускорения выполнения арифметических операций.
§ 3.3. РАЗНОВИДНОСТИ ДВОИЧНЫХ СИСТЕМ СЧИСЛЕНИЯ
Двоичная система счисления — система счисления, в которой для изображения чисел используются два символа и вес разрядов в которой меняется по закону 2±к (где k — произвольное целое число). Из определения следует, что для изображения чисел могут быть использованы не только символы 0, 1, но и символы 1, —1 или 0, —1^ Для удобства в дальнейшем символ —1 будем изображать как 1, а двоичную систему, в которой используются эти символы, называть системой (1, 1).
Рассмотрим такую систему. Если для ряда (3.3) положить, что а, принимает значения_1 или 1, то в случае q=2 число 99 запишется в виде Л=99= 1И 111 Ь.
Система (1, 1) отличается от естественной двоичной системы тем, что среди используемых символов отсутствует нуль. Это обстоятельство делает невозможным представление в системе (1, 1) некоторых чисел в виде конечного множества. В то же время существуют числа, которые не имеют единственного изображения, например, число 1 может быть представлено в виде
1 = 1 ГГ... Г= 100 ... 0— 1... 11 =.2* —(2* —2°), (3.15)
где k= 1, 2, ..., п.
Соотношение (3.15) выражает связь между естественной двоичной системой и системой (1, 1). Невозможность представить в виде конечного множества некоторые целые и дробные числа, например 20=11111,111...2, приводит к использованию бесконечных дробей, что обусловливает погрешность при представлении этих чисел в системе (1, 1).
2а-2‘-2~\ (3.16)
(=1
где а;={1, Т}.
Пример 3.11. Перевести число Аі— 100101 в систему (1, 1).
Решение. Используя соотношение (3.15), перевод сводится к замене комбинаций 001 и 01 комбинациями соответственно 111 и 11.
Ответ: Аід=111111.
Для перевода чисел в систему (1, Г) по методу Баньковского необходимо учитывать следующее: в случае нечетного числа перевод осуществляют по правилу (3.15), а затем в разряд і— — 1 записывают единицу; при переводе четного числа его сначала превращают в нечетное добавлением единицы в младший разряд и только после этого переводят в систему (1, 1) по правилу (3.15) как нечетное число._ Затем к полученному результату в разряд і— — 1 записывают 1.
Пример ЗХ?. Перевести в систему (1, 1) двоичное число Лз= 11000.
Решение. В соответствии с правилом Баньковского это число превращаем в нечетное число 11001. После этого заменяем в изображении числа комбинацию 001 ца комбинацию 111 и приписываем в разряд после запятой цифру 1.
Ответ: А и— 11111,1.
Избыточная система счисления с основанием q — система, где для записи чисел используется количество символов большее, чем q, например избыточная двоичная система с символами О, 1, 1 или избыточная троичная система с символами 2, 1, 0, 1, 2.
Избыточная двоичная система связана с обычной двоичной системой соотношением
UJy^J = 2 2' = 2*+1-2, = Щ0:Л. (3.17)
Формула (3.17) позволяет осуществлять переход от одной системы к другой, например Л= 111100012= 1000100011,о,г-
В избыточной двоичной системе одни и те же числа можно пред-ставить_ несколькими способами, например Л=0,011100112= = 0,10010011=0,10010101. Этот пример показывает, что при переходе к избыточной системе можно уменьшить количество единиц в изображении числа.
Избыточность системы счисления, характеризуемая симметричностью символов, дает возможность в ряде случаев упростить выполнение арифметических действий. Например, избыточную двоичную систему счисления используют в некоторых алгоритмах ускорения операции умножения (подробно она будет описана в § 5.7).
число
ЧИСЛО
В работах К. Шеннона [19] было показано, что в системе счисления с основанием q<L—\ и символами 0, —1, ..., —(q—1) можно представить любое действительное число, для чего используется выражение (3.3). Если некоторое число представляется в системе с целочисленным отрицательным основанием, то такое представление будет единственным для всех чисел, кроме чисел, равных X:
X = (±l)qk/(-q+l) + rqk+',
где q — основание системы (<7<с0); г и k — любые целые числа.
В самом деле, для системы счисления с основанием q——2 десятичное число X—l/z может быть представлено бесконечными дробями в виде
? _/0, 010101...;
Л("2)— 11, 101010.
Двоичную систему счисления с основанием q— —2, в которой используются символы 0, 1, назовем минус-двоичной системой счисления. В этой системе можно представлять как положительные, так и отрицательные числа (табл. 3.3).
Из таблицы видно, что методы перевода десятичных чисел в систему счисления с основанием q=—2 аналогичны методам перевода, рассмотренным ранее, но при переводе десятичных чисел необходимо учитывать следующее: при использовании метода последовательного деления на основание новой системы все остатки от деления на каждом шаге должны быть положительными числами, которые не превышают абсолютного значения нового основания q. Это правило распространяется и на случай перевода правильных дробей методом последовательного умножения на основе q, где появляющиеся целые части дробей также должны быть положительными числами, значение которых меньше величины q.
Решение.
В случае перевода правильной дроби (или дробной части смешанной дроби) необходимо, чтобы дробь на каждом шаге удовлетворяла требованию
|<7І/(|<7І + 1КЛ<1/(|9| + 1), или -2/3<Д<1/3, (3.18)
где А — дробь, переводимая в систему счисления с основанием q= —2.
Если ограничение (3.18) не выполняется, то дробь А представляют в виде А= 1 —А, где А должно лежать в указанных пределах.
Пример 3.14. Перевести десятичную дробь А = 0,625 в минус-двоичную систему счисления с точностью до трех знаков после запятой.
Решение. Исходная дробь не удовлетворяет неравенству (3.18). Преобразуем ее к виду: 0,625+1 —0,375.
(1) Х-\375
0,750 неравенство (3.18) не удовлетворяется;
(1) -0,250
х -2
0,500 неравенство (3.18) не удовлетворяется;
(1) -0,500
х -2
1,000 неравенство (3.18) удовлетворяется. Ответ: 0,625 =1,111.
§ 3.5. ФОРМЫ ПРЕДСТАВЛЕНИЯ ЧИСЕЛ
Число 0,028 можно записать так: 28-ІО-3, или 0,03 (с округлением), или 2,8-10"2 и т. д. Разнообразие форм в записи одного числа может послужить причиной затруднений для работы цифрового автомата. Во избежание этого нужно либо создать специальные алгоритмы распознавания числа, либо указывать каждый раз форму его записи. Второй путь проще.
Существует две формы записи чисел: естественная и нормальная. При естественной форме число записывается в естественном натуральном виде, например 12560—целое число; 0,003572—пра-
Задачу выбора масштабного коэффициента Ка усложняет необходимость сохранить соответствие разрядов всех чисел, которыми оперирует цифровой автомат. Пусть имеется цифровой автомат с разрядной сеткой длиной 12 двоичных разрядов (рис. 3.2, а). Надо определить масштабный коэффициент для чисел Аі= —1011,01111 Юг и
•42=0,110001101 г.
Для того чтобы выполнить условие (3.19), необходимо число, большее по абсолютному значению, записать в виде А і= = —0,10110111110-24. Отсюда [А,]ф=1,10110111110, что соответствует величине масштабного коэффициента /0ц = 24. Число Л2 должно войти в разрядную сетку автомата с сохранением соответствия разрядов, т. е. Ка?=Каі- Следовательно, А2= +0,0000110001101 -24, или [А2]ф = 0,00001100011 (рис. 3.2, б, в).
Из примера видно, что представление чисел в форме с фиксированной запятой может при?ести к погрешности представления. Так,
волом 0, а знак отрицательного числа «—» изображается символом 1.
Если на вход цифрового автомата поступают целые числа, например, как в ЕС ЭВМ, то в разрядной сетке (в формате машинного изображения) один разряд отводится под знак числа, а последующие разряды образуют после числа.
Номер
разряда
\t\f \ а\о\о\< ГЛоТЛ
вильная дробь; 4,89760 — неправильная дробь. При нормальной форме запись одного числа может принимать разный вид в зависимости от ограничений, накладываемых на ее форму. Например, число 12560 может быть записано так: 12560=1,256-104= 0,1256-105= = 125600-10"' и т. д.
Автоматное (машинное) изображение числа — представление числа А в разрядной сетке цифрового автомата. Условно обозначим автоматное изображение числа символом [А]. Тогда справедливо соотношение: А— [А] Ка, где Ка — коэффициент, величина которого зависит от формы представления числа в автомате.
Представление чисел с фиксированной запятой (точкой). Естественная форма представления числа в цифровом автомате характеризуется тем, что положение его разрядов в автоматном изображении остается всегда постоянным независимо от величины самого числа. Существует также другое название этой формы записи чисел — представление чисел с фиксированной запятой (точкой).
Чтобы упростить функционирование цифрового автомата, необходимо ограничить входную информацию какой-то одной областью чисел (на вход автомата желательно подавать либо целые числа, либо правильные дроби, либо любые числа), что позволит определить значения масштабного коэффициента Ка- Например, если на вход цифрового автомата поступают только правильные дроби, то
-1<[Л]Ф<1, (3.19)
где [А]ф — машинное изображение числа для формы представления с фиксированной запятой.
Тогда число А будет представлено в виде А— [Л]ф/Сл-
Величина масштабного коэффициента Ка, удовлетворяющего условию (3.19), определяет тот факт, что в машинном изображении запятая всегда стоит после целой части дроби, т. е. перед ее старшим разрядом. Следовательно, можно хранить только дробную часть числа (цифровую часть), а в разряде целой части писать дополнительную информацию.
Так как числа бывают положительные и отрицательные, то формат (разрядная сетка) автоматного изображения разбивается на знаковую часть и после числа (рис. 3.2, а). В знаковую часть записывается информация о знаке. Примем, что знак положительного
числа «-(-» изображается сим-
а) .Знаковая часть
«ЕЕ
>).Рис. 3.2. Представление чисел в форме с фиксированной запятой
Представление чисел в форме с плавающей запятой. В нормальной форме где тА — мантисса числа Л ; рА — порядок числа А (характеристика числа).
Как видно из ранее изложенного, такое представление чисел не однозначно; для определенности обычно вводят некоторые ограничения. Наиболее распространено и удобно для представления в ЭВМ ограничение вида
<Г‘<|/пл|<1, (3.21)
где q — основание системы счисления.
Нормализованная форма представления чисел — форма представления чисел, для которой справедливо условие (3.21).
Поскольку в этом случае абсолютное значение мантиссы лежит в пределах от q~{ до 1 — q~~n, где п — количество разрядов для изображения мантиссы без знака, положение разрядов числа в его автоматном изображении не постоянно. Поэтому такую форму представления чисел называют также формой представления с пла-
Порядок
5)
(3.22)
вающей запятой. Формат машинного изображения числа с плавающей запятой должен содержать знаковые части и поля для мантиссы и порядка (рис. 3.3, а). Выделяются специальные разряды для изображения знака числа (мантиссы) и знака порядка или характеристики (рис. 3.3, а, б). Кодирование знаков остается таким же, как было с фиксированной запятой.
а)
ІФ \г |з|Д|5|б| 7|fl|s|/g|//|/2l?j|/»|/ff|*
, t Поле мантиссы \ ' По/нГпоряЗка
оцак мантиссы_Арак порядка
Мантисса
Рис. 3.3. Представление чисел в форме с плавающей запятой
Рассмотрим пример записи чисел в форме с плавающей запятой. Пусть в разрядную сетку цифрового автомата (рис. 3.3) необходимо записать двоичные числа А\——10110,1 1112 и Л2 = =+0,0001100101112. Прежде всего эти числа необходимо записать в нормальной форме (рис. 3.3, в, г). Порядок чисел выбирают таким образом, чтобы для них выполнялось условие (3.21), т. е. А\ = = —0,101101111-2® и Л2 = +0,110010111-2~+ он должен быть записан в двоичной системе счисления. Так как система счисления для заданного автомата остается постоянной, то нет необходимости указывать ее основание, достаточно лишь представить показатель порядка (характеристику числа).
Поскольку для изображения порядка выделено пять цифровых разрядов и один разряд для знака, их машинные изображения и машинные изображения их мантисс соответственно
[Ра,)= 0 00101; [рАг]= Ю0011;
[т/1|]=1,101101111; [щЛ2] = 0,110010111.
§ 3.6. ПРЕДСТАВЛЕНИЕ ОТРИЦАТЕЛЬНЫХ ЧИСЕЛ
Одним из способов выполнения операции вычитания с помощью двоичного сумматора — замена знака вычитаемого на противоположный и прибавление его к уменьшаемому:
А — В=А+(—В).
Для машинного представления отрицательных чисел используют коды прямой, дополнительный, обратный. Рассмотрим применение этих кодов для чисел, представленных в форме с фиксированной запятой. Для простоты изложения в дальнейшем будут рассматриваться числа по модулю, меньшему единицы. Это существенно упрощает вычисление масштабных коэффициентов.
Прямой код числа Л=—0аіа2...а„— машинное изображение этого числа в виде [Л]пр=1, аіа2...ац Из определения следует, что в прямом коде все цифровые разрядЦ отрицательного числа остаются неизменными, а в знаковой чдети записывается единица. Например, если А— —0,101110, то [Л]пр = 1,101110. Положительное число в прямом коде не меняет своего изображения. Например, если Л=0,110101, то [Л]пр=0,110101.
В прямом коде в разрядную сетку цифрового автомата можно записать следующее максимальное по абсолютному значению число А„р max=0, 11 ... 1 = 12~", где п — количество разрядов разрядной сетки цифрового автомата.
Диапазон изменения машинных изображений для прямого кода лежит в пределах — (1— 2_'ІК[^]пр<(1-2~~п).
Ранее прямой код был использован для записи чисел в разрядной сетке цифрового автомата.
Правила преобразования чисел в прямой код можно сформулировать так:
А , если А ^ 0,
[А] „р = 11 + ІАI, если Л <0. (3.23)
Дополнительный код числа А = 0, а\а<і...ап — такое машинное изображение этого числа [Л]д— 1, аіа2...а„, для которого а* = 0, если а, = 1, и а, = 1, если а, — 0, за исключением последнего значащего разряда, для которого ak— 1 при ak= 1. Например, число Л = —0,101110 запишется в дополнительном коде так: [А]д = = 1,010010.
Дополнительный код является математическим дополнением основанию системы счисления:
ИІ+ [Л]д = <7, (3.24)
где |Л| — абсолютное значение числа Л.
Так как положительные числа не меняют своего изображения в дополнительном коде, то правила преобразования в дополнительный код можно записать следующим образом:
, ( А , если Л > 0,
<325)

(3.28)
(3.29)
Максимальное дополнительное число, представляемое при этом, равно (1 — 2~п).
Наибольшее отрицательное число, которое можно записать в дополнительном коде, определим следующим образом. Предположим, что наибольшее отрицательное число Л1 = —0,11...11. Тогда изображение этого числа в дополнительном коде [Л']д = 1,00...01. Если к числу А1 добавить единицу в самый младший разряд, то в результате получим число —1,00..0. Преобразовав это число по формальным правилам, получим [Л]д min= 1,00...0.
Следовательно, диапазон изменения машинных изображений чисел для формы представления с запятой, фиксированной перед старшим разрядом, в дополнительном коде — 1 <:[Л]д^(1 — 2_п).
Для ЕС ЭВМ машинные изображения чисел — всегда целые числа. При этом наибольшее положительное число состоит из целой части, все разряды которой равны единице, и знакового разряда, равного нулю (например, в случае 16 двоичных разрядов (два байта) максимальное положительное число имеет вид 0111111111111111, т. е. равно 215—1) ; наибольшее отрицательное число состоит из целой части, все разряды которой равны нулю, и знакового разряда, равного единице, т. е. имеет вид 1000000000000000. В этом случае говорят о форме представления чисел с фиксированной точкой. Таким образом, соотношение (3.24) для представления целых чисел в дополнительном коде принимает вид
ИІ+ И]д=<7* + '- (3.26)
где k — количество разрядов в целой части машинного изображения числа (k — 0,k).
Формула (3.24) —частный случай формулы (3.26) при k = 0.
Обратный код числа А = +0, аіа2...ап — такое машинное изображение этого числа [Л]06=1, а\а2...ап, для которого а, = 0, если а, = 1, и а, = 1, если а, = 0. Из определения следует, что обратный код двоичного числа является инверсным изображением самого числа, в котором все разряды исходного числа принимают инверсное (обратное) значение, т. е. все нули заменяются на единицы, а все единицы — на нули. Например, если Л = —0,101110, то [Л]об = = 1,010001. Для обратного кода чисел, представленных в форме запятой, фиксированной перед старшим разрядом, справедливо соотношение , , _
И1+ И] об = Я — Я > (3.27)
где |Л| — абсолютная величина Л; п — количество разрядов после запятой в изображении числа.
Правила преобразования чисел в обратный код можно сформулировать следующим образом:
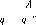
Пример 3.15. Найти обратный и дополнительный коды числа А = —0,111000г.
Решение. Используя определение обратного кода, получим [А]об = 1,000111.
Для нахождения дополнительного кода числа добавим единицу в младший разряд его изображения:
1,000111
+
[Л]д= 1,001000
Ответ: [Л]об= 1,000111; [Л]д= 1,001000.
В обратном коде можно изображать максимальное положительное число [Л]ов max = 0,11...1 = 1 — 2~п и наибольшее отрицательное число [Л]0б min = —0,11...1 = —(1—2~п), записываемое в виде 1ДЮ...0.
При проектировании цифровых автоматов необходимо учитывать неоднозначное изображение нуля в обратном коде: +0 изображается 0,00...0, —0 изображается 1,11... 1.
Использование различных способов изображения отрицательных чисел в цифровом автомате обусловливает целый ряд особенностей выполнения операции алгебраического сложения двоичных чисел.
§ 3.7. ПОГРЕШНОСТИ ПРЕДСТАВЛЕНИЯ ЧИСЕЛ
Представление числовой информации в цифровом автомате, как правило, влечет за собой появление погрешностей (ошибок), величина которых зависит от формы представления чисел и от длины разрядной сетки автомата.
Абсолютная погрешность представления — разность между истинным значением входной величины Л и ее значением, полученным из машинного изображения Лм, т. е. А [Л] = Л — Лм.
Относительная погрешность представления — величина
8 [Л] = А[Л]/ЛМ. (3.30)
Входные величины независимо от количества значащих цифр могут содержать грубые ошибки, возникающие из-за опечаток, ошибочных отсчетов показаний каких-либо приборов, некорректной, постановки задачи или отсутствия более полной и точной информации. Например, часто принимают я =3,14. Однако эта величина может быть получена с более высокой точностью (800 знаков и более). Если принять, что точное значение л= 3,14159265, то абсолютная погрешность равна А [я] =0,00159265.
Часто некоторая величина в одной системе счисления имеет конечное значение, а в другой системе счисления становится беско-
3—1569
б[А]п тіп = 0,5 • 2-прА/( 1 - 2-п)рА,
нечной величиной, например, дробь ‘/ю имеет конечное десятичное представление, но, будучи переведена в двоичную систему счисления, становится бесконечной дробью 0,0001100110011...
Следовательно, при переводе чисел из одной системы счисления в другую неизбежно возникают погрешности, оценить которые нетрудно, если известны истинные значения входных чисел.
В соответствии с (3.19) числа изображаются в машине в виде Ач=\А~\Кл, где масштабный коэффициент Ка выбирают так, чтобы абсолютное значение машинного изображения числа А в системе счисления с основанием ц = 2 было всегда меньше 1: Ая = = Ка [а-і<7~‘ + а-2<7“2 + -• + a-nq~n + ...].
Так как длина разрядной сетки автомата равна п двоичных разрядов после запятой, то, абсолютная погрешность перевода десятичной информации в систему с основанием q будет
А [А] = а („ + п<7 (л + п + a—(n + s)q~(n s) + —
= So*'. О-ЗІ)
і = —(я + 1)
Если q = 2, то при а, = 1 максимальное значение этой погрешности
— оо — оо
А[Л]|Ш1Х = 2 1-2' = 2"" 2 2‘ = 2~п. (3,32)
і = — (п +1) ! = — I
Из (3.32) следует, что максимальная погрешность перевода десятичной информации в двоичную не будет превышать единицы младшего разряда разрядной сетки автомата. Минимальная погрешность перевода равна нулю.
Усредненная абсолютная погрешность перевода чисел в двоичную систему счисления А [Л] = (0 + 2~л) /2 = 0,5 • 2~п.
Для представления чисел в форме с фиксированной запятой абсолютное значение машинного изображения числа
2-л<|[Л]ф|<1-2-л. (3.33)
Следовательно, относительные погрешности представления для минимального значения числа 6[Л]ф тіп = А[А]/[Л]Ф гаах = 0,5-2 “л/ /(1— 2~л).
Для ЭВМ, как правило, /г =16-^64, поэтому 1^>2 п, откуда 8[А]фтіп=0,5.2-л.
Аналогично, для максимального значения:
ЛЗ рА'* (3.36) где п — количество разрядов для представления мантиссы числа.
Из (3.36) следует, что относительная точность представления чисел в форме с плавающей запятой почти не зависит от величины числа.
Задание для самоконтроля
1. Перевести десятичное число А = 121 в двоичную систему счисления.
2. Перевести двоичное число 4 = 10001010111,01 в десятичную систему счисления.
3. Перевести десятичное число 4 = 135,656 в двоичную систему счисления с точностью до пяти знаков после запятой.
4. Сколько потребуется двоичных разрядов для изображения десятичного числа 4 = 10|в?
5. Перевести двоичное число 42=10111011 в десятичную систему счисления методом деления на основание.
6. Перевести восьмеричное число 48=345,766 в двоичную систему счисления.
7. Записать десятичное число 4 = 79,346 в двоично-десятичной форме.
8. Перевести десятичную дробь 4 = 639/б4 в двоичную систему счисления.
9. Перевести восьмеричную дробь 48 = 635/4о в двоичную систему счисления.
10. Перевести восьмеричное число 48 = 326 в троичную систему счисления.
11. Перевести восьмеричное число 48= 15,647 в двоичную систему счисления.
12. Перевести троичное число 43= 1211 в пятиричную систему счисления.
13. Для какой системы счисления с основанием q2 = x справедливо равенство 121 =441х?
14. Записать машинное изображение в форме с плавающей запятой или десятичного числа 4 = —3,375, если для мантиссы имеется шесть двоичных разрядов со знаком и для порядков — три двоичных разряда (со знаком).
15. Определить масштабные коэффициенты для чисел 42 = —10110,111010001 и В2 = 0,00111000110001 при условии, что машинное изображение числа содержит десять двоичных разрядов со знаком.
16. Перевести двоичное число 4г = 0,011000100 в систему (1, 1).
17. Перевести число 4і,[ = 11111,1 из системы (1,1) в двоичную систему счисления.
Из (3.34) видно, что погрешности представления малых чисел в форме с фиксированной запятой могут быть очень значительными.
Для представления чисел в форме с плавающей запятой абсолютное значение мантиссы
СЛОЖЕНИЕ ЧИСЕЛ НА ДВОИЧНЫХ СУММАТОРАХ
На основе правил двоичной арифметики можно записать правила сложения двоичных цифр так, как показано в табл. 4.1, где а„ Ь, — разряды операндов А я В соответственно; с, — разряд суммы; п, — перенос из данного разряда в соседний старший.
Двоичный полусумматор — устройство, выполняющее арифметические действия по правилам, указанным в табл. 4.1.
§ 4.1. ФОРМАЛЬНЫЕ ПРАВИЛА ДВОИЧНОЙ АРИФМЕТИКИ
Популярность двоичной системы счисления во многом определяется простотой выполнения арифметических действий:
сложение 0 + 0= 0
0+ 1 = 1
1+0= 1 1 + 1 = (1)0 перенос
вычитание 0-0= 0 1-0= 1 1-1= 0 0 — 1 =(і)і
заем
умножение
охо=о
охі=о
1X0 = 0 1X1 = 1
Обобщая вышеизложенное, можно сформулировать правила поразрядных действий при сложении операндов А я В:
в старший разряд
в старшем разряде
В основу арифметико-логического устройства любой ЭВМ может быть положен либо сумматор, либо вычитатель. И в том, и в другом случае могут быть разработаны алгоритмы выполнения арифметических операций. В выполнении арифметических действий всегда участвуют два числа или более. В результате арифметической операции появляется новое число
С = АЧВ, (4.І)
где ?— знак арифметического действия (сложение, вычитание, умножение, деление).
Операнд — число, участвующее в арифметической операции, выполняемой цифровым автоматом.
Так как цифровой автомат оперирует только автоматными изображениями чисел, то последние выступают в качестве операндов. Следовательно, для машинных операций более правильно выражение (4.1) написать в виде
[С]=[Л]?[В], (4.2)
где в квадратных скобках [ ] — обозначения автоматных изображений операндов.
Рассмотрим формальные правила выполнения арифметических операций сложения и вычитания на уровне разрядов операндов.
О-і + Ьі + п, —j — с, + л,-, (4.3)
где п, — 1 — перенос из (г — 1)-го разряда; п, — перенос в (/ + 1)-й разряд (переносы принимают значения 0 или 1).
Двоичный сумматор — устройство, выполняющее арифметические действия по правилам, указанным в табл. 4.2. Условные обозначения двоичных полусумматоров и сумматоров показаны на рис. 4.1,а и б соответственно.
Заем равносилен вычитанию единицы из старшего разряда. С учетом единицы заема из старшего соседнего разряда правила
разряда
-I
1
1
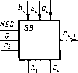
Решение.
вычитания двоичных цифр можно записать так, как показано в табл. 4.4 (чтобы отличить заем от переноса, перед единицей поставлен знак минус).
Если А—уменьшаемое (1-й операнд), В— вычитаемое (2-й операнд), то для поразрядных действий
ш — bi + zi = с, -f Zi + 1. (4.4)
Двоичный вычитатель — устройство, выполняющее арифметическое действие по правилам, указанным в табл. 4.4.
С точки зрения технической реализации всегда проще сложить два электрических сигнала, чем вычесть их друг из друга.
В машине «Иллиак» был использован вычитатель кодов и метод избыточного кодирования чисел. При этом любой разряд числа представляется двумя битами, один из которых является знаковым Si, а другой — значащим а*.
Таблица кодирования выглядит следующим образом (табл. 4.5).
Вместо сложения используется операция вычитания (условное обозначение вычитателя показано на рис. 4.2).
При этом
г,- = п, ® NEG, Сі = п, фйіф Ьі,
. п, _. 1 = (S/O,- V аД) G,n, = (s; + ,о, + 1 V V сц+ 1 bi+ 1 )G.
Символ ф принят для обозначения поразрядного сложения по модулю 2 (см. § 10.1).
Результат всегда получается в избыточной форме, т. е. С* = =А* — В, где С*, А* — избыточное представление.
С* — — (—А* — В).
В подавляющем большинстве ЭВМ основное устройство — двоичный или десятичный сумматор, в зависимости от принятой системы счисления.
§ 4.2. СЛОЖЕНИЕ ЧИСЕЛ, ПРЕДСТАВЛЕННЫХ В ФОРМЕ С ФИКСИРОВАННОЙ ЗАПЯТОЙ, НА ДВОИЧНЫХ СУММАТОРАХ
Рассмотрим несколько видов двоичных сумматоров.
Двоичный сумматор прямого кода (ДСПК) — сумматор, в котором отсутствует цепь поразрядного переноса между старшим цифровым и знаковым разрядами (рис. 4.3,а). На ДСПК можно складывать только числа, имеющие одинаковые знаки, т. е. такой сумматор не может выполнять операцию алгебраического сложения. В самом деле, пусть заданы операнды
[Д]пр = BgAa\a2...an, \_B~]np==SgB,b\b2’‘’bn,
где SgA, Sge — соответственно содержимое знаковых разрядов изображений для А и В (символ происходит от английского слова sign — знак); a,Д — цифровые разряды изображений.
Если SgA — Sge, то сумма чисел будет иметь знак любого из слагаемых, а цифровая часть результата получится после сложения цифровых частей операндов.
Пример 4.1. Сложить числа А =0,1011, В = 0,0100 на сумматоре прямого кода.
Решение.
[A] лр = 0,1011 SgA = 0,
+
[B] пр = 0,0100 SgB = о,
[C] пр = 0,1111 Sgc = 0.
Ответ: [С]пр = 0,1111.
При сложении чисел на ДСПК возможен случай, когда абсолютное значение суммы операндов превышает единицу. Тогда имеет место переполнение разрядной сетки автомата. Признак переполнения— наличие единицы переноса из старшего разряда цифровой
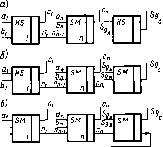
части сумматора. В этом случае должен вырабатываться сигнал переполнения <р= 1, по которому происходит автоматический останов машины и корректировка масштабных коэффициентов с таким расчетом, чтобы избежать появления переполнения.
Двоичный сумматор дополнительного кода (ДСДК) — сумматор, оперирующий изображениями чисел в дополнительном коде. Характерная особенность ДСДК — наличие цепи поразрядного переноса из старшего разряда цифровой части в знаковый разряд (рис. 4.3, б). Определим правила сложения чисел на ДСДК.
Теорема. Сумма дополнительных кодов чисел есть дополнительный код результата.
Доказательство. Предположим, что числа представлены в форме с фиксированной запятой, стоящей перед старшим разрядом. Рассмотрим возможные случаи.
1) Л>0, В>0, А+В< 1.
Так как [Л]Д=Л, [В]Д=В, то [Л]Д+[В]Д=Л+В=[Л+В]Д — результат положительный.
2) Л<О, В>0, \А\>В.
Здесь [A\=A+q, [В]Д=В. Тогда [Л]д+ [В]Д=Л —
результат отрицательный.
3) Л<0, В>О, \А\<В.
Здесь [A\=A+q, [В]д=В+<?. Тогда [Л]д + [В]д=Л+В+<?. Так как значение этой суммы больше q, то появляется единица переноса из знакового разряда, что равносильно изъятию из суммы q единиц, т. е. результат равен [Л]д +[В]Д=Л+В,
4) Л<0, В<0, И+В|<1.
Здесь [A\=A + q, [B\ = B+q. Тогда [Л]Д + [В]Д=Л + + ? + </ + <? = [Л-f- В]д — результат отрицательный (здесь появляется единица переноса из знакового разряда).
Пример 4.3. Найти сумму чисел Л = 0,1010, В=0,0100, используя сумматор дополнительного кода.
Решение. Складываются машинные изображения этих чисел:
(71^ = 0,1010
+
[В]д = 0,0100 [С]д = 0,1110
Ответ: С = 0,1110.
Пример 4.4. Найти сумму чисел А = — 0,1011, В = 0,0100 на сумматоре дополнительного кода.
Решение.
[Л]д= 1,0101
+
[В]д = 0,0100 [С]д= 1,1001
Ответ: С = —0,0111.
Пример 4.5. Найти сумму чисел Л =0,1011, В = — 0,0100 на сумматоре дополнительного кода.
Решение.
[4]д = 0,1011
+
[В]д=1,1100 [С]д = 0,0111
Ответ: С = 0,0111.
Двоичный сумматор обратного кода (ДСОК) — сумматор, оперирующий изображениями чисел в обратном коде. Характерная особенность ДСОК — наличие цепи кругового, или циклического, переноса из знакового разряда в младший разряд цифровой части (рис. 4.3, в).
Определим правила сложения чисел на ДСОК.
Теорема. Сумма обратных кодов чисел есть обратный код результата.
Доказательство. Рассмотрим следующие основные случаи:
1) Л>0, В>0, Л+В<1. Тогда [Л]об+[В]о6=Л+?=[Л+В]0б.
2) Л<0, В>0, \А\>В. Здесь \AU=q-q-a+A, [В]об=В.
Тогда [Л]об + [В]об = — Q~n-\- А-\- В = [А + В]об, так как результат отрицательный.
3) Л<0, В>0, |Л|<В. Здесь [Л]об=<7—q~n + А.
Тогда [Л]06+[В]об = <7-<Г'1 + Л+В. Так как [Лоб + [?]об положительна, то правая часть этого выражения становится больше q, что вызывает появление единицы переноса из знакового разряда. Поскольку в ДСОК существует цепь переноса из знакового разряда в младший разряд (величина переноса из знакового разряда равна q—q~n), то [Л]0б+[й]об = [4 + /?]об. результат положительный.
[Bl6 = q-q-n+B.
Следовательно, [A]o6+[B]o6—q — q~n + q—q^n+A+B. Здесь появляется единица переноса из знакового разряда, что равносильно изъятию из суммы величины а — а~п, т. е. [Л]об +
+ [й]об — [Л + В]об.
5)\А\=В, Л<0, В>0. Тогда [.A%6=q-q-n+A.
Следовательно, [A\o6+[B]o6=q—q~n+A + B=q — q~n — результат указывает на то, что сумма равна нулю (получим одно из изображений нуля в обратном коде).
Таким образом доказано, что на ДСОК машинные изображения чисел также складываются по правилам, приведенным в табл. 4.2.
Пример 4.6. Найти сумму чисел 4=0,0101 и 5=0,0111, используя сумматор, обратного кода.
Решение.
[4]о6 = 0,0101
+
[B] об = 0,0111
[C] об = 0,1100
Ответ: С = 0,1100.
[4]об= 1,1010 [В]об= 1,0111 1,0001 + 1
[С]об= 1,0010
Ответ: С = — 0,1101.
В дальнейшем для упрощения записи передача циклического переноса будет осуществляться сразу при получении результата и отдельно фиксироваться не будет.
§ 4.3. ПЕРЕПОЛНЕНИЕ РАЗРЯДНОЙ СЕТКИ
При сложении чисел одинакового знака, представленных в форме с фиксированной запятой, может возникнуть переполнение разрядной сетки.
I. Признак переполнения разрядной сетки сумматора прямого кода — появление единицы переноса из старшего разряда цифровой части числа.
Пример 4.10.
Іа. 4 = 0,1010 и 5=0,1101. 2а. 4 =—0,1100 и 5 =—0,1010.
[4]пР= 0,1010 [4]„р= 1,1100
+ +
[B] Пр = 0,1101 [В]„р = 1,1010
[C] „р^0,0111 [С]„р =44,0110
І5=гёдинйдаіпереноса Г^^ДІдиница переноса
[4] 0б = 1,1010
+
[5] об = 0,0111
0,0001 + 1
[С]о6 = 0,0010
Ответ: С = 0;0010.
Пример 4.8. Найти сумму чисел А =0,0101 и 5 = —0,0111, используя ДСОК. Решение.
[4] об = 0,0101
+
[5] 0б= 1,1000 [С]об=1,1101
Ответ: С — —0,0010.
За. 4 = 0,1011 и 5=0,1010. 4а. 4 = — 0,10! 1 и В = —0,1001.
[4 ]д = 0,1011 [4], = 1,0101
+ +
[В]д = 0,1010 [В]л= 1.01! I
[С]лф 1,0101 [С]д^0,1100
III. Признак переполнения разрядной сетки сумматора обратного кода — знак результата, противоположный знакам операндов.
5а. 4 = 0,0111 и 5 = 0,1101. 6а. 4 =—0,0110'и 5 =—0,1101.
[4] о6 = 0,0111 [4 ]об= 1,1001
+ +
[5] об = 0,1101 [В]об= 1,0010
[С]о0^0,Ю11
I
операцию называют нормализацией числа. Операция нормализации Ічисла состоит из проверки выполнимости условия (3.21) и сдвигаtзoбpaжeния мантиссы в ту или иную сторону. Сдвиги могут осуществляться на один разряд и более в левую или правую сторону Й пределах разрядной сетки машины.
Простой сдвиг — операция, выполняемая по следующим правилам:
Для обнаружения переполнения разрядной сетки в составе цифрового/ автомата должны быть предусмотрены аппаратные средства, автоматически вырабатывающие признак переполнения — сигнал ф.
Чтобы обнаружить переполнение разрядной сетки ДСОК и ДСДК, вводится вспомогательный разряд в знаковую часть изображения числа (рис. 4.4, а), который называют разрядом переполнения. На рис. 4.4, б, в соответственно представлены изображения положительного и отрицательного чисел. Такое представление числа называется модифицированным. Тогда в случае появления переполнения сигнал <р=1.
Знаковая
&) часть
Пале числа
'—1
Сдвинутая вправо на один разряд 0, 0аі...а„_і 0, 1аі...а„_і
Исходная комбинация 0, аіа2...ап \,а\а2...а„
Модифицированный сдвиг — операция над модифицированными изображениями, выполняемая следующим образом:
Сдвинутая вправо на один разряд
00, 0аі...а„_і 00, 1аі...а„_і
1,0а\...а„-1 1, 1а|...а„-і
Исходная
комбинация
00, аіа2...а„
01, а\а2...ап
10, а\а2...ап11, аіа2...а„
Сдвинутая влево на один ряд 0аь а2...а„0 \а\, а2...а„0 Оаі, й2...апа Іаі, а2...а„а
Sg\/\Sg2=l, Sgi Л Sg2—1;
в остальных случаях ф=0.
Это подтверждается следующими примерами.
(4.6)
№ = 00,1101 -[С]об = 01,0100 — 66. [Л]“б= 11,1001 — +
№=11.0010 -№=іо,ііоо -
36. (А)” = 00,1011 — модифицированное изображение операнда А;
[B] “ = 00,1010 — модифицированное изображение операнда В;
[C] J = 01,0101 — 01—признак переполнения в знаковых разрядах, <р=1; 46. [Л]" = 11,0101 — модифицированное изображение операнда А;
[B] ” = 11,0111 — модифицированное изображение операнда В;
[C] " = 10,1100 — 10 — признак переполнения в знаковых разрядах, ф=1; 56. [Л]об = 00,0111 — модифицированное изображение операнда Л;
модифицированное изображение операнда В;
01 — признак переполнения в знаковых разрядах, <р=1; модифицированное изображение операнда Л;
модифицированное изображение операнда В;
10 — признак переполнения в знаковых разрядах, tp = 1.
§ 4.4. ОСОБЕННОСТИ СЛОЖЕНИЯ ЧИСЕЛ, ПРЕДСТАВЛЕННЫХ В ФОРМЕ С ПЛАВАЮЩЕЙ ЗАПЯТОЙ
Числа, представленные в форме с плавающей запятой, изображаются двумя частями — мантиссой и порядком. При операции алгебраического сложения действия, выполняемые над мантиссами и порядками, различны. Следовательно, в цифровом автомате должны быть два раздельных устройства для обработки мантисс и для обработки порядков.
Так как для чисел с плавающей запятой справедливо условие (3.21), то всякий результат, не удовлетворяющий этому условию, должен быть приведен в соответствие с формулой (3.21). Такую
* Здесь и в дальнейшем тексте символ Д означает логическую функцию И , а черта над символом Sg •—функцию НЕ (см. §10.1).
Y=l. если SgiASg2=l; Sgi/\Sg2=l (4.7)
(в остальных случаях -у = 0), где у — признак нарушения нормализации числа справа, указывающий на необходимость сдвига числа вправо на один разряд.
Признак нарушения нормализации числа слева б (когда результат по собственной величине оказывается меньше '/q) — наличие одинаковых комбинаций в разряде переполнения и старшем разряде цифровой части сумматора (рі):
6=1, если Sg2 /\р\ = \\ Sg2 Д pi = 1 (4.8)
(в остальных случаях 6 = 0), где б — признак нарушения нормализации, указывающий на необходимость сдвига числа влево на один разряд.
Таким образом, операция нормализации числа состоит из совокупности сдвигов и проверки наличия признаков нарушения у и б.
Рассмотрим сложение чисел А = гпаРа и В — тврв, имеющих одинаковый порядок рА — рв• Обе мантиссы удовлетворяют условию нормализации.
Сложение мантисс осуществляется на соответствующем сумматоре по правилам, изложенным ранее для чисел, представленных в форме с фиксированной запятой. Если после сложения мантисса/ результата удовлетворяет условию нормализации (т. е. 6=0, у = 0)/ то к этому результату приписывается порядок любого из операндов^. В противном случае происходит нормализация числа.
Пример 4.11. Найти сумму чисел Л = 0,1000-г-' и В = — 0,1011 ¦2~'\ если мантиссы и порядок обрабатываются на сумматорах дополнительного кода (шесть разрядов для мантиссы и четыре разряда для порядка).
Решение. Сначала записываются машинные изображения операндов:
[тл]д = 00,1000; [рл]д= 1,101;
[ma];= 11,0101; [рв]д = 1,101, а затем мантиссы складываются:
00,1000
11,0101
[тс];= 11,1101
Здесь Sg2Api = U т. е. 6=1, у = 0, значит, необходим сдвиг мантиссы влево на разряд:
[m&]" = 11,1010, (6=1, ? = 0).
Одновременно со сдвигом влево нужна коррекция порядка, т. е. уменьшение его величины на-единицу (что равносильно прибавлению кода 1,111);
ІИ.,- 1.101
+ і,ііі
[р&= моо
Так как после сдвига снова 6=1, то осуществляется еще раз сдвиг и коррекция порядка:
-[mg]” = П ,0100, (6 = 0, у = 0), [ра = 1,100
+ 1,111
[ра= 1.011
Так будет продолжаться до тех пор, пока величина 6 не станет равной нулю. Следовательно, [та удовлетворяет условию нормализации и результат равен
[та=п,оюо; [Ра= сои.
Ответ: С = — 0,1100-2^5.
Пример 4.12. Найти сумму чисел А = — 0,1100-24 и В = — 0.1000-24, если числа складываются на сумматоре обратного кода (шесть разрядов для мантиссы и четыре разряда для порядка).
Решение. Машинные изображения операндов записываются в следующем виде:
[тл]”б= 11,0011; [рл]об = [Рв]о« = 0,100. [mB]"fi = 11,01111.
Затем складываются мантиссы:
,11,0011
' 11,0111
[тсЪ = 10,1011 (6 = 0, 7=1).
[т&Ь= 11,0101 (6 = 0, 7 = 0).
, Одновременно со сдвигом производится коррекция порядка результата на величину +0,001, или [рс]об = 0,100 + 0,001 =0,101, в результате получается окончательный результат.
Ответ: С = — 0,1010-26.
^ Рассмотрим наиболее общий случай сложения чисел, представленных в форме с плавающей запятой, когда их порядки не равны друг другу, т. е. рлфрв¦ Для операции сложения чисел необходимым условием является соответствие разрядов операндов друг другу. Значит, прежде всего нужно уравнять порядки, что, естественно, повлечет за собой временное нарушение нормализации одного из слагаемых. Выравнивание порядков означает, что порядок меньшего числа надо увеличить на величину Ар = \рА — рн\, что означает, сдвиг мантиссы меньшего числа вправо на количество разрядов, равное Ар.
Следовательно, цифровой автомат должен самостоятельно определять, какой из двух операндов меньший. На это укажет знак разности рА — рв: положительный знак будет при рА^рв, а отрицательный — при рлСрв-
Операции сложения и вычитания чисел в форме с плавающей запятой осуществляются зо всех современных машинах по изложенным выше правилам.
Пример 4.13. Сложить числа А =0,1011 -2~2 и В =—0,1001-2“3 на сумматорах обратного кода (шесть двоичных разрядов для мантиссы и четыре двоичных разряда для порядка).
Решение. Прежде всего записываются машинные изображения чисел и определяется, какой из двух порядков больше:
[тд]”б = 00,1011; [^]об= 1,101;
[тв;рб = 11,0110; [рв]об= 1,100,
[Др]о6 —= [Рліоб [Рвіоб-
Величину —[рв]об обозначим [рв]об, что означает изменение знака числа рв на обратный, т. е. [pBJo6 = 0,011. Тогда [Лр],,б= [р,]„о + [рД.6 = 0,001.
Так как величина Др положительна, то рА>Рв• Следовательно, надо сдвинуть мантиссу числа В вправо на количество разрядов, равное Др, т. е. на один разряд: [твЦб = 11,1011 (сдвиг модифицированный, стрелка над символом тв показывает сдвиг в соответствующую сторону). Теперь порядки операндов равны и дальнейшие действия производятся в последовательности, аналогичной последовательности, рассмотренной в примере 4.12.
Складываются изображения мантисс:
[тл]”б = 00,1011
+
[твЦб = 11,1011
[тсй = 00,0111 (6=1, 7 = 0).
Осуществляется нормализация мантиссы (6=1) и соответствующая коррекция порядка:
2-й такт
3-й такт
4-й такт
Так как нарушений нормализации нет, то получен окончательный результат.
Ответ: С = 0,1110-2-3.
Пример 4.14. Сложить числа А и В, заданные в форме с фиксированной точкой: «1/1 = 100110; Хд = 101; Хд = —111001; Хв = 011. Для выполнения опера -J ции сложения использовать сумматор дополнительного кода, имеющий семь битов для мантиссы со знаком, четыре бита для характеристики со знаком. Г
Решение. Запишем машинные изображения мантисс: [тдід = 00.100110; [тв]“ = 11.000111. Г
Исходные числа в памяти машины можно хранить либо в прямом, либо в обратной (дополнительном) кодах. Если числа хранятся в памяти машины в прямом коде, то при выполнении операции сложения (вычитания) на сумматорах обратного (дополнительного) кода необходимо произвести преобразование из прямого кода в обратный (дополнительный) код. По окончании операции должно производиться преобразование результата из обратного (дополнительного) кода в прямой.
При выполнении данного примера предполагается, что числа в памяти машины хранятся в дополнительном коде.
Прежде всего необходимо сравнить характеристики:
АХ = [Хд]д - [Хв]д = 0,101 + 1,101 = 0,010.
Разность характеристик — положительная: второй порядок меньше первого на 2. Следовательно, мантисса второго числа сдвигается на два разряда (сдвиг модифицированный) и после этого мантиссы складываются:
[та]д = 11,110001
+
[тд]д = 00,100110 [тс]д = 00,010110 (8=1, у = 0).
Так как 6=1, то производится сдвиг влево на один разряд с коррекцией характеристики:
Іт'с]л = 00,101110 (6 = 0, у = 0) [Хс\л = 0,101 + 1,111 =0,100.
Таким образом, окончательный результат получен в нормализованном виде.
Ответ: С = + 101110, Х0 = 100.
Пример 4.14 приведен для случая, когда мантисса — целое число и представляется в форме с фиксированной точкой перед старшим разрядом. Сформулированные выше правила выполнения алгоритма алгебраического сложения действуют в данном случае без существенных изменений.
При реализации операций сложения (вычитания) чисел, представленных в форме с плавающей запятой, может возникнуть переполнение разрядной сетки сумматора порядкор (характеристик) : мантисса получается нормализованной и правильной, а порядок (характеристика) не соответствует. Следовательно, необходимо вырабатывать сигнал переполнения сумматора порядков.
Нормализация результата операции сложения (вычитания) приводит и к исчезновению порядка (т.е. характеристика становится отрицательной), несмотря на то что мантисса отлична от нуля. В ЕС ЭВМ вводится специальный разряд, в котором записывается нуль или единица: при нулевом значении этого разряда в результате операции записывается истинный нуль, т. е. число с нулевой мантиссой, положительным знаком и нулевой характеристикой; при единичном значении этого разряда к характеристике прибавляется I Хтах •
t Уменьшить время на выполнение операции сложения можно разными путями. Идея, лежащая в основе многих методов ускорения Операции сложения, заключается в том, что осуществляется поэтапное получение условных сумм и переносов с последующей их раздельной обработкой. Наибольший эффект методы раздельной обработки условных сумм и переносов дают при параллельной или последовательно-параллельной обработке разрядов. Покажем эту идею на примере сложения чисел А и В:
А= 0011110100111010
+
В= 1001001101001101
с' = 1010111001110111 условная сумма
+
п' = 0010001000010000 переносы с" = 1000110001100111
+
п"= 0100010000100000 с"'= 1100100001000111
+
п'" = 0000100001000000 сІ? = 1100000000000111
+
п,? = 0001000010000000
с 1101000010000111 результат
0000000000000000 перенос
Весь процесс сложения прошел за пять тактов. Признак получения результата — нулевые значения поразрядных переносов. Метод раздельного сложения условных сумм и переносов в свое время послужил толчком для создания специальных сумматоров со сквозным переносом, в которых достигается существенное сокращение времени за счет удаления этапов передачи переносов через разряды, в которых условная сумма равна единице. Этот метод был впервые широко использован в ЭВМ БЭСМ-6.
Метод может быть усовершенствован, если использовать следующий прием. Для каждого разряда складываемых операндов
с? = аі®6і = 1, П2=аі-6і = 0, сі^с?® 1=0, по=а, у b\ = \ и т. д.
151413121110 98765432 10 Номер разряда
п° при условии а с' сумма и перенос п' при условии р
1-й такт
Рассмотрим пару соседних разрядов 0 и 1. Во втором такте входы в верхнюю половину первого разряда находим следующим
вычисляются две пары сумм и переносов: одна — в предположении, что перенос, вносимый в данный разряд, равен нулю (условие а), другая пара — в предположении, что перенос, вносимый в данный разряд, равен единице (условие Р). Исключение представляет нулевой разряд, в котором перенос равен только нулю
Таким образом, правила получения этих пар выглядят следующим/ образом:
для нулевого разряда
?о = ао?йо=1, условная сумма п“ = ао-Ьо=0, перенос;
Для первого такта условные суммы и переносы вычисляются для всех разрядов.
Во втором такте условные суммы и переносы определяются для пар соседних разрядов (0 и 1, 2 и 3 и т. д.) при условиях аир.
0011110100111010
1001001101001101
1010111001110111
0001000100001000 01010001 1000100 101111110111111
1001110101110111 0 10 10 0 10
2-й такт 01 100010100010 10 10 0 11
10010 001 100001 1 1 0 0 0 1
3- й такт 110100001000
1 1 1
1 1010 0 00100001 1 1 0 1
4- й такт 110 10 0 0 0
0
5- й такт 1 1010000100001 1 1 результат
0 1 1 11 или для другой четверки (4—7-й разряды):
0 111 0 0 10 0 0 0 1
В результате появляется возможность весь процесс суммирования реализовать на схемах типа И, ИЛИ, НЕ.
§ 4.6. ОЦЕНКА ТОЧНОСТИ ВЫПОЛНЕНИЯ АРИФМЕТИЧЕСКИХ ОПЕРАЦИЙ
Выбор системы счисления и длины разрядной сетки машины, а также формы представления числа в машине тесно связаны с обеспечением заданной точности вычислений. Важное значение имеет также оценка точности арифметических вычислений при использовании в машинах чисел, представленных в форме с фиксированной и плавающей запятой. При операциях сложения и вычитания с фиксированной запятой (при условии отсутствия переполнения в естественной форме) можно считать, что они выполняются точно.
Для чисел, представленных в форме с плавающей запятой, при операциях сложения и вычитания необходимо выравнивать порядки, что ведет к потере некоторых разрядов мантиссы при сдвиге. Поэтому при нормализованной форме представления чисел сама операция алгебраического сложения также является источником погрешностей.
(4.12)
(4.13)
бл + Я
(4.10)
Таким образом, причинами погрешностей вычисления на ЭВМ могут быть:
неточное задание исходных данных, участвующих в выполняемой операции (либо из-за ограниченности разрядной сетки машины, либо из-за погрешностей перевода информации из одной системы счисления в другую);
использование приближенных методов вычислений, что само по себе дает методическую погрешность (например, использование рядов Ньютона и Тейлора при интегрировании);
округление результатов элементарных операций, что, в свою очередь, может привести к появлению накопленных погрешностей;
сбои в работе ЭВМ (эта причина может быть устранена введением системы контроля выполнения любых операций).
Погрешности выполнения арифметических операций. Для определения этих погрешностей в цифровых автоматах будем рассматривать арифметические операции как элементарные операции над операндами.
Произведем арифметические действия над числами Л = [Л] + ДЛ и В = [В]-\- АВ, заданными с абсолютными погрешностями:
А + В = [Л ] + [В] + (ДА + ДВ), где абсолютная погрешность суммы Д(АЛ-В)= ДА + ДВ;
Л — В = [Л] — [В] + (АЛ —ДВ),
где абсолютная погрешность разности Д(Л—В)=ДА—ДВ.
Л В = [Л ] [В] + Л Д В + [В] Д Л + ДЛ Д В.
Так как произведение ДЛДВ на два порядка меньше чисел Л и В, то этим произведением можно пренебречь. Следовательно, ЛВ«[Л][В]+[Л]ДВ + [В]ДЛ, т.е. абсолютная погрешность произведения Д(ЛВ)=[Л]ДВ-)-[В]ДЛ.
При выполнении операции деления получаем
А ^ [Л] + АЛ __ [Л] + ДЛ /1 \
В [В] + ЛВ [В] ?і+ЛВДВ]/
Второй сомножитель в правой части уравнения разложим в ряд. После преобразований получим
A/В = [Л]/[В] - [Л]ДВ/[В]2 + [А](ДВ)2/[В]3 +
+ДЛ/[В]-ДЛДВ/[В]2-... (4.9)
Пренебрегая членами второго порядка малости, (4.9) можно упростить: Л/В«[Л]/[В] + ДЛ/[В] — [А]ДВ/([В])2. Отсюда абсолютная погрешность частного А(Л/В)'=ДА/[В] —[А]ДВ/([В])2.
Аналогичным образом можно вывести выражения для относительных погрешностей: при сложении — вычитании, при умножении и при делении соответственно:
[А] А А [В] ДВ .
[ЛИ-(В] [А] ± [Л] + [В] [В]’
Погрешности округления. Если предположить, что исходная информация не содержит никаких ошибок и все вычислительные процессы конечны и не приводят к ошибкам, то все равно присутствует третий тип ошибок — ошибки округления. Предположим, что вычисления производят на некоторой гипотетической машине, в которой каждое число представляется пятью значащими цифрами, и что необходимо сложить числа 9,2654 и 7,1625, причем эти числа точные. Сумма чисел равна 16,4279, она содержит шесть значащих цифр и не помещается в разрядной сетке машины. Поэтому шестизначный результат будет округлен до значения 16,428. В результате возникает погрешность округления.
Так как вычислительные машины всегда работают с конечным количеством значащих цифр, то потребность в округлении возникает довольно часто. Погрешность округления имеет смысл только для действительных чисел; это объясняется тем, что ЭВМ автоматически выравнивает порядки действительных чисел при сложении и вычитании.
Для чисел, представленных в форме с плавающей запятой, справедливы выражения Aq = mAqk, У<,< |/тілІ <1 ¦
Если для представления мантиссы используется только п разрядов, то изображение числа разбивается на две части:
Л,=[тл]<7п + [Ао?-'\ где [Ло]<7*-я = Ао — «хвост» числа, не попавший в разрядную сетку.
В зависимости от того, как учитывается величина А0 в машинном изображении, существует несколько способов округления.
1. Отбрасывание Ло. При этом возникает относительная погрешность, равная
8окР = Ио1<7*-7(|тлк*).
Так как q ‘^ІтДсІ; 0<|А0|<1, то
б <іі!І——
q-\цк —Ч
т. е. математическое ожидание погрешности округления не зависит от величины самого числа, а зависит только от количества разрядов в машине для любой системы счисления.
Дисперсия погрешности округления примерно равна q~2n/12.
2. Симметричное округление. При этом производится анализ величины Ло- Принимается, что
ГЛіІН?" , если |Ло|«г‘;
11'ПА]УП+Ук~п, если-|Ло|>^"''.
(4.15)
При условии |ЛоІ^<7“‘ производится прибавление единицы к младшему разряду мантиссы. Абсолютная погрешность округления при этом
Аокр
Максимально возможное значение модуля абсолютной погрешности равно 0,5qk~n. Математическое ожидание относительной погрешности округления
аь.Р<0,5<7*-7('Лл9*)=0,5<г<"-|>, (4.16)
т. е. ошибка не превышает половины единицы младшего разряда.
Способ симметричного округления наиболее часто используют на практике.
3. Округление по дополнению. В этом случае для округления берется информация, содержащаяся в (ц+1)-м разряде.
При q—2, если в (п+1)-м разряде содержится единица, в п-й разряд добавляется единица; если в (п+1)-м разряде находится нуль, содержимое разрядов правее «-го отбрасывается.
4. Случайное округление. Для такого округления необходимо иметь датчик случайных величин (1 или 0), который выдает единицу в самый младший разряд машинного изображения числа. Погрешность округления — случайная величина с нулевым математическим ожиданием.
Оценка накопленной погрешности при вычислениях на машине особенно затруднительна при использовании чисел в форме с плавающей запятой. При таком представлении возможно перемещение ошибки из младших разрядов мантиссы в старшие разряды. Это происходит, например, при вычитании друг из друга близких по значению мантисс. В результирующей мантиссе первые нулевые разряды оказываются сдвинутыми в правую часть разрядной сетки машины. При нормализации они перемещаются в левую часть разрядной сетки, давая большую погрешность результата.
Для автоматической оценки накопленной ошибки при вычислении чисел в форме с плавающей запятой в разрядной сетке машины кроме числовой информации записываются также информации об ошибке, содержащейся в числовой информации. При этом предполагается, что ошибки всех чисел — независимые величины и их распределение подчинено нормальному закону. Эти допущения весьма существенны, так как на практике ошибки при вычислениях, конечно, являются зависимыми величинами и их распределение может быть далеким от нормального. Кроме того, принимается, что все числа, записанные в разрядной сетке машины, имеют погрешность +0,5 последней значащей цифры. Значение этой вероятной ошибки записывается в исходных данных в разрядах, находящихся правее самого младшего разряда мантиссы. После арифметических операций нормализация осуществляется не всегда, а лишь в случаях, когда срабатывает критерий сдвига, оценивающий величину погрешности, вносимой в число в процессе нормализации.
другом. А
Задание для самоконтроля.
1. Написать изображения чисел А —— 0,101010 и В — 0,100010 в прямом, обратном и дополнительном кодах.
2. Возможно ли переполнение разрядной сетки, если числа с плавающей запятой складываются, умножаются, делятся?
3. Сложить на сумматоре прямого кода числа А — —0,11101 и В = 0,10100.
4. Сложить на сумматоре обратного кода числа А = 0,10110, и В — — 0,10110.
5. Сложить на сумматоре дополнительного кода числа 4=0,11001 и В =
= 0,10111.
6. Указать признак переполнения разрядной сетки на сумматоре обратного кода при сложении отрицательных чисел и положительных чисел.
7. Применимы ли понятия обратного, дополнительного и прямого кодов для представления чисел в минус-двоичной системе счисления?
УМНОЖЕНИЕ ЧИСЕЛ НА ДВОИЧНЫХ СУММАТОРАХ
§ 5.1. МЕТОДЫ УМНОЖЕНИЯ ДВОИЧНЫХ ЧИСЕЛ
Применительно к двоичной системе счисления наиболее известны следующие основные способы выполнения операции умножения:
1) умножение начиная с младших разрядов множителя:
?1101 — множимое,
*1101 — множитель,
поГ
0000
1101 — частные произведения,
1101
10101001 — произведение;
2) умножение начиная со старших разрядов множителя:
1101 — Множимое, '
*1101 — множитель,
1101
,1101 — частные произведения,
+ 0000 1101
10101001 — произведение.
В обоих случаях операция умножения состоит из ряда последовательных операций сложения частных произведений. Операциями сложения управляют разряды множителя: если в каком-то разряде множителя находится единица, то к сумме частных произведений добавляется множимое с соответствующим сдвигом; если в разряде множителя — нуль, то множимое не прибавляется.
Таким образом, кроме операции сложения чисел для получения произведения необходима операция сдвига чисел. При этом появляется возможность сдвигать множимое или сумму частных произведений, что дает основание для разных методов реализации операции умножения.
Метод 1. Пусть А — множимое (А>0), В — множитель (В>0), С — произведение. Тогда в случае представления чисел в форме
Отсюда
С=АВ=0, а,а2...а„(Ь1-2-' + г>2-2-2+- + 6п-2-п)=
=(2-1 - О, а\а2...ап)-Ь{+(2~2-0, сца2...ап)Ь2+---+(2-п-0, аіа2...ап)Ь„.
(5.1)
Умножение на 2~п означает сдвиг на п разрядов вправо числа, которое заключено в скобки, т. е. в данном случае сдвигается вправо множимое и умножение начинается со старших разрядов.
Структурная схема рассмотренного множительного устройства представлена на рис. 5.1, а.
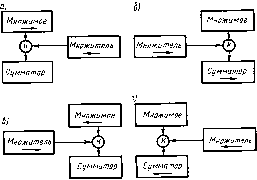
Множитель можно легко преобразовать, используя метод Горнера: ?=(...((Ь„-2~і+Ья_,)2“14-...-і-Ь2)2"і+Ьі)2~1. Тогда
С=ЛВ = (...((6„-0, аіа2...ап)2_14-6„_і -0, аіа2...а„)2-1 +
+ — + bi-0, аіа2...а„)2~'. (5.2)
Здесь умножение начинается с младших разрядов и сдвигается вправо сумма частных произведений. Структурная схема множительного устройства, реализующего этот метод, представлена на рис. 5.1, б.
Метод 3. Пусть А — 0, а\,а2...ап — множимое и В = 0,Ь\Ь2... ...Ьп — множитель.
Множитель, используя метод Горнера, можно записать так:
В = 2-п(Ь1-2п-х + Ь2-2п-2+.:+Ьп-1-2' + Ьп-2°)=
= 2-п(...(Ь1-21+Ь2)2'+...+ Ьп-ё1 + Ьп).
При умножении будут использованы метод 2 и устройство, показанное на
рис. 5.2.
Запись всех действий, выполняемых устройством, осуществляется с помощью условных обозначений, т. е.: = — оператор присваивания означает, что блоку,
В этом случае
С—АВ=2~п(Ьп-0, аіа2...ап+(2' -0, аіа2...а„)6„_і +
4-... + (2п“1 -0, аіа2...а„)-&і), (5.3)
что означает: умножение начинается с младших разрядов, и множимое сдвигается влево на один разряд в каждом такте. Схема множительного устройства представлена на рис. 5.1, в.
Метод 4. Пусть/1 = 0, аіа2...а„— множимое и J3 = 0, b\b2.--bn— множитель.
Если множитель В записать по методу Горнера:
С=ЛВ = 2-П((...(2‘(&, -0, аіа2...а„)+ b2-0, а\а2...ап)21 +
+ .1 -0, а\а2...ап)2{-\-Ьп-0, аіа2...ап), (5.4)
то умножение начинается со старшего разряда и в каждом такте’ сдвигается влево сумма частных произведений. Схема множительного устройства представлена на рис. 5.1,г.
Таким образом, для реализации операции умножения необходимо иметь сумматор, регистры для хранения множимого и множителя и схему анализа разрядов множителя. Сумматор и регистры должны иметь цепи сдвига содержимого в ту или иную сторону в соответствии с принятым методом умножения.
, Анализ формул (5.1) — (5.4) показывает, что с формальной точки зрения процесс умножения двух чисел может быть представлен:
при последовательном выполнении — в виде многократно повторяющегося по количеству разрядов цикла
S,=S,_i+i4A,, (5.5)
где S;_ 1, Si — суммы частных произведений на (г— 1)-м и і-м шагах соответственно;
при параллельном выполнении — суммой членов диагональной матрицы, для которой заданы по строкам А-2‘, а по столбцам — Ь-„ где і — текущий номер разряда.
В дальнейшем основное внимание будет уделено последовательному принципу выполнения операции умножения.
При точном умножении двух чисел количество цифр в произведении превышает количество цифр сомножителей не более чем в два раза. При умножении нескольких чисел количество цифр произведения может оказаться еще больше. Конечное число разрядов в устройствах цифрового автомата вынуждает ограничиваться максимально удвоенным количеством разрядов сумматоров.
При ограничении количества разрядов сумматора в произведение вносится погрешность. В случае большого объема вычислений погрешности одного знака накладываются друг на друга, в результате чего общая погрешность сильно возрастает. Поэтому существенное значение имеет округление результатов умножения, что дает возможность сделать погрешность произведения знакопеременной, а математическое ожидание погрешности округления при условий, что отброшенные младшие разряды могут с одинаковой вероятностью иметь любое из возможных значений — равным нулю. При этом предельное по абсолютной величине значение погрешности будет наименьшим из возможных при заданном количестве значащих цифр, т. е. равным половине значения младшего разряда.
§ 5.2. УМНОЖЕНИЕ ЧИСЕЛ, ПРЕДСТАВЛЕННЫХ В ФОРМЕ С ФИКСИРОВАННОЙ ЗАПЯТОЙ, НА ДВОИЧНОМ СУММАТОРЕ ПРЯМОГО КОДА
Пусть заданы машинные изображения двух чисел:
[A]np = SgA,a.\a2...an, [B]np = SgB, bib2...b„.
Тогда их произведение
Спр Sgc, С\С2'--Сп,
где Sgc=Sg/i ? Sg/j; ф — знак сложения по модулю 2.
При выполнении этой операции должны быть заданы структурная схема устройства, на котором производится операция, и метод умножения.
который указан слева от оператора,
присваивается значение,_^указанное
справа от оператора; [РгА] — сдвиг содержимого регистра Рг вправо на один разряд; [СМ] — содержимое сумматора СМ; И.П. — исходное положение.
Решение. Знак произведения определяем отдельно от цифровой части в соответствии с уравнением Sgc = SgA ф SgB= 1 Ф 0= 1.
Получение цифровой части можно показать в виде следующей записи. Пусть сумматор имеет 10 разрядов без учета знака, а регистры — 5 разрядов без знака. Введем обозначения соответственно изображения цифровой части множимого и цифровой части множителя.
Последовательность действий в процессе выполнения операции умножения представлена в виде табл, 5.1.
Ответ: [С]„р = 1,1010001010.
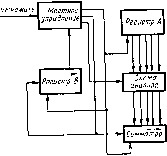
+
*4 = 0; [РгВ ]; [СМ];
*з = 0; [Р+6]; [СМ];
]а(;Д|:-|СМ|+|М|
1010001010
Конец
единица переноса из старшего разряда, то ее
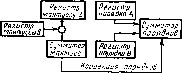
Во всех приведенных ниже примерах будет применяться рассмотренный способ.
§ 5.3. ОСОБЕННОСТИ УМНОЖЕНИЯ ЧИСЕЛ, ПРЕДСТАВЛЕННЫХ В ФОРМЕ С ПЛАВАЮЩЕЙ ЗАПЯТОЙ
Для чисел, представленных в форме с плавающей запятой, обязательным является представление в виде мантиссы и порядка (характеристики). При операции умножения действия, выполняемые над мантиссами и порядками, различны: мантиссы перемножаются, порядки складываются. Очевидно, что результат умножения может получиться ненормализованным, тогда потребуется нормализация с соответствующей коррекцией порядка результата. Следовательно, структурная схема множительного устройства должна измениться (рис. 5.3).
Пример 5.2. Перемножить числа А = — 0,11001-2“3 и В = 0,10011 -2+'.
В качестве множительного устройства используется схема, показанная на рис. 5.3, где РгА и РгВ — соответственно регистры для порядков рд и рв-
Решение. Мантиссы перемножаются по правилам, рассмотренным для чисел, представленных в форме с фиксированной запятой. Для перемножения мантисс используется сумматор прямого кода, а для сложения порядков — сумматор обратного кода.
Сначала записываются машинные изображения чисел:
[гпд]пр — 1,11001; [ра ] об ~ 1,100; ^
[тв]Пр= 0,10011; [рв]об = 0,001. '
Последовательность действий в процессе выполнения операции умножения мантисс представим в табл. 5.2.
После выполнения указанных действий находится мантисса произведения [тс]пр = 1,0111011011.
Одновременно с этим над порядками производится операция сложения: Ірс ] об = ІРа ] об + ІРв ] об = 1,100 + 0,001 = 1,101.
Так как мантисса результата не удовлетворяет условию нормализации (нарушена левая граница: 6=1, у = 0), то производится сдвиг мантиссы влево на один разряд: [от?-]Пр = 1,1110110110, и коррекция порядка [р'с] об = [рс] об+ + 1,110= 1,101 + 1,110= 1,110.
результата
в
Ответ: С = — 0,11110- 2"3.
в
11 .оооор
1; СМ:= [СМ] 4- [РгЛ];
[Р?3]; [САА];
Конец
если один из сомножителей равен нулю, то произведение также равно нулю. Следовательно, необходимо предусмотреть блокировку выполнения алгоритма умножения и формировать результат, равный нулю;
если порядок результата равен наибольшей отрицательной величине, то необходимо формировать машинный нуль.
Эти особые случаи можно предусмотреть в алгоритме операции введением анализатора сомножителей на нуль в начале операции (первый случай) или коррекцией произведения на основании признаков результата (второй и третий случаи).
§ 5.4. УМНОЖЕНИЕ ЧИСЕЛ, ПРЕДСТАВЛЕННЫХ В ФОРМЕ С ФИКСИРОВАННОЙ ЗАПЯТОЙ, НА ДВОИЧНОМ СУММАТОРЕ ДОПОЛНИТЕЛЬНОГО КОДА
В случаях, когда числа в машине хранятся в дополнительных кодах, целесообразно все операции над числами производить на сумматоре дополнительного кода. Однако при этом возникает ряд особенностей, которые необходимо учитывать.
Произведение дополнительных кодов сомножителей равно дополнительному коду результата только в случае положительного множителя.
Пусть множимое А—любое число, т. е. Л = [Л]Д, а множитель В>0. Тогда
ЛВ = [Л]д.0,б162...Ьп=[Л]д61.2^1 + [Л]дб2-2-2+-+[Л]дЬ„.2-я.
(5.6)
На основании теоремы о сложении дополнительных кодов можно утверждать, что в правой части уравнения: (5.6) стоит дополнительный код результата.
Таким образом, умножение на сумматоре дополнительного кода заключается в анализе разрядов множителя и при b<= 1 в прибавлении дополнительного кода множимого к содержимому сумматора. При этом должны осуществляться модифицированные сдвиги.
Пример 5.3. Умножить на сумматоре дополнительного кода (используется метод 2) числа А = — 0,10101 и В = 0,10011.
Решение. Сначала записываются машинные изображения чисел: [Л]д = = 11,01011; [В]" =00,10011.
Последовательность действий, производимых над числами, представлена в тзбл 5 3
Ответ: С = ЛВ = — 0,0110001111.
Теперь рассмотрим случай, когда_множимое А—любое число, а множитель В<0. Тогда [В]д = 1, Ь\Ьг...Ьп.
На основании (3.24) можно записать, что В=[В]Д—2, или В —0, bib2...bn. Следовательно, произведение чисел
ЛВ=Л(0, blbs...bn-i)=A-0,bibi...bn — A. (5.7)
Если множитель отрицательный, то произведение чисел на сумматоре дополнительного кода получается прибавлением поправки [Л] к произведению дополнительных кодов сомножителей.
Пример 5.4. Умножить на сумматоре дополнительного кода по методу 2 с использованием структурной схемы примера 5.1 числа А = — 0,10111 и В = — 0,11001.
Решение. Сначала запишем машинные изображения чисел: ІА]Д = 11,01001;
[?]д = 11,00111; [Л]дм = 00,10111.
Последовательность действий, производимых над числами, показана в табл. 5.4.
Ответ: С = АВ = 0,1000111111. Таблица 5.4
в
&5 = 1; СМ:= [СМ] + [Л]Г
04= 1; СМ:= [СМ] +[Л]”;
10.1011 г
11.01011
->11100
&з= 1; CM:,-- 1СМ] + ГА1”;
[СЛГ]; [РгВ];
Й2~ 0; [СМ]; [РгВ];
$ 5.5. УМНОЖЕНИЕ ЧИСЕЛ НА ДВОИЧНОМ СУММАТОРЕ ОБРАТНОГО КОДА
Рассмотрим правила умножения операндов, заданных в обратном коде.
Произведение обратных кодов сомножителей равно обратному коду результата только в случае положительного множителя.
Пусть множимое А — [А\о6, а множитель ?>0. Тогда
АВ = [Л]об • 0, bib2-..bn = [?4]об&і • 2 1 -(- [A]0gb2 • 2 2-\-...-\-\_A]ogbn-2~n.
По теореме о сложении обратных кодов в правой части данного уравнения получается обратный код результата.
Следовательно, умножение на сумматоре обратного кода также заключается в анализе разрядов множителя, и если оказывается, что очередной разряд множителя равен единице, то к содержимому сумматора добавляется обратный код множимого.
Пример 5.5. Умножить на сумматоре обратного кода (структурная схема взята из примера 5.1) числа А = —0,10011 и 5 = 0,11001.
Решение. Сначала записываются машинные изображения чисел:
№=П,01100; № = 00,11001.
Если множитель отрицательный, то произведение чисел на сумматоре обратного кода получается прибавлением поправок [Л] и [А]об-2~п к произведению обратных кодов сомножителей.
Пример 5.6. Умножить на сумматоре обратного кода (используется метод 2 и структурная схема из примера 5.1) числа А =—0,110101 и 5 = —0,101000. Решение. Сначала записываются машинные изображения чисел:
[Д]“б= 11,001010;
[В]"б = 11,010111;
№« = 00,110101.
Последовательность действий, производимых над числами, показана в табл. 5.6. Ответ: АВ = 00,100010.
Таблица 5.6
Примечания
Сумматор
Регистр В
И. П. СМ: = 0; РгА: = [А]"«; РгВ: = [В]”«; Добавление [А]“« в СМ, т. е. СМ:= [СМ] +[А]“6;
66=1; СМ:= [СМ] +№«;
[СМ]; [РНЗ[;
Ь5=1; СМ:=[СМ]+№«;
[СМ]; [РгВ];
*4=1; СМ:= [СМ] +№«;
[СМ]; [РИЗ];
63 = 0; [СМ[; [РгВ];
*2=1; СМ:= [СМ]¦+№«;
[CM]; [pTS] ; __
*, = 0; [СМ]; [РгВ];
СМ:= [СМ] +[А]“«;
Конец
010111
->-101011
-^110101
->-111010
->011101
->001110
->000111
Ml,001010 ,11,001010 11,001010 10,010101 ,11,001010 + 11,001010 10,0.10101'
, 11,001010 + 11,001010 10,010101
11,001010 ,11,100101 ^ 11,001010 10,110000
11,011000 , 11,101100 "+" 00,110101 00,100010
Ответ: №«=11,1000100100; С = АВ =—0,0111011011.
Таблица 5.5
в
§ 5.6. МЕТОД СОКРАЩЕННОГО УМНОЖЕНИЯ
В специализированных машинах иногда используют метод сокращенного умножения начиная со старших разрядов. Особенность этого метода состоит в том, что в произведении получается только п старших разрядов. Существуют разные пути выполнения сокращенного умножения. Рассмотрим наиболее распространенные.
Пусть А = [Л]об и В<0. Тогда [B~\o6 = l, b\b2...bn. В соответствии с (3.28) [В]об = 2+В—2~п. Следовательно, В = 0, b\b2...bn-\-2~n— 1.
А В = [Л]06 • 0, Ь\Ь2...Ьп + [А ]о6 • 2~п + А. (5.8)
о о 0 1
+ 01
О I
_0_0_
0,0 6/ 1 1 о -
^гпах
(5.9)
В некоторых машинах реализован метод, который можно объяснить с помощью следующей схемы.
Полная схема
А = 0 0,1 0 0 1 1 х
в - 0 0, 1 1 0 0 1
, , о, / о 0 1 1 + 0 0 1 0 01 1
Ь3=0 011Ю01
Ъ^О 0000000
ь5=1 0_1І 0 0 1 о
+ 0000000
0_і О 0 1 о о + 0 0 10 0 11 ОЦІ 1 0 1 1
Таким образом, Ав = 0,01110-25.
Из этой схемы видно, что произведение получается, если складывать только старшие два разряда от сумм, полученных на каждом шаге умножения (показано справа). В этом случае достаточно иметь только «-разрядный сумматор. Однако следует учитывать, что для получения « точных знаков в произведении необходимо ввести дополнительные разряды.
В самом деле, пусть А = 0, аіа2...ап и B = 0,b\b2...bn. Тогда, если все Ьі — 1, то
п—(п— I)
2»-і
При достаточно больших значениях « (5.9) может быть записано так:
Лтах««-2. (5.10)
Единицы переноса распространятся на х разрядов сумматора, и произведение будет содержать только «—х точных разрядов.
* = lg(n-2)/lg2. (5.11)
Ниже приведены результаты расчета по (5.11):
„ 24 32 40 48 64 72
г. . . 4,5 4,9 5,3 5,5 6,0 6,2
§ 5.7. УСКОРЕНИЕ ОПЕРАЦИИ УМНОЖЕНИЯ
В программах решения различных задач операции умножения встречаются достаточно часто. Поэтому методам выполнения умножения, его ускорению и рациональному построению множительных устройств всегда уделяется большое внимание.
По времени выполнения операцию умножения относят к длинным- операциям. Так, затраты времени на умножение двух чисел в прямом коде можно оценить следующей формулой (для случая последовательного анализа разрядов множителя):
^умн == 2 (^СДВ А~Рі^СЛ ) » (5.12)
1=1
где tc дв — время выполнения сдвига числа на один разряд; С л — время суммирования на сумматоре; р, — вероятность появления единицы в разрядах множителя; « — количество разрядов множителя.
Аналогичные формулы можно написать и для других методов умножения.
Анализируя (5.12), можно наметить следующие пути сокращения времени умножения: уменьшение затрат времени на сдвиг и суммирование операндов; уменьшение количества слагаемых в формуле, т. е. уменьшение разрядов множителя «. Этого можно добиться логическими или аппаратными (схемными) средствами. В дальнейшем тексте будет обращено внимание на логические средства.
Рассмотрим возможности изменения величин р, и Ап.
Наиболее простой способ изменения величин р, и Аі — пропуск тактов суммирования в случаях, когда очередная цифра множителя равна нулю. Этот способ может быть применен для систем счисления, содержащих нуль как одну из цифр, например, для систем (0, 1), (0, 1, 1) и т. п. Исключением в этом отношении являются симметричные системы (1, 1) и им подобные. Однако от системы (1, Г) можно осуществить переход к системе (0, 1) или (0, 1, Г), используя соотношения
1 Г Г Г ... Г = 0 00 ... 1. (5.13)
Такая возможность часто имеется независимо от длины последовательностей нулей или единиц. Для ускорения операции умно-
Ьі + 11>і
возможность сразу осуществить сдвиг на k разрядов, не производя операции, а последовательность вида ... 011...1 переходом к избы-
_ k
точной системе (0,1, 1) может быть заменена на последовательность вида ..Д 00...1, что также приводит к уменьшению количест-
к
ва операций сложений.
Таким образом, переход от одной разновидности двоичной системы счисления к другой при преобразовании множителя позволяет получить выигрыш во времени выполнения операции в целом.
При этом возникают определенной длины последовательности нулей или единиц, что приводит к необходимости одновременного анализа нескольких разрядов множителя и сдвигу на произвольное число разрядов.
Рассмотрим простую иллюстрацию этого положения. Пусть множитель В — 0,011110001110111000 необходимо преобразовать таким образом, чтобы получить меньшее количество единиц в его изображении^ Если представить этот множитель в системе счисления (0, 1, 1), то получим наименьшее число единиц в его изображении: В = 0,100010010011001000 (содержит_ только шесть единиц вместо десяти). Произведя замену 11 на 01, получим окончательно В = = 0,100010010001001000.
Чтобы оценить относительную эффективность того или иного логического метода ускорения умножения, можно воспользоваться формулой
2 Осдв ~Г Pjiсл)
= -, (5Л4)
2 Рсд° 4" Рісл)
; = 1
где т — число шагов при выполнении операций умножения ускоренным методом (количество групп для анализа); р} — вероятности появления в анализируемой і-й или /-й группе разрядов; а — коэффициент эффективности.
Если о < 1, то применяемый метод дает эффект; если же о^І — эффекта не будет.
Группировка разрядов множителя и анализ этих групп позволяют предложить несколько методов ускорения операции умножения.
Анализ двух разрядов множителя одновременно. На основании вышеизложенного можно составить следующие правила преобразсн вания разрядов множителя В = 0, b\, Ь2-..Ьп.
Разбиение множителя на группы длиной k разрядов означает переход к новой системе счисления с основанием • 2*. Если при этом удается сократить количество элементарных действий, выполняемых при операции умножения (сложения и сдвиги), то операция умножения ускоряется. Рассмотрим метод на примере одновременного анализа двух разрядов множителя, начиная с младших разрядов.
Комбинации вида 00 и 01 не преобразуются. Комбинация вида 10 означает, что необходим предварительно сдвиг множимого влево, сложение и затем сдвиг содержимого сумматора вправо на два разряда. Комбинация вида 11 заменяется на комбинацию вида 101, что означает запоминание единицы для следующей анализируемой пары цифр множимого и вычитание на данном шаге с последующим сдвигом на два разряда.
В табл. 5.7 представлены правила преобразования множителя для системы (0, 1, Г).
В результате преобразования множителя меняется характер действий, которые' должны выполняться при операции умножения, т. е. имеют место операции сложения и вычитания. Следовательно, такой способ умножения может быть реализован только на сумматорах обратного или дополнительного кода. Основной выигрыш во времени получается за счет того, что на каждом шаге умножения производится либо сложение, либо вычитание множимого и сдвиг на два разряда одновременно. Особенность — дополнительный сдвиг множимого в противоположную сторону в двух случаях из восьми и запоминание единицы для передачи в следующую пару разрядов множителя. Естественно, это потребует усложнения устройства местного управления умножением.
Пример 5.7. Умножить два числа с одновременным анализом двух разрядов множителя, начиная с младших разрядов на сумматоре дополнительного кода: Л = = 0,10011001, В = 0ДЩРП0,
Р е ш е И и е._ При?мтож’ении лисел потребуются следующие значения: [/1]“ = = 00,10011001; [Л)К = 11,0110011= 01,00110010.
сдвиг на 2 разряда; анализ 3-й пары — 01: СМ: = [СМ| + [Л];
сдвиг на 2 разряда; анализ 4-й пары — 01: СМ: = [СМ] + [Я]"
сдвиг на 2 разряда; анализ 5-й пары — 01: СМ: = [СМ] + [Л]”; Конец.
t>ibj+ 1
6j + 2
[й]„=оі,оГоГоідо.
В сумматоре выполняются следующие действия:
00,00000000 анализ 1-й пары— 10:
+01,00110010 . СМ:= [СМ] + [Л]”;
01,00110010 ,00,0100110010 +00,10011001
00,1110010110 ,00,001110010110 + 11,01100111
11,101000000110 ,
+ 11,11101000000110 11,01100111
11,01001111000110
,11,1101001111000110
+00,10011001
00,0110110011000110
Ответ: С = 0,0110110011000110.
Как видно из примера 5.7, количество шагов при умножении на единицу превышает количество пар разрядов в цифровой части множителя, так как предусматривается возможность появления 1 в знаковой части.
При одновременном анализе двух разрядов, начиная со старших, правила преобразования существенно изменяются. Прежде всего на характер действий влияет значение соседнего справа разряда по отношению к анализируемой паре разрядов. Если его содержимое равно нулю, комбинации вида 00 и 01 выполняются, как в предыдущем случае. Комбинация вида 10 заменяется равнозначной ей комбинацией вида ПО, что означает предварительный сдвиг множимого и вычитание его. Комбинация вида 11 заменяется комбинацией вида 101, что означает вычитание множимого на данном шаге. В случае, если значение соседнего справа разряда равно, единице, происходит изменение преобразуемых состояний и выполнение действий в соответствии с табл. 5.8.
Пример 5.8. Умножить два числа на сумматоре обратного кода с одновременным анализом двух разрядов множителя, начиная со старших разрядов: А =0,10010001; В = 0,10011101.
Решение. При умножении потребуются следующие величины:
[Л]ос = 00,10010001, [Л]"б = 01,00100010, [А]"6= 11,01101 ПО, [Я]”6= 10,11011101.
[В]„ = 01,Г0100Г01.
+00,0000000010010001
+00,0000000100100010
- k
ся сдвиг на k разрядов и вычитается множимое из содержимого сумматора. При анализе группы разрядов вида ...0 011 ...1 произво-
к
дится замена ее на новую группу вида ...100...1, что означает вы-
k
читание множимого на первом шаге, сдвиг на k разрядов и анализ группы следующих разрядов, образовавшейся после преобразования. Такой метод ускорения операции умножения требует создания сдви-тающего устройства, обладающего возможностью одновременного сдвига на произвольное количество разрядов.
Умножение в системе счисления с основанием q — 2k. В некоторых машинах ЕС ЭВМ используется переход на новое основание системы счисления вида q = 2k, за счет чего удается существенно сократить время1 выполнения операции умножения.
Пусть Дг = 4; это означает, что числа представляются в шестнадцатеричной системе счисления. При этом с помощью приема, аналогичного приему, использованному в случае одновременного анализа двух разрядов множителя, можно анализировать сразу тетраду (четыре двоичных разряда): рассматриваются текущая цифра (тетрада) множителя и его предыдущая цифра (тетрада). В зависимости от значений цифры множителя в предыдущем разряде (равна или больше восьми, т. е. старший разряд тетрады равен или нет единице) производятся разные действия (табл. 5.9). Для реализации этого приема требуется также предварительно готовить множимое А, увеличивая его в 1, 2, 3 и 6 раз.
руемая
цифра
руемая
тетрада
Пример 5.9. Умножить два числа /4 = 0,0001101 и В =—0,00001110 с одновременным анализом четырех разрядов множителя. Использовать сумматор дополнительного кода.
Решение. Для умножения потребуются числа: Л =0,00001101, 2Л =
= 0,00011010, ЗЛ =0,00100111, 6Л = 0,01001 ПО.
Множитель представляется в дополнительном коде [В]д= 1,11110010.
ЬI Й2
Шаг 1. Анализ первой цифры множителя для q = 24 (предыдущая цифра равна нулю): 62 = 0010 — на основании табл. 5.9 надо вызвать множимое + 2Л = = 0,00011010 и направить его в сумматор. Содержимое сумматора станет 0,00011010.
Шаг 2. Анализ второй цифры множителя (предыдущая цифра меньше восьми): 6і = 1111 —на основании табл. 5.9 надо вызвать множимое —Лі = 1,11110011, сдвинуть его на четыре разряда влево и направить в сумматор, где производится следующее действие:
,0,00011010 + 1,00110000
1,01001010
Ответ: ЛВ = —0,1011 ОНО.
§ 5.8. МАТРИЧНЫЕ МЕТОДЫ УМНОЖЕНИЯ
Существует ряд методов умножения, основанных на суммировании групп частных произведений с последующим объединением сумм вместе с переносами для получения произведения. Например, частные произведения группируются по три и подаются на входы цепочки сумматоров. Выходы цепочки сумматоров подключаются к регистрам, запоминающим отдельно получившиеся сумму и переносы в другие группы. Выходы этих регистров объединяются в группы по три и подключаются уже к другим сумматорам. В конце цепочки складываются только сумма и переносы для слагаемых. Такая раздельная обработка, промежуточных сумм и переносов требует так называемого «дерева сумматоров». Подобный метод умножения использован в вычислительных машинах ІВМ-360.
Существуют также ускоренные методы умножения, основанные на использовании матриц промежуточных результатов. Рассмотрим схему умножения на примере двух пятиразрядных чисел:
А = а5 а4 а3 а2 а{
В = ЬЪ Ъ4 Ьъ b2 b 1 ^аьЬі a4b 1 а3Ь\ а2Ь\ а\Ь\
аб&5 а4Ьь а3Ь$ а2Ьь а\Ьь
С— Сю Сэ - • С2 С\
Эту схему умножения можно представить также в виде матрицы (табл. 5.10).

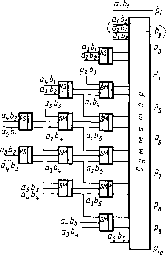
Наиболее известны среди матричных алгоритмов умножения алгоритмы Дадда, Уоллеса, матричный и алгоритм с сохранением переносов. На рис. 5.4 представлена структурная схема множительного устройства для реализации матричного алгоритма, а на рис. 5.5 — схема, с помощью которой может быть реализован алгоритм Дадда. Как видно из рисунков, алгоритмы отличаются друг от друга не только группировкой частных произведений, но и количеством ступеней преобразования: для матричного алгоритма количество ступеней преобразования равно четырем, т. е. на единицу меньше числа разрядов сомножителей, а для алгоритма Дадда — трем. Но с другой стороны, группировка разрядов по методу Дадда требует более сложного устройства управления операцией умножения.
Реализация матричных методов выполнения операции умножения требует большего количества оборудования, чем методов после-
довательного анализа разрядов или групп разрядов множителя и дает больший выигрыш во времени. Однако в связи с широким развитием микроэлектронных и особенно больших интегральных схем (БИС) ограничения по количеству оборудования становятся все менее строгими, поэтому рассмотренные выше методы применяют на практике.
ДЕЛЕНИЕ ЧИСЕЛ НА ДВОИЧНЫХ СУММАТОРАХ
Задание, для самоконтроля
1. Перемножить на сумматоре прямого кода числа Л =—0,1100011 и В — = —0,1011101.
2. Перемножить в обратном и дополнительном кодах числа Л =—0,11 и В — = -0,11.
3. Преобразовать множитель В = 0,110011101011 в избыточную двоичную систему (0, 1, 1).
4. Перемножить по способу одновременного анализа двух разрядов множителя числа Л = 0,1100011101 и В = — 0,1100100011: а) начиная с младших разрядов; б) начиная со старших разрядов.
5. Перемножить комбинированным методом с одновременным анализом произвольного количества разрядов множителя числа Л = —0,100000001 и В=0,011001110.
6. Перемножить числа Л =0,11001101 и В = 0,10001100, использовав промежуточную систему счисления с <? = 24 с одновременным анализом четырех разрядов множителя.
7. Перемножить числа Л = 0,1101101 и В = 0,1000111, используя формулу ЛВ = = 2ЛВ/2, если В — четное; ЛВ = 2Л(В— 1)/2 + Л, если В — нечетное.
8. Умножить числа Л =0,100101-25 и В = 0,110001 •2_:!, если задана разрядность: для мантиссы — семь двоичных разрядов со знаком и четыре двоичных разряда со знаком для порядка.
§ 6.1. МЕТОДЫ ДЕЛЕНИЯ ДВОИЧНЫХ ЧИСЕЛ
Деление двоичных чисел во многом аналогично делению десятичных чисел. Процесс деления состоит в том, что последовательно разряд за разрядом отыскиваются цифры частного путем подбора с последующим умножением этой цифры на делитель и вычитанием этого произведения из делимого.
Из множества разных методов выполнения операции деления рассмотрим наиболее распространенные.
Прежде всего это — «школьный» алгоритм деления, заключавшийся в том, что делитель на каждом шаге вычитается столько раз из делимого (начиная со старших разрядов), сколько это возможно для получения наименьшего положительного остатка. Тогда в очередной разряд частного записывается цифра, равная числу делителей, содержащихся в делимом на данном шаге. Таким образом, весь процесс деления сводится к операциям вычитания и сдвига.
Другой метод выполнения операции деления заключается в умножении делимого на обратную величину делителя. Здесь возникает новая операция — вычисление обратной величины, осуществляемая по известным приближенным формулам (например, разложением в биномиальный ряд Ньютона и т. п.). В этом случае в состав команд машины должна входить специальная операция нахождения обратной величины.
К наиболее распространенным методам выполнения операции деления относится также метод, заключающийся в использовании приближенной формулы для нахождения частного от деления двух величин. От метода умножения делимого на обратную величину он отличается только тем, что частное определяется по некоторой формуле, которая сводится к выполнению операций сложения, вычитания и умножения.
Фактически два последних метода пригодны для использования в специализированных машинах, в которых операция деления встречается не часто и ее целесообразно реализовать программным путем.
В универсальных вычислительных машинах, как правило, реализуется разновидность «школьного» алгоритма деления.
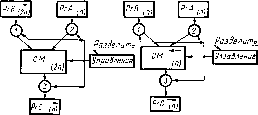
делимое— 1100100 1010 — делитель
делитель— 1010 1010 — частное
остаток— 0101
1010
— 1011
+
восстановление остатка 1010
01010
1010 0000
Здесь цифры частного получаются последовательно начиная со старшего разряда путем вычитания делителя из полученного остатка. Если получен положительный остаток, то цифра частного равна единице; если остаток отрицательный, то цифра частного равна нулю, при этом восстанавливается предыдущий положительный остаток.
В случае положительного остатка для получения следующей цифры частного последний остаток сдвигается влево на один разряд (либо делитель вправо на один разряд) и из него вычитается делитель и т. д.
В случае отрицательного остатка восстанавливается предыдущий положительный остаток прибавлением к отрицательному остатку делителя и восстановленный остаток сдвигается на один разряд влево (либо сдвигается делитель вправо на один разряд) и из него вычитается делитель. Такой алгоритм деления получил название алгоритма деления с восстановлением остатка. Формально все действия можно описать следующим образом.
Пусть А — делимое, В — делитель и С — частное, при этом А=0, а\а2...ап\ В = 0, b,b2...bn; С = 0, с\с2...сп.
Для реализации алгоритма деления двоичных чисел, представленных в форме с фиксированной запятой, необходимо, чтобы выполнялось условие \А\ < |Д|. Если это условие не выполняется, то в первом шаге возникает переполнение разрядной сетки и операция не выполняется. Если (4|<|б|, то на первом шаге операции производится сдвиг делителя и определяется остаток Аі = А — В • .
Пусть А1 > 0, тогда Сі = 1. Процесс деления продолжается дальше: А2 = А\ — В ¦ 2~2.
Пусть А < 0, тогда С2 = 0 и производится восстановление остатка А1 : А 2 = А 2 А В ' 2 2.
Таким образом, алгоритм деления можно описать в общем виде на і-м шаге:
А = Л-1 — В • 2~‘, (6.1)
если А ^ 0, то С, = 1 и переход к следующему шагу; если А < 0, то С, = 0 и восстановление остатка
А_і=А + В.2-', (6.2)
который принимается за остаток А' и процесс продолжается по формуле (6.1). Следовательно, операция деления сводится к последовательному выполнению вычитаний (сложений) в сумматоре и сдвигам делителя. Сдвиг делителя может быть заменен сдвигом содержимого сумматора в противоположную сторону.
Алгоритм деления, основанный на реализации формул (6.1) и (6.2), называется делением с восстановлением остатка.
Рассмотрим процесс восстановления остатка. Когда А < 0 и Сі = 0, то на следующем шаге выполняются действия по формуле А+1 =А'і — В ¦ 2-(і+1) = Л + В • 2-' — В ¦ 2-(,+|). После преобразования получим
А + 1 = А + в • 2~{і +1 \ (6.3)
Таким образом, появляется возможность алгоритм деления построить по следующей схеме: А = А-і—В • 2~‘, если АЛ^О, то С, = 1 и переход к следующему шагу; если А < 0, то С, = 0 и продолжение по формуле А+і = А А В • 2~(,+ |). При этом если А+і^0, то С/+І = 1 и переходим к формуле (6.1), если А+і<0, то Сі+1 = 0 и переходим к формуле (6.3). Такой алгоритм называется делением без восстановления остатков.
Реализация рассмотренных алгоритмов деления возможна с помощью двоичных сумматоров обратного или дополнительного кода. Для хранения делителя, делимого и накопления очередных разрядов частного выделяются регистры. Минимальный состав блоков, необходимый для выполнения делений, показан на рис. 6.1 в двух
а) 5)
іи
по
Таблица 6.1
с
[СМ]:=[СМ]+№
СМ:= [СМ] +[В]о6;
+ 1100110
Восстановление остатка
СМ: = [СМ] +[В]об;
Конец операции
Аі-і + в-г-1'-1* А,>0 А,-<0
Сі = 0 Сі = 1
А^ + в-г-''-»
А,;г 0 А,<0 Сі =1 с, = 0
Аі_, -v- В-2~Ч'-0 A;> 0 A, <0 c, = 0 Сі — 1
вариантах. Варианты отмечаются способом реализации сдвига. В варианте рис. 6.1,а осуществлен сдвиг содержимого регистра делителя, а в варианте рис. 6.1,6 — сдвиг содержимого сумматора. Стрелки на рисунке указывают направление сдвига. Индекс (п) указывает ориентировочное количество разрядов в цифровой части сумматора и регистра делителя. В дальнейших разделах при выполнении примеров, будет использована структура, показанная на рис. 6.1,а.
§ 6.2. ДЕЛЕНИЕ ЧИСЕЛ, ПРЕДСТАВЛЕННЫХ В ФОРМЕ С ФИКСИРОВАННОЙ ЗАПЯТОЙ, НА СУММАТОРАХ ОБРАТНОГО И ДОПОЛНИТЕЛЬНОГО КОДА
При делении знаковая и цифровая части частного получаются раздельно.
Знак частного образуется по формуле Sgc = SgA ® Sge.
Для образования цифр частного воспользуемся следующим соответствием, в котором приведены логические действия над остатками и делителем:
Пример 6.1. Разделить числа А = — 0,10011 и В = —0,11001 на двоичном суммам торе обратного кода с получением частного в прямом коде.
Решение. Для реализации примера воспользуемся структурной ¦ схемой рис. 6.1, а и методом деления с восстановлением остатка.
Представляем числа в обратных кодах: [А]”6= 11,01100; [В]"б = 11,00110; [В]“6ь= 00,11001.
Определим знак частного: Sgc = SgA ф SgB= 1 ф 1 =0.
При этом руководствуемся следующими правилами:
Что делать __
в СМ... Аі-\ + В-2-{!~''> Знак остатка А, . . . А«^0 А,< 0
Цифра частного с,.. с,- = 1 с, = 0
Требуется несколько интерпретировать правила определения цифры частного. В примере 6.1 производится сравнение знаков делимого и остатка на каждом шаге: при совпадении знаков в частном записывается единица, при несовпадении — нуль. Можно сравнивать знаки делителя и остатка, тогда единица в очередной разряд частного записывается при несовпадении знаков, а нуль — при совпадении.
Для получения частного, представленного в обратном коде, все действия должны осуществляться по следующим правилам:
1
ГІ = 0
II II
— о
”=0
II II
С іс
1
ОСТ.
ост.
ост.
ост.
где п — длина разрядной сетки; /сдв — время выполнения сдвига на один разряд; ісл — время выполнения операции сложения; р — вероятность появления нулей в разрядах частного.
На двоичных сумматорах дополнительного кода можно получить частное как в прямом, так и в дополнительном кодах. Знак частного образуется отдельно от цифровой части путем сложения знаковых разрядов по модулю 2.
Для получения частного в прямом коде правила остаются теми же, что и для сумматоров обратного кода (см. пример 6.1).
Пример 6.2. Разделить числа Л = —0,10101 и 6=0,11100 на двоичном сумматоре обратного кода с получением частного в обратном коде.
Решение. Структурная схема и метод деления те же, что в примере 6.1. Представим числа в обратных кодах:
№=11,01010; №=11,00011; №„ = 00,11100.
Знак результата Sgc=l ®0=1.
Последовательность действий при решении задачи показана в таблице 6.2.
Решение. Последовательность действий при решении примера показана в табл. 6.3
[71 ]д =00,10001; №=П,00101; [6]" = 00,11011. Используем алгоритм без восстановления остатка. Знак частного: Sgc=0© 1 = 1.
(ф = 0)
+ 1100011
-L:-
0100010
0000—
[СМ]; [Рг?];
[СМ]; [РгС];
[СМ]; [РгС];
[СМ]; [РгС];
2сдв-5, Конец
СМ: = [СМ] + [т]“;
СМ:=[СМ]+[тй]дм;
СМ:=[СМ] + (тя]дм;
''“00,1111
СМ:=[СМ]+[тй]дм;
Конец
Ответ: С = 0,100Ь2‘.
2275
0006825
k— 6825
1001
1001
k — 1
1)
2275
1003
k-\
0000
Алгоритм выполнения операции деления должен работать так, что, если делитель равен 0 или делимое равно максимальному отрицательному числу, то вырабатывается сигнал переполнения.
Сигнал переполнения должен вырабатываться и в тех случаях, когда делимое больше двигателя по абсолютной величине для чисел с фиксированной запятой.
§ 6.3. ОСОБЕННОСТИ ДЕЛЕНИЯ ЧИСЕЛ, ПРЕДСТАВЛЕННЫХ В ФОРМЕ С ПЛАВАЮЩЕЙ ЗАПЯТОЙ
Для получения частного от деления двух чисел, представленных в форме плавающей запятой, необходимо определить тс-тл/тв, рс = рА — рв.
Так как мантиссы делимого и делителя — нормализованные числа, то при делении возможны случаи, когда ІтлІ^ІШвІ; \гпА\<С\тв\.
Если мантисса делимого больше или равна мантиссе делителя, то в конце операции деления потребуется нормализация частного (нарушение правой границы). Таким образом, алгоритм деления начинается с операции вычитания делителя из делимого и записи единицы в целую часть частного. Все остальные действия над мантиссами аналогичны действиям над числами, представленными в форме с фиксированной запятой.
Если мантисса делимого меньше мантиссы делителя, то после операции вычитания на первом шаге получится отрицательный остаток, что означает нуль в целой части мантиссы частного и продолжение алгоритма деления по рассмотренным выше правилам для чисел, представленных в форме с фиксированной запятой. Таким образом, частное всегда получается в прямом коде, а действия над мантиссами осуществляются на ДСОК или ДСДК..
Так как при операции деления порядки чисел вычитаются (изображения складываются), то возможно переполнение разрядной сетки в сумматоре порядков. При переполнении в сторону отрицательных величин порядка мантисса результата превращается в машинный нуль, а порядку присваивается наибольшее отрицательное значение. Если делитель равен нулю, то также вырабатываются сигналы ср=1 и останов машины. Эти частные случаи предусмотрены при реализации алгоритмов в ЕС ЭВМ, где используется алгоритм деления без восстановления остатков. При этом мантисса делимого имеет длину в 2 раза больше, чем делитель, что иллюстрируется примером 6.4.
Пример 6.4. Разделить число А = 0,10001111-23 на В = 0,1111-22
Решение. Рассматривается случай, когда \тА\<\тв\. Прежде всего записываются машинные изображения мантиссы делимого [тл]“ = 00,10001111; мантиссы делителя [mB]“ = 00,1111 и [тв]“= 11,0001.
Все действия выполняются на сумматоре дополнительного кода втюследователь-ности, указанной в табл. 6.4.
Идея метода ускорения операции деления заключается в том, что в случае образования достаточно малого или достаточно большого по абсолютной величине остатка очередные цифры частного будут группой одинаковых цифр — либо нулей, либо единиц, поэтому продолжение процесса деления обычным способом излишне, так как эту группу цифр можно записать в частное сразу.
Рассмотрим примеры деления десятичных и двоичных чисел:
2) _1010001 1001
Щ1001
k—
1001 0000
Здесь на первом шаге получился малый по величине положительный остаток, который содержит нули в трех старших разрядах. В частном после первой цифры записаны нули в два следующих разряда. Можно утверждать, что при малом положительном остатке в частное можно сразу записать k^-l нулей в соответствующие разряды, остаток сдвинуть на k разрядов влево, вычесть из него делитель и далее продолжить операцию деления.
Если в результате вычитания на каком-то шаге получается большой положительный остаток, в котором k старших разрядов
В других случаях операция выполняется по обычному алго
цифр
частного
1000000000... 10001 10001 11110
011110
k
~ 10001
_011010
10001
010010
10001
000001...
ритму.
Рассмотренный метод ускорения операции деления может дать эффект только тогда, когда встречаются последовательности нулей или единиц в остатках.
Для ускорения операции деления можно воспользоваться также методом одновременного определения двух цифр частного, который является развитием изложенной выше идеи. Этот метод реализован в некоторых ЭВМ третьего поколения.
Пусть А — делимое; В — делитель; А_і — остаток на (г—1)-м шаге деления.
Для остатка справедливо 0^|Л,_||<?.
Если теперь остаток сдвинуть на два разряда, то 22 Ак-\. Тогда следующую пару цифр частного можно найти из условий, представ
-В<Л/=(Л,-В)< 0. (6.5)
Тогда коррекция остатка осуществляется следующим образом: если раньше проверялось условие /В<22Л,_і^(/+1)В, где j — 0, 1, 2, 3, то теперь проверяется эквивалентное ему условие
(/-4)В<22(Л;_,-В)<0-3)В. (6.6)
Можно сформулировать правила, представленные в табл. 6.6.
Операция извлечения квадратного корня как самостоятельная операция в систему, команд ЭВМ включается в случае, когда приходится относительно часто прибегать к ее выполнению (не менее 2% от общего числа операций). Такие ситуации могут встречаться при создании специализированных ЭВМ.
Основным приемом для приближенного вычисления квадратного корня в универсальных ЭВМ является метод итераций, основанный на использовании формулы Ньютона.
Пусть y=\fx. Тогда F(x,y)=y2—г=0, F'(x,y)=2y. Считая, что упжу есть приближенное значение искомой функции, по теореме Лагранжа можно определить F(x\ yn)=F(xi уп) —F(x, у)— ~ІУп—y)F'y(x, Уп), где уп — некоторое промежуточное значение между Уп и у.
Тогда уп+\=уп—{у1—х)/2уп, или
Уп+і = 0,5(уп~\~ х/уп), (6.7)
где л=0, 1, 2, ....
На практике используют и несколько иной метод. Пусть задано подкоренное число а = 0, а\а,2...ап. Предположим, что удалось найти (к— 1)-ю цифру значения корня, равную 0, b\b2-..bk-i- По условию, очередной остаток Ан-\ =А — 0, b\b2---bl~) >0. Очередная цифра bk может быть нуль или единица. Очевидно, что если Ak>0, то bk— 1. При этом
Ak = A-(0,bib2...bk-ll)2=A-(0,b\b2...bk^)2--2-2-k0,bibk...bk-i-2^?k,
или
Ак=Аь-і—2-<к-1Х), ЬіЬ2...Ьк-іОІ. (6.8)
Следовательно, для получения очередного остатка надо к уже найденному числу 0, b\b<i...bk-\ приписать пару цифр 01 и вычесть полученное число, предварительно сдвинутое на (к—1) разряд, из предыдущего остатка. При этом если А^О, то bk— 1; если Ak<0, то bk = 0.
Таким образом, (6.8) показывает, что операция извлечения квадратного корня напоминает операцию деления на переменный делитель, равный 0, 6ій2---&*-і01. Первое значение переменного делителя равно 0,01.
Пример 6.5. Извлечь квадратный корень из числа А = 0,100101 на сумматоре дополнительного кода.
Решение. См. табл. 6.7. Таблица 6.7
Задание для самоконтроля
1. Разделить заданные в прямом коде числа: а) [Л],,,, = 1,100011 и [В]пр = = 1,110011; б) [Л]пр = 0,100111 и [В]„р= 1,100011.
2. Разделить заданные в обратном коде методом с восстановлением остатков числа [Л]об= 1,011001 и [В]об = 0,11001.
3. Разделить заданные в дополнительном коде методом без восстановления остатков числа [Л]доп = 0,110000 и [В]доп= 1,000111.
4. Найти частное от деления чисел [Л]об = 0,1010001111 и [В]оЛ = 1,1010110010 с использованием ускоренного метода.
5. Можно ли применить правила двоичного деления к делению чисел, представленных в минус-двоичной системе?
6. Произвести на сумматоре обратного кода деление чисел А = —0,10011-2_6 и В = 0,100101 -2-4, представленных в форме с плавающей запятой.
7. Произвести деление на сумматоре дополнительного кода чисел А — = 0,101101-25 и В = —0,111001-23, представленных в форме с плавающей запятой.
8. Возможно ли переполнение разрядной сетки при делении чисел, представленных в форме с плавающей запятой?
9. Извлечь квадратный корень из числа А — 0,111111 на сумматоре обратного кода.
М 1,110000
СМ:= [СМ] +[—0,01]";
,00,001000
"МО,110010
Ml,001111
Конец
ВЫПОЛНЕНИЕ ОПЕРАЦИЯ НАД ДЕСЯТИЧНЫМИ ЧИСЛАМИ В ЦИФРОВЫХ АВТОМАТАХ
аі=а4а4 + аза3 + а2а2 + аіаі, (7.3)
где а, — вес разряда тетрады.
В табл. 7.1 представлено кодирование десятичных цифр в различных Д-кодах.
(система
8421)
(система
2421)
(система
5121)
(система
8421+3)
(система
53-21)
(система
75-31)
(система
5421)
Операции над десятичными числами (десятичная арифметика) часто включаются в состав основных команд универсальных ЭВМ. Кроме того, десятичная арифметика реализуется широко в электронных калькуляторах и персональных микроЭВМ. Поэтому кроме общей информации о возможности представления десятичных чисел разработчику необходимо знать и алгоритмы выполнения арифметических операций.
Д-код (двоично-кодированное представление) десятичного числа — такое его представление, в котором каждая десятичная цифра изображается тетрадой из двоичных символов:
Лд = {а4аза2аі}і{а4аза1а|}2...{а4аза2а"}я, (7.1)
где aj — двоичные разряды тетрады /; п — количество десятичных разрядов.
Количество различных Д-кодов определяется количеством возможных сочетаний по 10 из 16 комбинаций, которые допускает тетрада.
При образовании Д-кода следует исходить из общих требований, предъявляемых к системам счисления:
различным десятичным цифрам должны соответствовать различные тетрады;
большая десятичная цифра должна изображаться большей тетрадой (если разряды тетрады имеют вес по двоичной системе счисления);
— для десятичных цифр а={а4аза2аі} и 6={р4рзР2Рі}, связанных соотношением а + Ь = 9, должно удовлетворяться условие
г 0, если а,= 1
Р.= { (і= 1,2,3,4). (7.2)
1, если а, = 0
Для однозначности перевода чисел в Д-код и обратно жела-
Наличие разрешенных и запрещенных комбинаций — очень важное свойство Д-кодов. Оно отличает их от обычных позиционных систем счисления, в которых все комбинации — разрешенные.
Рассмотрим наиболее распространенные Д-коды.
Код Д, прямого замещения (система 8421). В коде Ді разрешенные комбинации соответствуют двоичным эквивалентам десятичных цифр с весами разрядов, равных степеням основания 2. Для этого кода не выполняется условие (7.2), так как цифры, являющиеся дополнением до 9, не получаются простым инвертированием наборов тетрад.
Код Д2 (система 2421). Для кода Дгвеса разрядов тетрады соответственно равны 2, 4, 2, 1; таблица кодирования делится на две части: от 0 до 4 — тетрады повторяют двоичные эквиваленты; от 5 до 9 — по сравнению с двоичной системой каждая тетрада содержит избыток ’+0110. Это дает возможность любую цифру одной части таблицы превратить в ее дополнение до 9 простым инвертированием.
Код Д4 (система 8421+3). Для этого кода все тетрады имеют значения на три единицы больше, чем тетрады кода Ді (отсюда название кода), и для него не существует целочисленных значений веса, которые удовлетворяли бы (7.3).
В вычислительных машинах разного назначения чаще всего используются коды Ді и Д4.
§ 7.2. ФОРМАЛЬНЫЕ ПРАВИЛА ПОРАЗРЯДНОГО СЛОЖЕНИЯ В Д-КОДАХ
Для определения формальных правил поразрядного сложения чисел, представленных в Д-коде, рассмотрим те особенности, которые присущи этим кодам.
1. Наличие разрешенных и запрещенных комбинаций.
Появление запрещенной комбинации при выполнении каких-то
действий над числами свидетельствует о возникновении ошибки или же о необходимости ввести корректировку результата.
2. При сложении тетрад возникает потетрадный перенос п/=16 вместо поразрядного переноса п,= 10. Это приводит к необходимости коррекции результата.
В самом деле, если складываются числа у4д = а„а„_і..-.аіао и Вл = ЬпЬп-\~.Ь\Ьо, то сумма Сл=Аа + Вл и
Ci=ai + bi + ni-l — niq, (7.4)
где Сі — і-й разряд суммы; п,_і — перенос из младшей тетрады; п, — перенос в старшую тетраду; п,__і = {0, 1}, п, = [0, 1], <7=10.
Далее выведем правила сложения применительно к Д-кодам.
При сложении чисел в коде Ді могут возникнуть следующие случаи.
1. Пусть а<+6;+п/_1<10, где щ, Щ — тетрады кода Ді. При сложении в данном разряде числа образуется сумма меньше 10. Если действия над разрядами тетрады производят по правилам двоичной арифметики, то правильный результат получают без коррекции.
Пример 7.1. Сложить тетрады и, = 0100 и ft, = 0101 при значении п,_і=0.
Решение, с, = а, + ft, 4-п,-_ і = 1001.
Ответ: сі =1001.
2. Пусть а;+Ь/+п,-_|^ 10, т. е. возникает десятичный перенос и сумма должна быть равна а,~-|-й;+п/_і — п,10, где п,= 1.
Свидетельством того что результат неправильный, является либо появление запрещенной комбинации, если 15^а/+&<+п,-_1^10, либо появление потетрадного переноса п/=16, что превышает значение десятичного переноса на 6. Следовательно, требуется коррекция результата в данной тетраде введением поправки, равной +0110.
Пример 7.2. Сложить тетрады а,=0101 и ft, = 1001 при значении п,_і = 1.
Решение. с, = а, + 6, + п<_ і = 1111.
(1) =0101. п,
т. е. результат равен 0101 в данной тетраде и образован перенос в старшую тетраду.
Ответ: с, = 0101, п,= 1.
Пример 7.3. Сложить тетрады а, = 0111, 6, = 1001 при значении п,-_і = 1.
Решение. с,'=а, + ft/ + п, _ і =(1)0001
п,'
Появление потетрадного переноса требует коррекции результата: с, = 0001 + 4-0110 = 0111.
Ответ: Сі = 0111, р,= 1.
Примеры, рассмотренные выше, дают возможность сформулировать следующие правила потетрадного сложения чисел в Ді-коде:
если при потетрадном сложении перенос в соседнюю старшую тетраду не возникает (п, = 0), то результат суммирования не требует коррекции;
коррекция результата потетрадного сложения путем добавления поправки +0110 требуется в случае, если:
а) возникает потетрадный перенос в старшую тетраду (п,—1);
б) возникает запрещенная комбинация.
Устройство, которое работает по сформулированным выше правилам, называется одноразрядным десятичным сумматором для Д-кода (рис. 7.1).
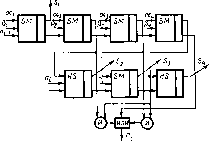
Пример 7.4. Сложить числа А =279 = 0010 0111 1001 и 5 = 581=0101 1000 0001, записанные в коде Ді.
Решение. Прежде всего производится потетрадное суммирование, а затем коррекция там, где это необходимо:
fl = + 0101 1000 0001
,0111 1111 1010
ОНО ОНО поправки
C = 1000 ^0110^-0000
Здесь стрелка указывает передачу единицы десятичного переноса.
Ответ: С = 860= 1000 0110 0000Дг
При сложении чисел в коде Д2 могут возникнуть следующйр случаи.
1. Пусть а/<5 и Ь'іС5, где а/, Ы — тетрады для кода Д2. Тогда:
если а!+5/+п,_і —результат сложения не требует коррекции;
если а/+6'+п,_і^5 — результат попадает во вторую часть таблицы кодирования, где с/ = с,-)-б.
Здесь необходима коррекция результата введением поправки ОНО. Признак этого — появление запрещенных комбинаций.
2. Пусть а,'>5 и Ь[<5; 15>а(-\-Ы п,_і^5.
Так как a/ = a,+6, то при суммировании поправка не требуется.
3. Пусть а/^5 и Ь[^5; п,= 1. Тогда:
если 10<+/+Ь/+ п;_і^15 — результат требует коррекции путем введения поправки — ОНО, так как появляется запрещенная комбинация;
если же а\ + Ъ\ + п,-1< 15 — результат не требует коррекции.
При потетрадном суммировании в Д2-коде результат суммирования без коррекции получается во всех случаях, кроме следующих:
если при отсутствии переноса в старшую тетраду (п,=0) возникает запрещенная комбинация, то требуется ввести поправку +0110;
если при наличии переноса в старшую тетраду (п,= 1) возникает запрещенная комбинация, то требуется ввести поправку —ОНО (1001 в обратном коде или 1010 в дополнительном коде).
Так как поправки бывают положительные или отрицательные, то их введение сопровождается блокировкой цепей межтетрадного переноса в период коррекции результата.
Пример 7.5. Сложить числа А =0010 0100 1110 и В = 0001 1100 1111, записанные в коде Д2.
Решение. Сначала производится потетрадное суммирование, а затем осуществляется коррекция:
Д== 0010 0100 1110
В = -Г0001 1100 1111
С= 0100^-0001^ 1101
Результат получился без коррекции.
Ответ: = 0100 0001 1101д>.
Решение. Сначала производится потетрадное суммирование, а затем коррекция:
+0101 + 1111 + 1010 0110 0000 1010 поправки
В младшей тетраде возникает перенос п,= 1 и запрещенная комбинация — вводится поправка 1010 в дополнительном коде; в старшей тетраде при п,=0 возникла запрещенная комбинация — поправка вводится 0110.
Ответ: С = 594 = 1011 НИ 0100Ді.
При сложении чисел в коде Д4 возможны следующие случаи. Пусть а"—щ + 3, &"=+,+3, где а" и Ь" — тетрады для кода Д4.
Тогда:
если а''+?"+п,_і<10, то c"=a,+3+fr/+3+n1-i — Оі+Ьі+п,-і+3+
Сі
+3; результат требует коррекции путем введения поправки —ООН; если ц^+бГ+п,—10, то с(/==Ц|+6(+П(—1+3+3.
Здесь возникает десятичный перенос, который, по условию, «уносит» с собой шесть избыточных комбинаций. Следовательно, в данном случае требуется коррекция результата путем введения поправки +0011.
Пример 7.7. Сложить числа Л = 35 = 0Н0 1000 и В — 28 = 0101 1011, записанные в коде Д4.
Решение. Сначала производится потетрадное сложение, а затем введение поправок:
Л= ОНО 1000 6 = ”' 0101 1011
1100 0011
— ООН + ООН поправки С= 1001 ОНО
Ответ: С=63=1001 0110Д).
Здесь поправки вводятся при блокировке цепей потетрадного переноса.
Правила введения поправок можно сформулировать так:
если цри сложении тетрад не возникает переноса (п,=0), то поправка равна —ООП (или дополнение +1101); если же возникает потетрадный перенос (п,=1), то поправка равна +0011.
Аналогичным образом можно рассмотреть правила суммирования для других Д-кодов.
Представление Д-кода в разрядной сетке машины может осуществляться в форме либо с фиксированной, либо с плавающей запятой. При этом отрицательные числа должны представляться в прямом, обратном или дополнительном кодах. Поэтому, если А = —0, аіач...аПу где а,- — тетрады, то
[Л]пр=1, а\а2...ап\
[Л]об= 1, ща2...й„\ (7.5)
[Л]д = 1, аіа2...а„,
где а, — дополнение до q— 1'во всех тетрадах; а, — дополнение до q— 1 во всех тетрадах, за исключением младшей, для которой это дополнение до q= 10.
Из правил преобразования (7.5) следует, что
a, + a,= ^—1. (тА)
Это означает, что для Д-кодов, для которых выполняется условие (7.2), обратный код получается простым инвертированием набора тетрад.
Пример 7.8. Найти обратный и дополнительный коды в коде Д2 для числа Л = = -0,127 = -0,0001 0010 1101Дг.
Решение. На основании (7.5) [Л]об= 1,1110 1101 0010.
Используя соотношение [Л]06 + Qn = lA\, находим дополнительный код: | Л ], =
= 1,1110 11010011.
Прибавление единицы в младшую тетраду при образовании дополнительного кода в коде Д2 осуществляется по правилам сложения для этого кода.
Ответ: {А\6 = 1,1110 1101 0010Ді; [Л]д= 1,1110 1101 0011Дг.
Пример 7.9. Найти обратный и дополнительный коды в коде Д4 для числа А = = —0,4591=0,0111 1000 1100 ОЮОд,.
Решение. На основании (7.5)
[Л]о6 = 1,1000 0111 ООП 1011;
[Л]д =1,1000 оі и ооп поо.
Прибавление единицы в младшую тетраду при образовании дополнительного кода в коде Д4 не требует коррекции.
Ответ: см. формулу (а) данного примера.
Код Ді отличается тем, что для' него не выполняется условие (7.2). Эта особенность кода влияет на образование обратного или дополнительного кода, так как инвертирование набора тетрад означает получение дополнения до 24—1 = 15. Следовательно, необходимо убрать разницу. Один из используемых при этом приемов состоит в том, что во все цифровые тетрады числа в коде Ді добавляется +0110 и после этого производится инвертирование набора. Полученное изображение представляет собой обратный код числа.
Пример 7.10. Получить обратный' код в коде Ді для числа А = —0,256= = —0,0010 01010110Д1.
0,0010 0101 ОНО
+ + +
ОНО оно оно
0,1000 1011 1100
После инвертирования этого набора получаем [А]0б?= 1,0111 0100 0011Ді.
Ответ: [Л+б= 1,0111 0100 0011ц,.
§ 7.4. ВЫПОЛНЕНИЕ ОПЕРАЦИЙ СЛОЖЕНИЯ И ВЫЧИТАНИЯ ЧИСЕЛ В Д-КОДАХ
Все арифметические действия в Д-кодах выполняются над операндами по формальным правилам десятичной арифметики, сформулированным выше.
Возникающие при этом специфические особенности целесообразнее рассмотреть на конкретных примерах.
Пример 7.11. Сложить в коде Ді на сумматоре дополнительного кода числа Л =—0,1000 0010 0101 и В = 0,1001 01000110.
Решение. Исходные числа представляются в дополнительном коде и их изображения складываются:
[Л+= , 1, 0001 0111 0101 [В]д = + 0, 1001 0100 оно
. 1, 1010 1011 1011
+ ОНО ОНО ОНО поправки
[С]д= О, - 0001 0010 0001.
Ответ: С = 0,0001 0010 ОООІд,.
Пример 7.12. Сложить в коде Ді на сумматоре обратного кода числа А = = —0,0100 1000 0111 и В = -0,0010 ООП ОНО.
Решение. Исходные числа представляются в обратном коде, и их изображения складываются:
[Л]о6 = 1, ,0101 0001 0010 4
[В]об= 1, +01П ОНО ООП
. 0, 1100 0111 ОНО
+ ОНО 0000 0000 поправки
[CJ,6= 1, ч- 0010 0111 ОНО.
При коррекции в коде Ді цепи межтетрадного переноса в сумматорах не блокируются.
Ответ получаем после преобразования результата из обратного кода.
Ответ: С = —0,0111 0010 0011Ді.
Пример 7.13. Сложить в коде Д2 на сумматоре дополнительного кода числа А = -0,0000 1101 ООН 1011 и В = —0,0000 1111 0010 1011.
Решение. Если все делать по правилам, то [Л]„= 1, 1111 0010 1100 0101. В последней тетраде получена запрещенная комбинация, что свидетельствует о необходимости коррекции путем введения поправки ОНО:
,0101
+ 0110
1011.
1,*г lUOtL ООН «т 101° -І ОНО
^ОООО '0000 ^ 1010 '1010 поправки
Производится обратное преобразование дополнительного кода.
Ответ: С==—0,0001 1100 1100 0000л.
Пример 7.14. Сложить на сумматоре обратного кода (система Д2) числа А =
= 0,1110 1011 0011Д! и В = —0,11000100 1011д2.
Решение. Сначала числа записываются в обратном коде и их изображения складываются:
[В]об= 1, ООП 1011 0100 ^^ = + 0, 1110 1011 ООП
, 0,-- 0010 ОНО -г ЮОО
+ 0000 +1010 'ОНО поправки
Соб= 0, 0010 0000 1110.
Ответ: [С]рб = 0,0010 0000 1110Ді.
Пример 7.15. Сложить в коде Д4 на сумматоре обратного кода числа А — = -0,1011 11000111 1001 и 5 = 0,0011 1000 1001 1010.
Решение. Сначала записываются в обратном коде и затем складываются изображения:
[A] об = , 1, 0100 ООН 1000 ОНО
[B] об = + 0, ООП 1000 1001 1010
1, 0111 1100 0010 0000 + 1101 +1101 +0011 +0011 поправки
[С]0б = 1, 0100 1001 0100 ООП.
При введении поправок цепи межтетрадного переноса блокируются и отрицательные поправки вносятся в виде дополнения (1101).
Ответ: С = — 0,1011 0110 1011 1100д,.
Рассмотренные выше примеры выполнения операций сложения в Д-кодах позволяют сделать ряд общих замечаний; коррекция результата может осуществляться автоматически либо программным путем, либо с помощью аппаратных средств. Первый метод потребует разработки специального блока управления, а второй — усложнения схемы собственно сумматора. Эту задачу разработчик решает в конкретной постановке в зависимости от требований. На практике чаще используется схемный метод коррекции.
По изложенным выше правилам реализуются алгоритмы сложения (вычитания) чисел, представленных в форме с фиксированной запятой на специальных десятичных сумматорах.
§ 7.5. УМНОЖЕНИЕ ЧИСЕЛ В Д-КОДАХ
Выполнение операций умножения в Д-кодах принципиально производится по классической схеме:
умножение чисел сводится к последовательному суммированию частных произведений, полученных при умножении множимого на очередную цифру множителя. Так как каждая цифра множителя представляется в виде (^РзРгРі);, где і — номер разряда, то умножение сопровождается расшифровкой значения очередной тетрады множителя и сдвигом на четыре разряда сразу. Расшифровку можно осуществить разными способами. Простейшим приемом является последовательное вычитание единицы из значения тетрады до получения нуля и соответственно прибавление множимого в сумматор на каждом такте. При умножении на сумматоре прямого кода надо предусмотреть дополнительную тетраду на случай местного переполнения.
Пример 7.16. Умножить на сумматоре прямого кода (код Д2) числа [Л]„р= 1, ООП 1101;
[В]пр = 0, 0010 0100.
Решение. При умножении используются сумматор прямого кода для кода Д2 на три тетрады и регистры на две тетрады.
Последовательность выполнения операции показана на табл. 7.2.
Т а б л и ц а 7.2
Примечание
пр
Регистр В
0001 +0011 1101
0001
, О ©1
і о о
. © —
1 — ©1
1
1110 0010 0001 шгг
_0001
ОТТО
1110 1110
Анализ тетрады Ьі
Конец анализа
Сдвиг на четыре разряда
Анализ тетрады 62
Конец анализа
Сдвиг на четыре разряда
Конец
( >) 0010
0001
0000
0100
1000
0000
0000
0100
1000 сдвиг
“'"ОНО
4101
“•“оно
поправки
“*"0110
поправки
“'“ОНО
сдвиг
поправки
0111
,0000
+0110
1000
поправки
ОНО попРавки
поправки
Ответ: АВ = 0001 0000 0011 0010.
цифра
множителя
цифра
множителя
При умножении в коде Ді анализ тетрад можно осуществлять с помощью реверсивного счетчика.
Ответ: [ЛВ]пр = 1,0000 1110 1110 1110.
В некоторых машинах единой системы при умножении десятичных чисел в коде Ді используется метод ускорения операции, при котором вся операция сводится к последовательному выполнению сложения или вычитания на сумматоре дополнительного кода в зависимости от величины очередной цифры множителя (табл. 7.3).
Таким образом, предварительно должны быть подготовлены множимое и удвоенное множимое. При этом если предыдущая цифра была больше пяти, то действие на очередном шаге надо увеличить на + 1А.
При умножении десятичных чисел часто используют другие приемы, позволяющие ускорить эту операцию, например, по формулам
ДВ = 2Д-у-, если В — четное число,
А В = 2 А в- 1 + А, если В — нечетное число.
Действия в соответствии с (7.7) можно рассмотреть на примере десятичных чисел: 35-42=2-35-(42/2)=70-21 = 140- 10+70=280Х X 5+70=560 • 2+280+70= 1120-1+280+70=1470.
При двоично-десятичном представлении чисел прием (7.7) может быть упрощен, так как удвоение числа означает сдвиг влево, а деление на 2—сдвиг вправо. Так как сдвиги производятся над двоичными кодами, то требуется коррекция тетрад на каждом шаге. Корректирующие поправки определяются для каждого Д-кода. Коррекция выполняется тогда, когда происходит сдвиг единицы из крайнего разряда данной тетрады в соседнюю тетраду. Например, для кода Ді корректирующая поправка равна +0110 для тетрад множимого и —ООП (или +1101) для тетрад множителя.
Пример 7.17. (см. [19]). Умножить числа А =0010 0100 и В = 0100 0011 методом (7.7) в коде Ді.
Решение. Схема умножения выглядит следующим образом:
Деление десятичных чисел в Д-кодах выполняется методом последовательного вычитания делителя из делимого на первом шаге и из остатков — на последующих шагах. Вычитание на каждом шаге производится до тех пор, пока не получится отрицательный остаток. Каждый раз при получении положительного остатка добавляется единица в специальный счетчик, где накапливается очередная цифра частного. Затем осуществляется сдвиг на четыре двоичных разряда и прибавление делителя до тех пор, пока не получится положительный остаток. Количество сложений (без последнего) является дополнением соответствующей цифры частного до 9, что заносится в счетчик очередной цифры частного.
Таким образом, процесс деления состоит из ряда последовательно чередующихся циклов сложения и вычитания со сдвигами. Знак частного получается как логическая сумма по модулю 2 знаков чисел.
Все действия при выполнении операции деления должны осуществляться на сумматоре дополнительного (обратного) кода, рабо-
Примечания
Сумматор
Делитель на і-м шаге
И. П. В-2“';
0,2425
0,2600
0,5200
0,2600
0,1300
0,0650
0,325
0,0162
0,0081
СМ: = [СМ] -В-2-';
остаток отрицательный Сі = 0; восстановление Rі;
В-2~2; СМ:= [СМ] —В-2”2; остаток положительный сг == 1:
В-2-'-, СМ:= [СМ] — В-2—3; остаток положительный Сз=1;
В-2-4; СМ: = [СМ] -В-2-4; остаток положительный сч=1;
В-2"5; СМ:= [СМ] —В-2~5;
остаток отрицательный Cs=0; восстановление Rr>;
В -2~6; СМ:= [СМ]-В-2~6;
остаток положительный Сб=1;
Конец
9,9825
0,2600
__0,2425
0,1300
0,1125
0,0650
0,0475
—0,0325 _0,0150
0,0162
,9,9938 '0,0162 _0,0150
0,0081 ' 0,0069
и т. д.
тающего по правилам сложения — вычитания соответствующего Д-кода.
Для простоты рассмотрим пример деления в десятичной системе счисления, не прибегая к представлению чисел в виде тетрад.
Пример 7.18. Разделить число Л =0,154675 на В=0,550.
Решение. Установка исходного положения.
Шаг 1. Осуществляется пробное вычитание: если результат будет положительный или равен нулю, то вырабатывается сигнал прерывания, если — отрицательный, то производится сдвиг на одну тетраду.
В данном случае получается отрицательный остаток (рассматриваете^ только цифровая часть чисел).
Остаток >0 Шаг 4:
Остаток <0
Алгоритм десятичного деления, подобный рассмотренному, используют в машинах ЕС ЭВМ.
Для ускорения операции деления применяют приемы, аналогичные приемам, употребляемым для ускорения выполнения операции умножения.
Пусть А — делимое, В — делитель, С — частное. Предположим, что удалось отыскать частное в виде С=0, С\С2--СП. Тогда
А = В • (с, • 2-1+с2 • 2~2+...+Сп ¦ 2")+/?„, (7.8)
где Rn — остаток от деления.
Пусть Rn=0. Положим, что с\=1, С2=Сз=...=0. Тогда остаток на первом шаге R\=A—2~1В.
Если Rі^0, то Сі^І; если R(<0, то сі=0. В последнем случае восстанавливается предыдущий положительный остаток. Затем принимаем, что С2=1, а остальные с,=0 и т. д.
/?,=Л-В2сг-2-‘. (7.9)
<=1
Таким образом, при делении десятичных чисел, заданных в Д-коде, результат получается в двоичной системе счисления.
Пример 7.19. Найти частное от деления /1=0,2425 на В = 0,5200.
Решение. Для наглядности выполним этот пример в десятичной системе счисления с записью результата в двоичном коде, предполагая, что при переходе к определенному Д-коду все операции над десятичными числами будут выполняться по правилам этого Д-кода.
Последовательность выполнения операции деления дана в табл. 7.4.
Таблица 7.4
Ответ: С=0,011101.
Так как при сдвиге чисел, представленных в Д-коде, приходится вводить поправки, то для хранения делителя целесообразно иметь самостоятельный сумматор, в котором при передаче единицы из одной тетрады в другую автоматически вносится поправка.
§ 7.7. ИЗВЛЕЧЕНИЕ КВАДРАТНОГО КОРНЯ В Д-КОДАХ
В основу алгоритмов извлечения квадратного корня в десятичной системе может быть с некоторыми уточнениями положена формула (6.8). Если для двоичной системы счисления в качестве
В десятичной системе счисления целое число можно представить в виде степенного полинома по основанию 10:
А = ап- 10"+...+аі • ІО'+ао-10°.
Квадрат числа А можно записать так:
А2 = а2- 102л+2ал- 10л(ал^і • 10"-‘ + ...аі • 10+а„)+
+(ал—і • 10" 1+...+йі • 10+Цо)2=йл • 102п+2ал(ал_і • 10” * + ...
...+аі *10 + а<)) + а2- і • Ю2(п_ 0 + 2а„_ і +10"_ 110"(ал_2‘ 10л~2 + ...
... + аі • 10 + а0) + ... + а2 • 106 + 2аз- 103(а2- ІО2 + аі • 10 + ао) +
+ а1-104 + 2а2.102(а,-10 + ао) + а?-102-102 + 2асЮ-ао + а§, где п — любое целое число.
Раскроем в этом выражении скобки и сгруппируем члены по убывающим степеням:
А2—а2п- 102л + йл-і • 10п^'(2ал- 10л+ал_і • 10"-')+
+а„_2- 10л-2(2ал- 10п+2а„-і • Ю^'+а^г- Ю""2) +
+ал_з- Юп~3(2ал. 10л+...+ал_3-10"~3)+...+
+ ао(2ал • 10п+2ал_і -ІО” 1 + ...+2аі • 10+Яо).
Здесь на каждом последующем этапе содержимое в г'-й скобке отличается от содержимого скобки на предыдущем этапе тем* что имеет дополнительные слагаемые ал_;+і • 10п-‘_1 и a„-r 10'1-'.
Обозначим скобку на каждом этапе через Ь, и примем Ьл+і=0 и ал+і=0, тогда
А2=(Ьп+і-\-ап+і • 10л+1+ал- 10").ал- 10л+(6л+ал. 10л+
+а„_і • 10л ‘)ал_і • 10" |+(йл_i+fln—1*10" * +
+ол_2,10л 2)ал_2- 10л 2+...+(Ь2+п2• Ю2+Ц| • 10)аі • 10+ +(Ьі+аі • Ю+ао)ао-
Вынося из скобок Ьі общие для скобки множители, получим
А2={Ь'п+1 • 10+ал+і • 10+ал)а„ • 102л+(Ьл • 10+а„ • 10+
+ал_і)а„_і • 102(л ^+-.-+(йі • 10+fli • 10+ао)ао-
Окончательно получим
А2= 2(^і+і • Ю+аі+1.10+а()а;- 102і, (7.10)
І
где Ы+1—коэффициент при а,-+і • 102(,+ 1), т. е. полученный на предыдущем этапе.
Алгоритм ручного вычисления квадратного корня по данной формуле можно представить следующим образом:
1. Произвести анализ двух старших разрядов числа А2, найти число ап, квадрат которого наиболее близко подходит к двум старшим разрядам числа А2, оставаясь меньше последнего.
2. Произвести вычитание из старших разрядов А2 квадрата числа ал.
3. Удвоить число а„.
4. Сдвинуть остаток от вычитания на два разряда влево, а величину 2ал — на один разряд влево.
5. Приписать справа от остатка вычитания два следующих старших разряда числа А2.
6. Произвести анализ полученного числа на равенство нулю.
7. Если полученное число не равно нулю, то, анализируя его, найти такое а„_і, которое, будучи умноженным на (2ал- 10+а„_і), даст в результате число, меньше полученного на пятом шаге, но наиболее близкое к нему по значению. Перейти к п. 3.
8. Если при анализе в п. 6 получено равенство, перейти к п. 4, предварительно приписав справа от ап нуль.
9. После получения количества цифр, равного д/2, прекратить вычисление.
При анализе в п. 1 и 7 можно использовать следующее соображение: если последовательно рассматривать квадраты чисел от 0 до 9, то переход от квадрата одного числа можно представить как прибавление к уже известному квадрату определенного числа, которое можно определить из формулы с=а2—&2=(а—6)(а+б); если a=b— 1, то а2=62+(а—6)(а+6)=62+(а+6), где а — предыдущее число, возведенное в квадрат.
Данный метод позволяет повысить точность результата. На шестиразрядном сумматоре можно получить в результате пять точных цифр, так как не все число во время выполнения над ним действий располагается на сумматоре.
К недостаткам метода относят довольно длительное время, необходимое для получения результата.
а2
СИ
«1
аі
аі
аі
Оз
а2
а2
а2
а2
аз
аз
Ct4
«3
Ct4
Оз
СІ4
аі
аз
0-3
а2
а2
а2
аз
Ct4
аі
аі
(24
а 4
ДЗ
а2
аз
«4
Оз
Рассмотрим некоторые вопросы перевода десятичных чисел, представленных в Д-коде, в двоичную систему счисления.
Пусть задано десятичное число А—а^а^аі, где десятичная цифра, которая должна быть представлена в Д-коде в виде а,=
= {<4u3<4ui}'-
Используя равенство 10=8-)-2=23+21, любое десятичное целое число можно записать как
Лд=(...((аГаГаГаГ,/(23+2|)+а/4"аГа^аГ)(23+21) + +аТа^аГ)(23+2')+а5а^а{).
Умножение на 2* означает сдвиг двоичного кода на k разрядов влево. Следовательно, перевод сводится к сдвигу соответствующих тетрад и их последующему суммированию. Это суммирование может быть выполнено по следующей схеме (для четырехразрядного числа): получаются последовательно одна за другой. При дробных числах эта операция видоизменяется таким образом, чтобы при умножении на число 1010 можно бьіло получить соответствующие цифры десятичных дробей).
Задание для самоконтроля
1. Какие комбинации являются запрещенными для кодов Ді, Д2, Дй?
2. Преобразовать число А = —0,6315 в дополнительный код в кодах Ді и Д2.
3. Преобразовать число В = —0,1234 в обратный код в кодах Д2 и Д4.
4. Сложить числа Л = — 0,6315 и В=0,1234 на сумматоре дополнительного кода
в коде Ді.
5. Сложить числа /1=0,6315 и В = — 0,1234 на сумматоре обратного кода в коде Д2.
6. Сложить числа /1=0,1245 и В = —0,1246 на сумматоре дополнительного кода в коде Д4.
7. Перемножить числа /1=0,12 и В=0,13 на сумматоре прямого кода в коде Ді.
8. Разделить число /1=0,1246 на В=0,13 на сумматоре дополнительного кода в
коде Д2.
9. Перемножить числа /1 =0,146 и В=0,178 ускоренным методом по (7.7) в коде Ді (сумматор обратного кода).
10. Извлечь квадратный корень из числа Л = 0,14412 на сумматоре обратного кода в коде Ді. Л
В схеме некоторые символы встречаются многократно. Так как при переводе осуществляется суммирование по столбцам, то пары одинаковых символов дадут единицы переноса в соседние разряды.
Таким образом, перевод числа в Д-коде осуществляется путем суммирования элементов тетрад по столбцам с передачей соответствующих переносов.
Подобные способы перевода реализованы в машинах ЕС ЭВМ, машинах фирмы «ІВМ» и т. д. При разработке схем перевода приходится решать вопросы создания суммирующего устройства на много входов. При переводе, например, восьмиразрядного десятичного числа количество слагаемых в столбце оказывается равным 13. Значит, надо иметь сумматор на 13 входов. Реализовать такую схему можно с помощью многоступенчатых схем. При этом возникают дополнительные задержки сигнала, что снижает скорость перевода чисел.
Перевод чисел из двоичной системы счисления в Д-код может осуществляться разными способами. В некоторых случаях для ряда последовательных операций над двоичным изображением числа может быть использована сама вычислительная машина (например, деление на число 1010 целых двоичных чисел; десятичные цифры
КОНТРОЛЬ РАБОТЫ ЦИФРОВОГО АВТОМАТА
§ 8.1. КОДИРОВАНИЕ ИНФОРМАЦИИ КАК СРЕДСТВО ОБЕСПЕЧЕНИЯ КОНТРОЛЯ РАБОТЫ АВТОМАТА
Коды как средство тайнописи появились в глубокой древности. Известно, что еще древнегреческий историк Геродот в V в. до н. э. приводил примеры писем, понятных лишь адресату. Секретная азбука использовалась Юлием Цезарем. Над созданием различных секретных шифров работали такие известные ученые средневековья, как Ф. Бэкон, Д. Кардано и др. Появлялись очень хитрые шифры и коды, которые, однако, с течением времени расшифровывались и переставали быть секретом. Первым кодом, предназначенным для передачи сообщений по каналам связи, был код С. Морзе, содержащий разное количество символов для кодирования букв и цифр. Затем появился код Ж. Бодо, используемый в телеграфии, в котором все буквы или цифры содержат одинаковое количество символов. В качестве символов может выступать наличие или отсутствие (пробел) импульса в электрической цепи в данный момент.
Коды, использующие два различных элементарных сигнала, называются двоичными. Эти сигналы удобно обозначать символами О или 1. Тогда кодовое слово будет состоять из последовательностей нулей и единиц.
Двоичное кодирование тесно связано с принципом дихотомии, который реализуется в графическом методе представления двоичной информации в виде графов.
В гл. 1 и 3 были рассмотрены общие и конкретные вопросы кодирования информации в цифровом автомате. Однако эти методы сами по себе еще не обеспечивают правильность выполнения того или иного алгоритма. Рассмотренные ранее алгоритмы выполнения арифметических операций обеспечат правильный результат только в случае, если машина работает без нарушений. При возникновении какого-либо нарушения нормального функционирования результат будет неверным, однако пользователь об этом не узнает, если не будут предусмотрены меры, сигнализирующие о появлении ошибки. Следовательно, с одной стороны, разработчиками машины должны быть предусмотрены меры для создания системы обнаружения возможной ошибки, а с другой стороны, должны быть проработаны меры, позволяющие исправить ошибки. Эти функции следует возложить на систему контроля работы цифрового автомата.
Поэтому система контроля должна строиться с таким расчетом, чтобы она позволяла обнаружить и по возможности исправить лю-ібые нарушения. При этом надо различать следующие виды ошибок результата:
1) возникающие из-за погрешностей в исходных данных;
2) обусловленные методическими погрешностями;
3) появляющиеся из-за возникнования неисправностей в работе машины.
Первые два вида ошибок не являются объектом для работы системы контроля. Погрешности перевода или представления числовой информации в разрядной сетке автомата приведут к возникновению погрешности й результате решения задачи. Эту погрешность можно заранее рассчитать и, зная ее максимальную величину, правильно выбрать длину разрядной сетки машины. Методические погрешности также учитываются предварительно.
Проверка правильности функционирования отдельных устройств машины и выявление неисправностей может осуществляться по двум направлениям:
профилактический контроль, задача которого — предупреждение появления возможных ошибок в работе;
оперативный контроль, задача которого — проверка правильности выполнения машиной всех операций.
Решение всех задач контроля становится возможным только при наличии определенной избыточности информации. Избыточность может быть создана либо аппаратными (схемными) средствами, либо логическими или информационными средствами.
К методам логического контроля, например, можно отнести следующие приемы. В ЭВМ первого и второго поколения отсутствие системы оперативного контроля приводило к необходимости осуществления «двойного счета», когда каждая задача решалась дважды и в случае совпадения ответов принималось решение о правильности функционирования ЭВМ.
Если в процессе решения какой-то задачи вычисляются тригонометрические функции, то для контроля можно использовать известные соотношения между этими функциями, например sin2a +
г! (п - ()!
+ cos2a==l. Если это соотношение выполняется с заданной точностью на каждом шаге вычислений, то можно с уверенностью считать, что ЭВМ работает правильно.
Вычисление определенного интеграла с заданным шагом интегрирования можно контролировать сравнением полученных при этом результатов с теми результатами, которые соответствуют более крупному шагу. Такой «сокращенный» алгоритм даст, видимо, более грубые оценки и по существу требует дополнительных затрат машинного времени.
Все рассмотренные примеры свидетельствуют о том, что такие методы контроля позволяют лишь зафиксировать факт появления ошибки, но не определяют место, где произошла эта ошибка. Для оперативного контроля работы ЭВМ определение места, где произошла ошибка, т. е. решение задачи поиска неисправности, является весьма существенным вопросом.
§ 8.2. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ КОДИРОВАНИЯ
Задача кодирования информации представляется как некоторое преобразование числовых данных в заданной системе счисления. В частном случае эта операция может быть сведена к группированию символов (представление в виде триад или тетрад) или представлению в виде символов (цифр) позиционной системы счисления. Так как любая позиционная система не несет в себе избыточности информации и все кодовые комбинации являются разрешенными, то использовать такие системы для контроля не представляется возможным.
Систематический код — код, содержащий в себе, кроме информационных, контрольные разряды.
В контрольные разряды записывается некоторая информация об исходном числе. Поэтому можно говорить, что систематический код обладает избыточностью. При этом абсолютная избыточность будет выражаться количеством контрольных разрядов k, а относительная избыточность — отношением k/n, где n=m-\-k — общее количество разрядов в кодовом слове (m — количество информационных разрядов).
Понятие корректирующей способности кода обычно связывают с возможностью обнаружения и исправления ошибки. Количественно корректирующая способность кода определяется вероятностью обнаружения или исправления ошибки. Если имеем «-разрядный код и вероятность искажения одного символа будет р, то вероятность того, что искажены k символов, а остальные п — k символов не искажены, по теореме умножения вероятностей будет
w = pk(\-p)n~k. (8.1)
Число кодовых комбинаций, каждая из которых содержит k искаженных элементов, равна числу сочетаний из п по k:
Р‘( 1 -р)""'.
Так как на практике р= 10-3-Е 10~ \ наибольший вес в сумме вероятностей имеет вероятность искажения одного символа. Следовательно, основное внимание нужно обратить на обнаружение и исправление одиночной ошибки.
Корректирующая способность кода связана также с понятием кодового расстояния.
Кодовое расстояние d(A, В) для кодовых комбинаций А я В определяется как вес такой третьей кодовой комбинации, которая получается' сложением исходных комбинаций по модулю 2.
Вес кодовой комбинации V (Л) — количество единиц, содержащихся в кодовой комбинации.
Пример 8.1. Найти вес и кодовое расстояние для комбинации А =011011100,
/1 = 100111001. 9 9
Решение. Вес для кодовых комбинаций V(A)= 2a, = 5; V(B)= 26і=5.
Находим кодовую комбинацию С=АфВ = 111100101, для которой определяется псе, равный кодовой расстоянию для А и В: V(C)=d(A, В)= 2 с, = 6.
Ответ: d(A, В) =6.
Коды можно рассматривать и как некоторые геометрические (пространственные) фигуры. Например, триаду можно представить в виде единичного куба, имеющего координаты вершин, которые отвечают двоичным символам (рис. 8.1). В этом случае кодовое расстояние воспринимается как сумма длин ребер между соответствующими вершинами куба (принято, что длина одного ребра равна 1). Оказывается, что любая позиционная система отличается гем свойством, что минимальное кодовое расстояние равно 1 (рис. 8.2, а).
В теории кодирования [10] показано, что систематический код обладает способностью обнаружить ошибки только тогда, когда минимальное кодовое расстояние для него больше или равно 21, т. е.
dmin>2t, (8.4)
где t — кратность обнаруживаемых ошибок (в случае одиночных ошибок t= 1 и т. д.).
Это означает, что между соседними разрешенными кодовыми словами должно существовать по крайней мере одно кодовое слово (рис. 8.2, б, в).
В тех случаях, когда необходимо не только обнаружить ошибку, но и исправить ее (т. е. указать место ошибки), минимальное кодовое расстояние должно быть
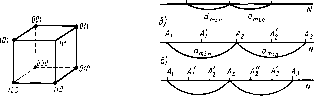
ское представление' кодов
Существуют коды, в которых невозможно выделить абсолютную избыточность. Пример таких кодов — Д-коды, где количество разрешенных комбинаций меньше количества возможных комбинаций. Неявная избыточность характерна также для кодов типа «& из /г». Примером является код «2 из 5», который часто ’используется для представления информации. Суть его в том, что в слове из пяти разрядов только два разряда имеют единичное значение.
В общем случае количество «-разрядных слов, имеющих k единичных разрядов, можно оценить по формуле (8.2).
§ 8.3. МЕТОДЫ ЭФФЕКТИВНОГО КОДИРОВАНИЯ ИНФОРМАЦИИ
Информационную избыточность можно ввести разными путями. Рассмотрим один из путей эффективного кодирования.
В ряде случаев буквы сообщений преобразуются в последовательности двоичных символов. Учитывая статистические свойства источника сообщения, можно минимизировать среднее число двоичных символов, требующихся для выражения одной буквы сообщения, что при отсутствии шума позволит уменьшить время передачи.
Такое эффективное кодирование базируется на основной теореме Шеннона для каналов без шума, в которой доказано, что сообщения, составленные из букв некоторого алфавита, можно закодировать так, что среднее число двоичных символов на букву будет сколь угодно близко к энтропии источника этих сообщений, но не меньше этой величины.
Теорема не указывает конкретного способа кодирования, но из нее следует, что при выборе каждого символа кодовой комбинации необходимо стараться, чтобы он нес максимальную информацию. Следовательно, каждый символ должен принимать значения 0 и 1 но возможности с равными вероятностями и каждый выбор должен быть независим от значений предыдущих символов.
Код строится следующим образом: буквы алфавита сообщений выписываются в таблицу в порядке убывания вероятностей. Затем они разделяются на две группы так, чтобы суммы вероятностей в каждой из групп были по возможности одинаковы. Всем буквам верхней половины в качестве первого символа приписывается 1, а всем нижним — 0. Каждая из полученных групп, в свою очередь, разбиваемся на две подгруппы с одинаковыми суммарными вероятностями и т. д. Процесс повторяется до тех пор, пока в каждой подгруппе останется по одной букве.
Рассмотрим алфавит из восьми букв (табл. 8.1). Ясно, что при обычном (не учитывающем статистических характеристик) кодировании для представления каждой буквы требуется три символа.
ности
комбинации
ности
комбинации
і=і
И среднее число символов на букву
/ср = 2 p(zi)n(zi) « 2,84,
; = і
где n(zi) — число символов в кодовой комбинации, соответствующей букве 2,.
Значения z и /ср не очень различаются по величине. Рассмотренная методика Шеннона — Фано не всегда приводит к однозначному построению кода. Ведь при разбиении на подгруппы
0,321 0,42/—J
0,101 0,101—1
— 0,061—1¦
2?
0,041
0.02/-I
разряд
можно сделать большей по вероятности как верхнюю, так и нижнюю подгруппу.
Множество вероятностей в предыдущей таблице можно было бы разбить иначе (табл. 8.2).
При этом среднее число символов на букву оказывается равным 2,80. Таким образом, построенный код может оказаться не самым лучшим. При построении эффективных кодов с основанием q>2 неопределенность становится еще больше.
От указанного недостатка свободна методика Д. Хаффмена. Она гарантирует однозначное построение кода с наименьшим для данного распределения вероятностей средним числом символов на букву.
Таблица 8.3
Для двоичного кода методика сводится к следующему. Буквы алфавита сообщений выписываются в основной столбец в порядке іедние буквы объединяются в одну приписывается суммарная вероятность. Вероятности букв, не участвовавших в объединении, и полученная суммарная вероятность снова располагаются в порядке убывания вероятностей в дополнительном столбце, а две последние объединяются. Процесс продолжается до тех пор, пока не получим единственную вспомогательную букву с вероятностью, равной единице.
Теперь, двигаясь по кодовому дереву сверху вниз, можно записать для каждой буквы соответствующую ей кодовую комбинацию:
гі 22 ¦ 2з Z4 25 2е Z7 2е
01 00 111 ПО 100 1011 10101 10100
§ 8.4. КОДИРОВАНИЕ ПО МЕТОДУ ЧЕТНОСТИ — НЕЧЕТНОСТИ
Если в математическом коде выделен один контрольный разряд {Аг = 1), то к -каждому двоичному числу добавляется один избыточный разряд и в него записывается 1 или 0 с таким условием, чтобы гумма цифр в каждом числе была по модулю 2 равна 0 для случая четности или 1 для случая нечетности. Появление ошибки в кодировании обнаружится по нарушению четности (нечетности). I Іри таком кодировании допускается, что может возникнуть только одна ошибка. В самом деле, для случая четности правильной будет юлько половина возможных комбинаций. Чтобы одна допустимая комбинация превратилась в другую; должно возникнуть по крайней мере два нарушения или четное^4исло нарушений. Пример реали-іации метода четности представлен в табл. 8.4.
Таблица 8.4
Можно представить и несколько видоизмененный способ контроля по методу четности — нечетности. Длинное число разбивается на группы, каждая из которых содержит / разрядов. Контрольные
і„.
2...
3.. .
4.. .
Увеличение избыточности информации приводит к тому, что появляется возможность не только обнаружить ошибку, но и исправить ее. Пусть произошла неисправность в каком-то из разрядов этого числа (представим, что разряд ащ изменил состояние, т. е. а 1 в = 1). Это приведет к тому, что при проверке на четность сумма s(a;+&,) по соответствующим строкам и столбцам изменится для ' значений, которые содержат элемент а|8, т. е. это будет четвертая сверху строка и третий слева столбец. Следовательно, нарушение четности по этой строке и столбцу можно зафиксировать, что в конечном счете означает обнаружение не только самой ошибки, но и места, где возникла ошибка. Изменив содержимое отмеченного разряда (в данном случае а\») на противоположное, можно исправить ошибку.
Пример 8.1. Определить и исправить ошибку в передаваемой информации вида
Для контроля использовать метод четности по строкам и столбцам (контрольный столбец 8, контрольная строка 6).
Решение. Прежде всего осуществим проверку на четность по каждой строке: ?і=0; /г2=1; &3 = 0; fc4 = 0; /г5 = 0.
Затем проверим на четность информацию по столбцам: ?6 = 0; Jfe7 = J; ?s = 0; ?9 = = 0; feio = 0; Лц = 0; &i2 = 0.
Проверка показывает, что ошибка возникла в информации второй строки и второго слева столбца. Следовательно, разряд, содержащий ошибочную информацию, находится на пересечении второй строки и второго столбца.
Ответ:
§ 8.5. КОДЫ ХЭМИНГА
Коды, предложенные американским ученым Р. Хэмингом, обладают способностью не только обнаружить, но и исправить одиночные ошибки. Эти коды — систематические.
Определить максимальное значение m для данного k можно из следующего:
Определим теперь позиции, которые надлежит проверить в каждой из k проверок. Если в кодовой комбинации ошибок нет, контрольное число содержит только нули. Если в первом разряде контрольного числа стоит 1, это означает, что в результате первой проверки обнаружена ошибка. Имея таблицу двоичных эквивалентов для десятичных чисел, мо>цно сказать, что, например, первая проверка охватывает позиции^!, 3, 5, 7, 9 и т. д., вторая проверка позиции 2, 3, 6, 7, 10.
Проверяемые разряды
1, 3, 5, 7, 9, 11, 13, 15...
2, 3, 6, 7, 10, 11, 14, 15, 18, 19, 22, 23.
4, 5, 6, 7, 12, 13, 14, 15, 20, 21, 22, 23. .
8, 9, 10, 11, 12, 13, 14, 15, 24... .
Теперь нужно’решить, какие из позиций целесообразнее применить для передачи информации, а какие — для ее контроля. Преимущество использования позиций 1, 2, 4, 8, ... для контроля в том, что данные позиции встречаются только в одной проверяемой группе символов.
В табл. 8.5 представлены примеры кодирования информации по методу Хэминга для семиразрядного кода.
Как видно из табл. 8.5, в этом случае л = 7, т = 4, і = 3 и контрольными будут разряды 1, 2, 4.
По методу Хэминга могут быть построены коды разной длины. При этом чем больше длина кода, тем меньше относительная избыточность. Например, для контроля числа, имеющего 48 двоичных разрядов, потребуется только шесть дополнительных (избыточных) разрядов. Коды Хэминга используют в основном для контроля передачи информации по каналам связи, что имеет место в вычислительных системах с телеобработкой данных или в системах коллективного пользования.
десятичная
информация
k\
*2
mi
*3
m2
Шз
т 4
Решение. Прежде всего определим контрольное число, производя проверки по правилам, указанным на с. 149: fc, = l; fe2 = 0; k3=l.
Контрольное число говорит о том, что произошла ошибка в разряде 5.
Ответ: правильная информация Л =0,111100.
Разнообразные задачи можно решать с помощью метода контроля, основанного на свойствах сравнений. Развитые на этой основе методы контроля арифметических и логических операций называют контролем по модулю.
Рассмотрим основные положения из теории сравнений.
Если целым числам А к В соответствует один и тот же остаток от деления на третье число р, то числа А и В равноостаточны друг другу по модулю р или сравнимы по модулю р:
А = B(mod р). (8.6)
Сравнения — уравнения типа (8.6).
Сравнимость двух чисел равносильна возможности представить их в алгебраическом виде
А = В + рІ- (8.7)
Сравнения обладают рядом свойств:
1. Сравнения можно почленно складывать. Если 7li = Bi(modp); /42 = B2(modp); ...; Ап == B„(modp), то А\ + Л2 + ... + Ап =В\ + + Ві + ... + B„(modp).
2. Два числа, сравнимые с третьим числом, сравнимы и между собой: если А = B(modp); С =г B(modp), то А = C(modp).
3. Сравнения можно почленно перемножить. Пусть Л,5з = Bi(modp); v42 = B2(modp). Тогда на основании (8.7) Ai — Bi + hp\ Ач = В2 -(- /2р.
После умножения получаем А\А2 — В\В2 + B\l2p + B2Up + ЫгХ ХРР- Следовательно, А\А2 ?= BiB2 -f Np, или в общем случае:
АіА2А3...Ат = ВіВ2Вз--Вт(тоёр).
Из свойства 3 также следует, что обе части сравнения можно умножить на одно и то же целое число.
Пусть А m B(modp); К = K(modp). Тогда АК = BK(modp).
4. Обе части сравнения и модуль можно умножить на одно и то же число: Л = В-Ир; Ат=Вт + трІ, т. е. Лт=Вт (modmp).
5. Обе части сравнения и модуль можно разделить на любой общий делитель. Пусть А = B(modp), где А — ad, В — bd\ Р = p\d. Тогда А = В + Ір.
Подставив в это выражение значения А, В и Р, получим
ad = bd + Ipid.
Разделив уравнение на d, имеем а == Ь + Ірі, т. е. а = fe(modpi).
6. Обе части сравнения можно возвести в степень. Если Л = B(modp), то А" = B"(modp).
Из свойства 6 следует, что над сравнениями можно произвести операцию извлечения корня п-й степени.
Рассмотренные выше свойства сравнений используются для осуществления операции контроля.
Существует два метода получения контрольного кода: числовой и цифровой.
Числовой метод контроля. При числовом методе контроля код заданного числа определяется как наименьший положительный остаток от деления числа на выбранный модуль р:
Га =А — {А/р}р, (8.8)
где в фигурных скобках {} — целая часть от деления числа; А — контролируемое число.
Величина модуля р существенно влияет на качество контроля; если р = q (q — основание системы счисления, в которой выражено число) и имеет место числовой контроль, то контролируется только младший разряд числа и контроль как таковой не имеет смысла; для р — qm справедливы аналогичные соображения, так как, если т <п, опять не все разряды числа участвуют в контроле и ошибки и разрядах старше т вообще не воспринимаются.
При числовом методе контроля по модулю р для определения остатка используют операцию деления, требующую больших затрат машинного времени. Для числового метода контроля справедливы основные свойства сравнений (сложение, умножение сравнений и т.д.). Поэтому, если А = rA (modp); B = rB(modp), где 0<гл< < р — 1; 0 < гв < р — 1, то А + В = гА + rB(modp). Отсюда
Аналогичным образом доказывается справедливость и следующих соотношений:
гА _ в = гА — rB(modp); (8.10)
rAB = rArB(modp). (8.11)
Пример 8.3. Для заданных чисел А = 125 и В = 89 определить контрольные коды самих чисел, их суммы и разности, если модуль р— 11.
Решение. Контрольные коды чисел определяем по (6.4):
Га = 125 — {125/11} 11=4; га = 89-{89/11}11 = 1.
Аналогично находим контрольные коды для суммы и разности:
А + В = 214, гл + в = 214-{214/11}11=5;
А-В = 36, гл _в = 36 — {36/11)11 =3.
Проверку правильности определения контрольных кодов суммы и разности можно произвести на основании (6.5) и (6.6):
гл+в = 4+ 1 = 5(mod 11); гл_в = 4— 1 =3(mod 11).
Ответ: гл = 4, rs=l, гл + в = 5, гл_в = 3.
Ц ровой метод контроля. При цифровом методе контроля контрольный код числа образуется делением суммы цифр числа на выбранный модуль:
г4—s®—}р
ИЛИ
г' = 2a,(modp). (8.12)
І
Возможны два пути получения контрольного кода: 1) непосредственное деление суммы цифр на модуль р; 2) суммирование цифр по модулю р.
Второй путь проще реализуется, так как если а,<р, то контрольный код получается только операцией суммирования.
Пример 8.4. Определить контрольные коды чисел /1=153 и В = 41, их суммы и разности, если р=11.
Решение. Контрольные коды исходных чисел определяем по (8.12). Для этого находим суммы цифр и делим их на модуль: 2а' = 9; 2*', = 5.
Следовательно, гА =9; г'в = 5. < ‘
Аналогично определяем контрольные коды суммы и разности:
С = А + В=194; rc = 3(modll);
?> = А —В = 112; 2d/ = 4; rb = 4(mod 11).
Ответ: rA — 9, r'B — 5, r'A + B = 3, гл_в = 4.
Пусть заданы числа А а В и соответственно их контрольные коды г а = 2а,(modp); гв = ^Ь{тоАр)\ С = А-\-В.
І
Найдем контрольный код г'с.
Видимо, когда есть результат операции, то найти г'с методом суммирования цифр подмодулю не сложно. Какова будет возможность получения Гс через контрольные коды слагаемых?
Сумму цифр Cj числа можно найти, зная цифры а, и 6, и количество переносов в каждом разряде. Каждый перенос уносит из данного разряда q единиц и добавляет одну единицу в следующий разряд, т. е. сумма цифр уменьшится на величину q — 1 на каждый перенос. Тогда
?і = І>+ t b,-l(q- 1), (8.13)
І — 1 i — 1 І = 1
где t — количество переносов, возникших при сложении.
Так как r'A = 2a;(modp); r'B = 2&,(modp), то r'c = 2c,{modp).
і і і
Подставив эти значения в (8.13), получим
г'с = [г'а + г'в — l(q — l)](modp). (8.14)
Аналогичными рассуждениями можно показать, что для разности чисел С=А — В
Гс = [гл — г'в-\- s(cj— l)](modp), (8.15)
где s — количество заемов при выполнении операции.
Пример 8.5. Определить контрольные коды чисел А =589 и В = 195, их суммы и разности, если р=11.
Решение. Контрольные коды исходных чисел определяем по (8.12). При этом используем второй путь, т. е. нахождение контрольного кода суммированием цифр но модулю:
2 а, = 5 0 8 ф 9 = 0(mod 11); гл = 0(mod И);
2 Ьі= 1 ф 9 ф 5 = 4(mod 11); rB = 4(modll).
Контрольный код суммы определяем по (8.14) — в этом случае 1 — 2:
А + В = 784; ^ + „ = 0 + 4-2(10- l)=8(mod 11).
В случае, когда имеет место отрицательный остаток, к сравнению надо добавить модуль р столько раз, сколько необходимо для получения ближайшего положительного остатка.
А — В = 394; г'а-в = 0 — 4+1(10—1) = 5(mod 11).
Ответ: г'а = 0, г’в = 4, г'А+в = 8, г'А-В = 5.
§ 8.7. ВЫБОР МОДУЛЯ ДЛЯ КОНТРОЛЯ
Достоинства числового метода контроля — в справедливости свойств сравнений для контрольных кодов, что облегчает контроль арифметических операций; в возможности достаточно просто получать контрольные коды без значительных затрат времени. Чтобы сохранить эти достоинства, необходимо выполнение условия гА — = ГА.
Так как rA=A{modp)\ гА = 2a,(modp), то 2ад'= 2a,(modp).
І
Это равенство возможно тогда, когда почленно обе части выражения равны: a,(j‘ = a,(modp), или <,‘ = l(modp).
Последнее выражение можно получить, если в сравнении q == = 1 (modp) возводить обе части в одну и ту же степень. Следовательно, q = 1 (modp), или
q = mp + 1, (8.16)
где m — целое число.
Из (8.16) следует, что
P = (q—\)/m. (8.17)
В результате получено, что для сохранения условия гА — г'А необходимо наложить ограничения на модуль р.
Анализ (8.17) показывает, что для двоичной системы счисления нет целочисленного решения. Это значит, что контролируемую информацию надо представлять в некоторой промежуточной системе счисления. Выбор промежуточной системы счисления определяется величиной модуля р.
К модулю р представляют следующие общие требования:
1) величина модуля р должна быть такой, чтобы возникновение любой арифметической или логической ошибки нарушало сравнимость контрольных кодов;
2) образование контрольного кода должно осуществляться по возможности простыми средствами;
3) величина модуля р должна быть по возможности небольшой, так как необходимость выполнения контрольных операций ведет к увеличению вспомогательного оборудования.
Ввиду того что цифровая информация в ЭВМ должна представляться символами двоичного алфавита, для контроля целесообразно перейти к системам счисления с основанием u = 2s, где s — некоторое целое положительное число (s^2). Переход от двоичного представления исходной информации к новому представлению с основанием q = 2s осуществляется разбиением информации на группы по s разрядов с последующим суммированием этих групп по модулю р==(2s— 1 )/m или при m— 1, р = 2s — 1.
Свертывание — процесс разбиения кодовой комбинации на группы и получения контрольного кода. Как правило, свертки (свернутые коды) образуются в результате суммирования выделенных групп (диад, триад и т. п.) по модулю р. В теории кодирования показано, что модуль можно выбирать из условия
p — (2f±l)/m. (8.18)
Рассмотрим частные случаи образования сверток при наиболее распространенных значениях модуля р.
1. Контроль модулю 3(от= 1, s = 2, р = 3). Здесь контролируемая информация представляется символами четвертичной системы и свертки образуются суммированием диад по модулю 3. Так как 22= l(mod3), то потребуется двухразрядный двоичный сумматор с цепью циклического переноса из старшего разряда в младший.
Пример 8.6. Найти контрольные коды для чисел А =46= 1011102, В = 29 =
= 011101 г, если р = 3.
Решение. Контрольные коды для чисел определяем по формуле (8.12) и цифры представляем диадами:
гА = 10 ф 11 © 10 = 01(mod)3;
Те = 01 ф 11 ® 01 = 10 (mod) 3.
Ответ: гл = 01, гв=10.
2. Контроль по модулю 7(m= 1, s = 3, р = 7). Здесь контролируемая информация разбивается на триады и представляется символами восьмиричной системы. Так как 23=1 (mod)7, то для получения свертки нужно иметь трехразрядный двоичный сумматор с цепью циклического переноса.
Пример 8.7. Найти контрольный код для числа С = 153 = 0111110012 при
Р = 7.
Решение. Исходное число разбиваем на триады, которые суммируются по mod 7: = 011 ф 111 ф 001 = 100(mod)7.
Ответ: /-(. = 100.
3. Контроль по модулю 5(m — 1, s — 2, р = 5). Из теории чисел известно, что для того чтобы число, выраженное в системе с основанием q, делилось на число <7+1, необходимо и достаточно, чтобы разность между суммой цифр, стоящих на четных и нечетных местах, или наоборот, делилась на величину q + 1 без остатка.
Из этого правила можно сделать следующий вывод: контрольный код по mod(<7+ 1) определяется по формуле
гА = 2 (—l)‘’b.-mod(<7 + 1), (8.19)
где Ьі — двоичное изображение цифр в системе с основанием 2s.
2°
а2
2'
s = 3 Вес о,
ап
22
0 0 0 1
00 10 000 100
который выполняется по 1а„_і ... азаг, происходит комбинации числа и кон-
Так как, по условию, rA<^.p — 1, то для получения свертки потребуется трехразрядный двоичный сумматор, работающий по модулю 5.
Пример 8.8. Найти контрольный код для числа А =0101101110 при Р = 5.
Решение. Сначала исходное число разбивается на диады:
А =01 01 10 11 10
Ьъ ЬА Ьл Ь2 Ьі
Затем диады суммируем по правилу (8.19): гА = Ь\ © Ь3 ® Ь5 ? b2 ? Ь\ = = 10 ф 10 ф 01 ? 01 ? 11 =001(mod 5).
Если получается отрицательный остаток, то его надо заменить на дополнение до модуля.
Ответ: Гл = 001.
§ 8.8. КОНТРОЛЬ ЛОГИЧЕСКИХ ОПЕРАЦИЙ
К логическим операциям относятся операции сдвига, логического сложения и умножения, выполняемые по правилам, описанным в других главах.
Несмотря на кажущуюся простоту этих правил, осуществление операций контроля сталкивается с рядом трудностей, объясняемых тем, что логические операции являются поразрядными операциями.
Операции сдвига. Пусть задано число А = а„а„_і...аіао, имеющее контрольный код гА = aks...akl.
Обозначим код чи^ла А, сдвинутый влево , через А (без циклического переноса) и Аа (с циклическим переносом) (при сдвиге вправо стрелка в обозначении будет повернута направо). Соответствующим образом обозначим и контрольный код: А = r^(mod)p; А = rA(modp)\ rj(modp); Хц = r;fu(modp).
Сдвиг влево двоичного числа эквивалентен умножению на два. Так как при сдвиге числа происходит потеря некоторых его разрядов, то можно предполагать, что контрольный код сдвинутого числа изменится на величину Л:
t~A + A(mod р), (8.20)
где ТА=2гА — сдвинутый влево контрольный код.
Величина Л зависит от значений ап и aks, которые при сдвиге выходят за пределы разрядной сетки.
Если при сдвиге «-разрядного числа старшая единица выйдет за пределы разрядной сетки, то это эквивалентно вычитанию апоп+і единиц из контрольного кода сдвинутого числа [где сгл+і — вес (п+1)-го разряда].
Если при сдвиге контрольного кода выходит за пределы разрядной сетки разряд п+=1, то это эквивалентно уменьшению контрольного кода на 2s. Такую потерю надо восстановцть прибавлением к контрольному коду единицы.
В общем случае (8.20) принимает вид
Гл = (гл — апОп+\ + a*s)mod(2s— 1). (8.21)
Ди—I dn— 2 —З-.-Чз
21 2° 22 ...22
В результате значения поправок Л для контроля выполнения левого сдвига по модулю будут:
?
Значение поправки Л можно заменить ее дополнением до модуля.
Для выполнения сдвига влево с циклическим переносом из старшего разряда в младший разряд необходимо уменьшить контрольный код на величину а„(о„+1 —1); так как оп+і=1, то этот член равен 0. Следовательно, формула (8.21) примет вид
гАи = ТА -+- aks mod (2s — 1). (8.22)
Пример 8.9. Найти контрольные коды для числа А = 1,01011010, сдвигаемого влево, при р = 7 (s = 3).
Решение. Сначала определяем контрольный код исходного числа путем сложения триад по модулю 7: гА з= 101 ф 011 ф 010 = 011 (mod 7).
Затем сдвигаем влево число Л^=0,10110100 и его контрольный код 7^ = 110.
На основании (8.21) при a„=l, ak= 0 определяем контрольный код сдвинутого числа: 110—1+000= 101(mod 7).
Производится сдвиг с циклическим переносом: = 0,10110101, для которого
контрольный код гД7, = 110 + 000= 110(mod 7).
При сдвиге вправо происходит потеря младших разрядов числа и контрольного кода этого числа. Так как сдвиг вправо эквивалентен делению на 2, то
а = (Л-9,)/2; fA —(гА — aks)/2. (8.23)
Эти потери надо компенсировать. Это означает, что контрольный код сдвинутого вправо числа-можно найти по формуле
г+=?І + Л(mod 2s—1). (8.24)
В зависимости от модуля поправка к контрольному коду в случае простого сдвига принимает следующее значение:
Значение щ . Значение а. Поправка Д для: р = 3 . . . р = 7 . . .
При модифицированном сдвиге вправо, правилу Л=1, а„_і, а„_2... агао; Х=1, также потеря младших разрядов кодовой
0
1
01
001
1
1
10
100
00
000
(8.25)
суммы двух чисел; гл — инверсия кон-произведения двух чисел со сдвигом
трольного кода. Для этого случая формула (8.24) сохраняет вид, но поправки должны быть следующими:
Поправка Ам для:
Пример 8.10. Найти контрольные коды для числа Л = 1,01110111101, сдвигаемого вправо, при р = 7.
Решение. Сначала определяем контрольный код для исходного числа путем сложения триад по модулю 7: гА = 101 ф 110 ® 111 0 101 =(mod 7). Затем сдвигаем вправо число Д = 0,10111011110 и его контрольный код 7^ = 001.
На основании (8.24) при оі = 1; а*, = 0, поправки Л —011 определяем контрольный КОД: гд^зООІ +011 = 100(mod 7).
Производим модифицированный сдвиг числа Л„ = 1,10111011110, для которого контрольный код находим при Л = 000: гл); = 001+000 = 001(mod 7).
Ответ: гА = 010, г^=100, гд*„ = 001.
Операция сложения по модулю 2. Операцию сложения по модулю 2 можно выразить через другие арифметические операции, например: А © В — А + В — 2(А Д В).
Если применить к этому выражению уже известные приемы, то получим А © В=(А + + А Д Всдв.
Тогда, используя переход от арифметических выражений к сравнениям, получим следующую формулу для образования контрольного кода:
г® = га+в + Гд (mod р),
где гА+в — контрольный код трольного кода логического влево на один разряд.
Пример 8.11. Найти контрольный код логической суммы чисел А=0100001іГи В~ 101110011 по модулю 7.
Решение. Прежде всего по изложенным выше правилам определим контрольные коды для исходных чисел: гА = 010, гй = 000, гА + 8 = 010.
Затем вычислим следующие величины: А Д 5=000000011, гЛ = 011; А Д Вс„, = = 000000110, Г,= 110.
После этого определим инверсное значение гЛ =001.
По формуле (8.25) находим контрольный код: г? =010 + 001 =01 l(mod 7). Ответ: гда = 011.
Операция логического умножения. Операцию логического умножения двух чисел можно выразить через другие арифметические и логические операции: А Д В=2~\А-\-В) — -2-1 (А® В).
Умножение на 2 1 означает сдвиг кода числа, стоящего в скобках, вправо на один разряд. После перехода к сравнениям контрольный код для логического умножения получается по формуле
г л =ГаТв + (mod р), (8.26)
где гА+в — контрольный код суммы, сдвинутый вправо на один раз-158
При выполнении сдвигов необходима коррекция контрольных 'кодов в соответствии с изложенными выше правилами.
Пример 8.12. Найти контрольный код логического произведения чисел по модулю 3: А = 10011001, /-л = 00, В = 0,001111, гв = 01.
Решение. Прежде всего найдем сумму чисел и контрольный код: А А-В — = 11101000, гА + в = 01.
Затем по 8.24 вычислим r.rps + Д = 10. Определим: А © В = 11010110, г®=01, + Д= 10, r-5f=01. Следовательно, контрольный код логического произведения гЛ = 10 -(— 10 s= 00(mod 3).
, Ответ: Гд = 00. ?
§ 8.9. КОНТРОЛЬ АРИФМЕТИЧЕСКИХ ОПЕРАЦИЙ
Арифметические операции выполняются на сумматорах прямого, обратного и дополнительного кодов. Предположим, что изображения чисел (операнды) хранятся в машине в некотором коде, т. е. операция преобразования в заданный код или обратно производится на выходе или входе машины. Методика реализации операций контроля представляется следующим образом.
Прежде всего рассмотрим изображение числа в соответствующем коде как единую кодовую комбинацию, к которой можно приложить все сформулированные выше правила получения сверток. При этом требуется только обязательная кратность общего числа разрядов избранному модулю.
Рассмотрим последовательность действий на примере сумматора прямого кода.
Так как на сумматоре прямого кода складываются только цифровые части изображений чисел, а знак сохраняется, то контроль можно осуществить двумя способами:
1) раздельный контроль знаковой и цифровой частей изображений результата;
2) обобщенный контроль всего изображения.
При раздельном способе для контроля знаковых разрядов можно использовать средства для обнаружения переполнения, так как в случае модифицированного кода появление ошибок в знаковых разрядах приведет к несовпадению информации в них. При проверке правильности обработки цифровых частей изображений также не возникает особых трудностей.
При обобщенном способе контроля требуется коррекция контрольного кода результата из-за того, что знак результата при сложении повторяет знак слагаемых. Следовательно, можно констатировать, что контрольный код суммы чисел должен быть
г(А+в)„р = rA + rB-Sg-Gs(mod р), (8.27)
где Sg — значение знакового разряда операндов; os — вес старшего разряда свертки.
Решение. Прежде всего определим по (8.12) контрольные коды исходных чисел: гл = НО, гв=101. Результат операции [Л+В]пр= 1,10011101. Тогда контрольный код результата по (8.12) ^+ fl= 110® 011 ф 101(mod7), или гл + 8 = 000.
На основании (8.27) находим г(/1+в)прз^ 110+ 101 — 1 • 100(mod 7), или +
Контрольные коды совпадают, что свидетельствует о правильном выполнении операции.
Ответ: гА + а — 000.
Обобщенный способ контроля может быть применен и для сумматоров обратного и дополнительного кодов.
Пример 8.14. Произвести контроль операции сложения кодов для сумматора обратного кода: [Л]об= 1,011001001; [В]об = 0,110001111, р = 3.
Решение. Определяем на основании (8.12):
гАоб= 10 ф И® 00© 10 ф 01 (mod 3); гАо6= 10, гяОб = 01 © 10© 00 © 11 © 11 (mod 3); гдоб = 00.
Результат: (Л + В)об = 0,001011001 и гІА f Я)об= 10.
Проверка: г(А + вы = гАо6 + гВоб = 10(mod 3).
Ответ: г(Л + В) = 10.
При сложении чисел на сумматоре дополнительного кода потребуется коррекция контрольного кода в случае, если знаковые разряды изображений содержат единицу, так как при этом возникает единица переноса из знакового разряда. Очевидно, что контрольный код суммы будет равен
7(л+в) = б4д.+ гВд — а, (8.28)
где а — коррекция (а=1, если возник перенос из знакового разряда, и а=0 — если переноса нет).
Пример 8.15. Произвести контроль операции сложения на сумматоре дополнительного кода: [Л]д= 1,00110001110; [В]д= 1,11101110111, р= 15.
Решение. Определим;
/+ = 1001© 1000© 1110(mod 15), гЛд = 0001, гВд = 1111 © 0111 © 0111 (mod 15), гВд = 1110.
Далее по результату операции определим контрольный код: [Л + В]д = = 1,00100000101 и г(Д + /,)= 1001 ©0000 ©0101 (mod 15), ли + в)=1110.
Проверка: г(в+В) = гИд + гВд—а = 0001 + 1110 — 0001 = 1110.
Ответ: Г(А + в) = 1110.
В случаях, когда операции преобразования в обратный или дополнительный код производятся в процессе вычислений, целесообразна проверка этих преобразований.
Рассмотрим операцию преобразования из прямого кода в обратный.
Пусть [А] „р = anan-\...а,а0—исходное число, представленное в прямом коде, для которого определяется остаток гА == = [т1]пр(тос1/о). Подобные выражения можно записать для обратного кода Гао6 = [Л]об (mod р) и инвертированного изображения ГА = [А] (mod р).
Тогда
[Д] = а„2п + Л'; (8.29)
[Л]об = а„2" +Л', (8.30)
гДе Л' — инвертированное изображение цифровой части числа.
Из (8.30) вычтем (8.29):
[Л]06 — [Л] = (а„ — а„)2п. (8.31)
Левую часть равенства (8.31) заменим сравнениями; rAo6—rA = &=(an—an)2n(modp).
Так как а„=1, то а„=0, следовательно, гАоб—гд = 2" (mod р).
Пусть 2" = fe(mod р). Тогда
0o6 = 0 + /e(mod р). (8.32)
Выражение (8.32) дает возможность найти контрольное число для обратного кода при известных значениях величины р:
п ... 5 8 10 15 18 20 25 30 40 р = 3 ... 2 1 1 1 112 1 1 р = 7. ..4 4 2114 212
Пример 8.16. Осуществить контроль преобразования числа А в обратный код: [+]„„= 1,01110010, р = 7.
Решение. Определяем следующие величины и соответствующие им контрольные коды:
[4]обР= 1,10001101, Гдоб= 101; [Л] = 0,10001101, гд = 001.
По (8.32) находим лЛо6 = гд + 6 = 001 + 100=101, где 6 = 100, так как л = 8.
Ответ: гдоб= 101.
Операцию преобразования в дополнительный код можно осуществить, используя соотношение (3.30) между обратным и дополнительным кодами: дополнительный код отличается от обратного на единицу младшего разряда. Следовательно, контрольное число можно получить из выражения
7+ = 7д k 1 (mod р). (8.33)
Рассмотренную выше методику определения контрольных чисел для таких операций, как умножение, или таких операций, как деление, можно применить для контроля работы ЭВМ, используя операционный контроль (контролем охватываются исходные числа и конечный результат) или шаговый контроль (проверяются все элементарные действия автомата при выполнении операции).
§ 8.10. АРИФМЕТИЧЕСКИЕ КОДЫ
: Контроль по модулю, рассмотренный ранее, позволяет эффективно обнаруживать одиночные ошибки. Однако одиночная ошибка в одном разряде может привести к группе ошибок в нескольких разрядах (например, ошибка в цепи циклического переноса). Поэтому целесообразно найти средства, которые позволяют обнаруживать не только одиночные ошибки, но и пакеты ошибок, которы? могут встречаться, например, при записи или считывании информации с магнитной ленты или магнитного диска. Для этого используются арифметические коды.
Арифметическим кодом 1-го вида будем называть код AN, где А — контролируемое число, N — модуль. Для таких кодов несколько изменяются понятия «расстояния» и «веса».
Весом арифметического кода принято считать количество ненулевых символов в кодовой комбинации, а расстояние, определяемое как вес разности кодовых комбинаций, называют арифметиче-\ ским расстоянием.
Если расстояние между двумя числами А\ и А2 равно d, то это означает, что переход от одного числа к другому достигается прибавлением величины d. В этом случае все комбинации чисел, находящиеся между А\ и А2, являются запрещенными. Следовательно, для обнаружения d-кратной ошибки необходимо иметь расстояние не меньше d+l. Если d—l, то такой код не сможет обнаруживать ошибок. Величина расстояния для кодов А-У?-вида зависит от величин А и N.
Предполагается (и это доказано в теории кодирования [10]), что для любого числа А в системе основания q—2 существует единственное представление вида
Aq = an- 2" —|—йп—1 • 2" 1°о, (8.34)-
где а(=±1 или 0, и в котором нет двух соседних коэффициентов, отличных от нуля.
Представление (8.34) содержит минимальное число ненулевых коэффициентов и называется каноническим. В каноническом представлении вес любого числа, начиная с 2'+1 и вплоть до числа 2‘+2‘“1, на единицу больше, чем вес чисел от 1 до 2'~'. Вес чисел, начиная с 2‘+2‘~1-]-1 и вплоть до 2,+ |, совпадает с весом чисел 2‘+2‘_1 — 1, 2‘+2‘-1—2 и т. д.
Количество разрядов для представления числа А • N равно log2 (А • У?)= log2 А + log2 У?, где log2 N — избыточность кода. Таким образом, выбор модуля определяет не только избыточность, но и расстояние. В качестве модуля целесообразно выбирать некоторое взаимно простое с основанием системы q число, превосходящее само основание. Можно положить, что для двоичной системы У?=3, и тогда любой код вида А-3 будет обнаруживать все одиночные ошибки. Следовательно, минимальная избыточность при произвольном основании определяется как log,(<7+l), т. е. всегда будет требоваться не менее одного, но и не более двух дополнительных разрядов.
Коды с минимальным расстоянием, большим двух, характеризуются величиной Mq{N, d). Величина Mq(N, d)— наименьшее число, которое при умножении его на N дает число, вес которого меньше d в представлении по основанию q. Другими словами, если число N имело вес d в представлении по основанию q, то произведение NMq(N, d) будет иметь вес меньше d по этому же основанию q.
В теории кодирования доказано, что
М2(У?, 3)=(2(Л/_|)/2-Ь 1)/І?. (8.35)
Основной способ для отыскания значения Mq — способ непосредственных вычислений. Рассмотрим его на конкретном примере.
Решение. Возьмем код с расстоянием 3. Тогда возможны случаи:
B — (2N~l —1)/У?. (8.36)
Рассмотрим B-N-код.
Число знаков в кодовом слове га=У?—1. Возьмем некоторое число /(0<1/<А). Тогда
1-В = Ьп- \ •2л~1 6„_2 • 2"~2 + ... +/>о, (8.37)
где 6, = (/-2л_1 mod A) mod 2.
И действительно: У?=11, В=(1024— 1)/11 = 93. Если /=10, то
/•В = 930 = 1-29 + 1-28 + 1-27 + 0-26 + 1 -25 + 0 - 24 + 0 - 23 +
+ 0-22 + 1-21 +0-2°.
Проверим коэффициенты bt по формуле (8.37) :
6о = (Ю-210 mod 11) mod 2 = 0; b i = (10-29 mod 1 l)mod 2=1;
62 = (10-28 mod 11) mod 2 = 0;
63 = (10-27 mod 1 l)mod 2 = 0;
Ьъ = (320 mod 11) mod 2= 1; fe6 = (160 mod 11) mod 2 = 0; fr7==(80mod ll)mod2=l;
68 = (40mod 11) mod 2= 1; bg = (20 mod 11) mod 2 = 1.
Итак, десятичное число 10 в двоичном представлении имеет вид 1010, в А-У?-коде будет иметь вид ІЮНЮ, а в B-N-коде при N— 11, В—93 число 10 будет представлено в виде 1110100010.
При использовании В-У?-кода коэффициенты 6, можно вычислять сразу же, не раскладывая числа в многочлен ?>, = (/-2'1~1mod/l)mod 2; n=N—1 известно заранее, так как B—(2N~l—1 )/N вычисляется через N.
Таким образом, при изображении числа / в B-N-коде половина знаков равна единице, а половина — нулю. Это следует из выражения
Ьі = {1• 2"~‘ mod N) mod 2,
так как 2 и N взаимно простые числа, значит остатки от деления чисел 2' на У? — целые числа от 1 до N—1. Так как число N — нечетное, то количество остатков — всегда четное число, а значит половина из остатков числа нечетные, а половина — четные числа. Следовательно, половина остатков по mod 2 дали единицу, а половина — нуль.
Пример 8.18. Пусть JV = 11, В = 93. Найти изображения чисел / от 1 до 10 в В -У?-коде.
Решение. Количество символов для изображения чисел в 93-Л(-коде =
Арифметический вес числа в В-У?-коде равен (У?— 1) /3, либо (У?-}-1)/3 в зависимости от того, какое из этих чисел целое (У?>3).
В случае В-У?-кодов по известному N можно не только определить количество символов и их вид, но и заранее определять арифметическое расстояние, что непосредственно влияет на корректирующие способности кода.
Существуют еще самодополняющиеся (А-ЛУ+В) коды. В этом случае код для дополнительного числа N — дополнительный код самого числа А.
qn-\-(A-N+B) = N(b-\-A)+B,
дополнение кодового числа код дополнительного числа
B=[qn— 1 —N(b— 1) ] /2.
Код возможен только при целых В.
Расстояния для (А-У?-f-B) кода те же, что и для А-У?-кода.
Пример 8.19. Пусть нужно найти (А ¦ N В)-двоичный код для кодирования десятичных знаков, исправляющий одиночные ошибки.
Решение. Возьмем 6 = 10. Чтобы исправлять одиночные ошибки, нужно иметь код с кодовым расстоянием d = 3.
Так как если 0^Д<АІ2(Л/, d), то при любых N и q расстояние 4-У?-кода равно по меньшей мере d.
По таблице ищем Mi(N, 3)> 10 (так как А — десятичный знак, т. е. от 1 до 9): М2(У?, 3) = 27, при этом /?=19. Наибольшее число в этом случае равно 19-9=171, для него потребуется по крайней мере 8 двоичных знаков (11010101).
Из формулы В = [у'1— 1 — N{b—1)]/2 получим: В = (28 — 1 — 19 - 9)/2 = 42.
A -JV + В = 9-19 + 42 = 213<28 (нужно 8 знаков двоичных, значит код возможен).
Окончательно таблица кодирования имеет такой вид:
Рассмотрим несколько случаев применения описанных выше кодов.
1. Пусть А\-\-Ад< 10, т. е. нет переноса в кодовых словах. Тогда N-А, + В + У?-А2 4- В = АУ(А, + А2) + 2В. Отсюда видно, что нужна поправка «—В».
Пример 8.20. Сложить числа А і и А2 в коде А ¦ N В, если 7? = 19, В —42 {А і =3, 4 г = 4).
Решение.
4,=3= ,01100011 42 = 4= ' 0111 ОНО
1101 1001 — запрещенная комбинация 00101010
/11-|-Л2 = 7= 1010 1111 —разрешенная комбинация, соответствует числу 7
,0110 0011 '''ОШ ОНО
1100 1001 —запрещенная комбинация 0010 1010
,1001 1111 —запрещенная комбинация наиболее близка к 1010 1111 1
1010 1111
Ответ: Л, +Л2= 1010 1111.
2. Пусть Аі-\-А2^\0. Тогда
N-Ai + B + N-A2 + B = N(Ai+A2)+2B=\0N + k-N + 2B.
уйдет в перенос
Следовательно, при переносе в старшее кодовое слово нужно добавить поправку -)-(Л— 1). В том слове, откуда происходит перенос, нужно сделать поправку —(N—1+В).
Пример 8.21. Сложить числа А|=328 и А2=563, N = 19, В=42.
Здесь N— 1 = 18(100102).
Решение.
А,= ,[328J=, 0110 0011 0101 0000 1100 00Ю
Л2=+[563] = ~~ 1000 1001 10011100 01100011
-)- В)-кодов необходимо умножить число на N, где N — простое число, прибавить В\ для представления четырехзначных чисел по величине используют восемь разрядов (см. пример. 8.21), помимо этого приходится осуществлять коррекцию (ввод поправок) при сложении, затем сравнение полученных комбинаций с эталонными, а затем производить исправление ошибок, если такие имеются. Но и (А ¦ N + В) -коды не всегда позволяют определить точное местоположение ошибки.
Проиллюстрируем вышесказанное на примере сложения двух чисел А\ и А2.
Аі= , ОНО ООП А2 +0111 оно
1100 1001 0010 1010
1001 1111 1010 1111 — ближайшая разрешенная
несовпадение комбинация
в 2-х разрядах
0010 1010 і~0001 0010 -г0001 0010
11000010 _1111 1111 0001 ООН
'-g-' 0010 1010 + 0010 1010
1101 0101 ООП 1101 9 І
Пусть при сложении произошли ошибки (они указаны знаком х~):
0110 0011 0101 0000 1100 0010
1000 1001 10011100 0110 0011
_1010 1100 _1110 1100 Ш100101
0010 1010 0010 1010 0001 0010
а) _1110 1001
“0010 1010
1011 1111 —запрещенная комбинация
б) _1101 1001
0010 1010
1010 1111 —соответствует эталонной комбинации
11000010 11010101 00111101 образец
Ответ: А,+А2= 1100 0010 1101 0101 ООП 1101.
Сравнив результат с образцом разрешенной комбинации, можно определить местоположение ошибки.
В современньіх вычислительных машинах используется контроль на четность и нечетность. Этот контроль позволяет лишь зафиксировать наличие ошибки, но не позволяет ее исправить. Но он нашел широкое применение благодаря своей простоте, так как и наличие информационной избыточности требует применения контрольной
,1100 0010 +01100011
1010 0101 — переноса не произошло 0010 1010
0111 1011 —вся комбинация запрещенная, отличается от разрешенных на три разряда
,1100 0010 "*"01100011
ЗАЩИТА ИНФОРМАЦИИ
Электронно-вычислительная машина часто входит как составная часть в системы обработки информации в виде систем коллективного пользования, либо вычислительных сетей. В таких случаях предъявляются достаточно жесткие требования по надежности и достоверности передаваемой информации.
Как было показано в гл. 1, любой канал связи характеризуется наличием в нем помех, приводящих к искажению информации, поступающей на обработку. С целью уменьшения вероятности ошибок принимается ряд мер, направленных на улучшение технических характеристик каналов: использование различных видов модуляции, расширение пропускной способности и т. д. При этом также принимаются меры по защите информации от ошибок или несанкционированного доступа. Доступ — получение возможности использовать информацию, хранящуюся в ЭВМ (системе).
Всякая информация в машине или системе требует той или иной защиты, под которой понимается совокупность методов, позволяющих управлять доступом выполняемых в системе программ к хранящейся в ней информации. Существуют методы физической защиты каналов связи, каналов передачи информации, помещений, где обрабатывается информация (например, экранирование).
Задача защиты информации в информационных и вычислительных системах решается, как правило, достаточно просто: обеспечиваются средства контроля за выполнением программ, имеющих доступ к хранимой в системе информации. Для этого используются либо списки абонентов, которым разрешен доступ, либо пароли. Это обеспечивает защиту информации при малом количестве пользователей. Однако при широком распространении вычислительных и информационных систем, особенно в такие сферы, как обслуживание населения, банковское дело и т. п., этих средств явно недостаточно. Система, обеспечивающая защиту информации, не должна разрешать доступ к данным пользователям, не имеющим такого права. Такая система защиты — неотъемлемая часть любой системы коллективного пользования средствами вычислительной техники, независимо от того, где они используются. Данные экспериментальных исследований различных систем коллективного пользования .показали, что пользователь в состоянии написать такие программы, которые дают ему доступ к любой информации, находящейся в системе. Как правило, это обусловлено наличием каких-то ошибок в программных средствах, что порождает возможность обхода установленных преград.
1. Простота механизма защиты. Так как средства защиты усложняют и без того уже сложные программные и аппаратные средства, обеспечивающие обработку данных в ЭВМ, то естественно стремление упростить эти дополнительные средства. Чем лучше совпадает представление пользователя о системе защиты с ее фактическими возможностями, тем меньше ошибок возникнет в процессе работы.
2. Разрешения должны преобладать над запретами. Нормальным режимом работы считается отсутствие доступа; механизм защиты основан на условиях, при которых доступ разрешается. Допуск дается лишь тем пользователям, кому он нужен.
3. Проверка полномочий любого обращения к любому объекту информации. Это означает, что защита выносится на общесистемный уровень и предполагает, что абсолютно надежно определяется источник любого обращения.
4. Разделение полномочий. Для любой программы и любого пользователя в системе определяется минимальный круг полномочий. Это позволяет уменьшить ущерба от сбоев и случайных нарушений и сокращает вероятность непреднамеренного или ошибочного применения полномочий.
5. Трудоемкость проникновения в систему. Фактор трудоемкости зависит от количества проб, которые нужно сделать для успешного проникновения. Метод прямого перебора вариантов может дать результат, если для анализа используется сама ЭВМ.
6. Регистрация проникновений в систему. Иногда считают, что выгоднее регистрировать случаи проникновения, чем строить сложные системы защиты.
§ 9.2. АППАРАТНЫЕ СРЕДСТВА ЗАЩИТЫ
Аппаратные способы шифрования информации применяются для передачи секретных данных по телекоммуникационной сети. Для реализации шифрования с помощью смешанного алфавита используется перестановка отдельных разрядов в пределах одного или нескольких символов.
На рис. 9.1 показана схема аппаратного шифрователя, использующего операцию перестановки разрядов в пределе одного байта информации. Для расшифровки сообщений применяется симметричная перестановка. Блок перестановки может быть сменным или управляемым. Блок управления БУ синхронизирует работу шифровального устройства. Возможное число перестановок для п-разряд-
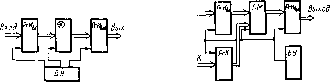
рователя
Для шифрования с помощью ключевых слов применяется операция сложения по модулю 2 (исключающее ИЛИ). Схема такого шифрования показана на рис. 9.2.
Ключевое- слово хранится в 64-разрядном регистре ключа РгК. Информация, подлежащая шифрованию, записывается в 64-раз-рядный регистр информации РгИвх. После заполнения этого регистра выполняется операция сложения по модулю 2 с содержимым регистра ключа. Результат представляет собой зашифрованную информацию, которая поступает в выходной 64-разрядный регистр РгИвых.
На практике используют несколько чередующихся операций запутывания и сложения по модулю 2 с различными ключами. Пример такой схемы приведен на рис. 9.3. Блок управления на рисунке не показан.
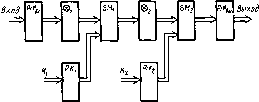
Ключевые слова для работы схем шифрования выбираются с помощью специальных генераторов случайных чисел и передаются в приемное устройство в зашифрованном виде по предыдущим ключам. Дешифрование информации выполняется в обратной последовательности.
§ 9.3. ПРОГРАММНЫЕ СРЕДСТВА ЗАЩИТЫ
Программные способы применяются для шифрования информации, хранящейся на магнитных носителях, которая может быть представлена в различных информационно-справочных системах АСУ, АСОД и пр. Программные способы шифрования сводятся к операциям перестановки, перекодирования и сложения по модулю 2 с ключевыми словами. При этом используются команды ассемблера TR (перекодировать) и ХС (исключающее ИЛИ).
Особое место в программах обработки информации занимают операции кодирования. Преобразование информации, в результате которого обеспечивается изменение объема памяти, занимаемой данными, называется кодированием. На практике всегда используется кодирование для уменьшения объема памяти.
Естественные языки обладают большой избыточностью. Не составит большого труда исправить все ошибки, которые есть в следующей фразе: «Есл нсклко бкв удлть, эт прдлжн ещ м б прчтно». Для экономии памяти, объем которой ограничен, имеет смысл ликвидировать избыточность текста или уплотнить текст.
Существует несколько способов уплотнения текста.
Переход от естественных обозначений к более компактным. Этот способ применяется для сжатия записи дат, номеров изделий, уличных адресов и т. п. Идея способа показана на примере сжатия записи даты. Часто мы записываем дату так: 22.09.83, что требует 6 байт памяти ЭВМ. Однако ясно, что для представления дня достаточно 5 бит, месяца — 4, года — не более 7, т. е. вся дата может быть записана в 16 бит, или в 2 байт.
Другой распространенный способ представления дат был предложен Жозефом Скалигером в 1582 г. дл^астрономических целей. По этому способу дата записывается как общее число дней, прошедшее к данному дню, считая с 1 января 4713 г. до н: э. По этой схеме 1 января 1983 г. записывается как 2 444 323. Обычно для реальных расчетов ограничиваются четырьмя последними цифрами этого представления. 24 мая 1967 г. записывается в виде 0000, и: отсчет дней от этой даты требует 16 бит в упакованном десятичном формате.
Подавление повторяющихся символов. В различных информационных текстах часто встречаются цепочки повторяющихся символов, например пробелы или нули в числовых полях. Если имеется группа повторяющихся символов длиной более трех, то ее длину можно сократить до трех символов. Сжатая таким образом группа повторяющихся символов представляет собой триграф SPN, в котором S — символ повторения; Р — признак повторения; N — количество символов повторения, закодированных в триграфе.
В других схемах подавления повторяющихся символов используют особенность кодов ДКОИ, КОИ-7, КОИ-8, заключающуюся в том, что большинство допустимых в них битовых комбинаций не используется для представления символьных данных. Обычно в коде ДКОИ не используются комбинации с нулем во второй
ХОХХХХХХ
Признак повторяемости
Кодирование часто используемых элементов данных. Этот способ ; уплотнения данных также основан на употреблении неиспользуемых комбинаций кода ДКОИ. Для кодирования, например, имен людей : можно использовать комбинации из двух байт диграф PN, где Р — признак кодирования имени; ІУ — номер имени. Таким образом может быть закодировано 256 имен людей, что обычно бывает ; достаточно в информационных системах. Если в байте N старший байт использовать в качестве признака пола, то можно этим байтом \ закодировать 128 мужских и 128 женских имен.
1 Другой способ основан на отыскании в тексте наиболее часто , встречающихся сочетаний букв и даже слов и замене их на неис-; .пользуемые байты кода ДКОИ.
, Посимвольное кодирование. Семи- и восьмибитовые коды не . обеспечивают достаточно компактного кодирования символьной і шнформации. Более пригодны для этой цели 5-битовые коды, на-Гпример международный телеграфный код МГК-2. Перевод информации в код МГК-2 возможен с помощью программного перекодирования или с использованием специальных элементов на основе больших интегральных схем (БИС). Пропускная способность каналов связи при передаче алфавитно-цифровой информации в коде МГК-2 повышается по сравнению с использованием восьмибитовых кодов почти на 40%.
Использование кодов переменной длины. Коды с переменным числом битов на символ позволяют достичь еще более плотной .упаковки данных. Метод заключается в том, что часто используемые символы кодируются короткими кодами, а символы с низкой частотой использования — длинными кодами. Идея такого кодирования была впервые высказана Хаффменом и соответствующий код называется кодом Хаффмена. Использование кодов Хаффмена позволяет достичь сокращения исходного текста почти на 80%.
ЛОГИЧЕСКИЕ ОСНОВЫ ЦИФРОВЫХ АВТОМАТОВ
Понятие автомата было введено в гл. 1 в качестве модели для описания функционирования устройств, предназначенных для переработки дискретной информации.
Для формального описания цифрового автомата широко применяют аппарат алгебры логики, являющейся одним из важных разделов математической логики.
Основное понятие алгебры логики — высказывание. Высказывание — некоторое предложение, о котором можно утверждать, что оно истинно или ложно. Например, высказывание «Земля — это планета Солнечной системы» истинно, а о высказывании «на улице идет дбждь» можно сказать, истинно оно или ложно, если указаны дополнительные сведения о погоде в данный момент.
Любое высказывание можно обозначить символом х и считать, что х = 1, если высказывание истинно, а х — 0 — если высказывание ложно.
Логическая (булева) переменная—такая величина х, которая может принимать только два значения: х = {0,1}.
Высказывание абсолютно истинно, если соответствующая ей логическая величина принимает значение х = 1 при любых условиях. Пример абсолютно истинного высказывания — высказывание «Земля — планета Солнечной системы».
Высказывание абсолютно ложно, если соответствующая ей логическая величина принимает значение х = 0 при любых условиях.
Например, высказывание «Земля — спутник Марса» абсолютно ложно.
Логическая функция (функция алгебры логики) — функция f(xі, 2, ¦ хп), принимающая значение, равное нулю или единице на наборе логических переменных х\, хч, ..., хп.
Логические функции от одной переменной представлены в табл. 10.1.
Функция /з(т), повторяющая значения логической переменной, — тождественная функция (/3(х) = х), а функция fi(x), принимающая значения, обратные значениям х,—логическое отрицание, или функция НЕ (fi(x) =Пх = х).
Логические функции 4 от двух переменных представлены в табл. 10.2.
Дизъюнкция (логическое сложение) — функция f8(x і, х2), которая истинна тогда, когда истинны илц хі, или х2, или обе переменные.
Дизъюнкцию часто называют также функцией ИЛИ и условно обозначают так: f8(xi, хч) = х\ + хч = х\ V хч.
От дизъюнкции следует отличать функцию f7(xі, хч), которая называется функцией сложения по модулю 2 (функцией разно-именности) и является истинной, когда истинны или х\, или хч в отдельности. Условное обозначение этой функции f7(xі, хч) = = Х\ -© х2.
которая истинна только тогда, когда и хі, и *2 истинны. Конъюнкцию часто называют также функцией И; условно обозначают так: Ь(хі, х2) = Х\Х2 = Х1&Х2 = х\ Дх2.
Пример 10.1. Имеются два высказывания: «Завтра будет холодная погода», «Завтра пойдет снег».
Дизъюнкция этих высказываний — новое высказывание: «Завтра будет холодная погода или пойдет снег». Соединительный союз, который образовал новое предложение, — ИЛИ.
Конъюнкция образуется следующим образом: «Завтра будет холодная погода и пойдет снег». Это высказывание образовано с помощью союза И.
Штрих Шеффера — функция /\ъ(х\, х2), которая ложна только тогда, когда х\ и х2 истинны. Условное обозначение функции Щеф-фера: /15(хі, х2) = хі/х2.
Немецкий математик Д. Шеффер на основе этой функции создал алгебру, названную алгеброй Шеффера.
Функция Пирса (Вебба) —функция /э(хі, х2), которая истинна только тогда, когда х\ и х2 ложны. Условное обозначение этой функции: f9(x 1, Х2) = Х\)Х2 = XtOX2.
Математики Ч. Пирс и Д. Вебб, независимо друг от друга изучавшие свойства этой функции, создали алгебру, названную алгеброй Пирса (Вебба).
Импликация — функция /и(хі, х2), которая ложна тогда и только тогда, когда хх истинно и х2 ложно. Условное обозначение: fu(X\, Х2) — X) х2.
Все логические функции, приведенные в табл. 10.2, — элементарные функции.
Две функции равносильны друг другу, если принимают на всех возможных наборах переменных одни и те же значения:
fі(хі, х2 ... х„)— f2(x 1, х2 ... х„).
Булевы переменные могут быть действительными или фиктивными. Переменная х; действительна, если значение функции f(x 1, ... х„ ... хп) изменяется при изменении х,. Переменная х, фиктивна, если значение функции f(xі„ ... xf, ... х„) не изменяется при изменении Х;.
Пример логической функции от трех переменных представлен в табл. 10.3.
Из таблицы видно, что переменные хі и х2 — действительные, а переменная хз — фиктивная, так как f(x 1, х2, 0) = /(хі, х2, 1) для всех наборов X,, х2. Таблица 10.3
Так как число значений переменных х, ограничено, то можно определить количество функций N от любого числа переменных п: N = 22".
Рассмотрим некоторые практические примеры использования алгебры логики.
Пример 10.2. В школе произошла неприятная история: разбито окно в одном из классов. Подозревают четырех учеников: Леню, Диму, Толю и Мишу. При опросе каждый из детей сделал по три заявления:
Леня:
1) я не виноват — Ль
2) я не подходил к окну — Л2;
3) Миша знает, кто разбил, — Л3.
Дима:
1) стекло разбил не я — Ді;
2) с Мишей я не был знаком до поступления в школу — Д2;
3) это сделал Толя — Д3. V
Толя:
1) я не виноват—Ті;
2) это сделал Миша — Т2;
3) Дима говорит неправду, утверждая, что я разбил окно, — Т3.
Миша:
1) я не виноват — Мj;
2) стекло разбил Леня — М2;
3) Дима может поручиться за меня, так как знает меня со дня рождения, — М3.
В дальнейшем все признали, что одно из трех заявлений является неверным.
Это пригодится при построении более сложных формул, поскольку показания каждого ученика в целом истинны только при условии, что два заявления истинны, а одно ложно. Используя элементарные логические функции, можно описать показания всех учеников в таком виде:
Л=ЛіЛіЛз + Л|Л2Л3-|- Л|Л2 л3
Д=Д1Д 2Д3 4- Д1Д 2Дз + Д1Д 2Д з;
Т=Т1Т2Т3 + Т1Т2Т3-|-Т1Т2Тз; м = МіМ2Мз + МіМ2Мз + М,М2Мз.
Теперь остается решить эту систему уравнений и определить, какие показания истинны. Для этого надо упростить выражения, используя аксиомы.
Рассмотрим третье уравнение. По условию, Т| = Т3, а значит Ті = Т3, но TiTt =0, ТіТі = Тi или Т = Т|Т2. Поэтому оно верно тогда, когда Ті = 1; Т2 = 0. Значит, Толя не виноват и Миша не виноват. Отсюда следует, что Д3 ложно, т. е. Д3=0 (Д3=1). Следовательно, Д = ДіД2Д3. Отсюда Д, = 1; Д2=1. Дима не виноват.
Д2 противоположно Мз, т. е. Д2—М3* Значит, М3 = 0 или M = M,M2M3. Оно верно только тогда, когда М| = 1; М2=1.
Ответ: стекло разбил Леня.
Пример 10.3. Предположим, что имеется система кондиционирования воздуха для помещения, где установлена ЭВМ, состоящая из двух кондиционеров малой и большой мощности и работающая при таких условиях: кондиционер малой мощности включается, если температура воздуха в помещении достигает 19°С; кондиционер большой мощности включается, если температура воздуха достигает 22°С (малый кондиционер при этом отключается); оба кондиционера включаются при температуре воздуха 30°С.
Пусть информация о температуре воздуха поступает от датчиков, которые срабатывают при достижении температуры соответственно 19, 22, 30°С. Каждый из этих
Таблица описывает функционирование системы управления без нарушений работы.
Впервые теория Дж. Буля была применена П. С. Эренфестом к анализу контактных цепей (1910). Возможность описания переключательных схем с помощью логических формул оказалась весьма ценной по двум причинам. Во-первых, с помощью формул удобнее проверять работу схем. Во-вторых, задание условий работы любой переключательной схемы в виде формул упрощает процесс построения самой переключательной схемы, так как оказалось, что существует ряд эквивалентных преобразований, в результате которых логические формулы упрощаются. При списании переключательных схем замкнутое состояние контакта принимается за истинное высказывание, а разомкнутый — за ложное, поэтому последовательное соединение контактов можно рассматривать как функцию И, а параллельное — как функцию ИЛИ.
Использование логических функций оказалось особенно полезным для описания работы логических элементов ЭВМ.
§ 10.2. СВОЙСТВА ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ АЛГЕБРЫ ЛОГИКИ
Из табл. 10.2 видно, что элементарные функции типа отрицания, дизъюнкции, конъюнкции, Шеффера, Пирса, импликации и т. д. находятся в определенной связи друг с другом. Рассмотрим эти связи и свойства исходных функций.
Конъюнкция, дизъюнкция, отрицание (фун к-ции И, ИЛИ, НЕ). Используя основные положения алгебры логики, нетрудно убедиться в справедливости следующих восьми аксиом. Пусть х — некоторая логическая переменная. Тогда
2. х + х = х; хх = х — правила подобных преобразований, которые позволяют сокращать длину логических выражений;
3. х + 0 = х;
4. х + 1 = 1;
5. х0 — 0;
6. х-1 = х;
7. хх = 0;
8. х + х = 1.
Дизъюнкция и конъюнкция обладают рядом свойств, аналогичных свойствам обычных арифметических операций сложения и умножения:
1) свойство ассоциативности (сочетательный закон):
х\ + (х2 4- *а) = (х\ + х2) + х3, Хі(х2х3) = (хіх2)х3;
2) свойство коммутативности (переместительный закон):
Х\ -(- х2 = х2 -|- Хи х\х2 = х2х\;
3) свойство дистрибутивности (распределительный закон):
для конъюнкции относительно дизъюнкции
Х\ &(х2 + Х3) == (хі &х2) + (х2&х3);
для дизъюнкции относительно конъюнкции
Хі + *2*3 = (*1 + *2>&(*1 + Хз).
Свойство дистрибутивности фактически определяет правила раскрытия скобок или взятия в скобки логических выражений.
Справедливость указанных свойств легко доказывается с помощью вышеизложенных аксиом.
Докажем, например, что
Х\ Н- х2хз = (хі 4- *2)&(хі + Хз).
В самом деле, (х\ + х2){хі + х3) = хіх, + х\х3 4- *і*2 + *2*3 = = Х\ -(- ХіХ2 -(- ХіХз 4- Х2Хз = 2Сі(1 -J- Х2 4" Хз) -(- х2хз.
Аналогично можно доказать и другие законы.
Несложно установить правильность соотношений, известных как законы де Моргана:
Х\Х2 — Хі 4- х2 , (10.1)
Хі 4- Х2 = ХіХг .
Из законов де Моргана вытекают следствия
хіх2 = хі + х2 . (Ю.2)
Х\ + х2 = Хі х2 ,
с помощью которых появляется возможность выражать конъюнк-
Законы де Моргана и следствия из них справедливы для любого количества переменных:
Х\ —(— ЛГ2 Хп = Хі &... &хп , ( 10.3)
Х\Хч ... Хп = Хі Х2 ...-Ь Хп ¦
Для логических функций устанавливаются соотношения, известные как законы поглощения:
X1 -j- ’X} Х2 = Хі , Х\{Х\ + Х2) = Хі
В табл. 10.4 показана справедливость законов поглощения.
Т аблиц.а 10.4
Функция сложения по модулю 2 — функция, выражаемая еле- , дующим образом:
Х\ ® Х2 = Х\Х2 + Х\Х2 = (Хі + Х2)(Хі + Х2) • (10.5) j
Функция сложения по модулю 2 обладает следующими свойст- j вами:
коммутативности (переместительный закон):
х\ ® Х2 — Х2 ? Хі ; ассоциативности (сочетательный закон):
хі ф (Х2 0 хз) = (хі 0 х2) 0 хз ; дистрибутивности (распределительный закон):
Хі(х2 © Хз) == (Х1Х2) © {х\Хз).
Для этой функции справедливы аксиомы:
хфх = 0; хф1=х; хфх==1; х ® 0 = х .
На основании аксиом и свойств можно вывести правила перевода функций И, ИЛИ, НЕ через функцию сложения по модулю 2 и наоборот: *, = х, 0 1 ;
Хі + х2 = Хі ф х2 0 Х1Х2 ;
Х1Х2 — {хі ф Х2) Ф {хі + х2) -
Для функции импликации справедливы аксиомы:
х ->- х = 1; х —>- 1 = 1; 0 -> х = 1;
х -*¦ х = х; х —0 = х; 1 -> х = х.
Из аксиом следует, что импликация обладает только свойством коммутативности (переместительный закон) в измененном виде: Х\ -*¦ Х2 = Х2 -> Хі.
Свойство ассоциативности для этой функции не справедливо (табл. 10.5).
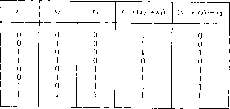
хіх2 = хі -> х2 ; (Ю.7)
Хі = хі 0.
Функция Шеффера (/) — функция, которая может быть выражена соотношением хі/х2 = хіх2.
Для нее характерны аксиомы:
х/х = х; х/х = 1; х/0 = 1;
х/1==х; х/0=1; х/1=х.
Для функции Шеффера справедливо только свойство коммутативности
хг/х2 = х2/хі,
однако для трех переменных и более
хі /(х2/хз) ф (хі /х2)/х3.
Для проверки справедливости свойства ассоциативности рассмотрим функцию трех переменных: (хі/х3)/х2 = (хі/х2)/х3.
Применяя правила преобразования для правой части выражения, находим (хі/х2)/х3 = (хТх2)х3 = хі-х2 + Хз-
І0, если номер набора не равен і. Например, F\ = xix2x3x4; F0 — xix2x3.
Соответственно то же самое находим для левой части выражения (хі/х3)/х2 = (xTxl)x2 = ХіХз + Х2. Следовательно, свойство ассоциативности не справедливо для трех переменных, а значит оно не справедливо и для п переменных.
При рассмотрении свойств дистрибутивности для функции Шеффера будем иметь в виду, что:
хі(х2 + х3) = (хі-х2) + (хіх3);
Х\ + (х2Х3) = (Хі 4- Х2)(Хі + Хз).
Приведем два примера преобразования выражений. Преобразуем выражение хі/(х2/х3), используя аксиому х==х/1:
Хі(х2Х3) = Х\ + Х2Хз = {х\ -f JC2)(Jci + Хз) =
= хі/х2&хі/х3 = хі/(х2/1)&хі/(х3/1) = [хі/(х2/1)/хі/(х3/1)]/1. Преобразуем выражение (хі/х2)/(хі/х3):
(XiX2)(XlX3) = XlX2 -f- Х\Хз — Х\{х2 + Хз) == Хі(х2Хз) =
= х, [(х2/1)/(хз/1)] = х, / [(х2/1 )/(хз/ 1)Т = {X, / [(х2/1 )/(хз/1)] } /1.
На основании этих двух примеров можно сделать вывод, что свойство дистрибутивности не справедливо для трех переменных, а значит и для п переменных.
Из основных свойств можно получить формулы преобразования:
ІХіХ2 = Хі/х2 — хі/х2/хі/х2; х = х/х; (10.8)
Xl + х2 = Хі -х2 = xi/x2 = xi/xi/x2/x2.
Функция Пирса (Вебба) (\ ) — функция, которая описывается выражением х\ \х2 = хі + х2 = хіх2.
Для этой функции легко показать справедливость аксиом:
1 х \ х = х;
2 х \ 0 = х;
3 х \ х = 0;
4 х I 1=0.
На основании аксиом можно показать, что для функции Пирса (Вебба) справедливо только свойство коммутативности: х\ \ х2 — = х2\ Хі.
Функции И, ИЛИ, НЕ выражаются через функцию Пирса (Вебба) следующим образом:
/ хіх2 = (хі I Хі) \ (x2 )• x2);
I x + x2 = (xi j x2) I (xi \ x2); (10.9)
[ x = x I x.
Существует много способов задания логических функций. Ранее был рассмотрен табличный способ, при котором каждому набору значений переменных в таблице истинности указывается значение самой логической функции. Этот способ нагляден и может быть применен для записи функций от любого количества переменных. Однако при анализе свойств функций алгебры логики (ФАЛ) такая запись не является компактной. Проще выглядит аналитическая запись в виде формул.
Рассмотрим фиксированный набор переменных (хі, х2 ... х„}, на котором задана функция алгебры логики. Так как любая переменная х, = {0, 1), то набор значений переменных фактически представляет собой некоторое двоичное число. Представим, что номером набора будет произвольное двоичное число і, получаемое следующим образом:
і = 2п 1 хі -|- 2™ 2х2 -Г 4~ хл. (10.10)
Пусть имеется функция Ф,(хі,х2, ..., х„):
ф І0, если номер набора равен і,
1 11, если номер набора не равен і.
Функцию Ф, называют термом.
Дизъюнктивный терм (макстерм)—терм, связывающий все переменные, представленные в прямой или инверсной форме, знаком дизъюнкции (иногда в литературе используется термин «конституэнта нуля»).
Например, Ф7 = хі V х2 V х3 V х4; Ф2 = хі V х2.
Конъюнктивный терм (минтерм) — терм, связывающий переменные, представленные в прямой или инверсной форме, знаком конъюнкции (иногда в литературе используется термин «конституэнта единицы»). Обозначается минтерм следующим образом:
F,={
Ранг терма г определяется количеством переменных, входящих в данный терм. Например, для минтерма Ею = хіх2х3х4Х5 г = 5, и для макстерма Ф2 = хі + х2 + х3, г = 3.
На основании вышесказанного можно сформулировать следующую теорему.
Теорема. Любая таблично заданная ФАЛ может быть представлена аналитически в виде
f(x,,x2, ...,х„) = Е, \J F2\/ ...V Fn= У Ft, (10.11)
1
где i — номера наборов, на которых функция равна 1; V -знак дизъюнкции, объединяющий все термы Е„ равные единице.
f(xI, Х'2, x3) = F(0, 0, ОІ + ИО, 1, 1 ) + /=¦( 1, 0, 0) = ХіХ2Х:і + ХіХ2Хз + ХіХ2Хз.
1
1
1
1
1
1
Нормальная дизъюнктивная форма (НДФ) —объединение термов, включающее минтермы переменного ранга.
Количество всех термов, входящих в состав (10.11), равно количеству единичных строк таблицы.
Пример 10.4. Записать в аналитическом виде функцию, заданную табл. 10.6.
Ответ: І(хі, х2, х3) = Х\Х2Х3 +хіх2х3-\-хіХ2Х3.
Для представления ФАЛ в (10.11) используется совокупность термов, объединенных знаками дизъюнкции (V или Можно использовать также другую элементарную логическую операцию. Сформулируем основные требования к этой операции.
Требование 1: если какой-либо терм F-t = 1, то функция f должна быть равна единице.
Требование 2: если какой-либо терм Д = 0, то функция может быть равна единице.
Необходимо, чтобы при значениях термов Fi=0 функция / была равна нулю.
Таблица 10.7 Таблица 10.8
Таким образом, получили, что искомой функцией, кроме функции ИЛИ, может быть функция разноименности и при этом справедливым становится такое следствие из теоремы (10.11):
Следствие: любая таблично заданная ФАЛ может быть представлена в следующей аналитической форме:
f(xh х2, ... x„)=FiAF2A ... AFk, (10.12)
где знак Д обозначает операции *?, 0.
Требования 1 и 2 можно обобщить и потребовать, чтобы аналитическое представление нулевых и единичных строчек таблицы различалось и чтобы выполнялось взаимно однозначное соответствие между нулевой единичной строкой и термом.
Требование 3: если какой-либо терм Ф, = 0, то функция f должна быть равна нулю.
Требование 4: если все термы Ф,= 0, то функция /=1.
Выполняя эти требования, можно прийти к двум другим возможным функциям: конъюнкции и равнозначности (табл. 10.9 и 10.10).
Таблица 10.9 Таблица 10.10
Теорема. Любая таблично заданная ФАЛ может быть задана в аналитической форме:
f(xі, х2, .. ,*„)=Ф1&Ф2& ... &Фк, (10.13)
где k — количество двоичных наборов, для которых5 Ф = 0.
Нормальная конъюнктивная форма (НКФ) —объединение термов (10.13), включающее в себя макстермы разных рангов.
Следствие: любая таблично заданная ФАЛ может быть представлена в аналитической форме:
f(xI, Х2, ... х„) = Фі =Ф2 = ... = фА( (10.14)
где k — количество нулевых значений функции.
§ 10.4. СОВЕРШЕННЫЕ НОРМАЛЬНЫЕ ФОРМЫ
Нормальные конъюнктивная, дизъюнктивная формы не дают однозначного представления функции. Такое представление получается только при совершенных нормальных формах (СНФ).
Если Xj
Таблица 10.11
Ответ: f(Xi, х2, хз) = ха2хз +хіх2х3 + хіх2хз.
Введем обозначения х°=х, х' — х.
Тогда в общем виде переменная может быть задана как некоторая функция
х, если а=1; х, если а = 0,
при этом
ха = ах + ах, (10.16)
где а — двоичная переменная.
Рассмотрим конъюнкцию вида х?1 х|2 ... *л", где (си, а2 ... а„} представляет собой двоичный набор; число наборов равно 2", т.е.
0 0 ... 0 0 0 0 0 ... 0 0 1 0 0 ... 0 1 0 . 0 0 ... 0 1 1
и т. д.
Если задать всем а, значение 0 и 1, то можно получить, например, дизъюнкцию вида
?х?1*? *?" = *1*2 Х°пУх\х% ... x'nVx ?Х2 ... лгі— lJCnV ... Vx(x2 ... x'n,
1 (10.17)
где V — символ обобщенной дизъюнкции по единичным строкам. Тогда справедлива следующая теорема.
Теорема. Любая ФАЛ может быть представлена в виде
f(x\X2...Xk..,Xn)='Vxal‘xf ...xtf(ai...akXk+i...Xn). (10.18)
Выражение (10.18) называют разложением функций алгебры логики по k переменным.
Доказательство. Прежде всего определим, при каких условиях выполняется равенство х“ = 1.
Очевидно, что это имеет место при х=а. В самом деле, если х = а, то аа = аа+аа = а + а=1; если х = а, то a“ = aa+aa = = aa = 0.
С учетом того, что х“=1 при х=а, можно утверждать, что конъюнкция вида хЧ'хг1 ... *?" равна единице при Xi = cti, х2=а2...х„= = а„.
Эти равенства можно подставить в правую часть выражения (10.18). В результате ухТхг2 ... х%*/(хіх2 ... xk ... *n)=f(*i*2---*fe---*n),
что и требовалось доказать.
Следствие 1: если k = \, то функция алгебры логики представляется в виде
f(xь *2, x„)=xif(l, х2 ... х„)?хі/(0, х2... Хп). (10.19)
Следствие 2: если k = n, то любая ФАЛ может быть представлена в виде
f(xi, х2, ... xn)=Vxf'x“2* ... x“„\ (10.20)
Рассмотрим основные свойства СНДФ:
в СНДФ нет двух одинаковых минтермов;
в СНДФ ни один минтерм не содержит двух одинаковых множителей (переменных);
в СНДФ ни один минтерм не содержит вместе с переменной й ее отрицание.
На основании этих свойств можно предложить следующий алгоритм получения СНДФ из таблицы истинности:
1. Положить номер строки вг таблице г=1, номер элемента в строке /= 1.
2. Выбрать из таблицы набор с номером і. Если f,— 1, то перейти к п. 3, если — к п. 5.
3. Сформировать терм F-,. Выбрать элемент строки с номером j.
(ГО, то Fi: = Fi/\Xj, (1, то Fi : = Fi/\Xj.
4. Вычислить /: = /4-1. Если і<Сп, то перейти к п. 3, если і^п, — к п. 5.
5. Вычислить г': = г -(-1. Если і<2", то перейти к п. 2, если і~^2п,— к п. 6.
6. Конец.
Рассмотрим СНФ для других функций.
Пусть имеется терм вида Ф,=х1]'V *г2 V V *?", где
ф ГО, если номер набора равен г;
1 (1, если номер набора не равен і.
Если х,=а; и а, — текущий элемент двоичного набора, то тогда
(Х;=0
a,= 1
хТ = Х; = 0
4) Хі=\ а ,= 1 а, = 0
2) Хі—0
щ== 1
3) Хі = 1 а, = 0 а, = 1
1) х,=0
а-, = 0 Х?і‘ = Хі= 1
Теорема. Любая ФАЛ, кроме абсолютно истинной функции, может быть представлена в совершенной конъюнктивной нормальной форме (СКНФ):
f(x, Х2, ... х„)= Л (*Т V xf V ... V 4")- (10.21)
Для представления логической функции используются операции И, ИЛИ, НЕ (Л, V, 1). •
Следствие: любая ФАЛ, кроме конституэнты 1, может быть представлена в виде
f(n, х2,...д„)==(4'?4!?-?Й). (10.22)
Здесь используются операции неравнозначности, дизъюнкции, отрицания ( = , V. П).
Пример 10.6. Найти СКНФ для функции (см. табл. 10.11).
Решение. Решение проводится по формуле (10.21)
f(x 1. *2, Х3)=(Х| ?й? Хз) (Xt V *2 V Хз) (х, V Х2 V Хз) А (Х| V *2 V Хз) (Х| V *2 V *з).
Это представление более громоздкое, чем представление этой функции в СНД<К так как в таблице много строк, для которых f = 0.
В рассмотренных ранее объединениях термов были использованы для записи термов Ftj и Ф1; операции ИЛИ, НЕ, а также И, НЕ. Можно использовать также набор из импликации (->-) и отрицания (НЕ).
Способы преобразования НФ в СНФ. Совершенная нормальная форма отличается от нормальной формы (НФ) тем, что всегда содержит термы только максимального ранга и дает однозначное представление функции.
Произвольная нормальная дизъюнктивная форма (НДФ) переводится в СНДФ следующим образом.
Пусть /НФ = Еь Тогда
/снф = Fixi V Fixh (10.23)
где Хі — переменная, которая не входит в данный терм Ft.
Пример 10.7. Логическую функцию, заданную в НДФ
/(Хі, Х2, хз, X4) = XtX2\/ Х2Х3Х4\/ ХіХ3Х4\/ ХіХ2ХзХ4,
Ft F2 F3 F4
преобразовать в СНДФ.
Решение. Воспользуемся приемом преобразования (10.23) поочередно к термам: Ft =Xix2(jc3 V хз)=хіх2хз V *1X2*3.
Оба члена полученного выражения умножим на (х4 V х4).
В результате получим
Fі= X1X2X3X4 V х,х2хзх4 V х,х2х3х4 V х\х2хзх4.
Аналогично,
F2=X2X3X4(Xt V Х\) — Х\Х2ХзХ4 V Х\Х2ХзХ4,
F3 = XlX3X4(x2 V Х2) = Х\Х2ХзХ4 V ХіХ2ХзХ4.
_ Ответ: ?(*і,_ х2, хз, х4)=х\х2хзх4 V Xtx2x3x4 V хіх2х3х4 V xtx2x3x4 V х\х2х3х4 V V ХіХ2ХзХ4 V ХіХ2ХзХ4 V XtX2X3X4.
Если максимальный ранг для функции равен г, а минималь-ный_ранг у-го терма равен k, то преобразование (10.23) необходимо применить к /-му терму (г — k) раз.
Произвольная НКФ переводится в СКНФ путем следующего преобразования.
Пусть /нкф = Ф\- Тогда
^снкф — Фі V ХіХі (Фі V Хі)(Ф 1 V Хі). (10.24)
Пример 10.8. Преобразовать в СКНФ логическую функцию f(x 1, Х2, Хз)=(х\ V х2) (х2 V Хз) (Х| ? Х2 V Хз).
Ф1 Ф2 Ф з
Решение. Применяем правило преобразований (10.24) поочередно к термам Ф1 и Ф2:
Фі=(хі ? Х2) ?хзХз=(хі ? х2? хз)(хі V х2 ? Хз);
ф2 = (х2 ? Хз) V XtXt =(xt ? х2 ? Хз) (Хі V Х2 ? Хз).
После упрощений СКНФ примет окончательный вид.
Ответ: )скнф(хі, х2, х3) = (х, V х2 V *з) (хі V х2 V хз) (хі V Х2 V Хз).
§10.5. СИСТЕМЫ ФУНКЦИЙ АЛГЕБРЫ ЛОГИКИ
Рассмотрим теорему Жегалкина, которая играет важную роль в алгебре логики.
Теорема Жегалкина. Любая булева функция может быть представлена многочленом вида f(x 1, х2... хп) = ko 0 ?1*1 Ф ? k2x2 0 ... 0 kn+\X\x2 ф kn+2x\X3 ф ... ф kn+mx\x2xn, где ki — коэффициенты, принимающие значения 0 или 1.
Теорема Жегалкина дает возможность представить любую логическую функцию в виде полиномов разной степени.
Существует несколько классов ФАЛ, которые также важны для логического анализа.
Класс линейных функций (Кл). Булева функция называется линейной, если она представляется полиномом первой степени:
f(X], Х2, ... Хп) = ko 0 kiX\ ф k2X2 ф ... ф knxn.
Количество линейных функций равно 2"+1. Например, для п = 2 количество линейных функций равно восьми, т. е.
1) f\(xi, х2) = 0; 2) f2(xt,x2) = xi; 3) f3(xi, х2) = х2;
4) f4(xi, х2) = хі ф х2, 5) f5(x\,х2)= 1 ф х;
6) f6(xkx2)= 1 ф х2; 7) f7(xі,х2)= 1 ф хі ф х2;
8) fB(x 1, х2)=1.
Класс функций, сохраняющих нуль (Ко). Если функция на нулевом наборе переменных равна нулю, то говорят, что функция сохраняет нуль: до, 0, ..., 0) = 0.
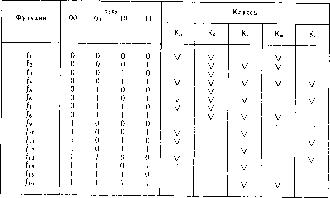
Класс функций, сохраняющих единицу (Кі). Если функция на единичном наборе переменных равна единице, то говорят, что такая функция сохраняет единицу: f(l, 1,... 1)= 1. Для двух переменных ТаКИМИ ФУНКЦИЯМИ ЯВЛЯЮТСЯ f2, f 4, f 6, fe, flO, f 12» f 14, f 16 (см. табл. 10.12).
Класс монотонных функций (К«). Функция алгебры логики называется монотонной, если при любом возрастании набора значения этой функции не убывают. Примером таких функций для двух переменных являются функции fi, f2, f4, fs, fs, fu (см. табл. 10.12).
Класс самодвойственных функций (К;) - Функция алгебры логики является самодвойственной, если на каждой паре противоположных наборов она принимает противоположные значения, т. е.
f(.X 1, Х2, ...,Хп) —- f(x 1, Х%, ...,Хя) .
Для двух переменных такими функциями являются /4, fs, fu, fіз.
Все названные выше классы функций обладают замечательным свойством: любая функция алгебры логики, полученная с помощью операции суперпозиции и подстановки из функций одного класса, обязательно будет принадлежать этому же классу.
Базисом называется полная система ФАЛ, с помощью которой любая ФАЛ может быть представлена суперпозицией исходных функций.
ФАЛ была полной, необходимо и достаточно, чтобы она содержала хотя бы одну функцию: не сохраняющую нуль, не сохраняющую единицу, не являющуюся линейной, не являющуюся монотонной, не являющуюся самодвойственной.
В табл. 10.12 представлены свойства функций двух переменных.
К базису относится система^ функций И, ИЛИ, НЕ (базис 1), свойства которых были изучены Дж. Булем. Поэтому алгебра высказываний, построенная на основе этих функций, названа булевой алгеброй. Базисами являются также системы, содержащие функции И, НЕ (базис 2), ИЛИ, НЕ (базис 3), состоящие из функции Шеффера (базис 4) и функции Пирса (Вебба) (базис 5). Это перечисление показывает, что базисы могут быть избыточными (базис 1) и минимальными (базисы 4 и 5).
Базис минимальный, если удаление хотя бы одной функции превращает систему ФАЛ в неполную.
Проблема простейшего представления логических функций сводится к выбору не только базиса, но и формы наиболее экономного представления этих функций.
Базис И, ИЛИ, НЕ является избыточной системой, так как возможно удаление из него некоторых функций. Например, используя законы де Моргана, можно удалить либо функцию И, заменив ее на функции ИЛИ и НЕ, либо функцию ИЛИ, заменив ее на функции И и НЕ.
Если сравнить в смысле минимальности различные формы представления ФАЛ, станет ясно, что нормальные формы экономичнее совершенных нормальных форм. Но, с другой стороны, нормальные формы не дают однозначного представления.
Минимальная форма представления ФАЛ -- форма представления ФАЛ, которая содержит минимальное количество термов и переменных в термах (т. е. минимальная форма не допускает никаких упрощений).
Например, функция f(xі, x2t ... х„) = х\ + х2 является минимальной формой и, наоборот, функция х\ -f х\х2 может быть упрощена, если к этому выражению применить распределительный закон, т. е. Хі + Х,Х2 = (Х, + Хі)(Хі + х2) — Хі + х2.
Следовательно, упрощение сложных логических выражений может быть осуществлено по основным законам и аксиомам, изложенным выше.
Пример 10.9. Упростить функцию f(A, В, С) = АВ-{-ВС-\-ВС-\-АВ в базисе 1.
Решение. Сначала применим правило (10.23), а затем упростим функцию.
f(A, В, С\=АВ + ВС + ВС(А+А) + АВ(С + С) = АВ+ВС + АВС + АВС + АВС + + АВС = АВ(\+С) + ВС(\+А) + АС(В + В) = АВ + ВС + АС.
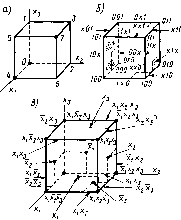
* 3

1------
X/
1
1
у
Пример 10.10. Упростить функцию f(A, В, С, D) = AB-\-C-\-ACD-\-BCD в базисе 1.
Решение. Нетрудно доказать, что х-\-ху = х-\~У-- Используя также теорему де Моргана, получим х-\-у = ху:
Тогда C + ACD = C + AD: C + BCD = C + BD. _
Следовательно, f(A, В, С, D)=AB + С + AD + BD = AB + D(A + В)+ С= = AB + DAB-\-C = AB + C+J>-
Ответ: {(А, В, С, D) = AB + C+D.
§10.6. ЧИСЛОВОЕ И ГЕОМЕТРИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ФУНКЦИЙ АЛГЕБРЫ ЛОГИКИ
Часто для упрощения записи функций алгебры логики вместо полного перечисления термов используют номера наборов, для которых функция принимает единичное значение. Например, функция, заданная табл. 10.5, может быть записана в виде }(хі, х2, хз) = = у Е(0, 3, 4); это означает, что функция принимает значение 1 на
наборах, номера которых равны 0, 3 и 4. Такую форму записи называют числовой.
Многие преобразования, выполняемые над булевыми функциями, удобно интерпретируются с использованием их геометрических представлений. Так, функцию двух переменных можно интерпретировать как некоторую плоскость, заданную в системе координат хі,х2 (рис. 10.1). Отложим по каждой оси единичные отрезки х\ и х2. Получится квадрат, вершины которого соответствуют комбинациям переменных. Из такого геометрического представления функций двух переменных следует: две вершины, принадлежащие одному и тому же ребру и называемые соседними, «склеиваются» по переменной, меняющейся вдоль этого ребра.
Таким образом, правила склеивания для минтермов можно записать для функции трех переменных в следующем виде:
*1X2*3 + *1*2*3 = *1*2-
Пример 10.11. Определить соседние минтермы и применить правило склеивания:
Решение. В соответствии с определением выпишем пары соседних термов: [і и /з; /2 и /4; )і и /5; /з и /4.
Применим правило склеивания к этим парам) получим новые термы.
Ответ:
*1*2X3 + -СіЛГг-іСз ==лгілг2;
XIX2X3 + * 1 *2X3 = X1 *2;
*1X2X3 + *і*2хз=хіх3;
*|*2*3 + *1*2*3 = *2*3-
Функция четырех переменных представляется уже в виде четырехмерного куба (рис. 10.3). В геометрическом смысле каждый набор хі*2... хп может рассматриваться как л-мерный вектор, определяющий точку n-мерного пространства. Исходя из этого все множество наборов, на которых определена функция п переменных, представляется в виде вершин n-мерного куба. Координаты вершин куба должны быть указаны в порядке, соответствующем порядку перечисления переменных в записи функций. Отметив точками вершины, в которых функция принимает значение, равное единице, получим геометрическое представление ФАЛ.
Терм максимального ранга принято называть 0-кубом (точкой) и обозначать К0.
Например, для f(x 1, х2, хз) = V (0, 4, 7)
*4! ? ?}¦
Если два 0-куба из комплекса К0 различаются только по одной координате, то они образуют 1-куб (отрезок): /('={*0 0}, где х — независимая координата.
Таблица 10.13
#12
#23
#123
#12
#23
#123
#12
0—
-ce
#123
#12
#123
#12
#23
#123
#123
. ш
к 123= 1,
/,00 I /,100_I .
#23 “Г #123— 1,
,00 . .010 ,
#із+ #123 = 1;
,00 . .00 , .000 ,
#13+#23 + #123= 1 •
Если два 1-куба имеют общую независимую компоненту и различаются только по одной координате, то они образуют 2-куб.
Таким образом, для построения одномерного единичного куба берут два 0-куба (точки) и соединяют отрезком прямой. Двумерный куб (грань) получается, если вершины двух 1-кубов соединить параллельными отрезками. Трехмерный куб получается при соединении соответствующих вершин двух двумерных кубов отрезками единичной длины. Геометрическое представление будет использовано при разработке методов минимизации с использованием минимизирующих карт.
§10.7. МЕТОД НЕОПРЕДЕЛЕННЫХ КОЭФФИЦИЕНТОВ ДЛЯ БАЗИСА И —ИЛИ —НЕ
На основании теоремы Жегалкина любую логическую функцию можно представить в нормальной форме. Например, пусть функция /С*і, *2, хз) записана в виде следующей нормальной дизъюнктивной формы (НДФ):
f(x 1, Х2, Х3) = k\x\ “Г ft?Xi kiXi “Г Й2Х2 4* кзХз “Г fe“x3 -f-4" ^ 12X1X2 4~ k\%X\X2 + Й12Х1Х2 4“ fe?2XiX2 4- к\зХ\Хз 4~
4~ /г 13X1X3 -)- 3X1X2 /г“3X1X3 4~ ^23X2X3 -Г 23X2X3 -Г /г“3X2X3 Д-
+ й^°х2Хз + k\llx\x2X3 + к 123X1 x'qX'3 + k\°2lx\x2x3 + (10.25)
4~ ЙІ23Х1Х2Х3 -f- /г!“3X1X2X3 4* /2123X1X2X3 -f- ^“23X1X2X3 4~
+ ^“23X1X2X3 -Г ^“23X1X2X3 ,
где f'fk1 — неопределенные коэффициенты, принимающие значение 0 или 1 и подбираемыел-ак, чтобы получающаяся после этого НДФ была минимальной.
Критерий минимальности — минимальное количество букв в записи НДФ. При определении НДФ пользуются следующими свойствами: хі + х2 + ... + х„ = 0, если х( = х2 = ... = х„ = 0, хі + Х2 + ... + хя = 1, если хотя бы один член уравнения равен' единице.
к\ 4~ к% 4~ к% 4" ^І2 4~ к\з 4~ кіз 4" ?12“ = /4(1,0, 0)
к\ 4~ к% 4- кз 4- к\% 4~ ?із 4~ &гз 4~ ^ігз = fb (1,0, 1)
k\ 4- k>2 4- *8 4- к\12 + Ді§ 4- kl2°3 + k\l2°3 = /в(1,1, 0)
к\ 4~ кг 4" кз 4- к\1 4" &1з 4" ^23 4~ к\1з == (1, 1, 1).
Если fi = 0 на соответствующем наборе переменных, то все коэффициенты, входящие в данное уравнение, равны нулю. Тогда в остальных уравнениях системы (10.26) надо вычеркнуть члены, содержащие нулевые коэффициенты, а из оставшихся уравнений, равных единице, найти коэффициенты, определяющие конъюнкцию наименьшего ранга в каждом из уравнений.
Выбрать очередную строку, в которой f/ = 0. Все коэффициенты этой строки приравнять нулю.
2. Если все нулевые строки просмотрены, то перейти к п. 3, если нет, то к п. 1.
3. Просмотреть строки, в которых /, = 1, и вычеркнуть из них все коэффициенты, встречающиеся в строках, где /, = 0.
4. Переписать все модифицированные уравнения.
5. Выбрать очередную строку fi — 1 и вычеркнуть максимально возможное количество коэффициентов так, чтобы ранг остающихся членов был минимальным.
Метод неопределенных коэффициентов наиболее применим для дизъюнктивной формы и практически непригоден для конъюнктивной формы.
Пример 10.12. Найти минимальную форму для функции
f(x 1, Х2, Хз)=?(0, 2. 4> 7)=*іХ2Хз + ХіХ2Хз + ХіХ2Хз + ХіХ2Хз.'
Результат: Ліз= 1; k23 = 1_; к!23 =} ¦
Ответ: f(xі, х2, хз)=хіх3 + х2хз + х 1X2X3.
термы
(ООП)
(0100)
(0111)
Импликанта функции — некоторая логическая функция, обращаемая в нуль при наборе переменных, на котором сама функция также равна нулю.
Поэтому любой конъюнктивный терм, входящий в состав СНДФ, или группа термов, соединенных знаками дизъюнкции, яв.4яются импликантами исходной НДФ.
Первичная импликанта функции — импликанта типа элементарной конъюнкции некоторых переменных, никакая часть которой уже не является импликантой.
Задача минимизации по методу Квайна состоит в попарном сравнении всех импликант, входящих в СНДФ, с целью выявления возможности поглощения какой-то переменной:
FХі V Fii = F. (10.27)
Таким образом, удается снизить ранг термов. Эта процедура проводится до тех пор, пока не останется ни одного члена, допускающего поглощение с каким-либо другим термом. Термы, подвергшиеся поглощению, отмечаются. Неотмеченные термы представляют собой первичные импликанты.
Полученное логическое выражение не всегда оказывается минимальным. Поэтому исследуется возможность дальнейшего упрощения. Для этого составляется таблица, в строках которой записываются найденные первичные импликанты, а в столбцах указываются термы исходного уравнения. Клетки этой таблицы отмечаются в случае, если первичная импликанта входит в состав какого-либо терма. После этого задача упрощения сводится к тому, чтобы найти такое минимальное количество первичных импликант, которые покрывают все столбцы.
Метод Квайна выполняется в несколько этапов, рассмотрим его применение на конкретном примере.
Пусть необходимо минимизировать логическую функцию, заданную в виде
/(X,, х2, *3, х4) = Y (з, 4, 5, 7, 9, 11, 12, 13) =
= Х1Х2Х3Х4 V Х1Х2Х3Х4 V Х1Х2Х3Х4 V Х1Х2Х3Х4 ? V Х1Х2Х3Х4 ? Х1Х2Х3Х4 V Х1Х2Х3Х4 V Х1Х2Х3Х4.
Задача решается в несколько этапов.
Этап 1. Нахождение первичных импликант. Прежде всего составляется таблица (табл. 10.14) и находятся импликанты четвертого и третьего ранга, т. е. снижается ранг членов, входящих в СНДФ.
Затем составляется другая таблица (табл. 10.15), которая включает все термы, не подвергшиеся поглощению, а также первичные импликанты третьего ранга. Составление таблиц продолжается до тех пор, пока нельзя будет применить правило (10.27). В рассматриваемом примере можно дойти до первичной импликанты второго ранга (табл. 10.15) — х2хз.
импликанты
/
импликанты
V
Этап 2. Расстановка меток. Составляется таблица, число строк которой равно числу полученных первичных импликант, а число столбцов совпадает с числом минтермов СНДФ. Если в некоторый минтерм СНДФ входит какая-либо из первичных импликант, то на пересечении соответствующего столбца и строки ставится метка (табл. 10.16).
Этап 3. Нахождение существенных импликант. Если в каком-либо из столбцов табл. 10.16 имеется только одна метка, то первичная импликанта в соответствующей строке является существенной, так как без нее не будет получено все множество заданных минтермов. В табл. 10.16 существенной импликантой является терм х2х3. Столбцы, соответствующие существенным импликантам, из таблицы вычеркиваются.
Этап 4. Вычеркивание лишних столбцов. После третьего этапа в результате вычеркивания столбцов 2, 3, 7 и 8 получается табл. 10.17. Если в таблице есть два столбца, в которых имеются метки в одинаковых строках, то один из них вычеркивается. Покрытие оставшегося столбца будет осуществлять отброшенный минтерм. В примере такого случая нет.
Этап 5. Вычеркивание лишних первичных импликант. Если после отбрасывания некоторых столбцов на этапе 4 в табл. 10.17 появляются строки, в которых нет ни одной метки, то первичные импликанты, соответствующие этим строкам, исключаются из дальнейшего рассмотрения, так как они не покрывают оставшиеся в рассмотрении минтермы.
Таким образом, минимальная форма заданной функции складывается из суммы существенных импликант (этап 3) и первичных импликант, покрывающих оставшиеся минтермы (этап 6):
f(x 1, *2, Хз, Х4) = Х2Х3 V Х1Х3Х4 ? *1*2*4-§ 10.9. МЕТОД КВАЙНА — МАК-КЛАСКИ
Недостаток метода Квайна — необходимость полного попарного ¦сравнения всех минтермов на этапе нахождения первичных импликант. С ростом числа минтермов увеличивается количество попарных сравнений. Числовое представление функций алгебры логики позволяет упростить этап 1 (см. § 10.7). Все минтермы записываются в виде их двоичных номеров, а все номера разбиваются по числу единиц на непересекающиеся группы, так как условие образования г-куба — наличие расхождения в (г — 1)-кубах только по одной координате в одном двоичном разряде и наличие общих независимых координат. Поэтому группы, которые различаются в двух разрядах или более, просто не имеет смысла сравнивать. При Этом в г-группу войдут все номера наборов, имеющие в своей двоичной записи і единиц. Попарное сравнение можно производить только между соседними по номеру группами.
Пример 10.13. Пусть задана функция
і(хи Х2, Хз, х4)=?(3. 4, 5, 7, 9, 11, 12, 13).
Решение. Сначала выпишем 0-кубы:
/(" = 0011, 0100, 0101, 0111, 1001, 1011, 1100, 1101.
Разобьем 0-кубы на три группы по количеству единиц в каждом двоичном наборе:
I 01И|
Х? = {0100}; *2 = Гдо}
(llOOj
Этап 1. Нахождение первичных импликант:
а) сравнение КЧ и Kb
0100* ООП
0101* 1001 1100*
Здесь и ниже символом «*» отмечены наборы, которые склеиваются.
На основании сравнения строим куб /Сі, в котором поглощенная координата заменяется символом X:
Х2 = {ХЮХ}.
Этап 2. Расстановка меток (табл. 10.18).
К\ =
оюх
хюо
Этап 3. Нахождение существенных импликант. Существенной импликаитой ранга 2 будет терм
{ХЮХ} = хх3.
ООП* 0111* 0101* 1011* 1001* 1101* 1100*
Этапы 4 и 5. Отстутствуют.
Этап 6. Выбирается минимальное покрытие оставшихся термов {10X1} и {0X11} (табл. 10.19).
Строим куб Кз-
импликанты
Х0Ш
XIOlJ
(пох
І10ХІ/
Х011
01X1
10X1
1X01
110Х
Х101
Первичный импликант ранга 4 нет;
в) разобьем все 1-кубы на четыре группы в зависимости от положения независимой координаты X:
К! =
г) сравнение КІ и КЧ, К* и КЧ внутри каждой группы:
ОЮХ 01X1* 0X11* ХЮО ПОХ 10X1* 1X01* Х0П*
Х101
На основании сравнения строим кубы Хі =ХЮХ; /Сі'? = Х10Х; КЧ и /(} не сравниваются.
Следовательно, символом «*» отмечены первичные импликанты ранга 3:
/(' = {01X1; 10X1; 0X11; 1X01; Х011 >; л) сравнение КЧ и /(fV:
№0
01
и
10
хх10
хіхгУ: ь — 1x00
Ул

Один из способов графического представления булевых функций от небольшого числа переменных — карты Карно. Их разновидность — карты Вейча, которые строят как развертки кубов на плоскости. При этом вершины куба представляются клетками карты, координаты которых совпадают с координатами соответствующих вершин куба. Карта заполняется так же, как таблица истинности: значение 1 указывается в клетке, соответствующей набору, на котором функция имеет значение единицы. Значение 0 обычно на картах не отражается. На рис. 10.4 показаны примеры условного размещения переменных на минимизирующих картах для двух (рис. 10.4, а), трех (рис. 10.4, б) и четырех (рис. 10.4, в) переменных. Примеры использования карт Карно для минимизации указанных ниже трех функций даны на рис. 10.5, а, в соответственно: -
¦0)
а)
*,і* 2
:*)
00 01 И 10
10X1
¦х00
Рис. 10.5. Минимизация логических функций с Рис. 10.6. Пример минимизации помощью карт для конъюнктивной формы
расширяя понятие соседних клеток, отыскивают минимальные термы для совокупности карт. Соседними клетками являются клетки, совпадающие при совмещении карт поворотом вокруг общего ребра.
При получении минимальной формы для СКНФ функция задается термами, принимающими нулевое значение на соответствующих наборах. Поэтому в клетках минимизирующей карты пишут нули.
^минимальную— конъюнктивную форму для функции 5, 6, 8, 9, 10, 12, 14) методом минимизирующих карт
Пример 10.14.
f(x 1, Х2, Хз, Х4>='
Найти
fi=x\X2V Хі'Х2=хі. (рис. 10.5, а);
f2 — х\х2Хз\/ хіх2х3\/ Хіх2Хз\/х\х2х3 (рис. 10.5,6); /з = ?(3, 4, 5, 7, 11, 12, 13) = X2*3V *і*з*4V*1*2*4
(рис. 10.5, в).
Карты Карно обычно используют для ручной минимизации булевых функций при небольшом числе переменных.
Правила минимизации следующие.
1. Две соседние клетки (два 0-куба) образуют один 1-куб. При этом клетки, лежащие на границах карты, также являются соседними по отношению друг к другу (пример образования 1-куба см. на рис. 10.5, а). Независимая координата обозначена символом X.
2. Четыре вершины могут объединяться, образуя 2-куб, содержащий две независимые координаты (пример образования 2-куба изображен на рис. 10.5, в).
3. Восемь вершин могут объединяться, образуя один 3-куб.
4. Шестнадцать вершин, объединяясь, образуют один 4-куб и т. д.
При числе переменных, равном или большем пяти, отобразить
графически функцию в виде единой плоской карты невозможно. В таких случаях строят комбинированную карту, состоящую из совокупности более простых карт, например четырехмерных. Процедура минимизации в этом случае состоит в том, что сначала находят минимальные формы внутри четырехмерных кубов, а затем,
Решение. 6" помощью минимизирующих карт находим
= *і*зХа V *з*4 V *1X3*4 V *2*з.
Применяя цравйла де Моргана, получаем: _ ___ _
f = Х 1X3X4 V *3*4 V *1*3*4 V *2*3 =— * 1 *3*4 А *3*4 А *1*3*4 А *2*3 =
= (*i V *3 V *4) А (*з V_*4) А (*і V *з У *4) А (*2 V *з).
Ответ: /(*1, *2, *3, *4) = (*1 V *3 V *4)(*3 V *4)Л(*1 V *3 V *4)(*2 V *з).
§ 10.11. МИНИМИЗАЦИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ, ЗАДАННЫХ В БАЗИСЕ ф, А. 1
Метод неопределенных коэффициентов может быть применен для минимизации функций, заданных в разных базисах.
Рассмотрим применение метода неопределенных коэффициентов на примере базиса ф, Д, 1. Функцию f(x\, х2, х3) представим в виде, аналогичном нормальной дизъюнктивной форме, где вместо дизъюнкции стоит знак операции сложения ф по модулю 2. Эта операция имеет особенности, отличающие ее от операций дизъюнкции:
где m = 2k — четное количество единиц; 1 = 1 0 1 ф 1 ф ... ф 1,
(3)
, А „ ,0» _ ,01 I .001 .
ІІ2 ф fel2® к23 “Р &123 :— 1 ,
где m = 2k-\-\ —нечетное количество единиц.
Для операции дизъюнкции всегда 1 = 1 V 1 V 1--- - Наличие свойств (2) и (3) операции сложения по модулю 2 усложняет минимизацию. Так как основными критериями минимизации по-прежнему являются минимальный ранг каждого терма и минимальное количество термов, то при минимизации в базисе ф, Д, ~] целесообразно приравнять нулю все коэффициенты на наборах, где /=0, так как тогда в единичных строках могут остаться термы высокого ранга. Поэтому особой разницы между выбором очередной строки нулевой или единичной нет. Количество коэффициентов, остающихся в нулевых строках, должно быть четным, а в единичных — нечетным. Лучше начать с единичных строк и оставлять те коэффициенты минимального ранга, которые чаще повторяются в этих строках.
Пример 10.15. Задана функция f(xi, х2, хз)=ф(0, 1, 5, 6).
Найти минимальное представление в базисе ф, Д,~|.
Решение. Составим табл. 10.20.
Ответ: f(xі, х2, Хз) = Х2®хіХз-
*§®^°2+*?2?
«123
«23
«12
«13
«23
«123
«12
«13
«23
«123
0 on
«12
«13
«12
«23
«12
«23
Для определения В-минтермов производится попарное сравнение всех Л-минтермов. Если в сумме Лі и Л2 имеются две единицы, то берется любой из минтермов Л і, Л2 и пишутся четыре минтерма, которые получаются из Лі или Л2 подстановкой на местах, соответствующих единицам, всех возможных комбинаций из 0 и 1. Тем самым определяется множество покрытая, ранг которого на две единицы меньше ранга исходного множества. Те из полученных минтермов, которые не являются Л-минтермами, — искомые мин-термы.
Пример 10.16. Пусть задана функция
f(xі, *2, хз)=®(0, 2, 4, 7) = хіх2Хз?хіХ2Хз® ХіХ2хз©ХіХ2Хз.
Исходные Л-минтермы {000, 010, 100, 111}. Найти минимальную форму. Решение.
Этап 1. Нахождение В-минтермов.
Производится попарное сравнение:
В таблице коэффициент кЧ повторяется три раза и его целесообразно оставить. В нулевой строке надо оставить еще какой-нибудь коэффициент минимального ранга, который также повторяется в тех единичных строках, в которых еще не было оставлено ни одного коэффициента. Для получения минимальной формы выполним следующие действия:
1. Посчитаем, сколько раз встречаются в единичных строках термы первого минимального ранга, и оставим те их них, которые встречаются максимальное число раз.
2. Найдем нулевые строки, в которых встречаются оставленные термы, и оставим в строках эти термы.
3. Рассмотрим нулевую строку, в которой остался хотя бы один единичный терм, и найдем в ней еще единичный терм (1 © 1) = 0, встречающийся максимальное число раз в единичных строках, в которых еще не было оставлено ни одного терма (строки 4, 6).
Результат получим в виде уравнений:
Лм?ЛІ°з?ЛІм = 1;
^?*23®ЙІ2°3=1;
а) 000 б) * то
000 в) 100
000 г) 11
100 д) _ 100 е) 010 *111
010
111
ОТО 100 ГТТ По ОТТ ГОГ
111}
В случаях г, д, е сумма имеет по две единицы. В результате
В = {011, 101, ПО}.
Этап 2. Нахождение первичных импликант: /С° = {000, 010, 011, 100, 101, ПО, А. Нахождение первичных импликант ранга 3:
КЧ = {000}; КЧ =
{0101
Ій!!
а) сравнение КЧ и КЧ'-000* 010* 100*
КІ = {0X0, Х00};
f(xI, *2, Хз) = ХіХ2®Хз-
Для сравнения приведем выражение минимальной формы для СНДФ: ^
f(xI, Х2, Хз) = ХіХз + Х2Хз + ХіХ2Х;,.
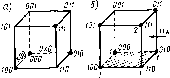
импликанты
010
100
111
101
011
110 хоо
1X0
Х10
0X0
V
V
V
V
V
V
\
V
10Х
XIX
010* 011*
100* 101*
ПО*
Л2'={01Х, Х10, 10Х, 1X0};
в) сравнение Кз и Kb
011* 111*
101*
ПО*
/Сз={Х11, 1X1, 1.11Х}.
Первичных импликант ранга 3 нет.
Б. Нахождение первичных импликант ранга 2.
Разобьем все множество импликант на три группы в зависимости от положения независимой координаты X:
(10Х) (0X0) (Х00)
/С1'= 01Х ; /«'=1X0} ; /«'= Х10 ;
IhxJ • UXlJ IxnJ
а) сравнение К", К? и Кз-
К!={1ХХ, XIX};
КІ={ХХ0, 1ХХ};
/СІ={ХХ0, XIX}.
Таким образом, Кг={\ХХ, XIX, ХХО}.
Этап 3. Расстановка меток, выбор покрытия (табл. 10.21).
ции двух переменных
Ответ: /(xi, Х2, хз)=хіх2®хз.
§ 10.12. МИНИМИЗАЦИЯ ФУНКЦИЙ В БАЗИСАХ ШЕФФЕРА И ПИРСА
Рассмотрим сначала функцию Шеффера:
Хі/Х2 = Хі&Х2-
Запись логической функции в базисе Шеффера осуществляется следующим образом:
1. Чтобы по таблице истинности записать терм в базисе Шеффера, переменные можно оставить без изменения.
2. Если задавать функцию на нулевых наборах, то в конце выражения следует ставить знак общего отрицания: (/(*))/1; если задавать функцию на единичных наборах, то инверсии не нужно.
Пусть функция задана следующей таблицей:
000 1 001 1 0 10 0
В базисе И — ИЛИ — НЕ эта функция имеет вид f(x 1, Х2, X3) = XiX2JC3 + XiX2X3.
В базисе Шеффера f(x\, х2, хз)=(хі/х^/х\і,)/{х\/х2)/{хъ/1)), или, после преобразований:
((Х,/Х2)/1)/((ХЗ/1)/ХЗ) = (Х1/Х2)/1.
Рассмотрим функцию Вебба:
Х\\Х2—Х\-\- Х2-
Запись логической функции в базисе Вебба происходит следующим образом:
1. Чтобы по таблице истинности записать терм в базисе Вебба, переменные в нем можно взять с инверсией.
2. Если функция задана на единичных наборах, то в конце выражения следует ставить знак общего отрицания: ([(х)Ц0.

Если функция задана на нулевых наборах, то инверсии не нужно.
Для заданной выше таблицы функция в базисе Вебба запишется так: (хі jx2j(x3jO))j(xi |х2|л:з)|0, или, после преобразований:
Для минимизации логических функций в базисах Шеффера или Вебба можно использовать метод Квайна — Мак-Класки.
После нахождения всех минимальных термов производится отыскание минимального покрытия с помощью частотно-минимального метода.
Обычно модели определяются своей матрицей инцидентности Q = в которой каждой строке взаимно однозначно соответ
ствует слово Мі, столбцу — буква т,.
1, если rrij^Mi,
О, если rrij^Mi.
При ранге матрицы г — 2 получается двумерная частотная матрица отношений.
Двумерная частотная матрица отношений F — f(i, j) связана с матрицей инцидентности Q = [</;,] так:
F = Q'Q,
где QT — транспонированная матрица.
Для булевой матрицы Q = [^I/], <7,;={0, 1} покрытием столбцов строками будем называть такое множество строк, что для каждого столбца найдется хотя бы одна строка, на пересечении с которой этот столбец имеет единицу, причем такое свойство множества строк отсутствует при вычеркивании хотя бы одного элемента из этого множества строк. Покрытие столбцов минимальным количеством строк в дальнейшем будем называть минимальным покрытием.
Одним из первых применений минимального покрытия было использование его при нахождении покрытий импликантных таблиц Квайна в связи с возникновением необходимости более компактных представлений булевых функций в практике построения логических схем, а именно, для нахождения МДНФ. Минимальное покрытие находится для матрицы Q, где строкам соответствуют найденные простые импликанты булевых функций, а столбцам — наборы аргументов, соответствующие единичным значениям минимизируемой функции:
1, если і-я простая импликанта содержит j-ю конституенту 1, О, в противном случае.
Простые импликанты, соответствующие строкам, которые входят в минимальное покрытие, соединяются знаками дизъюнкции и образуют МДНФ булевой функции.
Квайн предложил вычеркивать те столбцы из импликантных таблиц, часть которых полностью эквивалентна по 1 какому-либо другому столбцу, и для выбора строки в формируемое покрытие начинать просмотр со строк, имеющих максимальное количество единиц.
1) правило поглощения строк.
Если в матрице Q имеется такая пара строк Q‘ и Q', что Q‘^Q', то строка Q' вычеркивается (производится сжатие матрицы Q по строкам); У
2) правило поглощения столбцов.
Если в матрице Q имеется такая пара столбцов k‘ и k', что то столбец k’ вычеркивается (производится сжатие матрицы Q по столбцам).
Последовательным применением этих двух преобразований можно сжать исходную матрицу до «циклической» матрицы, которая содержит среди своих покрытий хотя бы одно из минимальных покрытий исходной матрицы Q.
Частотно-минимальный метод минимизации основан на изложенных выше положениях и содержит следующие этапы.
1. Из матрицы Q вычеркиваем те строки, которые полностью повторяют всю или часть любой другой строки (поглощаемые строки).
2. Из Q вычеркиваем те столбцы, которые полностью повторяют весь или часть любого другого столбца (поглощаемые столбцы).
Пункты 1 и 2 выполняются последовательно до тех пор, пока в матрице Q останутся только непоглощаемые строки и столбцы.
3. Из оставшихся столбцов матрицы Q-отыскиваем столбец, в котором находится минимальное количество единиц, находящихся в невычеркнутых строках.
4. Из всех невычеркнутых строк, имеющих единицу в выбранном согласно п. 3 столбце, находим ту строку, в которой имеется максимальное количество единиц. Если количество столбцов, удовлет-’ воряющих п. 3, больше одного, то строку, соответствующую условиям данного пункта, находим среди всех столбцов, выделенных по п. 3. Эту строку выбираем в оптимальное покрытие.
При равном количестве единиц в строках, удовлетворяющих п. 3 и п. 4, первая из них выбирается для оптимального покрытия или же за счет незначительного усложнения алгоритма подсчитывается вес строк Sk, которые имеют единицы в столбцах, удовлетворяющих п. 3. Затем выбираем строку, имеющую наибольший Sk в оптимальное покрытие. При одинаковых s* в оптимальное покрытие выбирается первая из них.
5. Найденную строку и все столбцы, в которых эта строка имеет единицу, вычеркиваем из Q.
6. Оставшиеся строки проверяем на количество единиц в строке. Если находится строка с числом единиц, равным числу невычеркнутых столбцов, то эта строка вносится в оптимальное покрытие и процесс поиска оптимального покрытия на этом заканчивается; если каждая строка имеет только по одной единице в каждом из оставшихся столбцов, то эти строки вносятся в оптимальное покрытие и процесс поиска также на этом заканчивается. Проверять специально после пяти пунктов алгоритма последнее условие необя-
рсб
§ 10.13. РЕАЛИЗАЦИЯ ЧАСТОТНО-МИНИМАЛЬНОГО МЕТОДА
Для реализации вышеизложенного алгоритма на ЭВМ используются частотные матрицы отношений F двух типов: FCT и Рб. Матрица FCT получается умножением Q на QT. Эта частотная матрица отношений дает информацию о взаимном влиянии строк Q друг на друга. На диагонали FCT находится число которое определяет количество единиц в і-й строке (f, — собственная частота /-Й строки). Элементы fq (fq— взаимная частота і-й строки с j-й строкой) матрицы Рт определяют количество единиц, которые находятся в тех же самых столбцах как в г'-й, так и в j-й строке. Матрица Рб. получается умножением QT на Q (P6 = QTQ) и дает информацию о взаимном влиянии столбцов. Здесь ft показывает количество единиц в г'-м столбце, а — количество единиц, которые находятся в тех же самых строках как в г'-м, так и в j-м столбцах.
В матрице Рт находим номера строк матрицы Q, которые, согласно п. 1 алгоритма, необходимо вычеркнуть. Это — )-е строки,
У КОТОРЫХ
В этом случае г'-я и /-я строки или полностью эквивалентны или /-я строка является частью г'-й строки- (ft>fj).
В матрице Рб находим номера столбцов матрицы Q, которые, согласно п. 2 алгоритма, необходимо вычеркнуть. Это — г'-е столбцы, у которых При этом условии /'-й столбец матрицы Q
будет покрыт теми же строками, которые будут покрывать j-й столбец.
Рассмотрим частотно-минимальный метод на примере.
Частотная матрица Q составляется следующим образом.
Если t-й терм входит в состав j-го выражения, то элемент матрицы Q <7,,= 1, иначе <7,7=0.
20121 2 000 1 1 1 32 3
Если fu=fij или fa—fji, то сравниваются диагональные члены fu и Іи.
Если fu>fjj, то из матрицы Q вычеркивается /-я строка.
Если то вычеркивается j-я строка.
В данном примере: fu = fu = 2; f44=3; /44>fn=>(3>2) и из матрицы вычеркивается 1-я строка:
/зз==/з4=/з5—1’> f44=3; /55=3; f44>f33;
/56>/зз=ф-(3> 1) и из матрицы Q вычеркивается 3-я строка.
Количество строк, покрываемых і-м минимальным термом, указывает f,-,; количество строк, покрываемых і-я и /-м минимальными термами, вместе указывает fq.
Равенство fu=fq или fu—fji показывает, что г'-й терм и г'-й и /-й термы вместе покрывают одинаковое количество строк. Если то выбираем /(/) минтерм, так как г'-й минтерм покрывает большее количество строк, чем /-й, и наоборот.
Составляем матрицу-столбец F®=QTQ.
1101010 10 100 2 02 1 1 00 4 2 2
Если fij—fu или fn=fji, то сравнивается fu и fq. Если fu>fq, то вычеркиваем г'-й столбец из матрицы Q.
В данном примере fu=fi3—fis> Лі</зз<^55- Из матрицы Q вычеркиваем 3-й и 5-й столбцы. f22=f24', f22=f44, из матрицы Q вычеркиваем 2-й столбец. f33=f35l fss>fзз — вычеркиваем 5-й столбец. fse=fев; fs5> fee — вычеркиваем 5-й столбец.
fu показывает, что г'-я строка исходной матрицы покрывается термами в количестве штук.
ftj показывает количество минимальных термов, покрывающих г и / строки вместе.
МК-М(М-)/2
MULTR
TABL
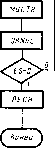
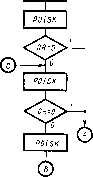
Если fu>fa (или наоборот), то вычеркиваем і-столбец матрицы Q, так как для покрытия і-й строки исходной матрицы требуется, большее количество термов, чем для покрытия j-й строки.
В результате этих операций получим новую матрицу Q:
0 1 О 00 1
1 0 0
Р2Т=
Поглощений нет.
Из матрицы Q следует, что оптимальное покрытие составляют минтермы 2, 4, 5, т. е.
F = X 2Хз-\-Х2Х4-\-ХХ4.
Алгоритм, реализующий минимально-частотный метод, представлен на рис. 10.8.
1. Вводятся исходные данные. В качестве исходных данных выступают следующие параметры: /1 — количество наборов переменных /1=2т, где т — количество переменных, N1 —количество переменных (т), N = N-\- 1, матрица ІА — таблица истинности.
2. Вызывается подпрограмма STOLB.
В этой подпрограмме осуществляется подсчет количества наборов логических переменных, на которых функция F{x) принимает значение «1» — «истина». Это число фиксируется с помощью переменной М, которая определяется путем подсчета единиц в крайнем правом столбце матрицы ІА.
3. Сравниваются М и 2т_|. На этом шаге определяется, на каких наборах задавать логическую функцию (1 или 0). Если Af<2т_|, то функция задается на единичных наборах (признак RK= 1). Если М^2т_|, то функция задается на нулевых наборах (/?*=0).
4. Вычисляются: МК=М(М —1)/2, определяющего максимальное количество промежуточных термов на одном шаге минимизации; определение IX, IY — матриц, в которых расположены минимальные термы.
5. Вызывается подпрограмма TABL.
В этой подпрограмме анализируется, на каких наборах задается функция, и в соответствии с этим переписываются строки матрицы ІА (строки — термы, образующие логическую функцию) в матрицу IT (матрица исходных термов) и далее будем использовать только матрицу IT. Анализ осуществляется через признак RK.
6. /11 —0. Переменная /11 определяет количество минтермов, находящихся в матрице ITERM.
POISK.
В этой подпрограмме осуществляется поиск минтермов путем склегрвания термов.
Под склеиванием термов понимается операция вида
ХіХ2 + ХіХ2 = Гі.
В машине это выглядит следующим образом:
110 1 1 1
Если хотя бы один раз произошло склеивание термов, то вырабатывается признак OR= 1, в противном случае OR = 0. Если после выполнения подпрограммы POISK OR = 0, то это означает, что все минтермы найдены. Можно переходить к поиску минимального покрытия.
Поиск минимальных термов проводится путем сравнения строк матрицы IT:
1-я строка сравнивается с 3, 4, 5,..., А4-Й, (М — 1)-я строка сравнивается с Л4-й.
Количество несовпадений по элементам строки фиксируется переменной IR. Склеивание термов произойдет лишь в том случае, если //?= 1.
При IR — 1 г'-строку матрицы IT переписываем в г-ю строку матрицы IX. В то место, где произошло склеивание, записывается цифра «2». Номер этой позиции фиксируется переменной IR.
Если при сравнении строк і и / строк IR — 0, т. е. і-я и j-я строки одинаковые, то переходим к работе с (і+1)-й строкой. Если при сравнении г'-й строки с другими хотя бы один раз произошло склеивание (//? = 1), то вырабатывается признак RV = 1.
Если RV=0, то г-ю строку переписываем в матрицу термов ITERM, проверив предварительно, не склеивалась ли данная г-я строка с предыдущими строками с 1-й по (г — 1)-ю. При сравнении г-й и /-й строк в случае склеивания номер / запомнится в одномерном массиве KR, на позиции под номером 17. Проверка осу-
0010
ООН
1001
1010
1011
IT=
ществляется путем поиска номера і в массиве KR по позициям от 1 до 17 текущего.
8. Если после работы подпрограммы POISK признак OR— 1, то подпрограмма POISK выполняется еще раз, но здесь работаем в подпрограмме с матрицей IX, а переписываем в матрицу IY. Если после этого шага OR — 1, то еще раз вызывается подпрограмма POISK, но производится перезапись из IY в IX. Это производится до тех пор, пока признак OR — 1. Чтобы на этом этапе выполнения программы избежать зацикливания, вводится переменная NRAZ-, она фиксирует количество обращений к подпрограмме POISK. Как только оно превысит заведомо большое число (100), то печатается сообщение ОШИБКА В ITERM и выполнение программы заканчивается.
9. 112=111 + 1, М1 = М +1.
Параметры 112 и Ml описывают матрицу покрытия IQ. Истинный размер матрицы IQ(IllXM), кроме этого необходимы дополнительные строка и столбец для обозначения номеров строк и столбцов матрицы IQ
10. Вызов подпрограммы QPOKR.
С помощью этой подпрограммы формируем матрицу покрытия IQ. Матрица образуется по следующему правилу: qi-,= 1 — если г-й минтерм входит в состав j неминимального терма; ^ = 0 — в противном случае.
11. Вызов подпрограммы MULTR.
С помощью этой подпрограммы формируется матрицы Рт, при этом 1-я строка IQ умножается на себя и попарные произведения суммируются, получаем элемент /п, затем 1-ю строку умножаем на 2-ю, 3-ю и т. д., 1-ю на 111, получаем элементы /|2, /із, ... /пи. Затем 2-ю на 2-ю, 2-ю на 3-ю, 2-ю на 4-ю, ..., Ill X ІИ- Это элемент /пі[і[• Размер матрицы Рт равен 111 X 111 -
12. Вызов подпрограммы OBNUL.
С помощью этой подпрограммы проводится вычеркивание (обнуление) строк матрицы IQ вплоть до 112 элемента.
Собственно обнуление проводит программа NR, которая вызывается подпрограммой OBNUL. Подпрограмма OBNUL указывает номер строки, которую необходимо обнулить. Поиск такой строки осуществляется следующим образом:
последовательно выбираются диагональные элементы /„ матрицы IFSTR;
fa сравнивается с элементами строки столбца, на пересечении которых fa находится;
если есть равенство /;, = /;,• или fu=fji, то вырабатывается' признак ES = 1 — признак наличия обнуления на данном этапе;
сравниваем /„ и fa; если fu>fa, то
выбор г-й строки из матрицы 1TERM;
сравнение каждого элемента этой строки с цифрой «2»;
подсчет количества «2» в этой строке — число их обозначим К', если К — четное число, то вырабатывается признак КСН— 1; если К — нечетное число, то КСЙ=0.
печать строки матрицы ITERM по элементам.
Пример 10.16. Пусть задцна функция: F(xі, хч, х3, л:4)=ч/(1, 2, 3, 9, 10, 11). Найти минимальную форму-трункции в базисе Шеффера (Вебба).
Решение.
1. Составляем матрицу ІА:
poooq
00011
00101
00111
оюоо
01010
01100
OHIO
10000
10011
10101
10111
11000
пою
11100
11110І
2. Af=6 (результат работы п/п. STOLB).
3.
(результат работы подпрограммы TABL).
4. Сравниваем 1-ю и 2-ю строки.
0001 два несовпадения 0010 IR—2.
Сравниваем 1-ю и 3-ю строки:
0001 //? = 1.
ООП JR=3.
Переписываем 1-ю строку в матрицу IX и на 3-ю позицию заносим «2».
ІХ= Ц0021II, KR(IY)=3.
Сравниваем 1-ю и 4-ю строки;
0001 IR = 1.
1001 УЯ=1.
•¦ННі- ** 2) = 4.
Сравниваем 1-ю и 5-ю строки:0001
1010
IR^= 3.
0001
1011
IR=2.
1Х =
Сравниваем 2-ю и 3-ю строки:
0010 IR = 1, JR = 4, /Щ3)=3, ООП
ІХ=
0021
2001
0012
3021
2001
0012
2010
2011
1021
1012
Сравниваем 2-ю и 4-ю строки:
0010 IR= 3. 1001
Сравниваем 2-ю
и 5-ю строки:
0010 /Я= 1, 1010 /7 = 4,
^//?=1.
К/?(4)=5.
0021
2001
0012
,2010
Сравниваем 2-ю и 6-ю строки:
0010 //?= 2. 1011
Сравниваем 3-ю и 4-ю строки:
ООП //? = 2. 1001
Сравниваем 3-ю и 5-ю строки:
ООП //?= 2. 1010
Сравниваем 3-ю и 6-ю строки:
ООП
1011
//?= 1, //?=!.
ІХ =
0021
2001
0012
Сравниваем 4-ю и 5-ю строки:
/Щ5) = 6.
1001
1010
IR—2.
Сравниваем 4-ю и 6-ю строки:
1001 /Я = 1, /Д=3, /С/?(6)= 1011
0021
2001
D012
2010
2011
1021
Сравниваем 5-ю и 6-ю строки:
1010
1011
//?= 1, //?= 4. KR(7)=6.
Из матрицы IX формируем IY. Сравниваем 1-ю и 2-ю строки
2021
2021
2021
2012І
IQ =
101101 И
011011 II •
7. Получаем матрицу 1FSTR:
1FSTR =
8. Получаем матрицу 1FSTB:
IFSTB =
4 2 II 2 4 II '
Сравниваем 4-ю и 5-ю строки:
2010 //?-= 1, JR — 4, KR(4)=5.
2011
IY=
2021
2021
2012
2012
101101
011011
112011
100101
311011
111112
Сравниваем 4-ю и 6-.ю строки:
fa =/i3=fi4=/i6;
/и</зз; /и = р44; /п</бб-
Из матрицы IQ вычеркиваем 3-й и 6-й столбцы, а также 4-й.
/22 = b3 = |:25=ff26-
/22 <7 /33; І22 = ІЪЪ', /22</б6-
2010 IR-= 3. 1021
Сравниваем 4-ю и. 7-ю строки:
2010 IR=2. 1012
Сравниваем 5-ю и 6-ю строки:
1021 /«=2.
2011
Сравниваем 5-ю и 7-ю строки:
2011 //?=2. 1012
Сравниваем 6-ю и 7-ю строки:
1021 /Я=2.
1012
Из 1Q вычеркиваем 5-й столбец. 9. Получаем новую матрицу:
IQ =
01
10
В минимальное покрытие вошли термы 2021, 2012.
1 Ответ: результат в базисе Вебба: (х-> |(л* 10))| (хз|(лц [ 0)), в базисе Шеффера: \{хі/\)/хі)/({хі/\)/хі).
Признак ЛУ=1, матрица ITERM пуста. Рассмотрим матрицу IY.
Сравним 1-ю и 2-ю строки:
2021 /Л=0.
2021
Сравниваем 2-ю и 3-ю строки:
2021 IR — 2, RV=Q.
2012
Задание для самоконтроля
1. Составить таблицу истинности для заданных функций:
•а) /,(*,*,*,)= VO. 2, 3, 5);
'б) [2(х,х2хз)=уо-2-3-5-6’7);
в) 3- 8’ 9’ 10’ И’ 12- 14)'
2. Доказать тождественность функций:
а) АС + ВС == АС + ВС;
б) (А + В) (А + С) = АС 4; АВ;__
в) АВ + ВС + АС = АВ + ВС + АС.
3. Найти минимальную форму для функций, заданных в примере 1.
4. Найти СДНФ и СКНФ для следующих функций:
а) fi(xix2x3)—xi + Х2Х3 + Х1Х2Х3 + Х1Х3.
б) f2(XiX2X3) = Xi+ х2\ _
в) (з(ХіХ2Хз)=(хіХ2+Х2Хз)&ХіХ2.
Терм 2021 является минимальным, его записываем в матрицу 1TERM. Сравниваем 3-ю и 4-ю строки:
2012
2012
ITERM =
IR = 0.
II 2021 И
11 2012 II '
Вх,
а)
Вх, А1
~Вх,
Вых
'
E'Epf
I - I !|
Вх, Д2
6)
х2
П?г)
Рис. 11.2. Схема дизъюнктора
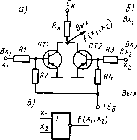
Схема работает следующим образом. В интервале времени от 0 до t\ (рис. 11.1,6) на входе действует почти нулевое напряжение. За счет делителя ?1—R2 и источника Е6 транзистор ПТІ закрыт и на выходе напряжение равно —?к, В момент 11 происходит изменение напряжения на
МЕТОДЫ ЛОГИЧЕСКОГО ОПИСАНИЯ ЭЛЕКТРОННЫХ СХЕМ
§11.1. ЛОГИЧЕСКИЕ ОПЕРАТОРЫ ЭЛЕКТРОННЫХ СХЕМ
По зависимости выходного сигнала от входного все электронные схемы [7, 17] можно условно разбить на:
схемы первого рода, содержащие комбинационные схемы — схемы, выходной сигнал в которых зависит только от состояния входов (наличия входных сигналов) в каждый момент времени;
схемы второго рода„ содержащие накапливающие схемы (элементы с памятью) — схемы, выходной сигнал в которых зависит как от входных сигналов, так и от состояния схемы в предыдущие моменты времени.
По количеству входов и выходов схемы бывают: с одним входом и одним выходом, с несколькими входами и одним выходом, с одним входом и несколькими выходами, с несколькими входами и выходами.
По способу осуществления синхронизации схемы бывают: с внешней синхронизацией (синхронные автоматы), с внутренней синхронизацией (асинхронные автоматы являются их частным случаем) .
Практически любая ЭВМ состоит из комбинации схем первого и второго родов разной сложности.
Рассмотрим некоторые конкретные прймеры.
На рис. 11.1, а показана принципиальная электрическая схема, выполненная на транзисторе.
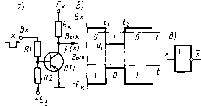
Таким образом, рассмотренная выше схема описывается функцией НЕ и называется инвертором (рис. 11.1, в).
На рис. 11.2, а показана схема дизъюнктора, описываемая логическим оператором ИЛИ (рис. 11.2, в). Временная диаграмма работы этой схемы представлена на рис. 11.2,6.
На рис. 11.3, а показана комбинация электронных схем дизъюнктора и инвертора, выполненная на транзисторах, а ее логический оператор ИЛИ—НЕ — на рис. 11.3, в. Временная диаграмма работы этой схемы дана на рис. 11.3,6.
q—
! *4
t
—
fe ! \a
i i i i i 1
1 1 1
1 1 1
1 ! 1
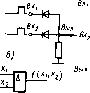
Mill ІІ|М
№
—I i i i I и
_KiiHL
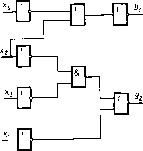
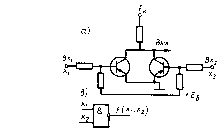
На основании вышеизложенного можно прийти к заключению, что различные электронные схемы или их комбинации на логическом уровне могут быть описаны с помощью логических операторов. Такое операторное описание электронных схем позволяет абстрагироваться от физической природы конкретных электронных элементов и осуществлять их анализ. При этом оказывается, что для анализа совсем не обязательно иметь саму схему. Для того чтобы получить значение функции на выходе какой-либо схемы, достаточно записать эту зависимость в виде логических операторов, связанных между собой в соответствии с выполняемой функцией.
Для анализа электронных схем с помощью аппарата алгебры логики нужно найти логическую функцию, описывающую работу заданной схемы. При этом исходят из того, что каждому функциональному элементу электронной схемы можно поставить в соответствие логический оператор. Этим самым устанавливается однозначное соответствие между элементами схемы и ее математическим описанием.
Анализ электронной схемы проводится в два этапа:
1) из принципиальной схемы удаляются все несущественны^
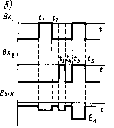
2) через логические операторы выражают все элементы, получая логическое уравнение, которое является моделью функции, выполняемой заданной схемой. Проводится анализ этой функции с целью устранения лишних частей.
Например, схема, представленная на рис. 11.6, может быть описана логическими выражениями у\ —
=дс2 + Х4; У2=х\ +Х2Х3. Однако с точки зрения инженерного проектирования чаще приходится решать обратную задачу, называемую задачей синтеза электронных схем.
Задачу синтеза электронных схем можно сформулировать следующим образом: при заданных входных переменных и известной выходной функции спроектировать логическое устройство, которое реализует эту функцию (при этом могут быть наложены дополнительные ограничения либо в виде системы логических элементов, которые используются, либо в виде требований по количеству логических операторов). Следовательно, в результате решения задачи синтеза возникает логическая схема-,
воспроизводящая заданную функцию.
Обычно, решая задачи анализа и синтеза, используют полные базисы функций. При этом каждую логическую функцию, входящую в базис, сопоставляют с некоторым физическим элементом. Значит, логическую схему можно заменить структурной схемой, состоящей из физических элементов.
Таким образом, удается соединить математическую задачу синтеза логической схемы с инженерной задачей проектирования электронной схемы. При разработке электронной схемы за основные критерии принимают минимум аппаратуры, минимум типов применяемых элементов, максимум надежности.
С точки зрения математической логики задача синтеза решается при обеспечении минимального числа логических операторов, минимального количества типов логических операторов. Можно сформулировать последовательно решаемые задали при синтезе электронной схемы:
составление математического описания (системы логических уравнений), адекватно отображающего процессы, происходящие в схеме;
анализ логических уравнений и получение минимальной формы для каждой из них в заданном базисе;
переход от логических уравнений к логической (структурной) схеме посредством применения логических операторов.
Таблица 11.1
Решение. Синтезируемую схему можно рассматривать как схему, состоящую из двух частей: схемы для получения поразрядной суммы с, (полусумматор) и схемы для получения переноса п,.
На основе теоремы (10.20) запишем СНДФ для функции с, и п,.
Используя минимизирующие карты Карно, получаем минимальные формы для каждой из функций с, и п, (рис. 11.8, а, б) :
Схемы с одним выходом и несколькими входами относятся к наиболее простым схемам. Основная сложность при синтезе этих схем состоит в том, чтобы найти выражение для выходной функции в заданном базисе.
Пример 11.1. Синтезировать схему в базисе «НЕ-импликация», если функция имеет вид /(jo, хг, хз)=х,~+(х,Х2 + х3).
Решение. Перейдем от смешанной системы логических функций к системе «НЕ-импликация» на основе правил перехода:
Xl^-X2 = Xi-jrX2 = XlX2, ХіХ2 = Хі->-Х2. (11.1)
Получим ф(хі, Х2, Хз) = Х,->~(хі->-Х2 + Хз) = Хі->~((х,->'Х2)->-Хз).
Функция ф(хі, X'j, х:і) может быть реализована на основе логических операторов «НЕ» и «импликация» (рис. 11.7).
Ответ: логическая схема на рис. 11.7.
Задача синтеза, как правило, имеет различные решения в зависимости от выбранной системы логических элементов. Однако для любой заданной функции алгебры логики почти всегда можно синтезировать cxetoy, соответствующую этой функции. Получение схемы с минимальным количеством логических связок требует нахождения минимальной формы для функции алгебры логики.
Некоторые более сложные схемы, имеющие несколько выходов, могут быть сведены в частном случае к набору схем с одним выходом. Тогда синтез осуществляется путем декомпозиции для каждой выделяемой схемы. Рассмотрим в качестве примера синтез одноразрядного двоичного сумматора методом декомпозиции.
J п,- = п, — ] (Пі Т* б;) -р а,б,.
Функции (11.2) могут быть реализованы схемой, представленной на рис. 11.9.
Ответ: логическая схема на рис. 11.10.
Однако способ решения задачи, который показан в примере 11.2, не всегда дает минимальное решение. Например, исходное выражение для с, может быть записано ийаче. Из табл. 11.1 видно, что поразрядная сумма с, равна единице тогда, когда одно из слагаемых аі, Ьі или перенос П;_і равен единице, а остальные слагаемые равны нулю и при этом п; = 0 (п; = 1) или когда все три слагаемых равны единице. Поэтому ct = (щ + &*-(- Пі_і)п; 4 афіЩ-ь
Таким образом, окончательное выражение имеет вид
с, = (а, + Ьі + п/_ 1) п,• + аДп,-,; I (И .3)
П; = П;_і(а, + Ьі) 4 O-ibi. J
Функции (11.3) могут быть реализованы логической схемой, представленной на рис. 11.10.
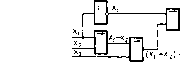

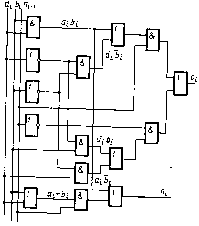
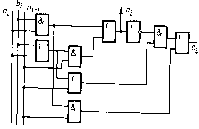
Задача синтеза схемы с п входами и k выходами отличается от задачи синтеза k схем с п входамии одним выходом тем, что при решении необходимо исключить дублирование в k схемах синтезируемых функций
Примером схем с несколькими входами и выходами служит схема дешифратора. Принцип работы дешифратора прост: при
у0—х\х2х3; уз=хіх2хз; у6 = ххх2х3-у\ = хіх2х3; у4 = х,х2х3; у7 — х\х2х3. У2 = XiX2xs; у § — ххх2хъ.
Реализация этих выражений в виде конъюнктора дает возможность создать логическую схему дешифратора (рис. 11.11).
Однако несложно убедиться н том, что такой подход к построению схем не дает оптимального решения из-за указанных выше особенностей схем с несколькими выходами.
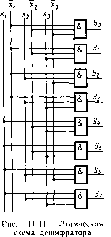
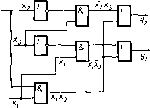
найти простые импликанты заданной системы функций;
выразить каждую заданную функцию через простые импликанты;
синтезировать схему, включающую только эти импликанты и связи между ними.
Пример 11.3. Синтезировать схему, функции на выходах которой имеют вид yi=fl(x\, *2, Хз) = Х>Х2Хз + ХіХ2Хз + ХіХ2Хз;
'/2=/2(Х|, *2, Х3) = ХіХ2 + Х2Х3.
В качестве базиса взять функции И, ИЛИ, НЕ. !
Решение. Найдем простые импликанты, разбив множество у> на три группЩ в соответствии с количеством единиц в каждой группе:
/С? = {100}; /(§ = {!10}; /(§ = {111}.
В результате сравнения групп получим
/('={1 Х0, 11 Х} = {хіХз + Х]Х2}.
Простых импликант ранга 3 нет.
Простые импликанты ранга 2
К'={хіх2; Х2Х3; хіхз].
Окончательный вид выходных функций:
yi—xixz + хіхз; И2=ХіХ?. + Х2Хз.
В полученных выражениях подчеркнут член, являющийся общим для обоих уравнений, что позволяет упростить окончательный вариант схемы, представленный на рис. 11.12.
Ответ: логическая схема на рис. 11.12.
Метод каскадов основан на теореме разложения функции алгебры логики по k переменным:
f(xu х2, ..., Xn) = Xnf(x,, Х'2, ..., Х„-и 1) V x„f(xu Х2, ..., Хп-1, 0).
Эта формула попеременно применяется к заданной функции столько раз, сколько необходимо, чтобы получить простые логические выражения, которые легко синтезировать, используя двухвходовые элементы И, ИЛИ:
f(x 1, х2, .... Х„) = Xnf 1 V х„/2; fi(xi, х2, x„-i) = х„_і/п V *«-1/12;
/г(Хі, X2, .... X„_l) = X„_|f2I V 1/22; ,
fllOl, X2, ••¦> X’n) == Xji—2^111 V —2^ 1 ^
f22(^1, X2, ..., Xn) = —2/221 V Xn-2/222;
/гі(хі, x2, ..., x„) — х„_2/2ц V xn_2/2i2;
схемы.
Процесс разложения происходит до тех пор, пока не будут получены функции fijk.i, зависящие только от двух аргументов. Далее синтезируется схема, соответствующая системе уравнений минимального ранга.
Пример 11.4. Синтезировать схему в базисе И—ИЛИ—НЕ, выходные функции которой заданы в виде уравнений:
фі =Х\Х2Хз V Х1Х2Х3 V Х1Х2Х3; <Р2=Х|Х2*з V Х1Х2Х3 V Х1Х2Х3; фз = ХіХ2-Хз V Х1Х2Х3? х 1X2X3.
Решение. Применим разложения (11.4) к заданным функциям:
1*2X3 V *з(хіХ2? Х1Х2); fu /12
ф2 =_?|Х2Хз V Хз(Х\Х2У Х\Х2):
^'фЗ = Хз(Х\Х2 V Х\Х2 V Х,Х2) fb 2=*і?Х2
После упрощений выходные уравнения можно записать так:
фі=хіх2хз V *2X3;
ф2=хіх2хз ?хгХз;
Фз=*з(хі ?х2).
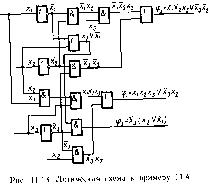
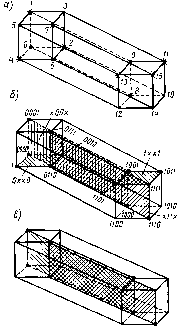
Не полностью определенная логическая функция п переменных — функция, заданная на числе наборов, меньших 2". Не полностью определенная функция алгебры логики содержит множество наборов, на которых она не определена. Встречаются такие функции достаточно часто. Если количество неопределенных наборов т, то путем различных доопределений можно получить 2т различных функций. В дальнейшем набор, на котором функция f(xi, х2, ..., х„) не определена, будем отмечать звездочкой (*). Для наборов, на которых функция не определена, значение логической функции может быть произвольным. Все зависит от некоторых других условий. Например, если взять какой-то десятичный код, то выходная функция определена на 10 из 16 возможных наборов. Остальные наборы — запрещенные. Значит, оставшиеся шесть наборов должны быть доопределены, так как иначе невозможно будет использовать аналитическое представление в виде совершенных нормальных форм (СНФ). Это доопределение очень важно, так как от него зависят результаты решения.
Пример 11.5. Доопределить следующую функцию:
Да:,, Jt2, *))=у(1*, 2, 3*. 4, 5, 7*). '
Решение. Рассмотрим, какие функции получаются, если отмеченные наборы доопределить.
На рис. 11.14, а представлено множество функций, соответствующих заданной функции f(xі, х2, хз). Если функцию f(xі, Х2, хз) доопределить на отмеченных наборах нулями, то получится в результате минимизации новая функция f6(xі, х2, х-3)= = х\хі V X)х2хз (рис. 11.14,6).
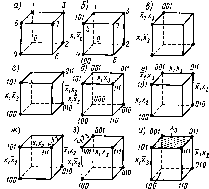
Другие части рис. 11.14 демонстрируют разные варианты доопределения. Минимальное решение для заданной функции: fr(xі, хг, Хз)—
= х\Х2 V х\Х2 (рис. 11.14, г).
Ответ: f2(xi, х2, хз) — х\х2 V
V *1X2.
Пример 11.5 показывает, что доопределение функции существенно влияет на конечный результат минимизации.
При доопределении функций можно руководствоваться следующим правилом: минимальная дизъюнктивная нормальная форма не полностью определенной функции f(xі, Х2, ..., Хп) получается как дизъюнция наиболее коротких по числу букв импликант функции фі(л:і, Х2, .... Хп), принимающей значение, равное единице, на всех наборах, где функция не определена, которые в совокупности покрывают все импликанты в совершенной нормальной форме для функции фо(хі, х2, ....
Хп), принимающей значение, равное нулю, на всех наборах, где f не определена.
В самом деле, функция фі(гі, х2, ..., хп) содержит все простые импликанты, которые могут встретиться в /-м покрытии f, а фо содержит минимальное число простых импликант. Поэтому надо выбрать из этого набора те импликанты из фі, которые оптимально покрывают фо-
Пример 11.6. Найти минимальную форму для функции четырех переменных: і(х,. хо. хз. Xa'\ = j(Q. 1*. 2*. 4*. в. 7*. 8*. 9. 11*. 13*. 14. 15*1
Решение. На рис. 11.15, а представлена функция f, отображаемая также табл. 11.3. Звездочкой на рисунке отмечены неопределенные значения. Для функции Фо(*і, *2, хз, *4) СНФ может быть получена из табл. 11.3 при замене символа * на 0:
Соответственно функция фі(хі, х2, *з, *4) определяется, если в табл. 11.3 символ * заменить на единицу. Этот случай изображен на рис. 11.15,6. Минимизируя показанную функцию, получим:
ф|(*|, *2, Хз, Х4) = Х2Х4 V Х2Хз V *2*3 V *1*4-
Решение. При решении будем использовать описание работы двоичного сумматора в виде табл. 11.1. Предположим, что схема, реализующая функцию т, уже синтезирована. Теперь построим таблицу для функции с? (табл. 11.5).
Введем обозначения: п, = уі, Сі = у2. Тогда =yf = bi,
п,_і, п,). Эта функция с? графически показана на рис. 11.16, а.
Доопределение функции сТ, записанное в СНДФ, имеет вид:

Ответ: f(x ь х2, х3, Хі) = х2хз\/ х2хз-
Пусть необходимо построить функциональную схему для системы, заданной уравнениями:
Уі = М*ь *2, •••» хп), Уч — h{x\, Х2, ..., хп). (11.5)
Предположим, что функция у, уже построена. Тогда новая функция
У? = f$(yі, хі, .... х„).
Функция yf — не полностью определенная и в таблице значений функции только половина значений определена. При этом уі используется в качестве (п + 1)-го аргумента, хотя фактически ff зависит только от п аргументов.
Последовательность этапов синтеза схемы будет такой.
Система уравнений вида (11.5) может быть задана либо аналитически, либо в виде таблицы. Теперь нужно построить таблицу значений функции у?, полагая, что у\ является аргументом, и значения yf не определены для тех строк таблицы, которые отсутствуют в таблице значений уг- Функция yf записывается в СНДФ:
У? = f$(x 1, Х2, ..., Хп, у,) == Y *('х?...*?"уТ, (11.6)
Положим, что на неопределенных значениях ff — 0, тем самым находим функцию <ро(хі, Хі, ..., хп) (см. § 11.5). Далее положим Уі = 1 и запишем СНДФ функции\/| (1). После этого найдем минимальную форму для /f (1) (рис. 11.15,6). Затем составим таблицу покрытия (0) и выделим минимальное покрытие (рис. 11.15, в). В завершение определим оптимальный набор неопределенных значений ff. При этом ff станет определенной на всех наборах. В результате находится соответствующая МДНФ, на основе которой синтезируется схема.
сГ(1)=у(1
с*(0)=у(2, 4, 8, 15).
Таблица 11.5
Теперь составим таблицу покрытия для функции с*(0) (табл. 11.6).
\
Таблица 11.6'
импликанты
По минимальному покрытию находим оптимальное доопределение функции с*(0), в соответствии с которым получаем окончательный вид уравнений (рис. 11.16, в). Ответ. Сі=(а + Ьі + п, _ 1) п, + аЬ,п, -1; п,=(а + Ьі) п, _ і + ab,-
у = ф(хі, Хе, .... хп, 1) = фото? фНі V V «Ps-iTs-i, (11.7)
где ф, — конъюнктивный или дизъюнктивный терм от переменных (хі, хе, ..., хп); ті — вспомогательная функция, принимающая значение ті={0, 1} в момент времени
ч Форма представления временных логических функций (11.7) позволяет применить к функциям у все методы упрощения и минимизации, рассмотренные ранер.
Пример 11.8. Преобразовать функцию, представленную табл. 11.7, в вид (11.7).
Таблица 11.7
ф(.С|, Х'2, I)
ф(Г|, *2, І)
функции:
(11.8)
§ 11.6. ВРЕМЕННОЕ БУЛЕВЫ ФУНКЦИИ
Ранее были рассмотрены способы анализа и синтеза схем первого рода (комбинационных), которые невозможно использовать при описании схем второго рода (схем с памятью). Основная особенность схем с памятью состоит в том, что алгоритм их работы зависит от времени. Следовательно, в число переменных, от которых зависит выходная функция схемы с памятью, должно входить время t. Но время не является двоичной переменной. Поэтому вводится понятие автоматного времени, принимающего дискретные целочисленные значения 0, 1, 2 и т. д. Это означает, что работа схемы с памятью распадается на ряд интервалов, в течение которых автоматное время условно принимает постоянное значение.
Временная булева функция (ВБФ) — логическая функция у— = <р(хі, х%, ..., х„, і), принимающая значение {0, 1} при 0s^/<s — 1, где s — количество интервалов автоматного времени.
Можно утверждать, что число различных ВБФ равно 2s2". В самом деле, если функция времени принимает s значений, т. е. t=0, 1, 2, ..., 5—1, и каждому интервалу времени соответствует 2" различных двоичных наборов, то всегда будет s2" различных наборов. Следовательно, общее число ВБФ равно 2s2\
фо(*і, х2)=хіХ2; фі(хі, xi)=xix2 V xix2; фг(хі, x2)=xlx2 \/xiX2=xi.
На основании (11.7) записываем окончательный вид временной логической
У = ХіХ2То V (Х\Х2 V ХіХ2)ті V Х|Т2. Ответ-, см. формулу (11.8).
Разложение (11.7) можно применить только к периодическим временным функциям. Переход к схеме от логического выражения вида (11.7) можно осуществить следующим образом.
Предположим, что на выходах некоторой схемы (дешифратора) в моменты времени t появляются сигналы если ^ 1 = 0, то на выходе 1 сигнал т0=1, при ті = 0, Т2=0; если /2=1. то на выходе 2 сигнал п = 1, при то=0, т2=0; если /з=2, то на выходе 3 сигнал x2=l, при т0—0, т,=0.
Для каждой функции ф, строим соответствующую логическую схему, не зависящую от переменной і. После этого все схемы соединяем между собой в соответствии с (11.7).
Рекуррентная булева функция (РБФ) — логическая функция, зависящая как от текущих значений xt, входных переменных, так и от предшествующих значений самой функции г/((_Полная аналитическая запись такой функции
1h == ф(*,,, ХН, ..., х,„ yt-i, Уі-2, ..., yt-k) , (11.9)
1U — {0, 1} при />0,
где х'и — текущие значения входных переменных; у,• — значения выходных функций в момент времени j = t — 1; t — 2 и т. д.
X(t)
№
^L-h-JL-hjL
Рис. 11.17. Схема с обратной связью
Чтобы представить необходимость рекуррентных булевых функций, рассмотрим некоторый физический элемент, работа которого описывается соответствием:
t... О 1 2/,
Х...ХІ) JT| -ХІ...Х1-І Хі
yt = f{x, t)...0 Xq X)...Xj — 2 xi— I
Следовательно, yt+\ = xt. Отсюда значение выходного сигнала в момент времени t -j- 1 равно значению входного сигнала в момент времени t. Такой элемент называют задержкой; D(t) — его логический оператор.
Рассмотрим логическую схему, имеющую цепь обратной связи с включенной в нее схемой задержки (рис. 11.17, а). Предположим, что в качестве схемы с функцией f(x, у) взята логическая*схема ИЛИ. Тогда в совокупности эта схема работает так, как показано на временной диаграмме (рис. 11.17,6), т. е. f(x, у) = xt+\ V У и
В схеме рис. 11.17 выходной сигнал зависит как от входного сигнала в данный момент времени, так и от выходного сигнала в предшествующий момент времени. В самом общем случае при наличии п входов и k цепей обратной связи, в которых осуществляется равная задержка, такие схемы могут быть описаны с помощью рекуррентных временных логических функций.
Следовательно, любая рекуррентная булева функция может быть реализована с помощью набора логических операторов функциональных элементов, представляющих обычные функции алгебры логики, и операторов схем задержки.
§ 11.7. ПОСЛЕДОВАТЕЛЬНОСТНЫЕ АВТОМАТЫ
Рассмотрим частный случай рекуррентной временной логической функции. Допустим, что на вход функциональной схемы входные переменные не подаются, а поступают только сигналы по цепям обратных связей, т. е. в момент времени t(t^= 0) все х, =^= 0. Тогда рекуррентная булева функция (РБФ)
Уі(і + 1) =4>і(уи, Ук/-1), .... Ущ-s), Учи .... ymt.....УпіЦ-з))- (11.10)
Для таких функций всегда необходимо задавать нулевые значения (т. е. при t = 0). Предположим, что обратная связь осуществляется только на один такт времейи. Тогда
Уі(І+\) = фі(Уі/, УЧІ, •¦, Уті)- (11.11)
На рис. 11.18 представлена логическая схема последовательностного автомата, описываемая системой уравнений вида (11.11).
Последовательностные автоматы — схемы, описываемые системой уравнений вида (11.11) при заданных начальных условиях.
При этом для каждого набора входных переменных можно определить значения выходных переменных, 'предполагая, что в этот момент цепи обратной связи условно разорваны. Предположим, что получилась следующая таблица состояний автомата (табл. 11.8).
На основании данных этой таблицы записывается СНДФ для всех выходных параметров:
Ущ+\) — УиУчіУзі V УиУчіУзі V УиУчіУзі V УиУчіУзй
Учц+і) = УиУчіУзі V УиУчіУзі V УиУчіУзі V УиУчіУзй (11.12)
Уз(і+[) = УиУчіУзі V УиУчіУзі V УиУчіУзі V УиУчіУзі-
Уравнения (11.12) справедливы для любого момента времени.
Используя методы минимизации, можно получить следующую минимальную форму:
У\(і+\) = УиУчіУзі V УиУчіУзі V УиУчіУзі V УиУчіУзі',
Учц+і) = узі; (11.13)
У3(1+1) == Учіузі V УиУзи
Теперь рассмотрим работу автомата последовательно в различные моменты времени, начиная с t = 0. По условию, при t = Она входе действуют: у\$ = 1, уч,о = 1, Уз,о == 1. Из табл. 11.9 видно, что
Т а б л и ц а 11.9
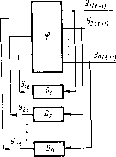
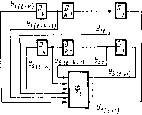
Таким образом, можно провести анализ работы автомата в любой фиксированный момент времени и получить полную таблицу.
Состояния автомата повторяются с определенным периодом (в данном случае он равен четырем). Периодичность и значение выходов зависят также от начального состояния автомата, в чем нетрудно убедиться, если задавать различные начальные условия.
Формулы (11.13), полученные в результате минимизации, позволяют построить схему автомата в выбранном базисе функций (И, ИЛИ, НЕ).
Таблицу состояний автомата можно также представить в виде диаграммы переходов, представляющей собой круг, разделенный на k равных частей, из которых каждая часть представляет- состояние входов автомата (соответственно выходов). Стрелками внутри круга соединяются входные наборы с соответствующими им выходными наборами.
§11.8. АНАЛИЗ ЭЛЕКТРОННЫХ СХЕМ, ОПИСЫВАЕМЫХ ВЫРОЖДЕННЫМИ РЕКУРРЕНТНЫМИ БУЛЕВЫМИ ФУНКЦИЯМИ
Можно представить некоторую логическую схему, которая задается следующей системой функций:
( У 1(<-Н) = фіО/іь уіи Узи */t(/-l), .... Уіу-к), i/sp-iy,-^., ys(t-k))\
................... (11.14)
1 ys(t-1) = <Ps(yu, yiu •••, yst, yu.t-1), ..., yi(t-k), ..., yS(t-1), ..., ys(t-k) .
При этом задаются начальные условия г/10, г/20, ...., у50, где ys0 = ={0, 1}.
Возможный вариант такой схемы изображен на рис. 11.19.
Если задана электронная схема последовательностного автомата, то анализ ее должен осуществляться в такой последовательности.
1. Написать систему уравнений вида (11.14), описывающих работу схемы, задать начальные условия.
2. Определить таблицу состояний или диаграмму переходов последовательностного автомата на основе полученной системы уравнений.
< </!(<+ () = У2іУЧІ- I) V </2(1-о;
\ t/2(( +1) —Ущ - 1)1/211/2(1- 11-
Ре ш е и и е. Определяем таблицу состояний (табл. 11.10) в общем случае, так как начальные условия не заданы.
Теперь в зависимости от различных обстоятельств можно задать начальные условия и получить конкретную таблицу состояний (табл. 11.11).
Пусть І/10= 0, (/20=1, </|(і-1)=1, У2(/-І) = °-Получился период повторения, равный трем.
Диаграмма переходов для данного случая представлена на рис. 11.21.
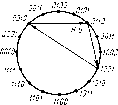
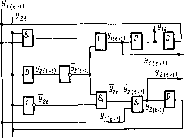
§11.9. АНАЛИЗ И СИНТЕЗ ЭЛЕКТРОННЫХ СХЕМ С ПОМОЩЬЮ РЕКУРРЕНТНЫХ БУЛЕВЫХ ФУНКЦИЙ
Рассмотрим некоторую обобщенную схему последовательностного автомата (рис. 11.22), которая описывается следующей системой:
В этой схеме выходные переменные зависят как от входных переменных, так и от внутренних состояний.
если qi = 0 при хі(/+і) = 1, то xj-p+i) не влияет; если qt = 1 при X2(t+i> = 1. то хці+1) не влияет.
Анализируя табл. 11.12, можно сделать вывод, что при 1і(,+ і) = = хга-і-і) = 1 переход триггера из одного состояния в другое зависит от значения qt. Если qt — 0, то qt+x = 1; если qt = 1, то qt+\ = = 0. Отсюда следует, что не обязательно подавать на входы триггера две независимых переменных, а достаточно подавать один сигнал на два выхода одновременно.
Выходная функция для этой схемы описывается уравнением
qt+i = Xi+\qt V xt+x qt. (11.17)
Триггеры со счетным входом — схемы, выходная функция для которых имеет вид (11.17).
Таблица состояний этой схемы имеет следующий вид (табл. 11.13).
На рис. 11.23 соответственно представлены условные обозначения триггера с двумя входами и триггера со счетным входом. Рассмотренные триггерные схемы — частичные случаи обобщенной схемы.
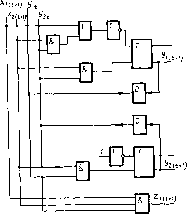
ма последовательностного схемы
автомата
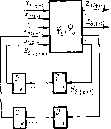
Выходная функция для этой схемы описывается уравнением
4t + l=Xi(t+l)X2(t+l)yt V X2(t+[)X2(t + \)yt V Х](І+\)Х2(1+І)Уі V V Xi(t+l)X2(t+i)yt,
которое после преобразования и минимизации имеет вид
Qt+i = X2(t+i)qt V (П.16)
Триггеры с двумя входами — схемы, выходная функция для которых имеет вид (11.16). Они обладают двумя устойчивыми
^<+1 = (*і,і+ь *2,<+і, -*п,і-иЬ
Yt = [уч, Учи ym,t};
^1+1 ={*/!,/+It </2,1+1, </m,l+l};
Zt+{ = {Zl,/+l, Z2./+2, -.-, Zk,t + \},
то система уравнений (11.15) может быть представлена в виде
'Yt+i = F{X,+ U Yt)\ Zt+, = Ф(Х1+[, Yt). (11.18)
Уравнения (11.18) называют каноническими уравнениями.
Пример 11.10. Уравнение уі(і + і)=*к<+і)Уп?*2(і + ч преобразовать так, чтобы его можно было реализовать с помощью триггера и других логических функций.
Решение. Так как триггер описывается уравнением yt+i—x2,t+iyt\/ хи + іуі, то, введя обозначения x2}t + i=yu+l, *і,і +1 =y{,t+ i, i/i,i +> =1/1,1+1 при yt = 1, и в результате подстановки ук=1 в исходное уравнение получим і/! + +1 =*і,і+1 V *2,і + і-Однако y2u + i=y,+ i при y, = 0. Значит, подставив yt = 0 в исходное уравнение, ПОЛуЧИМ y\j+l=X2,t+l-
Ответ: і/і,і+ і = (*і,і + 1 V *2,і + \)yt V *2,1 + ii/i.
: si"'-'
Теорема. Любую схему с памятью можно представить в виде совокупности схем И, ИЛИ, НЕ и триггеров.
Опираясь на теорему о разложении функции по k переменным, любое уравнение из системы уравнений (11.15) можно представить в виде
уs.t+1 = г/ифі(*и+ь *n/+j; 1> Уч.і, Ут.і) V
U2.!+ I
V </і,/фі(*и+1, *п,/+1; 0, y2.t, Ут.і)- (11.19)
Ml,( + l
В сокращенной записи (11.19) имеет вид
ys.t+1 = </2,l+l</l,l v U\.t+\y\.t,
что является уравнением триггера с двумя входами, при этом функции йі((+і) и «2(<+о — сигналы на входах триггера.
Произведя аналогичную операцию с другими уравнениями, придем к выводу, что все они могут быть записаны в виде (11.19).
Задание для самоконтроля
1. В чем заключается смысл введения логического оператора схемы?
2. Найти минимальную форму не полностью опредеЯенной функции:
а) А(*,вд)=У(1*, 2, 3*, 4, 5, 7*);
б) f2(x,x2x3x4) = Y(0, 1*, 2, 4, 6, 7*. 8, 9, 10*, 12, 14*);
в) /з(хіх2хз*4) = V(l*, 2, 5*, 6*, 8*, 12, 15).
3. Найти методом каскадов набор минимальных функций для следующих уравнений:
а) /і(хіх2хз) = /4В + SC + ЛС; б) fi(xix2x3) = AB + ВС; f2(x\x2x3) = ABC+ABC; f2(xix2x3) = AB С;
[з(хіх2х3) — А -(- В А~ С. /з(хі*2*з) = АВС АЁС.
Уці+ і) = *і(і + I)t/1/ V *2(i+ 1 )f/2;;
1/2(1+1) = *2(1+1)1/|1 V f/20
Z|(!+ 1) = *1(1 + 1)*2(1 + 1)1/21
построить электронную схему на элементах И, ИЛИ, НЕ и триггерах.
5. Используя элементы И, ИЛИ, НЕ и триггеры, синтезировать логическую схему, зада иную Системой уравнений:
1/1.1+1 ==*'1,1+1*’2,(+1І/1.( V 1/2,Г,
1/2,1+1 =*2,1+1 V 1/1,1-
6. Синтезировать логическую схему, заданную следующей таблицей состояний:
ВВЕДЕНИЕ В ТЕОРИЮ АВТОМАТОВ
Х = {х,(*)...хп(і)}Термин автомат, как правило, используется в двух аспектах. С одной стороны, автомат — устройство, выполняющее некоторые функции без непосредственного участия человека. В этом смысле мы говорим, что ЭВМ — автомат, так как после загрузки программы и исходных данных ЭВМ решает заданную задачу без участия человека. С другой стороны, термин «автомат» как математическое понятие обозначает математическую модель реальных технических автоматов [3, 4, 6]. В этом аспекте автомат представляется как «черный ящик», имеющий конечное число входов и выходов и некоторое множество внутренних состояний Q = {qi(t), q2(t)... qn(t)}, в которые он под воздействием входных сигналов переходит скачкообразно, т. е. практически мгновенно, минуя промежуточное состояние. Конечно, это условие не выполняется в реальности, так как любой переходный процесс длится конечное время. /
Автомат называется конечным, если множество его внутренних состояний и множество значений входных сигналов — конечные множества.
В практике часто используется понятие цифрового автомата, под которым понимают устройство, предназначенное для преобразования цифровой информации.
Входные сигналы в цифровых автоматах представляются в виде конечного множества мгновенных сигналов. Теоретически это означает, что входные сигналы не имеют длительности, хотя практически это не так. Такое допущение упрощает рассмотрение процессов, происходящих в автоматах, так как все события (состояния) должны относиться к фиксированному моменту времени t. Условно также принимается, что число выходных сигналов y(t) конечно и они возникают в результате действия входных сигналов. При этом следует учитывать, что одновременно с появлением выходного сигнала происходит скачкообразный переход автомата из состояния q\{t) в состояние q2{t).
Цифровой автомат называется правильным, если выходной сигнал y(t) определяется только его состоянием q(t — 1) или q(t) и не зависит от входных сигналов.
Пусть имеется цифровой автомат с одним входом (рис. 12.1).
^ и одним выходом
¦¦л
Математической моделью цифрового автомата является абстрактный автомат, заданный совокупностью шести объектов:
1) конечное множество X входных сигналов (входной алфавит автомата):
X = x2(t)... xn(t)};
2) конечное множество Y выходных сигналов (выходной алфавит автомата):
Y = {yi(t), y2(t)... yk{t)}\
3) произвольное множество Q состояний автомата:
Q={qi(t), q2(t)... qs(t));
4) начальное состояние автомата q0, как элемент множества Q:
q0(t)^Q;
5) функция б(q, х) (функция перехода автомата из одного состояния в другое);
6) функция Х(<7, х) (функция выходов автомата).
В начальный момент времени to автомат находится в состоянии qo¦ В каждый момент времени t автомат способен принять входной сигнал x(t) и выдать соответствующий выходнЬй сигнал y(t).
Через понятие «абстрактный автомат» реализуется некоторое отображение множества слов входного алфавита X в множество слов выходного алфавита Y.
Понятие состояния автомата используется для описания систем, выходы которых зависят не только от входных сигналов в данный момент времени, но и от некоторой предыстории, т. е. сигналов, которые поступили на входы системы ранее. Состояние автомата соответствует некоторой памяти о прошлом, позволяя устранить время как явную переменную и выразить выходные сигналы как функцию состояний и входных сигналов.
Работу абстрактного автомата следует рассматривать применительно к конкретным интервалам времени, так как каждому Интервалу дискретности t будет соответствовать свой выходной кигнал y(t). При этом предполагается, что выходной сигнал на одном из выходов автомата может появиться только после соответствующего этому же моменту времени входного сигнала с одновременным переходом из состояния q(t — 1) в состояние q(t).
Время для цифрового автомата имеет также важное значение. Для решения задач анализа и синтеза цифровых автоматов обычно вводится автоматное время. Функционирование автомата рассматривается через дискретные интервалы времени конечной продолжительности (интервал дискретности).
Общая теория автоматов при сделанных выше допущениях разбивается на две больших части — абстрактную теорию автоматов и структурную теорию автоматов. Различие между ними заключается в том, что в абстрактной теории мы отвлекаемся от структуры как самого автомата, так и его входных и выходных сигналов. Не интересуясь способом построения автомата, абстрактная теория изучает лишь те переходы, которые претерпевает автомат под воздействием входных сигналов, и те выходные сигналы, которые он при этом выдает. Абстрактная теория автоматов близка теории алгоритмов, является ее дальнейшей детализацией.
В противоположность абстрактной теории, в структурной теории автоматов рассматриваются прежде всего структуры как самого автомата, так и его входных и выходных сигналов. В структурной теории изучаются способы построения автоматов из элементарных автоматов, способы кодирования входных и выходных сигналов элементарными сигналами и т. п.
Автоматы классифицируют по двум наиболее распространенным признакам. \
1. Объем памяти. Памятью автомата называют число его состояний.
Рассмотренные выше автоматы Поста (или Тьюринга) являются бесконечными автоматами, так как имеют неограниченную память на ленте. Конечными автоматами являются отдельные части ЭВМ или вся машина.
2. Механизм случайного выбора. В детерминированных автоматах поведение и структура автомата в каждый момент времени однозначно определены текущей входной информацией и состоянием автомата. В вероятностных автоматах они зависят от случайного выбора.
В теории автоматов установлено, что для осуществления различных преобразований информаций совсем не обязательно каждый раз строить новые автоматы: в принципе это можно сделать на универсальном автомате с помощью программы и соответствующего кодирования.
В теории автоматов наиболее полно описаны синхронные автоматы. В зависимости от способа определения выходного сигнала в синхронных автоматах существует две возможности:
2) выходной сигнал y(t) однозначно определяется входным сигналом x(t) и состоянием q(t) в данный момент времени. Следовательно, закон функционирования абстрактного автомата может быть задан следующимчобразом: для автомата первого рода
q(t)=f>(q(t- 1), *(*)), y(t)=k(q(t- 1 ),х(0), *= 1,2...;
для автомата второго рода
|<7(0 = в(?(* — 1),*(0), (12.2)
\y(t) = k(q(t), x(t)), *=1,2....
Для дальнейшего анализа целесообразно рассмотреть вопрос о взаимоотношении автоматов первого и второго родов.
Предположим, что произвольный автомат 5 второго рода задан уравнениями (12.2). Для этого автомата построим новую функцию
h(qi, х)= k(b(q(t — 1), х(0), x(t)).
На основании закона функционирования (12.2)
у(і) = Щ(д(1-\), x(t)), x(t))=h(q(t-l), x(t)). (12.3)
Получили новый автомат R первого рода, заданный той же функцией перехода б(q,x) и функцией выходов k\(q,x).
Таким образом, для каждого автомата S второго рода существует эквивалентный ему абстрактный автомат R первого рода, функция выходов которого получается в результате подстановки функции переходов автомата S в его сдвинутую функцию выходов:
k\(q, х) = Х (б(<7, х), х).
Для дальнейшего изложения примем, что произвольные автоматы первого рода [формула (12.1)] будут называться автоматами Мили, а частный случай автоматов второго рода, для которых сдвинутая функция выходов X(q, х) не зависит от второй переменной х — автоматами Мура.
Закон функционирования автоматов Мура задается в виде: j?(0 = ЩЦ - 1), x(t)),
\y(t) = k(q(t)).
В отличие от автомата Мили, выходной сигнал в автомате Мура зависит только от текущего состояния автомата и в явном виде не зависит от входного сигнала.
Между моделями Мили и Мура существует соответствие, позволяющее преобразовать закон функционирования одного из них в другой или обратно. Такое преобразование порождает пару описаний законов функционирования, эквивалентных в том смысле, что им соответствует одинаковая зависимость между входной X и выходной Y последовательностями.
Q — {<7і, ... qs) — множество состояний;
X = {x\(t)... xn{t)\ — входной алфавит;
У = {у 1 (/)... yk(t)} — выходной алфавит типа 1;
U = {m(t) ... um(t)} — выходной алфавит типа 2;
б : QX^ Q — функция переходов, реализующая отображение ?)6^QXA в Q;
Хі : QXA Y — функция выходов, реализующая отображение DXlsQXA на У;
Я,2 : Q U — функция выходов, реализующая отображение
Z\EQ на U;
q0^Q —начальное состояние автомата.
Абстрактный С-автомат можно представить в виде устройства с одним входом, на который поступают сигналы из входного алфавита X, и двумя выходами, на которых появляются сигналы из выходных алфавитов У и (У (рис. 12.2).
-Ук^))г
U={u,(t)...un(t)}
Рис. 12.2. Совмещенная модель автомата с одним входом и двумя выходами
Отличие С-автомата от моделей Мили и Мура состоит в том, что он одновременно реализует две функции выходов Х| и А,2, каждая из которых характерна для этих моделей в отдельности. Этот автомат можно описать следующей системой уравнений:
q(t + 1) = б (q(t),x(t));
y(t) = Kx(q(i),x(t))[ (12.5)
u{t) = l2(q(t)).
Выходной сигнал и = X2(qs) выделяется все время, пока автомат находится в состоянии qs. Выходной сигнал yk = kt(qs, хп) выдается во время действия входного сигнала хп при нахождении автомата в состоянии qs. От С-автомата легко перейти к автоматам Мили или Мура (с учетом возможных сдвигов во времени на один такт), так же как возможна трансформация автомата Мили в автомат Мура, и наоборот.
В зависимости от способа задания функцией переходов и выходов (б и X) в настоящее время выделяют два класса языков — начальные языки и стандартные, или автоматные языки. В начальных языках автомат описывается на поведенческом уровне,
т. е функции переходов и выходов обычно в явном виде не заданы. Поведение автомата описывается в терминах входных и выходных последовательностей, реализуемых операторов (отображений) или управляющих последовательностей сигналов, воздействующих на операционный автомат. В автоматных языках поведение автомата задается путем явного задания функций переходов и выходов. Среди начальных языков следует выделить язык регулярных выражений алгебры событий, язык логических схем алгоритмов, язык граф-схем алгоритмов.
Рассмотрим кратко язык регулярных выражений алгебры событий. Для заданного конечного множества входных букв X = = {дсі ... хп} регулярное выражение задается следующим образом. Для построения языка регулярных выражений используются три операции над событиями (две бинарные и одна унарная):
1) А U В—объединение (дизъюнкция);.
2) АВ — умножение (конкатенация);
3) {Л} —итерация (обозначается также Л*).
Выражение, построенное из букв алфавита А и из символов операций объединения, умножения и итерации с использованием соответствующим образом круглых скобок, называется регулярным выражением в алфавите X. Всякое регулярное выражение R определяет некоторое событие S (S получается в результате выполнения всех операций, входящих в выражение R). События, определяемые таким образом, называются регулярными событиями над алфавитом X. Другими словами, регулярным событием называется событие, полученное из элементарных событий (однобуквенных слов Хі) применением конечного числа раз операций дизъюнкции, умножения и итерации. Например, в алфавите из трех букв х, у, г регулярное выражение х{х V у V z) {у V z) задает регулярное событие, состоящее из всех слов, которые начинаются буквой х и заканчиваются буквой у или z. Регулярные события и только они представимы в конечных автоматах.
Пусть необходимо описать автомат, выдающий сигнал (щ всякий раз, когда происходит изменение входной буквы с х\ на х2. Другими словами, сигнал соі должен выдаваться в ответ на любые входные последовательности, кончающиеся последовательностью х\х2. Фраза «любые входные последовательности» формализуется всеобщим, или универсальным, событием, состоящим из всех возможных слов в алфавите х\х2. Такое событие записывается как {*і V х2]. Тогда событие Sb в ответ на которое должен выдаваться сигнал ши будет описываться регулярным выражением:
S1 /о>і = {хі V Х2}Х\Х2.
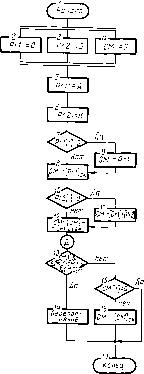
Порядок выполнения операций в автомате определяется программой (или микропрограммой), представляющей собой совокупность микроопераций и логических условий.
Под микрооперацией обычно понимается элементарный процесс переработки информации в одной из частей автомата, происходящий за время такта работы автомата. При этом устройство управления вырабатывает управляющие сигналы, которые обозначим символом V = [?\, ?2... vs). Ход выполнения микроопераций может нарушаться в зависимости от условий, задаваемых множеством Z = {Z\ ... zk).
Запись алгоритма, выполненная с учетом вышеизложенного, называется логической схемой алгоритма (ЛСА).
Логические схемы алгоритмов удовлетворяют следующим условиям:
1) содержат один начальный (ин) и один конечный оператор (Ик);
2) перед оператором ?н и после оператора ?к стрелок быть не должно;
3) вслед за каждым логическим условием всегда стоит верхняя стрелка;
4) не существует двух одинаковых (с одинаковыми цифрами) нижних стрелок;
5) для каждой нижней стрелки должна быть по крайней мере одна соответствующая ей (с одинаковой цифрой) верхняя стрелка;
6) для каждой верхней стрелки должна быть точнВ( одна соответствующая ей (с одинаковой цифрой) нижняя стрелка.
Описание поведения автомата с помощью ЛСА поясним на следующем примере:
V„Z\ \ V\ \ Z22\ V2V3Z3 f t>4 I ?Ь?К . (12.6)
Эта ЛСА имеет операторы начала и конца (ин и ок)> пять операторов (щ -Е Н5) и три логических условия (zi, Z2, 23). Начальному оператору соответствует некоторое начальное состояние автомата, при'котором никакие микрооперации не выполняются. Если в начальном состоянии на первый вход устройства придет сигнал, равный единице (z 1 = 1), то устройство перейдет в новое состояние, в котором выполняется оператор ?\ — первый справа после логического условия z\, а затем проверяется логическое условие 22. Если же z 1 = 0, то выходим по верхней стрелке f и входим по нижней стрелке с той же цифрой на проверку логического условия z2, минуя выполнение оператора гм. Если z2 = 0, то переходим к выполнению оператора ?ъ- Если же гг = 1, то выполняются операторы ?2 и ?з и проверяется оператор 23; если 23 = 0, то оператор гм не выполняется, происходит переход к оператору у5. После выполнения оператора о5 происходит переход к конечному оператору, т. е. работа дискретного устройства заканчивается.
Конечная, операторная и условная вершины имеют по одному торная вершины имеют по одному выходу, конечная вершина выходов не имеет, условная вершина имеет два выхода, помеченных символами 1 и 0. Граф-схема алгоритма удовлетворяет следующим условиям:
1) входы и выходы вершин соединяются друг с другом с помощью дуг, направленных всегда от выхода ко входу;
2) каждый выход соединен только с одним входом;
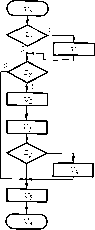
4) любая вершина графа лежит по крайней мере на одном пути из начальной к конечной вершине;
5) в каждой условной вершине записывается один из элементов множества логических условий Z={zi...zl}, разрешается в различных условных вершинах запись одинаковых элементов множества Z;
6) в каждой операторной вершине записывается один из элементов множества операторов V = (щ ... разрешается в различных операторных вершинах запись одинаковых элементов множества V.
На рис. 12.3 представлена граф-схема алгоритма, описанная выражением 12.6. Язык ГСА используется очень часто при описании алгоритмов функционирования как самого цифрового автомата, так и программ, выполняющих то или иное действие.
При проектировании различных устройств ЭВМ обычно используются содержательные граф-схемы алгоритмов, которые описывают не только формальные элементы, а также логические условия и микрооперации в содержательных терминах. Основные правила выполнения содержательных граф-схем алгоритмов и программ, которые студенты разрабатывают в процесс выполнения курсовой работы, представлены в соответствующих ГОСТах. В качестве иллюстрации на рис. 12.4 представлена содержательная граф-схема алгоритма операции сложения чисел, представленных в форме с фиксированной запятой.
§ 12.3. АВТОМАТНЫЕ ЯЗЫКИ ДЛЯ ЗАДАНИЯ АВТОМАТНЫХ ОТОБРАЖЕНИЙ
Среди автоматных языков наиболее распространены таблицы, графы и матрицы переходов и выходов.
Таблица переходов (выходов) представляет собой таблицу с двойным входом, строки которой нумерованы входными буквами, а столбцы — состояниями. На пересечении указывается состояние, в которое переходит автомат (в таблице переходов) или выходной сигнал, выдаваемый им (в таблице выходов).
Описание работы автомата Мили таблицами переходов и выходов иллюстрируется на примере автомата Si :
6: QXX-+Q* k:QXX -+Y*
На пересечении столбца qm и строки х/ в таблице переходов ставится состояние qs = б(qm, Xf), в которое автомат переходит
Иногда при задании автоматов Мили используют одну совмещенную таблицу переходов и выходов, в которой на пересечении столбца qm и строки х/ записываются в виде qs/yg следующее состояние и выдаваемый выходной сигнал. Так, для автомата Si имеем следующую совмещенную таблицу:
Так как в автомате Мура выходной сигнал зависит только от состояния, автомат Мура задается одной отмеченной таблицей переходов, в которой каждому ее столбцу приписан, кроме состояния qm, еще и выходной сигнал yg = X(qm), соответствующий этому состоянию. Пример табличного описания автомата Мура S2:
Для частичных автоматов, у которых функции б или X определены , не для всех пар (qm, Xf)?QXX, на месте неопределенных состояний и выходных сигналов ставится прочерк.
Часто автомат задают с помощью графа автомата. Этот язык удобен и нагляден. Граф автомата — ориентированный граф, вершины которого соответствуют состояниям, а дуги — переходам между ними. Две вершины графа автомата qm и qs (исходное состояние и состояние перехода) соединяются дугой, направленной от qm к <7.,, если в автомате имеется переход из qm в qs, т. е. если qs = = б(qm, Xf) при некотором х;?Х. Дуге (qm, qs) графа автомата приписывается входной сигнал Xf и выходной сигнал yg=X(qm, xf). При описании автомата Мура в виде графа выходной сигнал yg записывается внутри вершины qm или рядом с ней. На рис. 12.5, а, б приведены графы автоматов Si и S2, описанных ранее табличным способом.
Любой автомат может быть задан с помощью графа, но не всякий. граф в алфавитах Q, X, Y задает автомат. В графе автомата не должно существовать двух дуг с одинаковыми входными сигна-
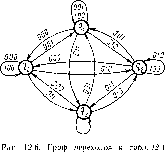
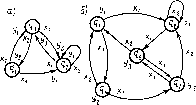
Иногда применяется способ задания автомата с помощью матрицы переходов и выходов, которая представляет собой таблицу с двумя входами. Строки и столбцы таблицы отмечены состояниями. Если существует переход из состояния qm под действием входного сигнала х\ в состояние qs с выдачей выходного сигнала Уі, то на пересечении строки qm и столбца qs записывается пара х)/Уі-
' Для автомата Мура используется матрица, столбцы которой отмечены выходными сигналами уіу а на пересечении ее строк и столбцов указываются только входные сигналы х/.
Ниже приведены матрицы переходов и выходов для рассмотренных ранее автоматов Si и S2:
Рассмотрим пример составления графа автомата.
Пусть задано некоторое устройство в виде табл. 12.1.
В табл. 12.1 три последние набора не имеют выходного значения, т. е. выходы не определены.
Рассмотрим последовательно входные наборы (рис. 12.6).
1) хіх2х3=000. Этому набору соответствует начальное состояние цо, которое не должно изменяться, что отображается дугой, выходящей и входящей в <70.
2) xiJt2X3=001. Состояние устройства меняется на q\. Значит, проводится дуга от состояния qo к состоянию q\ и помечается набором 001.
3) хіХ2Х3=010. Новое состояние обозначим <72, для чего соединим qo и дугой и обозначим ее набором 010.
5) хіХ2Хз= 100. В таблице этому входному набору соответствует два набора: либо 111, либо 000, что помечено звездочкой *(. Для определенности можно уточнить, что выбран набор 000, т. е. возврат в начальное состояние. Значит, надо отметить дугу, входящую и выходящую из q0 еще набором 100.
Аналогичным образом поступаем с остальными внутренними состояниями <7і, <72, <7з, в результате чего получаем окончательный граф переходов для рассматриваемого автомата (рис. 12.6).
На основании графа автомата можно составить таблицу переходов (табл. 12.2) или таблицу выходов.
Состояние автомата, вершина графа для которого имеет только Исходящие дуги, но не имеет входящих дуг, называется переходящим. В такое состояние попасть нельзя, из него можно только выйти.
Состояние автомата называется тупиковым, если соответствующая вершина графа не содержит исходящих дуг, но имеет хотя бы одну входящую дугу.
Таким образом, с помощью графов абстрактная модель автомата записывается в виде некоторого пространственного изображения, которое помогает при решении задач анализа или синтеза.
Любое разбиение множества состояний автомата на ряд подмножеств, объединяющих некоторые состояния, приводит к понятию подавтомата.
§12.4. СОЕДИНЕНИЕ АВТОМАТОВ
Существует несколько основных способов соединения автоматов.
Параллельное соединение автоматов Si и S2 представлено на рис. 12.7, а. Имеется общий входной алфавит X и некоторое устройство ф, объединяющее выходы автоматов ф: УіХ^г-^У-
Автоматы заданы:
Si = {Qi, Ху Yі, 6і, Я,і},
52=={Q2, X, Y2, 82, X2}.
В результате объединения получаем новый автомат S={Q, X, Y, 8, А,}, для которого заданы следующие параметры:
множество состояний Q = QiXQ2 образуется из всевозможных пар состояний автоматов Si и S2, т. е. Q={qm=(qmi, qm2)\qm\^Q\, <7т2бС?г};
входной алфавит Х\
выходной алфавит У=ф(Уі X У2);
функция переходов определяется правилом 8(qm, Xf) = (8\(qmly Xj), 82(qm2, Xj)), тле xf?X;
функция выходов определяется правилом X(qm\, x}y—q{Xi(qmi, Xj), X2{qm2, xf)).
Пусть два автомата, соединяемых параллельно, заданы следующими таблицами: табл. 12.3 — S\={B, X, 6і, Х\}, табл. 12.4 — S2 = {C, X, Y2, б,, X,}.
Таблица 12.3
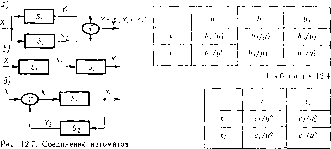
Q = BXC={(b 1, с,), (bu с2). (b2, ci), (b2, c2)y (b3, Ci), (b3, c2)} =
= Wi-<76};
X={xu x2};
У={Уі, г/2, Уз}-
Функция переходов 8 = QXX-+Q задается табл. 12.6.
Функция выходов X задается табл. 12.7:
Последовательное соединение двух автоматов представлено на рис. 12.7,6. В этом случае первый автомат Si, второй автомат S2, т. е. выходы первого автомата являются входом второго. Результи-
Q ~ Q1 X Q2, ИЛИ Q={qm = (qm\, qm2)\qm\ 6 Qt, 7/m2^Q2},
X = X;
У==У:
функция переходов:
8{qm\, Xf)~(8i(qni, xf), 62(</m2, к2{цт\, */)))> или
8(QX*)=(6i(QiXX), S^XMQ.X*)));
функция выходов X:
k(qm, x/)=k2(qm2, ki(qm 1, Xf)), или A,(QX^0=ta(Q2XM(Qi X*))-
В качестве примера рассмотрим те же автоматы Si и S2, заданные табл.12.8, 12.9.
___ ,_і_I_I
Результирующим автоматом последовательного соединения автоматов Si и S2 будет автомат S, для которого:Q = {(bu Сі), (bu с2), (bn, Ci), (62, c2), (63, Ci), (b3, c2)} = {qi...q6}; X={x\, x2}\
Y={yV; «#}•
Соединение автоматов с обратной связью представлено на рис. 12.7, в. В этом случае автоматы Sі = {Qі, Х\, Уі, бі, Ац} и S2= = {Q2, У1, У2, б2, А2}. Имеется некоторый функциональный преобразователь у, являющийся автоматом без памяти, который реализует отображение у:ХХУ2-^і- В этом случае, по крайней мере, один, из автоматов Si или S2 должен быть автоматом Мура. Пусть S2 — автомат Мура, у которого У2 = А,2(<32). Тогда результирующим автоматом такого соединения с обратной связью будет новый автомат S = {Q, X, У, б, А,}, для которого:
Q-Q 1 X Q 2 ==={qm —^ml, q т2)\ 1/ml 6 Ql, *7m2€Q2}»
У = У i;
функция переходов определяется следующим образом:
б(qm, x;) = (8i(qmi, y(xf, k2(qm2))), 82(qm2, ki(qmU y(xf, k2(qm2)))), или 6(QX2)=(6,(Q,Xv(^XMQ2))), 62(Q2X^(QiXy(^XMQ2))));
функция выходов определяется следующим образом: k(qm, х/)= ki(qmi, у(х[, k2(qm2))), или X X) = Xj(Qi ХтС^ХМФг))).
В качестве примера рассмотрим два автомата: Si = {B, Р, У, бі, кі} и S2={C, У, V, б2, к2}, которые заданы табл. 12.12 и 12.13.
-
Х(*2, Хі)))=(6і, б2(с, у2))=(Ьі, c2)=q2.
Функция выходов к определяется табл. 12.11:
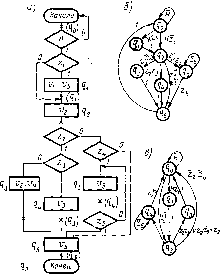
Х—{хі, х2, жз};
У={уь </2, уз};
функция переходов б: QXX~Q определяется следующим образом (табл. 12.15):
6(у3, і)=6((Ь2, Сі), Хі)=(6і(&2. у(ь ^г(сі))));
б2(сі, Xi(b2, ?(хь А,2(сі))))=(бі(б2, у(хи ?і), б2(сі, Х,(Ь2> у(х,, »ч)= —(бі(Ьг, V), 62(cj, Яі(б2, рі)))=(б2, б2(сі, х2))=(Ь2, с2)=Яз.
— функция выходов X-.QXX^Y задается табл. 12.16:
КЯъ, Х\)=А,((б2, Сі)хі)= Х,і(б2, у(хь А.2(сі)))=Хі(Ь2, у(хі, 0,))=
=Хі(Ь2, р1)=у2.
Управляющее устройство состоит из отдельных логических схем, вырабатывающих управляющие сигналы в заданной последовательности. Такое управляющее устройство можно рассматривать как управляющий автомат типа Мура или Мили.
Чтобы построить схему управляющего автомата, нужно задать микропрограмму работы операционного устройства. Микропрограмма может быть задана в виде граф-схемы (рис. 12.8, а). Микро-
СМ 1-
Рис. 12.9. Схема к примеру 12.1
Таблица 12.17
Операция
Сброс СМ Загрузить А Загрузить В С = АфВ С = А+В
Результат
Zo
Zi
Z2
Z3
Z4
Z5
1
2
3
4
5
6
Состояния
qi — Яі + І
Для автомата Мура выходной сигнал зависит только от внутреннего состояния, т. е. в нашем случае v = F(Q). Поэтому каждая операторная вершина граф-схемы алгоритма должна быть отмечена символом исходного состояния автомата с/і. На рис. 12.8, а слева от операторов дана отметка граф-схемы, интерпретируемой как автомат Мура. По этим отметкам можно построить граф переходов автомата Мура (рис. 12.8,6), где вершинами являются состояния автомата, а дугами — условия переходов из одного состояния в другое. Таким образом, функции выходов автомата Мура
Vj=\/qh
і
где <]і — состояние автомата, обеспечивающее выработку сигнала Vj.
Переход автомата из одного состояния в другое при отсутствии логических условий (безусловный переход) происходит под действием синхросигнала. Условный переход происходит в том случае, если соответствующее условие z,-=l.
Для построения автомата Мили следует помнить, что выходной сигнал зависит как от внутреннего состояния, так и от входного сигнала (т. е. условия zi): V=/?(Q, Z). Разметка граф-схемы для автомата Мили делается иначе, чем для автомата Мура. Символом qo отмечаются вход первой вершины графа, следующей за начальной, и вход конечной вершины. Выходы других операторных вершин отмечаются символом qi. На рис. 12.8, а автомат Мили отмечен символами, взятыми в скобки. Граф переходов автомата Мили показан на рис. 12.8, в. В автоматах Мили функции выходов, по которым вырабатываются сигналы микроопераций, определяются по формуле
Рі= У q{\Jzk),
‘ к
где qt — состояние автомата, сопровождающегося выработкой сигнала vf, Zk — логическое условие, определяющее выработку сигнала Vj при переходе автомата из состояния qt.
В случае безусловного перехода автомата из состояния qt сигнал Vj определяется только значением qt.
После построения автомата Мура или Мили функционирование управляющего автомата представляют в виде таблиц переходов и выходов. Для этого вначале производят кодирование состояний автомата двоичными кодами, определяют тип и количество триггеров. Затем по таблице переходов устанавливают значения сигналов на входах триггеров, при которых осуществляются переходы; определяют функции возбуждения триггеров и производят их минимизацию (упрощение). По найденным выражениям строится схема управляющего автомата на выбранных элементах.
Решение. Опишем операции сумматора в виде -..,„„„т,п„гпаммы (табл. 12.17).
Микропрограмма
МПо = Нщщ МПі =Ноіо2щ МПг =НщРзЩ МПз = Н'Щ020з0/, МГЦ = Ноі02оз040іг МГІ5 = Н ?5?к
_1_,_
В табл. 12.17 символ Н обозначает начальное логическое условие, инициирующее выполнение заданной операции при Н=1; символ ?к обозначает пустую микрооперацию, посредством которой управляющий автомат сигнализирует внешнему
устройству о завершении операции.
На основании табл. 12.17 составляем граф-схему микропрограммы (рис. 12.10, а). Производим отметку граф-схемы микропрограммы по указанным выше правилам для автомата Мура. Затем составляем граф переходов и таблицу переходов, в которых указываются все возможные переходы и соответствующие им условия
,п 1" « ¦¦ —«п 19 1КЗ
перехода
триггеров
0
1
1

Рис. 12.10. Алгоритм микропрограммы работы автомата (а), алгоритм переходов автомата Мура (б)
9о = 000; <7і == 001; <72 == 010; 9з = 011;
<74=100; <75 = 101; = 0 110.
По результатам табл. 12.18 напишем логические уравнения для сигналов на входах триггеров, которые после минимизации примут вид:
D1 =<70//V <7iZoZ2 V </2Zi;
?>2 = 90 V 9б V ?3Z4;
йъ = цШгъ V <JiZoV <?2Zi V 9з? 94 V 95-
Логическая схема управляющего автомата Мура дана на рис. 12.11. Расшифровку состояний автомата выполняет дешифратор, построенный на логических элементах И, который подключен к выходам Д-триггеров, и вырабатывает сигналы: v\=qi\ 1)2 = 92; нз = 9з; 1)4 = 94; ^5 = = 95. Для управления всех схем использован /?6-триггер, который под воздействием сигнала «Пуск» устанавливается в единичное состояние (Н=1) и возвращается в нулевое состояние (Н = 0) по сигналу конец операции (z^ = q&).
Ответ: схема на рис. 12.11.
Рис. 12.11. Логическая схема автомата Мура
1. Почему необходимо задавать начальное состояние автомата?
2. В чем состоит отличие автомата Мура от автомата Мили?
3. Что такое программа автомата?
4. Чем отличается операционный автомат от управляющего автомата?
5. Чем отличается граф автомата от содержательного графа автомата?
6. Что такое разметка граф — схемы автомата?
ЛИТЕРАТУРА
2. Балашов Е. П., Пузанков Д. В. Микропроцессоры и микропроцессорные системы.— М.: Энергия, 1981.
3. Баранов С. И. Синтез микропрограммных автоматов. — М.: Энергия, 1974.
4. Еаврилов М. А. Теория релейных и конечных автоматов. — М.: Наука, 1983.
5. Гивоне Д., Россер Р. Микропроцессоры и микрокомпьютеры/Пер. с англ. — М.: Мир, 1983.
6. Глушков В. М. Синтез цифровых автоматов. — М.: Наука, 1962.
7. Каган Б. М. Электронные вычислительные машины и системы.—М.: Энер-гоатомиздат, 1985.
8 Микропроцессоры/Под ред. Л. Н. Преснухина в 9-и кн. — М.: Высшая школа, 1984.
9. Дж. фон-Нейман. Теория самонастраивающихся автоматов. — М.: Мир, 1971.
10. Питерсон У., Уэлдон Э. Коды, исправляющие ошибки/Пер. с англ. — М.: Мир, 1976.
11. Поспелов Д. А. Арифметические основы вычислительных машин дискретного действия. — М.¦. Энергия, 1970.
12. Савельев А. Я. Арифметические и логические основы цифровых автоматов. — М.: Высшая школа, 1980.
13. Сяо Д., Керр Д., Мэдник С. Защита ЭВМ. — М.: Мир, 1982.
14. Темников Ф. Е„ Афонин В. А., Дмитриев В. И. Теоретические основы информационной техники. — М-: Высшая школа, 1979.
15. У оперли Д. Архитектура и программирование микро-ЭВМ/Пер. с англ.— М.: Мир, 1984.
16. ФистерМ. Логическое проектирование цифровых вычислительных машин. Киев, 1964.
17. Хоровиц Л., Хилл У. Искусство схемотехники в 2-х томах. — М.: Мир, 1983.
18. Хоффман Д. Д. Современные методы защиты информации. — М.: Советское радио, 1980.
19. Шоломов Л. Л. Основы теории дискретных логических и вычислительных устройств. М., 1980.
20. Энциклопедия кибернетики. Т. 1,2. Киев, 1975.
21. Яблонский С. В. Функции алгебры логики и классы Поста,—М.: Наука, 1966.
Автомат 248
— абстрактный 41
— дискретный 3
— конечный 248
— Мили 251
— Мура 251
— операционный 264
— последовательностный 240
— правильный 248
— управляющий 264
— цифровой 3 Автоматное время 249
— изображение числА 42, 60 Алгоритм 44
Базис 194 Бит 18
Вес кодовой комбинации 143
— — — арифметический 164
— разряда 48 Виженера квадрат 171 Высказывание 178 Вычислительная машина 15
— — аналоговая 31
— — гибридная 31
— — цифровая 31
— — электронная 31
— система 39
— — неразделимая 39
— — разделимая 39 Вычитатель двоичный 70
Глубина числа 18 Граф автомата 257 Граф-схема алгоритма 255
Декодирование 26
Диапазон представления числа 49
Дизъюнктор 225
Дизъюнкция 179
Дискретизация 22
Длина разрядной сетки 49
— числа 18, 49
Доступ 169
— де-Моргана 183
— переместительный 183
— поглощения 184
— распределительный 183
— сочетательный 183 Запрет (функция) 179
Избыточность информации 20. Инвертор 225 Информатика 15 Информация 16
— входная 36
— выходная 36
— дискретная 16
— непрерывная 16 Информационная модель канала 27
— система 15
Канал связи 27 Квайн 200 Квантование 22 Код арифметический 161
— двоичный 140
— десятичный (Д-код) 122
— систематический 142
— Шеннона—Фано 145
— Хэминга 148
— числа дополнительный 63
— — прямой 63
— — обратный 64 Кодирование 26 Кодовое расстояние 143
— арифметическое 162 Конъюнктор 226 Конъюнкция 180
Логическая переменная 178
— функция 178
— схема алгоритма 254 Логический оператор схемы 225
Масштабный коэффициент 60 Машина Поста 41
— Тьюринга 41 Машинный нуль 61 Мера информации 16
— геометрическая 17
— комбинаторная 17
— логарифмическая 18
— семантическая 20
— статистическая 18
— структурная 16
— Шеннона 21 Микрооперация 254 Микропрограмма 254 Микропроцессор 38 Минтерм 187
Нормализация числа 77 Нормальная форма 188
--дизъюнктивная 188
--конъюнктивная 189
— — совершенная 191
Округление 85 Операнд 68
Память автомата 252 Переполнение разрядной сетки 75 Подавтомат 260 Постулат Поста 44 Программа автомата 42 Пропускная способность 28 Процессор 37 Полусумматор 69
Ранг терма 187
Свертывание кода 155 Сдвиг простой 77
— модифицированный 77 Символ 16
Система контроля 141
— счисления 46
— — двоичная 54
— — десятичная 49
— — непозиционная 46
— — позиционная 47 Слово 16
Схемы комбинационные 221
— накапливающие 221 Сумматор Двоичный 69
— десятичный 125
— дополнительного кода 72
— обратного кода 73
— прямого кода 71
Теорема Жегалкина 193
— Котельникова 24
— Поста — Яблонского 195
— Шеннона 144 Теория сравнений 150
Устройство ЭВМ арифметико-логическое 36
— — ввода информации 36
— — вывода информации 37
— — запоминающее (память) 36
— — периферийное 37
— — подготовки данных 36
— — управления 37
Форма представления чисел естественная 59
— — — нормальная 59
— — — нормализованная 61
— — — с плавающей запятой 61
— — — с фиксированной запятой 60
— —---точкой 64
ЭВМ 31
— персональная 32
— проблемно-ориентированная 32
— универсальная 32 Энтропия 18
Александр Яковлевич Савельев
ПРИКЛАДНАЯ ТЕОРИЯ ЦИФРОВЫХ АВТОМАТОВ
Заведующая редакцией Н. И. Хрусталева. Редактор Е. В. Хвостова. Младшие редакторы Е. В. Судьенкова, Н. Е. Овчеренко. Художник А. А. Камаев. Художественный редактор В. И. Мешалкин. Технический редактор 3. В. Нуждина. Корректор В. В. Кожуткина.
ИБ №6156
Изд. № Стд-511 Сдано в набор 23.09.86. Подп. в печать 08.06.87.
Т—10499. Формат бОХЭО'/ів- Бум. офс. № 1. Гарнитура литературная. Печать офсетная. Объем 17 уел. печ. л. 17 уел. кр.-отт. 17,11 уч.-изд. л. Тираж 20 000 экз. Зак. № 1569. Цена 1 руб.
Издательство «Высшая школа», 101430, Москва, ГСП-4, Неглинная ул.,
д. 29/14.
Ярославский’ полиграфкомбинат Союзполиграфпрома при Государственном комитете СССР по делам издательств, полиграфии и книжной торговли. 150014, Ярославль, ул. Свободы, 97.
Глушков В. М. Синтез цифровых автоматов. М., Физматгиз, 1962. С. 7.
Английский математик А. М. Тьюринг в работе «О вычислимых числах с приложением к проблеме разрешения» и американский математик Э. X. Пост в работе «Финитные комбинаторные процессы» почти одновременно в 1936 г. дали уточнения понятия «алгоритм» на примере гипотетической машины с бесконечной лентой. Машина Тьюринга отличается от машины Поста тем, что ячейки заполняются не просто меткой, а символами из заданного множества.
Термин «алгоритм» произошел от имени узбекского математика Аль-Хорезми, который еще в IX в. сформулировал правила выполнения четырех арифметических действий. Появившееся несколько позже слово «алгорифм» связано с Евклидом, древнегреческим математиком, сформулировавшим правила нахождения наибольшего общего делителя двух чисел. В современной математике употребляют термин «алгоритм».
Первым два символа для кодирования информации применил известный философ XVII в. Ф. Бэкон, который использовал символы 0,L.
Здесь и в дальнейшем при записи десятичных чисел индекс опускается.
Величина а зависит от кода: для дополнительного кода а=0, для обратного кода а = 1.
Sklanskjj F. Conditional sum addition logic (RE Trans, on Electronic Comput. 1960, N 2, p. 226—231.
Название «Д-код» образовано от полного названия «десятичный код».
Исключение из этого случая возникает при а, + 6; +п,_ і = 15, когда не требуется вводить поправку, так как появится разрешенная комбинация.
Схемная избыточность будет рассматриваться в дисциплинах, в которых изучаются устройства ЭВМ. В данной главе описаны методы логического контроля, использующие информационную избыточность. . ,
Это определение совпадает с понятием кодового расстояния по Хэмингу. 1 Іоэтому в теории кодирования оно называется хэмйнговым расстоянием.
Определить вес и кодовые расстояния для: а) >4 = 01101111; 5=11101101-б) Л = 01010101; 5=10101010.
2. Произвести проверку правильности кода по методу Хэминга для чисел (номера разрядов идут слева направо): /1 = 101011001101010; 5=101011001101110; С = = 101011110101010.
3. Произвести контроль операций сложения, умножения, вычитания для чисел А и В, используя методы числового контроля, если А —122, 5 = 93, р= 11.
4. Определить контрольные коды для чисел /1 = 10010001, р = 7; 5=10101101 р = 5; С = 0,01001001, р = 7.
5. Определить контрольные коды числа /4=0,10010001, которое сдвигается влево и вправо при р = 7.
6. Найти контрольный код для логической суммы и логического произведения чисел >4 = 110011010 и 5 = 010011011.
7. Провести контроль операций сложения и вычитания чисел /4=0,100110011, р = 3 и 5 = —0,011110010, р = 3 на сумматоре обратного кода.
8. Провести контроль операции перемножения чисел Л =0,10011110, р = 7 и 5 =—0,11001101, р = 7 на сумматоре прямого кода.
9. Определить правильность выполнения операции сложения чисел /4 = = —0,100011011 и В = 0,11100011 при р = 3 на сумматоре дополнительного кода.
10. Можно ли использовать контроль по модулю для определения места, где произошла ошибка?
10111101 *0011 1101
Для реализации таких корректирующих кодов нужно большое количество дополнительного оборудования, что не всегда оправдано.
Задание для самоконтроля
Можно ли применить коды Хэминга для контроля операции сложения и умножения кодов? Если да, то как это осуществить?
Создатель алгебры логики — английский математик Дж. Буль (1815—1864). Поэтому алгебру логики называют также алгеброй Буля. В последние годы алгебра Буля получила значительное развитие благодаря работам таких ученых, как Э. Пост, К. Шеннон, Г. Л. Шестаков, В. М. Глушков [6], С. В. Яблонский [21] и др.
Функции )'э и /is не принадлежат ни одному из указанных классов.
В. Я. Хартов. Методические указания к лабораторным работам. Ч. 2. МВТУ, 1981. С. 14—16.
 Учет: Делопроизводство - Автоматизация - Софт
Учет: Делопроизводство - Автоматизация - Софт
- Управленческий учет
- Технологии управленческого учета
- Делопроизводство
- Стандарты делопроизводства
- Делопроизводство предприятия
- Секретарь и делопроизводство
- Автоматизация делопроизводства
- Документооборот
- Автоматизация
- Автоматизация управления
- Практика автоматизации
- Софт для автоматизации