
|
Лупал А. М. - Теория автоматов
В пособии приводятся основные понятия теории алгоритмов, раскрывается связь между алгоритмами и вычислительными машинами и различия между процессами, протекающими в машинах Тьюринга и автоматах фон Неймана. Рассматриваются также основы теории конечных автоматов, формальные методы проектирования автоматов на основе абстрактного и структурного синтеза, явление состязаний элементов памяти и гонок в структурном автомате, методы кодирования состояний автоматов и синхронизация автоматов. Приводятся примеры модификаций элементарных абстрактных и структурных автоматов в асинхронном и синхронизируемом исполнении.
1. КИБЕРНЕТИКА - НАУКА ОБ УПРАВЛЕНИИ
1.1. Создание кибернетики
Кибернетика - это наука об общих законах получения, хранения и передачи информации, т. е. о процессах, которыми характеризуется интеллектуальная деятельность как естественная, так и искусственная. Кибернетика явилась фундаментом, на котором выросла вся современная вычислительная техника и другие науки.Впервые представление об искусственном интеллекте появилось в научно-фантастической литературе, в частности американский ученый и писатель Айзек Азимов в 1974 году писал: “Я придумал в 1942 году три закона робототехники и написал на их основе несколько десятков рассказов, относясь ко всем этим роботам и искусственным интеллектам как к экзотическим плодам воображения. Я считал, что робот (или вычислительная машина, или искусственный интеллект) необходим человечеству. Затем я обнаружил, что, в конце концов, вычислительные машины смогут достичь интеллектуального уровня, сравнимого с человеческим... и даже намного превзойти его..., но, тем не менее, я должен открыть Вам одно обстоятельство: я никогда не верил в реальность всего этого - в этом отношении мое воображение отказало. Я никогда в действительности не предполагал, что искусственный интеллект возможен, и я совершенно определенно никак не предполагал, что застану время, когда люди будут серьезно работать в этой области” [1].
Научная теория по разработке искусственного интеллекта была провозглашена американским ученым Норбертом Винером в 1948 году. Тогда же он ввел понятие “кибернетики” как науки об общих закономерностях процессов управления и передачи информации в машинах, живых организмах и их объединениях. Вместе с этим словом более 50 лет назад в наш мир ворвался целый поток совершенно новых идей и представлений.
В России первые работы по кибернетике появились в 1956 году, причем сначала это были в основном переводы книг и статей американских ученых, а спустя некоторое время появились и собственные разработки. Одними из первых русских кибернетиков были советские ученые Аксель Иванович Берг, Виктор Михайлович Глушков и Александр Андреевич Ляпунов.
1.2. Предмет и методы исследования кибернетики
В качестве основных разделов кибернетики могут быть выделены:1. Теория информации, изучающая способы восприятия, хранения, преобразования и передачи информации.
2. Теория программирования, изучающая и разрабатывающая методы переработки информации и использования ее для управления, причем программирование работы любой системы управления в общем случае включает в себя определение и разработку условной математической схемы (алгоритма) нахождения решений и составление программы в коде, воспринимаемом данной системой.
3. Теория систем управления, которая изучает:
структуру и принципы построения систем управления, к которым относятся любые физические объекты, осуществляющие целенаправленную переработку информации, такие как нервная система животного, система автоматического управления движением самолета, электронная программно-управляемая вычислительная машина, система подразделений банка и т. п.;
процесс управления - понятие, которое определяет, каким требованиям должна удовлетворять последовательность действий (или ее описание), осуществляемых системой управления.
Кибернетика изучает абстрактные системы управления, которые представлены в виде математических схем (моделей). Основным свойством этих моделей является то, что они сохраняют информационные свойства соответствующих классов реальных систем, т. е. тех систем, которые моделируются с помощью этих моделей. В рамках кибернетики под влиянием запросов техники ЦВМ и управляющих вычислительных машин возникла специальная математическая дисциплина - теория автоматов, которая изучает специальный класс дискретных (цифровых) систем переработки информации, включающих в себя большое число элементов. Дискретные автоматы, изучаемые в теории автоматов, являются абстрактными моделями реальных систем как технических, так и биологических, которые перерабатывают цифровую информацию дискретными временными тактами.
Для того чтобы в вычислительной машине реализовать некоторый процесс управления, иначе говоря, соответствующий процесс переработки информации, необходимо построить такой алгоритм и осуществить такую же или примерно такую же переработку информации, как и исходный процесс, а затем оценить качество приближения.
Используемые в кибернетике методы исследования можно разделить на математические и экспериментальные, причем именно к последним относятся логический анализ и синтез систем управления. Поэтому дисциплины “Дискретная математика”, и “Теория автоматов” являются составными частями науки кибернетики.
2. ВВЕДЕНИЕ В ТЕОРИЮ АЛГОРИТМОВ
2.1. Определение алгоритма
Понятия теории алгоритмов всегда традиционно относились к “высокой” науке, считались слабо связанными с практикой и трудными для понимания. Однако жизнь опровергла эти представления, и это доказывается тем, что возникли прикладные ответвления этой теории, а именно, алгоритмические языки программирования и теория формальных исчислений, знание которых стало совершенно необходимым для любого исследователя, имеющего отношение к алгоритмизации процессов управления.По существу знание этих вопросов дает понимание того, что можно и чего нельзя сделать с помощью вычислительной машины. Сейчас, когда вычислительных машин больше чем людей, умеющих правильно их использовать, такое понимание особенно важно.
Алгоритм может быть определен как эффективная процедура, однозначно приводящая к результату. При разработке алгоритма необходимо формализовать процесс решения задачи, сведя его к применению конечной последовательности достаточно простых правил. Так, мы регулярно пользуемся алгоритмами выполнения основных арифметических операций над многозначными числами, разработанными еще в IX в. древневосточным математиком Аль-Хорезми (термин “алгоритм” произошел от имени этого ученого). До середины XIX в. все алгоритмы были вычислительными и имели дело, в основном, с числами. Поэтому все многообразие вычислений комбинировалось из 10-15 четко определенных операций арифметики, тригонометрии и анализа. Все было очевидно и не требовало специальных исследований.
Появление во второй половине XIX в. математики, имеющей дело с нечисловыми объектами (неэвклидова геометрия, теория групп, теория множеств) показало, что все не так просто и очевидно. Оказалось, что привычные рассуждения, применяемые к этим теориям, основанные на содержательном описании алгоритма, приводят к неразрешимым противоречиям (пример - так называемые противоречия теории множеств). Совершенно особым образом и крайне осторожно следует обращаться с таким понятием, как “бесконечность”. Были созданы так называемые финитные методы исследований, сущность которых заключается в том, что они допускают только конечные комплексы действий над конечным числом объектов. Все это потребовало уточнения понятия “алгоритм”.
2.2. Предмет теории алгоритмов
В технику термин “алгоритм” пришел вместе с кибернетикой. Если понятие “метода вычислений” не нуждалось в пояснениях, то понятие “процесса управления с помощью алгоритмов” пришлось вырабатывать практически заново. Неясность содержательного описания алгоритма послужила причиной уточнения понятия алгоритма, в результате чего был сделан вывод о существовании так называемой алгоритмической неразрешимости, т. е. о несуществовании единого алгоритма решения задач некоторого класса при возможности решения отдельных задач этого класса.Поэтому предметом теории алгоритмов, решающей задачу уточнения понятия “алгоритм”, является в первую очередь уточнение таких понятий, как “объект”, который подвергается преобразованию и “действие”, совершаемое над этим объектом. Поэтому, разрабатывая алгоритм, необходимо предварительно выяснить:
какие объекты следует считать точно определенными;
какие элементарные действия над ними следует считать точно определенными;
какими свойствами и возможностями обладают комбинации элементарных действий, т. е. что можно и чего нельзя сделать с помощью этих действий;
каким требованиям должна удовлетворять последовательность действий, чтобы считаться конструктивно заданной, т. е. иметь право называться алгоритмом.
В этом осознании огромную роль сыграла практика использования вычислительных машин, сделавшая понятие алгоритма ощутимой реальностью. Поэтому применительно к вычислительной технике можно сформулировать более корректное определение алгоритма: алгоритм -это точное предписание о выполнении в определенном порядке некоторой системы операций для решения всех задач некоторого заданного типа.
Тем не менее, нельзя считать алгоритмом любую инструкцию, разбитую на шаги. Поэтому необходимо определить основные требования, предъявляемые к алгоритмам.
1. Алгоритм применяется к исходным данным и выдает результаты. В привычных технических терминах это означает, что алгоритм имеет входы и выходы. Кроме того, в ходе работы алгоритма проявляются промежуточные результаты, которые используются в дальнейшем. Таким образом, каждый алгоритм имеет дело с данными - входными, промежуточными и выходными.
2. Необходимо уточнить понятие “данные”, т. е. указать, каким требованиям должны удовлетворять объекты, чтобы алгоритм мог с ними работать. Для этого объекты должны быть четко определены и отличимы как друг от друга, так и от “необъектов”.
Поскольку точное и полное словесное определение объекта дать достаточно сложно, в теории алгоритмов фиксируют конкретные конечные наборы исходных объектов, называемых элементарными и конкретный набор средств построения других объектов из элементарных объектов. Набор элементарных объектов образует конечный алфавит исходных символов (цифр, букв и др.), из которых строятся другие объекты.
Наиболее распространенный тип алгоритмических данных - слова конечной длины в конечных алфавитах (например, числа), причем число символов в словах (длина слова) - естественная единица измерения обрабатываемой информации. Более сложный случай алгоритмических объектов - формулы. Они также являются словами конечной длины в данном конечном алфавите, однако не каждое слово есть формула.
3. Данные для своего размещения требуют памяти, которая состоит из ячеек и каждая ячейка может содержать один символ алфавита данных. Таким образом, единицы измерения объема данных и памяти согласованы.
4. Алгоритм должен быть дискретным, т. е. должен состоять из множества элементарных шагов или действий, причем множество различных шагов конечно. Примером множества элементарных действий является система команд ЭВМ.
Последовательность шагов алгоритма должна быть детерминирована, т. е. после каждого шага указывается, какой шаг делать дальше либо дается команда остановки.
5. Алгоритм должен быть результативным, т. е. должен остановиться после конечного числа шагов с одновременным указанием того, что считать результатом.
В частности, всякий, кто предъявляет алгоритм решения некоторой задачи, например вычисления некоторой функции f(x), обязан показать, что алгоритм останавливается после конечного числа шагов (сходится) для любого х из области задания функции f
6. Алгоритм должен удовлетворять требованию массовости, т. е. алгоритм должен быть таким, чтобы его можно было применить для класса задач, различающихся лишь исходными данными.
7. В процессе создания алгоритма следует различать понятия:
описание алгоритма (например, инструкцию или программу);
механизм реализации алгоритма (например, ЭВМ), который включает в себя средства управления ходом вычислений, а именно: средства пуска, средства остановки, средства реализации элементарных шагов, средства выдачи результатов, обеспечения детерминированности;
процесс реализации алгоритма, представляющий собой последовательность шагов, которая будет порождаться при применении алгоритма к конкретным данным.
2.3. Блок-схемы алгоритмов, композиция алгоритмов
Для представления алгоритма и организации связи между его шагами используются блок-схемы. Блок схема алгоритма изображается в виде графа, в котором вершинам соответствуют шаги алгоритма, а ребрам - переходы между шагами. Вершины могут быть операторными или операторами (выходит одно ребро), условными или предикатам и (выходит два ребра), переключательными (выходит несколько ребер), единственный оператор начала (выходит одно ребро), единственный оператор конца (не выходит ни одного ребра).Важной особенностью алгоритма является то, что связи, описываемые блок-схемой, не зависят от того, являются ли шаги алгоритма элементарными или представляют собой самостоятельные алгоритмы (блоки).
В программировании известно понятие “разблочивания” сложного алгоритма, когда отдельные его блоки программируются разными лицами. И наоборот, с помощью блок-схемы можно несколько отдельных алгоритмов рассматривать как блоки, которые могут быть связаны в один большой алгоритм.
Например, блок-схема, вычисляющая функцию f=f2(fx(x)) , в которой в качестве аргумента используется другая функция и которая поэтому называется композицией функций, будет иметь вид, представленный на рис. 2.1.
 |
|
А1 - алгоритм вычисления функци if (х), f (х)- |
В такой блок-схеме входные данные (входы) алгоритма А2 есть результаты (выходы) алгоритма АІ.Такое соединение алгоритмов называется композицией алгоритмов.
На блок-схеме алгоритма хорошо видна разница между описанием алгоритма и процессом его реализации. Описание - это граф, а процесс реализации - это пути в графе, которые определяются логическими условиями. Если в процессе реализации вычислений не появляется условий, ведущих к концу, и процесс зацикливается, это означает отсутствие сходимости алгоритма.
2.4. Алгоритмические модели
В классическом варианте блок-схемы алгоритмов, при всей своей наглядности, отражают связи лишь по управлению (что делать в следующий момент, какому блоку передать управление), а не по информации (не содержат сведений ни о данных, ни о памяти, ни об используемом наборе элементарных шагов). Таким образом, представление алгоритма в виде блок-схемы не удовлетворяет перечисленным выше требованиям.Поэтому в теории алгоритмов принимается и другой подход к представлению алгоритма, позволяющий построить алгоритмическую модель процесса, когда удается удовлетворить всем требованиям, предъявляемым к алгоритмам. При построении алгоритмической модели производится уточнение детерминизма алгоритма:
выбирается конечный набор исходных объектов, которые называются элементарными;
выбирается конечный набор способов построения из них новых объектов;
фиксируется набор элементарных шагов;
разрабатывается способ создания памяти и выборки информации из памяти.
В результате этих действий создается конкретная алгоритмическая модель.
Можно выделить три основных типа алгоритмических моделей, которые различаются эвристическими соображениями относительно того, что такое алгоритм.
1. В первой модели понятие алгоритма связывается с наиболее традиционными понятиями математики - вычислениями и числовыми функциями. Наиболее широко используемая модель этого типа - рекурсивные функции. Рекурсивная функция описывается посредством так называемых индуктивных (или рекуррентных) определений, основанных на переходе от n к n+1. Слово “рекуррентный” означает “возвратный” от латинского слова recurso - “возвращаюсь, бегу назад”. И если алгоритм носит возвратный характер, то он и называется рекурсивным. Примером может служить алгоритм получения натурального ряда чисел: чтобы определить число 4, нужно сначала определить число 3, а чтобы определить число 3, нужно сначала определить число 2 и т.д. вплоть до 1.
Рекурсивные функции могут быть определены как некоторые новые функции, получаемые из уже имеющихся функций с помощью операции суперпозиции.
Оператором суперпозиции S^ называется подстановка в функцию от m переменных m функций от n одних и тех же переменных. Например, если имеем функции h(x1, x2, ...,xm), g1(x1, x2,..xn), g2(x1, x2, ...xn), ...,
gjxv XV ..., xn) , то Smm (h gp g2, ..., gm) = h(g1(xP xV ..., xn), g2(xP X2, ...,
Xn), ..., gm(xV X2, ...,Xn)) =AX1,xV ..., Xn).
2. Второй тип алгоритмической модели основан на представлении об
алгоритме как о некотором детерминированном устройстве, способном выполнять в каждый отдельный момент времени лишь весьма примитивные операции.
Эвристика этих моделей близка к ЭВМ и, следовательно, близка к инженерной интуиции. Основной теоретической моделью этого типа, созданной в 30-х годах, является машина Тьюринга.
3. Третий тип алгоритмических моделей - это преобразования слов в произвольных алфавитах, в которых элементарными операциями являются операции подстановки, т. е. замены части слова (подслова) другим словом. Примерами таких моделей являются конечные автоматы, созданные по алфавитному отображению.
3. МАШИНА ТЬЮРИНГА
В 1937 году английский математик А.М. Тьюринг, который был последователем теории о том, что машина способна мыслить и с ее помощью можно смоделировать психическую деятельность человека, предложил общую и вместе с тем очень простую концепцию вычислительной машины. В своем труде Тьюринг исходил из того, что предлагаемая им вычислительная машина уподобляется вычислителю, который выполняет операции в точном соответствии с некоторым строгим описанием. Работа машины Тьюринга напоминает действия вычислителя, который, будучи не в состоянии сразу обозреть всю, часто очень громоздкую систему данных и предписаний, производит каждый раз лишь какое-либо “элементарное” действие, причем только над некоторой “воспринимаемой” им частью данных (или промежуточных результатов). На следующем этапе он либо продолжает воспринимать ту же часть данных, либо переходит к другой части, находящейся рядом с ней.3.1. Структура машины
Машину Тьюринга можно представить состоящей из нескольких основных блоков.1. Управляющее устройство (УУ), которое может быть настроено на выполнение одной из множества возможных операций или, как принято говорить, может находиться в одном из состояний, образующих конечное множество Q = {q1, q2, ..., qn}.
Среди состояний УУ могут быть выделены начальное состояние q1 и конечное (пассивное) состояние qz с {q1, ..., qn}. В q1 машина Тьюринга находится перед началом работы, а, попав в qz, она останавливается. Очевидно, все состояния из множества Q, отличные от qz, являются активными.
Работа машины Тьюринга происходит в дискретном времени, когда состояния машины рассматриваются на конечном множестве временных отсчетов, называемых тактами машинного времени и обозначаемых t1, t2, ..., tp , ... .
2. Лента, разбитая на ячейки, в каждой из которых может быть записан один из символов конечного внешнего алфавита S = {s1, s2, ..., sm}. Символами этого алфавита кодируются как сведения, подаваемые в машину, так и те сведения, которые в ней вырабатываются. Среди знаков внешнего алфавита имеется пустой символ (пробел) X. Посылка (вписывание) этого символа в какую-либо ячейку ленты гасит (стирает) тот символ, который в ней раньше хранился, и оставляет ее пустой. Следует заметить, что X может принимать значение из алфавита S.
Лента бесконечна в обе стороны, однако в начальный момент времени только конечное число ячеек заполнено непустыми символами, остальные ячейки ленты пусты, т. е. содержат символ X (пробел). И в любой последующий момент времени лишь конечный отрезок ленты заполнен символами, поэтому важна не фактическая бесконечность ленты, а ее неограниченность, т. е. возможность писать на ней сколь угодно длинные, но конечные слова.
3. Устройство обращения к ленте, представляющее собой считывающую и записывающую головку, которая в каждый момент времени t( обозревает какую-либо ячейку ленты и в зависимости от символа в этой ячейке и состояния УУ выполняет следующие действия (рис. 3.1):
а) производит или запись в ячейку нового символа (может быть совпадающего со старым), или стирание символа (запись в ячейку пустого символа X),
б) сдвигает головку на ячейку вправо или влево, при этом УУ переходит в новое состояние.
Перечисленные действия в комплексе представляют собой шаг (элементарное действие) машины Тьюринга, который определяется парой (ЧР
лгч
. обозреваемая ячейка
головка
Рис. 3.1
Таким образом, сообразуясь с современными представлениями вычислительной техники, можно считать, что управляющее устройство и устройство обращения к ленте представляют собой Логический блок машины. Лента интерпретируется как внешняя память, в которой записываются исходные данные и окончательные результаты (данные - это слова, представленные в алфавите S). Внутренняя память машины Тьюринга может быть представлена в виде двух ячеек: ячейки сдвига D, в которую заносится знак (направление) сдвига, и ячейки состояния Q, отображающей текущее состояние машины. Элементарными шагами машины Тьюринга являются: считывание и запись символов, сдвиг головки на ячейку вправо или влево, или, иначе говоря, изменение адреса обозреваемой ячейки ленты на 1, переход УУ в новое состояние.
3.2. Детерминированность машины Тьюринга
Машина Тьюринга обладает свойством детерминированности, т. е. последовательность ее шагов определяется следующим образом.Для любого внутреннего состояния q. и символа алфавита Sj однозначно задана логическая функция, которая определяет следующее состояние q'; символ s', который должен быть записан; направление сдвига головки dk М {L, R, E}, где L - сдвиг влево, R - сдвиг вправо, Е -отсутствие сдвига; причем множество А = {L, R, E, q1, ..., qm} называется внутренним алфавитом машины Тьюринга.
Таким образом логическая функция машины Тьюринга сопоставляет каждой паре знаков (q;, sj) тройку знаков (s', q', dk) и может быть записана разными способами.
Первым способом записи логической функции является функциональная схема машины Тьюринга, представляющей собой таблицу, строкам которой соответствуют входные символы из множества S, столбцам - состояния из множества Q, а на пересечении строк и
столбцов записана тройка символов q' s' dk. (рис. 3.2).
| ||||||||||||||||||||||||||||||||||||
| Рис. 3.2 |
q . sj ^ q' s' dk, (1
где знак “^” читается “влечет за собой” или “приводит к ...”. Команда, соответствующая фрагменту функциональной схемы, представленной на рис. 3.2, имеет вид q2 s2 ^ q8 s7 L .
Третьим способом задания логической функции является блок-схема, называемая диаграммой (графом) переходов и изображаемая в виде графа, в котором состояниям машины Тьюринга соответствуют вершины (узлы), а командам вида (1)- ребра, ведущие из q{ в q', на которых записано Sj ^ s' dk
На рис. 3.3 приведен фрагмент диаграммы переходов машины Тьюринга, соответствующий фрагменту функциональной схемы, представленной на рис. 3.2.
>s7 L
Рис. 3.3
Таким образом, машина Тьюринга представляет собой максимально упрощенный вариант вычислительной машины, имеющей одноадресную структуру, с возможностью изменения адреса обозреваемой ячейки только на 1. Поэтому необходимое для процесса вычислений содержание какой-либо ячейки отыскивается путем постепенной проверки всех ячеек подряд до тех пор, пока не будет обнаружена нужная ячейка.
3.3. Работа машины Тьюринга
Рассмотрим работу машины Тьюринга на следующем примере.Пусть задана машина Тьюринга с алфавитом S = {1, а, в, X] и состояниями Q ={q1, q2, q3, q4, q5}.
Перед началом работы машины Тьюринга на ленту заносится начальная информация (например, пять единиц) и фиксируется начальная обозреваемая ячейка (например, 4-я), сдвиг отсутствует. Информация в этой ячейке отражает начальное состояние q1 машины Тьюринга.
| 5 4 3 2 1 | ||||||||||||
|
| ||||||||||||||||||||||||||||||
| Рис. 3.4 |
Рассмотрим первый способ описания работы машины Тьюринга, в котором в каждом состоянии машины указывается последовательность символов в ячейках ленты.
Такт 1- ?!
В ячейки состояния Q и сдвига D заносятся значения начального состояния q1 и начального сдвига Е и обозревается содержание начальной 4-й ячейки (символ “1”) при состоянии q1. В соответствии с функциональной схемой результатом данного шага будет q2 a E , т. е. выполняется Тьюрингова команда
q1 1 ^ q2 a E ,
где q2 указывает, на какую операцию перешли; a - что записали в обозреваемую ячейку; Е - направление сдвига головки.
Следовательно, сдвиг головки устройства обращения к ленте отсутствует, а символ “1” заменяется в 4-й ячейке на “a“.
Получим
| 5 4 3 2 1 | ||||||||||||
|
т
Такт 2- ?2Так как сдвига не было, то вновь обозревается 4-я ячейка, но уже в состоянии q2.
Результат: q2 a R, т. е. выполняется команда q2 а ^ q2 a R. Следовательно, головка передвинулась в 3-ю ячейку (вправо), в обозреваемой 4-й ячейке ленты остался символ а, а машина Тьюринга осталась в состоянии q2. Получим
5 4 3 2 1
| 1 | a | 1 | 1 | 1 |
т
Такт 3- t3Обозревается “1” из 3-й ячейки. Результат: q1 в E , т. е. выполняется команда q2 1 ^ q1 в E , сдвига нет. Получим 5 4 3 2 1
| 1 | a | в | 1 | 1 |
т
Такт 4- t4Вновь анализируется 3-я ячейка в состоянии q1 и обозревается символ в. Результат: q1 в L , т. е. выполняется команда q1 в ^ q1 в L , и осуществляется сдвиг влево. Получим 5 4 3 2 1
| 1 | a | в | 1 | 1 |
т
Такт 5- t5Анализируется 4-я ячейка в состоянии q1, обозревается символ а. Результат: q4 a L, т. е. выполняется команда q1 а ^ q4 a L, осуществляется сдвиг головки влево. Получим 5 4 3 2 1
| 1 | a | в | 1 | 1 |
т
Такт 6- t6Обозревается 5-я ячейка в состоянии q4. Там находится символ “1”, поэтому результат: q5 X R , т. е. выполняется команда q4 1 ^ q5 X R , и осуществляется сдвиг вправо. Получим
| 5 4 3 2 1 | ||||||||||||
|
т
Такт 7- t7Обозревается 4-я ячейка в состоянии q5. Там находится символ “а”, поэтому результат: q5 а E, т. е. выполняется команда q5 а ^ q5 а E , состояние и символ не меняются, сдвига нет. Получим 5 4 3 2 1
| X | а | в | 1 | 1 |
т
Состояние q5 является конечным состоянием машины Тьюринга или стоп-состоянием, так как после анализа символа а в состоянии q5, никаких изменений на ленте не происходит и в новое состояние машина не перейдет.Этот вывод подтверждается анализом последнего столбца функциональной схемы, из которого видно, что при возникновении состояния q5 произойдет остановка машины, так как любой обозреваемый символ не заменяется другим, а остается. Сдвига также не происходит, и машина снова и снова будет обозревать один и тот же символ. Это и есть стоп-состояние, сигнализирующее о результативном завершении процесса, о его сходимости. В этом случае говорят, что машина Тьюринга применима к информации, поданной на нее до запуска.
В результате работы машины Тьюринга была получена следующая схема изменения информации на ленте.
| 5 | 4 | 3 | 2 | 1 | |
| 1 | 1 | 1 | 1 | 1 | |
| 1 | а | 1 | 1 | 1 | |
| h | 1 | а | 1 | 1 | 1 |
| 1 | а | в | 1 | 1 | |
| 1 | а | в | 1 | 1 | |
| 1 | а | в | 1 | 1 | |
| а | в | 1 | 1 | ||
| а | в | 1 | 1 |
Удобнее пользоваться упрощенной записью Тьюринговых команд и функциональных схем, в которых не записываются выходные символы алфавита и новые состояния, если они не меняются, а также не фиксируется знак Е, указывающий на отсутствие сдвига. Это позволяет в таблице опустить столбец, соответствующий стоп-состоянию, само стоп-состояние отметить знаком “ ! ”, а в системе команд нет необходимости фиксировать последнюю команду.
Например, вместо q2a^q2aR можно писать q2a^R. Тогда упрощенная функциональная схема, представленная на рис. 3.4, будет иметь вид, показанный на рис. 3.5.
| |||||||||||||||||||||||||
| Рис. 3.5 |
3.4. Конфигурация машины Тьюринга
Конфигурацией (полным состоянием или машинным словом) машины Тьюринга называется совокупность ее следующих характеристик:внутреннего состояния;
состояния ленты (т. е. слова, записанного на ленте);
положения головки на ленте.
Конфигурация обозначается тройкой символов K = a1qi a2 , где qt -текущее внутреннее состояние, a1 - слово слева от головки; a2 - слово, образованное символом, обозреваемым головкой, и символом справа от него, причем, слева от a1 и справа от a2 нет непустых символов (т. е. либо записано X, либо ничего).
Например, если внутреннее состояние qt = abcde, а головка обозревает символ d, тогда конфигурация машины Тьюринга K = abcqf de, т. е.
| a | b | C | d | e |
aj a2
Стандартная начальная конфигурация обозначается как Kl=qla, где q1 - начальное состояние, а головка обозревает крайний левый символ. Стандартная конечная конфигурация имеет вид Kz=q a, где q - конечное состояние и вокруг обозреваемой ячейки пустые символы.
Работа машины Тьюринга может быть описана с помощью последовательности конфигураций.
Определение. Если к некоторой конфигурации машины Тьюринга K применима ровно одна команда, приводящая к конфигурации K’ , то говорят, что между конфигурациями K и K’ существует отношение K ^ K’ , что означает: K переходит в K’ по Тьюрингу.
Если же для K1 и Kn существует последовательность различных конфигураций такая, что K1 ^ K2^ K3 ^ ... ^ Kn, то такая последовательность обозначается K1 Kn. Последовательность конфигураций K1 ^ K2^ ... ^ Kn однозначно определяется исходной конфигурацией K1 и полностью описывает работу машины Тьюринга, начиная с K1.
В качестве примера рассмотрим систему команд Ет составленную на основе функциональной схемы, приведенной на рис. 3.4 (выписываем только те команды, которые понадобятся для иллюстрации):
q1 1 ^ q2 a E (1) q1 b ^ q1 в L (4) q4 1 ^ q5 X R (6)
q2 a — q2 a R (2) q. a — q4 a L (5) q5 a — q5 a E (7)
q2 1 — q. p E (3)
При заданной входной информации (11111) и начальной ячейке (4-й) получим следующую последовательность конфигураций машины Тьюринга:
1q1 1111 —— 1q2a111—— 1a q2 111—— 1 aq 1 в 11——
-К1- -К2- -КЗ- -К4—
—— 1 q 1 ap 11—— q41 ap 11—— Aq ap11——Aq^apn —К5— —К6— —К7— —— ! —
стоп-состояние
Следовательно, 1q11111 ^ Aq5ap11 .
3.5. Тьюрингово вычисление
Рассмотрим, как строится машина Тьюринга, реализующая некоторые простые алгоритмы.Алгоритм операции “Сложение”.
Исходные данные и результаты операции сложения являются натуральными числами.
Считаем, что в машине Тьюринга каждое натуральное число задано в виде набора “1” и отделяется от другого числа символом “*”. Таким образом, алфавит машины Тьюринга будет S = {1,*Д}. Состояния заданы множеством Q = {q0, q1, q2, q3, q4, q5}.
Рассмотрим пример.
Начальные условия: в начальном состоянии q0 на ленту машины Тьюринга подается пара чисел 6 и 4 и в поле зрения машины находится левая единица.
| 1 | 1 | 1 | 1 | 1 | 1 | * | 1 | 1 | 1 | 1 |
|
т Необходимо найти их сумму, т. е. записать подряд 10 единиц, получив | ||||||||||||||||||||
|
| ||||||||||||||||
| Рис. 3.6 |
Такт 1- ?1
q0 1 ^ q2 X R, т. е. вместо первой “1” устанавливается пробел и в состоянии q2 обозревается вторая “1”, так как сдвиг должен быть вправо.
Такт 2- ?2
q2 1 ^ R (записано в упрощенной форме), следовательно символ не меняется и состояние тоже, поэтому переходя направо от “1” к “1”, будем все время оставлять их в ячейках, оставаясь в состоянии q2. Попав на знак “*”, его тоже оставим, так как q2 * ^ R.
Этот сдвиг вправо будет продолжаться в течение 9 тактов до тех пор, пока в такте 11 не попадем в пустую ячейку.
Такты 1-10 (t1 - t10)
| ^ R | ||||||||||||||||||||
|
т т т ... т
Такт 11 - tn| X | 1 | 1 | 1 | 1 | 1 | * | 1 | 1 | 1 | 1 |
|
Такт 12 - t12 q2 X — q1 1, т. е. в пустую ячейку вписываем “1” и переходим в состояние q1 | ||||||||||||||||||||
|
Такт 13 - t13 q1 1 —— L
| ^ L | ||||||||||||||||||||
|
Далее в течение тактов t14 - t23 будет происходить обратный сдвиг (влево) через все 1 и * до тех пор, пока головка не окажется в левой пустой ячейке.
Такт 23 - t23
q1 1 — L, произвели последний сдвиг влево и оказались в пустой ячейке
| X | 1 | 1 | 1 | 1 | 1 | * | 1 | 1 | 1 | 1 | 1 |
q1 X — q0 R, переходим в состояние q0 и сдвигаемся вправо к первой
| ||||||||||||||||||||
| t24 (аналог t0) |
| Такт 25 - t25 | ||||||||||||||||||||
|
Т.е. цикл завершен, и с этого момента (t26) начинается новый цикл аналогичных операций. По окончании этого цикла еще одна “1” будет перенесена слева направо в конец последовательности.
Такт 47 - t47
| ||||||||||||||||||||
|
т т g Чі (аналог tn) |
| ||||||||||||||||||||
| t48 (аналог t0) t35 (аналог t10) |
| ||||||||||||||||||||
|
t49 t50 (аналог t2) t |
|
60 Предпоследний такт (t143) | ||||||||||||||||||||
|
q0 * ^ ! X, переходим в конечное состояние и помещаем пробел, вместо *
| X | X | X | X | X | X | X | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
ставлЯЮт Тцикл
n - число символов после
Длительность выполнения операции “Сложение” зависит от величины слагаемых, так как временные затраты на один цикл сложения со-2 (m+n+1) тактов, где m - число символов перед “*”,
Полностью на выполнение сложения понадобится Т = 2 (m+n+1) m +2m = 2m (m+n+2) тактов
/ \ время на подготовку к циклу
число циклов и на завершение цикла.
Поэтому в нашем примере Тцикл = 2-11 =22 (такта) и Тслож = 12-12 = =144 (такта).
Временные соотношения иллюстрируются табл. 3.1
| Таблица 3.1 | ||||||||||||||||||||||||||||||
|
| I цикл - | ^2 ^23 | IV цикл - | ?74 ?95 |
| II цикл - | ?26 - ?47 | V цикл - | ?98 - ?119 |
| III цикл - |
Ul o -Г* | VI цикл - | ?122- W ?144- конец |
3.6. Тезис Тьюринга
При реализации алгоритмов на машине Тьюринга может возникнуть вопрос для всех ли конструктивных процедур, т. е. для тех процедур, для которых можно построить алгоритм, можно разработать реализующие их машины Тьюринга. В тезисе Тьюринга, который является основной гипотезой теории алгоритмов, содержится утвердительный ответ на этот вопрос.Тезис формулируется следующим образом: всякий алгоритм может быть задан посредством Тьюринговой функциональной схемы и реализован в соответствующей машине Тьюринга. Доказать тезис Тьюринга нельзя, так как само понятие алгоритма является неточным. В формулировке тезиса Тьюринга идет речь, с одной стороны, о всяком алгоритме, т. е. об общем понятии алгоритма, которое не является точным математическим понятием; а с другой стороны, в этой же формулировке речь идет о точном математическом понятии - о Тьюринговой функциональной схеме.
Значение гипотезы как раз и заключается в том, что она уточняет общее, но расплывчатое понятие “всякого алгоритма “ через более специальное, но уже совершенно точное математическое понятие “Тьюринговой функциональной схемы” (и ее реализации в машине Тьюринга), т. е. общее расплывчатое понятие алгоритма отождествляется с точным понятием функциональной схемы машины Тьюринга.
Уверенность в справедливости тезиса Тьюринга основана главным образом на опыте. Все известные алгоритмы, которые были придуманы в течение многих веков истории математики, могут быть заданы посредством Тьюринговых функциональных схем. По своему характеру тезис Тьюринга напоминает об адекватности математических моделей физическим явлениям и процессам.
Исходя из тезиса Тьюринга, невозможность построения машины Тьюринга означает отсутствие алгоритма решения данной проблемы. Расшифруем это положение. В числе общих требований, предъявляемых к алгоритмам, упоминается требование результативности. Наиболее радикальной формулировкой здесь было бы требование, чтобы по любому алгоритму А и данным а можно было бы определить, приведет ли работа А при исходных данных а к результату или нет. Иначе говоря нужно построить алгоритм В, такой что В(А,а) = истина, если А(а) дает результат, и В(А,а) = ложъ, если А(а) не дает результата.
В силу тезиса Тьюринга задачу о том, приведет ли реализация алгоритма А при исходных данных а к результату или нет, можно сформулировать как задачу построения машины Тьюринга следующим образом [1].
Построить машину Тьюринга Т0 такую (с такой системой команд), что для любой машины Тьюринга Т с системой команд Ет и любых исходных данных а для машины Т Т0(Хт, а) = истина, если Т(а) - останавливается и Т0(Ет, а) = ложъ, если Т(а) не останавливается (происходит зацикливание).
Эта задача называется проблемой остановки, и если остановка невозможна, т. е. решаемая проблема является алгоритмически неразрешимой, никакое кодирование системы команд Ет и а в алфавите машины Т0 не приводит к успеху.
Но, тем не менее, если удастся разбить проблему на отдельные частные случаи, ее оказывается возможным решить, пользуясь разными средствами. Поэтому неразрешимость общей проблемы остановки вовсе не снимает необходимость доказывать сходимость предлагаемых алгоритмов, а лишь доказывает, что поток таких доказательств нельзя полностью автоматизировать.
Машина Тьюринга является прообразом любой вычислительной машины, так как каждая физически осуществимая вычислительная машина может быть рассмотрена лишь как некоторая приближенная модель машины Тьюринга. Именно в реальных машинах объем внешней памяти ограничен, в то время как в машине Тьюринга фигурирует бесконечная лента. Разумеется, техническое осуществление неограниченной памяти невозможно, но очевидна и современная, и прошлая тенденции к постоянному увеличению объема памяти и скорости вычислений по сравнению с уже достигнутым уровнем.
4. ВВЕДЕНИЕ В ТЕОРИЮ АВТОМАТОВ
Теория автоматов - это теория, на которой основаны экспериментальные методы исследования в кибернетике. При подходе к теории автоматов, как к части теории алгоритмов, центральной проблемой является изучение возможностей автоматов в терминах множеств слов, с которыми работают автоматы.Можно выделить два основных аспекта работы автоматов.
1. Автоматы-распознаватели, которые распознают входные слова, т. е. отвечают на вопрос, принадлежит ли поданное на вход слово данному множеству.
2. Автоматы-преобразователи, которые преобразуют входные слова в выходные, т. е. реализуют автоматные отображения.
Одной из задач теории автоматов является задача описания автомата и его реализации, т. е. представления автомата как структуры, состоящей из объектов фиксированной сложности (элементов). В этом отношении теория автоматов оказалась наиболее развитой ветвью теории алгоритмов.
Общая теория автоматов подразделяется на абстрактную теорию и структурную теорию автоматов. Абстрактная теория автоматов занимает промежуточное положение между алгеброй и логикой. С точки зрения приложений значение абстрактной теории автоматов отнюдь не сводится к удовлетворению запросов одной лишь вычислительной техники. Современная теория автоматов представляет собой математический аппарат для решения широкого класса комбинаторных проблем.
В частности, с помощью теории автоматов могут быть решены многие лингвистические задачи.
Например, пусть дано некоторое число фраз на незнакомом языке и их перевод на другой незнакомый язык. Требуется осуществить перевод некоторого числа новых фраз с первого языка на второй при условии, что в них используются лишь те слова и грамматические правила, которые встречаются в уже переведенных фразах. Решение этой задачи может состоять из следующих этапов.
1. В исходном множестве фраз первого языка выделяются различные входящие в них элементы языка (корни слов, окончания, суффиксы, префиксы и т.п.). Эти элементы объединяются в алфавит, называемый входным.
2. Аналогичным образом из исходных фраз второго языка формируется выходной алфавит.
Можно осуществлять и более мелкое дробление, используя в качестве входного и выходного алфавитов обычные алфавиты первого и второго языков, но тогда решение задачи становится более громоздким.
3. Перевод теперь представляется как установление соответствия между словами во входном и выходном алфавитах, что и делается на третьем этапе.
4. Используя алгоритм синтеза, по установленному соответствию строится осуществляющий его автомат А.
5. Используя алгоритм минимизации, производится оптимизация автомата А по числу состояний.
Полученный автомат будет осуществлять преобразование входных слов в выходные на более широкой области, включающей (при соблюдении оговоренных выше условий и соответствующих ограничений грамматики) все новые фразы, подлежащие переводу. Примером такого перевода было решение задачи перевода с венгерского языка на баскский, выполненное в Институте кибернетики в г. Киеве под руководством В.М. Глушкова. При ее решении по 10 парам исходных фраз был синтезирован автомат с 75 состояниями, который путем минимизации был приведен к 46 состояниям.
Структурная теория автоматов позволяет реализовать абстрактный автомат на элементах, принадлежащих к заранее заданному классу.
4.1. Алфавитные операторы и автоматы
Под абстрактным алфавитом понимают любую конечную совокупность объектов, называемых буквами данного алфавита. Слова в этом алфавите определяют как любые конечные упорядоченные последовательности букв. Число букв в слове называют длиной слова, причем, наряду со словами положительной длины (состоящими не менее, чем из одной буквы), рассматривают также пустое слово, не содержащее ни одной буквы. Слова единичной длины отождествляются с буквами алфавита.Алфавитным оператором, или алфавитным отображением, называют всякое соответствие (функцию), сопоставляющее словам в том или ином алфавите слова в том же самом или в некотором другом фиксированном алфавите. Первый алфавит называют при этом входным, а второй - выходным алфавитом данного оператора. Алфавитный оператор, сопоставляющий каждому входному слову (слову во входном алфавите оператора) не более одного выходного слова (слова в выходном алфавите оператора), называют однозначным. Если алфавитный оператор не сопоставляет данному входному слову никакого выходного слова (в том числе и пустого), то говорят, что он не определен на этом слове. Совокупность всех слов, на которых алфавитный оператор определен, называется его областью определения. Алфавитный оператор называют частичным, если его область определения не совпадает с совокупностью всех входных слов.
Всякий дискретный преобразователь информации, выдающий некоторый выходной сигнал (букву выходного алфавита) в ответ на каждый входной сигнал (букву входного алфавита), реализует некоторый алфавитный оператор. Такие преобразователи воспринимают и выдают сигналы лишь в моменты времени, разделенные промежутками ненулевой длительности, и называются автоматами.
В общем случае выходной сигнал автомата в каждый момент времени зависит от значений входного сигнала не только в данный, но и в предыдущие моменты времени. Эта зависимость проявляется в изменении у автомата его внутренних состояний таким образом, что сигнал на его выходе в каждый момент времени определяется как входным сигналом в тот же момент времени, так и состоянием, в котором оказался автомат к данному моменту времени в результате воздействия на его вход сигналов, поступивших в предыдущие моменты времени.
Если выходной сигнал автомата в каждый момент времени целиком определяется входным сигналом в тот же момент времени, то автомат имеет единственное внутреннее состояние и его называют комбинационной схемой.
Примером автомата с неединственным состоянием может служить устройство управления лифтом. Входными сигналами для него являются номера требуемых этажей Z1 < Z2 < ... < Zf < “. Реакция кабины лифта на каждый входной сигнал должна быть различной в зависимости от того, на какой этаж кабина приведена входными сигналами, поступившими к данному моменту времени. Если кабина находится ниже требуемого этажа она должна двигаться вверх до требуемого этажа, если выше - вниз до требуемого этажа, если на требуемом этаже -должна остаться на месте. Таким образом, выходные сигналы wуст-ройства управления лифтом можно считать равными разностям z. - zk, где zk - номер этажа, на котором находилась кабина лифта к моменту поступления очередного входного сигнала (номера требуемого этажа) z., при этом сигнал w. = 0 не включается в выходной алфавит (пустой символ). Появление каждого выходного сигнала зависит от входного сигнала, действующего в данный момент времени, и от номера этажа, на котором к этому моменту времени оказалась кабина лифта. По этой причине можно считать, что автомат управления лифтом имеет число состояний, равное числу этажей здания. Поскольку процесс движения кабины между этажами не представляет интереса, считается, что состояние автомата изменяется мгновенно в момент достижения кабиной очередного этажа и с этим же моментом времени отождествляется момент поступления входного сигнала, вызвавшего движение кабины к этому этажу.
4.2. Абстрактные автоматы
Автоматы, рассматриваемые безотносительно к их внутренней структуре, принято называть абстрактными автоматами.Абстрактный автомат работает в дискретном автоматном времени, последовательные моменты которого отождествляются с натуральными числами t = 1, 2, ... . В примере с лифтом моменты автоматного времени определяются кнопкой “пуск” либо моментами нажатия кнопок с номерами требуемых этажей.
Для задания абстрактного автомата нужно задать входной алфавит Z = {z1, z2, ..., zp}, выходной алфавит W = {w1, w2, ..., wG} и
множество A = {a1, a2, ..., aM} его внутренних состояний, называемое просто множеством состоянии автомата. В каждый момент времени t = 0, 1, 2, ... абстрактный автомат A находится в некотором состоянии at = a(t) из A. Состояние a0 = a(0) в начальный момент времени t = 0 называется начальным состоянием автомата A. Условно абстрактный автомат изображается в виде устройства (рис. 4.1) с одним входом и одним выходом.
Рис. 4.1
В каждый момент t автоматного времени, начиная c t = 1, на вход автомата поступает в качестве входного сигнала одна из букв zt = z(t) алфавита Z. Конечные упорядоченные последовательности входных букв z(l)z(2)...z(k) автомата будут входными словами. На вход автомата может подаваться любое входное слово из некоторого фиксированного множества допустимых входных слов. Каждое допустимое слово p = z(l)z(2)...z(k), поданное на вход данного автомата А, вызывает появление на выходе автомата выходного слова q = w(1)w(2)...w(k), представляющего собой некоторую упорядоченную конечную последовательность выходных сигналов автомата A (букв алфавита W), имеющего ту же самую длину, что и соответствующее ему входное слово p. Получаемое преобразование фА допустимых входных слов p в соответствующие им выходные слова q является алфавитным оператором, индуцированным автоматом А, или просто оператором автомата А.
В примере с лифтом оператор управляющего автомата можно задать явно. Из найденных выше соотношений между входными и выходными сигналами для этого автомата следует, что
w(t) = z(t) - z(t-l),
если принять z(0) = z1. Это и есть искомое преобразование входных слов автомата в выходные. Поскольку длина входных слов для этого преобразования не ограничена, множество допустимых входных слов для него бесконечно и даже несчетно при всяком F > 2.
Оператор фА однозначно определяется заданием функции переходов 5 и функции выходов X рассматриваемого автомата. Функция переходов определяет состояние a(t) автомата в некоторый момент t автоматного времени по входному сигналу z(t) в тот же самый момент и состояний a(t-l) в предыдущий момент автоматного времени
a(t) = 5(a(t-1), z(t)). (4.1)
Функция выходов определяет зависимость выходного сигнала от тех же самых переменных
w(t) = X(a(t-1), z(t)). (4.2)
Задавая любое выходное слово p = z(1)z(2)...z(k) и начальное состояние a(0) автомата, с помощью соотношений (4.1) и (4.2) можно последовательно определить все буквы соответствующего выходного слова
q = ФА(Р) = w(1)w(2)...w(k).
Таким образом, соотношения (4.1) и (4.2) действительно определяют оператор автомата A.
Функции переходов и выходов представляются обычно абстрактными частичными функциями 5(a, z) и X(a, z), задающими однозначное отображение некоторого множества пар (a, z)(aeA, zeZ) в множества A и W соответственно. Допустимыми входными словами для автомата A называют те и только те входные слова р, на которых с помощью функций 5 и X указанным выше способом можно определить соответствующие им выходные слова q = фA(p).
Автомат называют конечным, если конечны все три определяющие его множества Z, W, A.
Для примера с лифтом функции переходов и выходов определяются соответственно следующими равенствами:
a(t) = z(t), w(t) = z(t)-a(t-1).
Автомат управления лифтом конечен, хотя область определения его оператора состоит из бесконечного множества допустимых слов.
Поскольку дальше будут рассматриваться только конечные автоматы, слово “конечный” будет опускаться.
Автомат называют вполне определенным, если его функции переходов и выходов заданы на всех парах (a, z), и частичным - в противном случае.
Два абстрактных автомата считаются одинаковыми, если они отличаются друг от друга лишь обозначениями входных и выходных сигналов, состояний.
4.3. Способы задания абстрактных автоматов
Если заданы входной и выходной алфавиты автомата, а также множество его состояний, среди которых фиксировано начальное состояние a0, для задания абстрактного автомата остается задать функцию переходов 5 функцию выходов A .Автоматы, функции переходов и выходов которых удовлетворяют условиям (4.1), (4.2), называют автоматами Мили. Автоматы, у которых функции переходов и выходов удовлетворяют условиям
a(t) = 5(a(t-1), z(t)), (4.3)
называют автоматами Мура [2] .
Различие между автоматами Мили и Мура состоит в том, что выходной сигнал в автомате Мили зависит как от состояния в предыдущий момент времени, так и от входного сигнала в рассматриваемый момент времени, а в автомате Мура - только от состояния в рассматриваемый момент времени. Если подставить правую часть (4.3) в (4.4), то получится равенство типа (4.2). Таким образом, автомат Мура всегда можно свести к автомату Мили с тем же самым числом состояний и теми же самыми входным и выходным алфавитами. Для конечного автомата функции 5 и X определены на конечном множестве значений аргументов и принимают значения из конечных множеств. По этой причине для конечных автоматов функции 5 и X можно задать в виде таблиц.
Таблица 4.1 Таблица 4.2
| a(t-1) | zo | Z1 | Z2 | a(t-1) | Zo | Z1 | Z2 |
| ao | a2 | a3 | a1 | ao | w3 | W2 | W1 |
| ai | a3 | ao | a2 | a1 | w0 | W3 | wo |
| a2 | ao | a1 | a1 | a2 | w1 | wo | W2 |
| a3 | a2 | a2 | a3 | a3 | W2 | W1 | W3 |
Поскольку области определения функций 5 и X совпадают, таблицы переходов и выходов могут быть совмещены в одну таблицу переходов-выходов (табл. 4.3), в которой на пересечении i-й строки иj-го столбца (ie {0, 1, 2, ..., n}, je {0, 1, 2, ..., г}) записывается в числителе новое состояние автомата, а в знаменателе - выходной сигнал, выработанный при переходе в это состояние.
В табл. 4.4, 4.5 приведены примеры функций переходов 5 и выходов X автомата Мура. Функция выходов X автомата Мура зависит только от одного параметра a(t), поэтому при совмещении таблиц переходов и выходов достаточно столбцу состояний автомата поставить в соответствие столбец выходных сигналов (табл. 4.6).
| Таблица 4.3 | ||||||||||||||||||||
|
| Таблица 4.4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Таблица 4.5 | ||||||||||||||||
|
| z 0 I'M 0 |
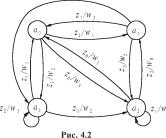 |
| z |
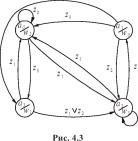 |
I j I
вершину aj проводится дуга, около которой в числителе указывается входной сигнал, вызывающий этот переход, а в знаменателе - возникающий при этом выходной сигнал.
Для автомата Мура вершины графа отмечаются состояниями и связанными с ними входными сигналами. Дуги графа отмечаются входными сигналами, под действием которых возникают рассматриваемые переходы.
В приведенных примерах функции 5 и X определены при всех значениях переменных a(t-1) и z(t), поэтому им соответствуют вполне определенные автоматы. Для частичных автоматов функции 5 и X определены не на всех парах a(t-1) и z(t). В этом случае на месте неопределенных переходов или выходов в таблицах ставятся прочерки. В графах же отсутствуют дуги, соответствующие неопределенным переходам, а вместо неопределенных выходных сигналов ставятся прочерки.
Если заданы функции переходов и выходов автомата, по ним можно построить оператор автомата. Однако не по всякому заданному алфавитному оператору можно построить функции переходов и выходов некоторого автомата.
4.4. Автоматные операторы
Пусть оператор jA автомата А удовлетворяет следующим четырем условиям.1. фА осуществляет однозначное отображение (вообще говоря, частичное) множества входных слов в множество выходных слов.
2. Область определения оператора фА удовлетворяет условиям полноты, т. е. вместе с любым содержащимся в ней словом содержит и все начальные отрезки этого слова (так, если области определения оператора фА принадлежит слово z1z2z3z4, то ей принадлежат и слова z1, z1z2, z1z2z3). Пустое слово всегда входит в область определения оператора
Фа.
3. фА сохраняет длину слова: любое входное слово р, на котором оператор фА определен, имеет ту же длину, что и его образ фА(р). В частности, пустое слово переводится оператором фА в пустое слово.
4. фА переводит любой начальный отрезок слова р, на котором он определен, в имеющий ту же длину начальный отрезок слова фА(р).
Эти четыре условия называют условиями автоматности оператора, а удовлетворяющий им оператор - автоматным оператором.
Если алфавитный оператор ф удовлетворяет условиям автоматно-сти, можно построить автоматы Мили и Мура (вообще говоря, бесконечные), индуцирующие оператор ф. В случае, когда область определения оператора ф конечна (конечно множество слов, на которых определен оператор ф), эти автоматы также могут быть выбраны конечными [2] .
Не всякий алфавитный оператор удовлетворяет условиям автомат-ности. Существует, однако, прием, позволяющий превратить любой алфавитный оператор в автоматный оператор.
Пусть ф - произвольный алфавитный оператор с конечными входным Z и выходным W алфавитами, P - область определения этого оператора. Будем применять к оператору ф две операции. Первая из них называется операцией выравнивания длин слов. Она заключается в том, что во входной и выходной алфавиты добавляется по одной пустой букве а и в соответственно, а затем к любому слову p из P приписываются справа mp экземпляров буквы а, а к его образу q = ф(р) приписываются слева nq экземпляров буквы в так, чтобы длины полученных в результате приписывания этих букв слов p1 и q1 совпали. Если, в частности, числа mp выбираются равными длине слова q, а числа nq равными длине слова p, то операция выравнивания длины слов называется стандартной.
После выполнения операции выравнивания длин слов строится новый оператор ф1, отображающий некоторое множество P1 слов в алфавите Z и {а} в множество слов в алфавите W и {в}. Он действует по правилу q1 = ф1(р1), где слова p1 и q1 получены выравниванием длин слов p и q, причем p пробегает все P. Оператор ф1 называется при этом выравненным оператором.
Вторая операция применяется только к выравненным алфавитным операторам, т. е. к таким операторам, у которых длины входных и соответствующих им выходных слов равны между собой. Ее называют операцией пополнения. Она заключается в распространении отображения ф на начальные отрезки слов. Это осуществляется следующим образом. Если S - произвольный начальный отрезок любого слова p из области определения оператора ф, то ф(?) полагается равным начальному отрезку слова ф(р), имеющим ту же, что и отрезок S, длину.
В результате применения операции пополнения к произвольному выравненному алфавитному оператору ф1 возникает оператор ф1', называемый пополнением оператора ф1. Если пополнение ф1' оператора ф1 является однозначным, то оно удовлетворяет, очевидно, всем четырем условиям автоматности. К сожалению, однако, в большинстве случаев пополнение оператора ф1 неоднозначно. Вместе с тем справедливо следующее утверждение [2]: в случае, когда оператор ф1 получен из некоторого однозначного алфавитного оператора в результате стандартной операции выравнивания длин слов, пополнение ф^ этого оператора однозначно и является автоматным оператором.
В ряде случаев при превращении заданного оператора в автоматный оператор можно применять не стандартную операцию выравнивания, а какой-нибудь более экономный (с точки зрения числа дописываемых букв) вариант операции выравнивания. В частности, если сам исходный оператор был автоматным, можно считать, что применяется нулевая операция выравнивания, при которой никакого дописывания пустых букв вообще не происходит.
Обычно на практике поступают следующим образом. Сначала операцию выравнивания проводят наиболее экономным образом, и, применяя затем операцию пополнения, проверяют (по признаку однозначности пополнения), получится ли в результате автоматный оператор. Если нет, то производят новое дописывание пустых букв, новую проверку пополнения и т.д. В результате продолжения подобного процесса обязательно будет получен автоматный оператор. Этот метод приведения алфавитного оператора к автоматному оператору называют методом последовательного приведения.
Для построенного таким методом оператора можно построить функции переходов и выходов.
5. АБСТРАКТНЫЙ СИНТЕЗ АВТОМАТОВ
5.1. Построение функций переходов и выходов по алфавитному оператору
Если область определения алфавитного оператора ф конечна, его чаще всего задают с помощью таблицы соответствия. В левой половине этой таблицы выписывают в том или ином порядке входные слова, на которых задан оператор ф, а в правой части таблицы - соответствующие им выходные слова.Рассмотрим процесс построения функций переходов и выходов по алфавитному оператору на конкретном примере. Пусть входной и выходной алфавиты состоят только из двух букв {z0, zj и {w0, w1} соответственно, а оператор (табл. 5.1) задан таблицей соответствия.
Таблица 5.1
| z(1) | z(2) | z(3) | w(1) | w(2) | w(3) |
| z0 | z0 | z0 | w1 | w0 | w0 |
| z0 | z0 | z1 | W0 | w0 | w0 |
| z0 | z1 | z0 | w1 | w0 | w0 |
| z0 | z1 | z1 | % | w1 | w1 |
| z1 | z0 | z0 | W0 | w0 | w1 |
| z1 | z0 | z1 | W0 | w1 | w1 |
| z1 | z1 | z0 | W0 | w1 | w0 |
| z1 | z1 | z1 | w1 | w0 | w1 |
Поскольку в табл. 5.1 при z(1) = z0 для второго и четвертого слов w(1) = w0, а для первого и третьего слов w(1) = w1, допишем справа к первым четырем входным словам а и слева к первым четырем, выходным словам в (табл. 5.2). Точно так же в табл. 5.1 при z(1) = z1 для пятого, шестого и седьмого слов w(1) = w0, а для восьмого слова w(1) = w1, поэтому справа к пятому, шестому, седьмому и восьмому входным словам припишем букву а и слева к соответствующим выходным словам припишем букву р. Если при этом считать, что z(1) преобразуется в в, то для однобуквенных начальных отрезков слов получилось однозначное преобразование (см. табл. 5.2).
| Таблица 5.2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
5.2 все различны, поэтому они преобразуются однозначно. То же самое относится к четырехбуквенным начальным отрезкам входных слов и к полным входным словам в табл. 5.3. Таким образом, задаваемый табл.
5.3 алфавитный оператор ф’, будет автоматным.
Если бы исходный оператор содержал не трехбуквенные, а четырехбуквенные входные и выходные слова, для приведения его к автоматному виду только что рассмотренным способом пришлось бы проверять однозначность преобразования и трехбуквенных начальных отрезков входных слов.
Построим теперь по табл. 5.3 графы автоматов Мили и Мура. Будем при этом предполагать, что последний символ каждого входного слова должен переводить автомат в начальное состояние. Начнем с графа автомата Мили (рис. 5.1).
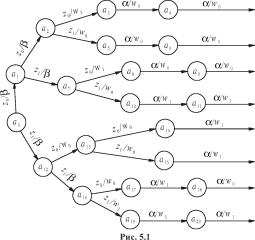
В момент t = 0 автомат находится в состоянии a0. При подаче в последующие моменты времени каждого входного сигнала z(t) автомат переходит в новое состояние и вырабатывает выходной сигнал w(t).
Поскольку для абстрактного автомата порядок нумерации состояний, отличных от a0, безразличен, можно считать, что буква z(1) = z0 первого входного слова из табл. 5.3 переводит автомат в состояние a1. При этом вырабатывается выходной сигнал w(1) = р. Буква z(2) = z0 переводит автомат из состояния a1 в состояние a2 и обеспечивает выработку выходного сигнала w(2) = р. Входная буква z(3) = z0 переводит автомат из a2 в a3. Этому переходу соответствует выходной сигнал w(3) = w1. Буквой z(4) = a автомат переводится в состояние a4 с выдачей выходного сигнала w(4) = w0. Последней во входном слове буквой z(5) = а автомат, согласно условию, должен переводиться в состояние a0. Этому переходу соответствует выходной сигнал w(5) = w0. Начальные отрезки z(1)z(2), w(1)w(2) второго входного и выходного слов совпадают с соответствующими начальными отрезками первого входного и выходного слов, поэтому первые два перехода для второго входного слова совпадают с уже построенными. Последующие переходы для этого слова строятся точно так же, как и для первого слова. Затем аналогичным образом строятся переходы для остальных входных и выходных слов (см. табл. 5.3).
Граф автомата Мура приведен на рис. 5.2. Он строится почти так же, как и для автомата Мили. Первое отличие состоит в том, что выходные сигналы записываются в вершинах, так как выходной сигнал автомата Мура в каждый момент времени определяется только состоянием и не зависит от входного сигнала.
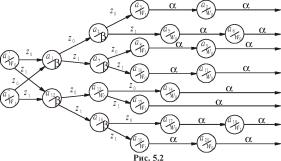 |
а 0 а о а о а о а 0 а 0 а0 а 0 |
Автоматы, соответствующие рис. 5.1 и 5.2, имеют входной алфавит {z0, z1, a}. Так как из каждой вершины этих графов выходят дуги, отмеченные не более чем двумя из этих символов, рассматриваемые автоматы будут частичными.
По графам, изображенным на рис. 5.1 и 5.2, легко можно построить таблицы переходов и выходов автоматов.
5.2. Постановка задачи о синтезе автоматов
Синтез автомата заключается в реализации автомата в виде устройства, соответствующего заданию. Для конечных автоматов заданием обычно служит представленный в виде таблицы соответствия алфавитный оператор. Процесс синтеза состоит из двух этапов: этапа абстрактного синтеза и этапа структурного синтеза.На этапе абстрактного синтеза входные и выходные сигналы рассматриваются просто как буквы входного и выходного алфавитов. При рассмотрении состояний интересуются их числом, считая, что при меньшем числе состояний реализация автомата проще. Этот этап синтеза заключается в построении функций переходов и выходов автомата по заданному алфавитному оператору и в нахождении абстрактного автомата с наименьшим числом состояний в некотором смысле эквивалентного исходному.
На этапе структурного синтеза выбирается способ представления входных и выходных сигналов через сигналы, принятые за элементарные, а также способ представления состояний автомата через состояния автоматов, принятых за элементарные. Конечной целью структурного синтеза является получение схемы, состоящей из минимального числа элементов заданного логического базиса.
Возможный путь решения первой части задачи абстрактного синтеза указан в подразд. 5.1. Решению второй части задачи необходимо предпослать несколько определений.
Два вполне определенных абстрактных автомата с общим входным и общим выходным алфавитами называют эквивалентными, если они имеют один и тот же алфавитный оператор.
Два частичных автомата с общим входным и общим выходным алфавитами называют эквивалентными, если их частичные алфавитные операторы имеют одну и ту же область определения и совпадают на этой области. Для частичных автоматов, однако, большее значение имеет не отношение эквивалентности, а отношение эквивалентного продолжения автоматов.
Говорят, что частичный оператор ф продолжает частичный оператор у, если область определения оператора ф включает в себя область определения D оператора у, и на области D оба оператора совпадают. Частичный автомат B называют эквивалентным продолжением частичного автомата A, если оператор автомата В продолжает оператор автомата A.
Абстрактный синтез автомата завершается нахождением автомата с минимальным числом состояний, эквивалентного заданному вполне определенному автомату или эквивалентно продолжающего заданный частичный автомат. Процесс нахождения такого автомата называется минимизацией абстрактного автомата, а полученный в результате его автомат называют минимальным автоматом.
Первым (предварительным) этапом всякой минимизации является выделение неопределенных выходных сигналов и состояний и внесение соответствующей неопределенности в таблицы переходов и выходов автомата таким образом, чтобы не изменить оператор автомата. С этой целью при задании частичного автомата Мили таблицами переходов и выходов нужно прочеркнуть все места в таблице переходов автомата, которым соответствуют прочеркнутые места в таблице выходов. Если для частичных автоматов Мура считать запрещенными состояния, для которых не определена функция выходов, то в таблице переходов автомата Мура нужно заменить черточками символы запрещенных состояний.
Пусть табл. 5.4 и 5.5 задают функции переходов и выходов час
| Таблица 5.6 | |||||||||||||||
|
| Таблица 5.5 | |||||||||||||||
|
| a(t-1) | Z0 | Z1 |
| ao | a0 | a1 |
| a, | a | a |
| 2 | 0 | |
| a2 | a0 | a2 |
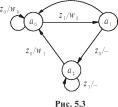
Если при каком-либо переходе выходной сигнал не определен, то и состояние, в которое перейдет автомат, не имеет значения. Поэтому после внесения неопределенности из табл.5.5 в табл.5.4 получим табл.5.6. Соответствующий табл.5.4 и табл.5.5 граф автомата Мили приведен на рис. 5.3. На рис. 5.4 приведен граф автомата, соответствующий табл. 5.5 и 5.6.
| z, /w 1 |
 |
| Z J /w J |
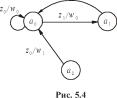 |
Таблица 5.7 Таблица 5.8
| ||||||||||||||||||||||||||||||||
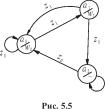
| Табл.5.7 соответствует граф автомата, приведенный на рис.5.5, а табл. 5.8- граф автомата, приведенный на рис. 5.6. |
| z | 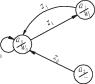 |
| Рис. 5.6 |
Для автомата Мили, заданного табл. 5.4, 5.5 или рис. 5.3, все состояния достижимы, поэтому автомат, заданный табл. 5.4, 5.5 или рис. 5.3, будет связным. Для автомата, заданного табл. 5.5, 5.6 или рис. 5.4, состояние а2 будет недостижимым, в силу чего автомат не будет связным.
Точно так же автомат Мура, заданный табл. 5.7 или рис. 5.5, является связным, а автомат, заданный табл. 5.8 или рис. 5.6, не будет связным, поскольку у него состояние а2 недостижимо.
После вычеркивания в табл. 5.5, 5.6 и 5.8 строки, соответствующей состоянию а2, получим связный автомат Мили, заданный табл. 5.9, 5.10 или рис. 5.7, и связный автомат Мура, заданный табл. 5.11 или рис. 5.8.
Таблица 5.9 Таблица 5.10 Таблица 5.11
| a(t-1) | Z0 | Z1 | a(t-l) | zo | z1 | w(t-l) | a(t-l) | zo | z, |
| ao | a0 | a | ao | wo | wo | wo | ao | ao | a1 |
| a | - | a0 | ai | - | w1 | w1 | ai | - | ao |
| z 0 /'W |  |
| Рис. 5.7 |
 |
| Рис. 5.8 |
Zi/'w о
Третьим этапом минимизации автомата является объединение в одно состояние множества совместимых состояний.
5.3. Классы совместимости автомата
Пусть A - произвольный абстрактный автомат, a - любое его состояние. Говорят, что слово p во входном алфавите автомата A применимо к состоянию a, если, подавая это слово на вход автомата A, установленного предварительно в состояние а, мы получим на выходе определенное слово q в выходном алфавите, имеющее ту же самую длину, что слово р. Слово q называют результатом применения слова p к состоянию a.Если слово р неприменимо к состоянию а, то результат применения слова р к состоянию а считается неопределенным (при этом безразлично, дают ли некоторые непустые начальные отрезки слова p в применении к состоянию а определенные результаты или нет).
Состояния аг1, ..., аы, входящие в автомат Мили, называются совместимыми, если все определенные (не считая неопределенных результатов) результаты применения слова р к состояниям аг1, ..., ain будут одними и теми же (зависящими только от слова p, но не от выбора состояния ак из данного множества состояний). Для автомата Мура, кроме этого условия, для совместимости данных состояний требуется, чтобы (не считая неопределенных отметок) все совместимые состояния имели бы одинаковые отметки. Совместимые состояния во вполне определенных автоматах называются также эквивалентными.
Для конечных автоматов существует конструктивный прием нахождения совместимых состоянии автомата Миля и Мура. Этот прием основан на использовании понятия /-совместимости состояний.
Состояния а;1, ..., аіп автомата Мили называются /-совместимыми для любого данного і = 1, 2, ..., если (с точностью до неопределенных результатов) результат применения любого слова длины i к состояниям а/1, ..., ап будет одним и тем же, находясь в зависимости лишь от выбо-
ра слова, но не от выбора состояния. Состояния автомата Мура называются 0-совместимыми, если (не считая неопределенных отметок) они одинаково отмечены; они называются /-совместимыми для любого i = 1, 2, ..., если они 0-совместимы и (с точностью до неопределенных результатов) результат применения любого данного слова длины i ко всем рассматриваемым состояниям одинаков.
Очевидно, /-совместимые состояния будут также и ф-совместимыми для любого j < i. Состояния тогда и только тогда совместимы, когда они /-совместимы для всех i =1, 2, ... . i-классом данного автомата Мили и Мура называется всякое максимальное множество i-совместимых между собой состояний автомата, т. е. такое множество, к которому нельзя добавить ни одного нового состояния без нарушения свойства i-совместимости. Всякое максимальное множество совместимых между собой состояний автомата называют финальным классом или классом совместимости автомата.
Непосредственно по таблицам выходов могут быть найдены 1-классы для автоматов Мили и 0-классы для автоматов Мура. В случае автомата Мили в один и тот же 1-класс зачисляются все состояния, одинаково обозначающие (с точностью до неопределенных выходных сигналов) строки таблиц выходов. В случае автомата Мура в один и тот же 0-класс зачисляются все одинаково отмеченные состояния и все состояния, отметки которых не определены (последние попадают, таким образом, во все 0-классы).
На этом примере видно, что для частичных автоматов i-классы, вообще говоря, пересекаются между собой. То же самое имеет место и для финальных классов. Для вполне определенных автоматов i-классы не могут пересекаться между собой.
Пусть K1(i), ..., Kp(i) - совокупности всех i-классов автомата (Мили или Мура). Говорят, что тождество N состояний ajl, ..., ajk, целиком содержащееся в одном из i-классов Kr(i) выдерживает умножение на входную букву zm, если все состояния b(aj1, zm), 6(aj2, zm), ..., 5(ajk, zm) (не считая тех, которые не определены) содержатся в одном и том же i-классе K(i), зависящем от выбора N и zm е N.
Нахождение максимальных подмножеств состояний каждого i-класса, выдерживающих умножение на все буквы z1, z2, ..., zF входного алфавита автомата называется операцией расщепления (разбиения) i-классов. Операция расщепления i-классов выполняются очевидным образом с помощью таблицы переходов рассматриваемого автомата.
В результате применения операции расщепления /-классов автомата Мили или Мура возникают все (/+1)-классы этого автомата (/ = 1, 2, ...). Ими является все максимальные множества, возникающие в результате расщепления.
Если применять последовательно операцию расщепления /-классов к конечному автомату Мили или Мура, отправляясь от 1-классов (для автомата Мили) или от 0-классов (для автомата Мура), то через конечное число шагов для некоторого k > 0 процесс расщепления k-классов даст в результате те же самые k-классы. Удовлетворяющие этому условию (нерасщепляемые далее) k-классы будут совпадать с финальными классами исходного автомата. Этот полученный В. М. Глушковым [2] результат является основой минимизации числа состояний конечных автоматов.
5.4. Автомат с минимальным числом состояний
Обозначим Ср c2, ..., cS финальные классы какого-либо автомата A с входным алфавитом Z = {z1, z2, ..., zp}. Так как финальные классы являются вместе с тем и j-классами для всех j = 0, 1, 2, ..., то для каждой буквы zk все состояния, входящие в любой финальный класс Cm, порождают один и тот же выходной сигнал (для автомата Мили) или отмечены одним и тем же выходным сигналом (для автомата Мура), либо соответствующие выходные сигналы не определены. Построим таблицу выходов некоторого автомата С, состояниями которого служат финальные классы c1, с2, ..., cS, а входными сигналами - буквы алфавита Z. Для автомата Мили относим каждой паре (cm, zk) выходной сигнал, соответствующий паре (av, zk) для любого an из класса cm, для которого этот сигнал определен. Если же для всех пар (av, zk) соответствующие им выходные сигналы не определены, то считаем, что выходной сигнал пары (cm, zk) также не определен. Для автомата Мура отмечаем каждый класс cm выходным сигналом, которым отмечен произвольный элемент av е ст. Если же все элементы, входящие в cm не отмечены, то будем считать отметку класса cm неопределенной.Таблицу 51 переходов автомата C построим по следующему правилу: переход из cm в 61(cm, zk) будет считаться неопределенным, если для состояний av, составляющих класс cm, переход из av в 5(av, zk) не определен. Если же хотя бы для одного состояния av е cm переход из av в 5(av, zk) определен, то переход из cm в 51(cm, zk) также будет считаться определенным, а в качестве состояния 51(cm, zk) будет приниматься любой из финальных классов с. (их может быть несколько), содержащий все определенные состояния вида 8(av, zk)(avecm). Очевидно, финальные классы с. с требуемыми свойствами всегда существуют.
За начальное состояние автомата С можно принять любой финальный класс, содержащий начальное состояние автомата A, либо принять за начальные состояния автомата С некоторые или все финальные классы, содержащие начальное состояние автомата A.
Совокупность E всех финальных классов автомата A удовлетворяет условию полноты и условию замкнутости. Первое условие означает, что каждое состояние автомата A принадлежит какому-либо из финальных классов. Второе условие означает, что для каждой буквы входного алфавита все состояния каждого финального класса (с точностью до неопределенных переходов) переходят в состояния, принадлежащие одному финальному классу (тому же самому или другому). Пусть Е0 - наименьшее подмножество E, удовлетворяющее условиям полноты и замкнутости. Условие замкнутости здесь означает, что для каждой буквы входного алфавита все состояния каждого финального класса из E0 (с точностью до неопределенных переходов) переходят в состояния, принадлежащие одному (тому же самому или другому) финальному классу из E0. Назовем минимальной нормальной формой автомата A нормальную форму, построенную по множеству финальных классов E0.
Если в минимальной нормальной форме С связного автомата A в качестве начального состояния выбран какой-либо финальный класс, содержащий начальное состояние автомата A, то автомат С будет иметь наименьшее число состояний среди всех автоматов, эквивалентно продолжающих автомат A.
Процесс минимизации автомата A можно разбить на два этапа. На первом этапе с помощью какого-либо эвристического приема строится эквивалентный автомату A автомат B с меньшим, чем у A количеством состояний, а на втором этапе стандартным методом осуществляется минимизация автомата A. При этом чем меньше количество состояний имеет автомат B, тем проще будет его последующая минимизация.
Наибольший объем работы по минимизации автомата связан с нахождением финальных классов. Для конечных автоматов эта работа может быть существенно упрощена с помощью треугольных таблиц. Правила составления и использования этих таблиц удобнее всего рассмотреть на конкретных примерах абстрактного синтеза автоматов.
5.5. Пример минимизации автомата Мили
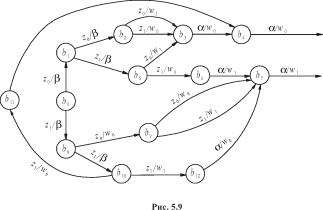
Пусть частичный автомат Мили A задан графом, приведенным на рис. 5.1. Это связный автомат без неопределенных выходных сигналов. Его минимизацию будем осуществлять в два этапа. Сначала построим эквивалентный автомату A автомат B с меньшим чем у A числом состояний.Согласно рис. 5.1, единственным применимым к состояниям a4, a6, a9 и a18 входным словом будет однобуквенное слово p = а с результатом применения q = w0. По этой причине состояния a4, a6, a9 и a18 совместимы, и их можно заменить одним состоянием b4. Точно так же убедимся в совместимости состояний a11, a14, a15 и a20, в силу чего их можно заменить одним состоянием b7. Для состояний a3, a5, a8 применимыми входными словами будут лишь двухбуквенное слово p1= аа, которому соответствует результат применения q1= w0w0, и однобуквенное слово p = а с результатом применения q = w0. Следовательно, состояния a3, a5, a8 совместимы, и их можно заменить одним состоянием b3. Переобозначив теперь на рис. 5.1 a0 на b0, a1 на b1, a2 на b2, a7 на b5, a 10 на b6, a12 на b8, a13 на b^, a16 на b10, a17 на b11 и aV9 на b12, получим граф автомата Мили B, изображенный на рис. 5.9.
| а/w 0 | |
 |
b О b О |
Других слов область определения оператора В не содержит. При этом каждому входному слову оператор автомата B сопоставляет то же самое единственное выходное слово, что и оператор автомата A.
Таблица 5.12
| b(t-1) | a | zo | Zi |
| bo | - | b/P | b/e |
| bi | - | b/в | b/e |
| Ь2 | - | b3/wi | b3/w0 |
| b3 | b4/W0 | - | - |
| Ь4 | b0w 0 | - | - |
| Ь5 | - | b3/W1 | b6/w0 |
| Ь6 | b7/w1 | - | - |
| b7 | bo/wi | - | - |
| Ь8 | - | b9/W0 | |
| b9 | - | b7/W0 | b7w i |
| bio | - | bii/wo | bi2/Wi |
| Ь11 | b4/W1 | - | - |
| bi2 | b7/wo | - | - |
Строки обозначаются состояниями b1, b2, ..., bh-1, а столбцы состояниями b0, b1, ..., bh 2, где h - число состояний автомата. На пересечении г-й строки и j-го столбца записываются условия, при которых возможно совмещение состояний А и bj. Если состояния нельзя совместить ни при каких условиях, ставится знак X, если совмещаются безусловно, то знак ?. Клетки, соответствующие пересечениям строк и столбцов с одинаковыми индексами, не заполняются. Окончательное совмещение состояний определяется на основании анализа непротиворечивости условий, записанных в клетках. Для рассматриваемого примера треугольная таблица (табл. 5.13) строится следующим образом.
Согласно табл. 5.12, состояниям b0 и b1 для каждого входного сигнала соответствуют одинаковые выходные сигналы, поэтому состояния b0 и b1 можно совместить, если при каждом входном сигнале они переходят в совместимые состояния, т. е. если можно совместить состояние b1 с b2 и состояние b8 с b5. Эти условия и записываются в верхнюю клетку, соответствующую столбцу для b0 (табл. 5.13). Поскольку для состояний b0 и b2 найдется входной сигнал, для которого (см. табл. 5.12) выдаются различные входные сигналы, эти состояния совместить невозможно, и соответствующая клетка табл. 5.13 отмечается символом х. Состояния b0 и b3 совмещаются безусловно, поскольку при каждом входном сигнале переход определен только для одного из них. В соответствующей клетке табл. 5.13 нужно поставить поэтому символ ?. Затем анализируются остальные пары состояний столбца табл. 5.13, отмеченного состоянием b0, после чего точно так же анализируются пары состояний, соответствующие остальным столбцам, начиная с верхней строки в каждом столбце. В результате этого анализа все клетки табл. 5.13 окажутся заполненными символами х, ? или условиями, при которых возможно совмещение состояний, соответствующих клеткам. После этого начинается анализ условий, записанных в клетках табл. 5.13.
Состояния b0 и b1 можно совместить в том случае, если совместимы состояния b1, b2 и b5, b8. Но в клетке, соответствующей состояниям b1, b2, стоит знакх, поэтому совместить состояния b0 и b1 невозможно и в соответствующей им клетке ставится символ х. Аналогичным образом находим, что и в клетке, отмеченной состояниями b2, b4, нужно поставить знак х. В клетке, отмеченной состояниями b0 и b4, стоит символ ?, поэтому в клетке, отмеченной состояниями b3 и b4, так же нужно поставить ?. В результате после такого анализа клеток, в которых записаны условия совместимости, в каждой клетке табл. 5.13 будет стоять символ х или символ ?. По такой треугольной таблице можно найти финальные классы.
Процедура нахождения минимального множества финальных классов, предполагающая полный перебор совместимых состояний, приведена в литературе [5]. Поскольку часто эта процедура оказывается гро-
| b | bb | |||||||||||
| b | X | X | ||||||||||
| b3 | V | V | V | |||||||||
| Ь4 | V | V | V | \V. | ||||||||
| Ь5 | X | X | X | V | V | |||||||
| Ь6 | V | V | V | X | X | V | ||||||
| b | V | V | V | X | X | V | V | |||||
| b8 | X | X | X | V | V | X | V | V | ||||
| Ь9 | X | X | X | V | V | X | V | V | X | |||
| bio | X | X | X | V | V | X | V | V | X |
b7, b11 b b12 |
| |
| Ь11 | V | V | V | X | X | V | bT | boVb4 | V | V | V | |
| Ь12 | V | V | V | bT | V | V | X | X | V | V | V | X |
| bo | b1 | b2 | b3 | b4 | b5 | b6 | b7 | b8 | b9 | b1o | b11 |
конкретных состояний в финальные классы. Предлагаемый способ может быть описан с помощью следующей процедуры.
1. Формируется множество пар совместимых состояний на основании разметки каждого столбца треугольной таблицы.
Для рассматриваемого автомата Мили (табл. 5.12) по табл. 5.13 находим следующие пары совместимых состояний:
| (b0, b3), | (bV bз), | (b2, b3), | (b3, b4), | (b4, b5), | (b5, | b6), |
| (b0, b4), | (bv b4), | (b2, b4^ | (b3, b5), | (b4, b8), | (b5, | b7), |
| (b0, b6), | (b1, Ьб), | (b2, b6), | (b3, b8), | (b4, b9), | (b5, | b11), |
| (b0, b7), | (b1, b7), | (b2, b7), | (b3, b9), | (b4, b10), | (b5, | b12), |
| (b0, b11), | (b1, b11), | (K b11), | (b3, b10), | (b4, b12), | ||
| (b0, b12), | (K b12), | (b2, b12), | ||||
| (b6, b7), | (b7, b8), | (b8, b11), | (b9, b11), | (b10, b11), | ||
| (b6, b8), | (b7, b9), | (b8, b12), | (b9, b12), | (b10, b12). |
(b6, bio), (b7, bn),
2. На основе полученного множества производится укрупнение групп совместимых состояний, в результате чего должна быть получена полная совокупность финальных классов, в каждом из которых все состояния совместимы между собой. Для уменьшения сложности этой процедуры возможно при формировании каждого очередного класса совместимых состояний не рассматривать состояния, уже вошедшие в какой-либо из сформированных классов. В частности, в рассматриваемом случае состояние b0 совместимо с состояниями b3 и b4, причем состояние b3 так же совместимо с состоянием b4, следовательно, их можно включить в один финальный класс K1. Состояние b0 совместимо и с состоянием b6, однако b6 не совместимо с состоянием b3 и не может входить в этот же финальный класс. Аналогичная ситуация обнаруживается при анализе совместимых с b0 состояний b7, b11, b12. Подобным же образом формируются и все остальные финальные классы. В результате будут получены следующие классы совместимых состояний:
K1 = {b0, К b4} K5 = {b8}
K2 = {bV b6, b7} K6 = {b9b K3 = {b2, Ь11} K7 = {b10}.
K4 = {b5, b12},
3. Производится анализ полученных финальных классов на удовлетворение условиям полноты и замкнутости. Проверка условия полноты очевидна и не вызывает затруднений, а проверка условия замкнутости выполняется по таблице переходов-выходов для всех состояний автомата. Если какие-либо два состояния, входящие в один из выбранных финальных классов, переводятся некоторым входным сигналом в состояния, принадлежащие разным классам, то нужно выбрать новое решение и проверить его на замкнутость.
Для рассматриваемого автомата при проверке финальных классов на замкнутость оказывается, что принадлежащие классу К2 состояния b6 и b7 сигналом а переводятся в состояния, принадлежащие разным классам (b6 -а^ b7 е К1, а b7 -а^ b0 е К2), т. е. условие замкнутости не выполняется. Следовательно, необходимо одно из этих состояний (например, b7) перенести в другой класс, не нарушая при этом условие замкнутости. Таким классом может быть класс К5. В результате будет получено окончательное множество финальных классов, совпадающих с состояниями минимизированного автомата C
С0 = К1 = {b0, b3, b4}, C3 = K4 = {b5, b12}, C6 = K7 = {b10}.
C1 = К2 = {bl, b6}, C4 = К5 = {b7, b8},
C0 = К3 = {b2, b11}, C5 = К6 = {b9}.
4. Строится таблица переходов-выходов минимизированной нормальной формы заданного автомата. Далее по этой таблице можно построить граф переходов минимизированного автомата. Состояния переходов и выходные сигналы в этом автомате определяются по переходам и выходным сигналам того состояния, которое наиболее полно определено.
Таблица 5.14
| c(t-1) | a | z0 | Z1 |
| С0 | c0 /w0 | c1 /Р | C4 ft |
| C1 | C4 /W1 | C2 /Р | c3 /Р |
| С2 | co /wi | c0 /w1 | c0/w0 |
| С3 | C4 /W0 | c0 /w1 | c1 /w0 |
| С4 | co/wi | c /w0 | C6 Q |
| C5 | - | C4 /W0 | C4 /W1 |
| C6 | - | C2 /W0 | c /w1 |
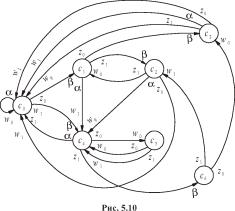
В рассматриваемом примере получены таблица переходов-выходов минимизированного автомата (табл. 5.14) и граф переходов (рис. 5.10).
5.6. Пример минимизации автомата Мура
Пусть частичный автомат Мура A задан графом, представленным на рис. 5.2. Поскольку все состояния этого автомата достижимы, а выходные сигналы определены для всех состояний, отпадает необходимость исключать недостижимые состояния. Будем опять минимизировать автомат в два этапа. Сначала построим эквивалентный автомату A автомат B с меньшим числом состояний.Согласно рис. 5.2, если автомат A установлен в любое из состояний a4, a6, a9, то единственным допустимым входным словом будет однобуквенное слово p = а, которому соответствует единственное однобуквенное слово p = 0. По этой причине состояния a4, a6, a9 совместимы и их можно заменить одним состоянием b4. Аналогичным образом находим, что совместимы состояния a11 и a15, a14 и a20.
Первую пару заменим состоянием b8, вторую - состоянием b13. Если автомат установлен в состояния a3 и a8, то допустимыми входными словами будут лишь двухбуквенное слово p1= аа, которому соответствует выходное слово q1= w0w0 и однобуквенное слово p = а, которому соответствует выходное слово q = w0. Следовательно, состояния а3 и а8 совместимы, и их можно заменить одним состоянием. Пе-реобозначив теперь на рис. 5.2 a0” на b0”, a0' на b0', a1 на bx, a2 на b2, a5 на b5, a7 на b6, a 10 на b7, an на b8, a12 на b9, a13 на b10, a16 на bn, a19 на b12, a20 на b13, a17 на b14, a18 на b15, получим граф автомата Мура B, изображенный на рис. 5.11.
Автомат B имеет 17 состояний вместо 22 у автомата A и эти автоматы эквивалентны.
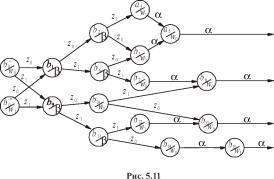 |
b b b b О |
Графу рис. 5.11 соответствует отмеченная таблица переходов (табл. 5.15) автомата B. Финальные классы автомата B будем находить с помощью треугольной таблицы (табл. 5.16), которая заполняется так же, как и для автомата Мили. Финальные классы находятся из нее для автомата Мура по тем же правилам, что и автомата Мили.
| w(t-1) | b(t-1) | a | Z0 | Z1 |
| W0 | V | - | b1 | b9 |
| V | - | b1 | b9 | |
| e | b1 | - | b2 | b6 |
| e | Ь2 | - | b3 | b5 |
| W1 | b3 | b4 | - | - |
| W0 | Ь4 | b0' | - | - |
| W0 | Ь5 | b4 | - | - |
| e | Ь6 | - | b3 | b7 |
| W0 | b7 | b8 | - | - |
| W1 | Ь8 | b0" | - | - |
| e | b9 | - | b10 | b11 |
| W0 | b10 | - | b13 | b8 |
| e | b11 | - | b14 | b12 |
| W1 | b12 | b13 | - | - |
| % | b13 | b0" | - | - |
| W0 | b14 | b15 | - | - |
| W1 | b15 | b0' | - | - |
(Ъ0, ь4), Фо", ьз), (b3, bi5), (b4, b5), (b5, bio),
(bo, b5), (b" b8)’ (b4’ b10)’
(bo', b7), (bo", bi2),
(bo', bi3), (bo", bi5),
(bo', b14),
(b7, Ьш), (Ьш, bi3), (bi3’ bi4).
(b7, bi3), (bio, bi4),
После проведения укрупнения групп совместимых состояний получим финальные классы и соответствующие им состояния минимального автомата C.
C0 = Ki = {bo'. b4’ b5}’ C5 = K7 = {b8}’
C/’ = K2 = W* b3’ bi5^? C6 = K8 = {b9}’
| X | |||||||||||||||
| X | X | ||||||||||||||
| X | X |
v- к к | |||||||||||||
| X | V | X | X | ||||||||||||
| V | X | X | X | X | |||||||||||
| V | X | X | X | X | V* | ||||||||||
| X | X |
b2 b3 2x 3 b6 bl |
b5 bl 5x 1 | X | X | X | |||||||||
| V | X | X | X | X | b.'xb, | V- | X | ||||||||
| X | V | X | X | 4b- | X | X | X | X | |||||||
| X | X |
b2XU bA |
xx bA | X | X | X |
xx brK | X | X | ||||||
|
b2’ b3 X 3 Kh | X | X | X | X | V | V | X | V | X | X | |||||
| X | X |
b2Xbl4 bAi |
b3Xbi4 bVb,2 | X | X | X | b3Xb14 b~1b, 2 | X | X | VX b11 b12 | X | ||||
| X | V | X | X | b4b13 | X | X | X | X | ‘•X- | X | X | X | |||
| V | X | X | X | X | b.'xb.- | b'b | X | ‘•Vb | X | X | V | X | X | ||
| V | X | X | X | X | b.Xb13 | b*Xb 15 | X | b-’X 15 | X | X | V | X | X | b.'Vb15 | |
| X | V | X | X | v* | X | X | X | X | bT | X | X | X | ‘•^13 | X | X |
C2 = K4 = {b2}, C8 = K10 = {b12},
C3 = K5 = {b6} C9 = K11 = {b13’ b14}
C4 = K6 = {b1 b10}
Полученное множество финальных классов удовлетворяет условиям полноты и замкнутости, в чем легко убедиться с помощью табл. 5.15. Для этого множества строим нормальную форму автомата, которая и будет минимальным автоматом эквивалентно продолжающим автомат A. Отмеченная таблица переходов минимального автомата приведена в табл. 5.17. По ней на рис. 5.12 построен граф минимального автомата Мура.
Таблица 5.17
| w(t—1) | c(t-\) | a | zo | z |
| wn | c' | C' | c | c |
| 0 | 1 | |||
| w1 | c ” c0 | Co' | c1 | c6 |
| в | c1 | - | C2 | C3 |
| в | c2 | - |
c" Co | Co' |
| в | c3 | - |
c Co | c4 |
| wn | c | c | c | c |
| 9 | ||||
| w1 | C5 |
c" c0" | - | - |
| в | C6 | - | C4 | c7 |
| в | C7 | - | C9 | c8 |
| w1 | C8 | c9 | - | - |
| WO | C9 |
c" c0" | - | - |
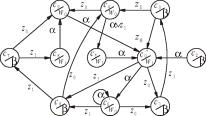
С помощью табл. 5.3 легко убеждаемся в том, что все допустимые входные слова оператора автомата A и их начальные отрезки принадлежат области определения оператора минимального автомата. По рис. 5.12 находим, что входное слово p = z^^aaa принадлежит области определения оператора минимального автомата. Согласно табл. 5.3, это слово не принадлежит области определения оператора исходного автомата A. Таким образом, минимальный автомат эквивалентно продолжает заданный.
6. СТРУКТУРНЫЙ СИНТЕЗ АВТОМАТОВ
6.1. Композиция автоматов
Структурный синтез автоматов осуществляется на базе структурной теории автоматов, в которой в отличие от абстрактной теории производится учет большого числа свойств реально существующих цифровых автоматов. Абстрактный автомат представляет собой математическую модель проектируемого устройства. В структурном же автомате учитывается структура входных и выходах сигналов, а также внутренняя структура автомата на уровне так называемых структурных схем. В структурной теории автоматов принят отсчет автоматного времени, начиная с 0 такта, т. е. t = 0, 1, 2, ...Главной задачей структурной теории автоматов является нахождение общих приемов построения структурных схем автомата на основе композиции элементарных автоматов, принадлежащих к заранее заданному конечному числу типов. Рассмотрим, как представляется автомат в структурной теории автоматов. У абстрактного автомата один входной и один выходной каналы. В структурной же теории как входные, так и выходные каналы автомата считаются состоящими из нескольких элементарных входных и соответственно элементарных выходных каналов. По этим каналам передаются элементарные сигналы. Набор всех возможных для данного автомата элементарных сигналов называется структурным алфавитом данного автомата. Каждый элементарный входной канал подсоединен к входному узлу автомата, а каждый элементарный выходной канал к выходному узлу автомата.
Сформулируем определение общего способа композиции автоматов. Пусть {Aj, A2, ..., An}(n > 0) - конечное множество автоматов. Необходимо произвести объединение этих автоматов в систему совместно работающих автоматов. Введем некоторое конечное множество узлов, которые назовем внешними входными узлами, и некоторое конечное множество других узлов, которые назовем внешними выходными узлами. Входные и выходные узлы автоматов Aj, A2, ..., An будем называть внутренними входными и выходными узлами.
Композиция автоматов состоит в том, что в полученной системе, состоящей из заданных автоматов Aj, A2, ..., An и внешних узлов, производится отождествление некоторых узлов (как внешних, так и внутрен-
них). У цифровых автоматов операции отождествления узлов соответствует соединение этих узлов проводниками.
После проведения отождествления узлов произвольная система автоматов превращается в так называемую схему или сеть автоматов. Будем считать, что автоматы, входящие в схему, работают совместно, если в каждый момент t автоматного времени (t = 0, 1, 2, ...) на все внешние входные узлы схемы подается какой-либо набор элементарных сигналов (структурный входной сигнал), а со всех внешних выходных узлов схемы снимается полученный на них набор элементарных выходных сигналах (структурный выходной сигнал). Если в каждый момент дискретного времени t = 0, 1, 2,... структурный выходной сигнал схемы однозначно определяется поступившей к этому времени конечной последовательностью структурных входных сигналов, начальными состояниями, входящих в схему автоматов, и сделанными при построении схемы отождествлениями (соединениями) узлов, то построенная схема может рассматриваться как некоторый автомат А и называется структурной схемой этого автомата. Автомат А, полученный описанным способом, есть результат композиции автоматов Ax, A2, ..., A .
Следует заметить, что операция отождествления узлов может быть выполнена неоднозначно. При отождествлении узлов необходимо соблюдать два условия, называемые условиями корректности построения структурных схем:
в любой момент автоматного времени на каждый узел схемы (как внешний, так и внутренний) поступает какой-либо элементарный сигнал;
неоднозначность элементарных сигналов в каком-нибудь узле схемы хотя бы один момент автоматного времени является недопустимой.
Первое условие корректности удовлетворяется в том случае, если любой узел схемы будет подключен через конечное число комбинационных схем или автоматов Мили к внешнему узлу, поскольку у автоматов Мили и комбинационных схем выходные сигналы возникают одновременно с поступлением сигналов на входы.
Неоднозначность элементарного сигнала в узле может появиться по двум причинам: к некоторому входному узлу подсоединено одновременно несколько выходных узлов, являющихся источниками элементарных сигналов, а также источником неоднозначности могут быть так называемые циклические цепи или петли структурных схем. Цепью называется последовательность автоматов, у каждого из которых один из выходных узлов соединен с входом последующего. Если выходной узел последнего автомата соединен со входным узлом первого, то такая цепь называется циклической или петлей (рис. 6.1).
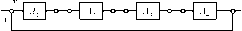 |
| Рис. 6.1 |
Схема, в которой выполняются все условия корректности, называется правильной.
6.2. Канонический метод структурного синтеза автоматов
Задачей структурного синтеза конечных автоматов является создание такой композиции некоторого множества автоматов, называемых элементарными, чтобы полученный автомат был эквивалентен заданному. Эта задача имеет решение, если система элементарных автоматов структурно полна.Одним из широко используемых методов структурного синтеза является так называемый канонический метод, теоретические основы которого были разработаны З.М. Глушковым, сформулировавшим и доказавшим теорему о структурной полноте [2].
Теорема: всякая система элементарных автоматов, которая содержит автомат Мура, обладающий полной системой переходов и полной системой выходов, и какую-нибудь функционально полную систему логических элементов (элементарных автоматов без памяти), является структурно полной системой. Существует общий конструктивный прием (канонический метод структурного синтеза), позволяющий в рассмотренном случае свести задачу синтеза произвольных конечных автоматов к задаче структурного синтеза комбинационных схем.
Полнота системы переходов в автомате означает, что для любой пары состояний (a;, aj) этого автомата найдется входной сигнал, переводящий один элемент этой пары в другой. Это положение справедливо, если i = j. Чтобы детерминированный автомат мог удовлетворять условию полноты переходов, число его входных сигналов должно быть не меньше числа состояний.
Полнота системы выходов в автомате Мура означает, что каждому состоянию автомата соответствует свой собственным выходной сигнал, отличный от выходного сигнала, соответствующего любому другому состоянию. Поэтому в автомате Мура с полной системой выходов можно отождествить внутренние состояния с выходными сигналами автомата. Для того, чтобы обеспечить в этом автомате полноту системы выходов, необходимо в выходном алфавите иметь число выходных сигналов не меньше числа состояний автомата.
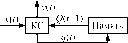
На основании теоремы о структурной полноте структурная схема всякого автомата А, синтезированного каноническим методом, будет состоять из двух частей: запоминающей части и комбинационной схемы (рис. 6.2). Запоминающая часть представляет собой совокупность элементарных автоматов Мура с полной системой переходов и выходов, а комбинационная часть представляет собой схему, построенную из логических элементов, составляющих функционально полный базис. Рассмотрим этапы структурного синтеза автомата каноническим методом.
1. Кодирование состояний абстрактного автомата. В процессе структурного синтеза различным состояниям заданного абстрактного автомата а. ставятся в соответствие различные упорядоченные последовательности состояний элементарных автоматов Q1, Q2, ..., Qp. Этот процесс называется кодированием состояний автомата.
Результатом кодирования состояний является возникновение структурных состояний автомата Ql = Q1l QR ... QR , где l = 0, 1, 2, ..., M (M+1) - число состояний абстрактного автомата. R = ]log2(M+1)[ и ]b[ означает ближайшее целое число, большее b или равное ему, если b - целое. Эти состояния можно отождествить со структурными выходными сигналами запоминающей части автомата.
В связи с тем, что каждый структурный выходной сигнал памяти автомата представляет собой совокупность элементарных сигналов, поступающих по отдельным каналам, будем считать структурный выходной сигнал памяти векторным сигналом Ql, в котором каждая компонента отождествляется с буквой структурного алфавита состояния Q = Qv ..., Qpb т. е. Q/е Q.
2. Кодирование абстрактных входных и выходных сигналов. Абстрактным входным и выходным сигналами ze Z и w . е W, где Z и W- входной и выходной абстрактные алфавиты, ставятся в соответствие внешние структурные входные и выходные сигналы автомата, обозначаемые соответственно X = x2j ... xLj, и У = yRyR... yNk, где j = 1, 2, ..., F, F - число символов входного абстрактного алфавита, к = 1, 2, ..., G , G - число символов выходного абстрактного алфавита, L = ]log2F[ и N = ]log2G[. Сигналы xj и ук являются векторными сигналами, компоненты которых xj и yR - соответственно элементарные входные и выходные сигналы на каждом элементарном входном или выходном канале, т. е. xj е X = {x1, x2, ..., xn}, а yRе Y = {y1, y2, ..., yr}, - гдеХ и Y- соответственно структурные входной и выходной алфавиты.
3. Составление кодированных таблиц переходов-выходов структурного автомата. В процессе синтеза необходимо обеспечить, чтобы переходы из одной последовательности состояний элементарных автоматов в другую происходили в полном соответствии с функцией переходов заданного абстрактного автомата, а значения структурных выходных сигналов вырабатывались в соответствии с заданной последовательностью абстрактных входных сигналов. Таким образом, должны быть обеспечены следующие законы функционирования для структурного автомата Мили:
QO+1) =5(Q(0, x(t)), y(t) = MQ(0, x(t))
(6.1)
и для структурного автомата Мура
Q(t+1) =5(Q(t), x(t)),
y(t) = ^(Q(t)). (6.2)
Закон функционирования структурного автомата может быть описан с помощью кодированных таблиц переходов-выходов, которые формируются на основании таблиц переходов-выходов абстрактного автомата и полученных на первых двух этапах структурных значений состояний и сигналов автомата. В клетках этих таблиц вместо символов, обозначающих абстрактные состояния и сигналы, записываются коды соответствующих им структурных состоянии и сигналов.
4. Формирование таблицы функций возбуждения структурного автомата. Из рис. 6.2 следует, что
q(t) = Y(Q(t) x(t)). (6.3)
Сравнивая выражение (6.3) с функцией переходов структурного автомата (6.1) или (6.2) можно сделать вывод, что именно сигналом q(t) можно осуществить требуемые переходы при условии формирования некоторой функции y(Q, x), называемой функцией возбуждения автомата A , в соответствии с функцией переходов 5(Q, x). В дальнейшем для упрощения формулировок сигнал q(t) будем также называть функцией возбуждения автомата A. Отдельные компоненты вектора q(t) являются входными сигналами используемых элементарных автоматов.
Функции возбуждения задаются о помощью таблицы, сформированной на базе структурной таблицы переходов проектируемого автомата, и таблицы переходов заданного элементарного автомата. В клетках таблицы функций возбуждения записываются значения структурных входных сигналов выбранных элементарных автоматов, обеспечивающие переходы их состояний в соответствии с кодированной таблицей переходов.
5. Получение логических выражений функций возбуждения и выходных сигналов автоматов. Сигнал q(t) является структурным выходным сигналом комбинационной схемы автомата А, отличающейся тем, что ее структурный выходной сигнал получается путем преобразования структурного входного сигнала x(t) автомата А и структурного выходного сигнала Q(t) его памяти. Реализуя схему преобразования в виде композиции заданных логических элементов, можно осуществить все те переходы, которые предусматриваются функцией переходов автомата А. Аналогично формируется структурный выходной сигнал y(t) на выходе комбинационной схемы автомата А. Требуемые значения выходного сигнала обеспечиваются соответствующим синтезом этой схемы.
Для получения логических выражений функций возбуждения и выходных сигналов необходимо воспользоваться соответственно таблицей функций возбуждения и кодированной таблицей выходов в качестве таблиц истинности.
Как известно, по таблице истинности можно получить только совершенную дизъюнктивную и нормальную форму (СДНФ) заданной функции. Для того чтобы минимизировать функцию, целесообразно воспользоваться диаграммой Вейча.
6. Построение структурной схемы. На основании полученных логических выражений строится схема структурного автомата из заданных элементарных автоматов и логических элементов функционально полного базиса.
Рассмотрим в качестве примера синтез структурной схемы автомата Мили, спроектированного в разделе 5, функции переходов которого описываются в табл. 5.14.
Обычно в качестве структурного алфавита используется двоичный структурный алфавит {0, 1}, а в качестве элементарного автомата используется автомат Мура с двумя состояниями.
Пусть имеем абстрактный элементарный автомат с входным алфавитом Г={?1,?2}, выходным алфавитом и алфавитом состояний С={срс2} и таблицей переходов-выходов (табл. 6.1).
Таблица 6.1
Произведем операцию кодирования состояний, входных и выходных сигналов у элементарного и исходного автоматов. Поскольку структурный алфавит двоичный, число элементарных входных каналов автомата определяется как L > ]log2F[, число элементарных выходных каналов определяется как N > ]log2G[, а число элементов памяти автома-
та - как R > ]log2(M+1)[.
Перейдем от абстрактного элементарного автомата к структурному. Закодируем абстрактные входные сигналы (табл. 6.2), выходные сигналы и состояния (табл. 6.3). Получим кодированную таблицу переходов-выходов элементарного автомата (табл. 6.4).
| Таблица 6.2 Таблица 6.3 Таблица 6.4 | ||||||||||||||||||||
|
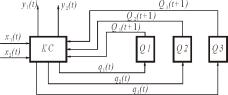 |
| Рис. 6.3 |
Таблица 6.5
| Таблица 6.7 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Таблица 6.8
.6 и 6.9 построим кодированную
| Таблица 6.9 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ф-Х) | a | Z1 | Z2 |
| С0 | c0 | C1 | C4 |
| ci | C4 | C2 | C3 |
| С2 | C0 | co | co |
| С3 | C4 | co | C1 |
| С4 | co | C5 | C6 |
| C5 | - | C4 | C4 |
| C6 | - | C2 | C3 |
| Таблица 6.10 | |||||||||||||||||||||||||||||||||||||||||||||||||
|
Чтобы получить минимальные ДНФ функций возбуждения q1, q2, q3 и выходных сигналов Q1, Q2, Q3, построим диаграммы Вейча для каждой из искомых функций. Аргументами всех функций возбуждения в соответствии с выражением (6.3) и табл. 6.12 являются состояния элементарных автоматов Qp Q2, Q3 и входные сигналы Xj и x2.
| Таблица 6.12 | |||||||||||||||||||||||||||||||||||||||||||||||||
|
4j = Yi(Qi(t\ Q2(0, Q3(t) х1(^ x2(t))’
Ч2 = 72(Q1(t)’ Q2(t), Q3(t) Х1(0з X2(t))’
?3 = 73(Q1(t)’ Q2(t) Q3(t) X1(t), X2(t)).
Аргументами для и у2 в соответствии с выражением (6.1) и табл. 6.11 также являются Q1, Q2, Q3, x1 и x2. Таким образом,
Y1(t) = MQ1(t)’ Q2(t) Q3(t) X1(t)’ X2(t))’
Y2(t) = ^2(Q1(t) Q2(t) Q3(t) X1(t)’ X2(t)).
В результате проведенной минимизации получим следующие логические выражения для функций возбуждения:
q1 X1Q2Q3 V XiQ2Q3 V X1Q1Q2Q3 V Q\Ql
q2 X1Q1Q3 V X2Q1Q2Q3 V QQ2 ’
Ч3 = X2Q1Q3 V X2Q1Q3 V X2Q1Q2 V X1X2Q1Q2 .
Поскольку на комбинационной схеме выходные сигналы вырабатываются практически одновременно с моментом поступления входных сигналов, временные соотношения могут быть в выражениях опущены.
Логическое выражение для выходного сигнала у2 целесообразно получать, минимизируя у2 по “0”, а не по “1”, поскольку в этом случае получается выражение с меньший рангом. В результате имеем
У1 = X1Q1Q2 V X2Q2Q3 > у2 X2Q1 V X1Q2Q3 V X1X2Q1 V X2Q1Q2 V X1X2Q2 V Q1Q2Q3 '
На базе полученных выражений можно построить структурную схему автомата в любом функционально полном базисе.
7. ЭЛЕМЕНТАРНЫЕ АВТОМАТЫ
Из теоремы о структурной полноте следует, что для структурной полноты системы элементарных автоматов необходимо включение в нее элементарных автоматов Мура с полной системой переходов и полной системой выходов. Теоретически такие автоматы, представляющие собой элементы памяти, могут обладать любым числом внутренних состояний, однако исходя из реальных возможностей современной технологии, оптимальным числом состояний элементарного автомата является два, а структурный алфавитом состояний автомата является двоичный алфавит.Рассмотрим некоторую обобщенную модель элементарного автомата, представляющую собой автомат Мура, заданный следующим множеством элементов:
A = {C, V, 5, X, cj,
где C = {cl, c2} - алфавит состояний; V = {vp v2, v3, v4} - входной алфавит, причем v1 - сигнал, не меняющий исходное состояние автомата, такой, что c1 = 5{c1, v1}, c2= 5{c2, v1}; v2 - сигнал, переводящий автомат в состояние, противоположное исходному, такой, что c1 = 5{c2, v2}, c2= 5{c1, v2}; v3 - сигнал, всегда переводящий автомат в состояние c1, такой, что c1 = 5{c1, v3}, c1 = 5{c2, v3}; v4 - сигнал, всегда переводящий автомат в состояние v4, такой, что c2 = 5{c1, v4}, c2 = 5{c2, v4}; c1 -
начальное состояние; 5 и X - функция переходов и функция выходов, определяемые с помощью графа переходов (рис. 7.1).
Поскольку в автомате Мура с полной системой выходов внутренние состояния отождествляются с выходными сигналами, для их обозначения использован один и тот же алфавит (в данном случае алфавит С).
На базе рассмотренной модели можно построить 16 элементов памяти с различными комбинациями абстрактных входных сигналов, но только
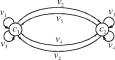 |
| Рис. 7.1 |
яний. Из автоматов с двумя входными сигналами только два из шести удовлетворяют приведенному требованию. Это автоматы, в которых в качестве входного алфавита используется алфавит V1 = {v3, v4} (автомат А1) и алфавит V2 = {vp v2} (автомат A2). Полным также является автомат А3 с тремя входными сигналами с алфавитом V3 = {v1, v3, v4}, а также автомат А4 с четырьмя входными сигналами.
Перечисленные элементарные автоматы и их модификации являются наиболее широко используемыми элементами памяти в современных цифровых устройствах.
Рассмотрим структурные особенности этих автоматов, считая, что любой структурный элементарный автомат с двумя состояниями имеет вид, представленный на рис. 7.2. Поскольку этот автомат является автоматом Мура, выходной сигнал задерживается относительно входного на один такт автоматного времени. В соответствии с теоремой о структурной полноте схему любого структурного элементарного автомата можно представить состоящей из двух частей: запоминающей части, в которой не производится логическое преобразование информации (элемент задержки сигнала t) и комбинационной схемы (рис. 7.3). Приведенная на рис. 7.3 функция возбуждения q (t) представляет собой собственную функцию возбуждения элемента памяти. Следует заметить, что для задания структурного элементарного автомата целесообразно использовать матрицу переходов, элементами которой являются значения структурных входных сигналов автомата, заданные на упорядоченных парах состояний структурного автомата и переводящие первый элемент соответствующей пары во второй.
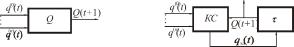 |
| Рис. 7.2 Рис. 7.3 |
| Q(t) | Q(+1) | q | 42 | 4k | 4m | |
| 0 — | 0 | *00 • | ¦ bk b00 | .. bm b00 | ||
| 0 | 1 | M = | *01 | *o2i • | ¦ bk • b01 | • • bm b01 |
| 1 — | 0 | b10 | *120 • | • bk • | ¦ • bm b10 | |
| 1 | 1 | *0i | *121 • | • bk b11 • | ¦ • bm b11 |
Элемент матрицы bkjj представляет собой значение входного сигнала qk, под действием которого автомат переходит из состояния i в состояние j. При этом каждый элемент матрицы может быть равен 1, 0 или неопределенному коэффициенту b. Неопределенные коэффициенты записываются в том случае, когда значения сигналов, поступающих на данный вход, не влияют на рассматриваемый переход.
7.1. Элементарные автоматы с двумя входными сигналами
Для проведения операции структурного синтеза с целью получения структурной схемы элементарного автомата Ах, граф переходов которого приведен на рис. 7.4, необходимо провести операцию кодирования состояний автомата и его входных сигналов. Поскольку абстрактному автомату с двумя входными и двумя выходными сигналами соответствует структурный автомат с одним входным и одним выходным каналом, результат операции кодирования входных сигналов и состояний будет иметь вид, представленный соответственно в табл. 7.1 и 7.2.
| Таблица 7.1 | Таблица 7.2 | ||
| V | q | C | Q |
| V3 | 0 | c | 0 |
| V4 | 1 | C2 | 1 |
На основании рис.7.4 и табл.7.1 и 7.2 можно составить кодированную таблицу переходов структурного элементарного автомата Ax (табл.7.3), кодированный граф переходов (рис. 7.5), а также его матрицу переходов
| 0 |
 |
| Рис.7.5 |
| ?з | |
| ?з |  |
| Рис.7.4 |
Q(+1)
q
0
1
0
1
(7.1)
Рассматривая табл. 7.3 и матрицу (7.1), можно заключить, что значение состояния автомата Q(t+1) и соответствующего ему выходного сигнала определяются значением входного сигнала q(t) и не зависят от состояния автомата Q(t), т. е. Q(t+1) = q(t). В то же время на основании анализа схемы, приведенной на рис. 7.3, можно сделать вывод, что
Q(t+1) = q^XO.
Следовательно,
q(t) = q^/0
и комбинационная схема в таком случае становится для автомата Ах излишней.
Таким образом, схема автомата приобретает вид, представленный на рис. 7.6, а сам автомат Ах представляет собой элемент задержки и называется триггером типа D (delay - задержка).
| Таблица 7.3 | |||||||||
|
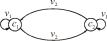 |
| Рис.7.7 |
Таблица 7.4 Таблица 7.5
| V | q | q | 0 | 1 |
| V1 | 0 | 0 | 0 | 1 |
| V2 | 1 | 1 | 1 | 0 |
Q(t+1) = q(t) Q (t) v q (t)Q(t) = q(t) © Q(t).
Поскольку в любом элементарном автомате
Q(t+1) = qjt^
можно записать
q^O = q(t) © Q(t).
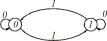 |
| Рис. 7.8 |
| |||||||||||||
| Рис. 7.9 |
7.2. Элементарные автоматы с тремя входными сигналами
Так же, как и для автоматов с двумя входными сигналами, в этом случае в зависимости от комбинаций и кодирования трех используемых входных сигналов можно спроектировать различные структурные схемы элементарных автоматов.Рассмотрим автомат A3, использующий входной алфавит V3 = {vp v3, v4}, граф переходов которого представлен на рис. 7.10.
Таблица 7.6
| V | q(0) | q(1) |
| V1 | 0 | 0 |
| V2 | 1 | 0 |
| V3 | 0 | 1 |
 |
| Рис. 7.10 |
(0)
(0)
Q(t)
о -Q(t+1)
0
(7.3)
| |||||||||||||||
| Рис. 7.12 |
| 00 |
 |
| Рис. 7.11 |
Логическое выражение для фикции q автомата А3 можно получить из табл. 7.7, доопределив неопределенные переходы единицами. В результате получим
?эл(0 = Qt+1) = q (0)(t)Q(t) V q(1)(t).
| Таблица 7.7 | ||||||||||||||||||||
|
Можно получить другое выражение для q автомата А , доопределив запрещенные наборы не единицами, а нулями. В результате имеем
q эл(t) = q(0)(t) V q (1)(t) Q (t). (7.4)
Взяв отрицание от обеих частей выражения (7.4) и переведя его в базис Пирса, получим
qjf) = P(q(0)(t), P(q(1)(t),Q(t))). (7.5)
Таким образом, комбинационная схема элементарного автомата представляет собой последовательное соединение либо элементов Пирса (для прямого значения входных сигналов), либо двух элементов Шеффера (для инверсного значения входных сигналов) и имеет два входных канала (рис. 7.12). Этот автомат получил название триггера с раздельными входами или триггера типа RS (set - установить; reset -сбросить), где с помощью R и S обозначены соответственно входы q(0) и q(1).
Наличие неопределенных состояний, отмеченных в табл. 7.7 прочерками, ограничивает функциональные возможности RS-триггера. В ряде случаев требуется, чтобы состояния триггера были определены при всех комбинациях входных сигналов, включая и те, которые запрещены для RS-триггера.
Для построения различных модификаций RS-триггера в этом случае делается дублирование одного из трех абстрактных входных сигналов: Vp v3 или v4 и кодирование дополнительного сигнала структурными символами 11. Каждая полученная при этом разновидность триггера считается самостоятельным типом и имеет свое наименование.
Рассмотрим получаемые таким образом автоматы. Переходы, осуществляемые дополнительными сигналами v\, v’3 или v’4, показаны на графах переходов абстрактных автоматов А4, А5, A6 соответственно на рис. 7.13, 7.14 и 7.15.
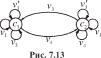
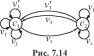
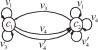 |
| Рис. 7.15 |
7.18.
Анализируя переходы автоматов на рис. 7.16, 7.17 и 7.18, можно заметить, что каждый дополнительный сигнал обеспечивает один из четырех возможных переходов. Автомат на рис. 7.16 под действием сигнала 11 остается в прежнем состоянии и называется триггером типа Е (іexclusive - исключительный, особенный), автомат на рис. 7.17 под действием сигнала 11 переходит в состояние 0 и называется триггером типа R, а автомат на рис. 7.18 переходит в состояние 1 и называется триггером типа S. Табл. 7.8 представляет собой общую кодированную таблицу переходов этих трех триггеров.
Таблица 7.8
| R | S | ^-триггер | R-триггер | S-триггер | |||
| 0 | 1 | 0 | 1 | 0 | 1 | ||
| 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 |
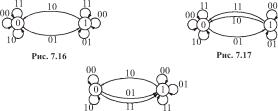 |
| Рис. 7.18 |
b1 b2 0 1 1 0 b2 b1
(7.4)
| Q(t) | Q(t+1) | R | S | R | S | ||
| 0 — | 0 | b | b2 | b | 0 | ||
| 0 | 1 M = | 0 | 1 | (7.5) | M = | b | i |
| 1 — | -0 | i | b | i | 0 | ||
| 1 | 1 | 0 | b | b2 | bi |
Автомат А4, представленный на рис. 7.13, может быть закодирован иначе, способом, предложенным в табл. 7.9. Тогда его кодированный граф переходов будет иметь вид, представленный на рис. 7.19, а таблица переходов - вид, представленный в табл. 7.10.
Таблица 7.9 Таблица 7.10
| V | q(1) | q(2) | qi | q(2) | 0 | 1 |
| v1 | 0 | 0 | 0 | 0 | 0 | i |
| V2 | 1 | 1 | i | 0 | 0 | i |
| V3 | 1 | 0 | 0 | i | 0 | 0 |
| v1' | 0 | 1 | i | i | i | i |
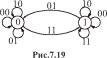
Если сравнить таблицу переходов этого автомата с таблицей переходов триггера типа D (табл. 7.3), можно заметить, что при q(2)(t) = 1 состояния автомата Q(t+1) в табл. 7.10 так же, как и в табл. 7.3, определяются только значениями входного сигнала q(1)(t). В то же время при q(2)(t) = 0 автомат переходит в режим хранения информации (его состояния не меняются) независимо от смены сигналов на входе q(1)(t).
В связи с этим рассматриваемый автомат представляет собой модификацию D-триггера и называется триггером типа DV (valve - вентиль, клапан), где буквами D и V обозначены соответственно входы q(1) и q(2). Вход V является разрешающим входом по отношению ко входу D. Матрица переходов триггера типа DV имеет вид
Q(t) Q(t+1)
(7.9)
где элементы Ъ1 и b2 могут принимать любые значения, кроме комбинации Ъ1 = Ъ2=1, т. е. Ъ1Ъ2 = 0, а элементы Ъ3 и Ъ4 должны удовлетворять
условию b 3Ъ4 = 0, т. е. недопустимо, чтобы Ъ3 = 0, а Ъ4 = 1 одновременно.
Функция возбуждения DV-триггера имеет вид
qjt) = q(1)(t) q(2)(t) v q (2)(t) Q(t) = Q(t+1)
или иначе
Q(t+1) = D(t)V(t) v V(t)Q(t).
7.3. Элементарный автомат с четырьмя входными сигналами
Элементарный автомат А7, граф переходов которого представлен на рис. 7.20, использует в качестве входного алфавита алфавит V4 = {v1, v2, v3, v4}, содержащий все четыре абстрактных входных сигнала описываемой модели. Закодировав символы входного алфавита в соответствии с табл. 7.11, построим на основании рис. 7.20, табл. 7.2 и 7.11 кодированный граф переходов автомата (табл. 7.12) и матрицу переходов (7.10) этого автомата.(0) q(1)
0b
(7.10)
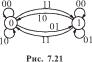
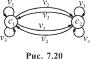
| Таблица 7.11 Таблица 7.12 | |||||||||||||||||||||||||||||||||||
|
вход q(0).
Функция возбуждения триггера JK имеет вид
qm(0 = q(1)(t) Q (t) v q (0)(t) Q(t) = Q(t+1)
или иначе
Q(t+1) = J(t) Q (t) v к (t)Q(t).
Структурная схема триггера реализуется обычно на базе триггера типа RS. В этом случае входы q(0)(t) и q(1)(t) RS-триггера будут иметь значения, определяемые следующими логическими выражениями:
q(0)Rs (t) = R(t) = K(t) Q(t), q(1)Rs (t) = S(t)=J(t) q (t).
Достаточно широкое применение в цифровых схемах находит элементарный автомат, полученный путем избыточного кодирования входных абстрактных сигналов автомата А7, представленного в табл. 7.13.
Любая комбинация, содержащая два единичных значения элементарных структурных сигналов, является запрещенной.
Таблица 7.13 Таблица 7.14
| V | q0) | q1 | q(2) | q<0) | q(1) | q(2) | 0 | 1 |
| Vi | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| V2 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 |
| V3 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| V4 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 |
| 000 | 000 | ||||
| to | f''" 001 001 | JJ | |||
| 100 | 100 | 4)10 | |||
| Рис. 7.22 | |||||
| Q(t) | Q(t+1) | q(0) | q(1) | q(2) | |
| 0 — | 0 | b | 0 | 0 | |
| 0 | 1 | M = | 0 | bi | bi |
| 1 — | 0 | b2 | 0 | b2 | |
| 1 | 1 | 0 | b | 0 |
Анализируя переходы автомата по табл. 7.14, можно заметить, что сигналы q(0) и q(1) работают аналогично сигналам R и S триггера типа RS, а сигнал q(2) изменяет состояние автомата на противоположное аналогично входному сигналу триггера Т. В связи с этим данный элемен-
q(1)
q(0)
| ||||||||||||||||||||
| Рис. 7.23 |
тарный автомат получил название счетного триггера с раздельной установкой или триггера типа RST.
Логическое выражение для функции возбуждения этого триггера может быть получено на основании табл. 7.14 с помощью диаграммы Вей-ча (рис. 7.23) и будет иметь вид
Q(t+1) = qjt) = q(1)(t) V q (0>(t) q (2)(t)Q(t) V q(2)(t) Q (t). (7.12)
Или иначе Q(t+1) = S(t) V T(t) Q (t) V R (t) T (t)Q(t).
Структурная схема RST-триггера реализуется обычно на базе RS-триггера.
8. ТЕХНИЧЕСКАЯ РЕАЛИЗАЦИЯ ЭЛЕМЕНТАРНЫХ
АВТОМАТОВ
Для устойчивой работы автомата необходима его синхронизация и введение дополнительных схем (конъюнкторов) [5]. Обычно дополнительные схемы и входы синхронизирующих сигналов предусматриваются в самом элементе памяти при его технической реализации. На основе характеристического уравнения RS-триггераQ(t+1) = S(S(S( R .„(О), Q(t)), S( S вХ (t))) можно построить асинхронную схему этого триггера на элементах Шеффера с управлением по входам, представленную на рис. 8.1.
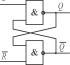
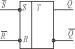
Рис. 8.1
Во избежание гонок [5] асинхронные триггеры обычно не используются в качестве элементов памяти в структурных автоматах. Подключая к входам асинхронного триггера схему управления, состоящую из логических элементов используемого базиса, можно получить синхронный (тактируемый) триггер. На рис. 8.2, а, б приведена схема синхронного RS-триггера и его логическая структура, в которых пунктиром обозначены побочные асинхронные входы. На рис. 8.2, в приведено условное изображение такого триггера. Входы S и R - информационные (входы функций возбуждения), а вход C - синхронизирующий (тактовый).
| а) S |
 |
|
б) _ в) с |
 |
| Рис. 8.2 |
С = 1. Побочные входы S и R триггера предназначены для асинхронной установки триггера в состояние 0 и 1, минуя информационные и тактирующий входы. Функционирование в этом случае соответствует асинхронному RS-триггеру с инверсным управлением. При синхронной работе на побочных входах должна поддерживаться нейтральная комбинация сигналов ( S = R = 1).
Помимо синхронизации для устранения гонок в автоматах используется двойная память. В этом случае все элементы памяти структурного автомата должны быть организованы в виде двухтактных (двухступенчатых) схем. Они строятся на основе двух синхронных триггеров, соединенных последовательно. Синхронизирующие сигналы поступают на эти триггеры в соответствии с условиями организации таких сигналов в схемах с двойной памятью: на вход C первого триггера поступает прямой сигнал, а на вход C второго триггера - инверсный. Двухтактная схема RS-триггера, ее логическая структура и условное изображение приведены соответственно на рис. 8.3, а, б и в.
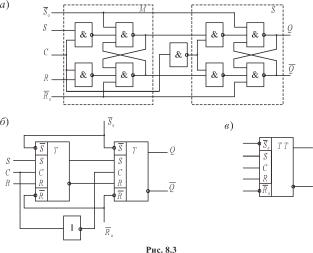
Первый триггер в двухтактной схеме называется ведущим M, а второй - ведомым S (М - master (хозяин), S - slave (невольник)).
Поскольку .RS-триггер устойчив по отношение к длительности входного сигнала, на его основе целесообразно строить различные варианты схем элементарных автоматов. Рассмотрим реализацию триггеров различных типов на основе синхронного RS-триггера.
На рис. 8.4 приведены схемы S- и R-триггеров, функционирующих в соответствии с табл. 7.8.
Функциональные схемы S-триггера и R-триггера одинаковы и конкретный тип триггера определяется наименованием входных и выходных каналов. На рис. 8.4 обозначения входов триггера без скобок соответствуют триггеру типа S, а обозначения в скобках - триггеру типа R.
На рис. 8.5 приведена функциональная схема R-триггера, работающего в соответствии с табл. 7.8.
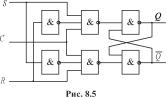
В этой схеме при одновременном сочетании на входах S = R = 1 обеспечивается режим хранения информации и состояние триггера не меняется.
Рассмотрим техническую реализацию триггеров типа D, DV, T, JK, синтезируя их каноническим методом структурного синтеза, используя в качестве элемента памяти триггер типа RS.
Структурная схема любого триггера на базе триггера типа RS имеет вид, представленный на рис. 8.6.
| |||||||||||||||||||||||
| Рис. 8.6 |
Таблица 8.1 Таблица 8.2
| 0 | 1 | D | 0 | 1 | |||
| 0 | 0 | 0 | R | S | R | S | |
| 1 | 1 | 1 | 0 | b | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | b |
R = D и S = D.
| ||||
| Рис. 8.8 |
| ||||
|
D -- Рис. 8.7 |
Таким образом, функциональная схема D-триггера на основе RS-триггера должна состоять из RS-триггера с дополнительным инвертором на входе R. Логическая структура такого D-триггера и его условное обозначение приведены на рис. 8.9, а и б.
| 'S а | TT | |
| D | ||
| C | ||
| >Яа |
1 С-
Рис. 8.9
Поскольку DV-триггер представляет собой модификацию D-триггера, его схему можно получить преобразованием последнего путем добавлением входа V, который должен быть логически связан операцией И с управляющим входом C (рис. 8.10).
2. Синтез триггера типа Т. Функционирование Г-триггера задается кодированной таблицей переходов (табл. 8.3).
Таблица 8.3 Таблица 8.4
| 1 | 0 | T | 1 | 0 | |||
| 0 | 1 | 0 | R | S | R | S | |
| 1 | 0 | 1 | 0 | 0 | b | b | 0 |
| 1 | 1 | 0 | 0 | 0 |
|
Q Q | ||||||||||||||||||||
| Рис. 8.10 |
| ||||
| Рис. 8.11 |
| ||||
| Рис. 8.12 |
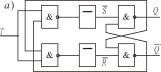
Рис. 8.13
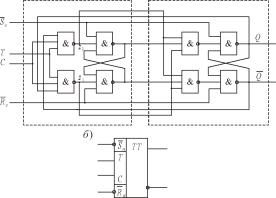 |
| Рис. 8.14 |
Условное обозначение двухтактного Г-триггера приведено на рис. 8.14, б.
3. Синтез триггера типа JK. Работа JK-триггера задается кодированной таблицей переходов (табл. 8.5).
Пользуясь матрицей переходов RS-триггера (7.3) и табл. 8.5, составим кодированную таблицу функций возбуждения JK-триггера (табл. 8.6).
Из табл. 8.6 с помощью диаграммы Вейча (рис. 8.15) можно найти логическое выражение для функции возбуждения S и с помощью другой диаграммы (рис. 8.16) - для функции возбуждения R.
| Таблица 8.5 | |||||||||||||||
|
| Таблица 8.6 | |||||||||||||||||||||||||||
|
|
J K | |||||||||
| |||||||||
| Рис. 8.16 |
| ||||||||||
| Рис. 8.15 |
В соответствии с этими выражениями схема асинхронного JK-триггера будет иметь вид, представленный на рис. 8.17, а. На рис. 8.17, б представлено условное изображение асинхронного JK-триггера.
б)
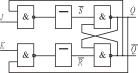
-О J к
Рис. 8.17
На практике описанный триггер не применяется из-за сложности изготовления и жестких требований к длительности входных сигналов. Так же, как и в случае Т-триггера, проблема устойчивости эффективно решается в триггерах с двухступенчатым управлением. Функциональная схема двухступенчатого JK-триггера показана на рис. 8.18, а, его условное обозначение - на рис. 8.18, б.
а)
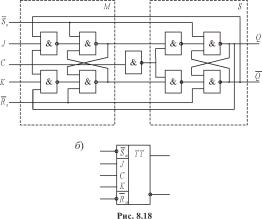
От двухступенчатого RS-триггера (рис. 8.3) она отличается наличием обратной связи с выходов Q и Q на входы элементов 1 и 2.
Следует заметить, что асинхронная установка любого двухступенчатого триггера в единичное и нулевое состояние (выходы R и S а) производится импульсами логического 0. Состояния остальных входов
при асинхронном управлении безразличны. Когда входы R и S неза-действованы, на них следует поддерживать уровень логической 1.
| ||||||||||||||||||||||||||||||||||||||||
| Рис. 8.19 Рис. 8.20 |
9. МИНИМИЗАЦИЯ ПОЛНОСТЬЮ ОПРЕДЕЛЕННЫХ
АВТОМАТОВ
Метод минимизации полностью определенных абстрактных автоматов изложен в литературе. Основная идея этого метода состоит в разбиении всех состояний исходного абстрактного автомата на попарно не пересекающиеся классы эквивалентных состояний и замене каждого класса эквивалентности одним состоянием. Таким образом, получающийся в результате минимальный автомат имеет столько же состояний, на сколько классов эквивалентности разбиваются состояния исходного автомата.Два состояния автомата am и а, называются эквивалентными (am= as), если k(am, = X(as, для всевозможных входных слов ^. Если ат и as не эквивалентны, они различимы. Более слабой эквивалентностью яв-
к
ляется ^-эквивалентность. Состояния а и а ^-эквивалентны (а = а ) если k(am, ^к) = k(as ^к) для всевозможных входных слов Ъ,к длины к. Если состояния k-эквивалентны, они к-различимы.
Введенные отношения эквивалентности и к-эквивалентности рефлексивны, симметричны и транзитивны, следовательно, они являются отношениями эквивалентности, а потому могут быть использованы для разбиения множества А состояний автомата на попарно не пересекающиеся классы (классы эквивалентности). Соответствующие разбиения на классы эквивалентных и k-эквивалентных состояний будем обозначать П и Пк. Разбиение П позволяет определить избыточные элементы в множестве состояний А. Пусть, например, am и as эквивалентны. Это значит, что с точки зрения реакций автомата на всевозможные входные слова неважно, находится автомат в состоянии am или as, и одно из них, например a, может быть удалено из множества A. Если каждый класс эквивалентности содержит только одно состояние, множество A несократимо. Если же один или несколько классов содержат более одного элемента, все элементы, кроме одного в каждом классе могут быть исключены из множества A , в результате чего получается автомат с минимальными числом состояний.
Алгоритм минимизации числа состояний автомата S = {ap A, Z, W, 5,
состоит из следующих шагов.
1. Находятся последовательные разбиения Пр П2, ..., Пк, Пк+1 множества A на классы одно-, двух-, ..., к, к+1-эквивалентных состояний, до тех пор пока на каком-то к+1-м шаге не окажется, что Пк+1= Пк. Нетрудно показать, что тогда разбиение Рк = P, т. е. что k-эквивалентные состояния являются в этом случае эквивалентными и число шагов к, при котором Пк = П, не превышает М-1, где M- число элементов в множестве A.
2. В каждом классе эквивалентности разбиения П выбираются по одному элементу, которые образуют множество A’ состояний минимального автомата S’={a^, A’, Z’, W, 5’, X’}, эквивалентного автомату S.
3. Функции переходов 5’ и выходов X’ автомата определяются на множестве A’xZ. Для этого в таблице переходов и выходов вычеркиваются столбцы, соответствующие не вошедшим во множество A’ состояниям, а в оставшихся столбцах таблицы переходов все состояния заменяются на эквивалентные из множества A’.
4. В качестве a^ выбирается одно из состояний, эквивалентное состоянию a1. В частности, удобно за а^ принимать само состояние а?
В качестве примера рассмотрим минимизацию автомата Мили S, заданного таблицами переходов и выходов (табл. 9.1 и 9.2). Непосредственно по таблице выходов получим разбиение П1 на классы одноэквивалентных состояний, объединяя в эквивалентные классы одинаковые столбцы: П1={В1,В2}, B1={a1, a2, a5, a7, a8}, B2={a3, a4, a6, a9, a10, an, a12}. Действительно, два состояния 1-эквивалентны, если их реакция на всевозможные входные слова длины 1 совпадают, т. е. соответствующие этим состояниям столбцы в таблице выходов должны быть одинаковы.
Таблица 9.1
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Таблица 9.2 |
| а1 | a | a | a4 | a | a6 | a | a | a | aiH | a11 | ai2 | |
| W | W | W | W | W | W | W | W | W | W | W | W | |
| W | W | W | W | W | W | W | W | W | W | W | W |
Таблица 9.3
| B | B. | |||||||||||
| a | a | a | a | a8 | a | a4 | a6 | a | ai0 | au | a1 | |
| B | B | B | B | B | B | B1 | B1 | B1 | B1 | B1 | ||
| Z | B | B | B | B | B | B | B | B | B | B1 | B | B1 |
C3={a3, a4, a6, a9, ai1}, C4={ai0, ai2}.
Аналогично построим n3={Dp D2, D3, D4, D5}, D1={a1, a2}, D2={a5, a7}, D3={a8}, D4={a3, a4, a6, a9, a11}, D5={a10, a12} (табл. 9.5) и, наконец, П4={Е1, E2, E3, E4, E5}, которое совпадает с П3. Процедура разбиения завершена. Разбиение П3 есть разбиение множества состояний автомата Мили S на классы эквивалентных между собой состояний.
Таблица 9.4
| C | C2 | C3 | C4 | ||||||||||
| a | ^2 | A | a | a8 | a3 | a4 | a6 | a9 | au | am | ai2 | ||
| Z, | C4 | C4 | C3 | C3 | C4 | C2 | C2 | C2 | C2 | C2 | C | C | |
| Z2 | C2 | C2 | C3 | C3 | C3 | C3 | C3 | C3 | C3 | C3 | C2 | C2 |
| Таблица 9.5 | |||||||||||||||||||||||||||||||||||||||||||||
|
При минимизации автоматов Мура вводится понятие 0-эквивалентности состояний и разбиения множества состояний на 0-классы: 0-экви-валентными называются любые одинаково отмеченные состояния автоматов Мура. Если два 0-эквивалентных состояния любым входным сигналом переводятся в два 0-эквивалентных состояния, то они называются 1-эквивалентными. Все дальнейшие классы эквивалентности состояний для автоматов Мура определяются аналогично приведенному выше для автоматов Мили. В результате применения алгоритма минимизации к автомату Мура S3 (табл.9.8), имеющему 12 состояний, получим автомат S4 с 4 состояниями (табл. 9.9). Опуская промежуточные таблицы, приведем лишь последовательность разбиений
|
Bv B3}. Таблица 9.8 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||
|
B1 {ai, a2, a8}; B2 {a6, a9, ai0, ai1, ai2}; B3 {a3, a4, «5, a7}; П1={С1, C2, C3, C4}; Ci={ai, a2, a8}; C2={a6, a9, al1}; C3={ al0, al2}’ C4 {a3, «4, «5, a7}? ^, Ац D4}; A=A; Di=Ci; D2=C2; D3=C3; D4=C4. |
| Таблица 9.7 | ||||||||||||||||||
|
| Таблица 9.6 | ||||||||||||||||||
|
| Таблица 9.9 | ||||||||||||||||||||||||
|
10. МЕТОДЫ КОДИРОВАНИЯ состояний АБСТРАКТНЫХ АВТОМАТОВ
Процесс кодирования состояний абстрактных автоматов является первым этапом канонического метода структурного синтеза автоматов. Кодирование заключается в установлении взаимно однозначного соответствия между множеством A = {a1, ..., am} состояний автомата и множеством ^-компонентных векторов {к1, ..., km}, km={A,m1, ..., XmR}, где A,mi - состояние r-го элемента памяти (триггера). Обычно кодирование производится с помощью символов двоичного структурного алфавита (km^ {1,0}), поскольку при этом решается задача определения необходимого числа триггеров, имеющих два устойчивых состояния. Зависимость числа триггеров от количества состояний заданного абстрактного автомата определяется формулой [2]:R ^ ]log2M[,
где ]b[ означает ближайшее целое число, большее b или равное ему, если b - целое.
Кодирование состояний автомата можно осуществлять различными способами. Это может быть произвольное кодирование, когда каждому состоянию ставится в соответствие случайный набор двоичных символов, количество которых равно R. Синтезированный на основе такого кодирования структурный автомат не будет оптимальным, так как, во-первых, его комбинационная схема может обладать повышенной сложностью и, во-вторых, при отсутствии синхронизации и двойной памяти в процессе функционирования этого автомата могут появиться состязания [4].
Явление состязаний возникает вследствие того, что элементы памяти имеют различные, хотя и достаточно близкие, времена срабатывания. Кроме того, различны также задержки сигналов возбуждения, поступающих на входные каналы элементарных автоматов по логическими цепям неодинаковой длины. Если при переходе автомата из одного состояния в другое должны изменить свои состояния сразу несколько триггеров (что характерно для произвольного кодирования), то между ними начинаются состязания. Тот триггер, который выигрывает эти состязания, т. е. изменит свое состояние раньше, чем другие элементы памяти, может через цепь обратной связи изменить сигналы на входах некоторых триггеров до того, как другие участвующие в состязаниях изменят свое состояние. Это может привести автомат в состояние, не предусмотренное графом. Тогда возникшие состязания называются критическими состязаниями или гонками.
Гонки могут быть устранены различными способами, в том числе и с помощью противогоночного кодирования.
10.1. Противогоночное кодирование методом развязывания пар переходов
В литературе [4] предлагается метод противогоночного кодирования, основная идея которого сводится к следующему.Пусть (а, в) и (у, 5) - две пары двоичных кодов произвольной длины, например
a - 1|0|1 1 у -0|1|1 1 в - 0|0|1 1 5 -0|1|0 0
Если некоторый г-й разряд кода принимает одно значение на паре (a, в) и противоположное - на паре (у, 5), то такие пары кодов называются развязанными.
Доказана следующая теорема [3]: в автомате, состояния которого закодированы двоичными кодами конечной длины, гонки отсутствуют тогда и только тогда, когда для любых двух переходов (am, as) и (ak, а), аФа, происходящих под действием одного и того же входного сигнала, соответствующие пары кодов развязаны. (Если автомат синхронный, то развязывать нужно пары переходов, для которых (am, as)n(ak, а)=0). В этой же работе приведен основанный на этой теореме алгоритм про-тивогоночного кодирования состояний конечных автоматов, основная идея которого достаточно проста: последовательно просматривая все пары переходов, для которых имеется хотя бы один общий входной сигнал, осуществляющий эти переходы, следует присвоить разрядам кодов такие значения, чтобы существующие пары кодов состояний были развязаны.
Алгоритм противогоночного кодирования заключается в последовательном развязывании подлежащих развязыванию пар переходов. На промежуточных этапах алгоритма состояниям автомата будут соответствовать коды, значения некоторых разрядов которых могут быть не определены. Такие коды будем называть неполными. В дальнейшем неопределенные разряды кодов отмечаются черточкой. Пусть (am, as), (ak, а) - пара переходов автомата S, а a, в, Y, 5 - соответственно четверка кодов (быть может, неполных) состояний ат, а, ак, а1 длины i.
Операция развязывания пары переходов (am, as), (ak, a) сводится к нескольким этапам.
1. Положить i = 0. Перейти к п.2.
2. Если i = 0, то переход к п.8, иначе переход к п.3.
3. Если при некотором r (1 < r < i) значения r-го разряда четверки а, в, у, 5 образует набор 0011 или набор 1100, то переход к п.9, иначе к п.4.
4. Если при некотором r (1 < r < i) значения r-го разряда четверки а, в, у, 5 образует один из наборов
| - 0 1 1 | - - 1 1 | - - - 1 |
| 0 - 1 1 | 0 - - 1 | 0 - - - |
|
1 о о | 0 0 - - | - 0 - - |
| 0 0 1 - | - 0 - 1 | - - 1 - |
| - 0 1 - | 0 - 1 - | ? |
5. Доопределить неопределенные значения r-го разряда четверки а, в, Y, 5 так, чтобы его значения образовывали набор 0011. Переход к п.9.
6. Если при некотором r (1 < r < i) значения r-го разряда четверки а,
в, Y, 5 образует один из наборов
- 1 0 0 - - 0 0 ---0
1 - 0 0 1 - - 0 1---
1 1 - 0 1 1 - - - 1 - -
1 1 0 - - 1 - 0 - - 0 -
- 1 0 - 1 - 0 - ----,
то переход к п.7, иначе переход к п.8.
7. Доопределить неопределенные значения r-го разряда четверки а, в, Y, 5 так, чтобы значения этого разряда образовывали набор 1100. Переход к п.9.
8. Дополнить коды состояний автомата одним неопределенным разрядом. Увеличить r на единицу. Переход к п.4.
9. Пара переходов (am, as), (ak, aj), развязана. Конец.
Длина кода, получаемая в результате применения изложенного алгоритма, в большинстве случаев оказывается неминимальной, так как при введении нового разряда кода могут развязываться пары переходов, которые уже были развязаны ранее. В связи с этим желательно минимизировать длину получаемых кодов состояний, что делается следующим образом. Исключаем один из разрядов кодов, в результате чего некоторые пары переходов могут оказаться связанными, и применяем алгоритм развязывания пар переходов. После этого исключаем еще один разряд, вновь применяем алгоритм противогоночного кодирования и т.д., до тех пор пока длина кода не перестанет уменьшаться. Если в результате работы алгоритма значения не всех разрядов будут определены, то их можно доопределить произвольно.
Проиллюстрируем алгоритм противогоночного кодирования на примере автомата, функция переходов которого задана табл. 10.1.
Таблица 10.1
| a | О, |
a3 | a4 | 0 5 | a6 | a7 | |
| Z, | c.l | a | a | a | a | a | |
| ai | a3 | a3 | ai | a3 | - | - | |
| Z3 | - | a5 | a7 | - | a5 | - | a7 |
| M1 | M2 | M3 |
| (a1, a2) | (a1, a1) | (a2, a5) |
| (a2, a2) | (a2, a3) | (a3, a7) |
| (a3, a4) | (a3, a3) | (a5, a5) |
| (a4, a4) | (a4, a1) | (a7, a7) |
|
(a5, a6) (a6, a6) | (a5, a3) |
Паре переходов (a1, a2), (a4, a4) соответствует четверка (0011) (табл.10.2), т. е. эта пара тоже развязана.
Пара (a1, a2),(a5, a6) образует четверку (00--). Для развязывания
этой пары доопределим эту четверку до (0011), для чего состояниям a5, a6 ставим в соответствие t1= 1 (табл. 10.3).
| Таблица 10.2 Таблица 10.3 Таблица 10.4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
После чего остальные переходы в M1 тоже развязаны. Аналогично для М2 и М3 получим табл.10.5 и 10.6.
Таблица 10.5 Таблица 10.6
| T1 | T | T3 | T1 | T2 | T3 | T4 | ||
| «1 | 0 | 1 | 1 | 1 | 1 | 1 | - | |
| 0 | 0 | 0 | a2 | 0 | 0 | 0 | 0 | |
| a3 | 1 | 0 | 0 | a3 | 1 | 0 | 0 | 1 |
| «4 | 1 | 0 | 1 | «4 | 1 | 0 | 1 | - |
| «5 | 1 | 1 | 0 | «5 | 1 | 1 | 0 | 0 |
| «6 | 1 | 1 | - | «6 | 1 | 1 | - | - |
| «7 | - | - | - | «7 | - | 0 | - | 1 |
Оказывается, что пара (a1, a2), (a5, a6) не развязана, в связи с чем добавляем переменную т5 и развязываем эту пару (табл. 10.8).
Все остальные пары развязаны. Далее исключаем переменную т2 и получаем табл.10.9 с тремя переменными т3,т4, т5, в которой после проверки оказываются развязанными все пары.
| Таблица 10.7 | ||||||||||||||||||||||||||||||||
|
| Таблица 10.8 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Таблица 10.9 | ||||||||||||||||||||||||||||||||
|
10.2. Противогоночное соседнее кодирование
Второй способ кодирования, позволяющий избавиться от гонок, -это кодирование соседних состояний автомата соседними кодами (соседнее кодирование). Соседние состояния - это состояния, связанные дугой на графе автомата, а соседние коды - это двоичные наборы, отличающиеся только одним разрядом. Расстояние по Хэммингу у таких кодов равно 1. При соседнем кодировании при переходе автомата из одного состояния в другое меняется состояние только у одного элемента памяти и состязания становятся невозможными. Соседнее кодирование не всегда оказывается возможным [4] и в этом случае приходится на графе между соседними состояниями автомата вставлять дополнительные, так называемые неустойчивые состояния. Неустойчивое состояние автомата (состояние ак, на рис. 10.1) отличается тем, что под действием некоторого входного сигнала Zk, по длительности превышающего время перехода в это состояние ak, автомат может его “проскочить”, перейдя сразу в следующее состояние as. |
| Рис. 10.1 |
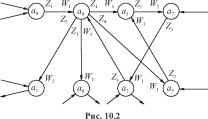
Состоянием с максимальным числом соседей (к = 6) является состояние a0. Следовательно, для кодирования удобно воспользоваться диаграммой Вейча размером 8x8=64=42 клеток (рис. 10.3). Поместим состояние a0 в произвольную клетку диаграммы, например соответствующую коду 110110 (QQ2 Q 3Q4 Q5 Q 6). Эта клетка имеет 6 соседних клеток, куда целесообразно помещать все состояния, соседние a0. Тогда получим следующие коды состояний:
k(a0) - 110110, k(a1) - 110100, k(a2) - 110010, k(a3) - 100110
_Q
_ 62
Q
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Рис. 10.3 |
Очевидно, коды состояний a1, a2, a3 отличаются от кода состояния a0 только одним разрядом. Поскольку состояние a5 является одновременно соседним и для a0, и для a1, необходимо поместить его в такую клетку, которая имела бы минимальные расстояния от обоих этих состояний. Такими клетками являются клетки с кодами 010100 и 010110. Выберем одну из них (например, 010110). Тогда, чтобы обеспечить соседнее кодирование, придется ввести дополнительное неустойчивое состояние b1, используя для него второй из этих кодов, а именно код 010100.
После этого оставшиеся состояния a4 и a6 можно поместить в клетки с кодами 110111 и 111110 соответственно. Состояние a7, соседнее состояниям a3 и a2, удачно помещается в клетку 100010, но при этом не получается требуемых соседних кодов у состояний a7 и a1. Поэтому на переходе a7 ^ a1 необходимо ввести дополнительные состояния (меньше двух при выбранном кодировании не получается) b2 и b3, расположенные соответственно в соседних клетках (a7 с b2, b2 с b3, b3 с a1).
В результате кодирования число состояний графа увеличилось на 4 (рис. 10.4), что, естественно, уменьшает быстродействие автомата.
107
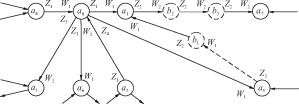 |
| Рис. 10.4 |
| Таблица 10.11 | ||||||||||||||||||||||||||||||||||||
|
1) кодируемое ложным кодом состояние (а) должно быть устойчивым по отношению к входному сигналу zk, (рис. 10.5); поскольку под действием zk автомат из at никуда перейти не может, состязания, если они и возникнут, являются некритическими;
2) из состояния а. отсутствует переход по сигналу zk;
3) из кодируемого ложным кодом состояния a. под действием сигнала zk автомат переходит в нужное состояние as (рис.10.6).
|
ООП 1001 |
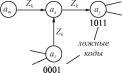 |
| Рис. 10.6 |
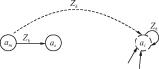 |
| Рис. 10.5 |
10.3. Кодирование состояний автомата, близкое к соседнему
Анализ канонического метода структурного синтеза автоматов показывает, что различные варианты кодирования состояний автомата приводят к различным выражениям функций возбуждения памяти и функций выходов. Эти выражения обладают различными рангами канонических форм записи, в результате чего реализованные по ним комбинационные схемы обладают различной сложностью, которая в итоге зависит от способа кодирования.Рассмотрим эвристический алгоритм кодирования состояний [4] и минимизирующий суммарное число изменений элементов памяти на всех переходах автомата.
Введем весовую функцию W = Xt, где tms = |Km-Ks|2 - расстояние между кодами состояний am и а, равное числу элементов памяти, изменяющих свое состояние на переходе (am, as); суммирование производится по всем переходам автомата. Введенная функция W может служить одной из оценок сложности комбинационной схемы автомата S, при этом упрощение комбинационной схемы будет тем больше, чем меньше W.
Алгоритм состоит из нескольких шагов.
1. Построим матрицу
аі Рі
ar вг
aR Pr
состоящую из всех различных пар номеров (ar, br), таких, что в автомате S есть переход из aar в а^г-
2. Переставим строки в матрице так, чтобы выполнялось условие
К, Рг}п{ар рі, ..., аг_і, ргЧ}*0, r=2, ..., R. (10.1)
Условие (10.1) означает, что хотя бы один из элементов r-й строки содержится в какой-нибудь из предыдущих строк. Имеются в виду только связные автоматы S, для которых такая перестановка всегда возможна.
3. Закодируем состояния из первой строки матрицы M следующим образом:
Ка1 = (00 ... 00); KP1 = (00 ... 01).
4. Вычеркнем из матрицы M первую строчку, соответствующую закодированным состояниям аа1, и а^1. Получим матрицу M’.
5. В силу условия (1) в начальной строке матрицы M закодирован один элемент. Выберем из первой строчки матрицы M’ незакодированный элемент и обозначим его через у.
6. Построим матрицу М^, выбрав из M’ строчки, содержащие у. Пусть
В = {у1, ..., Y, ..., yF} - множество элементов из матрицы М^, которые уже закодированы. Их коды обозначим КуР ..., ..., KyF соответствен
но.
7. Для каждого Kf (f= 1, ..., F) найдем - множество кодов, соседних с К^ и еще не занятых для кодирования состояний автомата.
F
Построим множество = U С . Если D^ = 0 , то строим новое мно-
F f=1
жество Dy = U С2 , где С^ - множество кодов, у которых кодовое
f=1
расстояние с кодом Kf равно двум. Если Dy = 0, строим аналогично Dy,... DY, до тех пор пока не найдется D^ Ф 0 (п = 1, 2, 3, ...). Пусть
D = { K81’ ..., Kg.... ЗД.
8. Для каждого K5g находим Wf = | Kbg - Kf |2 - кодовые расстояния между Kbg и всеми использованными кодами Kf (f = 1, ..., F). Если в автомате имеется переход из af в ау и из ау в af то Wf, входит дважды в Wg (см. ниже примеры переходов (a4, a5) и (a5, a4)).
9. Находим Wg = X Wf g = 1, ..., G.
10. Из DП выбираем K^ у которого Wg = min Wg. Элемент у (состояние aY) кодируем кодом K^.
11. Из матрицы M’ вычеркнем строчки, в которых оба элемента закодированы, в результате чего получим новую матрицу, которую такие обозначим через M’. Если в матрице M’ не осталось ни одной строчки, переходим к п.12, иначе к п. 5.
12. Вычисляем функцию W = Xtms, где tms = |Km- Ks|2.
13. Конец.
Оценкой качества кодирования по рассмотренному алгоритму может служить число k = W/p, где p - число переходов в автомате. Очевидно, что к > 1, причем чем меньше значение k, тем ближе кодирование к соседнему , при котором к = 1.
Без подробных объяснений приведем пример кодирования состояний автомата, граф которого изображен на рис. 10.7.
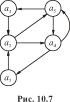
Кодирование будем иллюстрировать диаграммой Вейча.
| 00 | 01 | 11 | 10 | |
| 0 | 1 | 2 | ||
| 1 |
_ Q3
2 4
5 4 5 1
м' =
B4 ={2}.
Y = 4;
C21={101, 011}; Д} = C21={101, 011}. ^101=|101-001|2=1; ^011=|011-001|2=1. Выбираем K4=101.
| |||||||||||||||
|
Qi _ Q2 _ Q3 |
C2={011}; C4={100, 111}; C}={100, 010}; d} =C и C{u C/={011, 100, 111, 010}. fFo11=|011-001|2+|011-101|2+|011-10112+1011-000| 2= 1 +2+2+2=7; W100=|100-001|2+|100-101|2+|100-101|2+|100-000|2=2+1+1+1=5; Wn1=|111-001|2+|111-101|2+|111-101|2+|111-000|2=2+1+1+3=6; W010=|010-001|2+|010-101|2+|010-101|2+|010-000|2=2+3+3+1=9.
W100=min{ W001, W100, W111, W010}. Следовательно выбираем K5=100.
B3 ={2,4}.
Y = 3; M3
| 00 | 01 | 11 | 10 | |
| 0 | 1 | 2 | ||
| 1 | 5 | 4 |
W011=|011-001|2+|011-101|2=1+2=3;
W111=|111-001|2+|111-101|2=2+1=3.
W011=W111. Следовательно выбираем K3= 011.
| 00 | 01 | 11 | 10 | |
| 0 | 1 | 2 | 3 | |
| 1 | 5 | 4 |
10.4. Соседнее кодирование логически смежных состояний
Существует другой метод кодирования состояний, позволяющий упростить полученную в результате структурного синтеза схему [4]. Суть этого метода заключается в использовании двух следующих правил кодирования.Правило 1. Те состояния, из которых возможны переходы в одни и те же состояния хотя бы для одного значения входного сигнала, являются логически смежными и должны быть закодированы соседними кодами.
Правило 2. Логически смежными являются состояния, следующие для одного и того же состояния. Их необходимо кодировать соседними кодами.
Если при использовании этих правил невозможно закодировать соседними кодами все логически смежные состояния, то приоритет должен сохраниться за правилом 1.
В таблице переходов состояния, удовлетворяющие правилу 1, должны иметь одинаковые состояния перехода в какой-либо строке. Состояния, удовлетворяющие правилу 2, находятся в одном столбце таблицы переходов.
Рассмотрим таблицу переходов автомата (табл. 10.12).
| Таблица 10.12 | ||||||||||||||||||||||||||||||||||||||||
|
В нашем примере это:
(a0, а2) - оба переходят в а3 по сигналу “0”;
(a0, a3) - оба переходят в a4, по сигналу “1”;
(a2, a5) - оба переходят в a5 по сигналу “1”;
(a4, a6) - оба переходят в a8 по сигналу “1”;
(a3, a4) - оба переходят в a6 по сигналу “а “;
(a1, a2, a6) - все переходят в a1 по сигналу “a”.
Далее необходимо выписать группы состояний, находящихся в одних и тех же столбцах. В нашем примере это (a3, a4), (a2, a1), (a2, a3, a1),
(a3, a3, aj), (a5, a4, a6), (a2, a6)? (ai, a5).
Все состояния, находящиеся в каждой из сформированных групп, должны быть закодированы соседними кодами. Для этого на основе полученных групп следует составить классы состояний, логически смежных с каждым из состояний автомата, причем каждую пару логически смежных состояний целесообразно включать только в один класс. Сделав это в рассматриваемом примере, получим
| K | K | K3 | K4 K5 | |
| *(%. a) | *{al, a2) | *(a2- a5) | *(ay a4) | К a5) *Ц, a6) |
| *а a2) | *(av a6) | *(a2’ a6) | a a5) | *(a4’ a6) |
| a a5) | a a3) | |||
| a a3) |
Для кодирования логически смежных состояний целесообразно воспользоваться диаграммой Вейча, отдавая приоритет парам состояний, полученным по правилу 1. Проведя эту операцию, получим
| ai | a2 | a5 | a6 |
| a0 | a3 | a4 |
a _Q
2Оказалось, что в данном случае не удалось закодировать соседними кодами следующие пары логически смежных состояний:
(a2, a6), (a2, a3), (a5, a4), (a1, a5), (a1, a3).
В результате получили следующие коды состояний:
K(aj) = 000 (Q i Q 2 Q 3);
K(a2) = 100 (Qj Q 2Q 3);
K(a3) = 111 (Qj Q2 Q3);
K(aA )= 011 (q 1 02 в3);
K(a5) = 110 (Qi Q 2 Q 3);
K(a6) = 010 (Q 1 02 Q 3).
Процесс кодирования характеризуется качеством кодирования (k), которое рассчитывается по формуле где m - число пар логически смежных состояний, которые удалось закодировать соседними кодами; n - общее количество пар состояний, сформированных в классах K1, K2, ..., KN
9
В рассматриваемом примере к = ~ 0,69.
Хорошим можно считать кодирование, у которого k>0,5.
Библиографический список
1. Кузнецов О. П., Адельсон-Вельский Г. М. Дискретная математика для инженера. М.: Энергоатомиздат, 1988.2. Глушков В. М. Синтез цифровых автоматов. М.: Физматгиз, 1962.
3. Мацевитый Л. В., Денисенко Е. Л. О кодировании внутренних состояний некоторых многотактных устройств// Кибернетика. 1966. №1.
4. Баранов С. И. Синтез микропрограммных автоматов. Л.: Энергия, 1979.
5. Козин И. В., Лупал А. М. Проектирование цифровых автоматов управления и контроля/ ЛИАП. Л., 1985.
6. Мелехин В. Ф, Дурандин К. П. Вычислительные машины и системы. СПб.: Высшая школа, 1993.
 Учет: Делопроизводство - Автоматизация - Софт
Учет: Делопроизводство - Автоматизация - Софт
- Управленческий учет
- Технологии управленческого учета
- Делопроизводство
- Стандарты делопроизводства
- Делопроизводство предприятия
- Секретарь и делопроизводство
- Автоматизация делопроизводства
- Документооборот
- Автоматизация
- Автоматизация управления
- Практика автоматизации
- Софт для автоматизации