Л. О. Бабешко - Математическое моделирование экономических процессов

1. Вычисление рисковой надбавки тарифной ставки в рамках методики, рекомендованной Федеральной службой России по надзору за страховой деятельностью
Страховая компания принимает на себя риск неблагоприятного события, которое может нанести ущерб объекту страхования. Цена страховой услуги устанавливается в начале действия договора страхования и, в отличие от общества взаимного страхования, не меняется путем внесения дополнительных взносов при нехватке собранных средств на выплаты страховых возмещений [3, c.16]. Поэтому вопрос формирования тарифной ставки в рисковых видах страхования является особенно важным. В соответствии с методикой, рекомендованной Федеральной службой России по надзору за страховой деятельностью, структура тарифной ставки включает следующие составляющие:

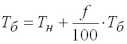
, т.е.

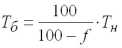
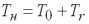
(1.0)
где

– брутто-ставка,

– нетто-ставка,

– чистая нетто-ставка,

– рисковая надбавка, f– нагрузка, идущая на выплаты сотрудникам. Как следует из (1.0), основная задача формирования структуры тарифной ставки связана с расчетом нетто-ставки

.
Алгоритм вычисления тарифной ставки по статистической информации включает следующие этапы (см., например, источники, указанные в списке литературы).
Подготовка статистических данных. На данном этапе, за определенный период времени (n лет), собирается информация о суммах страховых возмещений

и совокупной страховой сумме по рискам

, принятым на страхование, и вычисляется величина фактической убыточности страховой суммы за год t

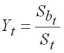
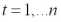
. (1.1)
Оценка модели линейной парной регрессии со спецификацией

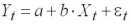
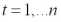
, (1.2)
где

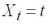
— независимая переменная (момент времени, к которому относится

— значение фактической убыточности страховой суммы за год t, a, b — параметры модели,

— случайное возмущение на момент t, удовлетворяющее условиям Гаусса–Маркова.
Оценка убыточности страховой суммы за год t в рамках модели (1.2) вычисляется по формуле

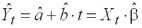
, (1.3)
где

– МНК-оценки параметров модели (1.2),

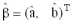
– вектор столбец оценок параметров, Xt=(1 t)— t-я строка матрицы регрессоров Х.
МНК-оценки вектора параметров определяются выражением

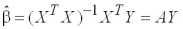
, где

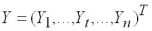
, (1.4)
и являются линейными несмещенными и эффективными в силу теоремы Гаусса–Маркова. Автоковариационная матрица оценок (1.4):

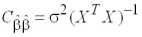
, (1.5)
где

– дисперсия возмущения.
Вычисление чистой нетто-ставки

. Чистая нетто-ставка (основная часть тарифной ставки) определяется как прогноз убыточности на

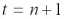
год

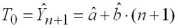
. (1.6)
Вычисление рисковой надбавки тарифной ставки Tr. Рисковая составляющая нетто-ставки рассчитывается по формуле

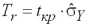
, (1.7)
где

– оценка среднего квадратического отклонения фактических значений убыточности от оцененных по формуле (1.3)

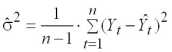
, (1.8)
где n – объем выборки,

– табличное значение статистики Стьюдента, выбираемое в соответствии с параметрами: (n-k) – число степеней свободы и (1-) – значение доверительной вероятности, с которой собранные взносы способны обеспечить выплаты страховых возмещений.
По существу, методика вычисления тарифной ставки представляет собой расчет правой границы доверительного интервала для индивидуального значения эндогенной переменной (убыточности страховой суммы) и выполняется в рамках эконометрических методов.
2. Вычисление рисковой надбавки тарифной ставки

в рамках эконометрических методов
Доверительный интервал среднего значения зависимой переменной.
Построим доверительный интервал для ожидаемого значения убыточности страховой суммы на момент времени t

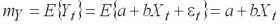
, где

,
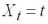
т.е. интервал, который с заданной доверительной вероятностью 1- будет накрывать ожидаемое значение зависимой переменной на данный момент. Для построения границ доверителного интервала используется стандартная процедура. Составляется дробь Стьюдента

(2.1)
– нормированная ошибка оценки (прогноза) среднего значения эндогенной переменной, где в числителе — истинная ошибка оценки (прогноза)

, (2.2)
в знаменателе — оценка среднего квадратического отклонения (ско) данной ошибки

.
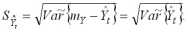
Точечная оценка (2.2) используется для формирования интервальной оценки, в соответствии с (2.1)

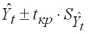
. (2.3)
Для того чтобы найти оценку ско

, поступим следующим образом. Запишем выражение для дисперсии оценки (2.2)

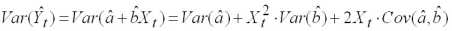
. (2.4)
Подставим в (2.4) выражения для дисперсий оценок параметров парной регрессионной модели и их взаимной ковариации (элементы матрицы (1.5)), выраженные через выборочные данные

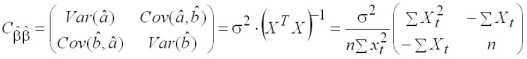
, (2.5)
где

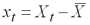
– центрированное по выборке значение регрессора (

– среднее по выборке), n– объем выборки,

– дисперсия возмущений.
Предварительно дисперсию оценки параметра а преобразуем к виду

,
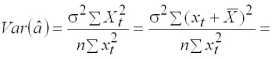
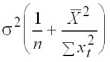
тогда

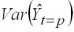
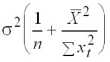
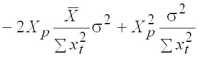
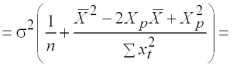
, (2.6)
где

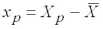
– центрированное по выборке значение регрессора, для которого определяется прогноз (оценка) ожидаемого значения зависимой переменной

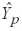
. Дисперсия (2.6) является диагональным элементом матрицы автоковариаций вектора оценок эндогенной переменной

,
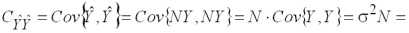
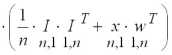
где

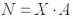
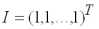
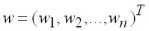
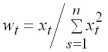
. Так, например, элементу

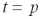
соответствует выражение (2.6). Заменяя значение дисперсии возмущения 2 его оценкой, получим выражение для оценки дисперсии

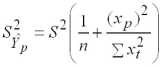
; (2.7)
Доверительный интервал индивидуального значения зависимой переменной.
Для определения границ доверительного интервала для отдельных (индивидуальных) значений зависимой переменной (например, на момент

), применяя стандартную процедуру, составляем дробь Стьюдента

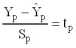
. (2.8)
Числитель дроби (2.8) представляет собой истинную ошибку прогноза индивидуального значения эндогенной переменной

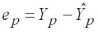
. (2.9)
Знаменатель дроби (2.8) — оценка ско истинной ошибки прогноза. Определим дисперсию данной ошибки

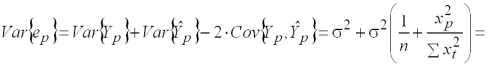
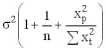
. (2.10)
Покажем, что

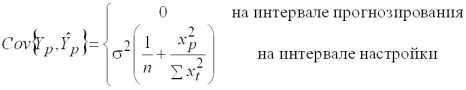
(2.11)
Интервал настройки модели:

.
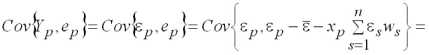
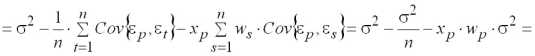
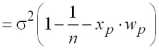
Здесь учтена взаимосвязь между остатками регрессии и случайными возмущениями [1, с. 30].
Интервал прогнозирования:

,
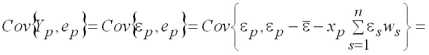
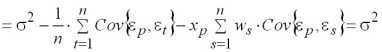
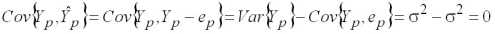
или, в матричной форме

Интервал настройки модели:

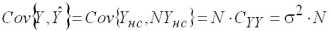
Интервал прогнозирования:

,
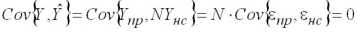
где

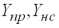
– векторы значений эндогенной переменной на интервалах прогнозирования и настройки, соответственно. Заменяя в (2.10) значение дисперсии возмущений 2 его несмещенной оценкой

,
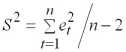
получим выражение для оценки дисперсии прогноза значения фактической убыточности для наблюдения

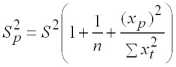
. (2.12)
Границы для доверительного интервала прогноза индивидуальных значений

определяются по формуле

,
и, следовательно, рисковая надбавка тарифной ставки в рамках регрессионных методов равна

. (2.13)
Таким образом, формула (1.8) учитывает лишь часть полной дисперсии прогноза, и рисковая составляющая тарифной ставки (1.7) дает заниженное значение относительно заданной доверительной вероятности по сравнению с (2.13).
Продемонстрируем это на следующих эмпирических данных.
Расчет значений фактической убыточности страховой суммы

t
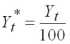1	227800	410	0,0018	0,179982
2	294200	765	0,0026	0,260027
3	275500	799	0,0029	0,290018
4	309400	1114	0,0036	0,360052
5	334600	1305	0,0039	0,390018

Стандартная форма оцененной регрессионной модели:

.
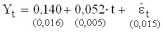
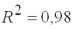
Прогноз значения фактической убыточности на следующий год

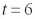
равен

% .
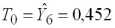
Значение рисковой надбавки тарифной ставки, рассчитанное по формулам (2.12) и (2.13):

.
Значение рисковой надбавки тарифной ставки, рассчитанное по формулам (1.7) и (1.8):

.
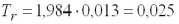
Из сравнения оценок надбавок тарифных ставок, рассчитанных по анализируемым методикам, следует, что методика, рекомендованная Федеральной службой России по надзору за страховой деятельностью, приводит к занижению рисковой надбавки тарифной ставки и, как следствие, к повышению риска страховых компаний, связанного с нарушением принципа эквивалентности между страховыми премиями и страховыми выплатами.
ЛИТЕРАТУРА
1. Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика: Начальный курс. М.: Дело, 1997.
2. Жданов А.И., Чудилина Т.В. Уточненный регрессионный метод расчета тарифных ставок в рисковых видах страхования // Страховое дело. 2001, декабрь.

С. 37-41.
3. Салин В.Н., Абламская Л.В., Ковалев О.Н. Математико-экономическая методология анализа рисковых видов страхования. М.: Анкил, 1997.
cb