Орлов В. П. - Основы страхования

1 Предварительные построения

Пусть имеется пять человек, при этом за год хотя бы один из них теряет необходимую вещь (например телевизор) стоимостью 10 единиц. Доход каждого из них 3 единицы, и они расходуются за год. Если не помогать друг другу, через 5 лет все останутся без телевизора. Для того чтобы иметь возможность возместить ущерб от потери владельцу телевизора, нужно собрать с каждого по 2 единииицы (в итоге 10 единиц) и вручить их пострадавшему для покупки нового телевизора. Эта процедура сбора средств для возмещения ущерба и является простейшим договором страхования.

Заметим, что если имеется всего один человек, то для возмещения ущерба ему самому нужно 10 единиц, чего у него нет. Для двух и для трёх человек эта схема тоже не работает. Нужно как минимум четыре человека, чтобы собрать необходимые 10 единиц. Для того чтобы выяснить сущность этой процедуры страхования, необходимо детально проанализировав ситуацию, выявить моменты, ее определяющие, и построить математическую модель, позволяющую осуществить точные расчёты.

Прежде всего отметим, что в этой процедуре страхования имеются два субъекта: тот кто даёт деньги, с тем, чтобы получить возмещение в случае беды, и тот, кто эти деньги собирает, а потом возмещает ущерб. Первый называется клиентом (страхователем), второй страховой компанией (страховщиком). Первый платит компании сумму р, называемую страховой премией, второй выплачивает сумму b, называемую страховой выплатой, в случае беды, или не платит ничего (платит 0), если ничего не случилось. Кроме двух субъектов этой процедуры, имеется ещё случай, от которого зависит, платить или не платить клиенту. Этот случай называется страховым случаем, и именно он является объектом страхования.

Таким образом, индивидуальный договор страхования связывает клиента, страховую компанию и случай, назовём его A, в зависимости от которого компания платит b или 0 клиенту, а клиент всегда платит р компании.

Возникает вопрос, сколько брать с клиента, чтобы выплатить ему компенсацию за ущерб? Вернёмся к нашему примеру. Если известно точно, что ломается только 1 телевизор в год, то ясно, что р = 2. Но предположим, что могут сломаться больше, чем 1 телевизор. Если их будет 2, то необходимо собирать по 4 единицы, если 3, то по б единиц и так далее. Пусть могут сломаться не более двух, да и то два ломаются раз в 100 лет.

Тогда разумно брать по 2 единиы, так как скорее всего два не сломаются. Правда, если сломаются, то тогда клиент останется без телевизора. Если же два ломаются 99 раз в 100 лет, то надо брать больше, чем по две единицы с клиента. На этом примере видно, что величина премии р существенно зависит от вероятности (частоты) с которой происходит случай A. Итак, мы с необходимостью пришли к понятиям теории вероятностей. А именно, нам нужно вероятностное пространство, которое порождает случай A.

В житейском смысле, страховой случай с точки зрения страховой компании является набором исходов, в зависимости от которых выплачивается та или иная сумма. Поэтому разумно считать, что это множество исходов по договору с клиентом, обозначим его номером i, является некоторым множеством Пц состоящим из множества исходов и, природа которого пока не важна. Для простоты можно считать это множество конечным, так что Q_i = {и¹,... ,и^Пі}, где n_i некоторое число. В зависимости от исхода и Е Q_i компания платит клиенту числовую величину X_i(u). При этом величина выплаты может быть разной (из области значения определённой на Q_i функции Х_і(и)).

В основу идеального взаимоотношения клиента и компании (на деле все несколько сложнее) положен принцип эквивалентности: клиенты платят компании столько же, сколько компания платит клиентам, то есть вся сумма собранных компанией премий идёт на выплаты клиентам по заключённым договорам.

С точки зрения компании не имеет значения, сколько платит конкретный клиент. С точки зрения клиента это как раз и важно. Заметим, что премия вносится клиентом под договор, то есть сначала договор (сколько клиент хочет получить в страховом случае), затем премия.

Один из принципов назначения премии за договор - тот же принцип эквивалентности: клиент платит премию в размере страховой выплаты. Но выплата - величина многозначная, эта функция X_i(u) на Qi, а премия величина однозначная. Поэтому логично говорить лишь о средней величине выплаты Xi(u).

Пример. Пусть X (и) принимает лишь два зн ачения: фи b₂. Для того чтобы говорить о среднем значении X(и), нужно знать вероятности pi и р₂, с которыми принимаются значения фи b₂ соответственно. Тогда среднее

- 7 -

значение EX функции X(и) определяется как

EX = bipi + b2P2.

Замечание. В этом примере Q состоит из двух элементов: иі и и₂. И X(и₁) = bp X(и₂) = b₂. При этом вероятность исхода и₁ равнapi, а исхода и₂ равна р₂.

На этом примере видно, что для определения среднего значения X(и) в общем случае на Q надо задать вероятность Р, числовую величину, определённую на некоторой совокупности Е (а-алгебре) подмножеств Q. В этом

случае среднее значение ы X(и) определяется числом EX = f X(и)dP(и) ,

о

где интеграл понимается в Лебеговском смысле. Напомним, что случайной величиной называется измеримая (относительно (а-алгебры Е) функция

X (и).

Мы ограничимся случаем, когда Q_i = {и₁, ...,и_Пі} (т. е. Qp- конечные множества) при этом будем считать, что случай иk G Q_i происходит с вероятностью р^і(ик). Тогда для функции Xp X^k) = bk,_i среднее значение EXi = ^2_i b_kjPⁱ(и_k). При этом об измеримости X(и) а- алгебре Е, интегралах Лебега говорить не приходится, что упрощает изложение. Величина p>_i = EXi называется нетто-премией по договору i.

Таким образом, компания, заключив договор с клиентом i о выплате X_i (и) в обмен на премию рр собирает капитал U = ^^N=_i рр где N - число клиентов, и собирается начинать выплаты. Оказывается, что так разумно устроенная компания прогорит с большой вероятностью. Ниже мы займёмся выяснением причин этого. Для этого мы дадим точные определения, построим математическую модель страхового дела и проведём количественный анализ этого дела. Для этого нам понадобятся некоторые сведения из теории вероятностей.

2 Необходимые сведения из теории вероятностей

Пусть Q = {ш} - конечное или счетное множество произвольной природы. Пусть для каждого элемента и_i (исхода) этого множества определено число P(и-і) > 0, называемое вероятностью этого элемента, так что Е°=₁Р(щ) = 1. Определим для каждого подмножества A (события) из Q его вероятность Р (A) формул ой Р (A) = ^2 _Шіе a Р (иі)-

Тогда на совокупности Е всех подмножеств множества Q определена неотрицательная функция P(Л) A ? Е, причем соотношение P(UAi) =

P(Aj), Ai П Aj = 0 выполняется для любой (конечной или, счет

ной) совокупности попарно пересекающихся множеств. При этом P(Q) = 1,

P (0) = 0.

Определение 2.1. Тройка (Q, E,P) называется вероятностным пространством. Элементы w множества Q называются элементарными событиями, подмножества A из Q, принадлежащие Е, называют случайными событиями, а число P(A) для A ? Е называется вероятностью события A.

Определение 2.2. Пусть A, D ? Е. Условной вероятностью P(A/D) события A при условном наступлении события D называется число

P (A/D) = P (AD)/P (D). (2.0.1)

В нашем случае справедливо назвать случайной величиной прозвольную функцию X(w) на Q.

Определение 2.3. Случайная величина X называется дискретной, если она принимает не более чем счетное число значений x_l, x₂,... x_n,....

Очевидно, что нашем случае любая случайная величина является дискретной.

Определение 2.4. Таблица вида

(2.0.2)

Xi Х2 ... Xn

Pi P2 ... Pn

называется распределением случайной величины X. Здесь p_k = P(w : X (w) = Xk).

Определение 2.5. Функцией распределения F(t) случайной величины X(w) называется определенная при t ? R¹ функция

(2.0.3)

F(t) = P{w : X(w) < t}.

Отметим основные свойства функции распределения: 1.0 < F(t) < 1;

2. F (t) непрерывна справа, то есть lim F (t) = F (t₀) для любо го t₀ G R¹, lim F(t) = 1, lim F(t) = 0;

3. F (t) неубывающая no t функция.

Функция распределения F (t) для дискретной случайной величины X будет кусочно-постоянной, имеющей скачки величиной pk в точках t = Xk-

Для случайной величины X(w) очень важным являются следующие характеристики, характеризующие ее в среднем. Это математическое ожидание - ее среднее значение на Q и дисперсия - среднее отклонение X(w) от ее среднего значения. Для дискретной случайной величины X справедливы следующие формулы:

E(X) = ^2 XiPi, (2.0.4)

і=і

(2.0.5)

(2.0.6)

D(X ) = YSXi, - E (X )fp„

i=1

D(X) = J2(x)P - ^ XiPi,

і=1

i=1

3 Основы страхования

3.1 Основные определения

Определение 3.1. Индивидуальным договором страхования называется тройка (Q,X,p). Здесь Q некоторое вероятностное пространство, X : Q ^ R¹ - функция, ар- число.

Множество Q описывает исходы страхового случая. Всюду ниже мы считаем для простоты, что Q является конечным или счетным множеством. Так как Q является вероятностным пространством, то это означает, что для каждого исхода ш_і определено число P(ш_і)₇ называемое вероятностью этого исхода.

Функция X(и_І) задаёт величину страховой выплаты в случае исхода и_І7 ар- величину страховой премии.

Определение 3.2. Функция X(ші) называется страховой выплатой, число р - страховой премией.

Определение 3.3. Случайная величина

L(u) = X (и) — p (3.1.7)

называется потерей компании на индивидуальном договоре (Q,X,p).

Определение 3.4. Число

p = EX = ^ bkPk ,bk = X (uk) (3.1.8)

k=1

называется нстто-прсмисй индивидуального договора (Q,X,p).

Из (3.1.7) и (3.1.8) вытекает, что если p = p, то

EL(u) = 0, (3.1.9)

т. е. потеря компании на индивидуальном договоре (Q,X,p) равна нулю.

Определение 3.5. Страховой компанией называется набор N индивидуальных договоров страхования (Q_i,X_i,p_i), i = 1,...,N.

Определение 3.6. Число

N

U = J2 Pi (3-1.10)

i=1

называется капиталом компании.

Для страховой компании важным является описание множества (Q_i состояний и, в котором находятся все клиенты. Пусть вероятностное пространство Q = Q₁ х ... х Q_n =, {и =(u¹, ...,u^N),и'Р Q_i = {u'1 ,..,и^гп.}}. Вероятность P(и) исхода и определяется как

N

P (и) = П P.(u Т (3.1.11)

i = 1

Рассмотрим на Q случайную величину

5 (и) = X1(u¹) + ... + Xn (uⁿ ). (3.1.12)

Определение 3.7. Случайная величина S(и) называется обязательством компании.

Определение 3.8. Числа

R = P(и : 5(и) >U),Q = P(и : 5(и) < U) (3.1.13)

называются, соответственно, вероятностью разорения и неразорения компании.

Ясно, что R + Q = 1. Оказывается, что при больших N подсчитать R и Q сложно, поэтому приходится пользоваться инструментами теории вероятностей.

3.2 Расчет вероятности разорения

Точный расчет величины R можно произвести, если известны характеристики величины Xi{wi). Однако эти вычисления очень громоздки (см. курс теории вероятностей). На практике при больших N имеются простые приближенные формулы, основанные на следующем факте.

Теорема 3.1. При больших N с большой степенью точности для функция распределения F{x) случайной величины

(3.2.14)

й 5 - E(5) ЦоЩ

справедливо соотношение

x
F(x) & Ф(х)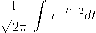
—оо

(3.2.15)

Мы не будем выяснять условий, при которых справедлива эта формула (см. по этому поводу [3]), заметим лишь, что для нормированной с.в. (это означает, что E(5) = 0 и D(5) = 1) формула (3.2.15) означает почти нормальное распределение. Ниже всюду считаем, что (3.2.15) выполнено.

Из формул (3.2.14) и (3.2.15)следует, что

U - E(5)

Q = P (w : 5 < U) & Ф

(3.2.16)

Действительно, так как 5(w) < U эквивалентно соотношению

5(w) - E(5) U - E(5)

?ощ < RD(S)

то

U - E(S)

EEm

S(w) - E(S) ^ U - E(S)

VDs) < уЩё)

P(w : 5(w) < U)

в силу (3.2.14) и (3.2.15).

Величина (3.2.16) означает вероятность Q неразорения компании. Исходя из (3.2.16), можно всегда подсчитать вероятность неразорения компании, если известен капитал компании и задана случайная величина

S.

Можно решить другую задачу: для заданной величины Q неразорения компании определить величину U капитала, обеспечивающего эту вероятность неразорения. Для этого, полагая Q =1 — R R Е (0,1) и R мало, определяют сначала xr как решение уравнения Ф(жд) = 1 — R. Решение xr уравнения Ф(xR) = 1 — R называется квантилью числа R.

Затем, пользуясь (3.2.14), выписывают соотношение

U - E(S)

\/ЩЩ

Q = P(w : S(w) < U) « Ф

Ф(XR).

Из последнего равенства, приравнивая аргументы, получаем, что

U = x^J D(S) + E (S). (3.2.17)

3.3 Принципы назначения страховых премий

Пусть капитал U компании складывается из полученных от клиентов премий. Если соблюдать принцип эквивалентности, суммарная величина премий, определенных как нетто-премия по формуле (3.1.8), и составит капитал компании, поскольку

N / N \

U = Y, E(Xi) = E = E(S). (3.3.18)

i=1 \i = 1 )

Пусть сначала премия по каждому договору является нетто-премией, т.е. Pi = pi = E(Xj). Тогда капитал U = ^^N=₁ E(Xi) = E ^^^N=₁ X^j = E(S). Из (3.2.16) получаем, что в этом случае

U - E(S)

VD(S)

E(S) - E(S) VDJS)

Ф(0) = 1/2.

В этом случае R & 1/2.

Это очень большая вероятность разорения. Дело здесь в том, что несмотря на одинаковые траты клиента и компании, клиент ничем не рискует, а компания при этом может не справиться с выплатой страховки. Поэтому страховая премия всегда включает надбавку l_i к нетто-премни рц именно

Pi = Pi + ^li = EXi + li. (3.3.19)

Определив через

N

l = li (3.3.20)

i=i

суммарную надбавку по всем договорам, получаем, что капитал компании

U = E (S) + l. (3.3.21)

В этом случае вероятность разорения компании R = 1 - P(S < U) = 1 - P(S < E(S) + l) & 1 - Ф

l

?ЩЁ)

(3.3.22)

Отсюда следует, что l/\JD(S) = xr, или

(3.3.23)

l = xr\J RD(S).

Таким образом, (3.3.23) дает суммарную величину надбавки, обеспечивающую заданную величину Q = 1 — R неразорения компании.

Величину l теперь необходимо разделить по договорам. Например, можно

ПОЛОЖИТЬ

li = kE (X )i, (3.3.24)

т.е. надбавку считать пропорциональной убытку. Тогда из (3.3.20) и (3.3.24) следует, что k ^ E(X_i) = kE(S) = l Поэтому, в силу (3.3.23)

k = x^J D(S)/E (S). (3.3.25)

Можно величину l_i определить как

(3.3.26)

li = kD(Xi)

т.е. надбавку считать пропорциональной дисперсии, или

(3.3.29)

До сих пор мы нигде не учитывали фактор времени. Рассматриваемые выше договора страхования мы будем называть кракосрочными.

При учете фактора времени приходится учитывать, во-первых, изменение стоимости денег с течением времени, а во-вторых, то обстоятельство, что сам страховой случай тоже может зависеть от времени. Перед тем, как заняться долгосрочным страхованием, мы рассмотрим некоторые вопросы, связанные с теорие процентных ставок.

4 Основные понятия финансовой математики

4.1 Общие положения

Всем хорошо известно, что помещенная при t = 0 в банк сумма S(0) растет и превращается в сумму S(t) в момент времени t > 0. Вид этой функции может быть самым разнообразным и определяется банком. Обычно определяют функцию C(t) такую, что C(0) = 1 и S(t) = S(0)C(t). То есть, C(t) означает, во что превратилась в момент времени t > 0 одна условная денежная единица (у.е.), взятая в момент времени t = 0.

Таким образом, каждый банковский счет определяется некоторой (своей) функцией C(t). Мы эту функцию C(t) и будем называть банковским счетом.

Определение 4.1. Банковским счетом называется функция C(t) > 0, определяющая стоимость одной денежной единицы во время t Е [0, +ж).

В зависимости от обстоятельств, поведение C(t) может быть самым разнообразным. Наиболее простые и важные функции C(t) имеют вид:

В первом случае

k = xr/у/ D(S)

(3.3.28)

во втором -

(4.1.1)

(4.1.2)

C (t) = (1 + ti)

C (t) = (1 + i)

где i > 0. При этом первая зависимость называется простым процентом, а вторая зависимость называется сложным процентом.

Для нас в дальнейшем интерес будет представлять вторая зависимость.

Часто возникает необходимость сравнивать денежные величины, взятые в разные моменты времени.

Определение 4.2. Сумма S(t_i), взятая в момент t\, и сумма S(t₂), взятая в момент t₂, называется эквивалентными относительно счета C(t), если существует такая сумма S(0), что S(ti) = S(0)C(ti) и

S (t₂) = S (0)C fe).

Определение 4.3. Задача нахождения суммы S(t₂), взятой в момент t₂, эквивалентной с умме S (t_i), взятой в мом ент t_iy t_i < t₂, называется задачей наращения суммы S(ti) к моменту t₂. Задача нахождения суммы S (t_i), взятой в мом ент t_iy эквивалентной с умме S (t₂), взятой в момент t₂, t_i < t₂, называется задачей дисконтирования суммы S(t₂) к моменту ti•

4.2 Теория сложных процентных ставок

Определение 4.4. Сложным процентом называется банковский счет, определяемый функцией

C (t) = (1 + i)^t. (4.2.1)

Определение 4.5. Число i называется эффективной процентной ставкой.

Определение 4.6. Промежуток времени [0,1] , за который 1 у.е. превращается в 1 + і, называется периодом конверсии.

Формула (4.2.1) означает, что одна денежная единица при t = 0 эквивалентна (1 + i)^t при t > 0. Другая формула банковской ставки (4.2.1) имеет

C (t) = e^st, 5 = ln(1 + i). (4.2.2)

Определение 4.7. Число 5 = ln(1 + і) называется интенсивностью процентной ставки і.

Для сложного банковского процента задача наращения решается с помощью вытекающих из (4.2.1) формул

S (t₂) = e^{d(t2-tl )}S (ti). (4.2.4)

Соответственно, задача дисконтирования решается с помощью формул

S (tl) = (1 + і)-(і2-і1^ (t2),	(4.2.5)
S (ti) = e-HU--tl>S (t2).	(4.2.6)
Определение 4.8. Число
v = (1 + і)-1	(4.2.7)

называется коэффициентом дисконтирования (для процентной ставки

і).

Очевидно, что

1 — v ,

і =-. (4.2.8

v

Формулы (4.2.5) (4.2.6) могут быть переписаны в виде

S (ti) = v^(t2-tl)S (t2). (4.2.9)

В рассчетах часто имеют дело со временем t_i = 0 и t₂ = t. Тогда, если имеется сумма S(0) в момент t_i = 0, ее наращенная стоимость в момент t > 0 определяется формулой

S (t) = (1 + ifS (0). (4.2.10)

Наоборот, если имеется сумма S(t) в момент времени t > 0, то ее приведенная стоимость S(0) определяется формулой

S (0) = v^fS (t). (4.2.11)

Определение 4.9. Эффективной ставкой дисконтирования называется число

d =^— = iv. (4.2.12)

1 + і ' ’

Смысл d - это выплата в момент t = 0 эквивалентной величины для процентов і, набежавших за год на 1 денежную единицу (проценты вперед).

Разобьем отрезок (0,1] на m чаетей [0, —, — ]. Выберем за единицу

времени [0, — ] и будем ^а 1 у.е. начислять проценты і^(— в момент 1/m. Эта процедура порождает банковский счет с эффективной процентной ставкой іІТ^ и периодом конверсии 1/т. Если мы возьмем время 7, то по банковскому счету (4.2.1) современная стоимость 1 у.е. равна C(t) = (1 + i)^f. Если мы возьмем новый счет Ci (t) с периодом

1 « -Ш) Гп j.1

конверсии m и ставкой il , то на промеж утке [0,t] промежуток конверсии [0, m] укладывается tm раз, и стоимость 1 у.е. в момент t по новому счету равна C₁(mt) = (1 + )^mt. Определим так, чтобы начисленная по

новому и старому счету суммы совпадали. Тогда должно быть C₁(mt) = C(t) или (1 + i) = (1 + il^m)^tm. Полагая t = 1, имеем (1 + i) = (1 + il^m^)^m. Отсюда легко следует, что

i^{m) = (1 + i)i - 1. (4.2.14)

Определение 4.10. Число il^m) = (1 + i) ™ — 1 называется эффективной процентной ставкой, выплачиваемой с частотой т.

Переписав (4.2.13) в виде

г(т)

Ci(t) = e^s* ^Т, (4.2.15)

и полагая т = m имеем C)(т) = в^* ^>m = в^ = C(1), откуда 6^(m) = Ь/т.

Определение 4.11. Интенсивностью процентной ставки, выплачиваемой с частотой т, называется число

(4.2.16)

б(^т = 6/т.

Аналогично ставке дисконтирования d, определенной через (4.2.12) на промежутке [0,1], вводится ставка дисконтирования на [0,1/т].

Определение 4.12. Эффективной ставкой дисконтирования на промежутке [0,1/т] называется число

• (ш)

ч

d(^m) =

(4.2.17)

В страховой математике для удобств записи формул используют не только эффективные, т.е. реальные, но и номинальные ставки.

Определение 4.13. Номинальной процентной ставкой называется число

Определение 4.14. Номинальной ставкой дисконтирования называется число

d^{m) = mdi^m\ (4.2.19)

Замечание 4.1. Поясним, откуда появляются номинальные процентные ставки. При периоде конверсии 1/m эффективная процентная ставка равна = (1 + i)m — 1. Так как по формуле Тейлора

(1 + i)^m = 1 +--i +--2— i²(1 + ?і)^m—2, 0 < ? < 1,

m m²

TO

i^(m) = mi^(m'⁾ = i — ^m—¹ i²(1 + ?і)^{m 2}

m

i.

Отсюда видно, что при малых i E (0,1) величина i^m приблизительно равна i. Это удобно для людей, имеющих дело с практическим счетом.

Замечание 4.2. Все выведенные выше определения основываются на банковском счете (4.2.1) и определяются процентной ставкой i, т.е. их все можно выразить через i. Точно так же, взяв в качестве определенной величины любую из выведенных, мы можем через нее выразить все остальные.

В заключение приведем сводку основных формул.

6 = ln(1 + i); i = e^s — 1; i =

(4.2.20)

1 - d’

(4.2.21)

(4.2.22)

(4.2.23)

(4.2.24)

(4.2.25)

i X

-; d =1— v; d =1 — e^—;

1 + i

i =(1 + іД) — 1;

i(^m = (1+ i) m — 1;

Am)

i*

d^ⁿ⁾ =

d(^m = 1 — (1 — d)^m;

"* 1 + 4^m) ’

d^(m) = m (1 — (1 — d)A) ; i^(m) = ({1 + i)m — Ц m.

4.3 Постоянные ренты

Всюду ниже предполагается, что имеется банковский счет C(t) = (1 + іД, относительно которого происходят расчеты.

Рассмотрим серию платежей a₁,a₂,... , a_k7 производимых в t_l7t₂,... ,t_n.

Определение 4.15. Приведенной к моменту времени t = 0 стоимость а конечной серии платежей a_l7a₂,... ,a_n в моменты врсмени t_1}t₂,... ,t_n называется число a = ^П=і a_kv^tk. Для бесконечной серии a_l7a₂,... во времена ti,t₂,... приведенная t = 0 стоимос ть a определяется формулой a = Y +=° a_kv^tk при условии сходимости ряда.

Определение 4.16. Приведенной к моменту времени t > t_k стоимость s серии платежей a₁,a₂, ...,a_n, в момсн ты t₁ ,t₂,...,t_n называется число s = Yⁿk=₁ ak (1 + i)^t-tk.

Определение 4.17. Серии платежей, производимые через равные промежутки времени и отличающиеся какой-либо однородностью, называются рентами.

Определение 4.18. Серия платежей величиной 1, производимых в моменты времени 0,1, 2, ...,n-1, называется упреждающей рентой. Приведенная стоимость упреждающей ренты обозначается как Йц и определяется формулой an = k-0 v = 1 + v +... + v^n-1.

Определение 4.19. Серия платежей величиной 1, производимых в моменты времени 1, 2,...,n, называется запаздывающей рентой. Приведенная стоимость запаздывающей ренты обозначается как an и определяется формулой a-ц = v + v² + ... + vⁿ.

Величину Йц удобно рассматривать как внесенную в пенсионный фонд в момент t = 0 для того, чтобы в течение n лет получать выплаты в размере 1 в начале каждого года. Величину aц удобно рассматривать как внесенную в банк в момент t = 0 для того, чтобы в течение n лет получать выплаты в размере 1 в конце каждого года.

Нетрудно подсчитать, рассматривая Йц и aц как геометрические прогрессии, что

..__1 - vⁿ /1 - vⁿ\ _ = v(1 - vⁿ) /1 - v<sup>n

(l</sup> '^{k 1} 1 - v \ d ) ’ ^a '^{k 1} 1 - v \ i

Определение 4.20. Серия платежей величиной 1, сделанных в моменты m, ...,m+n — 1, называется отсроченной упреждающей рентой. Приведенная к t = 0 стоимость _т\дц отсроченной упреждающей ренты определяется как _т\дц = v^m + ... + _?^т+^п—1_

Определение 4.21. Серия платежей величиной 1, сделанных в моменты m + 1, ...,m + n, называется отсроченной запаздывающей рентой. Приведенная к t = 0 стоимость _т\ац отсроченной запаздывающей ренты определяется как _т\ац = v^m+1 + ... + v^m+n.

Нетрудно показать, что

m \ ^аП\ = ^{? а}П\; m \ ^аЦ\ = ^{v а}ц] m \ ^аЦ\ = ⁽¹n+m \ ^{— а}П\ ^; m \ ^аЦ\ = ^ап+_т \ ^{— а}П\.

Интересно знать стоимость упреждающей и запаздывающей рент в момент времени t = n. Для этого надо их приведенные к t = 0 стоимости привести к моменту времени n по формуле наращения (4.2.9). Эти наращенные стоимости обозначаются так же, как приведенные, с заменой а на s. Соответствующие формулы имеют вид:

а_л = а_ц(1 + i)ⁿ, s^ = а_ц(1 + i)ⁿ.

Для отсроченных упреждающих и запаздывающих рент их наращенные к моменту m + n стоимости _т\ an и _т\ s-ц определяются как

т\ ^аЦ = ⁽¹ + ^i)n+mm\ ^аЦ^; т\ ^sn\ = ⁽¹ + 1^)П+тт\^аЦ. (4.3.2)

4.4 Постоянные ренты, выплачиваемые с частотой m

Определение 4.22. Серия из nm выплат величины m произведенных в моменты времени 0, —, —,......, ^пт—1 называется упреждающей рен

той, выплачиваемой с частотой m на промежутке [0,n]. Приведенная к t = 0 ее стоимость обозначается аЦС^, а наращенная к моменту времени

t = n стоимость обозначается .

п \

Определение 4.23. Серия из nm выплат велич ины m произведенных в моменты времени —, —,..., ^пт—1, n, называется запаздывающей рентой, выплачиваемой с частотой m на промежутке [0,и]. Приведенная Kt = 0 ее стоимость обозначается ац \ а наращенная к моменту времени t = n

стоимость обозначается s

П \

Подсчитаем величину (Ц \ Для этого рассмотрим упреждающую ренту, выплачиваемую с частотой ш, как обычную серию платежей на промежутке [0, ши] с промежутком конверсии [0,1/ш]. По определению, а^m =

^п\

1 1 1 1 _2 1 nm—1

—--1--—у m +--—у m + +--— у m

т m m m

Тогда = m (1 + уi + ... + у-^т—1)

1 /_л i nm-1 ч ^ i

= — (1 + У m + ... + У m ). ПуСТЬ У₁ = У m.

_ 1-v^nm

г(1-?і) ‘

Выражение в первых скобках - это обычная упреждающая рента на

промежутке [0,nm] с коэффициентом дисконтарования у₁. Соответству-

і 1_— ¹ і

ющая у₁ эффективная процентная ставка = ^1—1 = ^{1—v m} = —^{(1+г) m} =

Vi

X

(1+i)^m

(1+ i) m — 1. Для того чтобы в приведенной стоп мости ренты а—\ указать, что она приведена по процентной ставке i, пишут ац\_т. С учетом этого обо

• • (m)

значения 1 + у₁ + ... + у—^{п 1} = О—r@.(m). Для а—⁴ с учетом двух последних

і\@

п\

формул получаем, что аЦГ⁾ = —аn—_m(m). Если использовать номинальную процентную ставку i^(m) (4.2.18), то = — а-п^

_п\ m '^cnm\@i^(m)/m'

) 1 (m) _

\ m^а—т\@ii^{m) 7 а}п\ m^а nm\@i^(m)/m'

Аналогично показывается, что а^(—'⁾ = — а—_г@.(m), а^(—) = — а_пт@_і

5 Долгосрочное страхование

5.1 Основные определение.

Долгосрочное страхование является частным случаем общего типа страхования, приведенного в определении 3.1. Специфика долгосрочного страхования проявляется в следующем:

1) вероятностное пространство (случай) Q строится как множество моментов времени к = 1,2,... наступления страхового случая с заданной вероятностью Pk. Таким образом, можно считать, что Q = {0,1, 2,...} с вероятностями Pk, Pk > 0, ЕГ=о Pk = 1.

2) если страховой случай происходит в момент к, то страховая выплата размером bk выплачивается в момент времени т(к).

Поскольку выплаты производятся в разные моменты времени, для подсчёта премии их дисконтируют с коэффициентом у к нулевому моменту времени.

Определение 5.1. Договором долгосрочного страхования называется вектор вида (т(t),b_t, &,у,р), где:

1) Q - вероятностное пространство, описывающее страховой случай;

2) b_t - скалярная функция от t Е Q, определяющая величину страховой выплаты;

3) т (t) - скалярная функц ия от t Е Q, определяющая время выплаты страховой величины b_t;

4) v - коэффициент дисконтирования;

5) p - число, являющееся премией.

Определение 5.2. Случайная величина

Z(t) - btv^St(t),t Е Q (5.1.1)

называется приведённой стоимостью выплаты по договору долгосрочного страхования.

Таким образом, договором долгосрочного страхования можно рассматривать как вектор (Q, Z,p), т.е. договор долгосрочного страхования является частным случаем договора общего типа, приведенного в определении 3.1.

Определение 5.3. Нетто-премией A договора долгосрочного страхования называется число

Ж

A = EZ = ^ Z (k)Pk. (5.1.2)

k=0

Одними из основных задач в долгосрочном страховании является определение размера страховых премий и расчет вероятности неразорения компании.

В качестве примера долгосрочного страхования рассмотрим страхование жизни.

5.2 Долгосрочное страхование жизни

В долгосрочном страховании жизни объектом страхования является клиент возраста х. Для него вероятностное пространство Q = {0,1, 2,...} состоит из моментов n смерти клиента, при этом должна быть известна вероятность P_n смерти клиента в момент времени п. Эта вероятность определяется формулой

Здесь величины _np_x и q_x+_n определяются с помощью случайной величины K(х) - округленного время жизни клиента возраста x (это мы покажем ниже в б ниже).

Ясно, что ЕГ=о P_n = 1- В этом случае

Zk = bk v^{T k} (5.2.4)

Из формул (5.1.1), (5.1.2) и (5.2.3) следует, что согласно (5.2.4) разовая нетто-премия А имеет вид

Ж

A = EZ = ^ bkv^T(k)kPxqx+k. (5.2.5)

k=0

При конкретизации вида договора страхования жизни обозначение A нетто-премии снабжается индексами.

1. Если возраст клиента х, пишут A_x.

2. Если срок действия договора [0,п], пишут А_х.ц.

3. Если договор отсрочен на m лет, пишут _т\А.

Аналогично поступают с Z.

Рассмотрим некоторые типы договоров долгосрочного страхования жизни и найдем нетто-премии для этих договоров. Однако для этого нам придется дать процедуру определения вероятностей P_n. Это делается с помощью случайной величины K(х) - округленного остаточного времени жизни клиента возраста х.

6 Продолжительность жизни как случайная величина

6.1 Общие положения

Пусть Q = {uk : k = 1,...,N} - множество индивидуумов Uk- Очевидно, каждый из них проживёт X(uk) лет (это число может быть и не целым). Таким образом, определяется функция X(и) на множестве Q. Её естественно назвать функцией продолжительности жизни. Если мы наблюдаем группу Q в некоторый момент времени ?, то значения X(и) при фиксированном и наблюдателю неизвестны, и в этом смысле X(и) не определена (случайна), хотя это и есть самая обычная функция.

Иногда для этой функции известны не её конкретные значения X(и) при фиксированном и, а например часть F(t) группы (сама группа принимается за единицу) A_t = {и : X(и) < t}. Свойство и Е A_t означает, что и проживёт не более t лет.

В практической жизни для случайной величины X(и) предполагаются известными её значения Xk = X(ик) и вероятности pk-, с которыми эти значения принимаются. Таким образом, продолжительность жизни трактуется как дискретная (обычно счетнозначная) случайная величина, заданная распределением

х1	Х2		хп
pi	Р2		Pn

Здесь числа Xk означают количество прожитых лет, a pk - вероятность индивидуума прожить Xk лет.

Значения этой таблици берут из наблюдений за некоторой группой (обычно 100000, или 1 млн., или 10000), обозначая через l_x количество людей, доживших до возраста х. При этом через и обозначается предельный возраст, так что І_ш+і = 0. Число х > 0 берётся целым. Через d_x = l_x—_x+₁ обозначается число умерших в возрасте х. Число q_x = d_x/l_x означает долю числа умерших в возрасте х относительно числа доживших до возроста х. Эти данные записываются в таблицу

мужчины	женщины
х	lx	dx	qx	lx	dx	qx
0	100000	2047	0,02047	100000	1512	0,01512
1	97953	200	0,002042	98488	161	0,001635
2	97753	ИЗ	0,001156	98327	98	0,000997
3	97640

Наряду с этими числами вводятся величины:

p_x = 1 — q_x = l_x+₁/l_x - вероятность дожить до х +1 для человека возраста х;

_np_x = l_x+n/l_x = p_x • p_x+i, ¦ ¦¦,p_x+_n—1 - вероятность дож ить до х + n лет для человека возраста х (или, что то же, вероятность для человека возраста х прожить еще n лет);

_nq_x = 1 —_np_x = (l_x — l_x+_n)/l_x - вероятность умереть в течении следующих n лет для человека возраста х.

Понятно, что такая таблица полностью заполняется лишь тогда, когда вся наблюдаемая группа уже прожила своё время. Поэтому в реальной жизни для расчётов продолжительности используют таблици для уже проживших групп, которые по некоторым соображениям остаются совпадающими с наблюдаемой группой.

Важной характеристикой группы является средняя продолжительность оставшейся жизни.

Обозначим через T_x число

^{— d}x+1 + ^2dx+2 + ••• — ^lx=1 ^{— l}x + 2(0+2 ^{— l}x+l)--- ^{— l}x+1 + ••• + ¹ш — ? ^lx+k •

k=1

ЧиcлoT_x обозначает количество лет, которое проживут все члены группы, дожившие до возраста х.

Определение 6.1. Число

ex — Tx/lx (6.1.1)

называется средней продолжительностью оставшейся жизни для проживших х лет.

При вышеуказанном подходе к описанию продолжительности жизни считается, что смерти происходят в начале года. Иногда возникает необходимость учитывать то обстоятельство, что это событие может происходить и в любой момент года. Для этого делаются различные предположения. Например, вводятся величины:

dx⁽u) — udx ¦,

u^qx - ^uqx ⁵

0 < u < L

Тогда вероятность для человека возраста х дожить до возроста х + и определяется как:

^lx+u ^/lx <sup>1

l</sup>x+l ^lx

и + UPx•

uPx

Здесь полагается l_x+_u — l_x

6.2 Остаточное округленное время жизни.

Важное значение имеет случайная величина K(х) - остаточное округленное время жизни (усеченное время жизни).

Определение 6.2. Остаточным округленным временем жизни (усеченным временем жизни) называется случайная величина K(x), принимающая значения 0,1, 2,..., с вероятностями P_n = P(K(x) = n) =

^Pn n PxQx+n-

Число P_n =_n p_xq_x+_n означает вероятность для клиента возраста x умереть в момент времени n после заключения договора или, что то же, вероятность для клиента, дожившего до возраста x, умереть в возрасте x + n. В дальнейшем нам понадобится формула

k^px+m —m+k ^px^/m^pxi ^k,m > ⁰ (6.2.2)

для определения вероятности для клиента возраста x + m умереть через k лет (в возрасте x + m + k). Она выводится с помощью формулы _mp_x =

^lx+m ^/lx ¦

7 Разовые нетто-премии для договоров долгосрочного страхования жизни

7.1 Полное страхование жизни (пожизненное страхование)

Страховая выплата размером 1 выплачивается в конце года смерти. При этом момент смерти относится на начало года, в котором произошла смерть (т. е. K(x) = 0 означает, что клиент умер в течение года от начала заключения договора). Таким образом,

т(k) = k + 1,bk = 1,k = 0,1,... (7.1.3) Zx = vK (x)+1. (7.1.4) Нетто-премия имеет вид Ax = ^2 vk+1kpxQx+k. (7.1.5)

k=0

7.2 n- летнее накопительное страхование (чистое дожитие)

Страховая выплата размером 1 выплачивается в момент n, если клиент дожил до n, и не выплачивается ничего в противном случае. Здесь

1, k > n, 0, k < n.

0, k > n, vⁿ, k < n.

Z -1

x:n\

(7.2.7)

(7.2.8)

ж ж

A_xn vⁿkPxqx+kvⁿY, kPxQx+k = Vⁿ nPx.

k=n k=n

7.3 n-летнее временное страхование.

Страховая премия размером 1 выплачивается в конце года смерти, если она произошла до момента n и не выплачивается ничего в противном случае.

^т(к> =ⁿ + 1. ь_к = {0; ^{0 f} ><^n; (Т.3.9)

V К {^x) + l , K (x> < n;

О, K(x> > n.

Z¹ =

Нетто-премия A¹ -г имеет вид

x: n

(7.3.10)

n-1

Y,v^k+1k Pxqx+k.

k=0

i _ x:n \

(7.3.11)

4) n-летнее смешанное страхование. Если смерть наступит до момента n, выплата размером 1 выплачивается в конце года смерти. Если клиент дожил до n лет, выплата размером 1 выплачивается в момент n. Здесь

т (k> = min(k + 1,n>,b_k = 1, (7.3.12)

vⁿ ; K (x> > n ; v^-; K (X> < n.

Z¹-

x:n \

(7.3.13)

Z

x:n \

+ z ^

x:n \

Нетто-премия имеет вид

1 x:n \ ‘

A¹-

x: n \

(7.3.14)

x:n \

7.4 Отсроченное на m лет пожизненное страхование

Страховая выплата размером 1 выплачивается в конце года смерти, если она произошла до момента m от начала заключения договора и не выплачивается в противном случае. Здесь

п \ 7 1 / і 0, 0 < к

^Т (^к) = ^к + 1, ь_к Но, к>

vK(x')+l, K(x) > 0, K(x) <

< m, m. (7.4.15) n n. (7.4.16) (7.4.17) (7.4.18)

—Z^x =

т\

Нетрудно проверить, что

Л

x—\ *

_ryx _ гу Г71

Z - Zx Z \.

— \ ^X '

Поэтому нетто - премия имеет вид

_A^x _— A _ A¹_

—\ ^x x:m\

7.5 Кратные декременты

Рассмотрим еще один пример расчета разовой нетто-премии для следующего договора страхования. Предположим, что в момент времени к смерть клиента наступила по одной из m взаимоисключающих причин. Обозначим эти причины J и назовем причинами декремента (прекращения), т.е. J — {j — 1,... ,m}. В нашем случае вероятностное пространство страхового случая имеет вид Q — {j — 1,..., m}x — {к — 1,... , то}. Событием является пара (j,к) Е означающая смерть клиента в момент к по причине j. Пусть вероятность этого события (декремента) есть qj,k- Допустим, что при каждом фиксированном к для каждого j Е J известна вероятность qj,_x+k — 1 его наступления, так что Z—₌₁ qj,_x+k — 1. Таким образ ом, J при каждом к становится вероятностным пространством Jk. Если считать события смерть клиента и ее причину независимыми, то вероятность события ⁽j^{, к) Е} ^ естественно определить как kPx qj,_x+k-Пусть договор страхования заключается в выплате величины Cj,k₇ если смерть клиента произошла в момент к по причине j. Дисконтированная к 0 величина выплаты определяется выражением Cj,kv^K. Чтобы посчитать разовую нетто-премию A по такому договору, нужно стоимость страховой суммы Cjkv^k умножить на вероятность наступления события (j, к) и просуммировать по всем j и к:

m

^л = ЕЕ Cj,kv^k kPxQj,x+k. (7.5.19)

j=1 k=0

7.6 Расс чет вероятности разорения

Пусть компания имеет N договоров страхования. Пусть pk~ моменты

выплаты, величина выплаты и премия по к-му договору. Обозначим через U₀ капитал компании. Если U₀ = Z, Z = ^ ^N=₁ Zk , где

Zk = bk v^tk (7.6.1)

приведенная к t = 0 стоимость bk. Здесь использован принцип эквивалентности обязательств клиента и компании, согласно которому величина премии равна величине выплаты, а капитал компании складывается из собранных премий. Ясно, что если

N

Z = J2 Zk < Uo, (7.6.2)

k=l

то компания не разорится. Вероятность R разорения компании определяется числом

N

R = P(w Zk > Uo), (7.6.3)

k=1

а вероятность Q неразорения - соответственно числом

N

Q = P(w Zk < Uo), (7.6.4)

k=1

так же, как в случае краткосрочного страхования.

Нетто-премия pk для к-го договора определяется как

№ = E (Zk), (7.6.5)

исходя из эквивалентности обязательств клиента и компании. Страховую надбавку pk^S в простейшем случае определяют как

N / N \

Z°(Zk)/ Ее (Zk Л ,

k=1 \k=1 /

(7.6.6)

pk> = E(Zk) xr

т „ (n) . (s)

а премия pk определяется формулои pk = Pk + Pk ¦

- 30 -

7.7 Дисперсия приведенной стоимости

При расчетах вероятности разорения нужно подсчитывать величину дисперсии приведенной стоимости выплаты Z. Для этого используется величина EZ². Оказывается, нахождение величины EZ² можно заменить нахождением EZ, но по другой процентной ставке, что, в принципе, проще. Поясним суть дела.

Пусть имеется дискретная случайная величина K, принимающая целочисленные значения в R+. Пусть имеется случайная величина - выплата Ьк и случайная величина момент выплаты т(K), где, Ь^ и т(t) - некоторые функции. Тогда случайная величина

Z = Ьк ?^{т (к)} = Ьк в^{-6т (к)} (7.7.1)

является приведенной к моменту t = 0 стоимостью выплаты Ьк- Ее среднее значение

Am = E (Z@s) = E (Ьк е^{—т (к)}). (7.7.2)

Здесь мы знаком @ отметили зависимость A и Z от величины S (интенсивности процентной ставки). Для дисперсии случайной величины Z имеет место формула

D(Z_m) = E(Z@_s) - (E(Z@s))². (7.7.3)

Предположим, что Ь всегда принимает значения 0 или 1. Тогда Ь = Ь, j = 1, 2,..., и поэтому

Z@6^j = j v ^{-lSr (к)} = h_k e^{-i>T (к)} = Z@jS. (7.7.4)

С учетом (7.7.4), перепишем формулу (7.7.3) в виде

DZ@s = EZ@2§ — (EZ@s )² = A@2s — A@₅. (7.7.5)

При расчетах часто величина S является фиксированной, и ее опускают, полагая A@j$ = ^j A. С учетом этого (7.7.5) переписывается в виде удобной формулы

DZ = ² A — A². (7.7.6)

8 Пожизненные ренты (аннуитеты)

8.1 Общие положения

Выше рассматривались потоки платежей фиксированной длины, например ренты, ограниченные сроком и. В то же время широко распространены се-

рии платежей, длительность которых ограничена некоторой случайной величиной K. Если эта случайная величина связана с продолжительностью жизни, то ренты, ограниченные сроком K, будем называть пожизненными. В качестве K возьмем K(x) - дискретную случайную величину - округленное остаточное время жизни. Напомним, что распределение случайной величины K(x) определяется формулой

P (K (x) = к ) = kPx Ях+к, к = 0,1...,. (8.1.1)

Рассмотрим различные виды пожизненных рент. Как обычно, предположим наличие сложного банковского процента с коэффициентом дисконтирования v.

8.2 Прямой пожизненый аннуитет

Определение 8.1. Прямым пожизненным аннуитетом называется серия выплат размером 1, производимых в моменты t = 0,1,..., K(x).

Приведенная к t = 0 стоимость Y аннуитета есть

Yx = ¹ + ... + ^vK = ^aK+i\. (8.2.1)

Приведенная стоимость а_х аннуитета в этом случае определяется как

+то

^ах — ^EYx — ^Ea~K\xy+\\ — ^ ^ ^ак+1\ к^рх Ях+к. (8.2.2)

к=0

Ту же величину а_х можно выразить по-другому, записав (8.2.1) в виде

Y_x = J2 v^к I

(8.2.3)

{K (х)>к}.

к=0

Здесь

1, K(x) > к, 0, K(x) < к

I.

{K (х) >к}

индикаторная функция события K(x) > к. Так как

(8.2.4)

^EI{K(х)>к} ^PX^(K(x) > ^k) к^рх^,

то

^ах ЕУ^х ^ ^ ^{v EI}{k(х)>к} ^ ^ ^v к^рх'>

к=0 к=0

+ж

или, окончательно,

(8.2.5)

'dx = v^{к кРх}'

к=0

8.3 Отсроченная на m лет пожизненная рента

Определение 8.2. Отсроченной на m лет пожизненной рентой называется серия выплат по 1, производимых в мо менты t = m,m + 1,..., K(x) для K(x) > m.

Пусть _m\Y_x - приведенная к t = 0 стоимость такой ренты. Ясно, что если K(x) < m, то _m\Y_x = 0. Если же K(x) > m, то _m\Y_x = v^m + ... + v^K(x) = (v^m — v^{K (x}'⁾⁺¹')/d Отсюда следует, что

0, K(x) < m, (v^m — v^K(x'⁾⁺¹')/d, K(x) > n.

Yx

(8.3.1)

m\

Нетрудно видеть, что

\Y_x = Y_x _ Y —г.

\ ^{x x} x:m\

Поэтому для среднего значения _m\d_x величины _m\Y_x имеет место формула

m\^dx = ^{dx d}x:m\.

Выражая здесь соответствующие значения через нетто-премии, получаем, что

m\^dx = ^(Ax—\ _ ^Ax)/d.

Кроме того, можно выписать _m\d_x через распределение K(x). Действительно, из определения _m\d_x вытекает, что

Ж

m\^dx 'У ^ ^{v d}k_m+1\^Px^(K(x) = ^k).

k=m

Так как в силу (6.2.2)

Px(K(x) = k) = mPxPx+m(K(x + m) = k _ m),

TO

Ж

m\dx = mPxv^m^2 d_k-_m+i\Px+m(K(x + m) = k _ m) = k=m

го

^ь) — ^v m^px^dx+m.

(8.3.2)

= V^m _mp_x^2 aj+T\ Px+m(K (x + m)

i=0

Итак, мы установили формулу

m\^dx ^v m^px^ax+m-

8.4 Связь пожизненных аннуитетов с долгосрочным страхованием

8.4.1 Договор пожизненного страхования

Прямую пожизненную ренту можно рассматривать как договор долгосрочного страхования жизни, по которому компания выплачивает клиенту по 1 каждый год жизни клиента. Выплаты осуществляются в моменты времени t — 0,1,..., K. Сравним эту ренту с пожизненным договором страхования. Для договора пожизненного страхования приведенная стоимость выплаты

Zx — v^{K (x)+1} (8.4.1)

Так как (см.(4.3.1))

^dKxTT\ ^{— (1 - vK{:с)+1)/}^ (8.4.2)

то приведенная стоимость Y_x прямого пожизненного аннуитета есть

(8.4.3)

Yx — (1 - Zx)/d.

Отсюда следует, что рассчет характеристик пожизненного аннуитета сводится к рассчету пожизненного договора страхования. Например,

dx — EYx — (1 - EZx)/d — (1 - Ax)/d,

или

dx — (1 - Ax)/d, (8.4.4)

DY_x — DZx/d — (²Ax - A²x)/d. (8.4.5)

Здесь A_x — EZ_x.

8.4.2 n-летнее смешанное страхование

Для n-летнего смешанного страхования приведения стоимость выплаты

vⁿ, K(x) > П, v^K(xd⁺¹, K(x) < n.

(8.4.6)

^Z x:n\

В силу (4.2.9) приведенная стоимость прямого пожизненного аннуитета, ограниченного сроком n, есть

(1 — vⁿ)/d, K(x) > n, (1 — v^K(x'^)+v)/d, K(x) < n.

Y ш

x:n\

(8.4.7)

Следовательно, из (8.4.6) и (8.4.7) вытекает, что

(8.4.8)

(8.4.9) (8.4.10)

^Yx.n\ = Г ^{— Z}xn)l^d-

Поэтому

«x- =^{(1 —} ДДМ DY = DZ—ld² = (²A — A² -г)/d.

x:n\ x.ny v x:n\ x:ny'

8.5 Периодические премии

Выше отмечалось, что разовая нетто-премия A_xj эквивалентная обязательству компании, вносится клиентом в момент t = 0. Этот взнос A_x может быть заменен серией взносов величиной P(A_x) в моменты t = 0,1,.. .₇ приведенная стоимость которых к t = 0 равнa A_x. В случае, когда величина страховой выплаты равна 1, применим обозначение P_x = P (A_x).

Определение 8.3. Серия платежей величиной P_x, произведенных в моменты t = 0,1,... в срок действия договора, приведенная стоимость которых равна A_x, называется периодической нетто-премией.

Для договора пожизненного страхования 7.1 выплаты P_x = P(A_x) производятся в моменты времени t = 0,1,..., K(x). Приведенная средняя стоимость серии платежей

^Ax = ^Px Е⁽¹ + ^v + ... + ^vK(x)) == ^Px E⁽a_K(_x)+i\) = (8.5.1)

Ж

^Px ^ak+1\^{P (K (x) k) a}x^Px.

k=0

Из принципа эквивалентности следует, что

^^~x — aa x Px ¦ (8.5.2) Отсюда имеем Px = Ax/CLx- (8.5.3) 8.6 Расчет защитной надбавки для периодических нетто-премий

Пусть имеется N договоров индивидуального страхования. Обозначим через Lk индивидуальный убыток на k-ом договоре, определенный как разность между приведенной величиной Уь_{к) страховой выплаты bk и приве-

денной величиной ?С{к) потока премии, т.е. Lk = ?Ъ{к) — ?с(к) ¦ (8.6.1) Пусть S — Li + * * * + Ln¦ (8.6.2)

Мы хотим, чтобы вероятность неразорения компании была Q Е (0,1)

т.е. P(S < 0) — Q. Перепишем (8.6.3) в виде (8.6.3) P (S — E(S) ^ E(S) \ R R 1 Q 4 vm <—vm)R—1—Q (8.6.4) Считая Li независимыми, гак и ранее находим —E(S)/у/D(S) — что то же, Xr,j или, — (E (Li) + ¦ ¦ ¦ + E (ln ))/(D(Li) + ¦ ¦ ¦ + d(ln ))1/2 — xR* Здесь xr - квантиль числа R. Эта формула позволяет рассчитать защитную надбавку. (8.6.5)

Рассмотрим произвольный дискретный договор пожизненного страхования (7.1). В этом случае

L — v^{K (x)+1} — pa_x. (8.6.6)

Здесь премия pk = p^ + pk • ® простейшем случае защитная надбавка p^(s) полагается пропорционально нет то-премии p⁽ⁿ\ то ес ть p^(s = ?р^(п\ ? > 0. Таким образом, полная (нагруженная) премия

p = (1 + ?)р^(п). (8.6.7)

Формула (8.6.5) позволяет определить величину ?, поскольку при подстановке (8.6.7), (8.6.6), в (8.6.5), получается уравнение (для разных видов страхования разное) относительно неизвестной ?.

Полное страхование жизни. В этом случае для одного договора приведенная к t = 0 стоимость выплаты ?в = v^K(x)+1, приведенная стоимость потока нагруженных премий p ?с = p(1 — v^K(x'⁾⁺¹)d~¹. Следовательно, величина убытка на договоре

L = v^{K (x)+1} — p(1 — v^{K (x)+1})d^—1 = v^{K (x)+1}(1 + pd^—1) — pd^—1 =

= Z_x(1 + pd^-1) — pd^-1. (8.6.8)

В силу соотношения a_x = (1 — A_x)d^—1 имеем

E (L) = (1 + pd^—1)E (Zx) — pd^—1 = E (Zx) + (E (Zx) — 1)pd^—1 =

= Ax + (Ax — 1)pd^—1 = Ax — pax.

Отсюда получаем, что

E (L) = Ax — pax, (8.6.9)

D(L) = (²Ax — Al)(1+ pd^—1)². (8.6.10)

Так как в нашем случае p⁽ⁿ = P_xj а в силу (8.6.7), p = (1 + ?)Р_а;} то из (8.6.9) и (8.6.5) следует, что

EL = Ax — (1 + Q)Pxdx — ?Ax. (8.6.11)

Подсчитаем DL. Для этого заметим, что

1 + pd^—1 = 1 + (1 + ?) P_xd^—1 =

= ¹ + ⁽¹ + ^?)Лг^{(1 — A}x)^{(1 — A}x^{) 1} = ⁽¹ + ^?Дг^{)(1 — A}x⁾ (8.6.12)

Обозначим через L⁽⁰⁾ потери для не нагруженной премии, то есть для случая p = P_x. Тогда из (8.6.5) следует, что

(8.6.13)

DL^itt> = (²A_x — Ax)(1 — Ax)².

- 37 -

Из формул (8.6.10), (8.6.11) и (8.6.12) вытекает, что

DL = (1 + ?А_Х)² DL⁰\ (8.6.14)

Воспользуемся формулами (8.6.5), (8.6.11) (8.6.14) для определения ?. Пусть x(k) - возраст k-ro клиента. Обозначим



Л = ? DL|⁰⁾, і = ? Ax(i)DLf\





V = Е Ax^DL^, в = Е Ax(i) (8.6.15)



Подставляя (8.6.11) (8.6.14) (с соответствующими индексами) в (8.6.5) и пользуясь (8.6.15), имеем

?в (Л + 2р? + v?²) ^1/2 = x_R. (8.6.16)

Отсюда легко находим

? = (ц + (р² — Л? + Лв²(в^2xr² — v) ¹ • (8.6.17)

9 Резервы периодических премий

9.1 Общие положения

Рассмотрим индивидуальный договор страхования. Для индивидуального договора страхования на момент времени t образуется типичная ситуация: собранных за время [0, t) нетто-премий больше, чем сумма выплаченных за время [0, t) страховок, однако сумма будущих выплат при т > t больше, чем сумма ожидающихся при т > t премий. Недостающая для будущего сумма оказывается равной заработанной компанией в прошлом на разнице премий и выплат. При этом все суммы приводятся к моменту t. Эта накопленная на момент t > 0 сумма может быть рассмотрена как собственность клиента и, по его желанию, использована (конвертирована) для заключения нового договора вместо старого в качестве нетто-премии или выплачена деньгами.

Отметим здесь одно важное обстоятельство. Заработанные компанией на момент t > 0 средства в последующие моменты времени расходуются на оставшихся в живых клиентов. Поэтому при подсчетах сумм выплат и премий на индивидуальном договоре необходимо пользоваться не обычными, а актуарными коэффициентами накопления и дисконтирования.

Определение 9.1. Резервом периодической премии _tV на момент t > 0 на индивидуальном договоре страхования называется разность между актуарно приведенными к моменту t средним обязательством _ta_b компании по будущим выплатам и средним обязательством клиента _ta_c по будущим взносам, гп.е. числовая величина

t^V — t^ac t^ab• (9.1.1)

Определение 9.2. Формула для резерва (9.1.1) называется перспективной.

Эта формула называется перспективной, поскольку рассчитывается исходя из будущих обязательств.

Из принципа эквивалентности обязательств клиента и компании следует, что недостающие средства берутся из взносов клиентов. Таким образом, эти недостающие деньги должны быть получены из внесенных до t премий за вычетом произведенных до t выплат, т.е. должно выполняться соотношение

t^{V —} t^sc ^— (9.1.2)

Здесь _ts_c - актуарная накопленная к моменту t средняя сумма взносов клиента, сделанных на [0, t), _tSb - актуарная накопленная к моменту t средняя сумма выплат компании за время [0,t). Здесь вместо обычного приведения к моменту t берется актуарное накопление, так как средства будут использованы на покрытие страховок клиентов, оставшихся в живых.

Определение 9.3. Формула для резерва (9.1.2) называется ретроспективой формулой резерва периодической премии.

Формула (9.1.2) называется ретроспективой, поскольку рассчитывается, исходя из прошлых обязательств.

Для разных видов страхования _ts_c и _tSb имеют разный вид.

Всегда далее предполагается, что договор страхования заключен с клиентом возраста ж, что означает использование для подсчета _tV случайную величину K (ж). В этом случае в место _tV пишут _tV_x. Числ о t означает время, прошедшее с момента заключения договора. Величина _tV_x прямо зависит от вида страхования.

Величина резерва может быть рассчитана как по перспективной, так и по ретроспективной формулам. В качестве примера приведем расчет резерва

в случае, когда рассматривается дискретный договор полного страхования жизни клиента возраста х, при этом величина периодической премии задается как периодической нетто-премия P_x. Для расчетов нам понадобятся актуарное накопление и дисконтирование.

9.2 Актуарное накопление и дисконтирование

Пусть имеется группа людей, внесшая в банк по 1 условной единице на счет C(t) = (1 + i)^f. Пусть в момент времени t доля живых участников фонда равна p(t) так что 0 < p(t) < 1. Сколько денег приходится на каждого живого участника в момент времени t?

Пусть число участников А. Тогда накопленная ко времени t сумма S(t) = N(1 + i)^f. Число живых участников равно Np(t), и на каждого из них приходится сумма



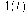
N (1 + i)^t = (1 + i)^t N p(t) p(t) '

Очевидно, A(t) > (1 + i) - накопленной суммы по ставке і.

Определение 9.4. Актуарным коэффициентом накопления для процентной ставки i и доли выживания p(t) на промежутке [0, t] называется число

(1+ i)^t p<sup>(t)

A(t)</sup>

(9.2.2)

Число A(t) означает сумму, приходящуюся на каждого живого к моменту времени t участника фонда, внесшего 1 у.е.

Определение 9.5. Актуарным коэффициентом дисконтирования d(t) на промежутке называется число

p^(t)

(1 + i)^t'

1

^A(t)



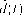
(9.2.3)

Число d(t) означает сумму, которую каждый участник фонда должен внести в момент времени t = 0, чтобы в момент врвмени t на каждого живого участника приходилась 1 единица накопленных денег. Обычно в математической теории страхования доля p(t) определяется формулой

Здесь T(х) - остаточное время жизни. В этом случае пишут A(t) — ^A(x,t),

d(t) —_t E_x. Из формул (9.2.2) - (9.2.4) вытекает, что

(1 + i)^t;

tPx

t^Ex ^v t^px

A(x, t)

(9.2.5)

При этом A(x,t) - актуарный коэффициент накопления для промежутка [0, t] для человека в возрасте х; _tE_x - актуарный коэффициент дисконтирования на промежутке [0, t] для человека в воз расте х. Нетрудно видеть, что A(x, t) больше обычного накопления (1 + i^ на [0,t], a _tE_x - меньше соответствующего коэффициента дисконтирования v^t на [0,t].

9.3 Расчет резерва по перспективной формуле (договор полного страхования жизни)

Пусть t > 0 целое число, означающее время после заключения договора.

Для подсчета _tV_x необходимо подсчитать _ta_c и _tab. Вычислим _ta_c и _tab. Нетрудно видеть, что приведенная к моменту 0 сумма выплачиваемых после t нетто-премий равна R\ — _t\a_xP_x. Следовательно, эта же сумма, приведенная к моменту t, равна R₂ — P_xt\d_xv^-t. Аналогичным образом приведенная к t величина выплат после t равна _t\A_xv^-t. Напомним, что A_x - это разовая нетто-премия по конкретному договору страхования для клиента возраста х, _t\A_x та же премия для отсрочеиного на t лет договора. Поскольку к моменту t от единицы клиента "остается"_tp_x-n часть, то на единицу клиента в момент t приходится соответственно, собранных премий

t^ac t\^ax^v I t^px (9.3.1)

и страховых выплат

t^ab — t\^Ax^{v 1} t^px• (9.3.2)

Так как

t\^ax — ^v dx+t t^pxi t\^Ax — ^v ^^x+t t^px^,

TO

t^Vx ^Ax+t ^Px^ax+t• (9.3.3)

Эту же формулу можно получить, если актуарно продисконтировать сумму будущих выплат и премий к моменту t с соответствующим коэффициентом _tE_x — _tp_xv^t. Мы это выше фактически сделали.

Формула (9.3.3) является реализацией перспективной формулы для договора пожизненого страхования.

Эту формулу можно получить из других соображений. Так как на момент ? возраст клиента равен х + t, то _tаь = A_x+_t.

По договору ежегодные премии равны P_x, поэтому сумма взносов клиента после момента t есть _ta_c = P_x d_x+t.

Таким образом, перспективная формула принимает вид (9.3.3).

Перспективную формулу (9.1.1) можно записать в другой форме.

Допустим, что компания заключит с тем же клиентом договор снова в момент t. Тогда возраст клиента будет x +1, обязательства компании A_x+tj ежегодная нетто премия P_x+_t = A_x+t/d_x+t. Поэтом у A_x+_t = d_x+tP_x+tj и формула (9.3.3) может быть переписана в виде

t^Vx = ^(Px+t ^{— P}x ^)dx+t¦ (9.3.4)

Эта формула называется формулой разности премий.

По-другому формула (9.3.4) может быть переписана как

tVx = (1 - Px/Px+t)Ax+t. (9.3.5)

Последняя формула удобна для конверсии в момент времени t текущего договора в договор пожизненного страхования с разовой нетто-премией величиной

t^Vx^/Ax+t = ^{1 — P}x^/Px+t¦ (9.3.6)

9.4 Расчет резерва по ретроспективной формуле (договор полного страхования жизни)

Рассмотрим договор полного страхования жизни и докажем, что (9.1.2) действительно справедливо.

Из формулы (9.3.4) видно, что _tV_x величина не отрицательная. Ясно, что P_x+_t > P_x, поскольку в возрасте x + t вероятность умереть больше, чем в возрасте х, то и страховой взнос P_x+_t должен быть больше, чем P_x. Поэтому средств, которые будут получены в будущем за счет премий, недостаточно для будущих страховых выплат. Подсчитаем сначала _ts_c. Эта величина определяется как

(9.4.1)

^Px ^s

t^sc

x:t\'

Здесь

^Sx:t| =М (9.4.2)

Актуарная приведенная к t стоимость обязательств компании есть

t^sb ^{- А}ІД ^A(x> ^t) = ^Al-I\ ^/ t^Ex. (9-4.3)

Таким образом,

tSc - tSb - Px S_xt\ - А^гх-\ / _tE_x. (9.4.4)

Выше A(x,t) и _tE_x - актуарные коэффициенты накопления и дисконтирования соответственно на промежутке [0, t]. Покажем, что левая часть (9.4.4) на деле равна _tVx. Для этого умножим (9.3.3) на _tE_x. Мы получим

t^Vxt^Ex ^Ax+tt^Ex ^px ^ax+t t^Ex. (9.4.5)

Так как

^Ax+tt^Ex t\^Axi ^ax+tt^Ex t\^axi (9.4.6)

то из (9.4.5) следует, что

t^Vxt^Ex t\^Ax ^Px t\^ax+t t^Ex. (9.4.7)

Так как очевидно A_x — P_x a_x, то из (9.4.7) следует, что

t^Vxt^Ex ^px (^ax t\^ax) ('^Ax t|^Ax) . (9.4.8)

Из соотношений

^ax t\^ax ^{- a}xд ^Ax t\^Ax ^{- A}x:f\ (9.4.9)

вытекает, что

tVxtEx - Px a_xt\- A^lx~y (9.4.10)

Отсюда в силу (9.4.4) следует, что _tV_x - _ts_c — _tSb.

Список литературы

[1] Фалин Г.И. Математические основы теории страхования жизни и пенсионных схем / Г.И.Фалин - М.: Московского ун-та, 1995. - 286 с.

[2] Гербер Х.Д. Математика страхования жизни / Х.Д.Гербер - М.: Мир, 1995. - 212 с.

[3] Гнеденко Б.В. Курс теории вероятностей / Б.В.Гнеденко - М.: Наука, 1981. - 456 с.

[4] Четыркин Е.М. Методы финансовых и коммерческих расчетов / Е.М.Четыркин - М.: Изд-во Дело ЛТД, 1995. - 386 с.

Автор: доктор физико-математических наук, профессор Орлов Владимир Петрович Редактор Тихомирова О.А.

    Биржевая торговля: Управление капиталом - Портфель - Риск - Страхование

• Теория управления капиталом
  
• Позиция как управление капиталом
  
• Правила управления капиталом
  
• Торговля и управление капиталом
  
• Управление капиталом в России
  
  
• Управление портфелем
  
  
• Управление риском
  
• Управление риском на рынках
  
• Методы управления риском
  
• Финансы и управление риском
  
  
• Страхование
  
• Риски страхования
  
• Российское страхование
  
• Страхование финансов
  
• Виды страхования