Как «сварить» VAR - ЕВГЕНИЙ ОБЖИРОВ

В предыдущих номерах [1, 2] был предложен новый метод определения величины Value-at-Risk (VAR). Границы его применимости охватывают широкий класс финансовых инструментов. Данная статья дает ключ к практическому использованию нового подхода - метода «лямбда-лапласа».

ЕВГЕНИЙ ОБЖКІРОВ, аналитик-консультант отдела программных разработок Центра информационно-финансовых технологий «И-Сток»

РИСУНОК 1 ОБЫКНОВЕННЫЕ АКЦИИ РАО «ЕЭС РОССИИ» 11.01 -30.12.2005

Как «сварить» VAR - ЕВГЕНИЙ ОБЖИРОВ


Итак, примем за основу гипотезу о том, что плотность распределения f симметричной (модифицированной) доходности любого рыночного актива X - (V. T-V.)/min(V1,V.|Т), где V - СТОИМОСТЬ актива, а Т - временной горизонт расчета VAR, имеет распределение Лапласа (симметричное показательное распределение) f(X) - 1/2 к е >|х.

Новый метод

Ранее [1, 2] было представлено несколько примеров на фондовом, валютном и товарном рынках, позволяющих сделать такое предположение.

Данное распределение зависит от единственного параметра к, поэтому метод вычисления меры рыночного риска VAR, основанный на данной гипотезе, по аналогии с. «дельта-нор-малыіым» методом логично назвать методом «лямбда-лапласа».

Важно отмстить, что по известному свойству данною распределения параметр к обратно пропорционален среднеквадратичному отклонению о распределения X, процедура вычисления которого не требует ни больших усилий, ни специальных навыков, т.к. содержится в любом, самом простом пакете программ статистической обработки информации. Из определения VAR можно легко получить формулу для его вычисления 111:

чальный момент времени. Например, для а - 95% данная формула приобретает следующий вид:

23а1 + 23а23А~VAR = -К = -К

1 + 23А~

и вычисление VAR становится «делом техники».

Однако есть одна серьезная проблема, к т.ч. присущая и «дельта-нормальному» методу" определения VAR: корректное определение статистической базы (или генеральной выборки) для расчета среднеквадратичного отклонения о. Особенно эта проблема актуальна для больших временных горизонтов расчета VAR - фактически от одного дня и более.

Например, для расчета недельного VAR для формирования приемлемой репрезентативной генеральной выборЕШ могут потребоваться исторические данные за период ДО нескольких десятков лет. При ЭТОМ харак-

r'ln(2-2a) ІГ

- V А

сг1п(2-2а)

VAR = V, (1)

1 1 -А. 1 Іп(2-2аг) ' 1-(7Іп(2-2сг)

доверительный уровень, обычно выбираемый

где а

в диапазоне 0.95-0.99, а

V,.

СТОИМОСТЬ актива в на-

40

тер динамики рынка за это время мог много раз кардинально меняться, что проявляется в известном эффекте кластеризации поведения волатильности рыночных активов. Поэтому приходится сталкиваться с неприятным выбором: или сужать генеральную выборку, как шагреневую кожу, или использовать для прогноза заведомо устаревшие исторические данные.

Любой из этих вариантов чреват серьезной потерей точности прогноза VAR.

Выход из этой ситуации лежит в фундаментальной природе изменчивости рыночных цеп статистические закономерности их движения па более продолжительных горизонтах времени (часы, дни и недели) с высокой точностью определяются статистикой малых интервалов времени (минуты).

Для подтверждения этого рассмотрим поведение распределений симметричной (модифицированной) доходности X обыкновенных акций РАО «ЕЭС России» для различных временных горизонтов Т.

На рисунке 1 представлены плотности распределения и их параметризации методом «лямбда-лапласа» для временных горизонтов 5, 15 и 60 минут. Видно, ЧТО С увеличением горизонта ПЛОТНОСТЬ распределения все более расширяется. Т.с. параметр X уменьшается, а среднеквадратичное отклонение увеличивается, при этом каждое из распределений с очень высокой степенью точности можно считать распределением Лапласа с Х(5) - 9.6; /,(15) - 6.0 и >,(60) -2.9. То есть характер распределения остается неизменным, меняется только параметр >,, который, вообще говоря, в этом случае должен быть функцией временного горизонта Т.

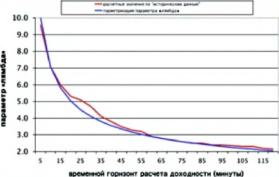
Чтобы определить эту функцию, для каждого временного горизонта Т из диапазона от 5 минут до 2 часов с шагом 5 минут был построен график плотности распределения симметричной доходности X и определен параметр X. На рисунке 2 красным цветом показан график зависимости полученных значений X от Т, а сипим - график следующей функции (X - 22.5):

4

?г

Как «сварить» VAR - ЕВГЕНИЙ ОБЖИРОВ


Таким образом, с использованием формулы (2) процедура вычисления VAR существенно упрощается. Определив параметр X. па малых горизонтах времени, статистическая база которых достаточна для корректной оценки, мы автоматически получаем возможность вычислить VAR для больших горизонтов времени из формул (1) И (2):

л/г? ln(2 — 2or)VAR = V° l-л/ГЛ,*1 In (2 - 2a) (3)

Для a - 95% и нашего примера получаем следующую приближенную функцию VAR(T) (при этом необходимо учесть, что поскольку величина X к наших вычислениях измерялась в процентах, то при подстановке в вышеуказанную формулу с уменьшением X параметр X должен быть обратно пропорционально увеличен в 100 раз):

FAR = —V, і о~3 ?у7 0 і + іо -3?г'

(2)

Анализируя формулы (1) и (3), из общих соображений можно легко оценить границу применимости метода:

I л/ГЯ,"' 1п(2 - 2cr) I « I ¦ (4)

что для выбранного нами примера с акциями РАО ЕЭС даст временной горизонт порядка двух недель. За его пределами применение метода «лямбда-лапласа» вместе с гипотезой (2) (для обыкновенных акций РАО «ЕЭС России») может оказаться некорректным. Тем пс менее, можно уверенно сказать, что как минимум на временных горизонтах в несколько дней описанный метод в данном конкретном случае будет давать достаточно точный прогноз VAR.

Таким образом, вышеизложенные факты делают очень перспективным использование метода «лямбда-лапласа» в рамках соблюдения условия (4) при расчетах VAR, поскольку это позволяет совместить простоту вычислений с высокой точностью прогноза, значительно увеличить скорость расчета и снизить операционные издержки на дорогое программное обеспечение.


    Биржевая торговля: Управление капиталом - Портфель - Риск - Страхование