Почему развивающимся странам трудно войти в "клуб" развитых? - Г.Ю. Трофимов

Статья нацелена на объяснение препятствий к экономической интеграции передовых и отсталых экономик на основе анализа качественно различных режимов экономического роста, присущих развитым и развивающимся экономикам. Под качественно различными режимами роста мы понимаем тот факт, что в одних экономиках существуют хорошо развитые сектора, являющиеся генераторами роста, тогда как в других они отсутствуют, либо неразвиты. Барьеры к интеграции рассматриваются здесь как, по существу, эндогенные, а недостаток потоков капитала из богатых в бедные страны объясняется неоднородностью механизмов, генерирующих рост в этих странах.

Мы используем и развиваем двухсекторную модель экономического роста с человеческим капиталом и промежуточным сектором производства и накопления знаний, изначально предложенную в Лукасом и Узавой. Для нас важно, что данный класс моделей допускает существование внутренних и краевых решений. Внутренним решением является равновесная траектория, на которой производству знаний индивидами уделяется положительная доля времени, и поэтому экономический рост является эндогенным. Рост вдоль траектории экзогенного роста происходит без затрат времени на производство знаний.

Мы показываем, что глобализация рынка капитала и выравнивание мировой процентной ставки ведет к очень тесной взаимосвязи стран в смысле поведения домохозяйств. Интеграция экономик посредством мирового рынка капитала требует выполнения двух условий: рост является эндогенным во всех странах и ни одна из них не накапливает экспоненциальный необеспеченный долг. Согласно первому условию, предельная продуктивность сектора знаний должна быть достаточно высокой в странах-участницах, и, согласно второму, она не должна существенно варьировать между странами. Эти условия ограничительны и выполняются, только если менее развитые экономики не участвуют в мировом рынке капитала. Важно то, что некоторые из них способны к эндогенному росту в условиях автаркии. Возможная интерпретация этих выводов заключается в том, что неоднородность стран в смысле эффективности сектора роста (в нашем случае — сектора знаний) представляет основной барьер на пути интеграции передовых и отсталых экономик.

При отсутствии международных эффектов перетока знаний экзогенно растущая национальная экономика может интегрироваться с мировым рынком капитала только очень специфическим образом, ко-

гда она превращается в экономику рантье. В таком случае все внутренние активы инвестируются за рубежом, весь производственный капитал исчезает из страны, а человеческий капитал перестает использоваться в производстве. Сравнительный анализ благосостояния показывает, что в условиях мирового рынка капитала некоторые страны могут предпочесть режим рантье, даже если они способны к эндогенному росту в автаркии. Это имеет место при низкой норме временного дисконта. В данном случае исчезает интуитивная связь между "бережливостью" и ростом, так как достаточно "терпеливые" домохозяйства предпочитают финансовое инвестирование созидательной деятельности.

Возможности для полноценной интеграции менее развитых стран с глобальной экономикой существенно расширяются благодаря международным перетокам знаний. Мы вводим в модель небольшой открытой экономики механизм перетоков, опосредованных прямыми иностранными инвестициями. Наш вывод заключается в том, что иностранные инвестиции позволяют снизить, но не устранить эндогенные барьеры к интеграции отсталых стран с передовыми. Благодаря данному механизму экономика может расти в эндогенном режиме, даже если она не имеет такой возможности в условиях автаркии. Кроме того, возможен экзогенный рост без трансформации в режим рантье.

Для каждого из режимов мы демонстрируем существование двух моделей переходного роста. Первая модель характеризуется интенсивным начальным притоком иностранного капитала в страну и относительно медленным ростом капитала при переходе к стационарному равновесию. Производственный капитал резко возрастает в начальный момент, когда экономика открывается, но в дальнейшем он растет с темпом более низким по сравнению с темпом глобального роста и внутреннего потребления. Такую модель мы называем моделью быстрого роста, поскольку открытие экономики ведет к немедленному притоку в нее капитала. Для второй модели активы в начальный момент уходят из страны, но при переходе к стационарному равновесию капитал накапливается быстрее внутреннего потребления. Мы называем этот тип переходной динамики моделью постепенного роста.

Мы показываем, что выбор модели переходного роста определяется начальным отношением знаний к активам домохозяйств: если оно высоко, экономика развивается быстро, иначе рост постепенный. Это является следствием принципа сравнительного преимущества: страна с относительным недостатком капитала привлекает потоки новых инвестиций на начальном этапе интеграции, тогда как страна с относительным избытком капитала на начальном этапе его экспортирует.

1. ВВЕДЕНИЕ

В статье обсуждается несколько закономерностей, характеризующих глобальную экономическую динамику. Во-первых, темпы роста производства сходятся для промышленно развитых стран и расходятся для всего мира. Во-вторых, большая часть международных инвестиций циркулирует между развитыми странами. При этом менее развитые страны сталкиваются с жесткими барьерами к интеграции с передовыми экономиками. В третьих, существуют различные модели интеграции, при которых одни страны могут претерпевать быстрый приток капитала и выпуска, а другие, наоборот, испытывают первоначальный отток капитала и лишь по прошествии определенного времени начинают наращивать темпы ВВП. В четвертых, рост в развивающихся и переходных экономиках неравномерен во времени.

Мы хотим показать, что эти феномены имеют общую природу и обусловлены качественно различными режимами экономического роста, присущими развитым и развивающимся экономикам. Под качественно различными режимами роста мы понимаем тот факт, что в одних экономиках существуют хорошо развитые сектора, являющиеся генераторами роста, тогда как в других они отсутствуют, либо неразвиты. Многие модели эндогенного роста предсказывают расхождение долговременных темпов для богатых и бедных экономик из-за различий в технологиях, наделенности факторами, предпочтений населения, политики государства и т.д. Большая часть подобных моделей изучает замкнутые экономики, игнорируя взаимосвязи международной торговли и роста. В то же время, в моделях торговли и роста (например, в рамках данного направления, Segerstrom et al. (1990), Young (1991) и Grossman, Helpman (1991)) анализировались различные эффекты влияния торговых барьеров на различия темпов роста богатых и бедных стран, но полученные выводы оказались неоднозначными.

Основной вопрос данной статьи является в некотором смысле обратным: могут ли различия в режимах роста быть серьезным препятствием на пути глобальной экономической интеграции посредством международного рынка капиталов? Барьеры к интеграции рассматриваются здесь как, по существу, эндогенные, а недостаток потоков капитала из богатых в бедные страны объясняется неоднородностью механизмов, генерирующих рост в этих странах. Для уп-

рощения анализа мы абстрагируемся от экзогенных барьеров на пути капитала, таких как политические риски и монопольный контроль во внешней торговле, которые подчеркивались, к примеру, в статье Lucas (1990).

Мы используем и развиваем двухсекторную модель экономического роста с человеческим капиталом и промежуточным сектором производства и накопления знаний, изначально предложенную в Lucas (1988) и Uzawa (1965). Для нас важно, что данный класс моделей допускает существование внутренних и краевых решений. Внутренним решением является равновесная траектория, на которой производству знаний индивидами уделяется положительная доля времени, и поэтому экономический рост является эндогенным. Рост вдоль траектории экзогенного роста происходит без затрат времени на производство знаний. Существование траекторий эндогенного и экзогенного роста для моделей типа Лукаса-Узавы было ранее продемонстрировано в следующих работах: Rebelo (1991), Caballe, Santos (1993), Goodfriend, Mcdermott (1995) и ladron-de-Guevara et al. (1999).

В данной работе используется вариант модели роста Лукаса-Узавы, в которой переменная свободного времени является аргументом функции полезности домохозяйств. Данный вариант был предложен в Rebelo (1991) и Jones et al. (1993), а затем развит в Benhabib, Perli (1994), Ortiguera, Santos (1997), Ladron-de-Guevara et al. (1999). Важной его особенностью является то, что уровень человеческого капитала не влияет на предельную полезность свободного времени, но при этом оказывает различное влияние на эффективность других сфер деятельности. Введя таким путем переменную свободного времени, Rebelo (1991) и Jones et al. (1993) исследовали долговременные эффекты налогообложения на рост, а Benhabib, Perli (1994) рассмотрели проблему неопределенности решений для широкой области значений параметров. Ladron-de-Guevara et al. (1999) выявили три траектории сбалансированного роста, две из которых внутренние, а одна краевая. Сравнительный анализ в последней работе сосредотачивался, главным образом, на внутренних решениях.

В отличие от Ladron-de-Guevara et al. (1999), мы делаем акцент на сравнении двух качественно различных режимов роста: эндогенного и экзогенного, соответствующих внутреннему и краевому решению. Это необходимо для выявления условий интеграции неоднородных экономик. Мы опираемся на сравнительно простой вариант модели эндогенного роста с переменной свободного времени, но пытаемся развить ее в двух направлениях. С одной стороны, предлагается анализ экзогенной траектории роста, а также развивается исследо-

вание переходных режимов для замкнутой экономики. Ниже показано, что экономика не способна к эндогенному росту, если предельная продуктивность сектора знаний невелика, а норма дисконта или эластичность свободного времени высоки. Кроме того, нетерпеливость индивидов и высокая склонность к отдыху влекут выбор в пользу режима экзогенного роста с точки зрения критерия благосостояния. Таким образом, неспособность или нежелание индивидов генерировать эндогенный рост является фактором, объясняющим отсталость некоторых стран в состоянии автаркии.

С другой стороны, модель замкнутой экономики обобщается на глобальный уровень со свободным перемещением капитала и иммобильным трудом. При этом считается, что национальные экономики могут различаться по продуктивности сектора знаний. Это обобщение аналогично модели глобальной экономики в Lucas (1993) с однородными странами, различающимися лишь по начальным значениям факторов производства. Модель нашей статьи также близка к динамическим моделям мировой экономики с международной торговлей товарами, выравнивающей цены факторов производства, например, в Stokey (1996), Ventura (1997) и Acemoglu, Ventura (2002).

Мы показываем, что глобализация рынка капитала и выравнивание мировой процентной ставки ведет к очень тесной взаимосвязи стран в смысле поведения домохозяйств. Это относится, главным образом, к выбору ими распределения затрат времени, и, по нашему мнению, объясняет некоторую стандартизацию поведения индивидов в странах, тесно связанных экономически. Предпочтение свободного времени оказывается важной предпосылкой модели, позволяющей дать реалистичное описание глобальной динамики, и в частности, переходных режимов роста. Если бы домохозяйства были безразличны к свободному времени, как в базовой модели Лукаса (Lucas, 1988), то механизм выравнивания процентных ставок приводил бы к неправдоподобной ситуации, когда весь мировой капитал и

производство в начальный момент концентрируется только в одной, наиболее развитой стране.

Интеграция экономик посредством мирового рынка капитала требует выполнения двух условий: рост является эндогенным во всех странах и ни одна из них не накапливает экспоненциальный необеспеченный долг. Согласно первому условию, предельная продуктивность сектора знаний должна быть в среднем достаточно высокой в странах-участницах, и, согласно второму, она не должна существенно варьировать между странами. Эти условия являются очень ограничивающими (при реалистичных значениях параметров модели) и выполняются, только если менее развитые экономики не участвуют в мировом рынке капитала. Важно то, что некоторые из них способны к эндогенному росту в условиях автаркии. Возможная интерпретация этих выводов заключается в том, что неоднородность стран в смысле эффективности сектора роста (в нашем случае — сектора знаний) представляет основной барьер на пути интеграции передовых и отсталых экономик. Неоднородность производственных технологий и предпочтений домохозяйств в данном случае не играет решающей роли. Мы показываем, что менее развитые экономики не могут участвовать в "клубе" развитых стран, потому что они не способны настроиться на динамику глобальной экономики посредством изменений свободного времени домохозяйств и финансовой позиции. В определенном смысле, недостаточно однородная глобальная экономика не в состоянии "выйти" на равновесную траекторию, приближающуюся к траектории сбалансированного роста.

При отсутствии международных эффектов перетока знаний (knowledge spillovers) экзогенно растущая национальная экономика может интегрироваться с мировым рынком капитала только очень специфическим образом, когда она превращается в экономику рантье. В таком случае все внутренние активы инвестируются за рубежом, весь производственный капитал исчезает из страны, а человеческий капитал перестает использоваться в производстве. По этой причине отношение активов к производственному капиталу домохозяйств стремится к бесконечности, а они сами посвящают все свое время

отдыху. При этом их душевые активы растут с темпом равным мировому темпу роста. Мы показываем, что такое стационарное состояние достигается за конечное время.

Сравнительный анализ благосостояния показывает, что в условиях мирового рынка капитала некоторые страны могут предпочесть режим рантье, даже если они способны к эндогенному росту в автаркии. Это имеет место при низкой норме временного дисконта. В данном случае исчезает интуитивная связь между "бережливостью" и ростом, так как достаточно "терпеливые" домохозяйства предпочитают финансовое инвестирование созидательной деятельности. Этот вывод модели существенным образом расходится с заключением Дж. Вентуры (Ventura, 1997, р. 76) о том, что весь секрет экономического чуда сводится к двум действиям: "открыть экономику и быть терпеливым".

Возможности для полноценной интеграции менее развитых стран с глобальной экономикой существенно расширяются благодаря международным перетокам знаний. Мы вводим в модель небольшой открытой экономики механизм перетоков, опосредованных прямыми иностранными инвестициями. Данный механизм, по сути, близок к предположениям о внешних эффектах прямых иностранных инвестиций, предложенным ранее в Findlay (1978) и Wang (1990). Эти авторы не использовали динамическую оптимизацию и опирались на модели роста с экзогенным техническим прогрессом. Они показали, что перетоки знаний, индуцируемые инвестициями в производство, устраняют разрыв в темпах развития богатых и бедных стран. Наши заключения аналогичны, но не так однозначны: иностранные инвестиции позволяют снизить, но не устранить эндогенные барьеры к интеграции отсталых стран с передовыми. Благодаря данному механизму экономика может расти в эндогенном режиме, даже если она не имеет такой возможности в условиях автаркии. Кроме того, возможен экзогенный рост без трансформации в режим рантье.

Для каждого из режимов мы демонстрируем существование двух моделей переходного роста. Первая модель характеризуется интенсивным начальным притоком иностранного капитала в страну и относительно медленным ростом капитала при переходе к стационарному равновесию. Производственный капитал резко возрастает в начальный момент, когда экономика открывается, но в дальнейшем он растет с темпом более низким по сравнению с темпом глобального роста и внутреннего потребления. Такую модель мы называем моделью быстрого роста, поскольку открытие экономики ведет к немедленному притоку в нее капитала. Для второй модели активы в

начальный момент уходят из страны, но при переходе к стационарному равновесию капитал накапливается быстрее внутреннего потребления. Мы называем этот тип переходной динамики моделью постепенного роста.

Мы показываем, что выбор модели переходного роста определяется начальным отношением знаний к активам домохозяйств: если оно высоко, экономика развивается быстро, иначе рост постепенный. Это является следствием принципа сравнительного преимущества: страна с относительным недостатком капитала привлекает потоки новых инвестиций на начальном этапе интеграции, тогда как страна с относительным избытком капитала на начальном этапе его экспортирует. Данный вывод согласуется с эмпирическими данными о том, что прямые иностранные инвестиции дают значимый положительный эффект на экономический рост в стране-реципиенте, только если величина человеческого капитала в этой стране превышает некоторый пороговый уровень, например, в Borensztein et al. (1998).

С точки зрения критерия благосостояния постепенный переход к стационарному состоянию предпочтительней, чем быстрый, если индивиды высоко ценят свободное время. Политическая рекомендация из анализа моделей переходного роста заключается в том, что не стоит возлагать слишком большие надежды на прямые иностранные инвестиции как основной источник быстрого роста в отсталой стране. Если такая страна не пытается развивать собственные сектора, генерирующие рост, она оказывается непривлекательной для иностранных инвесторов на начальных стадиях интеграции.

Статья далее включает три раздела и заключение. В Разделе 2 исследуется базовая модель замкнутой экономики, Раздел 3 обобщает ее на глобальный уровень, а в Разделе 4 анализируется механизм перетоков и модели переходного роста. Доказательства Утверждений собраны в Приложениях.

2. МОДЕЛЬ ЗАМКНУТОЙ ЭКОНОМИКИ

Рассматривается экономика с представительными агентами (домохозяйствами) наделенными двумя факторами производства: физическим капиталом и квалифицированным трудом. Агенты принимают решения о потреблении и инвестировании, максимизируя дисконтированную интегральную полезность на неограниченном горизонте

времени. Число работников предполагается равным численности населения, которое растет с постоянным темпом ?.

Задача принятия решений имеет вид:

max f е ^{(р ?)}(lnc + ? Inl)dt, (2.1) c,l,e,u,k,h 0 к = у - (d + ?)к - c , (2.2) h / h = g0 + ge , (2.3) и + e +1 = 1, (2.4) e > 0 . (2.5) Мгновенная полезность является лог-аддитивной функцией потребления c и свободного времени I. Индивидуальные предпочтения выражаются двумя показателями: эластичностью свободного времени ? и нормой дисконта р, р > ?. Величина 8 = р - ? является чистой нормой дисконта. Технология в секторе производства продуктов выражается функцией Кобба-Дугласа с нейтральным по Харроду техническим прогрессом: у = k^a(uh)^1-a, где у — выпуск, к — физический капитал и h человеческий капитал (знания) работника, а — доля физического капитала в выпуске, и — интенсивность затрат труда в производстве в единицах рабочего времени. Все переменные в производственной функции выражены в удельном отношении.

Динамические уравнения (2.2) и (2.3) это бюджетное ограничение и уравнение накопления человеческого капитала. Физический капитал обесценивается с темпом d, а человеческий капитал — с темпом — g₀. Параметр g₀ с положительным знаком отражает автономный технический прогресс, не зависимый от затрат времени на создание производство знаний е. Слагаемое gieh в (3.3) интерпретируется согласно Лукасу (1988), как однородная производственная функция в секторе знаний с единственным фактором производства — накопленным человеческим капиталом. Параметр gi > 0 отражает предельную продуктивность данного сектора. Уравнение (2.4) это условие баланса времени домохозяйств, которое распределяется между производством продуктов, накоплением знаний и отдыхом. Ограничение (2.5) исключает отрицательные затраты времени в производстве знаний. Затраты времени на производство продуктов и отдых в равновесии положительны и поэтому мы не учитываем ограничения на неотрица-

тельность для данных переменных в формулировке задачи. В зависимости от того, является ограничение (2.5) связывающим или нет, мы рассматриваем два режима экономического роста: эндогенный и экзогенный.

2.1. Эндогенный рост

Равновесная динамика в режиме эндогенного роста описывается следующими относительными величинами: нормой потребления x = c/k, (валовой) процентной ставкой r = ду/дк и свободным временем I.

Утверждение 1. Равновесная траектория эндогенного роста удовлетворяет системе







где

P = (1 - a)/a,



Мы изучаем переходную равновесную динамику чуть ниже, а сейчас рассмотрим траекторию эндогенного сбалансированного роста. Выпуск, потребление и оба вида капитала растут на этой траектории экспоненциально с одинаковым постоянным темпом, а распределение времени домохозяйств неизменно. Уравнения для данной траектории соответствуют стационарному состоянию сис-

темы (2.4), (2.6)-(2.9) х = в r + 8, (2.10) r = d + р + go + g1e, (2.11) u = 8 /g_b О e = 1 - (1 + ? + 8 ?/в r)8 /g₁, (2.13) / = ? (1 + 8/в r)8 /g1. (2.14) Уравнение (2.10) определяет стационарное потребление, как долю богатства домохозяйств. Согласно (2.11) процент является суммой нормы обесценения, нормы дисконта и темпа роста ВВП. Уравнения (2.12)-(2.14) определяют стационарное распределение времени. Долговременная норма потребления может быть представлена в виде функции затрат времени:

х = 8 //(/ - ? u). (2.15)

Это выражение окажется полезным в дальнейшем.

Комбинируя (2.11) и (2.13), получаем уравнение для долговременной ставки процента:

r² - (R - 8? )r + 8 ²?/в = 0, (2.16)

где R = d + v + go + Пусть Г| обозначает минимальный корень (2.16), а r2 — максимальный корень. Оба корня являются вещественными и положительными, если R - 8 ? > 28 (? /в)^1/2. Другими словами, система (2.6)-(2.9) имеет два стационарных состояния, если параметры производства знаний go и g1 не очень низки, либо эластичность свободного времени ? не очень велика.

Множественность стационарных решений обусловлена положительной взаимосвязью между процентной ставкой и темпом эндогенного роста, проявляющейся в уравнениях (2.11) и (2.13). Стационарные ставки процента Г1 и Г2 существенно отличаются для эмпирически оправданных значений параметров модели. Ladron-de-Guevara et a/ (1999) подчеркивают качественные отличия между траекториями стационарного роста, отвечающими данным корням. Однако минимальный корень (2.16) во многих случаях является неправдоподобным решением. Время на производство знаний должно быть положительно, что для стационарного состояния влечет:

g₁ > 8 (1 + ? + 8?/ЗИ^е)). (2.17)

Здесь и ниже верхний индекс (е) обозначает эндогенный стационарный рост. Если, например, 8 достаточно мало, то (2.17) выполне-

но для r₂, но не для Г|. Случай малой нормы дисконта важен как с теоретической, так и эмпирической точки зрения, но как раз в этом случае минимальный корень (2.16) должен быть отвергнут.

Темп эндогенного сбалансированного роста на душу населения получается из (2.3) и (2.13):

g^(e) = (go + gi) - (1 + ?) 5 - ? s²/p H^e). (2.18)

Чем выше норма дисконта или эластичность свободного времени, тем ниже эндогенный рост. Этот вывод интуитивно понятен: долговременный рост низкий, если индивиды нетерпеливы или слишком высоко ценят отдых. Третье слагаемое в правой части (2.18) отражает положительную связь между процентом и эндогенным ростом.

Рассмотрим числовой пример, который будет использоваться на протяжении всей статьи. Пусть go = 0, ? = 0, 5 = 0.025, в = 1.5, d = 0.03. Табл. 1 содержит значения переменных в стационарном состоянии для данного набора параметров и различных значений ? и g1. Эти два параметра подобраны таким образом, чтобы стационарная ставка процента была примерно одинакова для всех вариантов. Минимальный корень (2.16) Г1 не удовлетворяет (2.17) и поэтому r^(e) = r2 = 0.085. Норма потребления и темп эндогенного роста также примерно одинаковы для всех вариантов, и x^(e) = 0.153, g^(e) = 0.03. Отношение потребления к выпуску, соответствующее x^(e) равно x^(e) a/r^(e) = 0.72. Доля затрат времени на производство знаний варьирует между 0.23 и 0.3 для наиболее правдоподобного интервала эластичности свободного времени [1.5, 2.5], а доля свободного времени варьирует между 0.45 и 0.58.

Если домохозяйства индифферентны к отдыху, ? = 0, модель становится специальным случаем модели Лукаса (1988), в котором нет

внешних эффектов производства знаний (а полезность — логарифмическая функция). В этом случае исчезает положительная связь между долгосрочным процентом и эндогенным ростом, а стационарное состояние находится непосредственно. Темп роста тогда равен g^(e) = go + gi - 8 . Стационарная ставка процента равна И^е) = R, а распределение времени таково: u^(e) = 8/gi, е^(е) = 1 - 8/gi, /^(е) = 0. В данном случае оценка времени на производство знаний явно завышена: для приведенного выше примера e^(e) находится в интервале между 0.643 и 0.808 (и g^(e) принимает значения между 0.045 и 0.105, что также слишком высоко). Использование более общей изоэластичной полезности вместо логарифма не влияет на это свойство модели Лукаса .

2.2. Экзогенный рост

Режим экзогенного роста определяется как краевое решение задачи домохозяйства (2.1)-(2.5) с нулевой интенсивностью производства знаний вдоль всей равновесной траектории. В данном случае равновесная динамика определена переменными хи r, а доли времени домохозяйств и и / являются функциями данных переменных.

Утверждение 2. Траектория равновесного экзогенного роста удовлетворяет системе

x/x = x- pr-S,

(2.19)

(2.20)

a + p + g₀ + ux / x - r 1 + pu

Интенсивности производства и свободного времени равны

Pr

pr + ?x

?x

Pr + ?x'

(2.21)

Траектория сбалансированного роста в данном режиме является стационарным состоянием системы (2.19)-(2.20), (x<^x), И^х)), которое находится непосредственно:

x(^x) = р И^х) + S, (2.22)

И^х) = d + p + go (2.23)

(верхний индекс (х) обозначает стационарный экзогенный рост).

Темп сбалансированного роста равен g^(x) = go. Стационарная норма потребления может быть представлена как функция затрат времени (2.15). Соотношение между затратами времени для режимов эндогенного и экзогенного роста является различным. Например, при норме дисконта, близкой к нулю, свободное время близко к нулю в первом случае (для И^е) = r2) и к ?/(1 + ? ) во втором.

Для нашего численного примера и при ? = 2, g1 = 0.1 мы имеем: И^х) = 0.055, u^(x) = 0.277, l^(x) = 0.723. Норма потребления Ж^х) = 0.108 и отношение потребления к выпуску равно 0.78, что близко к эмпирическим оценкам для многих стран. Это свидетельствуют об адекватности оценок используемой нами модели для режимов стационарного роста.

2.3. Сравнительный анализ благосостояния

Режим эндогенного роста может быть менее предпочтителен для индивидов, даже если он может быть реализован. Если выигрыш интегральной полезности от увеличения свободного времени перевешивает потери от более низкого роста потребления, то домохозяйства выбирают экзогенный рост. Мы не можем аналитически оценить благосостояние для равновесной траектории, поэтому используем приближенные оценки для стационарных траекторий. Каждая из них определена соотношением начальных значений факторов ho/ko, что демонстрируется в следующем разделе. Для удобства примем (без потери общности), что начальные запасы капитала одинаковы для обеих стационарных траекторий, и отношение ho/ko может варьировать только из-за различий в ho. Различия в интегральной полезности для этих траекторий определяются двумя эффектами: роста и уровня. Первый обусловлен более быстрым увеличением потребления в эндогенном режиме, а второй — возможным более высоким уровнем свободного времени в экзогенном режиме. Темп эндогенного роста равен gie^(e), и интегральный выигрыш от роста потребления составляет

Je-^st Ine⁹'^e'^()tdt = g₁e^(e) Je ^sttdt = 8-²g₁e^{e). o o

Интегральный эффект уровня равен

' |(e) Y

l (x)

^V /

_x^(e)

IXT

J e⁸dt = 8^-1 In

dt = In

In

y-(x)

.(x)

l (x) V

l (x)

Эндогенный рост предпочтительней, если и только если эффект роста доминирует эффект уровня:

g₁e^(e) > 8 In(xM/x<^e))(l^(x)/l^(e))®. (2.24)

При низкой норме дисконта правая часть (2.24) положительная и мала. Хотя эффект уровня действует в пользу выбора экзогенного роста (поскольку при низких значениях 8 отношение l^(x)/l^(e) велико), эффект роста все-таки доминирует. Поэтому достаточно терпеливые домохозяйства предпочтут эндогенный рост. Как мы увидим ниже, это неверно для открытой экономики.

2.4. Переходная динамика

В режиме эндогенного роста начальный выбор индивида заключается в определении начальных значений нормы потребления, xo, и свободного времени lo, при начальном значении процента ro, задаваемом из условий экономического равновесия. Этот выбор предопределяется начальным соотношением знаний и капитала ho/ko. Процент и интенсивность производства продуктов являются решениями уравнений (2.9) и r = ду/дк, из которых вытекает следующее соотношение:

(2.25)

x = (р/В) (h/k)r_W (r)l,

где Цг) = (r/a)^-1/(1-a) = k/uh это структура производственных затрат. Соотношение h/k = ho/ko в (2.25) определяет поверхность начальных значений в пространстве (x, r, l).

Начальный выбор в режиме экзогенного роста заключается в определении начальных значений xo и Го при заданном соотношении ko/ho. Условие распределения капитала г = ду/дк и уравнение (2.21) влекут соотношение:

x = (p/0)r[(h/kMr) - 1], (2.26)

где h/k = ho/ko определяет кривую начальных значений в пространстве (x, г).

Локальные свойства переходной динамики для обоих режимов сформулированы в следующем Утверждении.

Утверждение 3. Траектория эндогенного роста, сходящаяся к (x<^e), И^е), l^(e)), является седловой, если и только если

8/И^е) < (в/?)^1/2. (2.27)

Траектория экзогенного роста, сходящаяся к (x<^x), И^х)), является седловой и единственной.

Условие (2.27) выполнено для И^е) = Г2. В противном случае R - 8? < 28 (?/в)^1/2 (поскольку И^е) > (R - 8?)/2), и уравнение (2.16) не имеет вещественных корней. Таким образом, равновесная траектория существует и единственна для максимального корня уравнения стационарного равновесия (2.16).

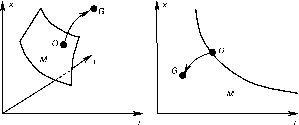
Утверждение 3 иллюстрируется на рис. 1, 2. Рис. 1 изображает фазовое пространство (x, г, I) и равновесную траекторию эндогенного роста. Ее начальная точка O = (xo, ro, lo) принадлежит поверхности начальных значений M определенной из (2.25) для ho/ko, и сходится к стационарной точке G = (x<^e), И^е), l^(e)). Режим экзогенного роста изображен на рис. 2, где показана кривая начальных значений M, определенная (2.26) и ho/ko, а также равновесная траектория. Начальное отношение знаний и капитала в данном случае достаточно высоко, и кривая M расположена достаточно далеко от начала координат. По этой причине переменные x и r убывают вдоль равновесной траектории¹°.

Рис. 1. Траектория эндогенного Рис. 2. Траектория экзогенного роста роста Недостаток модели эндогенного роста с человеческим капиталом (и свободным временем) заключается в том, что она генерирует слишком высокие темпы сходимости к стационарной траектории. Чтобы этого избежать, Ortiguera, Santos (1997) ввели в модель издержки новых инвестиций и получили темпы сходимости близкие к эмпирическим оценкам. Мы могли бы последовать их примеру, однако не делаем этого, поскольку преследуем иные цели. Поэтому в дальнейшем используется описанная выше версия модели, допускающая простое обобщение на глобальный уровень.

3. ГЛОБАЛЬНАЯ ЭКОНОМИКА

Рассмотренная выше модель экономического роста может быть полезна при объяснении препятствий к экономической интеграции между передовыми и отсталыми странами. Мы обобщаем эту модель для глобальной экономики, состоящей из N стран, и допускающей свободный перелив капитала. Как и в моделях Lucas (1993) и Barro, Sala-i-Martin (1995), наша модель глобальной экономики является однопродуктовой. Международная торговля при этом происходит, но ее смысл в том, чтобы сделать возможными международные кредиты и заимствования, предполагающие отклонения ВВП от ВНП или национальных сбережений от инвестиций в экономику. Иными словами, модель акцентируется исключительно на межвременных аспектах международного обмена, игнорируя вопросы, связанные со специализацией в производстве продуктов и знаний.

3.1. Модель глобальной экономики

Каждое домохозяйство в стране j наделено начальным запасом человеческого капитала hjo и активов ар. В начальный момент времени открывается международная торговля активами, и капитал перераспределяется согласно предельной отдаче. По этой причине капитал kjo, формирующийся в данный момент в стране j, отличается от начального запаса активов ajo в той же стране. Разрыв между данными величинами определяет положение страны как чистого экспортера или импортера капитала.

Предполагается, что страны имеют одинаковые технологии, предпочтения домохозяйств, темпы роста населения и экзогенного технического прогресса, но отличаются по предельным продуктивностям в производстве знаний д-\, а также начальных запасах hjo и ар и начальных размерах народонаселения Пр. Страны пронумерованы в соответствии с увеличением предельных продуктивностей д-, то есть д-і < д-2 < ... < g-N Задача домохозяйства в стране j имеет вид:

max fe ^st[Inc¦. + 0 InL]dt,

^cj ¦'j e u a ^h 0 (3.1) atj = raj + wujhj - (d + v)a_y - c. , (3.2) hj / hj = go + g-.e., (3.3) Uj + ej + lj = 1, (3.4) ej > 0, (3.5) j = 1, ..., N. В каждый момент времени глобальный рынок капитала уравновешивает общую сумму активов и производственного капитала:







Мировая процентная ставка выравнивает предельный продукт капитала между странами r = Эу/Эку, и капитал распределяется по этому принципу. Ставка оплаты труда также выравнивается благодаря идентичности технологий и линейной однородности производственной функции: w = dyj/d(ujhj) = (1 - a)(r/a)^-a/(1-a). Бюджетное ограничение (3.2) отражает накопление финансовых активов с чистой до-

ходностью r - d - ?. Слагаемое raj + wujhj в (3.2) это ВНП на душу населения.

Пусть

N

Pj = ⁿjYj ^/ ? ⁿkYk ^,

k=1

Xj = Cj/aj и Zj = aj/kj обозначают, соответственно, долю страны j в общемировом выпуске, норму потребления и финансовую позицию (отношение активов к производственному капиталу в стране). Для простоты мы не вводим ограничения на знак активов, допуская их отрицательные значения в переходном режиме. Тем не менее, в дальнейшем, мы рассматриваем ограничения на параметры модели, исключающие отрицательные значения aj, Xj, Zj в стационарном состоянии.

Утверждение 4. Если N стран растут в эндогенном режиме, то равновесная динамика интегрированной глобальной экономики определяется процентной ставкой r и набором специфических для каждой страны относительных переменных, Q = (Xj, j, Zj, jj, Uj, e_y)_y = 1, n, удовлетворяющих уравнениям:

Xj / Xj = Xj -pr / Zj. -8, (3.7) r / r = P(Rj - g_ylj - r), (3.8) !^{/ l}j = g_v^uj^-8, (3.9) Uj = prlj /?XjZj, (3.10) lj + Uj + ej = 1, (3.11) N ?^ZkPk = t (3.12) j = 1, ..., N и Rj = d + ? + go + gy. Уравнения равновесной динамики (3.7)-(3.12) по существу аналогичны полученным выше для случая автаркии. Уравнение (3.12) следует из условий рыночного равновесия (3.6) распределения капитала, kj = ay/r, и оно в явном виде отражает взаимосвязи между национальными экономиками. Согласно (3.12), средняя финансовая позиция, взвешенная с помощью долей стран в мировом выпуске, равна единице. Доли выпуска <Рк определяются на основе уравнений накопления человеческого капитала (3.3).

Динамическая система для глобальной экономики состоит из 6xN + 1 переменных и 6xN + 1 уравнений, включая (3.3). Уравнение процентной ставки (3.8) относится ко всем странам и совместимо, если выполнено N - 1 дополнительное условие:

01/(1 - I/) = Qik(1 - lk), (3.13)

j, к = 1, ..., N, j ф k. При этом число уравнений в системе не меняется, так как N уравнений процентной ставки (3.8) трансформируется в одно.

Условия (3.13) означают, что свободное время в каждой стране приспосабливается к глобальной динамике таким образом, что изменения процентной ставки одинаковы для всех стран. Выравнивание процентных ставок происходит мгновенно в начальный момент времени и сохраняется вдоль всей равновесной траектории. Однако свободное время является переменной управления, подчиняющаяся закону движения (3.9). Поэтому выравнивание процента происходит за счет приспособления интенсивности, входящего в уравнение (3.9). Ограничения (3.13) означают, что g_1j/_j = g_1ki_k . Это согласуется с (3.9) если

01/1/(01/0/ - 8) = g1klk(01kUk - 8), (3.14)

/, к = 1, ..., N, / ф к. Интенсивности производства, в свою очередь, зависят от переменных x/, г, I/ и финансовых позиций z, что следует из (3.10). Именно приспособление величин Zj для N - 1 стран в конечном итоге обеспечивают выравнивание процентных ставок для глобальной экономики. Финансовая позиция для "замыкающей" страны определяется из условия равновесия (3.12). В дальнейшем мы в явном виде вычисляем финансовые позиции стран для стационарного состояния.

Уравнения (3.13), (3.14), (3.11) означают, что распределение времени домохозяйств в N - 1 странах определяются распределением времени в замыкающей стране. Следовательно, глобализация рынка капитала и выравнивание процента приводит к тесной взаимозависимости поведения домохозяйств в различных странах.

Отсюда также видно, что механизм выравнивания процента через приспособление свободного времени важен для реалистичного описания динамики мировой экономики. Предположим опять, что ? = 0, как в модели эндогенного роста Лукаса (1988). Тогда I/ = 0 и уравнение процента (3.8) несовместимо для стран с различными g1. Поэтому применение модели Лукаса к глобальной экономике влечет неправдоподобный вывод, что весь капитал и производство концен-

трируется в самой передовой стране N, а процентная ставка изначально устанавливается на постоянном уровне r = Rn. В этом случае отсутствует механизм, устраняющий разрыв между r и величиной Rj для всех остальных стран.

Рассмотрим теперь режим экзогенного роста для открытой экономики, интегрированной с мировым рынком капитала.

Утверждение 5. Равновесная траектория для страны j, интегрированной и растущей в экзогенном режиме, является решением системы уравнений

(3.15)

(3.16)

Xj / Xj = Xj -pr / Zj -8,

_- . a + p + g₀ + Uj (Xj / Xj + Zj / Zj) - r r / r = P-^jjjjj-

¹ + PUj

Pr

(3.17)

^Uj pr

^?xj^zj

Выравнивание процента требует, чтобы правые части (3.16) и (3.8) совпадали. Это обеспечивается изменениями Zj и Zj /Zj в каждый

момент времени. Однако, как мы покажем ниже, переходная динамика становится взрывной: за конечный промежуток времени Zj достигает бесконечности, а интенсивность производства Uj снижается до нуля. Иначе говоря, производственный капитал "вымывается" из страны, которая полностью приостанавливает в какой-то момент времени производственную деятельность.

3.2. Стационарный эндогенный рост глобальной экономики

Предположим опять, что N экономик растут эндогенно и рассмотрим траекторию сбалансированного роста мировой экономики (И^е), Q^(e)). Она удовлетворяет уравнениям Xj = р r/Zj + 8, (3.18) r = ^Rj ^- g1j j, (3.19) Uj = 8/g_v, (3.20) noho^/ g_{v 1}

Zrf j N ’ (3.21) ‘=¹ ? ⁿk o^hko^/ g^k а также (3.10), (3.11) и (3.12).

Уравнения (3.18)-(3.20) аналогичны уравнениям (2.10)-(2.12), определявшим стационарную траекторию роста для закрытой экономики. Уравнение (3.21) является условием равновесия на рынке капитала для стационарного роста. Оно получается из (3.12), (3.20) и условия распределения капитала: у = (r/a)^-1/e Ujhj. Заметим, что равновесие автаркии с Zj = 1 для всех j является решением (3.21).

Уравнение равновесной процентной ставки для глобальной траектории сбалансированного роста выводится из соотношений (3.10),

(3.11) , (3.18)-(3.21):

r² - (R_a - ? + 82? /в = 0, (3.22)

где

N N

^Ra = ^d+^v + 90+9'^ 91a = X ⁿj 0^hj 0 ^/(X ⁿk0^hk 0 ^/ 91c⁾

j=1 k=1

— средняя гармоническая для g^. Уравнение (3.22) аналогично

(2.12) и имеет те же свойства. Как и выше, мы рассматриваем только максимальный корень Г2. Свободное время в стационарном равновесии составляет j^(e) = (?8 + z(^e'>o>)/g1j, где ю = ? 8²/в И^е). Поэтому 91j(1 - lj^(e)) = 91j - ? 8 - Zj^(eW Слагаемые g1j(1 - j^(e)) выравниваются, если выполняются следующие соотношения для z_y(^e), j = 2, .., N:

Zj ^(e) = 1 - (91a - 91j)M (3.23)

j = 1, ..., N. Таким образом, Zj <^e) возрастает по 9-^ ,и Zj <^e) < (>) 1 для стран с 91j < (>) 91a.

Мы накладываем ограничения на параметры модели, обеспечивающие положительность Xj и Zj в стационарном состоянии для всех стран. Эти переменные положительны в случае замкнутой экономики, но могут принимать отрицательные значения в случае открытой экономики. Такой исход в долговременном периоде означает экспоненциальное накопление необеспеченного долга какой-либо страной, что представляется неправдоподобным для интеграции через рынок капитала. Чтобы исключить такую возможность, введем огра-

ничение на финансовую позицию домохозяйств в стационарном режиме: z-j ^(e) > 0. Оно означает что

Яу > 9ia - ю, (3.24)

j = 1, N. Это неравенство выполнено, если предельная продуктивность производства знаний слабо варьирует между странами (Яі_а - Qij мало по абсолютному значению для всех j), либо эластичность свободного времени и норма дисконта достаточно велики.

Из (3.24) получаем стационарный темп эндогенного роста gW^e) = gia - (1 + ?)§ - ю,

j = 1, ..., N. Темп роста стран одинаков (из-за выравнивания процента) и положителен, если

Я1_а > (1 + ?)8 + ю. (3.25)

Это условие совпадает с условием (2.17), полученным для замкнутой экономики. Оно требует, чтобы предельная продуктивность исследований, усредненная по странам, была достаточно высока. В отличие от ограничений (3.24), специфических для каждой страны, (3.25) относится к мировой экономике.

Требования (3.24) и (3.25) представляют собой условия экономической интеграции посредством мирового рынка капиталов. Они ограничивают параметры предпочтений 8 и ? противоположным образом. Требование положительности мирового роста (3.25) выполнено, если индивиды терпеливы и склонны к продуктивной деятельности. Напротив, условие, исключающее экспоненциальное наращивание долга каждой из стран (3.24) выполнено, если индивиды нетерпеливы и склонны к отдыху. Таким образом, предпочтения потребителей неоднозначно влияют на существование долговременной траектории роста глобальной экономики.

3.3. Барьеры к интеграции

Предположим, что (3.24) выполнено для стран j = N*, ..., N и не выполнено для стран j = 1, ..., N* - 1, где N* индекс "пороговой" страны. Иначе говоря, будем считать, что глобальный рынок капитала

делит страны на две группы — более и менее развитых. Менее развитые страны 1, ..., N* - 1 не могут интегрироваться на основе эндогенного роста без экспоненциального наращивания долга. Эти страны могут оставаться в состоянии автаркии и расти эндогенно или экзогенно, в зависимости от имеющихся возможностей и предпочтений населения. Другая возможность заключается в интегрировании с мировым рынком капитала в очень специфической манере, когда в стране прекращается производство, производственный капитал из нее исчезает, а имеющийся человеческий капитал не используется. В таком режиме экономика растет экзогенно, поскольку интенсивность исследований также нулевая, а домохозяйства посвящают все время отдыху.

Подобный режим ассоциируется с понятием экономики рантье, в том смысле, что домохозяйства превращаются в чистых финансовых инвесторов, держащих только иностранные активы и живущих на получаемую с них ренту. Отношение активов к капиталу в стационарном состоянии равно бесконечности, а норма потребления, согласно (3.14), равняется 8 При этом активы и потребление растут с темпом мирового роста g^(e) = И^е) - d - р. Такой режим невозможен в замкнутой экономике, но он существует и может оказаться предпочтительней эндогенного роста в открытой экономике, интегрированной с мировым рынком капитала.

Передовые страны {N*, ..., N} участвуют в интеграции без накопления экспоненциального долга и могут не трансформироваться в режим рантье. Долговременное равновесие глобальной экономики, определенное выше для N стран непосредственно формулируется для данной группы. Условие интеграции (3.24) должно выполняться для подмножества {N*, ..., N} а средняя продуктивность сектора знаний gi_a относится только к данному подмножеству. Она зависит от порогового номера N*, gi_a = gi_a(N*), причем dgi_a(N*)/dN* > 0. Усиление условий интеграции (3.24) сокращает число стран, способных к полноценной интеграции. Если, к примеру, норма дисконта мала, неравенство (3.24) становится очень ограничивающим. Из него вытекает, что N* приближается к N, а gi_a(N*) — к giN. Поэтому лишь страны со значением giy близким к gi_a(N*) и giN могут участвовать в интеграции. В то же время, если норма дисконта или эластичность свободного времени достаточно велики, условие положительности мирового роста (3.25) выполняется лишь для у, близких к N. В данном случае также получается, что только наиболее продвинутые страны могут участвовать в интеграции.

Таким образом, при малой норме дисконта интегрирующиеся страны должны иметь почти одинаковые продуктивности исследовательского сектора, и быть наиболее продвинутыми в этом отношении. Данный вывод можно проиллюстрировать численным примером. Пусть 8 = 0.025, ? = 2, р = 1.5, И^е) = 0.085, N = 20 и значения g-j распределены равномерно согласно правилу: g- = g-- + 0.005, g-1 = 0.055, g-N = 0.15. Тогда со = 0.0098, gi_a(N*) е (0.14, 0.145) и g-N* = 0.135, и лишь четыре страны из двадцати могут интегрироваться: N - 3, ..., N. Заметим, что пороговый уровень g- эндогенного роста в автаркии составляет g-5 = 0.07, и при этом 14 стран могут расти в эндогенном режиме.

В качестве важнейшего препятствия для данного процесса часто рассматриваются несовершенства мировых рынков капитала. В нашей модели барьеры к интеграции связаны не столько с ограничениями на заимствования, сколько с неоднородностью стран. Если бы мы наложили такое ограничение, например, z(^e) > z_min, то условие аналогичное (3.24) влекло бы более жесткое ограничение на вариацию g- между странами. Если бы, с другой стороны, мы не принимали в расчет ограничение Zj^(e) > 0, нам надо было бы учитывать более слабое условие, что свободное время положительно. Для стационарного состояния это влечет условие на параметры g- > g-_a - со - 8?, которое в качественном отношении аналогично (3.24) .

Разброс стран по продуктивности исследований является решающим фактором, из-за которого нарушается (3.24). Данное условие было бы выполнено, если бы страны имели одинаковые g- = g-, отличаясь при этом по параметрам предпочтений и производства 8, ? или р. В таком случае страны различаются величинами о, а стационарные позиции капитала составляют Zj ^(е) = а/о_а > 0, где со_а это среднее арифметическое по ю_у- ^1е. Следовательно, именно неоднородность стран в продуктивности секторов, генерирующих рост, а не

в предпочтениях и технологиях производства является решающим барьером к их экономической интеграции.

Структурная неоднородность стран в рамках данной модели проявляется также в неравномерности распределения общего начального человеческого капитала страны n^h^- Если он концентрируется в одной из наиболее передовых стран N', то gi_a(N*) близко к g^, и N* близко к N'. По этой причине неравномерное распределение стран по численности населения может стать препятствием к интеграции.

Если либерализация мирового рынка капиталов откладывается, то условия интеграции все более ужесточаются. Это относится, прежде всего, к ограничению (3.24). Пусть экономики находятся в автаркии до открытия мировых рынков в момент t = 0, но растут неодинаковыми темпами. Это приводит к увеличению разрыва в уровнях знаний по мере откладывания либерализации, причем gi_a приближается к giN. Чем длиннее до-интеграционный период, тем больше вес наиболее передовых стран в gi_a, и тем значительней разрыв между ними и менее развитыми странами, то есть разность gi_a - gi. Следовательно, ограничение (3.24) ужесточается, а число менее развитых стран, способных к интеграции, со временем уменьшается.

3.4. Сравнительный анализ благосостояния

Передовая экономика, способная к интеграции, имеет три возможности: интегрироваться и расти эндогенно, интегрироваться и стать экономикой рантье, и оставаться в состоянии автаркии. Рассмотрим выбор между эндогенным ростом и режимом рантье для небольшой открытой экономики, не влияющей на мировую процентную ставку. Как и выше, мы сопоставляем эффекты роста и уровня для траекторий сбалансированного роста, предполагая одинаковые начальные запасы активов для этих двух режимов.

Поскольку темпы роста потребления одинаковы в обоих режимах, достаточно сравнить эффекты уровня. Режим рантье предпочтительней, если и только если выигрыш от увеличения свободного времени доминирует над потерями от уменьшения уровня потребления, то есть, согласно (2.24), (x^(e)/x^(r))(l^(e)/l ^(г))^? < 1.

Здесь верхний индекс (r) обозначает режим рантье. Норма потребления и свободное время в этом режиме составляют х(^г) = 8, /(^г) = 1. Из (3.18), (3.23) отношение уровней потребления выражается как x/^e)/x/^r) = (08 + ю + Дді_у-)/(ю + Agiy), где Agiy = giy - gi_a. Аналогично, отношение для свободного времени имеет вид

/y^(e)//y^(r) = (08 + ю (1 + Agij/a))/g_v = (08 + ю + Agiy)/giy.

Следовательно, режим рантье оказывается предпочтительней если

(08 + ю + Agiy)¹⁺⁰ < (ю + Agiy) g⁰ . (3.26)

Для 8 = 0 и Agiy > 0 это равносильно Agiy < giy или gi_a > О.Режим рантье, поэтому, более предпочтителен даже для достаточно передовых стран, если 8 достаточно мало. Это происходит из-за отсутствия эффекта роста и того, что "терпеливые" домохозяйства отдают предпочтение увеличению свободного времени по сравнению со снижением потребления в режиме рантье.

Численный пример, представленный в табл. 2, иллюстрирует зависимость между 0 и критическим значением 8, ниже которого режим рантье предпочтительней (все параметры такие же, как и в примерах выше, И^е) = 0.085, giy = 0.1, Agiy = 0). Как видно, пороговая норма дисконта для данного примера превосходит 0.01 для правдоподобных значений эластичности свободного времени.

Таблица 2 0 1.2 1.5 1.7 2 2.2 2.5 2.7 3 Критическое, 8x 10² 0.60 1.17 1.33 1.43 1.45 1.44 1.42 1.39 Следовательно, если норма дисконта невелика, режим рантье оказывается предпочтительней даже для страны, способной расти эндогенно в условиях глобального рынка капитала. В данном случае исчезает интуитивная связь между "бережливостью" и ростом, так как слишком бережливые домохозяйства предпочтут финансовые вложения созидательной деятельности.

3.5. Переходная динамика глобальной экономики

Выше мы показали, что при малой норме дисконта интеграция возможна только для стран с достаточно близкими предельными продуктивностями производства знаний (условие (3.24)). Поэтому мы анализируем переходную динамику глобальной экономики для простейшего случая, когда продуктивности сектора знаний одинаковы для всех стран, д_1у- = g₁, а национальные экономики отличаются лишь начальными значениями ajo и hjo ^1Э. Различия в начальных условиях не влияют на траекторию сбалансированного роста (И^е), Q^(e)), и в долговременном периоде относительные переменные состояния идентичны для всех стран. Это видно из (3.23), поскольку z_s = 1 для стран с однородным сектором знаний. Тем не менее, различия начальных условий влияют на характер переходной динамики глобальной экономики.

В рассматриваемом случае выравнивание процента влечет полную идентичность структуры времени домохозяйств в каждый момент времени. Это следует из условий (3.13), (3.14), означающих что Ij = І_к = I и Uj = u_k = и для всех j и к и обеспечивающих идентичность динамических уравнений для процента и свободного времени. Из (3.11) ej = вк = в для всех j и k, и поэтому в каждый момент человеческий капитал растет одинаково во всех странах. Производственный капитал и выпуск также растут одинаково, поскольку kj пропорционально uh. Таким образом, темпы роста ВВП выравниваются в начальный момент времени, и в переходном режиме страны различаются лишь по нормам потребления и финансовым позициям .

Обозначим агрегированную норму потребления как

N N

^Ха = ? ⁿj^Cj ^/ ? ⁿj^aj.

j=1 j=1

Агрегированная динамика глобальной экономики описывается переменными x_a, r, I, и, что демонстрируется в следующем Утверждении.

Утверждение 6. Агрегированная равновесная траектория глобальной экономики в эндогенном режиме удовлетворяет следующей системе

уравнений:

^Xa ^{/ X}a = ^Xa ^- Р^{Г -8,} (3.27) Г/г = Р(Я - г - дД (3.28) І /1 = ди-8, (3.29) и = вгІ /?x_a. (3.3о) Эта система идентична выведенной ранее для замкнутой экономики (2.6)-(2.9), а значит удовлетворяет Утверждению 3, характеризующему переходную динамику. Агрегированная равновесная траектория глобальной экономики отличается от траекторий для автаркии только тем, что она стартует с поверхности начальных условий, выраженной уравнением

*_а = (Ио/Ло)(Р/?)г_? (r)l, (3.31)

где у(г) = (г/а)^-1/(1_а) = kj/uhj — структура производственных затрат как функция процента, Н = ^ Pjhj, А = ^ — суммарные глобаль

ные запасы человеческого капитала и активов, Но/Ао — начальное отношение знаний к капиталу для мировой экономики.

Рассмотрим равновесную траекторию для страны j. Распределение времени домохозяйств определяется динамикой глобальной экономики. Норма потребления и финансовая позиция страны удовлетворяют уравнениям (3.7)и

и = (Р/?уі/XjZj. (3.32)

Из условия распределения капитала следует Zj = aj/hjuy (г), что вместе с (3.32) дает соотношение для нормы потребления, аналогичное (2.25):

Xj = (hj/aj)(P/ff)r_V(r)l. (3.33)

Траектория национальной экономики определяется переменными Xj, г, і, и, Zj, удовлетворяющими (3.7), (3.28), (3.29), (3.32), (3.33)²¹.

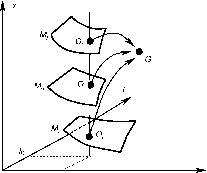
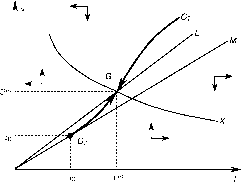
Фазовая диаграмма для глобальной и национальных экономик представлена на рис. 3, изображающем пространство (x, r, l), причем x = x_a или xj. Все траектории сходятся к одной и той же стационарной точке G, но стартуют с различных начальных точек. Агрегированная равновесная траектория берет начало в точке O_a, являющейся пересечением седловой глобальной траектории с поверхностью M_a, определенной (3.31). Данная точка задает начальные значения r = r₀ и l = l₀. Траектории национальных экономик стартуют с начальных точек Oj = (xjo, Го, Іо) на поверхностях Mj. определенных (3.33) и начальными отношениями hjo/ajo. Точка Oj задает начальную норму потребления xjo и финансовую позицию zjo для национальной экономики. Проекции траекторий национальных экономик на плоскость (l, r) совпадают с проекцией глобальной траектории на ту же плоскость.

го

г

Рис. 3. Глобальная траектория роста Из Утверждения 6 следует, что скорость сходимости для интегрированной глобальной экономики такая же, что и для замкнутой экономики. Важно, что эта скорость не является бесконечно большой, что означало бы мгновенное достижение стационарного состояния. Подобная ситуация характерна для моделей, непосредственно обобщающих стандартные модели роста на случай мировой или небольшой открытой экономики (например, Barro et al., 1995). Согласно же эмпирическим данным, темп сходимости для групп открытых экономик ненамного превышает этот темп для более замкнутых экономик. Аналогичный теоретический результат был получен ранее Barro et al. (1995) для случая небольшой открытой экономики при фиксированной ставке процента и ограничением на заимствования. В нашей модели процент определяется эндогенно, а экономики не сталкиваются с несовершенствами рынка капитала. Постепенная сходимость к стационарному состоянию обусловлена настройкой структуры времени домохозяйств и финансовых позиций различных стран.

3.6. Переходная динамика для режима рантье

Выше мы отмечали, что экономика, растущая экзогенно, может интегрироваться с мировым рынком капитала, только если она трансформируется в экономику рантье с нулевым производством. Рассмотрим переход к такому состоянию для небольшой открытой экономики. Предположим, что глобальная экономика уже находится в стационарном состоянии, то есть растет с постоянным темпом g и процентом г. Разрыв темпов роста составляет Ag = г - d - р - go. Принимая во внимание (3.17), представим уравнение процента (3.16) в виде:

jj /% = Ag(1 + (? / prtfj),

где jj = Cj/kj норма потребления, определенная как отношение потребления к производственному капиталу. Это уравнение решается в явном виде

jj=joe^Agt /[1 + (? / pr)jjo(1 - e^Agt)],

где jjo = (P/?)г[(hJo/aJo)w(г) - 1] начальная норма потребления. Траектория роста для данной страны взрывная, поскольку jj достигает бесконечности за конечный промежуток времени

T = ln(1 + pг/?j)/Ag = - ln(jo)/Ag.

Время перехода снижается с увеличением начального значения свободного времени и разрыва темпов роста. Табл. 3 демонстрирует время перехода (в годах) к режиму рантье для различных значений разрывов в темпах роста Ад и начальных значений /_у0, равных 0.4 или 0.6.

Таблица 3 Ад (%) 1.0 1.5 2.0 2.5 3.0 3.5 T (/j0 = 0.4) 92 61 46 37 31 26 T (/j0 = 0.6) 51 34 26 20 17 15 Полученные оценки демонстрируют, что переход к режиму рантье может произойти на достаточно коротком историческом интервале, а время перехода быстро сокращается с увеличением разрыва темпов роста.

4. ПЕРЕТОКИ ЗНАНИЙ И ИНТЕГРАЦИЯ

До сих пор мы не рассматривали механизм международных перетоков знаний, представляющих самостоятельный фактор роста и способствующих интеграции. Данный механизм был введен в модель глобальной экономики в работе Lucas (1993, p. 255), причем мировой уровень знаний рассматривался как фактор роста знаний внутри страны. Благодаря этому экономика с относительно низким (высоким) уровнем знаний должна расти быстрее (медленнее) мировой экономики. Не удивительно, что данное предположение позволяет легко обосновать сходимость темпов роста между странами, как это показано в той же работе. Эта гипотеза интуитивно прозрачна, но не подтверждается эмпирическими закономерностями (см., например, Durlauf, Quah, 1999, p. 265-268).

По этой причине мы дополняем нашу модель иным механизмом перетоков знаний, опосредованных прямыми иностранными инвестициями. Индуцированные прямыми инвестициями перетоки обычно отождествляются с трансфертом знаний, технологий, организационных мер, повышающих качество управления и рабочей силы в стране — получателе этих инвестиций. Данные трансферты особенно важны в том случае, когда прямые инвестиции идут от передовых стран к менее развитым. Проблема, исследуемая в данном разделе статьи, заключается в том, каким образом индуцированные инвестициями перетоки знаний влияют на возможности интеграции для небольшой открытой экономики. Мы изучаем небольшую открытую экономику и вводим перетоки знаний, допуская положительную обратную связь между приростом производственных инвестиций и знаний и считая, что иностранные инвестиции составляют некоторую долю от их общего объема.

Модифицируем уравнение человеческого капитала (3.3), предполагая для простоты, что до = 0:

h = gph + g2k.

Здесь и в дальнейшем мы не используем индекс страны. Последнее слагаемое в правой части этого уравнения отражает связь между производственными инвестициями и увеличением человеческого капитала. Коэффициент д2 > 0 отражает долю прямых иностранных инвестиций в их общем объеме, а также собственно влияние перетоков на накопление знаний. В темповом выражении данное соотношение имеет вид:

h / h = g₁e + g₂uy(r)k / k. (4.1)

Произведение g2uy (r) = e (u) является эластичностью знаний по отношению к производственному капиталу. Она увеличивается с интенсивностью производства в стране и уменьшается с мировой процентной ставкой.

4.1. Эндогенный рост

Предположим, что в момент t = 0 небольшая экономика выходит на мировой рынок капитала, а глобальная экономика уже находится в стационарном режиме с постоянным темпом роста g и процентной ставкой г. В данном случае потребление страны растет с момента t = 0 постоянным темпом g = г - d - р. В режиме эндогенного роста уравнение процента (3.8) модифицируется таким образом

г = R - g₁/ + ?(u)k / к.

Это уравнение отражает роль внешних эффектов инвестиций в механизме интеграции. В данном случае экономика может настраиваться на уровень мировой процентной ставки двумя путями: через распределение времени домохозяйств (второе слагаемое в правой части) и изменения производственного капитала (третье слагаемое). Поэтому распределение времени домохозяйств уже не связано жестким образом с процессом выравнивания процента между странами.

Эндогенный рост экономики описывается динамической системой:

z / Z = | / |-| / z + вг / z + S, (4.2) l /1 = g + (R - г - gi/)/?(u), (4.3) /// = gu-s, (4.4) u = в г//?|. (4.5) Здесь (4.2) это уравнение для нормы потребления (3.15), выраженное переменными | и z, (4.3) — уравнение процента и (4.4)-(4.5) — уравнения распределения времени домохозяйств. Подсистема (4.3)-(4.5) является автономной двумерной динамической системой с переменными | и /. На самом деле уравнение (4.2) имеет значение для определения начальных условий и анализа переходного режима, проводимого ниже.

Распределение затрат времени в стационарном состоянии имеет вид:

u^(e) = S/gi, e^(e) = [1 - ? (u^(e))]g/gi,

поскольку R - г = gi - g - S. Характерно, что стационарное распределение времени домохозяйств не зависит от эластичности свободного времени из-за экзогенности процента и темпа роста. Напомним, что взаимосвязь между этими величинами играет важную роль

в определении стационарного распределения времени для замкнутой и глобальной экономики.

Интенсивность производства знаний в стационарном состоянии положительна, если е ^(e) < 1 или

01 > Я2$?, (4.6)

где е ^(e) = е (u^(e)), у = у(г). В противном случае отпадает необходимость в проведении исследований внутри страны, так как накопление производственного капитала генерирует достаточно быстрый приток знаний, а значит e^(e) = 0.

Стационарная финансовая позиция и норма потребления равны:

(4.7)

_z(e) = в Г(/^(e) -0U^(e>) _у(e) = 8/<sup>(e)

Z</sup> ?8и^(і5) ’ * /^(e) -?и^

Обе эти величины положительны, если /^(e) > ? u^(e) или

01 > (1 - е ^(e))g + (1+?)8. (4.8)

Если g2 = 0, то е ^(e) = 0 и ограничение (4.8) трансформируется в (3.24), так что g1 > g1_a - со. Это означает, что для g2 > 0 перетоки знаний могут заметно сократить (но не устранить) барьеры к интеграции для страны с продуктивностью сектора знаний ниже мирового уровня (g1 < g1_a). Напротив, чем ближе эластичность человеческого капитала к единице, тем слабее ограничение (4.8).

Возвращаясь к примеру с 20 странами с равномерно распределенным g1 и предполагая, что е ^(e) = 0.5 и g = 0.03, можно видеть, что (4.8) выполнено для 12 стран. Напомним, что лишь 4 страны в том примере удовлетворяли аналогичному условию интеграции (3.24). На самом деле, (4.8) даже слабее условия эндогенного роста в автаркии (2.17), если (1 - е ^(e))g < со. В данном случае выход на рынок капитала позволяет выйти в режим эндогенного роста странам, не имеющим такой возможности в замкнутом состоянии.

4.2. Экзогенный рост

Перетоки знаний являются в данном случае единственным фактором роста. Комбинируя уравнение человеческого капитала (4.1) с уравнением процента (3.16), имеем: г = d + р + е(и)к/к + иЁ, /1 . Простые

преобразования приводят систему (3.15)-(3.17) к виду:

z/z = |/|-| /z + pr/z + 8, (4.9)

I/| = g - ^{9(? 1 вг}1, (4.10)

92V^{- 1}

где (4.9) это уравнение для нормы потребления, а (4.10) — уравнение процента. Последнее не зависит от z и может рассматриваться в качестве автономного. Оно глобально устойчиво, если

92V > 1, (4.11)

В противном случае экономика теряет устойчивость, трансформируясь за конечное время в режим рантье.

Стационарное распределение времени домохозяйств составляет u^(x) = 1/g2V, /^(x) = 1 - 1/92V, и поэтому е (u^(x)) = 1. Финансовая позиция и норма потребления x в стационарном режиме выражаются аналогично (4.7) и положительны, если /^(х) > ? u^(x) или

g2V > 1 + ?, (4.12)

что является достаточным для (4.11).

Ограничения (4.6), (4.8) (4.12) изображены на рис. 4. Зона 1 это область значений параметров, в которой все эти ограничения выполняются, и оба режима роста являются допустимыми. В зоне 2 возможен только эндогенный рост, а в зоне 3 — только экзогенный. Зона 4 соответствует случаю, когда все эти ограничения нарушаются,



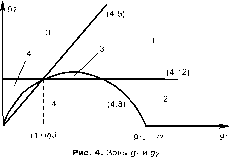
и страна может выбирать только между автаркией и режимом рантье. Долговременный эндогенный рост без экспоненциального наращивания долга возможен в зонах 1 и 2. Допустимая область значений параметра gi в данном случае заметно шире (для значительного интервала g2) по сравнению с моделью без эффекта перетоков (g2 = 0), которой соответствует ограничение (3.24) и жирная линия на рис. 4.

4.3. Сравнительный анализ благосостояния

Рассмотрим выбор между эндогенным и экзогенным стационарным ростом для стационарных траекторий. Темп роста одинаков для обоих режимов, и поэтому мы сравниваем только эффекты уровня. Из (2.24) экзогенный рост предпочтительней, если

(x ^(e)/x ^(x))(/^(e)//^(x))⁰ < 1. (4.13)

Левая часть (4.13) равняется [(/^(x) - ?и ^(x))/(/^(e) - ?и ^(e))](/^(e)//^(x))¹⁺⁰ и приближается к

(1 - gf

1 - (1+ ?)/g₂y (1 -1/ g_2W)^M

при 8 стремящемся к 0. Последний сомножитель данного выражения равен 1 для ? = 0 и меньше 1 для ? > 0. Поэтому (4.13) выполнено при небольших значениях 8. Экзогенный рост предпочтительней, поскольку доминирует эффект уровня свободного времени. Тем самым опять подтверждается вывод, что терпеливость отрицательно влияет на выбор эндогенного роста в условиях открытой экономики.

4.4. Модели переходной динамики

В режиме экзогенного роста равновесная траектория глобально устойчива. В режиме эндогенного роста стационарное состояние является седлом для широкой области значений параметров, что демонстрирует следующее Утверждение.

Утверждение 7. Равновесная траектория эндогенного роста является седловой, если

g1 > g + 8. (4.15)

Для каждого режима мы рассматриваем две модели переходного роста. Первая модель характеризуется высокой интенсивностью начального притока капитала в страну и более медленным его накоплением вдоль равновесной траектории. Производственный капитал резко увеличивается сразу после открытия экономики, но в переходной фазе он растет медленнее, чем мировая экономика и, соответственно, внутреннее потребление. Мы называем такой тип динамики моделью быстрого роста, поскольку открытие внутренних рынков капитала дает немедленный и достаточно быстрый приток инвестиций в страну. При второй модели роста вначале происходит отток активов из страны, но при переходе к стационарному состоянию капитал растет более быстрыми темпами по сравнению с мировой экономикой и внутренним потреблением. Мы называем такой тип развития моделью постепенного роста.

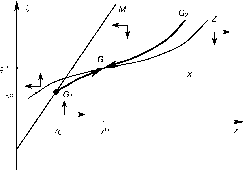
Рассмотрим, как выбор модели роста зависит от начального отношения знаний к активам h₀/ao, которое будет обозначаться о₀. Для удобства начнем с режима экзогенного роста. Фазовая плоскость системы (4.9)-(4.10) изображена на рис. 5, где горизонтальная линия X это множество, на котором | неизменно, а кривая Z — множество, на котором z неизменно (Z имеет отрицательный наклон, если выполнено (4.12)). Луч M является областью начальных значений, удовлетворяющей знакомому уравнению:

I = (Рг/?)(аоу z - 1). (4.16)

Рис. 5. Экзогенный рост для открытой экономики Начальная норма потребления и финансовая позиция являются пересечением луча M и устойчивой седловой траектории G-| или G2. Траектория G- соответствует модели быстрого роста, так как |₀ относительно мало (меньше^ ^(x)) и | возрастает вдоль этой траектории. Траектория G2 отвечает модели постепенного роста, потому что |о относительно велико (больше | ^(x)) и | убывает вдоль G2. Равновесная траектория совпадает с траекторией сбалансированного роста, если

Іо = I ^(x) = Ргд2уІ^(х)/? = (pr/? )(g2W - ¹) и, согласно (4.16), начальное отношение знаний и активов равно

а₀^(х) = 1/^u^(x)z^(x).

Утверждение 8. Эндогенный переходный рост является быстрым, если со >Og^x) , и постепенным, если со x) .

Данное Утверждение иллюстрирует рис. 5, где линия начальных значений M пересекает только одну из траекторий G- или G2. Согласно Утверждению 8, равновесный рост является быстрым в экономике с относительным избытком человеческого капитала, и он постепенный в экономике с относительным недостатком человеческого капитала. Более того, если z^(x) < 1, то Zo < 1 для G-, причем в момент 0 происходит приток капитала, не просто элиминирующий начальный дисбаланс знаний и активов, но и сразу же приводящий к обратному дисбалансу. Аналогично, начальный отток капитала из экономики с его избытком также слишком интенсивный, если z^(x) > 1, а значит Zo > 1 для G2. Таким образом, экономика с начальным избытком человеческого капитала испытывает в дальнейшем его относительный недостаток, поскольку капитал в дальнейшем притекает в нее с темпом ниже д. Начальный отток капитала из страны, относительно небогатой знаниями, также настолько интенсивен, что в дальнейшем капитал возвращается в нее с темпом выше д.

Мы связываем данный результат с принципом сравнительного преимущества, так как пороговый уровень начального отношения знаний к активам Og^x) определяется мировой процентной ставкой. модель переходного развития страны определяется сопоставлением ее начальной структуры факторов со с пороговым уровнем, определяемым характеристикой глобальной экономики.

Можно показать, что модель постепенного роста предпочтительней по критерию благосостояния модели быстрого роста, если эластичность свободного времени достаточно высока. Действительно, ожи-

даемая интегральная полезность в момент 0 составляет

je~^st(gt + Inx₀ + Ina₀)dt + e~^st InIdt =

0 0

= g/8² + [(In a0) + (In X0) + ?Е0 In I]/8,

где

E₀ In I = j (In l)e-^8tdt / j e ^8tdt 0 0

— ожидаемая полезность свободного времени, усредненная с помощью нормы дисконта. Ожидаемые интегральные полезности для данных моделей роста могут отличаться из-за различий в начальных уровнях потребления и ожидаемой полезности свободного времени. Начальная норма потребления Х0 выше для модели быстрого роста, так как отношение |)/^z0 = ^х0 больше для G-, что видно из рис. 5. Ожидаемая полезность свободного времени больше для модели постепенного роста. Это так, поскольку, согласно (3.17), на равновесной траектории величины I и | связаны соотношением: I = ?|/(?|+вг). Норма потребления | убывает вдоль траектории G2, поэтому свободное время также убывает вдоль этой траектории. Следовательно, для G2 выполнено: E0InI > InI^(x), тогда как E0InI < InI^(x) для G-, а значит E0InI выше для G2.

Ожидаемая полезность свободного времени входит в интегральную полезность с весом ?. Таким образом, модель постепенного роста предпочтительней модели быстрого роста, если индивиды высоко ценят свободное время, и наоборот. Другими словами, для страны с индивидами, не склонными к созидательной деятельности, начальное состояние с относительным избытком активов предпочтительней начального состояния с их недостатком.

Рассмотрим модели переходного роста для эндогенного режима. Соответствующие равновесные траектории изображены на рис. 6, показывающем фазовую плоскость для подсистемы (4.3)-(4.5). Кривая X это множество точек, для которых постоянно |, а луч L это множество постоянных I. Областью начальных значений является луч M, определенный как:

I = №/?)^оь Z0I. (4.17)

Две устойчивые седловые траектории соответствуют двум моделям переходного роста. Норма потребления | и свободное время воз-

Рис. 6. Эндогенный рост для открытой экономики растают вдоль первой траектории G- и убывают вдоль второй траектории G2. Как и для экзогенного режима, темп роста производственного капитала превосходит мировой темп роста g для второй траектории и ниже его для первой траектории. Равновесная траектория является траекторией сбалансированного роста, если

Іо = I ^(e) = Ргд₁/^(е)/?8 = (вг/?)/^(е)/и^(е) или, согласно (4.17),

Со Zo = 1М/^(е).

Выбор равновесной траектории определяется расположением луча M относительно луча L. Если первый имеет более низкий угол наклона, то выбирается траектория быстрого роста G-, в противном случае равновесной траекторией является G2, и переходный рост постепенный. В данном случае выбор модели роста осложняется тем, что наклон луча М зависит от произведения со и Zo. Первый сомножитель является экзогенной величиной, тогда как второй определяется эндогенно, совместно с |о и /о. Интуитивно, результирующий эффект вариаций со неоднозначен, так как, к примеру, увеличение со стимулирует приток капитала в страну, что ведет к снижению Zo. Следующее Утверждение показывает, что данный эффект достаточно сильный.

Утверждение 9. Пусть темп сходимости эндогенной траектории в окрестности стационарного состояния д^(е) удовлетворяет условию:

g < - д^(е) < g + pr/z^(e). (4.18)

Тогда рост является быстрым для о₀ >о0^е) ^ 1/^u^(e)z^(e) и постепенным для о₀ < о0^е).

Темп сходимости д^(е) это отрицательный корень характеристического уравнения подсистемы (4.3)-(4.5), приведенного в доказательстве Утверждения 7 (см. Приложение П1). Этот корень удовлетворяет условию -д^(е) > g - 8, и потому левое неравенство в (4.18) является лишь немного ограничивающим при малых 8. Его смысл в том, что темп сходимости должен быть выше мирового темпа роста. Однако правое неравенство в (4.18) может быть ограничивающим для ?<^е) близких к 1. Например, оно выполнено для нашего числового примера при g1 = 0.1 для ?<^е) = 0.5 (д^(е) = -0.126, z⁽^ = 1.02), и не выполнено для е^(е) = 0.8 (д^(е) = -0.096, z⁽^ = 1.94).

Рис. 6 иллюстрирует Утверждение 9 для случая 00 > о0^е). Согласно данному Утверждению, oz <о0^е) z⁽^ и M пересекает траекторию

быстрого роста G1. Как и в экзогенном режиме, модель быстрого роста реализуется для экономики с относительным избытком человеческого капитала. В экономике с его относительным недостатком переходный рост является постепенным (траектория G2).

Как и в режиме экзогенного роста, ожидаемая полезность для различных моделей перехода варьирует только благодаря начальной норме потребления Х0 и ожидаемой полезности свободного времени Е0ІП. Начальная норма потребления Х0 = Ia/z0 выше для модели быстрого роста (в окрестности стационарного состояния). Это так, поскольку в данной окрестности проекция равновесной траектории на плоскость (|, z) аппроксимируется линейной зависимостью | от z с положительным углом наклона и свободным членом (уравнение (П.13) в разделе П1). Поэтому отношение Iq/z0 убывает по z0, и оно выше для G1, поскольку в данном случае z0 ниже, чем для G2. Ожидаемая полезность свободного времени больше для траектории G2, поскольку в каждый момент величина свободного времени больше на G2, чем на G1, что видно из рис. 6. Таким образом, как и ранее, модель постепенного роста предпочтительней по критерию благосостояния, чем модель быстрого роста, если эластичность свободного времени высока и наоборот.

Сравнивая критические начальные значения отношения знаний к активам Og^x) и Og^e)) для режимов эндогенного и экзогенного роста,

можно показать, что, как правило, Og^x) > Og^{e) 28}. Это означает, что в

режиме экзогенного роста экономика должна иметь более высокое минимально возможное отношение знаний к активам, обеспечивающее начало быстрого роста, чем в режиме эндогенного роста. Если °о^х) > °о >°o^e), то модель быстрого роста реализуется лишь в режиме эндогенного роста. В этой ситуации страна, отказывающаяся от развития собственного сектора знаний и полагающаяся на приток прямых иностранных инвестиций в качестве основного источника быстрого роста, сталкивается с их недостатком в начальной фазе интеграции.

5. ЗАКЛЮЧЕНИЕ

В статье исследовались некоторые закономерности глобальной динамики с помощью анализа двух режимов экономического роста. Первый, эндогенный, основан на производстве знаний, второй, экзогенный — на других источниках. Мы показали, почему некоторые страны не способны развивать данный сектор и эффективно вписаться в мировую экономику. Имеется три типа препятствий: поведенческие, технологические и институциональные. К поведенческим барьерам роста относится нетерпеливость экономических агентов и высокая оценка ими свободного времени. Низкая продуктивность сектора знаний объясняется в большей мере технологическими и институциональными факторами. Рассмотренная в статье модель делает акцент на поведении домохозяйств, игнорируя роль корпораций, влияние государства, права собст-

венности и иные институциональные формы. Однако все эти факторы влияют на продуктивность секторов, генерирующих долговременный рост, которая играла в нашей статье ключевую роль.

Статья демонстрирует, что даже если темпы роста расходятся для набора замкнутых экономик, они сходятся для стран, участвующих в мировом рынке капитала (свойство клубной сходимости). Это, однако, требует достаточной близости стран-участниц клуба по показателю продуктивности в секторе роста, иначе какие-то из них начинают накапливать долг по экспоненте. На наш взгляд, введенное в статье ограничение на параметры модели (3.24), запрещающее такой исход, имеет непосредственное отношение к некоторым современным проблемам глобализации. Если какие-то экономики в реальном мире пытаются выйти на траекторию долговременного роста с экспоненциальным увеличением долга, то рано или поздно они оказываются близки к состоянию дефолта. Поэтому можно интерпретировать введенное ограничение на параметры как запрет на участие в мировом рынке капитала для стран с высоким риском дефолта. В соответствии с данной интерпретацией можно рассматривать финансовые кризисы как неудачные попытки интеграции в мировой рынок капитала стран, имеющих относительно низкие продуктивности секторов роста.

Введение в модель механизма перетоков знаний при посредстве прямых иностранных инвестиций важно в двух аспектах. Во-первых, данная модификация модели допускает переходную динамику для небольшой открытой экономики, воспринимающей постоянную ставку процента. Без такого предположения экономика моментально "перескакивает" на стационарное состояние, что очень нереалистично. Во-вторых, рассмотрение такого рода эффектов перетока интересно с практической точки зрения. Многие либеральные политики в переходных и развивающихся странах отстаивают идею интеграции в мировую экономику, выдвигая в качестве важнейшего аргумента позитивные эффекты перетоков знаний, технологий и навыков, индуцируемых прямыми иностранными инвестициями. Мы показали, что хотя подобные эффекты расширяют возможности экономической интеграции, они вовсе не являются панацеей от экономической отсталости.

Мы рассматриваем присоединение экономики к мировому рынку капитала не просто как формальное разрешение резидентам вкладывать в иностранные активы и, соответственно, приглашение войти нерезидентам. Речь идет также и об устранении институциональных барьеров внутри страны на пути иностранного капитала. Это обеспечивается глубокими реформами в системе права, корпоративного управления, налогообложении и т.д. При таком понимание выход экономики на

внешний рынок и начальное перераспределение капитала представляет собой длительный исторический процесс, тогда как в модели предполагалось, что все это происходит мгновенно, в начальный момент времени, t = 0. Конечно, можно было немного "дополнить" экономическую "сказку" модели, допуская, что либерализация торговли и начальное перераспределение капитала занимает некоторый конечный интервал времени [-to, 0], предшествующий переходному росту.

События, происходящие в этом "пред-переходном" периоде, остаются за рамками модельного описания, но в реальности именно они влияют на переходную динамику. Мы показали, что она может быть неравномерной во временном и межстрановом аспекте: возможен быстрый или постепенный рост на различных стадиях интеграции страны с мировым рынком. В определенном смысле, модель быстрого роста напоминает опыт некоторых успешных экономик, например, Восточно-Азиатских стран. Их выход на мировые рынки привел к быстрому притоку капиталов и росту производства, но в дальнейшем в ряде случаев происходило замедление этих процессов. Начальное отношение человеческого и производственного капитала в данных странах также было относительно высокое, что явилось одной из причин успеха. Конечно, рамки такой аналогии очень ограничены, поскольку наша модель рассматривала только рынок капитала, игнорируя международные товарные рынки, а значит и такой важный фактор интенсивного роста как экспортная экспансия (ее роль подчеркивалась, например, в работах Lucas (1993) и Ventura (1997)). С другой стороны, модель постепенного роста может ассоциироваться с менее удачными попытками интеграции развивающихся стран, приводящих вначале к оттоку капитала и замедлению роста. Однако, исходя из наших выводов, мы можем дать для таких стран оптимистичный прогноз: в последующих фазах интеграции должно происходить ускоренное накопление капитала и более быстрый рост производства.

Как было показано, выбор страной модели роста определяется сравнительным преимуществом страны в производстве знаний. По такой логике отток капитала из такой страны как Россия на начальных фазах интеграции объясняется (помимо прочего) отсутствием у нее подобных преимуществ. Это связано, прежде всего, с большими размерами ее активов на душу населения, включая природные ре-

сурсы. Россия, без сомнений, имеет абсолютные преимущества в ряде областей производства знаний (сформированные еще при социализме), но они элиминируются размерами ее активов. Данный результат модели позволяет прояснить отток капитала из нашей страны и недостаточно быстрый приток в нее иностранного капитала по сравнению с некоторыми другими переходными экономиками.

ПРИЛОЖЕНИЯ

П1. Доказательство Утверждения 1

Лагранжиан задачи (2.1)-(2.5) имеет вид

L = inc + ? in(1-u-e) + Яі(у - (d+v)k - с) + ^(go + gie)h + %e,

где Аі и %2 сопряженные переменные, относящиеся к (2.2) и (2.3), соответственно, х двойственная переменная, относящаяся к (2.5). Для режима эндогенного роста | = 0 и условия первого порядка таковы







Сопряженные уравнения имеют вид





Комбинируя (П2), (П3), получаем (1 - a)(k/uh)^a = g^/A^ Подставляя это в (П5), имеем



Беря логарифмические производные в обеих частях (П2), получаем ^2 / Ag =-І /1 - h/ h. Подставляя это в (П6), имеем (2.8).

Комбинируя (П1) и (П4), получаем



Разделим обе части (2.2) на k и вычтем (П7) из (2.2):

С / с - k / k = г - d - р - г/ а + d + ? + x = x - вг -8.

Это эквивалентно (2.6).

Чтобы получить (2.7), используем (П7), (2.3), уравнение распределения капитала

(П8)

(uh/k)^1-a = г/а

и возьмем логарифмические производные (П3):

І /r = Р(І /l+ V \ + h/h) = Р(І /l - д/c + h/ h) =

P(9V -S- r + d + 5 + go + 9P) = P(d + v + g₀ + g₁(1 -1) - r) Чтобы вывести (2.9), учитываем (П1) и преобразуем (П3):

? x/l = (1 - a)(k/uh)^a(h/k), и подставляем сюда (П8).

П2. Доказательство Утверждения 2

Для режима экзогенного роста х * 0, e = 0, а условиями первого порядка являются (П1), (П3) и ? /I = A-2g1h + х. Сопряженные уравнения — (П4), (П5). Уравнение (2.19) выводится так же как (2.6). Оптимальное правило (2.21) выводится аналогично (2.9). Дифференцируя (2.21) и преобразуя, получаем

и/u = l(r/r - X/x). (П9)

Дифференцируя (П8) и учитывая (П9), имеем І / r = (1 -a)(U/ и + h / h - k / k) =

= (1 - a)[l(r /r - X/ x) + g₀ - r /a + d + v + x] =

= (1 - a)[lr /r + (1 -1)x/x + g₀ + d + p - r].

Отсюда

_r , = (1 -a)(d + p + g₀ + ux/x-r)

1 - (1 -a)l '

Это эквивалентно (2.20).

П3. Доказательство Утверждения 3

Характеристическое уравнение для системы (2.6)-(2.9), линеаризованной около (x<^e), И^е), l^(e)) имеет вид

- px^(е)

Pr^(е) - д Sl^(е)/ r^(е)

0

pgr^(е) S - д

= 0,

0

-Sl^(e)/ x^(е)

где д — характеристический корень. Это кубическое уравнение: д³ - 25д² - В₁д - В₂ = 0,

где

В₁ = 5ДИ^е) - д^іЩ + (Pri^e))² - 8²,

B₂ = 8p(g₁і^(e)x^(e) - prgp^(e) - И^е)х<^е)) = 8р (д₁і^(е)8 - И^е)х<^е)).

Оно имеет один отрицательный вещественный корень, если и только если В₂ < 0, то есть

д-і^(е)8 - И^е)х<^е) < 0.

Благодаря (2.15) левая часть этого неравенства равняется

*<^е)(ді (і^(е) - ?и^(е)) - И^е)) = х^(е)(д-(і^(е) - ?и^(е)) - И^е)) = Ж^е)(?8²/рГ^(е) - И^е)).

Это выражение отрицательно, если и только если выполнено (2.27).

Рассмотрим переходную динамику для режима экзогенного роста. Преобразуем правую часть (2.20)

.. а п Г^Ы(Рг + ?Х) + Pr(X -8)

r / r = -Pr + p-—---—---

p(1 +P)r + ?Х

и возьмем производные (2.20) в точке (x<^x), И^х)):

P(r^(x) + x - 8)?х - P(1 + P)r^(х)?х

d(r / r)/Эг = -p + p

(P(1 + P)r + ?х)²

P(r^(x) + pr^(х))?х^(x) - P(1 + P)r^(х)?х^(x)

= -p + p

P,

(x) 2

(P(1 + P)r^(x) +?х ^(x))^:

d(r / r)/ Эх

(?г^(x) + pr)P(1 + P)r - ?вr(r^(x) - 8) (P(1 + P)r + ?х)²

Pr ^{x)(epr^(x) + pr^(x) + p²r^(x) + 8?) = (P(1 + P)r^(x) + ?х ^(x))² =

P0r^(x)х^(x) + p³(1 + P)r^(x)2 _=u < ₁ (P(1 + P)r^(x) + ?х^(x))^{2 _U<} .

Характеристическое уравнение для системы (2.19)-(2.21), линеаризованной около (хМ r<^x)) имеет вид

х^(x) ur^(x)

- px^(x) Pr^(x) - Д

-д

= 0.

Это квадратное уравнение д² - 8д + pX^(x)r(^x)(v - 1) = 0 с одним отрицательным вещественным корнем. Следовательно, (хМ, H^x)) седло.

П4. Доказательство Утверждения 4

Уравнение Эйлера — (П.7). Разделим (3.2) на aj и вычтем его из (П7):

Cj / Cj - aj / aj = r - d - p - r - (1 - a)r / azj + d + v + Xj = Xj - fir / Zj -S.

Это эквивалентно (3.7). Уравнения (3.8), (3.9) и (3.10) выводятся по аналогии с (2.7), (2.8) и (2.9). Уравнение (3.12) следует непосредственно из (3.6).

П5. Доказательство Утверждения 5

Уравнение (3.15) выводится аналогично (3.7); (3.16) и (3.17) выводятся аналогично (2.20) и (2.21), причем xj заменяется на XjZj.

П6. Доказательство Утверждения 6

Уравнения (3.28) и (3.29) следуют из тождества распределений времени между странами. Чтобы получить (3.27) и (3.30) для начала просуммируем (П7) и (3.2) по странам, что, соответственно, дает С/С = r - d-p, (П10)

N



j=1

где





— суммарное потребление и активы. Используя (П8), получаем



w? uhjnj / A = (1 - a)(r / a)^-a/(1-a) (r / a)^1/(1-a) ? / A = в r.



Подставляя это в (П11) и вычитая (П11) из (П10), имеем (3.27). Суммирование (3.10) по странам дает (3.30), так как lj = l.

П7. Доказательство Утверждения 7

Характеристическое уравнение подсистемы (4.3)-(4.4), линеаризованной около стационарного состояния, имеет вид

-д -д g /1^(e) - g Je^(e) = ₀

-S|⁽e)/^⁽e) S-Д

ИЛИ

д² + (д - 8)д - S(g - g/$^e + gii^(e)/d^e)$^e)) = 0.

Достаточное условие, чтобы это уравнение имело один отрицательный корень: g₁i^(e) > ge^(e), или g₁ - (1 - e^(e))g - 8 > ge^(e). Это эквивалентно g-| > g + 8.

П8. Доказательство Утверждения 8

Мы должны показать, что собственный вектор равновесной траектории в окрестности стационарного состояния имеет угол наклона меньше чем луч M (рис. 5). Собственный вектор, отвечающий корню д = -g, удовлетворяет уравнению:

8 + g -1 - g?z^(x)/ вг (g2V-1)' ' z - z^(x)' 1^{0 0} J ^-^^(x) \^{ь b J} = 0 . Наклон этого собственного вектора равен 8+g = 8+g

_z(x) =

П9. Доказательство Утверждения 9

Собственный вектор линеаризованной системы (4.2)-(4.4), соответствующей отрицательному характеристическому корню |^(e), удовлетворяет уравнениям:

Ф

"a.

i

CO - (1 + gz^(e) /^^(e)) z^(e)(g/l^(e) - g₁/e^(e))' ' z - z^(e)' o 1


1

aT g/1^(e) - g₁/_?^(e) 1 _ |(e) o

V - 8l^(e)/|^(e) 8 - |<sup>(e)

J</sup> l - l<sup>(e)

V J</sup> Комбинируя первое и второе уравнение в (П12), получаем

(8 - |^(e))(z - z^(e)) = [(1 + gz^(e)/^^(e)) - z^(e) (g + |^(e))](<^ - ^^(e))

или

C₁| = C₂z + C₃, (П13)

где

C1 = (1 + gz^(e)/^^(e)) - z^(e) (g + |^(e)),

C₂ = 8 - |^(e),

C₃ = [(1 + gz^(e)/^^(e)) - z^(e) (g + |^(e))]^^(e) - (8 - |^(e))z^(e). Коэффициенты C1 и C3 положительны благодаря (4.18) и тому, что

^^(e) = вг + 8z^(e).

Третье уравнение в (П12) можно представить как

l = C4^ + C5, (П14)

где

C₄ = 8l^(e)/$^e)(8 - |^(e)) > 0,

C₅ = -|^(e)l^(e)/(8 - |^(e)) > 0.

Начальная точка (zo, |o> lo) удовлетворяет (4.17), так как lo = Doo zoo, где D = (Рг/?)у.

Подставляя это в (П13) для z = zo и | = |o, имеем

(П15)

^C1^Dlo = ^C2^/oo + ^C3^/oo ^zo.

Подстановка (4.17) в (П14) для і = і₀ и | = |₀> и комбинирование полученного выражения с (П15) дает

^C1^C5^D___^сз _

^{1 - C}4^DoO^z0 Со^z0 ^oo

Левая часть этого уравнения возрастает по ooZo и, следовательно, это произведение монотонно убывает по oo. Произведение ooZo определяет угол наклона M. Если oo > oo^(e), то ooZo < oo^(e)Zo^(e), и M пересекает G1. В данном случае начальная точка принадлежит траектории быстрого роста (рис. 6). Если oo < oo^(e), M пересекает G2, и начальная точка находится на траектории постепенного роста.

СПИСОК ЛИТЕРАТУРЫ

Acemoglu D., Ventura J. (2002) The World Income Distribution, Quarterly Journal of Economics 117, 659-694.

Azariadis C., Drazen A. (1990) Threshold Externalities in Economic Development, Quarterly Journal of Economics 95, 354-379.

Barro R., Sala-i-Martin X. (2001) Economic Growth, McGraw-Hill, Third Printing.

Barro R., Mankiw G., Sala-iMartin (1995) Capital Mobility in Neoclassical Models of Growth, American Economic Review 85, 103-115.

Benhabib J., Perli R. (1994) Uniqueness and Indeterminacy: On the Dynamics of Endogenous Growth, Journal of Economic Theory 63, 113-142.

Borensztein E., De Gregorio J., Lee J.-W (1998) How Does Foreign Direct Investment Affect Economic Growth? Journal of International Economics 45, 115-135.

Caballe J., Santos M. (1993) On Endogenous Growth with Physical and Human Capital, Journal of Political Economy 101, 1042-1067.

Durlauf S., Quah D. (1999) The New Empirics of Economic Growth, in Handbook of Macroeconomics, Elsevier, 1A, 236-308.

Easterly W., Levine R. (2001) It’s Not Factor Accumulation: Stylized Facts and Growth Models, World Bank Economic Review 15 (2) 177-219.

Eicher Th., Turnovsky S. (1999) International Capital Markets and Non-Scale Growth, Review of International Economics 7, 171-188.

Findlay R. (1978) Relative Backwardness, Direct Foreign Investment, and the Transfer of Technology: a Simple Dynamic Model, Quarterly Journal of Economics 92, 1-16.

Goodfriend M., McDermott J. (1995) Early Development, American Economic Review 85, 116-133.

Grossman G., Helpman E. (1990) Comparative Advantage and Long Run Growth, American Economic Review 80, 769-815.

Howitt P. (2000) Endogenous Growth and Cross-Country Income Differences, American Economic Review 90, 829-846.

Jones L., Manuelli R., Rossi P. (1993) Optimal Taxation in Models of Endogenous Growth, Journal of Political Economy 101, 485-517.

Krugman P. (1991) History versus Expectations, Quarterly Journal of Economics 96, 651-667.

Ladron-de-Guevara A., Ortiguera S., Santos M. (1999) A Two-Sector Model of Endogenous Growth with Leisure, The Review of Economic Studies 66, 609-631.

Lucas R. (1988) On the Mechanics of Economic Development, Journal of Monetary Economics 22, 3-42.

Lucas R. (1990) Why Doesn’t Capital Flow from Rich to Poor Countries? American Economic Review 80, 92-96.

Lucas R. (1993) Making a Miracle, Econometrica 61,251-272.

Ortiguera S., Santos M. (1997) On the Speed of Convergence in Endogenous Growth Models, American Economic Review 87, 383-399.

Murphy K., Shleifer A., Vishny R. (1989) Industrialization and the Big Push, Quarterly Journal of Economics 94, 380-403.

Parente S., Prescott E. (2000) Barriers to Riches, The MIT Press.

Pritchett L. (1997) Divergence, Big Time, Journal of Economic Perspectives 11, 3-17.

Rebelo S. (1991) Long-Run Policy Analysis and Long-Run Growth, Journal of Political Economy 99, 500-521.

Segerstrom P., Anant T., Dinopoulus E. (1990) A Shumpeterian Model of the Product Life Cycle, American Economic Review 80, 290-304.

Stokey N. (1996) Free Trade, Factor Returns, and Factor Accumulation, Journal of Economic Growth 1,421-447.

Uzawa H., (1965) Optimum Technical Change in an Aggregate Model of Economic Growth, International Economic Review 6, 18-31.

Ventura J. (1997) Growth and Interdependence, Quarterly Journal of Economics 102, 57-84.

Wang J.-Y. (1990) Growth, Technology Transfer, and the Long-run Theory of International Capital Movements, Journal of International Economics 29, 255-271.

Young A. (1991) Learning by Doing and the Dynamic Effects of International Trade, Quarterly Journal of Economics 96, 369-405.

    Экономика: Знания - Циклы - Макроэкономика

• Введение в экономику
  
• Виды экономик
  
• Экология в экономике
  
• Экономическая теория
  
• Экономическая география
  
  
• Экономические знания
  
• Экономика России
  
  
• Циклы в экономике
  
  
• Макроэкономика
  
• Макроэкономика в России