
|
Печерский - Теория Игр Для Экономистов
Предисловие
В настоящее время огромный интерес привлекает теория игр, которая, с одной стороны, наряду с математическими моделями общего равновесия и теорией социального выбора, сыграла ключевую роль в создании современной экономической теории, а с другой, является одним из важнейших инструментов анализа огромного многообразия задач, возникающих не только в экономике, но и политике, социальных науках, военном деле, биологии и др.Суть теории игр (с экономической точки зрения) в том, чтобы помочь экономистам понимать и предсказывать то, что может происходить в экономических ситуациях, и сейчас вряд ли можно найти область экономики или дисциплины, связанной с экономикой, где основные концепции теории игр не были бы просто необходимыми для понимания современной экономической литературы.
В настоящий момент, если говорить об экономических приложениях, речь идет уже не только о применении теоретико-игровых методов к ставшим достаточно традиционными проблемам теории организации промышленности, но и, по сути дела, ко всему многообразию экономической проблематики. Теорию игр следует понимать как инструмент экономического анализа, который:
1) дает ясный и точный язык исследования различных экономических ситуаций;
2) дает возможность подвергать интуитивные представления проверке на логическую согласованность;
3) помогает проследить путь от ”наблюдений” до основополагающих предположений и обнаружить, какие из предположений действительно лежат в основе частных выводов.
При этом, как уже отмечалось выше, в настоящий момент область применения теории игр гораздо шире, чем только экономика.
Предлагаемый вниманию читателя вводный курс теории игр написан на основе лекций по теории игр, которые читались авторами на протяжении ряда лет на факультете экономики Европейского университета в Санкт-Петербурге, студентам кафедры экономической кибернетики Санкт-Петербургского государственного университета и студентам Новгородского государственного университета имени Ярослава Мудрого.
В данном пособии мы не ставили перед собой задачу детального и формального изложения различных аспектов теории игр. Наша главная цель состояла в том, чтобы познакомить студентов экономических специальностей с основами теории игр, представить им ’’первый набросок панорамной картины”, представляющей основные идеи и методы современной теории игр, на простых (порой даже примитивных) моделях продемонстрировать возможности теоретико-игрового моделирования различных экономических ситуаций и дать, тем самым, в руки ключ к двери, за которой простирается широчайшее многообразие теоретико-игровых моделей. Мы сознательно стремились минимизировать формализм, достаточно часто избегая формулировок соответствующих теорем или их доказательств. В то же время в дополнительных разделах к некоторым главам мы приводим достаточно подробно ряд важных, на наш взгляд, результатов, которые, безусловно, будут полезны тем, кто захочет более детально ’’прочувствовать” предмет.
К настоящему моменту написано огромное количество учебников по теории игр самого разного уровня, ориентированных на различных читателей. Многие из них приведены в списке литературы. Мы упомянем здесь пять, которые представляются нам наиболее удачными для тех, кто захочет познакомиться с гигантским айсбергом теории игр, лишь крохотную часть которого мы попытались представить в настоящем пособии. Это учебник выдающегося ученого и методолога, основателя советской теоретико-игровой школы — Николая Николаевича Воробьева, многие годы читавшего курс теории игр на экономическом факультете Ленинградского государственного университета (Воробьев, 1985). Далее это учебники Роберта Гиббонса (Gibbons, 1992), Мартина Осборна и Ариэля Рубинштейна (Osborn, Rubinstein, 1994), Дрю Фуднеберга и Жана Тироля (Fudenberg, Tirole, 1991) и, наконец, учебник Андрэ Мас-Колелла, Майкла Уинстона и Джерри Грина (Mas-Colell, Whinston, Green, 1995). Целый ряд задач и примеров в тексте заимствован нами именно из
этих учебников.
Мы хотели бы выразить глубокую признательность нашим студентам, которые помогали нам своими вопросами, комментариями и замечаниями и благодаря которым это пособие было написано.
Мы выражаем также глубокую благодарность Институту ” Открытое Общество”, в рамках мегапроекта которого ’’Развитие образования” стало возможным появление этого пособия.
ВВЕДЕНИЕ
В последние три десятилетия наблюдается стремительное повышение интереса к теории игр и значительное возрастание ее роли. Во многом это объясняется, тем, что без нее в настоящее время уже немыслима современная экономическая теория, причем область применения теории игр постоянно расширяется. Теория игр прошла путь от весьма формализованной теории, представлявшей интерес в первую очередь для математиков и ставшей источником целого ряда работ чрезвычайно глубокого математического содержания, до одного из важнейших инструментов анализа огромного многообразия задач, возникающих в экономике, политике, социальных науках и т. д. (разумеется, не утратив при этом своего математического содержания).1. Первыми исследованиями игр в экономической литературе, по-видимому, следует считать статьи Курно (Cournot, 1838), Бертрана (Bertrand, 1883) и Эджворта (Edgeworth, 1897), в которых рассматривались проблемы производства и ценообразования в олигополии. Правда, они рассматривались тогда как весьма специфические модели, и в некотором смысле существенно опередили свое время.
Анализ различных салонных игр проводился еще в Древнем Китае, но, видимо, первые работы, в которых нахождение оптимальных стратегий в играх формулировалось как математическая задача, появились только в XVII веке (Bachet de Mezirak, Lyon, 1612). Первым серьезным математическим результатом в этом направлении явилась работа Э.Цермело 1912 г. ”0 применении теории множеств к шахматной игре” (см. сб. ’’Матричные игры”, под. ред. Н.Н. Воробьева, М., 1961. С. 137-153). В ней он доказал, что в каждой позиции шахматной партии один из игроков может форсированно выиграть или обеспечить себе ничью, выбирая ’’правильные” ответы на любой ход противника. Хотя именно эта работа считается первой работой по теории игр, общепризнанным ’’годом рождения” теории игр стал 1944 г.
В 1944 году вышла в свет основополагающая монография Джона фон Неймана и Оскара Моргенштерна ” Теория игр и экономическое поведение” (von Neumann/Morgenstern, 1944), которая, по существу, заложила фундамент общей теории игр и обосновала возможность анализа огромного массива экономических вопросов с помощью теоретико-игровых моделей. А в 1950 г. Джон Нэш (будущий Нобелевский лауреат по экономике 1994 г.) ввел понятие ситуации равновесия, названной впоследствии его именем, как метода решений бескоалиционных игр (т. е. игр, в которых не допускается возможность создания коалиций). Ситуация, образующаяся в результате выбора всеми игроками некоторых своих стратегий, называется равновесной, если ни одному из игроков невыгодно изменять свою стратегию при условии, что остальные игроки придерживаются равновесных стратегий. Именно равновесие по Нэшу и его модификации признаются наиболее подходящими концепциями решения для таких игр.
За прошедшие с момента появления книги Дж. фон Неймана и О. Моргенштерна немногим более чем полвека теория игр прошла различные этапы своего развития и пережила несколько волн интереса к ней. Примерно 40-45 лет назад казалось, что теория игр дает чрезвычайно большие обещания экономике, однако эти обещания, увы, оказались тогда во многом лишь обещаниями, хотя в то же время был получен целый ряд очень глубоких математических результатов, представляющих значительный интерес даже вне экономических приложений. 30 лет назад ” теорию игр” можно было найти разве лишь в предметном указателе некоторых учебников по теории организации промышленности при рассмотрении олигополии по Курно, по Бертрану или по Штакельбергу. Однако за последние 20-25 лет произошел гигантский шаг вперед, и теперь вряд ли можно найти область экономики или дисциплины, связанной с экономикой, такой, скажем, как финансы, маркетинг . . . , в которых основные концепции теории игр не были бы просто необходимыми для понимания современной литературы.
Среди многочисленных определений того, что есть теория игр и каковы ее задачи, которые можно найти в различных статьях, учебниках и монографиях (см., например, Воробьев (1984, 1985), Aumann (1989), Dixit/Nalebuff (1991), Fudenberg/Tirole (1992), Myerson (1991), Rasmussen (1989) и многие другие) упомянем лишь четыре. Первые два — это определения теории игр, которые с некоторыми вариациями, по-видимому, наиболее часто встречаются в литературе и достаточно точно характеризуют общую проблематику, охватываемую теорией игр: ”Теория игр — это теория рационального поведения людей с несовпадающими интересами” (Aumann, 1989), и ’’Теория игр — наука о стратегическом мышлении” (Dixit/Nalebuff, 1991). Третье подчеркивает математическую природу теории игр: ’’Теория игр — это теория математических моделей принятия оптимальных решений в условиях конфликтов” (Воробьев, 1984). Наконец, четвертое определение выделяет роль теории игр именно в экономическом моделировании: ’’Суть теории игр в том, чтобы помочь экономистам понимать и предсказывать то, что будет происходить в экономическом контексте” (Kreps, 1990). В настоящий момент, если говорить об экономическом контексте, речь идет уже не только о применении теоретико-игровых методов к ставшим достаточно традиционными проблемам организации промышленности, но и, по сути дела, ко всему многообразию экономической проблематики. Так например, на микроуровне — это модели процесса торговли (модели торга, модели аукционов). На промежуточном уровне агрегации изучаются теоретико-игровые модели поведения фирм на рынках факторов производства (а не только на рынке готовой продукции, как в олигополии). Теоретико-игровые модели возникают в связи с различными проблемами внутри фирмы. Наконец, на высоком уровне агрегации, с международной экономикой связаны модели конкуренции стран по поводу тарифов и торговой политики, а макроэкономика включает модели, в которых, в частности, стратегическое взаимодействие рассматривается в контексте монетарной политики. ’’Аппарат теории равновесия и теории игр послужил основой для создания современных теорий международной торговли, налогообложения, и общественных благ, монетарной экономики, теории производственных организаций” (Полтерович, 1997, с. 11).
Разумеется, следует иметь ввиду, что в настоящий момент область применения теории игр гораздо шире, нежели только экономический контекст (который для нас представляет, естественно, особый интерес). Это и политический и социальный контексты, это и биология, и военное дело, и многое другое (см., например, Дюбин/Суздаль (1981), Shubik (1984), Moulin (1983, 1986), Ordeshook (1986), Rawls (1971), Maynard Smith (1974) и др.). Скажем, теоретико- игровой подход к изучению формирования коалиций — это уже своего рода традиция в социальных и политических науках (см., например, Riker (1962), Riker/Ordeshook (1973), De Swan (1973), Ordeshook (1978, 1992), Van Deemen (1997)). Здесь же следует упомянуть, например, книгу Game Theory and the Law (D. Baird, R. Gertner, C. Picker (1994)), в которой аппарат теории игр впервые применятся к анализу того, как законы влияют на поведение людей, партий и т. д.
2. Теория игр делится на две составные части: одна — это теория бескоалиционных (некооперативных) игр, а вторая — теория кооперативных игр. Это базовое деление, хотя подчас оно достаточно расплывчато, основано на том, что в бескоалиционной теории основной единицей анализа является (рациональный) ин-дивидуальныи участник, который старается сделать максимально хорошо себе в соответствии с четко определенными правилами и возможностями. Если происходит так, что индивиды принимают действия, которые можно было бы расценить как ”кооперацию” в обычном смысле этого слова, то это делается потому, что такое кооперативное поведение оказывается в интересах каждого из индивидов: каждый опасается ”расплаты” в случае нарушения кооперации (как это происходит, например, в повторяющихся играх).
В противоположность этому, в теории кооперативных игр основная единица анализа — это, как правило, группа участников, или коалиция; если игра определена, то частью этого определения является описание того, что каждая коалиция игроков может получить (чего она может достичь), без указания на то, как исходы или результаты будут влиять на конкретную коалицию.
Однако это деление ни в коем случае не следует рассматривать как исключающее: кооперативный и бескоалиционный подходы — это, если угодно, два взгляда на одну и ту же проблему. Как образно заметил И. Розенмюллер, игра — это ’’идеал”, двумя ’’тенями” которого являются кооперативный и бескоалиционный подходы.
Бескоалиционная теория стратегически ориентирована. Она изучает то, что, как мы ожидаем, будут делать игроки в игре. Кооперативная теория, с другой стороны, изучает исходы, которые мы ожидаем (см. Aumann (1997)). При кооперативном подходе мы смотрим непосредственно на пространство исходов, а не на то, каким образом они были достигнуты. Бескоалиционная теория — это своего рода микротеория; она включает детальное описание того, что происходит. В кооперативной теории нас интересует то, чего игроки могут достичь, то есть нас интересуют возможные (допустимые) исходы. То есть принимается во внимание все, что игроки могут получить, даже если у них нет соответствующих побудительных мотивов. Игроки могут вступать в коалицию и договариваться о совместных действиях, а значит, и относительно исходов; предполагается, что игроки должны соблюдать свои обязательства. Мы можем предполагать, что существует некий механизм типа суда, который форсирует выполнение контрактов, так что должны быть рассмотрены все возможные исходы.
Идея противопоставления кооперативного и бескоалиционного относится к началу 50-х годов, однако к концу 60-х годов это противопоставление начало сглаживаться. И если бескоалиционный подход можно сравнивать с микротеорией, то кооперативный (коалиционный) подход изучает игры с ”макро” точки зрения, фокусирующейся на возможных исходах, которые можно получить при обязывающих соглашениях.
Более того, в последнее время появляется все большее число работ, ’’наводя-тттих мосты” между бескоалиционной и кооперативной теорией (см., например, Gul (1989), Greenberg (1997), Hart/Mas-Colell (1995), Mas-Colell (1997), Reny (1997), Vohra (1997)).
3. Остановимся теперь чуть подробнее на проблемах приложения бескоалиционных игр, которые к настоящему времени занимают, пожалуй, большее место в экономическом моделировании. (Мы не приводим здесь формальные определения, которые будут даны ниже, а на интуитивном уровне прокомментируем лишь некоторые моменты).
Бескоалиционная теория игр — это способ моделирования и анализа ситуаций, в которых оптимальное решение каждого игрока зависит от его представлений или ожиданий от действий (игры) его оппонентов (партнеров). Важнейшей чертой этой теории является то, что она ”настаивает” на том, что игроки не должны иметь произвольных представлений относительно игры своих оппонентов. Напротив, каждый игрок должен пытаться предсказать игру своих оппонентов, используя свое знание правил игры и предположения, что его оппоненты рациональны, и поэтому пытаются сделать свои предсказания и максимизировать свои выигрыши.
Напомним, что цель теории игр — помочь нам понимать и предсказывать экономические феномены. Если применим критерий доминирования, то своего рода негласным соглашением является то, что агенты не будут выбирать стратегии, которые являются доминируемыми (т.е. те стратегии, которые хуже). И до тех пор, пока мы исходим из справедливости этой гипотезы, критерий доминирования дает четкий путь для предсказаний.
С равновесием по Нэшу, к сожалению, все обстоит несколько хуже. В некоторых ситуациях достаточно очевиден некоторый вполне определенный способ действия.
2 2
| ||||||||||||||||||
| А В |
В случае А, по-видимому, совершенно очевидно, что ”играть” надо левую нижнюю клетку (т.е. выбирать, соответственно, d и /), тогда как совершенно не понятно, что нужно играть во втором случае. И одна из возможностей состоит в разрешении предварительных переговоров. Но если бы понятие равновесия по Нэшу можно было оправдать, апеллируя только к предварительным переговорам, то значение этого понятия было бы достаточно низким, поскольку центральным становился бы вопрос о ’’силе договоренности”. Однако ’’оправдание” равновесия по Нэшу исходит из ряда других соображений, на которых мы остановимся, в частности, в главе 1. Мы не будем пытаться приводить сложные модели, а лишь упомянем некоторые возможные приложения. Рассмотрим следующую игру
| 1 | г | |
| и | 5,5 | -1,6 |
| 1 | ||
| d | 6,-1 | 0,0 |
В этом примере (мы впоследствии будем неоднократно возвращаться к такого типа игре) равновесие по Нэшу определяется стратегией d первого игрока иг — второго игрока. Действительно, если первый игрок выбрал стратегию d, то второму игроку невыгодно отклоняться от стратегии г , так как он вместо 0 получит выигрыш —1. Аналогично, если второй игрок придерживается стратегии г, то первому невыгодно вместо d играть и, так как он также вместо 0 проиграет Е
В тоже время ’’хорошая” ситуация (и, I) , когда игрок 1 выбирает и , а второй — I, не является ситуацией равновесия по Нэшу, так как, например, игроку 1 выгодно (при условии, что второй играет I) отклониться от и и сыграть d, поскольку вместо 5 он выиграет 6.
На этом простом примере мы видим, что ситуации равновесия по Нэшу могут приводить к тем исходам, которые представляются весьма неудачными. Однако здесь возникает целый ряд интересных возможностей, в частности, связанных с введением динамики, позволяющих уходить от таких ’’неудач”. Однако об этом нам предстоит подробнее говорить ниже.
Безусловно, следует специально подчеркнуть, что большая роль теории игр в экономике во многом объясняется тем, что теория игр дает язык для моделирования и технику анализа специфического динамического конкурентного взаимодействия. Скажем, в достаточно простом варианте это можно проиллюстрировать на следующем примере (см., Kreps (1990)). Представим себе монополиста (в классическом смысле), производящего некоторый товар для продажи. Для простоты будем считать, что спрос определяется кривой х = 13 — р. Структура затрат монополиста также весьма проста: с(х) = 6.25 + х . Стандартная теория предсказывает, что монополист, максимизирующий прибыль, будет выпускать 6 единиц готовой продукции и получит прибыль 29.75 (при цене 7). В то же время, если в данной ситуации рассмотреть возможность входа новичка (с такими же характеристиками), то ответ будет уже совершенно другим: укоренившийся монополист, предвидящий возможность входа, будет производить 7 единиц готового продукта (при цене 6), теряя несколько в прибыли в данном периоде, но обеспечивая себе большую прибыль в длительном периоде, поскольку новичок, считающий, что укоренившаяся фирма будет продолжать выпускать тот же объем продукции, воздержится от входа, так как его вход принесет ему нулевую прибыль.
Разумеется, здесь возникает, например, такой вопрос. А почему собственно-новичок должен верить в то, что монополист будет продолжать выпускать такой-то объем готовой продукции, если новичок все-таки ’’осмелится” войти в отрасль? Этот вопрос, безусловно, существенен для этой истории. Хотя простейшая модель не дает ответа на этот вопрос, тем не менее белее сложные модели входа со сложной динамикой, которые используют многошаговые игры, уже позволяют анализировать ситуации входа с различными гипотезами о поведении агентов. Скажем, если мы будем рассматривать двух-периодную модель, то уже появляется возможность рассматривать более сложное поведение. Например, возможен вариант, когда монополист в первом периоде выбирает технологию. Он может, к примеру, за счет высоких фиксированных затрат снизить предельные затраты. Высокие фиксированные затраты и низкие предельные затраты делают поведение монополиста более агрессивным во втором периоде. Далее монополист может в первом периоде предпринимать действия, порождающие ”потребительскую лояльность” (скажем, снижать цены) и т. д. и т. и. Известны многочисленные вариации на тему входа. Основной характеристикой соответствующих моделей является то, что в первом периоде монополист совершает действие, которое изменяет природу ”дальнейшей игры”, если новичок появляется, и которое может либо предотвратить вход совсем, либо позволит монополисту ”подготовиться” к входу так, чтобы иметь преимущество в образующейся впоследствии дуополии (см.: например, Dixit (1980)).
Другая вариация на эту тему — это рассмотрение ситуации, когда новичок не имеет точного знания характеристик монополиста. Например, новичок не знает структуры затрат монополиста. В этом случае он может воспринимать низкую цену в первом периоде как сигнал, говорящий о низких предельных затратах укоренившейся фирмы, а стало быть воздержаться от входа. Монополист, понимая это, может, даже в случае высоких предельных затрат, назначить достаточно низкую цену, сигнализируя тем самым о, якобы, низких затратах.
Следующий момент, который необходимо отметить — это момент, связанный с тем, что теория игр дала возможность моделировать ситуации, когда речь идет о том, верить или не верить тем или иным обещаниям или угрозам. Здесь речь идет о моделировании репутации (скажем работодатель и работник).
Следующий классический пример, связанный с повторяющимся взаимодействием участников — неявный сговор в олигополии. Он базируется на так называемой Folk Theorem (’’народной теореме”, ’’фольклорной теореме” — см. гл. 2), которая утверждает, что любые выигрыши двух фирм, которые дают каждой из фирм больше максиминного выигрыша и в сумме меньше, чем монопольная прибыль (за период) может поддерживаться в равновесии, если будущее ценится фирмами достаточно высоко. Как и во многих случаях, здесь возникает неприятный момент множественности равновесия, который, увы, оказывается весьма существенным и вынуждает пытаться вводить различные модификации равновесия по Нэшу.
Равновесия по Нэшу — это ’’согласованные” предсказания того, как игра будет разыгрываться, в том смысле, что если все игроки предсказывают, что возникнет определенное равновесие, то ни у одного из игроков не будет стимулов для отклонения. Таким образом, равновесие по Нэшу, и только оно, может обладать свойством, таким что игроки могут предвидеть его, их оппоненты предвидеть его и т. д. Напротив, предвидение того, что возникнет неравновесная ситуация, влечет за собой то, что по крайней мере один игрок сделает ’’ошибку”, либо в своем предсказании, либо в оптимизации своего выигрыша. Естественно, вряд ли можно считать, что такие ошибки никогда не возникают.
4. В то самое время, когда теория бескоалиционных игр становится стандартным инструментом в экономике, она подвергается значительной критике со стороны как теоретиков так и экспериментаторов. Бескоалиционная теория игр, подобно неоклассической экономике, базируется на двух ’’героических” предположениях: МАКСИМИЗАЦИИ (каждый экономический агент рационален и ясно представляет себе мир); и СОГЛАСОВАННОСТИ (представления агента, и, в частности, его ожидания относительно поведения остальных агентов правильны). Эти два предположения, по сути дела и оправдывают то, что общие образцы индивидуального оптимизирующего поведения формируют равновесие по Нэшу.
Основная проблема, с которой в настоящее время столкнулись теоретики — это проблема ’’неотразимого” обоснования этих двух предположений, ибо традиционные обоснования отнюдь не являются неотразимыми. В то же время без такого обоснования использование теории игр в приложениях становится проблематичным. Использование теории игр требует понимания того, когда эти предположения осмысленны, а в каких случаях — нет. Основной упрек, часто адресуемый экономической методологии, касается центральной роли гипотезы максимизации. Общий неформальный аргумент в пользу максимизации состоит в том, что любой не максимизирующий агент, и в частности, любая фирма, не максимизирующая прибыль, будет выдавлена рыночными силами. Это эволюционный аргумент, и как таковой, хорошо известен. Однако, работает ли такое оправдание? Является ли равновесие по Нэшу, или какое-либо связанное с ним понятие, хорошим предсказанием?
Аналогия между бескоалиционной теорией игр и неоклассической экономикой очевидна, но она не абсолютна. Конечно, вопрос о том, максимизируют ли агенты, по существу один и тот же. Более того, предположение согласованности появляется также в неоклассической экономике как предположение о том, что цены очищают рынок. Однако фундаментальное различие между неоклассической экономикой и бескоалиционной теорией игр в том, что многочисленные равновесия в конкурентной экономике почти всегда разделяют многие из свойств (скажем, эффективность или ее отсутствие), тогда как многочисленные равновесия в игре могут иметь существенно различные свойства. Неоклассическая экономика не ставит вопроса о выборе равновесия, теория же игр обязана это делать.
В настоящее время очень стремительно развивается эволюционная теория игр.
Большинство работ по эволюционной теории игр мотивированы двумя основными вопросами: 1. Действительно ли агенты играют равновесие по Нэшу? 2.Если агенты играют равновесие по Нэшу, то какое?
Эволюционная теория игр формализует и обобщает эволюционный аргумент, предполагая, что более успешное поведение имеет тенденцию превалировать. В канонической модели популяция игроков взаимодействует во времени, причем их поведение приспосабливается во времени в ответ на их выигрыши (полезности, прибыли и т. д.), к которым исторически приводил их выбор. Эти игроки могут быть работниками, потребителями, фирмами и т. и. В центре внимания находится динамическое поведение системы. Ключевыми предположениями являются предположения о том, что имеется популяция игроков, эти игроки взаимодействуют, и что поведение игроков наивно (в двух смыслах: игроки не верят, не понимают, что их собственное поведение потенциально влияет на будущее поведение их оппонентов, и игроки, типично, не принимают во внимание возможность того, что их оппоненты подобным же образом вовлечены в приспособление своего собственного поведения). Здесь важно заметить, что успешное поведение становится превалирующим не только потому, что рыночные силы производят отбор, исключая неуспешное поведение, но и потому, что агенты имитируют успешное поведение.
Поскольку эволюционная теория игр изучает популяции, ”играющие в игры”, она также полезна при изучении социальных норм и конвенций. Эволюция конвенций и социальных норм является примером игроков, обучающихся играть равновесие. Примеры включают популяцию потребителей, которые должны решить, какой тип товара покупать; популяцию работников, которые должны решить, какие усилия прилагать, и т. д.
Эволюционная теория игр дает положительный ответ на первый вопрос: во многих постановках игроки действительно играют равновесие по Нэшу. Таким образом, это дает оправдание равновесного анализа тогда, когда осмысленны эволюционные аргументы. Равновесие лучше всего рассматривать как устойчивое состояние сообщества, члены которого близоруко группируются ”по направлению” к максимизирующему поведению. И это существенно контрастирует с более ранним взглядом (у которого нет достаточного фундамента), в соответствии с которым теория игр и равновесный анализ представляют исследование взаимодействия ультра-рациональных агентов с ”большим запасом” знаний.
Вопрос о том, какое равновесие играется, широко обсуждается особенно в литературе, касающейся ”уточнений” (или ”утончений”) равновесия. Однако проблема их обоснования также относится к ним. Можно представить себе, например, что допускается пред-игровое общение, которое приводит к тому, что определяется, какое равновесие играется (скажем, все работники прикладывают максимум усилий, или, напротив, минимум, если, к примеру, общий выпуск определяется минимальным (среди всех работников) уровнем усилий). Такое оправдание равновесия, конечно, возможно и применимо к ряду приложений. Но это не покрывает все возможности, тем более, что неизбежны ситуации, когда договор может нарушаться, или, что просто может не быть возможности предварительного общения.
Второе оправдание само-осуществляющегося предсказания может проходить примерно следующим образом: если теоретически единственным образом предсказанное поведение игроков известно игрокам в игре, то она должна предсказывать равновесие по Нэшу. Трудность здесь в том, что такое оправдание требует теории, которая однозначно предсказывает поведение игроков, а в этом-то проблема как раз и состоит.
Оправдание с помощью ’’фокальной точки” (Т. Шеллинг) можно формулировать примерно так: ’’если есть очевидный путь играть в игре (либо в силу специфики постановки, либо в силу специальной структуры), то игроки будут знать, что будут делать другие игроки”.
Наконец, игроки могут научиться играть некоторое равновесие. Для того, чтобы научиться играть некоторое равновесие, игроки должны иметь возможность повторять розыгрыш этой или, по крайней мере, близкой, игры, чтобы иметь возможность получать нужный опыт. Если только игроки узнали, как играют их оппоненты, и если игроки максимизируют, то они должны оказаться в равновесии по Нэшу. В этой истории с обучением есть два момента. Первый — игроки максимизируют. Второй — это то, что при условии максимизирующего поведения игроков, игроки могут узнать поведение своих оппонентов. Это включает в себя дополнительные нюансы обучения. Даже если игрок знает, как его оппоненты играли, они могут не знать, каково было наилучшее действие. Наконец, само обучение меняет обстановку, которую агенты пытаются узнать, причем процесс обучения весьма тонок.
Мы остановились здесь на некоторых моментах, которые представляются нам важными, и на которых мы считали необходимым остановиться в преддверии формального изложения теории.
Глава 1
Статические игры с полной информацией
1.1 Способы задания бескоалиционных игр
Основная часть курса будет посвящена теории бескоалиционных игр. Это ни в коей мере не означает, что отсутствует интерес экономистов к ”некооперативному поведению”. Напротив, в настоящее время заметен существенный интерес к попыткам объяснить, каким образом кооперация может возникнуть как результат поведения индивидов, преследующих свои цели. Наконец, есть целый ряд важных задач, где роль теории кооперативных игр весьма существенна. Им мы посвятим заключительную часть курса.Теория бескоалиционных игр — это способ моделирования и анализа ситуаций, в которых оптимальные решения каждого участника (игрока) зависит от его представлений (или ожиданий) об игре его оппонентов. Как уже говорилось во введении, важнейшим моментом теории является акцент на то, что игроки не должны придерживаться произвольных представлений об игре своих оппонентов. Напротив, каждый игрок должен пытаться предсказать игру своих оппонентов, используя свои знания правил игры и исходя из предположений, что его оппоненты — сами рациональны, а потому пытаются сами также предсказать игру своих оппонентов и максимизировать свои собственные выигрыши.
Есть два способа задания игры. Первый — это позиционная форма игры. Позиционная форма задает: (1) порядок ходов, (2) ”альтернативы” (выбор), доступные
 |
|
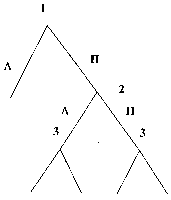
Рис. 1. Информационные множества отмечены пунктиром. 1, 2, 3 — номера игроков, имеющих право хода (здесь не указаны выигрыши в концевых вершинах дерева). |
Позиционная форма представляется деревом игры, которое можно рассматривать как обобщение дерева принятия решений, используемое в теории принятия решений, на случай нескольких игроков. Формальное определение мы приведем в гл. 2. ” Древесная структура” описывает, какая вершина следует за какой, какой игрок имеет ход, в соответствующей вершине. Информация, которую имеют игроки, описывается с помощью информационных множеств. (См. рис. 1). Если две вершины лежат в одном информационном множестве, то это означает, что игрок (в данном случае 3) не может сказать, какое из двух действий (Л или П) в действительности произошло (в этом смысле игрок не различает вершины дерева, лежащие в одном информационном множестве).
На рисунках 2 и 3 изображены недопустимые информационные множества: информационные множества не могут пересекаться (не различая вершины одного информационного множества и вершины другого информационного множества, которое пересекается с первым, игрок тем самым не различает вершины, лежащие в объ-
 |
| Рис. 4. В концевых вершинах указаны выигрыши игроков. |
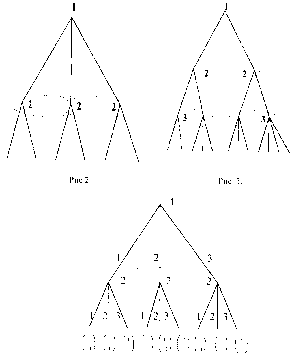
Приведем элементарный пример. Рассмотрим следующую игру: первый игрок выбирает одну из трех цифр — 1,2 или 3. Затем второй игрок, не зная выбора первого игрока, также выбирает одну из трех цифр — 1, 2, 3. Если сумма выбранных цифр четна, то первый игрок выигрывает у второго один рубль (доллар, фунт ...). Если сумма — нечетная, то наоборот — выигрывает второй. Дерево соответствующей игры изображено на рис. 4.
На рис.5 изображена модификация этой игры, в которой второму игроку стано-
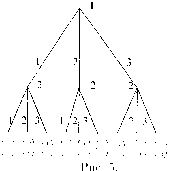
вится известно либо, что первый игрок выбрал цифру 2, либо, напротив, что цифру 2 он не выбрал.
Мы вернемся к позиционной форме в гл. 2 (поскольку в этой главе нас интересуют стаические игры с полной информацией, для которых позиционная форма — это некоторое излишество), а теперь перейдем ко второй возможной форме представления игры — нормальной или стратегической форме, которая ”суммирует” позиционную игру в трех элементах: множестве игроков / , множестве стратегий каждого игрока и функции выигрышей, ставящей в соответствие каждому набору стратегий игроков соответствующие выигрыши игроков.
1.2 Игры в нормальной форме
Итак, игра в нормальной (или стратегической) форме — это тройка {/, S = и = (щ,. . ., ип)} , где / = {1, . . . , п} — множество игроков, S) — множество стратегий (ходов), доступных игроку і = 1,... ,п , щ : S = Пщ/ _•* —функция выигрышей игрока і, ставящая в соответствие каждому набору стратегий s = (s 1,. . ., sn) , называемому также ситуацией, выигрыш этого игрока.
Стандартный пример здесь — дуополия по Бертрану и по Курно, когда стратегии — это цены или объемы выпуска, соответственно, а выигрыши — это прибыль (см. и. 1.8-1.10).
Важным предположением, которое играет ключевую роль в теории, состоит в предположении, что все игроки рациональны, в том смысле, что каждый игрок рассматривает имеющиеся в его распоряжении альтернативы, формирует представления относительно неизвестных параметров, имеет четко определенные предпочтения и выбирает свои действия в результате некоторого процесса оптимизации (максимизации своей целевой функции). Более того, не менее существенным является факт общеизвестности (общего знания) рациональности игроков, т. е. все игроки не только рациональны, но и знают, что другие игроки рациональны, что все игроки знают, что все игроки знают, что они рациональны и т. д. Формальное определение общеизвестности см. Aumann (1976).
Замечание 1.2.1. В последние годы появилось значительное число работ, посвященных исследованию моделей ограниченной рациональности. Основная мотивация этих работ — неудовлетворенность теорией, оперирующей с ” совершенно рациональным человеком”, поскольку мы является свидетелями весьма частого несоответствия реального поведения людей предположению ”совершенной рациональности”. Идея моделирования ограниченной рациональности восходит к работам Герберта Саймона (Simon (1955, 1956), см. также Simon (1972, 1976)). Обсуждение проблем, связанных с моделировнием ограниченной рациональности можно найти, например, в книге Rubinstein (1998). Различные взгляды на проблемы моделирования рациональных и ограниченных рационвльных игроков изложены в работах Binmore (1987, 1988), Auman (1996).
Обратимся к тому случаю, когда / = {1,2} и множества стратегий каждого из двух игроков — конечны. В этом случае игру можно ”изобразить” с помощью матрицы (см. рис. 6), где М = |S}| — число возможных стратегий игрока 1, К = Ібф —число возможных стратегий игрока 2, amk = и\(з[т\з^), = и2(з[т\з^),
к = 1,. . . , К , т = 1,. . . , М .
Эту же игру можно представить в виде двух матриц (поэтому такие игры называются часто биматричными), элементами которых являются элементы amk и bmk , соответственно.
Для конечной антагонистической игры, т. е. игры двух лиц такой, что
 |
| Рис. 6. |
к=1,...,К
ными (см. подробнее Дополнение (Раздел 1.13)).
Смешанная стратегия6 сц — это вероятностное распределение на множестве чистых стратегий Si . (Мотивацию введения смешанных стратегий мы оставляем на будущее). Рандомизация каждым игроком своих стратегий статистически независима от рандомизаций его оппонентов, а выигрыши, соответствующие профилю (набору) смешанных стратегий — это ожидаемое значение выигрышей соответствующих чистых стратегий (т.е. речь здесь идет об ожидаемой полезности). Одна из причин, по которой мы сосредотачиваемся на конечном случае — стремление избежать ’’осложнений”, связанных с теорией меры.
Будем обозначать пространство смешанных стратегий і -ого игрока через ^ •, а аі(зі) — веростность того, что выбирается стратегия щ . Пространство наборов смешанных стратегий — ^ = Пщ/ Si 5 элементы которого мы будем обозначать через а . Носитель смешанной стратегии сц — это множество тех чистых стратегий, которым ’’приписана” положительная вероятность.
Определение 1.2.1 Если Si — конечное множество чистых стратегий игрока і, то смешанная стратегия сц : Si —>¦ [0,1] ставит в соответствие каждой чистой стратегии зг- ? Si вероятность стДзД > 0 того, что она будет играться, причем = 1 .
(Обратим внимание на то, что индекс і означает здесь, что речь идет о стратегии игрока і. Поэтому, если мы будем говорить о разных стратегиях игрока і, то мы будем обозначать их s8-, s', s",. . .) . Нетрудно заметить, что множество смешанных стратегий игрока і — это (к( — 1)-мерный симплекс, где к( — число чистых стратегий і -ого игрока.
Выигрыш игрока і, соответствующий профилю (набору) стратегий а , есть
П
М*'И = (2-1)
sES j=1
(поскольку на наборах чистых стратегий значения этой функцими совпадают со значениями исходной функции выигрышей щ , мы сохраняем то же обозначение).
Важно отметить, что выигрыш і -ого игрока есть линейная функция от вероятностей (Ті , а также является полиномом от профиля, а потому непрерывен. Наконец, чистые стратегии являются вырожденными смешанными стратегиями, приписывающими вероятность 1 данной чистой стратегии и вероятность 0 — остальным.
Определение 1.2.2 Смешанным расширением игры Г = {/, S, и} называется игра Г = {/,ЕМ; где Е = Пщ/Ею а и{(т), где ст G Е); определяется равенством
(2.1).
Пример. Рассмотрим игру, изображенную на рис. 7.
L М Р
Рис. 7.
Пусть од = (это означает, что смешанная стратегия игрока 1 приписывает ему играть стратегии и , т и d с вероятностями 1/3), сг2 = (о, (эта
смешанная стратегия игрока 2 предписывает играть стратегии М и R с равными вероятностями и не играть стратегию L вовсе).
В данном случае мы получаем
, ч 1 / 1 1 \ щ(а) - -(0-4 + --5 + --б) +
-(о • 2 + -
8 + --3
1 1
3 + Г9 + -.'2) =
к°
—ио(сг) = —
1.3 Доминируемые стратегии
Посмотрим внимательно на приведенную выше игру (рис. 7). Независимо от того, как играет игрок 1, R дает игроку 2 строго больший выигрыш нежели М . В этом смысле стратегия М строго доминируема, поэтому ясно, что рациональный игрок 2 не должен играть М . Далее, если игрок 1 знает (т.к. он сам рационален и знает, что другой рационален...), что 2 не будет играть М, то для него и будет лучше, чем т или d. Наконец, если игрок 2 знает, что игрок 1 знает, что игрок 2 не будет играть М, то игрок 2 знает, что 1 будет играть и , а тогда 2 должен играть L . Этот процесс — последовательное удаление строго доминируемых стратегий (мы дадим позднее строгое определение и соответствующий экономический пример). Вопрос, естественно возникающий здесь: ”А не зависит ли множество стратегий, выдерживающих такое исключение доминируемых стратегий, от порядка исключения?” К счастью, нет, и дело здесь в том, что если стратегия щ строго хуже чем Д для всех стратегий оппонента из множества D , то она хуже чем Д и для любого подноже-ства множества D .Посмотрим теперь на следующую игру (см. рис. 8)
| L | R | |
| и | / (2,0) | (-1,0) |
| М | (0,0) | (0.0) |
| D | V (-1,0) | (2.0) |
| Рис. 8. |
Введем следующие обозначения: пусть і ? /, тогда через s_; ? S'-; — будем обозначать набор стратегий игроков из / \ {г}, (s',s_;) обозначает набор стратегий (щ, • • • , зг_і, s', s;+i, sn) . Аналогично, для смешанных стратегий (су', а_;) — это (су,. . . , су_і, су', су+і,. . ., (тп) . (Заметим, что в этих обозначениях s = (s;, s_;) ).
Определение 1.3.1 Чистая стратегия S; игрока і в игре Г строго доминируема (строго доминируется), если существует другая чистая стратегия s' такая, что
— 0 ^ —г) (3.1)
для всех s_; ? SA; .В этом случае говорят, что стратегия s' доминирует стратегию S; . Стратегия S; слабо доминируется, если существует такая s' , что (3.1) выполняется как нестрогое неравенство, но хотя бы для одного набора s_; - неравенство строгое.
Аналогично определение и для смешанных стратегий:
Опеределение 3.1’ Смешанная стратегия Оі строго доминируется в игре Г; если существует другая стратегия су- такая, что для всех а? У) ¦
гу(су',сг_Д > щ(су,сг_г).
Стратегия су называется строго доминирующей стратегией для игрока і в игре Г , если она строго доминирует любую другую стратегию из УД .
Заметим, что для того, чтобы проверить, что су строго доминируется стратегией су', нам нужно посмотреть на ” поведение” этих двух стратегий против чистых стратегий оппонентов игрока і.
Формально:
(A) щ(су, сг_Д > гу(су, ст_г) ?ст_г тогда и только тогда, когда
(B) іу(су', s_8) > iy(cy, s_8) Vs_8.
Действительно: рассмотрим разность
щ(сг', сг_Д - гу(су, СГ-Д = ^ (Д crfc(sfc))[u8(cr', s_8) - гу(су, s_8)].
<5 —г€5_г кфі
Тогда если (В), то (А), т.к. все [it4-(cP, 5_г-) — иг(сгг, з_г)] > 0 . (В) следует из (А), т.к. з_г- — вырожденный случай а_г- .
Задача. Докажите, что если чистая стратегия щ является строго доминируемой, то таковой же является и любая стратегия, использующая щ с положительной вероятностью.
Однако смешанная стратегия может быть строго доминируемой даже, если она использует с положительной вероятностью чистые стратегии, которые даже не слабо доминируемы. Действительно, рассмотрим следующую игру (рис. 9).
| L | R | |
| и | ( (1,3) | (-2,0) |
| М | (-2.0) | (1.3) |
| D | V (ОЗ) | (0.1) |
| Рис. 9. |
мости от того, что играет игрок 2, а следовательно строго доминируется стратегией
D.
Естественно, что строго доминируемые стратегии надо удалять. Если игра разрешима в смысле последовательного удаления строго доминируемых стратегий, т. е. каждый игрок остается с единственной стратегией, как в нашем первом примере, то, получившаяся ситуация будет хорошим кандидатом для предсказания того, как будет проходить игра.
Вернемся к игре, изображенной на рис. 7.
Нетрудно убедиться в том, что здесь в результате последовательного удаления строго доминируемых стратегий остается пара стратегий (u, L) . На первом шаге удаляется стратегия М (она доминируется стратегией R). Затем удаляется стратегия т (доминируемая стратегией и).На третьем шаге удаляется стратегия d (доминируется стратегией и). Наконец, на последнем шаге удаляется R.
Но, даже если такие ситуации представляют собой хорошие кандидатуры, все не обязательно произойдет в соответствии с их ” предписанием”, особенно если выигрыши могут принимать ”экстремальные” значения.
Рассмотрим, например, следующую игру (рис. 10).
L R (20,10) (15,20)
(-100,20) (40,30)
Рис. 10.
Очевидно, что здесь стратегия L доминиурется стратегией R, а потому ситуация (D}R) является хорошим кандидатом. Но ... Проигрыш игрока 1 в ситуации (Z), L) слишком велик, поэтому вполне можно допустить, что игрок 1 может не рискнуть сыграть стратегию d (допуская, например, возможность случайной ошибки игрока 2).
Все, конечно, изменится, если игроки могут договориться до того, как принять решение. В этом случае, конечно, все уже будет зависеть от ’’силы” договоренности.
1.4 Последовательное удаление слабо доминируе
мых стратегии
Рассмотрим следующую известную игру ’’Море Бисмарка”. Предыстория события такова: 1943 г. Адмирал Imamura получил приказ доставить подкрепление по морю Бисмарка на Новую Гвинею. В свою очередь адмирал Kenney должен был воспри-пятствовать этому. Imamura должен был выбрать между Северным (более коротким) и Южным маршрутами, a Kenney — решить куда посылать самолеты, чтобы разбомбить конвой. Причем в течение одного дня самолеты могут бомбить лишь на одном из двух направлений — либо на Северном, либо на Южном маршрутах (но не на двух). Поэтому, если Kenney посылает самолеты в сторону неправильного маршрута, то они могут вернуться, но число дней, когда возможна бомбежка, уменьшается. Описываемая ситуация моделируется следующей игрой. Считаем, что Северный маршрут займет 2 дня, а Южный — 3. (См. рис. 11).| С евер | 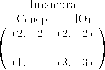 |
Рис. 11.
Вообще говоря — это матричная игра, т. е. антагонистическая игра с конечным множеством стратегий у каждого игрока. Ни один игрок не имеет доминирующей стратегии. Но здесь можно говорить о слабом доминировании: для Ітатиг’ы стратегия Ю слабо доминируема, так как для любой стратегии Kenney проигрыш Ітатиг’ы (число дней, когда конвой будет подвергаться бомбордировкам) не меньше для Ю, чем для С, но для стратегии Kenney Ю — проигрыш при С строго меньше, чем при ю.
Последовательное (итерированное) удаление слабо доминируемых стратегий проходит следующим образом: исключается одна из слабо доминируемых стратегий одного из игроков, затем из оставшихся стратегий исключается одна из слабо доминируемых стартегий и т. д.
Представим себе, что Kenney понимает это и считает, что Imamura выбирет Север. В этой новой ситуации Kenney имеет уже доминирующую стратегию — Север. Это и дает нам равновесие при последовательном удалении доминируемых стратегий. (В действительности, так и случилось: 2-5марта 1943 г. ВВС США и Австралии атаковали японский конвой, который шел по Северному пути и потопили все транспортные корабли и 4 эсминца: из 7000 чел. до Новой Гвинеи добрались 1000.)
Процедура последовательного удаления слабо доминируемых стратегий аналогична удалению строго доминируемых стратегий. Однако здесь есть одно весьма значительное отличие. А именно, множество стратегий, которые выдерживают последовательное удаление слабо доминируемых стратегий (то есть остаются) может зависеть от порядка удаления стратегий.
Действительно, рассмотрим следующую игру (рис. 12).
| L | я | |
| и | / (1,1) | (0,0) |
| М | (1Д) | (2,1) |
| D |
О О | (2,1) |
| Рис. 12, |
Рассмотрим несколько примеров. Мы начнем со знаменитой Дилеммы Заключенного — в некотором смысле чрезвычайно простой игры, которая в разных формулировках встречается в большинстве учебников по теории игр, которая приводится едва ли не в самом начале каждого курса и которую многие сразу же вспоминают, когда слышат словосочетание ”теория игр”.
Дилемма Заключенного. Ставший почти хрестоматийным сюжет этой стилизованной истории таков. Двое подозреваемых в совершении тяжкого преступления арестованы и помещены в одиночные камеры, причем они не имеют возможности передавать друг другу какие-либо сообщения. Их допрашивают поодиночке. Если оба признаются в совершении преступления, то им грозит, с учетом их признания, тюремное заключение сроком по 6 лет каждому. Если оба будут молчать, то они будут наказаны за совершение какого-то незначительного преступления и получат в этом случае по 1 году тюремного заключения. Если же один из них сознается, а другой — нет, то первый, за содействие следствию, будет вовсе освобожден от наказания, тогда как второй будет приговорен к максимально возможному за данное преступление наказанию — 10-летнему тюремному заключению.
Описанная история может быть представлена следующей игрой (рис. 13).
м с (-1,-1) (-10,0) (0,-10) (-6,-6)
Рис. 13.
Здесь нетрудно убедиться в том, что стратегия ”молчать” является строго доминируемой для каждого игрока (еще раз напомним, что они рациональны), поэтому каждый игрок выберет стратегию ”сознаться”. В результате оба заключенных получат по 6 лет тюремного заключения.
Как мы увидим ниже ситуация (”сознаться”, ”сознаться”), естественно, является ситуацией равновесия по Нэшу. При этом мы сразу же сталкиваемся с бросающейся в глаза проблемой: получающийся исход очень плохой — он дает максимальный суммарный срок заключения (разумеется, мы подчеркиваем это еще раз, не следует забывать предположение о рациональности игроков, поскольку здесь исключаются из рассмотрения проблемы предательства, и т. д.). Это послужило толчком к многочисленным исследованиям этой игры, поскольку, например, естественным желанием было бы получить в качестве исхода этой игры (или ее модификаций) ситуацию (”молчать”, ”молчать”), дающую каждому заключенному лишь по одному году заключения.
Следующая игра имеет уже ярко выраженный экономико-политический подтекст, хотя разделяет с дилеммой заключенного упомянутую выше специфику, поэтому мы позволим себе сохранить то же название:
” Дилемма заключенного - 2?. Рассмотрим две страны добывающие нефть, которые мы назовем, скажем, А и В. Эти две страны могут кооперироваться, договариваясь об объемах ежедневной добычи нефти, ограничиваясь, к примеру, добычей 2 млн. баррелей нефти в день для каждой страны. С другой стороны, страны могут действовать некооперативно, добывая, скажем, по 4 млн. баррелей в день. Такая ситуация может быть представлена следующей игрой, в которой указаны прибыли стран, в зависимости от их объемов добычи нефти (рис. 14).
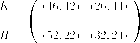 |
| Рис. 14. |
Легко видеть, что и здесь у каждого из игроков есть доминирующая стратегия — ”не кооперироваться”. В результате страны получают прибыль 32 и 24 (млн. долларов в день), что гораздо меньше, нежели в ситуации кооперативного поведения.
Феномен, с которым мы сталкнулись в этом примере, аналогичен дилемме заключенного, и именно поэтому второй пример мы также назвали ” дилеммой заключенного”: оба игрока играют свои доминирующие стратегии, максимизируя тем самым свои выигрыши, но в то же время исход для каждого из них хуже, нежели в ситуации, когда оба следуют доминируемым стратегиям.
Можно ли достичь ” кооперативного поведения” в дилемме заключенного? Как мы увидим в следующей главе — да.
Здесь мы ограничимся лишь еще одним примером на эту же тему.
” Дилемма заключенного - З?. Предположим, что есть 2 работника, которые могут ”работать” (щ = 1) и ”увиливать” (щ = 0) ( щ — уровень усилий, которые прикладывает работник г). Суммарный выпуск ”команды” 4(si + s2) делится поровну между работниками. Каждый работник несет издержки равные 3, если работает, и равные 0, если увиливает. Соответствующая матрица изображена на рис. 15.
Р У
Р / (1,1) (-1-2) \
V V (2.-1) (0.0) )
Рис. 15.
” Работать” — строго доминируемая стратегия для каждого работника.
Аукцион второй цены. У продавца есть одна единица неделимого товара. Есть п потенциальных покупателей, которые оценивают товар, соответственно, в 0 < ?\ < • • • < ?п и эти оценки являются ” общеизвестными”. Покупатели одновременно делают свои заявки (назначают цену) щ ? [0, +оо) . Назначивший максимальную заявку получает товар и платит вторую цену, т. е. если игрок і выигрывает (Si > maxj^i Sj ), то его полезность есть щ = гу — maxJ7^ щ, а остальные ничего не получают и ничего не платят (т. е. и3 = 0 ). Если несколько покупателей назначают высшую цену, то товар распределяется случайным образом (например, равновероятно).
Легко убедиться в том, что стратегия назначения своей оценки (щ = гу ) слабо доминирует все остальные. Действительно, пусть ту = maxJ7^ Sj . Пусть щ > гу . Тогда, если ту > зг- , то г-ый участник получает 0, что он получил бы и при щ = гу . Если Гі < ?{, то он получает гу — ту , что он опять же получает, назначив иг-. Если теперь гу < ту < зг-, то его полезность гг- — гг- < 0 , а если бы он назвал гу , то он бы получил 0. Аналогично и для щ < гу : если гу < щ или гу > иг-, то он получает ту же полезность, назвав гу вместо щ . Если же щ < гу < гу , то он упускает возможность получить положительную полезность.
Полезно в данном случае заметить, что поскольку назначение собственной оценки есть доминирующая стартегия, то не играет роль, имеют ли покупатели информацию об оценках других.
1.5 Рационализуемые стратегии
Мы обсуждали исключение строго доминируемых стратегий, исходя из того, что рациональный игрок никогда не выбрал бы такую стратегию, вне зависимости от того, как играют его оппоненты. Однако ”общее знание” структуры игры и того, что игроки рациональны, позволяет исключить больше. нежели просто последовательно удалить строго доминируемые стратегии, причем здесь опять же важную роль играет ’’общее знание”. Далее мы рассматриваем смешанное расширение Г игры Г .Определение 1.5.1 Стратегия сц является лучшим ответом игрока і на набор стратегий оппонентов сг_і , если иг(сгг, <т_г) > иДст', <т_г) при любых о[ ? ДЛ . Стратегия Оі является ”никогда не лучшим” ответом (далее НЛО), если не существует сг_і , для которых она была бы лучшим ответом.
Конечно же игрок не будет играть стратегию, которая является ’’никогда не лучшим ответом”.
Ясно, что строго доминируемая стратегия является ’’никогда не лучшей”. Разумеется, может случиться, что стратегия будет ’’никогда не лучшим ответом”, даже если она не является строго доминируемой (мы еще вернемся к этому). Таким образом, удаляя ’’никогда не лучшие ответы”, мы должны удалить по крайней мере и все стратегии, удаляемые при итерированном удалении строго домиинируемых стратегий. Более того, предполагая ’’общее знание”, мы можем итерировать удаление ’’никогда не лучших ответов”. Рациональный игрок не должен играть НЛО, как только он исключает возможность того, что его противники могут играть НЛО и т. д.
Стратегии, остающиеся после такого итеративного удаления, — это те стратегии, которые рациональный игрок может оправдать, или рационализовать, разумеется, при некоторых разумных предположениях о выборе своих противников.
Определение 1.5.2 Стратегии в ^Л ; которые выдерживают последовательное удаление НЛО назыаются рационализуемыми стратегиями.
Понятие рационализуемых стартегий было введено независимо Бернхеймом и Пирсом (Bernheim, 1984; Pearce, 1984).
Можно показать, что также, как и при последовательном удалении строго доминируемых стратегий, порядок удаления не существенен. Заметим, что множество рационализируемых стратегий не может быть шире, чем множество стратегий, ”выживающих” при последовательном удалении строго доминируемых стратегий, поскольку на каждом шаге процесса, определяющего множество рационализируемых стратегий, все стратегии, строго доминируемые на данном шаге, удаляются.
Пример (Osborn, Rubinstein) (см.рис. 16)
| Ьі | h | Ьз | к | |
| а\ | ( (ОТ) | (2,5) | (7,0) | (0,1) \ |
| а2 | (5,2) | (3,3) | (5,2) | (0,1) |
| а3 | (7,0) | (2,5) | (0,7) | (0,1) |
| а4 | 1 (0,0) | (0.-2) | (0,0) | (10,-1) / |
На 1 шаге исключения удаляется стратегия Ь4 , т. к. она является НЛО, поскольку она строго доминируется смешанной стратегией , 0, или ^|,|,0,0^ . Как
только исключено Ь4 можно исключить а4 , т.к. она строго доминируется а2 (поскольку Ь4 удалена). Но дальше мы уже не можем удалить ни одну стратегию, т.к. а\ — лучший ответ на Ь3 , а2 — на Ь2 и а3 — на Ь4 . Аналогично остаются Ь4 , Ъ2 , Ь3 . Таким образом, множество рационализуемых чистых стратегий есть {а>і, а2, а3} для игрока 1 и (bi}b2}b3) — для игрока 2.
Для каждой рационализуемой стратегии, игрок может построить последовательность ”оправданий” своего выбора, без ссылок на убеждение в том, что другой игрок не будет играть НЛО стратегию. Например, в этой игре игрок 1 может оправдать выбор а2 убеждением, что игрок 2 будет играть Ь2 , которое игрок 1 может оправдать убеждением, что игрок 2 будет думать, что он собирается играть а2 , что осмысленно, если игрок 1 убежден, что игрок 2 думает, что он, игрок 1, думает, что игрок 2 будет играть Ь2 и т. д.
Мы отметили, что множество рационализуемых стратегий не больше, чем множество стратегий, остающихся после последовательного удаления строго доминируемых стратегий. Однако в случае двух игроков (п = 2 ) эти два множества совпадают, так как в игре 2-х лиц (смешанная) стратегия сц является лучшим ответом
на некоторую стратегию противника, если су- не является строго доминируемой. Если чистая стратегия щ игрока і является НЛО для любой смешанной стратегии оппонента, тогда щ строго доминируется некоторой смешанной стратегией су- ? Ег- .
Посмотрим это на примере (Mas-Colell, Whinston, Green) (см. рис. 17).
Рис. 17.
У игрока 1 — три стратегии U, М и D . U лучшая против L, но худшая против R, D лучшая против R, и худшая — против L . С другой стороны М ” относительно неплоха” и против L и против R. Ни одна из этих трех стратегий не доминируется никакой другой. Но если разрешить игроку 1 рандомизацию, то игра U и D с вероятностями 1/2 каждая дает игроку 1 ожидаемый выигрыш 5, вне зависимости от стратегии второго игрока, тем самым строго доминируя М.
Предположим, что выигрыши от использования стратегии М изменены так, что М не является строго доминируемой. Тогда выигрыши от М лежат где-то выше, чем линия, соединяющая точки, соответствующие стратегиям U и D . Здесь оси соответствуют ожидаемым выигрышам игрока 1 в случае, если игрок 2 играет R (ось ur) и L (ось Ur) (см. рис.18). Является ли М здесь лучшим ответом? ДА.
Линия ab - это множество
{(ид, UL) : -UR + -Ur = ~щ(М, R) + ~щ(М, L)}
Действительно, земетим, что если игрок 2 играет R с вероятностью cr2(R) , тогда ожидаемый выигрыш игрока 1 от выбора стратегии с выигрышами ( ид, ид ) есть (t2(R)ur + (1 — сг2(і?))ид . Легко видеть, что М —это лучший ответ на а2(R) = 1/2; он дает ожидаемый выигрыш, строго больший, чем ожидаемый выигрыш, достижимый с помощью стратегий U и/или D . (В случае п > 2 это уже не так: могут быть стратегии, являющиеся НЛО, но не являющиеся строго доминируемыми; это связано с тем, что рандомизация независима).
1.6 Равновесие по Нэшу
Мы начнем со случая, когда рассматривается исходная игра Г , а к смешанному расширению обратися несколько позже.Определение 1.6Л Набор стратегий s = (щ,. . ., sn) образует равновесие по Нэшу (или ситуация s = (щ,. . ., sn) является равновесной по Нэшу) в игре Г = {/, {5/}, {щ}} ; если для любого і = 1,... п
S — г) Д '-’ — я) Д Л С *
Иными словами, если игрок водиночку решает отклониться от выбранной стратегии, то он разве лишь ухудшит свое положение.
В ситуации равновесия по Нэшу, выбранная каждым игроком стратегия является лучшим ответом на стратегии, действительно ’’играемые” соперниками. В этом принципиальное отличие от рационализируемости, которая следует из общего знания о рациональности друг друга и структуры игры, и требует только, чтобы стратегия игроков была лучшим ответом на некоторую разумную гипотезу о том, что его противник будет играть, причем под разумностью понимается, что гипотетическая игра его противников может быть также оправдана. Таким образом, равновесность по Нэшу добавляет к этому требование того, чтобы игроки были правы в своих гипотезах. (Далее мы для краткости будем писать р.Н. для обозначения равновесия по Нэшу).
Разумеется, полученные нами ситуации в рассмотренной ранее дилемме заключенного (во всех ее вариантах) являются равновесными по Нэшу.
Пример. ’’Семейный спор”. Этот пример также относится к числу традиционных примеров, различные вариации которого встречаются в большинстве учебников. История примерно такова. Он и Она независимо (мы оставляет в стороне вопрос о разумности или неразумности подобной постановки вопроса) решают, куда пойти — на балет (Б), или футбол (Ф). Если они вместе пойдут на футбол, то Он получит больше удовольствия, чем Она; если они вместе пойдут на балет, то — наоборот. Наконец, если они окажутся в разных местах, то они не получат никакого удовольствия. Рассматриваемая ситуация моделируется следующей игрой (см. рис. 19):
ОНА
Ф Б Ф / (2,1) (0,0)
°Н В V (0,0) М
Рис. 19.Легко видеть, что здесь есть 2 равновесия по Нэшу в чистых стратегиях — (Ф,Ф) и (Б,Б). Мы увидим ниже, что в этой игре есть еще одно равновесие по Нэшу — в смешанных стратегиях.
Пример. Рассмотрим следующую игру (рис. 20)
| 1 | m | Г | |
| и | (5,3) | (1,4) | (3,5) |
| м | (4,2) | (5.5) | (4.1) |
| D | (3,5) | (2.7) | (5.3) |
| рис | . 20. |
Пример. Вернемся к примеру, касавшемуся рационализуемости (рис. 16). В нем существует единственная (даже если разрешены смешанные стратегии) ситуация равновесия по Нэшу — (а2 , Ь2).
Этот пример иллюстрирует общее взаимоотношение между р.Н. и рационализуемыми стратегиями. Каждая стратегия, являющаяся частью р.Н., рационализуема, поскольку каждая стратегия игрока в ситуации р.Н. может быть ”оправдана” равновесными стратегиями других игроков. Таким образом, равновесие по Нэшу предсказывает как минимум не хуже, чем рационализуемость, впрочем очень часто эти предсказания оказываются значительно более ”четкими”.
Очень удобно следующее переопределение равновесия по Нэшу. Введем следующее многозначное отображение ” лучших ответов” Ьг- : S-i —>¦ Si (в игре Г ):
?') . щ(щ, S—i^j Э ut(sl7 S—i^j V } •
Тогда ситуация (щ,. . ., sn) является равновесием по Нэшу в игре Г , если щ ? Ьг(з_г) V і = 1,. . . , п .
Что же можно сказать по поводу того, а почему собственно нам нужно заниматься р.Н.? На самом деле это один из проблемных вопросов теории игр, несмотря на очень широкое использование р.Н.
(1) Равновесие по Нэшу, как последовательность рациональных выводов (умозаключений). Хотя это часто используется в качестве довода, тем не менее мы видим, что следствие общего знания — это необходимость играть рационализируемые стратегии. Рациональность не обязательно ведет к правильности предсказания.
(2) Равновесие по Нэшу как необходимое условие, если есть единственный предсказуемый исход игры. Если игроки думают и разделяют представления о том, что существует очевидный (в частности, единственный) способ играть игру, то это должно быть р.Н. Разумеется, этот аргумент подходит, если существует единственное предсказание, как игроки будут играть. Однако, вспомнив рационализуемость, мы придем к выводу, что этого недостаточно. Поэтому, этот аргумент полезен, если есть действительно повод считать некоторый набор стратегий очевидным способом сыграть в игру.
(3) Фокальные точки. Иногда случается так, что определенный исход является тем, что Шеллинг (1960) называет фокальным исходом (2-х человек просят назвать независимо какое-то место встречи, и если их выбор совпадет, то получают выигрыш). Это, конечно, явный кандидат, но только если он р.Н.
(4) Равновесие по Нэшу как самофорсирующее соглашение. Если игроки перед игрой имеют возможность предварительных необязыващих переговоров. Если они согласились на какой-то исход, то это, конечно, очевидный кандидат.
Чтобы он стал самофорсирующим нужно, чтобы он был р.Н. Хотя даже, если они договорились играть р.Н., они все равно могут отклониться, если ожидают, что другие могут тоже уклониться.
(5) Рановесие по Нэшу ак устойчивое социальное соглашение. Определенный способ играть в игу может возникнуть во времени, если игра разыгрывается повторно и появляется некоторое устойчивое социальное соглашение. Если это так, то для игроков может быть ’’очевидным”, что это соглашение будет поддерживаться. Это соглашение становится, так сказать, фокальным.
Более подробное обсуждение этой проблематики можно найти, например, в учебнике Mas-Colell, Whinston, Green.
1.7 Равновесие по Нэшу в смешанных стратегиях
Примеры, которые мы рассмотрели выше, продемонстрировали, что даже в очень простых играх равновесие по Нэшу в чистых стратегиях может быть не единственным. Однако, как мы увидим сейчас, равновесия в чистых стратегиях может не существовать вообще.Пример. ’’Игра в орлянку” или ’’Орел или решка”. 2 игрока одновременно, независимо выбирают либ ’’решку”, либо ’’орла”. Если их выбор различен, то первый игрок платит второму 1 рубль (доллар,...), если их выбор одинаков, то наоборот — второй платит первому столько же. Соответствующая игра имеет следующий вид (см. рис. 21).
Рис. 21.
Легко видеть, что в этой игре нет равновесия по Нэшу в чистых стратегиях, так как в любой ситуации одному из игроков выгодно отклониться от выбранной стратегии. Однако, как мы увидим, пара смешанных стратегий од = , <т2 =
2і 2) ’ в котоРЬІХ каждый из игроков играет свои чистые стратегии с равными вероятностями, образует равновесие по Нэшу в смешанных стратегиях.
Определение 1.7.1 Ситуация (набор смешанных стратегий) а = (сц,. . ., (тп) является равновесием по Нэшу в игре Г = {/, {ЕД, {иД}; если для любого і = 1
иДсц, сг_Д > иг(ст',сг_г) V ст' ? Ег.
Предложение 1.7.1 Пустъ Sf С Д — множество чистых стратегий, которые игрок і играет с положительной вероятностью в ситуации а = (од,. . ., (Тп) . Ситуация а является р.Н. в смешанном расширении Г игры Г тогда и только тогда, когда для всех і = 1,. . . , п
(1) Ui(si,a-i) = иг-(Д,<т_Д V s8,s' ? ?+
(2) Ui(si,cr-i) > иг(з',ст_г) V Si ? 5+4 ^ 5/.
Доказательство. Необходимость. Если бы одно из этих условий не выполнялось для некоторого і, то нашлись бы две стратегии зг- ? и s'pSi : Ui(sli,cr_i) > Ui(si,(T_i) , а значит, это не р.Н.
Достаточность. Предположим теперь, что (1) и (2) выполнены, но а — не р.Н. Тогда существует игрок і и стратегия <т' такая, что
щ(сг',сг_г) > щ(стг,сг_г).
Но если это так, то существует чистая стратегия s' , которая играется с положительной вероятностью при <т' и для которой u8(s', <т_г) > Ui((Ti, (т_і) . Так как иДщ, <т_Д = Ui(si,a-i) для любой Si ? Дг+ , это противоречит (1) и (2).
Таким образом, необходимые и достаточные условия того, что ситуация а — р.Н., состоит в том: 1) что каждый игрок при данном распределении стратегий, которые играют его противники, безразличен между чистыми стратегиями, которые он играет с положительной вероятностью; 2) что эти чистые стратегии не хуже тех, которые он играет с нулевой вероятностью.
Это свойство можно использовать для нахождения смешанного равновесия по Нэшу (т.е. равновесия по Нэшу в смешанных стратегиях).
Пример. Рассмотрим следующую игру (рис. 22).
Рис. 22.
Очевидно, что ситуации (А,А) и (В,В) являются равновесными по Нэшу (в чистых стратегиях). Найдем равновесия по Нэшу в смешанных стратегиях. Предположим, что в таком равновесии игрок 1 играет смешанную стратегию (р, 1 — р) , а второй — (g, 1 — q) , причем 0 < р, q < 1 .
Тогда, учивывая приведенное предложение мы, получаем, что ожидаемый выигрыш игрока 2 от игры А есть 1000р + 0(1 — р) , а от игры В есть 100 • (1 —р) + 0р , а значит
ЮООр + (1 — р) • 0 = 100 • (1 — р) + 0 • р.
Отсюда ПООр = 100 и следовательно р = 1/11 . Аналогично, q = 1/11 . Заметим, что в соответствии с предложением 1.7.1 у игроков в данном примере нет предпочтений относительно вероятностей, которые они приписывают своим стратегиям. Эти вероятности определяют ”равновесное рассмотрение”: необходимость сделать другого игрока безразличным относительно его стратегий.
Пример. Вернемся к игре ”Семейный спор”. Поступая как и в предыдущем примере, мы получаем, что Она, играя ”Ф”, получает 1 • р + 0(1 — р) , а играя ”Б”, получает 0-р+2(1— р) . Следовательно 2(1— р) =р. Отсюда Зр = 2 , а следовательно р = 2/3 . Аналогично получаем 2д + (1 — g)-0 = 0- g + (l — g)l , а значит 3q = 1 и q = 1/3 . Таким образом, в смешанном равновесии Он играет ”Ф” с вероятностью 2/3 , а Она играет ”Ф” с вероятностью 1/3 .
Замечание 1.7.1. В определении смешанного расширения или равновесия в смешанных стратегиях мы предполагаем, что игроки осуществляют рандомизацию своих чистых стратегий независимо. Иными словами, мы можем считать, например, что Природа передает игрокам индивидуальные, независимо распределенные сигналы (0і, ?2} ¦ ¦ • , ?п) G [0,1] х [0,1] X ... X [0,1], а каждый игрок г принимает решение в зависимости от различных возможных реализаций его сигнала ?г.
Предположим, однако, что есть некий общий сигнал ? ? [0,1] , который могут наблюдать все игроки. В этом случае появляются новые возможности. Так, к примеру, в упомянутой только что игре ”Семейный спор” оба игрока могут, например, решить идти на футбол, если, скажем, ? < { , и идти на балет, если ? > { . Выбор стратегии каждым игроком остается случайнм, тем не менее здесь мы имеем дело со вполне скоординированными действиями (Он и Она оказыаются вместе), явно имеющими равновесный характер, причем если один игрок решает следовать этому правилу, то и для второго оптимально придерживаться этого же правила. Это дает нам пример коррелированного равновесия (совместного равновесия) , введенного Р.Ауманом (Auman (1974)).
Формально такое равновесие — это специальный случай равновесия по Байесу-Нэшу, которое мы рассмотрим в главе 3.
Далее мы приведем важные результаты о существовании равновесий по Нэшу.
Предложение 1.7.2 В смешанном расширении Г любой игры Г с конечными множествами стратегий Si,...,Sn существует равновесие по Нэшу в смешанных стратегиях.
Это предложение непосредственно следует из следующего более общего результата, так как в игре Г множества стратегий игроков — это симплексы в соответствующем пространстве Им .
Теорема 1.7.1 Debreu (1952), Glicksberg (1952), Fan Ку (1952)). Если для каждого і = 1,. . . , п
(1) Si — непусто, выпукло и компактно (в некотором );
(2) Ui(.Si,. . ., sn) — непрерывна по (щ,. . ., sn) и квазивогнута по Si,
то в игре Г = {/, {ДДДщД} существует равновесие по Нэшу в чистых стратегиях.
Напомним, что функция / : ИА —>¦ Ш/ называется квазивогнутой, если для любого а множество {ж : /(ж) > а} — выпукло.
Доказательство этого предложения опирается на следующую лемму.
Лемма 1.7.1 Если выполнены условия Теоремы 1.7.1, то отображение лучших ответов Ьі непусто, выпукло-значно (т.е. множества — непусты и вы
пуклы) и полунепрерывно сверху.
Доказательство Леммы 1.7.1. Во-первых заметим, что ЬДзщ) — это множество тех стратегий г-го игрока, которые максимизируют иД-,5_г-) на компакте Si. Его непустота следует из непрерывности щ. Выпуклость множества bi(s-i) следует из квазивогнутости функции иД-,5_г-). Чтобы проверить полунепрерывность сверху, мы должны показать, что для любой последовательности: (s8fc,s(x) —> (spS-Д, такой что з) ? мы имеем зг- ? Ь(з_Д . Заметим, что \/k Ui(sj, > иг'(з',з^г) V s' ? Si. В силу непрерывности иД-) ,
^б(Дг'Л —г) Д ^ДСэ 5 — 0 *
Доказательство Теоремы. Определим отображение b : S —>¦ S формулой
6(si,...,sn) = 6i(s_i) х 62(5-2) х • • • х 6(s_n)
Ясно, что Ь(-) — многозначное отображение S = Si X • • • X Sn в себя. По лемме Ь(-) непусто, выпукло-значно, полунепрерывно сверху. Следовательно, по Т. Какутани о неподвижной точке существует неподвижная точка, т. е. набор стратегий s ? S : ¦s ? b(s) . Этот набор стратегий является равновесием по Нэшу, т. к. по построению
5 г ? 6 Д S _ Д V I 1, • • • , П.
Справедлива также следующая теорема.
Теорема 1.7.2 (Glicksberg (1952)). Если в игре Г множества Si стратегий игроков являются непустыми компактными подмножествами метрического пространства, а функции выигрышей щ непрерывны, то существует равновесие по ЕІэшу в смешанных стратегиях.
Пример. ” Голосование”. Рассмотрим следующую ситуацию — три игрока 1,2,3 и три альтернативы — А , D , С .
Игроки голосуют одновременно за одну из альтернатив, воздержаться невозможно. Таким образом, прстранство стратегий Si = {А, В, С}. Альтернатива, получившая большинство, побеждает. Если ни одна из альтернатив не получает большинства, то выбирается альтернатива А. Функции выигрышей таковы:
щ(А) = и2(В) = и3(с) = 2, т(В) = и2(С) = и3(А) = 1, щ(С) = и2(А) = и3(В) = 0.
В этой игре три равновесных исхода (в чистых стратегиях): А, В и С . Теперь посмотрим на равновесия (их больше 3): если игроки 1 и 3 голосуют за А, то игрок 2 не изменит исход, как бы он ни голосовал, и игроку 3 безразлично, как он голосует.
(А, А, А) и (А, В, А) —р.Н., но (А, А, В) —нер.Н., т.к. второму лучше голосовать за В.
1.8 Модель дуополии по Курно
Предположим, что две фирмы і = 1,2 производят однородный продукт и qi,q2 — объемы производства этого продукта. Обратная функция спроса имеет вид (для простоты) P(Q) = a - Q , где Q = + q2 , (P(Q) = a — Q , при Q < a , и P(Q) = 0 ,при Q > а). Функции затрат Ci(qi) = cqi (с < а) (нет фиксированных затрат и предельные затраты постоянны).
Фирмы выбирают qi одновременно и независимо. Здесь два игрока, стратегии Si = [0,+оо) . (В действительности ни одна фирма не будет производить дг- > а ). Фирмы максимизируют свои прибыли:
Qj) = ЧгіРІЯг + qj) - с) = qt[a - (qt + q3) - с].
Если пара (q*Aq2) —р.Н., то q* решает задачу
max TTi(qi,q*).
Предположим q* < а —с (можно доказать, что это действительно так), тогда условие 1 порядка дает нам дг- = |(а — q* — с) . Тогда
 | \{q - q*2 - с) |(а - q{ - с) |
<h
Заметим, что монопольный выпуск был бы (а — с)/2 .
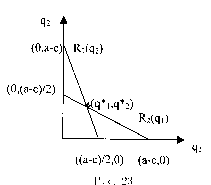
При исследовании дуополии по Курно важную роль играют функции лучших ответов (кривые реагирования) — это функции вида
1
2
1
2
(а - qi- с),
(а - q2- с).
Таким образом, Ri(qj) —это объем выпуска г-ой фирмы, максимизирующий ее прибыль при уловии, что j -ая фирма производит qj . Кривые реагирования изображены на рис. 23.
Точка пересечения кривых реагирования определяет равновесие по Курно, т. е. равновесие по Нэшу в модели дуополии по Курно.
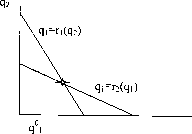 |
| Рис. 24. |
1.9 Равновесие по Нэшу в дуополии по Курно как результат обучения
Мы будем предполагать сейчас, что игроки пытаются предсказывать игру своих оппонентов, ’’используя свой предыдущий опыт”. Эта идея восходит еще к Курно, который рассматривал своеобразный динамический вариант нахождения равновесия. При этом игроки выбирали объем выпуска поочереди, как лучший ответ, исходя из выбора оппонента на предыдущем шаге, предполагая (’’гипотеза Курно”), что он (оппонент) оставит свой объем выпуска без изменения.Точнее, если игрок 1 делает ход в период 0 и выбирает , то выпуск игрока 2 в период 1 есть q\ = r2(g°) , где г2(-) — функция реагирования второго игрока. Затем
чі = п(чі) = ЫЫд?))
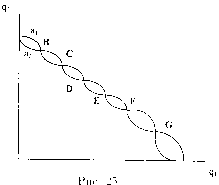
Если этот процесс сходится к (ф“, q%) , то q2 = г2((ф) и = щ(q%) , т.е. ((ф, q2) — р.Н. Если процесс сходится к некоторому состоянию (qi}q2) для любого начального состояния, достаточно близкого к нему, то говорят, что состояние (qi,q2) — асимптотически устойчиво, а сам процесс называется процессом нащупывания (см. рис. 24).
В общем случае картина может быть более сложной (см. рис. 25):
С , Е , G — неустойчивы (к ним процесс не сходится, если только не начинается в них самих), В , D и F — устойчивы.
Вообще говоря, достаточное условие устойчивости выглядит следующим образом:
| dr 1 | dr2 | |
| dq2 | dqi |
< 1.
Заметим, что если функции выигрышей дважды непрерывно дифференцируемы, то наклон функции реагирования і -ой фирмы есть
drt
dqj
U;
7Г
diTidqj / dqf
1.10 Дуополия по Бертрану
1. Парадокс Бертрана.Рассмотрим теперь ситуацию, когда две фирмы (как в дуополии по Курно) производят однородный продукт, но теперь мы предположим, что фирмы одновременно и независимо объявляют цену, по которой они готовы продавать свою продукцию. Тогда спрос, с которым сталкивается каждая фирма, определяется следующим образом:
{D(pi), если pi < pj,
D(pi)/ 2, если рг=р17 О, если pi > pj.
Иными словами, фирма, назначившая меньшую цену ”получает” весь спрос, а если цены одинаковы, то потребители покупают продукцию фирм равновероятно.
Предположим, что цены образуют равновесие по Нэшу. Во-первых, оче
видно, что р* > с, так как назначение цены ниже предельных затрат приведет к отрицательной прибыли, чего не может быть в равновесии, т. к. цена, равная предельным затратам, обеспечивает нулевую прибыль. Далее, ни одна из цен р* не может быть выше с. Действительно, предположим для определенности, что р\ > с, тогда если р2 > р\ , то фирма 2, сталкивающаяся в этом варианте в лучшем случае с половинным спросом, может ”перехватить” весь спрос, назначив цену р'2 = р\ — г для достаточно малого г > 0 и тем самым улучшив свое положение. Если же Рі > Р*2 > с, то фирма 1, аналогично, может назначить цену р2 — ? , ’’перехва-тывая” весь спрос.
Таким образом, в равновесии по Бертрану (или в равновесии по Нэшу в дуополии по Бертрану) р\ = р2 = с, и фирмы получают нулевую прибыль. Это и есть пардокс Бертрана.
Как можно избежать этой парадоксальной ситуации? Во-первых, можно ввести условие ограничения мощности фирм, то есть считать, что есть цены, при которых фирмы не могут обеспечить весь спрос. Во-вторых, можно снять условие однократности этой игры, и это, как мы увидим позднее в гл. 2, существенно меняет ситуацию. Наконец, можно избавиться от предположения об однородности продукции.
2. Рассмотрим ситуацию с дифференируемыми продуктами. Фирмы 1 и 2 выбирают цены рі и р2 одновременно и независимо. Спрос, с которым сталкивается фирма і, qi(pi,Pj) = а — рі~\~Ър2 , где b > 0 — отражает степень заменяемости г-ого продукта j -ым. (Мы не обсуждаем здесь реалистичность такой функции спроса). Предельные затраты есть с, с < а. Пространство стратегий — это S) = [0, оо) — фирмы выбирают цены. Тогда прибыль і -ой фирмы определяется равенством
Кг{Рг,Р3) = Чг{Рг,Р3)[Рг ~ с] = [а ~ рг + Ьр3][рг ~ С]. Пара (Рі,р2) ~ Р-Н., если ?г р* решает задачу
0<Рг<ОЭ
max 7Ті(рі,р*) = max[a - рг + Ьр*][рг - с].
П<С п ¦ / г?л J J
Решение задачи для і -ой фирмы есть
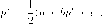
то есть
|
* Рі | 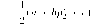 |
Р*2 = т;(а + ЪрІ +с).
Следовательно, р\ = р*2 = (а + с)/(2 — 6)1.11 Пример ’’Проблема общего”
Рассмотрим следующую очень стилизованную модель (Hardin (1968)). Представим себе, что есть п фермеров. Летом их козы (коровы) пасутся на зеленом поле. Обозначим через ді — число коз у і -ого фермера, тогда численность всего стада — G = щ + ••• + (/„ . Затраты на покупку и содержание козы равны с (независимо от числа коз у фермера). Ценность (стоимость) одной козы при общем числе коз G есть v(G).Предполагая, что козе необходим определенный уровень минимального пропитания (для выживания), считаем, что есть некоторое максимальное число коз, которое может прокормиться, Gmax : v(G) > 0 для G < Gmax , но v(G) = 0 для G > Gmax . Можно предположить, что если есть одна коза, то она спокойно прокормится; можно добавить еще одну ..., но с ростом числа коз, естественно считать, что v'(G) < О, (G < Gmax) и v"{G) < 0 .
Весной фермеры выбирают (одновременно и независимо), сколько заводить коз ( ді для г-ого фермера). Выигрыш фермера і есть
9і?(ді +----?дп)-сдг (*)
Следовательно, если (д^,. . ., д*) — р.Н., то д* должно максимизировать (*) при (ді,. .., </*_!,</*+!,• ..,<)• Условие / порядка есть
v(qt + q*_i) + qiv'(qi + q*_t) - с = О,
где
* \ Л *
Ч-г = 2^ qk-
кфі
Подставим в это равенство q* и, просуммировав по і, получаем (разделив на п)
v(G*) + -G*v'(G*)-c = 0. п
Рассмотрим теперь, что произойдет, если ”социальный плановик” будет искать социальный оптимум, то есть решать задачу нахождения
max Gv(G) — Gc.
CKGGooЗдесь условие / порядка есть:
c(G**) + G**v\G**) - с = 0.
Нетрудно проверить, что G* > G** , т. е. слишком много коз! Иными словами, общие ресурсы используются слишком интенсивно.1.12 Равновесие ’’дрожащей руки”
Мы уже обсуждали ранее слабо доминируемые стратегии и сейчас вновь обратимся к ним. Рассмотрим игру, изображенную на рис. 26.L R
и ( (2,2) (0,-2) \
D V (-2,0) (0,0) J
Рис. 26.Легко видеть, что в этой игре два р.Н. в чистых стратегиях (it, L) и (D, R) , причем второе равновесие характерно тем, что оба игрока выбирают свои слабо доминируемые сттратегии.
Мы остановимся сейчас на определении совершенного равновесия (по Нэшу) дрожащей руки игры в нормальной форме, определение которого восходит к работе Рейнхарда Зельтена Selten (1975). Такое равновесие ’’выдерживает” возможность того, что с некоторой очень небольшой вероятностью игроки делают ошибки (грубо говоря, ’’дрожащей ркуой” не попадая на нужные кнопки).
Для произвольной игры в нормальной форме Г = {/, (ЕД, (щ)} можно определить ’’возмущенную” игру Ге = {/, (Е?), (щ)} , выбирая для каждого игрока і и каждой
чистой стратегии щ ? Si числа ?і(зі) ? (0,1) так, что J^s-es-?*(5*) < 1, и затем, определяя множество ” возмущенных” стратегий как ?
= {сгг- ? ?; : сгг-(5і) > ?i(si) для всех щ ? St и
І
=и-
Иными словами, в игре Ге каждый игрок і играет каждую свою стратегию щ с вероятностью не меньшей чем некоторая минимальная вероятность ег(зг) , которая интерпретируется как неизбежная вероятность сыграть щ по ошибке.
Определение 1.12.1 Равновесие по Нэшу а в игре (в нормальной форме) Г = {/, (Ег-), (щ)} называется равновесием дрожащей руки, если существует такая последовательность возмущенных игр {Гед.}^11; сходящихся к Г (в том смысле, что Ііте)’(щ) = 0 для любых і ? I и Si ? Si), что существует последовательность равновесий (в соответствующих играх ?ек) {ак}<^_1 , сходящаяся к а, т.е. limcrfc = а .
Таким образом, рассматриваемые равновесия — это те равновесия по Нэшу, которые ”выживают” при возможных ошибках.
Заметим, что в определении требуется лишь существование возмущенных игр, имеющих равновесия, близкие к а. Более сильным было бы требование ’’выживания” при всех возмущениях исходной игры.
Предложение 1.12.1 (Selten 1975). В смешанном расширении любой игры Г = {/, {Si}, (щ)} с конечными множествами стратегий Si,...,Sn существует равновесие дрожащей руки.
Предложение 1.12.2 (Selten (1975)). Равновесие по Нэшу а в игре в нормальной форме Г = {/, (Ег), (щ)} является совершенным равновесием дрожащей руки (в игре в нормальной форме) тогда и только тогда, когда существует последовательность таких вполне смешанных стратегий ак (т.е. стратегий, в которых все чистые стратегии играются с положительными вероятностями), что ак —у а и gі является лучшим ответом на любой элемент последовательности {ст(іг}^Т1 для любого і = 1,. . . , п .
Предложение 1.12.3 (Selten (1975)). Если а = (сц,. . . , (тп) — совершенное равновесие дрожащей руки (в игре в нормальной форме), то Оі не является слабо доминируемой ни для какого і = 1,. . ., п .
1.13 Дополнение: Антагонистические игры
К числу достаточно простых и потому наиболее изученных игр относятся антагонистические игры. В случае антагонистических игр, в отличие от произвольных игр, можно достаточно много сказать о качественном характере равновесий по Нэшу. Напомним определение игр с ”нулевой суммой”.Определение 1.13.1 Игра Г = {/, {S}}, {иг-}} называется игрой с нулевой суммой, если для любого s G S выполняется условие ?Г= ;1 ui(s 1, ^2, • • • , sn) — 0 .
Иными словами, такая игра представляет собой замкнутую систему: все то, что кто-нибудь выиграл, должно быть кем-то проиграно. Большинство салонных игр являются играми такого типа.
Будем далее считать, что / = {1,2} .
Определение 1.13.2 Игра Г двух лиц с нулевой суммой называется антагонсти-ческой.
В такой игре интересы игроков диаметрально противоположны, поскольку ui(si, s2) + u2(s1, s2) = 0 или ui(si,s2) = — u2(si, s2), Vsi G Si,s2 G S2 . К числу примеров антагонистических игр можно отнести игру ’’Орел или Решка”. В этой игре каждый из двух игроков выбирает, независимо от другого, монетку, повернутую вверх либо ’’Орлом”, либо ’’Решкой”. Если выбор игроков различен, то игрок 1 платит игроку 2 один доллар. Если выбор совпадает, то — наоборот. Матрица выигрышей такой игры представлена на Рис. 27.
’’Орел” ’’Решка”
’’Орел” /(-1,1) (1,-1) \
’’Решка” у (1,-1) ( — 1,1) J
Рис. 27.
Как уже отмечалось, конечная антагонистическая игра называется матричной. Будем говорить, что игрок і выбирает максиминную стратегию, если эта стратегия является наилучшей для него в предположении, что игрок j будет выбирать свою стратегию так, чтобы максимально навредить игроку і.
Рассмотрим такую стратегию на примере игры, представленной на рис. 28.
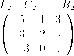 |
| Рис. 28. |
L - 1 С\ Ri
Здесь приведена матрица выигрышей 1-го игрока. Как выбирает максиминную стратегию 1-ый игрок? Он может рассуждать следующим образом: ’’Если я выберу свою стратегию L\ , то сколько я смогу получить?” Поскольку его противник выбирает свою стратегию так, чтобы навредить игроку 1 насколько возможно, то он в ответ на Ь\ ответит своей стратегией С2 . В этом случае игрок 2 проиграет лишь 1. Аналогично, если игрок 1 задумает сыграть С\ , в ответ игрок 2 ответит С2 , тогда 1-ый игрок сможет выиграть лишь 2. Если же игрок 1 задумает сыграть R\ , то противник накажет его, сыграв Ь2 . В этом случае 1 игрок проиграет 3, а следовательно, 2-ой игрок выиграет 3. Очевидно, что для игрока 1, наилучшим будет выбор такой стратегии, которая даст ему максимальный выигрыш из тех минимальных, которые позволит ему выиграть игрок 2, т.е. стратегии С\ .Аналогичные рассуждения применимы и для игрока 2 при выборе им своей мак-симинной стратегии.
Покажем, что если в антагонистической игре Г существует равновесие по Нэшу, то пара стратегий будет являться равновесной тогда и только тогда, когда стратегия каждого игрока — максиминная. Этот в некотором смысле удивительный результат обеспечивает связь между индивидуальным принятием решения и рассуждением, объясняющим причину введения такого понятия как равновесия по Нэшу. Мы докажем заодно, что все равновесные ситуации в антагонистических играх приводят к одним и тем же выигрышам. Это свойство редко выполняется в неантагонистических играх.
Определение 1.13.3 Пустъ Г — антагонистическая игра. Стратегия ? Si
является максиминной для игрока 1, если
min 'иДзДзД > min s2), V Si ? S\.
S2^S2 S2E.S2
Стратегия S2 G S2 является максиминной для игрока 2, если
min u2(si, S2) > min u2(si, s2), V s2 ? 52.
siGSi siGS1!
T. e. максиминная стратегия для игрока і является стратегией, обеспечивающей ему максимальный гарантированный выигрыш. Следовательно, максиминная стар-тегия игрока 1 решает задачу:
max min s2).
siGSi S2es2
Аналогично максиминная стратегия 2-го игрока решает задачу:
max min u2(s 1, s2).
s2G52siG5i
Следующая очевидная лемма показывает, что нахождение максимального среди минимальных выигрышей игрока 2 эквивалентно нахождению минимума среди максимальных выигрышей игрока 1.
Лемма 1ЛЗЛ Пустъ Г = {{1,2}, {А;}, {щ}} — антагонистическая игра, тогда maxS2eS2 minsie5l u2{s1, s2) = - minS2es2 maxSieSl иДзі, s2).
Доказательство этой леммы немедленно следует из следующих очевидных свойств:
1) mmz(-f(z)) = - max, /(z)
2) arg minz(-f(z)) = arg max, f(z) .
Из этого результата следует, что стратегия s2 ? S2 является решением задачи нахождения maxS2es2 minSl?51 u2(s\, s2) тогда и только тогда, когда эта стратегия s2 является решением задачи minS2es2 maxSlG51 иДщ, s2) . Поэтому при поиске такой стратегии можно воспользоваться той же матрицей выигрышей игрока 1 следующим образом: сначала в каждом столбце найти максимальный элемент, затем из всех максимальных элементов выбрать минимальный. Полученное значение является ’’наименьшим гарантированным проигрышем” игрока 2. Это означает, что если игрок 2 будет придерживаться стратегий, соответствующих этому минимаксному значению, то при любом поведении противника он проиграет не больше этого значения.
Следующий результат устанавливает связь между равновесием по Нэшу в антагонистической игре и множеством пар максиминных стратегий.
Предложение 1.13.1 Пустъ Г — антагонистическая игра.
a. Если (s^s^) —равновесие по Нэшу в Г; тогда s^ —является максиминной стратегией игрока 1, а — является максиминной стратегией игрока 2.
b. Если (s^s^) —равновесие по Нэшу в игре Г; тогда
maxminui(si, s2) = minmaxui(si, s2) = иДзД s^)
Sl S2 S2 Si
и таким образом все равновесия по Нэшу в игре Г дают одни и те же выигрыши.
c. Если maxSl тіщ2 Ui(si, s2) = тіщ2 maxSl s2); — является максиминной стратегией игрока 1, — является максиминной стратегией игрока 2,
тогда (s^s^) является равновесием по Нэшу игры Г.
Доказательство.
а,Ь. Пусть (s^s^) — равновесие по Нэшу, тогда
и2(зД з2) > u2(sl, s2), V s2 G S2 или (т. к. U2 = —Ui )
(st, s2) < Ui(s^,s2), V s2 G S2.
Следовательно,С другой стороны,
(st, s2) Д ^i(si, s2), V Si G Si.
Следовательно, it^s^s^) > minS2 u1(s1,s2), V Sj G Д , поэтому
Sl S2
Таким образом, из (1) и (2) следует, что = maxSl тіщ2 Ui(si, s2) и
является максиминной стратегией игрока 1. Аналогично можно показать, что является максиминнои стратегией игрока 2.
Т. к. u2(s\, S2) = maxS2 minSl it2(si, s2) = —Ui(s^, s^) , to ^2) = — maxS2 minSl u2(si, s2) = minS2 maxSl Ui(si, s2) . с. Обозначим через v* = maxSl minS2 Ui(si,s2) = minS2 maxSl i4i(si,s2) . Из леммы следует, что maxS2 minSl u2(si,s2) = —v* . Поскольку — максиминная стратегия 1-ого игрока, то Ui(s^,s2) > ?* для всех s2 ? S2 ¦ Аналогично, s*2 — максиминная стратегия 2-ого игрока, поэтому
u2(si, S2) > —?*, для всех Si ? S\.
Положим в этих неравенствах s2 = и Si = , тогда > ?* и
> —?*. Но так как и\ = — и2 , то < ?* . Отсюда следует,
что гг 1 (s^, s^) = ?* . Получим Ui(s^,s2) > и2(з^, зД или, подставляя U\ = — и2 имеем, и2(з^, З2) > i42(si,s2). А из второго неравенства ^(s^s^) > — или
y>i(з^, зД > tii(si, зД . Значит пара (s^s^) является равновесием по Нэшу.
Заметим также, что из свойств (а), (с) следует, что равновные стратегии являются взаимозаменяемыми в том смысле, что если (si,s2) и (s^s^) образуют равновесия, то и (si, зД , (s^s^ — также образуют равновесия по Нэшу.
Свойство (Ь) показывает, что
maxminui(si, s2) = minmaxui(si, s2)
Sl S2 S2 Si
для всех антагонистических игр, в которых существует равновесие по Нэшу.
В более общем случае, когда равновесия по Нэшу в чистых стратегиях нет, выполняется более общее свойство:
maxminui(si, s2) < minmaxui(si, s2).
Sl S2 S2 Sl
Действительно, т. к. для любого имеем
iti(si,s2) < maxiti(si,s2), V s2 ? S2,
si
поэтому
minu^s), s2) < minmaxu1(s1, s2) V s) ? S\.
S2 S2 Si
Наличие равновесной ситуации предполагает выполнение противоположного неравенства. В примере ’’Орел или Решка” мы видим, что
maxminui(si, s2) = —1 < minmaxui(si, s2) = 1.
Sl S2 S2 Si
Значит в этой игре равновесия по Нэшу в чистых стратегиях не имеет, а вот во втором примере мы получаем, что
maxminui(si, s2) = 2 = minmaxui(si, s2),
Sl S2 S2 Sl
когда игрок 1 играет C\ , а игрок 2 играет С2 . Ситуация (С\,С2) здесь является равновесной по Нэшу.
Если оказывается, что в антагонистической игре Г
maxminui(si, s2) = minmaxui(si, s2) = v*,
Sl S2 S2 Sl
то говорят, что этот равновесный выигрыш 1-ого игрока является значением игры. И как следует из доказательства предложения, если ?* является значением антагонистической игры, то это значит, что любая равновесная стратегия игрока 1 гарантирует ему выигрыш по крайней мере не меньше его равновесного выигрыша ?* , а любая равновесная стратегия игрока 2 гарантирует ему не меньше его равновесного выигрыша — ?* .
Поэтому любая такая стратегия игрока 2 гарантирует, что игрок 1 получит выигрыш не больше его равновесного. В неантагонистических играх равновесные стратегии игроков такими свойствами уже не обладают.
1.14 Дополнение. Решение биматричных игр 2x2
В этом параграфе мы подробно остановимся на анализе решений биматричных игр, в которых у каждого из игроков есть только две стратегии. Разумеется эти игры представляют собой частный случай рассмотренных ранее игр, но здесь появляется возможность дать наглядную графическую интерпритацию поиска равновесных ситуаций в игре. (Наше изложение здесь саледует книге Воробьева (1985).) Рассмотрим биматричную игру 2 X 2 с матрицей/ (ац,Ьц) (аі2,Ьі2) \
\ («2і, Ь2і) (а22, Ъ22) J
или, как мы уже отмечали, игру, выигрыши в которой можно задать с помощью двух матриц:
/ ЙЦ, Иі2 \ / Ьц, Ьі2
\ °21, «22 J \ &21, ^22
первая из которых описывает выигрыши игрока 1, а вторая — вымгрыши второго.
Очевидно, что смешанные стратегии игроков в случае игр 2x2 полностью описываются вероятностями р и q выбора игроками своих первых чистых стратегий. (Вторые чистые стратегии выбираются, соответственно, с вероятностями 1 — р и 1 — q .) Поэтому, поскольку 0 < р , q < 1 , каждая ситуация в смешанных стратегиях в биматричной игре 2x2 представляется как точка на единичном квадрате.
Напомним, что пара смешанных стратегий = (р*,1 — р*) и (т^ = (<Д, 1 — q*) является равновесием по Нэшу, если смешанная стратегия а* одного игрока является лучшим ответом на смешанную стратегию о* другого игрока, т. е. выполняются следующие неравенства:
Ні(сгі,сг*) < Ні(сгГ,сг*) ?сгі и U2(o-l,a2) < Ui{al,a*2) ?сг2.
Рассмотрим уже знакомый нам пример ’’Орел или Решка”. Пусть игрок 1 считает, что игрок 2 будет выбирать ’’Орла” с вероятностью q и ’’Решку” с вероятностью 1 — q. Ожидаемый выигрыш игрока 1 от разыгрывания ’’Орла” будет ( — l)q + 1 • (1 — q) = 1 — 2q , а от разыгрывания ’’Решки” 1 • q + ( — 1) • (1 — q) = 2q — 1 . Если 1 — 2q > 2q — 1 , т. e. q < | , то лучшей чистой стратегией игрока 1 будет Орел, а если q > | , то Решка, и игроку 1 будет все равно, что разыгрывать, если q = I . Рассмотрим возможные смешанные стратегии игрока 1 . Пусть (р, 1 — р) обозначает смешанную стратегию, в которой игрок 1 разыгрывает ’’Орла” с вероятностью р. Для каждого значения q мы можем вычислить значения р = p*(q)} такие что, (р, 1 — р) будет являться лучшим ответом игрока 1 на (g, 1 — q) игрока 2.
Ожидаемый выигрыш игрока 1 от разыгрывания (р, 1 — р) , когда игрок 2 разыгрывает (g, 1 — q) будет
(-І)р • q+ 1 -р • (1 - q) + 1 • (1 -р) • q+ (-1) • (1 -р)( 1 ~ q) =
= (2q - 1) + р • (2 - 4q)
Ожидаемый выигрыш игрока 1 повышается (в зависимости от р), если 2 — 4д > 0 и уменьшается, если 2 — 4q < 0 , поэтому лучший ответ игрока 1 (среди всех стратегий, как чистых, так и смешанных), есть р = 1 (т.е. Орел), если q < 4 , но р = 0 (т.е. Решка), если q > Этим значениям р соответствуют два горизонтальных отрезка на рис. 29.
p*(q)
орел 1
решка
1 q
решка
орел
рис. 29.
Так как при q = 1/2 ожидаемый выигрыш игрока 1 не зависит от его стратегии, мы получаем, что игроку 1 безразлично, выбрать ли одну из своих чистых стратегий, или же выбрать какую-нибудь смешанную стратегию (р, 1 — р) . Это означает, что если q = | 5 то смешанная стратегия (р, 1 — р) является лучшим ответом на смешанную стратегию (g, 1 — q) при любом значении р от 0 до 1 . Поэтому р*(4) представляетсобой вертикальный отрезок, изображенный на рис. 29. Таким образом, ломаная линия на рис. 29 представляет собой многозначное отображение (поскольку при q = \ мы имеем целый отрезок) лучших ответов (в зависимости от q).
рис. 30.
Похожими рассуждениями и в силу симметрии матрицы выигрышей игрока 2 получаем аналогичное отображение лучших ответов игрока 2 . На рис. 30 это ломаная q*(p) . Рис. 30 показывает, что равновесие по Нэшу в игре ’’Орел или Решка” возникает, если игрок 1 разыгрывает смешанную стратегию (|,|) и игрок 2 разыгрывает такую же стратегию, что, по-видимому, было естественно ожидать в силу симметричности игры. Важно заметить, что этот пример иллюстрирует, что неслучайно, если один из игроков выбирает свои стратегии равновероятно (т. е. придерживается своей равновесной стратегии), то второму игроку при этом абсолютно безразлично как играть. Это следует из свойства, доказанного ранее (см. и. 1.7) в общем случае:
орел
q*(p)
решка
1 q
орел
решка
Ui{si,(T*2) = Ul{(T*l,(T*2)
Ui{a*i,s2) = Ui{al,a*)
для тех Si, которые входят в равновесную ситуацию с ненулевыми вероятностями. Для тех же s' , которые входят в равновесную ситуацию с нулевой вероятностью верны неравенства:
(2)
iMs'^cr*) < Ні(сг*,сгД,
Uiicrl.s'i) < г/і(сг*, сг|)
Формулы (1), (2) дают действенный способ определения равновесных ситуаций в произвольных биматричных играх 2x2.
Ожидаемый выигрыш игрока 1 от разыгрывания од = (р, 1 — р) , когда игрок 2 разыгрывает <т2 = (g, 1 — q) :
^і(сгі, сг2) = р(ац<2 + (1 - <?)а2і + а22))(р ~ 1),
Ui{cri,a2) — Ui(si,a2) = (бц2 — а22 + q(an — ai2 — a21 + a22))p.Введем обозначения: С = йц — бд2 — а21 + а22, а = а22 — аі2 .
Лучший ответ игрока 1 на произвольную стратегию а2 игрока 2 можно получить из условий неотрицательности:
Ui(cri,cr2) - Ui(si,cr2) > 0;
^і(сгі,сг2) - Ui(s2,a2) > 0.
С учетом введенных обозначений они выглядят следующим образом:
(Р ~ l)(Cq - а) > 0,
p(Cq — а) > 0 ^Аналогично можно поступить для нахождения лучшего ответа игрока 2 . Ожидаемый выигрыш игрока 2 от игры а2 = (g, 1 — q) , когда игрок 1 играет <ті = (р, 1 - р) :
U2(cr1, сг2) = q(bnp + (1 - p)b2i) + (1 - q)(bi2p + (1 - р)Ъ22) =
= ь22 + (b12 - b22)p + (b21 - b22 + p(bn - b12 - b21 + b22))q.
Из условий (неотрицательности)
U2(o-1,a2) - Si) > 0,
Ui((Ti,a2) - Ui{(Ti,s2) > 0,
обозначив D = Ъц — bi2 — b21 + 622, fi = b22 — b21 , получаем аналогичные неравенства для нахождения лучшего ответа игрока 2 на произвольную стратегию а = (р, 1 — р) игрока 1:
(q-l)(Dp-(3)>0,
q(Dp — (3) > 0. ^
Тогда, для того чтобы пара од = (р, 1 —р), сг2 = (g, 1 — д) определяла равновесную ситуацию необходимо и достаточно одновременное выполнение систем неравенств (3), (4) , а также 0 < р < 1, 0<д<1.
Рассмотрим лучшие ответы каждого игрока, которые, разумеется, зависят от того, как устроены матрицы выигрышей игрока 1 и игрока 2 . Начнем с неравенств (3).
Возможны три случая:
1) р = 1 , Cq > а;
2) 0 < р < 1 , Cq = а; (5)3) р = 0 , Cq < а.
В свою очередь, в зависимости от соотношений между Сна, возможны следующие случаи и соответствующие лучшие ответы игрока 1 в каждом из них.
I. Если С > 0, а > 0 , то лучшие ответы изображны на рис. 31-33:
| ||||||||
| а/С > 1 рис. 31. |
| |||||||
| а/С = 1 рис. 32. |
а/С < 1 рис. 33.
II. Если С < 0, а < О , то лучшие ответы изображены на рис. 34-36:
| Р |
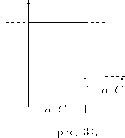 |
а/С = 1 рис. 35.
| Р |
 |
IV. Если С ф 0, а = О , то лучшие ответы игрока 1 , имеющие вид зигзагов, проходят по смежным сторонам квадрата — рис. 39 и 40. :
| р | Р | |||
| С > 0 | qr | с < 0 | qr | |
| эис. 39. | эис. 40. |
| р | р | |||
| а > 0 | г q | а < 0 | qr |
VI. Наконец, если С = О, а = 0 , то любая точка квадрата является решением системы — рис. 43.
Р
q
С = 0, а = О рис. 43.
Анализируя рисунки 31-42, можно отметить, что качественно различных решений могут быть три вида: горизонтальный отрезок вдоль одной из сторон квадрата, любые две смежные стороны квадрата, ”возрастающий” (рис. 33) и ”убывающий” (рис. 36) зигзаги.
При решении неравенств (4) также возможны три случая:
1) q= 1 , Dp > (3 ;
2) 0 < q < 0 , Dp = (3;
3) q = 0 , Dp < (3 .
Аналогично, лучшие ответы игрока 2 в зависимости от соотношений между D и /3 выглядят следующим образом:I. Для D > 0, (3 > 0 , лучшие ответы игрока 2 изображены на рис. 44-46:
| ||||||||||
| рис. 44. рис. 45. |
| ||||||||
| f3/D < 1 |
Р
(3/D
, q
I
Р/D > 1
рис. 47.
I
| р |
1 1 1 1 | |
| P/D | ||
| _ , ^ |
рис. 49.
III. Если D > О, P < 0 , то см. рис. 50; если D < 0, P > 0 — то рис. 51.
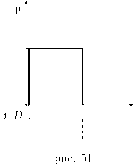
P/D
рис. 50.
IV. Если D ф 0, /3 = 0, то лучшие ответы игрока 2 проходят по смежным сторонам квадрата — рис. 52 и 53:
| р | р |
і і і і | ||
|
: q : d > о |
: q d < о : |
V. При D = 0,(3 ф- 0 зигзаги вырождаются в прямые на рис. 24,25. При решении неравенств (4) возможен случай 3) когда (3 > 0 , либо 1), когда (3 < 0 .
| р | ; | р | ||
|
: q : [з > о |
: q [з < о : |
VI. Если D = 0, (3 = 0 , то мы получаем любую точку квадрата — рис. 56.
Исключая тривиальный VI случай, убеждаемся, что и для игрока 2 возможны три различных вида лучших ответов: вертикальный отрезок вдоль одной из сторон квадрата, любые две смежные стороны квадрата, ”возрастающий” (рис. 46) и ”убывающий” (рис. 49) зигзаги.
q
D = 0, (3 = 0
рис. 56.
Равновесным ситуациям графически соответствуют точки пересечений множеств лучших ответов игроков. Совмещая графики лучших ответов игрока 1 (рис. 31-43) с любым графиком наилучших ответов игрока 2 (рис. 34-56), мы получаем всевозможные варианты множеств равновесных ситуаций биматричной игры 2x2.
Рассмотрим геометрический смысл условий (3) и (4) на примере описанной выше игры ”Дилемма Заключенного”. Напомним, что ситуация, сложившаяся в этой игре, задается матрицей
/ молчать сознаться \
Молчать I (-1,-1) ( — 10,0) I Сознаться у (0,-10) (—6 — 6) J
Имеем С = -1 - (-10) - 0 + (-6) = 3, а = -6 - (-10) =4, ?> = -1-0-(-10) + (-6) = 3, (3 = -6 = (-10) = 4
Тогда условия (3), (4) выглядят следующим образом:(Р — 1)(3<? — 4) > 0, (q — 1)(3р — 4) > 0, p(3q — 4) > 0, q(3p — 4) > 0,
Отсюда получаем, что при р = 1, q > | , при 0<р<1, q = | , при р = 0, q < | ; при q = 1, р > I , при 0<д<1, р = | , при q = 0, q < | Полученные лучшие ответы изображены на рис. 57.
р
4
3 Г
I
I
1
рис. 57.Как видно из сказанного выше, такой рисунок можно получить совмещением рис. 31 и рис. 44, где пунктиром отмечены участки зигзагов, не принадлежащих единичному квадрату. Из рисунка видно, что существует единственная ситуация равновесия р = 0, q = 0 . Это ситуация, в которой каждый из игроков выбирает вторую чистую стратегию — Сознаться.
Из анализа всевозможных ситуаций видно, что биматричная игра всегда имеет по меньшей мере одну точку равновесия по Нэшу, что является наглядной иллюстрацией теоремы Нэша о существовании равновесия. Отметим при этом несколько качественных особенностей, существующих равновесий.
1) Единственное равновесие по Нэшу в чистых стратегиях — например, рис. 37 и рис. 44 дают равновесную точку р = l,q = 0. ” Дилемма Заключенного” относится к такому случаю (здесь р = 1 , q = 1).
O' і
С 1
рис. 58.
2) Единственное равновесие по Нэшу в смешанных стратегиях, например, рис. 36 и рис. 46 когда накладывается ’’убывающий” зигзаг на ’’возрастающий” зигзаг. Игра ’’Орел” или ’’Решка” является примером такого случая.
3) Три равновесия по Нэшу — два в чистых стратегиях и одно — в смешанных. Такая ситуация образуется, когда накладываются два ’’возрастающих” или два ’’убывающих зигзага”, например, рис. 33 и рис. 46. Такого типа ситуация возникает в игре ’’Семейный спор” (см. рис. 59).
¦ф
-**
Т)
а/С
рис. 59.
4) Два равновесия по Нэшу в чистых стратегиях. Его можно получить, например, наложением рис. 9 и рис. 22 . Такая ситуация возникает, в частности, когда в матрице А выигрышей игрока 1 а 12 = а22 , а в матрице В выигрышей игрока 2 Ьі2 = Ъ22 ¦ См. рис. 60.
Р
I
I
I
-ф---
1)
I
: с > о рис. 60.
5) Континуум равновесий по Нэшу в (смешанных стратегиях). Примеров такого рода равновесий можно предложить очень много. Скажем, совмещение рис. 36 и
рис. 53 дает множество равновесных точек, где р = 0, q ? \%Л\ и р = 1, g = Ои т.п. См. рис. 61
| D |
 |
Этого нельзя сказать о случаях четного и бесконечного числа равновесных ситуаций. В этих случаях малейшее изменение элементов матриц выиграшей может приводить к совершенно иным качественным ситуациям. Например, ситуация изображенная на рис. 60 может перейти в ситуацию либо с одним чистым равновесием, если а = 0, (3 < 0 (Ь22 < Ь2і) , (см. рис. 62), либо в ситуацию с тремя равновесиями, если а > 0, (3 > 0 (а22 < «2і) (см. рис. 63), либо в ситуацию с континуумом равновесий, если а > 0,(3 = 0 (см. рис. 64)
| Р | |||||||
| |||||||
| рис. 64. |
рис. 63.
Замечание 1.14.2. Рассмотрим наиболее интересный случай, когда С и D не равны нулю. Тогда равновесная ситуация определяется двумя формулами р = jj, q = ^7 из которых следует, что в равновесной ситуации выбор игрока 1 определяется элементами матрицы выигрышей игрока 2 и не зависит от элементов собственной матрицы, а выбор игрока 2 в равновесной ситуации полностью определяется элементами матрицы игрока 1 и не зависит от элементов собственной матрицы. Иными словами, равновесная стратегия обоих игроков определяется не столько стремлением увеличить собственный выигрыш, сколько держать под контролем выигрыш другого игрока (минимизировать его). Таким образом, в биматричной игре мы сталкиваемся не с антагонизмом интересов, а с антагонизмом поведения.
1.15 Задачи
1. Какие стратегии в следующей игре, представленной в нормальной форме, выживают после последовательного исключения строго доминируемых стратегий? Найдите все равновесия по Нэшу.
2. Игроки I и II торгуются по поводу того, как поделить один доллар. Оба игрока одновременно называют доли, которые они бы хотели иметь, Si и S2 , где 0 < Si , S2 < 1 . Если Si + S2 < 1 , то игроки получают названные доли; если Si + S2 > 1 , то оба игрока ничего не получают. Каковы равновесия по Нэшу в этой игре?
3. Рассмотрим модель олигополии по Курно с п фирмами. Пусть дг- объем произведенной продукции фирмой і и пусть Q = qi + • • • + qn - общий объем продукции на рынке. Предположим, что функция обратного спроса имеет вид P(Q) = а — Q (для Q < а , иначе Р = 0 ). Полные затраты фирмы і на производство продукции в размере дг- есть C(qi) = с- qi} то есть постоянных затрат нет, а предельные затраты постоянны и равны с, причем с < а . Фирмы выбирают свои объемы производства одновременно. Найдите равновесие по Нэшу? Что будет происходить, если п стремится к бесконечности?
4. Рассмотрим следующий конечный вариант модели дуополии по Курно. Допустим, что каждая из фирм должна выбрать, производить ли половину монопольного объема продукции, qm/2 = (а — с)/4, либо равновесный по Курно объем, qc = (а — с)/3. Другие объемы производства в такой модели невозможны. Показать, что эта игра с двумя ходами эквивалентна дилемме Заключенного: каждая фирма имеет строго доминируемую стратегию и в равновесии обе фирмы оказываются в менее выгодном положении, нежели в ситуации, когда бы они выбрали сотрудничество (кооперацию).
5. Рассмотрим модель дуополии по Курно с функцией обратного спроса P(Q) = а — Q . Будем считать, что фирмы имеют ассимметричные предельные затраты: Сі для /-ой фирмы и с 2 II - ой фирмы. Что будет являться равновесием по Нэшу, если 0 < сг- < а/2 для каждой фирмы? Что если с\ < с2 < а , но 2с2 и -)- С\ ?
6. Рассмотрим совокупность избирателей, равномерно распределенных вдоль ”идеологического спектра” слева (ж = 0) направо (ж = 1) . Одновременно каждый из кандидатов на одну должность (пост) выбирает платформу компании (т.е. точку на линии между ж = 0 и ж = 1 ). Избиратели наблюдают выборы кандидатов и затем каждый избиратель голосует за того кандидата, чья платформа является ближайшей к позиции избирателя на спектре. Если имеется два избирателя и они выбрали, например, платформы Х\ = 0, 3 и ж2 = 0, 6 , то все избиратели, расположенные левее ж = 0,45 голосуют за кандидата 1, а все избиратели правее этой точки голосуют за кандидата 2 и кандидат 2 выигрывает выборы с 55 процентами голосов. Предположим, что кандидаты хотят только быть выбранными — в действительности они не интересуются платформами совсем! Если имеется два кандидата, то каково равновесие по Нэшу в чистых стратегиях? Если имеется три кандидата, отыщите равновесие по Нэшу в чистых стратегиях. Считаем, что любые кандидаты, которые выбрали одну и ту же платформу поровну делят голоса, отданные за эту платформу, и что ничьи среди лидирующих кандидатов разрешаются с помощью подбрасывания монеты).
7. Показать, что в ” Дилемме Заключенного” и в играх на рис. 65 и 66.
| ||||||||||||||||
| Рис. 65 Рис. 66 |
8. Найти равновесие по Нэшу в смешанных стратегиях для следующей игры, представленной в нормальной форме:
L R
T ( (2,1) (0,2) \В V (1,2) (3,0) )
9. На каждой из двух фирм имеется по одной вакансии. Допустим, что фирмы предлагают различные зарплаты: фирма і предлагает зарплату ну, причем 1 < w2 < 2wi . Предположим, что есть два работника, каждый из которых может обратиться только в одну фирму. Работники одновременно решают обратиться в фирму 1 или фирму 2. Если в фирму обращается только один работник, то он получает работу; если оба работника обращаются в одну и ту же фирму, фирма нанимает одного работника случайным образом и другой работник остается безработным (имеет нулевой выигрыш). Найдите равновесие по Нэшу в игре работников, представленной в нормальной форме.
Обратиться Обратиться в фирму 1 в фирму 2
Обратиться в фирму 1 Обратиться в фирму 2
(w2,w1)
(w1}w2)
[\w2,\w2)
10. Показать, что для равновесия по Нэшу в смешанных стратегиях верно следующее утверждение: стратегии, сыгранные в положительной вероятностью в равновесии по Нэшу в смешанных стратегиях выживают в процессе последовательного исключения строго доминируемых стратегий.
11. Аукцион первой цены. Оценки игроков объекта аукциона упорядочены щ > ?2 > ¦ ¦ ¦ > ?п > 0 . Участники одновременно делают заявки, назначая цену, которую они готовы заплатить за объект. Выигрывает назначивший наибольшую цену, которую он и платит (в случае, если несколько участников называют одну наивысшую цену, объект получает тот из участников, у которого наименьшая оценка).
12. Армия А обладает единственным самолетом, который она может направить для атаки одной из трех целей. У армии В есть единственное зенитное орудие, которое она может установить для защиты одной из целей. Ценность цели к есть Vk , так что щ > ?2 > ?3 > 0 . Армия А разрушает цель только, если она атакует незащищенную цель. Армия А стремится максимизировать ожидаемый ущерб от нападения, а В стремится его максимизировать. Найдите равновесие по Нэшу в смешанных стратегиях соответствующей игры.
Глава 2
Динамические игры с полной информацией
2.1 Позиционная форма игры
Прежде чем перейти непосредственно к теме этой главы, мы должны сделать небольшое отступление, касающееся терминологии, поскольку мы будем встречаться с терминами полная информация, совершенная информация, неполная, несовершенная информация и т. д. Чтобы избежать возможных недоразумений, отметим следующее.Информационную структуру игры можно охарактеризовать несколькими способами. Первый подразделяет игры на игры с совершенной и игры с несовершенной информацией. (Хотя мы еще не дали строгого определения позиционной формы игры, мы кратко описали ее в начале гл. 1.).
В игре с совершенной информацией каждое информационное множесто одноточечно. В противном случае игра является игрой с несовершенной информацией.
В игре с совершенной информацией каждый игрок всегда знает точно, в каком месте дерева игры он находится, нет одновременных ходов, и все игроки наблюдают ходы Природы (если таковые есть).
В игре с неполной информацией Природа делает ход первой и он ненаблюдаем по крайнем мере одним из игроков. В противном случае игра является игрой с
полной информацией.
Игра с неполной информацией является игрой с несовершенной информацией, так как информационные множества некоторых игроков содержат более одной вершины.
Необходимо особо подчеркнуть, что термин ”неполная информация” используется в литературе часто и в старом смысле, согласно которому в игре с полной информацией, все игроки знают правила игры, а в противном случае игра называется игрой с неполной информацией. До 1967 г. об играх с неполной информацией (в этом смысле) говорили, когда хотели сказать, что их невозможно анализировать. Затем Дж. Харшаньи заметил, что любая игра с неполной информацией может быть переформулирована как игра с полной, но несовершенной информацией просто за счет добавления начального хода Природы, когда Природа выбирает между различными правилами. Подробнее по этому поводу см. Rasmussen (1989).
Итак, рассмотрим теперь более подробно позиционную форму игры.
Рассмотрим простейший пример — игру ”крестики-нолики” на поле 3x3. Перенумеруем соответствующие клетки
| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | GO | 9 |
Мы не изображаем это дерево полностью, поскольку очевидно, как оно строится. Разумеется, как только выстраивается ряд из трех крестиков или ноликов, то игра заканчивается и победивший игрок получет, скажем, от проигравшего 1 рубль (доллар ...). В случае ничьей, соответствующие выигрыши — это (0,0).
Формально позиционная форма игры описывается с помощью следующих элементов: списка игроков; дерева игры; указания для каждой вершины номера игрока
| N |
 |
Таким образом, мы считаем, что
1. / = {1,...,п} — конечное множество игроков.
2. Мы имеем дерево игры с конечным множеством вершин X и конечным множеством ходов А.
При этом должно быть определено отображение р : X —>¦ {tU0} , которое каждой вершине х ставит в соответствие единственную непосредственно предшествующую вершину р(х) , за исключением начальной вершины х0 , для которой р(х) = 0 . Далее — непосредственно следующие за х вершины тривиально определяются по р: s(х) = р~1(х) . Чтобы у нас действительно была древесная структура необходимо, чтобы множество всех предшествующих и множество всех последующих вершин не пересекались для каждой вершины х (они могут быть найдены с помощью итераций
pus). Множество терминальных (окончательных) вершин Т = {ж : з(ж) = 0} .
3. Далее мы должны иметь отображение а : X \ {ж0} —>¦ А, ставящее в соответствие каждой вершине ж , кроме начальной, ход, который из непосредственно предшествующей вершины р(ж) приводит к ж и такой, что если ж', х" ? з(ж) и х' ф х", то а(ж') ф <ч(х") .
Множество возможных ходов, доступных в вершине ж , есть с(ж) = {а ? А : а = а(ж') для некоторого х' ? Дж)} •
4. Набор информационных множеств Л и отображение Н : X —>¦ Л , ставящее в соответствие каждой вершине (кроме терминальной) информационное множество Н( ж) ? Л . Информационные множества образуют разбиение множества X \ Т . Необходимое требование: все вершины, лежащие в одном информационном множестве имеют одни и те же допустимые ходы, т. е. формально, с(ж) = с(ж') , если Н( х ) = н( х') . Мы можем, таким образом, определить выбор, который доступен игроку в информационном множестве Н :
с(Н) = {а ? А : а ? с(ж) для ж ? Н}.
5. Отображение р : Л ^ I U {0} , ставящее в соответствие каждому информационному множеству Н ? Л игрока (или Природу, т.е. игрока і = 0), который должен ходить в вершине из этого множества. Будем обозначать через Лі = {Н ? Л : р(Н) = г}, те информационные множества, в которых очередь хода принадлежит игроку і.
6. Функция р : Ло X А —У [0,1] , ставящая в соответствие ходам в информационных множествах Природы вероятности, удовлетворяющие условию
р(Н,а) = 0 для а (jt С(Н) и
^2 р(н’а) = 1 V Н (ЕЛо
аеС(Н)
7. Набор функций выигрышей и = {iti(-),. . ., un(-)} , щ(-) : Т —> IR.
Здесь следует заметить, что, формально говоря, мы определили все для конечных множеств, но данные определения могут быть перенесены и на случай бесконечных множеств (вершин, ходов, игроков). Нарисовать дерево уже было бы, разумеется, невозможно (хотя, впрочем, как мы видим, даже для простейшего варианта
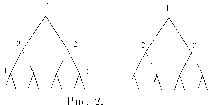
”крестиков-ноликов” это не очень просто), но все формальности можно было бы соблюсти, приписывая, скажем, выигрыши не терминальным вершинам, а путям, соответствующим разыгрыванию игры.
Важно также отметить, что мы ограничиваемся рассмотрением игр с полной помятъю, в которых игроки не забывают то, что они раньше знали, включая свои собственные ходы, сделанные ранее. Игры, изображенные на рис. 2, таковыми не являются.
Определение 2.1.1 Игра в позиционной форме называется игрой с совершенной информацией, если каждое информационное множество состоит из единственной вершины. В противном случае игра называется игрой с несовершенной информацией.
Здесь мы должны сделать очень важное отступление и остановиться на центральном для бескоалиционной теории игр понятии стратегии. Стратегия — это полный возможный план, который описывает то, как игрок будет действовать в каждых возможных обстоятельствах, когда ему, может быть, придется ходить.
С точки зрения игрока, множества возможных обстоятельств представлены набором его информационных множеств, причем каждое информационное множество представляет различные различимые обстоятельства, в которых ему может потребоваться ходить. Тем самым стратегия игрока сводится к описанию того, как он планирует ходить в каждом из его информационных множеств.
Определение 2.1.2 Пустъ BLi — семейство всех информационных множеств игрока і, Л —множество всех возможных ходов (действий) в игре, С(Н) С Л — множество ходов, возможных в информационном множестве Н . Стратегия игрока і — это отображение щ : BLi —У Л, такое что вфН) ? С(Н) для каждого
V не Ні.
То, что стратегия — это полный возможный план нельзя недооценивать, особенно, как мы увидим, это будет важно в дальнейшем. Определение игроком своей стратегии подобно написанию перед игрой инструкции относительно того, как его представитель может действовать, просто заглядывая в эту инструкцию. Или, иначе, определение игроком і своей стратегии можно трактовать следующим образом: в каждом информационном множестве игрока і находится его агент, которому он сообщает, какой ход должен будет сделать этот агент, если ему придется делать ход, т.е. игра ’’дойдет” до соответствующего информационного множества.
Здесь очень важно иметь ввиду следующее. Как полный план, стратегия часто определяет действия игрока в информационных множествах, которые могут быть даже не достигнуты во время действительного разыгрывания игры. Так в крестиках-ноликах стратегия игрока О описывает, в частности, то, что он будет делать если на І-ом ходу X сыграет в центр. Но в действительной игре можно сыграть вовсе не в центр. Более того, стратегия игрока может включать планы действий, которые его собственная стратегия делает неуместными. Опять же в ’’крестиках-ноликах” стратегия игрока X включает описание того, что он будет делать после того, что он сыграет на первом ходу в центр , а (J ответит в левый нижний угол”, даже, если X на первом ходу играет ’’верхний левый”. Это, возможно, кажется странным, но играет очень важную роль в динамическом случае. Итак еще раз:
Стратегия — это полный возможный план действий, который говорит, что игрок будет делать в каждом его информационном множестве.
Рассмотрим следующую простую игру (рис. 3).
У первого игрока две стратегии: Я и Г. А у игрока 2 их четыре; поскольку у него 2 информационных множества, следовательно, каждая стратегия должна определять ход в каждом из этих информационных множеств:
Отметим здесь чрезвычайно важное обстоятельство. Имея набор стратегий каждого игрока, мы можем построить нормальную форму данной игры: поскольку выбор игроками своих стратегий определяет ход в каждом информационном мно-
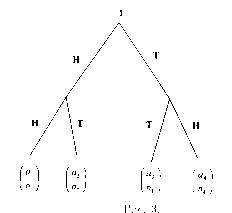
жестве, значит полностью определяет ’’путь”, по которому будет развиваться игра. Нормальная форма игры, изображенной на рис. 3 есть
Каждый набор стратегий определяет траекторию ” движения” по дереву и тем самым, определяет исход игры.
Прежде чем обратиться к более подробному рассмотрению равновесия по Нэшу приведем теорему существования.
Теорема 2.1.1 (Kuhn, 1953). В конечной игре с совершенной информацией существует равновесие по Нэшу в чистых стратегиях.
Мы начнем со следующего примера, который покажет, что равновесие по Нэшу не всегда дает разумное предсказание.
Пример (Mas-Colell, Whinston, Green). Фирма Е (entrant) — новичок — рассматривает вопрос о том, входить ли на рынок, где в текущий момент есть одна единственная укоренившаяся фирма / (incumbent). Если Е решается на вход, то / может ответить двумя способами: она может предоставить вход, отдавая часть
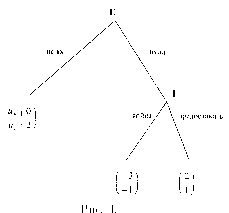
своих продаж, но не изменяя цену, либо она может вступить в хищническую войну, которая приведет к ” драматическому” снижению цен. Дерево, соотетствующее рассматриваемой ситуации, изображено на рис. 4.
Соответствующая нормальная форма имеет следующий вид (рис. 5):
| ||||||||||||
| Рис. 5. |
Для того, чтобы исключить ситуации типа (нет; война, если да) мы рассмотрим ’’принцип последовательной рациональности”: стратегия игры должна предписывать оптимальный ход в каждой вершине дерева. Т. е. если игрок находится в некоторой вершине дерева, его стратегия должна предписывать оптимальный выбор, начиная с этой точки, при данных стратегиях его оппонентов. В этом смысле
| Е |
 |
| Рис. 6. |
uF f О ut 1^2
стратегия ”война, если вход” таковой не является, ибо после входа единственная оптимальная стратегия для / — ”предоставить”. В нашем примере, сделать все очень просто: начнем с того, что определим оптимальное поведение для / в игре на этапе ” после входа” — это, очевидно, ”предоставить”. Теперь мы можем определить оптимальное поведение фирмы Е до этого момента, с учетом предвидения того, что произойдет после входа. Это можно сделать, рассмотрев ’’редуцирован-ную” позиционную форму, где ”пост-входное” принятие решения / заменено на соответствующие выигрыши, которые возникают при оптимальном ”пост-входном” поведении фирмы / (рис. 6). А это уже простейшая задача принятия индивидуального решения, причем решение — ’’вход”.
Этот тип процедуры, которая начинается с нахождения оптимального поведения ”в конце игры”, а затем определения оптимального поведения на более ранних шагах, в предвидении того, что будет происходить дальше называется обратной индукцией. (Подчеркнем, что сказанное относится к конечным играм с совершенной информацией, т. е. конечным играм с ”одновершинными” инормационными множествами).
Однако, прежде чем остановиться на обратной индукции более подробно, мы должны отметить следующее достаточно существенное обстоятельство, касающегося смешанных стратегий. А именно, если мы рассматривали игры в позиционной форме, то игроки могут регулировать свои чистые стратегии способом, отличным от стандартного, в котором используются смешанные стратегии, приписывающие каждой чистой стратегии игрока (множество которых может быть очень большим) вероятноть того, что игрок будет ей играть. В позиционной форме появляется возможность рандомизации раздельно в каждом информационном множестве. Такой способ рандомизации приводит к стратегиям поведения.
Определение 2.1.3 В игре в позиционной форме Іф стратегия поведения игрока і определяет для каждого информационного множества Н ? Иі и альтернативы а ? С(Н) вероятность Аг(а, Н) > 0 ; причем ^2аеСцн) ^і(аі Н) = 1 для всех Н ? Иі .
Оказывается (Kuhn, 1953; см. также, например, Петросян, Зенкевич, Семина (1992)), что для игр с полной помятью эти два типа рандомизации эквивалентны. (Важно подчеркнуть, что полная память играет здесь ключевую роль.) А именно, для любой стратегии поведения игрока і, существует его смешанная стратегия, дающая в точности такое же распределение выигрышей для любых стратегий (смешанных или стратегий поведения), которые могут играться отдельными игроками, и наоборот.
Это соответствие можно установить следующим образом. Будем, как всегда, обозначить чистые стратегии игрока і через щ . Пусть сц — некоторая его смешанная стратегия. Будем называть некоторую вершину х дерева Іф возможной для Si, если существует такой набор стратегий s = (зг,з_г) , что траектория, определяемая этим набором, проходит через s . Обозначим множество всех возможных для Si вершин через Р(щ) .
Информационное множество Н называется существенным для щ , если оно содержит некоторую возможную для щ вершину. Множество существенных для щ информационных множеством обозначим через і?(зг) .
Пусть (Ті — некоторая смешанная стратегия игрока і. Тогда стратегия поведения Аг' , соответствующая смешанной стратегии сц , опрделяется следующим образом. Если Н ? R((Ti) , то
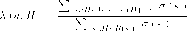
Если Н R((Ti) , то знаменатель этой дроби обращается в ноль, поэтому стратегию А,- можно определить произвольно, например,
А і(а,Н)= ^2
{st:st(H) = a}
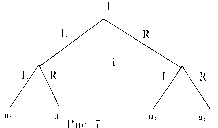
Если Аг' — стратегия поведения, то сц можно определить как
Ci(si) = Y[\i(si(H),H).
н
При этом Аі оказывается стратегией поведения, соответствующей сц . Поэтому в играх с полной памятью (а именно такие игры мы и рассматриваем) безразлично, каким способом рандомизировать. Терминологически мы всегда будем говорить о смешанных стратегиях.
В игре с неполной памятью могут существовать смешанные стратегии, для которых нет эквивалентных им стратегий поведения.
Пример. (Osborn, Rubinstein). Рассмотрим игру, изображенную на рис. 7. Пусть смешанная стратегия игрока а определяется следующим образом: с вероятностью 1/2 играется L, а потом еще раз L, и с вероятностью 1/2 играется R, а потом еще раз R. Исходом, соответствующем этой стратегии, явлдяется распределение (|,0,0,|) на множестве терминальных вершин. Но такой подход не может быть обеспечен ни одной стратегией поведения: стратегия поведения ((р, 1 — p),(g, 1 — q)) инициирует распределение на множестве терминальных вершин, в которых исход соответствующий и2 , имеет вероятность 0 в случае только, если р = 0 или q = 1 , но тогда вероятность (й, L) или (i?, R) есть 0 .
2.2 Обратная индукция и конечные игры с совершенной информацией
Для того, чтобы внимательнее посмотреть на обратную индукцию в конечной игре с совершенной информацией, начнем с определения оптимального ” действия” в последних вершинах дерева, где принимается решение (т. е. тех вершин, для которых последователи — это только терминальные вершины). Решение, принимаемое игроком в такой вершине, не зависит уже от стратегического взаимодействия и потому является простой задачей принятия решения. Затем мы можем обратиться к ”предпоследней” вершине и найти оптимальное решение там, предвидя, естественно, ход, который будет сделан в последней вершине. И так далее.Рассмотрим пример (рис. 8).
Обратная индукция дает нам ситуацию (од , <т2 , сг3 ):
(Т\ = R, <т2 = (а, если 1 играет R),
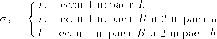 |
| Обратим внимание на то, что это есть равновесие по Нэшу. Но есть и еще равновесия по Нэшу в чистых стратегиях: |
или
Однако можно проверить, что они не удовлетворяют принципу последовательной рациональности. Общая теорема здесь выглядит следующим образом:
Предложение 2.2.1 В любой конечной игре с совершенной информацией Г^; существует ситуация равновесия по Нэшу в чистых стратегиях, которая может бытъ найдена с помощью обратной индукции. Более того, если ни один из игроков не имеет одинаковых выигрышей ни в одной из терминальных вершин, то существует единственное р.Н., которое может бытъ получено таким образом.
2.3 Совершенное под-игровое равновесие по Нэшу
Рассмотрим ситуацию, которая у нас уже была с входом в рынок. Но теперь модифицируем ее слегка, считая (см. Mas-Colell, Whinston, Green), что теперь после входа обе фирмы могут выбирать, воевать или нет (принять) (рис. 9). |
| Рис. 8. |
Нормальная форма игры с одновременными ходами (после входа Е ) есть (рис. 10)
| I | ||||||||||||||||||
|
((нет; принять если вход), (война, если Е входит)),
((нет; война, если вход), (война, если Е входит)),
((вход; принять если вход), (принять, если Е входит)).
Первые две стратегии для Е довольно глупы, но стратегии — это, по определению полный план.
Заметим, что (принять, принять) — единственное р.Н. в игре с одновременными ходами. Поэтому, естественно ожидать, что обе фирмы сыграют ’’принять”, следуя за входом Е . Но если это так, то фирма Е должна входить. Поэтому логика последовательной рациональности говорит, что только последнее равновесие должно быть разумным предсказанием.
Итак перейдем к формальным определениям.
Определение 2.3.1 Под-игрой игры Іф в позиционной форме называется такое поддерево дерева исходной игры, что:
(1) его начальная вершина — одноточечное информационное множество, и оно содержит все последующие (непосредственно и далее) за ней вершины и только их;
(2) если вершина х лежит в под-игре, то все вершины х' ? Н(х) тоже лежат в этой под-игре, где Н(х) — информационное множество, содержащее х .
На рисунке 11 две под-игры — сама игра и игра с одновременными ходами. Объединенная пунктиром часть дерева не является под-игрой.
Заметим, что в игре с совершенной информацией каждая вершина (кроме терминальной) инициирует под-игру.
Легко видеть, что в соответствии с определением стратегий в позиционной игре, любая стратегия игрока в позиционной игре индуцирует стратегию в под-игре, получающуюся сужением исходной стратегии на информационные множества игрока, оказывающиеся в под-игре.
Определение 2.3.2 Ситуация (набор стратегий) а = (од,. . ., (Тп) в игре в позиционной форме называется совершенным (под-игровым) равновесием по Нэшу, если она индуцирует равновесие по Нэшу в каждой под-игре.
Далее мы для краткости будем писать СПРН вместо ” совершенное под-игровое равновесие по Нэшу”. Заметим, что СПРН является р.Н., но не каждое р.Н. является СПРН.
В конечных играх с совершенной информацией множество СПРН совпадает с множеством р.Н., которые могут быть получены с помощью обратной индукции.
Предложение 2.3.1 В любой конечной игре с совершенной информацией Г^; существует СПРН в чистых стратегиях. Если все выигрыши всех игроков различны в любых двух терминальных вершинах, то оно единственно.
Для определения множества СПРН в общей (конечной) динамической игре Г^; , процедура обратной индукции может быть обобщена следующим образом:
1. Начинаем с конца дерева игры, и определяем равновесия по Нэшу для каждой из ’’концевых” под-игр, т.е. под-игр, не имеющих собственных под-игр.
2. Выбираем одно из равновесий по Нэшу в каждой из этих ’’концевых” под-игр и рассматриваем редуцированную игру, в которой эти ’’концевые под-игры” заменяются выигрышами, получающимися в этих под-играх, когда игроки используют эти равновесные стратегии.
3. Повторяем шаги 1 и 2 для редуцированных игр. Продолжаем эту процедуру до тех пор, пока не будут определены все ходы в игре Іф . Набор ходов в каждом из информационных множеств игры Іф образует СПРН.
4. Если ни на одном из шагов процесса не возникала множественность равновесий по Нэшу, то полученное СПРН единственно. Если же множественность равновесий имела место, то множество всех СПРН получается с помощью повторения этой процедуры для каждого возможного равновесия, возникающего в рассматриваемых под-играх.
Предложение 2.3.2 Рассмотрим игру в позиционной форме Г^; и некоторую ее под-игру S . Предположим, что набор as стратегий является СПРН в под-игре S и пустъ — редуцированная игра, образованная заменой S терминальной вершиной с выигрышами, равными выигрышам, возникающим при игре as . Тогда
(1) в любом СПРН а игры Те , в которой as — это набор стратегий, которые играются в под-игре S, ходы игроков в информационных множествах вне S должны образовывать СПРН игры Г^; /
(2) если а — СПРН в Те , то набор а, приписывающий ходы в соответствии с as в информационных множествах из S и ходы в соответствии с б в информационных множествах вне S является СПРН в Г^; .
Доказательства этих предложений можно найти, например, в учебнике Mas-Colell, Whinston, Green.
Рассмотрим модификацию нашего примера. Предположим, что есть две части рынка, две ниши малая ниша (м.н.) и большая ниша (б.и.) (см. рис. 12).
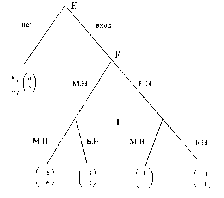 |
| Рис. 12. |
В любом СПРН в этой под-игре должно индуцироваться одно из этих равновесий по Нэшу. Предположим сначала, что фирмы играют (б.и., м.н.), а следовательно редуцированная игра будет иметь вид, изображенный на рис. 13. В этом случае Е выбирает входить, следовательно, СПРН — это (ае} сг/) = ((вход, б.и.), (м.н., если Е вошла).
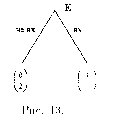
Во втором случае редуцированная игра представлена на рис. 14
Следовательно СПРН ( ае} <т/)= ((не вх., м.н.), (б.н., если Е вошел).
Разумеется, как всегда, не все так просто с СПРН. Рассмотрим следующую игру (Rabin (1988)) (см. рис. 15).
В ” координационной игре” с одновременными ходами между 1 и 3 игроками три равновесия по Нэшу: два в чистых стратегиях, приводящих к выигрышам (7,10,7) и равновесие в смешанных стратегиях, дающее выигрыши (3.5, 5, 3.5). Если мы выбираем равновесие, в котором игроки 1 и 3 успешно координируются, то игрок 2 играет L , а игрок 1 - R , ожидая выигрыш 7. Если же мы выбираем неэффективное равновесие в смешанных стратегиях, то игрок 2 сыграет R, а 1 - снова L , ожидая выигрыш 8. Поэтому во всех СПРН игрок 1 играет R.
Но ... тем не менее игроку 1 будет осмысленно сыграть Е, если он не увидел возможности координации на 3-ем шаге, а поэтому ожидает выигрыш 3| , но опасается того, что игрок 2 может верить, что при игре на 3-ем шаге будет достигнуто эффективное равновесие.
(8,6,8)
 |
G R |
| (0,0,0) (7,10,7) (7,10,7) (0,0,0) Рис. 15. |
Суть здесь в том, что ”под-игровое совершенство” предполагает не только, что игроки ожидают р.Н. во всех под-играх, но также и что все игроки ожидают одно и то же равновесие.
2.4 Примеры 1. Дуополия по Штакельбергу. Эта ситуация — модификация дуополии по Курно, рассмотренной нами в гл. 1. Теперь мы считаем, что есть лидер, который делает ход первым. Затем, зная этот выбор, другой выбор игрок делает свой ход. Итак, игра протекает следующим образом:
1) фирма 1 выбирает щ > 0 ;2) фирме 2 становится известно это щ , и после этого она выбирает q2 > 0 ;
3) выигрыш фирмы і есть
где P(Q) = а — Q ; Q = qi + q2 , с — постоянные предельные затраты.
Для нахождения равновесия здесь мы воспользуемся обратной индукцией. Вычислим вначале функцию реагирования фирмы 2, решая задачу

тах7г2(ці, q2) = таxq2[a — щ — q2 — с].
Легко видеть, что
а — qi — с
2
-^2(91)
То же самое было и в случае дуополии Курно. Разница, однако, в том, что это действительная, а не гипотетическая функция реагирования фирмы 2.
Фирма 1, естественно, также может вычислить эту функцию реагирования, а следовательно, задача фирмы 1 на первом шаге выглядит так:
a — qi — c
c\ = max qi-
q 1 2
тах7Гі(<2і, R2(qi))
Яі
тахщ[а — q\ — R2(qi)
41
что дает
и R2(q*1) =
<h =
Прибыль в случае дуополии по Штакельбергу:
а — с г 1
7г 1 = - —(а — с)
2 Uv ;
ТГ2 =
16
-с _ (а —с)2
|(а-с)?
Заметим, что прибыль в случае дуополии по Курно: з?^ —
Этот пример показывает существенное различие между принятием единоличного решения и решения при нескольких участниках. Здесь ’’лишняя” информация для игрока и знание того, что другие имеют больше информации, могут ухудшить положение игрока.
2. Последовательный торг (Rubinstein, 1982).
Рассмотрим следующую игру. Игроки 1 и 2 торгуются о разделе 1 доллара: 1ый предлагает некоторый способ деления, 2-ой либо принимает это предложение, либо нет; если нет, то он предлагает способ деления, а 1-ый принимает, либо нет, ... Каждое предложение занимает один период, но при этом есть дисконтирующий множитель. Итак, формально рассмотрим следующую трех-периодную игру.
(Іа) В начале І-ого периода игрок 1 предлагает ’’свою долю” щ доллара, оставляя 1 — Si игроку 2.
(lb) Игрок 2 принимает предложение, тогда игра заканчивается, либо отклоняет его. В этом случае игра переходит ко 2-ому периоду.
(2а) В начале второго периода игрок 2 предлагает долю s2 , которую получает игрок 1, оставляя себе 1 — s2 .
(2Ь) Игрок 1 либо принимает предложение, либо нет. В последнем случае игра переходит к 3-ему периоду.
(3) Игроки в 3-ем периоде получают доли (s , 1 — s ), 0 < 5 < 1 , причем s задан экзогенно.
Мы будем решать задачу с помощью обратной индукции. Вначале вычисляем, что происходит, если дело доходит до 2-ого периода. Игрок 1 может получить s , если отклонит s2 , но стоимость при этом будет 8s (в сравнении с предыдущим (вторым) периодом). Следовательно, игрок 1 примет s2 тогда и только тогда, когда s2 > 8s (считаем, что принимает, если равенство). Значит, задача игрока 2 состоит в выборе между получением 1 — 8s (предлагая первому игроку s2 = 8s ) и получением 1 — s в следующем периоде (предлагая s2 < 8s). Дисконтированная стоимость последнего ” действия” есть Й(1 — s) , что меньше чем 1 — 8s , а потому 2-ой игрок во 2-ом периоде предлагает s^ = 8s .
Таким образом, если игра доходит до 2-ого периода, то 2-ой игрок предложит s^ и 1-ый игрок примет это предложение.
Однако 1-ый игрок может предвидеть, что игрок 2 может получить 1 — во втором периоде, отклоняя предложение si , но ’’стоить” это будет только Й(1 — s^) в следующем периоде. Значит 2-ой игрок принимает 1 — si тогда и только тогда, когда 1 — si > Й(1 — s^) , или Si < 1 — Й(1 — s^) .
Поэтому задача 1-ого игрока в периоде 1 состоит в выборе между получением 1 — Й(1 — S2) в этом периоде (предлагая 1 — si = Й(1 — зД игроку 2) и получением s^ в следующем периоде (предлагая 1 — si < Й(1 — s^) игроку 2). Дисконтированная стоимость последнего есть ^s^ = S2s , что меньше, чем 1 — Й(1 — зД = 1 — Й(1 — 8s) . Значит, оптимальное предложение в певом периоде есть s^ = 1 — Й(1 — зД = 1 — Й(1 — 8s). Следовательно, на первом ходу 1-ый игрок предлагает s^ , 2-ой принимает это предложение и получает 1 — s^ . Таким образом, выигрыш игроков есть 1 — 8 + S2s и 8 — S2s , соответственно.
Задача. Докажите, что если бы игра продолжалась бесконечно (здесь уже нет экзогенно заданного s ), то игрок 1 на 1-ом шаге предложил бы s* = 1/(1 + й) , оставляя второму 1 — s* = 8/(1 + й) и второй игрок принял бы это предложение.
3. ’’Инвсторы и банк” (Diamond, Dybvig, 1983). Представим себе следующую ситуацию. Два инвестора вкладывают по D долларов в банк. Банк инвестировал
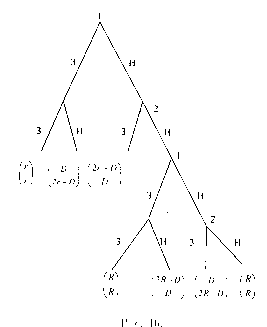
эти депозиты в долгосрочный проект. Если ”форс-мажорные” обстоятельства заставляют банк ликвидировать свои инвестиции до того, как проект ”созревает”, то он может покрыть сумму 2г, где D > г > D/2. Если банк позволяет проекту ” созреть”, то проект принесет 2 і? , где R> D .
Есть 2 даты, когда вкладчики могут забрать свой вклад: дата 1 — до ”созревания”, дата 2 — после. Для простоты считаем, что нет дисконтирования. Если оба вкладчика забирают вклады в момент 1, то оба получают по г и игра заканчивается. Если только один вкладчик забирает в момент 1,то он получает D , а второй — 2г — D . Наконец, если ни один вкладчик не забирет в момент 1, то проект созревает и оба вкладчика забирают в момент 2, то каждый получает по R . Если только один вкладчик забирает в момент 2, то он получает 2R — D , другой получает D . Если, наконец, ни один не забирает в момент 2, то банк возвращает по R каждому.
Дерево этой игры изображено на рис. 16. Неформально, для момента 1 игру можно попытаться изобразить следующим образом (см. рис. 17):
2г — D,D (шаг 2)
забирать
г, г D, 2г — D
нет
забирать
нет
Рис. 17.
Для момента 2 игра изображена на рис. 18:
забирать нет
забирать / R} R D, 2R — D, D
R} R
D,2R - D
нет
Рис. 18.
Начнем с момента 2: так как R > D (и 2R — D > R), то ’’забирать” строго доминирует ’’нет”. Значит единственное р.Н. — это (забрать, забрать), давая выигрыши (і?, R) . Поскольку нет дисконта, то можно просто подставить в ’’первую игру” (см. рис. 19)
3.
н.
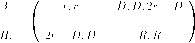 |
| Рис. 19. |
1) оба вкладчика ’’бегут” в банк в момент 1;
2) оба забирают в момент 2.
Первое можно интерпретировать как ’’бежать в банк”: если вкладчик верит в то, что другой побежит, то ему тоже надо бежать, хотя, конечно, обоим лучше подождать.
2.5 Повторяющиеся игры
Рассмотрим следующий вариант дилеммы заключенного (рис. 20). Будем считать, что игра повторяется дважды, причем, игроки наблюдают исход первого розыгрыша до того, как начинается второй. Считаем пока, что нет дисконта и, поэтому, выигрыши есть просто сумма выигрышей в первом и втором разыгрывании, т. е. мы имеем дело с двухпериодной или двухшаговой дилеммой заключенного.Ri R2 Ri ( (1Д) (5,0) \
R2 { (0,5) (4,4) )Рис. 20.
Следуя той логике СПРН, которая у нас была ранее, посмотрим, что происходит на втором шаге игры. Ясно, что исход игры второго шага будет р.Н., т. е. (Lі, Ь2) ¦ А это значит, что игра на первом шаге сводится к тому, что к каждому элементу исходной матрицы нужно добавить выигрыши второго шага, т.е. (1,1) .
Таким образом, матрица становится
/ (2,2) (6,1) Л
V (1-6) (5,5) )
а в ней р.Н. единственно — (Ті,Т2), значит СПРН в этой двухшаговой дилемме Заключенного — это (Lі, Ь2) на 1 шаге и (Lі, Ь2) — на втором.
Теперь отвлечемся на время от двукратного повторения игры. Пусть G = (Аі,. . ., Ап; iti,. . ., ип) — статическая игра с полной информацией, в которой игроки одновременно выбирают ходы щ из своих пространств стратегий Аі и соответствующие выигрыши есть . . ., ап) . Будем называть G — ’’базовой” игрой.
Определение 2.5.1 Конечной повторяющейся игрой G(T) базовой игры G называется игра, в которой G разыгрывается Т раз и перед началом каждого очередного розыгрыша игрокам известны исходы всех предыдущих розыгрышей, т. е. известны стартегии, избранные игроками, и полученные выигрыши. Выигрыши в игре G(T) определяются как сумма (или дисконтированная сумма) выигрышей на каждом шаге.
Рассмотренная выше ситуация на самом деле характерна и для общего случая.
Предложение 2.5.1 Если базовая игра G имеет единственное равновесие по Нэшу, то для любого конечного Т повторяющаяся игра G(T) имеет единственное СПРН: на каждом шаге играется р.Н.
Рассмотрим теперь ситуацию, когда базовая игра G имеет несколько равновесий
(Gibbons).
| Ь2 М2 В |
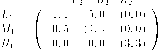 |
Предположим, что эта игра повторяется дважды, причем исход первой игры известен до того, как разыгрывается вторая. Для нас важно, что может существовать СПРН, в котором на первом шаге играется (Мі,М2). Это тот самый нюанс, который важен для нас, поскольку он, так сказать, разделяет дух того, что происходит в случае бесконечного разыгрывания игры G.
Как и раньше (поскольку речь идет о СПРН) предполагаем, что игроки считают, что исход второго розыгрыша — это р.Н. базовой игры. Вообще говоря, можно предположить, что игроки могут ожидать, что различным исходам 1 этапа будут соответствовать разные исходы 2-ого этапа. Предположим, например, что игроки ожидают, что (R\, Я2) будет исходом, если первый исход был (Мі, М2) , но Ь2) если один из 8 оставшихся был исходом 1 этапа. В этом случае игра на І-ом шаге сводится к игре,
12 М2 R•
1j2 Ш 2 Гі 2
и
Мх
Яі
(2,2) (6,1) (1,1) (1,6) (7,7) (1,1) (1,1) (1,1) (4,4)
Здесь (3,3) добавлено к выигрышам, соответствующим (Мі,М2) и (1,1) — к 8 остальным элементам исходной матрицы.
В этой игре уже 3 р.Н. — (Li,L2), (Мі,М2), (R\,R2). Эти три р.Н. соответствуют СПРН в первоначальной повторяющейся игре. Обозначим ((ш, ж)(у, z)) — исходы в повторяющейся игре — (ш, х) — на І-ом шаге, (у, z) — на 2-ом. Равновесие (Ьі,Ь2) соответствует ”совершенному под-игровому” исходу ((йі, Ь2), Ь2))
в повторяющейся игре. Аналогично р.Н. (і?і,і?2) соответствует ”совершенному под-игровому” исходу ((і?і, R2), (Li, Ь2)) в повторяющейся игре. Эти два исхода просто ’’наследуют” р.Н. базовой игры. Но третий исход — качественно другой: (Мі,М2) — соответствует ’’совершенному под-игровому” (СП) исходу ((Mi, M2), (i?i, i?2)) в повторяющейся игре, т. к. ’’предвидимый” исход 2-ого шага — это (Ri,R2) вслед за (Мі,М2).
Иными словами, кооперацию можно достичь на 1-ом шаге СП исхода повторяющейся игры. А это уже дает пример более общей природы: если G — статическая игра с полной информацией и множественными р.Н., то может существовать СП исход в игре G(T) , в которой на любом шаге t < Т исход шага t — не является р.Н.
Основной вывод здесь такой — угрозы или обещания, которым можно верить в будущем, могут влиять на текущее поведение. Второй вывод, однако, состоит в том, что ”под-игровое совершенство” может не воплощать достаточно сильные определения ’’правдоподобия”. Говоря, например, о СП исходе ((МІ5 М2), (і?І5 R2)) мы предполагали, что игроки предвидят, что (і?і,і?2) будет исходом на втором шаге, если исход первого шага был (М1?М2) , а (Гі,Г2) — исходом второго шага игры, если любой другой из 8 оставшихся исходов возникает на первом шаге. Однако игра (Lі, Ь2) на втором шаге может показаться достаточно глупой, если (і?і, R2) с выигрышем (3,3) также возможно в равновесии на втором шаге игры. Далее можно рассуждать следующим образом. Если (М1?М2) не стало исходом первого шага, так как (Гі,Г2) предположительно будет играться на втором шаге, то каждый игрок может считать, что ’’что прошло, то прошло” и предпочтительная для обоих игроков ситуация (і?і,і?2) должна разыгрываться на 2-м шаге. Но если і?і,і?2) будет исходом 2-го шага после любого исхода розыгрыша, то пропадают стимулы играть (Мі,М2) на 1-м шаге: розыгрыш І-го шага сводится просто к добавлению к каждому исходу (363). А тогда Li есть лучший отчет игрока і на Mj игрока j .
Прежде чем перейти к бесконечным повторяющимся играм, вернемся к нашему определению и введем коэффициент дисконтирования. Считаем, что игроки дисконтируют будущие выигрыши с общим дисконтом 8. Иногда бывает удобно рассматривать не просто суммарный выигрыш
V(cC),
t=1
но нормировать его для того, чтобы рассматривать среднюю полезность за период,
т. е.
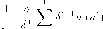 |
| і=1 |
Если ” Дилемма Заключенного” разыгрывается один раз — то нужно ” сознаваться”. Если разыгрывается конечное число раз, то ”под-игровое совершенство” требует в последний раз ”сознаться”, а обратная индукция говорит, что единственное СПРН — это ” сознаваться” всегда. Если игра разыгрывается бесконечное число раз, то ”сознаться” остается СПРН. Более того — это единственное равновесие такое, что игра на каждом шаге не меняется в зависимости от того, что игралось на предыдущих шагах. Но если горизонт бесконечен и 8 > 1/2, то, как мы увидим ниже, следующий набор стратегий оказывается тоже СПРН: ’’молчать” (кооперироваться) на 1-ом шаге и продолжать ’’молчать” (кооперироваться) до тех пор, пока никто не предал. Если только кто-то предал, то далее предавать всегда.
Пример.
| L | м | R | |
| и | ( (0,0) | (3,4) | (6.0) |
| М | (4.3) | (0.0) | (0.0) |
| D | \ (0,6) | (0.0) | (5.5) |
Если эта игра разыгрывается один раз, то здесь 3 равновесия: (М, L), (С, М) и с выигрышами (4,3), (3,4) и соответственно. Здесь
запись |М^ означает, что с вероятностью | играется ” U ” и с вероят
ностью I - играется ”М”. Эффективный набор выигрышей (5,5) не достижим. Однако в двухшаговой игре с 8 > 7/9 следующий набор стратегий является СПРН: ’’Играть (D,R) на первом шаге. Если исход первого шага (D,R) , то играть (М, L) во втором шаге; если исход первого шага — не (D, R) , то играть ((3/7U, 4/7М), (3/7Е, 4/7М)) на втором шаге”.
По построению, эти стратегии используют р.Н. на 2-ом шаге. Отклонение этой стратегии на 1-ом шаге увеличивает текущий выигрыш на 1 и уменьшает следующие выигрыши игроков 1 и 2, соответственно, с 4 или 3, до 12/7. Поэтому игрок 1 не будет отклоняться, если 1 < ^4 — Щ^8 или 8 > 7/16 , а второй не будет отклоняться,
если 1 < ^3 — й или й > 7/9 .
Имеет место следующее уточнение: если в базовой игре G есть несколько равновесий по Нэшу, то может существовать СПРН в повторяющейся игре G(T) такое, что для любого t < Т исход шага t не является равновесием по Нэшу. В бесконечно повторяющихся играх справедлив более сильный результат: даже если в базовой игре G есть единственное равновесие по Нэшу, то может существовать СПРН бесконечно повторяющейся игры, в которой никакой ”по-шаговый” исход не будет равновесием по Нэшу.
Итак рассмотрим вариант ”дилеммы заключенного”, повторяющейся бесконечно, причем для любого t исходы t — 1 предыдущего шага игры известны до начала разыгрывания шага t.
Li i?2
К /(1.1) (5,0) \
Я, V (0,5) (4,4) )
Разумеется, в бесконечном случае уже без дисконтирующего множителя не обойтись.
Определение 2.5.2 Если 8 — коэффициент дисконтирования, то приведенная стоимость бесконечной последовательности выигрышей тті, 7Г2, - - - есть
ОО
t=l
В нашем варианте дилеммы заключенного мы покажем, что ”кооперация” (i?i, R2) на каждом шаге может быть СПРН бесконечно повторяющейся игры (хотя единственный равновесный исход в базовой игре — это (Аі, й2) ). А именно, если игроки кооперируются сегодня, то они кооперируются и завтра и т. д., а в противном случае они играют ”плохое” равновесие.
Предположим, что игрок і начинает игру, кооперируясь, и продолжает так только и если только оба игрока кооперировались на любом предыдущем шаге. Формально его стратегия описывается следующим образом:
Играть Ri на 1-м шаге. На шаге t, если все предыдущие t — 1 исхода были (Ді,Д2), играть Ri ; в противном случае играть Li .
Это так называемая триггерная стратегия (стратегия переключения). Если игроки придерживаются этой стратегии, то в бесконечно повторяющейся игре равновесным исходом будет (іД, R2) на каждом шаге.
Мы вначале покажем, что если 8 достаточно близко к 1, то это есть равновесие по Нэшу в бесконечно повторяющейся игре для обоих игроков, придерживающихся этой стратегии. А затем покажем, что это СПРН.
Чтобы показать, что это есть равновесие по Нэшу в бесконечно повторяющейся игре, предположим, что і -ый игрок использует триггерную стратегию, и покажем, что если 8 достаточно близко к 1, то для j-ого игрока лучшим ответом будет тоже применять такую стратегию. Так как игрок і будет играть Li всегда, как только на каком-то шаге исход отличается от (і?і,і?2) , то лучшим ответом j-ого будет тоже играть Lj всегда после нарушения (і?і,і?2). Т.е. осталось определить лучший ответ j -ого игрока на 1-ом шаге и на всех шагах таких, что все предыдущие были (RuR2) ¦ Игра Lj даст 5 на этом шаге, но переключит на ”некооперативное поведение” игрока і (а значит и j ) навсегда. Следовательно, на любом будущем шаге выигрыш будет 1; так как 1+й + й2 + ••• + ••• = 1/(1 — й) , то приведенная стоимость последовательности выигрышей есть 5 + й + й2 + -- - = 5 + у^у .
С другой стороны, ответ R3 дает выигрыши 4 и аналогичный выбор между Lj и R3 на следующем шаге. Пусть V — приведенная стоимость выигрыша j -ого игрока, если он играет оптимально. Если игра R3 оптимальна, то V = 4 + 8V. Следовательно,
4
Т^8'
Если Lj оптимальна, то V = 5 + у^у следовательно R3 оптимальна в том и только в том случае, если
8
Т^8
1
4'
>5 +
илиПусть теперь G — игра с полной информацией, в которой игроки одновременно выбирают ходы. Если дана базовая игра G, то G(oo}8) — это бесконечно повторяющаяся игра, в которой G повторяется всегда, и у игроков общий коэффициент дисконтирования 8 . Для любого t исходы предыдущих t — 1 шагов наблюдаются до начала шага t. Выигрыш каждого игрока — приведенная стоимость его выигрышей.
Как хорошо известно, в любой игре стратегия — полный план действия. В статической игре с полной информацией — это просто ходы. В динамике, разумеется, все сложнее. Скажем в двухшаговой дилемме заключенного стратегию можно записать как пятерку (v,w,x,y,z):
? — на І-ом шаге;
w — ходить w , если исход был (Lі, Ь2) ;
х — ходить х , если — (Lі, R2);
у — ходить у , если — (і?і, Ь2) ;
z — ходить z , если — (і?і, R2) .
Это можно представить себе, как набор команд агентам: 1-ый ходит на 1 шаге, 2-ой — на втором и т. д.
В повторяющейся игре G(T) или G(oo,8) история игры до шага t — это ”за-пись” ходов игроков до шага t. В конечно повторяющейся игре G(T) или бесконечно повторяющейся игре G(oo,8) стратегия игрока описывает действие игрока, которые он предпринимает на каждом шаге, для любой возможной истории. (В этом смысле история соответствует информационному множеству: каждая история приводит к вполне определенному информационному множеству (одноточечному), а каждому информационному множеству (одноточечному) соответствует вполне определенный путь (история), который приводит именно к этому информационному множеству).
Для конечно повторяющейся игры G(T) под-игра, начинающаяся на шаге t + 1; — это конечно повторяющаяся игра, в которой G разыгрывается Т — t раз, и которая обозначается G(T — t) .
В G(oo,8) каждая под-игра, начиная с шага t-\- 1 — идентична G(oo,8) . Игр, начинающихся с t + 1 столько же, сколько историй. Разумеется каждая под-игра осмысленна вместе с предысторией.
Таким образом, здесь, как и ранее, равновесие по Нэшу является СПРН, если соответствующие стратегии игроков образуют равновесие по Нэшу в любой подигре.
СПРН является уточнением равновесия по Нэшу в том смысле, что стратегии игроков должны, во-первых, образовывать равновесие по Нэшу, а кроме того, ”вы-
держивать” дополнительный тест — в под-играх.
Вернемся к дилемме заключенного и к триггерной стратегии, рассмотренной выше. Здесь все под-игры можно разбить на 2 группы:
(1) под-игры, в которых все исходы предыдущих шагов были (i?i, R2) и
(2) под-игры, в которых хотя бы один из предыдущих исходов был не (i?i, R2) .
Если игроки используют триггерную стратегию во всей игре, то 1) стратегии
игроков в под-игре первой группы тоже оказываются триггерными стратегиями, которые формируют равновесие по Нэшу во всей игре; 2) стратегии игроков в подигре второй группы просто ’’навечно” повторяют ’’пошаговое” равновесие (Li7L2) , которое также является равновесием во всей игре. Поэтому равновесие по Нэшу в триггерных стратегиях является СПРН.
Набор выигрышей (ад,. . ., хп) называется достижимым в базовой игре G , если он является выпуклой комбинацией выигрышей в ситуациях в чистых стратегиях игры G. На рис. 21 изображено множество достижимых выигышей в дилемме заключенного — это параллелограмм.
Средний выигрыш (за период) бесконечной последовательности выигрышей 7іц, 7г2, 7г3, . . . при данном коэффициенте дисконтирования 8 есть
ОО
t=1
Преимущество среднего выигрыша по сравнению с приведенной стоимостью в том, что средний выигрыш непосредственно можно сравнивать с пошаговыми выигрышами. В рассмотренном нами варианте дилеммы заключенного оба игрока могут получать выигрыш 4 в каждом периоде. Такая последовательность выигрышей дает средний выигрыш 4, а приведенную стоимость 4/(1 — й). С другой стороны, средний выигрыш — это просто приведенная стоимость с некоторым множителем; максимизация среднего выигрыша эквивалентна максимизации приведенной стоимости.
Мы можем сформулировать теперь знаменитую теорему, которая носит название народной (фольклорной) — Folk Theorem, которая столь хорошо известна специалистам, что ее авторство считается ’’народным”, хотя, по-видимому, первым ее для СПРН доказал Джеймс Фридман.
Теорема 2.5.1 (Friedman, 1971). Пустъ G конечная, статическая игра с полной информацией. Пустъ (еі,...,еп) выигрыши в состоянии равновесия по Нэшу, и пустъ (жі,...,жп) — любой достижимый вектор выигрышей в G . Если ж г- > ег-для любого і и 8 — достаточно близко к 1, то существует СПРН в игре бг(оо, й), дающее (жі,...,жп) в качестве среднего выигрыша.
Доказательство этой теоремы можно найти, например, в учебнике Gibbons (1992). На рис. 19 множество возможных СПРН заштриховано.
Пример. Сговор Курно-дуополистов
Вспомним статическую дуополию по Курно. Спрос на рынке P(Q) = а — Q , где Q = qi~\~q2 , Q < а , у фирм постоянные предельные затраты с , и нет фиксированных затрат. В единственном равновесии по Нэшу каждая фирма производит qc = (а — с)/3. Поскольку суммарный объем в равновесии 2(а — с)/3 превышает монопольный объем, qm = (а — с)/2 , обеим фирмам было бы лучше, если бы каждый производил половину монопольного выпуска qi = qm/2 .
Рассмотрим бесконечно повторяющуюся игру, в которой базовая игра — это рассматриваемая дуополия по Курно, причем у обеих фирм общий коэффициент дисконтирования 8. Мы сейчас вычислим значение 8, для которых в совершенном ”под-игровом” равновесии по Нэшу этой бесконечно повторяющйся игры играется (обеими фирмами) следующая стратегия:
Производить половину монопольного объема, qm/2 , в первом периоде. В периоде t играть qm/2 , если обе фирмы производили qm/2 в каждом из предыдущих t — 1 периодов; в противном случае производить qc.
Прибыль фирмы, когда обе фирмы производят qm/2 , есть (а —с)/8 , которую мы обозначим через 7гт/2 . Прибыль фирмы, когда обе производят qc, есть (а — с)/9 , которую мы обозначим ттс. Далее, если фирма і собирается производить qm/2 в этом периоде, то объем, максимизирующий прибыль фирмы j , решает задачу
c)q3.
max^a - q3 - -qm 4j I
Решением этой задачи является q3 = ^ag с~* , с соответствующей прибылью 7ід = 9(a64c) . Таким образом, ситуации, в которых фирмы играют триггерную стратегию, приведенную выше, является равновесием по Нэшу, если
1 1 8
Т^8 2Пт -nd + Т^8П'
_9_
17 '
Подставляя ттт
lid , получаем
7Г г
2.6 Задачи
1. Предположим, что родитель и ребенок играют в следующую игру. Сначала ребенок выбирает действие А, которое приносит ему доход ІС(А) и доход для родителя Ір(А) . Далее, родитель наблюдает доходы /с и Ір и затем выбирает награду В для ребенка. Функция выигрыша ребенка U(IC + В) , родителя — ?(Ір — B)AkU(IcAВ), где к > 0 отражает ’’родительское участие в благополучии ребенка”. Допустим, что действие ребенка — это выбор неотрицательного числа А > 0 ; функции доходов строго вогнуты ІС(А) и ІР(А) и достигают максимумов при Ас > 0 и Ар > 0 , соответственно. Награда В может быть положительной или отрицательной; функции полезности U и V возрастающие и строго вогнуты. Докажите, что обратная индукция дает следующий исход: ребенок выбирает действие, которое максимизирует семейный совокупный доход, /ДА) + /ДА).Ui(Ic — S) + U2(S + B). Выигрыш родителя: V(Ip — B) + k[Ui(Ic — S) + U2(S + B)] . Допустим, что функции полезности U\ , U2 , V возрастающие и строго вогнутые. Показать, что исход обратной индукции следующий: ребенок сохраняет слишком мало, чтобы побудить родителя оставить большую награду (т. е. обе функции выигрыша родителя, и ребенка могут быть увеличены, если S будет выбрано больше, а В выбрано меньше).
3. Допустим, что игроки в бесокнечной игре торга по Рубинштейну имеют различные дисконтирующие множители ф и ф Для первого и второго игрока, соответственно. Показать, что обратная индукция дает следующий результат игрок 1 предлагает соглашение
( 1 -Ф ф(1-ф)\
\1 — ФФ ’ 1 — ФФ /
игроку 2 и тот принимает его.
4. Рассмотрим олигополию по Курно с 3 участниками и обратной функцией спроса P(Q) = а — Q , где Q = щ + q2 + qz и — объем продукции, произведенной фирмой і. Каждая фирма имеет постоянные предельные затраты с и не имеет фиксированных затрат. Фирмы выбирают объем производства следующим образом:
(1) фирма 1 выбирает щ > 0 ; (2) фирмы 2 и 3 наблюдают щ и затем одновременно выбирают q2 и q3 , соответственно. Что является совершенным под-игровым исходом в этой игре?
5. Допустим, что профсоюз является единственным поставщиком труда во все фирмы в олигополии (например, Объединенные Авто Рабочие имеются в General Motors, Ford, Chrysler и т.п.). Пусть последовательность ходов будет следующей
(3) выигрыши (w — wa)L для профсоюза, где wa —зарплата, которую члены профсоюза могут заработать на альтернативной работе и L = L\ + Ь2 + • • - + Ьп — общая занятость в объединенной фирме, и прибыль 7г(гг, Li) для фирмы і, которая устанавливается исходя из следующего предположения: все фирмы имеют производственную функцию дг- = Li. Рыночная цена P(Q) = а — Q , где Q = щ + • • • + qn . Для простоты будем предполагать, что фирмы не имеют никаких других затрат, кроме заработной платы рабочим.
Что является совершенным под-игровым исходом в этой игре? Как (и почему) количество фирм влияет на функцию полезности профсоюза в совершенном под-игровом исходе?
6. Рассмотрим две страны и будем считать, что возможны две ситуации.
В ситуации 1 обе страны устанавливают такие высокие тарифные ставки, что никакой торговли между ними не происходит. В каждой стране зарплата и занятость определяются как в задаче 5. В ситуации 2 тарифных ставок нет. Каждый профсоюз устанавливает зарплату в совей стране, но каждая фирма производит продукцию для обоих рынков.
Допустим, что в каждой стране обратная функция спроса P(Q) = a — Q . Пусть производственная функция для каждой фирмы будет q = L , поэтому выплаты зарплаты — единственные затраты фирмы, и пусть функция полезности профсоюза будет U(w}L) = (w — w0)L , где w0 альтернативная заработная плата рабочих.
Найти исход с помощью обратной индукции в ситуации 1.
Теперь рассмотрим следующую игру в ситуации 2. Сначала два профсоюза одновременно выбирают зарплаты, ид и w2 . Затем фирмы наблюдают зарплаты и выбирают продукции для домашнего и иностранного рынков, обозначенных hi и ві для фирмы в стране і. Вся продукция і -ой фирмы производится дома, поэтому общие затраты есть гщ(/ц + ег) . Найти совершенное под-игровое равновесие этой игры. Показать, что зарплаты, занятость и прибыль (и поэтому также полезность профсоюза и потребительский излишек) увеличиваются, по мере исчезновения тарифных ставок.
7. Статическая игра с одновременными ходами (см. рис. ) разыгрывается дважды, причем исход первого шага наблюдается перед началом второго шага. Предположим, что нет дисконтирования. Переменная х > 4, поэтому (4,4) не является равновесным выигрышем в ”базовой” игре. Для каких значений х следующая стратегия (сыгранная обоими игроками) будет СПРН?
Сыграть Qi на первом шаге. Если исход первого шага (Qi, Q2) , играть Рі на
втором шаге. Если на первом шаге исход (у, Q2) , где у ф Q\ , играть і?г- на
втором шаге. Если на первом шаге исход (Qi,z) , где z ф Q2 , играть S) на
втором шаге. Если на первом шаге исход (у, z) , где у ф Qі , z ф Q2 , играть
Рі на втором шаге.
| Р2 | Q 2 | Й2 | ч | |
| Рі | ( (2,2) | (і,0) | (-1.0) | (0,0) \ |
| Q1 | (0,ж) | (4,4) | (-1.0) | (0,0) |
| Ri | (0,0) | (0,0) | (0.2) | (0,0) |
| S1 | V (о,-і) | (о,-і) | (-1.-1) | (2,0) / |
й>±.
9. Игра ”Верю-неверю”
Имеется две карты, скажем ”туз” и ’’шестерка”. Играет два игрока. Сначала игрок 1 наугад выбирает одну карту и не показывает ее игроку 2. Если игрок 1 вынул ’’туза”, то он говорит об этом игроку 2 и требует выигрыш 1$ . Если игрок 1 вынул ’’шестерку”, то у него имеется две возможности: обмануть игрока 2, сказав, что у него ”туз” и потребовать 1$ или признаться, что у него шестерка и тогда уплатить 1$ игроку 2.
Если игроку 2 предлагают 1$ , то он принимает его. Если же у игрока 2 требуют 1$ , то он либо верит, что у противника ”туз” и отдает 1$ , либо не
верит и просит показать карту. В этом случае, если у игрока 1 действительно был ”туз” , игрок 2 выплачивает 2$ игроку 1 (за то, что зря сомневался). Если же у игрока 1 оказалась ’’шестерка”, то наказанием за обман является выплата им 2$ игроку 2.
Представьте позиционную и нормальную формы этой игры и найдите равновесие по Нэшу.
10. Игра ’’Четное-нечетное”
Первый ход: игрок 1 выбирает одно из чисел {1,2} . Второй ход (случайный): бросают монету, если выпал ’’Орел”, то второму игроку сообщают, что выбрал игрок 1. Третий ход: игрок 2 выбирает одно из чисел {3,4} . Четвертый ход (случайный): выбирается случайным образом одно из чисел {1,2,3} с заданными вероятностями 0,4; 0,2; 0,4, соответственно. В результате игры числа, выбранные на первом, третьем и четвертом ходе складываются и игрок 2 выплачивает полученную сумму игроку 1, если она четная; если же сумма оказалась нечетной, тогда игрок 1 выплачивает ее игроку 2.
Представьте позиционную и нормальную формы игры. Найдите равновесие по Нэшу в смешанных стратегиях.
11. Найдите совершенное под-игровое равновесие в следующей игре, известной под названием ” Сороконожка”.
12. Следующая игра с одновременными ходами разыгрывается дважды, причем исход первого розыгрыша известен до начала второго розыгрыша
L С R /(3.5,2.5) (1,1) (3,2) \ (3,2) (5,5) (2,6)
V (2,3) (6,2) (4,4) /
Могут ли выигрыши (5,5) достигаться на первом шаге в совершенном равновесии по Нэшу в чистых стратегиях? Ответ поясните.
13. Три игрока делят пирог, следуя следующей процедуре. Игрок 1 предлагает распределение, затем игроки 2 и 3 одновременно отвечают либо ”да”, либо ’’нет”. Если оба — и игрок 2 и 3 — говорят ”да”, то распределение принимается. В противном случае никто ничего не получает. Найдите совершенное под-игровое равновесие.
Глава 3
Статические игры с неполной информацией
3.1 Байесовы игры
До сих пор мы считали, что у игроков была вся ”необходимая” информация друг о друге, включая выигрыши игроков. В реальных ситуациях, конечно, все далеко не так, и фирмы, например, могут не знать затраты других фирм, и т. д. Поэтому здесь возникает ситуация, в которой участники могут и, по-видимому, должны иметь какие-то представления относительно предпочтений других участников, должны иметь представления об их представлениях о предпочтениях других и т. д. Здесь мы приходим к понятию Байесовых игр (пока статических), введенных Дж.Харшаньи (Harsanyi (1967)).Вернемся к нашей дуополии по Курно с обратной функцией спроса P(Q) = a — Q , Q = qi + q2 , и рассмотрим следующую ее модификацию. Предположим теперь, что функция затрат фирмы 1 есть G\(q\) = сщ , и будем считать, что функция затрат второй фирмы есть 6Д(<?2) = СнЧі с вероятностью ? и 6Д(<?2) = 6Дщ2 с вероятностью 1 — ? , причем СД < C# ¦ Кроме того будем предполагать, что фирма 2 знает свою функцию затрат и функцию затрат фирмы 1, но фирма 1 знает только свою функцию затрат и вероятности ? и 1 — ? того, что предельные затраты второй фирмы есть C# и Cl , соответственно. При этом все это общеизвестно: фирма 1 знает, что 2 имеет ’’больше” информации, фирма 2 знает, что 1 знает это и т. д.
Разумееется, естественно было бы ожидать, что фирма 2 будет принимать раз-
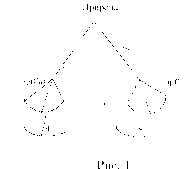
личные решения в зависимости от своего типа, т. е. от уровня своих предельных затрат. То есть в данном случае под стратегией следует понимать отображение, которое ставит в соответствие каждому из двух возможных уровней предельных затрат Сн и Cl некоторый объем выпуска, который определялся бы фирмой 2 в случае, если бы ее предельные затраты были высокими — Сн или низкими — Cl ¦ Забегая несколько вперед, отметим, что такое понимание стратегии близко к пониманию стратегии в играх в позиционной форме. Связано это с предположением, что игра протекает как бы следующим образом: вначале Природа ”выбирает” с вероятностью ? и 1 — ? соответствующий уровень предельных затрат и ” сообщает” выбранный уровень только фирме 2, а затем уже фирмы принимают свои решения о выпусках. В этом смысле соответствующую игру можно весьма условно представить следующим образом (см. рис. 1)
Пусть q^Cn) и ^(СА) , соответственно, выбор фирмы 2, а — выбор фирмы
1.
Если предельные затраты высоки, то ^(Сф) (в равновесии по Нэшу) решает задачу
тах((а — q{ — q2) — Cn)q2-
42
Аналогично дфСФ) решает задачу
max((a - щ - q2) - CL)q2-
42
Для фирмы 1 ql решает задачу
max ?[(а - qi - ql{CH)) - фі + (1 - ?)[а - qi - ql{CL)) - фі-q i
Условие первого порядка дает нам
| а — |
1 * 1—і | - Сн |
| 2 | ||
| а — |
1 * 1—і | -сь |
| 2 | 5 | |
| ?[а | - <?2(Ся | |
| , мы имеем | ||
| а — | 2 Сн | + с |
| 3 | ||
| а — | 2 Сь | + с |
чЦСн) =
q\\{Cl) =*
<h =
¦(Сн — Cl),
<h (Ся) — -7Г--ь
q\\{CL) =
3
a — 2c + ?Ся + (1 — ?)СД3 '
Если бы у нас была полная информация с затратами с\ и с2 соответственно, то было бы
а — 2 Сі + Cj
3
Заметим, чтосі — 2 Сн с
ЧІ(Сн) >
Это происходит потому, что при высоких затратах фирмы 2 конкурент (фирма 1) ’’недопроизводит”, а при низких затратах — ” перепроизводит”. Связано это с тем, что фирма 1 не знает точно структуру затрат фирмы 2, а знает, что они могут бытъ (с соответствующими вероятностями) либо высокими, либо низкими. Поэтому, принимая решение об объеме выпуска своей продукции, фирма должна учитывать потенциально обе возможности, при этом, если ее выпуск при высоких затратах конкурента (фирмы 2) был бы qf , то, учитывая возможность низких затрат у конкурента, фирма 1 должна уменьшить этот объем выпуска. Именно в этомсмысле фирма 1 недопроизводит продукцию при высоких затратах конкурента. Аналогично, при низких затратах конкурента фирма производит ’’лишнюю” продукцию.
Напомним, что для игр с полной информацией нормальная форма игры — это G = {Si,. . . , Sn, iti,. . . , ип} , где Si — пространство стратегий игрока г, а Ui(s 1,. . . , sn) — выигрыш игрока і в ситуации (зІ5. . . , sn) . (Мы опускаем здесь фиксированное множество игроков /). Если мы рассматриваем игру с одновременными ходами, то Si = Аі — множество ходов. Игра с полной информацией проходила так:
(1) — игроки одновремнно выбирали ходы;
(2) — игроки получали свои выигрыши щ(аі,. . . , ап) , і ? / .
Теперь мы хотим описать ситуацию с неполной информацией. Мы должны, для начала, учесть как-то тот факт, что игрок знает свою функцию выигрыша, но может не знать функций выигрыша остальных игроков. Пусть возможная функция выигрыша игрока і имеет вид
U’ii&ll • • • •} Т) ч
где ti — тип игрока, А ? Т) — множество (пространство) возможных типов игрока
і.
В приведенном выше примере с дуополией по Курно: Т\ = {с} , Т2 = {(7ц, Сн} ¦ Сказать, что игрок і знает свою функцию выигрыша, означает, что он знает свой тип. Аналогично, если игрок не знает функций выигрышей других игроков, то, соответственно, он не знает их тип, т. е. он не знает
t—і (ti, . . . , ti—1, ti-|_i • • • , tn ^j ? T—i,
где T-i — множество возможных значений .
Введем теперь понятие предпставлений. Представления (или система представлений) игрока і о типах остальных игроков — это вероятность Pi(t-i\ti) того, что типы остальных игроков описываются вектором t-i = itі, . . ., С_!, С+1,. . . Sn) i при условии, что і -ый игрок имеет (и знает свой) тип ti. В большинстве случаев, обычно предполагается, что эта вероятность не зависит от типа самого игрока, т. е. мы можем писать не условную вероятность, а просто Pi(t-i) ¦
Определение 3.1.1 Байесова игра п -лиц в нормальной форме определяется: набором множеств (пространств) ходов А1?...,Ап; набором множеств (пространств) типов Т\,. . . ,Тп игроков; представлениями рі,...,рп игроков; функциями выигрышей щ,. . ., ип .
Тип ti ? Ті игрока і известен игроку і и определяет функцию выигрышей щ(аі,. . . ,an':ti) . Представления pi(t_i\ti) игрока і описывают неопределенность относительно типов t_i оставшихся п — 1 игрока, при данном типе ti игрока і . Эту игру будем обозначатъ G = {А, Г, р, и} ; где А = Аі х • • • х Ап , Т = Ті х • • • х Тп , р=(р1,...,рп), и = (щ,. . . ,ип) .
Следуя Харшаньи, мы предполагаем, что игра протекает следующим образом:
(1) Природа выбирает вектор типов t = (П,. . . , tn) ? Т = Ti X • • • X Тп ;
(2) Природа сообщает каждому игроку і его тип ti (и никому другому);
(3) Игроки одновременно выбирают свои ходы (соответственно, г-ый игрок из
А);
(4) Игроки получают выигрыши щ(аі,. . . , ап; ti) , і ? / .
Введение этапов (1) и (2) сводит нашу игру к игре с несовершенной информацией. Вообще говоря, можно рассматривать и случай, когда функция щ зависит от ти
пов и других игроков, т. е. функции выигрышей имеют вид щ(аі,. . ., ап; П,. . . , tn) .
Однако мы не будем останавливаться на этом.
Обычно предполагается, что типы t выбираются в соответствии с априорным вероятностным распределением pit) , и это общеизвестно.
Когда Природа ” объявляет” игроку і его тип ti, то он может вычислить представление p(t-i\ti) , используя формулу Байеса
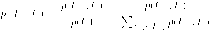
Далее, другие игроки могут также вычислить различные представления, которые игрок і может иметь, в зависимости от типа ti. Мы обычно будем считать, что типы игроков независимы, т.е. не зависит от ti.
Определение 3.1.2 В статической Байесовой игре G = . . . ,Тп ,
Рі,. . . ,рп , щ,. . . , гщ} стратегия игрока і — это функция Si : Ті —У Аі , которая для каждого типа ti ? Ті определяет ход из Аі , который был бы выбран игроком і, если бы Природой был выбран его тип ti . Символически Si = Aj' .
Принято выделять стратегии разделяющие, когда различные типы ti выбирают различные ходы, и объединяющие, когда все типы выбирают одно и то же действие. (Это различие будет существенным для нас в динамических играх).
Здесь следует заметить следующее: на первый взгляд кажется, что после того, как Природа выбрала тип и сообщила его игроку, ему уже не нужно думать о тех ходах, которые он выбрал бы, если бы был выбран другой его тип. Но, игрок і должен рассматривать действия других игроков, а это уже зависит от того, что будет делать игрок і, имея любой из возможных типов ti ? Ті : поскольку остальные игроки не знают выбранный Природой тип игрока і, они обязаны ориентироваться не все возможные типы игрока і (вспомним ”перепроизводство” и ”недопроизводство” в дуополии по Курно, рассмотренной в начале этой главы). Поэтому игрок і должен будет подумать и о том, что бы он делал, если бы были выбраны другие его возможные типы.
В нашей модели дуополии по Курно, как уже отмечалось, стратегия игрока 2 — это пара (q$(Cн), q$(CL)) ¦
Теперь мы можем дать определение Байесова равновесия, или точнее — равновесия по Байесу-Нэшу, или БН-равновесия. Центральная идея все та же: стратегия каждого игрока должна быть лучшим ответом на стратегии других игроков, т. е. БН-равновесие — это просто равновесие по Нэшу в Байесовой игре.
Определение 3.1.3 В статической Байесовой игре G = {А,Т,р, и}, ситуация (т.е. набор (чистых) стратегий) s* является БН-равновесием, если для любого і и любого типа ti ? Ті s*(ti) решает задачу
max щЦЦЦ),.
at Q.Ai
І-геТ-г
Часто бывает удобным БН-равновесие определять следующим эквивалентным образом:
Определение 3.3* Равновесие по Байесу-Нэшу (или БН-равновесие) в игре с неполной информацией с конечным множеством типов Ті у каждого игрока і ? /; апириорным распределением р и пространством чистых стратегий і -ого игрока Si{= Аі) есть равновесие по Нэшу в ”расширенной игре”, в которой пространство стратегий игрока — это Sf' (т. е. множество всех отображений из Ті в Si).
Таким образом, если дана ситуация s(-) и произвольная стратегия s'(-) ? Sj' , то обозначим, как всегда, через
(4(-),М0)
ситуацию, в которой игрок і играет з'(-) , а другие следуют s(-) . Пусть(Ale)} ^ —г'(^ —г')) (^і(П)? • • • •) $і — 1 (С — і)? 'й'(Т')? ^г + 1 (С+1) ? • • • ? ^п(Б))
обозначает ’’реализацию” этой ситуации при t = (С,С_і). Тогда ситуация (профиль) s(-) есть равновесие по Байесу-Нэшу, если для любого игрока іSi(-) ? Arg max У^ У^ р(Б, t_8)u8(s'(T), s_8(t_8); (A, t_8)), ti t_t
где Arg max обозначает множество стратегий, доставляющих максимум указанной двойной сумме.
Существование БН-равновесия немедленно следует из теоремы существования равновесия по Нэшу.
3.2 Альтернативный взгляд на смешанные стратегии
Мы сейчас поговорим немного об идее Харшаньи оправдания смешанных стратегий: равновесие по Нэшу в смешанных стратегиях в игре с полной информацией (почти всегда) может интерпретироваться, как БН-равновесие в чистых стратегиях в некоторой ’’близкой” игре с ’’чуть-чуть” неполной информацией. (’’Почти всегда” в том смысле, что можно игнорировать те редкие случаи, когда такая интерпретация неуместна).Основная черта равновесия по Нэшу в смешанных стратегиях — это даже не то, что игрок j выбирает стратегию случайно, а то, что игрок і сталкивается с некоторой неопределенностью относительно выбора игрока j , причем эта неопределенность может возникнуть или в силу наличия рандомизации, или в силу ”некоторой неполноты” информации, как в следующем примере.
Вернемся к хорошо знакомой нам игре ” Семейный спор” (см. рис.2).
|
ОНА Ф Б | ||||||
|
Здесь есть два равновесия по Нэшу в чистых стратегиях — (Ф,Ф) и (Б,Б), и одно в смешанных стратегиях при котором:
Он играет ”Ф” с вероятностью 2/3 и ”Б” с вероятностью 1/3;
Она играет ”Ф” с вероятностью 1/3 и ”Б” с вероятностью 2/3.
Теперь представим себе, что, хотя они знают друг друга достаточное время, они не вполне уверены относительно точного значения выигрышей друг друга. В частности, предположим, что Его (ему будет далее соответствовать индекс с) выигрыш, когда оба идут на футбол есть 2 + tc, причем tc приватно известно ему; Ее выигрыш (ей соответствует индекс р), если оба идут на балет, есть 2 + tp , что известно приватно ей. Будем считать, что tc и tp равномерно распределены на [О, ж] . (В действительности, равномерность не по существу, но главное то, что tc и tp слегка ”возмущают” выигрыши). Все остальные выигрыши — те же. В терминах абстрактной Байесовой статической игры в нормальной форме имеем:
(А {Ас, Ар, Ес, Е/, рс, Рр, нс, Up\,
где
Ас = Ар = {Ф, Б}; Тс = Тр = [0, ж];
представления есть
Pc{tp) = Pp{tc) = 1/ж
для любых tc и tp , а выигрыши определены так, как это представлено на рис. 3.
| ОНА | ||||||||||||
|
х — с 2 х — р 2
х х-м 3 х х-м 3
Представим себе, что оба игрока играют описанные стратегии. Для данного х мы определим значения сир такие, что описанные стратегии будут образовывать равновесие по Байесу-Нэшу. Если она играет такую стратегию, то Его ожидаемый выигрыш от игры Ф есть
(2 + tc) +
0 = -(2 +Д),
х
а Его ожидаемый выигрыш от игры Б есть
• 1 = 1-*.
X
1-Г
X J
1-0 +
X
Поэтому, играть Ф оптимально тогда и только тогда, когда tc > | — 3 . Следовательно, с — — — 3 .
’ р
Аналогично, если Он играет указанную стратегию, то Ее ожидаемый выигрыш от игры Б и игры Ф — это соответственно
С г . с ,
• 0 -|—[2 + tp] = —(2 + tp)
-14— - 0 = 1 —
Таким образом, играть Б оптимально в том и только том случае, если
X
tp>~- 3. с
т. е. р = ^ — 3 . Следовательно, мы имеем систему из 2 уравнений с двумя неизвестными
' c=f-3,
й=?-3,
, и это дает р = с и р2 + Зр — ж = 0 .
Решая относительно р , получаем, р = ~3+Л^9+4- вероятность того, что Он играет Ф, а Она играет Б, т.е., соответственно, и равны 1 — ~3+^9+4~ , что стремится к 2/3 при х —У 0 . Действительно, рассмотрим ^9^4ж~3 . Домножив числитель и знаменатель на 3 + л/9 + 4ж , получаем
9 + 4ж - 9 2 1
2ж(л/9 + 4ж + 3) л/9 + 4ж + 3 3
Следовательно,
л/9 + 4ж — 3
2ж
Таким образом, по мере ” сокращения” неполноты информации, поведение игроков в этом равновесии по Байесу-Нэшу в чистых стратегиях ” стремится” к поведению в равновесии по Нэшу в смешанных стратегиях в исходной игре с полной информацией.
3.3 Замечание о коррелированном равновесии
Теперь мы можем вернуться к коррелированному равновесию, упомянутому в Замечании 1.7.1. Вообще говоря, совершенно не обязательно, чтобы информация игроков была бы вполне коррелированной как в Замечании 1.7.1. Возможна более общая ситуация. Предположим, например, что случайная величина может принимать 3 возможных значения — ж1 , ж2 , ж3 , а игрок 1 знает, что реализация есть либо ж1 , либо одно из значений ж2 или ж3 . В то же время игрок 2 знает, что реализация есть либо ж3 , либо одно из значений ж1 или ж2 . Это можно интерпретировать как наличиеинформационного разбиения у первого игрока {{ж1}, {ж2, ж3}} и информационного разбиения у второго игрока {{ж1, ж2}, {ж3}} . В этом случае стратегия игрока 1 будет состоять из двух действий - того, которое он будет предпринимать, если он знает, что реализация есть ж1 и того, которое он предпримет, если узнает, что реализация есть элемнт {ж2, ж3} . Аналогично, стратегия второго игрока — это два действия в зависимости от реализации ж3 или из {ж1, ж2} . В этом случае стратегия игрока будет оптимальной, если при данной стратегии второго игрока, при любой реализации его сигнала он не может сыграть лучше, нежели так, как предписывает ему его стратегия.
Например, предположим, что вероятности реализации ж2 и ж3 есть /З2 и /З3 , а стратегия игрока 2 состоит в выборе а2 , если он знает, что реализация есть элемент {ж1, ж2} и а2 — если ж3 . Тогда, если игрок 1 информирован о том, что реализуетя либо ж2 , либо ж3 , он выбирает действие, оптимальное при условии, что игрок 2
выбирает а2 с вероятностью р2+рз (вероятность ж2 при условии {ж2, ж3}) и а2 —
/З3
с вероятностью р2+^з ¦
Определение 3.3.1 Коррелированным равновесием в игре {/, {АД, {щ}} называется набор {(О, л), {cri}iej} , состоящий из конечного верояностного про
странства О (пространства состояний) и вероятностей меры тт на О; информационного разбиения ?і для каждого игрока і = 1,...,п пространства 0; и функций (Ті : О —>¦ Аі , і = 1,...,п обладающих свойством (тф?и) = (тф?и') для w, w1 ? Рі для некоторого Рі ? ?і (сгі — стратегия игрока і), такой что для любого і ? / и любой функции ті : О —>¦ Аі , для которой гг(гт) = тф?о') для w,w ? Рі из некоторого Рі ? ?і (т. е. для любой стратегии игрока і)
^2 n(w)ui(cri(w),cr-i(w)) > n(w)ui(Tj(w), (7-i(w)).
Следующий результат принадлежит Р.Ауману (Aumann (1974)).
Предложение 3.3.1 Для любого равновесия по РІэшу в смешанных стратегиях а конечной бескоалиционной игры {/, {Аг}, {иг}} существует коррелированное равновесие {(0,7г){'Рг}, {щ}} , в котором для каждого игрока і ? / распределение на Аі , индуцированное сц ; есть щ .
Иными словами, множество коррелированных равновесий содержит множество равновесий по Нэшу в смешанных стратегиях.
В игре ” Семейный спор три равновесия по Нэшу в смешанных сратегиях дают выигрыши (2,1), (1,2) и ^|,|^ . Кроме того, одно из коррелированных равновесий дает выигрыши ^|, . Действительно, пусть О = {ж1, ж2} , -лДж1) = 7г(ж2) = | ,
?\ = ^{{ж1}, {ж2}} , сгДж1) = Ф , сгДж2) = В , г = 1,2. Это равновесие можно интерпретировать следующим образом: игроки наблюдают за подбрасыванием монеты и в зависимости от того, что выпадет, выбирают, какое из двух ’’чистых” равновесий по Нэшу играть.
Заметим также, что множество всех коррелированных равновесий в игре выпукло.
3.4 Примеры
1. ’’Аукцион” (Gibbons). Представим себе, что есть 2 покупателя і = 1,2. Покупатель оценивает некоторый неделимый товар в щ (единиц), т.е. если он получает товар, заплатив ф, то его выигрыш есть щ — ф. Будем считать, что оценки покупателей распределены независимо и равномерно на отрезке [0,1]. Считаем также, что ?і > 0 . Покупатели одновременно представляют свои заявки. Назвавший большую цену, платит эту цену и получает товар. Другой — не получает (и не платит) ничего. Если оба называют одну и ту же цену, то бросают монетку. (Покупатели нейтральны по отношению к риску). Все это общеизвестно.Сформулируем это как Байесову игру, т. е. определим пространства ходов, пространства типов, представления и функции выигрышей. Действия игрока — заявить цену ф (р оставляем для представлений), а тип есть щ . Поскольку оценки независимы, то игрок і считает, что Vj распределено равномерно на [0,1] вне зависимости
ОТ ?і .
Выигрыши игрока і есть:
{?і-Ьі, Ьі > bj,
(vt-bi)/2, bi = bj,
0, Ъг < bj.
Определим пространство стратегий. В соответствии с определением, стратегия игрока і — это функция 6Д-) , ставящая в соответствие каждому щ цену ЬДщ) , которую готов заплатить игрок і, если он оценивает товар в щ . В равновесии по
Байесу-Нэшу б(-) — это лучший ответ на стратегию 2-ого Ъ2(-) и наоборот. Формально, пара (Ьі(-), Ь2(-)) — равновесие по Байесу-Нэшу, если для любого щ в [0,1], Ьі(?і) является решением задачи
тах(у - Ъі)Р{Ъі > b3(v3)} + ~(?г - б)Р{б = Ь3(?3)}.
ь, А
Мы будем искать линейное равновесие, то есть равновесие, образуемое линейными стратегиями 6Д-) и Ь2(-) :
Ъг(?і) = щ + Сі?і и Ъ2(?2) = а2 + С2?2.
(Заметим, что мы не ограничиваем пространство стратегий линейными стратегиями. Мы допускаем любые, но ищем равновесие, которое будет линейным. В действительности, в силу равномерности распределения оценок, окажется что равновесие не только существует, но и единственно (в смысле, который станет понятным ниже)). Мы получим, что ЬДщ) = у .
Предположим, что j использует стратегию Ь3(?3) = а3 + с3?3 . Для данного значения щ лучший ответ і есть решение задачи
тах(щ — Ъі)Р{Ъі > а3 + с3?3}
ьг
(поскольку P{bi = b3(v3)} = 0, так как Ь3(?3) = {Ьг- > а3 + с3?3} и ?3 равномерно распределено, а значит и Ь3 распределено равномерно).
Поскольку для игрока і бессмысленно назначать цену ниже минимального назначения j и глупо - выше максимального, то а3 < б < а3 + с3 , и следовательно
б - а3
сз
б ~ а3
Р{Ъг > а3 + гг)
?3 <
следовательно, лучший ответ игрока г есть
если ?і > а3,
vt + a3
б{уЛ
2 ’
a,j, если ?і < а3
Если 0 < а3 < 1 , то существуют некоторые щ такие, что щ < а3 , а тогда 6(?і) — не линейна (она равна а3 вначале, а потом возрастает). Значит, поскольку мы ищем линейное равновесие, мы должны теперь считать, что либо а3 > 1 , либо а3 < 0 . Однако первое неравенство в равновесии невозможно: поскольку для более высокого типа оптимально назначать по крайней мере столько же, сколько оптимально для более низкого типа, то с3 > 0 , но тогда а3 > 1 давало бы Ь3(?3) > Vj , что не может быть оптимальным. Следовательно, если мы хотим, чтобы ф(-) была линейной, то должно быть a,j < 0 , следовательно
?г + a,j
_ I _L
~ 2 2 ’ а это значит, что
a, ,
a% = —, c% = 1/2.
Повторив то же для j , предполагая, что i использует стратегию
Ъг{?і) = а% + с%?%
получаем, что аг- < 0,а3 = y,Cj = 1/2 , и следовательно аг- = а3 = 0 , сг- = су = 1/2 . Таким образом Ьг(гг) = гг/2 .
Теперь мы обратимся к поиску симметричного равновесия, т. е. равновесия, в котором оба игрока играют одинаковые стратегии. Предположим теперь, что оба игрока j используют стратегию Ь(-) , причем Ь(-) — строго возрастающая и дифференцируемая функция. Следовательно для данного гу оптимальная заявка игрока і решает задачу
тах(щ - Ъі)Р{Ъг > Ь(?3)}.
Ьг
Пусть b~lihj) обозначает оценку, которую должен иметь j , чтобы заявить Ъ3 . Т.е.
Ъ~1(Ъз) = ?з (если К?з) = Ъз )•
Т.к. vj равномерно распределено на отрезке [0,1], то
Р{Ьі > b(Vj)} = Р{Ь-\Ь,) > ?3} = Ъ~\Ъі).
Условие 1-ого порядка для задачи первого игрока есть
-Ъ~1(Ъі) + (?і - Ъі)-^-Ъ~1(Ъі) = 0.
clbi
Далее, не слишком вдаваясь в детали, мы имеем: поскольку мы ищем симметричное равновесие, то ф = Ь(гу) , следовательно
-Ь_1(Ь(щ)) + (щ - Ь(гг))-^-Ь_1(Ь(щ)) = 0.
doЗаметим, что 6 (Ь(иг)) = гу , и следовательно
-гу + (гу-6(гу))—Ц- = 0 o'{Vi)
или Ъ'{?і)?і + Ъ{?і) = ?і . Таким образом, учитывая, что Ъ'{?і)?і + Ъ{?і)) = (Ъ{?і) • ?і)' , мы получаем
Ъ{?і)?і = -гу2 + к.
Для исключения к нам нужны граничные условия. Ясно, однако, что никто заявлять цену выше своей оценки не будет, следовательно 6(гу) < гу для любых гу . В частности, 6(0) < 0 , а в силу неотрицательности 6 имеем 6(0) = 0 , а тогда к = 0 И 6(іу) = f .
2. ”Производство публичного продукта в условиях неполной информации”. (Fu-denberg, Tirole). Два игрока і = 1,2 одновременно решают вопрос о том, вкладывать или нет в производство публичного продукта, причем это решение — это 0 — 1 решение, т.е. 0, если не вкладывать, и 1, если вкладывать. Выгода каждого игрока есть 1, если хотя бы один решил вкладывать, и 0, если никто не вкладывает. Затраты і -го игрока на вложение есть <у . Выигрыши изображены на рис.4.
в кл нет
вкл / (1-сді -С2) (І-СфіП нет \ (1,1-Сг) (0,0) )
Рис. 4
Выгода от наличия публичного продукта - 1 каждому - общеизвестна, но затраты каждого игрока известны только ему. В то же время оба игрока считают общеизвестным, что <у выбираются независимо, в соответствии с непрерывной, строго возрастающей кумулятивной функцией распределения Р{-) на [с, с] , где с < 1 < с (поэтому Р(с) = 0 и Р(с) = 1 ). Затраты <у — это тип игрока і.
Чистая стратегия в этой игре — это функция зДсД , ставящая в соответствие каждому возможному типу <у ? [с, с] решение вкладывать (1) или нет (0). Выигрыш г-го игрока есть
Ui(si,Sj,Ci) = max(s1,s2) - ctst.
Байесово равновесие — это пара стратегий (^Д-), зД-)) такая, что для каждого игрока і и каждого возможного типа <у стратегия з*(сД максимизирует ожидаемый выигрыш ECjUi{si, s*{cj),Ci) . Пусть Zj = Prob(s*(cj) = 1) — равновесная вероятность того, что игрок j вкладывает. Для максимизации своей ожидаемой ползности игрок і будет вкладывать, если его затраты сг- меньше, чем 1 • (1 — Zj) , что представляет собой выгоду от наличия публичного продукта, умноженную на вероятность того, что j не будет вкладывать. Тогда з*(сг) = 1 , если сг- < 1 — Zj , и, обратно, -s*(ci) = 0 , если сг- > 1 — Zj . (Заметим, что тип сг- = 1 — Zj безразличен между тем, вкладывать или нет, но поскольку Р(-) непрерывна, то вероятность того, что тип будет именно таким (или любым другим определенным типом) равна 0). Это значит, что типы игрока і, которые будут вкладывать, лежат в интервале [с, с*] . Аналогично, j будет вкладывать тогда и только тогда, когда с3 ? [с, с*] .
Поскольку Zj = Prob(c < Cj < с*) = Р(с*) , то с* = 1 — Р(с*) . Таким образом, с* и С2 должны удовлетворять уравнению с* = 1 — Р(1 — Р(с*)) . Если существет единственное решение этого уравнения с* , то необходимо должно быть с* = С* = 1 — Р(с*) . Например, если Р равномерно на [0,2] ( Р(с) = с/2 ), то с* единственно и равно 2/3. Игрок не вкладывает, если его затраты лежат в промежутке (|, і] даже если его затраты меньше, чем его выгода, и даже если 2/3 — это вероятность того, что публичный продукт не будет ”предложен” другим игроком.
Если же вместо с = 0 предположить с > 1 — Р(1) , то в игре будет два ассиме-тричных равновесия. В них один игрок никогда не вкладывает, а другой вкладывает при всех с < 1 . Например, равновесие, в котором игрок 1 не вкладывает, есть сі = 1 — Р(1) < с и с] = 1 .
3.5 Задачи
Е Найдите все БН равновесия (в чистых стратегиях) в следующей статической Байесовой игре:Игра 1
Игра 2
2. Рассмотрите дуополию по Курно, действующую на рынке с обратной кривой спроса вида P(Q) = а — Q , где Q = щ + q2 . Общие затраты фирм имеют вид сі(Яі) = сЧі 1 однако спрос неопределен: он высокий (а = ац) с вероятностью р и низкий ( а = бщ ) с вероятностью 1 — р. Кроме того информация несимметрична: фирма 1 знает, является ли спрос высоким или низким, а фирма 2 — нет. Все это общеизвестно. Обе фирмы выбирают объем производства одновременно. Каково равновесие по Байесу-Нэшу в этой игре?
3. Рассмотрите следующую модель дуополии по Бертрану с асимметричной информацией и дифференцированной продукцией. Спрос на продукцию фирмы і есть qi(pi,Pj) = a — pi — biPj . Затраты нулевые для обеих фирм. Чувствительность спроса і -ой фирмы относительно цены j -ой фирмы либо низка, либо высока, то есть Ьі равно либо Ъц , либо Ъц,, где Ь# > Ьь > 0 . Для каждой фирмы Ъі = Ън с вероятностью ? и fe; = Д с вероятностью 1 — ? (независимо от реализации Ъ3 ). Каждая фирма знает свое Ьі , но не знает Ь3 конкурента. Все это общеизвестно. Каковы пространства действий (ходов), пространства типов, представления и функции выигрышей в этой игре? Каковы пространства стратегий? Какие условия определяют симметричное равновесие по Байесу-Нэшу (в чистых стратегиях) в этой игре?
4. Рассмотрите следующий вариант аукциона второй цены, когда участник і знает свою оценку щ , однако не имеет полной информации об оценках других участников и считает, что множество возможных оценок есть конечное множество V , а оценки других игроков выбираются независимо, в соответствии с одним и тем же распределением не V . Опишите Байесову игру, соответствующую такому аукциону, и пологайте, что в этой игре существует БН равновесие а* , в котором а*(?і) = щ для любого і и ц ? У = Т,.
5. Найдите множество последовательных равновесий в следующей игре, называемой ”лошадью Зельтена”:
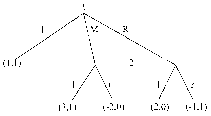
Глава 4
Динамические игры с неполной информацией
4.1 Совершенное Байесово равновесие
В этой главе наша цель — рассмотрение совершенного Ваисова равновесия.Прежде чем обратиться непосредственно к теме данной главы, заметим следующее. Мы начинали с равновесия по Нэшу, затем, по мере усложнения рассматриваемых нами игр, мы обратились к совершенному под-игровому равновесию по Нэшу, далее к равновесию по Байесу-Нэшу и, наконец, к совершенному Байесову равновесию в динамических играх с неполной информацией. Однако это вовсе не означает, что мы вводили новые концепции. В действительности, мы лишь усиливали соответствующие определения, чтобы исключать ”неуместные” равновесия в играх с более сложной структурой. В каждом случае более сильное равновесие отличается от более слабых только в случае более сложных игр. Поэтому, конечно, нужно отдавать себе отчет в том, что совершенное Байсово равновесие эквивалентно Б.Н.-равновесию в статических играх с неполной информацией, эквивалентно совершенному равновесию по Нэшу в динамических играх с полной и совершенной информацией и эквивалентно равновесию по Нэшу в статических играх с полной информацией.
Рассмотрим следующую динамическую игру с полной, но несовершенной информацией (Gibbons):
1) Игрок 1 выбирает L , М или R : Если он выбирает R , то игра заканчивается. Если же он выбирает L или М, то игрок 2 узнает, что R не выбрано, но не знает что выбрано — L или М , а затем выбирает L' или R' и игра заканчивается (см.
рис.1).
Нормальная форма этой игры есть
Легко видеть, что здесь два равновесия по Нэшу: (й, L') и (i?, R') .
В этой игре нет под-игр, значит и (й, L') и (і?, R') — совершенные под-игровые равновесия по Нэшу. Но, безусловно, (і?, R') — не достоверная, т.к., если 2-ой получает ход, то V — доминирует R', а поэтому R не будет играться, так как в этом случае первый игрок получает 2, вместо 1 в случае игры R.
Таким образом, нам нужно исключить (і?, R1) . Для этого введем дополнительные требования:
R1. В каждом информационном множестве игрок, которому принадлежит очередь хода, должен иметь представление о том, какая вершина информационного множества достигнута. Для неодноэлементного множества, представление — это вероятностное распределение на множестве вершин информационного множества; для одноэлементного информационного множества, представление игрока равно 1.
R2. При данных представлениях игроков, стратегии игроков должны быть последовательно рациональны, т. е. в каждом информационном множестве ход, сделан-
ный игроком (действие предпринятое игроком), и последующая стратегия игрока должна быть оптимальна, при данном представлении игрока в этом информационном множестве и последующих стратегиях остальных игроков (где под ”последующей стратегией” понимается полный план действий, покрывающий все возможности, которые могут возникнуть после того, как данное информационное множество было достигнуто).
В нашем примере требование R1 дает следующую ’’картину” (см. рис.2).
При данных представлениях игрока 2, ожидаемый выигрыш от игры R' есть р • 0 + (1 — р)-1 = 1 — р, а ожидаемый выигрыш от игры L' есть р-1 + (1— р)-2 = 2 — р. Так как 2 — р > 1 — р при любых р, то требование R2 препятствует выбору R'.
В соответствии с R1 и R2 у игроков должны бытъ представления и игроки должны действовать оптимально при этих представлениях, однако ничего не говорится относительно осмысленности самих представлений.
Определение 4.1.1 Для данного равновесия в данной игре в позиционной форме, будем говоритъ, что информационное множество лежит на равновесной траектории (пути), если оно достигается с положительной вероятностью, (или с вероятностью 1, если играются чистые стратегии), если игра разыгрывается в соответствии с этими равновесными стратегиями, и лежит вне равновесной траектории, если она достоверно (с вероятностью 1) не будет достигнута, если игра разыгрывается в соответствии с этими равновесными стратегиями (причем здесь ’’равновесие” может означатъ равновесие по Нэшу, СПРН, ВН-равновесие или совершенное Байесово равновесие).
R3. В информационном множестве на равновесном пути, представления определяются по правилу Байеса и равновесными стратегиями игроков.
В совершенном равновесии по Нэшу (L, L') в нашем случае, естественно, должно быть р = 1 . Представим себе на минуту, что есть еще некоторое равновесие в смешанных стратегиях, в которых игрок 1 играет L с вероятностью щ , М — с вероятностью q2 , a R — с вероятностью (1 — щ — q2) . Тогда R3 дает нам р = йі/(qi~\~q2) ¦ Как правило, в простых экономических приложениях эти три требования и определяют совершенное Байесово равновесие, хотя в более сложных приложениях требуется еще одно требование — R4 (или его модификация). Заметим, что, как мы увидим, формулировка четвертого требования весьма туманна.
R4. В информационных множествах, лежащих вне равновесной траектории, представления определяются правилом Байеса и равновесными стратегиями, где только возможно.
Последние слова в формулировке этого тредования достаточно расплывчаты, поэтому, чтобы проиллюстрировать R4, мы рассмотрим пример, хотя предварительно приведем определение совершенного Байесова равновесия.
Определение 4.1.2 Совершенное Байесово равновесие состоит из стратегий и представлений, удовлетворяющих требованиям R1-).
Рассмотрим игру, представленную на рис.З.
Здесь одна под-игра, начинающаяся с вершины, в которой ходит игрок 1. В этой под-игре одно равновесие — (L, R1) , значит единственное совершенное равновесие по Нэшу есть (D, L, R1) . Эти стратегии и представления р = 1 удовлетворяют R1-R3, а требование R4 — выполнено тривиально.
Теперь рассмотрим набор стратегий (A, L, L') вместе с представлением р = 0 . Эти стратегии определяют равновесие по Нэшу: ни одному из игроков не выгодно оклоняться. Для этих стратегий и указанного представления требования R1-R3 выполнены (игрок 3 имеет представления и действует при них оптимально, а 1 и 2 действуют оптимально при данных последующих стратегиях других игроков). Но это не совершенное равновесие по Нэшу, так как единственное равновесие по Нэшу
| А |
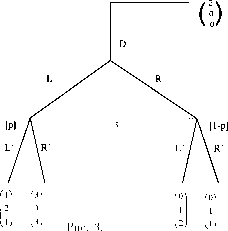 |
Итак, мы начали некий разговор о совершенном Байесовом равновесии, при этом нельзя скзать чтобы мы ”грешили” чрезмерной строгостью. Что мы имеем ввиду? Наши рассуждения о совершенности равновесия носили пока достаточно, если угодно, предварительный характер. Все дело в том, что в играх с неполной информацией, даже если игрок наблюдает действия другого игрока, он все равно не знает тип игрока, и начало периода не формирует хорошо определенную подигру до тех пор, пока не сформированы апостериорные представления, а поэтому
 |
| Рис. 4. |
Итак, в каком-то смысле, мы начинаем заново. Рассмотрим следующий пример: это вариант примера, который у нас был ранее.
Пример (Mas-Colell, Whinston, Green). В отрасли есть две фирмы: / — укоренившаяся фирма, и новичок Е , который может входить или не входить в отрасль, причем входить она может 2 способами (см. рис.4).
Здесь, как и в той игре, которую мы уже рассматривали, два равновесия по Нэшу в чистых стратегиях:
(не входить; война, если вход),
(вхі ; принять, если вход).
Первое кажется не очень осмысленным: независимо от того, какую стратегию входа использует Е , / предпочтет не воевать.
Критерий под-игрового совершенства здесь абсолютно бесполезен, так как единственная под-игра здесь — вся игра, а значит, оба равновесия в чистых стратегиях — совершенны.
Поэтому для того, чтобы исключить ”неосмысленное” равновесие мы можем поступить следующим образом: в духе последовательной рациональности было бы считать, что действие укоренившейся фирмы после входа должно быть оптимальным для некоторого представления, которое она может иметь относительно той стратегии входа, которую использовала Е. (В нашем примере, ’’война, если вход” не оптимально ни для какого возможного представления /).
Таким образом, чтобы сделать это, мы должны считать, что в любой момент игры стратегия игрока приписывает оптимальные действия с этого момента, при данных стратегиях его оппонентов и его представлениях о том, что произошло в игре, и что его представления согласуются с разыгрываемыми стратегиями.
Итак, дадим формальные определения.
Определение 4.1.3 Система представлений р в игре в позиционной форме есть набор вероятностей р(х) ? [0,1] для каждой вершины игры х :
^д(ж) = 1
х?Н
для каждого информационного множества Н .
Для того, чтобы определить последовательную рациональность, удобно ввести следующее обозначение: Е(щ\Н, р, сц, <т_г) — ожидаемая полезность (ожидаемый выигрыш) игрока і, при начале в его информационном множестве Н, если его представления, касающиеся условных вероятностей нахождения в различных вершинах Н , заданы р , при условии, что он следует стратегии сц , а его оппоненты
СГ-г ¦
Определение 4.1.4 Набор стратегий (ситуация) а = (од,. . ., (Тп) в игре в позиционной форме называется последовательно рациональным в информационном множестве Н при данной системе представлений р, если
E(Uj(H)\H} р}СГДЯ), <7_ДЯ) > E(Uj(H)\H, Д, СГДЯ), СГ_ДЯ))
для любой &j(H) ? Y^j(H) > г(^е чеРез j(H) обозначен игрок, который ходит в информационном множестве Н, а — множество смешанных стратегий игрока к . Если ситуация а удовлетворяет этому условию для всех информационных множеств Н, то а, по определению, последовательно рациональна, при данной системе представлений р .
Иными словами, набор стратегий а = (од,. . . ,(тп) является последовательно рациональным, если ни один из игроков не считает целесообразным, если достигнуто одно из его информационных множеств, пересмотреть свои стратегии, при данных представлениях (в смысле того, как это воплощено в ц) о том, что уже произошло, и стратегиях оппонентов.
Теперь мы можем определить слабое совершенное Байесово равновесие (чуть позднее будет ясно, почему мы говорим о ”слабости”). Это определение включает 2 условия: во-первых, стратегии должны быть последовательно рациональны. Во-вторых, когда это возможно, представления должны быть согласованы с этими стратегиями: в равновесии у игроков должно быть правильные представления относительно выбора стратегий их оппонентами.
Для описания такой согласованности рассмотрим специальный случай, когда равновесная стратегия каждого игрока приписывает строго положительную вероятность каждому возможному действию в каждом из его информационных множеств (так называемая вполне смешанная стратегия). В этом случае каждое информационное множество достигается с положительной вероятностью. Естественное понятие согласованности представлений с такой ситуацией равновесия а выглядит так: для каждой вершины х в данном информационном множестве Н , игрок должен вычислить вероятность достижения этой вершины при данном разыгрывании набора стратегий а, РгоЬ(ж|<т), а затем, используя формулу Байеса, приписать условную вероятность нахождения в каждой из этих вершин, при условии, что при разыгрывании достигнуто это информационное множество:
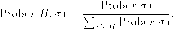
В качестве иллюстрации рассмотрим наш пример, когда Е использует вполне смешанные стратегии, которые приписывают ’’НЕТ” — вероятность 1/4, ” вхі ” — 1/2, ” вх2 — 1/4”. Тогда вероятность достижения информационного множества игрока / есть 3/4. По правилу Байеса, вероятность нахождения в левой вершине этого информационного множества, при условии, что оно достигнуто, равно 2/3, а условная вероятность нахождения в правой вершине равна 1/3. Для представлений / , следующих за входом и согласованных со стратегией Е , представления / должны приписывать именно эти вероятности.
Если стратегии не вполне смешанные, то некоторые информационные множества могут не достигаться (с положительной вероятностью) и мы не можем использовать формулу Байеса. На интуитивном уровне эта проблема соответствует следующей идее: даже, если игроки разыгрывали бы игру неоднократно, то ”равновесный розы-грътттт” не порождал бы опыта, на основе которого игроки могли бы основывать свои представления в этом информационном множестве. Слабое Байесово равновесие позволяет приписывать любые представления в таких информационных множествах (и в этом смысле, в частности, используется прилагательное ”слабое”).
Определение 4.1.5 Набор стратегий и система апостериорных представлений (<т, р) является слабым совершенным Байесовом равновесием в игре в позиционной форме Іф ; если
(1) а — последовательно рациональна при данной системе представлений р.
(2) Система представлений р выводится из набора а по правилу Байеса, когда только это возможно. То есть для любого информационного множества Н такого, что РгоЬ(і7|сг) > 0 (где РгоЬ(і7|сг) — вероятность того, что достигуто информационное множество Н)
РгоЬ(ж|<т)
РгоЬ(і7|сг)
р(х)
V х ? Н.
(Заметим, что слабое равновесие определяется как пара (<т, р) ).
Следующее предложение (см., например, Mas-Colell, Whinston, Green) характеризует связь между слабым совершенным Байесовым равновесием и равновесием по Нэшу.
Предложение 4.1.1 Набор стратегий а является равновесием по Нэшу в игре в позиционной форме Г^; тогда и только тогда, когда существует система представлений р такая, что:
(1) а — последовательно рациональна при данной системе р во всех информационных множествах Н таких, что РгоЬ(і7|сг) > О/
Продолжим рассмотрение нашего примера: ясно, что / должна играть ”принять, если вход” в любом ССБР, так как это оптимальное действие фирмы /, начиная с ее информационного множества при любой системы представлений. Таким образом, равновесные по Нэшу стратегии (нет; война, если вход) не могут быть частью никакого ССБР. Теперь посмотрим пару стратегий на (вхі ; принять, если вход). Чтобы доказать, что это есть часть ССБР нам нужно снабдить эти стратегии системой представлений, удовлетворяющей условию (2) в Определении 4.1.5, и которое бы сделало эти стратегии последовательно рациональными. Заметим, во-первых, что для того, чтобы удовлетворить критерию (2), представления / должны приписывать вероятность 1 нахождению в левой вершине ее информационного множества, так как это информационное множество достигается с положительной вероятностью при данных стратегиях (вхі ; принять, если вход). Более того, эти стратегии, в действительности, последовательно рациональны при данной системе представлений, и эта пара ”стратегии-представления” — единственное ССБР.
Далее рассмотрим еще 2 примера.
Пример 2 (М as-Colell,Whinston,Green). Считаем, что появился 2-ой потенциальный новичок Е2 и теперь ситуация такова: фирма Е1 обладает достаточными возможностями, чтобы войти в рынок самостоятельно, но ей не достает некоторых возможностей, которые имеет фирма Е2. Как результат, фирма Е1 рассматривает вариант предложения о создании с Е2 ”совместного предприятия”, причем в случае создания такого предприятия, Е2 делит с Е1 ее ”возможности”, и эти обе фирмы делят получающийся доход. Е1 имеет 3 варианта действий: не входить, войти самостоятельно или предложить кооперацию. Если она предлагает кооперацию, то Е2 может либо принять предложение, либо отвергнуть. Если Е2 принимает предложение, то Е1 входит вместе с Е2; если Е2 отвергает, то Е1 решает входить ли самостоятельно или нет. / может наблюдать вошла ли Е1, но не знает вошла ли фирма ’’отдельной единицей”, или ’’совместным предприятием” (рис.5).
Для определения ССБР заметим, что в любом ССБР Е2 должна принять предложение Е1, так как в этом случае Е2 гарантирует положительный выигрыш независимо от стратегии /. Но тогда в любом ССБР Е1 должна предложить кооперацию, так как, если Е2 принимает предложение, то Е1 получает больше независимо от ”пост-входной” стратегии /. Далее, эти два вывода приводят к тому, что информационное множество игрока / достигается с положительной вероятностью (в дей-
ствительности равной 1) в любом ССБР. Теперь, используя правило Байеса в этом информационном множестве, мы заключаем, что это правило должно приписывать вероятность 1 нахождения в средней вершине. В этом случае, в любом ССБР стратегия фирмы / должна быть’’принять, если вход”. Наконец, если / играет’’принять, если вход”, то Е1 должна входить, если она предложила кооперацию, но Е2 отвергла. Следовательно единственное ССБР в этой игре есть набор стратегий (<Т?і, <Т?2, &і) = ((предложение кооперации; вх., если Е2 отвергнуто), (принять), (принять, если ’’вход”) и система представлений ц (средняя вершина) = Е
Заметим, что это не единственное равновесие по Нэшу (а потому и не единственное СПРН). Например, ((Теі,&Е2,&і) = ((нет, нет, если Е2 отклонит), (отклонить), (война, если ’’вход”)) является СПРН в этой игре.
Пример 3 (М as-Colell, Whinston, Green). В приведенных выше примерах все было совсем просто, так как кто-то из игроков имел оптимальную стратегию, которая была независима от его представлений и/или дальнейшей игры оппонентов. Рассмотрим теперь следующую игру (см. рис.6)
Чтобы решить эту игру, найдем ’’неподвижную точку”, при котором поведение,
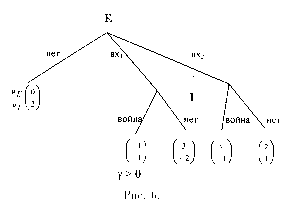
порожденное представлениями, согласовано с этими представлениями. Считаем, что
7 > 0 .
Пусть ар — вероятность того, что фирма / воюет после входа.
Пусть ц 1 — преставление фирмы /, что стратегией входа был вхі (если он состоялся), и пусть <т0, од, <т2 — вероятности, с которыми фирма действительно выбирает ”нет”, вхі , вх2 соответственно.
Заметим, что / захочет воевать с положительной вероятностью, тогда и только тогда, когда —1 > —2ці + 1(1 — ц\) , т.е. если ці > 2/3 .
Предположим, что ці > 2/3 в ССБР. Следовательно, фирма / должна играть ” войну” с вероятностью 1. Но тогда Е должна играть вх2 с вероятностью 1 (т. к. 7 > 0) и тогда ССБР требует чтобы ці = 0 . Предположим теперь, что ц 1 < 2/3 в ССБР, следовательно / должна играть ’’принять” с верояностью 1. Но тогда Е должна играть ” вхі ” с вероятностью 1 и ССБР требует, чтобы ці = 1 . Значит в любом ССБР ці = 2/3 . Следовательно, Е должна рандомизировать в этом равновесии, приписывая вхі и вх2 положительную вероятность, причем вхі должно быть ’’вдвое вероятнее”, чем вх2 . Это означает, что вероятность играть ’’войну” должна делать Е безразличной между вхі и вх2 , следовательно, —ар + 3(1 — ар) = устf + 2(1 — ар), или ар = 1/(у + 2) .
Выигрыш Е от игры вхі или вх2 есть (З7 + 2)/(7 + 2) > 0 и, следовательно, Е должна играть ’’нет” с вероятностью 0. Значит, единственное ССБР в этой игре,
когда 7 > 0 , есть
2
3'
2
’ 3’
(<т0,<ті,<т2) = (О
1/3),
(?F = 1/7 + 2 /іі
Мы называли равновесие слабым, так как требования согласованности были минимальны: единственное требование для представлений, кроме неотрицательности и равенства суммы вероятностей единице в информационном множестве, состояло в том, что они должны быть согласованы с равновесными стратегиями на равновесном пути, в том смысле, что они должны выводится из формулы Байеса. При этом не было никаких ограничений на представления вне рановесного пути. Однако, это иногда желательно. Но мы на этом подробно останавливаться не будем.
Пример 4.4 (Mas-Colell, Whinston, Green).
Чистые стратегии и представления, отмеченные на Рис.7 стрелками образуют ССБР.
Представления удовлетворяют свойству (2): только информационное множество игрока 1 достигается с положительной вероятностью, а его представления отражают вероятностное распределение на множестве ходов Природы.
Представления 2-ого не очень осмысленны. Информационное множество второго игрока может быть достигнуто только, если 1 отклонился, выбирая у с положительной вероятностью, причем отклонение должно быть независимо от действительного
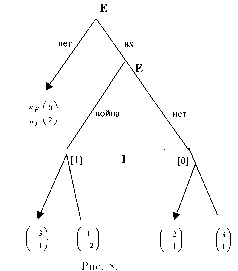
выбора Природы. Поэтому игрок 2 осмысленно может иметь только представления, которые приписывают равные вероятности этим двум вершинам в его информационном множестве, значит желательно требовать ” структурной согласованности” вне равновесного пути в том смысле, что существует некоторое субъективное вероятностное распределение на наборах стратегий, которое может порождать вероятности, согласованные с представлениями.
Заметим также, что ССБР не обязательно является совершенным под-игровым равновесием. Рассмотрим игру, изображенную на рис.8.
ССБР здесь есть ((Тщсг/) = ((нет, принять если вход), (война, если вход)) вместе с указанными представлениями. Но это не совершенное под-игровой равновесие, так как оно не дает равновесия по Нэшу в ”пост-входной” под-игре.
Проблема в том, что ”пост-входные” представления фирмы I относительно игры фирмы Е не ограничены ССБР, так как информационное множество фирмы I — вне равновесного пути.
Значит ССБР может быть слишком слабым.
В приложениях обычно вводятся дополнительные требования согласованности, чтобы избежать этих проблем. Получающееся равновесие и называют совершенным Байесовым равновесием. Формальные определения и обсуждение некоторых понятий совершенного Байесова равновесия можно найти в книге Fundenberg, Ті-role.
Мы рассмотрим подробное совершенное под-игровое равновесие на примере сигнальных игр, где оно совпадает с последовательным равновесием2 Вилсона-Крепса, на котором мы сейчас кратко остановимся).
4.2 Последовательное равновесие
Важным, тесно связанным понятием равновесия, которое в то же время усиливает понятие слабого совершенного Байесова равновесия за счет введения дополнительного условия согласованности представлений, является понятие последовательного равновесия (Wilson, Kreps (1982)). В противоположность совершенному Байесову равновесию, в понятии последовательного равновесия эта согласованность вводится не прямым, а косвенным образом через сходящиеся последовательности стратегий.Определение 4.2 Л Пара (<т, р) , состоящая из набора стратегий и системы представлений называется последовательным равновесием в позиционной игре Г^;; если: (1) набор стратегий а последовательно рационален при данной системе представлений р ; (2) существует последовательность вполне смешанных стратегий (то есть стратегий, в которых каждая чистя стратегия играется с положительной вероятностью) {crfc}^l1 такая, что Іііщ-юо crk = а, причем р = limfc-j.oo pk , где pk — представления, выводимые из набора стратегий ак по правилу Байеса.
По существу, речь идет о том, что последовательное равновесие требует, чтобы представления возникали из некоторого множества ” близких” к а вполне смешанных стратегий. Это можно рассматривать как требование того, что игроки определяют свои представления, делая, с некоторой малой вероятностью, ошибки в выборе своих стратегий. Важно отметить, что каждое последовательное равновесие является ССБР, поскольку предельные представления в точности совпадают с представлениями, выводимыми из равновесных стратегий а по правилу Байеса на траектории, определяемой профилем а . Обратное, вообще говоря, неверно.
Sequential equilibrium
Последовательному равновесию удается избежать тех осложнений, с которыми мы столкнулись в двух последних примерах. Действительно, вернемся к игре, изображенной на рис. 7. В этой игре все представления, которые можно вывести из любой последовательности вполне смешанных стратегий, приписывают равные вероятности двум вершинам из информационного множества игрока 2. Поэтому в любом последовательном равновесии игрок 2 должен играть г , а игрок 1 должен играть у . В действительности, пара стратегий (г, у) и представления, приписывающие равные вероятности вершинам каждого из двух информационных множеств, определяют единственное последовательное равновесие в этой игре.
Что касается примера, изображенного на рис.8, то стратегии единственного последовательного равновесия в этой игре являются стратегиями единственного СПРН: ((вход; нет, если вход), (нет, если Е играет вход)). Чтобы убедится в этом, рассмотрим любую вполне смешанную стратегию а и любую вершину х в информационном множестве /, которое мы обозначим через Я/ . Пусть z обозначает вершину, следующую за входом игрока Е (т. е. начальную вершину под-игры, следующей за входом). Тогда представления ца , соответствующие а в информационном множестве Я/ , определяются следующим образом:
Рг(х\а )
Pr(x\z} cr )Pr(z\a ) Рг(Я/ф, a')Pr(x\a') ’
Рг{Ні\(т')
где Pr(x\z,a ) — вероятность достижения вершины х в случае применения стратегий а , при условии достижения вершины z . После сокращения и с учетом того факта, что Рг(Я/ф,сг ) = 1 , мы получаем уа{х) = Pr((x\z}cr ) . Но это как раз и есть вероятность того, что фирма Е выбирает действие, приводящее к вершине х в стратегии а . Поэтому любая последовательность вполне смешанных стратегий {сг }^11 , сходящаяся к а , должна порождать предельные представления фирмы I, которые совпадают с игрой в вершине z , предписываемой реальной стратегией ае ¦ Из этого немедленно следует, что стратегии в каждом последовательном равновесии должны определять равновесное по Нэшу поведение в этой ”пост-входной” под-игре, а поэтому должны образовывать СПРН.
Предложение 4.2.1 (Kreps, Wilson (1982)^. В каждом последовательном равновесии (<т, у) позиционной игры Г^; набор равновесных стратегий а образует совершенное под-игровое равновесие по Вэшу.
Таким образом, последовательное равновесие усиливает и понятие СПРН и понятие СВР: каждое последовательное равновесие является и СРПН, и ССБР.
4.3 Сигнальные игры
Сигнальная игра — это динамическая игра с неполной информацией, включающая двух игроков: S (Sender) - ведущего (посылающего сигнал) и R (Receiver) — получателя сигнала. Игра протекает следующим образом:1. Природа выбирает тип Т для ведущего из множества возможных типов Т =
в соответствие с вероятностным распределением р(Т) : р(Т) > О для любого і и p(ti) + • • • + p(ti) = 1 .
2. Ведущий наблюдает Т и выбирает сигнал пг^ из множества возможных сообщений М = {ші,. . . , rrij} .
3. Получатель наблюдает (получает сигнал) mj (но не Т ) и затем выбирает действие qk из множества А = {щ,. . ., а к} ¦
4. Определяются выигрыши Us(ti,rrij,ak) и йф(й', т.,-, щ) ¦
Разумеется, естественно бывает считать, что множество возможных сообщений зависит от типа игрока, а множество возможных действий зависит от полученного сигнала. Так, скажем, в модели сигнализирования на рынке труда S — рабочий, а R — это перспективный рынок занятости, тип — это производительность рабочего, а сообщение — это выбор уровня образования, и наконец, действие — это уровень заработной платы. В модели корпоративных капиталовложений и структуры капиталов, S — фирма, нуждающаяся в финансировании нового проекта, R — потенциальный инвестор, тип — прибыльность имеющихся активов фирмы, сообщение — это предложение фирмы долевой ставки отдачи, а действия — решения инвестора вкладывать или нет. В некоторых случаях сигнальная игра может быть частью более сложной игры, т. е. например, может быть некоторое действие получателя до выбора сообщения ведущим S .
Мы остановимся на простом случае:
Т = {ti,t2}, М = {ші, m2}, А = {аі,а2}, РгоЬ{П} = р.
|
ai ai |
 |
Как всегда, стратегия игрока — это полный план действий: стратегия предписывает допустимое действие в каждом случае, когда игроку может понадобиться ходить. В сигнальной игре, чистая стратегия игрока S — это функция то(Д) , указывающая, какое сообщение будет выбрано для каждого типа, который может выбрать Природа, а чистая стратегия игрока R — это функция а(т3) , указывающая, какое действие будет выбрано для каждого возможного сообщения S. В изображенной игре может быть всего 4 (чистых) стратегии у каждого из игроков:
Первая стратегия S — сыграть піі , если Природа выбрала Д и сыграть піі , если Д.
Вторая стратегия S — сыграть піі , если Природа выбрала Д и сыграть т2 , если Д.
Третья стратегия S — сыграть т2 , если Природа выбрала Д и сыграть піі , если Д.
Четвертая стратегия S — сыграть т2 , если Природа выбрала Д и сыграть т2 , если Д .
Первая стратегия R — сыграть щ , если S выбрала піі и сыграть щ , если т2 .
Вторая стратегия R — сыграть щ , если S выбрала т\ и сыграть а2 , если т2 .
Третья стратегия R — сыграть а2 , если S выбрала т\ и сыграть щ , если т2 .
Четвертая стратегия R — сыграть а2 , если S выбрала т\ и сыграть а2 , если т2 .
Первая и четвертая стратегии S — объединяющие , так как каждый тип посы-
4 ?
лает один и тот же сигнал, а вторая и третья — разделяющая , так как каждый тип посылает разные сигналы. В моделях с более, чем двумя типами могут быть частично объединяющие (или полу-pa,зделяюттще) стратегиии, когда все типы в некотором подмножестве типов посылают один и тот же сигнал, но разные подмножества типов посылают различные сообщения. Есть также гибридные стратегии, например Д посылает т\ , a t2 — рандомизирует т\ и т2 .
Поскольку S знает всю историю игры и его выбор осуществляется в одноточечном информационном множестве, то вопрос о его представлениях не возникает. Что касается Д, то он выбирает действие после наблюдения сообщения S, но не знал тип S , значит выбор R происходит в неодноточечном информационном множестве. Поэтому теперь мы можем переформулировать требования, которые мы рассматривали в начале этой главы для сигнальных игр.
Сигнальное требование 1. После наблюдения каждого сообщения mj из М, R должен иметь представление о том, какой тип мог послать сообщение mj . Обозначим соответствующее вероятностное распределение через /ДД|гаД , где /ДД|гаД > О для любого С ? Т и
цех
(n(ti\mj) —вероятность того, что сообщение mj послано типом С).
При данном сообщении S и представлении R оптимальное действие характеризуется с помощью требования последовательной рациональности:
Сигнальное требование 2 R. Для любого mj ? М действие R, a*(nij) , должно максимизировать ожидаемую полезность R при данном представлении от
носительно того, какой тип мог послать сообщение mj . То есть a*(nij) решает задачу
тах? ц(Т|тДСд(Т, rrij, ак).
au(zA ' J
иет
Требование последовательной рациональности применимо и к S, но S имеет полную информацию, а следовательно тривиальные представления, а кроме того он ходит только в начале игры, значит стратегия S должна быть оптимальна при данной стратегии R.
Сигнальное требование 2 S. Для любого типа Д ? Т сообщение S, т*(Д) , должно максимизировать полезность S, при данной стратегии R, a*(rrij) . Т.е. то*(Д) решает задачу
ttij GM
Наконец, при данной стратегии S m*(ti) , обозначим через Tj множество типов, которые посылают сообещние rrij . Т.е. Д ? Tj , если m*(ti) = rrij . Если Tj — непусто, то информационное множество, соответствующее сообщению nrij , лежит на равновесном пути; в противном случае nrij не посылается никаким типом, и соответственно, информационное множество находится вне равновесного пути. Поэтому требование 3 можно переписать для R следующим образом.
Сигнальное требование 3. Для любого nrij в М, если существует Д в Т такой, что то*(Д) = nrij , то представление R в информационном множестве, соответствующем rrij , должно определяться по правилу Байеса и исходя из стратегии S , т. е.
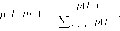
Определение 4.3.1 Совершенное Байесово равновесие (в чистых стратегиях) в сигнальной игре есть пара стратегий m*iti), a*{nrij) и представление n{ti\mj) , удовлетворяющее сигнальным требованиям 1, 2 R , 2S и 3.
Если стратегия S является объединяющей, или разделяющей, то равновесие называется объединяющим или разделяющим, соответственно.
Пример (Gibbons). Рассмотрим сигнальную игру, изображенную на рис. 10.
Здесь потенциально может существовать 4 совершенных Байесовых равновесия в чистых стратегиях.
(1) объединяющее на I;
(2) объединяющее на г ;
(3) разделяющее с Д , играющим I, и t2 , играющим г ;
(4) разделяющее с Д , играющим г , и Д , играющим I.
(2,1)
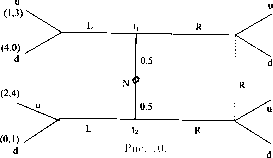
(0,0)
(1,0)
(1,2)
Рассмотрим эти возможности поочередно.
(1) Объединяющее на I. Предположим, что есть равновесие, в котором стратегия S есть (/, I) , т. е. Д играет ( и і2 играет I. (Запись (га', т") означает, что тип 11 посылает сигнал т', а тип t2 посылает сигнал т" ). Тогда информационное множество R, соответствующее I, лежит на равновесном пути, поэтому представление (р, 1 — р) в этом информационном множестве определяется правилом Байеса и стратегией S : р = 0.5 — априорное распределение. При таком представлении (или любом другом представлении), лучший ответ R на I — это сыграть и, так что типы 11 и t2 получают, соответственно 1 и 2. Чтобы определить, будут ли оба типа действительно играть I, нам надо уточнить еще, как R реагировал бы на г . Если ответ Л на г есть и , то выигрыш типа Д от игры г есть 2, что превосходит выигрыш 11 от игры I, поэтому если ответ й на г есть и , то типу П играть I не следует. Но если ответ й на г есть й, то П и t2 получают 0 и 1 от игры г, тогда как они получают 1 и 2 (соответственно) от игры I. Таким образом, если существует равновесие, в котором стратегия S есть (/, I), то ответ й на г должен быть й, а значит стратегия R должна быть (щй) (где (а', а") означает, что R играет а' на I и а" на г). Остается определить те представления R в информационном множестве, соответствующем г , при которых для него оптимально играть й. Легко видеть, что играть й оптимально для R при любом q < 2/3. Действительно, для данных представлений R \q} 1 — q] ожидаемый выигрыш R от игры и есть 1 • q + 0(1 — q), от игры й есть 0 • q + 2(1 — q). Значит, играть й оптимально, если 2(1 — q) > 1 • q , т. е. q < | .
Следовательно, [(/,/), (щй), р = 0.5, q] является объединяющим совершенным Ваисовым равновесием для любого q < 2/3 .
(2) Объединяющее на г: Предположим теперь, что стратегия S есть (г, г) , значит q = 0.5, и значит (т.к. 0.5 < 2/3 у R лучший ответ на г есть d, давая 0 для Л и 1 для t2 . Но А может получить 1, играя I, так как лучший ответ R на I есть и для любого значения р, значит равновесия с (г, г) не существует.
(3) Разделяющее с А , играющим I. Если S играет (/, г) , то оба информационных множества — на равновесном пути, следовательно оба представления определены правилом Байеса и стратегией S: р = 1 , q = 0 . Лучший ответ R на эти представления есть и и d, соответственно, так что оба типа S получают по 1. Остается проверить, является ли эта стратегия S оптимальной при данной стратегии R (и, d) . Но это не так: если Л отклонится от г играя I, то R отвечает и , поскольку его стратегия - (и, d) , давая Л выигрыш 2, что превосходит выигрыш 1 для t2 от игры г .
(4) Разделяющее с Л , играющим г . Если S играет (г, I) , то представления R должны быть р = 0 и q = 1 , так что лучший ответ R есть (и, и) и оба типа получат 2. Если бы Л отклонился, играя I, то R отреагировал бы и ; выигрыш Л тогда был бы 1, значит нет стимулов для Л отклоняться от игры г. Аналогично, если бы Л отклонился бы, сыграв г , то поскольку R играет и , то выигрыш t2 был бы 1, а значит Л нет смысла отклоняться от игры I. Значит [ (г, I) , (и, и), р = 0 , g = 1 ] — разделяющее совершенное Байесово равновесие.
Пример. Модель ограничивающего ценообразования Милгрома-Робертса (Міі-grom, Roberts, (1982)), см. также, например, Тироль (2000).
Мы приведем несколько упрощенную модель и опишем ее достаточно схематично. Предположим, что есть два периода времени и две фирмы. Фирма 1, укоренившаяся, является монополистом в момент времени 1. Она выбирает цену р\ своей продукции в первом периоде. Затем фирма 2, новичок, решает вопрос о том, входить или нет во втором периоде. Если она входит, то во втором периоде мы имеем ситуацию дуополистической конкуренции, если же нет, то фирма 1 остается монополистом.
Предположим, что затраты фирмы 1 могут быть низкими (с вероятностью х ) или высокими (с вероятностью 1 — ж). Пусть М\(рі) обозначает монопольную прибыть укоренившейся фирмы, если она назначает цену р\ , причем t = L или Н в зависимости от того, являются ли затраты фирмы низкими (L) или высокими Н , то есть
а^ы = (рі-сГ)в;"ы,
где -D™(') —монопольный спрос. Пусть далее р^ и р^ —монопольные цены, назначаемые укоренившейся фирмой в зависимости от уровня затрат. Хорошо известно, что р1^ < pH . Обозначим через М^ и М^ — прибыль монополиста (в зависимости от типа затрат), который максимизирует свою прибыть, то есть = М\(ргт) . Будем считать, что М((щ) строго вогнута по р\ .
Фирма 1 знает свои затраты. Фирма 2 не знает затрат фирмы 1. Следуя Милгрому- Робертсу, считаем, что фирма узнает затраты фирмы 2 после входа, если она решается на вход; считаем также, что дуополистическая конкуренция по цене (после входа, если он происходит) не зависит от цены первого периода. Обозначим через D\ и D\ дуополистические прибыли фирм при условии, что тип первой фирмы — t. (Можно считать, что D\ включает затраты на вход).
Будем считать, что решение фирмы 2 относительно входа зависит от представлений относительно затрат фирмы 1 следующим образом
D** > 0 > Dl2.
То есть, в условиях симметричной информации фирма 2 вошла бы, если бы затраты первой фирмы были высокими (общий коэффициент дисконтирования есть а).Поскольку фирма 1 предпочитает быть монополистом ( М\ > D\ , t = L} Н), она, конечно же, хочет передать информацию о том, что ее затраты низки. Однако проблема состоит в том, что у нее нет прямого механизма сделать это, даже если у нее действительно низкие затраты. Косвенный способ состоит в сигнализировании путем назначения низкой цены р^ . В нашем примере фирма 1 может захотеть назначить р\ , даже если у нее высокие затраты. Потеря прибыли в первом (монопольном) периоде может быть перекрыта во втором периоде за счет сохранения своего монопольного положения. Но означает ли это, что назначение цены р^ предотвратит вход? Это, увы, совершенно не очевидно. Рациональный новичок, зная, что в интересах укоренившейся фирмы ” обмануть” подобным образом новичка, может не поддаться на такую уловку. Но, укоренившаяся фирма понимает, что новичок знает о соответствующей заинтересованности укоренившей фирмы обмануть и т. д.
В такого рода модели есть два типа потенциальных равновесий (не считая третьего случая, когда укоренившаяся фирма использует смешанные стратегии) — разделяющие, когда укоренившаяся фирма назначает различные цены в зависимости от своего типа, и объединяющее, когда цена первого периода не зависит от типа фирмы. В первом случае цена первого периода выявляет затраты новичку. Во втором, напротив, новичок ничего не узнает относительно затрат и его апостериорные представления остаются неизменными (он приписывает вероятность х низким затратам).
Начнем с разделяющего равновесия. Мы имеем два необходимых условия: тип L не хочет назначать равновесную цену типа Н , и наоборот. (Затем мы завершим описание равновесия, выбирая представления вне равновесного пути, т. е. для цен, отличающихся от потенциальных равновесных цен, которые будут препятствовать отклонению обоих типов от их равновесных цен). Ясно, что в разделяющем равновесии цена, назначенная типом Н , индуцирует вход, поэтому укоренившаяся фирма играет pH и получает прибыть Мф + (если он назначает меньшую цену, то
он может увеличить свою прибыль в первом периоде без неблагоприятного влияния на вход). Пусть р^ — цена, назначаемая типом L . Тип Н , назначая эту цену, предотвращает вход и получает Мффф) + ЙМф . Таким образом, необходимое условие равновесия есть Мф + ЙП>ф > Мффф) + 8Мф или
Мф - Mf(pf) > й(Мф - ?>ф). (3.1)
Аналогично, тип L максимизирует свою прибыль, выбирая р^ . Поскольку он может назначить свою монопольную цену и получить в худшем случае (р1т в худшем случае индуцирует вход) Мф + Й-Df , и поскольку в равновесии он получает М^(р\)-\-8М1 , мы должны иметь
3.2
Мф + ФСф < Мффф) + <Шф или
Мф-Мффф) < й(Мф — Df)
При некоторых предположениях неравенства (*) и (**) определяют некоторый интервал [рі,рі] цен р± , причем рі < рф . Это означает, что для того, чтобы ’’разделять”, тип L должен назначать цену ниже своей монопольной цены, чтобы сделать ’’объединение”, т.е. назначение низкой цены, весьма затратным для типа
Н.
 |
| Рис. 11. |
Заметим, что в точке р\ неравенство (3.1) превращается в равенство, и р\ на-
о о g
зывается разделяющей ценой наименьших затрат , так как из всех разделяющих цен тип L предпочел бы цену р\ (ближайшую к р1т ).
Предположим, что тип Н выбирает рф , а тип L — цену р\ ? [pl5pi]. Когда наблюдается цена, отличная от этих двух цен, представления произвольны. Простейший способ получить равновесие — выбрать представления, которые индуцируют вход, поэтому будем считать, что если рі ф рф и рі ф р\ , то апостериорные представления х' есть 0 (фирма 2 считает, что укоренившаяся фирма имеет тип Н).
Хотя мы получаем тем самым континуум разделяющих равновесий, все-таки ”разумным” представляется только одно из них — с раздеяющей ценой наименьших затрат.
Таким образом, подводя итоги нашего достаточно краткого анализа разделяющего равновесия, заметим следующее: существует единственное ”разумное” равновесие, при этом тип Н назначает свою монопольную цену и ’’разрешает” вход, тип
L назначает наибольшую цену pi .
Обратимся теперь к объединяющему равновесию. Его существование зависит от выполнения условия
х+ (1 — x)D2 < 0 (3.3)
Предположим, что это условие не выполнено. Тогда при объединяющей цене фирма 2 получает строго положительную прибыль, если входит. Это означает, что вход не предотвращен, стало быть, оба типа не могут сделать ничего лучшего, нежели назначить свои монопольные цены. Так эти цены различны, то объединяющее равновесие не существует.
Следовательно, предположим, что (3.3) имеет место, так что объединяющаяся цена рі сдерживает вход. Необходимое условие того, что цена р\ является ценой объединяющего равновесия, состоит в том, что ни один из типов не хочет назначать свою монопольную цену.
Если бы один из них сделал бы это, то это, в худшем случае, допустило вход. Значит рі должна удовлетворять условию (3.2) и аналогичному условию для типа
Я:
Mf - Mf(m) < ?(Mf - T>f). (3.4)
Если выполнено условие
мf - M?(pLJ < S(Mf - D?)
(см. также сноску на стр. 126), то существует интервал цен ’’вокруг” р1т , удовлетворяющих обоим неравенствам.
Можно показать, что если рі удовлетворяет условиям (3.2) и (3.4), то р\ может быть частью объединяющего равновесия. Предположим, что как только фирма 1 назначает цену, отличную от рі (цена вне равновесного пути), то фирма 2 считает, что фирма 1 имеет тип Я . Тогда фирма 2 входит, а фирма 1 может назначить монопольную цену. Таким образом, из условий (3.2) и (3.4) следует, что ни один из типов не будет отклоняться.
Модель Спенса (Spence,1974). Спенс предложил следующую модель выбора уровня образования. Первый игрок S (работник) выбирает уровень образования
оу > 0 . Его затраты на инвестирование оу единиц в образование есть oy/Q, где Q —его тип ” способностей”. Производительность работника в фирме равна Q (для простоты не зависит от уровня образования). Второй игрок R (фирма) старается минимизировать квадрат разности между ставкой заработной планы а2 , предлагаемой работнику (в зависимости от его производительности), и его производительностью. Игрок 2 предлагает ожидаемую производительность оу(а2) = E(Q\a\) . Функция выигрыша работника есть а2 — cii/Q ¦ S может иметь один из двух возможных типов Q' или Q" , причем 0 < Q' < Q" ; вероятности этих типов — р и р , соответственно. S знает свой тип, но Л — нет.
Пусть су и су обозначают равновесные стратегии типов Q и Q . Заметим, что если оу ? suppcy и а ? suppcy (где supply — носитель стратегии оу , т. е. множество тех чистых стратегий, которые играются с положительными вероятностями), то flj < flj . В самом деле, в равновесии
а2(бу) - a^/Q' > а2(а") - a[/Q'
a2(a1)-a1/Q > а2(аі) - aJQ . Складывая эти два неравенства, получаем
(1 /Q — 1/Q(ll)(a1 — оу) > 0 или оу < а1.
В разделяющем равновесии, низкопроизводительный работник выявляет свой тип и получает зарплату Q' . Он, поэтому, должен выбрать оу = 0 ; если бы он поступил иначе, то смог бы выиграть, выбрав оу = 0 , поскольку он бы сэкономил на затратах на образование и получил бы зарплату, являющуюся необходимо выпуклой комбинацией Q и Q и поэтому, как минимум, равна Q .
Пусть оу > 0 означает равновесное действие типа Q" (заметим, что в разделяющем равновесии тип Q не может играть смешанную стратегию, поскольку все
его равновесные действия приносят зарплату О
, и поэтому тип Q предпочитает самый низкий уровень образования. Для того, чтобы (оу = 0, оу) было частью разделяющего равновесия, тип Q не должен предпочитать оу (в сравнении с оу):
Q > Q — axjQ или
«і > Q\Q" - Q') (3.5)
Аналогично, тип Q не может предпочитать од (в сравнении с од) :а[ < Q"(Q" ~ Q') (3.6)
Следовательно, Q'(Q" — Q') < од < Q"(Q" — Q') ¦
Обратно, предположим теперь, что од лежит в этом интервале.
Рассмотрим представления
|«і) = 1, если од ф- од, ji{Q |од) = 0}.
Ясно, что оба типа предпочитают од = 0 любому од ф. {0,од} , поскольку любой такой од дает зарплату Q . Поскольку для Q 0 предпочтительнее од (см. (3.5), а для Q од предпочтительнее 0 (см. (3.6)), то мы имеет континуум разделяющих равновесий. Этот континуум иллюстрирует, как определение представлений вне равновесного пути приводит к множественности равновесий. Мы использовали ”пессимистичное” представление, согласно которому любой сигнал, кроме од , убеждает R в том, что S имеет тип Q . Однако разделяющие равновесия могут основываться на менее экстремальных апостериорных представлениях. В частности, мы можем считать, что n(Q |од) = 0 для всех од > од .
Интересно отметить, что из этого континуума разделяющих равновесий все, кроме одного с наименьшими затратами, когда од = Q (Q — Q ) = а\ , могут быть исключены по следующим соображениям.
Независимо от того, какой уровень образования выбирает S , игрок R никогда не выбирает уровень зарплаты вне интервала [Q , Q ] . Когда игрок S осознает это, то тип Q' никогда не выберет а > а\. Когда игрок R осознает, что это так, то он должен отвечать на од > а\ зарплатой Q ; в этом случае тип Q никогда не выберет од > а\ .
В объединяющем равновесии оба типа выбирают одно и то же действие сд =
/ и „
од = од . оарплата в этом случае есть
\ ’гл’ " Г\’
а2(од) = р Q + р Q
Простейший способ ”поддержать” а, как объединяющий исход — это формирование пессимистичного представления n(Q |од) = 1 для любого од ф сіі , так как это минимизирует (для обоих типов) соблазн отклониться. Поэтому сд является уровнем образования объединяющего равновесия тогда и только тогда, когда для любого Q
Q < р Q + р Q - ai/Q.
Так как Q' < Q" , Q' наиболее склонен отклониться к од = 0 , минимизировать затраты на образование и связывающее ограничение есть ед < р Q (Q — Q ) , так что существует также континуум объединяющих равновесий.
4.4 Задачи
1. Для следующей игры укажите нормальную форму игры, все равновесия по Нэшу, совершенные под-игровые и совершенные Байесовы равновесия (в чистых стратегиях).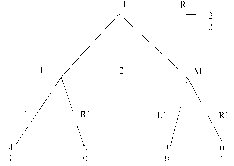 |
| 2. Укажите объединяющее Байесово равновесие, в котором оба типа Sender’a играют г в следующей сигнальной игре. |
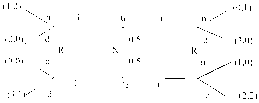
3. Опишите все объединяющие и разделяющие совершенные Байесовы равновесия (в чистых стратегиях) в следующей сигнальной игре.
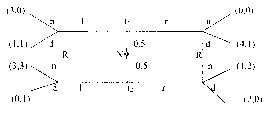
4. Опишите все объединяющие и разделяющие совершенные Байесовы равновесия (в чистых стратегиях) в следующей сигнальной игре.
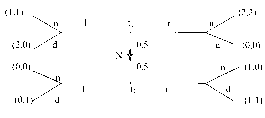
5. Для следующей игры укажите нормальную форму игры, все равновесия по Нэшу, совершенные под-игровые и совершенные Байесовы равновесия (в чистых стратегиях).
Глава 5
Элементы эволюционной теории игр
5.1 Обучение и эволюция
В этой главе мы очень кратко коснемся того направления развития теории игр, которое касается моделей обучения и эволюции. Большая часть бескоалиционной теории игр фокусируется на равновесии в играх и, в первую очередь, на равновесии по Нэшу и его уточнениях типа совершенного равновесия. Это, собственно, порождает вопрос о том, когда и почему мы можем надеяться на то, что наблюдаемое поведение в игре будет соответствовать одному из таких равновесий. Достаточно традиционное объяснение возникновения равновесия состоит в том, что оно является результатом анализа и самоанализа игроками в ситуации, когда правила игры, рациональность игроков, функции выигрышей игроков общеизвестны. Разумеется, и концептуально, и эмпирически здесь возникает целый ряд проблем. Во-первых, основная концептуальная проблема возникает в случае множественности равновесий, так как в отсутствие объяснения того, каким образом игроки приходят к одному и тому же равновесию, действия игроков вообще могут не соответствовать никакому равновесию. Во-вторых, крайне сомнительно, чтобы гипотеза общеизвестности выигрышей и рациональности была применима к многим играм, а ослабление этого условия, даже до ”почти” общеизвестности, приводит уже к значительно более слабым заключениям. Наконец, теория равновесия очень плохо объясняет игру на ранних этапах большинства экспериментов, хотя значительно лучше работает на более поздних раундах, (подробнее см., например, Fundenberg, Levine (1998)).Исследование ограниченно рационального процесса приспособления к равновесию по Нэшу стало полем активных исследований последних лет. Появляющуюся литературу можно весьма условно разделить на две категории: обучение и эволюцию. В литературе по обучению обычно предполагается, что игроки могут вычислить наилучший ответ и проверить, как игроки совершенствуют свои представления о стратегиях своих оппонентов в фиксированном ’’матче”. Напротив, эволюционный подход не предполагает обязательную способность оптимизировать и анализирует эволюцию поведения через пробы и ошибки и естественный отбор в популяции игроков.
Как мы уже отмечали, хотя равновесный анализ доминирует в исследованиях стратегических игр, очень многих не удовлетворяет и беспокоит предположение о том, что игроки немедленно и безошибочно идентифицируют и играют определенный набор равновесных стратегий. Изучение процесса обучения является альтернативным и в некотором смысле дополняющим подходом к анализу поведения в играх. Типичный анализ рассматривает игру, разыгрываемую ’’повторно” (неоднократно) и постулирует некоторые специфические правила, в соответствии с которыми игроки формируют ожидания, касающиеся того, каким будет текущий выбор игроков как функция предыдущих розыгрышей. Далее предполагается, что игроки пытаются максимизировать свои текущие выигрыши при данных ожиданиях; это определяет динамический процесс, порождающий последовательность розыгрышей, и анализ концентрируется на изучении поведения этой последовательности. Сходится ли такой розыгрыш? Если да, то приводит ли этот подход к поведению, предсказываемому равновесным анализом?
Этот подход столь же почтенен, как и сам равновесный анализ: исследование Курно дуополии (Cournot, 1838) по существу ’’явило миру” и равновесие по Нэшу, и специфический процесс обучения (см. раздел 1.9). Курно исходил из того, что в каждом ’’раунде” каждая фирма выбирает объемы производства, которые максимизируют ее прибыль в предположении (’’гипотеза Курно”), что конкурент продолжает выпускать тот же объем продукции, что и в предыдущем раунде. Называемая теперь ’’динамикой лучшего ответа”, эта динамика до сих пор привлекает внимание как одна из моделей обучения в играх (Bernheim (1984), Moulin (1986)). В то же время представляется неразумным предполагать, что реальные фирмы будут вести себя таким специфическим образом, как это описано у Курно. Это относится к ситуации, когда динамика лучшего ответа приводит к несходящемуся, циклическому поведению, что может случиться при некоторых специфических функциях затрат и спроса.
Циклы — это не единственная проблема, возникающая в моделях обучения. Например, Фуденберг и Крепе показали, что модели типа стационарного Байесова обучения, в соответствии с которым игроки анализируют прошлые наблюдения, как если бы поведение их конкурентов было стационарным, порождают такую последовательность, которая может сходиться, но к набору стратегий, отличному от любого совершенного равновесия (Fudenberg, Kreps (1988)).
В действительности, ”рациональность” каждого процесса обучения ситуативна: алгоритм, ведущий себя хорошо в некоторых ситуациях, может в других ситуациях работать скверно. Другим важным аспектом существующих моделей обучения является то, что они, по сути дела, ’’вынуждают” игроков не быть ’’искушенными”, то есть игроки могут использовать только информацию о прошлой игре, не придавая никакого значения информации относительно информации конкурентов, выигрышей, рациональности. Подход, основанный на равновесии по Нэшу или рационали-зуемости, напротив, придает значение только информации о выигрышах. Реальные же игроки часто используют оба типа информации.
Обратимся к играм двух лиц. Естественной точкой отсчета можно считать двух игроков, разыгрывающих игру повторяющимся образом и пытающихся предсказать игру соперника, исходя из предшествующей игры. Такую модель можно назвать моделью с фиксированными игроками (мы следуем здесь Fudenberg, Levine (1998)). В подобного рода ситуации игроки должны рассматривать не только то, каким образом будет играть в будущем оппонент, но также возможность того, что их собственная игра будет влиять на будущую игру оппонента. Например, игроки могут думать, что если они ’’ведут себя хорошо”, то они будут вознаграждены ’’хорошим поведением” оппонентов в будущем, или что они могут ’’научить” своих оппонентов играть лучший ответ на определенное действие, разыгрывая его снова и снова.
Рассмотрим следующую игру (рис.)
L R
и ( (1,0) (3,2) \ d 1 (2,1) (4,0) )Практически во всех моделях обучения игрок 1, игнорирующий повторяющееся разыгрывание, будет играть d, поскольку d - доминирующая стратегия, а потому максимизирует текущий ожидаемый выигрыш первого игрока при любых представлениях относительно оппонентов. Если, а это представляется правдоподобным, игрок 2 в конце концов ”выучит”, что игрок 1 играет d, то система сойдется к (й, L) , причем выигрыш игрока 1 будет 2. Но если игрок 1 терпелив и знает, что второй ”наивно” выбирает в каждом периоде ход, максимизирующий выигрыш в этом периоде при условии прогнозирования вторым игроком хода первого игрока, то игрок 1 может добиться большего, всегда играя и , что в конце концов ”вынудит” второго играть R, давая первому игроку 3.
Теория обучения, как правило, абстрагируется от такого рода рассмотрений, экплицитно или имплицитно опираясь на модель, в которой стимул к попытке изменить будущую игру оппонентов слишком мал. Один класс моделей этого типа - это тот, в котором игроки ограничены в своем выборе Д а дисконтирующие множители малы в сравнении с максимальной скоростью, с которой система может приспосабливаться. Второй класс моделей - это модели, в которых большое число игроков, взаимодействующих относительно анонимно, причем размер популяции (игроков) велик по сравнению с множителем дисконтирования.
Мы можем погрузить игру двух (или п ) лиц в такую ” обстановку”, уточняя механизм, в соответствии с которым пары игроков из популяции выбираются для разыгрывания этой игры. Здесь есть целый ряд моделей.
Модель с одной парой. В каждом периоде одна пара игроков выбирается случайным образом для разыгрывания игры. В конце раунда, ходы игроков становятся известными всем. Здесь, если популяция велика, то скорее всего, игроки, играющие сегодня, долгое время будут оставаться неактивными. Даже для терпеливых игроков не будет целесообразным жертвовать текущим выигрышем, чтобы повлиять на будущую игру оппонентов, если размер популяции достаточно велик в сравнении с дисконтирующим множителем.
Совокупная статистическая модель. В каждом периоде все игроки случайным образом разбиваются на пары. В конц раунда объявляется совокупный выигрыш популяции. Если популяция велика, каждый игрок незначительно влияет на выигрыш популяции, а следовательно, мало влияет на будущую игру. Вгрокам нет смысла
Пример этого - процесс нащупывания Курно (см. раздел 1.9), когда фирмы ограничены условием дважды подряд (на своем, а затем на чужом шаге) сохранять объем выпуска неизменным.
отклоняться от близорукого поведения.
Модель случайного выбора пар. В каждом периоде все игроки случайным образом разбиваются на пары. В конце раунда каждый игрок наблюдает только исход своего собственного матча. То, как игрок играет сегодня, будет влиять на то, как его оппонент будет играть завтра, но маловероятно, чтобы игрок снова попал в пару к своему текущему оппоненту или кому-то, кто играл с текущим оппонентом. Снова, близорукая игра ”почти” оптмальна в конечной, но большой по сравнению с дисконтирующим множителем, популяции. Этот подход наиболее часто используется в теоретико-игровых экспериментах.
С технической точки зрения есть два типа обычно используемых моделей больших популяций - конечные популяции и континуальные популяции. Важный модельный момент связан с тем, каким образом популяции, из которых выбираются игроки, соотносятся с числом ’’игровых ролей” в игре. Можно различать агента в игре, соответствующего определенной роли игрока, и действительного игрока, принимающего на себя роль агента в конкретном матче. Если игра симметрична, то можно считать, что есть одна популяция, из которой выбираются два агента. В этом случае говорят об однородной популяции. С другой стороны, мы можем считать, что каждый агент выбирается из отдельной популяции. В этом случае говорят об ассиметричной популяции.
В симметричной игре, в дополнение к крайним случаям однородных и неоднородных популяций можно также рассматривать смесь этих двух случаев, когда каждый игрок имеет какие-то шансы встретиться в матче с оппонентом из другой популяции и какие-то шансы - с оппонентом из той же популяции.
Мы остановимся сейчас (весьма кратко) на одном специфическом процессе динамического приспособления - так называемом фиктивном разыгрывании, полностью основанном на идее обучения, а затем перейдем к модели, основанной на идее эволюции.
В процессе фиктивного разыгрывания агенты ведут себя так, как будто они считают, что они сталкиваются со стационарным, но неизвестным, распределением на множестве стратегий агентов.
Итак предположим, что мы имеем бескоалиционную игру {{1,2}, {Si, 62}, {ui,u2}}. Модель фиктивного разыгрывания предполагает, что игроки выбирают свои ходы в каждом периоде из условия максимизации ожидаемого выигрыша в этом периоде при данной их оценке распределения действии оппонента в этом периоде, причем эта оценка имеет следующий специальный вид: у игрока і есть экзогенно заданная начальная функция весов кг0 : S-i —>¦ IR+ . Эти веса модифицируются путем добавления 1 каждой стратегии оппонента каждый раз, как только эта стратегия играется, то есть
K(s-i
1, еслиз^-1 = з_г-О, в противном случае.
Вероятность того, что игрок і предсказывает оппоненту игру з_г- в момент t есть
Ш-і)
Фиктивное разыгрывание - это правило р\{ у)), так что p\(Yt) ? BR( 7)) (здесь BR -best response). Важно заметить, что такое правило может быть не единственным, поскольку может существовать более одного лучшего ответа на каждую оценку.
Ключевой вопрос, возникающий здесь, состоит в том, сходится ли такой процесс.
Состояние процесса фиктивного разыгрывания есть вектор оценок игроков, а не стратегии, играемые в период t, поскольку их хватает для определения будущей эволюции системы. Тем не менее, несколько пренебрегая формальностями терминологии, будем говорить, что набор стратегий является устойчивым состоянием, если он играется в каждом периоде, начиная с некотороо конечного момента времени Т .
Предложение 5.1.1 (Fudenberg, Kreps (1990)). 1) Если s - строгое равновесие по Нэшу и s играется в момент t в процессе фиктивного разыгрывания, то s будет играться далее всегда. 2) Любое устойчивое состояние фиктивного разыгрывания в чистых стратегиях должно бытъ равновесием по Нэшу.
Упомянем здесь еще один вариант фиктивного разыгрывания. Милгром и Робертс (Milgrom, Roberts (1991)) рассматривают адаптивное обучение. Прогноз (относительно выбора стратегий оппонентом) называется адаптивным, если этот прогноз приписывает очень малую вероятность любой стратегии оппонента, которая не игралась длительное время. Формально, прогноз адаптивен, если для любого г > 0 и любого t существует T(e,t) такой, что для любого t' > T(e,t) и любой истории до момента t', прогноз 7\ приписывает веоятность не больше г множеству чистых стратегий оппонента игрока і, которые не игрались между моментами tut1. Для адаптивного прогноза сохраняется второе утверждение предложения 5.1: если прогнозы адаптивны и разыгрывание сходится к набору чистых стратегий, то этот набор должен быть равновесием по Нэшу.
Перейдем теперь от моделей, базирующихся на обучении к моделям, связанным с идеей эволюции.
Основная идея эволюционного подхода состоит в том, что агенты могут не оптимизировать сознательно, но вести себя так, как если бы они были рациональны, поскольку (экономическая) конкуренция отберет оптимизирующих агентов.
Существенным толчком к исследованию таких процессов послужила биология. Мейнард Смит и Прайс (Maynard Smith, Price (1973)) ввели понятие эволюционно устойчивой стратегии и пришли к выводу о том, что наблюдаемые черты поведения животных и растений можно объяснить с помощью равновесия по Нэшу в соответствующим образом определенной игре. Идея состоит в том, что комбинация естественного отбора и мутации приводит популяцию к эволюционно устойчивому состоянию в длительном периоде. Эта точка зрения была подтверждена многочисленными полевыми исследованиями. Здесь ’’как если бы” — это вполне реальное описание действительности. Вдохновленные успехом биологии, многие экономисты включились в активные исследования эволюционной теории игр. Почему же эволюционная теория привлекает такое внимание?
Только после глубоких и длительных исследований теория игр прояснила, что значит рациональность в стратегических ситуациях и каковы ее последствия. Рациональность сама по себе не оправдывает равновесие по Нэшу, и нужно искать что-то другое, что объясняло бы равновесное поведение.
Кроме того, необходимость равновесного отбора, которая стала доминирующей темой в многочисленных приложениях теории игр к многообразию конкретных задач, это то, чего предшествующая литература по динамике приспособления не учитывала.
5.2 Эволюционно устойчивые стратегии
Как мы уже отмечали и во введении, и в предыдущем разделе, эволюционная теория игр представляется чрезвычайно привлекательным подходом к обучению. В типичной для эволюционной теории игр модели, есть популяция агентов, выигрыш каждого из которых является функцией не только его поведения, но и того, как ведут себя агенты, с которыми он взаимодействует. В каждый момент времени, поведение в популяции распределено в соответствии с различными стратегиями, или типами поведения. Если популяция конечна, то состояние (популяции) представляет собой описание того, какие агенты какое поведение выбирают. Если популяция бесконечна, то состояние — это описание долей популяции, которые играют каждую стратегию. Если игрок может максимизировать и знает состояние, то он может выбрать лучший ответ. Если он не знает состояния популяции, тогда он должен сделать заключение о состоянии, исходя из информации, которой он обладает. Кроме того, даже зная состояние, игрок может быть не в состоянии вычислить лучший ответ. Вычисление лучшего ответа требует, чтобы игрок знал все доступные стратегии и соответствующие выигрыши. Наблюдаемая история игры становится важной по двум причинам.Во-первых, история передает информацию о том, каковы ожидания относительно игры оппонентов. Во-вторых, наблюдаемый успех или неудача выбора различных действий помогает игрокам определить, что может быть хорошей стратегией в будущем. Имитация часто является важной частью обучения: успешному поведению будут учиться. До той степени, до которой игроки имитируют успешное поведение и не вычисляют явно лучшие ответы, у игроков нет необходимости различать знания, получаемые от разыгрывания игры, и знания того, как играют оппоненты. Игроки должны только знать, что было успешным, а не почему оно было успешным.
Важным моментом является то, что эволюционная динамка ни в каком аспекте не опирается на какие-либо предположения о поведении или знания, отличные от базового принципа дифференцированного отбора — явное успешное поведение должно ”увеличивает свое представительство” в популяции, в то время как неуспешное — нет.
Существенным аспектом эволюционной динамики является то, что (в больших популяциях) если она имеет тенденцию сходиться, то она сходится к равновесию по
Нэшу. Это свойство является необходимым условием для любой осмысленной модели социального обучения. Предположим, что у нас есть модель, в которой поведение ” сходится” к чему-то, что не является равновесием по Нэшу. Поскольку обстановка в конечном счете становится стационарной и есть стратегия (тип поведения), доступная какому-либо агенту, дающая ему больший выигрыш, то в конце концов этот агент отклонится.
Понятие равновесия, наиболее часто используемое в эволюционной теории игр, как уже отмечалось выше, было введено Мейнардом Смитом и Прайсом и впервые достаточно подробно изложено в книге Мейнарда Смита ” Эволюция и теория игр” (Maynard Smith (1982)). Мейнард Смит исследовал поведение фенотипов (фенотип — совокупность всех признаков и свойств организма, сформировавшегося в результате его индивидуального развития). В частности, он изучал фенотип в популяциях, которые эволюционно устойчивы в том смысле, что они не могут быть ”побеждены” (’’захвачены”) другим фенотипом. Здесь ’’победа” означает, что какой-то другой тип поведения оказывается более успешным и агенты применяют его. Поскольку ’’тип поведения” переводится в теоретико-игровых терминах термином стратегия, то речь, по сути дела, идет об эволюционно устойчивых стратегиях3.
Основная идея, лежащая в основе этого понятия, состоит в том, что эволюционно устойчивая стратегия (ЭУС) — это стратегия, которая будучи используемой в некоторой популяции не может быть ’’побеждена” другой стратегией, поскольку она не может быть улучшена. Так, если популяция использует стратегию х , то ’’мутанты” , использующие какую-то другую стратегию у , не могут распространиться в популяции.
Будем обозначать набор возможных стратегий (типов поведения) через S, а выигрыш агента, выбирающего стратегию х ? S, в случае, если его противник выбирает стратегию у, через и(ж,у). Предполагаем, что S — конечно. Любая стратегия из S называется чистой. Смешанная стратегия — это вероятностное распределение на множестве чистых стратегий. (Мы считаем, говоря о смешанных стратегиях, что в них с положительной вероятностью используются как минимум две чистые стратегии). Смешанные стратегии имеют две возможные интерпретации: либо популяция мономорфна, и в ней каждый член играет одну и ту же смешанную стратегию, либо популяция полиморфна, и в ней каждый участник играет некую
Evolutionary stable strategies — ESS
чистую стратегию, причем доля популяции, играющая каждую чистую стратегию, равна вероятности, приписываемой этой чистой стратегии смешанной стратегией.
Смысл ключевого понятия эволюционной теории игр — эволюционно устойчивой стратегии (ЭУС) — состоит в следующем. Предположим, что индивиды (агенты) повторяющимся образом выбираются случайно из большой популяции, чтобы разыграть симметричную игру двух лиц (то есть игру Г = {{1, 2}, А, {щ і = 1, 2}} , где А — множество стратегий и первого и второго игрока, причем гаі(ж,у) = га(ж,у) и га2(ж,у) = га(у, х) для некоторой (непрерывной) функции и), и предположим, что первоначально все индивиды ” генетически запрограммированы” играть определенную чистую или смешанную стратегию. Теперь ” добавим” некоторую малую долю популяции, которая запрограммирована играть некоторую другую чистую или смешанную стратегию. ”Укоренившаяся” стратегия называется эволюционно устойчивой, если для любой такой ”мутантной” стратегии, существует такой положительный ’’барьер вторжения”, что если доля популяции индивидов, играющих ’’мутантную” стратегию, падает ниже этого барьера, то ’’укоренившаяся стратегия дает больший выигрыш, чем ’’мутантная” стратегия.
Такой подход фокусируется на симметричных попарных взаимодействиях в некоторой популяции. В частности, он не сосредотачивается на взаимодействии более, чем двух индивидов в момент времени. Кроме того, критерий эволюционной устойчивости опирается на тесную связь между выигрышами в игре и ’’степени распространенности” стратегии в популяции.
Какова же роль величины популяции? Здесь есть два элемента: один ’’механический”, а другой — ’’стратегический”. Во-первых, чтобы говорить о барьере вторжения (выражаемом в долях популяции) нужно, чтобы такой барьер превосходил 1/га, где га — численность популяции. Во-вторых, популяция должна быть столь велика, чтобы возможный эффект от текущего индивидуального действия на дальнейшие действия остальных был бы пренебрежим.
Помимо биологического аспекта, эволюционная устойчивость дает надежный критерий поведения людей в широком спектре ситуаций, включая многочисленные взаимодействия в области экономики. В социальной ли экономической обстановке эволюционная устойчивость требует, чтобы малые группы индивидов, которые пытаются использовать другую стратегию, преуспевают меньше, чем те индивиды, которые используют ”status quo стратегию”. Следовательно, те индивиды, которые используют превалирующие стратегии, не стремятся их менять, поскольку их положение лучше, чем у ”экспериментаторов”, а экспериментаторы стремятся вернуться к ”укоренившимся” стратегиям.
Итак, предположим, что небольшая группа мутантов появилась в большой популяции индивидов, каждый из которых запрограммирован играть некоторую одну и ту же ”укоренившуюся” стратегию ж ? А (чистую или смешанную). Предположим, что все мутанты запрограммированы играть некоторую другую (чистую или смешанную) ” мутантную” стратегию у ? А . Пусть доля мутантов в ”пост-входной” популяции есть г ? (0,1) . Пары индивидов в этой биморфной (представлены две стратегии) популяции выбираются (повторяющимся образом) случайно, чтобы разыгрывать игру, причем все индивиды выбираются равновероятно. Следовательно, если некоторый индивид выбран разыграть игру, то вероятность того, что его оппонент будет играть ”мутантную” стратегию у, есть е, а вероятность того, что будет играть ”укоренившуюся” стратегию, есть 1 — г . Выигрыш в матче (схватке) в такой биморфной популяции совпадает с выигрышем в матче с индивидом, играющим смешанную стратегию
w = еу + (1 — е)х ? А.
Таким образом, ”пост-входной” выигрыш для ”укоренившейся” стратегии будет u(x,w), а для ’’мутантной” стратегии — u(y,w) (и — непрерывная функция выигршей). По-видимому, интуитивно, ясно, что ’’сила эволюции” выступает против ’’мутантной” стратегии тогда и только тогда, когда ”пост-входной” выигрыш меньше, нежели выигрыш ’’укоренившейся” стратегии, то есть
и(х, еу + (1 - е)х) > и(у,еу + (1 - е)х). (2.1)
Стратегия ж ? А эволюционно устойчива, если это неравенство выполнено для любой ’’мутантной” стратегии уф ж , при условии, что популяция мутантов достаточно мала.
Определение 5.2.1 Стратегия ж ? А называется эволюционно устойчивой, если для любой стратегии у ф х существует такой Тф ? (0,1), что неравенство (5.1) выполнено для любого г ? (0,?^) .
Достаточно просто проверить, что ЭУС оптимальна против себя самой: если ж не оптимальна против себя самой, то существует некоторая стратегия у , дающая больший выигрыш против х . Следовательно, если доля г такой ”мутантной” стратегии достаточно мала, то, по непрерывности и , она даст больше против смеси w = еу + (1 — е)х , нежели х , а значит х — не ЭУС.
Приведенное выше определение можно переформулировать следующим образом.
Определение 5.2.1*. х ? А называется эволюционно устойчивой, если (ж, ж) является равновесием по Нэшу игры Г и и(у,у) < и(х,у) для любого наилучшего ответа у на ж (уф х).
Пример. Рассмотрим следующую игру, которую можно интерпретировать по-разному. Ее (или ее модификации) иногда называют игрой ’’цыплята”, или ’’ястреб-голубь” .
Я Г
Я /(-2,-2) (2,0) Л Г I, (0.2) (1,1) уі
Одна из интерпретаций ’’цыплят” такова. Навстречу друг другу на машинах мчатся ’’храбрецы”. Если никто не сворачивает (оба ведут себя как ястребы), то печальный исход приводит, как минимум, к серьезным травмам. Если оба сворачивают (голуби), то, хотя это не столь эффектно, но, по крайней мере, оба живы и здоровы. Наконец, если только один сворачивает, то он — проигравший (но здоров), а другой — победитель, который ’’получает все”.
Другая интерпретация состоит в следующем. Идет борьба, скажем, за наследство, оцениваемое в 2 единицы. Если никто не хочет уступать (оба ястреба), то борьба связана с серьезными затратами, например, судебными издержками. Если претенденты договариваются (оба голуби), то они делят наследство пополам. Наконец, если один уступает, то второй ’’получает все”.
В этой игре три равновесия по Нэшу — (л, г), (г, я) и смешанное равновесие, когда ”я” играется с вероятностью 1/3.
Чтобы посмотреть на ЭУС, предположим, что агенты из некоторой популяции случайным образом взаимодействуют друг с другом. Предположим, что агенты не знают, какую стратегию использовать. Они просто начинают использовать какую-то стратегию или вероятностную смесь этих стратегий, и они приспосабливают свои стратегии, используя процесс обучения методом проб и ошибок. Есть два способа ввести процесс обучения. Либо мы можем представить себе, что некоторая часть р (О < р < 1) популяции использует стратегию ”я”, а другая 1 —р использует ”г”, и предположить, что агенты переключаются с одной стратегии на другую в зависимости от результата использования той или иной стратегии. Второй вариант — мы можем предположить, что каждый индивид использует смешанную стратегию и приспосабливает вероятностную смесь на основе своего опыта использования каждой чистой стратегии (то есть увеличивает р, если ”я” дает большую отдачу, и наоборот).
Разумеется, такая рациональность не отражает осознанное обучение; в биологическом смысле речь идет о том, что те, кто лучше приспособился, быстрее воспроизводится.
Как будет развиваться использование этих стратегий в процессе такого обучения? Рассмотрим ожидаемую отдачу от стратегии, когда вероятность встретить ”я” есть р (либо потому, что такова доля популяции, использующая эту стратегию, либо потому, что такова средняя вероятностная стратегия, используемая агентами в популяции):
Е(л) = р(—2) + (1 — р)2 = 2 — 4р,
Е(г) = р(0) + (1 — р)1 = 1 — р.
Это означает, что выигрыш от ’’бытия ястребом” превышает таковой для голубя, если2 — Ар > 1 — р или р < 1/3,
а тогда большее число агентов будет стремиться использовать ”я”, то есть р будет расти. Обратно, для ”г” р > 1/3 и больше агентов будет стремиться использовать ”г”, а значит, р будет уменьшаться. Следовательно, р = 1/3 определяет ЭУС.
Таким образом, возможно несколько неожиданно, эволюционное разыгрывание этой игры ’’поддерживает” равновесие по Нэшу в смешанных стратегиях.
Мы весьма неформально и кратко коснулись понятия эволюционно устойчивых стратегий. Подробное изложение основ эволюционной теории игр можно найти в книге Weibull (1995).
Эволюционная теория игр еще достаточно молода, чтобы можно было судить обо всех ее возможностях. Многочисленные проблемы ждут своего решения. По-видимому, на данный момент времени ’’эволюционное моделирование” еще слишком стилизовано, чтобы непосредственно использоваться в приложениях. Однако следует отметить, что во многих интересных играх существуют многочисленные равновесия, и эволюционная теория игр играет важную роль в понимании того, какие равновесия являются значимыми в различных обстоятельствах.
Задача. Покажите, что в каждой симметричной игре, в которой у каждого игрока есть две чистые стратегии, а выигрыши, соответствующие четырем наборам стратегий, различным, существет смешанная стратегия, являющаяся эволюционно устойчивой.
Глава 6
Элементы теории кооперативных игр
В этой главе мы приведем основные определения и некоторые результаты, касающиеся теории кооперативных игр, а затем (в разделе 4) перечислим некоторые их возможные приложения. Поскольку на первый взгляд может показаться, что сфера приложений кооперативных игр не столь обширна как сфера приложения бескоалиционных (стратегических) игр, мы не приводим детальное описание какого-то одного или двух достаточно простых примеров, как мы обычно поступали ранее, а, напротив, приводим весьма обширный список многочисленных задач, при исследовании которых используются методы теории кооперативных игр.Как уже отмечалось во введении, в теории кооперативных игр основная единица анализа — это, как правило, группа участников, или коалиция. Если игра определена, то частью этого определения является описание того, что каждая коалиция игроков может получить (чего она может достичь), без указания на то, как исходы или результаты будут влиять на конкретную коалицию. То есть здесь нас не интересует стратегический аспект игры.
6.1 Классические кооперативные игры
Классической кооперативной игрой или кооперативной игрой с побочными платежами называется пара Г = (/, ?), состоящая из конечного множества / = {1, 2,. . . , п} и вещественной функции ? : 21 —У IR, определенной на множестве всех подмножеств множества /, причем с(0) = 0. Элементы множества / называются игроками, подмножества S С / — коалициями, а сама функция ? — характеристической функцией игры Г .Стандартная интерпретация состоит в следующем. Игроки из множества / могут объединяться в различные коалиции с целью так согласовать свои действия, чтобы получить максимальный выигрыш. Если образуется коалиция S , то известна величина v(S), которая и интерпретируется как тот максимальный суммарный выигрыш игроков из S, который они могут обеспечить себе, действуя совместно. При этом мы абстрагируемся от того, каким образом должны действовать игроки, чтобы обеспечить себе выигрыш v(S) , то есть отыскание оптимальных действий игроков из S лежит вне данной модели. Кроме того, в определении классической кооперативной игры предполагается, что полезности игроков обладают свойством трансферабельности, то есть измеряются по одной шкале и могут передаваться от одного игрока другому без потерь и без ограничений (побочные платежи), поэтому такие игры называются также играми с трансферабельной полезностью, или кратко ТП играми. В таком случае игрокам из каждой коалиции важно максимизировать суммарный выигрыш, так как в дальнейшем они могут распределять его между собой произвольным образом. Ниже, в разделе 6.2 мы рассмотрим игры более общей природы — игры без побочных платежей, или так называемые игры с нетрасфера-бельной полезностью.
Заметим, что характеристическая функция может иметь самое разнообразное происхождение. В частности, она может возникать при рассмотрении бескоалиционных игр. А именно, рассмотрим бескоалиционную игру Г = {/, {^г}г-е/,
(здесь мы отступаем от нашего традиционного обозначения множеств стратегий через Si, поскольку мы обозначаем буквой S —коалиции). Предположим что игроки, составляющие коалицию S С /, объединяют свои усилия в общих интересах. Какой наибольший суммарный выигрыш может обеспечить себе эта коалиция, независимо от того, каким образом действуют оставшиеся игроки, то есть игроки из / \ S ? Объединение игроков в одну коалицию означает, по сути дела, что они превращаются в единого игрока, для которого мы сохраним то же самое обозначение S. То, что они действуют совместно, означает, что стратегиями этого игрока являются всевозможные комбинации стратегий, составляющих эту коалицию игроков, то есть пространство стратегий Zs игрока S есть Zs = Пг'е5 • Следовательно, выигрыш игрока S есть Us(z) = Yljcs ui(z) •
Нас интересует тот наибольший выигрыш, который может обеспечить себе эта коалиция. Ясно, что в худшем для игрока S случае оставшиеся игроки могут тоже объединиться в коалицию I \ S с диаметрально противоположными интересами, то есть Ui\s(z) = —Us(z) . В результате вопрос о нахождении наибольшего гарантированного выигрыша игрока S сводится к нахождению значения (если таковое существует) антагонистической игры ГД = {Zs, Zi\s, Us} , или
max min Us(zs, zns),
zs z^s
где Zs , Zj\s множества стратегий игрока S и / \ S, соответственно, a Us — функция выигрышей игрока S (см. Дополнение 1.13 к главе 1). Так определенный выигрыш игрока S зависит в конечном счете только от коалиции S (и, конечно, от самой исходной бескоалиционной игры Г ), являясь ее функцией. Эта функция и есть характеристическая функция бескоалиционной игры Г , которая обозначается через гг.
Первоначально именно так определяемая характеристическая функция игры представляла для исследователей особый интерес, однако по мере развития теории кооперативных игр, вопрос о том, каким образом возникает характеристическая функция, отошел в тень (хотя он, безусловно, представляет самостоятельный интерес при рассмотрении конкретных моделей, когда возникает необходимость исследовать специфику моделируемой ситуации), и, как мы уже отмечали, стратегический аспект остается вне ”сферы интересов” теории кооперативных игр.
Далее мы будем часто говорить об игре ? без указания множества игроков /. В случае необходимости, мы будем обозначать множество игроков в игре с характеристической функцией ? через І? .
В зависимости от свойств, накладываемых на характеристическую функцию, рассматриваются различные классы кооперативных игр с побочными платежами. Так, игра называется несущественной, если
щ) = Е с ({г}) для любой коалиции S С I. ies
В дальнейшем мы будем использовать сокращенную запись ?(і) и r(S'Ui) вместо с({г}) и v(S U {г}) и т. д., соответственно.
Игра ? называется супераддитивной, если для любых коалиций S и Т, таких что S П T = 0 , выполняется неравенство
v(SUT) > v(S) + v(T).
Заметим, что определенная выше характеристическая функция бескоалиционной игры обладает свойством супераддитивности, что без труда можно проверить, исходя из свойств операций взятия максимума и минимума.
Игра называется выпуклой, если для любых коалиций S и Т , выполняется неравенство
v(S и Г) + v(S ПТ)> v(S) + ?(Т).
Заметим, что выпуклая игра является супераддитивной, так как г(0) = 0 .
Игра называется простой, если характеристическая функция ? принимает только два значения: 0 и 1 .
Пусть IR обозначает |/|-мерное эвклидово пространство, координаты которого заиндексированы элементами из множества /. Часто бывает удобно рассматривать вектор ж ? Ш как несуществующую игру, определенную формулой
х (S) = хі для всех S С /.
ies
Дележом в игре ? называется вектор х ? IR1, удовлетворяющий условиям групповой и индивидуальной рациональности, то есть:
1) х(І) = ?(І) и 2) хі > ?(і) для всех і ? /.
Далее мы введем следующие обозначения:
IR5 = {ж ? IRn : хі = 0 для і (jt S'} , S С /;
X(v) = {ж ? IR : ж(/) = г(/), жі > ?(і) для любого г ? /} — множество дележей в игре ?;
Х*(?) = {ж ? IR : ж(/) = г(/)} — множество распределений (пред-дележей) в игре ? .
Если G — некоторый класс кооперативных игр (вообще говоря, не обязательно с побочными платежами), то под решением на G обычно понимается отображение F (однозначное, или, быть может, многозначное), которое ставит в соответствие каждой игре ? ? G некоторый вектор или непустое множество F(v) в пространстве Ш, которое называется решением или значением (в случае однозначности) игры v . Разумеется, отображение F должно обладать некоторыми определенными свойствами, чтобы ’’иметь право” называться решением. Компонентам Fi(y) вектора F(y) (в случае однозначности решения), или компонентам вектора х ? F(y) в случае многозначности) можно давать различные интерпретации. Так, например, можно считать, что Fi(y) есть априорная оценка игроком і выгодности для него игры ? . Можно считать Fi(y) в некотором смысле средним выигрышем игрока в игре. Можно также интерпретировать Fi(y) как ’’справедливую” долю игрока і в игре ? . Выбирая ту или иную интерпретацию и формализуя интуитивные представления о тех свойствах, которыми должно обладать решение, то есть вводя те или иные аксиомы, можно получать различные отображения F .
Мы приведем определение ряда наиболее известных решений. Исторически первым и одним из наиболее важных понятий решения является решение, введенное Л. Шепли в его классической работе Shapley (1953). Шепли рассматривал Fi(y) как априорную оценку игроком і выгодности для него игры ? . Он предложил три аксиомы, которым должна удовлетворять функция F .
А1 (симметричность). Если г — такая перестановка множества І? , что для любой коалиции А, v(tS) = г(А), то Fri(y) = Fi(y) для любого і ? І? .
А2 (носителя). Если коалиция К — носитель игры г, то есть г(А) = г(А П К) для любой коалиции S, то ^2ieK Fi(y) = v(K) .
АЗ (линейность). Если для всех S , w(S) = v(S) + u(S), то для всех і
Fi(w) = Ft(v) + Fi(u).
Смысл первой аксиомы заключается в том, что оценка игроком игры не должна зависеть от того, каким индексом он обозначен. Вторая аксиома эквивалентна одновременному выполнению двух следующих аксиом.
А2’ . Если игрок j в игре ? таков, что v(S U j) = v(S) для любой коалиции А, то Fj(v) = 0 .
А2” . Е.б/СИ = ?(І).
Последнюю аксиому называют условием групповой рациональности, или Парето оптимальности, или также эффективности. Игрок j из аксиомы А2’ называется ”болваном” в игре ? . Этот игрок ничего не получает сам, так как v(j) = с(0) = О и никак не влияет на выигрыш коалиции, к которой присоединяется. Таким образом, аксиома А2’ требует, чтобы игрок, являющийся болваном, ничего не получал при распределении выигрышей. Аксиома эффективности А2” просто означает, что игроки делят между собой величину ?(І). Именно эту аксиому мы будем в дальнейшем называть аксиомой эффективности. Заметим, что для супераддитивных игр ?(І) есть максимум того, что игроки могут получить суммарно. Аксиома АЗ означает, что оценка игры, являющейся суммой двух игр, есть просто сумма оценок каждой из игр-слагаемых.
Например, рассмотрим следующую весьма простую игру трех лиц / = {1, 2, 3} : с(1) = 0, ?(2) = ?(3) = 1 , ?(2) = с(13) = 1 , с(23) = 3, с(123) =3.
В этой игре носитель — это коалиция {2, 3} , игрок 1 — болван.
Перестановка, меняющая местами игроков 2 и 3, сохраняет игру без изменения. Поэтому, если значение Шепли (т. е. функция, удовлетворяющая этой системе) существует, то игрок 1 (в силу А21) должен получить 0, игроки 2 и 3 (в силу А1) поровну, а суммарно (в силу А2”) они должны получить 3, т. е. игроки 2 и 3 должны получить по 1.5.
Шепли доказал (доказательство приводится в разделе 6.5), что этим трем аксиомам удовлетворяет единственная функция, называемая значением (или функцией, или вектором) Шепли, а именно:
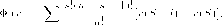 |
| S:?S |
Функцию Ф можно интерпретировать не только как оценку игры, но и как функцию, задающую средний выигрыш игроков при следующей вероятностной схеме. Равновероятно выбираем любого из игроков. Далее равновероятно выбираем любого из оставшихся игроков и присоединяем к уже выбранному. Продолжаем этот процесс, пока не исчерпаем все множество /. При этом, если игрок і был выбран именно после того момента, когда была уже образована коалиция А , то он получает выигрыш, равный величине, на которую возрастает выигрыш коалиции из выбранных игроков в результате его присоединения, то есть v(S U г) — v(S) .
Замечательное свойство значения Шепли, на котором основан целый ряд существенных обобщений значения Шепли, и в частности, определение многозначных аналогов значения Шепли (см. Pechersky, Sobolev (1995)) дает следующее предложение.
Предложение 6.1.1 (Keane, 1969) Значение Шепли совпадает с решением задачи минимизации функционала
Q(x,v) = (s — 1)!(п — з — 1)!(г(5') — x(S))2
вфі,г
на множестве распределений Х*(?) .
Доказательство этого предложения можно найти в книге Печерский/Соболев (1983). При доказательстве используется метод множителей Лагранжа, строгая выпуклость функции Q и проверяется выполнение всех аксиом Шепли. В частности, аксиома болвана однозначно определяет коэффициенты (s — 1)!(п — s — 1)!.
В качестве решения используются также и другие функции вида
Рг{?) = 7(S’ U 0 - ?($)],
S:i(S
где y(s,n) — некоторые коэффициенты. В частности, если y(s,n) = 1/2”, то получается так называемый вектор Банзафа (Banzhaf (1965), Owen (1975)). Однако среди всех этих функций значение Шепли, безусловно, заслуживает наибольшего внимания, так как обладает многими важными свойствами. Так, например, значение Шепли обладает свойством (сильной) ковариантности, то есть, если две игры ? и ?' таковы, что
v\S) = cv(S) + a(S) для некоторых с > 0 и а ? IR”,
то
Ф,-(0 = сФДс) + аг.
Заметим также, что очень интересный класс решений представляет семейство значений наименьших квадратов, получающихся при минимизации функций, аналогичных приведенной выше функции Q , но с произвольными коэффициентами wn,s Д 0 (см. например, Ruiz, Valenciano, Zurzuelo (1998)).
Прежде чем обратиться к некоторым другим понятиям решений кооперативных игр, необходимо сделать небольшое отступление.
При исследовании решений кооперативных игр используются два базовых метода. Первый — это аксиоматический метод, когда желательные свойства решений формулируются в виде аксиом и исследуется вопрос существования решений, удовлетворяющих этим аксиомам. Такие исследования обычно приводят к так называемым характеризационным теоремам, то есть теоремам, описывающим определенное решение (или класс решений), являющееся единственным решением (или, соответственно, единственным классом решений), которое удовлетворяет введенным аксиомам. (Прекрасным примером здесь является только что определенное значение Шепли). Часто такие характеризационные теоремы могут иметь форму теорем существования, указывающих в явном (или неявном) виде решение, удовлетворяющее желаемым свойствам. В соответствии с этим методом, первичными являются свойства решений, и эти свойства используются как основной образующий блок для построения решений.
Второй метод — ”противоположно направлен”, это своего рода обратный аксиоматический метод. Применяя его, обычно исходят из тех решений, которые выбраны на основе каких-то интуитивных соображений или формальных представлений о схемах, используемых в реальной практике, а лишь затем уже изучают те свойства, которым эти решения удовлетворяют (хотя это уже не является центральным моментом исследований). Здесь, однако, следует особо отметить, что граница, разделяющая эти два метода весьма и весьма расплывчата в том смысле, что очень часто второй метод естественно переходит в первый: исследование свойств выбранного решения приводит к тому, что полученные свойства (или некоторые из них) становятся аксиомами, которые однозначно и определяют то самое решение, с которого процесс начинался. В этом смысле, о втором методе можно тоже достаточно естественно говорить как об аксиоматическом методе, не разделяя строго ”прямой” и ”обратный” аксиоматический методы. (Мы проиллюстрируем ниже применение аксиоматического метода еще на примере арбитражной схемы Нэша).
К числу важнейших понятий решения для кооперативных игр относится понятие с-ядра, определение которого опирается на отношение доминирования на множестве дележей. Это отношение определяется следующим образом.
Пусть ж и у — два дележа, а S — некоторая коалиция. Говорят, что ж доми-пирует, у по коалиции S, если
(1) хі> уі для всех і ? S,
(2) х(S) < v(S).
Второе условие означает, что распределение, соответствующее х , действительно может быть обеспечено коалицией S. В этом случае говорят также, что коалиция S блокирует дележ х .
Говорят, что х доминирует у, если найдется такая коалиция S, что х доминирует у по коалиции S .
Определение 6.1.1 С -ядром игры ? называется множество всех ее недоминируемых дележей и обозначается через С(?) .
На самом деле нетрудно доказать, что
С(?) = {ж ? IR1 : х(/) = г(/), x(S) > v(S) для всех S С /}.
Если игра ? выпукла, то значение Шепли игры ? лежат в с-ядре игры ? (Shap-ley, 1971). Заметим, что в случае, например, супераддитивности игры ? вектор Ф(с) может даже не принадлежать непустому с-ядру. Более подробно о выпуклых играх см. раздел 6.6.
Классическим результатом о непустоте с-ядра кооперативных игр с побочными платежами является теорема, доказанная впервые О. Бондаревой (Бондарева, 1963), а затем, независимо, Л. Шепли (Shapley, 1967), утверждающая, что кооперативная игра имеет непустое с-ядро тогда и только тогда, когда она сбалансирована. Понятие сбалансированности вводится следующим образом (см., например, Розен-мюллер (1974)) (см. также и. 6.3).
Набор коалиций В С 21 называется сбалансированным, если найдутся такие неотрицательные числа ps , S ? В , что ^2SeB pses = е , где е = е1 = (1,1,. . . , 1) ? IR1, a es — характеристический вектор коалиции S, то есть
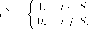
Кооперативная игра ? называется сбалансированной, если для любого сбалансированного набора коалиций В имеет место неравенство
< ?(І).
SEB
(Мы еще вернемся к понятию сбалансированности в разделе 6.3).
Наряду с с-ядром существенную роль играет е-ядро (или се-ядро) игры, определяемое для произвольного вещественного г следующим образом:
С?(?) = {х ? Ш1 : х(/) = ?(І), x(S) > v(S) — е для всех S ф 0, /}.
Ясно, что С(?) = С'о(г) . Кроме того, С?(?) D С?>(?) , если ? > г', причем включение строгое, если С?(?) ф 0. Очевидно также, что С?(?) ф 0 для достаточно больших ? и, напротив, начиная с некоторого ? (быть может, отрицательного) становится пустым.
На основе понятий угрозы и контругрозы дается определение переговорного множества: пусть х — дележ в игре ? .
• Пара (у, S) , где S — коалиция, а, у — достижим для S, т.е. y(S) = v(S) , называется угрозой і против j относительно х , если S Э *, но S ф j и ук > хкУк G S'.
• Пара (z,T), где Т —коалиция, a z — Г-достижим, называется контругрозой относительно угрозы (у, S) игрока і против j , если Т Э J , но Т ф і и zk > хкУ k ? T\S, zk > ук У к ? Т Г\ S.
Предложение 6.1.2 Переговорным множеством называется множество дележей х таких, что для любой угроды (у, S) игрока і против любого другого игрока j относительно х существует контругроза игрока j относительно (у, S) .
Переговорное множество всегда непусто и содержит с-ядро.
Другими, чрезвычайно важными понятиями решения кооперативных игр являются понятия п-ядра (the nucleolus) и к-ядра (the kernel), а также их модификации — пред п-ядро (prenucleolus) и пред-?;-дсфо (prekernel). Введенное Д.Шмайдлером понятие п-ядра игры (Schmeidler (1969)) опирается на понятие эксцесса коалиции. Для классической кооперативной игры ? стандартный эксцесс (или функция эксцесса) определяется естественным образом: e(S, х) = v(S) — x(S). Величина e(S, х) называется эксцессом коалиции Sex и интерпретируется как мера неудовлетворенности коалиции распределением выигрышей, которое предписывается вектором ж . Заметим здесь, что чем больше х , тем меньше эксцесс, и, тем самым, ’’меньше неудовлетворенность”. В этом смысле мы можно говорить, что эксцесс монотонен по г и антимонотонен по х .
Пусть X — произвольное непустое замкнутое множество в Ш/. Для любого х ? X и любой кооперативной игры ? определим вектор ?(х) следующим образом
?(х) = (e(S1,x),e(S2,x),...,e(S2n,x)),
где различные эксцессы всех коалиций расположены в убывающем (невозрастающем) порядке. Компоненты вектора ?(х) определены и непрерывны. Будем говорить, что ?(х) лексикографически меньше чем ?(у), и обозначать это как ?(х) <іех ?(у) , если существует такое натуральное число у, что ф(х) = ф(у) для любого і < q и ?д(Х) < ?д(у) .
Тогда п -ядром игры ? относительно множества X (и данного семейства эксцессов е(Д,-),Д С /) , которое мы будем обозначать через N(X,v), называется множество тех векторов из множества X , для которых соответствующие вектора ? минимальны относительно определенного лексикографического порядка, то есть
N(X,v) = {ж ? X : ?(х) <іех ?(у) для всех у ? X}.
Если X = Х(?) , то N(X, ?) := N(v) называется п -ядром игры ? . Если X = Х*(?) , то N(X}v) := PN(v) = N*(v) называется пред-п -ядром игры ? .
Теорема 6.1.1 Если X компактно, или если оно замкнуто и ж(/) < const для всех х ? X, то N(X, ?) непусто. Если, кроме того, X выпукло, то N(X,v) состоит из одной точки и непрерывно зависит от характеристической функции (см., Schmeidler (1969), Kohlberg (1971), Maschler (1992)).
Важнейшим свойством п -ядра и пред- п -ядра является следующее следствие из этой теоремы.
Следствие 1 п-ядро игры ? (и пред-п -ядро игры ?) одноточечно и лежит в с-ядре игры ? , если оно непусто.
Докажем для примера одноточечность п-ядра.
Пусть ? — ТП игра и ж, у ? N(v) =?¦ Q(x) = Q(y) . Мы покажем, что е(Д, ж) = е(Д, у) ?Д и в частности е(г,ж) = е(г,у) =4* ? = у. Пусть S* : е(Д*,ж) ф е(Д*,у)
и рассмотрим дележ ж = |(ж + у). Обозначим через Вфх),. . . , Вк(х) разбиение множества всех коалиций S такое, что S,S ? Вк(х) -<=>¦ е(0, ж) = е(0 , ж), т.е. ?А G Вк( ж) е(0, ж) = ац(ж) . Считаем ац(ж) > а2(ж) > ... > ац(ж) . Ясно, что ац(ж) = ац(у) ?А; и |_??*,(ж)| = |.ЕС(г/)| ?А;. Но, так как е(?*,ж) ф е(?*,у), то существует минимальное к* , для которого Вк*(ж) ф Вк*(у) . Если Вк*(ж) П Вк*(у) ф 0 , то = Вк*(х) П С , если Вк*(х) П Вк* П Вк*(у) = 0 то ад*(.г) <
ак*(у) = ак*(у).
В любом случае ?(г) <іех ?(х) .
Еще одно полезное свойство n-ядра дается следующим утверждением.
Предложение. Пусть и и ? — две игры такие, что и(І) = ?(І) и v(S) = u(S) + а для всех S ф I и некоторого числа а . Тогда N*(v) = N*(u) .
Интересно, что определение n-ядра можно дать в терминах угроз и контругроз (см. Osborne, Rubinstein (1994)). А именно, пусть ж — дележ в игре ? .
Пара (0, у) , состоящая из дележа у и коалиции S, называется угрозой относительно х , если е(0, ж) > е(0, у) (то есть y(S) > x(S)).
Коалиция Т называется контругрозой относительно угрозы (0, у) , если е(Т, у) > е(Т, ж) (то есть ж(Т) > у(Т)) и е(Т, у) > е(0, ж) .
Тогда п -ядром игры ? называется такой дележ ж , что для каждой угрозы (0, у) относительно ж найдется контругроза.
/Т-ядро и пред-А;-ядро исследовалось во многих работах начиная со статей М. Дэвиса и М. Машлера (Davis/Maschler, 1965), М. Машлера и Б.Пелега (Maschler/Peleg, 1966, 1967), М. Машлера, Б.Пелега и Л. Шепли (Maschler/Peleg/Shapley, 1972, 1979). В действительности, исторически А;-ядро предшествовало n-ядру: один из неожиданных результатов статьи Maschler/Peleg (1966) состоял в том, что если для произвольного е множество С?(?) ПІ(г) непусто, то А;-ядро пересекает это множество (неожиданных потому, что определение А;-ядра никак не опирается на понятие с-ядра). Исследуя именно этот факт, Шмейдлер и дал определение n-ядра, которое, с одной стороны, является ’’уникальной” точкой к-ядра, а с другой стороны, как оказывается, весьма тесно связано с концепцией с? -ядра. (Говоря неформально, именно на некоторым образом сконструированном процессе трансформации непустого с? -ядра построена геометрическая характеризация п -ядра (см. Maschler, Ре-leg, Shapley (1979). При такой трансформации грани непустого с? -ядра для достаточно большого е начинают рановерно с одинаковой скоростью (за счет уменьшения
е) сдвигать параллельно себе до тех пор, пока множество, ограничиваемое этими гранями, не станет пустым, либо не ” отделится” от с-ядра. Далее некоторые грани сдвигать уже становится невозможным, поэтому продолжают сдвигать оставшиеся до тех пор, пока множество, ограничиваемое гранями, не станет пустым, либо не ” отделится” от с-ядра. И так далее, пока не останется единственная точка. Эта точка и будет п -ядром).
Пусть ? — произвольная кооперативная игра. Обозначим для любых двух различных игроков г,д ? / через 7Д множество тех коалиций, которые содержат г, но не содержат j , то есть
Tij = {S:ScI,ieS,j? S}.
Для каждого распределения ж ? Х*{?) определим ’’максимальное преимущество игрока і над j”:
Sn(x) = тахе(з,ж).
; seTij V ’ ;
Величину Sij(x) можно интерпретировать как максимум того, что игрок і может надеяться выиграть (минимум проиграть, в случае отрицательности), если он отклонится от ж и образует коалицию, которая не нуждается в согласии игрока j , в предположении, что другие участники этой коалиции удовлетворены тем, что им дает ж. Игроки і и j находятся в равновесии для ж, если щДж) = зд(ж).
Если вместо множества распределений Х*(?) взять множество дележей Х(г), то условие равновесия переписывается в виде двух неравенств:
Мж) - sAx)][xj - v(j)] < о
и аналогичного неравенства с перестановкой гид.
К -ядром К {у) игры ? называется множество тех дележей ж ? Х(?) , для которых любые два игрока находятся в равновесии. Пред-к -ядром К*{у) игры ? называется множество тех пред-дележей ж ? Х*(?) , для которых любые два игрока находятся в равновесии, то есть
К*(?) = {ж ? Ш1 : max- MS) - x(S)) = max (г(Д) - ж(S)),i,j ? I;x(I) = v(I)}.
К-ядро и пред-к-ядро всегда непусты. Для любой игры ? имеет место равенство К {у) П С{у) = К* (у) П Сіу). Кроме того А;-ядро лежит в переговорном множестве.
Прежде чем привести некоторые примеры решений необходимо отметить, что мы ничего не сказали относительно аксиоматического подхода к определению таких решений, как с-ядро, n-ядро, А;-ядро и т. д. Мы отсылаем по этому поводу читателя к работам МагсЫег (1992), Pechersky/Sobolev (1995), Peleg (1986, 1992), и многими другими. Заметим, что к -ядро может иметь весьма своеобразное строение, как показывает пример 4 в конце этого раздела. При этом необходимо подчеркнуть, что применение систематического подхода оказывается чрезвычайно плодотворным. Мы остановимся на этом четь подробнее в п. 6.4.
Приведем несколько простых примеров решений.
Пример 1. Простая игра. Кооперативная игра ? называется простой, если v(S) принимает только значения 0 и 1 для любой коалиции S / J и v(J) = 1 ; коалиции S, для которых v(S) = 1, называются выигрывающими. Игрок, принадлежащий всем выигрывающим коалициям называется вето-игроком. Тогда
a) Если в игре нет вето-игрока, то С(?) = 0 (докажите!)
b) Если множество вето-игроков в игре ? непусто, то с-ядро состоит из векторов выигышей, дающих 0 всем остальным игрокам (докажите!).
Пример 2. Мажоритарная игра 3-х лиц.
a) Пусть / = {1,2,3}, ?(І) = 1, v(S) = а ? [0,1] для любой коалиции S, состоящей из двух игроков, и ?(і) = 0 для любого і ? /. Тогда с-ядро С(?) непусто тогда и только тогда, когда а < 2/3 (докажите!).
b) Пусть теперь а = 1 . Тогда с-ядро такой игры пусто. Можно показать, что переговорное множество этой игры состоит из единственного вектора (3,3,3)-
Действительно, предположим, что ж-дележ и (у, S) — это угроза і против j относительно ж. Тогда S = {г,й}, где h — оставшийся игрок и yh < 1 — жг- (т.к. Уі > хі и y(S) = v(S) = 1)- Для того, чтобы у j нашлась контругроза на (у, S) мы должны иметь ул, + Xj < 1 . Следовательно, для того, чтобы ж принадлежал переговорному множеству необходимо, чтобы для всех игроков i,j,h было выполнего неравенство уд <1 — Xj как только уд < 1 — жг-, а это означает, что 1 — жг- < 1 — Xj или жі > Xj для любых гид так что ж = (|, |, |) .
Пример 3. Взвешенная мажоритарная игра. Такая игра представляет собой простую игру ? , для которой
, п\ _ f 1, если w(S) > q, у 1 0, в противном случае
для некоторого числа q и w ? IR+ , где v(S) = Y2ieswi Для каждой коалиции S. Интерпретация такова: Wi — число голосов, имеющихся у игрока і, а q — число голосов, необходимых для победы. Взвешенная мажоритарная игра (ВМИ) является однородной, если w(S) = q для любой минимальной выигрывающей коалиции S (т.е. коалиции, не содержащей никаких выигрывающих коалиций). ВМИ является игрой с нулевой суммой, если для любой коалиции S либо v(S) = 1 , либо v(I\S) = 1 , но не одновременно. Предположим, что ? — однородная ВМИ с нулевой суммой, в которой Wi = 0 для каждого игрока і, не принадлежащего ни одной минимальной выигрывающей коалиции. Тогда N(v) = . . .,
Пример 4. Рассмотрим следующую игру семи лиц.
г; (124) = с(235) = с(346) = с(457) = с(561) = с(672) = с(713) = 1,
v(S) = 1 для любой коалиции S, содержащей перечисленные выше коалиции,
v(S) = 0 в остальных случаях.
А;-ядро состоит из 7 отрезков, соединяющих (1/7,1/7,. . . , 1/7) с точками, в которых минимальная выигрывающая коалиция делит свой выигрыш поровну.
Определение 6.1.2 Однозначное решение монотонно, если увеличение ?(І) при сохранении значений остальных S не уменьшает выигрыш ни одного из игроков.
Легко убедиться в том, что значение Шепли монотонно. Однако п-ядро этим свойством уже не обладает. Действительно, рассмотрим следующий пример (Maschler, 1992).
Пример 5. / = {1,..., 9} . Пусть х = (1,1,1,2,2,2,1,1,1)
v(S) = 6 для Де {123,14, 24, 34,15, 25, 35, 78} , v(S) = 9 для Д G {12367,12368,12369,456} ,
0(1) = 12. v(S) = Y,,es х(г) — 1 в остальных случаях.
w(I) = ?(І) + 1 , w(S) = v(S). Тогда
N(v) = x , N(w) = (l|, 1|, 1|,2|,2|, If, 1|, 1|, 1|) .
Пример 6. Задача о банкротстве. Любопытно, что задачи банкротства имеют очень давнюю историю. Приведем решение задачи банкротства, которая восходит к Талмуду (см. например, Aumann/Maschler (1985), Maschler (1992)), где описана следующая ситуация. Три вдовы одного мужа предъявляют требования на имущество, оставшееся после смерти мужа, в размере 100, 200 и 300 единиц, соответственно. Рассматриваются три случая, когда имущество оценивается в 100, 200 и 300 единиц.
Талмуд приписывает в первом случае распределение (33|, 331, 331) , во втором — (50, 75, 75) и в третьем — (50,100,150). Оказывается, что если определить кооперативную игру для множества игроков (жен) / = {1,2,3} по формуле
v(S) = max{”имущество минус сумма требования членов / \ S'”, 0},
то приведенные выше распределения являются п -ядрами соответствующих кооперативных игр.
Пример 7. (Littlechild, Owen, 1973). Предположим, что п авиакомпаний должны распределить затраты на строительство взлетно-посадочной полосы, причем для обслуживания самолетов, принадлежащих авиакомпании і, достаточно, чтобы длина взлетно-посадочной полосы была равна сг-. Будем считать, что затраты пропорциональны длине и, без ущерба для общности, что
С-п А Сп — і А ... А С\.
Таким образом, если образуется коалиция S , то затраты этой коалиции есть c(S) = тахге5{сг} .
Можно проверить, что это игра выпукла. Вектор Шепли w здесь оказывается следующим:
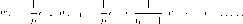 |
| для всех і = 1,. . ., п, |
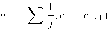 |
|
3=і причем мы считаем сп+1 = 0. |
6.2 Игры без побочных платежей
Очень часто, однако, приходится сталкиваться с ситуациями, когда рассмотрение игр с побочными платежами ставит чрезмерно жесткие ограничения. А именно, может случиться так, что игроки не могут вообще или не могут без потерь перераспределять между собой полученные в ходе игры выигрыши. Иными словами, не все побочные платежи оказываются возможными. Это может быть вызвано, например, следующими причинами. Во-первых, может не иметься единого средства обмена, а во-вторых, даже если такое средство обмена существует (например, деньги), то полезности игроков могут не быть возрастающими линейными функциями денег. Наконец, побочные платежи могут быть запрещены (например, законом) или быть ограниченными. В такой ситуации задачу распределения выигрышей уже нельзя рассматривать как классическую кооперативную игру, а приходится обращаться к более сложной модели, а именно к так называемым кооперативным играм без побочных платежей (играм с нетрансферабельной полезностью, или, как мы будем их часто сокращенно называть, НТП-играм). Разумеется, классическую кооперативную игру можно рассматривать как частный случай кооперативной игры без побочных платежей, при этом основные идеи теории классических кооперативных игр переносятся и на игры без побочных платежей, но здесь возникает целый ряд проблем, связанных, например, со спецификой аппарата, используемого в теории НТП-игр, который, в последнем случае, гораздо сложнее. Помимо этого, в рамках теории кооперативных игр без побочных платежей оказываются содержательными такие задачи, которые для классических кооперативных игр достаточно просты или даже тривиальны.Кооперативной игрой без побочных платежей (или НТП-игрой) называется пара (/, У) , где / = {1,2,. . . , гг} — множество игроков, а У — многозначное отображение, которое ставит в соответствие каждой коалиции S С / множество У (S'), удовлетворяющее следующим условиям:
(1) У(А) с Н5 = {х ? Ш1 : Хі = 0 для г <? S} ;
(2) У (S') — непустое, замкнутое и исчерпывающее множество в IR5 , то есть из х ? У (S') , у ? IR5 и у < х следует у ? У (S') (или, что то же самое, У (S') = V(S)-Rs+).
Часто бывает удобно использовать слегка модифицированное определение игры без побочных платежей, рассматривая вместо множеств V(S) С Ш5 соответствующие цилиндры ?Л(5') = V(S') + Н1''5 .
Множество V(S) обычно интерпретируется как множество векторов полезностей (множество векторов выигрышей, выраженных в терминах полезностей), которые коалиция S может обеспечить своим членам, то есть пространство IR1 рассматривается как пространство полезностей. Мы будем иногда называть множества V(S) игровыми подмножествами. По классической кооперативной игре ? можно стандартным образом построить игру без побочных платежей, положив
У(5) = {ж ? Н5 : x(S) < г(б')}.
Здесь множества V(S) являются полупространствами в IR5 , граничные гиперплоскости которых имеют соответствующие единичные нормали es , где е = (1,1,...,1).
Важный частный случай НТП-игр представляют арбитражные схемы. Арбитражной схемой п лиц называется пара (g, Q), где q ? IR1, a Q С IR1. Компоненты арбитражной схемы имеют следующий смысл: игроки получают (или уже имеют) выигрыши, соответствующие координатам вектора q, если они не договорились о создании коалиции /, объединяющей всех игроков. Точка q называется точкой status quo. Если же игроки объединились в единую большую коалицию / , то они имеют возможность получить выигрыши в соответствии с любым вектором из множества Q . Арбитражная схема (g, Q) естественным образом порождает следующую игру без побочных платежей:
= {х ? : хі ^ ЧіА ^ -S'}, S ф /,
?(І) = {ж ? Ш/ : Зу ? Q,x < у}.
Нетрудно видеть, что любая коалиция S ф- I в такой игре может обеспечить любому игроку г ? А выигрыш, не превышающий дг-, но такие же выигрыши игроки могут получить и самостоятельно, не объединяясь ни в какие коалиции, отличные от {г} . Лишь объединившись в коалицию /, игроки могут добиться большего. Соответственно, вопрос о решении арбитражной схемы сводится к вопросу об определении некоторой точки из множества Q , которую можно было бы считать в некотором смысле ” справедливым” распределением выигрышей.
Арбитражные схемы (или задачи о сделках, или задача торга5) представляют особый интерес. Не останавливаясь на них подробно, отметим, тем не менее, следующий важный момент. Одной из причин, по которой упомянутые игры называются ”арбитражными схемами”, является следующее. Как правило, для решения подобного вида игр используется аксиоматический метод, то есть формулируется ряд свойств, которым должно обладать решение таких игр. А значит, нахождение решения такой игры можно трактовать следующим образом: ” справедливое” распределение определяет некий беспристрастный арбитр, руководствуясь некоторыми правилами (сформулированными в виде аксиом).
В качестве примера рассмотрим классическую арбитражную схему Нэша. Нэшем (Nash (1950)) была предложена система аксиом, которой должно удовлетворять значение (решение), определенное на множестве G2 арбитражных схем (далее АС) двух лиц с выпуклыми компактными множествами допустимых векторов выигрышей Q , в которых существует хотя бы один вектор ж > q. Значением Нэша (или арбитражным решением Нэша) называется функция г : G2 —У IR2 , (мы будем обозначать r(g, Q) = q = (ф, q2)) , удовлетворяющая следующим шести аксиомам.
N1 (индивидуальная рациональность), q > q .
N2 (допустимость), q ? Q .
N3 (Парето оптимальность), q ? ttQ , где ttQ — множество Парето оптимальных точек множества Q .
N4 (независимость от посторонних альтернатив). Если q б Q С Qi и q — решение АС (g, Qі) , то q является решением и АС (g, Q).
N5 (независимость от аффинного преобразования). Пусть Qі получается из Q с помощью аффинного преобразования
X1 = Оі\Х\ А /А, од > 0,
х'2 = а2х2 + /32, а2 > 0.Тогда, если q — решение (g, Q), то (ац(д + /А, а27Н+/А) является решением (ф, Qі) .
N6 (симметричность). Пусть множество Q таково, что (жі,ж2) ? Q тогда и только тогда, когда (ж2, Х\) ? Q , и пусть q\ = q2 . Тогда q\ = q2 .
bargaining games
Нэш доказал, что существует единственная функция г, удовлетворяющая аксиомам N1 -N6, причем
(Ш - Яі)ІЯ2 - Й2) = тах(жі - q1)(x2 - q2)-
xEQ
Аналогичная теорема имеет место и в случае п > 2 .
Существует широкий спектр различных арбитражных решений, каждое из которых определяется своей системой аксиом (см., например, Roth (1979), Печерский, Соболев (1983) и др.).
Игру с побочными платежами ? , но нетрансферабельной полезностью также можно рассматривать как игру без побочных платежей. Если щ(Ь) есть полезность Ь единиц для игрока і (г = 1, 2,. . . , га ) и функция полезности такова, что щ(у) = ифуі) , у ? IR1, то множество
V(S) = {ж ? IR5 : 3 у ? IR7,y(S) = г;(S'), ж < us(y)}
представляет собой множество векторов полезностей, достижимых коалицией S.
Под решением игры без побочных платежей, как и под решением классической кооперативной игры, понимается некоторый вектор или множество векторов ж ? IR1. Различные понятия решений, возникающие в классических кооперативных играх, можно перенести и на игры без побочных платежей. Это может быть сделано, вообще говоря, различными способами, хотя при этом возникает целый ряд как технических, так и концептуальных трудностей. Так, например, определение с-ядра, основанное на понятии доминирования, непосредственно переносится на НТП-игры, а именно, с -ядро игры без побочных платежей V есть множество
С(V) = {ж ? ?(І) : VS не существует у ? V(S) такого, что гд > жг- V г ? S}.
Однако в этом случае гораздо сложнее решается вопрос непустоты с-ядра (см. по этому поводу, например, Scarf (1967), Shapley (1973)). (Соответствующие теоремы также связаны с понятием сбалансированности и выпуклости, однако условия непустоты оказываются достаточными, но не необходимыми).
Мы приведем две теоремы о непустоте с-ядра НТП-игры, аналогичные теореме о непустоте с-ядра выпуклой ТП-игры. В случае игр без побочных платежей выпуклость можно определить двояко.
НТП-игра называется ординально выпуклой, если V S', Г С J
V{S) П ?(Т) С V(S П Г) U V(S П Г),
где ?(0) = 0о •
Игра V называется кардинально выпуклой, если V S', Г С
+ УЛ(Т) С Ул(? П Г) + U Г),
где Ул(0) = {0} и Ул(5') = У(б') + MAS .
Заметим, что кардинальная выпуклость и ординальная выпуклость не эквивалентны. Рассмотрим следующие две игры (Ichiishi, 1992).
(1) J = { 1, 2, 3} , V(j) = {ж е : х3 < 0} ,
V(i,j) = {х ? : ху < 1,жг- < 1} lkz і ф j ,
У(1, 2, 3) = {х ? Ш3 : х3 < l,j = 1,2,3}.
(2) J = { 1, 2, 3,4} , V(2, 3) = {ж ? Н4 : ж2 < 1, ж3 < 3} ,
У(1, 2, 3) = {ж ? Н{1’2’3} : Ж! < 1, ж2 < 2, ж3 < 2} ,
?(2, 3,4) = {ж ? Н{2’3’4} : ж2 < 2, жз < 2, ж4 < 1} ,
V(J) = {ж ? ШУ : жі < 1,ж2 < 2,ж3 < 2,ж4 < 0} U U {ж ? IRJ : ж4 < 0, ж2 < 2, ж3 < 2, ж4 < 1} U U {ж ? IRJ : ж4 < 1,ж2 < З,ж3 < 1,ж4 < 1},
V(S) = {ж ? Rs : ж4 < 0, г ? S} для остальных S.
Первая игра ординально выпукла, но не является кардинально выпуклой, а вторая — напротив, кардинально выпукла, но не является ординально выпуклой! Хотя в случае ТП-игры эти понятия эквивалентны.
Теорема 6.2.1 (Волков, 1977). Пусть V — НТП-игра, и Ъ ? IRJ определен так, что Ьі = sup{Tj ? IR : x3 ? V{j)} , j = 1 , и с-ядро игры V непусто, если
(1) 3 M G IR такое, что V S С J из х ? ?ДД) и х >b следует, что хг- < М для любого і ? S;
(2) V — ординально выпукла.
Кардинально выпуклая игра также имеет непустое с-ядро.
Обобщение значения Шепли на случай НТП-игр, а также n-ядра, А;-ядра и других решений, опирающихся на понятие эксцесса, сталкивается уже с проблемами другого рода. Так, например, здесь нет столь же естественного, как в случае классических игр, определения понятия эксцесса, поэтому до сих пор вопрос о том, каким же должен быть эксцесс, остается нерешенным (см. по этому поводу Печерский (2000)). Мы приведем здесь лишь определение аналога значения Шепли для игр без побочных платежей — так называемого ( А -трансферабельного или транс-ферабельного значения Шепли. Оно было введено Л. Шепли в статье Shapley (1969) следующим образом.
Пусть V — игра без побочных платежей. Подвергнем полезности игроков изменению масштабов измерения, а именно, умножим полезность каждого игрока г ? / на неотрицательный множитель Аг- . Далее постулируем: значением игры может быть такой и только такой вектор F(V) , который одновременно допустим, эффективен и справедлив для некоторых множителей А* , і ? /. Это означает, что:
(a) F(V')€V-(/)|
(b) вектор F(V) х А* = (іД(?)А^,..., Fn(V)А*) максимизирует суммарную полезность коалиции / в игре с побочными платежами с измененными масштабами полезностей;
(c) вектор FiV) X А* есть значение Шепли соответствующей игры с побочными платежами.
Так определенное А -трансферабелъное значение Шепли существует для достаточно широкого класса НТП-игр (см., например, Печерский, Соболев (1983)). Впрочем здесь тоже возникает целый ряд проблем, связанных, например, с возможностью возникновения нулевых весов Аг- (см. по этому поводу Печерский, Яновская (2000), где кроме того определен ряд других трансферабельных значений и, в частности, трансферабельные значения наименьших квадратов, трансферабельное (пред-) га -ядро для НТП игр).
2
6.3 Нечеткие коалиции
В этом разделе мы остановимся на понятии нечетких коалиций, нечетких кооперативных игр и сбалансированности.Мы начнем с формального определения нечетких коалиций и нечетких кооперативных игр (с побочными платежами), а затем остановимся подробнее на различных интерпретациях нечетких коалиций. Пусть, как всегда, / = {1,. . . , га} — конечное множество игроков. Поскольку каждая коалиция S является подмножеством множества игроков / , то она может быть отождествлена с ее характеристическим вектором es ? {1,0}п , то есть
s _ Г 1, г ? S
1 ~ \ о, s.
Мы определяем нечеткую коалицию и нечеткие кооперативные игры, следуя Ж,-П. Обену (Aubin, 1979, 1981а,b). Нечеткая коалиция (то есть нечеткое подмножество (в смысле Л.Заде (Zadeh (1965)) множества I) — это вектор г ? [0,1]”. Число тг-рассматривается как ”степень участия” игрока г в г.
Нечеткая кооперативная игра — это положительно однородная функция V : [0,1]” —>¦ IR, которая ставит в соответствие каждой нечеткой коалиции г ее выигрыш ?(т).
Как и в стандартном случае, функцию V будем называть характеристической функцией. Положительная однородность функции V означает, что У(0) = 0 ? И” (ср.с(0) = 0 в случае стандартных кооперативных игр) и У(Ат) = А У (г) для А ? И_|_ . Последнее предположение позволяет нам продолжить характеристическую функцию V с единичного куба [0,1]” на IR+ , полагая
?(т) = ) для т^°-іеі \2-^іеіТг /
Нечеткие кооперативные игры в различных контекстах изучались многими авторами (см., например, Васильев (1984), Данилов/Сотсков (1983), Экланд (1983),
Aubin (1979, 1981a,b), Aumann/Shapley (1974), Baudier (1973), Billot (1992), Owen (1972), Pechersky (1986), Rosenmueller (1977), Shapley/Shubik (1969) и др.).
(Безусловно, требование положительной однородности не является обязательным, однако семейство положительно однородных нечетких кооперативных игр само по себе достаточно обширно и представляет самостоятельный интерес).
Введение в рассмотрение нечетких коалиций — это в некотором смысле попытка ’’убить двух зайцев”: с одной стороны, рассмотрение нечетких коалиций представляет собой один из возможных способов отказа от довольно жесткого условия участия игрока лишь в одной коалиции, а с другой — это один из возможных способов обхода трудностей, связанных с конечностью множества всех коалиций, структура которого очень бедна, что приводит к тому, что получающиеся результаты, по замечанию Обена, ’’либо тривиальны, либо очень сложны” (Обен (1988)).
Один из вариантов интерпретации следующий (см., например, Ауман, Шепли (1974), Обен (1988)). Поскольку мы интерпретировали всякое подмножество множества / как коалицию игроков, то всякое нечеткое подмножество — своего рода идеализированное множество, заданное с помощью указания для каждой точки множества некоторого веса, значение которого лежит в промежутке между Опіи который означает ’’степень принадлежности” точки множеству — мы будем (в соответствии с определением) интерпретировать г как нечеткую коалицию игроков, а числа тг- — как степень участия (принадлежности) игрока і в коалиции г . Игрок полностью участвует в г , если тг- = 1 , он совсем не участвует в ней, если тг- = 0 , и он участвует в ней частично, если тг- ? (0,1) . Так как множество нечетких коалиций [0,1]п представляет собой выпуклую оболочку множества обычных коалиций {0,1}п , то всякую нечеткую коалицию можно записать в виде
т = ^/ще5, где /Щ > 0,^ц5 = 1.
S S
Тогда степень участия игроков тг-, і ? / определяется по формуле
Тг = ?з-
s-.ies
Следовательно, если /щ интерпретировать как вероятность того, что образуется коалиция S , то степень участия игрока і — это сумма вероятностей формирования коалиций S, которым і принадлежит.
Достаточно удачной представляется возможная интерпретация соответствующих компонент ті как времени, то есть тг- — это то время, которое игрок і ”готов трудиться” на коалицию г . Иными словами — это своего рода ” совместительство”.
Перейдем теперь к обсуждению понятия сбалансированного набора коалиций (в духе Экланда), нечетких коалиций, определим каноническое представление стандартных кооперативных игр и рассмотрим еще одну полезную интерпретацию нечетких коалиций.
Предположим, что коалиции представляют своих участников (или интересы своих членов). Предположение, что каждый игрок является участником только одной коалиции очень сильно. Обычно один и тот же индивид может участвовать в нескольких коалициях, организациях, принимать участие в различной деятельности, причем каждая такая коалиция ”защищает” его интересы. Однако, если индивид і является участником одновременно двух коалиций, скажем, Si и S2 , то он не может быть полностью представлен по отдельности, ни коалицией Si ни коалицией S2 , поскольку каждая из этих коалиций считает его своим членом. (Далее, как и всегда, мы будем называть участников игроками). Иными словами, (см. Данилов/Сотсков (1983)) участник не обязан полностью включаться в одну коалицию, а может делить свою активность (и соответственно, получать вознаграждение в виде каких-то результатов деятельности коалиций) между несколькими различными коалициями (”играть несколько ролей”). Поставим в соответствие каждому игроку і и каждой из этих двух коалиций такую степень участия
/4 > 0,/4 > °, что /й5і + /4 = 1.
Это равенство означает, что эти две коалиции полностью представляют і. Если /4 = 0 , то і (ji S; если же /4 = 1 , то эта коалиция полностью представляет игрока і.
Предположим теперь, что /4 + ц'3 < 1 . Это неравенство соответствует тому случаю, когда игрок і не представлен полностью этими двумя коалициями. Ясно, что этот подход может быть легко обобщен на случай более чем двух коалиций, а поэтому мы можем связать с каждой коалицией S семейство таких чисел
цг3 , что цг3 есть степень участия игрока і в коалиции S.
Потребуем теперь, чтобы каждая коалиция представляла своих участников в равной степени, то есть чтобы выполнялось равенство цг3 = ц33 для всех г,д ? S. Это общее значение будем обозначать через ps ¦ Как отмечает А.Билло (Billot (1992)): ”... ничто не дает нам повода для экономического объяснения, почему агенты принадлежат к различным уровням принадлежности коалиции”. (В этом смысле ”вре-менная” интерпретация степени участия приводит к тому, что разное время участие вызывает, так сказать, ’’распад” коалиции). Таким образом, каждый игрок і ’’разделен” между коалициями и полностью представляется семейством S коалиций S, если
S »s = 1-
iese z
Неравенство < 1, означает, естественно, что игрок і лишь ’’частично”
представлен семейством S .
Ясно, что такое семейство коалиций S и соответствующий набор чисел {ps}sez определяет нечеткую коалицию г следующим образом
Vs = Тг'
s-.iesez
Более того, любая нечеткая коалиция г ? [0,1]п определяется некоторыми наборами S и {fJ>s}sez 5 которые могут, разумеется, быть не единственными. Мы будем называть такие семейства — представляющими семействами (для г). Для любой коалиции S число ps будет называться уровнем реализуемости коалиции S.
Пусть ? — стандартная кооперативная игра с множеством игроков / = {1,. . ., га} . Каноническое представление игры ? — это нечеткая кооперативная игра, определенная следующим образом. Представим себе, что:
(1) если выигрыш (доля или дивиденды) игрока і в коалиции S Э і есть t, то его выигрыш в той же коалиции с уровнем реализуемости ps , равняется pst;
(2) каждый игрок получает выигрыши (дивиденды) от каждой коалиции, в которой он участвует.
Предположим теперь, что {?, (ps)sez} задано. Ясно, что суммарный выигрыш, который это семейство может гарантировать своим членам есть
J2^sv(s)-
sez
Каноническим представлением игры ? называется нечеткая кооперативная игра ?* : [0,1]п —>¦ IRn , которая ставит в соответствие каждой нечеткой коалиции г максимальный суммарный выигрыш, который могут гарантировать представляющие ее семейства. Из определения и свойств (1) и (2) сразу следует, что ?* определяется формулой
?*(т) = sup{^2/j,sv(S) : ps > 0,^2 pseS = т}. s s
Нетрудно проверить, что функция ?* суперлинейна, то есть вогнута и положительно однородна (мы еще вернемся к игре ?* ниже).
Эта функция, ее модификации и ее сужение на вершины единичного куба используются при рассмотрении проблем, связанных со сбалансированностью стандартных игр (см., например, Aubin (1981а,b), Drissen (1985), Ichiishi (1993), Shapley/Shubik (1969)).
Нельзя обойти вниманием еще одну, возможно самую популярную, интерпретацию нечетких коалиций, по крайней мере в ситуации экономики обмена. Мы приведем эту интерпретацию, не ограничиваясь рамками собственно экономики обмена, а кратко дадим еще определения соответствующей игры рынка и ядра экономики.
Соответствующая экономическая ситуация такова (см., например, Экланд (1983)): каждый из п агентов, характеризуется своей функцией полезности (предположение о том, что отношения предпочтения агентов представимы с помощью соответствующих функций полезности абсолютно не существенны в данном контексте), зависящей только от его набора товаров ж* ? IR+ , где к — число товаров, а г — номер агента и обладает начальным набором товаров шг ? IR+ . Общие ресурсы в такой экономике (производства нет) определяются равенством ш1 + • • • + шп = О . Каждый из участников стремится максимизировать свою полезность за счет возможного обмена с другими участниками.
В экономике обмена коалиция S С / блокирует распределение (ж1,. . ., хп) , если существует такой набор товаров у1 ? IR+, і ? S, что щ(уг) > щ(хг) для любого і ? S, и ^2іе3уг = Распределение (ж1,..., ж”) называется допустимым,
если = Егеіи% ¦
Ядром экономики обмена называется множество допустимых распределений, которые не блокируются никакой коалицией. Аналогия с с-ядром кооперативных игр очень сильная: любой экономике обмена можно поставить в соответствие кооперативную игру без побочных платежей таким образом, что ядро одной будет соответствовать с-ядру другой. Действительно, положим для любой коалиции S ф- 0
R(S) = {(у%3:уг еШк+,ге S и ]Гф = ]ГсУ},
U(S) = {(щ(у%е3 : (у%3 ? R(S)}. ^
R(S) — это множество перераспределений, которые может реализовать коалиция S. При S = I получаем R(I) = R — множество допустимых распределений. Множество U(S) С Ш1 —множество векторов полезностей, которые коалиция S может гарантировать своим членам.Игрой рынка, соответствующей экономике обмена, называется кооперативная игра без побочных платежей, определяемая формулой
У(Д) = U(S) - IRj, S С /,
где
U(S) = {ж ? IR5 : (ж *) j g 5 = (ui)ies для некоторого и ? U(S)}.
Хорошо известно следующее предложение (см., например, Розенмюллер (1974), Экланд (1983)), которое формализует соотношение между ядром экономики и с-ядром соответствующей игры рынка.
Предложение 6.3.1 Если (ж1,..., ж”) принадлежит ядру экономики, то вектор (иДж1),. . ., ип(хп)) принадлежит с-ядру игры рынка. Если (щ,. . ., щ) принадлежит с-ядру игры рынка, то в ядре экономики найдется такое распределение (ж1,. . . , хп), что Vj < Uj (ж3) для всех j ? / .
Следствие 2 Ядро экономики обмена непусто тогда и только тогда, когда непусто с-ядро соответствующей ей игры рынка.
Понятие блокирования очевидным образом переносится с обычных коалиций на случай нечетких коалиций. А именно, говорят, что нечеткая коалиция блокирует распределение (ж1,. . ., хп) , если существуют такие наборы товаров у1 ? IR^_ , і ? S , что
иі{уг) > Ui(xl) для любого г ? S',
Y1Тгу1 = S t%uj1->
ies ies
где S — носитель коалиции г , то есть множество тех игроков і ? /, для которых Гг Ф 0 .
Нечетким ядром экономики называется множество допустимых распределений, которые не блокируются никакими нечеткими коалициями.
Интерпретация нечетких коалиций (в контексте экономики обмена), о которой говорилось выше, состоит в следующем (см. Экланд (1983)). Представим себе общество Іт , построенное по образцу /, но содержащее в т раз больше индивидов: для каждого j ? / в этом обществе будет m участников типа j , то есть т участников, наделенных одной и той же функцией полезности и3 и таким же начальным ресурсом и3 . Любая коалиция А из Іт определяется заданием типов ее участников и числом участников каждого типа, то есть коалицией S' из / и целыми числами amj < т для каждого j ? S . Тот факт, что коалиция А может гарантировать набор товаров у3 каждому из своих членов типа j , выражается равенством (в котором левая и правая часть поделены на т) mj j
jes
—0J3}
m или, если положить ат1/т = Tj , равенством
^2ТзУ3 = J2T3uj3-
jes jes
Пусть каждый участник типа j имеет набор товаров хг ? , тогда этот набор
блокируется коалицией А, если найдется такое распределение у , что
и фу3) > ифх3) для любого j ? S.
Таким образом, если принять во внимание то, что вещественные числа можно сколь угодно точно аппроксимировать рациональными, то мы можем выбрать целые числа amj так, что при m —> +оо мы будем получать желаемую аппроксимацию для любых Tj . В этом смысле можно сказать, что нечеткие коалиции представляют собой коалиции в экономике, аналогичной первоначальной экономике, но с очень большим числом индивидов.
Наконец, определение нечеткого ядра формулируется следующим образом (мы используем положительную однородность функции V ).
С -ядром нечеткой кооперативной игры V (или нечетким ядром игры V) называется множество
С(?) = {ж ? Ш1 : Жі + • • • + хп = ?(е), хт > ?(т) для всех т ? IR+}.
Предположим теперь, что ? — стандартная кооперативная игра. Непосредственно из определений следует, что эта игра сбалансирована, если ?(І) = ?*(е) . Она вполне сбалансирована, или тотально сбалансирована (то есть сбалансирована любая ее под-игра с множеством игроков S С /, определяемая сужением исходной игры на 5), если v(S) = v*(es) для всех S . Конечно же v(S) < с*(е5) для любой S. Функция ?* является наименьшей суперлинейной (то есть вогнутой и положительно однородной) функцией, большей чем дискретная функция ? .
Как уже отмечалось разделе 6.1, следующее предложение хорошо известно (см. Бондарева (1963), Shapley (1967), Aubin (1981а)).
Теорема 6.3.1 С -ядро С(?) (стандартной) кооперативной игры ? непусто тогда и только тогда, когда ? сбалансирована. В этом случае С(?) = С(?*) .
Мы приведем здесь набросок доказательства этой теоремы. Как мы отмечали только что, сбалансированность означает, что ?(І) = ?*(е) .
Если V — суперлинейная нечеткая игра, то (см. Aubin (1981а)) ее с-ядро совпадает с супердифференциалом д?(е) функции V в точке е = (1,. . . , 1) , то есть
С(?) = д?(е).
причем супердифференциал вогнутой функции / в точке г определяется формулой
д/(т) = {ж ? RA : /(г) - f(t) > (, г - t), V ж ? RA}-
поскольку очевидно, что С(?*) С С(?) (поскольку в нечетком случае просто больше ограничений или они более сильные, т.к. v(S) < г*(е5) ), то из непустоты супердифференциала вогнутой функции следует непустота L(y*) .
Пусть ? — стандартная игра. Множество
А{?) = {ж ? К1 : x(S) > v(S), ?А С 1}
называется (см. Aubin (1981а), Sharkey (1981)) множеством приемлемых векторов (или приемлемых исходов), или просто приемлемым множеством.
Для нечеткой кооперативной игры V — приемлемое множество АІ?) определяется следующим образом
А(?) = {ж ? R1 : жт > ?(т), V т ? [0,1]”}.
Очевидно (см. Рокафеллер (1973), Aubin (1981а,b)), что нижняя опорная функция р множества АІ?) , определяемая равенством
Ра(?){т) = inf {(ж,т) : ж G А(?)},
совпадает с функцией ?* . Более того, Ра(?)(т) = Ра(?*){т) , а следовательно А(?) = А(?*) . Ясно, что А(?) — непустое, замкнутое, выпуклое множество. Оно R+ — устойчиво, то есть А(?) = А(?) + R+ .
Супердифференциация д?*(е) есть множество тех точек ж множества А(?*) = А(?), для которых жі = г*(1) = г(1). А это и есть как раз с-ядро (или нечетное с-ядро), т.е. С(?) = С(?*).
Замечание 6.3.1. Нетрудно заметить, что если игра тотально сбалансирована, то нечетная игра ?* является продолжением стандартной кооперативной игры ? с вершины единичного куба на весь куб. Существуют и другие варианты продолжения игры ? на куб. Так, например, хорошо известно мультилинейное расширение Оуэна (Owen, 1972), определяемое для игры ? слдующим образом:
%) = 5Zpstv{s),
S
где Ps(t) = Пщ5 ті ELeJ—s(l — ті) ¦ Интересно, что при этом вектор Шепли оказывается равным интегралу от градиента функции ? по главной диагонали куба
[О, If-
Замечание 6.3.2. Необходимо упомянуть еще одно обобщение кооперативных гр, связанное с рассмотрением бесконечных множеств игроков. Игры с континуумом участников используются, в частности, для моделирования ситуаций с очень большим числом участников (см. например, Ауман, Шепли (1977)).
6.4 Приложения кооперативных игр
Многочисленность различных экономических приложений кооперативных игр во многом связана, например, с тем, что многие решения, имеющие общественную значимость, вряд ли могут приниматься на основе рыночных механизмов, ибо не будут в достаточной мере использоваться кооперативные возможности, что может приводить к неэффективности при самостоятельных действиях агентов. Простейшим примером здесь может служить производство публичных продуктов (общественных благ или продуктов общественного потребления — public goods). Чтобы исправить эти недостатки рыночных механизмов, предлагается множество нормативных решений, которые представляются уместными в различных ситуациях принятия решений.Прежде, чем остановиться подробнее на приложениях кооперативных игр мы приведем определение согласованности решений кооперативных игр, которое играет очень важную роль в современных исследованиях кооперативных игр и их приложений и которые нельзя не упомянуть даже в столь кратком курсе. Мы кратко опишем здесь свойство согласованности в достаточно общем форме (подробный обзор результатов, касающихся этой проблематики можно найти в работе В.Томсона
(Thomson (1996)). Пусть М--бесконечное множество ”потенциальных” агентов.
Мы считаем, что М = N, где N — множество натуральных чисел. Пусть S — семейство всех конечных подмножеств множества N, элементы которого мы будем обозначать N, N', IV",.... Для любой группы N ? S обозначим через XN множество альтернатив, доступных группе N , из которого группа должна осуществить свой выбор. Пусть Dn — семейство всех возможных задач, с которыми могут столкнуться члены N . Каждый элемент DN задается допустимым множеством, то есть некоторым подмножеством XN , удовлетворяющим каким-либо условиям, а также данными, описывающими окружающую обстановку, включающими, как правило, предпочтения участников на допустимом множестве.
Для данной группы N ? S и задачи D ? DN мы хотим определить, какую допустимую альтернативу из D группа N выберет как компромисс или, в зависимости от интерпретации, какую альтернативу из D будет рекомендовать им беспристрастный арбитр.
Обозначим Е = 1Ддге:Е DN и X = 1Ддге:Е XN .
Решением на Е называется функция <р : Е —>¦ X , которая ставит в соответствие каждому N ? S и D ? альтернативу (или множество альтернатив, если говорить о многозначном решении) из допустимого множества D . Эта альтернатива обозначается через <p(D) и называется решением D .Неформально, свойство согласованности можно описать следующим образом. Решение будет обладать свойством согласованности, если для любой задачи, с которой сталкивается некоторая группа N , всякий раз, когда оно (решение) будет рекомендовать некоторый исход ж в качестве решения этой задачи, оно будет любой подгруппе N' С N рекомендовать сужение х на N' в качестве решения ” редуцированной задачи”, с которой сталкивается N', то есть задачи, возникающей из исходной задачи, если участникам дополнения N \ N1 ”атрибутировать их компоненты х". (Здесь, конечно, нужно иметь ввиду, что решение должно быть разложимым в том смысле, что можно говорить о соответствующих компонентах).
Для формального описания согласованности нам понадобится понятие редуцированной задачи. Пусть N, N' ? S , N' С N, Д ? DN , х ? D . Редуцированной задачей D относительно N' и х является задача, состоящая из тех альтернатив из D , для которых все компоненты, соответствующие дополнению N \ N1, являются соответственными компонентами х . Такую задачу мы будем обозначать через r(D, N', х).
Решение <р : Е —> X удовлетворяет свойству согласованности (а в случае кооперативных игр часто говорят также о свойстве редуцируемости или свойстве редуцированной игры — reduced game property), если имеет место следующее свойство. Если для всех групп N, N' ? S , таких что N' С N и всех задач D ? DN , через х обозначить решение D , то ж|дг является решением редуцированной задачи D относительно N' и х , если редуцированная задача лежит в DN : для любых N, N' ? S , таких что N' С N, для любой задачи D ? DN и для любого х ? D
<p(D), r(D, N', х) ? Dn ==5> ж|дг/ = <p(D, N', ж).
Если, например, ? — кооперативная игра с множеством игроков /, то редуцированная игра может быть определена различными способами. Скажем, по Дэвису-Машлеру, редуцированная на S' в ж игра (S', vxs) определяется следующим образом
(см., например, Maschler (1992)):
да = Ж(Я
?%(Т) = max [v(T U Q) — x(Q)\, 0 ф T C S', T ^ S, S С I \ S.
QCI\S
Это определение служит основой для широкого спектра модификаций понятия согласованности. Так, например, существенную роль играет не только свойство согласованности, но и так называемое свойство обратной согласованности, которое имеет дело с ”двойственной операцией”: желательность какого-то исхода для некоторой задачи выводится из желательности его сужения на все подгруппы, состоящие из двух участников, для редуцированных задач, с которыми сталкиваются эти подгруппы. Формально говоря, решение <р удовлетворяет свойству обратной согласованности, если для любой группы IV ? S, любой задачи D ? DN и любого допустимого х ? D выполняется следующее условие: если для любой группы N' С N такой, что \N'\ = 2 , r(D, IV', x) ? DN> и ж|дг = <f(D, N', x), то x = <p(D) .
Именно на согласованности или на свойстве редуцированности основаны многочисленные системы аксиом, определяющие с-ядро, n-ядро, А;-ядро и т. д. (см., например, Maschler (1992), Peleg (1992) и др.).
Как уже говорилось, спектр приложений кооперативных игр в настоящее время огромен и перечислить все известные к настоящему моменту приложения просто невозможно, тем более, что он постоянно расширяется. Поэтому мы ограничимся здесь лишь кратким перечислением некоторых из них, не давая подробных комментариев и не указывая различных подходов к исследованию соответствующих моделей. Более того, мы укажем лишь те модели, формулировки которых не требует больших формальностей.
По-видимому, начать это перечисление следует с общего экономического равновесия. Классические результаты о совпадении равновесия, ядра и значения в больших экономиках, о совпадении множества равновесий по Вальрасу с нечетким ядром экономики обмена, о связи ядра экономики обмена с с-ядром соответствующей игры рынка давно уже занимают важное место в экономической литературе (см., например, Ауман/Шепли (1977), Васильев (1984), Гильденбранд (1986), Розенмюллер (1974), Экланд (1983), Aubin (1979), Mas-Colell/Whinston/Green (1995) и др.).
Один из важнейших классов приложений составляют задачи распределения затрат. Однако прежде чем рассмотреть несколько подробнее задачи распределения затрат, упомянем некоторые приложения относительно простых классов кооперативных игр. К простейшим кооперативным играм относятся аксиоматические задачи торга (или арбитражные схемы), о которых мы упоминали в разделе 6.2. При всей простоте своего определения, аксиоматические модели торга — это весьма существенный и наиболее продвинутый инструмент исследования в теории благосостояния (см, например, Мулен (1991)). Они нашли также свое применение и в теории фирмы, и в теории организации промышленности (скажем, при рассмотрении взаимоотношений между поставщиком и покупателем (см., например, Тігоіе (1988)).
Следующие приложения, которые следует упомянуть — это приложения, связанные с проблемами банкротства и налогообложения. Задачи, возникающие в этом контексте, можно сформулировать следующим образом. Задача банкротства (см., например, Thomson (1996)) — это пара (с, Е) ? IR+ хИ+ , такая что ^2іеІ Сі > Е , где / = {1,2,. . . , гг} — множество претендентов на собственный капитал Е (то есть стоимость имущества за вычетом обязательств) обанкротившейся фирмы, а сг- — требование г-ro претендента. Задачи банкротства рассматривались, например, в работах Aumann/Maschler (1985), Chun (1988), Chun/Thomson (1990), Dagan/Volij (1993), Thomson (1995) и других. (См. также пример 6 в разделе 6.1.)
Если по-другому интерпретировать соответствующую пару в IR+ X IR+ , то мы приходим к задаче налогообложения. А именно, задача налогообложения — это пара (ш,Т) ? IR+ X И_|_ , причем > Т ; / — это множество налогоплательщиков,
Wi — доход і -го агента, а Т — затраты, которые должны быть покрыты за счет налогов. Задачам налогообложения посвящены, например, работы Young (1986, 1987, 1988, 1994).
С задачей налогообложения тесно связана и задача распределения прибыли. Задача такого типа — это пара (w, S) ? IR+ X И+ , где ну — инвестиции агента і в совместное предприятие, а S > 0 — прибыль, приносимая этим предприятием (см. Moulin (1985а), Herrero/Maschler/Villar (1995)).
Другой весьма существенный круг приложений, занимающих важное место и упоминавшихся уже ранее, связан с задачами распределения затрат. Начнем со случая так называемых квазилинейных затрат. Соответствующая задача в ситуации, скажем, с 3 агентами и двумя проектами может быть сформулирована следующим образом. Представим себе, что три агента сталкиваются с выбором между двумя проектами щ и а2, затраты на осуществление которых есть щ и с2 , соответственно. Выгода (в терминах полезности), получаемая агентами, есть, соответственно, U\ = (и\,и\) , и2 = (и\,и22) , и3 = (гД,^) , при этом допускаются монетарные тренсферты между агентами.
Общее определение таково. Если А — конечное множество общественных проектов, то квазилинейная задача распределения затрат — это пара (и, С) ? X ,
причем С интерпретируется как вектор затрат, каждая координата которого соответствует затратам на осуществление соответствующего проекта. Кроме того, есть индивидуальный товар, называемый ”деньгами”, и предпочтения агента і ? /, определенное на произведении А X IR допускают представление с помощью квазилинейной функции полезности: для данного проекта а ? А и имеющейся у агента суммы денег ггц ? IR полезность агента есть иг-(а) + гаг-. Если обозначить через М1 класс таких задач, то решение — это функция, ставящая в соответствие каждому множеству I и каждой задаче (и, С) ? М1 вектор х ? IR1 такой, что
Хг < max{u,(a) - Са)}. іеі
Анализ этого класса задач можно найти в работах Э.Мулена (Moulin (1985, 1985а)).
В достаточно общей постановке задачу распределения затрат можно кратко сформулировать следующим образом. Группа агентов (это могут быть фирмы, государства, какие-либо организации) хочет реализовать некий проект, реализация которого дает возможность обеспечивать участников некоторым специфическим продуктом (это может быть, к примеру, здание, шоссе, дамба, аэропорт, электростанция, телефонная станция и т.п.) Каким образом следовало бы распределить затраты между участниками этого проекта? Здесь следует отметить, что некоторые понятия, играющие важную роль в теории кооперативных игр и ее приложениях, возникли до того, как сформировался концептуальный аппарат кооперативных игр. Так например, понятие с-ядра было введено Джиллисом (Gillies (1959)), но его аналог по существу рассматривался уже в конце 30-х годов при изучении проблемы распределения затрат между участниками проекта, связанного с развитием бассейна реки Теннеси. В процессе работы над этим проектом был уже сформулирован так называемый принцип отсутствия субсидий, утверждающий, что никакая группа потребителей не должна платить меньше, чем дополнительные затраты на ее обслуживание (то есть разница в затратах с учетом этой коалиции и без нее). См. по этому поводу обзор Straffin/Heaney (1981), Driessen (1988).
Формально задача распределения затрат может быть сформулирована следующим образом. Пусть С : {О, I}1 —> И+ , где / = {1, 2,. . . , п} , неубывающая функция затрат, (7(0) = 0 и С —пространство всех таких функций затрат. Решением является отображение <р : С ? С —>¦ <р(С) ? IR+ так что + <f2(C) + • • • + <рп(С) =
(7(e), где е = (1,1,. . . , 1) .
Эту задачу можно сформулировать в еще более общей форме (см., например, Moulin (1996)). А именно, предположим, что С : IR+ —> IR+ , причем вектор ж = (жі,...,жп) ? IR+ интерпретируется как вектор спроса агентов на продукт (услугу), а продукт производится в соответствии с технологией, которая описывается функцией затрат С. В этом случае решением является отображение щСх IR+ —> <р(С, ж) ? IR+ , так что
(Ді((7,ж) + Ір2 (Т*, ж) + • • • + (рп(С,х) = (7(жі, . . . ,Хп).
Такое обобщение не только расширяет спектр приложений, но и, что, на наш взгляд, представляется также достаточно интересным, дает еще один важный довод в пользу необходимости рассмотрения кооперативных игр общего вида (например, нечетких или обобщенных кооперативных игр). Обсуждение различных способов распределения затрат можно найти, например, в работе Moulin/Shenker (1994).
Исследование многопродуктового случая началось с работы Колпина (Kolpin (1994)), который предложил характеризацию обобщения так называемого серийного метода распределения затрат. (При серийном методе агент 1 платит 1/га-ую часть затрат, необходимых для производства nd\ . Агент 2 платит 1 /(п — 1)-ую часть разности между затратами на производство d\ + (п — l)d2 и тем, что заплатил агент 1 и т.д.). Вербально, метод Колпина состоит в следующем: каждой коалиции потребителей сопоставляется некоторое имплицитное ” социальное бремя” (затраты на производство), которое было бы результатом, если бы спрос общества в целом ”отражал” бы спрос членов этой коалиции; это отправное бремя используется для вычисления тех прав, которые коалиции имеют по отношению к защите от ’’затрат”; эти права имеют приоритеты и коалиция, обладающая высшим приоритетом распределяет свое бремя равномерно между своими членами; оставшиеся затраты распределяются между оставшимися агентами последовательным применением этого правила.
В этом же контексте необходимо упомянуть задачи ценообразования. Формальная модель такова. Предположим, что / — множество товаров (commodities). Для данного а ? IR+ , интерпретируемого как вектор максимального выпуска, определена функция затрат С : {ж ? IR+ : х < а} —У IR1 , такая, что (7(0) = 0. Число С(х) интерпретируется как затраты на производство вектора выпуска х .
Механизм ценообразования — это функция <р , которая ставит в соответствие каждой задаче ценообразования ((7, а) вектор Р(С} а) ? IR1. Примерами таких механизмов являются механизм Шепли и механизм Аумана-Шепли. Первый назначает вектор цен, і -ая координата которого есть
Shi(v(Ct0l))
Sh* * (с, а)где Sh(-) — значение кооперативной игры, определяемой формулой V(c,a)(S) =
0(0^, as).
Если ограничиться задачами, в которых функции затрат бесконечно дифференцируемы и таковы, что существует интеграл J1 C(ta)dt, то можно определить механизм Аумана-Шепли, который назначает вектор цен так, что его і -ая координата есть J”1 Ci(ta)dt, где (7; — частная производная по г-ой координате. Обзор литературы, посвященной анализу этой модели можно найти в обзоре Я.Таумана (Tauman (1988)).Поскольку речь здесь идет о ценообразовании, то уместно было бы упомянуть столь важный класс приложений кооперативных игр как, проблема ценообразования в регулируемой монополии. Понятие регулируемой монополии возникло в связи с двумя противоположными тенденциями, возникающими в случае, если технология производства обладает свойствами возрастающей отдачи от масштабов производства. В этом случае технологически выгодно слияние производств в одно крупное производство, в результате чего появляется монополия. (В.Баумоль, Дж.Пансар и Р.Виллиг определяют отрасль как естественную монополию, если в определенных пределах выпуска функция затрат субаддитивна (Baumol/Panzar/Willig (1982)). Это определение правильно для хорошо информированного плановика, то есть плановика, которому точно известна функция затрат. У плановика нет причин для того, чтобы иметь несколько фирм, производящих продукцию, когда весь выпуск может быть более дешевым способом осуществлен одной фирмой (см. Тігоіе (1988))). Однако с усилением монополизации отрасли перестает работать механизм конкуренции. В этой ситуации возможны два способа: либо искусственно сдерживать монополизацию, либо отдать отрасль на откуп монополии, но в этом случае отобрать у нее право ценообразования. Так возникает регулируемая монополия: государство не вмешивается в технологические проблемы, но в его руках находится ценообразование.
Традиционные подходы к проблемам регулируемой монополии следуют традициям теории конкурентного рыночного равновесия. В случае публичного блага мы приходим к равновесию по Линдалю, когда каждый агент имеет свою персональную цену публичного продукта и при этих персональных ценах спрос на этот публичный продукт одинаков. В случае индивидуального продукта (продукта индивидуального потребления — private good) это приводит к правилам предельного (маргинального) ценообразования.
Кооперативная теория приводит к различным типам решений, связанных с проблемами регулируемой монополии. В их числе методы, включающие методы ценообразования, основанные на предельной полезности: равновесие по Линдалю и долевое равновесие, обобщающее равновесие по Линдалю для модели с общественным продуктом, а также конкурентное равновесие, в котором каждый агент владеет одной и той же долей общественной фирмы в модели с индивидуальным продуктом. Проблемы связанные с регулируемой монополией обсуждаются в книге Мулена (1991).
Следующий класс проблем, интерес к которым в последнее время постоянно возрастает — это экономические модели справедливого распределения. Упомянем здесь три модели: модель, в которой агенты имеют классические предпочтения на п-мерном пространстве товаров, модель с единственным товаром и ”одно-пиковыми” предпочтениями агентов и, наконец, модель с неделимыми товарами.
Начнем с распределения ”социального фонда” ресурсов (social endowment) между агентами с равными правами на них (например, распределение долей между группой наследников). Предположим, что есть к товаров и группа агентов /. Предпочтения каждого агента г G / описываются некоторым отношением предпочтения і?г- на IR+ . (Как правило, эти предпочтения предполагаются непрерывными, выпуклыми и монотонными). Есть также социальный фонд О ? IR+ . Задача справедливого распределения — это пара (R, О) , причем эту модель следует отличать от стандартной модели, в которой каждый агент изначально имеет некоторое распределения товаров или ресурсов общества.
Указанную модель можно обогатить, если ввести возможность производства, при этом возникает множество разнообразных решений. Среди работ, посвященных этим моделям следует указать работы Thomson (1988, 1992), Fleurbaey (1995), Fleuerbaey/Maniquet (1994) и Maniquet (1996). Причем здесь любопытно отметить, что проблемы согласованности рассматриваются в этих моделях не только в связи с возможностью варьирования числа агентов, но и варьированием числа товаров, с соответствующей переформулировкой свойств согласованности решений (см., Roemer (1986а, 1986b)).
Задачу справедливого распределения в экономике с ”одно-пиковыми” предпочтениями мы проиллюстрируем на следующем примере (см. Thomson (1994)). Представим себе, что для выполнения некой работы формируется группа из трех работников, при этом суммарно потребуется Т часов работы. Каждый работник получает фиксированную почасовую оплату, а его ”неудовольствие” (disutility) от работы является вогнутой функцией от отработанного им времени. Как результат, его полезность является вогнутой функцией от предлагаемого им труда. Каким образом работу следует распределить между этими тремя работниками, если помимо эффективности нас волнует еще и ” справедливость”. Исследованиями моделей этого типа моделей посвящены работы Thomson (1994), Sonmez (1994), Dagan (1996) и др.
Задачу справедливого распределения в ситуации с неделимыми товарами в простейшей форме можно представить следующим образом. Есть три работы, на выполнение которых следует назначить трех работников одинаковой квалификации. Работы не являются идентичными и предпочтения работников относительно сочетаний ”работа — заработная плата” различны. Заработная плата может быть выбрана так, чтобы компенсировать агентов в случае назначения их на менее желательную работу, причем суммарная заработная плата должна находиться в рамках некоторого определенного бюджета. Каким образом следовало бы назначить работников для выполнения этих работ и какова должна была бы быть их заработная плата? Решение задач этого типа обсуждается в работах Tadenuma/Thomson (1991, 1993, 1995), Aragones (1995) и др.
Конечно же невозможно перечислить все известные к настоящему времени приложения теории кооперативных игр и тем более пытаться подробно описать каждое из них. Однако, представляется, что даже приведенный список моделей демонстрирует то обширное многообразие возможных приложений теории кооперативных игр.
В заключении отметим еще несколько, на наш взгляд, важных моментов. Так, например, чрезвычайно интересный подход к изучению природы фирмы, базирующий на теории кооперативных игр, исследован Т.Ихииши в монографии Ichiishi (1993).
Наконец мы опишем несколько хорошо известных моделей, формулировка которых базируется на использовании игр без побочных платежей.
Один из классических примеров — игру рынка, мы уже упоминали выше. Рассмотрим теперь другую модель — модель с производством (Boehm (1974)).
Экономика с производством описывается набором
Ep = ({X^u^w^}j€l,{Y(S)}sci),
где X3 С IRfc — потребительское множество, и3 : X3 —> IR — функция полезности, w3 ? IRfc — начальный ресурс агента j ? /, a Y(S) — технологическое множество каждой из коалиций S . Если в данной экономике не вводится никаких механизмов, то кооперативное поведение агентов в Ер можно моделировать с помощью НТП-игры V , определяемой следующим образом:
У(б') = {и ? еЦх3 :3у eY(S) :
jes
(4.1)
х3 < w3 + у и Vj ? S : и3 < и3(X3)}.
jes jes
Если каждое из множеств X3 выпукло, каждая функция и3 квазивогнута, а технология сбалансирована, то есть для каждого сбалансированного семейства коалиций В с соответствующими весами {As}ses имеет место включение
УМЩЦС VI.I),
SEB
то игра V сбалансирована, а значит (см. например, Scarf (1957), Iduishi (1992)), с-ядро этой игры непусто.
Следующий пример взят из Champsaur (1975). Рассмотрим экономику с производством с одним первичным продуктом, одним конечным продуктом и конечным множеством / экономических агентов. Все коалиции S С / являются потенциальными производственными единицами и могут производить в соответствии с
производственной функцией д : И+ —> IR+ , которая предполагается строго возрастающей. Конечный продукт является публичным, а первичный продукт — индивидуальным. Функция полезности каждого агента и3 : IR+ —у IR зависит от потребления и первичного продукта и потребления конечного продукта (можно рассматривать, скажем, в качестве индивидуального продукта — деньги, а значит, полезность агента зависит от имеющейся у него суммы денег и количества публичного продукта, которое он может потребить) и является неубывающей функцией. Предположим, кроме того, что w3 ? IR+ — начальный запас (ресурс) первичного продукта у агента j . В экономике нет начального запаса публичного продукта. Соответствующая игра без побочных платежей V определяется следующим образом
< zy ’
jes
jes
У(^)
Vj ? S : Uj < u3 (x3, g(^^ w3 — x3 j)
jes jes
Модель, приводимая ниже (см. Ichiishi (1993)), по существу аналогична предыдущей, но теперь, чтобы сделать ”бесплатный проезд” (free ride) ”платным” (costly ride), смягчая тем самым классическую проблему, возникающую при производстве публичных продуктов, когда каждый из агентов, принимающих участие в производстве публичного продукта, старается ”недобложить” в его производство, пользуясь при этом произведенным всеми агентами продукт, в модель вводится ”контролирующий орган”. Предположим, что коалиция S предполагает выйти из коалиции /, если последняя решает использовать набор хА индивидуальных продуктов. Поскольку участники коалиции S могут ”бесплатно” пользоваться количеством g(Y2jei\s(w:> ~ х“0) публичного продукта, произведенного коалицией / \ S, то контрольный орган вынуждает коалицию S осуществить передачу доли a'l2jeI\s(w3~x3) затРат коалиции /\S , где налоговая ставка а? [0,1] установлена заранее. Предположим, что функции полезностей агентов неубывающие и квазивогнутые, а функция д вогнута. Игра без побочных платежей, параметризованная хА , определяется следующим образом:
V(S) = ? IR5 : '^/х3 < нй ~ ° (wJ ~ х^)і
I jes jes jei\s
V j G S : u3 < u3(x3,g( w3 — tAj)) +
j—inS jes
+ _ ж^) _ X^)) I •
j&s jei\s jes I
6.5 Дополнение. Существование и единственность вектора Шепли
Мы докажем здесь без особых подробностей существование и единственность значения Шепли (более подробно см., например, Воробьев (1995)).Найдем сначала вектор Шепли для характеристической функции вида cur , где с > 0 , а vr — простейшая характеристическая функция, т. е. функция вида
,Г 1, если S D R, vr{S) - <
[ U, в противном случае
Легко видеть, что число различных простейших характеристических функций на / равно 2п — 1 , т. е. числу непустых коалиций. Следующие два предложения мы приведем без доказательств.
Предложение 6.5Л. Все 2п — 1 простейших характеристических функций на I линейно независимы.
Предложение 6.5.2. Для любой характеристической функции ? имеет место единственное представление
? = Аr(v)vr,
RcJ
где
МИ =
ScR
Иными словами, это предложение утверждает, что каждую характеристическую функцию на J можно представить, и притом единственным образом, в виде линейной комбинации простейших характеристических функций.
Теорема 6.5.1 Если vr — простейшая характеристическая функция, то
щ если і ? R, О, если і ? R
Ф i(cuR)
(6.5.1)
Доказательство. Множество R является для сиг носителем. Поэтому по аксиоме эффективности:
фі(сия) = cur(R) = с. (6.5.2)
ieR
Ясно также, что перестановка любых двух игроков из R не меняет значения характеристической функции cur . Поэтому, по аксиоме симметрии слева в (6.5.2) все слагаемые равны друг другу, и мы получаем верхнюю строку (6.5.1). Наконец, все игроки, не входящие в R, являются в cur болванами, и это дает нам нижнюю строку (6.5.1).
Следствие 3 Для простейшей характеристической функции ur и с > 0 Ф(сгщ) =
сФ(гщ) •
Доказательство следует непосредственно из (6.5.1.).
Из аксиомы линейности последнего следствия вытекает, что при любых сд Д О должно быть
Ф(У^ crUr) = ф(crUr) = Сдф(гщ). (6.5.3)
R R R
Распространим эту формулу на случай коэффициентов cr с произвольными знаками.
Лемма 6.5Л Если и' и ?" - характеристические функции, а их разность и' - ?" также является характеристической функцией, то
ф(г/ - у") = ф(ф) - ф(ф'). (6.5.4)
Доказательство. По условию мы имеем тождественно ?' = ?" + (?' — и") . Справа здесь стоит сумма двух характеристических функций, и по аксиоме линейности мы имеем
Ф(ф) = ф(ф') + ф(ф - ф'),
откуда и следует (6.5.4).
Следствие 4 Формула (6.5.3) остается справедливой, если знаки коэффициентов cr произвольные, а сумма ^rcrUr является характеристической функцией.
Доказательство. Имеем
? = ^2 crijr = ^2 CRVR - '^2 (_C^W-
Здесь во второй сумме все числа — cr являются положительными, так что вычитаемая сумма оказывается характеристической функцией. Поэтому по лемме 6.5.1
ФИ
Ф( ^ CRRR) — Ф( ^2 ( — cr)ur) =
R
cr<0
г
CR>°
Теорема 6.5.2 Каждая характеристическая функция имеет не более одного вектора Шепли.
Доказательство. То, что каждая простейшая характеристическая функция имеет не более одного вектора Шепли, следует из теоремы 6.5.1. Но, в силу предложения 6.5.2, произвольная характеристическая функция представима в виде линейной комбинации простейших единственным способом. Поэтому из доказанного выше следует, что каждая характеристическая функция имеет не более одного вектора Шепли.
Нам остается доказать существование вектора Шепли для любой характеристической функции.
Теорема 6.5.3 Для любой характеристической функции ? на I = {1,. . . , п} компоненты вектора Шепли определяются формулой
ф.’М = ^ -—М/й) - и(К\ г)). (6.5.5)
^' пі
іексі
Доказательство. Проверим сначала, что вектор Ф(гД с компонентами из (6.5.5) удовлетворяет всем аксиомам Шепли.
Докажем эффективность вестора Ф(гД . Для этого рассмотрим
ДяЮ-ЛКЛ))-
(п - \K\)l(\K п\
Еф‘(і/) = Е Е
іеі іеі іексі
(6.5.6)
Во всей двойной сумме выражение у (К) встречается в роли уменьшаемого \К\ раз (по числу входящих в К элементов) и тем самым приобретает коэффициент
ітП(п-\К\)К\К\-1)1 (п-\К\)\К\\
\к I-;-=-;->
пі пі
который при \К\ = га, т.е. при К = /, очевидно, равен единице. В роли же вычитаемого оно встретится п — \К\ раз (по числу не входящих в К элементов) и тем самым приобретает коэффициент
— (га
и коэффициент, 0, если п = |КТаким образом, правая часть (6.5.6) равна у(і) :
если п ф- IК
- \К\
п\
п\
У]ф,М = ЦЛ. (6.5.7)
іеі
и вектор Ф(г/) оказывается эффективным.
Проверка аксиомы болвана тривиальна. Пусть в игре ? игрок і является болваном. Тогда для любой коалиции К С /
іу(К) — іу(К \ г) = О
а следовательно, каждое слагаемое в (6.5.5) для этого і равно 0. Поэтому
Ф(і/) = 0.
Проверим теперь аксиому симметричности. Пусть / — перестановка J такая, что ?(ттК) = ?(К) для любой коалиции К . Тогда вместе с К коалиция ттК также пробегает все подмножества /, и мы можем (6.5.5) переписать какЖ / 5 - !)!// , , USX -х\\
Ф^’Н = -~\-((фА)-ф(А\ф).
тгіЕтгКС.!
С другой стороны, поскольку и(ттК) = ?(К) , и 17ГКI = \К\ , ТО 7Гг И 7ГК под знаком суммирования можно обратно переименовать соответственно в і и К . Окончательно мы имеем
(п - \К\у.(\К\ - 1)!
Е
ксі
{іу{К) - у {К \ г)) = Фг(г/).
Ф,
п\
Аксиома линейности следует из того, что компоненты вектора Ф(гД зависят от значений характеристической функции ? линейно.
Таким образом, вектор Ф(гД действительно является для характеристической функции ? вектором Шепли, существование которого тем самым доказано.
6.6 Выпуклые игры
1. Пусть / = {1,. . . , га) — множество игроков, а ? — выпуклая игра, т.е. для любых S,T С (/)v(S) + v(T) А v(S U Т) + v(S П Т). (6.1)
Множество всех выпуклых игр мы будем обозначать через С . Оправданием такому названию может служить тот факт, что для выпуклой игры ”первые разности”v(S + T) -v(S) (6.2)
при фиксированном Т монотонно возрастают по S. (Заметим, что если/ : R+ ^ R+
выпуклая функция, т.е./(аж + (1 - а)у) А а/(ж) + (1 - a)f(y)
при всех ж, у ? R+ и О А а А 1 , то ”первые разности” этой функции
/(ж + у)-/(ж) (ж,у<ЕІІ+)
при фиксированном у монотонно возрастают по ж).
Соотношение (6.2) наводит на мысль, что с-ядро выпуклой игры непусто. Дей-
7
ствительно, можно заметить, что условие
(v(S + {*}) - v(S)) (6.3)
равносильно монотонности (6.2). Утверждение же (6.3) означает, что игроку і целесообразно присоединяться к все большим коалициям; отсюда вытекает стремление
73десь и далее запись А(х) У будет означать, что функция А(х) монотонно возрастает по переменной х .
к образованию большой коалиции, охватывающей вообще всех игроков. Поэтому естественно ожидать, что образуется максимальная коалиция, а меньшие коалиции этому не будут препятствовать. Следовательно, можно ожидать, что с-ядро непусто.
Теорема 6.6.1 Если ? ? С, то С(?) ф
Доказательство ведется по индукции. Для п = 1 доказывать нечего. Предположим, что теорема доказана для п — 1 игроков. Пусть / = {1,. . . , га} , а Т — коалиция из п — 1 игроков. Тогда, в силу индуктивного предположения, функция
г°(Д) = v(SnT)
имеет непустое с-ядро, т.е. существует такой вектор пг° ? Ит , что
m°(S) Д v°(S), (6.4)
'(Г) = m°(J) = v°(T) = v°(E).Определим вектор m ? ПИ, положив
(6.5)
ГГЦ =
m° г ? Г,
?(Г)-?(Т), ііТ.
Тогда мы имеем
m(I) = nij = m° + ?(І) — ?(Т) = іеі іет
= гп°(Т) + ?(І) - ?(Т) = ?(І) (6.6)
и для S С Т в силу (6.4)m(S) = m°(S) Д v°(S) = v(S).
Кроме того, для S (фТ мы имеем, считая что Т = / \ {г0} ,
m(S) = m°(S П Т) + гпі0 Д
Д v°(S П Т) + гпі0 = v(S П Т) + ?(І) — ?(Т) =
= viS \ {*o}) + v(I) - v(I \ {г0}) Д v(S),причем последнее неравенство в цепочке следует из (6.3). Теорема доказана.
Идея доказательства здесь достаточно прозрачна: выигрыш делится между членами коалиции Т соответственно некоторому дележу из С(?°) , а вновь присоединяющемуся игроку і0 выплачивается все то, что он приносит большой коалиции.
А это позволяет подойти к следующей конструкции.
Теорема 6.6.2 Пустъ
0 = S0 C Si C S2 С • • • C Sn = I (6.7)
— строго возрастающая последовательность коалиций из I, для которой |S) \ Si-11 = 1 при всех і = 1,. . ., п . Тогда равенстваX (Si \ Si-!) = v(Si) - v(Si-i) (6.8)
определяют некоторый дележ х ? С(?) .Доказательство аналогично доказательству предыдущей теоремы.
Процесс, описываемый цепочкой (6.7), достаточно нагляден: пустая коалиция So за счет вступления в нее новых игроков последовательно увеличивается каждый раз на одного игрока. Этот порядок вступления определяет некоторую перестановку игроков л . Перестановка тт , соответствующая (6.7), однозначно определяется равенством
К (Si \ Si-i) = г (г = 1 ,...,п). (6.9)
Пусть теперь тт : I —У I — некоторая перестановка. Ясно, что она порождает некоторый порядок игроков. Обозначим множество первых (согласно этому порядку) і игроков черезЦ = {к : к(к) s >}.
Если л получено из соотношения (6.7) на основании (6.9), то из к ? Si, А; ? Sj \ Sj-1 (для некоторого j Д і) вытекает
ТТІк) = ТГ (Sj \ Sj-1) = j "Si.
ОтсюдаS? = Si.
Поэтому справедлива следующая теорема.
тт : I —У I дележ х? , (6.10)
Теорема 6.6.3 (Shapley, 1979). Для любой перестановки задаваемый равенством
<-і(0 = - v(Si-i),
принадлежит С(?) .Замечание. Легко видеть, что
х\ = ?(Бф)) - v(Syky1). (6.11)
Теорема 6.6.4 (Shapley, 1979). Каждый дележ х? , описываемый равенством вида (10), является крайней точкой множества С {у), и все крайние точки могут бытъ получены таким путем.
Доказательство. Множество С является ограниченным замкнутым выпуклым многогранником в R” . Известно, (см., например, Рокафеллар (1973)), что крайние точки можно получить как единственные решения системы п уравнений, получаемых из неравенств, задающих многогранник. При этом необходимо еще проверить, принадлежат ли найденные таким образом точки многограннику.
В силу равенства (6.8) для заданных х? = х и S( = S) мы имеем
v(Si),
'(Si) — x(Si \ Si-i) + x(Si-i \ Si-2) + • • • + x(Si \ So)
т.е. x является решением системы n уравнений. Из равенства (6.10) следует, что х является единственным решением этой системы. Наконец, по теореме 6.6.3 х ? С , так что х является крайней точкой с-ядра.
Пусть, наоборот, х — некоторая крайняя точка с-ядра. Рассмотрим систему коалиций
а = сг(ж) = {8 С I\x(S) = r(S')}. (6.12)
Эта система замкнута относительно операций объединения и пересечения. Действительно, пусть S,T ? а ; тогда
v(SUT) Д x(SUT) = x(S) + x(T)-x(Sr\T) Д
Д v(S) + v(T)-v(SnT) < v(SUT) (6.13)и, следовательно, S U Т ? а .
Точно так же доказывается, что и S П Т ? а . Пусть
0 = До С Ді С • • • С Sm = I (6.14) — строго возрастающая последовательность коалиций из а, имеющая наибольшую длину. Если т = п , то наша теорема доказана. Если т < п , то найдется такое Sk , ЧТО
\Sk+i\Sk\ Д2.
Пусть, например, {г, j} С Sk+i \ Sk ¦
Ввиду того, что х как крайняя точка является единственным решением системы
Xj = v(S) (S' ? cr), (6.15)
ies
существует хотя бы одно такое S ? а , что (не нарушая общности)
ieS, j?S.
Множество Т = (S U 5Й) П б'й+і является элементом а ввиду замкнутости семейства а относительно операций объединения и пересечения. Кроме того, для Т имеет место включение
Sk с Т С Sk+1,
а это невозможно в силу того, что (6.14) — последовательность наибольшей длины. Поэтому случай m < п невозможен, и теорема доказана.
Теорема 6.6.5 Пустъ функция ? ? С такова, что для S,T ? В, для которых S \ Т ф- 0 и Т \ S ф- 0 ; всегда имеет место
v(S) + v{T) < v(SUT) + v(S ПТ). (6.16)
Тогда все дележи х? различны. В этом случае С имеет ровно п\ крайних точек.
Доказательство. Пусть множества S' и Г удовлетворяют условиям теоремы, аж — некоторая крайняя точка С . Покажем, что если х — крайняя точка С , a S', Г ? <т(ж) , то либо S С Т , либо S D Т .
Действительно, из ж (S') = v(S) и х(Т) = ?{Т) на основании свойств <т(ж) следовало бы, что х(S U Г) = v(S U Г) и х(S П Г) = v(S П Т) . Отсюда в свою очередь вытекало бы
v(S) + ?(Т) = ж (S') + х(Т) = x(S U Г) + x(S П Г) =
= v(S U Г) + v(S П Г),
а это противоречит (6.16).
Поэтому множества из <т(ж) можно упорядочить так:
0 = S0 С Si С • • • С Sm = I.
Мы уже видели, что должно быть т = п и, следовательно, соответствие между крайней точкой х и системой (6.7) является взаимно однозначным.
Следствие 5 Если ? ? С и выполнено (6.16), то значение Шепли игры ? есть центр тяжести с-ядра С(?).
Доказательство немедленно следует из теоремы и формулы, определяющей значение Шепли.
6.7 Задачи
1. Вычислите значение Шепли следующей кооперативной игры трех лиц: ?(і) =0 , г(12) = г(13) = 4 , г(23) = 5 , г(123) = 6 .
2. Докажите, что если кооперативная игра трех лиц такова, что ?(і) = 0 для любого г = 1, 2, 3 , и 0 < v(S) < и(/) для любой коалиции S , состоящей из двух игроков, то для n-ядра либо три эксцесса, соответствующие двух-элементным коалициям равны, либо два из них равны, третий больше. Если ?(І) < 2v(S) , то все три эксцесса равны.
3. Вычислите значение Шепли следующей игры трех лиц: ?(і) = 0 для любого
1 = 1,2,3, с(12) = с(23) = 3, с(13) = 4, ?(І) = 6. Что можно сказать о непустоте (или пустоте) с-ядра этой игры.
4. Докажите, что с-ядро игры трех лиц г, в которой ?(і) = 1 для любого і = 1, 2, 3 , с(12) = 3.5 , с(23) = 2.5 , с(13) = 3 , ?(І) = 4 пусто.
5. а) Дана следующая кооперативная игра ? : / = {1,2,3} ,
гД1) = ?(2) = с(З) = 1, с(1, 2) = с(1, 3) = 4, ?(2, 3) = 6, ?(І) = 7.
Вычислите вектор Шепли и п -ядро этой игры.
Ь) Вычислите n-ядро следующей кооперативной игры w : I = {1,2,3} , ш(1) = г?(2) = ш(3) = 0, w( 1,2) = ш(1,3) = 3, і?(2,3) = 5 ,w(I) = 7.
Литература
1. Ауман Р., НІепли Л. (1977). Значения для неатомических игр. М.: Мир. (М)2. Бондарева О.Н. (1963). Некоторые приложения методов линейного программирования к теории кооперативных игр // Проблемы кибернетики. 10. 119-139.
3. Васильев В.А. (1984). Модели экономического обмена и кооперативные игры. Новосибирск: Изд-во НГУ.
4. Вилкас Э.Й. (1990). Оптимальность в играх и решениях. М.: Наука.
5. Вилков В.Б. (1974). У-ядро в кооперативных играх без побочных платежей // Журнал вычислительной математики и математической физики. 14. № 5. 1327-1331.
6. Воробьев Н.Н. (1984). Основы теории игр: бескоалиционные игры. М.: Наука. (М)
7. Воробьев Н.Н. (1985). Теория игр для экономистов-кибернетиков. М.: Наука.
(У)
8. Гильдебранд В. (1986). Ядро и равновесие в большой экономике. М.: Наука. (М)
9. Данилов В.И. (1981). Экономическое равновесие и обобщенные цены // В кн.: Исследования по стохастической теории управления и математической экономике. М.: ЦЭМИ АН СССР, 25-42.
9Буквы М и У в скобках после названия обозначают, что указанное издание — монография или учебник, соответственно. Список включает некоторые названия, не упомянутые в тексте.
10. Данилов В.И., Сотсков А.И. (1983). Конкурентные равновесия в коалиционных играх // В кн.: Категории общественной полезности: вопросы методологии и структуризации. М.: ЦЭМИ АН СССР, 147-167.
11. Данилов В.И., Сотсков А.И. (1987). Уравновешенные состояния и теоремы о ядре // Оптимизация. 41 (58). 36-49.
12. Дюбин Г.Н. (1988). О существовании значения Шепли // Оптимизация. 43 (60), 102-118.
13. Дюбин Г.Н., В.Г.Суздаль В.Г. (1981). Введение в прикладную теорию игр. М.: Наука. (У)
14. Мулен Э. (1985). Теория игр с примерами из математической экономики. М.: Мир. (У)
15. Мулен Э. (1991). Кооперативное принятие решений: аксиомы и модели. М.: Мир. (У)
16. Наумова Н.И. (1971). О ядре со счетным числом игроков // Докл. АН СССР. Т. 197. № 1. 4-42.
17. Обей Ж.-П. (1988). Нелинейный анализ и его экономические приложения. М.: Мир.
18. Оуэн Г. (1971). Теория игр. М.: Мир. (У)
19. Партасаратхи Т., Рагхаван Т. (1974). Некоторые вопросы теории игр двух лиц. М.: Мир. (У)
20. Петросян Л.А., Зенкевич Н.А., Семина Е.А. (1998). Теория игр. М.: Высшая школа, Книжный дом ’’Университет”. (У)
21. Петросян Л.А., Данилов Н.Н. (1985). Кооперативные дифференциальные игры. Томск: Из-во Томского университета.
22. Печерский С.Л. (2000). Функции эксцесса для кооперативных игр без побочных платежей: аксиоматический подход //В кн. Экономика-математические исследования: математические модели и информационные технологии. СПб.: Наука. 65-82.
23. Печерский С.Л., Соболев А.И. (1983). Проблема оптимального распределения в социально-экономических задачах и кооперативные игры. Л.: Наука. (М)
24. Печерский С.Л., Яновская Е.Б. (2000). Трансферабельные значения для игр с нетрансферабельными полезностями // Экономические исследования: теория и приложения. СПб.: Европейский университет в СПб. 310-349.
25. Полтерович В.М. (1997). Кризис экономической теории / Труды семинара ”Не-известная экономика”. Отделение экономики РАН. М.: ЦЭМИ РАН.
26. Соболев А.И. (1975). Характеризация принципов оптимальности в кооперативных играх посредством функциональных уравнений // Математические методы в социальных науках. 6. Вильнюс. 94-151.
27. Соболев А.И. (1976). Нелинейные аналоги аксиоматики Шепли / В кн.: Современные направления теории игр. 119-126. Вильнюс: Мокслас.
28. Соболев А.И. (1978). Нелинейные аналоги функции Шепли / В кн.: Теоретикоигровые вопросы принятия решений. 9-18. Л.: Наука.
29. Сотсков А.И. (1985). Игры со смешанным участием игроков в коалициях / В кн.: Проблема равновесия и принятия экономических решений. 52-58. М.: ЦЭМИ АН СССР.
30. Розенмюллер И. (1974). Кооперативные игры и рынки. М.: Мир. (М)
31. Экланд И. (1983). Элементы математической экономики. М.: Мир. (У)
32. Яновская Е.Б. (1985). Аксиоматическая характеризация максиминного и лексикографически максиминного решения арбитражных схем // Автоматика и телемеханика. № 9. 128-136.
33. Aragones Е. (1995). A Derivation of the Money Rawlsian Solution // Social Choice and Welfare. 12. 267-276.
34. Arrow K. (1951). Social Choice and Individual Values. NY: Wiley. (M)
35. Arrow К., Debreu G. (1954). Existence of Equilibrium for a Competitive Economy // Econometrica. 25. 265-290.
36. Aubin J.-P. (1979). Mathematical Methods of Game and Economic Theory. Amsterdam: North-Holland. (M)
37. Aubin J.-P. (1981a) Cooperative Fuzzy Games // Mathematics of Operations Research. 6. 1-13.
38. Aubin J.-P. (1981b). Locally Lipschitz Cooperative Games // Journal of Math. Econ. 8. 241-262.
39. Aumann R.J. (1974). Subjectivity and Correlation in randomized strategies. Journal Of Math. Economics, 1, 67-96.
40. Aumann R.J. (1985). An Axiomatization of the Non-Tranferable Utility Value // Econometrica. 53. N 3. 667-678.
41.
42.
Aumann R.J. (1989). Lectures on Game Theory. San Francisco: Westview Press.
(У)
Aumann R.J. (1996). Rationality and Bounded Rationality, Nancy Schwartz Lecture, Kellog Fundation.
43. Aumann R.J. (1997). Introductory Remarks. In Cooperation: Game-Theoretic Approaches”. (S.Hart, A.Mas-Colell eds.) NATO ASI Series, Series F: Computer and Systems Sciences. 155. Springer. 5-8.
44. Aumann R.J., Maschler M. (1985). Game theoretic analysis of a bankruptcy problem from the Talmud // Journal of Economic Theory. 36. 195-213.
45.
46.
Aumann R.J., Shapley L.S. (1974). Values for Non-Atomic Games. Princeton University Press. (M)
Banks J.S., Sobel J. (1987). Equilibrium Selction in Signalling Games // Econometrica. 55. 647-661.
47. Banzhaf J. (1965). Weighted Voting Doesn’t Work: a Mathematical Analysis // Rutgers Law Review. 317-343.
48. Baudier Е. (1973). Competitive Equilibrium in a Game // Econometrica. 41. 10491068.
49. Baumol W., Panzar J., Willig B. (1982). Contestable Markets and the Theory of Industry. NY: Harcourt Brace Jovanovich. (M)
50. Beja A., Gilboa I. (1990). Values for Two-Stage Games: Another View of the Shapley Axioms // International Journal of Game Theory. 19. 17-31.
51. Bernheim B.D. (1984). Rationalizable Strategic Behavior // Econometrica. 52. 1007-1028.
52. Bertrand J. (1883). Theorie mathematique de la richesse sociale // Journal des Savants. 499-508.
53. Billera L.J. (1972). A Note on a Kernel and the Core for Games Without Side Payments. Technical Report 152. Dept, of Operations Research. Cornell University, Ithaca. New York.
54. Billot A. (1992). Economic Theory of Fuzzy Equilibria. Lecture Notes in Econ. and Math. Syst. V. 373.
55. Binmore K. (1987). Modeling Rational Players, I. Economics and Philosophy, 3, 179-214.
56. Binmore K. (1988). Modeling Rational Players, II. Economics and Philosophy, 4, 9-55.
57. Binmore K. (1990). Essays on the Foundations of Game Theory. Oxford, Basil Blackwell. (M)
58. Boehm V. (1974). The Core of an Economy with Production // Review of Economic Studies. 41. 429-436.
59. Bondareva O.N. (1989). The Nucleolus of a Game Without Side Payment. Working Paper N 176. Institute of Mathematical Economics. Bielefeld University, Germany.
60. Braithwaite R. (1955). Theory of Games as a Tool for Moral Philosopher. Cambridge: Cambridge University Press. (M)
61. Champsaur P. (1975). How to Share the Cost of a Public Good? // International Journal of Game Theory. 4. 113-129.
62. Chun Y. (1988). The proportional solution for rights problems // Mathematical Social Sciences. 15. 231-246.
63. Chun Y., Thomson W. (1990). A consistent solution to claims problems. University of Rochester, mimeo.
64. Cornes R., Sandler T. (1986). The Theory of Externalities. Public Goods and Club Goods. Cambridge: Cambridge University Press. (M)
65. Cournot A. (1838). Recherches sur les Principles Mathematicues de la Theorie des Richesses. Paris.
66. Dagan N. (1992). Consistency and the Walrasian Allocations Correspondence. Hebrew University of Jerusalem Mimeo, September 1992.
67. Dagan N. (1996). A Note on Thomson’s Characterizations of the Uniform Rule // Journal of Economic Theory. 96. 255-261.
68. Dagan N., Volij 0. (1994). Bilateral comparisons and consistent fair division rules in the context of bankruptcy problems. Hebrew University of Jerusalem, mimeo, February 1994.
69. Davis M., Maschler M. (1965). The Kernel of a Cooperative Game // Naval Research Togistics Quarterly. 12. 223-259.
70. G. Debreu (1952). A Social Equilibrium Existence Theorem // Proceedings of the National Academy of Sciences, 38, 886-893.
71. Debreu G. (1959). Theory of Value. NY: Wiley. (M)
72. de Swan A. (1973). Coalition Theories and Cabinet Formations. Amsterdam: North-Holland.
73. Dixit A. (1980). The Role of Investment in Entry Deterrence, Economic Journal, 90, 95-106.
74. К. Han (1952). Fixed Point and Minimax Theorem in Locally Convex Topological Linear Spaces // Proceedings of the National Academy of Sciences, 38, 121-126.
75. Dixit A., Nalebuff B. (1991). Thinking Strategically: The Competitive Edge in Business, Politics and Everyday Tife. NY: Norton. (M)
76. Driessen T. (1988). Cooperative Games, Solutions and Applications. Dorderecht: Kluwer Academic Publishers. (M)
77. Dubey P. (1975). On the Uniqueness of the Shapley Value // International Journal of Game Theory. 4. 131-139.
78. Dubey P. (1980). Asymptotic Semivalues and a Short Proof of Kannai’s Theorem // Mathematics of Operations Research. 5. 267-270.
79. Dubey P., Neyman A., Weber R. (1981). Value Theory without Efhcience // Mathematics of Operations Research. 6. 122-128.
80. D. Diamond, P. Dybvig (1983). Bank Runs, Deposit Insurance, and Liquidity // J. of Political Economy, 91, 401-419.
81. Edgeworth F. (1897). La Theoria pura del monopolio // Giornale degli Economisti. 13-31.
82. Fan Ky (1952). Fixed Point and Minimax Theorem in Locally Convex Topological Linear Spaces Proceedings of the National Academy of Sciences, 38, 121-126.
83. Fleurbaey F. (1995). The Requisites of Equal Opportunity, in Social Choice, Welfare, and Ethics / (W. Barnett, H. Moulin, M. Salles, and N. Schofield, eds). Cambridge University Press. 37-53.
84. Fleurbaey F., Maniquet F. (1994). Fair Allocation With Unequal Production Skills: the Solidarity Approach to Compensation. Universite de Cergy-Pontoise mimeo, December 1994.
85. Friedman E., Moulin H. (1995). Three Methods to Share Joint Costs (or Surplus). Mimeo. Duke University.
86. Friedman J.W. (1971). A Non-Cooperative Equilibrium for Supergames // Review of Economic Studies. 38. 1-12.
87. Friedman J.W. (1990). Game Theory wih Application to Economics. 2-nd ed. Oxford. Oxford University Press.
88. Fudenberg D., Kreps D. (1988). Learning, Experimentation, and Equilibrium in Games. Mimeo. Stanford University.
89. Fudenberg D., Kreps D. (1990). Lectures on Learning and Equilibrium in Strategic Form Games. Mimeo CORE Lectures Series.
90. Fudenberg D., Levine D.K. (1998). The Theory of Learning in Games, Cambridge, MA: The MIT Press (M).
91. Fudenberg D., Tirole J. (1991). Game Theory. Cambridge, Massachusetts: The MIT Press.
92. Fudenberg D., Tirole J. (1989) Noncooperative Game Theory for Industrial Organization: An Introduction and Overview. / In: Handbook of Industrial Organization / Ed. by R.Schmalensee and R.Willig. Elsevier Science Publishers, 1989.
93. Gevers L. (1986). Walrasian Social Choice: Some Simple Axiomatic Approaches / Social Choice and Public Decision Making: Essays in homor of K. Arrow / W.Keller et al eds. V. 1. Cambridge University Press.
94. Gibbons R. (1992). Game Theory for Applied Economists. Princeton, Princeton University Press.
95. Gillies D. (1959). Solution to General Non-Zero Sum Games // Annals of Mathematical Studies. 40. 47-85. Princeton University Press.
96. Glicksberg I. L. (1952). A Further Generalization of the Kakutani Fixed Point Theorem with Application of Nash Equilibrium points // Proceedings of the National Academy of Sciences, 38, 170-174.
97. Green J. (1983). A Theory of Bargaining with Monetary Transfers. HIER Discussion Paper, N 966.
98. Green J. (1991). Compensatory Transfers in Group Decision Problems. Working Paper. Dept, of Economics. Harvard University, March 1991.
99. Greenberg J. (1997). Situation Approach to Cooperation, In Cooperation: Game-Theoretic Approaches / (S.Hart, A.Mas-Colell eds.). NATO ASI Series. Series F: Computer and Systems Sciences. 155. 143-168. Springer.
100. Gul F. (1989). Bargaining Foundations of Shapley value // Econometrica. 57 81-95.
101. Hardin G. (1968). The theory of the Commons // Science, 162, 1243-1248.
102. Harsanyi J.C. (1963). A Simplified Bargaining Model for N-person cooperative Games // International Economic Review. 4. 194-220.
103. Harsanyi J.C. (1967). Games with Incomplete Information Played by Bayesian Players. Part I, II, III // Management Science, 14, 159-182, 320-334, 486-502.
104. Harsanyi J.C. (1973). Games with Randomly Distributed Payoffs: A New Rationale for Mixed Strategy Equilibrium Points. International Journal of Game Theory, 2, 1-23.
105.
106.
Hart S. (1985). An Axiomatization of Harsanyi’s Non-Transferable Utility Solution // Econometrica. 53. N 6. 1295-1314.
Hart S., Mas-Colell A. (1989). Potential, Value and Consistency // Econometrica. 57. 589-614.
107. Hart S., Mas-Colell A. (1995). Bargaining and Value. Hebrew University of Jerusalem. Discussion Paper. N 66, January 1995.
108. Herrero C., Maschler M., Villar A. (1995). Personal rights and collective ownership: the rights-egalitarian solution. University of Alicante, mimeo.
109. Ichiishi T. (1993). The Cooperative Nature of the Firm. Cambridge University Press. (M)
110. Kalai E. (1973). Excess Functions, Nucleolus, Kernel and e-Core of Non-Sidepayments Cooperative Games // Technical Report. N 12. Department of Statistics. Tel-Aviv University.
111. Kalai E. (1975). Excess Functions for Cooperative Games Without Sidepayments // SIAM J. Appl. Math. 29. N 1. 60-71.
112. Kalai E. (1977). Non-Symmetric Nash Solutions and Replication of Two-Person Bargaining // International Journal of Game Theory. 6. 129-133.
113. M. Keane (1969). Some Topics in N-Person Game Theory. Thesis, Northwestern University, Evanston, Illinois.
114. Keiding H. (1986). An Axiomatization of the Core of a Cooperative Game // Economics Tetters. 20. 111-115.
115. de Koster R., Peters H., Tijs S., Wakker P. (1983). Risk Sensitivity, Independence of Irrelevant Alternatives and Continuity of Bargaining Solutions // Mathematical Social Sciences. 4. 295-300.
116. Kohlberg E. (1971). Oh the Nucleolus of a Characteristic Function Game // SIAM Journal of Applied Mathematics. 20. N 1, 62-66.
117. Kolpin V. (1994). Coalitional Equitable Cost Sharing of Multi-Service Facilities. University of Oregon, mimeo, October 1994.
118. Kreps D. (1990). Game Theory and Economic Modelling. Oxford: Clarendon Press. (M)
119. Kreps D.M. (1990). A Course in Microeconomic Theory. Princeton: Princeton University Press. (У)
120. Kreps D.M., Wilson R.B. (1982). Sequential Equilibrim// Econometrica. 50. 863— 894.
121. Lensberg T. (1988). Stability and the Nash Solution // J. of Economic Theory. 45. 330-341.
122. S.C. Littlechild, G/ Owen (1973). A Simple Expression for the Shapley Value in a Special Case // Management Sci., 20. 370-372.
123. Mailath G.J. (1998). Do People Play Nash Equilibrium? Lessons From Evolutionary Game Theory // J. of Economic Titerature. XXXVI (September 1998). 1347-1374.
124. Maniquet F. (1996). Horizontal Equity and Stability When the Number of Agents is Variable in the Fair Division Problem // Economics Letters. 50. 85-90.
125. Maschler M. (1992). The Bargaining Set, Kernel, and Nucleolus // Chapter 18 in Handbook of Game Theory / R. Aurnann and S. Hart, eds. Elsevier.
126. Maschler M., Owen G. (1989). The Consistent Shapley Value for Hyperplane games // Int. J. of Game Theory. 18. 389-407.
127. Machsler M., Owen G. (1992). The consistent Shapley value for games without side-payments // Rational Interactions / R. Selten, ed. Springer-Verlag. 5-12.
128. Maschler M., Peleg B. (1966). A Characterization, Existence Proof and Dimension Bounds for the Kernel of a Game // Pacific J. of Mathematics. 18. 289-328.
129. Maschler M., Peleg B. (1967). The Structure of the Kernel of a Cooperative Game // SIAM Journal for Applied Mathematics. 15. 569-604.
130. Maschler M., Peleg B. , Shapley L. (1972). The Kernel and the Bargaining Set for Convex Games // Int. J. of Game Theory. 1. 73-93.
131. Maschler M., Peleg B. , Shapley L. (1979). Geometric Properties of the Kernel, Nucleolus and Related Solution Concepts // Mathematics of Operations Research. 4. 303-338.
132. Mas-Colell A. (1980). Efficiency and Decentralization in the Pure Theory of Public Goods // The Quarterly J. of Economics. XCIV. 4. 625-641.
133. Mas-Colell A. (1997). Bargaining Games, In Cooperation: Game-Theoretic Approaches” // S.Hart, A.Mas-Colell eds. / NATO ASI Series, Series F: Computer and Systems Sciences. 155. Springer. 69-90.
134. Mas-Colell A., Silvestre J. (1989). Cost Share Equilibria: A Lindahlian Approach //
J. of Economic Theory. 47. 239-256.
135. Mas-Colell A., Silvestre J. (1991). A Note on Cost-Share Equilibrium // J. of Economic Theory. 54. 204-214.
136. Mas-Colell A., Whinston M., Green J. (1995). Microeconomic Theory. Oxford University Press. (У)
137. Maynard Smith J. (1974). The Theory of Games and Evolution in Animal Conflicts // J. of Theoretical Biology. 47 209-221.
138. Maynard Smith J. (1982). Evolution and the Theory of Games. Cambridge, Cambridge University Press. (M)
139. Maynard Smith J., Price G.R. (1973). The Logic of Animal Conflict // Nature. 246. 15-18.
140. McKenzie L.W. (1954). On Equilibrium in Graham’s Model of World Trade and Other Competitive Systems // Econometrica. 22. N 1.
141. McLean R., Sharkey W. (1992). Alternative Methods for Cost Allocation in Stochastic Service Systems. Mimeo, Rutgers University.
142. McLean R.P., Postlewaite A. (1989). Excess Functions and Nucleolus Allocation of Pure Exchange Economies // Games and Economic Behavior. 1. 131-143.
143. Milgrom P., Roberts J. (1982). Limit Pricing and Entry under Incomplete Informa-ton // Econometrica. 50. 443-460.
144. Milgrom P., Roberts J. (1991). Adaptive and Sophisticated Learning in Normal Form Games // Games and Economic Behavior. 3 82-100.
145. Moulin H. (1983). The Strategy of Social Choice. Advanced Textbooks in Economics. N 18. Amsterdam: North-Holland. (У)
146. Moulin H. (1985). The separability axiom and equal sharing methods // J. of Economic Theory. 36. 120-148.
147. Moulin H. (1985a). Egalitarianism and utilitarianism in quasi-linear bargaining // Econometrica. 53. 49-67.
148. Moulin H. (1986). Game Theory for Social Sciences. NY University Press. (У)
149. Moulin H. (1987). A Core Selection for Pricing a single output monopoly // Rand J. of Economics. 18(3). 397-407.
150. Moulin H. (1995). On Additive Methods to Share Joint Costs // Jap. Economic Review. 46. 4. 303-332.
151. Moulin H. (1996). Incremental Cost Sharing: Characterization by Coalition Strategy-Proofness. Discussion Paper. Duke University. Dept, of Economics, March 1996.
152. Moulin H. (1995). Cooperative Microeconomics: a Game Theoretic Introduction. Princeton University Press and Prentice-Hall. (У)
153. Moulin H., Shenker S. (1994). Average cost pricing versus serial cost sharing: an axiomatic comparison // J. of Economic Theory. 64. 178-201.
154. Myerson R. (1981). Utilitarianism, Egalitarianism and the Timing Effect in Social Choice Problem // Econometrica. 49. N 2. 883-897.
155. Myerson R. (1991). Game Theory: Analysis of Conflict. Harvard University Press.
(У)
156. Nagahisa R. (1991). A Local Independence Condition for Characterization of Walras Allocation Rule // J. of Economic Theory. 54 106-123.
157. Nash J.F. (1950). The Bargaining Problem // Econometrica. 28. 155-162.
158. von Neumann J., Morgenstern 0. (1944). Theory of Games and Economic Behavior. Princeton University Press. (Русский перевод: Дж. фон Нейман, О. Моргенштерн (1970) Теория игр и экономическое поведение, М.: Наука). (М)
159. Neyman А. (1977). Continuous Values Are Diagonal // Mathematics of Operations Research. 2. 338-342.
160. Ordeshook P. (ed.) (1978). Game Theory and Political Theory. NY. (M)
161. Ordeshook P. (1986). Game Theory and Political Theory: An Introduction. Cambridge University Press.
162. Ordeshook P. (1992). A Political Theory Primer. NY-london: Routledge.
163. Osborne M., Rubinstein A. (1994). A Course in Game Theory. The MIT Press.
(У)
164. Owen G. (1972). Multilinear Extension of Games // Management Sciences. 18. 64-79.
165. Owen G. (1975). Multilinear Extensions and the Banzhaf value // Naval Research Logistics Quarterly. 22. N 4. 741-750.
166. Pechersky S. (1986). Positively Homogeneous Quasidifferentiable Functions and their Applications in Cooperative Game Theory // Math. Programming Study. 29. 135-144.
167. Pechersky S., Rubinov A. (1993). Solution Concept for Generalized Multi-Stage Games Without Side Payments // J. of Math. Economics. 25. 403-420.
168. Pechersky S., Sobolev A. (1995). Set-Valued Nonlinear Analogues of the Shapley Value // Int. J. of Game Theory. 24. 57-78.
169. Peleg B. (1985). An Axiomatization of the Core of Cooperative Games Without Side-Payments // J. of Math. Economics. 14. 203-214.
170. Peleg B. (1986). On the Reduced Game Property and its Converse // Int. J. of Game Theory. 15. 187-200.
171. Peleg B. (1992). Axiomatizations of the Core. // Chapter 13 in Handbook of Game Theory. R. Aurnann and S. Hart, eds. Elsevier. 398-412.
172. Peleg B., Tijs S. (1996). The Consistency Principle for Games in Strategic Form // Int. J. of Game Theory. 25. 13-34.
173. Peters H. (1985). A Note on Additive Utility and Bargaining // Economics Letters. 17. 219-222.
174. Peters H. (1986). Simultaneity of Issues and Additivity in Bargaining // Economet-rica. 54. N 1. 153-169.
175. M. Rabin (1988). Consistency and robustness Criteria in Game Theory. Mimeo. MIT
176. Rasmussen E. (1989). Games and Information: An Introduction to Game Theory. Oxford: Basil Blackwell. (У)
177. Rawls J. (1971). A Theory of Justice. Harvard University Press. (Русский перевод: Дж. Ролз (1995) Теория справедливости, Новосибирск: Изд-во НГУ). (М)
178. Reny Р. (1997). Two Lectures on Implementation Under Complete Information: Ganeral Results and the Core // In Cooperation: Game-Theoretic Approaches, (S.Hart, A.Mas-Colell eds.) NATO ASI Series, Series F: Computer and Systems Sciences. 155. Springer. 91-114.
179. Riker W. (1962). The Theory of Political Coalitions. New Haven. (M)
180. Riker W., Oredeshook P. (1973). Introduction to Positive Political Theory. New Jersey: Prentice-Hall.
181. Roemer J. (1986a). The Mismarriage of Bargaining Theory and Distributive Justice // Ethics. 97. 88-110.
182. Roemer J. (1986b). Equality of Resources Implies Equality of Welfare // Quarterly J. of Economics. 101. 751-784.
183. Rosenmueller J. (1977). Extreme Games and Their Solutions // Tecture Notes in Economics and Mathematical Systems. 145.
184. Rosenthal E.C. (1990). Monotonicity of the Core and Value in Dynamic Cooperative Games // Int. J. of Game Theory. 19. 35-57.
185. Roth A. (1979). Axiomatic Models of Bargaining // Tecture Notes in Economic and Mathemathc Systems. 170. Springer Verlag. (M)
186. Rubinstein A. (1982). Perfect Equilibrium in a Bargaining Model // Econometrica, 50, 97-109.
187. Rubinstein A. (1998). Modeling Bounded Rationality, Cambudge, MA: The MIT Press (M).
188. Ruiz L.M. , Valenciano F., Zurzuelo J.M. (1998). The Family of Least Square Values for Transferable Utility Games // Games and Economic Behaviour, 24, 109-130.
189. Scarf H. (1967). The Core of an N person game // Econometrica. 35. 50-69.
190. Selten R. (1965). Spieltheoretische Behandlung eines Oligopolmodells mit Nachge-tragheit // Zeitschrift fur die Gesamte Staatswissenschaft, 121, 301-324.
191. Selten R. (1975). Reexamination of the Perfectness Concept for Equilibrium Points in Extensive Games // Int. J. of Game Theory, 4, 25-55.
192. Sen A. (1970). Collective Choice and Social Welfare. San Francisco: Holden Day. (M)
Utilitarianism and Beyond. Cambridge Univer-
193. Sen A., Williams B. (eds.) (1982). sity Press.
194. Shapley L. (1953). A value for n-person games // in Contributions to the Theory of Games II / Annals of Math. Studies 28, ed. by H.W. Kuhn and A.W. Tucker. Princeton: Princeton University Press, 307-317.
195. Shapley L. (1967). On Balanced Sets and Cores // Naval Research Togistics Quarterly. 14. 453-460.
196.
Shapley L. (1969). Utility Comparision and the Theory of Games / Та Decision: Agregation et dinamique des orders da preference. Paris. 251-264.
197. Shapley L. (1971) Cores of Convex Games // Int. J. of Game Theory. 1. N 1. 11-26.
198. Shapley L. (1973). On Balanced Games without side payments // Mathematical Programming: Proc. Of Advances Seminar. Madison, 1972. 261-290.
199. Shapley L., Shubik M. (1969). On Market Games II J. Econ. Theory. 1. 9-25.
200. Sharkey W. (1982). Cooperative Games with Large Cores // Int. J. of Game Theory. 11. 175-182.
201. Shelling T.C. (1960). The Strategy of Conflict. Cambridge, Harvard University Press.
202. Shubik M. (1984). Game Theory in the Social Sciences. Princeton University Press. (M)
203. Simon H.A. (1955). A Behavoiral Model of Rational Choice, Quartely Journal of Economics, 69, 99-118.
204. Simon H.A. (1956). Rational Choice and the Structure of the Enviroument, Psychological Review, 63, 129-138.
205. Simon H.A. (1972). Theories of bounded Rationality // C.B.McGruire and R.Radner eds. Decision and Organization, Amsterdam: North-Holland, 161-176.
206. Simon H.A. (1973). From Substantive to Procedurial Rationality // S.J.Laties ed., Methods and Appraisal Economics, Cambridge University Press, 129-148.
207. Sonmez T. (1994). Consistency, Monotonicity and the Uniform Rule // Economics Letters. 46. 229-235.
208. Spence A.M. (1974). Market Signalling. Harvard University Press. (M)
209. Strafhn P., Heaney J. (1981). Game Theory and the Tennessee Valley Authority // Int. J. of Game Theory. 10. 35-43.
210. Tadenuma K., Thomson W. (1991). No-envy and Consistency in Economies with Indivisible Goods // Econometrica. 59. 1755-1767.
211. Tadenuma K., Thomson W. (1993). The Fair Allocation of an Indivisible Good when Monetary Compensations are Possible // Mathematical Social Sciences. 25. 117-132.
212. Tadenuma K., Thomson W. (1995). Refinements of the No-envy Solution in Economies With Indivisible Goods. 39. 189-206.
213. Tauman (1988). The Aumann-Shapley prices: a survey // in The Shapley value: Essays in Honor of Lloyd Shapley / A.E. Roth, ed. Cambridge University Press. 279-304.
214. Tirole J. (1988). The Theory of Industrial Organization. Cambridge: The MIT Press. (Имеется русский перевод: Ж.Тироль Рыночная власть: теория организации промышленности. СПб.: Экономическая школа, 2000). (У)
215. Thomson W. (1988). A study of choice correspondences in economies with a variable number of agents // J. of Economic Theory. 46. 247-259.
216. Thomson W. (1994). Consistent solutions to the problem of fair division when preferences are single-peaked // J. of Economic Theory. 63. 219-245.
217. Thomson W. (1995). The axiomatic analysis of bankruptcy and taxation problems. University of Rochester, Discussion Paper.
218. Thomson W., Lensberg T. (1992). The Theory of Bargaining with a Variable Number of Agents. Cambridge University Press. (M)
219. Van Deemen Ad.M.A. (1997). Coalition Formation and Social Choice. Dorderecht: Kluwer Academic Publishers. (M)
220. Van den Nouweland A., Peleg B., Tijs S. (1996). Axiomatization of the Walras Correspondence for Generalized Economies // J. of Economic Theory. 25. N 3. 355-372.
221. Van den Nouweland A., Tijs S., Wooders M. (1995). Axiomatizations of Tindhal and Ratio Equilibria in Public Good Economies. Mimeo, Department of Econometrics. Tilburg University.
222. Vasil’ev V.A., Weber S., Wiesmeth H. (1995). Core Equilibrium with Congested Public Goods // Economic Theory. 6. N 3. 373-387.
223. Vohra R. (1997). Coalitional Non-Cooperative Approaches to Cooperation // In Cooperation: Game-Theoretic Approaches / S.Hart, A.Mas-Colell eds. NATO ASI Series, Series F: Computer and Systems Sciences. 155. Springer. 127-142.
224. Weber R. (1988). Probabilistic Values for Games // The Shapley Value (Essays in Honor of Tloyd S.Shapley) / A.E.Roth (ed.). 101-119, Cambridge Univ. Press. Cambridge, U.K.
225. Weber S., Wiesmeth H. (1991). The Equivalence of Core and Cost Share Equilibria in an Economy with a Public Good // J. of Economic Theory. 54. 180-197.
226. Weibull J.W. (1995). Evolutionary Game Theory. Cambridge, The MIT Press. (У)
227. Yanovskaya E. (1997). Consistency Properties of the Nontransferable Cooperative Game Solution // Game Theoretical Applications to Economics and Operation Research / T.Parthasarathy at al. (eds). Kluwer Academic Publishers. 67-84.
228. Yanovskaya E. (1997a). Set-Valued Analogues of the Prenucleolus // Game Theory and Applications. 3 / L.Petrosjan, V.Mazalov eds. NY. Nova Science Publishers. 161-175.
229. Young P. (1986). Taxation and bankruptcy. University of Maryland, Mimeo, July 1986.
230. Young P. (1987). On dividing an amount according to individual claims or liabilities // Mathematics of Operations Research. 12. 398-414.
231. Young P. (1988) Distributive justice in taxation // J. of Economic Theory. 48. 321-335.
232. Young P. (1994). Equity: how groups divide goods and burdens among their members. Princeton University Press. (M)
233. Zadeh L. (1965). Fuzzy Sets // Information and Control. 8. 338-353.
253
¦'Далее мы будем ссылаться на эти книги без указания года издания.
В англоязычной литературе общепринятыми являются названия Industrial Organization или Industrial Economics. Соответствующие русские названия курсов — это уже упомянутая теория организации промышленности, структура отраслевых рынков, теория организации отраслевых рынков и другие. Здесь и далее мы будем в сносках указывать английские соответствия основным используемым понятиям.
(feasible outcomes)
Приложения кооперативных игр мы достаточно подробно рассмотрим в гл. 6.
-'шли расширенная форма — extensive form
normal form representation
В настоящей главе, в которой рассматриваются статические игры , то есть игры, в которых игроки ходят один раз, одновременно и независимо, стратегия игрока и его ход — это одно и то же. Принципиальная разница, как мы увидим ниже, возникает в динамическом случае.
Разумеется, в общем случае, мы не должны исключать случаи S ^ П Sі , соответствующие ’’играм с запрещенными ситуациями”. Однако мы здесь такие игры не рассматриваем.
common knowledge
mixed strategy
never а best response
razionalizable strategies
(correlated equilibrium)
Русский перевод статьи Гликсберга опубликован в сборнике ’’Бесконечные антагонистические игры (1963). Под ред. Н.Н.Воробьева. М.: Физматгиз. В русских переводах можно встретить две версии транскрипции Fan Ку: Фань Цзи (см., например, упомянутый выше сборник) и Ки Фань (см., например, Обей Ж.-П., Экланд И. Прикладной нелинейный анализ. М.: Мир, 1988).
Многозначное отображение F называется полунепрепрывным сверху (п.н.св.), если из хп —у х , Уп ? F{xn) , уп -Ч у следует у ? F(x) .
Вообще говоря, под исходом следует понимать полное описание ’’результата” игры: и выбранные стратегии и соответствующие выигрыши игроков и, возможно, какие-то другие атрибуты (например, объявление о том, что победил такой-то игрок X ). В данном случае мы имеем ввиду победившую альтернативу.
Мы всегда будем ограничиваться рассмотрением лишь условия I порядка (в тех случаях, когда это необходимо), считая, что они определяют решение (не упоминая условия II, поскольку в тех ситуациях, которые мы будем рассматривать, это действительно, будет иметь место).
Вообще говоря, этот процесс можно рассматривать и без чередования ходов, когда каждая фирма на следующем шаге выбирает объем выпуска, как лучший ответ на предыдущий выбор конкурента (см., например, Fudenberg, Levine (1998)).
Normal form trembling hand perfect Hash equilibrium.
Р.Зельтен - лауреат Нобелевской премии по экономике 1994 года.
perfect information
imperfect information,
incomplete information
complete information.
Джон Харшаньи (J.Harsanyi) — лауреат Нобелевской премии по экономике 1994г.
Мы придерживаемся здесь обозначений, использованных в учебнике Mas-Collel, Whinston, Green.
Русский перевод статьи Куна см. сборник ’’Позиционные игры” (1967). Под ред. Н. Н. Воробьева и И. Н. Врублевской. М.: Наука - Физматгиз.
backword induction
subgame
subgame perfect Nash equilibrium
п3аметим, что СПРН называется иногда также абсолютным равновесием (см., например, Петросян, Зенкевич, Семина (1998)).
Вообще говоря, триггерные стратегии допускают неоднократные переключения с одного хода на другой. Указанная стратегия называется иногда жесткой (или жестокой) стратегией (grim strategy)
Допустим теперь, что родитель и ребенок играют в другую игру. Пусть до
ходы /с и Ір — фиксированы экзогенно. Во-первых, ребенок решает сколько из дохода /с сохранить для будущего (А), потребляя остаток (/с — S) сегодня. Во-вторых, родитель наблюдает выбор ребенка S и выбирает награду В . Выигрыш ребенка — это сумма текущей и будущей полезности:
профсоюз устанавливает единую ставку заработной платы, гг, которую предлагает всем фирмам;
фирмы наблюдают (и принимают) w и затем одновременно выбирают уровень занятости, Li , для фирмы і;
Belief или system of beliefs
Separating — разделяющие, pooling — объединяющие
Bayesian Nash equilibrium
Harsanyi (1973)
Природа определяет, какими являются выигрыши: как в Игре 1, или как в Игре 2, причем обе игры равновероятны.
2. Игрок 1 (но не игрок 2) узнает, какую из двух игр выбрала Природа.
3. Игрок 1 выбирает Т или В ; игрок 2 одновременно выбирает L или R.
4. Игроки получают выигрыши, выбранные Природой.
Фдесь и далее под апостериорными представлениями понимаются представления, формируемые игроками, в отличие от априорных, связанных с ходами Природы и общеизвестных всем игрокам
Система представлений р выводится из а с помощью формулы Байеса, когда это возможно.
Подчеркнутая часть — это единственное отличие от Определния 4.1.5: для равновесия по Нэшу мы требуем последовательную рациональность только на равновесном пути, следовательно, слабое совершенное Байесово равновесие (ССБР) является равновесием по Нэшу, но не каждое равновесие по Нэшу является ССБР.
pooling
separating
В частности, д^Мі ^PlgpM1 l'Pl^ > 0 и Мф — Atf1 (р1^) < ?(Мф — ?)ф) .
least-cost separating price.
Для простоты будем считать, что имеет место строгое неравенство.
ным лучшим ответом на s_8- . Заметим, что строгое равновесие может быть только равновесием в чистых стратегиях, т.к. если смешанная стратегия является лучшим ответом, то таковой же является и любая чистая из носителя смешанной стратегии.
Равновесие по Нэшу называется строгим, если для каждого игрока г , 8{ является единствен
Mmputation
preimputation
the core
bargaining set
Consistency
Точка х называется крайней точкой некоторого множества X , если не существует таких различных х1, х" ? X , что х = (х1 + х")/2 .
 Экономика: Знания - Циклы - Макроэкономика
Экономика: Знания - Циклы - Макроэкономика
- Введение в экономику
- Виды экономик
- Экология в экономике
- Экономическая теория
- Экономическая география
- Экономические знания
- Экономика России
- Циклы в экономике
- Макроэкономика
- Макроэкономика в России