
|
Петросян - Теория Игр

Книга представляет собой краткое и сравнительно элементарное учебное пособие, пригодное как для первоначального, так и для углубленного изучения теории игр; в ней проводится исследование математических моделей принятия решений в условиях конфликта. Впервые в отечественной научной литературе дано систематическое изложение единой теории статических и динамических игр. Рассмотрены конечные и бесконечные антагонистические игры, многошаговые игры, бескоалиционные и кооперативные игры, дифференциальные игры. В каждой главе содержатся задачи разной сложности.
Книга предназначена для студентов и аспирантов университетов, экономических и технических учебных заведений, представляет интерес как для математиков, работающих в области теории игр, так и для специалистов в области экономики, теории управления и исследования операций.
ПРЕДИСЛОВИЕ
Математическая теория игр является составной частью исследования операций. Она находит широкое применение в различных областях человеческой деятельности, таких, как экономика и менеджмент, промышленность и сельское хозяйство, военное дело и строительство, торговля и транспорт, связь и т. д.
Несмотря на наличие богатой монографической и специальной литературы по теории игр, учебных пособий, посвященных этому разделу математики, сравнительно немного и в них рассматриваются в основном отдельные разделы теории игр. Настоящее учебное пособие восполняет этот пробел. В нем отражено большинство современных направлений теории игр. Пособие методически построено так, что понятие модели конфликта (игры) развивается от простой (матричные игры) до наиболее сложной (дифференциальные игры).
Большинство учебных программ вузов предполагает чтение отдельных разделов или специальных курсов по теории игр. Данное учебное пособие построено таким образом, чтобы каждая глава могла служить основой такого курса. Для предварительного ознакомления с теорией игр достаточно изучить материал гл. I. Типовой курс по теории игр может быть построен на основе гл. I, Ш и TV. Наиболее подробно изложена теория антагонистических игр (гл. I, II, IV, V). В курсах «Системный анализ» и «Модели принятия решений» целесообразно использовать гл. Ill и IV. Теория неантагонистических игр изложена в гл. Ill, IV, а теория динамических игр — в гл. IV, V. В пособии не отражены результаты теории дифференциальных игр многих лиц, поскольку этот класс игр еще недостаточно изучен. Однако имеющиеся в этом направлении работы широко представлены в списке литературы [38, 45, 51, 77, 87, 88]. При построении курса лекций по приложениям теории игр полезно также воспользоваться специальной литературой [5, 10, 12, 20, 27, 34, 52, 53].
Во всех главах содержатся многочисленные примеры, иллюстрирующие основные положения теории. Некоторые из них представляют самостоятельный интерес. В конце каждой главы приведены упражнения для индивидуальной работы, расположенные в порядке изложения материала и возрастания сложности. В ряде случаев они существенно дополняют содержание главы. Систематическое решение этих упражнений является важной формой изучения теории игр.
Для усвоения основных понятий и результатов, приведенных в учебном пособии, достаточно знания курса математики в объеме университетской программы. Наиболее сложной в математическом отношении является гл. II, которая предназначена для студентов математических специальностей. Материал, набранный петитом, при первоначальном изучении может быть опущен.
В списке рекомендованной литературы приведены основная (учебники и задачники), дополнительная (монографии и учебные пособия) и справочная (справочники, обзоры, сборники статей) литература. В список дополнительной литературы включены также статьи, которые цитируются в основном тексте книги. Вместе с тем библиография не претендует на полноту. Библиографические ссылки можно найти в справочной литературе.
Пособие может быть использовано как для первоначального, так и для углубленного изучения теории игр. Оно предназначено для студентов и аспирантов, специализирующихся в области прикладной математики, будет также полезно студентам экономических и технических специальностей, факультетов менеджмента, изучающим математические методы принятия решений в сложных системах. Книга заинтересует специалистов, занимающихся вопросами теории игр, исследования операций, теории управления, математической экономики, теории менеджмента и их приложениями.
Учебное пособие написано на основе курсов «Теория игр и исследование операций», «Системный анализ», «Математические модели принятия решений в экономике и управлении», а также ряда специальных курсов по разделам и приложениям теории игр, прочитанных Л. А. Петросяном и Н. А. Зенкевичем студентам старших курсов и аспирантам на факультете прикладной математики — процессов управления Санкт-Петербургского государственного университета. Параграфы 7, 9 гл. I, § 5, 10 гл. Ш, § 4 — 6, 8 и 9 гл. IV, § 2 — 6, 8 гл. V написаны совместно с Е. А. Семиной.
Авторы
ВВЕДЕНИЕ
В.1. В настоящем учебном пособии изложены основные понятия и результаты теории игр. Теория игр — это раздел математики, в котором исследуются математические модели принятия решений в условиях конфликта, т. е. в условиях столкновения сторон, каждая из которых стремится воздействовать на развитие конфликта в своих собственных интересах. Теорию математических моделей принятия оптимальных решений принято называть исследованием операций, поэтому теорию игр следует рассматривать как прикладную математическую теорию — составную часть исследования операций.
В.2. Задачи исследования операций можно классифицировать по уровню информации о ситуации, которой располагает субъект, принимающий решение. Наиболее простыми уровнями информации о ситуации являются детерминированный (когда условия, в которых принимаются решения, известны полностью) и стохастический (когда известно множество возможных вариантов условий и их вероятностное распределение). В этих случаях задача сводится к нахождению экстремума функции (или ее математического ожидания) при заданных ограничениях. Методы решения таких задач изучаются в курсах математического программирования или методов оптимизации.
Наконец, третий уровень — неопределенный, когда известно множество возможных вариантов, но без какой-либо информации об их вероятностях. Такой уровень информации о ситуации является наиболее сложным. Эта сложность оказывается принципиальной, так как могут быть не ясны сами принципы оптимального поведения. Следуя определению Н. Н. Воробьева, теория игр — это теория математических моделей принятия решений в условиях неопределенности, когда принимающий решение субъект («игрок») располагает информацией лишь о множестве возможных ситуаций, в одной из которых он в действительности находится, о множестве решений («стратегий»), которые он может принять, и о количественной мере того «выигрыша», который он мог бы получить, выбрав в данной ситуации данную стратегию.
Установление принципов оптимального поведения в условиях неопределенности, доказательство существования решений, удовлетворяющих этим принципам, указание алгоритмов нахождения решений, их реализация и составляют содержание теории игр.
В.З. Неопределенность, с которой мы встречаемся в теории игр, может иметь различное происхождение. Однако, как правило, она является следствием сознательной деятельности другого лица (лиц), отстаивающего свои интересы. В связи с этим под теорией игр часто понимают теорию математических моделей принятия оптимальных решений в условиях конфликта. Таким образом, моделями теории игр можно в принципе содержательно описывать весьма разнообразные явления: экономические, правовые и классовые конфликты, взаимодействие человека с природой, биологическую борьбу за существование и т. д. Все такие модели в теории игр принято называть играми.
Математическое описание игры сводится к перечислению всех действующих в ней игроков, указанию для каждого игрока всех его стратегий, а также численного выигрыша, который он получит после того, как игроки выберут свои стратегии. В результате игра становится формальным объектом, который поддается математическому анализу.
В.4. Игры можно классифицировать по различным признакам. Во-первых, бескоалиционные игры, в которых каждая коалиция (множество игроков, действующих совместно) состоит лишь из одного игрока. Так называемая кооперативная теория бескоалиционных игр допускает временные объединения игроков в коалиции в процессе игры с последующим разделением полученного выигрыша или принятие совместных решений. Во-вторых, коалиционные игры, в которых принимающие решение игроки согласно правилам игры объединены в фиксированные коалиции. Члены одной коалиции могут свободно обмениваться информацией и принимать полностью согласованные решения.
По выигрышу игры можно разделить на антагонистические и игры с ненулевой суммой.
По характеру получения информации — на игры в нормальной форме (игроки получают всю предназначенную им информацию до начала игры) и динамические игры (информация поступает игрокам в процессе развития игры).
По количеству стратегий — на конечные и бесконечные игры.
Начнем изучение теории с простейшей статической модели — матричной игры, в которой участвуют два игрока, множество стратегий каждого из игроков конечно, а выигрыш одного игрока равен проигрышу другого.
ГЛАВА I
МАТРИЧНЫЕ ИГРЫ
§ 1. ОПРЕДЕЛЕНИЕ АНТАГОНИСТИЧЕСКОЙ ИГРЫ В НОРМАЛЬНОЙ ФОРМЕ1.1. Определение. Система
Г=(Х, Y, К), (1.1)
где X и Y — непустые множества, и функция К:Хх Y-*Rl называется антагонистической игрой в нормальной форме.
Элементы хеХ и yeY называются стратегиями игроков
1 и 2 соответственно в игре Г, элементы декартового произведения XxY (т. е. пары стратегий (х, у), где хеХ и yeY— ситуациями, а функция К — функцией выигрыша игрока 1. Выигрыш игрока
2 в ситуации (х, у) полагается равным [—К(х, у)], поэтому функция К также называется функцией выигрыша самой игры Г, а игра Г — игрой с нулевой суммой. Таким образом, используя принятую терминологию, для задания игры Г необходимо определить множества стратегий X, Y игроков 2 и 2, а также функцию выигрыша К, заданную на множестве всех ситуаций XxY.
Игра Г интерпретируется следующим образом . Игроки одновременно и независимо выбирают стратегии хеХ, yeY. После этого игрок 1 получает выигрыш, равный К(х, у), а игрок 2 — (-Цх.у)).
Определение. Игра Y' = (X', Y', К') называется подыгрой игры. Г=(X, Y, К), если X’ с У, Г с У, а функция К':Х'х Y'-*Rl является сужением функции К на X' х Y'.
В данной главе будут рассматриваться главным образом антагонистические игры, в которых множества стратегий игроков конечны.
1.2. Определение. Антагонистические игры, в которых оба игрока имеют конечные множества стратегий, называются матричными.
Пусть игрок 1 в матричной игре (1.1) имеет всего т стратегий. Упорядочим множество X стратегий первого игрока, т. е. установим взаимно однозначное соответствие между множествами М={ 1, 2, ..., т} и X. Аналогично, если игрок 2 имеет и стратегий, то можно установить взаимно однозначное соответствие между множествами N={1, 2,..., п} и Y. Тогда игра Г полностью определяется заданием матрицы A = {fxLj}, где txij=K(xi, yj), (i,j)eMxN, (xh y)eXx Y, ieM,
jeN (отсюда и название игры — матричная). При этом игра Г реализуется следующим образом. Игрок 1 выбирает строку іеМ, а игрок 2 (одновременно с ним) — столбец jeN. После этого игрок 1 получает выигрыш ау, а второй — (—ау). Если выигрыш равен
отрицательному числу, то речь идет о фактическом проигрыше игрока.
Игру Г с матрицей выигрышей А обозначим и назовем (тхл)-игрой (по размерности матрицы А). Если из изложения понятно, об игре с какой матрицей идет речь, то ивдекс А будем опускать.
Нумерация стратегий в матричной игре может производиться различными способами, поэтому каждому отношению порядка, строго говоря, соответствует своя матрица. Таким образом, конечная антагонистическая игра может быть описана различными матрицами, отличающимися друг от друга лишь порядком строк и столбцов.
1.3. Пример 1. (Оборона города.) Этот пример известен в литературе под названием «игра полковника Блотто» [4]. Полковник Блот-то имеет т полков, а его противник — п полков. Противник защищает две позиции. Позиция будет занята полковником Блотто, если на ней наступающие полки окажутся в численном превосходстве. Противоборствующим сторонам требуется распределить полки между двумя позициями.
Определим выигрыш полковника Блотто (игрока 1) на каждой позиции. Если у него на позиции полков больше, чем у противника (игрока 2), то его выигрыш на этой позиции равен числу полков противника плюс один (занятие позиции равносильно захвату одного полка). Если у игрока 2 полков на позиции больше, чем у игрока 1, то игрок 1 теряет все свои полки на этой позиции и еще единицу (за потерю позиции). Если обе стороны имеют одинаковое число полков на позиции, то имеет место ничья и каждая из сторон ничего не получит. Общий выигрыш игрока 1 равен сумме выигрышей на обеих позициях.
Игра, очевидно, антагонистическая. Опишем стратегии игроков. Пусть, для определенности, т>п. Игрок 1 имеет следующие стратегии: х0 = (т, 0) — послать все полки на первую позицию, хі=(т— 1,
1) —(т— 1) полков послать на первую позицию, а один — на вторую, х2 = (т—2, 2),..., хт_х = (\, т—\), хт=(0, т). Противник (игрок
2) имеет такие стратегии: у0 = (п, 0), y1 = (n — 1, 1), ..., у„ = (0, и).
Пусть игрок 1 выбрал стратегию х0, а игрок 2 — стратегию у0. Вычислим выигрыш а00 игрока 1 в этой ситуации. Поскольку т>п, на первой позиции выигрывает игрок 1. Его выигрыш равен л + 1 (единица — за удержание позиции). На второй позиции — ничья. Поэтому а00 = л-|-1. Вычислим а01. Так как т>п— 1, то на первой
позиции выигрыш игрока 1 равен п — 1 +1 = п. На второй позиции выигрывает игрок 2. Поэтому проигрыш игрока 1 на этой позиции равен единице. Таким образом, а01=и —1. Рассуждая аналогично, получаем <x0j=n—j+1 — 1 =n—j, Далее, если т—\>п, то
аю=п+1 +1 =и + 2, а11 = п—\ + \=п, аи=п— j+1 — 1 — 1 =п—j— 1,
2<_/< л. В общем случае (для любых тип) элементы а,-у, і = 0, т,
j=0, п матрицы выигрышей вычисляются следующим образом:
| &ij=K(xit yj) |
|
| To | У i | Уг | Тз | |
| *0 | " 4 | 2 | 1 | 0“ |
| *i | 1 | 3 | 0 | -1 |
|
4 II | -2 | 2 | 2 | -2 |
| *3 | -1 | 0 | 3 | 1 |
| _ 0 | 1 | 2 | 4 _ |
принимает вид
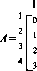
2 3 4
Пример 3. {Дискретная игра типа дуэли.) Игроки продвигаются навстречу друг другу на п шагов. После каждого сделанного шага игрок может выстрелить или нет, но во время игры он может выстрелить только один раз. Считается, что вероятность того, что игрок попадает в своего противника, если выстрелит, продвинувшись на k шагов, равна k/n (&<п).
Стратегия игрока 1{2) заключается в принятии решения стрелять на і-м (/-м) шаге. Пусть i<j и игрок 1 принимает решение стрелять на і-м шаге, а игрок 2 — на j-м шаге. Тогда выигрыш ау игрока
1 определяется формулой
Л _ А і _п(ні)+?
^ п) п п2
| I |
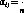 |
если положить л=5, то матрица этой игры, умноженная на 25, имеет вид
| 0 | -3 | -7 | -11 | -15 |
| 3 | 0 | ; | -2 | -5 |
| 7 | -1 | 0 | 7 | 5 |
| 11 | 2 | -7 | 0 | 15 |
| 15 | 5 | -5 | -15 | 0 |
Тогда задача выбора объекта нападения (для игрока 1) и объекта защиты (для игрока 2) сводится к матричной игре с матрицей выигрышей
|
И і_ | *1 | ...tj - |
| *2 | Plxl | ...т2 |
| ЪЯ | -РпЪш |
'“/?!-*і -ь -ь- ~Т1
-т2 afi2- z2 -z2... -z2
—- Zjt —Тд Тд... aP„ Тд
Пример б. (Поиск «шумного» объекта.) Предположим, что игрок 1 ведет поиск подвижного объекта (игрок 2) с целью его обнаружения. Игрок 2 преследует противоположную цель (т. е. стремится уклониться от обнаружения). Игрок 1 может двигаться со скоростями а, = 1, а,=2, а3 = 3, а игрок 2 — соответственно со скоростями /?і = Г, /?2 = 2, /?3 = 3. Дальность действия средства обнаружения игрока 1 в зависимости от скоростей движения участников игры приведена в матрице
Рі Рг Ръ
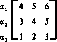
Z)=aJ 3 4 5
a, Ll 2 3.
Стратегиями игроков являются скорости движения, а в качестве выигрыша игрока 1 в ситуации (а,-, /9)) примем производительность поиска ау=аі8у, і= 1, 3, j—\, 3, где 5„ — элемент матрицы D. Тогда
задача выбора скоростей игроков при поиске — уклонении может быть представлена матричной игрой с матрицей
Pi Pi Рг
§ 2. МАКСИМИННЫЕ И МИНИМАКСНЫЕ СТРАТЕГИИ
2.1. Рассмотрим антагонистическую игру Г=(X, Y, К). Здесь каждый из игроков выбором стратегии стремится максимизировать свой выигрыш. Но для игрока 1 он определяется функцией К(х, у), а для второго — (—К(х, >»)), т. е. цели игроков прямо противоположны. При этом заметим, что выигрыш игрока 1(2) определен на ситуациях (х, у) eX Y, складывающихся в процессе игры. Но каждая ситуация, а следовательно, и выигрыш игрока зависят не только от его выбора, но и от того, какая стратегия будет выбрана противником. Поэтому, стремясь получить возможно больший выигрыш, каждый игрок должен учитывать поведение противника.
Поясним сказанное на примере игры «оборона города». Если игрок 1 хочет получить максимальный выигрыш, то он должен принять стратегию х0 (или хА ). В этом случае, если игрок 2 применит стратегию у0(у3), то первый получит выигрыш, равный 4 единицам. Но если игрок 2 применит стратегию уъ (соответственно _у0), то игрок 1 получит выигрыш, равный 0, т. е. потеряет 4 единицы. Аналогичные рассуждения можно провести и для игрока 2.
В теории игр предполагается, что оба игрока действуют разумно, т. е. стремятся к получению максимального выигрыша, считая, что соперник действует наилучшим (для себя) образом. Что может себе гарантировать игрок 11 Пусть игрок 1 выбрал стратегию х. Тогда в худшем случае он выиграет min К(х, у).
Поэтому игрок 1 всегда может гарантировать себе выигрыш max min К(х, у). Если отказаться от предположения достижимости
* У
экстремума, то игрок 1 может всегда получить выигрыш, сколь угодно близкий к величине
? — sup inf К(х, у), (2.1)
- хеХ yeY
которую будем называть нижним значением игры. Если же внешний экстремум в (2.1) достигается, то величина ? называется также максимином, принцип построения стратегии х, основанный на максимизации минимального выигрыша,— принципом максимина, а выбираемая в соответствии с этим принципом стратегия х — мак-симинной стратегией игрока 1.
Для игрока 2 можно провести аналогичные рассуждения. Пусть он выбрал стратегию у. Тогда в худшем случае он проиграет шах К(х, у). Поэтому второй игрок всегда может себе гарантиро-
X
вать проигрыш — min max К(х, у). Число У х
5= inf sup К(х, у) (2.2)
уеГ хеХ
называется верхним значением игры Г, а в случае достижения внешнего экстремума в (2.2) и минимаксом. При этом принцип построения стратегии у, основанный на минимизации максимальных потерь, называется принципом минимакса, а выбираемая в соответствии с этим принципом стратегия у — минимаксной стратегией игрока 2. Подчеркнем, что существование минимаксной (максимин-ной) стратегии определяется достижимостью внешнего экстремума в (2.2) ((2.1)).
Пусть задана матричная (/ихл)-игра Г^. Тогда экстремумы в (2.1) и (2.2) достигаются, а нижнее и верхнее значения игры соответственно равны
“ 1 <«7И 1
Минимакс и максимин для игры могут быть найдены по следующей схеме:
| max min ау=ю. і J ~ |
--v-тг—
min тахау=?
j ‘
Так, в игре с матрицей
1
5
_6
О 4 3 8 О 1_
нижнее значение (максимин) ? и максиминная стратегия /0 первого игрока равны ?=3, /0=2, а верхнее значение (минимакс) ? и минимаксная стратегия j0 второго игрока — v — 3,j0 — 2.
2.2. Для любой игры Т=(Х, Y, К) справедливо следующее утверждение.
Лемма. В антагонистической игре Г
?^? (2.5)
или
sup inf K(x, ^<inf sup K(x, y). (2.6)
xeX yeY yeY xeX
Доказательство. Пусть xeX— произвольная стратегия игрока 1. Тогда имеем
К(х, у) ^sup К(х, у).
хеХ
Отсюда получаем
inf К(х, у) ^inf sup К(х, у).
yeY yeY хеХ
Теперь заметим, что в правой части последнего неравенства стоит константа, а значение хеХ выбиралось произвольно. Поэтому выполняется неравенство
sup inf К(х, jXinf sup К(х, у).
хеХ yeY yeY хеХ
§ 3. СИТУАЦИИ РАВНОВЕСИЯ
3.1. Рассмотрим вопрос об оптимальном поведении игроков в антагонистической игре. Естественно считать оптимальной в игре Г= (X, Y, К) такую ситуацию (х*. у*) еХ- Y, от которой ни одному из игроков невыгодно отклоняться. Такая ситуация (х*, у*) называется равновесной, а принцип оптимальности, основанный на построении равновесной ситуации,— принципом равновесия. Для антагонистических игр, как это будет показано ниже, принцип равновесия эквивалентен принципам минимакса и максимина. Конечно, для этого необходимо существование равновесия (т. е. чтобы принцип оптимальности был реализуем).
Определение. В антагонистической игре Г=(Х, Y, К) ситуация {х*, у*) называется ситуацией равновесия или седловой точкой, если
К(х,у*НК(х*,у*); (3.1)
К(х*,у)^К(х*,у*) (3.2)
для всех хеХ и ye Y.
Множество всех ситуаций равновесия в игре Г обозначим через Z(H, г(Г)с=Х- Y.
Для матричной игры речь идет о седловых точках матрицы выигрышей А, т. е. таких точках (г*, /*), что для всех іеМ и jeN выполняются неравенства
а,/<af*>
В седловой точке элемент матрицы а,*}* является одновременно минимумом в своей строке и максимумом в своем столбце. Напри-
П О <Г|
ситуация (2.2) является равновес-
мер, в игре с матрицей 5 3 8
|_6 0 1
ной.
3.2. Множество ситуаций равновесия в антагонистической игре Г обладает свойствами, которые позволяют говорить об оптимальности ситуации равновесия и входящих в нее стратегий.
Теорема. Пусть (х?, _у*), (xf, УІ) — две произвольные ситуации равновесия в антагонистической игре Г. Тогда
1) ад. Я)=ад. А); ВД. УГ)=К(А, а);
2) (х*, y*)eZ(r), (х5, yf)eZ(r).
Подставим в левую часть неравенства (3.3) х|, в правую—yf, в левую часть неравенства (3.4) — х* и в правую у}. Тогда получим
К(х>>?)<K(xf, yt)^K(xf, yt)^K(xt, у$)<К(х%, >>?).
Откуда следует равенство
ад. я)=ад. у*)=к(х%, я)=ад, аі (з.5)
Покажем справедливость второго из утверждений. Рассмотрим ситуацию (х$, _уі). Тогда из (3.3) — (3.5) имеем
к(х, яхад. уг)=ад. уГ)=к(хі яхад. у) (з.б)
для всех хеХ, ye Y. Доказательство равновесности ситуации (х*. у*) проводится аналогично.
Из теоремы следует, что функция выигрыша принимает одно и то же значение во всех ситуациях равновесия. Поэтому разумно ввести следующее определение.
Определение. Пусть (х*. у*) — ситуация равновесия в игре Г. Тогда число
? = К(х*,у*) (3.7)
называется значением игры Г.
Из второго утверждения теоремы следует, в частности, такой факт. Обозначим А”* и У* проекции множества Z(T) на X и Y соответственно, т. е.
X• = {х*|х* еХ, Зу* g Y, (х*, у*) е Z(Г)},
У* = {>’*!>’* е Y, Зх* е X, (х*, у*) е Z(T)}.
Тогда множество Z(T) можно представить в виде
Z(T)=X* х Y*. (3.8)
Доказательство (3.8), как следствие второго утверждения теоремы, предоставим читателю.
Определение. Множество X*(Y*) называется множеством оптимальных стратегий игрока 1(2) в игре Г, а его элементы — оптимальными стратегиями игрока 1 (2).
Заметим, что равенство (3.S) указывает на взаимозаменяемость оптимальных стратегий, т. е. любая пара оптимальных стратегий образует ситуацию равновесия, а выигрыш в ней равен значению игры.
33. Оптимальность поведения игроков не изменится, если в игре множества стратегий остаются прежними, а функция выигрыша умножается на положительную константу (или к ней прибавляется постоянное число).
Лемма (о масштабе). Пусть Г=(Х, Y, К) и Y' = (X, Y, К1) две антагонистические игры, причем
К = рК+а, /?>0, ос=const, /?=const. (3.9)
Тогда
Z(T')=Z(Г), *r=R+«. (3.10)
Доказательство. Пусть (х*, у*) — ситуация равновесия в игре Г. Тогда имеем
К'(х*. у*)=рК(х*, у*)+а^рК(х*, у)+а=К'(х*, у),
К\х, у*)=рК(х, у*)+а^рК(х*, у*)+а=К’(х*, у*)
для всех хеХ и ye Y. Поэтому (х*, y*)eZ(Г*), Z(T)c=Z(r'). Обратно, пусть (х, y)eZ(Г'). Тогда
К(х,у)=(1/Р)К'(х,у)-а/р
и, рассуждая аналогично, получаем, что (х, y)eZ(T). Поэтому Z(T)=Z(T'), при этом выполняется равенство
?Г=К'(х*, у*)=рК(х*, у*) + а=р?г+а.
Содержательно данная лемма говорит о стратегической эквивалентности двух игр, отличающихся лишь началом отсчета выигрышей, а также масштабом их измерения.
3.4. Теперь установим связь между принципом равновесия и принципами минимакса и максимина в антагонистической игре.
Теорема. Для того чтобы в игре Г=(Х, Y, К) существовала ситуация равновесия, необходимо и достаточно, чтобы существовали минимакс и максимин
min sup К(х, у), max inf К(х, у) (3.11)
ух X у
и выполнялось равенство
v=max inf К(х, y)=min sup К(х, y)=v. (3.12)
“ X у ух
Доказательство. Необходимость. Пусть (х*, y*)eZ(T). Тогда для всех хеХ и у е Y выполняются неравенства
(3.13) отсюда
sup К(х, у*) < К(х*, у*). (3.14)
X
Вместе с тем имеем
(3.15)
(3.16)
(3.17)
inf sup К(х, у) < sup К(х, у*).
ух X
Сравнивая (3.14) и (3.15), получаем
inf sup К(х, y)<sup К(х, у*)^К(х*, у*).
Рассуждая аналогично, приходим к неравенствам
К(х*. y*)<inf К(х*, y)<sup inf К(х, у).
у X у
Таким образом,
inf sup К(х. у) ^ sup inf К(х, у).
У* х у
С другой стороны, всегда выполняется обратное неравенство (2.6). Итак, получаем
sup inf К(х, y)=inf sup К(х, у), (3.18)
х у ух
при этом неравенства (3.16), (3.17) выполняются как равенства inf sup К(х, у) = sup К(х, у*)=К(х*, у*),
ух X
sup inf К(х, y)=inf К(х*, у)=К(х*, у*),
X у У
т. е. внешние экстремумы у минимакса и максимина достигаются в точках у* и х* соответственно.
Достаточность. Пусть существуют минимакс и максимин
max inf К(х, y)=inf К(х*, у); (3.19)
min sup К(х, у) — sup К(х, у*) (3.20)
и выполняется равенство (3.12). Покажем, что ситуация (х*, у*) является равновесной. Действительно,
Щх*. у*)>М К(х*. у)—max inf К(х, у); (3.21)
К(х*, y*)<sup К(х, y*)=min sup К(х, у). (3.22)
х ух
Согласно равенству (3.12) минимакс равен максимину, а из (3.21), (3.22) следует, что он равен также и величине К(х*, у*), т. е. неравенства в (3.21), (3.22) выполняются как равенства. Теперь имеем
К(х*. j>*)=inf К(х*, у)^К(х*, у),
У
К(х*. y*)=sup К(х, у*)^К(х, у*)
X
для всех хеX и ye Y, т. е. (х*, y*)eZ(T)-
Заметим, что в ходе доказательства показано, что общее значение минимакса и максимина равно К(х*, у*)=? — значению игры, при этом любая минимаксная (максиминная) стратегия у*(х*) в условиях теоремы является оптимальной, т. е. ситуация (х*, у*) является равновесной.
Из доказательства теоремы получаем следующее утверждение.
Следствие 1. Если минимакс и максимин в (3.11) существуют и достигаются науих соответственно, то
max inf К(х, у)<К(х, y)<min sup К(х, у). (3.23)
х у ух
Игры, в которых существуют ситуации равновесия, называются вполне определенными. Поэтому данная теорема устанавливает критерий вполне определенной игры и может быть переформулирована следующим образом. Для того чтобы игра была вполне определена, необходимо и достаточно, чтобы существовали минимакс и максимин в (3.11) и выполнялось равенство (3.12).
Заметим, что в матричной игре Гд экстремумы в (3.11) всегда достигаются, поэтому теорема принимает следующий вид.
Следствие 2. Для того чтобы матричная (тх и)-игра была вполне определена, необходимо и достаточно выполнение равенства
min max atf= max min аи. (3.24)
l, 2..,, n i»l, 2..., m i»l, 2, m /-U 2, n
1 4 1
2 3 4 0-2 7
ситуация (2,1) является
Например, в игре с матрицей равновесной. При этом
max min ay=min max ау=2.
‘ j j I
не имеет ситуации равно-
С другой стороны, игра с матрицей весия, поскольку
min max а,?= 1 >max min ау=0.
J ‘ ‘ і
Заметим, что игры, сформулированные в примерах 1 — 3 (п. 1.3), не являются вполне определенными, а игра в примере 6 вполне определена и ее значение ? = 6.
§ 4. СМЕШАННОЕ РАСШИРЕНИЕ ИГРЫ
4.1. Рассмотрим матричную игру Г*. Если в ней существует ситуация равновесия, то минимакс равен максимину, причем согласно определению ситуации равновесия каждый из игроков может сообщить свою оптимальную (максиминную) стратегию противнику и от этого ни один из игроков не может получить дополнительную выгоду. Теперь предположим, что в игре Г* не существует ситуации равновесия. Тогда согласно теореме п. 3.4 и лемме п. 2.2 имеем
min max ау—max min ау>0. (4.1)
j ‘ ‘ J
В этом случае максиминная и минимаксная стратегии не являются оптимальными. Более того, игрокам бывает невыгодно их придерживаться, так как они могут получить больший выигрыш. Однако сообщение о выборе стратегии противнику может привести к еще большим потерям, чем в случае максиминной или минимаксной стратегии.
Действительно, пусть матрица А имеет вид
Для такой матрицы min max ay = 5, max min а,7=3, т. е. ситуации
J і i j
равновесия не существует. Обозначим через f максиминную стратегию игрока 1 {і* = 1), а минимаксную стратегию игрока 2 через j* (j* = 2). Пусть игрок 2 придерживается стратегии j* = 2, а игрок 1 выберет стратегию і—2. Тогда последний получит выигрыш 5, т. е. на 2 единицы больше, чем максимин. Однако если игрок 2 догадается о выборе игрока 1, то он изменит стратегию на j= 1, и тогда первый получит выигрыш лишь 2 единицы, т. е. на единицу меньше, чем в случае максимина. Аналогичные рассуждения можно провести и для второго игрока. По существу вопрос стоит о том, как разделить между игроками выигрыш (4.1)?
Оказывается, что в этом случае игрокам разумно действовать случайно, что обеспечивает наибольшую скрытность выбора стратегии. Результат выбора не может стать известным противнику, поскольку до реализации случайного механизма не известен самому игроку.
4.2. Определение. Случайная величина, значениями которой являются стратегии игрока, называется его смешанной стратегией.
Так, для матричной игры ГА смешанной стратегией игрока 1 является случайная величина, значениями которой являются номера строк іеМ, М={ 1, 2, ..., т) матрицы А. Аналогично определяется смешанная стратегия игрока 2, значениями которой являются номера jeN столбцов матрицы А.
Учитывая только что введенное определение смешанных стратегий, прежние стратегии будем называть «чистыми». Так как случайная величина характеризуется своим распределением, то будем отождествлять в дальнейшем смешанную стратегию с вероятностным распределением на множестве чистых стратегий. Таким образом, смешанная стратегия х игрока 1 в игре есть m-мерный вектор
т
х=(?? .... QeiT. ? {,= 1, i=l.....т. (4.2)
t-і
Аналогично, смешанная стратегия у игрока 2 есть л-мерный вектор
П
У=(*І1.....H.J. I (4.3)
j= 1
При этом 0 и — вероятности выбора чистых стратегий іеМ и JeN соответственно при использовании игроками смешанных стратегий хи у.
Обозначим через X и Y соответственно множества смешанных стратегий первого и второго игроков. Нетрудно заметить, что множество смешанных стратегий каждого игрока — компакт в соответствующем конечномерном евклидовом пространстве (замкнутое, ограниченное множество).
Определение. Пусть х=(?1, .... ?т)$Х—смешанная стратегия игрока 1. Тогда множество индексов
(4.4)
Мх={і\іеМ, {,>0},
где М={ 1, 2, ..., т}, назовем спектром стратегии х.
Аналогично для смешанной стратегии у= (г]и .... г}„) е Y игрока 2 спектр Ny определяется следующим образом:
Ny = {j\jeN,r,j>Q}, (4.5)
где N={ 1, 2, ..., л}. Спектр смешанной стратегии состоит из таких чистых стратегий, которые выбираются с положительными вероятностями.
Для любой смешанной стратегии х спектр МхФ0, поскольку вектор х имеет неотрицательные компоненты, сумма которых равна 1 [см. (4.2)].
Рассмотрим смешанную стратегию иі = (?1.....6, .... <^m)еX, где
6=1, ^=0,]фі, і=1, 2, ..., т. Такая стратегия предписывает выбор і-й строки матрицы А с вероятностью 1. Естественно отождествлять смешанную стратегию щеХ с выбором z-й строки, т. е. с чистой стратегией іеМ игрока 1. Аналогично отождествим смешанную
стратегию wJ=(rji, .... rjj.....rj„)eY, где fy=l, г\и = 0, іф], j=\, ..., л,
с чистой стратегией jeN игрока 2. Тем самым мы получили, что множество смешанных стратегий игрока есть расширение его пространства чистых стратегий.
Определение. Пара (х, у) смешанных стратегий игроков в матричной игре называется ситуацией в смешанных стратегиях.
Определим выигрыш игрока 1 в ситуации (х, у) в смешанных стратегиях для матричной (т х л)-игры как математическое ожидание его выигрыша при условии, что игроки используют смешанные стратегии соответственно х и у. Выбор стратегий игроками осуществляется независимо друг от друга, поэтому математическое ожидание выигрыша К(х, у) в ситуации (х, у) в смешанных стратегиях х=(^, .... ?m), y = (t]t, .... равно
т л
К(х, у)=? ? “</ & (хА)У=Х(АУ)- (4.6)
(-1 j-1
При этом функция К(х, у) является непрерывной по хеХ и ye Y. Заметим, что выигрыши К(і, у), К(х, j) при применении одним из игроков чистой стратегии (і или j соответственно), а другим — смешанной стратегии (у или х) имеют вид
Л
Щі, у)=К(ии у)= ? аиЪ=Ъу, і'=1, ..., т,
j-1
т
K(x,j)=K(x, Wj)=Y, cnj?i=xaJ,j=l, ..., л,
1-1
где а„ aJ — і-я строка и у-й столбец соответственно (т х ^-матрицы А.
Таким образом, от матричной игры ТА = (М, N, А) мы пришли к новой игре Гд = (У, У, К), где X и У — множества смешанных стратегий в игреТ^, а К — функция выигрыша в смешанных стратегиях. Игру ГА будем называть смешанным расширением игры Г^. Игра ГА является подыгрой для Г^, т. е. Г^сГ^.
4.3. Определение. Ситуация (х*, у*) в игре образует ситуацию равновесия, а число ? = К(х*, у*) является значением игры Г^, если для всех хеХи уе У
К(х,у*)^К(х*,у*)^К(х*,у). (4.7)
Из теоремы п. 3.2 следует, что стратегии (х*. у*), входящие в ситуацию равновесия, являются также оптимальными. Более того, согласно теореме п. 3.4 стратегии х* и у* являются соответственно максиминной и минимаксной, поскольку внешние экстремумы в (3.11) достигаются (функция К(х, у) непрерывна на компактных множествах У и У).
В п. 3.3 была показана стратегическая эквивалентность двух игр, отличающихся лишь началом отсчета выигрышей, а также масштабом их измерения (лемма о масштабе). Оказывается, что если две матричные игры и находятся в условиях этой леммы, то их
смешанные расширения стратегически эквивалентны. Формально этот факт устанавливается следующим утверждением.
Лемма. Пусть и Г/ — две матричные (т х п)-игры, причем А' = аА + В, а>0, a=const,
а В — матрица с одинаковыми элементами /?, т. е. ptJ= /? для всех г и j. Тогда Z(T A-)=*Z(T А), ?А=а?А + 0, где ТА и — смешанные расширения игр ТА-и соответственно, а ?А, ?А — значения игр ТА и ГА.
Доказательство. Обе матрицы А я А' размерности тхл, поэтому множества смешанных стратегий в играх Г А я ГА совпадают. Покажем, что для любой смешанной ситуации (х, у) выполняется равенство
К'{х,у) = аК(х, у)+Р, (4.8)
где К' я К — выигрыши игрока 1 в играх и соответственно.
Действительно, для всех хеХ я уе У имеем
К'(х, у)=хА’у=а(хАу)+хВу—аК(х, у)+/?.
Тогда из леммы о масштабе следует, что Z(rA ) = Z(rA), vA-=o(vA+fi.
Пример 7. Проверим, что стратегии у*=(.4г* V* ?Д **= —( І2> 1/4, LU) оптимальны, а ? = 0 — значение игры с матрицей
1
-1
_-1
-1 -1 -1 3
3 -1_
Упростим матрицу А (с целью получения максимального числа нулей). Прибавляя ко всем элементам матрицы А единицу, получим матрицу
2 О 0І 1'= 0 0 4 • _0 4 oJ
Каждый элемент матрицы А’ разделим на 2. Новая матрица принимает вид
100
А"=\ 002.
І_0 2 oJ
По лемме значение игр связано равенством «^*=1/2 vA‘ = vj2(yA + \).
Таким образом, требуется проверить, что значение игры Гл- равно 1/2. Действительно, К(х*. у*)=х* A"y* = iL. С другой стороны, для каждой стратегии yeY, y=(rjт\2, т]ъ) имеем К(х*, у) = = 1І2ТІ1 + 1І2ТІ2 + 'І2ТІЗ = 1І2 І = 1І2, а для всех х=(?1, %2, f3J, хеХ, К(х, у*) = т/2^і + T/2?2 + /2?з = /2- Следовательно, указанные стратегии х*, у* являются оптимальными, а »^=0.
В дальнейшем, говоря о матричной игре Г^будем предполагать, что речь идет о ее смешанном расширении Г^.
§ 5. НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ВЫПУКЛЫХ МНОЖЕСТВ И СИСТЕМ ЛИНЕЙНЫХ НЕРАВЕНСТВ
Этот параграф носит вспомогательный характер и при первом чтении может быть опущен. Однако для понимания доказательств последующих утверждений полезно напомнить широко распространенные понятия и результаты. Большинство из них будет приведено без доказательств, в необходимых случаях даны ссылки на специальную литературу.
5.1. Множество Мс/і* называется выпуклым, если вместе с любыми двумя точками этого множества xt, х2еМ в нем содержатся все точки отрезка
A*i+(1 — X)x2, 0<2<1. Понятие выпуклого множества можно сформулировать и в более общем, но эквивалентном виде.
Множество Мназывается выпуклым, если вместе с точками хі.... х* из М оно содержит и все точки вида
к к
*= ? *і>°> ? Л = Ь
і-1 і-1
называемые выпуклыми линейными комбинациями точек х2,х*.
Пересечение выпуклых множеств всегда выпукло.
Рассмотрим систему линейных неравенств
хА^Ь
ИЛИ
xa^Pj.jeN, ЛГ={1.....я}. С5-1)
где А=1J, jeN\—(тх л)-матрица, хе Л™, b = (f)i, .... Р„) еЛ". Обозначим ЛГ = {х|хЛ<6} множество решений системы (5.1). Непосредственно из определения следует, что X — выпуклое множество. Множество X называется выпуклым многогранным множеством, заданным системой ограничений (5.1).
5.2. Точка х 6 М, где М — выпуклое множество, называется крайней точкой, если из условия x=Ax!+(1—А)х2, хіеМ, х2еМиО<2<1 следует, что х, = х2=х. Содержательно определение означает, что хеМ — крайняя точка, если не существует отрезка, содержащего две точки из М, для которого х является внутренней.
Заметим, что крайняя точка выпуклого множества всегда является граничной, обратное неверно.
Пусть X — выпуклое многогранное множество, заданное системой ограничений (5.1). Тогда справедливы следующие утверждения.
Теорема. Множество X имеет крайние точки тогда и только тогда, когда rank A =\J, _/е .І?]=лі[16, с. 69].
Теорема. Для того чтобы точка хаеХ была крайней, необходимо и достаточно, чтобы она была решением системы
Последняя теорема дает алгоритм нахождения крайних точек множества X. Для этого необходимо рассмотреть столбцовые базисы матрицы А, решить систему линейных уравнений (5.2) и проверить выполнение неравенств (5.3). Однако такой способ понска крайних точек многогранного множества мало пригоден для практики, поскольку он связан с полным перебором всевозможных столбцовых базисов матрицы А.
5.3. Выпуклой оболочкой множества Р будем называть пересечение всех выпуклых множеств, содержащих Р, и обозначать conv (Р). Данное определение эквивалентно следующему. Выпуклая оболочка множества Р состоит из всех выпуклых линейных комбинаций всевозможных точек из Р, т. е.
Л Л
conv (Р)={х\х= ? A,Xj, ? 2 =1, 2,^0, х,еР}.
(-1 і-1
Выпуклая оболочка конечного числа точек называется выпуклым многогранником, порожденным этими точками. Выпуклый многогранник порожден своими крайними точками. Так, если рассмотреть множество X смешанных стратегий игрока
1 в (тлхл)-игре, то Х=сст?{и1,.... и„}, где и, = (0.....0, 1,0,...,0) — орты пространства
К” или чистые стратегии игрока 1. Множество X является выпуклым многогранником размерности (т— 1) и называется также (т-І)-мерным симплексом (или фундаментальным симплексом). При этом все векторы и,- (чистые стратегии) являются крайними точками многогранника X. Аналогичные утверждения справедливы для множества Y смешанных стратегий игрока 2.
Конусом С называется множество таких точек, что если хе С, А^О, то ХхеС. Содержательно конус С — это такое подмножество Л™, которое вместе с точкой х содержит и всю полупрямую (х), где
(х) ={у\у=Хх, 2»0}.
Конус С называется выпуклым конусом, если выполняется условие: для всех х, уе С справедливо х+уеС. Другими словами, конус С — выпуклый, если он замкнут относительно операции сложения. Можно дать и другое эквивалентное определение. Конус называется выпуклым, если он является выпуклым множеством. Сумма выпуклых конусов С1+С2 = (с\с = сі + с2, с1еСі, сеС2} и их пересечение Ctf]C2 также являются выпуклыми конусами.
Непосредственной проверкой определения можно показать, что множество С = {х| хЛ<0} решений однородной системы линейных неравенств, соответствующей (5.1),_является выпуклым конусом.
Пусть X — выпуклое многогранное множество, заданное системой ограничений (S.1), записанной в эквивалентной форме
т
Z ha^b, (5.4)
і-і
где х=({2, .... {„Jeff", а,-— і-я строка матрицы А, і= 1.....т. Предположим, что
rank А=г^т, и векторы а,,..., а, образуют строчечный базис матрицы А. Разложим остальные строки по базису
(5.5)
aJ**Y. Sijai.j^r+l.....т.
і-і
Подставляя (5.5) в (5.4), получим эквивалентную (5.4) систему неравенств
l(fi+ I «aW*-
1-1 \ 1-Г+І /
(5.6)
Обозначим через Х0 множество векторов х=(?,, .... і^)еК”, удовлетворяющих неравенствам (5.6) и условию (j=0,j=r+i, т. По теореме п. 52 множество Х0 имеет крайние точки. Справедлива следующая теорема {16, с. 70 — 74}. „
Теорема о представленіи многогранного множества. Пусть Xмногогранное множество, заданное системой ограничений (5.4). Тогда
Х=М+С,
Из теоремы, в частности, следует, что если множество X решений системы (5.4) ограничено, то X — выпуклый многогранник.
5.4 Напомним, что задача нахождения min сх при ограничениях
где А— (тх лJ-матрица, сеR™, xeRm, belt" называется прямой стандартной задачей линейного программирования, а задача, заключающаяся в определении max Ау при ограничениях
где уеК1 — двойственной задачей линейного программирования для (5.7).
Вектор хе К”, удовлетворяющий системе (5.7), называется допустимым решением задачи (5.7). Аналогично вводится понятие допустимого решения у eJc задачи (5.8). Допустимое решение х(у) называется оптимальным решением задачи (5.7) [(5.8)], если на нем достигается минимум (максимум) функции сх(Ьу) на множестве всех допустимых решений.
Справедливо следующее утверждение [16].
Теорема двойственности. Если обе задачу (5.7), (5.8) имеют допустимые решения, то они обе имеют оптимальные решения х, у соответственно, при этом
сх—Ьу.
5.5. В заключение параграфа приведем одно свойство выпуклых функций. Сначала напомним, что функция <р: где МаК” — выпуклое множество, называет
ся выпуклой, если
q>(Axj 4-(I-Х)х2) ^Xq>(xj + (\-k)<p(x2) (5.9)
для любых xlt x2eMи А,е[0,1]. Если же в (5.9) выполняется обратное неравенство, то функция q> называется вогнутой.
Пусть q>i(x) —выпуклые на М функции і = 1.....п. Тогда верхняя огибающая
ф(х) этого семейства функций
ф(х) = max <Рі(х) (5.Ю)
І-І, ..., (I
является выпуклой на М.
Действительно, по определению выпуклой функции для х2, х2еМ и ае[0, 1] имеем
<рі(сис1 + (1 - а)х2) < aq>i(x,J + (1 - Фі(х2) <
<а max q>i(xj +(1 — a) max <Рі(х2).
і і
Отсюда получаем
ф(qeXj 4*(1 <х)х2) =max «ptfax^fl-aJxtX
^аф(х1) + (1-а)ф(х2), что и требовалось доказать.
Аналогично можно показать вогнутость нижней огибающей (в (5.10) берется минимум по 0 семейства вогнутых функций.
§ 6. СУЩЕСТВОВАНИЕ РЕШЕНИЯ МАТРИЧНОЙ ИГРЫ В КЛАССЕ СМЕШАННЫХ СТРАТЕГИЙ
Докажем, что произвольная матричная игра вполне определена в классе смешанных стратегий.
6.1. Теорема. Всякая матричная игра имеет ситуацию равновесия в смешанных стратегиях.
Доказательство. Пусть ГА—произвольная (т хи)-игра со строго положительной матрицей А = {аи), т. е. ау>0 для всех і= 1, т
и 7=1, п. Покажем, что в этом случае теорема справедлива. Для этого рассмотрим вспомогательную задачу линейного программирования
(6.1)
шіпхи, xA^w, х>0 и двойственную ей задачу (п. 5.4)
maxyw, Ay^u, y^ 0, (6.2)
где u = ( 1, ... lje/f", w = (l, ..., 1)еЛ". Из строгой положительности матрицы А следует, что существует такой вектор х>0, для которого xA^w, т. е. задача (6.1) имеет допустимое решение. С другой стороны, вектор у = 0 является допустимым решением задачи (6.2) Поэтому по теореме двойственности линейного программирования (см. п. 5.4) обе задачи (6.1) и (6.2) имеют оптимальные решения х, у соответственно, при этом
xu=yw = 9> 0. (6.3)
Рассмотрим векторы х* = х/? и у*=у/? и покажем, что они являются оптимальными стратегиями игроков 1 и 2 соответственно в игре Г*, при этом значение игры равно 1/0.
Действительно, из (6.3) имеем
х*и=(хи)/?=(yw)/6=y*w = 1,
1 и 2 в игре ГА.
Вычислим выигрыш игрока 1 в ситуации (х*. у*):
С другой стороны, из допустимости векторов х и у для задач (6.1), (6.2) и равенства (6.3) имеем
Таким образом, хАу=?, из (6.4) получаем, что
Пусть хеХ и yeY—произвольные смешанные стратегии игроков 1 и 2. Тогда выполняются неравенства
а из допустимости хи у для задач (6.1), (6.2) следует, что х*—х/?^0 и у*=у/?^0, т. е. х* и у* — смешанные стратегии игроков
Сравнивая (6.6) — (6.8), получаем, что (х*. у*)—ситуация равновесия, а 1/0 — значение игры со строго положительной матрицей А.
Теперь рассмотрим (тхп)-игру с произвольной матрицей
A' = {aJj}. Тогда существует такая константа В> 0, что матрица А=А' + В — строго положительна, где В={/?,у} — (тхп) -матрица,
Вц=В. і= 1, tn,j= 1, п. В игре ГА существует ситуация равновесия (х*.
у*) в смешанных стратегиях, а значение игры равно ?^=1|/0, где 0 определяется как в (6.3).
Из леммы п. 4.3 следует, что (х*, y*)eZ(Г^) — ситуация равновесия в игре Гл- в сметанных стратегиях, а значение игры равно ?Л'=?л — Р=1/?—р. Теорема доказана.
Неформально факт существования решения в классе сметанных стратегий означает, что игроки всегда могут снять неопределенность выбора стратегии, с которой они столкнулись перед началом игры, рандомизируя множество чистых стратегий. Следует отметить, что не всегда в антагонистических играх существует решение в сметанных стратегиях. Примеры таких игр с бесконечным числом стратегий приведены в § 3, 4 гл. II.
Заметим также, что доказательство теоремы конструктивно, поскольку сводит решение матричной игры к задаче линейного программирования, при этом алгоритм решения игры Гл- следующий.
1. По матрице А' строится строго положительная матрица А = А' + В, где В={Ри}, Рц=Р> 0.
2. Решаются задачи линейного программирования (6.1), (6.2). Находятся векторы х, у и число ? [см. 6.3)].
3. Строятся оптимальные стратегии игроков 1 я 2 соответственно
х* = х/?, у*=у/?.
4. Вычисляется значение игры
?А=\ /?-р.
Пример 8. Рассмотрим матричную игру ГА, определенную матрицей
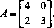
Соответствующие ей задачи линейного программирования имеют следующий вид:
min^ + ^2,
4?1+2?2>1,
?і?2^0»
тахт]1+ті2,
4»h<l,
2?/і+3?/2<1,
Заметим, что эти задачи в эквивалентной форме могут быть записаны для ограничений типа равенств:
тахт]1+гі2,
4f/i + f/3 = l,
min^ + ^2,
4{1 + 2*2-{э = 1,
2f/i + 3f/2 + f/4=l,
3{а-{4»1.
ІХ>0, {2>0, {3>0, u>0,
*h>0, Ц2>0, f/3^0,
*І4,> 0.
Таким образом, любой метод решения задач линейного программирования может быть приспособлен для решения матричных игр. Наиболее распространенным методом решения таких задач является симплекс-метод, систематическое изложение которого можно найти в [16, 25, 73].
6.2. Задача линейного программирования в определенном смысле эквивалентна матричной игре Г^. Действительно, рассмотрим следующие прямую и двойственную задачи линейного программирования
гшп хи
xA^w, (6.9)
х^О; maxyw
(6.10)
у>0.
Пусть Іи 7 — множества оптимальных решений задач (6.9) и (6.10) соответственно. _ Обозначим (ІІ?)Х={хІ?\хеХ}.
(\І?)Г={^І?\уеУ],?>0. 1
Теорема. Пусть — (тхп)-игра с положительной матрицей А (все элементы положительны) и даны две двойственные задачи линейного программирования (6.9) и (6.10). Тогда имеют место следующие утверждения.
1. Обе задачи линейного программирования имеют решение (ХФ0 и УФ0), при этом
0=min xu=max yw.
X у
2. Значение ?А игры Г* равно
®д = 1 І?’
а стратегии
х*=х/?, у*=у/?,
являются оптимальными, где хеХ — оптимальное решение прямой задачи (6.9), ayeY— двойственной задачи (6.10).
3. Любые оптимальные стратегии х*еХ* и у* eY* игроков могут быть построены указанным способом, т. е.
Х* = (1/?)Х, Y* = (l/e)Y.
Доказательство. Утверждения 1, 2 и включения (1/?)Х^Х*, 1/?УсУ* непосредственно следуют из доказательства теоремы п. 6.1.
Покажем обратное включение. Для этого рассмотрим векторы х* = (€і, и x=(git .... L), где х=?х*. Тогда для всех jeN
имеем
ха^вх*а^6(1/в)= 1,
при этом jc>0, так как 0>О и х*>0. Поэтому х — допустимое решение задачи (6.9).
Вычислим значение целевой функции
хи=?х*и = ?=т’т хи,
т. е. хеХ— оптимальное решение задачи (6.9). _
Аналогично доказывается включение У* с (1/0,) У. Теорема доказана.
§ 7. СВОЙСТВА ОПТИМАЛЬНЫХ СТРАТЕГИЙ И ЗНАЧЕНИЯ ИГРЫ
Рассмотрим свойства оптимальных стратегий, которые в ряде случаев помогают находить значение игры и ситуацию равновесия.
7.1. Пусть (х*, у*)еХх У— ситуация в смешанных стратегиях в игре Г^. Оказывается, что для проверки ситуации (х*, у*) на равновесность неравенства (4.7) достаточно проверять не для всех хеХ и уеУ, а лишь для іеМ и jeN, поскольку справедливо следующее утверждение.
Теорема. Для того чтобы ситуация (х*, у*) была равновесной в игре Гл, а число ? = К(х*, у*) —значением игры необходимо и достаточно выполнение следующих неравенств для всех іеМ и jeN:
Щ у*)^К(х\ y*)^K(x*,j), (7.1)
Доказательство. Необходимость. Пусть (х*. у*) — ситуация равновесия в игре Г*. Тогда
К(х, у*)^К(X*. у*)^К(х*, у)
для всех хеХ, уе У. Поэтому, в частности, для щеХ в WjeY имеем Щ, у*) = К(иь у*)^К(х\ у*)^К(X*. wji = K{x*,j) для всех іеМ в jeN.
Достаточность. Пусть (х*, у*) — пара смешанных стратегий, для которой выполняются неравенства (7.1). Пусть также х=(?1, ... ..., ?т)еХи у=(>11, .... (|„)еУ — произвольные смешанные стратегии игроков 1 и 2 соответственно. Умножая первое и второе неравенства
(7.1) на и t\j соответственно и суммируя, получаем
(7.2)
I T,jK(x\J)^K(x\ у*) X ц,=Я(х*, 7*). (7.3)
у-і
При этом имеем
(7.4)
(7.5)
5>,*(**,_/) = ?(**, у).
Подставляя (7.4), (7.5) в неравенства (7.2) и (7.3) соответственно и учитывая произвольность стратегий хеХa ye Y, получаем равновесность ситуации (х*. у*).
Следствие 1. Пусть (i*. j*) — ситуация равновесия в игре Гд. Тогда ситуация (/*, j*) равновесна и в игре Г*.
Пример 10. (Решение игры на уклонение.) Предполагается, что игроки выбирают целые числа і и j между 1 и и, а игрок 1 выигрывает величину dij=\i—j\, т. е. расстояние между числами і и j.
..., 0, 1/2). Тогда
К(х*. j)= 1/211 -j\ +1/21n-jI = 1/20-1) +1/2(n-D=(n-1)/2
Пусть первый игрок придерживается стратегии х* = (1/2, 0, ...
для всех 1 </^и.
а) Пусть n—2k+1 — нечетно. Тогда игрок 2 имеет чистую стратегию j* = (n+\)jl — k+1 такую, что
OLij* = I / — (и +1)/21 = I /—fc — 11 ^ (и —1)/2
для всех і=1, 2, ..., п.
б) Предположим, что п = 2к — четно. Тогда игрок 2 имеет такую стратегию у* = (0, 0, ..., 1/2, 1/2, 0, ..., 0), где rfk=l/2, nU\ = ll2> *Jj = 0, j?ik + j^k, что
Щ y*)=l/2\i-k\.+ l/2\i-k-l\^I/2к +1/2(к-1) = (и¦-1)/2 для всех 1^/^и.
Теперь, используя теорему, нетрудно убедиться, что значение игры ? = (п —1)/2, игрок 1 имеет оптимальную стратегию х*, а оптимальная стратегия игрока 2 равна j*, если п=2к+1, и у*, если п=2к.
7.2. Приведем результаты, являющиеся непосредственным следствием теоремы п. 7.1.
Теорема. Пусть ГА-(тхгі)-игра. Для того чтобы ситуация в смешанных стратегиях (х*. у*) была равновесной в игре ГД) необходимо и достаточно выполнение равенства
max К(і, у*) = min К(х*. j). (7.6)
Доказательство. Необходимость. Если (х*, у*) — ситуация равновесия, то согласно теореме п. 7.1 имеем
K(i,y*)^K(x*,y*HK(x*,j)
для всех і6 {1, ..., m},je{\, п}. Поэтому
К(і, у*НК(х*,Л
для каждого і и j. Предположим противное, т. е. (7.6) не выполнено. Тогда max К(і, у*) < min К(х*, j).
КМ 1</<л
Следовательно, имеют место неравенства
К(х*. у*)= ? ?К(І, у*)^ max К(і, у*)< min K(x*,j)^
/-1 1</<л
4,*J5:(jc*./)=A(x* у*).
J-1
Полученное противоречие и доказывает необходимость утверждения теоремы.
Достаточность. Пусть пара смешанных стратегий (х, у) такова, что max K(i, y)=min К(х, j). Покажем, что в этом случае
(.х, у) — ситуация равновесия в игре Г^.
Справедливы соотношения
min К(х, /К ? ijj К(х, J) = К(х, у)=
= ? ІК(і. Ж max К(і, у).
Поэтому имеем
K(i, y)^max K(i, у)=К(х, y)=min K(j, x)^K(x,j)
для всех 1 ^i^m и тогда по теореме п. 7.1 (х, у) — ситуация
равновесия в игре Г^.
7.3. Теорема. Для матричной игры справедливы следующие соотношения:
X j у І
причем экстремумы по смешанным стратегиям х иу в (7.7) достигаются на оптимальных стратегиях игроков.
Теорема является следствием теорем п. 3.4, 7.2, и ее доказательство предоставляем читателю.
7.4. Теорема. В матричной игре ГА множества оптимальных смешанных стратегий X* и Y* игроков являются выпуклыми многогранниками.
Доказательство. Согласно теореме п. 7.1 множество X* является множеством всех решений системы неравенств
xal'^vA,jeN, хи — 1, х^О,
где и=(1, ..., 1)е7?т, ?Л — значение игры. Таким образом, X* — выпуклое многогранное множество (п. 5.1). С другой стороны, Х*<=-Х, где X—выпуклый многогранник (п. 5.3). Поэтому X* — ограничено. Следовательно, по теореме п. 5.3 множество X* — выпуклый многогранник.
Аналогично доказывается, что Y* — выпуклый многогранник.
7.5. В качестве примера использования теоремы п. 7.3 приведем геометрическое решение игр с двумя стратегиями у одного из игроков ((2 х и)- и (т х 2)-игры). Такой подход в литературе также называется графоаналитическим методом решения игр. В основе графоаналитических методов лежит свойство оптимальных стратегий х* и у* доставлять внешние экстремумы в равенстве
«4=тах min K(x,j)=mm max К{і, у).
Пример 11. ((2хп)-игра). Рассмотрим игру, в которой игрок 1 имеет две стратегии, а игрок 2 — и стратегий. Матрица имеет вид
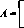
*11 *12 ¦" *1"
Пусть игрок 1 выбрал смешанную стратегию х=(<!;, 1 — 0» а игрок 2 чистую стратегию jeN. Тогда выигрыш игрока 1 в ситуации (х, j) равен
Геометрически он представляет собой прямую в координатах (0 К). Таким образом, каждой чистой сратегии j соответствует своя прямая. Графиком функции
Я(0=тіп K(x,j)
j
является нижняя огибающая семейства прямых (7.8). Эта функция вогнута как нижняя огибающая семейства вогнутых (в данном случае линейных) функций (п. 5.5). Точка ?*, в которой достигается максимум функции #(?) по ^ е [0, 1], и дает требуемое оптимальное решение =
| к | |
| 3\ | 4/ |
| г/ | |
| V | |
| 1 | |
| \ 3 | |
|
2 h |
//гм /і \ I ?ч I \\ ' 1 \ V |
| ] | 0"|* 1 \ К ^ 1 |
|
\? ІСЛ \—^ |
-В
Для определенности рассмотрим игру с матрицей
3 1 4"
2 14 0
Для каждого j= 1, 2, 3, 4 имеем: К(х, 1)= —? + 2, К(х, 2) = 2?+1, К(х, 3) = — 3?+4, К(х, 4)=4?. Нижняя огибающая Н(?) семейства прямых рис 1 {Щх, j)} и сами прямые К{х, j),
j= 1, 2, 3, 4, изображены на рис. 1. Максимум #(?*) функции Н(?) находится на пересечении первой и четвертой прямых. Таким образом, ?,* — решение уравнения
?л-
4€*=-{* + 2 = і;,
Откуда получаем оптимальную стратегию х* = (2/5, 3/5) игрока
1 и значение игры ?л — &/5. Оптимальную стратегию игрока 2 най
дем из следующих соображений. Заметим, что в рассматриваемом случае К(х*. 1) = ?(х*, 4)=?л = 8/5. , , , ,
Для оптимальной стратегии y* = (ri\, r{2, і/*3, rj,\) должно выполняться равенство
?А^К(х*. у*) = п\ К(х*, 1 ) + п2 К(х*, 2) + т& К(х*. 3) + ^ К(х*, 4).
При этом К(х*, 2)>8/5, К{х*, 3)>8/5, следовательно, rf2 = rj\ = 0, a rj j, т)\ можно найти из условия (7.1)
^ + 4^=8/5, 2f/l = 8/5.
Таким образом, = 4/5 и г\\= 1/5 и оптимальная стратегия игрока
2 равна /* = (4/5, 0, 0, 1/5).
Пример 12. ((т х 2)-игра.) В этом примере Две стратегии имеет игрок 2, а игрок 1 — т стратегий. Тогда матрица А имеет вид
| ’«и | «12 | |
| «21 | «22 | |
| А = | &т\ | ®т2 |
К(і, у) = апг] + an(l -rj) = (ос,, - аа)г] + аа.
График функции К(і, у) — прямая. Рассмотрим верхнюю огибающую этих прямых, т. е. функцию
Щч) =тах [(а,, - аа)ч + ас].
і
функция Н(ч) выпуклая (как верхняя огибающая семейства выпуклых функций).
Точка минимума ч* функции Н(ч) дает оптимальную стратегию у* = (ч*, l — rj*) и значение игры ?А=Н(ч*)~ тпіп Н(ч).
7.6. Приведем результат, полезный при отыскании решения игры.
Теорема. Пусть дг* = (<!;І,..., О иу* = 0/І,..., rfo — оптимальные стратегии в игре ГА и ?А — значение игры. Тогда для любого і, при котором К(і, у*)<?А, имеет место равенство ?*=0, а для любого j такого, что ?А<К(х*. j), имеет место равенство г\]=0.
Обратно, если ?¦ >0, то К(і, у*)=?Л, а если г\]>0, то K(x*,j)=vA.
Доказательство. Допустим, что для некоторого і0еМ выполнено К(і0, У*)<?л и при этом ?*о#0. Тогда получаем, что
К(і0,у*)?<?л?,
Для всех іеМ К(і, у*)^?А, поэтому
К(і,у*)?*ь?АС
Следовательно, К(х*. у*)<?А, что противоречит тому, что ?А — значение игры. Вторая часть теоремы доказывается аналогично.
Этот результат является аналогом теоремы о дополняющей нежесткости [73] или, как ее еще называют, канонической теоремой равновесия для задачи линейного программирования [25].
Определение. Чистая стратегия іеМ (jeN) игрока 1 (2) называется существенной или активной стратегией, если существует оптимальная стратегия х* = (^, ..., О (у* = (ч\, .... ч„)) этого игрока, для которой ?*>0 (ч]>0).
Из определения и последней теоремы следует, что для каждой существенной стратегии і игрока 1 и любой оптимальной стратегии У* е Y* игрока 2 в игре ГА выполняется равенство
К(і, у*)=ау*=?л.
Аналогичное равенство имеет место для любой существенной стратегии jeN игрока 2 и оптимальной стратегии х*еХ* игрока 1
K(x*. j) = aJ х* =?л.
Если для чистой стратегии іе Ми смешанной стратегии yeY выполняется равенство а{у=?л, то говорят, что стратегия і уравновешивает смешанную стратегию у в игре Г^.
Таким образом, в данной терминологии теорему можно переформулировать следующим образом. Если чистая стратегия игрока существенна, то она уравновешивает любую оптимальную стратегию противника.
Знание спектра оптимальной стратегии упрощает нахождение решения игры. Действительно, пусть Мх. — спектр оптимальной
стратегии х* игрока 1. Тогда каждая оптимальная стратегия y*=(Tj\, .... г\я) игрока 2 и значение игры ? удовлетворяют системе неравенств а<у*=„, іеМ*.
ау*^?, іеМ\М Ё Ъ = 1, qj^OJeN.
і-1
При этом в спектр любой оптимальной стратегии х* могут
входить лишь существенные стратегии.
7.7. В заключение параграфа приведем аналитическое решение игры «нападение — защита» (см. пример 4 п. 1.3)
Пример 13. Рассмотрим игру с (и х и) мат
эицей А
Т2 Рі
*1
Т,
Рп Ти_
Здесь Т/>0 — ценность, а 0 < Д,< 1—вероятность поражения объекта Ch /= 1, 2, ..., и, при условии, что он защищен. Пусть т1^т2<...^тя. Определим функцию <р от целых чисел 1, 2, ... ..., п следующим образом:
= Ы1-А)}-1. (7.9)
и пусть /е{1, 2, ..., и}—целое число, доставляющее максимум функции <p(k), т. е.
<?(/)= max <р(к). (7.10)
Jfc-1, 2, .... я
Установим свойства функции <p(k). Обозначим символом R один из знаков отношения порядка {>, =, <}. В этом случае 38
Заметим, что коэффициент в (7.13), стоящий после квадратных скобок, положительный. Поэтому из (7.13) получаем эквивалентность соотношений (7.11) и (7.12).
Теперь так как 1) или (р(Г)^<р(1+1) (в этом случае
т/_і ^ ^>(/— 1) или т,> (pit)), то из соотношений (7.10), (7.11) имеем
неравенство
T,_,<(j()(/)<T/. (7.14)
Найдем оптимальные стратегии в игре Г^. Напомним, что мы предполагаем выполненными неравенства т 1<т2<...<тя. Тогда оптимальными сметанными стратегиями х* = (?*і, .... Cm) и y* = (t]\> игроков 1 и 2 соответственно являются следующие:
Го, ;=і, .... /-1,
(p(k)R(p(k +1)
тогда и только тогда, когда
ткК(р(к), к= 1, 2, и-1, то = 0.
Действительно, из (7.9) получаем
т о-аг1 л ,,, ,, , 1Ч, (1-лг1
-----+ ф) = (р(к+1)+—-
(7.11)
(7.12)
I {Ф-РдУ1
і-к+l
I {ф-РдУ1
і-к+l
Тогда имеем
[т-‘Ь
(1 -Рк)~
(7.13)
+ (р(к)=(р(к+1).
I W1-A)}-1
і-к+ 1
(7.15)
(7.16)
[ф-Р))У\ і=і .... п;
.=|о,;=і...../-1,
Пі \[у-тНф-Р))), J=i. .... п.
а значение игры равно
?л = <р(1)-
Действительно, ?*>0, і= 1, 2,..., п и ? С = 1. Из определения q>(t)
I- 1
П
и (7.14) получаем, что 2, ..., п и ? ^*=1.
Пусть K(x*,j) — выигрыш игрока 1 в ситуации аналогич
но К(і, у*) — выигрыш в ситуации (г, у*).
Подставляя (7.15), (7.16) в функцию выигрыша и используя предположение о неубывании ценностей объектов, а также (7.14), получаем
I ?;=«>(/)+Г ? {т/1-/у}-‘]>Ф(0. 7= 1, /-1, і=/ L,=/ J
*(**.7)='
I 7=7 я;
/-/
А(/. ?*)=
/=1. /-1,
.*і-*і(1-0іК=9>(О, і=7 я-
Таким образом, для всех i,j= 1, я выполняются неравенства
Тогда по теореме п. 7.1 х* и у* — оптимальные стратегии игроков и vA = q>([) — значение игры. Игра решена.
§ 8. ДОМИНИРОВАНИЕ СТРАТЕГИЙ
Сложность решения матричной игры возрастает с увеличением размеров матрицы А. Вместе с тем в ряде случаев анализ матрицы выигрышей позволяет сделать вывод, что некоторые чистые стратегии не входят в спектр, оптимальной стратегии. Это приводит к замене первоначальной матрицы на матрицу выигрышей меньшей размерности.
8.1. Определение. Говорят, что стратегия х' игрока 1 доминирует стратегию х" в (тхп)-игре Г^, если для всех чистых стратегий je (\, ..., я} игрока 2 выполняются неравенства
х?>х?. (8.1)
Аналогично, стратегия у' игрока 2 доминирует его стратегию у", если для всех чистых стратегий іе{1, ..., т} игрока 1
ау'^ау". (8.2)
Если неравенства (8.1), (8.2) выполняются как строгие, то говорят о строгом доминировании. Частным случаем доминирования стратегий является их эквивалентность.
Определение. Будем называть стратегии х' и х" игрока 1 эквивалентными в игре Г^, если для всех je {1, ..., л}
х?=х?,
и обозначать х'~х".
Для двух эквивалентных стратегий У и х" выполняется (для каждого у е У) равенство
К(х', у) = К(х", у).
Аналогично, стратегии у' и у" игрока 2 эквивалентны (у1 ~у") в игре ГА, если для всех /е{1, т}
y'ai=y"aj.
Отсюда имеем, что для любой смешанной стратегии хеХ игрока 1 выполняется равенство
К{х, у') = К(х, у").
Для чистых стратегий введенные определения трансформируются следующим образом. Если чистая стратегия Г игрока 1 доминирует стратегию і", а чистая стратегия / игрока 2 — стратегию /' того же игрока, то для всех і=1, m;j= 1, и выполняются неравенства
OLtj>arj, aty ^aiij..
Это можно записать в векторной форме следующим образом:
af >?*,-• и d'^d".
Эквивалентность пар стратегий V, и означает
выполнение равенства а,- = а,- (с/ = cf).
Определение. Будем говорить, что стратегия х"(у") игрока 1 (2) доминируема, если существует стратегия х' Фх"(у' Фу") этого игрока, которая доминирует х"(у"). В противном случае стратегия х"(у") недоминируема.
Аналогично стратегия х" (соответственно у,г) игрока 1 (2) называется строго доминируемой, если существует стратегия х'(у') этого игрока, которая строго доминирует х"(у"), т. е. для всех
j= 1, п(і= 1, т) выполняются неравенства
x'd>x"ci, йіу'<йіу".
В противном случае говорят, что стратегия х"(у") игрока 1 (2) недоминируема строго.
8.2. Покажем, что игроки могут не использовать доминируемые стратегии. Этот факт устанавливает следующее утверждение.
Теорема. Если в игре стратегия х' одного из игроков доминирует оптимальную стратегию х*, то стратегия х' также оптимальна.
Доказательство. Пусть, для определенности, х' и х* — стратегии игрока 1. Тогда в силу доминирования для всех 7=1, п. Откуда в силу оптимальности стратегии х* (см. п. 7.3) получаем
?л=тіп x*aJ^min x'a^min x*aJ=vA
j j j
для всех j— 1, n. Поэтому согласно теореме п. 7.3 стратегия х' также оптимальна.
Итак, оптимальная стратегия может быть доминируема лигш. оптимальной стратегией. С другой стороны, никакая оптимальная стратегия не является строго доминируемой, поэтому игроки не должны использовать строго доминируемые стратегии.
Теорема. Если в игре Гл стратегия х* одного из игроков оптимальна, то х* — недоминируема строго.
Доказательство. Пусть, для определенности, х* — оптимальная стратегия игрока 1. Предположим, что х* — строго доминируема, т. е. существует такая стратегия х'еХ, что
x'aJ>x*aJ, У=1, 2, ..., п.
Откуда
min jcV>min x*aJ. j J
Но в силу оптимальности x*eX выполняется равенство
min x*aj=vA. Поэтому справедливо строгое неравенство j
max min xaJ> ?Л,
* j
что противоречит тому, что ?А — значение игры (п. 7.3). Полученное противоречие доказывает теорему.
Понятно, что обратное утверждение, вообще говоря, неверно. Так, в игре с матрицей
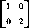
1-я и 2-я чистые стратегии игрока 1 недоминируемы строго, но они неоптимальны.
С другой стороны, интуитивно понятно, что если і-я строка матрицы А (j-й столбец) доминируема, то нет необходимости приписывать ей (ему) положительную вероятность. Таким образом, для нахождения оптимальных стратегий вместо игры достаточно решить подыгру Г?, где А' — матрица, получаемая из матрицы
А вычеркиванием доминируемых строк и столбцов.
Прежде чем перейти к точной формулировке и доказательству этого результата, введем понятие расширения смешанной стратегии х на і-м месте. Если x=(?lt .... t,m) еХ и 1< і^т + 1,_то расширением стратегии jc на і-м месте будем называть вектор Хі=(?? .... <*,_ь
О, 6, .... ?т) еі?т+|. Так, расширением вектора (1/3, 2/3, 1/3) на 2-м месте является вектор (1/3, 0, 2/3, 1/3); расширением на 4-м месте — вектор (1/3, 2/3, 1/3, 0); расширением на 1-м месте — вектор (0, 1/3, 2/3, 1/3).
8.3. Теорема. Пусть Гл — (т х п)-игра. Предположим, что і-я строка матрицы А доминируема (т. е. доминируема чистая стратегия і первого игрока) и пусть — игра с матрицей А', получаемой
из А вычеркиванием і-м строки. Тогда справедливы следующие утверждения.
1. ?Л = ?Л .
2. Всякая оптимальная стратегия у* игрока 2 в игре Г? является оптимальной и в игре Гл.
3. Если х* — произвольная оптимальная стратегия игрока 1 в игре ГА и X* —расширение стратегии х* на і-м месте, то
х* — оптимальная стратегия этого игрока в игре Гл.
4. Если і-я строка матрицы А строго доминируема, то произвольная оптимальная стратегия х* игрока 1 в игре Гл может быть получена из некоторой оптимальной стратегии х* в игре Г? расширением на і-м месте.
Доказательство. Не нарушая общности, можно предположить, что доминируемой является последняя т-я строка. Пусть х=(?1,.... ?т) — смешанная стратегия, которая доминирует строку т. Если <*т=0, то из условия доминирования для всех j— 1, 2, ..., и получаем
т т— 1
&ij ^ &mj»
(8.3)
ія—1
Ц 6=1, 6^0, і— 1, ..., т-1.
I-і
В противном случае (?m>0) рассмотрим вектор х'=(?,[, .... ?Д), где
(8.4)
W-U, іФт,
0, і=т.
Компоненты вектора неотрицательны (?/>0, і=1, ..., т) и ? 6=1-
Іш 1
С другой стороны, для всех7 = 1, п имеем
или
/я —1
1 т— 1 і т — 1
—г I tithiXbJT-r I &
1" Cm і«і l — Cm r-1
Учитывая (8.4), получаем
т—1 /я-І
(8.5)
і-1 т — \
і-і
Таким образом, всегда из доминирования т-й строки следует, что она не превосходит выпуклую линейную комбинацию остальных т— 1 строк [(8.5)].
Пусть (х*, y*)eZ(TA) — ситуация равновесия в игре Г^ , х*=(^],
С-і). У*=(ір. .... tl'n)- Для доказательства утверждений 1, 2, 3 теоремы достаточно показать, что К (х'т, у*)=?А^ и
(8.6)
для всех і=1, ..., т; j— 1, ..., п.
Первое равенство очевидно, а из оптимальности стратегий (х*. у*) в игре Г? следует выполнение неравенств
Из (8.7) очевидным образом следует правое из неравенств (8.6). Докажем левое неравенство. Для этого достаточно показать, что
Е ОтЛі^?Л'-
7-1
Из неравенств (8.3), (8.5) получаем
Е «mjfjj^E Ё <*vC nj< Ё ?*?і = ?Л'.
7-1 7-1 і— l i-l
что и доказывает первую часть теоремы.
Для доказательства второй части теоремы (утверждение 4) достаточно заметить, что в случае строгого доминирования т-й строки неравенства (8.3), (8.5) выполняются как строгие для всех j= 1, и. 44
Поэтому
Е “ч/ *lj < Ё Е “(/' < ®4-
У-1 У=1 i-1
Тогда из теоремы п. 7.6 получаем, что у любой оптимальной стратегии игрока 1 в игре т-я компонента равна нулю. Теорема доказана.
Сформулируем теорему о доминировании для второго игрока, доказательство которой опустим.
Теорема. Пусть — (тхп)-игра. Предположим, что j-й столбец матрицы А доминируем и пусть Г? игра с матрицей А',
получаемой из А вычеркиванием j-го столбца. Тогда справедливы следующие утверждения:
1. ?А—?Л'.
2. Всякая оптимальная стратегия х* игрока 1 в игре Гл> является оптимальной и в игре Г^.
3. Если_у* — произвольная оптимальная стратегия игрока 2 виг-ре Г^, и У] —расширение стратегии у* на j-м месте, то у) —
оптимальная стратегия игрока 2 в игре Г^.
4. Далее, если j-й столбец матрицы А строго доминируем, то произвольная оптимальная стратегия у* игрока 2 в игре ГА может быть получена из некоторой оптимальной стратегии у* в игре Га¦ расширением на j-м месте.
8.4. Обобщим полученные результаты. Подведем итоги. Теоремы п. 8.3 дают алгоритм понижения размерности матрицы игры. Так, если строка (столбец) матрицы не больше (не меньше) некоторой выпуклой линейной комбинации остальных строк (столбцов) этой матрицы, то для нахождения решения игры можно эту строку (столбец) вычеркнуть. При этом расширение оптимальных стратегий в игре с усеченнной матрицей даст оптимальное решение исходной игры. Если неравенства выполнялись как строгие, то множество оптимальных стратегий в первоначальной игре можно получить расширением множества оптимальных стратегий усеченной игры, в противном случае при такой процедуре оптимальные стратегии можно потерять. Поясним применение данных теорем на примере.
Пример 14. Рассматривается игра с матрицей
"2 1 1 О"
2 3 13 А= 3 12 0’
.0 3 0 6.
Так как 3-я строка а3 превосходит первую (a3^at), то, вычеркивая первую строку, получаем
Р 3 1 зі I 3 1 2 0 1. Lo 3 0 6J
В этой матрице 3-й столбец а3 не превосходит 1-й столбец а1. Поэтому получаем
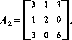
В последней матрице никакая строка (столбец) не доминируется другой строкой (столбцом). Вместе с тем 1-й столбец а1 превосходит выпуклую линейную комбинацию столбцов а2 и а3, так как а1^ 1/2а2 + 1/2а3, поскольку 3> 1/2+1/2-3, Ы1/2-2+1/2.0, 3=0-1/2+1/2.6. Исключая 1-й столбец, получаем
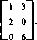
В этой матрице 1-я строка эквивалентна смешанной стратегии х=(0, 1/2, 1/2), поскольку 1 = 1/2-2+0-1/2, 3 = 0-1/2+6-1/2. Таким образом, исключая 1-ю строку, получаем матрицу
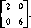
Оптимальные стратегии х* и у* игроков в игре с этой матрицей равны х*=у* = (Ъ/4; 1/4), при этом значение ? игры равно 3/2.
Последняя матрица получена вычеркиванием первых двух строк и столбцов, поэтому оптимальными стратегиями игроков в исходной игре являются расширения указанных стратегий на 1-м н 2-м местах, т. е. х!2=у^=(0, 0, 3/4, 1/4).
§ 9. ВПОЛНЕ СМЕШАННЫЕ И СИММЕТРИЧНЫЕ ИГРЫ
Знание спектра оптимальной стратегии упрощает нахождение решения игры. В спектр оптимальной стратегии могут входить лишь существенные чистые стратегии игрока. При этом никакая существенная стратегия не является строго доминируемой, что непосредственно следует из теорем § 8.
9.1. Рассмотрим класс игр, в котором знание спектра достаточно для нахождения решения игры.
Определение. Стратегия х (у) игрока 1(2) называется вполне смешанной, если ее спектр состоит из множества всех стратегий игрока, т. е. Mx = M(Ny=N).
Ситуация равновесия (х*, у*) называется вполне смешанной, если стратегии х* и у* — вполне смешанные. Игра называется вполне смешанной, если каждая ситуация равновесия в ней является вполне смешанной.
Следующая теорема утверждает, что вполне смешанная игра имеет единственное решение.
Теорема. Вполне смешанная (т х п)-игра имеет единственную ситуацию равновесия (х*, у*) и квадратную матрицу (т=п). Если ?ЛфО, то матрица А невырожденная и
| иА~1 | |
|
х*= ; иА~хи | (9.1) |
| _ A~lu | |
| У-иА->и' | (9.2) |
|
1 VA= ¦ uA и | (9.3) |
xaJ=?А, хи— 1, х>0,у = 1, ..., n; (9.4)
ydi=vA, yw=\, y>0, i=l, ..., m, (9.5)
где ы=( 1, ..., 1)е2Г, w=(l, ..., 1)еЛ".
Покажем, что решение вполне смешанной игры (х*, у*) единственно. Множества X*. Y*, заданные (9.4) и (9.5), являются непустыми выпуклыми многогранниками и, следовательно, имеют крайние точки. Согласно второй из теорем п. 5.2 имеем
/я<rang [а1, ..., (Г, u]=rang [Л, ы]</я, (9.6)
л<rang[а^ .... От, w] = rang[^, н>]<л. (9.7)
Теперь из этой же теоремы следует, что множества X*, Y* имеют по одной крайней точке и, следовательно, состоят только из них (как выпуклые многогранники, содержащие единственную крайнюю точку). Единственность решения (х*. у*) доказана.
Пусть ?л = 0. Тогда однородная система
xaJ=vA,j=TTn
имеет ненулевое решение, откуда rang (А)<т. Так как rang[A, иТ] = т, имеем: rang(4)=m — 1. Аналогично, из (9.5) и (9.7) следует, что rang (А)—и — 1. Отсюда п=т.
Пусть ?А^0. Тогда
rang(A)=rang[A, vAu] = ia.ng[A, и]=т,
rang (А)=rang [A, vAw]=rang[A, >?]=л.
Отсюда имеем n=m=tang(A), т. е. А — невырожденная матрица. Система уравнений х*А=?ли имеет решение
х*=?лиА~і.
Запишем решение системы Ау*—?ли:
у*=?лА~1и.
Так как х*и = 1 = ?.иА~1и, то ?А =—-—.
Л Л иА-'и
Теорема доказана.
Справедливо и обратное утверждение, доказательство которого предоставляем читателю.
Теорема. Пусть в (т х т)-игре матрица А является невырожденной. Тогда, если игрок 2 имеет в вполне смешанную оптимальную стратегию, то игрок 1 имеет единственную оптимальную стратегию х* (9.1). Если в игре вполне смешанную оптимальную стратегию имеет игрок 1, то игрок 2 имеет единственную оптимальную стратегию у* (9.2), при этом значение игры ?А равно
(9.3).
Пример 15. ((2 х 2)-игра.) Пусть дана (2 х 2)-игра с матрицей
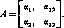
Произвольная смешанная стратегия х игрока 1 может быть записана в виде х=(?, 1—0, где 1. Аналогично, смешанная стратегия игрока 2 имеет вид у=(ц, l—ij), где 1. Выигрыш в ситу
ации (х, у) равен
Цх, y)=Z[anri + al2(\-ri)]+(\-Z)[a21ri + a22(\-*)].
Предположим теперь, что в игре ГА нет ситуации равновесия в чистых стратегиях (в противном случае решение просто найти из равенства минимаксов) и пусть х*=(0> 1 — 0). У* = (0> 1—0) — произвольные оптимальные стратегии соответственно первого и второго игроков. Ситуация (к*, у*) и игра являются вполне смешанными (О>0 и tj*> 0). Поэтому по теореме п. 9.1 в игре существует единственная пара оптимальных смешанных стратегий, которые являются решением системы уравнений
“иЧ*+0-О*12=®л-
“21^* +0 —rl*)a22 = vA’
ail^ + 0-^)a21 = v^
aiaf* + 0-«*)«22 = ^-
Если добиваться, чтобы ?АфО (например, если все элементы матрицы А положительны, то это неравенство выполняется), то решение игры
?А=——, х*=?лиА \ и,
і::] А,:
иА Іи
нет
Тогда
где м=(1, 1). Так, легко проверить, что у матрицы А
седловой точки. Обратная матрица А 1 равна А *,= 1/3, х* = (2/3, 1/3), у* = (1/3, 2/3).
9.2. Исследуем частный класс игр с матрицами специального вида.
Определение. Игра ГА с квадратной матрицей А называется симметричной, если матрица А — кососимметричная, т. е. если tXjj= — а,/і для всех і и j.
В этом случае все диагональные элементы матрицы А равны О, т. е. а„=0 при всех і. Для кососимметричной матрицы А всегда
выполняется условие Аг= — А. Поскольку матрица А квадратная, множества смешанных стратегий игроков совпадают, т. е. Х= Y.
Докажем теорему о свойствах решения симметричной игры ГА, которая полезна при отыскании ситуации равновесия.
Теорема. Пусть Г\, — симметричная игра. Тогда
?л
=0
и множества оптимальных стратегий игроков совпадают, т. е.
X* = Y*.
Доказательство. Пусть А — матрица игры и хеХ— произвольная стратегия. Тогда хАх=хАГх= —хАх. Поэтому хАх=0.
Пусть (х*, y*)eZ(A) — ситуация равновесия, а ?А — значение игры. Тогда
? А = х*Ау* < х*Ау, ?А=х*Ау* > хАу*
для всех хеХ, уе У. Следовательно,
*^,<х*^х* = 0, ?Л^у*Ау* = 0.
Откуда получаем *^ = 0.
Пусть стратегия х* оптимальна в игре Г., тогда (см. теорему п. 7.1)
х*А^0.
Однако отсюда следует, что х*(—Ат)^0, поэтому jc*^r<0. Таким образом, получаем
Значит, по той же теореме п. 7.1 х* — оптимальная стратегия игрока 2. Таким образом, доказано, что X*cY*. Обратное включение доказывается аналогично.
В дальнейшем на основании равенства X* = Y*, говоря об оптимальной стратегии игрока в симметричной игре, мы не будем указывать, о каком именно игроке идет речь.
Пример 16. Решим игру с матрицей
Го-' П А = \ 1 о -1 I
L-1 1 oJ
Пусть jc* = (^i, ?2, ?3) — оптимальная стратегия в игре Г^. Тогда должны выполняться неравенства
Г2-Гз>0,
-<Гі+<Гз>о,
Гі-Г2>0, (9.8)
Й+Й+Гз=1, Й>0, fi>0, Гз>0.
Покажем, что эта игра вполне сметанная. Действительно, пусть ?і = 0. Тогда из системы неравенств (9.8) получаем систему
Й-Гз>0,
Гз>0,
-Й>0,
Й+Й+Гз=1,
которая не имеет неотрицательного решения. Аналогичные рассуждения показывают невозможность случаев ?2 = 0 или ?3 = 0. Поэтому игра ГА — вполне смешанная. Следовательно, компоненты Й, ?2, й являются решением системы
Й-Й=о,
-Й+Й=о,
Й-Й=о,
Й + Й + Й=1,{«>0,/=1,2, 3.
Эта система имеет единственное решение. Оптимальной стратегией является вектор jc*=(1/3, 1/3, 1/3).
Пример 17. Решим дискретную игру типа дуэли с пяти шагов и одним выстрелом у каждого игрока, сформулированную в п. 1.4 (см. пример 3). Матрица А выигрышей игрока 1 является симметричной и имеет вид
| 0 | -3 | -7 | -11 | -15' |
| 3 | 0 | 1 | -2 | -5 |
| 7 | -1 | 0 | 7 | 5 |
| 11 | 2 | -7 | 0 | 15 |
| 15 | 5 | -5 | -15 | 0 |
го 1-2 -5“
-10 7 5
А'= 2-7 О 15
5 -5 -15 0
не все стратегии являются существенными.
Действительно, из симметричности игры Г? следует, что ?А=0.
Если бы все стратегии были существенными, то оптимальная стратегия х* была бы решением системы уравнений
x*aJ=0,j=2, 3, 4, 5,
І й-i,
1-2которая решения не имеет.
Перебирая варианты, остановимся на существенной подматрице А", составленной из строк и столбцов матрицы А с номерами 2, 3 и 5:
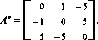
Игра с матрицей_/1" является вполне смешанной и имеет единственное решение у=х=(5/1 1, 5/11, 1/11).
Теперь в исходной игре рассмотрим стратегии **=>’* = (0, 5/11, 5/11, 0, 1/11), которые и являются оптимальными.
Таким образом, окончательно имеем: ?А = 0, ситуация равновесия (х*, у*) единственная. С точки зрения правил игры получаем, что дуэлянту не следует стрелять на 1-м шаге, он должен стрелять с равной вероятностью после 2-го и 3-го шагов, никогда после 4-го шага и лишь с малой вероятностью стрелять в упор.
§ 10. ИТЕРАТИВНЫЕ МЕТОДЫ РЕШЕНИЯ МАТРИЧНЫХ ИГР
Распространенный способ решения матричной игры путем сведения ее к задаче линейного программирования обладает тем недостатком, что процесс решения задачи линейного программирования существенно усложняется для матриц большой размерности. В таких случаях обычно используют методы декомпозиции задачи линейного программирования, когда вместо решения задачи с исходной матрицей строится координирующая задача с матрицей, у которой мало строк, но много столбцов. На каждой итерации координирующей задачи решается некоторая совокупность вспомогательных задач линейного программирования с матрицами меньших размерностей. К сожалению, декомпозиционные методы эффективны лишь для матриц специального вида (например, блочнодиагональных).
10.1. Итеративный метод Брауна — Робинсона (метод фиктивного разыгрывания). Идея метода — многократное фиктивное разыгрывание игры с заданной матрицей выигрыша. Одно повторение игры будем называть партией. Пусть разыгрывается игра с (тх л)-матрицей А = {а0}. В 1-й партии оба игрока выбирают совершенно
произвольные чистые стратегии. В к-й партии каждый игрок выбирает ту чистую стратегию, которая максимизирует его ожидаемый выигрыш против наблюдаемого эмпирического вероятностного распределения противника за (к— 1) партий.
Итак, предположим, что за первые к разыгрываний игрок 1 использовал і-ю стратегию раз (і=1, ..., т), а игрок 2—j-ю стратегию rft раз (/=1, ..., л). Тогда в (к+ 1)-й партии игрок 1 будет использовать г*+ Гю стратегию, а игрок 2 — свою у*+і-ю
стратегию, где
U*=max ? *і]ГІ}=Х
«*=min ? а.у#=? «у*+1 &
Пусть ? — значение матричной игры Г*. Рассмотрим отношения
vk/k=mm ? ctiJtflk = '? ctljk+, tf/k.
“ І i I
Векторы хк=(?кЦк, .... ?*/?) и yk=(riilk, .... rfjk) являются смешанными стратегиями игроков / и 2 соответственно, поэтому по определению значения игры имеем
Таким образом, получен некоторый итеративный процесс, позволяющий находить приближенное решение матричной игры, при этом степень близости приближения к истинному значению игры
определяется длиной интервала J^max v klk, minl3*/^J- Сходимость
алгоритма гарантируется теоремой [64].
Теорема.
lim
к-* со
= V.
(min ?к/к ] = lim [ max ?к/к к ) k—tx> V к ~ .
Пример 18. Найти приближенное решение игры с матрицей
а b с
2 1 3
3 0 1 1 2 1
Обозначим а, /?, у стратегии игрока 1 и а, Ъ, с — стратегии игрока 2. Пусть сначала игроки выбрали стратегии а и а соответственно. Если игрок 1 выбрал стратегию а, то игрок 2 может получить один из выигрышей (2, 1, 3). Если игрок 2 выбрал стратегию а, то игрок 1 может получить один из выигрышей (2, 3, 1). Во 2-й и 3-й партиях игрок 1 выбирает стратегию /?, а игрок 2 — Ъ, поскольку эти стратегии обеспечивают наилучший результат и т. д.
В табл. 10.1 приведены результаты разыгрываний, в этой таблице указаны стратегия игрока, накопленный выигрыш и средний выигрыш.
Таким образом, за 12 партий мы получили приближение решения х12 = (1/4,1/6, 7/12), у12 = (1/12,1/2, 5/12), а точность может быть оценена числом 1/2. Основным недостатком рассмотренного метода является его малая скорость сходимости, которая уменьшается с ростом размерности матрицы. Это_ является также следствием немонотонности последовательностей ?к/к и vkjk.
Рассмотрим другой итеративный алгоритм, который избавлен от указанного недостатка.
10.2. Монотонный итеративный алгоритм решения матричных игр.
Рассмотрим смешанное расширение ГА=(Х, Y, К) матричной игры с(шхи)-матрицей А.
Обозначим х?=(?і, .... ?%)еХ приближение оптимальной стратегии первого игрока на N-й итерации и с* eR", .....fJ-
всномогательный вектор. Алгоритм позволяет находить (точно и приближенно) оптимальную стратегию игрока 1 и значение игры ?.
В начале процесса игрок 1 выбирает произвольную чистую стратегию і0, т. е. х°=(0, 1, ..., 0) = м/() и вспомогательный вектор
вида с° = аіо, где а,о — строка матрицы А, имеющая номер і0.
Итеративный процесс строится следующим образом. Пусть выполнена І?— 1 итерация и получены векторы х**~ , cN_1. Тогда Xs и с* вычисляются но следующим итеративным формулам:
xw=(l-aJV)xw-1 + aJvxw; (10.1)
cN=(l—aN)cN~1 + aNcN, (10.2)
где параметр 0<aN<l. Векторы х'? и сі? будут получены ниже.
| Таблица 10.1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Рассмотрим вектор с* 1 = (уі \ .... і) и выберем такие индексы jk, на которых достигается минимум |
7-1, П
Обозначим через
А= min yf 1 (10.3)
” >*1, .. , п
и = .., Л} множество индексов, на которых (10.3) до
стигается.
Пусть Г^сГд — подыгра игры Гд с матрицей Ал = {а,^ '}, г = 1, т, а индекс/?_1 е/*-1. Решаем подыгру и находим оптимальную стратегию Xs еХ игрока 1. Пусть х*=(?і, ..., ?*).
т
Вычислим вектор сЛ= ? і*Оі. Пусть вектор cN имеет компоненты сІ?=(Уь ..., у%). Рассмотрим (2 х л)-игру с матрицей
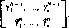
Найдем оптимальную стратегию (aN, 1 — aN), 0 < а,, < 1, игрока 1 в этой подыгре.
Подставляя найденные значения Xs, с**, а* в (10.1), (10.2), находим х* и с*. Процесс продолжаем до тех пор, пока не выполнится равенство aN=0 или не будет достигнута требуемая точность вычислений. Сходимость алгоритма гарантируется следующей теоремой [65].
Теорема. Пусть {i>N}, {х*} — итеративные последовательности, определяемые (10.1), (10.3). Тогда справедливы следующие утверждения.
1. vN>vN~1, т. е. последовательность {i>N_1} строго монотонно
возрастает. ~
2.
lim vN=v—v. (10.4)
N—co
3. lim x*=x*, где x*eX* — оптимальная стратегия игрока 1.
N-*co
Пример 19. Решим, используя монотонный алгоритм, игру с матрицей
2 1 3
А= з о 1 _1 2 1-
Итерация 0. Пусть игрок 1 выбрал 1-ю строку матрицы А, т. е. х° = (1, 0, 0) и c° = a1 = (2, 1, 3). Вычислим «°=min yj = y% = 1, 7° = {2}.
~ J
Итерация 1. Рассмотрим подыгру Г1 с:Г' с матрицей
V
А1 =
о
L2.
Оптимальной стратегией х1 игрока 1 является вектор х1 = (0, 0, 1).
[2 1 3~1 12 11
Заметим, что 3-й столОец матрицы доминируем, поэтому рас-
Г2 1_І
смотрим матрицу .
В силу симметрии оптимальной стратегией игрока 1 в этой игре является вектор (aN, 1 —<xN) = (lj2, 1/2)-
Вычисляем х1 и с1 по формулам (10.1), (10.2). Имеем
х1 = 1/2х°+1/2*1 = (1/2, 0, 1/2),
с1 = 1/2с°+1/2с1 = (3/2, 3/2, 2),
v1=min у/ = УІ = уі=3/2> ?° = 1.
Множество индексов имеет вид /1 = {1, 2}.
Итерация 2. Рассмотрим подыгру Г2 с: Г с матрицей
А2 =
Первая строка в этой матрице доминируема, поэтому достаточно рассмотреть подматрицу
Оптимальной стратегией игрока 1 в этой игре является вектор (V*. 3/Д поэтому х2 = (0, \U,
Вторая стратегия игрока 1 доминирует
Вычислим с = /4а2+ /4аз = (3/2, 3/2, 1) и рассмотрим (2x3)-Гз/2 з/2 Г
игру с матрицей
[_3/2 З/2 2_
первую, поэтому а2=0. Таким образом, вычисления закончены х* = х1 = (1/2, 0, */2), значение ? игры равно ?=?1 = Ъ/2, а оптимальная стратегия игрока 2 имеет вид у* = (1/2, 1/2, 0) (см. пример 18).
Упражненіи ¦ задачи
1. Каждый из двух игроков показывает другому т пальцев на руке (1 <т<5) и одновременно называет число пальцев, которое, по его мнению, может показать противник. Если один игрок угадывает правильно, а другой неправильно, то тот, который угадал, выигрывает сумму, равную числу пальцев, показанных обоими игроками. Во всех остальных случаях выигрыши обоих игроков считаются нулевыми.
а) Сколько стратегий имеет каждый игрок при л=3?
б) Построить матрицу игры для л=2.
2. Распределеше поисковых усилий. В одной из л ячеек игрок 2 прячет предмет.
Игрок I имеет в распоряжении г ищущих, которые должны быть распределены по ячейкам для поиска предмета. Например, в первую ячейку могут быть направлены (г— 1) ищущих, один - во вторую ячейку, а в остальные ячейки — ни одного и т. п.
Предполагается, что известна вероятность обнаружения предмета в і'-й ячейке (если он там находится) при поиске одним ищущим. Обнаружение предмета каждым из ищущих — независимые события.
Выигрыш игрока 1 — вероятность обнаружения предмета при заданном распределении ищущих.
а) Вычислить число т чистых стратегий игрока 1.
б) Построить матрицу игры.
3. Поиск многих предметов. Игрок 2 прячет т черных шаров в п урнах. Общее количество шаров (черных и белых), находящихся в j-й урне, равно Ip j= 1, ..., п. Игрок 2 должен распределить т черных шаров между л урнами, при этом общее количество шаров в каждой урве постоянно и равно Ір Ц>т.
Противник (игрок 1) старается обнаружить максимальное число черных шаров, имея возможность проверить одну из урн. При проверке і-й урны игрок 1 наугад (равновероятно) выбирает т шаров из и его выигрыш равен математическому ожиданию количества черных шаров в выборке из т шаров.
а) Пусть в і-й урне спрятаны Рі черных шаров. Вычислить вероятность Ру того,
что выбранная из і-й урны группа г шаров содержит ровно j черных.
б) Построить матрицу игры.
4 Противовоздушная оборони. В системе ПВО объекта могут применяться три типа средств поражения воздушной цели (1, 2, 3), которые должны быть распределены между двумя стартовыми установками. У противника (игрока 2) имеется два типа самолетов (тип 1 и тип 2). Вероятности поражения самолетов одним средством сведены' в матрицу
[! 2 0,3 0,5І
0,5 0,3 •
0,1 0,6J
Предполагается, что возможно нападение только одним из самолетов.
Выигрыш игрока 1 — вероятность поражения самолета системой ПВО. а) Построить матрицу игры.
б) Выяснить, имеется ли решение в чистых стратегиях.
5. Найти ситуации равновесия и значения следующих игр:
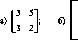 |
1/2 0 1/2 1 3/2 1/2 0 -1 7/4- |
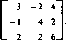
7. Пусть А'(А") — подматрица матрицы А, получающаяся вычеркиванием ряда строк (столбцов) А. Показать, что выполняются неравенства ?А'^?л^?А-, где ?А>,
?А- — значения игр Гд-, ГА- соответственно.
8. Рассматривается игра ГА> с матрицей
-1 3 2 О 2 1
3
3
О-
Значение игры ?л = \ я оптимальная стратегия игрока 1 есть х* —(1/3, 2/3, 0). Найти оптимальную стратегию у* игрока 2.
9. Решить графически игру с матрицей
"-4 0'
3 -2
5 -3 '
-1 -1
10. Показать, что строго доминируемая стратегия не может быть существенной!
11. Показать, что 3-я строка матрицы А доминируема, где
20 0 0 8 _ 4 5_
12. Показать, что выбор 1-го столбца эквивалентен смешанной стратегии у=(0, 1/3, 2/3), где матрица игры имеет вид
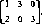
13. Используя понятие доминирования, найти решение игры с матрицей
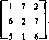
14. Доказать теорему п. 7.3.
15. Решить игру поиска с одной попыткой. Игрок 2 прячет предмет в одну из п ячеек. Игрок 1 ищет его в одной из этих ячеек, при этом вероятность обнаружения предмета в і-й ячейке равна 0(>О, і = 1, ..., п (при условии, что он там находится). Показать, что рассматриваемая игра вполне смешанная. Найти решение игры.
16. Решить игру дискретного поиска (пример 5, п. 1.3) в предположении а0,-Т|#О, і=1, ..., п.
Указание. Воспользоваться результатом п. 7.7.
17. Игра поиска двух предметов. Игрок 2 прячет два предмета в п ячейках (можно оба в одной ячейке). Цель игрока 1 — обнаружить хотя бы один предмет, при этом он имеет возможность проверить одну ячейку (fit> 0 — вероятность обнаружения одного предмета в і-й ячейке) (при условии, что он там находится). Если в і-й ячейке находятся одновременно два предмета, то вероятность их одновременного обнаружения равна fif. Таким образом, матрица А = {ог^,}, a-(i.J).i.j-1, ....«, имеет вид
ЧЬ»“ 0, i=j, іфк, *ka = Pt, І=к. ІФІ.
<*ka = PJ.j",k, i*j. «*o=A(2-W. i=j=k.
Решить игру.
18. Решить игру поиска многих предметов (см. упр. 3).
19. Игра поиска нескольких множеств на плоскости. Заданы набор п фиксированных компактных выпуклых множеств К?, К2, ..., f^aR1 и система т конгруэнтных между собой компактных выпуклых множеств 7\, .... Tm^R2. Дискретная одновременная игра поиска заключается в следующем. Игрок 2 прячет т множеств Т} (7=1,
в п множествах К-, (1=1,..., п) таким образом, что они пересекают Kj. Тот факт, что Рі множеств спрятаны в Kh означает, что совокупность множеств {7}} в количестве рі единиц бросается на плоскость случайно. Чистая стратегия а игрока 2 имеет вид
а=(Рі.р2.....Л,)еЛ", ? Рі=т'
і-і
где Рі — количество множеств Tj, спрятанных в множестве kt.
Игрок 1 может проверить одно из множеств Kh бросая случайно в Кі точку х. Выигрыш игрока 1 — математическое ожидание числа множеств {Tj, которым принадлежит х.
Найти решение игры.
20. Игра поиска с двумя попытками у ищущего. Игрок 2 прячет предмет в одной из п ячеек, а игрок 1 (ищущий) производит поиск в одной из этих ячеек, имея возможность просмотреть две ячейки (повторный просмотр ячейки не допускается).
Множество чистых стратегий игрока 1 состоит из несовпадающих пар (/, J), і= 1, ..., п, /=1, ..., л, и содержит С2 элементов. Множество чистых стратегий игрока 2 определяется индексом к, к= 1,..., л, и содержит л элементов. Матрица выигрышей имеет вид ?={/?(,-, Л *}, где
Р(.!¦№=
ок, если і=к или j=k,
0 — в противном случае.
Решить игру в предположении и \/о1 + \/о2>\/ап.
21. В игре поиска с двумя попытками у ищущего рассмотреть случай, когда множество чистых стратегий игрока 1 состоит из всевозможных пар (i, f) и содержит л2 элементов. Решить игру в предположении
л—1
Е anlak< 1-к-1
22. В игре на уклонение (и. 7.1) показать, что игрок 1 всегда имеет единственную оптимальную стратегию.
ГЛАВА II
БЕСКОНЕЧНЫЕ АНТАГОНИСТИЧЕСКИЕ ИГРЫ
§ 1. БЕСКОНЕЧНЫЕ ИГРЫ1.1. В этой главе рассматриваются антагонистические игры, которые отличаются от матричных тем, что в них один или оба игрока имеют бесконечное (счетное или континуум) множество стратегий. С теоретико-игровой точки зрения это отличие малосущественно, поскольку игра остается антагонистической и проблема состоит в использовании более сложного аналитического аппарата исследования.
Таким образом, будем исследовать общие антагонистические игры, т. е. системы вида
Г=(Х, Y, Н), (1.1)
где Іи У — произвольные бесконечные множества, элементы которых являются стратегиями игроков 1 и 2 соответственно, а Н: X х Y->Rl — функция выигрыша игрока 1. Напомним, что правила антагонистической игры изложены в п. 1.1 гл. 1. Выигрыш игрока 2 в ситуации (х, у) равен [—Н(х, у)], хеХ, уе У (игра антагонистическая). В этой главе будем рассматривать такие игры, у которых функция Н ограничена.
12. Пример 1. (Одновременная игра преследования на плоскости.) Пусть St и S2 — множества на плоскости. Игра Г заключается в следующем. Пусть 1 выбирает некоторую точку xeSu а игрок 2 — точку у 6 S2. При совершении выбора игроки 1 и 2 не имеют информации о действиях противника, поэтому подобный выбор удобно интерпретировать как одновременный. Точки хеSt, yeS2 являются в этом случае стратегиями игроков 2 и 2 соответственно. Таким образом, множества стратегий игроков совпадают с множествами St и S2 на плоскости.
Целью игрока 2 является минимизация расстояния между ним и вторым игроком (игрок 1 преследует противоположную цель). Поэтому под выигрышем Н(х, у) игрока 1 в этой игре будем понимать евклидово расстояние р(х. у) между точками xeSt и у 6 S2, т. е. Н(х, у)=р(х, у), xeSt,yeS2. Выигрыш игрока 2 полагаем равным выигрышу игрока 1, взятому с обратным знаком (игра антагонистическая).
Пример 2. (Поиск на отрезке.) Простейшей игрой поиска с бесконечным числом стратегий является следующая игра.
Игрок 2 (прячущийся) выбирает точку уе[0, 1], а игрок 1 (ищущий) выбирает одновременно и независимо точку Jte[0, 1]. Точка у считается «обнаруженной», если |jc—у|</, где 0</<1. В этом случае игрок 1 выигрывает величину -I-1, во всех остальных случаях его выигрыш полагается равным 0. Игра антагонистическая.
Таким образом, функция выигрыша имеет вид
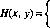 |
1, если |дг—>>| </, 0 — в противном случае. |
Пример 3. (Поиск на сфере.) Пусть в R3 задана сфера С радиуса R. Игрок 1 (ищущий) выбирает систему из точек xY, х2, .... х,е С, а игрок 2 — одну точку у е С. Выборы точек осуществляются игроками одновременно и независимо друг от друга. Игрок 2 считается обнаруженным, если точка у е С оказывается в r-окрестности одной из точек Xj, j= 1, .... s. Здесь под r-окрестностью точки Xj будем понимать сферический сегмент с вершиной в точке Xj и радиусом основания г (рис. 2). В дальнейшем r-окрестность точки Xj будем обозначать через S(xjt г).
Целью игрока 1 является обнаружение игрока 2. Игрок 2 преследует противоположную цель. В соответствии с этим положим выигрыш игрока 1 равным
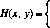 |
1, если уеМх, 0 — в противном случае, |
| S |
Пример 4. (Шумная дуэль.) Каждому из двух дуэлянтов разрешается выстрелить только один раз. Предполагается, что оба они имеют «шумные» пистолеты, так что каждый знает, когда выстрелил его противник. Предполагается также, что функция меткости Рі(х) (вероятность попадания при стрельбе в момент времени х) игрока 1 определена на [0, 1], непрерывна, монотонно возрастает по х и рх(0) = 0, Рі(1)= 1. Аналогично, точность выстрела игрока 2 описывается функцией р2(у) на [0, 1], где р2(0) = 0, р2(\)—\. Если игрок
1 поражает игрока 2, то первый получает выигрыш +1; если игрок
2 поражает игрока 1, то игрок 1 получает —1, если оба игрока стреляют одновременно и с одинаковым результатом (успешным или нет), то выигрыш игрока 1 равен 0.
Структура информации в этой игре (тот факт, что оружие шумное) принимается во внимание при составлении функции выигрыша Н(х, у). Если х<у, то вероятность того, что игрок 1 поразит противника, равна р^х) и выигрыш игрока 1 равен 1 ¦ р2(х); вероятность того, что игрок 1 промахнется, равна \—р2(х). Если игрок
бі
2 еще не стрелял и знает, что игрок 1 больше не может выстрелить, то игрок 2 будет увеличивать свои шансы на успех, ожидая, пока у не станет равным 1. Таким образом, если игрок 1 промахнется в момент х, то он наверняка будет поражен игроком 2, если х<у, следовательно,
Щх, jO=Pi(x) + (-1)[1-Pi(*)]» х<у.
Аналогично имеем
Щх, у)=р2(у) (—1) + [1 —р2(у)] • 1) *>У
Щх, У)=Рі(х)[\-рг(у)\+рг(у)[\ —.Pi(*)](—1), Х = у. Таким образом, функция выигрыша Щх, у) в игре равна
I 2рі(х)-1, х<у,
Щх, У)=ір1(х)-р2(у), х=у,
Ll-2p2(y), лоу,
где хе[0, 1], уе[0, 1].
Пример 5. (Бесшумная дуэль.) Снова каждому из дуэлянтов разрешается выстрелить только один раз, но в этом случае ни один из дуэлянтов не может определить, выстрелил его противник или нет.
Предположим для простоты, что функции меткости заданы следующим образом: р1(х)=р2(х) = х. Тогда функция выигрыша, описывающая игру, имеет вид
{jc— (1 —х)у, если х<у,
О, если х=у,
—у+(1 — у)х, если х>у,
где хе[0, 1], уе[0, 1]. Построение функции выигрыша Щх, у) в этой игре производится так же, как и в примере 4, за исключением того, что в данном случае ни один из игроков не может определить момента выстрела противника, если только этот выстрел не оказался успешным.
Пример 6. (Поиск «шумного» объекта.) Рассматривается задача поиска «шумного» объекта (игрок 2) подвижным средством обнаружения (игрок 1). Дальность действия 1(х, у) средства обнаружения в зависимости от скоростей хе[х0, xj и уе[у0, у(\ игроков 1 и 2 соответственно имеет вид
(*!-*)
где 1(у) = 10 + Р(У-Уо)’ Р = (Іі~1о)І(Уі-Уо)’ Іі = КУі)> 10 = 1(Уо)- Положительные числа х0 <х1( у0 <у1( /0 < Іі считаются заданными. Таким образом,
Цо(Уі-у)+Іі(у-Уо))
(Уі~Уо)
(xt-x)
К*, у)
(xt-x0)
В качестве функции выигрыша Н(х, у) игрока 1 понимается производительность поиска, т. е. просмотренная площадь в единицу времени Н(х, у)=2х- 1(х, у). Выигрыш игрока 2 полагаем равным [—Н(х, у)]. Таким образом, получаем игру с функцией выигрыша
Н(х, у)=2х
і0(Уі-У)+іі(У-Уо) (Xj-x) (Уі~Уо) (*і-*о)’
гдехе[х0, xj, у Фо> УН-
13. В заключение отметим специальный класс антагонистических игр, в которых X=Y=[0, 1]. В этих играх ситуации суть пары чисел {х, у), где х, уе[0, 1]. Эти пары задают точки единичного квадрата. Поэтому такие игры называются играми на единичном квадрате. Класс игр на единичном квадрате во многом характеризует бесконечные антагонистические игры и поэтому является базовым при исследовании бесконечных игр. В частности, примеры 2, 4, 5 — примеры игр на единичном квадрате. Пример 6 также игра на единичном квадрате, если положить х0=у0 = 0, х1=у1 = 1.
§ 2. СИТУАЦИЯ 6-РАВНОВЕСИЯ, Б-СЕДЛОВЫЕ ТОЧКИ И в-ОПТИМАЛЬНЫЕ СТРАТЕГИИ
2.1. Как и во всякой антагонистической игре Г = (Х, Y, Н), в бесконечной игре принципом оптимального поведения игроков является принцип равновесия. Оптимальной (равновесной) является такая ситуация (х*. у*), для которой выполняются неравенства
Щх, у*)^Н(х*, у*)^Н(х*, у) (2.1)
при всех хеХ, yeY. Этот принцип реализуется в игре Г в том и только в том случае, когда
? = ? = ?9
v=max inf Н(х, у), (2.2)
~ х У
v=min sup Н(х, у),
У X
т. е. внешние экстремумы максимина и минимакса достигаются
63
и нижнее значение игры ? равно верхнему значению ?. Такая антагонистическая игра Г называется вполне определенной, а число ? — значением игры (см. п. 3.4 гл. 1).
Для матричных игр существование и равенство максимина ми-нимаксу было доказано в классе смешанных стратегий (см. § 6 гл.
I), поэтому решение игры заключалось в нахождении их общего значения ? и тех стратегий х*, у*, на которых достигаются внешние экстремумы в (2.2).
Для бесконечных игр существование внешних экстремумов в (2.2), вообще говоря, не обязательно.
2.2. Пример 7. Пусть каждый из игроков 1 и 2 выбирает число из открытого интервала (0, 1), после чего игрок 1 получает выигрыш, равный сумме выбранных чисел. Таким образом, получаем игру на открытом единичном квадрате с функцией выигрыша Н(х, у) игрока 1
Щх, у)=х+у, хе(0, 1), уе(0, 1). (2.3)
Здесь ситуация (1, 0) была бы равновесной, если бы 1 и 0 входили в число стратегий игроков, а значение игры ? было бы ?= 1. В действительности внешние экстремумы в (2.2) не достигаются, а верхнее и нижнее значения игры равны между собой. Поэтому ?=1 и игрок 1, выбирая число 1 — е, е>0, достаточно близкое к 1, всегда может получить выигрыш, достаточно близкий к значению игры. С другой стороны, игрок 2, выбирая число е>0 достаточно малым (близким к 0), может гарантировать, что его проигрыш будет сколь угодно близким к значению игры.
23. Определение. Ситуация (х„ у,) в антагонистической игре Г=(X, Y, Я) называется ситуацией е-равновесия, если для любых стратегий хеХ и уе У игроков 1 и 2 соответственно выполняется неравенство
Щх, у.) - б < Я(х„ у,) < Я(х„ у) + е. (2.4)
Точка (х„ у,), для которой имеет место (2.4), называется е-седловой точкой, а стратегии х, и у, — е-оптимальными стратегиями игроков 1 и 2 соответственно.
Полезно сравнить определения ситуации равновесия (2.1) и б-равновесия (2.4). Если отклонение от оптимальной стратегии приводит лишь к уменьшению выигрыша этого игрока, то отклонение от Б-оптимальной стратегии может привести к его увеличению, но не более чем на б.
Так, ситуация (1 — е, е), 0<е<1, является s-равновесной в примере 7, а стратегии х, = 1 — б, у,=б — е-оптимальными стратегиями игроков 1 и 2 соответственно.
2.4. Заметим, что для двух стратегически эквивалентных игр Г = (Х У, Я) и Г'—(Х, Y, Н), где Я' = /?Я+а, /?>0, справедливы следующие результаты. Если (х„, у,) — ситуация е-равновесия в игре
Г, то она является ситуацией (/?е)-равновесия в игре Г' (ср. с леммой о масштабе § 3 гл. I).
2.5. Основное свойство е-оптимальных стратегий дает следующая теорема.
Теорема. Для того чтобы sup inf Н(х, у) =
* У
= mf sup/T(x,y)=i;< + оо, необходимо и достаточно, чтобы для лю-
У *
бого ? > 0 существовали е-оптимальные стратегии х„ у, игроков 1 и 2, при этом
lim Н(х8, уе)=?. (2.5)
в—»0
Доказательство. Необходимость. Пусть игра Г имеет конечное значение «. Для любого ?>0 выберем стратегию у, из условия
хеХ
и стратегию xt из условия
yeY
Из (2.2), (2.6), (2.7) получаем неравенство
для всех стратегий х, у. Следовательно,
Из неравенств (2.8), (2.9) следуют соотношения (2.4), (2.5).
Достаточность. Если для любого числа е>0 выполняются неравенства (2.4), то
sup inf Н(х, у)=inf sup Н(х, у)=? < + оо
х у ух
?-inf sup Н(х, y)^sup Н(х, у,)^Н(х„ У,) + Е^
У X
^ inf Н(х„ у)+2е < sup inf Щх, у) + 2е=? + 2е. (2.10)
У х у
Отсюда заключаем, что но согласно лемме п. 2.2 гл. I справедливо противоположное неравенство. Таким образом, остается доказать, что значение игры Г конечно. Возьмем такую последовательность {е„}, что lim ?„=0. Пусть Е*б{ел}, е*+те{ея}, где т —любое
л-юо
фиксированное натуральное число. Имеем
Н(хЧс+т> З'е*:) + +m ^ Щх,к+т, Уек+п)^^(Х‘к’ У‘к+п) ~ Ёк + т, н(хч> У*к+т)+.^Н(хек, У,к)>Н(хек+т, yek)-sk.
Таким образом, \Н(х,к, у.к)-Н(х,к+т, Уек+т)\^?к+?к+т = 5кт. Так как Ііт 8кт = 0 при любом фиксированном значении т, то существует
fc-»oO
конечный предел lim Н(хе, уе). Из соотношения (2.10) получаем 8—*0
неравенство \Н(хе, у,)—г|г%?, следовательно, и=1іт Щхе, yt). Теоре-
8—>О
ма доказана.
2.6. Для иллюстрации приведенных в этом параграфе определений рассмотрим подробно пример 1 п. 1.2.
Пример 8. Предположим, что множества S2 и S2 представляют собой замкнутые круги с радиусами Rx и R2 (Rx <R2). Найдем нижнее значение игры
u=max тіп р(х, у).
хе,У, yeS2
Пусть Тогда min р(х0, у) достигается в точке у0 пересече-
У
ния прямой, проходящей через центр 02 круга S2 и точку х0, с границей круга S2. Очевидно, что величина min р(х0, у) достигает
j>eSj
максимального значения в точке MeS2, являющейся точкой пересе-
 |
| Рис. 3 |
чения линий центров 001 (рис. 3) с границей круга іУІ5 наиболее удаленной от точки
Таким образом, v = \01M\ — R2.
Для вычисления верхнего значения игры
t>=min max р(х, у)
yeS3 хeSs
рассмотрим два случая.
Случай 1. Центр О круга St принадлежит множеству S2 (рис. 4).
Для каждого y0eS2 точка хо> доставляющая max р(х, у0), строится
следующим образом. '
Пусть Хо и xq — точки пересечения прямой Оуу0 с границей круга Sy, a jcq — точка пересечения прямой Оу0 с границей круга Su наиболее удаленная от точки у0. Тогда х0 определяется из условия
р(х0і^=ш Р(^О.Уо)-
/-1, 2, 3
По построению, для всех у0 е S2
max р(х, у0)=р(х0, y0)>Ry
х 65,
Однако при уо=0 получаем
max р(х, OJ =Rlt
хе St
поэтому
min max p(x, у) =v=Rl.
yeS2 xe5t
Непосредственно видно, что, поскольку OeS2, в случае 1 v=Ry'^\OlM\—R2=v. При этом равенство возможно лишь при условии, что О принадлежит границе множества S2.
Таким образом, если в случае 1 точка О не принадлежит границе множества S2, то значения игры и ситуации равновесия не существует. Если же точка О принадлежит границе множества S2, то существует ситуация равновесия, при этом оптимальная стратегия игрока 1 заключается в выборе точки М, лежащей на пересечении линии центров 00 у с границей множества 51 и наиболее удаленной от точки Оу. Оптимальная стратегия игрока 2 заключается в выборе точки yeS2, совпадающей с центром О круга St. Значение игры при этом равно v=v=v = Ry +R2 — R2 = Ry.
Случай 2. Центр круга ОфБ2. Этот случай рассматривается как вариант случая 1, когда центр круга S< принадлежит границе множества S2. Вычислим величину ? (рис. 5).
Пусть y0eS2. Тогда точка х0, доставляющая max р(х, у0), со-
xeS2
впадает с точкой пересечения х0 прямой, проходящей через у0 и центр О круга Su с границей круга St, наиболее удаленной от точки у0. Действительно, круг радиусом ХдУо с центром в точке у0 содержит S1 и его граница касается границы круга S1 в единственной точке х0. Очевидно, что величина max р(х, у0) =р(х0, у0)
JC6 Sl
достигает минимума в точке М2 пересечения отрезка 01М с границей круга S2. Таким образом, в рассматриваемом случае
r=min max р(х, y) = \OlM\—R2=v. **
yeS2 xeSl
Оптимальные стратегии заключаются в выборе точек MeS1 и MieS2 игроками 1 и 2 соответственно.
Если в качестве множеств стратегий в примере 1 п. 1.2 рассматривать открытые круги S2 и S2, то в случае 2 значение игры существует и равно
t> = sup inf р(х, у) — inf sup р(х, у) =v = \OlM\ — R2 = v.
хе?, yeS2 yeS2 xeSt
Однако оптимальных стратегий не существует, поскольку M4S2,
Тем не менее для любого б>0 существуют е-оптимальные стратегии — это точки из е-окрестности точек М и М? принадлежащие соответственно можест-вам S2 и S2.
2.7. В заключение отметим, что игра в примере 6 имеет ситуацию равновесия в чистых стратегиях (см. упр. 7), а игры в примерах 1 — 5, вообще говоря, не имеют ситуации равновесия и значения игры. Так, в примере 2 лишь при 1/2 у игрока
1 есть оптимальная стратегия х* = і/2, а значение игры равно единице (у игрока
2 оптимальной является любая стратегия).
§ 3. СМЕШАННЫЕ СТРАТЕГИИ
3.1. Рассмотрим антагонистическую игру Г = (X, Y, Н). Если она не имеет значения, то ?>?. Для увеличения своего гарантированного выигрыша в таких случаях каждому игроку, как уже отмечалось в § 4 гл. I, важно знать намерение противника. И хотя правила игры не представляют такой возможности, при достаточно частом повторении игры с одним и тем же противником можно статистически оценить возможность выбора той или иной стратегии и поступить определенным образом. Как же должен поступить игрок, не желающий, чтобы его намерение было раскрыто? Единственным разумным способом в этом случае является выбор стратегии случайным образом, в соответствии с определенным случайным механизмом, т. е. необходимо использовать смешанные стратегии.
Дадим формальное определение смешанной стратегии для бесконечной игры.
3.2. Пусть х — некоторая а-алгебра подмножеств множества X (включающая в себя одноточечные множества хеХ) и ? — а-алгебра подмножеств Y (уе?, если yeY). Обозначим через Хи і множества всех вероятностных мер на ег-алгебрах у и ? соответственно, и пусть функция Н измерима относительно а-алгебры X х ?. Рассмотрим интеграл
К(ц, vj = j* j*Н(х, y)dp(x)dv(y), реХ, ?е X, (3.1)
X г
представляющий собой математическое ожидание выигрыша Н(х, у) по мерам р, ? [85].
Определение. Смешанным расширением игры Г—(X, Y, Н) называется антагонистическая игра в нормальной форме с множествами стратегий X, Т и функцией выигрышей К(р, ?), т. е. игра Г=(Х, ?,К).
Поведение игроков в смешанном расширении игры Г можно интерпретировать следующим образом. Игроки выбирают независимо друг от друга меры реХ и ?еХ. В соответствии с этими мерами они реализуют (например, с помощью таблицы случайных чисел) случайный выбор стратегий хеХ и ye Y. После этого игрок 1 получает выигрыш Н(х, у). Стратегии реХ, ?еТ называются смешанными, а хеХ, ye Y — чистыми стратегиями в игре Г.
Введете смешанного расширения бесконечной игры требует определенных пояснений. Множества X и Т зависят от того, на каких (7-алгебрах х и ? рассматриваются вероятностные меры. В случае матричных игр (множества X и Y конечны) в смешанном расширении игроки выбирали свои стратегии согласно вероятностным распределениям на множествах X и Y. Если X — бесконечное множество и мы будем поступать так же, как в конечном случае, то необходимо рассматривать меры, для которых измеримы все подмножества бесконечного множества X. Однако таких мер сравнительно мало: это меры, сосредоточенные на не более чем счетных множествах точек. Используя только такие меры, игроки обедняют свои возможности (и далеко не всегда могут гарантировать существование ситуации равновесия в смешанных стратегиях). Поэтому используют менее обширные (7-алгебры, на которых определяют вероятностные меры. Тогда возможных вероятностных мер существенно больше (и, как правило, гарантируется существование ситуации равновесия в смешанных стратегиях). Однако в этом случае не всякая фуЕцщия Н на Ху. Y окажется измеримой, поэтому нельзя определить математическое ожидание выигрыша и тем самым понятие равновесия, значения игры и оптимальных стратегий. Таким образом, здесь необходим известный компромисс. С точки зрения проблемы нахождения решения желательно, чтобы смешанные стратегии имели наиболее простой вид и в то же время в этом расширении существовало, по крайней мере, значение игры.
Строго говоря, интеграл в (3.1) должен браться по мере ц х ? на декартовом произведении Тх У. Однако согласно правилам антагонистической игры смешанные стратегии (меры) д и ? игроками выбираются одновременно и независимо друг от друга, т. е. вероятностные меры д и ? — стохастически независимы.
Определение. Ситуацией (ц,?) в смешанных стратегиях называется пара вероятностных мер реХ.?еХ, которые стохастически независимы.
Таким образом, в ситуации (р, ?) в смешанных стратегиях выигрыш К(р, ?) равен повторному интегралу (3.1). Одноточечные множества принадлежат <т-алгебре подмножеств множества стратегий, на которой определяются вероятностные меры, поэтому каждой чистой стратегии х(у) можно поставить в соответствие вероятностную меру рхеХ(?уеі), сосредоточенную в точке хеХ (yeY). Отождествляя стратегии х и рх, у и ?у, видим, что чистые стратегии являются частным случаем смешанных, т. е. справедливы включения Ісі, Ус: Т. Тогда выигрыши игрока 1 в ситуациях (х, ?) и (р, у) равны соответственно математическим ожиданиям:
|
К(х, ?) =К(рх, ?) — • |
Н(х, y)dv(y); г | (3.2) |
| К(р, у)=К(р, ?у) = | Щх, y)dp(x), | (3.3) |
где интегралы в (3.1), (3.2), (3.3) понимаются в смысле Лебега — Стилтьеса. Если же распределения р(х), ?(у) имеют плотности f(x) и g(y), т. е. dp(x)=f(x)dx и dv(y) =g(y)dy, то интегралы в (3.1), (3.2), (3.3) понимаются в смысле Римана — Стилтьеса. Таким образом, Гс= Г — подагра своего смешанного расширения Г. Будем считать, что все интегралы в (3.1) (3.2), (3.3) существуют, каковы бы ни были вероятностные меры р и ?.
Определение. Пусть Г= (X, У, Н) — антагонистическая игра, а Г = (X, Т, К)—ее смешанное расширение. Тогда ситуация (р*, у*) еХ х У называется ситуацией равновесия в игре Г в смешанных стратегиях, если для всех реХи?еХ выполняются неравенства
К(р, ?*) <К(р* ?*; ^К(р*. ?), (3.4)
т. е. (р*, ?*) — ситуация равновесия в смешанном расширении игры
Г, а /і*(?*) — оптимальная стратегия игрока 1 (2) в Г.
Аналогично, ситуация (д*, ?*) е X х У) называется ситуацией е-равновесия в игре Г в смешанных стратегиях, если для всех ре X и ?еТ выполняются неравенства
К(р, ?*) ~Е^К(р*„ v'J^Kfpl vJ+E, (3.5)
т. е. pi, (yf) — е-оптимальная стратегия игрока 1 (2) в Г.
3.3. Подобно тому, как это доказывалось для матричных игр, можно показать, что если функции выигрыша игр Г=(Х, У, Н) и Г' = (X, У, Н) связаны равенством И(х, у) = <хН(х, у) + /?, а>0, то множества ситуаций_равновесия у игр Г и Г' в смешанных стратегиях совпадают, т. е. Z(T') =Z(T), а значения игр связаны соотношением «(^=№(0+^ (см. § 4 гл. I).
3.4. Ситуации равновесия в смешанных стратегиях обладают такими же свойствами, как и в случае матричных игр, что следует из приведенных ниже теорем.
Теорема. Для того чтобы пара (р*, ?*), р*еХ, ?*еТ была ситуацией равновесия (е-равновесия) в смешанных стратегиях в игре Г, необходимо и достаточно для всех хеХ, у е У выполнение неравенств
К(х, ?*) К(р*, ?*; ^К(р\ у); (3.6)
(КОС, ?*)-Е<К(р*, V*; ^К(р*, У) + Е). (3.7)
Доказательство. Необходимость теоремы очевидна, поскольку чистые стратегии являются частным случаем смешанных. Докажем достаточность для (3.6) (для (3.7) это доказывается аналогично). Пусть р и ? — произвольные смешанные стратегии игроков 1 и 2 соответственно. Тогда из (3.1), (3.2) и (3.6) получаем
К(р, ?*) = JК(х, v*)dp(x)^K(p*, ?*), х
К(р*, v)=^K(p*, y)dv(y)>K(p*, V*).
Y
Отсюда вытекают неравенства (3.4), что и требовалось доказать.
Из теоремы, в частности, следует, что если (х*. у*) — ситуация равновесия (е-равновесия) в чистых стратегиях в игре Г, то она является и ситуацией равновесия (е-равновесия) в смешанном расширении Г, при этом значение игры ? сохраняется.
Заметим, что смешанное расширение Г является антагонистической игрой, поэтому относительно Г справедливо понятие вполне определенной игры (п. 2.1), а также теорема п. 2.5, только речь теперь идет о ситуации равновесия и значении игры в смешанных стратегиях.
3.5. Теорема. Для того чтобы игра Г=(Х, Y, Н) имела значение ? в смешанных стратегиях, т. е. sup inf К(р, v)=infsup K(p, ?)=?,
Ц V V ft
необходимо и достаточно выполнение равенства
Если при этом игроки имеют оптимальные стратегии, то внешние экстремумы в (3.8) достигаются и равенства
У
sup К(х, ?*)=? (3.10)
являются необходимыми и достаточными условиями оптимальности смешанных стратегий р* е X и ?* е Т.
Доказательство. Пусть ? — значение игры. Тогда по определению
v = sup inf К(р, ?). (3.11)
fi У
Для фиксированной стратегии р множество {К(р, ?)|?е?} —выпуклая оболочка чисел К(р, у), yeY. Так как точная нижняя граница любого множества действительных чисел совпадает с точной нижней границей выпуклой оболочки этих чисел, то
inf К(р, у) — inf К(р, у). (3.12)
?е Т yeY
Равенство (3.12) можно получить также из следующих соображений. Поскольку Ус У, имеем
inf K(p, vj^inf K(p, у).
?е 7 yeY
Предположим, что неравенство строгое, т. е.
inf К(р, v)<inf К(р, у).
у у
Это значит, что при некотором достаточно малом е>0 выполняется неравенство
inf К(р, v) + e<inf К(р, у).
V у
Таким образом, при всех yeY
Теперь, переходя к смешанным стратегиям в (3.13), получаем inf K(fi, v)^inf К((1, ?) +Е.
V V
Полученное противоречие и доказывает (3.12).
Возьмем супремум по у в равенстве (3.12). Тогда
v=sup inf K(fi, у).
У У
Аналогично доказывается правое из равенств в (3.8). Обратно, если (3.8) выполнено, то из (3.12) следует, что ? — значение игры.
Пусть теперь у*, ?* — оптимальные стратегии игроков 1 я 2 соответственно. По теореме п. 3.4 гл. I внешние экстремумы в (3.8) достигаются, а (3.9), (3.10) являются необходимыми и достаточными условиями оптимальности смешанных стратегий у* и ?*.
В п. 3.2 отмечалось, что введение смешанных стратегий в бесконечной антагонистической игре зависит от способа рандомизации множества чистых стратегий. Однако из (3.8) следует, что значение ? игры не зависит от способа рандомизации. Так, для доказательства его существования достаточно найти хотя бы одно смешанное расширение игры, для которого выполнялось бы равенство (3.8).
Следствие. Для любой антагонистической игры Т=(Х, Y, Н), имеющей значение ? в смешанных стратегиях, справедливо неравенство
sup inf Н(х, yj^v^inf sup Н(х, у). (3.14)
* У У*
Доказательство. Из теоремы п. 3.5 следует:.
sup inf Н(х, yj^sup inf К(у, y)=v=
х у ц у
=inf sup К(х, v) <inf sup H(x, у).
? х У X
З.б. Из (3.14) следует один из способов приближенного решения антагонистической игры. Действительно, пусть внешние экстремумы в (3.14) достигаются, т. е.
?~ =max inf Н(х, у) =inf Н(х°, у); (3.15)
X у у
?+ =тіп sup Н(х, у) =sup Н(х, у0) (3.16)
ух X
и пусть а=?+ —?~. Тогда максиминная стратегия х° игрока 1 и ми-
нимаксная стратегия у0 игрока 2 с точностью до а описывают оптимальное поведение игроков и могут быть взяты в качестве приближенного решения игры Г. Таким образом, в этом случае задача сводится к нахождению максиминных и минимаксных стратегий игроков 1 я 2 соответственно, а точность приближенного решения определяется величиной а=?+— ?~, при этом значение игры ? согласно (3.14) лежит в интервале и е [и-, и+]. Способам нахождения решения задач (3.15), (3.16) посвящена теория минимак-са [31, 30].
3.7. Как и в случае матричных игр, для бесконечных игр важную роль играет понятие спектра смешанной стратегии.
Определение. Пусть Г = (X, Y, Н) — антагонистическая игра. Тогда чистую стратегию х0еХ (y0eY) игрока 1 (2) называют точкой концентрации его смешанной стратегии р (?), если р (х0) >0 (?(уо)>0).
Определение. Чистая стратегия х0еХ (y0eY), где X (соответственно Y) — топологическое пространство, называется точкой спектра смешанной стратегии р (?), заданной на борелевской а-алгебре подмножеств множества X (Y), если для любой измеримой окрестности ш точки х0 (у0) имеет место неравенство

Спектром смешанной стратегии р(?) назовем наименьшее замкнутое множество, р-мера (?-мера) которого равна единице.
Точки концентрации смешанной стратегии являются точками спектра; обратное, вообще говоря, неверно. Так, чистые стратегии, в которых смешанная стратегия имеет положительную плотность, являются точками спектра, но они не являются точками концентрации. ?
Спектр смешанной стратегии р (соответственно ?) будем обозначать Хц (У?).
Докажем аналог теоремы п. 7.6 гл. I о дополняющей нежесткости для бесконечных игр.
Теорема. Пусть Т=(Х, Y, Н) — антагонистическая игра, имеющая значение ?. Тогда, если х0еХ, а ?* — оптимальная смешанная стратегия игрока 2 и
(3.17)
К(х0, ?*)<«,
то х0 не может быть точкой концентрации какой-либо оптимальной стратегии игрока 1.
Аналогичный результат справедлив и для точек концентрации оптимальных стратегий игрока 2.
Доказательство. Из оптимальности смешанной стратегии ?*е У следует, что для всех хеХ выполняется неравенство
К(х,
Интегрируя его по оптимальной смешанной стратегии (мере) /х* игрока 1 на множестве Z\{x0}, получаем
J К(х, ?*)ф*(х)<і> J dfi*(x).
Пусть fi*(x0)> 0, т. е. х0 —точка концентрации оптимальной смешанной стратегии р* игрока 1. Тогда из (3.17) имеем
К С*0. ?*)д* (х0) < ?ц* (х0).
Складывая два последних неравенства, получаем противоре'&е $К(х, v*)dp*{x)=K(p*, ?*)=?<?.
X
Поэтому р*(х0)=0 для всех оптимальных стратегий р*еХ.
3.8. Для бесконечных антагонистических игр можно ввести по
нятие доминирования стратегий аналогично тому, как это делалось в § 8 гл. I. _
Определение. Стратегия р?еХ игрока 1 строго доминирует стратегию ргеХ(д1>д2), если
Н(р1,у)>Н(р2,у)
для всех yeY. Аналогично, стратегия ?2е У игрока 2 строго доминирует стратегию ?2е У (?!>?2), если
Н(х, ??)<Н(х, ?2)
для всех хеХ. Стратегии д2 и ?2 называются строго доминируемыми, если существуют р^рг и Vj>v2.
Если последние неравенства выполняются как нестрогие, то говорят, что д2 доминирует д2 (р^р2) и ?і доминирует ?2 (v^v^.
Приведем без доказательства теоремы о доминировании, аналогичные теоремам п. 8.3.
Теорема. Для бесконечной антагонистической игры, имеющей решение, ни одна строго доминируемая чистая стратегия игрока не содержится в спектрах его оптимальных смешанных стратегий.
Теорема. Пусть Г=(Х, Y, Н) — бесконечная антагонистическая игра, имеющая решение (X в Y — топологические пространства), и каждый элемент открытого множества Х° с X доминируется некоторой стратегией д°, спектр которой не пересекается с Х°. Тогда всякое решение игры Г'=(Д\Т°, Y, Н) является решением игры Г. Аналогичная теорема верна и для стратегий игрока 2.
3.9. В этом параграфе рассмотрены свойства оптимальных (ё-оптимальных) смешанных стратегий в предположении существования решения игры. Матричная игра вполне определена в смешанных стратегиях, т. е. всегда существуют значение и ситуация равновесия, что следует из теоремы п. 6.1 гл. I. Возможности решения бесконечных антагонистических игр в смешанных стратегиях ограничены, что показывает следующий пример.
Пример 9. {Игра, не имеющая значения в смешанных стратегиях.) Рассмотрим игру Г = (Х, Y, Н), где Х= Y— {1, 2...} — множество натуральных чисел, а функция выигрышей имеет вид
И{х,у)=\
1, если х>у, О, если х=у,
. — 1, если х<у.
Эта игра не имеет значения в чистых стратегиях. Покажем, что она> не имеет значения и в смешанных стратегиях.
Пусть р — произвольная смешанная стратегия игрока 1,,
и dp(x)=8x, где <5*^0 и ? <5* = 1- Возьмем е>0 и найдем у, такое, что х”‘
Тогда
K(p,yd=t Ь*Н{х,у^= ? 8хН(х, yt) +
Хш\
+ ? SxH{x,yt)=- ? Sx+ ? Sx< — l + 2e.
x>y, x<ye x >y,
В силу произвольности e>0 и так как Н{х, у) не принимает значений, меньших — 1, имеем
infK{p, y)=-l.
У
Следовательно, поскольку стратегия р произвольна,
w=sup iafK(p, у)= — 1.
М У
Рассуждая аналогично, получаем
i3=inf supjRT(jc, v)= 1.
V X
Так как v>v, то игра Г не имеет значения в смешанных стратегиях.
Как будет показано в следующем параграфе, непрерывности функции выигрыша и компактности пространства стратегий достаточно для того, чтобы игра имела решение (значение и оптимальные стратегии) в смешанном расширении.
§ 4. ИГРЫ С НЕПРЕРЫВНОЙ ФУНКЦИЕЙ ВЫИГРЫША
4.1. В данном параграфе рассмотрим антагонистические игры Г=(Х, Y, Н) в предположении, что пространства стратегий Хи Y — метрические компакты (чаще всего они будут подмножествами евклидовых пространств), а функция Н непрерывна по обеим переменным. Под множествами X, Y смешанных стратегий игроков 1 и 2 будем понимать множества вероятностных мер, заданных на <т-алгебрах % и ? борелевских множеств пространств X и Y соответственно. Тогда выигрыш К{р, ?) игрока 1 в ситуации (р, v)elx Y в смешанных стратегиях — измеримая функция относительно боре-левской (Т-алгебры хХ?, она определяется интегралом (3.1) и представляет собой математическое ожидание выигрыша по вероятностной мере рх?.
Игру Г—(X, Y, Н), определенную указанным выше способом, будем называть непрерывной игрой.
42. Теорема. Если Г=(Х, Y, Н) — бесконечная антагонистическая игра, имеющая значение ? и ситуацию равновесия (р*, ?*), а функции К(р*, у), К(х, ?*) — непрерывны соответственно по у и по х, то справедливы равенства
где Ys, Хр — спектры смешанных стратегий ?* и р* соответственно.
Доказательство. Из теоремы п. 3.4 следует, что неравенство
выполняется для всех точек yeY. Если (4.1) не выполнено, то существует такая точка у0е У„., что К(р*, у0)>?. В силу непрерывности функции К(р*, у) неравенство (4.3) в некоторой окрестности со точки Уо — строгое. Из того, что у0 е У?. точка спектра смешанной стратегии ?*, следует ?*(св)>0. Отсюда и из неравенства (4.3) получаем
?=К(р*, v*) = J К(р*, y)dv*(y)>v.
Y
Противоречие доказывает справедливость (4.1). Равенство (4.2) доказывается аналогично.
Данный результат является аналогом теоремы о дополняющей нежесткости п. 7.6 гл. I. Напомним, что чистая стратегия х, входящая в спектр оптимальной стратегии, называется существенной. Таким образом, теорема утверждает, что для существенных стратегий должны быть выполнены равенства (4.1), (4.2).
Теорема п. 4.2 справедлива для любой непрерывной игры, поскольку справедливо следующее утверждение.
4.3. Лемма. Если функция H:XxY-+Rl непрерывна на XxY, то интегралы К(р,у) и К(х, ?) являются соответственно непрерывными функциями от у и х для любых фиксированных смешанных стратегий реХ и ?е У.
Доказательство. Функция Н(х, у) непрерывна на компакте XxY, поэтому она равномерно непрерывна.
Возьмем произвольное е>0 и найдем такое <5>0, что как только р2(Уі, у2)<&, то для любого х выполняется неравенство
IН(х, Уі)—Н (х, у2)\<в, (4.4)
где р2 ( ) — метрика в пространстве Y.
Тогда
\К(р, y^-Kip, >-2)| = |J Н(х, yv)dp{x)-х
- J Н(х, y2)dp(х)| = IJ [Н(х, у^-Щх, y2)]dp(х)|<
Следовательно, функция К(р, у) непрерывна по у.
Аналогично доказывается непрерывность функции К (х, ?) по х.
4.4. Сформулируем основную теорему данного параграфа. Теорема. Бесконечная антагонистическая игра Г=(X, У, Н), где
X, Y — метрические компакты, а Н — непрерывная функция на их произведении, имеет решение в смешанных стратегиях (значение и оптимальные стратегии).
Доказательство теоремы основано на аналитических свойствах смешанного расширения игры Г=(X, Y, К) и некоторых вспомогательных результатах.
4.5. Напомним, что последовательность борелевских мер щ,, п = 1,2,..., заданных
на борелевской д-алгебре % компактного метрического пространства X, называется слабо сходящейся, если
Лемма. В условиях теоремы п. 4.4 множества смешанных стратегий Xи Y(mho-жества борелевских вероятностных мер) — метрические компакты в топологии слабой сходимости.
Приведем схему доказательства для множества смешанных стратегий 7 (для 7 — рассуждения аналогичны).
Пространство борелевских мер 7, заданных на борелевской ^-алгебре х компактного метрического пространства X, метризуемо, поскольку в X можно ввести метрику
p O', д")=тах(р', р”),
где р' я р“ — нижние границы таких чисел г* я г* соответственно, что для любого замкнутого множества Fc.X
p'(F)<p"(Vг(F))+/, p"(.F)<tf(Vf¦ (F)) +/',
где Vr(F)={xeX]: minp, (x, z)<r), r>0, a pj () — метрика в пространстве X. zeF
Известно [85], что сходимость в этом метрическом пространстве равносильна слабой сходимости, а семейство мер р на борелевской с-алгебре пространства X слабо компактно (т. е. компактно в описанном выше метрическом пространстве всех борелевских мер) тогда и только тогда, когда это семейство равномерно ограничено
р(Х)<с (4.7)
н равномерно плотно, т. е. для любого е>0 существует такой компакт А Я X, что
р(Х\АНе. (4.8)
Условие (4.8) следует из компактности X, а (4.7) — из того, что меры pelt нормированы {р (X) = 1).
4.6. Заметим, что в условиях теоремы п. 4.4 множество смешанных стратегий 7(7) игрока I (2) является компактом и в обычном смысле, поскольку в данном случае слабая сходимость последовательности мер {дя}, п=1, 2, ..., равносильна сходимости в обычном смысле:
Кт р„(А)=р(А)
л-*оо
для любого борелевского множества АяХ такого, что его граница А' имеет меру нуль: р(Аг)=0.
Доказательство этого результата представляет определенные технические сложности. Его можно найти, например, в [4, с. 367].
4.7. Обозначим через ? я ? соответственно нижнее и верхнее значения игры Г=(X, Y, К):
»=sup inf К (ji, у), i;=inf sup^(x, v). (4.9)
НУ » X
Лемма. В условиях теоремы п. 4.4 экстремумы в (4.9) достигаются, поэтому
u=max тіп К (р, у), S=min тахЛДдс, ?). (4.10)
” неХ yeY ?е Г хеХ
Доказательство. Так как Н(х, у) непрерывна, то по лемме п. 4.3 для любой меры ре Xфункция
К(р, y) = \H(x,y)dp(x) х
непрерывна по у. Так как Y— компакт, то К(р, у) в некоторой его точке будет достигать минимума.
По определеншо ? для любого л существует такая мера Р»еХ, что “
minK(ji„, у)^«-1/л.
У
Поскольку X — компакт в топологии слабой сходимости (лемма п. 4.5), то из последовательности {p„}ZL і, д„еУ, можно выбрать слабо сходящуюся подпоследовательность. Пусть сама последовательность {дя}*-і слабо сходится к некоторой мере д0еХ. Тогда
lim К(дя, у) = lim IН(х, у)</д„(х)={Я(х, y)dp0 (х) = К(д0, у), уе У.
п-юо п-*аоХ X
Но К(цо, у) не меньше ? для каждого уе У. Следовательно, min ^(до, у) >і; и на д0 е X достигается требуемый максимум.
Аналогично доказывается, что inf sup в (4.9) можно заменить на min max.
4.8. Перейдем непосредственно к доказательству теоремы п. 4.4. Доказательство. Так как X и У — метрические компакты, то для любого целого л существуют конечные (1/л)-сети
У„={х1, х*Гп], Хя с X, У„={Уь ..., у?}, У, с: У,
соответственно множеств Хи У. Это означает, что для любых точек хе А" и уе У найдутся такие точки х?еХ„ и у?е Уя, что
Рі (х, х7)<“, д2 (у, yj) < (4.11)
л л
где дг ( ), д2 ( ) — метрики пространств У и У соответственно.
Для произвольного целого л построим матричную игру с матрицей An={tfj}, где
а7,=Я(х?, У!), ^еХя, у?е Y„. (4.12)
Игра с матрицей Ая имеет значение ?я и оптимальные смешанные стратегииря = (..., ппГг), /„=(?",..., т^) игроков 1 и 2 соответственно (см. теорему п. 6.1 гл. I).
Функция Н (х, у) непрерывна на декартовом произведении X х У метрических компактов, поэтому она равномерно непрерывна, т. е. для заданного е>0 можно найти такое <5>0, что как только
Рі(х, х0<<5, р2(у,у’)<5,
то
\Н(х,у)-Н(х',У)\<8. (4.13)
Выберем и_настолько большим, чтобы 1/л <5, и определим стратегию ц„еХ по правилу
М*)= ? (4.14)
для каждого борелевского множества .F пространства X. Имеем
(4-15)
І-1
Если р2{у, У])<д, то согласно (4.4), (4.5) и (4.13) получаем
IН(х, у) — Н(х, у])\ < е,
\К(рп,у)-К(рп, уГ)|<е.
Следовательно, для любого ye Y (Y„—(1/л)-сеть множества Y)
К(р„,у)>?я-Е. (4.16)
Так как min К(р„, у) достигается (лемма п. 4.7), то
У
?>?„ — е. (4-17)
Аналогично можно показать, что
?<?„ + е. (4.18)
Из (4.17) и (4.18) получаем
?>? — 2г.
Но по лемме п. 2.2 гл. I неравенство ?^? выполняется всегда. Учитывая произвольность г>0, получаем-
? = ?; (4.19)
тогда из леммы п. 4.7 и (4.19) следует утверждение теоремы (см. п.
2.1).
4.9. Следствие. Имеет место равенство
? = lim ?„, (4.20)
л-юо
где ?„=? (А„) — значение матричной игры с матрицей (4.12).
4.10. Из доказательства теоремы п. 4.4 следует, что непрерывную игру можно с любой степенью точности аппроксимировать конечными играми. Более того, справедлив следующий результат.
Теорема. Бесконечная антагонистическая игра Г= (Х, Y, Н), где X, Y — метрические компакты, а Н — непрерывная функция на их произведении, при любом е>0 имеет е-оптимальные смешанные стратегии с конечным спектром.
Доказательство теоремы следует из доказательства (п. 4.8) теоремы п. 4.4. Действительно, по игре Г построим матричные игры с матрицами А„ и смешанные стратегии р„еХ, определяемые соответственно (4.12), (4.14) для произвольного целого п. Стратегии ?„е У игрока 2 по аналогии определяются следующим образом:
?„(С7)= ? I?, (4.21)
?уеО,]ГеТя}
где *я=(ті, ..., — оптимальная смешанная стратегия игрока
2 в игре с матрицей Ап и значением ?„.
По построению имеем
?»=Е ?«*7=^0™ v„), . (4.22)
/-1 j-\
где K(ji, v) — выигрыш в смешанных стратегиях (р, ?) в игре Г. Из (4.16) и аналогичного неравенства для стратегии ?„ получаем, что
для произвольного е>0 найдется номер п такой, что
К(х,?„)-Е<?я<К(рту)+е (4.23)
для всех хеХ и yeY. Учитывая, что стратегии и ?„ имеют
конечный спектр ХЙ и Y„ соответственно (Х„ и Y„ — конечные (1/л)-
сети соответственно множеств X и У), получаем утверждение теоремы (см. п. 3.4).
4.11. Объединяя результаты теорем п. 4.4 и 4.10, можно сделать вывод, что бесконечная антагонистическая игра с непрерывной функцией выигрыша и компактными множествами стратегий для любого ?>0 имеет е-оптимальные стратегии игроков, являющиеся смесями конечного числа чистых, а также смешанные оптимальные стратегии в классе борелевских вероятностных мер. В частности, эти результаты справедливы для игр на квадрате (п. 1.3) с непрерывной функцией выигрыша.
4.12. Имеется большое число работ, в которых доказывается существование значения бесконечных антагонистических игр. Наиболее общий результат в этом направлении принадлежит Сайону [66]. Для игр с компактными пространствами стратегий и полунепрерывными функциями выигрыша известны результаты [50, 75, 90]. Покажем, что в некоторых направлениях они не поддаются обобщению.
Пример 10. {Игра на квадрате, не имеющая значения в смешанных стратегиях [67]). Рассматривается антагонистическая игра Г=(ЛГ, Y, Н), где X=Y=[0, 1], а функция выигрыша Н имеет вид
{—1, если х<у<х+1/2,
0, если х=у или х=х+1/2,
1, если у<х или х+\І2<у.
Эта функция имеет разрывы на прямых у=х и у=х+1/2. Покажем, что
sup inf.K(/i, v)=l/3; inf supK{p, v)=3/7. (4.24)
/IV V /I
Пусть p— вероятностная мера на [0, 1]. Если р ([0, 1/2))^1/3, то положим Уц=1. Если же р ([0, 1/2))>1/з> то выберем 5>0, чтобы
р (№, 1/2 —^])> 1/з, и положим у<1=1/2 — <5. В каждом из этих случаев получаем неравенства
inf К(р, ?)^К(р, у^ 1/3,
которые доказываются непосредственной проверкой.
С другой стороны, если р выбрано так, что р ({0}) = д ({1/2})=д ({1}) = */3, то для всех уе[0, 1] имеем
} Н{х, y)dp(x)= 1/3[Я(0, у)+Н{ 1/2, у) + Н{ 1, у)]> 1/3. о
Следовательно, доказано первое из равенств (4.24).
Теперь пусть ? — какая-либо вероятностная мера на [0, 1]. Если ?([0, 1))>3/7, то положим х,= 1. Если ? ([0, 1))<3/7, то ?({1})>4/7,
и в этом случае положим х?=0, если ?([0, 1/2))< 1/7; если же ?([0,
1/2))> 1/7, то выберем (5>0 так, чтобы ?(JO, 1/2 —<5])> 1/7, и положим Ху= 1/2—S. В каждом из указанных случаев убеждаемся, что
sapK(p, v)^K(xv, v)S?3/7. м
С другой стороны, если ? выбрано так, что
? ({1/4}) = 1/7, ? ({1 /2}) = 2/7, ? ({1})=4/7,
то для любого хе[0, 1] имеем 1
jff(x,y)dv(y)=l/7[ff(x, 1/4)+2 Н(х, 1/2)+4 Н{х, 1)]<3/7. о
Таким образом, доказано второе из равенств (4.24).
§ 5. ИГРЫ С ВЫПУКЛОЙ ФУНКЦИЕЙ ВЫИГРЫША
В § 4 при достаточно общих предположениях было доказано существование решения в бесконечных антагонистических играх с непрерывной функцией выигрыша и компактными множествами стратегий. Вместе с тем представляет теоретический и практический интерес выделение таких классов игр, когда один или оба игрока имеют оптимальные чистые стратегии. Такие игры рассматриваются в данном параграфе.
5.1. Определение. Пусть Ха рГ, Yc.R" — компакты, множество Y — выпукло, функция Н:Хх Y->Rl непрерывна по совокупности аргументов и выпукла по yeY при любом фиксированном значении хеХ. Тогда игра Г (X, Y, Н) называется игрой с выпуклой функцией выигрыша (выпуклая игра).
Приведем симметричное определение относительно игрока 1.
Определение. Если Хс-РГ, Yc.Rn — компакты, множество X выпукло, функция выигрыша Н непрерывна по совокупности аргументов и вогнута по хе X при любом фиксированном yeY, то игра Г=(X, Y, Н) называется игрой с вогнутой функцией выигрыша (вогнутая игра).
Если же ХаРГ, YcR” — выпуклые компакты, а непрерывная по совокупности аргументов функция выигрыша Н(х, у) вогнута по х при любом фиксированном у и выпукла по у при каждом х, то игра Г (X, Y, Н) называется игрой с вогнуто-выпуклой функцией выигрыша (вогнуто-выпуклая игра).
Рассмотрим игры с выпуклой функцией выигрыша. Аналогичные результаты справедливы и для вогнутых игр.
Теорема. Пусть Т = (Х, Y, Н) — выпуклая игра. Тогда игрок 2 имеет оптимальную чистую стратегию, при этом значение игры равно
?=шіп шахЯ(х, у). (5.1)
yeY хеХ
Доказательство. Так как X и Y—метрические компакты (в
метрике евклидовых пространств РГ и PC), а функция Я непрерывна на произведении Хх Y, то согласно теореме п. 4.4 в игре Г существует значение ? и оптимальные смешанные стратегии р*, ?*. Известно, что множество вероятностных мер с конечным носителем всюду плотно в множестве всех вероятностных мер на Y [85]. Поэтому
существует последовательность смешанных стратегий ?" с конечным
спектром, слабо сходящаяся к ?*. Пусть спектр стратегии ?" состоит из точек у*, ..., yj", и они выбираются с вероятностями rf[, ..., rfkn. Тогда в силу выпуклости функции Я имеем
К(х, v)= § г\]Н(х, уп)^Н(х, у"),
(5.2)
7-1 я
где у"= ? г)]У„. Переходя к пределу при л-»оо в неравенстве (5.2)
7-1
(если необходимо, то следует рассмотреть подпоследовательность {у"}), получаем
где у — предельная точка последовательности {у"}. Из (5.3) и леммы п. 4.2 имеем
Пусть неравенство (5.4) строгое. Тогда
»=тахК(х, ?*)>тахН(х, у)>тіп тахК(х, ?)=і>,
что невозможно. Таким образом, тахЯ(х, у)=тах АГ(х, ?*)=? и из
теоремы п. 3.5 получаем, что у — оптимальная стратегия игрока 2.
Установим справедливость равенства (5.1). Так как уе У— оптимальная стратегия игрока 2, то
D=max#(jc, y)>min тахЯ(х, у).
х ух
С другой стороны, выполняется неравенство
t)=min max AT (те, v)<min max Я (x, у).
V X ух
Сравнивая последние неравенства, получаем (5.1).
5.2. Напомним, что функция ср: У-+Л1, У a Rn, У—выпуклое
множество, строго выпукла, если для всех Яе(0, 1) выполняется строгое неравенство
<Р (4Уі + 0 - %г) < (Уі) + (1 - Х)<Р (Уг); УіУг е Y> Уі ^Уг-
Теорема. Пусть Г= (Х, Y,H) — выпуклая игра со строго выпуклой функцией выигрыша. Тогда игрок 2 имеет единственную оптимальную стратегию, которая является чистой.
Доказательство. Пусть р* —оптимальная стратегия игрока /, 9 (у) = К(р*, у) и ? — значение игры. Если у — точка спектра оптимальной стратегии игрока 2, то выполняется равенство (п.4.2).
K(ji*, y) = i;.
Однако для всех ye У имеем неравенство K(ji*, у)>?, поэтому
ф(у)=тіп<р(у)=?.
yeY
Функция (p(y) является строго выпуклой, поскольку для Ае (О, 1) имеет место неравенство
(р (Хуу + (1 - Х)у2) = J Н(х, Ху у + (1 -X)y2)dp* (х) <
X
<х f Н(х, yyW* (х) + (1 —X) I Н(х, у2№* (х) =
= Х(р(уу) + (1-Х)(р(у2). (5.5)
Из (5.5) следует, что функция q>(y) не может достигать минимума в двух различных точках. С другой стороны, существование точки минимума у функции (р(у) гарантируется теоремой п. 5.1, что завершает доказательство.
5.3. Приведем без доказательства результаты, симметричные теоремам по п. 5.1 и 5.2 для вогнутых и вогнуто-выпуклых игр.
Теорема. Пусть Г = (Х, Y, Н), X с= FT, Y с= Л" — вогнутая игра. Тогда значение игры ? вычисляется по формуле
v=max тіп#(х, у), (5.6)
* У
каждая чистая стратегия х*. на которой достигается max min (5.6), является оптимальной для игрока 1. Если, кроме того, функция Н(х, у) строго вогнута по х при каждом фиксированном yeY, то оптимальная стратегия игрока 1 единственна.
Теорема. Пусть Г = (ЛГ, У, Н), XczlC, Y с= Л" — вогнуто-выпуклая игра. Тогда значение игры ? равно
?=тіп тах#(х, у)=тах тіп#(х, у). (5.7)
ух X у
В игре Г всегда существует ситуация равновесия (х*, у*) в чистых стратегиях, где х* е X, у* е У — чистые стратегии игроков 1 и 2, на которых достигаются внешние экстремумы в (5.7). Если при этом функция Н(х, у) строго вогнута (выпукла) по переменной х (у) при любом фиксированном уеУ (хеХ), то игрок 1 (2) имеет единственную оптимальную стратегию, которая является чистой.
5.4. Выясним структуру оптимальной стратегии игрока 1 в выпуклой игре Г=(Х, У, Н).
Теорема. В выпуклой игре Г = (Х, У, Н), У с= R" игрок 1 имеет оптимальную смешанную стратегию р* с конечным спектром, состоящим не более чем из (л + 1)-й точки множества X.
Доказательство этого результата основано на известной теореме Хедли о выпуклых множествах, которую мы приведем без доказательства [63, с. 210; 3, с. 107]*. Теорема (теорема Хелли). Пусть К— семейство из не менее чем п + 1 выпуклого
множества в R , причем каждое множество из К компактно. Тогда, если каждые п+1 из множества семейства К имеют общую точку, то существует точка, общая всем множествам семейства К.
Прежде чем перейти непосредственно к доказательству теоремы, докажем ряд вспомогательных утверждений.
Пусть функция Н(х, у) непрерывна на произведении XxY компактных множеств X с Rm, Y с R". Обозначим X' = Хх ... хХ декартово произведение г множества X.
Рассмотрим функцию <р: X' xX-*Rl:
(р(хи ..., х„ у)=тахН(хи у).
Лемма. Функция <р(х 1(хг, у) непрерывна на X' xY.
Доказательство. Функция Н(х, у) непрерывна на компактном множестве X х Y, поэтому и равномерно непрерывна на нем. Тогда для любого е>0 найдется <5>0 такое, что из неравенств р2 (х, х)<8, Р2(Уі, Уг)<Ь следует неравенство |Н(х, у2)-Щх, у2)\ <е, где р2(),
р2 (') — расстояния в Л” и Л" соответственно.
Имеем
|<р(*і, ..., х„ у2)-(р(х2, ..., х, у2)| =
= |тахЯ(х„ yJ-тахНІХі, у2)| = \H(xh, y2)-H(xk, у2)j,
1</<г 1<І<Г
где
H(xh, у1)=тглН(хІ, у2), Н(х,2, у2)=тахН(хі, у2).
1 </<г 1^і<г
Если р2 (х„ хі)<& для і= 1,..., г, рг (у1г у2)<8 и если Я(х„ у^>Щхіг, Уг), то
0^Я(хч, у2)-Н(хІ2, y2)^H(xh, Уі)-Н(xti, у2)<е. Аналогичные неравенства имеют место в случае H(xit, ух) ^ Н(хіг, у2). Лемма. В выпуклой игре Г=(Х, Y, Я), Y с R" значение игры
’Вопросы, связанные с обобщениями и приложениями теоремы Хелли, подробно изложены в книге: Данцер Л., Грюнбаум Б., Кли В. Теорема Хелли. М., 1968.
? равно
v=min max Я (л, у) = max min max H(xhy), (5.8)
У X .....*я+1 У 1</<я + 1
где ye Y, xteX, і-1, п+1.
Доказательство. Обозначим через
?= max min max H(xh у).
*t *П + 1 У 1<і<л + 1
Так как min max H(xt, y)^min max# (x, y)=v для каждой систе-
у 1<і<л + 1 % ух
мы точек (хІ5 ..., jc„+i)gX"+1, то
?^?. (5.9)
Для произвольного фиксированного набора стратегий xteX, і= 1, ..., л + 1, рассмотрим систему неравенств относительно у
Н (хиу)^?, ye Y, і= 1, ..., л+1. (5.10)
Покажем, что система (5.10) имеет решение.
Действительно,
?^тіп max H(xhy) = max Н(хи у)^Н(х{, у), і= 1, л +1.
у 1<і«5я+1 1<І<Я+1
Таким образом, у удовлетворяет системе (5.10).
Следовательно, система (5.10) имеет решение для любых х,еX,
і=1, 2, ..., л + 1.
Зафиксируем х и рассмотрим множество Dx={y:H(x, у)^?}.
Функция Н(х, у) выпукла и непрерывна по у, поэтому множество Dx выпукло и замкнуто при каждом х. Множества {Dx} образуют
систему выпуклых компактных множеств в R", причем в силу того, что неравенства (5.10) всегда имеют решение, любой набор по (л+ 1)-му множеству системы {Dx} имеет непустое пересечение. Поэтому по теореме Хелли существует точка у0 е Y, общая для всех множеств Dx, т. е. такая, что
Н(х,у0)^? (5.11)
при любых хеХ. Предположим, что ?ф?. Тогда из (5.9) и (5.11)
0<v=min тахН(х, у)^тахН(х, у0)^:?,
имеем
ух X
г. е. ?<?. Полученное противоречие и доказывает (5.8).
Перейдем к доказательству теоремы.
Доказательство. Из предыдущей леммы имеем
?= max min max H(x„ y)=min max H(xh y)=
xx, xn+\ у 1</<Л +1 у
л+ 1
=min max ? H(xh y)nh (5.12)
у p <=i
где х1г ..., Зёл+, —векторы, на которых достигается внешний максимум в (5.8),
р = (п1, ..., ял+і)еЛ"+1, я.^0, ? я<=1- (5-13)
і-=1
Рассмотрим функцию
КІР, у) =Y,H(Я, у)щ, yeY, ре Р,
і-і
где Р — состоит из векторов, удовлетворяющих (5.13). Функция К(р, у) непрерывна по р и у, выпукла по у и вогнута по р, а множества Y с рС, Р с Л"+1 — компакты в соответствующих евклидовых пространствах. Поэтому по теореме п. 5.3 и из (5.12) имеем
я+1 я+1
0=min max ? H(xh у)я,=тах min ? Н (xh у)щ. (5.14)
У Р 1-1 Р У І-І
Из (5.8) и (5.14) следует существование таких р*еР и у* eY, что для всех хе Хи yeY выполняется неравенство
Н(х, y*)^v^ ? н(Я> У)п*-1-1
Теорема доказана.
Сформулируем теорему о структуре оптимальной стратегии игрока 2 в вогнутой игре Г = (Х, Y, Н).
Теорема. В вогнутой игре Г = (Х, Y, Н), X с Rm игрок 2 имеет оптимальную смешанную стратегию ?* с конечным спектром, состоящим не более чем из (т+1)-й точки множества Y.
Доказательство теоремы аналогично доказательству предыдущей теоремы.
5.5. Суммируем результаты теорем для выпуклых игр, доказанные в этом параграфе.
Теорема. Пусть Г=(Х, Y, Н), X а RT, Y с R" — выпуклая игра. Тогда значение ? игры Г определяется по формуле
v=min тахЯ(х, у).
У *
Игрок 1 обладает оптимальной смешанной стратегией р0 с конечным спектром, состоящим не более чем из (п+ 1)-й точки множества X. В то же время все чистые стратегии у0, на которых достигается min max Н(х, у), являются оптимальными для игрока 2. Если,
кроме >того, функция Н(х, у) при каждом фиксированном хеХ строго выпукла по у, то оптимальная стратегия игрока 2 единственна.
Проиллюстрируем эти результаты на примере.
Пример 11. Рассмотрим частный случай примера 1 (см. п. 1.2). Пусть Si = S2 = S и множество S представляет собой замкнутый круг на плоскости с центром в точке О и радиусом R.
Функция выигрыша Н(х, у)=р (х, у), xeS, у eS, где р ( ) — функция расстояния в R2, является строго выпуклой по у при любом фиксированном х, a S — выпуклое множество. Поэтому согласно теореме п. 5.5 значение игры ? равно
u=min max р (х, у). (5.15)
yeS хеS
Вычисляя min max в (5.15), получаем, что v=R (см. пример 8 п. 2.6). При этом точка y0eS, на которой достигается минимум выражения
max р (х, у), единственная и совпадает с центром круга S (т. е.
xeS
точкой О). Эта точка и является оптимальной стратегией игрока 2 (минимизирующего). Теорема утверждает, что у игрока 1 (максимизирующего) существует оптимальная смешанная стратегия, предписывающая положительную вероятность не более чем трем точкам множества S. Однако вследствие симметрии множества S в действительности оптимальная смешанная стратегия д0 игрока 1 предписывает с вероятностью 1/2 выбирать любые две диаметрально противоположные точки на границе множества S. Для доказательства оптимальности стратегий /х0, у0 достаточно установить, что К(х, у0)^К(р0, УоНК{р0, у) для всех х, у eS, где К — математическое ожидание выигрыша, К(р0, y0)=R/2 + R/2 = R. Действительно, К(х, у0)=р(0, x)^R и К(р0, у)=р(х2, у)/2+р(х2, y)/2^R, где х1 и х2 — произвольные диаметрально противоположные точки на границе круга S. Оптимальность стратегий р0 и у0 доказана.
5.6. Рассмотрим частный случай выпуклой игры Г=(Л', Y, Н),
когда 7= У=[0, 1], т. е. выпуклую игру на единичном квадрате. Из теоремы п. 5.5 следует, что игрок 2 всегда имеет оптимальную чистую стратегию уое[0, а игрок 1 — смешанную, сосредоточенную не более чем на двух точках, при этом значение игры равно
?= min max Н(х, у). (5.16)
уе(0, Ч *е[0, 1]
Множество всех существенных стратегий {х} <= [0, 1] игрока 1 является подмножеством решений уравнений (п. 4.2)
tf(x,yo)=*,xe[0, 1], (5.17)
где Уо — оптимальная стратегия игрока 2. Чистые стратегии х игрока 1, удовлетворяющие равенству (5.17), иногда называются уравновешивающими. Множество всех уравновешивающих стратегий игрока 1 замкнуто и ограничено, т. е. компактно. Оптимальной чистой стратегией игрока 2 является любая точка уо = [0, 1]> на которой достигается (5.16).
Обозначим через Щ (х, у) частную производную функции Н по у (при у=0 и у= 1 понимается соответственно правая и левая производные).
Лемма. Если у0 — оптимальная стратегия игрока 2 в выпуклой игре на единичном квадрате с функцией выигрыша Н, дифференцируемой по у и уо>0, то найдется уравновешивающая стратегия х' игрока 1, для которой
Я;(х\у0КО. (5.18)
Если же Уо<1, то существует такая уравновешивающая стратегия х" игрока 1, что
Щ(х",уо)>0. (5.19)
Доказательство. Докажем (5.18). (Вторая часть леммы доказывается аналогично.) Предположим противное, а именно: для каждой уравновешивающей стратегии х игрока 1 выполняется неравенство Ну(х, у о) > 0, т. е. функция Н(х, •) в точке ^ строго возрастает. Это означает, что найдутся такие е^х) > 0 и ?(х)>0, что для уе[0, 1], удовлетворяющих неравенству ?(х)>у0—у>0, выполняется неравенство
Н(х,у)<Н(х, Уо)-е(х).
В силу непрерывности функции Н имеем, что для каждой уравновешивающей стратегии х и е(х)/2 найдется такое 8 (х)> 0, что при ?(х)>у0—у>0 выполняется неравенство
Н (х, у)<Н (х, у) - Е (х)/2 < Я (х, у о) - Е (х)/2 =
=Н(х, у0) — Е (х)/2
для всех, уравновешивающих стратегий х, для которых |х—х| <8 (х).
91
Множество уравновешивающих стратегий компактно, поэтому его можно покрыть конечным числом таких д (х)-окрестностей. Пусть Е — наименьшее из всех соответствующих чисел е(х). Тогда имеем неравенство, справедливое для всех уравновешивающих стратегий х (в том числе и для всех существенных стратегий)
Н(х, у)^Н(х, у о)-е/2, где jo-mm0(x)<j<jo.
Пусть До — оптимальная сметанная стратегия игрока 1. Последнее неравенство справедливо для всех точек спектра стратегии д0, поэтому, интегрируя, получаем
Я (До, y)^K(ji0, Jo)—е/2=?—е/2,
что противоречит оптимальности стратегии д0.
Теорема. Пусть Г—выпуклая игра на единичном квадрате с функцией выигрыша Н, дифференцируемой по у при любом х, jo — чистая оптимальная стратегия игрока 2,а? — значение игры. Тогда:
1) если jo = 1, то среди оптимальных стратегий игрока 1 имеется чистая стратегия х', для которой выполняется (5.18);
2) если jo=0, то среди оптимальных стратегий игрока 1 имеется чистая стратегия х", для которой выполняется (5.19);
3) если 0<jo< 1, то среди оптимальных стратегий игрока 1 найдется такая, которая является смесью двух существенных стратегий х1 их",удовлетворяющих (5.18), (5.19), с вероятностями а и 1 —а, ае[0, 1]. При этом а является решением уравнения
аЯ;(У, J0) + (1 — а)я;(х", jo)=0. (5.20)
Доказательство. Пусть j0= 1. Тогда найдется уравновешивающая стратегия х! игрока і, для которой выполняется (5.18). Тогда из выпуклости функции Н(х', у) следует, что она не возрастает по у на всем промежутке [0, 1], достигая при j= 1 своего минимума. Это означает, что
Н(х?, jo) < Н(х\ у) (5.21)
при всех je[0, 1]. С другой стороны, из (5.17) следует, что
Н(х, jo) <Я(х', Jo) (5.22)
при всех хе[0, 1]. Неравенства (5.21), (5.22) показывают, что (х> У о) — ситуация равновесия.
Случай jo=0 исследуется аналогично. Перейдем к случаю 3. Если 0<jo<1, то имеются две уравновешивающие стратегии х? и х", удовлетворяющие (5.18), (5.19) соответственно.
Рассмотрим функцию
<Р(Р) = Щ(Х’, J0)+(1-№(*", Jo).
Из (5.18), (5.19) следует, что q>(0)^t0, (р(1)^0. Функция (р(Р) непрерывна, поэтому найдется <хе[0, 1], для которого (р(а) = 0.
Рассмотрим смешанную стратегию д0 игрока 1, заключающуюся в выборе стратегии х' с вероятностью а и стратегии х" с вероятностью 1 —а. Функция
KQi0, y)=aH(xf, y)+(l — oi)H(x", у)
выпукла по у. Ее производная по у в точке у=у0 равна
К'уіМо, Уо) = аЯ;(х', у0)+(1 -а)Н'у(хГ, уо)=0.
Следовательно, в точке у0 функция К(р.0, у) достигает минимума. Отсюда, учитывая (5.17), имеем
K(ji0, УоНК0іо,у),
К(Мо, У)—Н{х, у0)=?=тахН(х, у0)>Н(х, у0)
при всех хе[0, 1] и уе[0, 1], что и доказывает оптимальность стратегий д0 и у0.
5.7. Теорема п. 5.6 дает способ отыскания оптимальных стратегий, который мы проиллюстрируем на примере.
Пример 12. Рассмотрим игру на единичном квадрате с функцией выигрыша Н(х, у)=(х—у)2. Это есть одномерный аналог примера 11, только в качестве функции выигрыша здесь взят квадрат расстояния. Поэтому естественно ожидать, что значение ? игры будет равно ?=1/4, оптимальной стратегией игрока 2 является середина отрезка у0= 1/2, а оптимальной стратегией игрока 1 — выбор с вероятностью 1/2 крайних точек 0 и 1 отрезка [0, 1]. Покажем это, используя теорему п. 5.6.
Заметим, что д2Н(х, у)/ду2 = 2>0, так что игра Г — строго выпуклая, поэтому игрок 2 имеет единственную оптимальную стратегию, которая является чистой (теорема п. 5.5). Пусть у — фиксированная стратегия игрока 2. Тогда
тах(х—у)2 =
(1-у)2, если у<1/2, у2, если у^ 1/2.
Таким образом, из (5.16)
тіп у2
min (1 -у)2,
v=min
Оба внутренних минимума достигаются на у0= 1/2 и принимают значение 1/4. Поэтому ю=1/4, а у0 = 1 /2 — единственная оптимальная стратегия игрока 2.
Найдем оптимальную стратегию игрока 1. Для этого заметим, что 0<уо<1 (у0= 1/2). Найдем существенные стратегии игрока 1. Уравнение (5.17) в данном случае принимает вид (х—1/2)2= 1/4. Откуда хх =0 и х2= 1, т. е. существенными для игрока 1 являются крайние точки отрезка [0, 1].
Вычислим производные
я;(хІ5>-0)=і>о, н'у(х2, у2)=-і<о.
Составим уравнение (5.20) относительно а. Имеем 2а —1 = 0, откуда а =1/2. Таким образом, оптимальная стратегия игрока 1 состоит в выборе им чистых стратегий 0 и 1 с вероятностью 1/2.
5.8. В заключение параграфа приведем результат, аналогичный п. 5.6 для вогнутой игры.
Теорема. Пусть Г — вогнутая игра на единичном квадрате с функцией выигрыша Н, дифференцируемой по х при любом фиксированном у, х0 — чистая оптимальная стратегия игрока 1, а ? — значение игры. Тогда:
1) если х0= 1, то среди оптимальных стратегий игрока 2 имеется чистая стратегия у', для которой выполняется неравенство
У)> 0; (5.23)
2) если jco = 0, то среди оптимальных стратегий игрока 2 имеется чистая стратегия у", для которой
Н'х(х0,у")^ 0; (5.24)
3) если 0 < х0 < 1, то среди оптимальных стратегий игрока 2 найдется такая, которая является смесью двух существенных стратегий у' и у", удовлетворяющих (5.23), (5.24), с вероятностями (іи 1 — /?. При этом число ре[0, 1] является решением уравнения
/?я;(*0,/НО-№(*„, Л=о.
§ 6. ОДНОВРЕМЕННЫЕ ИГРЫ ПРЕСЛЕДОВАНИЯ
В этом параграфе приведено решение некоторых одновременных игр преследования, у которых функция выигрыша или множества стратегий игроков невыпуклые. К таким играм не применимы результаты § 5, поэтому решение для обоих игроков находится в классе смешанных стратегий. Существование решения в этом классе гарантируется теоремой п. 4.4.
6.1. Пример 13. (Одновременная игра преследования в кольце.) Эта игра является частным случаем примера 1 п. 1.2, когда множества S1 = S2 = S и S представляют собой кольцо. Радиусы внешней и внутренней окружностей кольца S обозначим соответственно Лиг, R>r.
Покажем, что оптимальными стратегиями игроков 1 и 2 являются выборы точек с равномерным распределением на внутренней (для игрока 2) и внешней (для игрока 2) окружностях кольца
S. Обозначим эти стратегии д* (для игрока 1) и ?* (для игрока 2). При указанных стратегиях среднее значение выигрыша (расстояния) равно
K(jj*, v*)=~ J” j* л/R2+Г2—2/ircos {(p — \j/)d(pd4> =
(6.1)
=^~ J y/R2 + r2 —2Rr cos { d? = Ф (г, Л), 0
где фа q> — полярные углы чистых стратегий игроков Іа 2 соответственно. Если игрок 1 выбирает точку х с полярными координатами р, ф, то ожидаемое расстояние (игрок 2 придерживается стратегии ?*) равно
2я
К(х, ?*) = Ф (г, Р)=~ J" \Л2 + Р2—2pr cos ? d?. о
При функция <р(р)=р2 + г2 —2prcos? монотонно возрастает. В частности, (р) < <р (R) при Отсюда имеем Ф(г,
р)<Ф(г, R). Поэтому для любой стратегии игрока 1 ожидаемое расстояние не больше Ф (г, R).
Рассмотрим теперь ситуацию (р*, у), в которой у е S, р и <р — полярные координаты точки у. Имеем
2 я
К(ц*,у)=Ф{р, Л)=^ j*\jR2 + p2 — 2Rpcos ?d?,
о
Зафиксируем R а рассмотрим функцию Ф(р, R) на отрезке O^p^R. Дифференцируя по р, можно убедиться, что
ешю=о ^ф(р. 0
др ’ др2 :
Поэтому функция Ф (р, Л) монотонно возрастает по р, следовательно, Ф(г, Л)<Ф (Р, Л)
*(*, ?*)^К(р.*, ?*НК(ц*, у)
для всех х, yeS1. Таким образом, оптимальность стратегий р* и ?* доказана, а значение игры и равно ? = К(р*, ?*), где К(р.*, ?*) определяется (6.1). В частности, если 5—окружность радиуса R (случай r=R), то значение игры равно 4R\n.
6.2. Пример 14. Рассмотрим одновременную игру, когда игрок 2 выбирает пару точек у = {ух, у2}, где ух е S, у2 е 5, а игрок 1, не зная выбора игрока 2,— точку хе5. Выигрыш игрока 1 полагаем равным min (г (х, у,). Приведем решение для случая, когда множество
і-1, 2 '
5 представляет собой круг радиуса R с центром в начале координат (точке О): 5=5(0, R).
Рассмотрим функцию Ф (г, р) — г2 + р2—4гр/п, где rap принимают значения из промежутка г, ре [О, Л]. Установим свойства функции Ф (г, р).
Лемма 1. Функция Ф(г, R) (как функция переменного г) является строго выпуклой и достигает абсолютного минимума в единственной точке r0 = 2Rln.
Доказательство. Имеем д2Ф/дг2=2>0. Следовательно, функция Ф(г, р), ге[0, Л] строго выпукла, а производная
(6.2)
ЭФ (г, R) „ 4Л
---= 2 Г--
дг п
строго монотонна. Очевидно, что функция (6.2) в единственной точке r0 = 2R/n обращается в нуль. В силу строгой выпуклости Ф(г, R) точка г0 является единственной точкой абсолютного минимума. Лемма доказана.
Лемма 2. Функция Ф(г0, р) строго выпукла по р и достигает абсолютного максимума в точке p0=R.
Доказательство. В силу симметрии функция Ф (г, р) строго выпукла по р. Поэтому максимум этой функции достигается в одной из точек 0 или R. Имеем
Ф(г0, Л)-Ф(г0, 0)=Го + R2 —4г0Л/я — г% —
=R2 -4/я (2R/n)R = R2 (я2 - 8)/я2 > 0.
Лемма доказана.
Из лемм 1, 2 вытекает, что пара (г0, К) является седловой точкой функции Ф:
Ф(г0, рКФ(г0, К)<Ф(г, R).
Теорема. Оптимальными смешанными стратегиями являются: для игрока 2 — выбор точки yt с равномерным распределением на окружности 5(0, г0) с центром в точке О и радиусом г0(у1= —у2), для игрока 1 — выбор точки х с равномерным распределением на окружности 5(0, R). Значение игры равно величине Ф (г0, R).
Доказательство. Указанные в теореме стратегии обозначим через р* и ?* для игроков 1 а 2 соответственно. Пусть игрок 1 придерживается стратегии р*, а игрок 2 — произвольной чистой стратегии у={у2, у2}, y, = (r(cos <р„ r,sm <р,), і=1, 2. Рассмотрим сначала случай, когда уг =у2. Обозначим через г число г2 + г2, а через q> — угол (рі=(р2. Выигрыш игрока 1 равен
2я
К(р*, У)=~ J* [R2 + г2 —2Rr cos (ф — (р)]іі/г = о
Тогда по лемме 1 имеем К(ц*, у) >Ф (r0, R).
В дальнейшем будем предполагать, что yL Фуг. Введем на плоскости полярную систему координат следующим образом. За начало координат возьмем точку О, за полярную ось — луч, выходящий из точки О перпендикулярно хорде АВ (множеству равноудаленных от у1 и у2 точек круга S(О, R)). Для простоты записи предположим, что и относительно новой системы координат точка yt имеет те же
координаты (г,cos <р„ r,sin(pi). Тогда (рис. 6) выигрыш первого игрока равен
2іГ
К(р*,у) =
2n
1 1 min [R2 + г2 — 2Rr,cos (ф — <p,)] chj/ =
i=l, 2
P
=— [R2 + r2 —2Rr2 cos (ф — (р2)]4ф +
2n J
2я—?
2n
[i?2 +r\—2Rr1 cos (ф — (pi)] йф.
Пусть .
FtІФ) = [(^2 + Л)Р~2Rr2sinPcoscp]/n, -p^cp^P;
F2(cp) = [(i?2 + r2)(n~P) + 2Rrt sinPcos (p]/n, P^(p^2n—p.
Стационарными точками функций Ft и F2 являются 0 и я соответст-
2
венно, так как имеем 0<Р<п/2 и функция F[ (cp) = Rr2sinР sin q>,
F'z (ф) = — Rrl sin /? sin q>, причем 0 и я — точки абсолютного мини-
П
мума функций К, и F2 (F[ (q>) < 0 при q> е (—/?, 0), F[ (ф) > 0 при q> е (0, /?); аналогично, Р2 (ф)< 0 при фе(/?, я), F2(q>)>0 при фе(я, 2я —/?)). Следовательно,
КОЛ у) = ^ (ф2)+К2 (ф,)^Л (0) + F2 (я) =
1
2я
(і?2 + г2 — 2і?г2 cos ф)(іф +
| 2я—j? | ||
|
1 +— 2я | 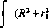 | —2Лгх cos — п))<іф, |
т. е. игрок 1 при использовании игроком 2 стратегии у1=(—г1, 0) у2 = {г2, 0} получит меньший выигрыш, чем при использовании стратегии
Уі=(гfCOs фі, гj sin ф|), i— 1, 2.
Пусть теперь точки у,и у2 лежат на диаметре круга 5(0, R) и расстояние между ними 2г. Обозначим через 2а центральный угол, опирающийся на дугу, стягиваемую хордой _АВ (рис. 7). Предположим, что y1 = (Kcosa —г, 0), y2 = (i?cosa+r, 0). Тогда выигрыш первого игрока равен
| а | |
| 2п | 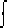 |
2я —а
1
+-
2я
[(Kcos^ — Л cos a+г)2 + Л2 sin 2ф]<іф =
|
а а | |
|
1 2я | 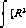 |
| 7п—а |
1
+-
2я
[Л2 — 2R cos ф (R cos a—г) + (R cos a—г)2] (іф=
{[Л2 + {R cos a + r)2]a—2Л sin а (Л cos a + r) +
+[Л2 + (R cos a—г)2] (я — a) + 2R sin a x (R cos a—r)}.
Покажем, что функция ф(щ, г) при фиксированном г достигает минимума по а при а = я/2. В результате элементарных вычислений получим 8il/l8a = {2Rsma[(n—2a)r — nRcosa]}ln, поэтому для достаточно малых значений а имеем дф(а, г)/да<0, так как sin а > О, r(n — 2a) — nRcosa<0 (в предельном случае гя—яЛ<0). Вместе с тем 8ф(п/2, г)/8а = 0.
При каждом фиксированном г функция 8ф(а, г)/8а не имеет нулей по а, кроме <х=я/2. Предположим противное. Пусть а1 — нуль этой функции в интервале (0, я/2). Тогда при <х=а1 обратится в нуль и функция G(a) = (n—2a)r—nRcosa. Таким образом, G (oti) = G (я/2) = 0.
Очевидно, что G (а) > 0 для всех ае(а1, я/2). Это противоречит выпуклости функции G(а) (G" (а) = nR cos а > 0). Поэтому дф (а, г)/8а<0 при ае(0, я/2) и дф(я/2, г)/8а=0. Следовательно, функция ф(а, г) достигает абсолютного минимума по а при <х=я/2: ф (а, г)^ф (я/2, г). Значит, и в этом случае имеем
К{ц*, у)=ф(а, г)>ф(пІ2, г) = Ф(г, Л)>Ф(г0, Л). (6.5)
Из соотношений (6.3) — (6.5) вытекает, что для любой чистой стратегии у={у\, у2} справедливо неравенство
(6.6)
K(ji*,y)><b(r0,R).
Пусть игрок 2 применяет стратегию ?*, а игрок 1 — произвольную чистую стратегию х=(рсо&ф, psinф). Тогда игрок 1 получает выигрыш
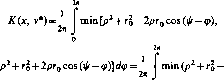 |
| о |
(6.7)
К(х, ?*)=Ф (г0, рКФ(г0, R).
Из неравенств (6.6) и (6.7) получаем, что р* и ?* являются оптимальными стратегиями игроков, а Ф(г0, R) — значение игры. Теорема доказана.
6.3. Пример 15. Пусть игрок 2 выбирает набор из т точек у={уІ5 ..., ут], где Уіе S, і= 1, ..., т, а игрок 1 одновременно с ним — точку xgS. Выигрыш игрока 1 полагаем равным min р(х, уі). Решим игру в случае, когда множество S совпадает с отрезком [—1, 1].
Теорема. Оптимальная смешанная стратегия ?* игрока 2 заключается в равновероятном выборе двух наборов из т точек:
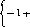 |
4/ 2т— 1 |
2т—\
Оптимальная стратегия р* игрока 1 состоит в выборе точек
\2т-2і-\ 2т— 1
, 2=0, 1, ..., 2т— 1
с вероятностями 1/(2/я). Значение игры равно l/(2m— 1).
Доказательство. Пусть р* и ?* — смешанные стратегии игроков 1 и 2 соответственно, оптимальность которых нужно доказать. Введем следующие обозначения:
2т—2і—\ 2т—2і+і"1 2т—\ ’ 2т—1 J
1,2,
, 2т— 1.
Покажем вначале, что К(х, ?*)^ 1/(2т — 1) для всех хе[— 1, 1]. Действительно, при хе/, имеем
| К(х, ?*)=- min |
|
-2да+4і+1 2т— 1 | ||||||
| 2\ 2т—\ ) 2\ 2т—1 ) 2т-1 |
Пусть теперь игрок 1 выбирает смешанную стратегию р*, а игрок 2 — произвольную чистую стратегию у={уи .., ут).
Обозначим
2т—2j— 1 2т—I ’
7=0, 1,
, 2т— 1.
Тогда
2m—1
KQi*,y)= I
тіп р (х;, >>,)
1 <і<т
J- о
Е тіп р(хУ-,,Уі)+ min р{ху_2,
j— I 1<і<т
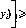
1
2т
(6.9)
1 2 1 >— • т ¦-=-.
2т 2т— 1 2т — 1
Из неравенств (6.8), (6.9) вытекает утверждение теоремы.
§ 7. ОДИН КЛАСС ИГР С РАЗРЫВНОЙ ФУНКЦИЕЙ ВЫИГРЫША
Для игр, у которых функции выигрыша разрывны, нельзя гарантировать существование значения игры в смешанных стратегиях (см. пример п. 4.12). Однако часто именно разрывность функции выигрыша позволяет найти оптимальные стратегии и значение игры. Нахождению решения помогают также эмпирические предположения о виде оптимальных стратегий игроков.
7.1. В данном параграфе будут исследованы игры с выбором момента времени или игры типа дуэли (см. примеры 4.5 п. 1.2). Основной особенностью этого класса игр на квадрате является разрывность функции выигрыша Н(х, у) вдоль диагонали х=у.
Рассмотрим игру на единичном квадрате с функцией выигрыша
Н(х,у) =
(7.1)
Ф(х, >0, если х<у, (р(х), если х=у, .?(х, у), если х>у,
где ф(х, у) — определена и непрерывна на множестве 1,
функция <р непрерывна на [0, 1], а ?(х, j) определена и непрерывна на множестве 0<>><х< 1. Предположим, что игра Г=(Х, Y, Н), где X=Y—[0, 1], Н—задана (7.1), имеет оптимальные смешанные стратегии д*, ?* игроков 1 и 2 соответственно. Более того, предположим, что оптимальные смешанные стратегии д*, у* являются распределениями вероятностей, которые имеют непрерывные плотности J* (х) и g* (х) соответственно.
Далее в этом параграфе будем обозначать искомую стратегию / (соответственно g), понимая под этим плотность распределения. Выясним свойства оптимальных стратегий.
Пусть /— стратегия игрока 1. Для >>е[0, 1] имеем
Предположим, что / и g — оптимальные стратегии игроков 1 и 2. Тогда для любой точки у0, в которой
(точки спектра стратегии g), выполняется
где ? — значение игры. Но равенство (7.3) строгое, поэтому существует <5>0 такое, что для всех у: [у—>>0|<:<5, неравенство (7.3) сохраняется. Таким образом, для этих у сохраняется и неравенство
(7.4), т. е. выполняется равенство K(f, у)=?. Это означает, что
dK(f, у)/ду=0. (7.5)
Уравнение (7.5) перепишем в виде
[?(у, у)~Ф(у, У)?(у) = \ Фу(х, y)f(x)dx +
О
+№,(х, y)f(x)dx,yeS(у0, 8). (7.6)
У
Следовательно, получено интегральное уравнение (7.6) относительно искомой стратегии /.
| ф(х, у)=х-у+ху; | (7.7) |
| ?(х,у)=х-у-ху; | (7.8) |
| ф(х) = 0. | (7.9) |
Заметим, что данная игра является симметричной, поскольку Я (х, у) = — Н (у, х) (кососимметричная функция выигрыша). Поэтому анализ, аналогичный проведенному в п. 9.2 гл. 1, показывает, что значение ? игры, если оно существует, равно нулю, а оптимальные стратегии игроков (если они также существуют) должны быть одинаковыми.
Имеем: фу(х,у)=-1 + х; ?у(х,у)=-1-х;?(у,у)-ф(у,у)=-2у2 и интегральное уравнение (7.6) принимает вид
-2y2f(y) = j (x-l}f(x)dx-f (x+Vjf(x)dx. (7.10)
о У
Будем искать стратегию / в классе дифференцируемых плотностей распределения, принимающих положительные значения в интервале (а, /?) с: [0, 1] (интервал (а, /?) — спектр стратегии Д Тогда (7.10) можно записать следующим образом:
-2y2f(y) = ] (x-\)f(x)dx-\(х+ \)f(x)dx. (7.11)
а у
Дифференцируя обе части (7.11) по у, получим дифференциальное уравнение вида
-4yf-2y2f = (y-l)f+(y+l)f
или
>/'=-3/(у*0). (7.12)
Интегрируя уравнение (7.12), имеем
f(y) = yy~3> (7.13)
где у — некоторая константа.
Теперь осталось найти а, /? и у. Напомним, что оптимальные стратегии игроков в рассматриваемой игре одинаковы. Из нашего предположения о спектре стратегии / следует, что
К(Г,У) = 0 (7.14)
для всех уе(а, ft).
Пусть /?< 1. Поскольку функция K(f, у) непрерывна по у, из (7.14) имеем К О, /0=0. Следовательно,
J (x-f} + fix)f(x)dx=0. (7.15)
а
Однако в случае /?< 1 из (7.15) следует
K(f, 1) = J (x-l+x)f(x)dx<0,
ос
что противоречит оптимальности стратегии /. Таким образом, f}= 1 и K(f, 1)=0. Тогда, подставляя (7.13) в (7.15) при /?=1, получаем
1
Г 2х-1 , Л Л у dx=0, у#0.
Откуда вытекает
(7.16)
За2—4а+1=0.
Решая уравнение (7.16), найдем два корня а=1 и а = 1/3, первый из которых посторонний. Следовательно, а= 1/3. Коэффициент у находится из условия нормировки f(y)
J fiy)dy=y J y~*dy=l,
1/3 1/3
откуда у = 1/4.
Таким образом, получено решение игры примера 5 п. 1.2: значение игры равно ? = 0, оптимальные стратегии /и g обоих игроков (как плотности распределения) равны между собой и имеют вид
/(*) =
0, если jc< 1/3, 1/(4х3), если х> 1/3.
7.3. Пример 17. Найдем решение игры «шумная дуэль» (см. пример 4 п. 1.2) для функций меткости р1 (х)=х и р2 (у)=у- Функция выигрыша Н(х, у) в игре имеет вид (7.1), где
ф(х, у)=2х-1; (7.17)
?(х,у)=1~2у; (7.18)
Ф(*) = 0. (7.19)
юз
Игра является симметричной, поэтому « = 0, а оптимальные стратегии игроков совпадают. Здесь оба игрока имеют чистую оптимальную стратегию х*—у* = 1/2. Действительно,
#(1/2, у)=?(1/2, у)= 1 —2j>>0, если у<1/2,
#(1/2, у)=(р (1/2) = 0, если у=1/2,
#(1/2, у)=ф (1/2, у)=0, если *>1/2.
С точки зрения интерпретации игры решение предписывает дуэлянтам стрелять одновременно, когда каждый пройдет половину дистанции до барьера.
В заключение следует отметить, что класс игр с выбором момента времени хорошо изучен (см. [6, 3, 23]).
§ 8. РЕШЕНИЕ БЕСКОНЕЧНЫХ ОДНОВРЕМЕННЫХ ИГР ПОИСКА
В этом параграфе будет приведено решение игр поиска с бесконечным числом стратегий, сформулированных в п. 1.2. Первая из рассматриваемых игр интересна тем, что в ней оба игрока имеют оптимальные смешанные стратегии с конечным спектром.
8.1. Пример 18. {Поиск на отрезке). Рассмотрим задачу поиска на отрезке (см. пример 2 п. 1.1), которая моделируется игрой на единичном квадрате с функцией выигрыша Н{х, *) вида
1, если /е(0, 1),
О в противном случае.
Н{х,у)=
(8.1)
Заметим, что при 1/2 у игрока 1 имеется чистая оптимальная; стратегия х* = 1/2 и значение игры равно единице, поскольку в этом случае Н(х*, у)=Н{ 1/2, *)= 1, так как [у—1/2|< 1/2</для всех *е[0, 1]. Предположим, что /< 1/2. Заметим, что стратегия х=1 доминирует все чистые стратегии х</, а стратегия х= 1—1 — все стратегии х> 1—1. Действительно,
Н(х, у)=Н(1, у)=
(1 при *е[0, 21),
(О в противном случае, и если х<1, то
*(*,,)={' Пр«^[0, /+*],
(О в противном случае.
Таким образом, при х<1: Н{х, *)<#(/, *) для всех *е[0, 1]. Аналогично имеем
1 при ye[l-2l, 1],
О в противном случае,
Н(х,у)=Н(1-1,у)=
и если хе[1 —/, 1], то
лий={;"риуф-‘’11
(О в противном случае.
Таким образом, при xe[\—l, 1] Н(х, у)^Н(1 —/, >>) для всех >>е[0, 1].
Рассмотрим следующую смешанную стратегию д* игрока 1. Пусть l=xt<x2<... <хт—1 —!— точки, для которых расстояние
между любой парой соседних точек не превосходит 21. Стратегия д* выбирает каждую из этих точек с равными вероятностями 1/т. Очевидно, что при этом любая точка >>е[0, 1] попадает в /-окрестность хотя бы одной точки Хк. Следовательно,
К(ц*,у)>1/т. (8.2)
Пусть теперь ?* — стратегия игрока 2, которая состоит в равновероятном выборе точек 0=у1<у2<...<у„=1, причем расстояние
между парой соседних точек больше 21. Тогда, очевидно, существует не более одной точки у*, в /-окрестности которой содержится точка
х. Следовательно,
К(х, ?*)^1/и. (8.3)
Если бы удалось построить стратегии д*, ?* так, чтобы т—п, то величина 1/и была бы значением игры, а стратегии д*, ?* — оптимальными стратегиями игроков.
Оказывается, такие стратегии действительно можно построить. Для этого достаточно взять
(8.4)
(1/(2/), если 1/(2/) — целое,
|[1/(2/)]+1 в противном случае. Здесь [а] — целая часть числа а. Точки
*/=/+^—7 (*-1), *=1, 2, ..., и,
л—1
(8.5)
отстоят друг от друга не более чем на 21, а расстояние между соседними точками
У]=—\, І— 1, 2, ..., и, (8.6)
л—1
строго больше 21. Таким образом, 1/и — значение игры, а оптимальные стратегии д*, ?* являются равновероятными смесями чистых стратегий, определяемых формулами (8.5), (8.6).
8.2. Пример 19. Рассмотрим обобщение предыдущей задачи в том случае, когда игрок 1 (ищущий) выбирает систему из s точек хх, .., xs, х,е[0, 1], і=1, ..., s, а игрок 2 (прячущийся) выбирает независимо и одновременно с игроком 1 точку у еГО, 1]. Игрок 2 считается обнаруженным, если находится такое у'е{і, s}, что [у — Xj\^l, />0. В соответствии с этим функция выигрыша (выигрыш
игрока 1) определяется следующим образом:
{1, если min \у—х^|</,
J (8.7)
О в противном случае.
Предположим, что игрок 1 располагает точки хи ..., х, в точках
х,= /+(1 — 21)(і— 1)/(п— 1), Кі^п, являющихся точками спектра
стратегии д* из предыдущего примера. Очевидно, что располагать две точки xh, xj2 в одной точке отрезка [0, 1] (т. е. выбирать
совпадающие точки) невыгодно. Пусть д, — стратегия игрока 1,
выбирающая равновероятно любые 5-наборы не равных друг другу точек {Зс,}. Если s^n, то, расположив в каждой из точек Зс, по точке
Xj, игрок 1 полностью покроет отрезок [0, 1] интервалами длины 2/
с центрами в точках Зс, и тем самым обеспечит, что для любой точки
уе[0,1] будет иметь место min \xj—у|</, т. е. в этом случае значение
игры равно единице. Поэтому будем считать, что s<n. Число всевозможных различных выборов 5-наборов точек из множества {Зс,} равно С?. Имеем
К(л*, у)=Ш{хч, ..., х,,; у)
Действительно, точка у обнаруживается, если она попадает_ в /-окрестность хотя бы одной из выбранных стратегией [if точек {Зс,}.Для того чтобы это произошло, необходимо игроку 1 выбрать точку Зс, из /-окрестности точки у. Число наборов, удовлетворяющих
этому требованию, не менее C*„z\.
Предположим теперь, что игрок 2 использует стратегию ?* из предыдущего примера, а игрок 1 — произвольную чистую стратегию х=(х? ..., х,). Тогда
Я 1 5
K(xlt..., хЛ; v*)= ? Щху, ..., х,; у]) ^ .
і-1 " я
Таким образом, значение игры равно s/n и д*, ?* — оптимальные стратегии игроков. Значение игры линейно зависит от количества выбираемых ищущим игроком точек.
8.3. Пример 20. (Поиск на сфере). Рассмотрим игру поиска на сфере (см. пример 3 п. 1.2). Функция выигрыша Н(х, у) имеет вид
{1, если уеМх,
(8.8)
О в противном случае,
S
где x=(xt, ..., xs — набор s точек на сфере С и Ms= 1J S(xy, г); S(xj, г) — г-
сферическая окрестность точки xj. Множество смешанных^ стратегий игрока 1 представляет собой семейство вероятностных мер {М}, определенных на декартовом
произведении s сфер Сх Сх... х C—Q, т. е. на fl=C*.
Множество смешанных стратегий игрока 2 определим как семейство вероятностных мер {?}, определенных на сфере С.
Рассмотрим конкретную пару стратегий (д*, ?*). В качестве стратегии ?* выберем равномерную меру на сфере С, т. е. потребуем, чтобы
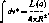 |
| А |
где L(a) — лебегова мера (площадь) множества А.
Будем предполагать, что параметры игры s, г и R таковы, что можно выбрать систему точек x—(xlt х2,..., ха), удовлетворяющих условию
S
L(MX)= ? L(S(Xj, г)), (8.10)
У-1
(сферические сегменты S(xj, г) не пересекаются).
Зафиксируем фигуру Ms на некоторой сфере С. Тогда смешанная стратегия д*
порождается случайным бросанием этой фигуры Мх аа сферу С. Для этого в фигуре
Мх фиксируется некоторая внутренняя точка z, с которой жестко связываются два
неколлинеарных вектора а, Ъ (с углом ір> 0 между ними), расположенных в касательной плоскости к Мх в точке z.
Точка z «бросается» на сферу С в соответствии с равномерным распределением, т. е. плотностью 1/(4nR2). Пустъ в результате реализуется точка z'eC. Фигура Мх с фиксированными на ней векторами параллельно переносится на сферу С так,
чтобы точки z и z' совпали. Таким образом, векторы а, Ъ будут лежать в касательной плоскости к сфере С в точке z1.
Затем на промежутке [0, 2л] выбирают в соответствии с равномерным распределением угол <р\ и вектор b в касательной плоскости поворачивают вместе со связанной с ним фигурой Мх на угол <р' по часовой стрелке. В результате фигура
Мх и вектор b переходят в новое положение на сфере С. Случайное размещение множества Мх на сфере в соответствии с описанной двухэтапной процедурой и порождает случайный выбор точек х’1, х!2, ..., У, соответствующих смешанной стратегии д*, а именно: игрок 1 выбирает точки У,,..., У еС, в которых оказались центры хи ..., х) сферических окрестностей S(xj, г), составляющих множество Мх.
Мера д*, построенная таким образом, оказывается инвариантной, т. е. вероятность покрытия множеством Мх любой точки у е С не зависит от у*. Действительно, найдем вероятность этого события. Пусть П={со} — пространство всевозможных размещений Мх на сфере С. Тогда средняя площадь, покрываемая на сфере С при
бросании на нее множества Мх (математическое ожидание площади), равна L (Мх),
в то же время
L (Мх) = J J J(y, <»)dydf, (8.11)
Q С
где J (у, со) — характеристическая функция множества на сфере С, покрываемого областью Мх- По теореме Фубини имеем
\ lJ(y, <o)dydp = J J J(y, со)dpdy. (8.12)
Q C C 5
Однако в силу инвариантности меры ft интеграл J Jiy, co)dp, совпадающий с вероятностью покрытия точки у множеством Мх, от‘у не зависит и равен р. Тогда из (8.11), (8.12) имеем
L(MX) I L(S(Xj, г))
(8.13)
_=2=1_
4nR2 4 nR2
Обозначим через К(р, ?) математическое ожидание выигрыша при использовании игроками смешанных стратегий ре{р) и ?е{?}. Если один из игроков использует чистую стратегию, то
К(х, v)=J Н(х, y)dv= J dv=Pi(yeMx), с Мх
К(м, у)= J Н(х, y)dp = J J{x, y)dp=Рг(у6Мх), 3 п
и в этом случае математические ожидания соответственно имеют смысл вероятностей попадания случайной точки в фиксированную область и накрытия случайной областью фиксированной точки. Для всех у и x=(xlt ..., х,) в силу условий (8.9)
и (8.13) имеем
L(MX) I L(S(xj, rll
|
4 nR2 4nR2 3 L L(S(.Xj, г)) К(м*,у) = f'-- --- 4 nR2 | 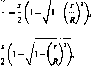 |
так как L{S(Xj, r))=2nR(R—y/R1—r1).
Из определения седловой точки и полученного неравенства К(р, у)~^К(х, ?) следует, что смешанные стратегии р и ? являются оптимальными и
*0J'-$)
— значение рассмотренной игры поиска.
8.4. Рассмотрим вариант предыдущей игры, полагая, что игрок 2 выбирает некоторое односвязное множество Ус С и целью игрока 1 является максимизация площади пересечения
MiWJ-WVl U S(xj,r)
' і-1
Цель игрока 2 противоположна. В остальном игра совпадает с игрой, рассмотренной в начале параграфа. Стратегия ц* игрока 1 совпадает с таковой в предыдущей игре. Смешанная стратегия ?* игрока 2 строится аналогично стратегии д* и заключается в случайном бросании множества У на сферу (в предыдущем случае игрок 2 случайно выбирал точки уеС). Таким образом, ?* строится как инвариантная мера, которая состоит из случайного (в соответствии с равномерным распределением на С) выбора одной из фиксированных точек множества У на С и далее поворота У вокруг этой точки на случайный угол (в соответствии с равномерным распределением на [0, 2л]). Пусть К(х, ?), K(jt,y) соответствуют математическим ожиданиям площади пересечения 2-(У|)А/х). Тогда
L(T)L(A/X)
2я R1
*0Л у)=К{х, ?*)=*(д*, ?*)=
Если У— г-окрестность точки у, то значение игры равно
К(р*, ?*)=яj (R-y/lP-r3).
Упражнения ¦ задачи
1. Игра нападения ¦— защиты. Игрок 1 силами А единиц намерен атаковать один из объектов Ct.....С*, ценность которых определяется числами т, >0, т2>0,.... тл>0,
причем Хі^х2> — >х„. Чистой стратегией х игрока 1 является вектор x=({t.....(„),
П
Yj Іі=А, где (і — часть сил, выделенных для атаки объекта Q. Суммарные силы
обороняющейся стороны (игрок 2) равны В. Чистой стратегией у игрока 2 является выбор набора неотрицательных чисел у=(^,..... %), удовлетворяющих условию
Л
Y Щі=В, где r\j—часть сил, предназначенных для защиты объекта Cj. Результат іітаки на объект Q пропорционален разности ^ если силы атакующих превосходят силы защищающихся, а в остальных случаях он равен нулю. Построитъ функцию выигрыша.
2. Игра на единичном квадрате имеет функцию выигрыша Н(х, у)=ху—1/Здс—1/2у.
Показать, что (1/2, 1/3) — ситуация равновесия в этой игре.
3. Показать, что игра на единичном квадрате с функцией выигрыша
Н(х, y) = sign(jc-y)
имеет седловую точку.
4. Показать, что игра на единичном квадрате типа дуэли с функцией выигрыша
Г-1/х2, х>у, ^(JC, >-)- = ^ 0, х=у,
I 1ІУ1, х<у
имеет ситуацию равновесия (0, 0).
5. Показать, что игра на единичном квадрате с функцией выигрыша Я(х, у)=(х—у)2 не имеет ситуации равновесия в чистых стратегиях.
6. Показать, что в игре на единичном квадрате с функцией выигрыша
Г Х+У, х*И, у#0,
Ч J 1/2+У, Х=1, у#0,
Я(х,у)=-Ч , „
I 1/2 + х, х#1, у=0,
^ 2, х=1, у=0
пара (х„ у,), где х6 = 1 —«, у,=г, является ситуацией г-равновесня. Имеет ли эта игра значение?
7. Решить игру «поиска шумного объекта», сформулированную в примере 6 п. 1.2.
8. Вычислить выигрыш игрока 1 в игре на единичном квадрате с функцией выигрыша Н(х, у) в ситуации (F(x), G (у)) (F и G — функции распределения), если:
а) Н(х, у)=(х+у)/(4ху), F(x)=x2, G(y)=y2;
б) Я(х,у) = |х-у| (1-Іх-уІ), F(x) = x, G(y)=y;
в) Н(х, у)=(х—у)2, F(x) = 1/2/0 (х)+l/2/j (х),
G(y) = /l/2(x),
где /*(х) — ступенчатая функция.
9. Игра дискретного поиска. Рассматривается следующая бесконечная игра. Стратегия игрока 2 заключается в выборе точки, равномерно распределенной на окружности радиуса у, где у может принимать значения из интервала [0, 1]. Игрок 1 может просмотреть в единичном круге односвязную область Q, площадь которой а (Q) = а=const, где а<А, А = л — площадь единичного круга. Его стратегия х заключается в выборе формы области Q, имеющей площадь а, которая целиком лежит в единичном круге. Выигрыш Н{х, у) игрока 1 равен вероятности обнаружения, т. е. Н(х, y)=Pr(y6Q). Под смешанной стратегией g(y) игрока 2 будем понимать функцию плотности распределения случайной величины у е [0, 1]. Найти решение игры.
10. Доказать теорему Хелли п. 5.4.
11. Рассмотрим непрерывный аналог игры «обороны города» (п. 1.3 гл. 1). Игрок 1 должен направить силы х, хе[0, 1] в наступление на первую позицию и силы П — х) — в наступление на вторую позицию. Игрок 2 должен направить силы у, у 6 [0, 1] для обороны первой позиции и силы (1 —у) — для обороны второй, на которой уже расположены постоянные оборонительные силы размером 1/2. Один игрок платит другому единицу на каждой позиции, если его силы на этой позиции меньше сил противника, и ничего не платит, если их силы равны.
Построить функцию выигрыша Н(х, у) игры на единичном квадрате. Показать, что данная игра не имеет решения в смешанных стратегиях.
Указание. Воспользоваться результатом примера 10 п. 4.12.
12. Показать, что в непрерывной игре с функцией выигрыша
Я(х,у)=[1+(х+у)2]-1
стратегии F* (х) = % (х), (т*(у)=1/2/0(у) + 1/2/2(у) — оптимальны для игроков 1 и 2 соответственно.
ПО
13. Доказать, что значение симметричной непрерывной игры на единичном квадрате равно нулю, а оптимальные сметанные стратегии совпадают (игра симметричная), если функция выигрыша кососимметрична, т. е. Н(х, у) = —Н(у, х).
14. Определить оптимальные стратегии и значение игры на единичном квадрате с функцией выигрыша Н(х, у)=у3 — Зху+х3.
15. Показать, что в игре с функцией выигрыша
Н(х, у)=еУ * у/і-^/у2, хе[х0, хх], уе\у0, yj, у>0,
игрок 2 имеет оптимальную чистую стратегию. Выяснить вид этой стратегии в зависимости от параметра у > 0. Что можно сказать об оптимальной стратегии игрока 1.
16. Проверить, что функция выигрыша из примера 11 п. 5.5
Н(х, у) = р(х, у), хе5(0,1), yeS(0, I),
где 5(0, /) — круг с центром в 0 и радиусом /, />(•) —расстояние в R1, строго выпукла по у при любом фиксированном х.
17. Показать, что сумма двух выпуклых функций выпукла.
18. Доказать, что если выпуклая функция ср: [a, ограничена, то она
непрерывна в любой точке хе (л, /Г). Вместе с тем на концах а и /? промежутка (а, Р) выпуклая функция ср полунепрерывна сверху, т. е.
lim <р(х)^<р(еі)
х-*а
(аналогично при x-*fS).
19. Пусть дана игра Г = {Х, Y, Н), X=Y=[0, 1] с выпуклой ограниченной функцией выигрыша Н(х, •): [0, \]-*Р2. Показать, что игрок 2 в этой игре имеет либо оптимальную чистую стратегию, либо для каждого s>0 чистую е-оптимальную стратегию. Относительно игрока 1 справедлив результат теоремы п. 5.6.
Указание. Использовать результат упр. 18 и рассмотреть вспомогательную игру Г0 = (*, Y, Н0), где г #(*, у\ если уе(0, 1),
Но(х, у)=
lim Н(х, у„), если у=0 или у= 1.
'¦>і—>
20. Решить игру «нападение — защита», сформулированную в упр. 1.
21. Рассматривается одновременная игра преследования на плоскости (см. пример 1 п. 1.2), когда множества стратегий Sl=S2 — S, где S — некоторое замкнутое выпуклое ограниченное множество.
а) Показать, что значение рассматриваемой игры равно R, где R — радиус минимального круга S (О, R), содержащего S, оптимальная стратегия игрока 2 является чистой и заключается в выборе центра О круга 5(0, R).
б) Показать, что оптимальная стратегия игрока 1 является смешанной и является смесью либо двух диаметрально противоположных точек касания множества 5 с кругом 5(0, R) (если такие точки хх и хг существуют), либо таких трех точек касания Хх, х!г, х!г, что точка О лежит внутри треугольника, вершинами которого являются данные точки.
22. Решить одновременную игру преследования на плоскости, рассмотренную
в упр. 21, в предположении, что игрок 2 выбирает не одну точку yeS, а т точек ух.....
Уте$- Функция выигрыша игры имеет вид
Щх,у)=- ? р2(х,У,), т і- 1
где р (•) — расстояние в R2.
23. Игрок 1 выбирает системы х из т точек промежутка [—1, 1], т. е. х=({,, ... ..., fт, f;6[—1, 1], і'=1, ..., т. Одновременно и независимо от него игрок 2 выбирает
систему у из п точек того же промежутка [—1, 1], т. e.y = (rju ..., гі„), »7,е[—1, 1],у= 1, 2, п. Функция выигрыша Н(х, у) имеет вид
Н(х, у) = 1/2 I max min fy|+max min ц\).
' • i i i
Найти решение игры.
24. Рассмотреть обобщение задачи п. 8.3, а именно игру поиска, в которой игрок 2 выбирает систему у из к точек у = (у1, ..., у*) на сфере С, а игрок 1, как и прежде,
систему гизз точек х = (хг, ..., xs) на сфере С. Функция выигрыша имеет вид H{x,y) = {M\M=\{y^\-.yieS{xj, r);j= 1, ..., s},
где 5 (Xj, т) — сферический сегмент с вершиной в точке xj и радиусом основания г; (запись |{у;}| означает количество точек множества {у,}). Точка у,- считается обнаруженной, если yjeS(xj, г) хотя бы для одного Xj. Таким образом, значение
функции выигрыша имеет смысл числа обнаруженных точек в ситуации (х, у). Найти решение игры.
ГЛАВА III
НЕ АНТАГОНИСТИЧЕСКИЕ ИГРЫ
§ 1. ОПРЕДЕЛЕНИЕ БЕСКОАЛИЦИОННОЙ ИГРЫ В НОРМАЛЬНОЙ ФОРМЕ1.1. В предыдущих главах были рассмотрены антагонистические игры двух лиц, т. е. игры, в которых интересы сторон прямо противоположны. Однако реальные задачи принятия решения в условиях конфликта характеризуются большим числом участников и, как следствие этого, неантагонистичностью конфликтной ситуации. Если говорить о конфликте двух лиц и его моделях, то можно заметить, что он также не исчерпывается только антагонистическим случаем. Дело в том, что интересы игроков могут пересекаться, но не быть обязательно противоположными. Это, в частности, может приводить к ситуациям, взаимовыгодным обоим игрокам (в антагонистическом конфликте это невозможно), что делает осмысленным кооперирование (выбор согласованного решения), приводящее к увеличению выигрыша обоих игроков. Однако возможны такие конфликты, когда кооперация или соглашение невозможны по правилам игры. Поэтому в неантагонистических играх различают бескоалиционное поведение, когда соглашения между игроками запрещены правилами (см. § 1 — 5), и кооперативное поведение игроков, когда разрешается кооперация типа выбора совместных стратегий (см. § 6 — 8) и совершения побочных платежей (см. § 9 — 11). Рассмотрим первый случай.
1.2. Определение. Система
Г=(N,
в которой N={\, 2, ..., п} — множество игроков, Xt— множество стратегий игрока i, Hi — функция выигрыша игрока і, определенная
П
на декартовом произведении множеств стратегий игроков X=Y[ Xt
i-і
(множество ситуаций игры), называется бескоалиционной игрой.
Бескоалиционная игра п лиц происходит следующим образом. Игроки одновременно и независимо друг от друга выбирают свои стратегии xt из множеств стратегий Xh г = 1, 2, ..., и, в результате
из
чего формируется ситуация л:= (xt, ..., х„), x,е Xt. После этого каждый игрок і получает выигрыш Н, (х). На этом игра заканчивается. Если множества чистых стратегий игроков X, конечны, то игра
называется конечной бескоалиционной игрой п лиц.
1.3. Бескоалиционная игра Г, в которой принимают участие два игрока, называется игрой двух лиц. Таким образом, бескоалиционная игра двух лиц Г в нормальной форме определяется системой Г= (Х1, Х2, Н1} Н2), где Xt — множество стратегий первого игрока, Х2 — множество стратегий второго игрока, Х1хХ2 — множество ситуаций игры, a Hl: Xl х X2-*Rl, H2:Xlx X2-*Rl — функции выигрыша соответственно 1 и 2 игроков. Конечная бескоалиционная игра двух лиц называется биматричной. Это объясняется тем, что перенумеровав множества чистых стратегий игроков числами 1, 2, ..., т и 1, 2, ..., п соответственно, функции выигрыша можно записать в виде двух матриц
| |||||||||
| При этом элементы ау и /?у матриц А, В являются соответственно |
В соответствии с изложенным выше биматричная игра происходит следующим образом. Первый игрок выбирает номер і строки, а второй (одновременно и независимо) номер j столбца матрицы. Тогда игрок 1 получает выигрыш aij=Hl (хи у}), а игрок 2 — выигрыш рІГН2(хь yj).
Заметим, что биматричную игру с матрицами А и В можно также задать (in х п) матрицей (А, В), каждый элемент которой есть пара (аф /=1, 2, ..., т\ j= 1, 2, ..., іі. Игру, определяемую
матрицами А а В, будем обозначать Г (А, В).
Если бескоалиционная игра Г двух лиц такова, что Н1(х, у)= —Н2(х, у) для всех хеХ? уеХ2, то Г оказывается антагонистической игрой, рассмотренной в предыдущих главах. В частном случае, когда в биматричной игре ау = — /?„, мы получаем матричную игру, рассмотренную в гл. 1.
1.4. Пример 1. («Семейный спор».) Рассматривается биматричная игра с матрицей
«2
(А, В) =
. ^1 02 (4, 1) (0, 0)
.(0, 0) (1, 4)
Имеются различные интерпретации этой игры, но наиболее известная [44] следующая. Муж (игрок 1) и жена (игрок 2) могут выбрать одно из двух вечерних развлечений: футбольный матч (а1; /?j) или театр (<х2, /?2). Если они имеют разные желания (а15 /?2) или (а2, /?j), то остаются дома. Муж предпочитает футбольный матч, а жена — театр. Однако обоим гораздо важнее провести вечер вместе, чем участвовать в развлечении (хотя и предпочтительном) одному.
Пример 2. (Игра «перекресток» [10]J Два автомобилиста двигаются по двум взаимно перпендикулярным дорогам и одновременно встречаются на перекрестке. Каждый из них может остановиться (1-я стратегия otj или Pj) и ехать (2-я стратегия а2 или /?2).
Предполагается, что каждый из игроков предпочитает остановиться, а не пострадать в аварии и проехать, если другой сделал остановку. Этот конфликт может быть формализован биматричной игрой с матрицей
/»і
(1, 1)
(2, 1-е)
Рг
(1-е, 2)
(О, 0) _
“і
<х2
(А, В) =
(неотрицательное число ? соответствует неудовольствию от того, что игрок остановился и пропустил партнера).
Пример 3. (Выбор способа передвижения /іо городу [10] J Пусть число игроков п велико и каждое из множеств X, состоит из двух
элементов: ^,={0, 1} (для определенности: 0 — воспользоваться
автомобилем, 1 — использовать общественный транспорт). Функция выигрыша определяется следующим образом:
га(/) при х,= \,
Ь(і) при х, = 0,
Хп) =
1 "
где t= У xj.
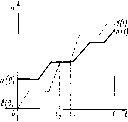 |
| Рис. 8 |
Пусть а и Ь имеют вид, изображенный на рис. 8. Из вида функций а(і) и b(t) следует, что если доля игроков, выбирающих 1, больше tv то уличное движение настолько свободно, что водитель чувствует себя лучше, чем пассажир в общественном транспорте. Если же доля автомобилистов больше 1 —10, то движение настолько интенсивное (при естественном приоритете общественного транспорта), что сравнение теперь в пользу пассажиров общественного транспорта.
Пример 4. (Распределение ограниченного ресурса с учетом интересов потребителей [52].) Предположим, что п потребителей имеют возможность расходовать (накапливать) некоторый ресурс, объем которого ограничен величиной А> 0. Обозначим объем ресурса, который расходует (накапливает) і-й потребитель, через xt.
В зависимости от значений вектора х=(хх, х2, ..., х„) потребители
получают выигрыш, который оценивается для і-го потребителя функцией А*(хІ9 х2, ..., х„), если общий объем израсходованного
(накопленного) ресурса не превосходит заданной положительной величины ?<А, т. е.
I-1
Если выполняется противоположное неравенство, то выигрыш і-го потребителя вычисляется с помощью функции gi(xt, х2, ..., хп). При
этом предполагается, что полезность ресурса резко снижается, если
Я
? Х)>0, т. е. в этом случае
i-i
g,(x2, x2, ..., xm)<hi(xi} x2, ..., xj.
Рассмотрим неантагонистическую игру в нормальной форме
Г=(ЛГ, {ЛГ,},в№ {#,},**),
в которой функции выигрыша игроков имеют вид
\ht(xu ..., х„), ?
Ні(хіг х2, ..., *„)=< '-1
L&(*1, Хп), Ё Х‘>?’
/-1
ЛГ,=[0, aj, 0<а,<Л, X а,=А, N={ 1, 2.....л}.
і-t
Игроками в этой игре являются потребители ресурса.
Пример 5. (Теоретико-игровая модель охраны воздушного бассейна от загрязнений [52].) В промышленном районе расположено л предприятий, каждое из которых имеет один источник, выбрасывающий в атмосферу вредную примесь. В районе имеется экологически значимая зона П, уровень загрязнения в которой не должен превышать предельно допустимого значения. Усредненное по времени и области значение концентрации вредной примеси в атмосфере при наличии л источников можно приближенно рассчитать по формуле
q=Y, c‘xh » = 1, 2, n, 0<x,<a,.
(-1
П
Пусть ? < см — значение предельно допустимой концентрации
t-i
(ПДК) вредной примеси.
Считая предприятия игроками, построим игру, моделирующую конфликтную ситуацию загрязнения атмосферы. Предположим, что каждое предприятие і может снижать свои эксплуатационные расходы, увеличивая выброс х,, однако если в зоне Q уровень загрязнения превышает ПДК, на предприятие накладывается штраф 5,>0.
Пусть игрок / (предприятие) имеет возможность выбирать значения х, из множества ЛГ,=[0, а]. Функции выигрыша игроков
имеют вид
hi(xu х2, hi(xu х2,
; *я),
.., x„)-sh q>e,
где A,(xl5 х2, ..., хп) — непрерывные и возрастающие по аргументу Хі функции.
§ 2. ПРИНЦИПЫ ОПТИМАЛЬНОСТИ В БЕСКОАЛИЦИОННЫХ
ИГРАХ
2.1. Известно, что для антагонистических игр принципы минима-кса, максимина и равновесия совпадают (если они реализуемы, т. е. существует равновесие, а максимин и минимакс достигаются). В таком случае они определяют единое понятие оптимальности и решения игры. В теории неантагонистических игр нет единого подхода к выработке принципов оптимальности. По существу имеется целое множество таких принципов, каждый из которых основывается на некоторых дополнительных предположениях о поведении игроков и структуре игры.
Естественно предположить, что в игре Г каждый из игроков стремится к достижению ситуации х, в которой значение его функции выигрыша было бы наибольшим. Однако функция выигрыша Ні зависит не только от стратегии і-го игрока, но и от стратегий, выбираемых другими игроками, поэтому ситуации {jc}, дающие большее значение выигрыша для і-го игрока, могут не быть таковыми для других игроков. Таким образом, так же как и в случае антагонистической игры, стремление игроков получить наибольший выигрыш носит конфликтный характер и сама формулировка того, какое поведение является «хорошим» или оптимальным в игре, является проблематичной. Здесь имеется несколько подходов. Одним из них является равновесие по Нэшу и его различные обобщения. В случае, когда игра Г является антагонистической, равновесие по Нэшу совпадает с понятием равновесия, которое представляет собой основной принцип оптимальности в антагонистической игре. Пусть х=(х1, ..., Хі_{, xh xi+l, ..., х„) — произвольная ситуация
в игре Г, а х( — некоторая стратегия игрока і. Построим ситуацию,
которая отлична от х только тем, что стратегия х{ игрока і заменена
на стратегию х|. В результате мы получаем ситуацию (хи ..., х,_,, х-,
х,+і, ..., х„), которую будем обозначать через (x||xj). Очевидно, что
если Xj и x'j совпадают, то (x||xj)=x.
Определение. Ситуация х* = (х*, ..., xf, ..., xf) называется ситуацией равновесия по Нэшу, если для всех xf е Xt и і=1,.... п имеет
место неравенство
Н,(х*)>Н(х* ||х;). (2.1)
Пример 6. Рассмотрим игру примера 3 п. 1.4. Равновесными по Нэшу здесь являются ситуации, для которых выполняется условие
(2.2) где t*=(l/n) ? xf. Из условия (2.2) следует, что переключение
7-1 „ „
каждого отдельного игрока с одной чистой стратегии на другую при условии, что другие игроки своих стратегий не изменяют, не влияет на его выигрыш.
Пусть в игре реализовалась ситуация х, которой соответствует
R
t=(l/n) ? Xj, te{t0, fj}, и пусть величина 8 — доля игроков, решивших переключиться со стратегии 0 на стратегию 1. Заметим, что если 8 таково, что b(i) = a(i)<a(t+8), то выигрыши этих игроков увеличиваются при таком переключении, если стратегии остальных игроков останутся прежними. Однако если это переключение действительно произойдет, то у тех же игроков возникает желание переключиться со стратегии 1 на стратегию 0, поскольку выполнено условие а (t+8)<b(t+8). Если же это желание осуществится, то
доля (1/л) ¦ ? Xj игроков уменьшится и вновь попадет на отрезок
г п
['о, *1І-
Аналогично, пусть 8 — доля игроков, переключившихся цо каким-либо причинам (например, из-за случайных ошибок) со стратегии 1 на стратегию 0, причем t—8<t0. Тогда в силу условия b(t—8)<a(t~ 8) у игроков появится желание переключиться обратно на стратегию 1. При осуществлении этого желания доля
П
1/и ¦ Y, хі увеличится и вновь вернется на отрезок [/0, /J.
ill. Из определения ситуации равновесия по Нэшу следует, что ни один из игроков і не заинтересован в отклонении от стратегии х,*, входящей в эту ситуацию (согласно (2.1) его выигрыш при использовании стратегии xf вместо х* разве лишь уменьшится при условии, что остальные игроки придерживаются стратегий, образующих ситуацию равновесия х*). Таким образом, если игроки договорились предварительно об использовании стратегий, входящих в ситуацию равновесия х*, то индивидуальное отклонение от договора невыгодно отклонившемуся игроку.
Определение. Стратегия х* е Хі называется равновесной, если
она входит хотя бы в одну ситуацию равновесия по Нэшу.
Для бескоалиционной игры двух лиц Г = (АГ1, Х2, ЯІ5 Я^ ситуация (х*, у*) является ситуацией равновесия, если неравенства
Н1 (х, у'НН, (.х*, у*), Я2(х*. уНН2(х*, у*) (2.3)
выполняются для всех хеХ2 и ye Y2.
В частности, для биматричной (т х л)-игры Г (А, В) пара (/*, /*) будет ситуацией равновесия по Нэшу, если неравенства
(2-4)
выполняются для всех номеров строк іеМ и столбцов jeN. Так, в примере 1 равновесными являются ситуации (аІ9 Р2) и (а2, /?2), в примере 2 — (аІ9 и (а2, /?2).
Напомним, что для антагонистической игры Г = (АГ1, Х2, Н) пара (х*, у*) е Хх хХ2 является ситуацией равновесия, если
Н(х, у*)^Н(х*, /)а(х*, у), хеХ2, уеХ2.
При этом имеют место следующие основные свойства антагонистических игр.
1°‘. Игроку невыгодно информировать своего противника о стратегии (чистой или смешанной), которую он собирается применить. (Конечно, если игрок собирается использовать оптимальную стратегию, то его выигрыш не уменьшится от того, что он объявит об этом, но он ничего и не выигрывает.)
2°. Если (х, y)eZ(Г), (х', у')еZ(Г) — ситуации равновесия в игре Г, а г — значение игры, то
(x',y)eZ(T),(x,y')eZ(Г); (2.5)
?=Н(х, у)=Н(хг, /) = Я(х, /)=Я(х', у). (2.6)
3°. Игроки не заинтересованы в общении перед началом игры для выработки совместных действий.
4°. Если в игре Г существует ситуация равновесия, ах — мак-симинная и у — минимаксная стратегии соответственно 1 и 2 игроков, то (х, у) 6 Z (Г) — ситуация равновесия, и наоборот.
Выясним, выполняются ли эти свойства для биматричных игр.
Пример 7. Рассмотрим игру «семейный спор» (см. пример 1 и п. 1.4). Как уже отмечалось, в ней есть две равновесные ситуации (als Рі) и (a2, Р2)- Однако 1-я ситуация выгодна игроку 1, а 2-я — игроку
2. Это противоречит (2.6), поскольку выигрыши игроков в этих ситуациях различны. Далее заметим, что, несмотря на равновесность ситуаций (al5 /?2), (а2, Р2), пары (al5 /?2) и (а2, /?2) не являются ситуациями равновесия по Нэшу, т. е. не выполнено свойство 2 (см.
(2.5)).
Если игрок 1 информирует партнера о намерении выбрать стратегию а2 и если игрок 2 убежден, что тот будет упорствовать, то ему ничего не остается, как объявить первую стратегию /?2. Аналогичные рассуждения можно провести и за игрока 2. Таким образом, каждому из игроков выгодно первому объявить свою стратегию, что противоречит свойству 1° для антагонистических игр.
Предположим, что игроки не общаются до начала игры, а делают выбор одновременно и независимо друг от друга (как и предусмотрено правилами бескоалиционной игры). Проведем рассуждения за игрока 1. Ему выгодно, чтобы реализовалась ситуация (al5 Р2). Но игроку 2 выгодна ситуация (а2, /?2). Поэтому, если игрок 1 выберет стратегию al5 то игрок 2 может выбрать стратегию /?2, и они оба проиграют (вектор выигрышей (0, 0)). Тогда игроку 1 имеет смысл выбрать стратегию а2, поскольку в ситуации (а2, /?Д он получает выигрыш 1. Но игрок 2 может рассуждать аналогично и выбрать Pt, тогда в ситуации (а2, /?2) они оба опять проиграют.
Таким образом, имеет место случай, когда ситуация выгодна (и поэтому неустойчива) для игрока 1. Аналогично (с точки зрения игрока 2) можно исследовать ситуацию (а2, /?2). Поэтому игрокам выгодно общаться перед началом игры и договариваться о совместном плане действий, что противоречит свойству 3°. Затруднения возникают также из-за того, что пара максиминных стратегий не является равновесной.
Таким образом, мы имеем пример игры, когда не выполнено ни одно из свойств 1° — 4° антагонистической игры.
Итак, в различных ситуациях равновесия по Нэшу векторы выигрышей игроков могут быть различны. Кроме того, множество ситуаций равновесия по Нэшу в отличие от множества ситуаций равновесия в антагонистической игре не является прямоугольным. Если х=(х15 ..., х„ ..., х„) и х' = (х'1, ..., x'j, ..., х’„) — две различные
ситуации равновесия, то ситуация х", состоящая из стратегий, которые образуют ситуации х и х', и не совпадающая ни с одной из этих ситуаций, равновесной может не являться. Ситуация равновесия по Нэшу является множественным принципом оптимальности в том смысле, что различные ситуации равновесия могут быть в разной степени предпочтительными для различных игроков. Таким образом, остается не решенным вопрос: какую из ситуаций равновесия можно принять как устраивающий всех игроков принцип оптимальности? В дальнейшем будет показано, что множественность принципа оптимальности является существенной характерной чертой оптимального поведения в конфликтных управляемых процессах со многими участниками.
Заметим также, что в отличие от антагонистического случая равновесная стратегия /-го игрока х* далеко не всегда обеспечивает получение, по крайней мере, выигрыша Д (х*) в ситуации равновесия по Нэшу, поскольку это существенно зависит от того, выберут ли остальные игроки стратегии, входящие в данную ситуацию равновесия по Нэшу. Поэтому равновесную стратегию не следует трактовать как оптимальную стратегию /-го игрока. Такая трактовка осмыслена только для набора стратегий игроков, т. е. для ситуаций.
2.3. Важная особенность ситуации равновесия по Нэшу заключается в том, что отклонение от нее двух игроков и более может привести к увеличению выигрыша одного из отклонившихся игроков. Пусть S <= N — некоторое подмножество множества игроков (коалиция) и пусть х=(х15 ..., хп) — ситуация в игре Г. Обозначим
через (х||х^) — ситуацию, которая получается из ситуации х при замене в ней стратегий xh ieS, на стратегии x,ieXi, ieS. Иными
словами, в ситуации (х||х') игроки, входящие в коалицию S, заменяют свои стратегии xt на стратегии jcJ. Если х* — ситуация равновесия по Нэшу, то из (2.1) вовсе не следует, что
Д(х*) ^ Н(х* ||xs) для всех / е S. (2.7)
Это будет показано далее на простейших примерах.
Можно усилить понятие равновесия по Нэшу, потребовав выполнения условия (2.7) или ослабленного условия (2.7) хотя бы для одного из игроков ieS. Тогда мы приходим к следующему определению.
Определение. Ситуация х* называется сильно равновесной, если для любых коалиций S а N и xse ]~[ X, выполняется неравенство
ieS
ІД(**)^ІД(** ||х,). (2.8)
ieS IeS
Условие (2.8) гарантирует нецелесообразность соглашения между игроками с целью вступления в некоторую коалицию S, так как в любой коалиции находится игрок /, которого это соглашение не устраивает. Любая сильно равновесная ситуация является равновесной.
Если бы сильное равновесие существовало в достаточно широком классе игр, то оно могло бы явиться приемлемым принципом оптимальности в бескоалиционной игре. Однако оно существует крайне редко.
Пример 8. Рассмотрим биматричную игру с матрицей
fll
(5, 5) (10,0)
Рг
(0, 10)1
(1, 1) I
(А, ?) =
Здесь одна ситуация равновесия (ос2, /?2) (не сильно равновесная), которая дает игрокам вектор выигрышей (1, 1). Однако если оба игрока сыграют (<хІ9 /1Д то они получат вектор выигрышей (5, 5), что выгодно обоим. Эта ситуация не является равновесной, но она лучшая для обоих игроков. Таких парадоксов в антагонистических играх не бывает. Если говорить об этом конкретном случае, то данный результат является следствием того, что при одновременном отклонении от равновесной стратегии каждый из игроков может выиграть еще больше.
2.4. Пример 8 приводит к мысли о возможности других принципов оптимальности в бескоалиционной игре, приводящих к ситуациям, более выгодным обоим участникам, чем в случае равновесных ситуаций. Таким принципом оптимальности является оптимальность по Парето.
Рассмотрим множество векторов {Я(х)} = {(Ях (х),
П
Н„ (х))}х еХ, Х= J~[ Xh т. е. множество значений вектор-выигрышей
игроков во всех возможных ситуациях хеХ.
Определение. Ситуация х в бескоалиционной игре Г называется оптимальной по Парето, если не существует ситуации хеX, для которой имеют место неравенства
Ні (х)>Ні(х) для всех ieN и Яіо(х)>Яіо(х) хотя бы для одного i0eN.
Множество всех ситуаций, оптимальных по Парето, будем обозначать через Xе. _
Содержательно принадлежность ситуации х множеству Xе означает, что не существует другой ситуации х, которая была бы предпочтительнее ситуации х для всех игроков.
Следуя [2], отметим содержательное различие понятий ситуации равновесия и ситуации, оптимальной по Парето. В первой ситуации ни один игрок, действуя в одиночку, не может увеличить своего выигрыша, во второй — все игроки, действуя совместно, не могут (даже не строго) увеличить выигрыш каждого.
Заметим также, что соглашение о выборе фиксированной ситуации равновесия удерживает каждого индивидуального игрока от отклонения от нее. В оптимальной по Парето ситуации отклонившийся игрок может в некоторых случаях получить существенно больший выигрыш. В то же время сильно равновесная ситуация безусловно является и оптимальной по Парето. Так, в примере 8 ситуация (а2, /?2) равновесна, но не оптимальна по Парето. Вместе с тем ситуация (аІ5 Ру), наоборот, оптимальна по Парето, но не является равновесной. В игре «семейный спор» обе равновесные ситуации (а2, Ру), (а2, Р2) сильно равновесны и оптимальны по Парето, но, как уже отмечено в примере 7, не являются взаимозаменяемыми. Такая же картина имеет место и в следующем примере.
Пример 9. Рассмотрим игру «перекресток» (см. пример 2 п. 1.4). Ситуации (а2, /?,), (а2, /?2) равновесны и оптимальны по Парето (ситуация (al9 Ру) оптимальна по Парето, но не равновесна). Для каждого игрока равновесной является стратегия а у, Ру «остановиться», если другой игрок решил проехать перекресток, и, наоборот, выгодно выбрать стратегию а2, /?2 «ехать», если другой игрок остановился. Однако выигрыш в две единицы каждый из игроков получает только при выборе стратегии а2 (fi2) — «ехать», поэтому здесь неизбежна борьба за лидерство, т. е. каждый из игроков заинтересован первым заявить, что он выбрал стратегию «ехать».
Заметим, что точно к такому же выводу мы пришли при анализе игры «семейный спор» (см. пример 7).
2.5. Проанализируем поведение типа лидер — ведомый в игре двух лиц Г=(ЛГ1, Х2, Ну, Н2). Обозначим Z1, Z2 множества наилучших ответов игроков 1 и 2 соответственно, где
zl = {(*i, х2)\Ну(ху, x2) = sup Нуіуу, х2)}- (2.9)
yt
Zz = {(xlt х2)\Н2(ху, x2) = sup Н2(ху, у2)} (2.10)
Уі
(предполагается, что супремумы в (2.9) и (2.10) достигаются).
Определение. Назовем ситуацию (х1, х2)еХуХ Х2 і-равновеси-ем по Штакельбергу в игре двух лиц Г, а Н і-выигрышем, если (ху,
x2)ezf и выполняется равенство
~Hi—Hj (ху, х2)= sup Н(уу,у2), (2.11)
(Уі.
где і= 1, 2, іфj.
Понятие /-равновесия можно интерпретировать следующим образом. Игрок 1 (лидер) знает функции выигрыша обоих игроков Ну,
Н2, а тем самым и множество наилучших ответов Z2 игрока 2 (ведомого) на любую стратегию х1 игрока 1. Тогда он, обладая этой информацией, максимизирует свой выигрыш, выбирая стратегию jc1 из условия (2.11). Таким образом, Я,— это выигрыш г'-го игрока, действующего оптимально в качестве «лидера» в игре Г.
Лемма. Пусть Z(T) — множество ситуаций равновесия по Нэшу в игре двух лиц Г. Тогда
Z(T)=Zlf]Z2, (2.12)
где Z1, Z2 — множества наилучших ответов (2.9), (2.10) игроков 1, 2 в игре Г.
Доказательство. Пусть (xl5 jc2)eZ(T) — ситуация равновесия по Нэшу. Тогда неравенства
Яі(*і, х2К#і(*і, Х2І Л2(хі> *2)^2(*і» хг)
выполняются для всех x'l^Xl a x,2eX2. Откуда получаем
H1 (xv x2)=sup H2 (x’1, x2); (2.13)
¦*1
H2 (xl5 x2)=sup H2 (xlt xf2). (2.14)
•*»
Таким образом, (jc2, x2) e Z1 и (xl5 x2)eZ2, t. e. (xl5 x2)eZ1f)Z2.
Обратное включение непосредственно следует из (2.13), (2.14). Лемма доказана.
Определение. Будем говорить, что в игре двух лиц Г=(ЛГ1, Х2, Н? Н2) имеет место борьба за лидерство, если не существует такой ситуации (хІ5 х2)е Хі*Х2, что
Н^ЪІх,, х2), і=1,2. (2.15)
Теорема. Если игра двух лиц Г=(Х2, Х2, ЯІ5 Н2) имеет по крайней мере две оптимальных по Парето и равновесных по Нэшу ситуации (х1( х2), (у2, у2) с различными векторами выигрышей
(#і (xlt х2), Н2 (х15 х2))ф(Н1 (у15 у2), Н2 (уи у2)), (2.16)
то в игре Г имеет место борьба за лидерство.
Доказательство. В силу (2.12) для всякой ситуации равновесия по Нэшу (z2, z2)eZ(T) справедливы неравенства
Я,(г1; z2)<Ни i=l, 2.
Предположим противное, т. е. что в игре Г нет борьбы за лидерство. Тогда существует ситуация (z2, z2) еХ1 х Х2, для которой
z2); (2.17)
Я,(Ух, yJ^H,^Hi(zlt z2), (2.18)
j=l, 2. Ho (xj, x2), (уи у?) — ситуации, оптимальные по Парето. Поэтому неравенства (2.17), (2.18) выполняются как равенства, что противоречит (2.16). Теорема доказана.
В заключение заметим, что игры «семейный спор» и «перекресток» (п. 1.4) удовлетворяют условиям теоремы п. 2.5, поэтому в них имеет место борьба за лидерство.
§ 3. СМЕШАННОЕ РАСШИРЕНИЕ БЕСКОАЛИЦИОННОЙ ИГРЫ
3.1. Рассмотрим бескоалиционную игру двух лиц Г=(АГ1, Х2, Н2, Яг). В антагонистическом случае мы уже убедились, что ситуация равновесия в обычных чистых стратегиях, вообще говоря, не существует. Даже матричные игры в общем случае имеют ситуацию равновесия лишь в смешанных стратегиях. Поэтому естественно искать равновесие по Пэшу в бескоалиционной игре в классе смешанных стратегий.
Как и в случае антагонистических игр, смешанную стратегию игрока мы отождествляем с вероятностным распределением на множестве чистых стратегий. Предположим для простоты, что множества стратегий X, конечны, и введем понятие смешанного расширения игры. Пусть
Г=(Я, {Xt}leN, {Ht}leN) (3.1)
— произвольная конечная бескоалиционная игра. Для определенности предположим, что игрок 1 в игре Г имеет щ стратегий.
Обозначим через д, произвольную смешанную стратегию игрока
і, т. е. некоторое вероятностное распределение на множестве стратегий Xh которые назовем чистыми стратегиями. Через д((х() будем
обозначать вероятность, которую стратегия д, приписывает конкретной чистой стратегии xteXi. Множество всех смешанных стратегий игрока / будем обозначать через Xt.
Пусть каждый из игроков ieN применяет свою смешанную стратегию д,, т. е. выбирает чистые стратегии с вероятностями
д,(х,). Будем предполагать, что вероятность появления ситуации х=(х1, х„) равна произведению вероятностей выборов составля
ющих ее стратегий, т. е.
д (х) = Ді (Хі) х д2 (х2) х... х д, (хя). (3.2)
Формула (3.2) определяет вероятностное распределение на мно-
Я
жестве всех ситуаций 3^=П определяемое смешанными страте-
j-i
гиями ц1г р2, .... Рп- Набор р—ір^ ..., рп) называется ситуацией
в смешанных стратегиях. Ситуация в смешанных стратегиях р реализует различные ситуации в чистых стратегиях с некоторыми вероятностями, поэтому значение функции выигрыша каждого из игроков оказывается случайной величиной. В качестве значения функции выигрыша і-го игрока в ситуации р принимается математическое ожидание этой случайной величины:
*і(/0=Е Н,(х)р(х)= ? ... ? Н,(хи .., х„)х
хеХ х,еХ, хяеХп
х рх (хх) х ...хря(хя), ieN, х=(х1.....х„)еХ. (3.3)
Введем обозначение
кы*}= I... I I ... Е ад № П №(**)¦ (3-4)
*,бХ, xj_ieXj^i xj+ieXj+i хяеХя k+J
Пусть fij — произвольная смешанная стратегия игрока j в игре Г. Умножив (3.4) на Pj(xj) и просуммировав по всем хJeA), получаем
_ _
Определение. Игра Г=(N, {Xi}ieN{K,}iefi), в которой N — множество игроков, Хі — множество смешанных стратегий каждого
игрока і, а функция выигрыша определяется равенством (3.3), называется смешанным расширением игры Г.
Если для любой чистой стратегии xt игрока і имеет место
неравенство А)(д||х{)<а, то для любой смешанной стратегии р', выполняется неравенство Kj(p\\pj)^a. Справедливость этого вытекает
из (3.3) и (3.4) стандартным переходом к смешанным стратегиям.
3.2. Для биматричной (тхп) игры Г (А, В) можно определить множества смешанных стратегий Х1г Х2 соответственно 1 и 2 игроков в виде
Xl = {х | xw = 1, х^О, хеЛ"1},
X2 = {y\yw=\, у^О, уеВ"},
где м = (1, ..., 1)еВГ, w = (l,..., 1)еЛ", а также выигрыши игроков К1 и К2 в ситуации (х, у) в смешанных стратегиях как математическое ожидание выигрыша
Кі (х, у)=хАу, К2(х, у)=хВу, хеХи уеХ2.
Следовательно, формально построено смешанное расширение Г (А, В) игры Г (А, В), т. е. бескоалиционная игра двух лиц Г (А, В) = Х2, Ки К^.
Для биматричной игры (как и для матричной) множество Мх={і\? >0) будем называть спектром смешанной стратегии
х=(Л\., ?m) игрока 1, а стратегию х, для которой МХ=М, М—{\,
2, т) —вполне смешанной. Аналогично, Ny={j\tjj>0} —спектр
смешанной стратегии п„} игрока 2 в биматричной (т х п)-
игре Г (А, В). Ситуацию (х, у), в которой обе стратегии хи у вполне смешанные, будем называть вполне смешанной.
Покажем на примере игры «семейный спор», что введение смешанных стратегий не снимает те трудности, которые возникают при анализе бескоалиционной игры (см. пример 7 п. 2.2).
Пример 10. Пусть в игре «семейный спор» игрок 1 хочет максимально увеличить свой гарантированный выигрыш. Это означает, что он намерен выбрать смешанную стратегию х° = (^°, 1 — ?°), 1 так, чтобы максимально увеличить наименьшую из двух величин К2 (х, /?х) и К2 (х, /?2), т. е.
, max min {АГі (х, /?Д К^х, 02)}=тіп {К^х0, ^), К2(х0, 02)}.
X
Максиминная стратегия х° игрока 1 имеет вид х°=(1/5, 4/5) и дает ему средний гарантированный выигрыш 4/5. Если игрок 2 выберет стратегию /?1; то выигрыши игроков будут равны (4/5, 1/5), если же он воспользуется стратегией /?2, то (4/5, 16/5).
Таким образом, если игрок 2 догадается, что его партнер придерживается стратегии х°, то он выберет в, и получит выигрыш 16/5 (Если игрок 1 может обосновать выбор р2 за игрока 2, то он может улучшить и свой выбор.) Аналогично, пусть игрок 2 придерживается максиминной стратегии, она имеет вид yQ = (4/5, 1/5), и если игрок 1 выбирает стратегию аІ5 то выигрыши игроков равны (16/5, 4/5), а если а2, то (1/5, 4/5), поэтому ему выгодно против максиминной стратегии у0 применять свою стратегию а.?
Если оба игрока будут рассуждать таким образом, то они приходят к ситуации (а2, /?2), в которой вектор выигрышей (0, 0). Здесь ситуация (х°, у0) в максиминных смешанных стратегиях не является ситуацией равновесия по Нэшу.
3.3. Определение. Ситуация р* называется ситуацией равновесия по Нэшу в смешанных стратегиях в игре Г, если для любого игрока і и для любой его смешанной стратегии р, имеет место
неравенство
кірцрд^кір*), 1=1,..., п.
Как показывает пример 10, ситуация в максиминных смешанных
стратегиях не обязательно является ситуацией равновесия по Нэшу в смешанных стратегиях.
Пример 11. В игре «перекресток» (см. пример 9 п. 2.4) имеются две ситуации равновесия по Нэшу в чистых стратегиях: (al5 р2) и (а2, Рі). Эти же ситуации оптимальны по Парето. В смешанном расширении игры возникает еще одна ситуация равновесия, а именно пара (х*, j>*):
* * 1~Е 1 х*=у*=-— Wl+-— и2
2-е
2-е
где М! = (1, 0), и2 = (0, 1) или х*=у* = ((1-е)/(2-е), 1/(2-б)).
Действительно, имеем
2—6 У)=2
1— е „ в
Более того, так как для любых смешанных стратегий х=(?, 1— ?) и у=(rj, 1 — т\) выполняются равенства
К, (х, у*) = ?КХ (а15 у*) + (1 - № («2,
2 — 8
К2(х*, у) = Т]К2(х*, W + 0-Т])К2(х*,
2 — 8
то получаем
К, (х, у*)=К1 (х*, у*), К2 (х*, у)=К2 (.х* >>*)
для всех смешанных стратегий хеХ^ и уеХ2. Поэтому (х*, у*) — ситуация равновесия по Нэшу. Более того, это вполне смешанная ситуация равновесия. Однако ситуация (х*, у*) не является оптимальной по Парето, так как вектор К(х*, /*)=( 1 ——, 1 —— 1
\ 2—е 2—в)
строго меньше (покомпонентно) вектора выигрышей (1, 1) в ситуации (at, Ді).
Пусть К(р*) = {Кі(ц*)} —вектор выигрышей в некоторой ситуации равновесия по Нэшу. Обозначим і>i=Ki(ji*) и Заметим, что если в антагонистических играх значение ? функции выигрыша в ситуации равновесия было одним и тем же для всех ситуаций равновесия, а следовательно, осуществлялось единственным образом для каждой антагонистической игры, в которой существовала ситуация равновесия, то в неантагонистических играх вектор ? определяется неоднозначно. Таким образом, здесь можно говорить лишь о равновесном выигрыше ?, = К,(ц*) игрока і в ситуации равновесия д*, fi* еХ, Т= П-^>- Та*, в игре «перекресток» в ситу-
і-і
ации равновесия (а1? j82) вектор равновесных выигрышей (?1г ?,) имеет вид (1 — е, 2), а в ситуации (х*, у*) он равен (1 ——, 1 —— )
\ 2-е 2-г/
(см. пример 11).
3.4. Если в бескоалиционной игре Г = (Xlt Х2, Н?, Н2) пространства стратегий бесконечны, например Xl с: Rm, Х2 с: R", то, как и в случае бесконечных антагонистических игр, сметанные стратегии игроков отождествляются с вероятностными мерами, заданными на борелевских ст-алгебрах множеств Xt и Х2. Если д и ? — смешанные стратегии игроков 1 и 2 соответственно, то выигрыш игрока і" в этой ситуации -К,(д, ?) — математическое ожидание выигрыша, т. е.
Ki(ji,v)=\\Hi(x,y)dv(y), (3.5)
х, х2
где интегралы понимаются в смысле Стильеса. Заметим, что в ситуациях (х, ?) и (д, у) выигрыши игроков имеют вид
Кі(х, ?)= J Ні(х, у) dv(y),
Кі(ц, у)= { Ні(х, y)dn(x), і= 1, 2.
(Предполагается, что интегралы существуют.)
Таким образом, формально смешанное расширение бескоалиционной игры Г двух лиц может быть задано системой Г= (Х1; X,, Ки К2), где Х1 = {д), F2 = {v), a Kt и К2 определяются (3.5). Игра Г является бескоалиционной игрой двух лиц, поэтому ситуация (д*, ?*) равновесна тогда и только тогда, когда выполнены неравенства, аналогичные (2.3).
§ 4. СУЩЕСТВОВАНИЕ СИТУАЦИИ РАВНОВЕСИЯ ПО НЭШУ
4.1. В теории антагонистических игр для существования ситуации равновесия в смешанных стратегиях было достаточно непрерывности функции выигрыша и компактности множеств стратегий (см. п. 4.4 гл. II). Оказывается, что этих условий достаточно и для существования ситуации равновесия по Нэшу в смешанных стратегиях для бескоалиционной игры двух лиц. Вместе с тем вопрос о существовании ситуации равновесия в бескоалиционной игре двух лиц является правомерным. Уже приводился пример антагонистической игры, которая- не имеет ситуации равновесия в смешанных стратегиях (см. п. 4.12 гл. II).
Сначала докажем существование ситуации равновесия в смешанных стратегиях для биматричной игры. Это доказательство опирается на известную теорему Какутани о неподвижной точке, которую приведем без доказательства [49].
Т еорема. Пусть S — компактное выпуклое множество в R иф — многозначное отображение, переводящее точки S в компактные выпуклые подмножества S и удовлетворяющее условию: если x„eS, хя-*х, у„еф (хя), у„-+у, то у еф (х).
Тогда существует такое х* eS, что х* еф (х*).
Теорема. Пусть Г (А, В) — биматричная (тх л)-игра. Тогда существуют смешанные стратегии х*еХ1и у* е Х2 игроков 1 и 2 соответственно, такие, что пара (х*, у*) является ситуацией равновесия по Нэшу.
Доказательство. Множества смешанных стратегий Xt и Х2 игроков 1 ш 2 — выпуклые многогранники, поэтому множество ситуаций Х1 х Х2 — компактное выпуклое множество.
Пусть ф — многозначное отображение,
ф-.Х^Х^хХ» определяемое соотношением
| Ф '• (*0» У о) | 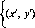 |
х.
К2(х0, /)=тах К2(хй, у), т. е. образ отображения ф состоит из пар наилучших ответов игроков на стратегии у0 и х0 соответственно.
Функции Kt и К2 как математические ожидания выигрышей в ситуации (х, у) билинейны похиу.а следовательно, образ ф(х0, j0) ситуации (х0, у0) при отображении ф представляет собой выпуклое компактное подмножество в Хх х Х2. Более того, если последовательности пар {(х”0, j5)}, (х"0, Уо)еХіхХ2 и {(х^, у'я)}, (х!п, у'п)еф{^, jo) имеют предельные точки, т. е.
lim (х?, jo)=(*0> У о)* ton 04 4) = (4 У),
л-» со л-*со
то в силу билинейности функций К1 и К? и компактности множеств Х1 и Х2 имеем, что (х', у')еф(х0, у0). Тогда по теореме Какутани существует ситуация (х*, у*) е Х1 хХ2, для которой (х*, у*)еф(х*, у*), т. е.
К,(х*, у*)^К1 (х, у*), К2(х*, у*)^К2(х*, у)
для всех xeXt и уeY2. Теорема доказана.
4.2. Предыдущая теорема может быть обобщена на случай непрерывных функций выигрыша Н1 и Н2. При доказательстве этого результата потребуется хорошо известная теорема о неподвижной точке, принадлежащая Брауэру [49].
Теорема. Пусть S — компактное выпуклое множество в R , имеющее внутренность. Если ср — непрерывное отображение S в себя, то существует неподвижная точка х* отображения <р, т. е. х* eS и х*=д>(х*).
Теорема. Пусть Г=(ЛГ1, Х2, Ни Н2) — бескоалиционная игра
двух лиц, пространства стратегий Х2 с ВТ, Х2сВ" — компактные выпуклые подмножества, а множество Х2 х Х2 имеет внутренность. Пусть также функции выигрыша H1 (jc, у) и Н2 (х, у) непрерывны на Х2 х X2, причем Н2 (х, у) вогнута по х при каждом фиксированном у, а функция Н2(х, у) вогнута по у при каждом фиксированном х.
Тогда в игре Г существует ситуация равновесия по Нэшу (jc*, у*). _ Доказательство. Пусть р = (х, у)еХ2хХ2 и q = (x, у)еХ1хХ2 — две ситуации игры Г. Рассмотрим функцию
9(p,q)=H1 (х, у)+Н2 (х, у).
Покажем прежде всего, что существует ситуация q* = (x*, у*), для которой
max ?(р, q*)=9(q*, q*).
peXi xjfj
Действительно, пусть это не так. Тогда для каждого qeX1x.X2 найдется такое реХ2 хХ2, p^q, что ?(р, q)>9(q, q). Введем в рассмотрение множество
GP = {q\9{p, q)>9(q, q)}.
Так как функция 9 непрерывна (Н2 и Н2 непрерывны по совокупности переменных), a Xt х Х2 — выпуклый компакт, то множества Gp открыты. Более того, согласно сделанному предположению,
Х1 х Х2 покрыто множествами Gp.
Из компактности Ху х Х2 следует, что найдется конечная совокупность этих множеств, которая покрывает Х2 х Х2. Пусть это множества GPi, ..., Gfk. Обозначим
<Pj(q)=max{9(pj, q)-9(q, q), 0}.
Функции q>j(q) не отрицательны, и по определению Gp в каждой точке q по крайней мере одна из функций ср} принимает положительное значение.
Определим отображение ф множества Х2 х Х2 в себя следующим образом:
Ф(я)=— Z <рАя)р*
ф(я) j
где <jо (я) —Yd Ч>Ая)- Функции (pj непрерывны, поэтому ф — непрерывное отображение Х1 х Х2 в себя. Согласно теореме Брауэра о неподвижной точке, найдется такая точка q^Xl хІ2, что ф(ц)=ц, т. е.
q = (l/(p(q)) Yj фАя)Р)-j
Следовательно,
Hl й=в (ik ? «}
Но функция ?(р, q) вогнута по р при фиксированном q и, следовательно,&(q, Я)>~^=: Z 9/ (?)? (Рр Я)- (4.1)
<PW j
С другой стороны, если <р/5)>0, то 6(q, q)<6(pj, q), а если (pj(q)=0, то q>j(q)e(pj, q) = %(q) ? (q, q). Поскольку q>j(q)>0 для некоторого j, мы приходим к неравенству
?(Я,Я)<~р: Z я>Ая)в(рр Я),
?(я) у
которое противоречит (4.1).
Таким образом, всегда существует q*, для которого
max ?(р, q*)-Q{q*, q*).
реЛT, xJT2
Это означает, что
(x, y*)+H2 (x*, y)^H1 (x*, y*)+H2 (x*, y*)
при всех xeX^ и ye Y2. Последовательно полагая в последнем неравенстве х=х* и у=у*, получаем неравенства
Н2 {х*, у)^Н2 (х*, у*), Н2 (х, y*)^Ht (х*, у*),
справедливые для всех хеХ1и уеХ2. Теорема доказана.
Для бескоалиционных игр двух лиц, разыгрываемых на компактных множествах (в частности, на единичном квадрате) с непрерывной функцией выигрыша, справедлив следующий результат.
Теорема. Пусть Y=(XU Х2, Ни Н2) — бескоалиционная игра двух лиц, где Ht и Н2 — непрерывные функции на Х1 х Х2; Хи Х2 —
132 компактные подмножества конечномерных евклидовых пространств. Тогда игра Г имеет ситуацию равновесия (р, ?) в смешанных стратегиях.
Эту теорему приведем без доказательства, поскольку оно основывается на непрерывности и билинейности функций
К,(р, ?)= J J Ні(х, y)dp(x)dv(y), i = l, 2,
_ _ х' х>
на множестве Х1хХ2 и почти дословно повторяет доказательство предыдущей теоремы.
Мы не будем подробно останавливаться на построении смешанных стратегий в бескоалиционных играх п лиц с бесконечным числом стратегий и доказательстве существования ситуации равновесия по Нэіпу. Отметим только, что если функции выигрыша
П
игроков Н, (х) непрерывны на декартовом произведении Л'=]_[ X,
і-і
компактных множеств чистых стратегий, то в такой бескоалиционной игре всегда существует ситуация равновесия по Нэшу в смешанных стратегиях. Для существования ситуаций, оптимальных по Парето, достаточно компактности множества (#(х)}, хеХ, что, в свою очередь, может быть обеспечено компактностью в некоторой топологии множества всех ситуаций X и непрерывностью в этой же топологии всех функций выигрыша Кі, і= 1, 2, ..., п. Очевидно,
что для конечных бескоалиционных игр это всегда имеет место.
§ 5. СВОЙСТВА ОПТИМАЛЬНЫХ РЕШЕНИЙ
5.1. Приведем свойства ситуации равновесия, которые помогают находить решение бескоалиционной игры двух лиц.
Теорема. Для того чтобы ситуация (р.*, ?*) в смешанных стратегиях в игре Г = (ЛГ1, Х2, Н2, Н2) была ситуацией равновесия, необходимо и достаточно, чтобы для всех чистых стратегий хеХ2 и у еХ2 игроков выполнялись следующие неравенства:
V*); (5.1)
K2Qi*,y)^K2Qi*,V*). (5.2)
Доказательство. Необходимость очевидна, поскольку каждая чистая стратегия является частным случаем смешанной и, следовательно, должны быть выполнены неравенства (5.1), (5.2). Для доказательства достаточности необходимо перейти к смешанным стратегиям игроков I и 2 соответственно в неравенствах (5.1), (5.2).
Эта теорема (как и в случае антагонистических игр) показывает, что для доказательства равновесности ситуации в смешанных стратегиях достаточно проверить неравенства (5.1), (5.2) только для чистых стратегий партнера. Для биматричной (т х л)-игры Г (А, В) эти неравенства принимают соответственно вид
(»\ y*) = aty* ^х*Ау*=К1 (х*, у*); (5.3)
K2(x*,j)=x*ti^x*By* = K2(x*, у*), (5.4)
где а,{У) — строки (столбцы) матрицы А (В), і= 1, ..., т\ 7=1, ..., п.
5.2. Напомним, что для матричных игр каждая существенная чистая стратегия уравновешивает любую оптимальную стратегию противника (см. п. 7.6 гл. I). Аналогичный результат справедлив и для биматричных игр.
Теорема. Пусть Г (А, В) — биматричная (т х п)-игра и пусть (х, y)eZ(T) — ситуация равновесия по Нэшу в смешанных стратегиях. Тогда выполняются равенства
для всех іеМх и jeNy, где Mx(Ny) — спектр смешанной стратегии х(у).
Доказательство. По теореме п. 5.1 имеем
для всех і 6 Мх. Пусть выполняется хотя бы одно строгое неравенство в (5.7), т. е.
где і0еМх. Обозначим & компоненты вектора x=(?t, ..., ?т). Тогда
&о>0 и
K1(x,y)=t^jK1(i,y) =
1-1
= 1 ?іК1(і,у)=К1(х, у) ? Ь=К2(х, у).
іеМх івМх
Противоречие доказывает справедливость (5.5). Равенства (5.6) доказываются аналогично.
Данная теорема дает способ нахождения оптимальных сметанных стратегий игроков в игре Г (А, В). Действительно, предположим, что мы ищем ситуацию равновесия (х, у), считая спектры стратегий Мх, Ny заданными. Тогда оптимальные стратегии должны
удовлетворять системе линейных уравнений
Уйі=? і,
хУ=?2, (5.9)
где ieMx,jeNy, vitv2 — некоторые числа. Если же ситуация равновесия (х, у) вполне смешанная, то система уравнений (5.9) принимает вид
Ау = ?1и, (5.10)
xB=v2w,
где ы = (1, ..., 1), w = (l, ..., 1) — векторы соответствующей размерности, составленные из единиц, числа ?1 = хАу, ?2 = хВу — выигрыши игроков в ситуации равновесия (х, у).
| х=?2иВ | (5.П) |
| у = ?1А~1и, | (5.12) |
| = 1 j(uA ~ 1u), v2 = 1 j(uB~ 1u). | (5.13) |
Обратно, если для векторов х, уеВГ, определяемых равенствами (5.11) — (5.13), справедливо х^О, у^О, то пара (х, у) образует ситуацию равновесия в смешанных стратегиях в игре Г (А, В) с вектором равновесных выигрышей (?1, ?2).
Доказательство. Если (х, у) — вполне смешанная ситуация равновесия, то х и у с необходимостью удовлетворяют системе (5.10). Умножая первое из равенств (5.10) на А~1, а второе — на В-1, получаем (5.11), (5.12). С другой стороны, поскольку хи= 1 и уи — 1, находим значения для ?2 и ?2. Единственность вполне смешанной ситуации (х, у) следует из единственности решения системы (5.10) в условиях теоремы.
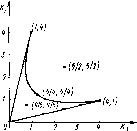 |
| Рис. 9 |
Согласно теореме п. 5.1 для того, чтобы ситуация (х, у) являлась ситуацией равновесия в смешанных стратегиях в игре Г (А, В), достаточно выполнения условий
аіу = К1(і, у) < хАу, і=1, т, хУ=К2 (х, J) < хВу, У=1, т,
или
Ау^(хАу)и, хВ^(хВу)и.
Проверим справедливость этих соотношений для х=——
иВ~1и
А'Іи
и у=-—. Имеем
иА~1и
(иВ~іАА~іи)и (иВ~1 и) (иА ~1 и)
и
иА~1и
~(рсАу)и,
Ay —
(иВ~1ВА~1и)и
(иВ~*и)(иА~*и)
и
иВ~1и
хВ=
= (хВу)и,
что и требовалось доказать.
Проиллюстрируем применение теоремы на примере игры «семейный спор» п. 1.4. Рассмотрим смешанное расширение игры. Множество точек, соответствующих векторам выигрышей в смешанных стратегиях, можно изобразить графически (рис. 9, упр. 6). Нетрудно заметить, что игра удовлетворяет условиям теоремы, поэтому здесь имеется единственная вполне смешанная ситуация равновесия (х, у), вычисляемая по формулам (5.11) — (5.13): х=(4/5, 1/5), у=( 1/5, 4/5), (?и ?2) = (4/5, 4/5).
5.4. Рассмотрим свойства различных принципов оптимальности. Заметим, что определения оптимальности ситуации по Парето и Нэшу, приведенные в § 2, касаются произвольной бескоалиционной игры (в частности, двух лиц), поэтому они справедливы и для смешанного расширения Г. Следовательно, для игры двух лиц
z(T)=zLf)z2
(где Z (Г) — множество ситуаций равновесия по Нэшу, Z1 и Z2 — .множества наилучших ответов игроков 1 и 2 соответственно в игре Г) и справедлива теорема о борьбе за лидерство (см. п. 2.5).
В более сложном отношении находятся ситуации, равновесные по Нэшу и оптимальные по Парето. Из примеров § 2 следует, что возможны случаи, когда ситуация равновесна по Нэшу, но не оптимальна по Парето, и наоборот. Вместе с тем возможно, что одна и та же ситуация оптимальна и в том и в другом смысле (п. 2.4).
В примере 11 п. 3.3 было показано, что дополнительная ситуация равновесия, возникающая в смешанном расширении игры Г, не является оптимальной по Парето в смешанном расширении Г. Оказывается, что это довольно распространенное свойство бимат-ричных игр.
Теорема. Пусть Г (А, В) — биматричная (тхгі)-игра. Тогда почти для всех (тхп)-игр (за исключением не более чем счетного множества игр) справедливо следующее утверждение.
Ситуации равновесия по Нэшу в смешанных стратегиях, которые не являются равновесными в исходной игре, не являются оптимальными по Парето в смешанном расширении.
Доказательство теоремы основано на том, что ее результат справедлив для множества Q так называемых регулярных игр, которое открыто и всюду плотно в множестве биматричных (т х л)-игр. Полное доказательство этой теоремы можно найти в [10].
5.5. Приведем без доказательства утверждения, касающиеся бескоалиционных игр п лиц, которые являются обобщением соответствующих теорем из теории биматричных игр, рассмотренных в данном и предыдущем параграфах.
Теорема. Для того чтобы ситуация р* в игре Г = (І?, {Х,}іб№ {Ні}іeN) была ситуацией равновесия в смешанных стратегиях, необходимо и достаточно, чтобы для любого і и любой чистой стратегии Xj е Хі выполнялось неравенство
WWx^W).
Теорема. В любой конечной бескоалиционной игре существует хотя бы одна ситуация равновесия по Нэшу в смешанных стратегиях.
Теорема. Если равновесная стратегия р* игрока і входит в ситуацию равновесия р* и приписывает положительную вероятность чистой стратегии х,еХ, (р* (х,)>0), то
5.6. В заключение параграфа рассмотрим пример решения биматричных игр с малым числом стратегий, который во многом поучителен.
Пример 12. (Биматричные (2 х 2)-игры [10].) Рассмотрим игру Г (А, В), в которой у каждого из игроков по две чистые стратегии. Пусть
Здесь индексами Slf S2, ?L, т2 обозначены чистые стратегии игроков 1 и 2 соответственно.
Предположим для простоты, что числа а1І5 а12, а21, а22 (/?1І5 /?12, hi, hi) различны.
Случай 1. В исходной игре Г, по крайней мере, один игрок, пусть игрок 1, имеет строго доминирующую стратегию, скажем <5± (см. § 8 гл. I). Тогда игра Г и ее смешанное расширение Г имеют единственную ситуацию равновесия по Нэшу. Действительно, нера-
венства аіі>а2и аіг>а22 приводят к тому, что в игре Г чистая стратегия д? строго доминирует все остальные смешанные стратегии первого игрока. Поэтому ситуацией равновесия является пара (<5l5 tJ, если >^12, и (<5і5 т2), если <^12.
Случай 2. Игра Г не имеет ситуации равновесия по Нэшу. Здесь
возможны два взаимоисключающих случая а) или б):
а) ®21"^а11» а12<-а22> Pll<'Pl2’ ^22^^21»
б) а11"^а21» а22"^а12> @21<'Р22>
причем деіАфО, detB^O и поэтому выполняются условия теоремы п. 5.3. Поэтому в игре существует ситуация равновесия (х*, у*), где
 |
| (5.15) |
Рі1~Рі1 Pll~Pl2
Pll+Pl2—P21~Pl2 Pll+P22~P21~Pt2
a22~ai2 ®11 ®21
9
all+a22 —a21 —®12 all+a22 — ®21— ®12
а соответствующие равновесные выигрыши и ?2 определяются по формулам
®11®22 ®12®21 . PllP22~Pl2P2l
Vj =-, v2~-.
а11 + ®22 —®12 —®21 Pll+P22~Pl2~P21
Случай 3. Игра Г имеет две ситуации равновесия по Нэшу. Этот случай получается, когда выполнено одно из условий:
а) 0t2l"^ail> а12"^а22>
б) *u«*21> а22<-а12> 011<-$22> $12<-$21‘
В случае а) равновесными будут ситуации (<5Х, тД (д2, т2), а в случае б) — ситуации (<52, т2), (<52, тД Однако в смешанном расширении есть еще одна вполне смешанная ситуация равновесия (х*, у*), определенная формулами (5.14), (5.15).
Рассмотренные случаи исчерпывают изучение (2х2)-игры при условии, что элементы в матрицах различны.
§ 6. РАВНОВЕСИЕ В СОВМЕСТНЫХ СМЕШАННЫХ СТРАТЕГИЯХ
6.1. Продолжим рассмотрение игр двух лиц. Как уже отмечалось в § 2, даже если ситуация равновесия является недоминируемой (оптимальной по Парето), возможны случаи, когда одна ситуация равновесия выгодна игроку 1, а другая — игроку 2. Это затрудняет нахождние взаимоприемлемого решения, возникающего неантагонистического конфликта на уровне формализации бескоалиционной игры. Поэтому исследуем неантагонистический конфликт в формализации, разрешающей игрокам принимать совместные решения. 138
Проиллюстрируем этот подход на примере игры «семейный спор» (см. пример 1 п. 1.4).
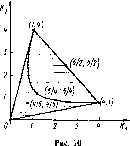
Пример 13. Рассмотрим смешанное расширение игры «семейный спор».
Множество точек, соответствующих векторам выигрышей в смешанных стратегиях в игре, можно изобразить графически (см. рис. 9 п. 5.3). На рисунке изображены две ситуации равновесия по Нэшу с векторами выигрышей (1) 4), (4, 1) в чистых стратегиях и одна вполне смешанная равновесная ситуация с вектором выигрышей (4/5, 4/5)
(ищется с использованием теоремы п.
5.3), которая менее предпочтительна для игроков, чем каждая из ситуаций равновесия в чистых стратегиях. Напомним, что равновесными здесь являются ситуации: (аІ5 /? Д (а2, /?2), СУ УХ где л* = (4/5, 1/5), У = (1/5, 4/5), а ситуации (аІ5 0Д (а2, р2) также оптимальны по Парето.
Если игра повторяется многократно, то игрокам имеет смысл сделать совместный выбор: с вероятностью 1 /2 выбирать ситуацию (al5 Pi) или (a2, /?2). Тогда средний ожидаемый выигрыш игроков будет (5/2, 5/2). Однако эта точка не лежит в множестве точек, соответствующих возможным ситуациям бескоалиционной игры (рис . 9), т. е. не может быть реализована, если игроки выбирают смешанные стратегии независимо.
Под совместной смешанной стратегией игроков будем понимать вероятностное распределение на множестве всевозможных пар (і, j) (ситуаций в чистых стратегиях), не обязательно порожденное независимыми случайными выборами чистых стратегий игроками 2 и 2. Такие стратегии могут быть реализованы посредником до начала игры.
Обозначим М совместную смешанную стратегию в игре Г (А, В). Тогда ожидаемые выигрыши К2 (Л/), К2 (М) игроков 1 и 2 при использовании совместной смешанной стратегии соответственно равны
*і(М) = Е К2{М) = ^ Рфч,
і, J і> J
где А = {ay}, В= {p,j} — матрицы выигрышей игроков, М= {р?}, при
этом uMw=\, Л/>0, ц = (1, ..., I)e2?m, w = (l, ..., 1)еі?л. Геометрически множество точек, соответствующее множеству векторов выигрышей в совместных смешанных стратегиях,— это выпуклая оболочка множества точек возможных выигрышей в чистых стратегиях. Для игры примера 13 оно примет вид, как на рис. 10.
=[?0 У
Заметим, что совместная смешанная стратегия М* ¦
является оптимальной по Парето и ей соответствует вектор выигрышей (5/2, 5/2). Таким образом, М* может быть рекомендована в качестве решения игры «семейный спор».
Определение. Для биматричной (тхл)-игры Г (А, В) обозначим через М= {ну} совместное вероятностное распределение на парах (і, у), і=1, ..., т; у = 1, ..., и. Через д((/) обозначим условную вероятность реализации стратегии у при условии, что реализовалась стратегия і. Аналогично, через ?/(і) обозначим условную вероятность реализации стратегии і при условии, что реализовалась стратегия у. Тогда
' /Я Я
ft0)=
Рф если X
I J-l j-I
п;
. 0, если Ду=0,7=1,
Ни/Е ?ф если ?
?Ді)=<
(-1
0, если ду=0, і=1,
т.
Будем говорить, что М* = {д*} — ситуация равновесия в совместных смешанных стратегиях в игре Г (А, В), если выполнены следующие неравенства:
Ё <*фТ 0) > Ё 0), Ё № (0 > Ё Р??* (0 (б- О
j-і j-1 (-1 (-1
для всех i, fell, 2, ..., /и} иу,у'е{1, 2, ..., я}.
6.2. Игру Г (Л, 5) в совместных смешанных стратегиях можно интерпретировать следующим образом. Пусть игроки договорились об использовании стратегии М* = {р*} и пусть также в результате реализации случайного механизма выпала пара (і, у), т. е. первый (второй) игрок получил номер і (/) стратегии. Заметим, что каждый из игроков знает только свою реализацию. Этот игрок, вообще говоря, может не согласиться с реализацией і (соответственно у) совместной стратегии и выбрать стратегию f (/')• Тогда, если М* — равновесная ситуация, то каждому из игроков невыгодно отклоняться от предложенной реализации і (соответственно у), что следует из (6.1), где в левой части неравенства стоит ожидаемый
выигрыш игрока 1 (игрока 2) в случае согласия с реализцией i(j). Теперь предположим, что стратегия і игрока 1 такова, что д,у=0
для всех 7=1, 2, ..., л. Тогда первое из неравенств (6.1), очевидно, выполняется. Аналогично, если Цц=0 для всех і= 1, т, то второе из неравенств (6.1) выполняется. Подставим выражения для ц,{]) и ?Ді) через цц в формулы (6.1). Тогда получаем, что необходимым и достаточным условием равновесности ситуации M* = {p!}j} является выполнение неравенств
Z «ітм*. Z Z м*=1.
j-i j- 1 i-\j- 1
Z Z Pvti’ (6-2)
(-1 (-1
для всех i, Ге{1, 2, ..., mYajJ 'e{l, 2, .... л}.
Обозначим через ZC(T) множество равновесных ситуаций в совместных смешанных стратегиях.
Теорема. Справедливы следующие утверждения.
1. Множество Ze(T) равновесных ситуаций в совместных смешанных стратегиях в биматричной (т х п)-игре Г (А, В) является
непустым выпуклым компактом пространства ЕГ*п.
2) Если (х, у) — ситуация в смешанных стратегиях игры Г (А, В), то определяемая по ней ситуация М={ду} в совместных смешанных стратегиях будет равновесной тогда и только тогда, когда (х, у) — ситуация равновесия по Нэшу в смешанных стратегиях в игре Г (А, В).
Доказательство. Пусть (х, у), х=(^, ..., {„), y=0h, ..., ц„) — ситуация в смешанных стратегиях игры Г (А, В), а М={ри} — соответствующая ситуация в совместных стратегиях, т. е. т/у, г=1,
..., m;j=l, ..., л. Необходимым и достаточным условием равновесности М является система неравенств (6.2), т. е.
№(/, у)>^К2(Г, у), г\, К2 (х, J) ^ r}jK2 (х, 7'), (6.3)
где і, і'е{1,2,..., m};j,j'e{l,..., л}. Если ?,=0 (tjj= 0), то неравенства
очевидны. Поэтому система неравенств (6.3) эквивалентна следующей:
К! (/, у)>К, (Г, у), К2 (х, j)>K2 (х, j'), (6.4)
і, Гб{1, ..., /л}; 7, 7'б{1, ..., л}, где і и j принадлежит спектрам стратегий хи у. Предположим, что (х, у) — ситуация равновесия по
Нэшу в смешанных стратегиях в игре Г (А, В). Тогда согласно теореме п. 5.2
KL (і, у) = К1 (х, у), К2 (х, f) = К2 (х, у)
для всех і и j из спектров оптимальных стратегий. Поэтому неравенства (6.4) выполнены и MeZc(Г).
Обратно, если (6.3) выполнено, то, суммируя неравенства (6.3) по і и j соответственно и применяя теорему п. 5.1, получаем, что ситуация (х, у) равновесна по Нэшу.
Выпуклость и компактность множества Zc(Г) следует из того,
что Zc (Г) — множество решений системы линейных неравенств
(6.2), которое ограничено, а непустота — из существования ситуации равновесия по Нэшу в смешанных стратегиях (см. п. 4.1). Теорема доказана.
Г ?2 0 1
Отметим, что совместная смешанная стратегия Л/* = І ^ х
равновесна в игре «семейный спор» (см. пример 1 п. 1.4), что просто установить проверкой неравенств (6.2).
§ 7. ЗАДАЧА О ПЕРЕГОВОРАХ
7.1. Основной вопрос, который мы рассмотрим в данном параграфе, заключается в том, как прийти к соглашению разумным игрокам при совместном выборе решения в ходе переговоров. Перед тем как сформулировать задачу, еще раз вернемся к игре «семейный спор».
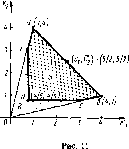
Пример 14. Рассмотрим множество R, соответствующее возможным векторам выигрышей в совместных смешанных стратегиях для игры «семейный спор» (область, заштрихованная на рис. 11). Действуя совместно, игроки могут реализовать любой выигрыш в смешанных стратегиях в области R. Однако это не означает, что они могут договориться о любом исходе игры. Так, игроку 1 наиболее предпочтительна точка (4, 1), а игроку 2 — точка (1, 4). Ни один из игроков не согласится с результатами переговоров, если его выигрыш будет меньше максиминного значения, поскольку этот выигрыш он может получить самостоятельно (независимо от партнера). Максиминные смешанные стратегии игроков в этой игре jc° = (1 /5, 4/5) и / = (4/5, 1/5) соответственно, а вектор выигрышей в максиминных
стратегиях (?°, ?°) равен (4/5, 4/5). Поэтому множество S, возможное для переговоров, ограничено точками a, b, с, d, е (см. рис. 11). Назовем его переговорным множеством игры. Далее, действуя совместно, игроки всегда могут договориться выбирать точки на отрезке ab, поскольку это выгодно обоим (отрезок ab соответствует ситуациям, оптимальным по Парето). _ _
7.2. Назовем задачу выбора точки (?х, ?2) из 5 в результате переговоров задачей о переговорах. Таким образом, мы пришли к следующей проблеме. Пусть для биматричной игры Г (А, В) задано переговорное множество S и вектор максиминных выигрышей («і, ?2). Требуется найти правило, решающее задачу о переговорах, т. е. необходимо найти функцию q>, такую, что
q>(S,v\,v\)=(vі, ю2). (7.1)
Оказывается, что при некоторых разумных предположениях задача (7.1) разрешима в силу справедливости следующей теоремы.
Теорема. Пусть S — выпуклый компакт в R2, (?°, ?\) — вектор максиминных выигрышей в игре Г (А, В). Множество S, пара (»lf ?2) и функция <р удовлетворяют следующим условиям:
1) (®1,®2)Х®1»®2)-
2) (v1,v2)es.
3) Если (®lf v2)eS и (®lf v2)>(vl, ?2), то (v15 v2) = (vlt v2).
4) Если (®lt v2)eSc:S и (ylt v2)=q>(S, v°, v°), то (vlt v^ = (p(S, v°,
A
5) Пусть T получается из S с помощью линейного преобразования v'1 = a1v1+fll, ?2 = а2?2 + Р2; ^>0, а2>0. Тогда, если q>(S, ?\, ?2) = (?1, «Д, то
<р(Т, + а2?2+Р2)=(аі®і + Ри аг®2 + Рг)-
6) Если из (vlt v2)eS следует (у2, v^eS для всех (»lf v2)еS; ?°=?°
и (p(S, »5, ®°)=(®1» ?2), то ?2 = ?2.
Тогда существует единственная функция <р такая, что
<P(S, ?°, «°)=(«і, ?2).
Функция (р, которая отображает игру с переговорами (S, ?°, ?°) в множество векторов выигрышей (ои ?2) и удовлетворяет условиям 1) — 6), называется арбитражной_схемой Нэша [11], условия 1) — 6) — аксиомами Нэша, а вектор (vL, ?2) — арбитражным вектором выигрышей. Таким образом, арбитражная схема — это реализуемый принцип оптимальности в игре с переговорами.
Прежде чем перейти к доказательству теоремы, обсудим ее условия на примере игры «семейный спор» (см. рис. 11). Условия 1 и 2 означают, что вектор выигрышей (»lf ?2) находится в множест-
143
ве, ограниченном точками а, Ь, с, d, е. Ограничение 3 показывает, что (и1( ?2) лежит в множестве точек, оптимальных по Парето. Условие 4 говорит о независимости функции ср от посторонних стратегий, т. е. если («1# ?2) — арбитражный вектор выигрышей для множества ~S, то при расширении множества переговоров до S реше; нием будет либо («1# ?2), либо другая точка, но не принадлежащая S. Ограничение 5 говорит о том, что если функции выигрыша отличаются лишь масштабом измерения и началом отсчета, то также отличаются и результаты переговоров. Свойство 6 указывает на равноправность обоих игроков.
Доказательство теоремы п. 7.2 основано на следующих вспомогательных результатах.
7.3. Лемма. Если существуют точки (vlt v2)еS, что ?2 >?°
и ?2>?2, то существует единственная точка (?2, ?2), максимизирующая функцию
0(«1, ?2) = (?1-?Ч)(?2-?Ч)
на подмножестве S2 <= S, S2 = {(uj, v2)\(vlt v2)eS, ?^?Ч).
Доказательство. По условию Sx — непустой компакт, а 0 — непрерывная функция, поэтому она достигает на нем своего максимума 9. По предположению, ff положительно.
Пусть существуют две точки максимума («і, ?'2) и (у\, ?2) функции 0 на Sx. Заметим , что ?\ Ф?"2, поскольку в противном случае из вида функции 0 имеем ?'2=?2.
Если ?\ <?\, то ?'2>?2. Так как множество Sx — выпукло, то (vlf v2)eS1, где ?1 = (?’1 + ?'1)/2, ?2=(?'2+?2)/2. Имеем
?(у1г ?2)=
:--1---1---
Каждое из первых двух слагаемых последней суммы равно 0/2, а третье слагаемое положительно, что невозможно, поскольку 0 — максимум функции 0. Таким образом, точка (й1, ?2), максимизирующая функцию 0 на множестве Sl5 единственна.
J7.4. Лемма. Пусть S удовлетворяет условиям леммы п. 7.3, а (vlt ?2) — точка максимума функции 0 (?2> ?2) и пусть
й0>1> ?2) = (?2-?'Ч)?1 + (?1-?Ч)?2.
Если (?2, ?2) е S, то имеет место неравенство
<5(«і> ?г)-
Доказательство. Предположим, что существует такая точка (»1# ?2)еS, что v2)>S(v1, ?2). Из выпуклости S имеем:
144
(®і, v'2)eS, где ®і —®і + Е(®і_®і) и ?'2 = ?2 + е(?2 —®2), 0<е<1. В силу линейности 5(и1 —?1, ?2—?2)>0. Имеем
?(?'і, ?'2) = ?(?1, ?^ + ед^і-?^ ?2-?2) + е2(?1-?1)(?2-?2).
Последнее слагаемое — бесконечно малая величина порядка 0 (е). Поэтому при достаточно малом е>0 получаем неравенство ?(?\, ?2)>?(?1, ?2), но это противоречит максимальности ?(?1, ?2).
7.5. Перейдем к доказательству теоремы п. 7.2. Для этого покажем, что точка (54, ?2), которая максимизирует ?(?1, ?2), является решением задачи о переговорах.
Доказательство. Предположим, что выполнены условия леммы п. 7.3. Тогда определена точка (54,_®2), которая максимизирует 0(®і, ?2). Можно проверить, что (®1( ?2) удовлетворяет условиям
1) — 4) теоремы п. 7.2. Она также удовлетворяет условию 5 этой теоремы, так как если ?'1 = а,1?1 + р2 и ?'2 = а2?2 + р2, то
?' («1, ®і) = [®І — («1®? + Pi)] [®2 — (a2v2 + P2)] = ala2 ® (®i> ®г)>
и если 04, ®2) максимизирует ?(?1г ®2), то («і, ?'2) максимизирует
& (?\, ?2). Покажем, что (й1г ®2) удовлетворяет условию 6. Пусть множество S симметрично в смысле условия 6 и «°=®2. Тогда (?2,
и 0(54, ?2) — ?(?2, «,). Так как (54, ®2) — единственная точка, которая максимизирует ?(?2, ®2) на S2, то (®lf «2) = («2» ?і)> т- е-«1 = ®2- _ _
Таким образом, точка («lf ®2) удовлетворяет условиям 1) — 6). Покажем, что это единственное решение задачи о переговорах. Рассмотрим множество
Л = {(®і > «2) I <5 (®і, ?2) ^ 8 (®і , ®2)}. (7.2)
По лемме п. 7.4 имеет место включение S с R. Пусть Т получается из Л с помощью преобразования
| ®і | 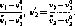 |
Выражая ?2 и «2 из (7.3) и подставляя в (7.2), получаем, что
Т = {(®і, ®г) I «і + ®2 ^ 2}
и ®'1о=«2° = 0. Так как Т симметрично, то из свойства 6 имеем, что решение (если оно существует) должно лежать на прямой «і=«'2, а согласно свойству 3 оно должно быть точкой (1, 1), т. е. (1,
1) = (р (Г, 0, 0). Обращая преобразование (7.3) и применяя свойство 5,
получаем, что (54, v2) = (p(R, ?°, ®°). Так как (®lf v2)eS, а Sc R, на
основании свойства 4 пара (54, ®2) является решением для (S, «°, ®°). Предположим теперь, что условия леммы п. 7.3 не выполнены,
т. е. не существует точек («15 v2)eS, для которых >?° и ?2>?2. Тогда возможны следующие случаи.
а) Существуют точки, у которых ?1>?° и ?2=?2. Тогда в качестве (t>1; ?2) возьмем точку в S, которая максимизирует ?1 при ограничении ?2 = ?°.
б) Существуют точки, у которых ?1=?° и ?1>?°. В этом случае в качестве (vt, ?2) возьмем точку в S, которая максимизирует ?2 при ограничении ?1 =«°.
в) Переговорное множество S вырождается в точку (?°, ?°) мак-симинных выигрышей (например, случай матричных игр). Полагаем
«2=«2-
Непосредственно можно проверить, что эти решения удовлетворяют свойствам 1) — 6), при этом из свойств 1) — 3) следует единственность. Теорема доказана.
В игре «семейный спор» (см. пример 14) схема Нэша дает арбитражный выигрыш (vlt ?2) = (5/2, 5/2) (см. рис. 11).
§ 8. ИГРЫ В ФОРМЕ ХАРАКТЕРИСТИЧЕСКОЙ ФУНКЦИИ
В § 6 и § 7 на примере игр двух лиц было показано, как, используя возможность согласованного выбора стратегий, игроки могут прийти к взаимоприемлемому решению возникающего неантагонистического конфликта (стратегический подход). Теперь будем считать, что условия игры допускают совместные действия игроков и перераспределение выигрыша. Это предполагает, что полезности различных игроков могут быть оценены единой шкалой (трансфера-бельные выигрыши), и поэтому взаимное перераспределение выигрышей не искажает содержательной постановки первоначальной задачи. Представляется естественным, что объединение игроков в максимальную коалицию (в коалицию, состоящую из всех игроков) с целью получения максимального суммарного выигрыша приведет к наилучшим результатам также и с точки зрения каждого игрока, при этом нас будет интересовать не столько как коалиция игроков добивается своего суммарного выигрыша, сколько как он будет распределен между членами коалиции (кооперативный подход).
В § 8 — 10 рассмотрена кооперативная теория игр п лиц. В ней исследуются условия, при которых объединение игроков в максимальную коалицию является целесообразным, а отдельные игроки не будут иметь желания создавать меньшие группировки или действовать индивидуально.
8.1. Пусть N= {1,..., л} — множество всех игроков. Любое непустое подмножество ScN называется коалицией.
Определение. Характеристической функцией игры п лиц будем называть вещественную функцию ?, определенную на коалициях SczN, при этом для любых непсресекающихся коалиций Т, S (TczN,
S<^N) выполняется неравенство
v(T) + v(S)<v(T\)S),v(0) = V. (8.1)
Свойство (8.1) называется свойством супераддитивности. Оно необходимо для содержательной интерпретации числа ?(Т) как гарантированного выигрыша коалиции Т в случае, когда она действует независимо от остальных игроков. При такой интерпретации неравенство (8.1) означает, что коалиция имеет не меньше
возможностей, чем две непересекающиеся коалиции S и Т, действующие независимо.
Из супераддитивности ? получаем, что для любых непересека-ющихся коалиций Si} ..., Sk
^v(S,Hv(N).
i-l
Отсюда, в частности, следует, что не существует такого разбиения множества N на коалиции, чтобы суммарный гарантированный выигрыш этих коалиций превышал максимальный выигрыш всех игроков ? (N).
8.2. Рассмотрим бескоалиционную игру Г= (N, {X^ieN, {H,}ieN).
Пусть игроки, составляющие некоторую коалицию SaN, объединяют свои усилия с целью увеличения своего суммарного выигрыша. Установим, какой наибольший выигрыш они могут себе гарантировать. Совместные действия игроков из коалиции S означают, что коалиция S, действуя от имени своих членов как один игрок (обозначим его 1), имеет в качестве множества чистых стратегий всевозможные комбинации стратегий, составляющих ее игроков из S, т. е. элементы декартового произведения
ieS
Общность интересов игроков из S означает, что выигрыш коалиции S (игрока 1) есть сумма выигрышей игроков из S, т. е.
Я5(*)=І ДМ,
іб5
где xeXN, x = (x1, ..., х„) — ситуация в чистых стратегиях.
Нас интересует тот наибольший выигрыш, который игроки из S могут себе гарантировать. В худшем для игрока 1 случае оставшиеся игроки из N \S могут также объединиться в коллективного
игрока 2 с множеством стратегий Х^= П ^ и интересом, диаме-
іеЯ \S
трально противоположным игроку 1 (у.е. выигрыш игрока 2 в ситу-яіши х равен — Hs (x)). В результате таких рассуждений вопрос
0 наибольшем гарантированном выигрыше коалиции S превратился в вопрос о наибольшем гарантированном выигрыше игрока 1 в антагонистической игре Г5 = (Xs, XHs). В смешанном расширении
TS=(XS, XN\5> Ks) игры Гя гарантированный выигрыш v (S) игрока
1 может разве лишь увеличиться по сравнению с игрой Г5, поэтому в дальнейшем будем рассматривать смешанное расширение игры Г$. Заметим, в частности, что при такой интерпретации ?(5) совпадает со значением игры Гя (если оно существует), а ? (N) — максимальный суммарный выигрыш игроков. Очевидно, что ? (5) зависит в результате только от коалиции S (и еще от самой исходной бескоалиционной игры, которая в наших рассуждениях остается одной и той же), являясь ее функцией. Убедимся, что эта функция является характеристической функцией бескоалиционной игры. Для этого достаточно показать выполнение условия (8.1).
Заметим, что для каждой бескоалиционной игры, построенной выше, ?(0)=О. Действительно, по определению,
Я0(*)=Х Щх),
<е0
но последняя сумма не содержит слагаемых, откуда Н0 (х) тождественно равно нулю, поэтому и ?(0)=О.
Лемма (о суперадднтнвности). Для бескоалиционной игры Г=(N, М<6№ {H,}leN) построим функцию
V(S)=sup inf Ks(ps, v^s), SczN, (8.2)
Ms
где pssXs, v^eX^s, Fs=(Xs, X^s, Ks) — смешанное расширение
антагонистической игры Г5. Тогда для всех 5, TczN, для которых iSQ Т=0, имеет место неравенство
v(S[]T)^v(S)+v(T). (8.3)
Доказательство. Заметим, что
?(5(j7) = slip inf K,(ps\jT,
T yN \(MJT) ieSUT
где ps(jT — смешанные стратегии коалиции T, т. е. произвольные вероятностные меры на X^jT, — вероятностные меры на
Xn\(s[JT), К, — выигрыш игрока і в смешанных стратегиях. Если ограничиться только такими вероятностными мерами на Х$^т, которые являются произведениями независимых распределений ps и ?г на декартовом произведении Xs х Хт, то область изменения переменной, по которой производится максимизация, сузится и супремум разве лишь уменьшится. Таким образом, имеем
V 7) ^ sup sup inf ? Ki (jisXfiT, ?„ U4J71).
to to vtt\i$jT) ieS{jT
Отсюда v T)^ inf Z Ki(jis XfiT, Vtf\(s\ji)) —
?ЛМЯ_И ieSlJr
= inf
v«\(sUri
( Z x ?т, ?/Л(^ил)+ Z X Vt, VtMS(Jn
\ieS ieT ,
Так как сумма инфимумов не превосходит инфимум суммы, имеем
v(S\jT)^ inf ^ Ki(jisxцт, vff\(S\jT))+
vA\(SUn ieS
+ tirf Z Ki (^S X Рт’ VN\(S\JT))-
v*\(Hjr) ieT
Минимизация первого слагаемого в правой части неравенства по цт, а второго — по ц8 (для единообразия переименуем их соответственно ?т и vs) приводит к соотношениям
? 0SU Т) ^ inf inf Z К (jis xvr, Vn\(s\jt>)+
Vj vM(JUn ieS
+ inf inf Z Кі(?8хцт, ?Щ5[)7$>
v* v*unji) іеГ
>inf Z Kites, VN\s)+inf Z Kiter, vn\t)-
yN\S ,6^ ?Л\Г *6^
Последнее неравенство справедливо при любых значениях мер fis в первом слагаемом и цт — во втором. Следовательно, по этим мерам можно перейти к супремумам
?(S(JТ)>sup inf Z Kites, Vjv\s)+sup inf YKter, Мт)-
to ieS to v^T ieT
Откуда, используя (8.2), получаем
v(S\jT)>v(S)+v(T)
и супераддитивность доказана.
Заметим, что неравенство (8.3) также справедливо, если функция ? (S) строится по правилу
v(S)=sup inf Н, (xs, x^g), ScN,
x5 X.Vi,S
где xseXs, x^seX^s, rs=(Xs, X^s, Hs), при этом доказательство
дословно повторяет приведенное выше.
8.3. Определение. Бескоалиционная игра Г—(N, [X,}liN, {H,},eN
называется игрой с постоянной суммой, если
X Ht(x)=c=const
ieN
для всех xeXN, f] Xt.
ieN
Лемма. Пусть Y={N, {А”,},6№ {Hj}ieN) — бескоалиционная игра
с постоянной суммой, функция v{S), S<^N, определена, как в лемме п. 8.2, а игры Г5, S^-N, имеют значения в смешанных стратегиях. Тогда
v(N)=v(S)+v(N\S), ScN.
Доказательство. Из определения игры с постоянной суммой получаем, что
г(І?)=? Я,()=Х **(ц) = с
ieN ieN
для всех ситуаций х в чистых и р — в смешанных стратегиях. С другой стороны
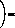
? (S)=sup inf X К, Os, vn\s)=sup inf I c - X Ki Os. v\s)
<4 vMJ ieS Ms vMJ \ ieN\S
= c-inf sup X Ki(jis,VN\s) = c-v(N\S),
vN\s Ms ieN\S
что и требовалось доказать.
8.4. В дальнейшем под кооперативной игрой будем понимать просто пару (N, ?), где ? — характеристическая функция, удовлетворяющая неравенству (8.1), поскольку содержательная интерпретация характеристической функции, обосновывающая свойство (8.1), не имеет принципиального значения.
Пример 15 [10]. (Игра «джаз-оркестр».) Директор клуба обещает 100 руб. певцу S, пианисту Р и ударнику D за совместное выступление41. Дуэт певца и пианиста он оценивает в 80 уел. ед., ударника и пианиста в 65 уел. ед. и одного пианиста — в 30 уел. ед. Другие дуэты и солисты не рассматриваются, поскольку присутствие фортепиано директор клуба считает обязательным. Дуэт певец — ударник зарабатывает 50 уел. ед., а певец — в среднем 20 уел. ед. за вечер. Ударник один ничего не может заработать.
Обозначая цифрами 1, 2, 3 игроков S, Р и D соответственно, мы имеем дело с кооперативной игрой (N, ?), где N= {1, 2, 3}, ?(1, 2, 3) = 100, і»(1, 3)= 50, ?(1) = 20, «(1, 2)=80, ?(2, 3)=65, и(2) = 30, „(3) = 0.
Основная задача кооперативной теории игр п лиц заключается в построении реализуемых принципов оптимального распределения максимального суммарного выигрыша ? (N) между игроками.
Пусть а, — сумма, которую получает игрок і при распределении
максимального суммарного выигрыша v(N), N={1, 2, ..., и}.
Определение. Вектор а=(а1; ..., аД удовлетворяющий условиям
({*})» (8.4)
t а,=«(Л0, (8-5)
І—1
где «({/}) — значение характеристической функции для одноэлементной коалиции ?={/}, называется дележом.
Условие (8.4) называется условием индивидуальной рациональности и означает, что, участвуя в коалиции, каждый игрок получает по меньшей мере столько, сколько он мог бы получить, действуя самостоятельно и не заботясь о поддержке каких-либо других игроков. Должно также выполняться условие (8.5), так как в случае
? a{<v(N) существует распределение а', при котором каждый иг-
ieN
рок ieN получит больше, чем его доля а,. Если же ? at>v(N), то
/бЛГ
игроки из N делят между собой нереализуемый выигрыш, и поэтому вектор а неосуществим. Следовательно, вектор а может считаться допустимым только при выполнении условия (8.5), которое называется условием коллективной (или групповой) рациональности.
На основании условий (8.4), (8.5) для того, чтобы вектор а = (аІ5 ..., о^) был дележом в кооперативной игре (N, ?), необходимо
и достаточно выполнение равенства
“/=«({*}) + У/, ieN>
причем
,ieN, ?y,=i»(fl)-5>({/})•
ieN ieN
Определение. Игра (N, ?) называется существенной, если
5>({I})<0(JV).
(8.6)
ieN
В противном случае игра (N, ?) называется несущественной.
Для любого дележа а через а (S) будем обозначать величину
? а,= а(5), а множество всех дележей — через D. Несущественная
игра имеет единственный дележ а=(?({1}), «({2}), «({и})).
Во всякой существенной игре с более чем одним игроком множество дележей бесконечно. Поэтому будем анализировать такие игры с помощью отношения доминирования.
Определение. Дележ а доминирует дележ /? по коалиции S (обозначение а^/?), если s
а, > /?,, і е S, а (S) ^ ? (S). (8.7)
Первое из условий в определении (8.7) означает, что дележ ос лучше дележа /? для всех членов коалиции S, а второе отражает реализуемость дележа а коалицией S (т. е. коалиция S на самом деле может предложить каждому из игроков ieS величину а,).
Определение. Говорят, что дележ а доминирует дележ /?, если существует коалиция S, для которой а^/?. Доминирование дележа
S
Р дележом а обозначается как а ^/?.
Доминирование невозможно по одноэлементной коалиции
и множеству всех игроков N. Действительно, из а^=/? следовало бы Рі<аі^?({/}), что противоречит условию (8.4). А из ос^=/? следовало бы, что аі>Рі для всех ieN и поэтому ? ос,> ? Pi=v(N), что проти-
ieN ieN
воречит условию (8.5).
8.5. Объединение кооперативных игр в те или иные классы существенно упрощает их последующее рассмотрение. В качестве таких классов можно рассмотреть классы эквивалентных игр.
Определение. Кооперативная игра (N, ?) называется эквивалентной игре (N, ?1), если существуют положительное число кип таких произвольных вещественных чисел си і е N, что для любой
коалиции S а N выполняется равенство
t/(S) = b(S)+X с, (8.8)
ieS
Эквивалентность игры (N, ?) и (N, ?') будем обозначать как (N, ?) ~ (N, ?) или ?~?.
Очевидно, что ?~?. Чтобы убедиться в этом, достаточно положить в формуле (8.8) с, — 0, к= 1, ?—?. Такое свойство называется
рефлексивностью.
Докажем симметрию отношения, т. е. что из условия ?~? следует ?'~?. Действительно, полагая к! = 1/к, с,'= —cjk, получим
v{S)=k'v'{S)+Y,t>
ieS
т. е. ?г~?.
Наконец, если ?~?' и ? ~?", то ?~?". Это свойство называется транзитивностью. Оно проверяется последовательным применением формулы (8.8).
Так как отношение эквивалентности рефлексивно, симметрично и транзитивно, оно разбивает множество всех игр п лип на взаимо-непересекающиеся классы эквивалентных игр.
Теорема. Если две игры ? и ?' эквивалентны, то отображение а-* а!, где
a.'i = kai+Ci, ieN,
устанавливает также взаимно однозначное отображение множества всех дележей игры ? на множество дележей игры ?, так что из
а^Р следует сс'^0'.
S S
Доказательство. Проверим, что а' является дележом в игре (N, ?). Действительно,
OL^koLi+Ci^ kv ({*}) + ct=v' ({*'}),
I «;= ? (kai+cd = kv(N)+ I Ci=v (N).
ieN ieN ieN
Следовательно, для а' условия (8.4), (8.5) выполнены. Далее, если а^р, то
аі>Рі, ieS, Yai^v(S),
ieS
поэтому
o' = ka.i -I- c, > kPi+c,=P'i (k> 0),
? a,' = A; ? a, + ? c, < fo (S') + Z c,=v (S),
ieS ieS ieS ieS
т. е. а'Взаимная однозначность соответствия следует из существования обратного отображения (оно было использовано при доказательстве симметрии отношения эквивалентности). Теорема доказана.
8.6. При разбиении множества кооперативных игр на попарно непересекающиеся классы эквивалентности возникает задача выбора наиболее простых представителей из каждого класса.
Определение. Игра (N, ?) называется игрой в (0 — ^редуцированной форме, если для всех ieN
v({i}) = 0,v(N) = l.
Теорема. Каждая существенная кооперативная игра эквивалентна некоторой игре в (0 — ?уредуцированной форме.
Доказательство. Пусть
k=--->0,
•W- I«(И)
ieN
С---—-, «Ч5)=Ь(5)+?с*
•w-1 «(W) ,eS
ieN
Тогда ? ({і}) = 0, ? (N) = 1. Теорема доказана.
Из теоремы следует, что свойства игр, включающие понятие доминирования, можно изучить на играх в (0 — 1 )-редуцированной форме. Если ? — характеристическая функция произвольной существенной игры (N, ?), то
«(¦S)- Z *'({'})
v'(S)=-^-, STcN, (8.9)
• W- I «((О)
ieN
есть (0 — 1) — нормализация, соответствующая функции ®. При этом дележом оказывается любой вектор а = (а1,..., а„), компоненты
которого удовлетворяют условиям
а,>0, ieN, ?а,= 1, (8.10)
ieN
т. е. дележи можно рассматривать как точки (п — 1)-мерного симплекса, порожденного ортами и>,=(0, ..., 0, 1, 0,..., 0),у = 1, п пространства R".
Перейдем к рассмотрению принципов оптимального поведения в кооперативных играх. Как уже отмечалось в п. 8.4, речь будет идти о принципах оптимального распределения максимального суммарного выигрыша между игроками.
9.1. Возможен следующий подход. Пусть игроки в кооперативной игре (N, ?) пришли к такому соглашению о распределении выигрыша всей коалиции N (дележу а*), при котором ни один из дележей не доминирует а*. Тогда такое распределение устойчиво в том смысле, что ни одной из коалиций S невыгодно отделиться от других игроков и распределить между членами коалиции выигрыш ?(5). Это рассуждение наводит на мысль о целесообразности рассмотрения множества недоминируемых дележей.
Определение. Множество недоминируемых дележей кооперативной игры (N, ?) называется ее С-ядром.
Имеет место следующая теорема, которая характеризует С-ядро.
Теорема. Для того чтобы дележ а, принадлежал С-ядру, необходимо и достаточно выполнение для всех SczN неравенств
t,(SKa(S)=2> (9.1)
ieS
Доказательство. Для несущественных игр теорема очевидна, и в силу теоремы п. 8.6 достаточно провести ее доказательство для игр в (0 — 1)-редуцированной форме.
Докажем достаточность утверждения теоремы. Пусть для дележа а выполнено условие (9.1). Покажем, что дележ а принадлежит
С-ядру. Пусть это не так. Тогда найдется такой дележ /?, что /?^а,
т. е. f}(S)>a(S) и f}(S)^v(S). Но это противоречит (9.1).
Покажем необходимость условия (9.1). Для любого дележа а, не удовлетворяющего (9.1), существует коалиция S, для которой a (S)<v(S). Положим
Pi —0С,*+ , Z6o, Pi—
|S|
\N\-\S\
где 151 — число элементов множества S. Легко видеть, что /? (І?) = 1, /?/>О и /?^а. Отсюда следует, что а не принадлежит С-ядру.
Из теоремы п. 9.1 следует, что С-ядро является замкнутым, выпуклым подмножеством множества всех дележей (С-ядро может быть пустым множеством). '
9.2. Пусть игроки договариваются о выборе кооперативного соглашения. Из супераддитивности ? следует, что такое соглашение
приводит к образованию коалиции N всех игроков. Решается вопрос о способе дележа суммарного дохода v (N), т. е. о выборе вектора
aeRn, для которого ? a,=v(N).
ieN
Минимальным требованием для получения согласия игроков выбрать вектор а является индивидуальная рациональность этого вектора, т. е. условие а,({/}), ieN. Пусть игроки договариваются
о выборе конкретного дележа а. Против выбора дележа может возражать некоторая коалиция S, требующая для себя более выгодного распределения. Коалиция S выдвигает это требование, угрожая в противном случае нарушить общую кооперацию (это вполне реальная угроза, так как для достижения дохода v(N) требуется единодушное согласие всех игроков). Предположим, что остальные игроки N\S реагируют на эту угрозу объединенными действиями против коалиции S. Тогда максимальный гарантированный доход коалиции S оценивается числом ? (5). Условие (9.1) означает существование стабилизирующей угрозы коалиции S со стороны коалиции N\S. Таким образом, С-ядром игры (N, ?) является множество устойчивых в смысле коалиционных угроз распределений максимального суммарного дохода ? (N).
Приведем еще один критерий принадлежности дележа С-ядру.
Лемма. Пусть а — дележ игры (N, ?). Тогда а принадлежит С-ядру в том и только в том случае, когда для всех коалиций S<zN выполняется неравенство
?а,<*(Л0-*(І?\5). (9.2)
i€S
Доказательство. Так как ?а,-=«(і?), то приведенное выше
ieW
неравенство можно записать в виде
v(N\S)s$ ? а,-.
ieN\S
Теперь утверждение леммы следует из (9.1).
Из условия (9.1) видно, что если дележ а принадлежит С-ядру, то ни одна коалиция S не может гарантировать себе выигрыш, превосходящий ?a,=a(S), т. е. суммарный выигрыш, который обеспечи-
іб s
вается членам коалиции дележом а. Это делает нецелесообразным существование коалиций S, отличных от максимальной коалиции N.
Теорема п. 9.1 дает достаточные основания для использования С-ядра как важного принципа оптимальности в кооперативной теории. Однако во многих случаях С-ядро может оказаться пустым, а в других случаях оно представляет собой множественный принцип оптимальности и остается всегда открытым вопрос, какой все-таки дележ из С-ядра необходимо выбрать в конкретном случае.
Пример 16. Рассмотрим игру «джаз-оркестр» (см. пример 15 п. 8.4). Суммарный доход трех музыкантов максимален (и равен 100 руб.) в случае их совместного выступления. Если певец выступает отдельно от пианиста с ударником, то все втроем они получают 65 + 20 руб., если пианист выступает один, то 30 + 50 руб. Наконец, суммарный доход равен 80 руб., если пианист и певец отказываются от участия ударника. Какое распределение максимального общего дохода следует признать разумным, учитывая описанные возможности игроков в смысле частичной кооперации и индивидуального поведения?
Вектор л = (л1, <х2, а3) в игре «джаз-оркестр» принадлежит С-ядру тогда и только тогда, когда
{а4>20, а2>30, а3>0,
а1 + а2 + а3 = 100,
аі + «2^80, а2 + а3>65, ах + а3>50.
Это множество является выпуклой оболочкой следующих трех дележей: (35, 45, 20), (35, 50, 15), (30, 50, 20). Таким образом, выигрыши всех игроков определяются с точностью до 5 руб. Типичным представителем ядра является центр (среднеарифметическое крайних точек) С-ядра, а именно: а* = (33,3; 48,3; 18,3). Для дележа а* характерно, что все двуэлементные коалиции имеют одинаковый дополнительный доход: <х, + ау—?({/, j}) = l,6. Дележ а* является
справедливым компромиссом внутри С-ядра.
9.3. Из того, что С-ядро пусто, не следует невозможность кооперации всех игроков N. Это просто означает, что никакой дележ не может быть стабилизирован с помощью простых угроз, описанных выше. Пустота ядра имеет место тогда, когда промежуточные коалиции слишком сильны. Это утверждение поясняется следующим образом.
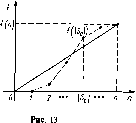
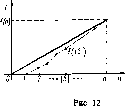
Пример 17 [10]. (Симметричные игры.) В симметричной игре коалиции с одинаковым числом игроков имеют одинаковый выигрыш. Характеристическая функция ? имеет следующий вид:
v(S)=f(\S\)
для всех SaN, где |5] — число элементов множества S.
Предположим без потери общности, что/(1)=0 и jV={1, л}.
Тогда множеством дележей игры (N, ?) является следующий симплекс в R":
?а,=/(л)=«(Л0, а,>0, і=1, ..., п.
і-і
С-ядром является подмножество множества дележей, определенное линейными неравенствами (9.1), т. е. это выпуклый многогранник. В силу симметричности v(S) С-ядро также симметрично, т. е. инвариантно относительно любой перестановки компонент аІ9 ..., а„.
Учитывая, кроме того, выпуклость С-ядра, можно показать, что оно не пусто в том и только в том случае, когда содержит центр а* множества всех дележей (а*=/(л)/л, і=1, ..., л). Возвращаясь к системе (9.1), получаем, что С-ядро не пусто тогда и только тогда, когда для всех |5| = 1, ..., л имеет место неравенство
(1/|?))/(|?|Х(1/л)/(л). Таким образом, С-ядро непусто тогда и только тогда, когда не существует промежуточной коалиции S, в которой средняя доля каждого игрока больше соответствующей величины в коалиции N. Рис. 12 (13) соответствует случаю, когда С-ядро непусто (пусто).
9.4. Пример 18 [2]. Рассмотрим общую игру трех лиц в (0 — 1)-редуцированной форме. Для ее характеристической функции имеем »(0)=«(1)=«(2)=»(3) = О, »(1, 2, 3)= 1, »(1, 2)=с3, »(1, 3) = с2, «(2, 3)=с1, где 0<с,<1, і=1, 2, 3. На основании теоремы п. 9.1, чтобы
дележ а принадлежал С-ядру, необходимо и достаточно выполнение следующих неравенств:
а1 + а2^с3, Яі + аз>с2, а2 + а3^с1
или
я3^ 1 с3,я2^1 ^2, ®і^ 1 (9.3)
Складывая неравенства (9.3), получаем
<*і + а2 + а3 ^ 3 — (с2 + с2 + с3),
или, поскольку сумма всех а„ і= 1,2, 3, тождественно равна единице,
сі + с2 + с3<2. (9.4)
Последнее неравенство является необходимым условием существования в рассматриваемой игре непустого С-ядра. С другой стороны, если (9.4) выполняется, то существуют такие неотрицательные ?15 \г, ?3, что
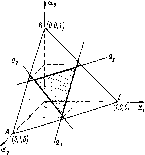 |
| Рис 14 |
i-i
Положим /?,= 1 — с, —f=l, 2,
3. Числа /?, удовлетворяют неравенствам (9.3), так что дележ Р=(Рі, Р2’ Рз) принадлежит С-яд-ру игры. Таким образом, соотношение (9.4) является также достаточным для существования непустого С-ядра.
Геометрически множество дележей в рассматриваемой игре есть симплекс: а1 + а2 + а3 = 1, а,^0, і= 1, 2, 3 (треугольник АВС, рис. 14).
Непустое С-ядро представляет собой пересечение множества дележей (ААВС) и выпуклого многогранника (параллелепипеда) 0<а,<1— с„ і=1, 2, 3. Это часть треугольника АВС, вырезаемая
линиями пересечения плоскостей
а,= 1-с„ і=1, 2, 3 (9.5)
с плоскостью А АВС. На рис. 14 через а„ / = 1, 2, 3, обозначена
прямая, образованная пересечением плоскостей а,= 1 — с,
и а1 + а2 + а3 = 1. Точка пересечения двух прямых а, и а, принадлежит
треугольнику АВС, если неотрицательна к-я (кфі, кФj) координата этой точки, в противном случае она находится за пределами А АВС (рис. 15, 16). Таким образом, С-ядро имеет вид треугольника, если совместное решение любой пары уравнений (9.5) и уравнения ?Хі+а2 + а3 = 1 состоит из неотрицательных чисел. Это требование выполняется при
Сі + с2^1, Ci+Cg^l, с2 + с3^1. (9.6)
В зависимости от различных случаев (а всего их может быть восемь) С-ядро будет приобретать тот или иной вид. Например, если не выполняется ни одно из трех неравенств (9.6), то С-ядро оказывается шестиугольником (рис. 16).
9.5. Другим принципом оптимальности в кооперативных играх является Н — M-решение. Н — M-решение, так же как и С-ядро, является множественным принципом оптимальности в множестве всех дележей. Хотя элементы С-ядра и не доминируются никакими другими дележами, однако нельзя утверждать, что в С-ядре для любого наперед заданного дележа а найдется доминирующий его дележ. Поэтому оказывается целесообразной формулировка принципа оптимальности, который бы учитывал и это последнее обстоятельство.
Определение. Подмножество дележей L кооперативной игры (N, ?) называется Н — М-решением, если:
1) из а>р следует, что либо афЬ, либо рфЬ (внутренняя устойчивость);
2) для любого а фЬ существует такой дележ рфЬ, что р^а (внешняя устойчивость).
К сожалению, применение понятия Н — М-решения на практике невозможно. Оно несет скорее философский, нежели практический смысл.
Между С-ядром кооперативной игры и ее Н — М-решением имеется известная связь. Например, если С-ядро не пусто и Н — М-решение существует, то оно содержит С-ядро. Действительно, пусть дележ а принадлежит С-ядру; тогда если бы он не принадлежал Н — М-решению L, то согласно свойству 2) нашелся бы такой дележ а', что а'^а. Однако это противоречит принадлежности а С-ядру как множеству недоминируемых дележей.
Теорема. Если для характеристической функции игры (N, ?) в (0 — 1 )-редуцированной форме (|ЛЧ = л) выполняются неравенства
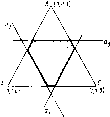
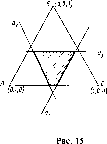
v(S)^
1
л-|5| + Г где |S| — число игроков в коалиции S, то С-ядро этой игры не пусто и является ее Н — М-решением.
Доказательство. Возьмем произвольный дележ а, лежащий вне С-ядра. Тогда существует непустое множество коалиций {5}, по которым можно доминировать а, т. е. это те и только те коалиции S, для которых а(S)<v (S). Множество {S} частично упорядочено по включению, т. е. Si>S2, если S1^S2. Возьмем в нем какой-нибудь минимальный элемент S0, который, очевидно, существует. Пусть к— число игроков в коалиции S0. Очевидно, 2^/с^и— 1. Построим дележ /? следующим образом: „ , «(S0)~a(S0)
а,-|----, іеі0,
/?,= •
к
us
п-к ’ t$s°’
Так как P(SQ)=v(S0), ^,>а„ ieS0, то /? доминирует а по коалиции
S0. Докажем, что /? содержится в С-ядре. Для этого достаточно показать, что P(S)^v(S) при произвольном S. Пусть сначала Заметим, что /? не доминируется по S0, так как ft (SQ)=v(SQ) и не может доминироваться ни по какой коалиции 5<=50, поскольку /?, > а, (ieS0), a S0 — минимальная коалиция, по которой можно
доминировать а. Если же хоть один игрок из S не содержится
п—к+\
^v(S).
п—fc+І п— |S1 + 1
п—к
п—к
Таким образом, Р не доминируется ни по какой коалиции, содержащей не более к игроков.
Пусть теперь Если S^S0, то
GS\-k)(l-v{S0)) , ,ow|51-fc^
P(S)=----\-v(S0)^-3s
n—k ^v(S).
n—k
JSl-*+Jk-|S| + l_ n—k+k—|S| + 1 n—|S| + 1
Если же S не содержит S0, то число игроков множества S, не содержащихся в S0, не меньше |^ — к+1, поэтому
п—к+1 л—151 + 1
Р\0)^ - ^
Таким образом, Р не доминируется ни по какой коалиции S. Следовательно, /? содержится в С-ядре. Кроме того, /? доминирует а. Итак, доказано, что С-ядро непусто и удовлетворяет свойству 2, характеризующему множество Н — А/-решений. Свойству 1 С-ядро удовлетворяет автоматически в силу определения. Теорема доказана.
9.6. Определение. Игра (N, и) в (0 — \)-редуцированной форме называется простой, если для любых S^N v(S) принимает лишь одно из двух значений 0 или 1. Кооперативная игра называется простой, если проста ее (О — 1 )-редуцированная форма.
Пример 19 [2]. Рассмотрим простую игру трех лиц в (0 — 1)-редуцированной форме, в которой коалиция, состоящая из двух и трех игроков, выигрывает (?(5) = 1), а коалиция, включающая только одного игрока, проигрывает (? ({/}) = 0). Для этой игры рассмотрим три дележа:
а12 = (1/2, 1/2, 0), а13 = (1/2, 0, 1/2), а23 = (0, 1/2, 1/2). (9.7)
Ни один из этих трех дележей не доминирует никакого другого. Множество дележей (9.7) имеет и следующее свойство, любой дележ (кроме трех дележей а,у) доминируется одним из дележей ау. Чтобы
это проверить, рассмотрим какой-нибудь дележ а=(аІ9 а2, а3). Так как мы рассматриваем игру в (0 — 1)-редуцированной форме, то а,^0 и а1 + а2 + а3 = 1. Следовательно, не более двух компонент
вектора а могут быть не меньше 1/2. Если их действительно две, то каждая из них равна 1/2, в то время как третья равна 0. Но это означает, что а совпадает с одним из ау. Если же а — какой-нибудь
иной дележ, то он имеет не более одной компоненты, не меньшей чем 1/2. Значит, по крайней мере две компоненты, например, ос, и ocj,
где і</, меньше 1/2. Но в этом случае а(;>а. Таким образом, три
V
дележа (9.7) образуют Н — Л/-решение. Но это не единственное Н — Л/-решение.
Пусть с — любое число из отрезка [0, 1/2]; легко проверить, что множество
Ьъ, с={(а, \-c-a, с)|0^а^1—с}
также является Н — Л/-решением. Действительно, в это множество входят дележи, при которых игрок 3 получит постоянную с, а игроки 1 и 2 делят остаток во всевозможных пропорциях. Внутренняя устойчивость следует из того, что для любых двух дележей а и Р из этого множества имеем: если а2>^І5 то а2</?2. Однако доминирование по коалиции, состоящей из единственного участника, невозможно. Чтобы доказать внешнюю устойчивость L3j „ возьмем какой-либо дележ РфЬі'С. Это означает, что либо /?3>с, либо /?3<с.
Пусть /?3 >с, например /?3 = с + е. Определим дележ а следующим образом:
аі~Рі + еІ2, а2=Р2 + е/2, а3=с.
Тогда, aeL3j с и а^Р по коалиции {1, 2}. Пусть теперь /?3<с. Ясно,
что либо P1^lj2, либо 02^1/2 (ибо в противном случае их сумма была бы больше 1). Пусть 1/2. Положим а = (1 —с, 0, с). Так как 1 — с>1/2^Р1} то а^Р по коалиции {1, 3}. Очевидно, что aeLiC.
Если же Р2^ 1/2, то можно показать аналогично, что у^/?, где у = (0, 1 — с, с). Итак, кроме симметричного Я — Л/-решения, рассматриваемая игра имеет еще целое семейство решений, при которых игрок 3 получает фиксированное количество с из отрезка 0^с<1/2. Эти Я — Л/-решения называются дискриминирующими; говорят, что игрок 3 при этом дискриминирован. В случае множества Я, „ говорят, что игрок 3 полностью дискриминирован или исключен.
Из соображений симметрии очевидно, что существуют также два семейства Я — Л/-решений Lu с и La, „ в которых дискриминируются игроки 1 и 2 соответственно.
Предшествующий пример показывает, что у игры может быть чрезвычайно много Я — Л/-решений. Совершенно неясно, какое из них следует выбрать. Когда же Я — Л/-решение выбрано, остается непонятным, какой из него выбрать дележ.
Существование Я — M-решений в общем случае до сих пор не доказано, однако получены некоторые частные результаты. Одни из них касаются существования Я — Л/-решений для конкретных классов игр, другие — существования решений определенного типа [5].
§ 10. ВЕКТОР ШЕІШИ
10.1. Множественность рассмотренных ранее принципов оптимальности С-ядра и Я — Л/-решения в кооперативных играх, а также жесткие условия существования этих принципов стимулируют попытки поиска принципов оптимальности, существование и единственность которых были бы обеспечены в каждой кооперативной игре. К таким принципам оптимальности относится вектор Шепли. Вектор Шепли определяется аксиоматически.
Определение. Носителем игры (N, ?) называется такая коалиция Т, что v(S) = v(Sf]T) для любой коалиции SczN.
Содержательно определение утверждает, что любой игрок, не принадлежащий носителю, является «болваном», т. е. не может ничего внести ни в какую коалицию.
Рассмотрим произвольную перестановку Р упорядоченного множества игроков Я={1, 2, ..., п}. С этой перестановкой связана подстановка я, т. е. такая взаимно однозначная функция я: N-*N, что для ieN значение n(i)eN представляет собой элемент из N, в который переходит ieN в перестановке Р.
Определение. Пусть (N, ?) — игра п лиц. Р — перестановка множества N, ап — соответствующая ей подстановка. Тогда через
(N, nv) обозначим такую игру (N, и), что для любой коалиции Sc.N,
S={it, i2, ..., Q
“({"('А я(і2), ..., я (/,)})=«(5).
По существу игра (N, л?) отличается от игры (N, ?) лишь тем, что в последней игроки поменялись ролями в соответствии с перестановкой Р.
С помощью этих определений можно изложить аксиоматику Шепли. Сначала заметим, что так как кооперативные игры п лиц, в сущности, отождествляются с вещественными (характеристическими) функциями, то можно говорить о сумме двух или большего числа игр, а также о произведении игры на число.
10.2. Поставим в соответствие каждой кооперативной игре (N, ?) вектор <р[?]=((рі [і>], ..., q>„[?]), компоненты которого будем интерпретировать как выигрыши, полученные игроками в результате соглашения или решения арбитра. При этом будем считать, что указанное соответствие удовлетворяет следующим аксиомам.
Аксиомы Шепли.
1. Если S — любой носитель игры (N, ?), то
ЕфіМ=®65)-
teS
2. Для любой подстановки п и ieN
Фп(оМ=Ф(Н-
3. Если (N, и) и (N, ?) — две любые кооперативные игры, то
<Рі[ы+?] = <рі[и] + <Рі[?].
Определение. Пусть q> — функция, ставящая в соответствие согласно аксиомам 1 — 3 каждой игре (N, ?) вектор ф[?]. Тогда <р[?] называется вектором значений или вектором Шепли игры (N, ?).
Оказывается, что этих аксиом достаточно для определения единственным образом значения для всех игр п лиц.
Теорема. Существует единственная функция q>, определенная для всех игр (N, ?) и удовлетворяющая аксиомам 1 — 3.
10.3. Доказательство теоремы опирается на следующие результаты.
Лемма. Пусть для любой коалиции Sc.N игра (N, ws) определяется следующим образом:
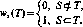
(Ю.1)
Тогда для игры (N, wa) аксиомы 1, 2 однозначно определяют вектор (р К]:
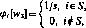
где 5= |5| — число игроков в S.
Доказательство. Ясно, что S — носитель w„ как и любое
множество Т, содержащее множество S. Тогда по аксиоме 1, если ScT, то
іеТ
Но это означает, что <jp)[ws]=0 для іфБ. Далее, если я— любая подстановка, которая переводит S в себя, то nws=ws. Следовательно, в силу аксиомы 2 для любых i, jeS имеет место равенство <Рі[н’з']=фЛн’х]- Так как этих величин всего s= |5|, а сумма их равна 1,
то <Pi[ws]=l/5, если /е?.
Игра с характеристической функцией ws, определяемой (10.1),
называется простой игрой п лиц. Таким образом, лемма утверждает, что для простой игры (N, ws) вектор Шепли определяется формулой (10.2). Вектор Шепли для игры (N, ws) определяется единственным образом.
Следствие. Если с^О, то
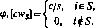
Доказательство очевидно. Таким образом, (р [cwy]=cq> [и>5] для
с^О.
Теперь покажем, что если csws является характеристической функцией, то 8
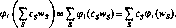
(10.3)
В случае cs>0 первое равенство в (10.3) постулируется аксиомой 3, второе следует из следствия. Далее, если и, ? и и—? — характеристические функции, то согласно аксиоме 3 имеем <р[и—?] = (р[и] — (р[?]. Отсюда следует справедливость (10.3) для любых cs. Действительно, если — характеристическая функция, то
| поэтому |
|
{S|cs>0} {S|cs<0} S
10.4. Лемма. Пусть (N, v) — любая игра, тогда найдутся 2*— 1 вещественных чисел cs, таких, что
?= Е csws> (10.4)
SciV
где ws определены (10.1), а суммирование ведется по всем подмножествам S множества N, исключая пустое множество. При этом представление (10.4) единственно.
Доказательство. Положим
с*= Е (-1Г'«(І) (10.5)
{Г|Т<=5}
(здесь t — число элементов в Т). Покажем, что эти числа cs удовлетворяют условиям леммы. Действительно, если U — произвольная коалиция, то
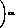
Е w(tf)= Е с®= Е ( Е (-іГ'«(і)
{5|5<=W} {5|5<=С7} {S|J<=C7} \{r|TcS}
= Е Г Е (-іН«(Г).
{7’|7’<=C7}L{S|7’<=S<=C7} J
Рассмотрим теперь величину в квадратных скобках в последнем выражении. Для каждого значения s между /им имеется С*if таких множеств S с s элементами, что Та ?<= U. Следовательно, выражение в скобках можно заменить следующим выражением:
Е <^ (-1 Г'=Е Q -«(-1 Г‘.
но это биномиальное разложение (1 — 1)“_/. Следовательно, для всех t<u оно равно 0, а для t=u равно 1. Поэтому для всех U<=N
Е csws(U) = v(U).
{5|5<=W}
Докажем единственность представления (10.4). Любой характеристической функции ? соответствует элемент пространства
д2п-і Действительно, упорядочим коалиции T<zN. Тогда каждой непустой коалиции T<zN соответствует компонента вектора, равная ?(Т). Эти векторы будем обозначать, как и функции, через ?. Очевидно, что простейшим характеристическим функциям ws соответствуют векторы, у которых компоненты равны либо нулю, либо единице. Докажем, что простейшие характеристические функции (точнее, соответствующие им векторы) линейно независимы. Действительно, пусть
? ^sws(Tr)=Q ДОЯ всех TczN.
ScN
Тогда для Т={і} имеем ws({/}) = 0, если S^{i), и ws({/})=l, если S={i). Поэтому 1{і) = 0 для всех i<zN. Продолжим доказательство
методом индукции. Пусть 2S=0 для всех S<zT, БФТ. Покажем, что Хт=0. Действительно,
? ^sws(T)— S ^sws(^)=^r=0-
scat s=r
Таким образом, мы имеем 2я—1 линейно независимых вектора
в R2 -1, поэтому любой вектор, а значит и любая характеристическая функция ? единственным образом выражается в виде линейной комбинации (10.4) простейших характеристических функций ws. Лемма доказана.
10.5. Перейдем к доказательству теоремы п. 10.2. Лемма п. 10.4 показывает, что любая игра может быть представлена в виде линейной комбинации игр ws, причем представление (10.4) единственно. Согласно п. 10.3 функция д>[«] единственным образом определяется соотношениями (10.3), (10.2).
Пусть (N, ?) — произвольная игра. Получим теперь выражение для вектора <р[?]. Согласно п. 10.3, 10.4
ФіМ= ? cs<jp,[ws]= Z cs(l/s),
{S|S<=W} {SlieScW)
но cs определены формулой (10.5). Подставляя (10.5) в это выражение, получаем
<Рі[?]= I (1/*)Г I (-1ГУ7) =
Положим
y,(T)= Z (-ІГ'(ІЛ).
(10.6)
{S|7lJi6S<=Ar}
Если іфТ' и Т= то у,(Т')= ~Уі(Т). Действительно, все
члены в правой части (10.6) в обоих случаях одни и те же, и только t=t'+1, следовательно, они отличаются лишь знаком. Таким образом, имеем
9, М= I у,(7)[«(7)-«(Г\{і»].
{г|ібГ<=лг}
Далее, если і е Т, то ровно Q.Z1, таких коалиций S с s элементами, что Тс 5. В результате получаем хорошо известный определенный интеграл:
У.О)=Е(-1) «-.(1/*)
1 1 «ь
= E(-ir'Q-'t \x~ldx= ft(-iy-ta-.ltx-ldx= о 0
1 1 = X (- Vf-'C-JtX*~‘dx=JV"1 (1 -x)n~‘dx.
Таким образом, имеем (бета-функция)
0!
(/_1)>(я-
л!
УіІТ)=
и, следовательно,
<Рі[?]= Z \{ф]. (10.7)
(T\ieT<=N) л!
Формула (10.7) определяет компоненты вектора Шепли в явном виде. Это выражение удовлетворяет аксиомам 1 — 3 п. 10.2.
Заметим, кроме того, что вектор ср [?] всегда является дележом. Действительно, в силу супераддитивности функции ?
(<-1)!(л-<)!
-=?
л!
(f—1)!(л—<)! л!
Z
{г|ібГ<=лг}
»({*}) Z С*»-1
[»]>»({*})
(«)•
10.6. Если отвлечься от аксиоматического определения, то вектору Шепли, выраженному формулой (10.7), можно дать следующее содержательное истолкование. Предположим, что игроки (элементы множества N) решили встретиться в определенном месте в определенное время. Естественно, что из-за случайных отклонений все они будут прибывать в различные моменты времени; однако предполагается, что все порядки прибытия игроков (т. е. их перестановки) имеют одну и ту же вероятность, а именно 1/(л!). Предположим, что если игрок і, прибывая, застает на месте членов коалиции Т\ {/} (и только их), то он получает выигрыш ?(Г)—? (7\ {/}); иначе говоря, его выигрышем является предельная величина, которую он вносит в коалицию. Тогда компонента вектора Шепли р,[«] представляет
собой математическое ожидание выигрыша игрока і в условиях этой рандомизационной схемы.
10.7. Для простой игры (п. 9.6) формула для вектора Шепли особенно наглядна. Действительно, ?(Т)—?(Т\ {і\) всегда равно либо 0, либо 1, причем это выражение равно 1, если Т — выигрывающая коалиция, а коалиция 7\ {/} не является выигрывающей. Следовательно, имеем
т
где суммирование распространяется на все такие выигрывающие коалиции Гз і, для которых коалиция 7\ {/} не является выигрывающей.
Пример 20 [2]. (Игра с главным игроком.) В игре участвуют п игроков, один из которых называется «главным». Коалиция S выигрывает 1, если она либо содержит главного игрока и хотя бы одного кроме него, либо всех п— 1 «неглавных». Если главный игрок имеет номер п, то характеристическая функция этой игры записывается в следующем виде:
{1, 5э{і, п}, іфп,
1, 5з{1, ..., п 1},
0, в остальных случаях.
Ясно, что для всякой коалиции !Гз {л} условия ?(Т)=1 и ?(7\{л}) = 0 выполняются тогда и только тогда, когда 2<|7)<и—1. Поэтому
Щп-р!
л!
п—2
п
<Рп[?]=іа-\-
/-2
Поскольку игра имеет (0 — 1)-редуцированную форму,
я — I
? Фі Н = 1 — ц>п [и] = 2/л.
і-1
Все неглавные игроки равноправны, поэтому в силу симметрии
Фі[?] =
л-1.
1, •
п(п-1)
Таким образом «монопольное» положение главного игрока обеспечивает ему в (л — 1)(л —2)/2 раз больший выигрыш, чем «рядовым» участникам игры.
10.8. Пример 21 [2]. («Помещик и батраки».) Предположим, что имеются л— 1 батраков (игроки і— 1, ..., л— 1) и помещик (игрок л) и что помещик, наняв к батраков, получит от урожая доход f(k) (f(k) — монотонно возрастает), а батраки сами дохода получить не могут. Это описывается следующей характеристической функцией:
ft
(|S|-1), neS,
, в противном случае.
v(S)=
Здесь для всех 7Ъ{п}, |71>1, ?(7)-?(7\{л})=/(/-1), где /=|Г|, и из (10.7) следует
ч>М=Іс-_\ ВД”—*>!/(,_1)=1 ? т
г-і
,_2 я! П
На основании условия эффективности и симметрии всех батраков
<Рі[?] = ?(п-1)-- ? fit)), i= 1, ..., л-1.
я-1 п
Упражнения ¦ задачи
1. Два объединения производят разведку полезных ископаемых на п месторождениях. Фонды средств на разведку у 1-го н 2-го объединения составляют а и Р соответственно. Прибыль от добычи полезных ископаемых на і-м месторождении равна Уі > 0, она распределяется между объединениями пропорционально доле средств,
которые они вложили в і месторождение. При этом если в і месторождение обоими не вложено никаких средств, то и прибыли, полученные обоими объединениями на і-м месторг едении, также равны нулю.
ь) Спи зтъ указаний конфликт в виде игры двух лиц, считая выигрышем каждого объединения суммарную прибыль, полученную от добычи полезных ископаемых на всех месторождениях.
б) Найти ситуацию равновесия по Нэшу.
Указание. Воспользоваться вогнутостью функций Н1 по х и Н2 по у.
2. В экологически значимом районе имеется п промышленных предприятий, на каждом из которых один источник загрязнения. Значение концентрации qt вредной
примеси, выбрасываемой і-м предприятием, пропорционально величине выброса 0<х(<Ді, і = 1 п, этого предприятия. Потери і-го предприятия складываются из
расходов на переработку отходов производства (/Кх^)) и налога за загрязнение,
который пропорционален суммарной концентрации q вредной примеси от выброса всех предприятий. Величина ? не должна превышать q — значения предельно допустимой концентрации вредной примеси. В противном случае і-е предприятие дополнительно платит штраф Sj.
Описать указанный конфликт в виде бескоалиционной игры п лиц, считая проигрышем каждого предприятия суммарные затраты на природоохранные мероприятия.
Указание. Воспользоваться результатом примера S п. 1.4.
3. Найти множества всех ситуаций равновесия по Нэшу (в чистых стратегиях) в следующих (т х л)-биматричных играх с матрицами А = {а^} и В=
а) Матрицы А в В — диагональные и положительные, т. е. т=п, ау= Д^=0, іф]
и а,і> 0, Рц>0, /=1, 6)
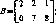
в)
| А = | 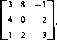 |
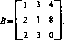
4 Показать, что в биматричной игре с матрицами
[1 2 0“| ГЗ 4 0"| 131, 5= 1 3 2
2 2 ljj Ll 3 oj
ситуация (2, 2) является равновесной. Является ли она сильно равновесной?
5. В биматричной игре с матрицами
найти все ситуации, оптимальные по Парето в чистых стратегиях. Есть ли в этой игре равновесные ситуации в чистых стратегиях?
6. Изобразить графически в координатах (Alf К2) множество всевозможных векторов выигрышей в смешанных стратегиях в игре «семейный спор» (см. п. 1.4).
Указание. Произвольные смешанные стратегии хи у игроков 1 и 2 соответственно могут быть записаны в виде x=(f, 1 — f), y=(ri, 1 —rj), (, »;e[0, 1]. Записывая функции выигрыша At и К2 в смешанных стратегиях и исключая один из параметров, получаем однопараметрическое семейство отрезков, объединение которых и есть искомое множество (см. рис. 9). Криволинейная часть границы представляет собой огибающую этого семейства отрезков и является частью параболы: 5А* + 5Ц- ЮК2К2—18 (Aj + К2)+45=0.
7. В оиматричной игре с матрицами
найти вполне смешанную ситуацию равновесия по Нэшу. Имеет ли эта игра еще ситуации равновесия в смешанных стратегиях?
Указание. Найти сначала вполне смешанную ситуацию равновесия (х, у), x=(fj, ?3), y=(tj2, rj2, tj3), затем такую равновесную ситуацию, для которой =0, ит. д.
8. «Игра на оригинальность» [23]. Рассматривается бескоалиционная игра п лиц
r«(W, {*i}/6№ где ЛГ,= {0, 1}, /7,(0, .... 0|l)-ft>0, /7,(1, 1||0) = Л(>0,
i i
/7, (x)=0 в остальных случаях, где || означает, что замена производится на і-м месте.
а) Интерпретировать игру в терминах рекламного дела.
б) Найти вполне смешанную ситуацию равновесия.
9. В п. 10.1 гл. I было показано, что игры двух лиц с нулевой суммой можно решать методом «фиктивного разыгрывания». Рассматривая биматричную игру с матрицами
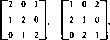
показать, что этот метод не может быть использован для нахождения ситуаций равновесия в биматричных играх.
10. Игра «музыкальные стулья» [10]. Имеются два игрока и три стула, помеченные цифрами 1, 2, 3. Стратегия игрока состоит в выборе номера стула. Оба игрока несут потери при выборе одного и того же стула. Если же их выборы различны, то тот игрок, например і, чей стул следует сразу за стулом игрока j, выигрывает вдвое больше, чем игрок j (предполагается, что стул 1 следует за стулом 3). Получаем биматричную игру Г (А, В),
[(0, 0) (1, 2) (2, 1Л
(2, 1) (0, 0) (1, 2) .
(1, 2) (2, 1) (0, 0)J
а) Показать, что единственное вполне смешанное равновесие по Нэшу состоит в равновероятном выборе стульев каждым игроком.
б) Показать, что равновесие в совместных смешанных стратегиях имеет вид
(1/6, если i+j,
п ¦ •
( 0, если і=7-
в) Показать, что выигрыши в ситуации равновесия по Нэшу не являются оптимальными по Парето, а равновесие в совместных смешанных стратегиях приводит к выигрышам (3/2, 3/2), оптимальным по Парето.
11. Равновесие в совместных смешанных стратегиях не обязывает игроков придерживаться чистых стратегий, реализовавшихся в результате принятой совместной смешанной стратегии (см. определение п. 6.1). Если же мы обязаны придерживаться результатов конкретной реализации совместной смешанной стратегии, то можно обобщить «равновесие в совместных смешанных стратегиях». Для всех ieN обозначим через ft (N\ {>}) сужение распределения /і на множество Хщц = ["[ Хь а именно
іеМЙ
ХіеХі
для всех хе J~[ Х(. Будем говорить, что р есть слабое равновесие в совместных ieN
смешанных стратегиях, если выполнены следующие неравенства для всех ieN иуіеХ,:
L Я,ОФМ> I Н(х\\у^(Щ{і}).
хеПХі хеЦХі
Га* iaN
а) Доказать, что всякое равновесие в совместных смешанных стратегиях является слабым равновесием в совместных сметанных стратегиях.
б) Пусть д=(д,, цп) — векторная ситуация в смешанных стратегиях в игре Г.
Показать, что вероятностная мера П № на множестве Х= Хі является слабым
_іеЫ іеЫ _
равновесием в совместных сметанных стратегиях и равновесием в совместных
стратегиях тогда и только тогда, когда ситуация fi=(jiu //„) равновесна по Нэшу.
12. а) Доказать, что в игре, сформулированной в упр. 10, множество ситуаций равновесия по Нэшу, множество ситуаций равновесия в совместных стратегиях и множество ситуаций слабо равновесных в совместных смешанных стратегиях различны и не совпадают между собой.
6) Показать, что множество вектор-выигрышей, оптимальных по Парето среди выигрышей в ситуации равновесия в совместных смешанных стратегиях, покрывает отрезок [(s/3, 4/3), (4/3, 7з)1, а выигрыши, оптимальные по Парето среди слабо равновесных в совместных смешанных стратегиях, покрывают отрезок [(2, 1), (1, 2)1.
Г 2 ~г
13. Найти арбитражное решение биматричной игры с матрицами А=\ ,
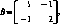 | используя схему Нзша. |
..pf:» і
«2 L(2. 1) (-5. 0)JЭто модификация игры «перекресток» (см. пример 2 п. 1.4), отличие которой заключается лишь в следующем. Водитель легкового автомобиля (игрок 1) и грузового (игрок 2) по-разному оценивают результаты аварии (ситуация (а,, /?2)). Показать, что анализ игры в стратегиях угроз предписывает ситуацию (<tu j}2), т. е. грузовому автомобилю «ехать», а легковому — «остановиться».
15. Пусть ядро имеет непустое пересечение со всеми гранями щ=к ({і}) множества
дележей. Показать, что в этом случае оно является единственным Н— М-решением.
16. Для кооперативной игры (N, ?) определим полудележ как вектор a=(aj.....
а„), для которого а*>«({/}) и ? а(<»(Я). Показать, что если L есть Н-M-решение
игры (N, и) и а — полудележ, не1 принадлежащий L, то существует такой дележ fteL, что /?>гз.
17. Для игры (N, ?) определим pt равенством
Рі= max [»(5y{j})-»(5)].
S^{i)
Показать, что если найдется і, для которого а,- >ft, то дележ а не может
принадлежать ни ядру, ни одному из Я — M-решений.
18. Пусть (N., ?) — простая игра в (0 — 1)-редуцированной форме (см. п. 10.6). Игрок і называется «вето»-игроком, если v(N\{i}H=Q.
а) Доказать, что для того, чтобы С-ядро в простой игре было непустым, необходимо и достаточно, чтобы в игре существовал хотя бы один «вето»-игрок.
б) Пусть S — множество всех «вето»-игроков. Показать, что дележ л = {л1,..., а„)
принадлежит С-ядру, если ? а, = 1, а,>0, для ieS, и щ—0, для i?S.
19. В игре (N, ?) под квазидележом будем понимать вектор а=(а,, ..., ац), такой,
что ? аi=v(N). Для каждого «>0 определим строгое в — ядро С, («О, как множество ieN
квазидележей таких, что для каждой коалиции
ieS
а) Показать, что если «<«', то С, («) <= Q, (?).
б) Показать, что существует наименьшее число, для которого Са(е)**0. При таком в множество С, («О называется минимальным «-ядром и обозначается через МС(?).
в) Найти минимальное «-ядро в игре (N, ?), где N={1, 2, 3};
»({/})= 0, »({1, 2}) = 50, .({1, 3})=80, .({2, 3})=90, *{N} = 100.
г) Пусть (N, v), (N, ?) — две кооперативные игры и для некоторых « и «' выполняется равенство С, («/) = Q («О »*0. Показать, что в этом случае для всех <5>0,
Cts(v) = Cj_s(v')- В частности, МС{?)=МС{?).
20. Показать, что если (N, ?) — игра с постоянной суммой (см. л 9.3), то вектор Шелли <р определяется по формуле
„ Г(л—j)!(s—1)! И
лМ-2 I \--7-„(5) -«(Л).
{S:S<zN, ieS) L И- J
21. Игра (N, v) называется выпуклой, если для всех S, Та N
v(S\jT)+v(SC\T)>v(S)+v(T).
а) Доказать, что выпуклая игра имеет непустое С-ядро и вектор Шелли принадлежит С-ядру.
б) Показать, что (N, ?) — выпуклая игра, если
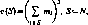
а т={ти тп) — неотрицательный вектор.
22. Рассмотрим простую игру (N, ?) в (0 — 1)-реАудированной форме. Под «скачком» игрока і будем понимать такое множество SaN, для которого е (?)=1, a v(S \{і})=0. Обозначим через 0,- число скачков игрока і в игре. Тогда вектор
/?(«)=(/?, («),..., /?„(»)), где Рі(?)=?і Y, 0/называется вектором Банзафа для простой
I j-1
игры.
а) Для простой игры четырех лиц (N, ?), в которой коалиция S выигрывает, если она состоит либо из двух игроков и игрока {1} eS, либо из трех игроков или четырех игроков, показать, что 0, =6, ?2=?3 = ?А=2и, следовательно /?(«0=0/2,1/6,1/6,1/6).
б) Показать, что 0 (?) совпадает в игре упр. (2.2 а) с вектором Шепли.
23. Пусть (N, и) — простая игра трех лиц, в которой коалиции (1, 2), (1, 3), (1, 2, 3) являются единственными выигрывающими коалициями. Показать, что в этой игре 0j=3, 02 = 03 = 1 и, следовательно, вектор Банда фа имеет вид /f(t>) = (3/5, 1/5, 1/5), а вектор Шепли равен <р[«]=(2/3, 1/6, 1/6).
24. Рассмотрим неотрицательный вектор р=(я,, ..., щ,) и число 0>О. Пусть
О <04 ? я,-. Взвешенной игрой большинства будем называть простую игру (N, и), в которой характеристическая функция ? определяется по правилу
| v(S)= | 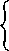 |
ies
1, если ?
ieS
Пусть 0=8 и р=(4, 3, 3, 2, 2,1), л=6. Вычислить вектор Шепли и вектор Банзафа для простой взвешенной игры большинства.
ГЛАВА IV
ПОЗИЦИОННЫЕ ИГРЫ
§ 1. МНОГОШАГОВЫЕ ИГРЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ1.1. В предыдущих главах нами рассматривалась игра в нормальной форме. К такой форме в принципе может быть сведен динамический (т. е. протекающий в течение некоторого времени, а не мгновенно) конфликтно-управляемый процесс формальным введением понятия чистой стратегии. В тех немногочисленных случаях, когда мощность пространства стратегий невелика и имеется возможность численного нахождения решений, такой подход является вполне допустимым. Однако в большинстве задач поиска оптимального поведения участников конфликтно-управляемого процесса переход к нормальной форме, т. е. сведение задачи к однократному выбору чистых стратегий как элементов пространств больших размерностей или функциональных пространств, не приводит к эффективным способам нахождения решений, хотя и позволяет наглядно иллюстрировать те или иные принципы оптимальности. В ряде случаев общие теоремы существования решения для игр в нормальной форме не позволяют находить или даже конкретизировать оптимальное поведение в играх, нормализацией которых они являются. Как будет показано ниже, в «шахматах» существует решение в классе чистых стратегий. Однако этот результат невозможно получить прямым исследованием матричной игры. Еще более отчетливо это обстоятельство проявляется при исследовании дифференциальных игр преследования, для которых в ряде случаев удается находить решения в явной форме, однако нормальная форма дифференциальной игры является настолько общей, что получение конкретных результатов оказывается практически невозможным.
1.2. Математические модели конфликтов, учитывающие динамику, исследуются в теории позиционных игр. Наиболее простым классом позиционных игр является класс конечношаговых игр с полной информацией. Для определения конечношаговой игры п лиц с полной информацией потребуются элементарные сведения из теории графов.
Пусть X — некоторое конечное множество. Правило/, ставящее в соответствие каждому элементу хеХэлемент/(х)еX, называется однозначным отображением X в X или функцией, определенной на
X и принимающей значения в X. Многозначное отображение F множества X в X — это правило, которое каждому элементу хеХ ставит в соответствие некоторое подмножество FxaX (при этом не
исключается возможность Fx=0). В дальнейшем для простоты
будем употреблять термин «отображение», понимая под ним «многозначное отображение».
Пусть F — отображение X в X, а А аХ. Под образом множества А будем понимать множество
FA={JFX.
хеА
По определению полагаем F(0) = 0. Можно убедиться в том, что если AidX, і= 1, п, то
Н 0 0 FA„ f( П А= П FA,.
\;-i / i-i Vi—l / i-i
Определим отображения F2, Fa, ..., /*, следующим образом:
tf=F(Fx), F?=F(F?\ ..., Fkx=F(Fkx~% ... (1.1)
Отображение /'множества Xв Xназывается транзитивным замыканием отображения F, если
^=WU^U^2U-U^U- (1-2)
Отображение F~l, обратное отображению F, определяется как
F;l = {x\yeFx},
т. е. это множество тех точек х, образ которых содержит точку у. Аналогично отображению Fx определяется отображение (F~*)*, т. е.
(F-l)2=F-l((F~%), (1.3)
(/-1)>3=/'-1((^1)>2), (F-lfy=^((F-l)r).
Если ВаХ, то полагаем
F-1(B) = {x\Fx()B*0}. (1.4)
Пример 1. (Шахматы.) Каждая позиция на доске определяется как количеством и составом фигур каждого игрока, так и их расположением в данный момент и указанием того, кто из игроков должен в этот момент играть. Пусть заданы: X — множество позиций, Fx, хеХ — множество тех позиций, которые могут реализоваться непосредственно после позиции х. Если в позиции х число белых и черных фигур равно нулю, то Fx=0. Тогда Fx, определяемое (1.1), есть множество позиций, которое может быть получено из х за к ходов; Fx — множество всех позиций, которые могут быть
получены из х\ F~l (A) (AczX) — множество тех позиций, из которых за один ход возможен переход в позиции из множества А (см. (1.2) и (1.4)).
Изображая позиции точками и соединяя стрелкой две позиции хи у, у eFx, теоретически можно построить граф игры, исходящий
из начальной позиции. Однако из-за очень большого числа позиций нарисовать такой граф невозможно.
Использование многозначных отображений над конечными множествами позволяет представить структуру многих многошаговых игр: шахмат, шашек, игры «го» и др.
Определение. Пара (X, F) называется графом, если X — некоторое конечное множество, a F — отображение X в X.
Граф (X, F) будем обозначать символом G. В дальнейшем элементы множества X будем изображать точками на плоскости, а пары точек х и у, для которых yeFx, соединять непрерывной
линией со стрелкой, направленной от х к у. Тогда каждый элемент множества X называется вершиной или узлом графа, а пара элементов (х, у), в которой yeFx — дугой графа. Для дуги р = (х, у)
вершины х и у называются граничными вершинами дуги, причем х — начало, а у — конец дуги. Две дуги р и q называются смежными, если они различны и имеют общую граничную точку.
Множество дуг в графе будем обозначать Р. Задание множества дуг в графе G=(X, F) определяет отображение F и, наоборот, отображение F определяет множество Р. Поэтому граф G можно записывать как в виде G=(X, F), так и в виде G=(X, Р).
Путем в графе G—(X,F) называется такая последовательность Р=(Рі> Рг> •••> Рк, ¦••) Дуг, что конец каждой предыдущей дуги
совпадает с началом следующей. Длина пути р=(р1г ..., Рк) есть
число 1(р)=к дуг последовательности; в случае бесконечного пути р полагаем 1(р)= со.
Ребром графа G = (X, Р) называется множество из двух элементов х, уеХ, для которых или (х, у)еР, или (у, х)еР. В отличие от дуги для ребра ориентация роли не играет. Ребра будем обозначать буквами р, q, а множество ребер — Р. Под цепью будем понимать последовательность ребер (р? р2, ...), в которой у каждого ребра Рк одна из граничных вершин является также граничной для рк~\,
а другая — граничной для рк+і.
Цикл — это конечная цепь, начинающаяся в некоторой вершине и оканчивающаяся в той же вершине. Граф называется связным, если любые две его вершины можно соединить цепью.
Дерево или древовидный граф, по определению, есть конечный
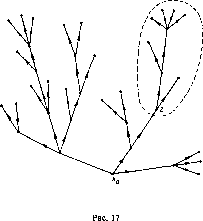
связный граф без циклов, имеющий не менее двух вершин. Во всяком древовидном графе существует единственная вершина х0, такая, что FXo = X. Вершина х0 называется начальной вершиной графа G.
Пример 2. На рис. 17 изображено дерево или древовидный граф с началом х0. Точками отмечены узлы хеХ или вершины графа. Дуги графа изображены отрезками со стрелкой, выделяющей начало и конец дуги.
Пример 3. Шашки или шахматы, вообще говоря, не могут быть изображены с помощью древовидного графа, если под вершиной графа понимать расположение фигур на доске в данный момент и указание хода, поскольку одно и то же расположение фигур может быть получено различными путями. В то же время, если под вершиной графа, изображающего структуру шашек или шахмат, понимать расположение фигур на доске в данный момент, указание хода и всю предысторию игры (все последовательные расположения фигур на предыдущих ходах), каждая вершина будет достигаться из начальной единственным способом (т. е. существует единственная цепь, ведущая из начальной вершины в любую заданную), поэтому соответствующий граф игры не содержит циклов и является деревом.
1.3. Пусть zeX. Подграфом Gz древовидного графа G = (X, F)
называется граф вида {Xz, F:), где XZ=FZ, a Fzx=Fxf]Xz. На рис. 17
штриховой линией обведем подграф, берущий начало из вершины z. В древовидном графе для всех xeXz множество Fx и множество Fzx
совпадают, т. е. отображение Fz является сужением отображения
F на множество Хг. Поэтому для подграфов древовидного графа
будем использовать обозначение GZ=(XZ, F).
1.4. Перейдем теперь к определению многошаговой игры с полной информацией на древовидном конечном графе.
Пусть G—(X, F) — древовидный граф. Рассмотрим разбиение
я+1
множества вершин X на п+1 множество Xt, ..., Х„, Х„+и (J Х,=Х, Xkf]X,= 0, кфі, где Fx=0 для хеХя+1. Множество Х„‘ і= 1, ...,
п называется множеством очередности і-го игрока, а множество Х„+\ —множеством окончательных позиций. Па множестве окончательных позиций Хя+1 определены п вещественных функций Н1(х), ..., Ня(х), хеХя+1. Функция Ні(х), і=1, ..., п, называется выигрышем і-то игрока.
Игра происходит следующим образом. Задано множество N игроков, перенумерованных натуральными числами 1, ..., і, ..., п (в дальнейшем І?={1, 2, ..., п}). Пусть x0eXtl, тогда в вершине (позиции) х0 «ходит» игрок ij и выбирает вершину x1eFx>. Если xt е ХІ2,
то в вершине х. <аодит» игрок іг и выбирает следующую вершину (позицию) хгеРХі, и т. д. Таким образом, если на k-м шаге вершина
(позиция) еХ^, то в ней «ходит» игрок і* и выбирает следующую
вершину (позицию) из множества Рч? Игра прекращается, как
только достигается окончательная вершина (позиция) х,еХя+и т. е.
такая, для которой Fx,=0.
В результате последовательного выбора позиций однозначно реализуется некоторая последовательность х0, ..., хк, ..., xh определяющая путь в древовидном графе G, исходящий из начальной позиции х0 и достигающий одной из окончательных позиций игры. Такой путь в дальнейшем будем называть партией. Из-за древовид-ности графа G каждая партия однозначно определяет окончательную позицию хі, в которую она приводит, и, наоборот, окончательная позиция хі однозначно определяет партию. В позиции xt каждый из игроков і, і=1, ..., п, получает выигрыш Hi(xt).
Будем предполагать, что игрок і при совершении выбора в позиции хeXt знает эту позицию х, а следовательно, из-за древовид-
ности графа G может восстановить и все предыдущие позиции. В таком случае говорят, что игроки имеют полную информацию. Примером игр с полной информацией служат шахматы и шашки, поскольку в них игроки могут записывать ходы, и поэтому можно считать, что они знают предысторию игры при совершении каждого очередного хода.
Определение. Однозначное отображение и„ которое каждой
вершине (позиции) хеХ, ставит в соответствие некоторую вершину
(позицию) yeFx, называется стратегией игрока і.
Множество всевозможных стратегий игрока і будем обозначать через U,.
Таким образом, стратегия і-го игрока предписывает ему в любой позиции х из множества его очередности X, однозначный выбор
следующей позиции.
Упорядоченный набор м=(м1, и„ ..., ц,), где ще Uh называется
П
ситуацией в игре, а декартово произведение U=Y\Ut — множе-
і-і
ством ситуаций. Каждая ситуация и = (и2, ..., и,-, ..., и„) однозначно
определяет партию в игре, а следовательно, и выигрыши игроков. Действительно, пусть x0eXti. Тогда в ситуации и=(м1, ..., и„ ..., ип)
следующая позиция jq определяется однозначно по правилу м,, (jc0)=-*i- Пусть теперь х1еХ,і. Тогда х2 определяется однозначно
по правилу и,1(х1)=х2. Если теперь на k-м шаге реализовалась
позиция хк_! е Х±, то хк определяется однозначно по правилу
Хк=и,к(хк_0, и т. д.
Пусть ситуации и=(и2, ..., и„ ..., и„) в указанном смысле соответствует партия х0, х2, ..., JC/. Тогда можно ввести понятие функции выигрыша К, игрока і, положив ее значение в каждой ситуации и равным значению выигрыша І7, в окончательной позиции партии х0, ..., хі, соответствующей ситуации м=(м1, ..., ы„), т. е.
K,(ult ..., и„ ..., ц,)=Я,(xfi, і=1, ..., п.
П
Функции Кіг і= 1,..., л, определены на множестве ситуаций U= и и,.
і-і
Таким образом, построив множества стратегий игроков U, и определив на декартовом произведении функции выигрыша К„ і=1, ...,
п, получаем некоторую игру в нормальной форме
г = (N, {Ui}ieS,
где N={ 1, і, ..., п} — множество игроков, С/, — множество стратегий игрока і, Кі — функция выигрыша игрока і, і= 1, п.
1.5. Для дальнейшего исследования игры Г необходимо ввести в рассмотрение понятие подыгры, т. е. игры на подграфе графа G основной игры (ср. с. п. 1.1 гл. I).
Пусть zeX. Рассмотрим подграф GZ = (XZ, F), с которым свяжем
подыгру Гг следующим образом. Множества очередности игроков в подыгре Г2 определяются по правилу Yz, = Xt[)Xz, і= 1, ..., п, множество окончательных позиций Yzn+l=Xn+if}Xz, выигрыш игрока і Щ (х) в подыгре полагается равным
Hzi(x) = Hi(x),xeYz„+l,i=l, ..., п.
В соответствии с этим стратегия и] і-то игрока в подыгре Гг определена как сужение стратегии щ і-то игрока в игре Г на множество Y], т. е.
uz,(x) = Ui(x), хе Г^ХіОХ,, i’=l, ..., п.
Множество всех стратегий і-го игрока в подыгре обозначается через Щ. В результате с каждым подграфом Gz мы связываем подыгру
в нормальной форме
TZ=(N, {C/f}, {КІ}), .
где функции выигрыша К\, і— 1, п, определены на декартовом
П
произведении ifUz.
i-l
§ 2. СИТУАЦИЯ АБСОЛЮТНОГО РАВНОВЕСИЯ
В гл. Ill было введено понятие равновесия по Нэшу для игры п лиц в нормальной форме. Оказывается, что для многошаговых игр можно усилить понятие равновесия, введя понятие абсолютного равновесия.
2.1. Определение. Ситуация равновесия по Нэшу и* = (и\,..., и*) называется ситуацией абсолютного равновесия по Нэшу в игре Г,
если для любого zeX ситуация («*/ = ((«*/, ..., (u*)z), где (и*)1 — сужение стратегии и* на подыгру Гг, является ситуацией равновесия по Нэшу в подыгре Г*.
Имеет место следующая основная теорема.
Теорема. В любой многошаговой игре с полной информацией на конечном древовидном графе существует ситуация абсолютного равновесия по Нэшу.
Прежде чем перейти к ее доказательству, введем понятие длины игры. Под длиной игры Г будем понимать длину наибольшего пути в графе G=(X, F).
Доказательство проведем индукцией по длине игры. Если длина игры Г равна 1, то может ходить лишь один из игроков, который, выбирая следующую вершину из условия максимизации своего выигрыша, будет действовать согласно стратегии, образующей абсолютное равновесие по Нэшу.
Пусть теперь игра Г имеет длину к и x0eXit (т. е. в начальной
позиции х0 ходит игрок /Д Рассмотрим семейство подагр Г„ zeFXo,
длина каждой из которых не превосходит к— 1. Предположим, что теорема справедлива для всех игр, длина которых не превосходит к— 1, и докажем ее для игры длины к. Поскольку подагры Г„ zеFX(i,
имеют длину не более к— 1, по предположению индукции для них теорема справедлива и тем самым существует ситуация абсолютного равновесия по Нэшу. Обозначим для каждой подыгры Гх,
z е FX(t, эту ситуацию через
(0Z=[(K?)Z, .... Юг]. (2.1)
Используя ситуации абсолютного равновесия в подаграх Гх, построим ситуацию абсолютного равновесия в игре Г. Пусть и?(х) = (и?(х)У, для хеХ{[)Ха zeFXo, i= 1, ..., п, u?t(x0)=z*, где z* находится из условия
^1*[(«*)1=тах^і[(н*)1]. (2.2)
*eFx0
Функция и* определена на множестве Х(, і= 1, ..., л, очередности
і-го игрока, а при каждом фиксированном xeXt значение и* (х) е Fx.
Таким образом, и*, і= 1,..., л, является стратегией і-го игрока в игре
Г, т. е. и* е Ut. По построению, сужение (u*)z стратегии м* на
множество Хі[)Хг является стратегией, входящей в абсолютное
равновесие по Нэшу игры Г„ zeFXo. Следовательно, для завершения
доказательства теоремы достаточно показать, что стратегии и*, /=1, ..., л, построенные по формулам (2.2), образуют ситуацию равновесия по Нэшу в игре Г. Пусть іфі^. По построению стратегии и* после выбора игроком і? позиции z* на первом шаге игра Г переходит в подыгру Г... Поэтому
К,(и*) = К? {(и*)1*} {(и* II и/} =*,(ц*1к),
м.е U„ і=\, ..., п, іФіи (2.3)
так как (u*)z — ситуация абсолютного равновесия в подыгре Гг.. Пусть ин е Uh — произвольная стратегия игрока і1 в игре Г. Обозначим z0 = uh(x0). Тогда
Кн (и*) = К( =max К\ {(и*)1}
-cFx,
(2.4)
Утверждение теоремы следует теперь из (2.3), (2.4).
2.2. Пример 4. Пусть игра Г происходит на графе, изображенном на рис. 18, и пусть множество N состоит из двух игроков: N={\, 2}. На рис. 18 определим множества очередности. Изобразим вершины множества Х1 в виде кружков, а вершины множества Х2 — в виде квадратиков. Выигрыши игроков записаны в окончательных пози-
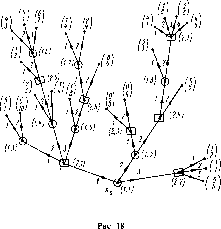
циях. Перенумеруем двойными индексами позиции, входящие в множества Х1 и Х2, а дуги, выходящие из каждой вершины,— одним индексом. Выбор в вершине х эквивалентен выбору следующей вершины x’eFx, поэтому будем предполагать, что стратегии
указывают в каждой вершине номер дуги, по которой следует двигаться дальше. Например, стратегия ul = (2, 1, 2, 3, 1, 2, 1, 1) игрока 1 предписывает ему выбор дуги 2 в вершине 1, дуги 1 — в вершине 2, дуги 2 — в вершине 3, дуги 3 — в вершине 4 и т. д. Так как множество очередности первого игрока состоит из восьми вершин, то его стратегия представляет собой восьмимерный вектор. Аналогично, любая стратегия игрока 2 представляет собой семимерный вектор. Всего у первого игрока 864 стратегии, а у второго игрока — 576 стратегий. Таким образом, соответствующая нормальная форма оказывается биматричной игрой с матрицами размера 864x576. Естественно, что решение таких биматричных игр методами, предложенными в гл. Ill, не только затруднительно, но и невозможно. Вместе с тем рассматриваемая игра достаточно проста и ее можно решить, используя попятную процедуру построения абсолютного равновесия по Нэшу, предложенную при доказательстве теоремы 1 п. 2.1.
Действительно, обозначим через ?2 (х), ?2 (х) выигрыши в подыг-ре Г* в некоторой фиксированной ситуации абсолютного равновесия. Сначала решаем подыгры rJ6, rJ7, Г2.7. Как легко убедиться,
«і(1-7) = 6, ю2(1-6)=2, «з(1.7)=2, «2(1.7)=4, ?,(2Л) = 1, «2(2.7) = 8. Далее решаем подыгры Т2 5, Г2.6, Гі 8. В подыгре Г2 j два равновесия
по Нэшу, поскольку игроку 2 безразлично, какую альтернативу выбрать. Вместе с тем его выбор оказывается существенным для игрока 1, поскольку при выборе игроком 2 левой дуги первый игрок выигрывает +1, а при выборе игроком 2 второй дуги +6. Отметим это обстоятельство и предположим, что игрок 2 «благожелателен» и выбирает в позиции (2.5) правую дугу. Тогда w1(2.5)=w1(1.6) = 6, ?г (2-5)=?2 (1.6)=2, (2.6)=«3 (1.7)=2, «2(2.6)=«2(1.7)=4,
«з(1.8) = 2, ?2(1.8) = 3. Далее решаем игры Гі3, Гі4, Г23, Ги, Г24.
В подыгре Г] з два равновесия по Нэшу, поскольку игроку 1 безразлично, какую альтернативу выбрать. Вместе с тем его выбор оказывается существенным для игрока 2, так как при выборе игроком 1 левой альтернативы он выигрывает 1, а при выборе правой — 10. Предположим, что игрок 1 «благожелателен» и выбирает в позиции (1.3) правую альтернативу. Тогда ?2 (1.3) = 5, «2 (1.3) = 10, ?і(1-4) = ?і(2.5) = 6, ?, (1.4)=?2 (2.5)=2, «3 (1.5)=*. (2.6) = 2,
v2(1-5) = «2(2.6)=4, «3(2.35 = 0, «2(ІЗ) = 6, «з(2.4) = 3, «,(2.4)=5. Далее решаем игры Г2Ь Г12, Г22: «1(2.1)=«1(1.3) = 5,
«2(2.1) = «2(1.3) = 10, «з (1.2)=«з (2.4) = 3, t,2(1.2)=«2(2.4) = 5, vl(2.2)=— 5, «2 (2.2) = 6. Теперь решаем игру Г=Гы- Здесь
«1(1.1) = і;1(2.1) = 5, «2 (1.1)=«2 (2.1) = 10.
В результате мы получаем ситуацию абсолютного равновесия по Нэшу (и*, и*), где
ы? = (1,2,2,2,2,3,2,1), «5 = (1,3,2,2,2,1,2). (2.5)
В ситуации (и*, и*) игра развивается по пути (1.1), (2.1), (1.3). В процессе построения было замечено, что стратегии и*, /= 1, 2, «доброжелательны» в том смысле, что игрок і при совершении своего хода, будучи в равной степени заинтересован в выборе последующих альтернатив, выбирает ту из них, которая более благоприятна для игрока 3 — і.
В игре Г существуют ситуации абсолютного равновесия, в которых выигрыши игроков будут другими. Для построения таких равновесий достаточно снять условие «доброжелательности» игроков и заменить его обратным условием «недоброжелательности». Обозначим через (х), ?2 (х) выигрыши игроков в подыгре Гх при
использовании игроками «недоброжелательного» равновесия. Тогда имеем: »,(1.6)=»,(1.6)=6, t>2(1.6)=t>2(1.6)=2,
«і(1.7)=йі(1.7)=2, v2(\J)=v2 (1.7)=4, ^(2.7)=-2,
«2 (2.7)=«2 (2.7) = 8. Как уже отмечалось, в подыгре Г25 два равновесия по Нэшу. В отличие от предыдущего случая предположим, что игрок 2 «недоброжелателен» и выбирает ту из вершин, в которой при его максимальном выигрыше выигрыш игрока 1 минимален. Тогда (2.5) = 1, Z1(2.5)=2, Vl (2.6)=?і (1.7)=2, ?2 (2.6)=?2 (1 -7)=4, «2 (1.8)=«і(1.8)=2, «2(1.8)=«2(1.8) = 3. Далее ищем решение игр Ги,
Гы, Г]5, Г2.з, Г^. В подыгре Г]3 два равновесия по Нэшу. Как
и в предыдущем случае, выберем «недоброжелательнее» действия игрока 1. Тогда имеем: », (1.3)=», (1.3) = 5, «2(1.3) = 1, »,(1.4) = 2, »2(1.4) = 3, «2 (1.5)=«2 (2.6)=», (1.5)=2, »2 О-5)=?2 (2.6)=»2(2.6)=4, «2 (2.3)=«2 (2.3)=0, «2 (2.3)=«2 (2.3) = 6, «2 (2.4)=«2 (2.4) = 3,
«2 (2.4)=«2 (2.4) = 5. Далее решаем игры Г2.ь Г]2, Г2.2. Имеем:
Іі(2.1)=Іі(1.5)=2,_ «2 (2-1)=«2 (1 • ^)_= 4, «і (1 -2)=«2 (2.4) = 3,
«2(1.2)=«2(2.4) = 5, «2(2.2)=»2(2-2) ==6, »2 (2.2) =_у1 (2.2) =_— 5. Теперь решаем игру Г=Ги. Здесь «2(1.1)=«2(1-2) = 3, »2(1.1)=«2(1.2) = 5.
Таким образом, получена новая ситуация равновесия по Нэшу
й* С) = (2,2,1,1,2,3,2,1), «5 (')=(3,3,2,2,1,1,3). (2.6)
Выигрыши обоих игроков в ситуации (2.6) меньше таковых в ситуации (2.5). Ситуация (2.6), так же как и ситуация (2.5), является ситуацией абсолютного равновесия,-
2.3. Очевидно, что кроме «доброжелательных» и «недоброжелательных» ситуаций абсолютного равновесия по Нэшу существует целое семейство промежуточных ситуаций абсолютного равновесия. Интересным является вопрос о том, когда можно утверждать отсутствие двух различных ситуаций абсолютного равновесия, отличающихся выигрышами игроков.
Теорема. Пусть выигрыши игроков Н,(х), і = 1, ..., п, в игре
Г таковы, что если существует такое і0 и такие х, у, что Hh(x) = Hh(y), то Я,(х) = Я,(у) для всех ieN. Тогда в игре Г выигрыши игроков во всех ситуациях абсолютного равновесия совпадают. Доказательство. Рассмотрим семейство подыгр Г* игры
Г и доказательство проведем индукцией по их длине 1(х). Пусть l(x)= 1 ив единственной нетерминальной позиции х ходит игрок і? Тогда в ситуации равновесия он осуществляет выбор из условия
Я,і(х)=тахЯіі(х').
SeFx
Если точка х единственная, то единствен и вектор выигрышей в ситуации равновесия, равный в данном случае Н(х) = {Н1 (х), ..., Ял(3с)}. Если существует такая точка хфх, что Я,і(Зс)=Я,і(х), то
имеется еще одна ситуация равновесия с выигрышами Я(Зс) = {Я1(Зс), ..., Я,ДЗс), ..., Ял(х)}. Однако из условия теоремы
следует, что если H,i(x) = Hil(x), то Н,(х)=Ні(х) для всех ieN.
Пусть ? (jc) = {«f (jc)} — вектор выигрышей в ситуациях равновесия в одношаговой подыгре Гх, который, как уже показано, определяется единственным образом. Покажем, что если для некоторого і0 выполнено равенство ?Іо(х')=?,і)(х"), (х', х" таковы, что длины
подыгр Гу, Г*- равны единице), то ?,(х')=?і(х") для всех ieN. Действительно, пусть х' е Хі%, х" е Х^, тогда
«і, (?) = Ни (?)=max Hk (у),
% (?')=Н,г (?) =тахЯіі (у)
и ?-,(?) = Ні(?), ?,(х")=Ні(х") для всех ieN. Из равенства ?,о(х')=?іа(х”) следует, что Я,о (?) = Я,о (х"). Но тогда по условию теоремы Я,(?)=Я,(?') для всех ieN. Отсюда ?с(х") = ?,(х") для всех ieN.
Предположим теперь, что во всех подыграх Гх с длиной l(x)^k— 1 вектор выигрышей в ситуациях равновесия определяется единственным образом и если для каких-нибудь двух подыгр Гу, Гх- с длиной, не превосходящей к= 1, ?іо(х,)=?іа(х") для некоторого і0, то и, (х')=?і (х") для всех ieN.
Пусть игра ГХо имеет длину к и в начальной позиции х0 ходит игрок іх. По предположению индукции для всех zeFXoa игре Гг выигрыши в ситуациях равновесия по Нэшу определяются единственным образом. Пусть вектор выигрышей в ситуациях равновесия по Нэшу в игре Гг равен {«i(z)J. Тогда, как это следует из (2.2), игрок іх
в вершине х0 выбирает следующую вершину zeFXa из условия
vil^)=maxi;il(z). (2.8)
zeF*<,
Если точка z, определяемая (2.8), единственна, то вектор с компонентами ?і(х0)=?і(і), і=1..... и, и является единственным век
тором выигрышей в ситуациях равновесия по Нэшу в игре ГХо. Если же существуют две вершины z, z, для которых vit (z)=vit (z), то по предположению индукции, поскольку длины подыгр Г; и Г. не превосходят к—1 из равенства vi{ (z)=(z), следует равенство Vi(z)=Vj(z) для всех ieN. Таким образом, и в этом случае выигрыши в ситуациях равновесия vt(х0), ieN, определяются единственным образом.
§ 3. ОСНОВНЫЕ ФУНКЦИОНАЛЬНЫЕ УРАВНЕНИЯ
3.1. Рассмотрим многошаговые антагонистические игры с полной информацией. Если в условиях п. 1.4 множество игроков состоит из двух элементов Af={l, 2} и Н2(х)= —Нх (х) для всех хеХ3 (Х3 — множество окончательных позиций в игре Г), то
t=<n, ии КЪ
оказывается антагонистической многошаговой игрой с полной информацией. Очевидно, что этим же свойством обладают и все подыгры Гг-игры Г.
Так как из условия Н2 (х) = —Нх (х) немедленно следует, что К2(их, и2)=-Кх(их, и2) для(всех MjGC/j, u2eU2, то в ситуации равновесия по Нэшу (и\, и'2) выполняются неравенства Кх(их, U2)^K1(u'l, ul)^Kx(ul и2) для всех uxeUx, u2eU2. Пару (иь и2) в этом случае будем называть ситуацией равновесия или седловой точкой, а стратегии, образующие ситуацию равновесия, оптимальными. Значение функции выигрыша в ситуации равновесия обозначим буквой ? и назовем значением игры Г.
3.2. Из теоремы п. 2.1 следует, что в антагонистической многошаговой игре с полной информацией на конечном древовидном графе существует ситуация абсолютного равновесия, т. е. такая ситуация (uj, и\), сужение которой на любую подыгру Гг игры
Г образует в Гг ситуацию равновесия. Для любой подыгры Г, можно также определить число ? (у), представляющее значение функции выигрыша в ситуации равновесия этой подыгры и называемое значением подыгры Гг Как было показано в п. 3.2 гл. I, значение
антагонистической игры (т. е. значение функции выигрыша игрока 1 в ситуации равновесия) определяется единственным образом, поэтому функция ? (у) определена для всех уеХ^, уеЛГ2 и является однозначной функцией.
3.3. Выведем функциональные уравнения для вычисления функции и (у). Из определения ?(у) следует, что
ч>о=*т «и;/, («;/)=-к\««:/, с«у),
где ((и*/, (и'2У) — ситуация равновесия в подыгре Г,, являющаяся
сужением ситуации абсолютного равновесия (и*, и^).
Пусть уеХ1 и zeFy. Тогда, как это следует из (2.2),
имеем
?(у)=тах К\ ((мІ)г, (u\f)= -max v(z). (3.1)
zeFy zeFy
Для yeX2 аналогично получаем
®(у)= -К\ ((«!/, (иУ)= -max К\ {{и\)\ (иЭ*)-
zeFy
zeFy zeFy
Из (3.1) и (3.2) окончательно имеем
zeFy
zeFy
Уравнения (3.3), (3.4) решаются при граничном условии
Система уравнений (3.3), (3.4) с граничным условием (3.5) позволяет осуществить попятную рекуррентную процедуру нахождения значения игры и оптимальных стратегий игроков. Действительно, пусть значения всех подыгр Гг длиной l(z)^k— 1 известны и равны
v(z), пусть Г, — некоторая подыгра длины Цу) = к. Тогда если
уеХ2, то ?(у) определяется по формуле (3.3), если же уеХ2, то ?(у) находится по формуле (3.4). При этом значения функции v(z) в формулах (3.3), (3.4) известны, поскольку соответствующие подыг-ры имеют длину не более чем к— 1. Эти же формулы указывают способ построения оптимальных стратегий игроков. Действительно, если уеХ2, то игрок 1 (максимизирующий) должен выбрать в точке у вершину zeFy, для которой значение следующей подыгры
максимально. Если же у еХ2, то игрок 2 (минимизирующий) должен выбрать позицию zeFy, для которой значение следующей подыгры минимально.
В случае, когда выборы игроков в антагонистической многошаговой игре чередуются (поочередная игра), уравнения (3.3), (3.4) могут быть записаны в виде одного уравнения. Действительно, рассмотрим подагру Г, и пусть, для определенности, хеХ? Тогда
в следующей позиции ходит игрок 2 или эта позиция является (игра поочередная) окончательной, т. е. Fxcz X2\JХ3. Поэтому можно
записать
zeFy
Подставляя (3.7) в (3.6), получаем
yeFx zeFy
Если xeX2, то аналогично имеем
yeFx zeFy
Уравнения (3.8), (3.9) эквивалентны и должны рассматриваться с начальным условием ? (х) |х6*,=Н2 (х).
3.4. Теорема п. 2.1, рассматриваемая применительно к антагонистическим поочередным многошаговым играм, позволяет утверждать существование ситуации равновесия в «шахматах», «шашках», в классе чистых стратегий, а уравнения (3.8), (3.9) показывают путь для нахождения значения игры. Вместе с тем очевидно, что никогда в обозримом будущем решение указанных функциональных уравнений для нахождения значения игры и оптимальных стратегий не будет реализовано на ЭВМ и мы так и не узнаем, может ли 190 какой-либо игрок «белый» или «черный» гарантировать победу в любой партии или всегда возможна «ничья»? Однако в шахматах и шашках делаются небезуспешные попытки построения приближенно оптимальных решений путем создания программ, думающих на несколько шагов вперед, и использования всевозможных (полученных, как правило, эмпирическим путем) функций оценки текущих позиций. Такой подход возможен и при исследовании общих антагонистических многошаговых игр с полной информацией. Последовательное итерирование оценочных функций на несколько шагов вперед может привести к желательным результатам.
§ 4. СТРАТЕГИИ НАКАЗАНИЯ
4.1. В п. 2.1 доказано существование ситуации абсолютного равновесия (по Нэшу) в многошаговых играх с полной информацией на конечном древовидном графе. В то же время при исследовании конкретных игр этого класса можно обнаружить целое семейство ситуаций равновесия, сужения которых необязательно являются ситуациями равновесия во всех подаграх исходной игры. К числу таких ситуаций равновесия относятся равновесия в стратегиях наказания. Проиллюстрируем это понятие на примере.
Пример 5. Пусть игра Г происходит на графе, изображенном на рис. 19. Множество ?? = {1, 2} состоит из двух игроков. Как и в примере п. 2.2, на рис. 19 кружками изображены вершины, составляющие множество Х1; квадратиками — множество Х2. Вершины графа перенумерованы двойными индексами, дуги — одинарными.
(/) (D® (?) а) т) со
Нетрудно убедиться в том, что ситуация ы[ = (1, 1, 2, 2, 2), и2 — {\, 1) является абсолютно равновесной в игре Г. При этом выигрыши игроков равны 8 и 2 единиц соответственно. Рассмотрим теперь ситуацию й1 = (2, 1, 2, 1, 2), ы2 = (2, 2). В этой ситуации выигрыши игроков равны соответственно 10 и 1, тем самым игрок 1 получает больше, чем в ситуации (ии и2).
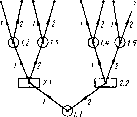
Ситуация (м1, ~й2) является равновесной в игре Г, но не является абсолютно равновесной. Действительно, в подагре Гх 4 сужение стратегии й х диктует игроку 1 выбор левой дуги, что не является для него оптимальным в позиции
1.4. Такое действие игрока 1 в позиции 1.4 можно интерпретировать как угрозу «наказания» игрока 2, если он отклонится от желательного для игрока 1 выбора дуги 2 в позиции 2.2, лишив тем Рис. 19
самым игрока 1 максимального выигрыша 10 единиц. Однако по существу такую угрозу «наказания» едва ли следует считать действенной, поскольку наказывающий (игрок 1) при этом сам может потерять в выигрыше пять единиц (действуя не оптимально в Г\
4.2. Дадим строгое определение стратегий наказания. Для простоты ограничимся случаем неантагонистической игры двух лиц. Пусть задана неантагонистическая многошаговая игра двух лиц
Г=<С/1( и2, к? к2у.
С игрой Г свяжем две антагонистические игры Г2 и Г2 следующим образом. Игра Г2 — это антагонистическая игра, построенная на основе игры Г, в которой игрок 2 играет против игрока 1, т. е. К2=—К? Игра Г2 — это антагонистическая игра, построенная на основе игры Г, в которой игрок 1 играет против игрока 2, т. е. К1 = —К2. Графы игр ГІ5 Г,, Г и множества стратегий в них совпадают. Обозначим через (ии, ««) и (и\г, и2т) ситуации абсолютного равновесия в играх Г2 и Г2 соответственно. Пусть Г1х, Г2* —
подыгры игр Г2, Г2; ?2(х), ?2(х) — значения этих подыгр. Тогда ситуации {(«п)Л> (и 2іи {(«Іг)*, («22)*} являются равновесными в играх Ги, соответственно и »і(х)=ЛГ*((мп)*, (u21)*),
?2(х)=Ши\дх, (и'п)1).
Рассмотрим произвольную пару (ы1, и2) стратегий в игре Г. Разумеется, эта пара стратегий является таковой и в играх Г2, Г,. Пусть Z—(x0=z0, zv .... Z/) — путь, реализуемый в ситуации (и2, и2).
Определение. Стратегия й1(-) называется стратегией наказания игрока 1, если:
M1(zJt)=z*+1 для zkeZ[]X2, (4.1)
йі O’) = Щ2 O’) Для у 6 Х2, у ф Z.
Стратегия «2( •) называется стратегией наказания игрока 2, если:
й2 (z*)=z*+1 для zkeZf]X2, (4.2)
м2O’) = u2iO’) Для уеХ2, уфZ.
4.3. Из определения стратегий наказания сразу получаем следующие свойства:
Г. К, («!(•)), й2(•))=#!О/), к2(й,(•), й2(-))=#20,).
2°. Пусть один из игроков, например игрок 1, использует стратегию и2 (•), для которой позиция zke является первой в пути Z,
где п1(-) диктует выбор следующей позиции z*+1, отличной от выбора, диктуемого стратегией й^), т. е. z*+1 Тогда из
определения наказывающей стратегии й2 (•) следует, что
(4.3)
•^1 (И1 ( ' )> **2 ( ' )) ^ ?1 (2к)•
Аналогично, если игрок 2 использует стратегию и2(-) для которой позиция zkeZf]X2 является первой в пути Z, где и2( ) диктует
выбор следующей позиции z'k+u отличной от диктуемой стратегией и2(-)> т. е. z'k+i^z/c+u то из определения наказывающей стратегии
йі (•) следует, что
К2 («і (¦), и2 (• Ж ?2 (.zk). (4.4)
Отсюда, в частности, получаем следующую теорему.
Теорема. Пусть («j^ (•), й2()) — ситуация в стратегиях наказания. Для равновесности ситуации (й2(-), й2 (')) достаточно, чтобы для всех fc=0, 1, ..., /—1 выполнялись неравенства
*і(йі(-),й2(-))^іЫ (4-5)
•^2 0*1 (" )> И2 ( " )) ^ ?2 (zk),
где z0, zv ..., zt — путь, реализовавшийся в ситуации (й2 (•), м2(')).
4.4. Пусть Мп(-) и «22(*) — оптимальные стратегии игроков 1 и 2 во вспомогательных антагонистических играх Гх и Г2 соответственно и Z = {z0, zlt .... z,j—путь, соответствующий ситуации
(«11 (•), Ми (•)).^Предположим, что стратегии наказания й2 (•) и й2 (•) таковы, что u1(zk) = u,n(zk) для zkeZf]X1 и ti2(zk) = u*22(zk) для zkeZf]X2. Тогда ситуация (й1 (¦), й2(-)) образует ситуацию равновесия по Нэшу в стратегиях наказания. Для доказательства этого утверждения достаточно показать, что
*1 («;¦(•), И22(-)) = *і(йі(-)Л(-))^і&), (4.6)
к2(«;.(•), н22(-))=^2(йі(-), й2(-))2?2&),
k=0, 1, ... l-l,
и воспользоваться теоремой п. 4.3. Неравенства (4.6) следуют из оптимальности стратегий Мп(-) и и^(-) в играх Tj и Г2 соответственно, обоснование предлагаем в качестве упражнения. Таким образом, получена следующая теорема.
Теорема. В игре Г всегда существует ситуация равновесия в стратегиях наказания, при этом выигрыши в этой ситуации равны Kt(un(-), и22(*)), где ы*і(•) и и22(*) — оптимальные стратегии игроков 1 и 2 во вспомогательных антагонистических играх Г2 и Г2 соответственно.
Смысл стратегий наказания заключается в том, что игрок заставляет партнера придерживаться определенного пути в игре (определенных выборов), используя постоянную угрозу переключения на стратегию, оптимальную в антагонистической игре против партнера. Множество ситуаций равновесия в классе стратегий наказания достаточно представительно, однако эти стратегии не следует считать очень «хорошими», поскольку, наказывая партнера, игрок может еще сильнее наказать самого себя.
§ 5. ИЕРАРХИЧЕСКИЕ ИГРЫ
Важнейшим подклассом неантагонистических многошаговых игр являются иерархические игры. Иерархические игры моделируют конфликтно управляемые системы с иерархической структурой. Такая структура определяется последовательностью уровней управления, следующих друг за другом в порядке определенного приоритета. В математической постановке иерархические игры классифицируются по числу уровней и характеру вертикальных связей. Простейшей из них является двухуровневая система, схема которой изображена на рис. 20.
5.1. Двухуровневая конфликтно управляемая система функционирует следующим образом. Управляющий (координирующий) центр А0, находящийся в первом уровне иерархии, выбирает вектор u = (uY,и„) из заданного множества управлений U, где ut — управляющее воздействие центра на подчиненные ему подразделения Д,
і=1, 2, ..., п, находящиеся на втором уровне иерархии. В свою очередь, Д, і=1, ..., п, выбирают управления ?,е K,(u,), где Vj(u,) —
множество управлений подразделения Д, предопределенное управлением и центра А0. Таким образом, управляющий центр имеет право первого хода и может ограничивать возможности подчиненных ему подразделений, направляя их действия в нужное русло. Цель центра А0 заключается в максимизации по и функционала К0 (и, vL,..., ?„), а подразделения Д, /= 1,..., п, обладая собственными целями, стремятся максимизировать по ?, функционалы Д (ы„ ?,).
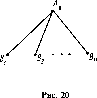
5.2. Формализуем эту задачу как бескоалиционную игру Г(л+1)-го лица (административного центра А0 и производственных подразделений Д, ..., Д) в нормальной
форме.
Пусть игрок А0 выбирает вектор ueU, где
U={u = (uY, .... u„):ui>0, и,-еЛ', і=1, ..., п, — множество стратегий игрока А0 в игре Г. Вектор и, будем интерпретировать как набор ресурсов / наименований, выделяемых центром А0 для /-го производственного подразделения.
Пусть в исходной задаче п. 5.1 каждый из игроков Ви зная выбор
А0, выбирает вектор ?{е К,(и,), где
?і(иі) = {?{еRn:vtAt^Ui+OLi, v^O}. (5.1)
Вектор vt интерпретируется как производственная программа z'-го
производственного подразделения по различным видам продукции; Aj — производственная или технологическая матрица z'-го производственного подразделения (А^О); а(— вектор наличных ресурсов z'-го производственного подразделения (<х,^0).
Под стратегиями игрока В{ в игре Г будем понимать множество функций ?і(•), ставящих в соответствие каждому элементу u, : (ulf..., ы„ ..., u„)e Uвектор ?,(и,)е Vt(tz,). Множество таких функций будем обозначать через Vit z'=l, ..., л.
Определим функции выигрышей игроков в игре Г. Для игрока А0 функция выигрыша имеет вид
Ко («. »і (О.-. ?* (')) = Е ?і (“О.
i-l
где di^Q, ateRm — фиксированный вектор, z'=l, ..., л; а(?,(м,) — скалярное произведение векторов а,- и ю,(ы,). Функцию выигрыша игрока Ві полагаем равной
Кі(и, »!(•), ?п( )) = Сі?і(ид,
где Сі^О, CieRm — фиксированный вектор, z=l, ..., л.
Таким образом, игра Г имеет вид Г=(U, ?1,.... ?„, К0, Klt.... Кп).
5.3. Построим ситуацию равновесия по Нэшу в игре Г.
Пусть ?’ (ut) е Vt (и,) — решение задачи параметрического линейного программирования (параметром является вектор ц)
(5.2)
П,
шах с, ?і=с, ?* (Ui), z= 1, ....
v,eV,(ui)
a u*eU — решение задачи
max К0(и, «!(•)» «»(•))•
(5.3)
Для простоты предполагаем, что максимумы в (5.2) и (5.3) достигаются. Заметим, что (5.3) — задача нелинейного программирования с существенно разрывной целевой функцией (максимизация ведется по и, а ?*(и;)> вообще говоря, — разрывные функции
параметра и,). Покажем, что точка (и*, ?’,(¦), ..., «*(¦)) является
| ситуацией равновесия в игре Г. Действительно, |
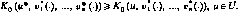 |
| Далее, при всех /= 1, ..., п справедливо неравенство |
 |
Ви невыгодно в одностороннем порядке отклоняться от ситуации
(и*. «!(•)> ««(•))> т- е- она является равновесной. Заметим, что эта
ситуация также устойчива против отклонения от нее любой коалиции Scz{Blt..., В„}, поскольку выигрыш Kt /-го игрока не зависит
от стратегий vj(),je{l, ..., п},}фі.
§ 6. ИЕРАРХИЧЕСКИЕ ИГРЫ (КООПЕРАТИВНЫЙ ВАРИАНТ)
В этом параграфе рассматривается кооперативный вариант ряда простейших иерархических игр (в том числе игры, определенной в п. 5.1, 5.2). Строятся характеристические функции и исследуются условия существования непустого С-ядра.
6.1. Исходя из содержательного смысла задачи п. 5.1, 5.2 и с использованием стратегией, образующих равновесие по Нэшу, для каждой коалиции SczN= {А0, В? .... В„} определим ее гарантированный доход ? (S) следующим образом:
’ 0, если S= {40};
(6.1)
(6.2)
? с, vf (0), если А0фБ;
max ? (а.
? (a,+ c,) v* (и,), если A0 e S, (6.3)
{ueU: 5] u,-=i} i.BjeS i:BeS
где ?- (и,), і= 1,п — решение задачи параметрического линейного программирования (5.2).
Равенство (6.1) имеет место, поскольку коалиция {Blt ..., В„) может добиться получения нулевого выигрыша игроком А0, выбирая все ?,=0, і= 1, ..., п; равенство (6.2) справедливо, так как игрок А0 всегда может гарантировать для S выигрыш не более чем (6.2), направляя каждому Де S нулевой ресурс; равенство (6.3) имеет
место, поскольку коалиция S, содержащая в своем составе А0, всегда может обеспечить распределение всего ресурса только между своими членами.
Пусть S — произвольная коалиция, содержащая А0. Обозначим через и =(и\, ..., и3„) вектор, доставляющий максимум в задаче нелинейного программирования (6.3) (для i\Bt$S выполнено условие ы} = 0). Тогда для любой коалиции 5с=5, $ФА0, A0eS справедливо следующее выражение:
Е (at+Ci)v*(uO> Е (о,+Сі)?/ (Ы() =
l-.B/eS l:B/eS
= Е (<*і+сі)?*(Ы()+ Е (<И-<*)«<(0).
UBieS i:BteS\S
Пусть S, R<=N, Sf]R=0 и A0eS^A0. Тогда A0$R. Принимая во внимание условия а,^0, с,^0, v^O, z — 1, ..., п, имеем
*(SU*)= I (щ+сУ(и^)> Е (а,+^К(и»=
i:BieS\jR i:BteS\jR
= Е (а<+с<)«*(«?)+ Е (а.+с,)«?(0) =
(:B,6S i.BjeR
=v(S)+v(R)±- Е а,v',(0)^v(S)+v(R),
i-.BieR
где Е а>?і(0)^0 — прибыль центра А0 от «нефинансируемых»
I! Bj € R . .
предприятий. В случаях A0fS\jR или S=A0$R неравенство ? (Sjj)?) (5)+? (Л) очевидно.
Таким образом, функция ? (5), определяемая (6.1) — (6.3), супераддитивна и можно рассмотреть кооперативную игру ({Л0, В? .... В„}, ?) в форме характеристической функции ?.
6.2. Рассмотрим (п+ 1)-мерный вектор
? = (ЕаУ, (й,), сі?\(й,), ..., сУ„(щ)), (6.4)
/-1
где u = uN. Вектор ? является дележом, поскольку выполнены следующие сотношения:
1) ??*=2>гЬс,к&)=1>(Л0;
*-0 і-1
2) ?о=ІіаУі (“,)>0=vUo),
1-1
?,=с,і;*(ы()>с,і>*(0)=і>(В(), /'= 1, п.
Напомним условие принадлежности дележа С-ядру. Согласно теореме п. 10.1 гл. Ш необходимым и достаточным условием принадлежности дележа (?0, ..., ?п) С-ядру является выполнение
неравенства
Z&>"(•*) (6.5)
ieS
для всех коалиций 5<={Л0, Ву, .... В„}.
Выведем условие, при котором дележ принадлежит С-ядру. Если {^40}, либо S<={BV .... В„), то условие (6.5) выполнено,
поскольку
?о = Z а<®* (“>) > 0=« ({^о})»
І-1
Z&= Z °i»*(“<)> Z c<®*(0)=®(5)-
ieS iiBjeS i.BjtS
Если A0eS^A0, то условие (6.5) можно записать в виде
^аУ,(йд+ ? сі®*(“()=
і«1 i:BjeS
= X *(“()+ Z ci®*(“i)+ z аі?‘(йі)> z (fli+c<K(Mi).
<:Л(е5 i:B,65 <:Л,е5
Следовательно, дележ (6.4) принадлежит С-ядру, если для всех S:A0eS выполнено неравенство
Z Z (я,+Сі) [«*(ыО-і>,*&)]•
l-.BitS i-.BteS
Заметим, что в данном случае мы определили характеристическую функцию игры, используя выигрыш в ситуации равновесия по
Нэшу, и величина v(N)=max ? (а,+с()?* (м,), вообще говоря, мень-
“ і-і
ше максимального суммарного выигрыша всех игроков, равного max max ?(а*+с*)?*
ueU ЩбУад [ji.!
(в этом отличие от принятого в гл. Ill определения характеристической функции).
6.3. Характеристическую функцию игры можно построить и обычным способом, а именно: для каждой коалиции S определить ее как значение антагонистической игры между этой коалицией и коалицией остальных игроков N\S. Построим теперь характеристическую функцию именно таким образом. При этом несколько обобщим предыдущую задачу, введя в рассмотрение произвольные функции выигрышей участников игры.
Как и ранее, будем предполагать, что центр А0 распределяет ресурсы между подразделениями Blt.... В„, которые используют эти
ресурсы для производства продукции. Выигрыши управляющего центра А0 и «производственных» подразделений Blt.... В„ зависят от
продукции, производимой Вк, .... В„. Вектор ресурсов, имеющийся
в распоряжении центра А0, обозначим через Ь. Центр (игрок) А0 выбирает систему л векторов u=(u1, ..., u„) из множества
U={u=(ult .... Un):uk^0, ы*еЛ', к=ТГп).
к-1
Здесь Uk интерпретируется как вектор ресурса, выделяемый центром А0 производственному подразделению Вк. Возможности предприятия (игрока) Вк определяются ресурсом щ, получаемым от А0, т. е. предприятие Вк выбирает свою производственную программу хк из
множества Вк(ик) <= ВТ неотрицательных векторов. Будем предполагать, что множества Вк (ик) при всех щ содержат нулевой вектор и монотонно возрастают по включению, т. е. из uk>uk следует Вк(ик) Вк(ик), кроме того, выполнено условие Вк (0) = 0 (невозможность производства при отсутствии ресурсов).
Пусть x=(xlt х„). Выигрыш игрока А0 определяется с помощью неотрицательной функции /0 (х)^0, а выигрыши игроков Вк полагаем равными 4(х*)>0, к = 1, ..., л (выигрыш игрока Вк зависит лишь от производственной программы). Для простоты будем считать, что выигрыш центра А0 удовлетворяет условию
ш=іы,
k=1
где слагаемое / (х*) интерпретируется как выигрьпп игрока А0, получаемый от игрока Вк. Предположим также, что / (хк) $= 0 для всех хкеВк(ик) и 4(0) = 0, /(0) = 0, к= 1, ..., п.
Подобно тому как это сделано в § 5, представим иерархическую игру п. 6.3 в виде бескоалиционной игры (п + 1) лица в нормальной форме, где стратегиями игрока А0 будут векторы ueU, а стратегиями игроков Вк — функции из соответствующих множеств. Построим характеристическую функцию ?( ) этой игры, следуя п. 9.2 гл. III. Для каждого подмножества S игроков ?(5) будет равно значению (оно существует в условиях п. 6.3) антагонистической игры между коалициями S и N\S, в которой выигрыш коалиции S определяется как сумма выигрышей, принадлежащих множеству S игроков.
Пусть N={A0, Bt, .... Вп}. Тогда
v(N) = sup sup
{ие?/: ? ust=*} xkeBk(uit)
*¦* 1 k= 1..... n
Заметим, что для всех Sa{B1, .... Вп), v(S)=0, поскольку игрок
А0 всегда может распределить весь ресурс b среди членов коалиции N\S, в которую он входит, лишив, таким образом, коалицию S ресурсов (т. е. А0 всегда может положить ик=0 для k:BkeS, что
приводит к Вк (0) = 0 для всех BkeS). Рассуждая аналогично, имеем
?(?4о) = 0, поскольку игроки В? .... В„ всегда могут сделать выигрыш
центра А0 равным нулю, полагая х*=0 для к= 1, ..., п (не производя
продукции). В том случае, когда коалиция S содержит центр А0, очевидно, что А0 будет распределять весь ресурс среди членов коалиции. Это соображение приводит к следующей формуле:
v(S)= sup sup I X [/(**) +4 (**)]
{ueU: ? %=*} xkeBk{uk) ^k:BkeS k.BkeS k:BkeS
для S: A0 e S.
Можно показать, что при таком определении характеристической функции С-ядро множества дележей
П
ос = (а0, а15 ..., а„):а,^0, г'=0, 1, п, ? *і=?(Щ
1 = 0
всегда непусто.
6.4. Иерархические системы с подразделениями двойного подчинения называются ромбовидными (рис. 21). Управление подразделения двойного подчинения С зависит от управления Ві и от управления В2. Можно представить ситуацию, в которой центр Bt представляет интересы отрасли, а В2 — региональные интересы, включающие вопросы охраны окружающей среды. Простая ромбовидная система управления является примером иерархической системы с тремя уровнями принятия решений. На высшем уровне находится административный центр, располагающий материальными и трудовыми ресурсами. Он воздействует на деятельность двух подчиненных ему центров, принадлежащих следующему уровню. От решений, принимаемых этими центрами, зависит объем производства предприятия, находящегося на последнем уровне иерархической системы.
Будем рассматривать этот процесс принятия решений, как некоторую игру четырех лиц. Обозначим ее через Г. Переходя к игровой постановке, условимся считать, что на 1-м шаге ходит игрок А0 и выбирает элемент (стратегию) и = (и^, и2) из некоторого множества U, где U — множество стратегии игрока А0. Элемент и е U ограничивает возможности выборов игроков В2 и В2 на следующем шаге. Другими словами, множество выборов игрока В1 оказывается функцией параметра и1 (обозначим его через Bt (и2)), и, аналогично, множество выборов игрока В2 оказывается функцией параметра и2 (обозначим его через В2 (и2)). Через соі е Ві (и2) и ю2 е В2 (и2) обозначим элементы множества выборов игроков Bt и В2 соответственно. Параметры си1 и со2, выбираемые игроками В1 и В2, задают ограничения на множество выборов игрока С на 3-м шаге игры, т. е. это множество оказывается функцией параметров со1 и ю2. Обозначим его через С (ш1; ю2), а элементы этого множества (производственные программы) — через ?.
 |
| Рис. 21 |
С зависят только от производственной программы ?, выбираемой игроком С, и равны соответственно 12 (?), 12 (?), /3 (?), /4 (и), где /,(?)>0.
Такую иерархическую игру можно представить как бескоалиционную игру четырех лиц в нормальной форме, если считать стратегиями игрока А о элементы м = (м1, и2) е U, а стратегиями игроков В? В2 и С — функции со1 (мД со2(и2) и ? (ш1, со2) со значениями в множествах
Bl (о Д B2(u2), С (со 2t co2) соответственно (обозначим множества таких функций через В1; В2, Q, которые каждому возможному выбору игрока (или игроков), находящегося на более высоком уровне, ставят в соответствие выбор данного игрока. Полагая
К,(и, соД), со2(•), ДО^ОДсоДиД со2(и2)), і=ТА,
получим нормальную форму игры Г
Г=(С/,В1,В2, С, K^K^K^KJ.
6.5. Будем искать ситуацию равновесия по Нэшу в игре Г. Для этого выполним вспомогательные построения.
Для каждой фиксированной пары (соІ5 со2), (сои со2)е (J В2 (uj) х В2(ц2) обозначим через v* (соІ5 со2) решение параме-
ие?
трической экстремальной задачи
max /4(?)=14(?* (соlf со2)). (6.6)
?еС(ш? <aj
(Считаем, что максимум в (6.6) достигается.) Решение v* ()=?* (со1, со2) задачи (6.6) оказывается функцией параметров со,, со2 и ?* ()е С.
Рассмотрим вспомогательную параметрическую (с параметрами щ, и2) неантагонистическую игру F(«lf ц2)={ВДыД В2 (и,), /2, /3} двух лиц В1 и В2, где /2 = /2 (?* (со1, со2)), /3 = /3(?* (coj, со2)). Стратегиями игрока В2 в F^j, и2) являются элементы со1 eBj (иД стратегиями В2 — элементы со2еВ2(ц2). Предположим, что в игре Г' (ult и2) существует ситуация равновесия по Нэшу, которую обозначим (со? (и,), со? (и2)). Отметим, что со* (¦) является функцией параметра и, и со, (•)еВ„ і=1, 2.
Пусть, далее, и* = (и*, и?) — решение следующей экстремальной задачи:
max /j («* (со?(ыД со? (и2))). (6.7)
ие?
Лемма. Совокупность (и*, со? (¦), со? (•), ?* (•)) является ситуацией равновесия по Нэшу в игре Г.
Доказательство. Согласно определению и* из (6.7) следует соотношение
К2 (и*, со? (•), со? ( ), г* ( )) =тах (г* (со? (и Д со? (и2)))>
^/ДгДйДОсД со?(н2))) Лдн, со?О, со?О, V* (¦))
для всех ие U. Поскольку со? (и?), со? (и?) образуют ситуацию равновесия по Нэшу во вспомогательной игре Г'(и|, и2), для любой функции соДОеВ^ со2 (и?) = со1еВ1(и?) выполняются соотношения
К2(и*. со?О, со?(•), г*(.)) = /2(**(со?(н?), со? (*?))>
>1г (®* ("ъ (и?))) = *2 (и*, (.), со? (•), «;* (¦))•
Аналогичное неравенство справедливо и для игрока В2.
По определению функции ?* из (6.6) имеем:
*4(«Л со? (•), ш? (•), »*(•)) =(«*). о* («?))) =
= max /4 (*) > /4 (*)=Я4 (и*, со? (¦), со? (•), * (•))
?е С(ш* (ц*), ш* (up)
для любой функции ?(-)еС, v(cof(uf), со* (и?))=іеС (со* (и*),
со? («?)).
Лемма доказана.
6.6 Применяя максиминный подход, для каждой коалиции 5с{Л0< В? Вг, С) определим v'(S) как наибольший гарантированный выигрыш S в антагонистической игре между коалицией S, выступающей в качестве максимизирующего игрока, и коалицией S' = (a0, В1, В2 C}\S. Предположим, что существует такое ?0еС(со1, со2) для всех со1, со2, что /;(г0) = 0, і= 1, 2, 3, 4.
Будем различать два вида коалиций:
I) S: С ф S; 2) S: С е S.
В первом случае 5 с {А0, В1, В2} и игрок С, являющийся членом коалиции N\S, может выбрать стратегию ?0: /,(?о)=0, і=1, 2, 3, 4,
поэтому r'(5)=0.
Во втором случае определим характеристическую функцию ? (5) следующими равенствами:
а) 5= {С}
?' (5)=min min min max /4(r)
ueU ш,€В,(и,) ш2gB2(м2) ”SC(wi,w2)
(здесь и далее предполагаем, что все max и min достигаются);
б) 5={Л0, С)
? (5)=max min min max (l2 (r) + /4(i>));
ueU ш,еВ,(и,) oijeBjtuj) ибС(ш„Ші)
в) S={Blt C}
r'(5)=min max min max (/2(?) + А*00);
ueU ш,еВ,(и,) o>2eB2(u2) иеСЦ.ш^
г) S={B2, C}
v (5)=min max min max (/3 (i;)+/4(f));
ueU m1eBI(u1) t>eC(a),,a>2)
д) S={B1,B2, C}
і)'(5)=пс
U<
е) S={A0, Blt C}
v (5)=min max max max ?/;(г);
ueU ш,еВ,(и,) <u2eB2(u2) иеС(ш,,шJ іш2
r'(S)=max max min max ? /,(»);
ueU <u,eB,(u,) <U]eB2(u2) veC(<u,,<u2) 1 = ] 24
Ж) 5={^[0, B2, C}
v(S)=max max min max ? /,(r);
ueU OjeBj^j) а^еВ^к,) ебС(си,,<и1) 3 4
З) iS’={y40, B2, B2, C}
4
r'(*S')=max max max max ? /,(»).
ueU cojeB,^,) ш2еВ2(и2) oeC^.ajj)
При таком определении характеристическая функция обладает свойством суперадцитивности, т. е. для любых S,Ra {Л0, В? В2, С}, для которых Sf~)R=0, имеет место неравенство «(5иЛ)>і;(5)+і;(Л).
§ 7. МНОГОШАГОВЫЕ ИГРЫ С НЕПОЛНОЙ ИНФОРМАЦИЕЙ
7.1. В § 1 — 4 рассматривались многошаговые игры с полной информацией, определенные на конечном древовидном графе (г=(Х, F), в которых каждый из игроков в момент совершения своего хода точно знал, в какой позиции или в какой вершине дерева он находится. Именно поэтому удалось ввести понятие стратегии игрока і как однозначной функции ы, (х), определенной на множестве
очередности Xt со значениями в множестве Fx. Однако если попытаться исследовать многошаговую игру, в которой игроки при совершении своих выборов не знают точно позиции, в которой они совершают ход, или могут лишь предполагать, что эта позиция принадлежит некоторому подмножеству А множества очередности Xt, то реализация стратегии игрока как функции от позиции хеХ,
окажется невозможной. Таким образом, желание усложнить информационную структуру игры неизбежно приводит к изменению понятия стратегии. Для точных формулировок необходимо в первую очередь формализовать понятие информации в игре. Важную роль здесь играет понятие информационного множества. Проиллюстрируем это на нескольких простейших, ставших классическими в учебной литературе по теории игр примерах [9].
Пример 6. (Игра антагонистическая). Делая 1-й ход, игрок 1 выбирает число из множества {1, 2}. Второй ход делает игрок 2. Зная выбор игрока 1, он выбирает число из множества {1, 2}. Третий ход опять делает игрок 1. Зная выбор игрока 2 и помня свой выбор, он выбирает число из множества {1, 2}. На этом игра прекращается, и игрок 1 получает выигрыш Н (игрок 2 — выигрыш (—Н), т. е.
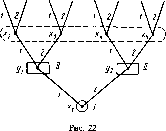
| игра антагонистическая), где функция Я определяется следующим образом: | ||||||||||||
|
Пример 7. Несколько изменим информационные условия примера 6. Игра антагонистическая. Делая первый ход, игрок 1 выбирает число из множества {1, 2}. Второй ход делает игрок 2. Зная выбор игрока 1, он выбирает число из множества {1,2}. Третий ход делает игрок 1. Не зная выбора игрока 2 и забыв свой выбор, он выбирает
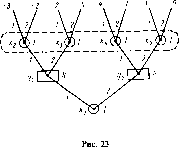
число из множества {1, 2}. На этом игра прекращается и выигрыш определяется по формуле (7.1), так же как и в игре примера 6.
Граф G = (X,F) игры не изменяется, однако, находясь в узлах х2, хъ, х±, х5 (на 3-м ходе игры), игрок 1 не может определить, в каком из этих узлов он на самом деле находится, но, зная очередность хода (3-й ход), он может быть уверен, что не находится в узле х1. На графе G мы обведем узлы х2, хъ, х5 пунктирной линией (рис. 23). В результате узел х2 оказался обведенным кружком, что можно интерпретировать как точное знание игроком 1 этого узла, когда он в нем находился. Узлы у2, у2 обведены квадратиками, что также означает, что игрок 2, находясь в одном из них, при совершении своего хода может отличить его от другого. Объединяя узлы хг, л:3, jc4, jc5 в одно множество, мы иллюстрируем факт их неразличимости для игрока 1.
Множества, на которые разбиты узлы, будем называть информационными множествами.
Перейдем теперь к описанию стратегий. Состояние информации игрока 2 не изменилось, поэтому множество его стратегий то же, что и в примере 6, т. е. оно состоит из четырех векторов (1, 1), (1, 2), (2, 1), (2, 2). Информационное состояние игрока 1 изменилось. На 3-м шаге игры он знает лишь номер этого шага, но не знает позиции, в которой находится. Следовательно, он не может реализовать выбор следующей вершины (или выбор числа из множества {1, 2}) в зависимости от позиции, в которой находится на третьем шаге. Поэтому на 3-м шаге ему остается независимо от в действительности реализовавшейся позиции выбирать одно из двух чисел {1, 2}. Поэтому его стратегия представляет собой пару чисел (/', j), /е{1, 2}, у'е{1, 2}, где число і выбирается в позиции х2, а число j на 3-м шаге одинаково во всех позициях х2, х3, jc4, jc5. Таким образом, выбор числа j оказывается функцией множества
| и может быть записан как и {х2, | х3> | х5} = | j. В данной игре у обоих | ||
| игроков по четыре стратегии и матрица игры имеет вид | |||||
| (1.1) | (1.2) | (2.1) | (2.2) | ||
| (1.1) | " -3 | -3 | 2 | 21 | |
| (1.2) | -2 | -2 | -5 | -5 | |
| (2.1) | 4 | 1 | 4 | 1 | |
| (2.2) | 1 | 5 | 1 | 5 |
1 есть вектор (0, 0, 4/7, 3/7), а оптимальная смешанная стратегия игрока 2 равна (4/7, 3/7, 0, 0). По сравнению с примером 6 гарантированный выигрыш игрока 1 уменьшается. Это вызвано ухудшением его информационного состояния.
Интересно заметить, что матрица игры примера 7 имеет размер 4 х 4, в то время как матрица игры примера 6 имеет размер 32 х 4. Таким образом, уменьшение доступной информации уменьшает размер матрицы выигрышей, следовательно, и облегчает решение самой игры, что противоречит распространенному мнению о том, что уменьшение информации приводит к усложнению принятия решений.
Изменяя информационные условия, можно получить другие варианты игры, описанной в примере 6.
Пример 8. Делая первый ход, игрок 1 выбирает число из множества {1,2}. Второй ход делает игрок 2, который, не зная выбора игрока 1, выбирает число из множества {1, 2}. Далее, совершая 3-й ход, игрок 1 выбирает число из множества {1,2}, зная выбор игрока
2 и помня свой выбор на первом шаге. Выигрыш определяется так же, как и в примере 6 (рис. 24). Поскольку при совершении третьего хода игрок знает позицию, в которой он находится, позиции третьего уровня обведены кружками, два узла, в которых ходит игрок 2,
мы обвели штриховой линией, включив их в одно информационное множество.
Пример 9. Делая первый ход, игрок 1 выбирает число из множества {1, 2}. Второй ход делает игрок 2, не зная выбора игрока 1. Далее, совершая третий ход, игрок 1 выбирает число из множества (I, 2}, не зная выбора игрока 2 и не помня свой выбор на 1-м шаге. Выигрыш определяется так же, как в игре из примера 6 (рис. 25).
Здесь стратегия игрока 1 состоит из пары чисел (г, J), где /-выбор на 1-м шаге, а j — на 3-м шаге игры. Стратегия игрока 2 есть выбор числа j на 2-м шаге игры. Таким образом, у игрока 1 — четыре стратегии, а у игрока 2 — две стратегии. Игра в нормальной форме имеет матрицу размера 4x2:
2
2"
-5
1
5
1
-3
-2
4
1
(1.1)
(1.2)
(2.1)
(2.2)
Значение игры равно 19/7, оптимальная смешанная стратегия игрока 1 (0, 0, 4/7, 3/7), оптимальная стратегия игрока 2 (4/7, 3/7).
В этой игре значение оказалось таким же, как и в игре из примера 7, т. е. оказалось, что ухудшение информационных условий игрока 2 не улучшило состояние игрока 1. Это обстоятельство в данном случае носит случайный характер и вызвано спецификой функции выигрыша.
Пример 10. В предыдущем примере игроки не различают позиции, находящиеся на одном уровне дерева игры, однако они все-таки знают, какой ход совершают. Можно построить игру, в которой игроки проявляют большее незнание.
Рассмотрим антагонистическую игру двух лиц, в которой игрок 1 — один человек, а игрок 2 — команда из двух человек А и В. Все трое изолированы друг от друга (находятся в изолированных помещениях) и не могут общаться между собой. В начале игры посредник входит в помещение, где находится игрок 1, и предлагает ему выбрать число из множества {1, 2}. Если игрок 1 выбирает 1, то посредник заходит сначала в помещение, где находится А, и предлагает ему выбрать число из множества {1, 2}, затем заходит к В и предлагает ему сделать выбор из множества {1, 2}. Если же игрок 1 выбирает 2, то посредник предлагает игроку В сделать выбор первому. После того как три числа выбраны, игрок 1 выигрывает величину К (х, у, z), где х, у, z — выборы игрока 1 и членов команды 2 А и В соответственно. Функция К(х, у, z) определяется следующим образом:
*0,1,1)=1, К (1,2,1) = 7,
К(2,1,1) = 5, К (2,2,1)=6,
К (1,1,2)=3, К (1,2,2) = 9,
К (2,1,2)= 1, К (2,2,2) = 7.
Из правил игры следует, что, когда одному из членов команды А и В предлагается сделать выбор, он не знает, совершает ли он выбор на 2-м или 3-м шаге игры. Структура игры изображена на рис. 26. Таким образом информационные множества игрока 2 содержат вершины разного уровня, что соответствует незнанию номера хода в игре. Здесь игрок 1 имеет две стратегии. Игрок 2 имеет четыре стратегии, они состоят из всевозможных комбинаций выборов членов команды А, В, т. е. его стратегии суть пары (1,1), (1,2), (2,1), (2,2).
Для того чтобы понять, как определяются элементы матрицы выигрышей, рассмотрим ситуацию {2, (2,1)}. Так как игрок 1 выбрал 2, то посредник идет в комнату к В, который согласно стратегии (2.1) выбирает 1. Далее он идет к А, который выбирает 2. Таким образом, выигрыш в ситуации {2, (2,1)} равен К (2, 1, 2) = 1. Матри-
| 1 3 7 9 5 1 6 7 |
 |
(1,1) (1,2) (2,1) (2,2)
1 Г 1 3 7 9]
2 L 5 6 1 7 j
Значение игры равно 17/5, и оптимальные смешанные стратегии игроков 1 и 2 соответственно равны (2/5, 3/5), (3/5, 0,2/5,0).
Заметим, что в многошаговых играх с полной информацией (см. теорему п. 2.1) существует ситуация равновесия по Нэшу в классе чистых стратегий, а в случае антагонистических многошаговых игр — просто ситуация равновесия в чистых стратегиях. Вместе с тем во всех играх с неполной информацией, рассмотренных в примерах 7 — 10, ситуации равновесия в чистых стратегиях не существует.
7.2. Дадим теперь формальное определение многошаговой позиционной игры.
Определение. Многошаговая позиционная игра п лиц Г определяется:
1) Заданием древовидного графа G = (X, F) с начальной вершиной х0, называемой начальной позицией игры.
2) Разбиением множества всех вершин X на п + 1 множество X,, Х2, .... Х„, Хп+І, где множество X, называется множеством очередности і-го игрока і= 1, ..., л, а множество X„+l = {x: Fx— 0} — множеством окончательных позиций.
3) Заданием вектор-функции К(х) = (К1 (х),..., К„ (х)) на множестве окончательных позиций хеХп+1; функция Kt(x) называется выигрышем і-го игрока.
4) Подразбиением каждого множества Х„ і=1, ..., л, на непересе-
кающиеся подмножества Х{, называемые информационными множествами і-го игрока. При этом для любых позиций одного и того же информационного множества множество следующих за ними вершин должно содержать одно и то же число вершин, т. е. для любых х, у еХ{\ — число элементов множества Fx), и никакая
вершина информационного множества не должна следовать за некоторой другой вершиной этого же множества, т. е. если хеХ\,то не существует другой вершины у в Х{ такой, что yeFx (см. п. 1.2).
Определение многошаговой игры с полной информацией (см. п. 1.4) отличается от приведенного здесь лишь условием 4, где вводятся дополнительные разбиения множеств очередности игроков Xt на
информационные множества. Как видно из примеров, содержательный смысл такого разбиения заключается в том, что при совершении своего хода в позиции хеХ, игрок і в условиях неполной информации не знает самой позиции jc, а знает лишь, что эта позиция находится в некотором множестве XJ,cX,(xe Х{). На информационные множества игрока условие 4 накладывает определенные ограничения. Требование |^| = |^| для любых двух вершин
одного информационного множества вводится для того, чтобы вершины х, yeXJ, были неразличимы. Действительно, при \FX\ ф |
игрок і мог бы различить между собой вершины х, у еХ{ по числу выходящих из них дуг. Если бы в одном информационном множестве существовали две такие вершины х, у, что у eFx, то это означало
бы, что партия игры может пересекать дважды одно информационное множество, а это, в свою очередь, равносильно тому, что игрок і не помнит номера своего хода в данной партии, что трудно Представимо в реальной игре.
§ 8. СТРАТЕГИЯ ПОВЕДЕНИЯ
Продолжим исследование многошаговой игры с неполной информацией и покажем, что в случае полной памяти у всех игроков она имеет ситуацию равновесия в стратегиях поведения.
8.1. Для дальнейшего исследования необходимо ввести ряд дополнительных понятий.
Определение. Альтернативами в вершине хеХ называются дуги, инцидентные с х, т. е. {(jc, y):yeFx}.
Если \Fx\ = k, то в вершине х имеется к альтернатив. Будем
считать, что если в вершине jc имеется к альтернатив, то они нумеруются целыми числами 1, ..., к, причем вершина jc обходится по часовой стрелке. В вершине jc0 первая альтернатива может быть указана произвольно. Если некоторая вершина хфх0 обходится по часовой стрелке, то первой альтернативой в jc считается та, которая следует за единственной дугой (Fxl, jc), входящей в jc (рис. 27).
Будем считать, что в игре Г все альтернативы перенумерованы указанным способом. Пусть Ак— множество всех вершин хеХ,
| имеющих поино к альтепнатив. т е, _ |
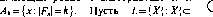 |
Рис 27
сЛ",}—множество всех информационных множеств игрока і. Под чистой стратегией игрока і будем понимать функцию и„ отображающую
I, в множество положительных чисел, так что ц,(Х^^к, если Х\<^Ак. Будем говорить, что стратегия и, выбирает
альтернативу / в позиции хеХ{, если и,(Х§—1, где / — номер альтернативы.
Так же как это было сделано в п. 1.4, можно показать, что каждоЁ ситуации и() = (и1(), ..., щ,(•)) единственным образом соответствует партия со, следовательно, и выигрыш в окончательной позиции этой партии.
Пусть хеХ„+і — некоторая окончательная позиция и со — единственный путь (F — дерево), ведущий из х0 в х. Условие принадлежности позиции у пути со будем записывать в виде уесо или у<х.
Определение. Позиция хеХ называется возможной для щ(),
если существует ситуация м( ), содержащая м(( ), такая, что в ситуации и (•) реализуется путь со, который содержит позицию х, т. е. хе со. Информационное множество Х{ называется существенным для щ (•), если некоторая позиция хеХ{ возможна для и, (•).
Множество позиций, возможных для ы((), обозначим через Poss Ui( ), а семейство информационных множеств, существенных для М.(-),— через Rel щ( ).
Лемма. Позиция хеХ возможна для щ( ) тогда и только тогда, когда щ (•) выбирает альтернативы, лежащие на отрезке партии сох от х0 до х во всех своих информационных множествах, пересекающих сох.
Доказательство. Пусть xePossM((). Тогда существует ситуация и(-), содержащая «, (•), такая, что партия со, реализовавшаяся
в этой ситуации, проходит через х: а это и означает, что на своих информационных множествах, пересекающих отрезок партии сох,
стратегия ы, ( ) выбирает альтернативы (дуги), принадлежащие сох.
Пусть теперь и{( ) выбирает все альтернативы игрока / в со,. Для того чтобы доказать возможность х для «,(¦), необходимо построить ситуацию «(•), содержащую и, ( ), в которой партия проходила бы через х. Для игрока кФі построим стратегию и*(), которая на информационных множествах Х{, пересекающих отрезок пути со,,
выбирает альтернативы (дуги), лежащие на этом пути, а в остальном произвольна. Поскольку каждое информационное множество пересекает путь со лишь однажды, это всегда можно сделать. В полученной ситуации и(-) партия со обязательно пройдет через х. Следовательно, мы показали, что хе Poss u,().
8.2. Смешанные стратегии в многошаговой игре с неполной информацией Г определяются так же, как и в п. 4.2 гл. I для конечных игр.
Определение. Смешанной стратегией р, игрока і называется
вероятностное распределение на множестве чистых стратегий игрока і, которое каждой его чистой стратегии щ() ставит в соответствие вероятность qUj (•) (в дальнейшем для простоты будем писать просто qu).
Ситуация р=(р1, .... р^) в смешанных стратегиях определяет
распределение вероятностей на всех партиях со (следовательно, и на окончательных позициях Х„+\) по формуле
V
где Ри (со) = 1, если партия со реализуется в ситуации ы( ), и Ри (со)=О в противном случае.
Лемма. Обозначим через РДх) вероятность реализации позиции х в ситуации р. Тогда имеет место формула
рЛх)= ? _Чи,..Чип= п Е Яи, (8.1)
{и о: хе Ром и/О, /-1,в) /-1 {и(:хеРоми,}
Доказательство этого утверждения непосредственно следует из леммы п. 8.1.
Математическое ожидание выигрыша Et(p) игрока / в ситуации р равно
Е}{р)= X ВДРДх), (8.2)
*6*В+1
где Рм(х) вычисляется по формуле (8.1).
Определение. Позиция хеХназывается возможной для ph если существует ситуация р в смешанных стратегиях, содержащая pit такая, что Рм(х)>0. Информационное множество игрока і называется существенным для ph если некоторое хеХ{ является возможным для р,.
Множество возможных для д, позиций обозначим через Poss pt, а множество существенных для р, информационных множеств — через Rel pi.
8.3. Исследуя многошаговые игры с полной информацией (см. 3.3), мы показали, что выбор стратегии может осуществляться на каждом шаге в соответствующей позиции игры, а при решении конкретных задач необязательно (да и практически невозможно) определять заранее стратегию, т. е. полный набор рекомендуемого поведения во всех позициях (информационных множествах), поскольку такое правило (см. пример п. 2.2) «страдает сильной избыточностью». Можно ли сделать аналогичное упрощение в играх с неполной информацией, т. е. строить стратегию не как заранее фиксированное правило выбора во всех информационных множествах, а формировать ее по мере попадания в соответствующее информационное множество? Оказывается, что в общем случае этого сделать нельзя. Однако существует класс игр с неполной информацией, где такое упрощение возможно. Введем понятие стратегии поведения.
Определение. Под стратегией поведения р, игрока і будем
понимать правило, которое каждому информационному множеству Х{<=.Ак игрока і ставит в соответствие систему из k чисел
Ь(Х\, ?)^0, ? = 1, ..., k, таких что
5>(П?) = 1,
где Ak={x:\Fx\ = k}.
Числа Ь{Х{, ?) могут интерпретироваться как вероятности выбора альтернативы ? в информационном множестве Х{сzAk, каждая
позиция которого содержит ровно к альтернатив.
Любой набор Р=(Рк, рп) стратегий поведения для и игроков
определяет вероятностное распределение на партиях игры и окончательных позициях следующим образом:
П Ь(Х{ ?). (8.3)
Здесь произведение берется по всем Х\м? таким, что Х\[\соФ0, и выбор в точке Х{ Р)ш альтернативы с номером ? приводит в позицию, принадлежащую пути со.
В дальнейшем под понятием «путь» удобно подразумевать не только набор составляющих его позиций, но и набор соответствующих альтернатив (дуг).
Ожидаемый выигрыш Et(P) в ситуации Р = (РХ, ...» р„) в стратегиях поведения определяется как математическое ожидание
Е,(Р)= ? К,(х)Р?(сох), і=1,...,п,
*е*и+1
где сох — партия, завершающаяся позицией хеХ„+1.
8.4. Каждой смешанной стратегии д, можно сопоставить некоторую стратегию поведения /?,.
Определение. Стратегией поведения /}„ соответствующей смешанной стратегии д, = {?„,} игрока і, называется стратегия поведения, определенная следующим образом.
Если A^eRel д,, то
Z 9щ
Ь (Х{, ?)=(8.4) Е Чщ
{щ-.Х^КАи,}
Если Х{ ф Rel д,, то на множестве Х{ стратегию /?, можно определить произвольным, отличным от (8.4) образом. (В случае Х{ ф Rel Ді знаменатель в выражении (8.4) обращается в нуль.) Для определенности будем полагать
Ь(П?)= ? qu, (8.5)
Приведем без доказательства следующий результат.
Лемма. Пусть /?,• — стратегия поведения игрока і, а Д/={?«,} —
смешанная стратегия, определяемая формулой
Ящ=ПЬ(ХІ щ(Х$).
Тогда Pi — стратегия поведения, соответствующая д,.
8.5. Определение. Игра Г называется игрой с полной памятью для і-го игрока, если для любых ы((.), Х{, х из условий ATjeRel
Ui и хеХі следует, что хеPossц.
Из определения следует, что в игре с полной памятью для і-го игрока любая позиция из существенного для щ( ) информационного
множества является возможной для ы, (•). Термин «полная память»
подчеркивает то обстоятельство, что, очутившись в любом своем информационном множестве, і-й игрок может точно восстановить, какие альтернативы (т. е. номера) он выбирал во всех своих предыдущих ходах (в силу однозначного соответствия). Игра с полной памятью для всех игроков превращается в игру с полной информацией, если все ее информационные множества содержат по одной вершине.
8.6. Лемма. Пусть Г — игра с полной памятью для всех игроков; со — некоторая партия в Г. Пусть хеХ\ — последняя позиция в пути со, в которой ходит игрок і, и пусть он выбирает в х дугу ?есо.
215
Положим
Ті(со)={иі-.Х\еШи„иг(Х>) = ?}.
Если в (о нет позиций из Х„ то через 7} (со) обозначим множество
всех чистых стратегий игрока і. Тогда партия со реализуется в тех и только тех ситуациях и (•) = (мх (•),..., и„ ()), для которых и, е Г, (со).
Доказательство. Достаточность. Достаточно доказать, что если и,е Г, (со), то стратегия и, выбирает все дуги (альтернативы)
игрока і, входящие в партию со (если, конечно, игрок і вообще имеет ход в со). Однако если ы,е Т(со), то A^eRel иь и так как игра Г имеет
полную память, то хе Poss щ (хесо). Значит, согласно лемме п. 8.1, стратегия ы, выбирает все альтернативы игрока і, входящие в партию со.
Необходимость. Предположим, что партия со реализуется в ситуации м(), у которой и,фТі(со) для некоторого і. Поскольку
A'jeRelUj, это означает, что щ(ХІ)ф?. Но тогда путь со не реализуется. Полученное противоречие завершает доказательство леммы.
8.7. Лемма. Пусть Г — игра с полной памятью для всех игроков. Пусть ? — альтернатива (дуга) в партии со, инцидентная х е Х{, где хе со, и следующая позиция игрока і (если она существует) в пути со есть уеХ,. Рассмотрим множества S и Т, где
5={Mi:^eRelui, щ(Х^=?),
7’={ui:ArfeRel м<}.
Тогда S=T.
Доказательство. Путь u,eS. Тогда A^eRel ut, и так как Г имеет полную память, то хе Poss щ. Следовательно, по лемме п. 8.1 стратегия щ выбирает все дуги, инцидентные к позициям игрока і на пути от х0 до х и Ui(X{)=v. Таким образом ы, выбирает все дуги,
инцидентные к позициям игрока і на пути от х0 до у, т. е. у еPoss Uj, A'feRel щяще Т.
Пусть ще Т. Тогда JTfeRel ы,, и так как Г имеет полную память, то у е Poss Uj. Однако это означает, что xePossuj и щ(Х{) = ?, т. е. ц,е5. Лемма доказана.
8.8. Теорема. Пусть Р — ситуация в стратегиях поведения, соответствующая ситуации в смешанных стратегиях р в игре Г (в которой все позиции имеют по крайней мере две альтернативы).
Тогда для того чтобы
Е,(Р)=Е,(ц), /=1, п,
необходимо и достаточно, чтобы Г была игрой с полной памятью для всех игроков.
Доказательство. Достаточность. Пусть Г — игра с полной памятью для всех игроков. Фиксируем произвольное д. Достаточно показать, что Рр (со) = Ру. (со) для всех партий со. Если в со существует
позиция игрока і, принадлежащая несущественному для д, информационному множеству, то найдется Х{ е Rel/i,, Х{(~)со^0, такое, что для стратегии поведения рь соответствующей д,, вьшолняется равенство Ъ{Х\, ?) = 0, где veto. Отсюда имеем Рр(со) = 0. Справедливость соотношения Ру (со)=0 в этом случае очевидна.
Будем теперь считать, что все информационные множества z'-ro игрока, через которые проходит партия со, существенны для Ді, і=1, 2, ..., п. Пусть игрок і в партии со ходит по порядку в позициях, принадлежащих множествам X],..., Х\, и выбирает в множестве Х{ альтернативу vJt j= 1, ..., s. Тогда согласно формуле (8.4)
и лемме п. 8.7 имеем
П b(Xi,Vj)= ? Чщ.
J-1 цеГДш)
Действительно, поскольку в партии со игрок і свой 1-й ход делает из множества X), оно является существенным для всех щ (•), поэтому
знаменатель в формуле (8.4) для b(X}, vj равен единице. Далее в силу леммы п. 8.7 в формулах (8.4) числитель Ь(Х{, у,) равен
знаменателю b(X{+l, vJ+i),j=l, ..., s. Согласно формуле (8.3) окончательно получим
Р?(а)=І\ ? Чщ,
і-І щеТ{(т)
где Г,(ш) определено в лемме п. 8.6.
В то же время на основании леммы п. 8.6
= - 4u„Pu(a>)= ? Чщ-Чип,
“О и щеТі(<о)
/=1, ,п
т. е. Рм(ш)=Рд(ш), и достаточность доказана.
Необходимость. Пусть Г не является игрой с полной памятью для всех игроков. Тогда существуют игрок і, стратегия щ, инфор-
217
мационное множество A'-'eRel и, и две позиции х, уеХ\ такие, что
хе Poss и„ уфPoss и,. Пусть и\ — стратегия игрока і, для которой
у е Poss и и со — соответствующая партия, проходящая через у в ситуации и'. Обозначим через д, смешанную стратегию игрока і,
которая предписывает с вероятностью 1/2 выбирать стратегию и, либо и,. Тогда Pultli{y)-PuUi{co)=\j2 (здесь и'||д,— ситуация,
в которой чистая стратегия и, заменена на смешанную д,). Из условия у ф Poss и, следует, что путь со, реализующийся в ситуации и'||и„ не проходит через у. Это означает, что существует Хк такое, что Хк(~]со = Хк(~]соФ0 и и1(Хк)Фи1(^'Г)- Отсюда, в частности, следует Хке Rel и„ Хк е Rel и'. Пусть /?, — стратегия поведения, соответствующая д,. Тогда b(Xf, ut(Xk)) = 1/2. Не ограничивая общности, можно считать, что и,(Х\)фй,(Х\). Тогда b{X\, u,(XJ)) = 1/2. Обозначим через Р ситуацию в стратегиях поведения, соответствующую ситуации в смешанных стратегиях м'Цд,. Тогда Рр(со)^ 1 /4, в то
время как PU'itli (<о)= 1/2. Теорема доказана.
Из теоремы п. 8.8, в частности, следует, что для нахождения ситуации равновесия в играх с полной памятью достаточно ограничиться классом стратегий поведения.
§ 9. ФУНКЦИОНАЛЬНЫЕ УРАВНЕНИЯ ДЛЯ ОДНОВРЕМЕННЫХ МНОГОШАГОВЫХ ИГР
Теорема о стратегиях поведения, доказанная в предыдущем параграфе, в общем случае не дает возможности непосредственно решать многошаговые игры с полной памятью, однако при простой структуре информационных множеств она обосновывает вывод функциональных уравнений для значения игры и основанные на этих уравнениях методы нахождения оптимальных стратегий. Наиболее простыми играми с полной памятью, не считая игр с полной информацией, являются так называемые одновременные многошаго-

вые игры. Выведем функциональное уравнение для значения таких игр и рассмотрим несколько широко известных [5, 11] примеров, где эти уравнения поддаются решению.
9.1. Содержательно одновременная многошаговая игра представляет собой антагонистическую многошаговую игру, в которой на каждом шаге игры игроки 1 и 2 выбирают свои действия одновременно, т. е. не имея информации о выборе противником позиции в этот момент. После того как выборы сделаны, они становятся известными обоим игрокам, и игроки вновь совершают одновременный выбор и т. д.
Условно такую игру будем изображать с помощью графа, имеющего одно из двух представлений (рис. 28, а, б). Граф изображает поочередную игру с четным числом ходов, в которой информационные множества игрока, совершающего первый ход, являются одноэлементными, а информационные множества другого игрока двухэлементными. В такой игре Г оба игрока обладают полной памятью, поэтому в ней согласно теореме п. 8.8 при отыскании ситуации равновесия можно ограничиться классом стратегий поведения.
Пусть, для определенности, в Г первым ходит игрок 1. С каждым хеХу связывается подыгра Г* с той же информационной
структурой, что и игра Г. Нормальная форма любой антагонистической конечно-шаговой игры с неполной информацией представляет собой матричную игру, т. е. антагонистическую игру с конечным числом стратегий, поэтому во всех подыграх Г*, хеХу (включая
игру Г=ГІ(і) существует ситуация равновесия в классе смешанных
стратегий. Согласно теореме п. 8.8 такая ситуация равновесия существует и в классе стратегий поведения и значения игры (т. е. значения функции выигрыша в ситуации равновесия в классе смешанных стратегий и в классе стратегий поведения) равны между собой.
Обозначим значение игры Г* через ? ¦ (х), хвХх и составим
функциональные уравнения для ? (jc).
Для каждого хеХу следующая позиция У, в которой ходит игрок 1 (если таковая вообще существует), принадлежит множеству F\. Позиция х' реализуется в результате двух последовательных выборов: игроком 1 — дуги, инцидентной к вершине х, и игроком 2 — дуги в позициях ysFx, образующих информационные множества игрока 2. Поэтому можно считать, что позиция х? получается в результате отображения Тх, зависящего от выборов а, /) игроков
1 и 2, т. е.
х' = Тх(а, р).
Так как число различных альтернатив а и /9 конечно, то можно рассмотреть для каждого хеХх матричную игру с матрицей выиг-
219
рышей Ax = {v[Tx(a, fi)]}. Пусть ft (x) = {b\(x, a)}, P'„(x) =
= {b'!!(x, f})} —оптимальные смешанные стратегии в игре с матрицей Ах. Тогда имеет место следующая теорема о структуре оптимальных стратегий в игре ГЛ.
Теорема. В игре Г оптимальная стратегия поведения игрока 1 в точке х (каждое информационное множество игрока 1 в игре Г состоит из одной позиции xeXj) предписывает каждой альтернативе а вероятность в соответствии со смешанной оптимальной стратегией игрока 1 в матричной игре Ах, т. е.
a) = bf(x, a).
Оптимальная стратегия поведения {Ь2(Х{, /?} игрока 2 в игре Г предписывает каждой альтернативе Р вероятность в соответствии с оптимальной смешанной стратегией игрока 2 в игре с матрицей Ах, т. е.
Ь2(Х{, Р) = Ь*П(х, Р),
где x=F~\ если уеХ{.
Значение игры удовлетворяет следующему функциональному уравнению:
®(*)=?а1 {?[Тх(а, Р)]}, хеХ,, (9.1)
с граничным условием
®(*W,=#(x). (9.2)
(Здесь ?аі А — значение игры с матрицей А).
Доказательство проводится по индукции и вполне аналогично доказательству теоремы п. 2.1.
9.2. Пример 11. (Игра инспектирования). Игрок Е (нарушитель) хочет совершить некоторое запрещенное действие. Имеется N периодов времени, в которые это действие может быть осуществлено. Игрок Р (инспектор), желающий предотвратить это действие, может провести только одну инспекцию в любой из этих периодов времени. Выигрыш игрока Е равен 1, если запрещенное действие произошло и осталось необнаруженным, и равен ( — 1), если нарушитель пойман (это будет в том случае, когда для совершения действия он выбирает тот же самый период времени, что и инспектор для проверки); выигрыш равен нулю, если нарушитель не действует вовсе. Обозначим такую ^-шаговую игру через rw.
В первом периоде (на 1-м шаге) каждый игрок имеет две альтернативы. Игрок Е может предпринимать действие или не предпринимать его; игрок Р может инспектировать или не инспектировать. Если игрок Е действует и игрок Р инспектирует, то игра заканчива-
ется и выигрыш равен —1. Если игрок Е действует, а игрок Р не инспектирует, то игра заканчивается и выигрыш равен 1. Если игрок Е не действует, а игрок Р инспектирует, то игрок Е может предпринять действие в следующий период времени (в предположении, что N> 1) и выигрыш также равен 1. Если игрок Е не действует и игрок Р не инспектирует, то переходят к следующему шагу игры, который отличается от предыдущего только тем, что до конца игры остается меньшее число периодов времени, т. е. попадают в подыг-ру ГІ?_1. Следовательно, матрица для 1-го шага игры выглядит следующим образом:

Уравнение (9.1) в этом случае принимает вид
’»=?а1["і «І-J 9Л>
Здесь ? (х) одинаково для всех позиций игры одного уровня и поэтому зависит только от числа периодов до конца игры. Поэтому вместо ?(х) записано Далее будет показано, что vN_1< 1, следовательно, матрица в (9.4) не имеет седловой точки, т. е. игра с матрицей (9.4) является вполне смешанной. Отсюда получаем (см. п. 9.1 гл. I) рекуррентное уравнение
«w-1 + І -?„_і + з’
(9.5)
VN =
которое вместе с начальным условием
определяет vN. Преобразуем уравнение (9.5) с помощью подстанов-
ки tN—-. Получим новое рекуррентное уравнение tN=tN_1—,
tl= — 1. Это уравнение имеет очевидное решение tN= — (N+1)/2, откуда имеем
(9.7)
N-1 ' N+1
Теперь можно вычислить оптимальные стратегии поведения на каждом шаге игры. Действительно, матрица игры (9.4) принимает
Г-1 11
ВИДІ , „Ч(жг , оптимальные стратегии поведения таковы:
|_ 1 (N-2)/N J
',sj_L Л.
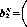 |
i N+1 N + l |
Пример 12. (Теоретико-игровые особенности оптимального расхода ресурса). Пусть первоначально игроки 1 и 2 имеют соответственно г и R—г единиц некоторого ресурса, а также по две чистые стратегии. Допустим, что если игроки выберут одинаковые по номеру чистые стратегии, то ресурс игрока 2 уменьшится на единицу. Если же игроки выберут разные по номеру чистые стратегии, то на единицу уменьшится ресурс игрока 1. Игра заканчивается после того, как ресурс одного из игроков станет равным нулю. При этом игрок 1 получает выигрыш, равный 1, если ресурс игрока 2 станет равным нулю, и выигрыш — 1, если станет равным нулю его собственные ресурс.
Обозначим через Г*/ многошаговую игру, в которой игрок
1 имеет k(k=l, 2, ..., г) единиц, а игрок 2 —1(1=1, ..., R—r) единиц ресурса. Тогда
?а1Г*_и-|
Vairfc/_J’
?аІГ*/_ь ?а1Г*_м
?а1Г*,,=?а1
где Val Г*,о= 1, Val Г0,/= — 1.
Рассмотрим 1-й от конца шаг, т. е. когда у обоих игроков осталось по одной единице ресурсов. Очевидно, что на этом шаге
г Г 1 -п
разыгрывается следующая матричная игра: Гіл = I .
Игра Ги является симметричной, ее значение, которое мы обозначим через ?1>ь равно нулю, а оптимальные стратегии игроков совпадают и равны (1/2, 1/2).
На 2-м от конца шаге, т. е. когда у игроков осталось три единицы ресурсов, разыгрывается одна из двух матричных игр Гід или Г2,і. При этом
|
-1 П | 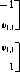 |
*>і,і — 1__1 2 _ 2* «4,1 + 1 _1 2 — 2 |
®2>1=?а1Г2>1 = ?а1
На 3-м от конца шаге (т. е. когда у игроков имеется в общей сложности четыре единицы ресурса) разыгрывается одна из следующих трех игр: Г]3, Г^, Г31. При этом
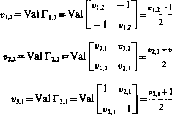 |
4 3 |
Продолжая аналогичные вычисления далее до N-го шага от конца, получим следующее выражение для значения исходной игры:
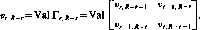
В силу симметричности матрицы выигрышей игры Г,, х_, имеем
і?.д-,=- (в,.*-,-1+І?-1,я—г),
оптимальные стратегии поведения игроков на каждом шаге совпадают и равны (1 /2, 1/2).
Пример 13. В шуточной игре играют две команды: игрок 1 (т1 женщин и т2 кошек); игрок 2 (п1 мышей и п2 мужчин). На каждом шаге каждый из игроков выбирает своего представителя. Один из двух выбранных представителей «устраняется» согласно следующим правилам: женщина «устраняет» мужчину; мужчина «устраняет» кошку; кошка «устраняет» мышь; мышь «устраняет» женщину. Игра продолжается до тех пор, пока в одной из групп не останутся игроки только одного типа. Когда группа не имеет больше выбора, другая группа, очевидно, выигрывает.
Обозначим значение исходной игры ?(т1, т2, п? п2). Будем полагать
?(т2, т2, п2, 0)=?(т2, т2, 0, п2)= 1, если т2, т2>0, ^ g^
?(т2, 0, п2, п2)=?(0, т2, п2, п2)= — 1, если и1, и2>0.
Введем следующие обозначения: «(/Их — l)=v(m1—1, т2, п? п2), ?(т2-\)=?(т? т2 — 1, п2, п2), ?(п1-1)=?(т1, т2, п2-1, п2), ?=(п2 — \)=?(т1, т2, п2, п2 — 1). Согласно теореме п. 9.1 справедливо соотношение
Можно показать, что рассматриваемая игра является вполне смешанной. Согласно теореме п. 9.1 гл. I имеем
v(mlt т2, tiy,
?{тх — 1) ?(т2 — 1)— «(/ij — 1) v(n2 — 1) v(niy— 1)+?(да2 — 1)— «(/ij — 1)—v(n2 — 1)
Учитывая граничные условия (9.8), отсюда получаем
v(n2-\) v(m2- 1)
v(mlt m2, n1,
и2)=?а1
?(ту, 1, 1, 1) =
«(ffij-ll+l —V (nty —1) + 3
и?(1, 1, 1, 1)=0. Но эти уравнения совпадают с уравнениями (9.5),
(9.6), следовательно, ?(т, 1, 1, 1) = (тя— \)/(т+1) и оптимальные стратегии в этом случае также совпадают с приведенными в примере 11.
Упражненія н задачи
1. Найти все ситуации абсолютного равновесия по Нэшу в примере 4 п. 2.2.
2. Доказать, что в неантагонистической конечно-шаговой игре двух лиц с полной информацией выигрыши во всех «благожелательных» (неблагожелательных) ситуациях равновесия по Нэшу равны между собой.
3. Пусть (х), ?2(х), ..., ?„(х) — значения функций выигрыша игроков 1, 2, ...,
л в подагре Гх в ситуации абсолютного равновесия в игре Г.
а) Показать, что функции ?,(х), і’= 1,2,..., л, удовлетворяют следующей системе функциональных уравнений:
і!,(х)= max vi(xr), хеХи i=l, 2,..., n, (10.1)
xerx
при граничном условии
Ч(х)\хехя+1=Н,(Х). (10.2)
б) Привести пример игры, в которой выигрыши игроков в ситуации равновесия в стратегиях наказания не удовлетворяют системе функциональных уравнений (10.1) при граничном условии (10.2).
4. Построить пример неантагонистической многошаговой игры двух лиц, в которой в ситуации равновесия в «стратегиях наказания» наказывающий игрок при наказании противника за отклонение от выбранного пути еще сильнее наказывает самого себя.
5. Построить Парето-оптимальные множества в игре из примера 4 п. 2.2.
6. Построить пример многошаговой неантагонистической игры, в которой ни одна из ситуаций равновесия по Нэшу не приводит к Парето-оптимальному решению.
7. Построить отображение Т, которое каждой подагре Гг игры Г ставит в соответствие некоторое подмножество ситуаций Ut в этой подагре. Пусть ГІГ) = UXa.
следует, что uk()eUzk, где «"*(¦)=(«!*(¦), ..., и„к()) - сужение ситуации и() на подыгру Т-к, <о0 = {х0, 2,, .... z*} — партия, реализовавшаяся в ситуации u()eUXo. Показать, что если отображения Т каждой подыгре Г,А ставит в соответствие
множество Парето-оптимальных ситуаций Urx, то оно динамически устойчиво.
8. Отображение Т, определенное в упр. 7, называется сильнодинамически устойчивым, если для любой ситуации и (¦) е UXo, любого z* е {z,} = со, где {z,} = at — партия
в ситуации и(-), ситуации ик (¦) е U,k существует ситуация й (¦) е UXa, для которой
zk
ситуация й (•) является ее сужением на позициях подыгры Г1к и позиция z* возможна в ситуации й(-).
Показать, что если отображение Т каждой подыгре ГІк ставит в соответствие
множество ситуаций равновесия по Нэшу, то оно сильнодинамически устойчиво.
9. Построить пример, когда отображение Т, ставящее в соответствие каждой подыгре Г2 множество Парето-оптимальных ситуаций равновесия, сильнодинамически устойчивым не является.
10. Для каждой подыгры Гг введем в рассмотрение величины v({i},z), /=1,..., п,
представляющие собой гарантированный выигрыш і-го игрока в подыгре Гг, т. е.
z) — значение антагонистической игры, построенной на графе подыгры Г, между игроком і и игроками N\i, действующими как один игрок. При этом
множество стратегий коалиции игроков N\ і есть декартово произведение множества стратегий каждого из игроков ke{N\i), J~[ щ, функция выигрыша игрока
/ в ситуации (и,-, и ну,) определяется как ff’Cu,-, unffik функция выигрыша коалиции N\i полагается равной — Н\ (ц, ину).
Построить функции »({і}, z) для всех подыгр Гг из примера 4 п. 2.2.
11. Показать, что если в некоторой многошаговой неантагонистической игре Г с неотрицательными выигрышами (Д,->0, і= 1, ..., п) »({/}, z) = 0 для всех /= 1, ...
Л
..., п и ze У Xh то любая партия может быть реализована в некоторой ситуации
і=і
равновесия в стратегиях наказания.
12. Формализовать fc-уровневую древовидную систему управления в виде иерархической игры, в которой управляющий центр, находящийся на /-м уровне (/= 1.....
к— 1), распределяет ресурсы между подчиненными ему управляющими центрами следующего уровня при і<к— 1 и между подчиненными ему производственными подразделениями при і=к— 1. Выигрыш каждого производственного подразделения зависит только от своего производства, а выигрыш управляющих центров — от подчиненных им производственных подразделений.
13. Найти ситуацию равновесия по Нэшу в построенной в упр. 12 fe-уровневой
иерархической древовидной игре. _
14. Показать, что вектор выигрышей a = {v(N), 0, ..., 0} принадлежит С-ядру двухуровневой иерархической древовидной игры с характеристической функцией « (5). Показать, что ситуация равновесия, построенная в двухуровневой древовидной иерархической игре, является также ситуацией сильного равновесия.
15. В ромбовидной иерархической игре построить характеристическую функцию, используя ситуацию равновесия по Нэшу.
16. Описать множество всех ситуаций равновесия по Нэшу в двухуровневой
древовидной иерархической игре. Учесть возможность «наказания» центра Аа игроками 7?,, .... В„ (например, прекращение выпуска продукции при распределении ресурсов, не отвечающих интересам игрока і).
17. Построить матрицу выигрышей игроков в игре примера б п. 7.1. Найти оптимальные чистые стратегии и значение получившейся матричной игры.
18. Привести к матричной форме и решить игру из примера 8 п. 7.1.
19. Рассмотрим следующую антагонистическую многошаговую игру с задержкой информации о местоположении одного из игроков. Имеются два игрока: мишень Е и стрелок Р. Мишень может двигаться только по точкам оси Ох с координатами О, 1,2,..., причем если игрок Е находится в точке і, то в следующий момент времени он может переместиться только в точки /+1, /—1 или остаться на месте. Стрелок Р имеет у' патронов, у‘=О, 1, ..., и может производить не более одного выстрела в каждый момент времени. Считается, что стрелок попадает в ту точку, в которую целится.
В каждый момент времени игрок Р знает только точное местоположение игрока Е на предыдущем шаге, т. е. если Е находился на предыдущем шаге в точке і, то игроку Р необходимо целиться в точки і+1, і и і—1. Игрок Е знает количество патронов, которые имеет игрок Р в каждый момент времени, но не знает, куда целится игрок Р. Выигрыш стрелка Р равен числу попаданий в мишень. Таким образом, цель стрелка Р — максимизировать количество попаданий в мишень Е до того, кяк она достигнет «бункера». Цель мишени противоположна. Здесь под «бункером» понимается точка О, в которой мишень недостижима для стрелка Р.
Обозначим символом Г^, у) описанную выше игру при условии, что мишень
Е в начальный момент времени находилась в точке с координатой і, а стрелок Р имел j патронов. Символом v (і, у) обозначим значение игры Г,-у (если оно существует).
Нетрудно заметить, что ?(/, 0)=0, і= 1, 2.....u=(l,y)=0,y'= 1,2.....На каждом шаге
игры Гij, і=2, 3.....7=1, 2, .... стрелок имеет четыре стратегии (на самом деле
больше, но они неразумны), а игрок Е — три стратегии. Стратегии стрелка Р таковы: выстрелить в точку і—1, выстрелить в точку і, выстрелить в точку і+1, не стрелять на данном шаге. Стратегии мишени: передвинуться в точку і—1, оставаться в точке і, передвинуться в точку і+1. Следовательно, на каждом шаге игры разыгрывается матричная игра с матрицей выигрышей
1+»(і —1, у—І)
•>(«-1,7-1) •>(«-1,7-1) •>(«'—1, 7)
•>(«', 7-1) *>(«'+!, 7-1)
1+•>(«, 7-1) •>(«+1,7-1)
•>(«', 7-1) 1+*>(« + 1, 7-1)
•>(«', у) *>(«'+!, У) -
Символами xl (і, у), х2 («, у), хъ (i, J), x4 (i, j) обозначим вероятности, с которыми стрелок Р использует свои 1, 2, 3 и 4-ю стратегии, а символами Уі (і, у), y2(i, у), Уз (i, j) — вероятности, с которыми мишень E использует свою 1, 2, и 3-ю стратегии (стратегии поведения игроков Р и Е соответственно есть функции информационных множеств {і,у}).
а) Показать, что значение игры ?(і, у) и оптимальные стратегии поведения стрелка Р (xt (i, j), х2 (i, J), хъ (i, j), xK (i, J)) и мишени E 0>t (j, J), y2 («', j), y3 («, J)) связаны между собой следующими соотношениями:
(1 H-t>(/—1,7—1)) JCj-HuO*—1,7— 1) JC2 + »(i-1,7-1) -*3+•>(« —1,7") xA>v(i,j), v(«', у-1) xj + (1 + «(/, у-1)) x2 + v(/, j-1) x3 + •>(i, j) x^v(i, J),
•>(« + 1,7-1) Jci+»(«’+l,7 —1) *2+(l + •>(« +1,7-1)) x3+v(i+l,j) x4>v(i,j), *і+*2 + *з+** = 1> x2>0, x3^0, x4>0;
(1 + v (/-1,7-1)) Уі + •> (i, 7-1) T>2 + •> («+1,7-1) 7>з <•> («, 7),
V (i-1, j-1) yt + (1 + V (i, j-1)) y2 + ® (І + 1, j- 1) Уз < ® («, J), У!+?(І^-1) y2 + (l+v(i+l,j-l)) y3<v(i,j),
*>(1-1,7) Уі+®(л 7) У2+®0+ 1,7) Уз<®O',7),
J>i +^2 Н-Уз =1, J>i >0, y2 > 0, Уз > 0.
Указание. Трудность решения этой игры состоит в том, что для определения ®(і, ]) необходимо знать «0+1, у), для определения ®(і+1, j) необходимо знать ®(і+2,у) и т. д. В приводимых ниже упражнениях дано решение игры Г(/,у) и приводятся некоторые его свойства.
б) Пусть ф(і, j), i'=l, 2, ..., 7'=0, 1.....— двойная последовательность, определя
емая соотношениями
4>(і, 0)=0, і=1, 2, ...; <р(1,у)=0,7=1, 2, ...,
Ф (і, т) =min {(1 + ф O'-1,7 -1) + Ф (*, 7-1)+Ф (/+1,7-1 ))/3, (1+ф(і-и~1)+ф(і,]-Щ2}.
1) Доказать, что ®(і, у)=<Р(і, у), и если ®(і, 7)=(1+®(і—1, у—l)+»(i, у'—1)+ +®(i+l,y'-l))/3, то
O', 7)=® O', J) -® 0-1. У — 1), *2 O', 7) =» 0, 7) ~® O', j~ 1),
*3 O', 7)=® 0, 7) - ® (i+1,7-1), -^4 0, 7)=o,
Ti 0, J)=у 2 0. у)=Тз 0, у)=і/3;
2) Доказать, что ®(і,7)=р(1,у), и в0™ *(і.7)=(1+®(1— 1,7—1)+®(і,7—1))2, то
*і(і.7)=»(і.7)-®(і- і,7-і), JC2O, 7)=®0'. у)-®0, у- і)> -*30,у) 0,у) =*0.
>>, о, /)—Уі 0. у)=1/2; Уз 0, у)=0.
в) Доказать, что при любом 7=0, 1, 2,... справедливы следующие соотношения:
1) ®0',У)=У/3. і'=у'+1,у'+2,...;
2) ®(1.7)<®(і+1,7), 1=1, 2, ...;
3) »0,У)<®0,У'+1), 1=2, 3, ...;
4) ® 0,7) +® 0+2, у) « 2® 0+1, у), 1=1, 2,... .
г) Доказать, что:
1) lim » 0, У) =7/3 при любом фиксированном 7=0, 1, 2,...;
,/-» + 0О
2) lim ®0.7)=1-1 при любом фиксированном і=1, 2, ....
j-* — ОО
20. Рассмотрим обобщение игры о стрелке и мишени, когда мишень Е, занимая положение і, может из него передвинуться максимум на к единиц вправо или влево,
т. е. перейти в каждую из следующих точек і—к, і—к+1..... і, i + l, ..., i+k.
Остальные цели и возможности стрелка Р и мишени Е остаются прежними с учетом нового определения стратегии игрока Е.
Символом G (i, j) обозначим игру при условии, что мишень в начальный момент времени занимает і-ю точку, а стрелок имеет у' патронов. Символом v (і, j) обозначим значение игры G (i, у). Из определения G (i, f) имеем
«(/, 0)=0 і=1, 2..... ®(і,7)=0, і = 1, 2,.... Л;7=1, 2.....
На каждом шаге игры G(і, у), i=Jk+l, ...,7=1, ... стрелок Р имеет 2к+2 чистые стратегии, а мишень Е(2к+1) — чистую стратегию. Чистыми стратегиями игрока Р являются: стрельба в точку і—к, стрельба в точку і—к+1,..., стрельба в точку i + fe, отказ от выстрелов на данном шаге. Стратегиями Е являются: перемещение в точку і—к, перемещение в точку і—к+1, перемещение в точку і+к.
Таким образом, на каждом шаге игры разыгрывается игра с матрицей {атп (:, J)}
размера (2к+2) х (2к+1), где
а) Показать, что игра G (/, j) имеет значение, равное v (і, j), в том и только в том случае, если существуют (х1г х2,.... х2*+ 2), (у и У2,.... У2к+і) такие, что:
2к+2
X Omnii.j) Х„л = 1, .... 2к+ 1, ш+1 2к+2
X *m = l, хт>0, т=1, ..., 2к+2, т* 1 2к+1
X am„{i,j) Уп<?(і.А т-1, 2fc+l,
П-1
2*+1
X >я=1.>л>°. и = 1, •••, 2fc+l.
Л— 1
Указание. Обозначим символами Xj(/, 7), х2(i, j).....JQjt+zO'. J) оптимальные
стратегии поведения (если они существуют), с которыми стрелок Я использует свои 1-ю, 2-ю, ..., (2fc+2)-io стратегии в информационном состоянии (і, 7), а символами >і(<> А У2 О* А —, У2к+10. 7) — оптимальные стратегии поведения, с которыми
мишень Е использует свою 1-ю, 2-ю, ..., (2к+ 1)-ю стратегии в информационном состоянии (і, 7). В приводимых ниже упражнениях приведено решение игры G(i, 7) и его свойства.
б) Символом <р(і, т), 7=0, 1, ...; j —1, 2, ..., обозначим следующую двойную последовательность:
q>(i, 0)=0, і=1, 2,...;
<г>0'.т)=0, і= 1, 2.....fc;7'=l, 2,...;
/ *+r
(10.3)
Ч» (»',/) = min [(\+YJv(i+t-k-\,j~l))l(k+2)
r-l, ,*+l \
i'=fc+l, k+2, ...,7= 1, 2.....
Доказать, что
1) «0',7)=<г>0‘. A
2) при i=fc+l, ...;7=1, 2, .., имеем xm(i, j)=v(i, j)—v(i+m—к— 1, j— 1) при
m=l, ..., к+r*, иначе xm(i, 7)=0, y„(i,J)=l/(k+r*) при л = 1,..., k+r*, иначеy„=0.
Здесь r=r* — точка, в которой достигается минимум в (10.3).
в) Доказать, что при 7=0, 1, ...:
1) «(»./)>0, і=1, 2,...;
2) ?(і, j)—jj(2k+l), i=kj+l, kj+2, ...;
3) 1=1. 2> •••;
4) v(i,j)^v(i,j+l), i=k+1 к+2,
5) vb,j+lHv(i,j)+l/(2k+l), i= 1, 2.....
г) Игра G(j, со). Доказать, что Umv(i, j)=w{t) при каждом і = 1, 2, .... где
j-?QО
іе (0 — решение линейного разностного уравнения
к
*w(i)“ X w(/-p) = l, i=fc+1, fc+2, ...
p-i
с начальными условиями:
w(k)=0.
ч>(1)*=ч>(2)
ГЛАВА V
ДИФФЕРЕНЦИАЛЬНЫЕ ИГРЫ
§ 1. АНТАГОНИСТИЧЕСКИЕ ДИФФЕРЕНЦИАЛЬНЫЕ ИГРЫ С ПРЕДПИСАННОЙ ПРОДОЛЖИТЕЛЬНОСТЬЮДифференциальные игры являются обобщением многошаговых игр на случай, когда число шагов в игре становится бесконечным (континуум), и игроки 1 и 2 (будем обозначать их буквами Е и Р) соответственно имеют возможность принимать решения непрерывно. В такой постановке траектории движения игроков представляют собой решения систем дифференциальных уравнений, правые части которых зависят от параметров, которые находятся под контролем игроков.
1.1. Пусть xelC, yeRn, ueUcR?, veVcR1, f(x, и), g(y, v) —
вектор-функции размерности n, заданные на R" x U и R? x V соответственно. Рассмотрим две системы обыкновенных дифференциальных уравнений
x=f(x, и); (1.1)
>’=?0'. ?) (1.2)
с начальными условиями jc0, у0. Игрок Р(Е) начинает движение из фазового состояния jc0 (у0) и перемещается в фазовом пространстве
R? согласно (1.1) или (1.2), выбирая в каждый момент времени значение параметра ueU(veV) в соответствии со своими целями и информацией, доступной в каждом текущем состоянии.
Наиболее просто поддается описанию случай полной информации. В дифференциальной игре это означает, что игрокам в каждый момент времени t при выборе параметров ие U, ?е? известно время t и фазовые состояния свое и противника. Иногда требуют знание одним из игроков, например игроком Р, в каждый текущий момент t значения параметра v е V, выбранного игроком Е в этот же момент. В таком случае говорят, что игрок Е дискриминирован, а сама игра называется игрой с дискриминацией игрока Е.
Параметры ueU, ?е? называются управлениями игроков
Р и Е соответственно. Функции х (/), у (/), удовлетворяющие уравнениям (1.1), (1.2) и начальным условиям, называются траекториями движения игроков Р, Е.
1.2. Цели в дифференциальной игре определяются с помощью выигрыша, который может различным образом зависеть от реализовавшихся траекторий x(t), у(і). Например, предполагается, что процесс игры продолжается некоторое заранее предписанное время Т. Пусть х(7), у (7) — фазовые состояния игроков Ри Ев момент окончания игры Т. Тогда выигрыш игрока Е полагается равным Н{х{Т), у (ТО, где Н(х, у) — некоторая функция, заданная
на R" х R". В частном случае, когда
Н(х(Т), у(Т)) = р(х(Т), у {ТО, (1.3)
где р{х{Т), у(Т))=(х,(Т)—у,(Т))2—евклидово расстояние
между точками х (7), у (7), игра описывает процесс преследования, в котором целью игрока Е является уклонение от игрока Р к моменту окончания игры на максимальное расстояние. Во всех случаях будем предполагать дифференциальную игру антагонистической. В случае выполнения условия (1.3) это означает, что цель игрока Р — максимальное сближение с игроком Е к моменту окончания игры Т.
При таком определении выигрыш зависит лишь от конечных состояний процесса и каждому игрцку не засчитываются результаты, достигнутые им в процессе игры до момента Т. Поэтому логичной является и такая постановка задачи, в которой выигрыш игрока Е определяется как минимальное расстояние между игроками в процессе игры:
min р {х (і), у (/)).
Существуют игры, в которых ограничение на продолжительность игры не является существенным и игра продолжается до
достижения игроками определенного результата. Пусть в R2" задана ш-мерная поверхность F, которую будем называть терминальной. Положим
= {min t: (х (t), у (0) eF), (1.4)
т. е. tn — первый момент попадания точки (х (/), у (/)) на F. Если при всех />0 точка (х(/), у(/))фF, то tn полагаем равным + оо. Для
реализовавшихся траекторий х (/), у (/) выигрыш игрока Е полагаем равным t„ (выигрыш игрока Р равен — /„). В частности, если F представляет собой сферу радиуса /> 0, заданную уравнением
Ji(x,-y)2 = l,
то имеет место задача преследования, в которой целью игрока Р является скорейшее сближение с игроком Е на расстояние /> 0. Если 1=0, то под встречей понимается совпадение фазовых координат игроков РъЕ, при этом игрок Е стремится оттянуть момент встречи. Игры преследования этого типа будем называть играми преследования на быстродействие.
В теории дифференциальных игр рассматриваются также задачи определения множества начальных состояний игроков, из которых игрок Р может обеспечить встречу с игроком Е на расстоянии /, и определения множества начальных состояний игроков, из которых игрок Е может гарантировать, что встреча с игроком Р на расстоянии / за конечное время не произойдет. Первое множество называется областью встречи или захвата и обозначается (С, Z), второе — областью убегания и обозначается (Е, Z). Очевидно, что эти области не пересекаются, однако важным является вопрос, покрывает ли объединение замыканий областей встречи и убегания все фазовое пространство? Ответ на этот вопрос будет дан ниже, а пока заметим, что для адекватного описания такого процесса достаточно определить выигрыш следующим образом. Если существует /„ < оо
(см. (1.4)), то выигрыш игрока Е полагаем равным —1. Если же /п = оо, то выигрыш равен +1 (выигрыш игрока Р равен выигрышу
игрока Е с обратным знаком, так как игра антагонистическая). Игры преследования с таким выигрышем называются играми преследования качества.
1.3. Фазовые ограничения. Если дополнительно потребовать, чтобы в процессе игры фазовая точка (х, >>) не покидала некоторого
множества Fa Л2”, то получим дифференциальную игру с фазовыми ограничениями. Частным случаем такой игры является игра с «линией жизни». Она является антагонистической игрой качества, в которой выигрыш игрока Е полагается равным +1, если ему удается достичь границы множества F («линии жизни») до встречи с игроком Р. Таким образом, целью игрока Е является достижение границы множества F до встречи с игроком Р (сближение с игроком Р на расстояние /, /> 0), цель же игрока Р — сближение с игроком Е на расстояние /, пока последний еще находится в множестве F. Предполагается, что в процессе игры игрок Р не может покинуть множества F.
1.4. Пример 1. (Простое движение). Игра происходит на плоскости. Движение игроков Р и Е описывается системой дифференциальных уравнений
х1=и1, х2 = и2, uj + ul^a2,
Уі = ?і, У2 = ?2> ?} + ?\^Р2,
х1(0)=х°1, х2(0) = хЪуі(0)=у°1, у2(0)=у°2, (1.5)
С физической точки зрения уравнения (1.5) означают, что игроки РяЕперемещаются в плоскости с ограниченными скоростями, при этом максимальные скорости а и /? постоянны по величине и максимальная скорость игрока Е не превосходит скорость игрока Р.
Выбирая в каждый момент времени управление и = (иі, и2), стесненное ограничением + (множество U), игрок Р может
изменять направление движения (направление вектора скорости). Аналогично, игрок Е, выбирая в каждый момент времени управление « = («!, ?2), стесненное ограничением ?} + ?\^р2 (множество V), может также в каждый момент времени изменить направление движения. Очевидно, что если <х>/?, то множество захвата (С, Z) совпадает со всем пространством, т. е. игрок Р всегда может гарантировать для любого / /-встречу с игроком Е за конечное время. Для этого достаточно выбрать движение с максимальной скоростью айв каждый момент времени t направлять вектор скорости на преследуемую точку у (t), т. е. осуществлять преследование по погонной линии. Если а</?, то множество убегания (Е, Z) совпадает со всем пространством игры за вычетом точек (jc, у), для которых р(х, у)</. Действительно, если в начальный момент р(х0, Уо)>1, то игрок Е всегда может гарантировать избежание захвата, удаляясь от игрока Р вдоль прямой, соединяющей начальные точки хо> Уо, с максимальной скоростью ft.
Здесь проявляется характерное свойство, которое будет встречаться и в дальнейшем. Для формирования управления, гарантирующего игроку Е избежание захвата, достаточно знать лишь начальные состояния х0, у0, в то время как игроку Р в случае а>/? для формирования управления, гарантирующего встречу с игроком Е, необходимо иметь информацию о своем состоянии и состоянии противника в каждый текущий момент времени.
Пример 2. Игроки Р и Е представляют собой материальные точки с единичными массами, которые перемещаются на плоскости под действием ограниченных по модулю сил и силы трения. Уравнения движения игроков имеют вид
х2=х3, х2=х4_, х3 = сш1~крх3, х4=аи2 —fcPx4, uf+u^a2,
Уі=Уъ> У2=Уа.> Уъ=Р?і~кЕУъ, (1.6)
У4 = Р?2~кЕУ4. «1+«2</?2,
где (jc1, х2), (у2, у2) — геометрические координаты, (х3, jc4), (у3, у4) — импульсы точек Р и Е соответственно, кР и кЕ — коэффициенты трения, а и /? — максимальные силы, которые могут быть приложены к материальным точка Р и Е. Движение начинается из состояний х, (0) = х”, у, (0) =у<!, /=1, 2, 3, 4. Здесь под состоянием
понимается не геометрическое местоположение игроков Р и Е, а их фазовое состояние в пространстве координат и импульсов. Множества U, V представляют собой круги U—{u=(ul, м2):м, + М2^а2}, ?—{? = (?1, ?2):?}+?\^р2}. Это означает, что игроки Р и Ев каждый момент времени могут выбирать направления прилагаемых сил, однако максимальные значения этих сил ограничены константами а и р. В такой постановке, как это будет показано в дальнейшем, условия а >Р (превосходство в силе) недостаточно для завершения преследования игроком Р из любого начального состояния.
1.5. Пока не указан способ выбора управлений ие U, ?е? игроками Р и Ев процессе игры в зависимости от поступающей информации. Иначе говоря, не дано определение понятия стратегии в дифференциальной игре.
Существует несколько разных подходов к определению этого понятия. Остановимся на тех интуитивно очевидных теоретикоигровых качествах, которыми оно должно обладать. Как уже отмечалось в гл. IV, стратегия должна характеризовать поведение игрока во всех информационных состояниях, в которых он может оказаться в процессе игры. В дальнейшем будем определять информационное состояние каждого игрока фазовыми векторами x(t), y(t) в текущий момент t и временем t—t0, прошедшим с момента начала игры. Тогда естественно было бы рассматривать стратегию игрока Р(Е) как функцию и(х, у, і) (?(х, у, /)) со значениями в множестве управлений Щ?). Именно таким образом определяется стратегия в [1]. Стратегии этого типа будем называть синтезирующими. Однако этот способ определения стратегии обладает рядом существенных недостатков. Действительно, пусть игроки Р и Е выбрали стратегии и(х, у, /), ?(х, у, і) соответственно. Тогда для определения траектории движения игроков, следовательно, и выигрыша (который зависит от траекторий) подставим функции и(х, у, 0, ?(х, у, t) в уравнения (1.1), (1.2) вместо управляющих параметров и, ? и попытаемся их проинтегрировать при начальных условиях х0, у0 на отрезке времени [0, 7]. Получим следующую систему обыкновенных дифференциальных уравнений:
x=f(x, и(х, у, 0), y=g(y. ?(х, у, 0). (1.7)
Для существования и единственности решения системы (1.7) необходимо наложить определенные условия на функции f(x, и), g(y, ?) и стратегии и(х, у, і), ? (х, у, t). Первая группа условий не ограничивает стратегических возможностей игроков, относится к постановочной части задачи и оправдывается физической природой рассматриваемого процесса. По-иному обстоит дело с ограничениями на класс функций (стратегий) и(х, у, і), ?(х, у, t). Ограничения возможностей игроков не согласуются с принятым в теории игр представлением о свободе выбора поведения и приводят в ряде случаев к существенному «оскудению» множеств стратегий. Например, если ограничиться лишь непрерывными функциями и(х, у, t), ? (х, у, t), то встречаются задачи, в которых не существует решения в классе непрерывных функций. Допущение же более широкого класса стратегий приводит к невозможности обеспечить существование единственного решения системы (1.7) на отрезке [/0, 7]. Иногда для преодоления этой трудности рассматривают множества таких стратегий и(х, у, t), ?(х, у, t), при которых система (1.7) имеет единственное решение, продолжимое на отрезок [f0, Т\. Однако такой подход (помимо неконструктивности определения множества стратегий) не является достаточно обоснованным, поскольку множество всех пар стратегий и(х, у, (), ?(х, у, t), при которых система
(1.7) имеет единственное решение, оказывается непрямоугольным.
1.6. В качестве стратегий в дифференциальной игре будем рассматривать кусочно-программные стратегии.
Кусочно-программная стратегия м( ) игрока Р состоит из пары {а, а), где а — некоторое разбиение 0=t0<t\<...<tn<... полуоси времени [0, со) точками ік, не имеющими конечных точек сгущения; а — отображение, ставящее в соответствие каждой точке ік и фазовым состояниям х(4), у (4) некоторое измеримое программное управление u(t)eU при t е [ік, **+і) (измеримую функцию и (t), принимающую значения из множества U). Аналогично, кусочно-программная стратегия »(•) игрока Е состоит из пары {т, Ь}, где т — некоторое разбиение 0 = t'0< t\ <... < t„ <... полуоси времени [О, оо) точками ік, не имеющими конечных точек сгущения; Ъ — отображение, ставящее в соответствие каждой точке tk и позициям x(tk), у (ік) некоторое измеримое программное управление ?(і)е? на отрезке [і(к, 4+і) (измеримую функцию v(t), принимающую значения из множества V). Используя кусочно-программную стратегию, игрок реагирует на изменение информации не непрерывно во времени, а через интервал [tk, f*+i), длину которого он определяет сам.
Обозначим множество всех кусочно-программных стратегий игрока Р через Р, а множество всех возможных кусочно-программных стратегий игрока Е — через Е.
Пусть и(і), и(0 — пара измеримых программных управлений игроков Р и Е (измеримых функций со значениями в множествах управлений U, V). Рассмотрим систему обыкновенных дифференциальных уравнений
x=f(x, и(f)), y=g(y, v(t)), t>0. (1.8)
На правые части систем (1.8) наложим следующие ограничения. Вектор-функции f(x, и), g(y, ?) непрерывны по всем аргументам и равномерно ограничены, т. е. f{x, у) непрерывна на множестве
R" х U, a g{y, ?) непрерывна на множестве Rn х V и \[f(x, u)||<a,
IIg(y, v I) (здесь II z II — норма вектора в R"). Кроме того, вектор-функции f{x, и) и g(y, ?) удовлетворяют условию Липшица по х и у соответственно независимо от и, ?, т. е.
Щх, u)-f(x2, lOIKaJXj-xJ, ueU,
ІІв’Оі- v)-g(y2> «Ж/УРі-РгІІ* «еК.
Из теорем существования и единственности Каратеодори следует, что при выполнении указанных условий для любых начальных состояний х0, у0, любых измеримых программных управлений и(і), v(t), заданных на отрезке \Т2, TJ, 0^Т.<Т2, существуют единственные абсолютно непрерывные вектор-функции x (t), у(і), которые удовлетворяют почти всюду (т. е. всюду, за исключением множества меры нуль) в промежутке [T’jT’J системе дифференциальных уравнений
*(<)=/(*(0, и(0), Ht)=g(y(0, «(/)) (1.9)
и начальному условию х(Т1)=х0, УІТ1)=Уо (см. [68, 36]).
1.7. Пусть (х0, у0) — пара начальных условий для уравнений
(1.8) . Система S={x0, у0; иі), «(•)}, где ы()еР, «()еЕ, называется ситуацией в дифференциальной игре. Каждой ситуации S единственным образом соответствует пара траекторий x(t), y(j) таких, что х(0)=хо, у (0)=jo, и при почти всех /е[0, 7], !Г>0 выполнены соотношения (1.9).
Действительно, пусть м()={й, а}, «() = {т, Ь}. Пусть
О = t0<t1<...<tk<... —разбиение полуоси [0, оо), являющееся объединением разбиений 8, т. Решение системы (1.9) строится следующим образом. На каждом отрезке [/*, /*+і), к= 0, 1, ..., образы
отображений а, Ь представляют собой измеримые программные управления и(і), v(t), поэтому на отрезке [/0, t2) система уравнений
(1.9) при х(0)=хо, у (0)=уо имеет единственное решение. На отрезке [/j, t2), взяв в качестве начальных условий x{t1)= Ііш x(t),
/-v/,-0
y(t1)= Ііш у it), строим решение (1.9), вторично используя измери-
1-.1, -О
мость управлений и it), ?іі) как образов отображений а и b на отрезках [/*, tk+l), к= 1, 2, ... . Полагая х(/2)= Ііш x(f),
о
yit2)= Ііш у it), продолжаем этот процесс, в результате чего нахо-о
дим единственное решение x(f), у ІО такое, что х(0)=хо, у(0)=>>о. Любую траекторию х ІО (у ІО), соответствующую некоторой ситуации {х0, у0; иі), «(•)}, будем называть траекторией игрока Р (игрока Е).
1.8. Функция выигрыша. Как уже было показано, каждая ситуация S=(x0, у0', иі), ?()} в кусочно-программных стратегиях однозначно определяет траектории хіО, у ІО игроков Р и Е. Степень
предпочтительности этих траекторий будем оценивать функцией выигрыша К, которая каждой ситуации ставит в соответствие некоторое вещественное число — выигрыш игрока Е. Выигрыш игрока Р равен (—К) (это означает, что игра антагонистическая, поскольку сумма выигрышей игроков Р и Е в каждой ситуации равна нулю). Будем рассматривать игры с функцией выигрыша четырех видов.
Терминальный выигрыш. Заданы некоторое число Т>0 и непрерывная по (х, у) функция Н(х, у). Выигрыш в каждой ситуации S = {х0, у0; и (•), ? (•)} определяется следующим образом:
К(х0, у0; ы( ), ? (•)) = Н(х (Т), у(Т)), где x(T)=x(t)\,шТ, у(Г)=у(0\,шТ (здесь x(t), у(і) — траектории игроков Р и Е, соответствующие ситуации S). В случае, когда функция Н(х, у) представляет собой евклидово расстояние между точками хи у, имеет место задача преследования.
Минимальный результат. Пусть Н(х, у) — вещественная непрерывная функция. В ситуации S={x0, у0; и (•), ? (•)} выигрыш игрока Е полагается равным min Н(х(і), у it)), где Т’>0 — заданное число.
Если Н(х, у)=р (х, у), то игра описывает процесс преследования.
Интегральный выигрыш. В PC xtC заданы некоторое многообразие F размерности т и непрерывная функция Н(х, у). Пусть в ситуации S={x0, у0; «(•), «(•)}, tn — первый момент попадания
траектории (x(t), y(t)) на F. Тогда
К(х0, у0; и О, «(•))=/ H(x(t),y(t)) dt о
(если f„ = oo, то К = оо), где *(/), у (/) — траектории игроков Р и Е,
соответствующие ситуации S. В случае Н= 1, K=t„ имеет место
задача преследования^ на быстродействие.
Качественный выигрыш. Функция выигрыша К может принимать только одно из следующих трех значений: +1,0, — 1 в зависимости
от расположения (x(t„), y(t„)) в Р" х R". В R” xR” заданы два многообразия F и L размерности тг и т2 соответственно. Пусть в ситуации S={x0, у0; и( ), ? (¦)} tn — первый момент попадания траектории (x(t), у (/)) на F. Тогда
Г + 1, если (x(t„),y(tn))eL.
К(хо, у0; и(•), «(•))=¦( 0, если /в = со,
(-1, если (x(t„), y(Q)$L.
1.9. Определив множества стратегий игроков Ри?и функцию выигрыша, можно определить дифференциальную игру как игру
237
в нормальной форме. В. п. 1.1 гл. I под нормальной формой Г мы понимали тройку Г = <Х, Y, К), где XxY — пространство пар всевозможных стратегий в игре Г и К — функция выигрыша, определенная на XxY. В рассматриваемом случае функция выигрыша определена не только на множестве пар всевозможных стратегий в игре, но и на множестве всех пар начальных позиций х0, у0.
Поэтому каждой паре (х0, y0)eRnxRn соответствует своя игра в нормальной форме, т. е. фактически определяется некоторое семейство игр в нормальной форме, зависящее от параметров
(*о. У^іГхРГ.
Определение. Под нормальной формой дифференциальной игры Г(х0, Уо), заданной на пространстве пар стратегий РхЕ, будем понимать систему
Г{хо, Уо)=(х0, у0; Р, Е, К(х0, у0; «(•), «О»,
где K(xQi у0; и( ), «(•)) — функция выигрыша, определенная любым из четырех описанных выше способов.
Если функция выигрыша К в игре Г терминальная, то соответствующая игра Г называется игрой с терминальным выигрышем. Если функция К определяется вторым способом, то имеем игру на достижение минимального результата. Если функция К в игре Г является интегральной, то соответствующая игра Г называется игрой с интегральным выигрышем. Когда функция выигрыша в игре Г качественная, соответствующая игра Г называется игрой качества.
1.10. Естественно, что в классе кусочно-программных стратегий (ввиду некомпактности множества) оптимальных стратегий может не существовать. Однако удается показать, что в достаточно большом числе случаев для любого е>0 существуют ситуации е-равно-весия.
Напомним определение ситуации е-равновесия (см. п. 2.3 гл. II). Определение Пусть задано некоторое е>0. Ситуация S,=
= {jc0, Уоі (•), »,(•)} называется ситуацией е-равновесия в игре Г (х0, у0), если для всех и()еР и ?()еЕ имеет место неравенство
К(х0, у0; «(•), ?'()) + е^К(х0, у0; «,(•), «,(•))> (1.10)
>К(х0, у0; «,(•), ?( ))- е.
Стратегии «,(•), «,(•), определенные в (1.10), называются е-оп-
тимальными стратегиями игроков Р и Е.
Следующая лемма является перефразировкой теоремы п. 2.5 гл. П для дифференциальных игр.
Лемма. Пусть в игре Г(х0, у0) для каждого е>0 существует ситуация е-равновесия. Тогда существует предел
lim K(x0, y0; «,(.), «.(•))•
e-*0
Определение. Функция V(x, у), определенная в каждой точке
(х, у) некоторого множества D<zRn хР" по правилу
lim К(х, у; и.(•), *.(•))= ?(х. у), (1.11)
8-*0
называется функцией значения игры Г (х, у) на множестве начальных условий (х, у) е D.
Существование при любом е>0 ситуации е-равновесия в игре Г (х0, у0) эквивалентно (см. п. 2.5, гл. П) выполнению равенства
sup inf K(x0,y0;u(),v())= inf sup K(x0, y0; u(), »(¦)).
«QeE и()ёР u()eP«QeE
Если в игре Г(х0, у0) для любого е>0 существуют е-оптималь-ные стратегии игроков Р и Е, то будем говорить, что игра Г (х0, у0) имеет решение.
Определение. Пусть и* (•); ?* (•) — пара таких стратегий, что К(хо, у0; «О» ?*(У)Ж(х0, у0; и*(), ?*())>
Ж(х0, у0; и*( ),?(.)) (1.12)
для всех и( )е Р и ?()еЕ. Тогда ситуация S* = (x0, у0; «*(•), »*(•)) называется ситуацией равновесия в игре Г (х0, у0). Стратегии и* (•) е Р и ?* (•) е Е из (1.12) называются оптимальными стратегиями игроков Р и Е.
Существование ситуации равновесия в игре Г (х0, у0) эквивалентно (см. п. 3.4 гл. I) выполнению равенства
max inf К(х0, у0; и( ), «(•))=
«(•)еЕи()ёР
= min supA:(x0, y0; «(•), «(•)).
u(.)gEu()eP
Очевидно, что если существует ситуация равновесия, то для любого ?>0 она является и ситуацией е-равновесия, т. е. функция ?(х, у) в данном случае просто совпадает с К (х, у\ и* (•), ?* (•)) (см. п. 2.3 гл. И).
1.11. Рассмотрим синтезирующие стратегии.
Определение. Пара (и* (х, у, t), ?* (х, у, /)) называется ситуацией равновесия в дифференциальной игре в синтезирующих стратегиях, если имеет место неравенство
К(х0, у0; и(х, у, t), ?*(х, у, і))Ж(х0, у0; и*(х, у, t),
®* (X, у, /)) >К(х0, у о, и* (х, у, і), V (х, у, 0) (1.13)
для всех ситуаций (и (х, у, І), ?* (х, у, і)) и (и* (х, у, і), ? (х, у, /)), для которых сугцествует единственное, продолжимое на [0, оо) решение
системы (1.7) из начальных состояний х0, JV Стратегии и* (х, у, t), ?* (х, у, О называются оптимальными стратегиями игроков Р и Е.
Установим различие понятий ситуации равновесия в кусочнопрограммных и синтезирующих стратегиях. Заметим, что определить ситуацию равновесия в обычном смысле в классе функций и {х, У, 0) ?(х, у, 0 невозможно из-за непрямоугольное™ пространства ситуаций, т. е. в синтезирующих стратегиях невозможно потребовать выполнения неравенства (1.13) для всех стратегий и (х, у, /), ? (х, у, /), поскольку некоторые пары (и*, ?), (и, ?*) могут не быть допустимыми (система уравнений (1.7) в соответствующей ситуации может не иметь решения вообще или не иметь единственного решения).
В дальнейшем, если специально не будет оговорено, во всех случаях будем рассматривать классы кусочно-программных стратегий. Прежде чем перейти к доказательству существования ситуации e-равновесия в дифференциальной игре, рассмотрим один вспомогательный класс многошаговых игр с полной информацией.
§ 2. МНОГОШАГОВЫЕ ИГРЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ И БЕСКОНЕЧНЫМ ЧИСЛОМ АЛЬТЕРНАТИВ
2.1. Рассмотрим класс многошаговых игр с полной информацией, представляющих собой обобщение игр с полной информацией из § 1 гл. IV. Игра происходит в л-мерном евклидовом пространстве
¦К". Будем обозначать через xeR" местоположение (позицию) игрока 1, а через уеіС — местоположение игрока 2. Пусть для каждых xeR", у eR* определены множества Ux, ?у соответственно, которые будем предполагать компактными множествами евклидового пространства R". Игра начинается из позиции х0, у0. На 1-м шаге игроки 7 и 2 выбирают точки хх е UXo и ?Уа. При этом выбор
игрока 2 сообщается игроку 1 до выбора им точки x1 е Uxy В точках
х1,уі игроки 1 и 2 выбирают точки x2eUXi и уге ?Уі, и выбор игрока
2 сообщается игроку 1 перед выбором им точки х2 е UXl и т. д. На
к-м шаге в позициях хк_и ук_х игроки выбирают хке UXk_{, уке ?Ук_?
и выбор игрока 2 сообщается игроку 1 перед выбором им точки Хк^иХк_у Процесс заканчивается на N-м шаге выбором xNe UXi/ i,
yNe ?Уііі и переходом в состояние xN, yN.
Семейства множеств UXI Vy, xeR", yeRn предполагаются непрерывными в метрике Хаусдорфа по х, у. Это означает, что для любого б>0 найдется такое <5>0, что при |х—х0|<<5 ([у—УоІ<^)
(UXo)^Ux, т,^их- (?УХ^?у,
Здесь Ue (Vt) — ?-окрестность множества U(V).
Следующий результат хорошо известен в анализе (см. [12]). Лемма. Пусть fix', у1) — непрерывная функция на декартовом произведении Ux х ?г Тогда если семейства {?/*}, {?у} — непрерывны
по Хаусдорфу по х, у, то функционалы
Fy (х, y)=max min fix', у'),
У е?у Уе Ux
F2ix, у) = min min fix!, у')
уеих уе?у
непрерывны_по х, у. _
Пусть х=(х0, .... xN) и у = іу0, .... yN) — траектории игроков 1 и 2 соответственно, реализовавшиеся в процессе игры. Выигрышем игрока 2 является величина
max fixk, yk)=F(x, у), (2.1)
где fix, у) — непрерывная функция от х, у. Выигрыш игрока 1 равен І—F) (игра антагонистическая).
Будем предполагать, что данная игра с полной информацией, т. е. в каждый момент времени (на каждом шаге) игрокам известны позиции хк, ук и момент времени к+1, а игроку 1, кроме того,
известен выбор у*+1 игрока 2 в этот момент.
Стратегиями игрока 1 являются всевозможные функции ы(х, у, t) такие, что ы(х*_ь ук, к)е UXk_r Стратегиями игрока 2 —
всевозможные функции ?(х, у, t) такие, что ?іхк_,, ук_и к)е Ууь-?
Эти стратегии будем называть чистыми стратегиями (в отличие от смешанных).
Пусть игроки 1 и 2 применяют чистые стратегии и (х, у, t), ? (х, у,
і). В ситуации іи (•), ? (•)) игра происходит следующим образом. На 1-м шаге игрок 2 из состояния у0 переходит в состояние у1=і;(х0, у0
1) и игрок 1 — из состояния х0 в состояние х1 = м(х0, ук 1) = ы(х0, ?(х 0, у о, 1), 1) (поскольку игрок 1 знает выбор игрока 2). На 2-м шаге игроки переходят в состояния y2=i;(JC і< У и 2), х2 = м(х1, у2,
2) = и(х1, ? (х1# у2,2), 2) и т. д. На к-м шаге игроки 1 и 2 переходят из состояний х*_ь у*_, в состояния ук=?іхк.,, у*-,, к), хк=иіхк_и ук,
к) = иіхк_І5 ?(х/t_i, ук-х, к), к). Таким образом, каждой ситуации (ы (•), «(•)) однозначно соответствуют траектории игроков 1 и 2: х=(х0, ...
xs) и у—іуо> •••. yN), следовательно, и выигрыш Кіи(¦), vQ=F(х, у), определяемый по формуле (2.1).
Рассматриваемая игра зависит от двух параметров: начальных
241
позиций (хр, у0) и продолжительности N, поэтому будем обозначать ее через Г (х0, у0, N). Для дальнейшего исследования каждую игру Г (х0, у0, N) удобно отнести к семейству игр Г (х, у, Т), зависящих от параметров х, у, Т.
2.2. Справедлив следующий результат, являющийся обобщением теоремы п. 2.1 гл. IV для конечных игр с полной информацией.
Теорема. В игре Г(х0, _у0> N) существует ситуация равновесия в чистых стратегиях и значение игры ?(х0, у0, N) удовлетворяет рекуррентному соотношению
У(х0. Уо' k)=max{f(x0, у0), max min ?(х, у, k-1)}, (2.2)
у еУУ„ xeU*0
k= 1, ..., V; V(x,y, 0)=f(x,y).
Доказательство проведем методом индукции по числу шагов игры. Пусть N=1. Определим стратегии и* ( ), ?* (•) игроков в игре Г (х0, _у0, 1) следующим образом:
min fix, y)=f(u* (х0, у, 1), >>), уе ?л; если max min f(x, y)=f(u* (x0, у*, 1), у*), то v* (x0, y0, 1 )=y*. Тогда
уе?уо xeUXa
K(u* (•), v* ())=max {f(x0, y0), max min f(x, y)}
yeVy<) xeUXo
и для любых стратегий и( ), ? (•) игроков в игре Г (х0, у0, 1) справедливы соотношения
Кіи* О, vQ)^Kiu*i-), ?*і.))<Кіиі\ ,*(¦))•
Тем самым утверждение теоремы справедливо при N= 1.
Предположим теперь, что утверждение теоремы справедливо при и докажем ее для N=n+1, т. е. для игры Г(х0, у0, п+1). Рассмотрим семейство игр Г(х, у, и), xeUXa, у е ?Уо. Обозначим
через й%у(), ?^і) ситуацию равновесия в игре Г (х, у, и). Тогда Кій^уі ), ?ху (•)) = V(х, у, и), где F(x, у, и) определено соотношениями (2.2). Используя непрерывность функции /(х, >>) и лемму п. 2.1, нетрудно доказать непрерывность функции F(x, у, и) по х, у.
Определим стратегии й"+1( )> »"+,Q игроков в игре Г(х0, у0, и + 1) следующим образом:
min ?іх, у, п)=У(йя+\х0, у, 1), у, и), уе ?л;
xeUx0
если max min ?іх, у, и)= Г(й"+І (х0, у, 1), у, и), то й"+І (х0, у0, 1 )=у, у е?Уо xeUx0
для х^х0, у?=у0 функции й"+1(х, у, 1) и й"+1(х, у, 1) определим произвольно:
и+\; к) = йяХіУі(; к-1), к = 2, ..., п+1,
®"+4. к)=?пХіУі (., к-1), к=2, ..., п+1.
Здесь хі е UXo, yL е F>0 — позиции, которые реализовались после 1-го шага в игре Г(х0, у0, n+1). По построению,
К(й"+1 (¦), ?"+1 ())=max {f(x0, у0), max min V(x, у, и)}. (2.3)
Фиксируем произвольную стратегию и() игрока 1 в игре Г(х0, у0,
п+1). Пусть и(х0, у, l)=xls где у=?я+' (х0, у0, 1), и и^О — сужение стратегии и( ) на игру Г (х, у, л), хе С/,0, уе ?Уо.
Справедливы следующие соотношения:
К(йя+' (•), в"+І (•))<max {f(x0, у0), V(х? у, л)} = =тах{/(х0, >0). K(u”xJ (¦), <*()Ж ^max{f(x0,y0), К(ияХіУ(¦), <,(•))} = *(«(•), "+‘0). (2.4)
Аналогично доказывается неравенство
К(и+І О, Г+І (•))>К(и+10,!,(.)) <2.5)
для любой стратегии «(•) игрока 2 в игре Г (х0, у0, л+1). Из соотношений (2.3) — (2.5) следует справедливость утверждения теоремы для N= n+1. Тем самым доказательство теоремы по индукции закончено. _
Рассмотрим теперь игру Г(х0, у0, N), которая отличается от игры Г(х0, у0, N) тем, что в ней сообщает свой выбор игрок 1. Таким образом, в игре Г (х0, у0 N) на каждом шаге к игрок 2 кроме состояний хк~и Ук-і и шага к знает состояние х*е UXk_v выбранное
игроком 1. Игрок 1 на каждом шаге к знает лишь х*_,, Ук-\-Аналогично, теореме п. 2.5 можно показать, что в игре г (*„_ yQi ДГ) существует ситуация равновесия в чистых стратегиях и значение игры V (х0, у0, N) удовлетворяет рекуррентному уравнению V (х0, у0, k)=max{f(x0, у0), min max V (х, у, А:— 1)},
к=1, ..., N, V (.х, у, 0)=/(*, у). (2.6)
2.3. Рассмотрим игры Г' (х0, у0, N) и Г' (х0, у0, N), которые отличаются от игр Г(х0, у0, N) и Г (х0, у0, N) соответственно лишь видом функции выигрыша. Предположим, что в этих играх выигрыш игрока 2 равен расстоянию между ним и игроком 1 на последнем шаге игры, т. е. р (xN, yN). Тогда утверждение теоремы п. 2.2 и ее следствие сохраняют силу и вместо рекуррентных уравнений (2.2),
(2.6) справедливы уравнения
?'(х, у, к)=max min V'(xf, у', к — 1),
/е?у x!<=Ux
k = 1, V'(x,y,0)=p(x,y>, (2.7)
V'(x, y, k) = min max V'(xf, у', k— 1),
x'et/j /6 Vy
k= 1, .... N, V'(x, у, 0) = p(x, y) (2.8)
Пример 3. Рассмотрим дискретцую игру преследования, в которой множества Ux представляют собой круги радиуса а с центром
в точке х, а множества ?у — круги радиуса /? с центром в точке
>>(<*>/}). Это соответствует игре, в которой игрок 2 (убегающий) перемещается на плоскости со скоростью, не превосходящей /?, а игрок 1 (преследователь) — со скоростью, не превосходящей а. Скорость преследователя превосходит скорость убегающего, и игрок 1 ходит вторым. Игра такого типа называется дискретной игрой «простое преследование» с дискриминацией убегающего игрока. Игра продолжается N шагов, и выигрыш игрока 2 равен расстоянию между игроками на последнем шаге.
Найдем значение игры и оптимальные стратегии игроков, используя функциональное уравнение (2.7).
Имеем
?(х, у, l)=max тіп р(х', /). (2.9)
/е?у *eUx
Так как Ux и ?у — круги с центрами в х и у и радиусами а и /}, то, если их^?у, имеем ?(х, у, 1)=0, если же ІІхф?у, то ?(х, у, 1)=
р(х, у)+Р~ а=р(х, у) — (а—р) (см. пример 8 п. 2.6 гл. П). Таким образом,
?(х, у, 1)=
О, если Ux=> ?у, т. е. р(х, y)—(a—fi)^Q, р(х. у)-(а-р), если ІІхф ?у,
или, что то же самое,
?(х, у, 1)=тах[0, р(х, у)-(а-р)]. (2.10)
Докажем, применив индукцию по числу шагов к, что имеет место следующая формула:
?(х, у, fc)=max[0, р(х, у)-к(а~Р)], к^2. (2.11)
Пусть (2.11) выполнено при к=т— 1. Покажем, что формула справедлива для к=т. Воспользовавшись уравнением (2.7) и соотношениями (2.9), (2.10), получим
?(х, у, m)=max min ?(х', у', m—\) =
Уе?у Уе?х
=max min {max[0, p(x', y') — (m — 1) (a—P)]} —
Уе?у Уе?х
=max [0, max min {p (x', /)} — (m — 1) (a—/?)] =
Уе?у УеUx
=max[0, max{0, p(x, y) —(a—/?)} —(m —l)(a —/?)] =
=max [0, p(x, y)-m(ct-P)], что и требовалось доказать.
Если ?(х0, у0, т)—р (х0, у0)-т(а-Р), т. е. р(х0,у0)~ —т(а — р)>0, то оптимальная стратегия игрока 2 диктует ему выбирать на к-м шаге игры точку ук пересечения линии центров
yk-\ с границей Vyk-p наиболее удаленную от jc*_i. Здесь jc*-i, yk_i—позиции игроков после (к— 1)-го шага, к = 1, ..., N. Оптимальная стратегия игрока 1 диктует ему на к-м шаге игры выбирать точку из множества UXk_v наиболее близкую к точке ук. Если оба
игрока действуют оптимально, то последовательность выбранных точек х0, х? .... xN, у0, у? yN лежит на прямой, проходящей через jc0, у0. Если ?(х0, у0, т)=0, то оптимальная стратегия игрока 2 произвольна, а игрока 1 — та же. При этом после некоторого шага к выполняется равенство max min р(х, у)=0, поэтому, начи-
уеУук xeUXk
ная с (fc+ 1)-го шага, выбор игрока 1 повторяет выбор игрока 2.
§ 3. СУЩЕСТВОВАНИЕ СИТУАЦИЙ е-РАВНОВЕСИЯ В ДИФФЕРЕНЦИАЛЬНЫХ ИГРАХ С ПРЕДПИСАННОЙ ПРОДОЛЖИТЕЛЬНОСТЬЮ
3.1. В данном параграфе будет доказано существование ситуаций e-равновесия в дифференциальных играх преследования с предписанной продолжительностью в классе кусочно-программных стратегий, определенных в п. 1.6. Рассмотрим подробно случай, когда выигрыш игрока Е — расстояние р (х (7), у (Г)) в последний момент игры Т.
Пусть динамика игры задается следующими дифференциальными уравнениями:
для Р: х =/ (х, ы); (3.1)
для E:y=g(y,v). (3.2)
Здесь х (0, у (0 е Л", и (t) е U, ? (t) е V, где U, V — компактные множества евклидовых пространств Rk и R1 соответственно, /е[0, оо). Пусть выполнены все требования п. 16.
Определение. Обозначим через ёР(х0) множество точек xeRn,
для которых существует измеримое программное управление и (0 е U, переводящее точку х0 в х за время t, т. е. х (tQ) = xQ,
х (t0 + t)=x. Множество С’Р (х0) называется множеством достижимости игрока Р из начального состояния х0 за время t.
Аналогично определяется множество достижимости С ‘Е (у0) игрока Е за время t из начального состояния у0.
Предположим, что функции /, g таковы, что множества достижимости ёР(х0), С'е (уо) игроков Р и Е соответственно удовлетворяют следующим условиям:
1) С1Р (х0), С‘Е (у0) определены при всяких х0, у0 е R", t0, / е [0, оо)
(t0 ^ /) и являются компактными множествами пространства Л";
2) отображение СР (х0) непрерывно по совокупности аргументов
в метрике Хаусдорфа, т. е. для любых е>0, х0 е R", /е[0, оо) существует такое <5>0, что если |/ —1'\<6, р (х0, Xq)<5, то р* (С‘Рх^, СР (х „))<?. То же выполняется для С ‘Е (у0).
Напомним, что метрика Хаусдорфа р* в пространстве компактных подмножеств R" задается так:
р* (А, В)= шах (р' (А, В), р' (Я, А)), р' (А, В)=шах р (а, В)
аеА
и р (а, В) = min р {а, Ь), где р — стандартная метрика в R".
ЬеВ
Теорему существования будем доказывать для игры преследования Г (х0, уо, Т) с предписанной продолжительностью, где х0,
уо е Rn — начальные позиции игроков Р и Е соответственно, а Т — продолжительность игры. Игра Г (х0, у0, Т) протекает следующим образом. Игроки Р и Е в момент времени /0 = 0 начинают перемещаться из позиций х0, уо в соответствии с выбранными кусочнопрограммными стратегиями. В момент времени t=T игра заканчивается, при этом игрок Е получает от игрока Р выигрыш, равный р (х (7), у (Г)) (см. п. 1.8). В каждый момент времени /е[0, 7] игры
Г (х0, Уо, Т) обоим игрокам известны момент времени t, своя позиция и позиция противника. Обозначим через Р (jc0, to, t) (Е (yn, to, 0) множество траекторий системы (3.1) ((3.2)), исходящих из точки Хо (уо) и определенных на интервале [*„, t],
3.2. Фиксируем некоторое натуральное и>1. Положим <5 = 772" и введем в рассмотрение вспомогательные по отношению к игре Г (х0, Уо, Т) игры Г? (х0, Уо, Т), і= 1, 2, 3.
Игра rf (х0, Уо, Т) протекает следующим образом. На 1-м шаге
игрок Е, находясь в позиции уй, выбирает у^ из множества С| (у0),
а игрок Р, находясь в позиции х0 и зная выбор у{ игрока Е на этом шаге, выбирает точку xi е Cf. (х0). На к-м шаге, к = 2, 3, ..., 2", игрок
Е, зная позицию игрока Р х*._, е С\ (х*_2) и свою позицию yt_,eCl 0*_2), выбирает точку ykeCsE (ук-\)- Игрок Р, зная х*_ь
Ук-и Ук, выбирает x*eCf> (х*_,). На 2"-м шаге игра заканчивается,
и игрок Е получает выигрыш, равный р (х (Т), у (Г)), где х {Т) — х „, У (Т)=у2„. 2
Отметим, что выбор игроками на к-м шаге точек хк, ук из
множеств достижимости Cj> (х*_,), С| (у*_і) можно трактовать как
выбор ими соответствующих траекторий из множеств Р (х*_і,
(к—1)8, к8), Е (ук_,, (к—1) 8, к8), оканчивающихся в точках хк,
ук в момент t = k8 (или выбор управлений и (•), ? (•) на [(?— 1) 8, к5\,
которым эти траектории соответствуют согласно (3.1), (3.2)).
Игра rf (х0, у о, Т) отличается от игры Tf (х0, уа, Т) тем, что на
к-м шаге игрок Р выбирает xkeCj> (х*_,), зная х*_І5 ук-\, а игрок Е,
зная, кроме того, хк, выбирает уке СдЕ (у*_і).
Игра rf (х0, уо, Т) отличается от игры rf (х0, у0, Т) тем, что на
2"-м шаге игрок Р выбирает x2„eCf> (х2Л і), после чего игра заканчивается и игрок Е получает выигрыш р (х (7), у (Т— 8)), где х (7)=х у (Т-8)=у2„
3.3. Лемма. В играхТf (х0, у о, Т), і= 1, 2, 3, существуют ситуации равновесия при всех х0, уо, Т< со и значение игры Val Tf (х0, у о, Т) есть непрерывная функция х0, Уо^В". При всяком и^О выполняется
неравенство
Val rf (хо, уо, TKVal rf (х0, у0, Т), Т=2п8. (3.3)
Доказательство. Игры Г? (х0, у0, Т), і=1, 2, 3, принадлежат
классу многошаговых игр, определенных в § 2. Существование ситуации равновесия в играх Г f (х0, у0, Т) и непрерывность функций
Val Г? (х0, Уо, Т) по х0, Уо непосредственно следует из теоремы п. 2.2
и ее следствия. Для значений игр Г? (х0, у0, Т), і= 1, 2 справедливы
рекуррентные уравнения
?аі Г* (х0, уо, Т)= max min Val Г? (х, у, T—S),
>еС^0) «ЭД
?аі Г f (х0, уо, Т)= min max Val Г2 (х, у, Т—8)
*еС'(*о> ХбС* 0-^
при начальном условии ?аі Г, (х, у, 0)=?а1 Г* (х, у, 0)=р (х, у). Применяя последовательно лемму п. 2.2. гл. I, убедимся в справедливости неравенства (3.3).
3.4. Лемма. При любом целом л^О справедливы неравенства Val Tf" (х0, уо, 7)^Val rf»+i (х0, у0, Т),
?аі (хо, уо, І)^?а1 Г|"+' (х0, у0, Т),
где 5к=ТІ2к.
Доказательство. Покажем справедливость первого из неравенств. Второе неравенство доказывается аналогично. Во избежание
громоздкости обозначений будем далее полагать С* (у;)=С^ (у,), С* (х;)=С^ (х,), і=0, 1, 2" —1. Имеем
>,6С с0) х^С (*„)
max min Val Г?в+1 (x2, y2, T—25n+l)^
>,eC (у,,) >2eC
min min Val rf«+‘ (x2, y2, T—2Sn+l)=
= max min Val rf"+1 (x,, yu T— 8„).
vc"(V
Продолжая этот процесс, получим
Val rf"+1 (jco, y0, T)^ max
min
ft
yieC typ Jti6C (*(P
... max min p (x2„, y2„)=Val Tf" (x0, y0, T).
ft ft
(Ууя_|) *2n^^ (•Г2Л_1^
3.5. Теорема. При всех х0, уоеR", Т< оо справедливо равенство пределов:
lim Val Г?» (х0, ^о, Г) = 1іт Val Г|я (хо, у0, Т),
П-*СО Л-ЮО
где б„= Г/2".
Доказательство. Фиксируем некоторое л^О. Пусть и (•), ? (•) — пара стратегий в игре Г|я (х0, у0, 7). Эта пара является
таковой и в игре Г з" (хо, у0, 7). Пусть в ситуации и (•), ? (•) реализуется последовательность х0, х{, х2„, у0, уь .... у2„. Обозначим
функции выигрышей в играх Г|я (х0, у0, Т)-> Гзя (х0, у0, Т) соответственно через К2 (и (•), v ()) = р (х2„, у2„), Къ (и (•), v ()) = р (х2Л, J2„_,). Тогда
К2 (и (•), ? (Ж^з (и (•), ? ())+р (у^,, у2„).
В силу произвольности и (•), ? (-) отсюда имеем:
Val Г$* (х0, Jo, 7)<Val Г?я (х0, j0, 7) +
+ max max р (у, у'). (3.4)
уеСж'*‘0’0> y'eCZM
Пусть yfreCfy (j0), тогда CTE~in (jfB) с Cj(j0). Запишем неравенство (3.4) для игр с начальным состоянием х0, у f". Учитывая предыдущее включение, получим
Val Г*” (хо, jf", TKVal (х0, уf", 7) +
+ max max р (у, у'). (3.5)
З’бС^О’о) УбС^О’)
Из определения игр Г?я (х0, у0, 7) и Гзя(х0, у0, 7) вытекает равенство
Val Г?» (x0, Уо, T)= max Val Г|» (x0, j>f", 7).
(3.6)
•*’!*бСг 6(p
В силу непрерывности no t функции С‘Е (у) и выполнения условия С°е(у)=У второе слагаемое в (3.5) стремится к нулю при и-юо. Обозначим его через еі (и). Из (3.5), (3.6) получаем
Val Г?» (хо, уо, Г)>?а1 Т\” (х0, yfr Г)-е, (и). (3.7)
В силу непрерывности функции ?аІ Г^1 (х0, уо, Т) из (3.7) имеем неравенство
?аІ Г?" (хо, уо, Т)>?аІ Г(х0, у0, Г)- е, (и)-е2 (и), (3.8)
где Ё2 (ті)—>О при п-юо. Переходя в (3.8) к пределу при л-* со
(что возможно на основании лемм п. 3.3, 3.4 и теоремы о существовании предела у монотонной ограниченной последовательности), получаем
Ііш ?аІ Г ?» (х0, уо, Т) > Ііш ?аІ Гf» (*ь, у0, Г). (3.9)
«->СО Я->СО
Из леммы п. 3.3 вытекает противоположное неравенство. Следовательно, оба предела в (3.9) совпадают.
3.6. Утверждение теоремы п. 3.5 доказано в предположении, что последовательность разбиений интервала [0, 7]
O'n={^0 = 0<fi<...<fN=7^, и=1, ...,
удовлетворяет условию tJ+l — tj=T/2",j=0, 1,..., 2"—1. Утверждения
тес ремы г. 3.5 и лемм п. 3.3, 3.4 справедливы для всякой последовательности ап измельчающихся разбиений интервала [0, 7], т. е.
такой, что ff„+1 => ff„ (это означает, что разбиение ап+і получается из
<т„ добавлением новых точек)
И у (<х„)=тах (/,+ ,- О -¦ 0.
/ и-юо
Рассмотрим теперь таите любые последовательности разбиений интервала [0, Т\ {а„} и {а „}.
Лемма. Имеет место равенство
lim ?аІ Г?" (х0, Уо, 7) = lim Val rf" (х0, у0, Т),
«->00 «->ОО
где Хо, УоеЯ", 74 оо.
250
Доказательство проведем от противного. Допустим, что утверждение леммы неверно, и предположим для определенности, что выполняется неравенство
lim Val Г"" (х0, Jo, Т)> lim Val ГГ" (*о, Jo, Т)..
Л-400 л-400
Тогда согласно теореме п. 3.5 имеем
lim Val Г?" (х0, j0, Т)>lim Val Г 5'" (х0, Jo, Т).
Л-400 л-*оо
Отсюда найдутся натуральные числа ти л, такие, что выполнено неравенство
Val Г?-і (х0, jo, 7)>Val rf»i (x0, j0, T).
Обозначим через Ъ разбиение интервала [О, Т\ точками, принадлежащими как разбиению ащ, так и разбиению а„. Для него выполняется неравенство 1
Val Г \ (х0, Jo, 7)sgVal ГГ'"і (х0, j0, Т)<
<Val ГГ«і (xq, jo, ГК Val Г? (x0, j0, T).
Откуда
Val Г \ (xo, jo, T) < Val Г1 (x0, j0, T).
Это противоречит (3.3), следовательно, сделанное предположение неверно и утверждение леммы справедливо.
3.7. Теорема. При всех х0, j0, Т< со в игре Г (х0, j0, Т) существует ситуация е-равновесия для любого е>0. При этом
Val Г (х0, jo, 7) = lim Val Г?" (х0, jo, Т), (3.10)
Л-400
где {<т„} — любая последовательность измельчающихся разбиений интервала [0, Т\.
Доказательство. Зададим произвольно выбранное число е>0 и покажем, что найдутся такие стратегии и, (¦) и vs (•) игроков
Р и Е соответственно, что для всех стратегий м()еР и ? ( )еЕ выполняются неравенства
к (х0, jo, и, (•), ? (¦))-кл: (х0, jo, ие (¦), ?, (Ж
< К (Xo, Jo, и (•), V, О) + е. (3.11)
В силу теоремы п. 3.5 найдется такое разбиение а интервала [0, 7], что
Val Г2 (*о, Уо, 7)—lim Val Г?" (х0, у0, Т)<~,
п~*ао 2
lim Val Г"" (х0, уо, 7)-?а1 ГГ (х0, у0, Т)<~.
я-»оо 2
Положим и (•) = (ет, ац»), v () = (<r, bj), где а^, — оптимальные
стратегии игроков Р и Е соответственно в играх Г? (х0, уо, 7)
и Г? (х0, Уо, 7).
Тогда справедливы соотношения:
К (х0, уо, и (•), ? (•))«$ Val Г\ (х0, уо, Т)<
<lim Val Г|" (х0, уо, T)+^,v QeE; (3.12)
К (ль, Л, и (•), «* (-))>?а1 ГГ (ль, Уо, Г)>
>lim Val ГГ" (х0, уо, 7)--, и ()еР. (3.13)
Я-ЮО 2
Из (3.12), (3.13) и теоремы п. 3.5 имеем
-~<К(хо, уо, ы (•), «,' (•))- Urn Val ГГ" (ль, Уо, Г)<-. (3.14)
2 я-,00 2
Из соотношений (3.12)—(3.14) следует (3.11).
В силу произвольности е из (3.14) следует (3.10). Теорема доказана.
3.8. Замечание. При доказательстве теоремы существования нигде не был использован специфический вид выигрыша р (х (7), у (7)). Существенной является лишь непрерывная зависимость выигрыша от реализованных траекторий. Поэтому теорема п.3.7 остается справедливой, если вместо р (х (7), у (7)) рассмотреть любой непрерывный функционал траекторий х (/), у (/). В частности, таким
функционалом может быть min р (х (/), у (/)), т. е. минимальное
расстояние между игроками в процессе игры. Поэтому результат данного параграфа остается в силе и для дифференциальной игры преследования на достижение минимального результата с предписанной продолжительностью.
§ 4. ДИФФЕРЕНЦИАЛЬНЫЕ ИГРЫ ПРЕСЛЕДОВАНИЯ НА БЫСТРОДЕЙСТВИЕ
4.1. Дифференциальные игры преследования на быстродействие представляют собой частный случай дифференциальных игр с интегральным выигрышем, определенных в п. 1.8. Классы стратегий Р и Е те же, что и в игре с предписанной продолжительностью.
Предположим, что в R.” х R." задано множество F= {(х, у): р (х, у)^1, />0}, и пусть х (/), у (0 —траектории игроков Р и Е в ситуации (и (•), ? (•)) из начальных состояний х0, у0.
Обозначим
tn (*о, То; и (¦), V ( ))=min {t: (х (0, У (O)e-F}; (4.1)
если не существует такого t, что (х (0, у (t))eE, то t„ (х0, у0; и (•), ? (•))
полагается равным +оо. В дифференциальной игре преследования на быстродействие выигрыш игрока Е полагают равным
К (х0, То; и (•), ? (¦)) = t„ (х0, То; и (•), ? (•)). (4.2)
Выигрыш игрока Р в ситуации 5=(х0, у0, и (•), ? (•)) равен { — К (5)} (игра антагонистическая).
Игра зависит от начальных состояний х0, То, поэтому будем обозначать ее через Г (х0,Уо)-
Из определения функции выигрыша (4.2) следует, что в игре Г (х0, То) целью игрока Е является максимизация времени сближения с игроком Р на заданное расстояние />0. Игрок Р, наоборот, стремится минимизировать это время.
4.2. Между игрой преследования на быстродействие Г (х0, То)
и игрой преследования с предписанной продолжительностью на достижение минимального результата существует прямая связь. Пусть Г (хо, То, Т) — игра преследования с предписанной продолжительностью Т на достижение минимального результата (выигрыш игрока Е равен min р (х (0, у (0)- Было показано, что для игр о
такого типа при любом е>0 в классе кусочно-программных стратегий существует ситуация Е-равновесия (см. п. 3.8). Пусть V (х0, То,
Т) — значение такой игры, а V (х0, То) — значение игры Г (х0, То),
если оно существует.
Лемма. При фиксированных х0, То функция V (х0, То, Т) непрерывна и не возрастает по Т на отрезке [0, оо].
Доказательство. Пусть 7’і>7'2>0. Обозначим через ?[‘ (•) стратегию игрока Е в игре Г (х0, Уо, Т{), которая гарантирует игроку Е, что расстояние между ним и игроком Р на отрезке [О, Т{] не меньше max [О, V (х0, уо, Т\) — е]. Следовательно, она тем более гарантирует расстояние max [О, V (х0, у0, Т{) — е] между ними на отрезке [О, TJ, где Т2<ТХ. Поэтому
V (х0, Уо, Т2)^max [О, V (х0, у0, Г,)-е] (4.3)
(е-оптимальная в игре Г (х0, у0, ^і) стратегия не обязательно е-оптимальна в игре Г (jc0, у о, Т2)). Поскольку е может быть выбрано
произвольным, из (4.3) следует второе утверждение леммы. Непрерывность V (х0, Уо, Т) по Т доказывать не будем. Отметим лишь,
что это свойство можно получить, используя непрерывность V (х0, Уо, Г) по Хо, Уо-
4.3. Рассмотрим уравнение
V (х0, Уо, Т) = 1 (4.4)
относительно Т. Возможны следующие три случая:
1) уравнение (4.4) не имеет корней;
2) имеет единственный корень;
3) имеет более одного корня.
В случае 3) из невозрастания и непрерывности функции V (х0, Уо, Т)
по Т следует, что уравнение (4.4) имеет целый сегмент корней, т. е. функция V (х0, уо, Т) как функция от Т имеет интервал постоянства.
Рассмотрим каждый случай отдельно.
Случай 1. В этом случае возможно:
а) V (х0, Уо, Т)<1 для всех 7>0; б) inf V (х0, Уо, Т)>1;
Г5> 0
в) inf V (х0, уо, Т) = 1. т> о
В случае а) имеем
У (*о, Уо, 0 )=р (х0, у о) < /,
т. е. t„ (х0, у0; и (•), ? ( ))=0 для всех и (•), ? (•). Тогда значение игры Г (*о, Уо) равно V (х0, у0)=0.
В случае б) выполняется равенство
inf V (х0, уо, 7)=lim V (х0, у0, Т)>[.
0 Г—00
Отсюда для любого Т> 0 (сколь угодно большого) у игрока Е найдется соответствующая стратегия ? ()еЕ, которая гарантирует ему избежание /-встречи на отрезке [0, 7]. Но тогда игрок Р не имеет стратегии, которая бы гарантировала ему /-встречу с игроком Е за конечное время. В то же время нельзя утверждать, что игрок Е обладает стратегией, гарантирующей избежание /-встречи за любое время. Вопрос о нахождении начальных состояний, в которых такая стратегия существует, сводится к решению игры качества для игрока Е. Таким образом, при /dim V (х0, у0, Т) можно лишь
Г-*0О
утверждать, что значение игры Г (х0, у0), если оно существует,
больше любого наперед заданного Т, т. е. равно +оо; в) рассмотрим совместно со случаем 3).
Случай 2. Пусть Го — единственный корень уравнения (4.4). Тогда из невозрастания и непрерывности по Г функции V (х0, уа, Т) следует, что
V (х0, Уа, Т)> V (х0, уа, Г0) при всех Г< Г0,
(4.5)
V (х0, Уа, Т)<? (х0, Уа, Г0) при всех Т> Т0;
lim V (х0, уа, Т)=? (х0, Уа, Г0). (4.6)
Т~То
Фиксируем произвольное Т>Т0. Рассмотрим игру преследования Г (х0, Уа, Т). Она обладает ситуацией е-равновесия в классе кусочнопрограммных стратегий для любого е>0. Это означает, в частности, что для любого е>0 существует стратегия и, (-)еР игрока Р,
которая гарантирует ему сближение с игроком Е на расстояние V (х0, уа, Т) + е, т. е.
К (и. (•), « (•)) < V (х0, уа, Т) + е, ? (•) g Е, (4.7)
где К (и (•), ? (•)) — функция выигрыша в игре Г (х0, у0, Т). Из (4.5),
(4.6) следует существование е > 0 такого, что для любого е < е найдется число Т (е), Г0< Т (е)< Г, при котором
е=? (х0, уа, TQ)~ V (х0, у0, Т (е)). (4.8)
Из (4.7), (4.8) следует, что для любого е<ё
К (и, (•), ? (¦))< V (х0, уа, Г) + е< V (.х0, Уа, Т (е)) + е=
= V (Хо, Уа, То) = 1, ? (¦) ? Е,
т. е. стратегия и, (¦) обеспечивает /-встречу за время Г. Отсюда,
в силу произвольности Т> Та следует, что для любого Т> Тп найдется отвечающая ему стратегия и (•) е Р, которая гарантирует /-встречу за время Т. Иными словами, для любого Ь > 0 существует щ (•) е Р
такая, что ^ ^ ^ щ q, ? (,))^.т0+8 при всех ? (•) еЕ. (4.9)
Аналогично доказывается существование vs ()еЕ такого, что
tn (х0, у0; и (•), ?6 (¦)) ^Tq-S при всех и ()еР. (4.10)
Из (4.9), (4.10) следует, что в игре преследования на быстродействие Г (х0, Уо) Для любого ё>0 существует ситуация s-равновесия
в кусочно-программных стратегиях и значение игры равно Т0, где
Та — единственный корень уравнения (4.4).
Случай 3. Обозначим через Го минимальный корень уравнения
(4.4). Теперь, вообще говоря, мы не можем утверждать, что значение игры ?аі Г (х0, Уо) = Та. Действительно, из V (х0, у0, Г0) = / следует лишь, что в игре Г (х0, Уо, Г0) у игрока Р для любого s>0 существует стратегия ие (•), гарантирующая ему за время Г0 встречу
с игроком Е на расстоянии не более чем /+е, а из существования более одного корня уравнения (4.4) и монотонности V (х0, Уо, Г) по
Г получаем существование интервала постоянства функции V (х0, Уа, Т) по Ге[Г0, Г]. Поэтому увеличение продолжительности игры Г (х0, уа, Т0) на 5, где 8<Т{ — Т0, не приводит к уменьшению гарантированного сближения с игроком Е, т. е. для всех Ге[Г0, Г] игрок
Р может лишь обеспечить сближение с игроком Е на расстояние /+ е (для любого Е > 0), и нет основания считать, что при каком-то Ге[Г0, Гі] величина s окажется равной нулю. Если бы в игре Г (jc0,
Уо, Т0) существовала ситуация равновесия (а не ситуация s-равновесия), то значение игры Г (jc0, у0) было бы равно Г0 и в случае 3.
4.4. Модифицируем понятие ситуации равновесия в игре Г (jc0, Уо). Далее в этом параграфе удобнее использовать запись Г (х0, у0, /) вместо Г (хо, уо), подчеркивая, что игра Г (х0, Уо, 0 заканчивается
при сближении игроков на расстояние /.
Пусть t'„ (jc0, Уа’, и (¦), ? (•)) — время до момента сближения на
расстояние / в ситуации (и (•), ? (•)) и заданы е^О, 8^0. _ _
Определение. Будем говорить, что пара стратегий й\ (•), ?дв (•) образует ситуацию е, 8-равновесия в игре Г (х0, Уо, /), если
t‘n+s (*o, Уй, U (•), vi (•)) + ?> t‘n+s (xQ, y0; ы? О, ?і (¦))>
(¦*о, Уо, йі О, V (•)) — е,
для всех стратегий и ()еР, ? ()еЕ.
Определение. Пусть существует такая последовательность {<5*}, <5*>0, 5k->0, что во всех играх Г (jc0, у o', l+Sfc) для любого е>0
существуют ситуации е-равновесия. Тогда предел lim V {ха, уо, /+4)= V (х0, уо, I)
к-*оо
называется значением игры Г (х0, уо, I) в обобщенном смысле.
Заметим, что величина V (х0, у0, I) не зависит от выбора последовательности {<$*} вследствие монотонного убывания функции
V {хо, уо, О по /.
Определение. Будем говорить, что игра Г (х0, Уо, I) имеет
значение в обобщенном смысле, если существует такая последовательность {<5*}, что для любого е>0 и <5*е {<5*} в игре Г (jc0, у0,1)
существует ситуация е, 5к-равновесия.
Можно показать, что если игра Г (jc0, у о, /) имеет значение в обычном смысле, то значение ее V (х0, уо, /) (в обобщенном смысле) существует и равно
lim tln+tk (х0, у0; й6е (•), Zs, (•))= V (x0, y0, /).
i-»0
6k-A
Из определения значения и решения игры Г (jc0, у0, /) (в обобщенном
смысле) вытекает, что если в игре Г (х0, у0, /) для любого е>0
существует е-ситуация равновесия в обычном смысле (т. е. решение в обычном смысле), то V (jc0, у0, /)= V (х0, у0, /) (достаточно взять
последовательность 5к=0 для всех к).
Теорема. Пусть уравнение (4.4) имеет более одного корня и Т0 — наименьший корень, Т0 < со. Тогда существует значение
V (х0, уо, /) (в обобщенном смысле) игры преследования на быстродействие Г (*о, Уо, I) и V (*о, Уо, /)= Тй.
Доказательство. Из монотонности и непрерывности функции
V (х0, уо, Т) по Т следует существование такой последовательности
Г*-» Го слева, что V (х0, у0, Г*)-> V (х0, у0, Г0)=/и в точках Тк функция V (х0, у0, Г*) строго монотонна. Пусть
8к=?(х0, Уо, Г*)-/>0.
Из строгой монотонности функции V (х0, у0, Т) в точках Тк вытекает, что уравнение V (х0, у0, Т)=1+5к имеет единственный корень Г*. Это означает, что для любого в играх Г (х0, у0, 1+8к)
существует ситуация е-равновесия для любого е>0 (см. случай 2) п. 4.3). Значит, в игре Г (х0, у0, /) существует решение в обобщенном
смысле:
lim V(х0, уо, /+й*)= lim Тк= Т0= V (х0, у0, /)
*-юо к-*ао
и теорема доказана.
Рассмотрим теперь случай в) п. 4.3. Имеем: inf V (х0, у0, Т)=1.
т
Пусть Тк~* оо. Тогда lim V (х0, у0, Тк) = 1. Из монотонности и непре-
Jk-юо
рывности V (х0, уо, Г) по Г следует, что последовательность {Г*}
можно выбрать так, что в точках Тк функция V (х0, у0, Т) строго
монотонна. Тогда как и при доказательстве теоремы п. 4.4 можно показать, что существует такая последовательность {5*}, что
lim V (х0, уо, /+(5*) = 1іт Тк=Т0= со.
*-юо к-*оо
Таким образом, и в данном случае обобщенное решение существует, а обобщенное значение игры Г (х0, Уо, О равно бесконечности.
4.5. Часто оказывается важным определить, может ли игрок Р гарантировать /-встречу из данных начальных позиций х, у за фиксированное время Г. Если это невозможно, то может ли игрок Е гарантировать избежание /-встречи в течение заданного времени.
Пусть V (х, у, Т) — значение игры с предписанной продолжительностью Г из начальных состояний х, у еі?" с выигрышем
min р (х (t), у (/)). Тогда возможны следующие альтернативы:
0«Е КГ
1) ?(х,у, Т)>1;
2) ?(х,у, T)^l.
Случай 1. Из определения функции V (х, у, Т) следует, что для любого б>0 найдется такая стратегия игрока Е, что для всех стратегий и (•) справедливо неравенство
К (х, у; и (•), ?'в (•))> V (х, у, Т)-в.
Выбрав Е достаточно малым, можно добиться выполнения неравенства
К (х, у; и (•), г,* (•))> V (х, у, Т)—е>1
для всех стратегий и ()еЕ игрока Р. Из вида функции выигрыша К следует, что, используя стратегию ? * (•), игрок Е может гарантировать выполнение неравенства min р (х (/), у (/)) > / независимо
от действий игрока Р, т. е. в рассматриваемом случае игрок Е гарантирует избежание /-встречи на отрезке времени [0, 7] независимо от действий игрока Р.
Случай 2. Пусть Т0 — минимальный корень уравнения V (х, у, Т)=1 при фиксированных х, у (если р (х, у)<1, то Т0 полагаем равным 0). Тогда из определения V (х, у, Т0) следует, что в игре Г (х, у, Т0) игрок Р при любом ё>0 обладает стратегией и* (•), гарантирующей выполнение неравенства
К (х, у; иі (•), ? (•))< V (х, у, 7,о) + е=1+Ё
для всех стратегий ? ( )еЕ игрока Е. Из вида функции выигрыша К следует, что, используя стратегию и \ (•), игрок Р может гарантировать выполнение неравенства min р (х (/), у (/)) ^ /+Е независи-
0<»<Г0
мо от действий игрока Е. Продолжая произвольным образом стратегию и \ (•) на отрезок [7о, Т\, получаем, что в случае 2 игрок Р при
любом е>0 может гарантировать (/+Е)-встречу с игроком Е за время Т независимо от действий последнего.
Фактически доказана следующая теорема (об альтернативе).
Теорема. Для любых х, уеИ", Т>0 справедливо, по крайней мере, одно из следующих утверждений:
1) из начальных состояний х, у игрок Е может в течение времени Т гарантировать избежание 1-встречи независимо от действий игрока Р;
2) при любом ё>0 игрок Р может гарантировать (1+е)-встречу с игроком Е из начальных состояний х, у за время Т независимо от действий последнего.
4.6. Для каждого фиксированного Т> 0 все пространство R" х R" делится на три непересекающиеся области: область А = {х, у: V (х, у, 7)</}, которую будем называть зоной захвата; область В= = {х, у: V (х, у, Т)>1), которую естественно назвать зоной избежания захвата, и область С={х, у:? (х, у, Т)=1) —зону нейтрального исхода.
Пусть х, уеА. По определению А при любом е>0 игрок Р обладает такой стратегией ы* (•), что
К (х, у; и,* (), ? ( Ж V (х, у, Т) + г
при всех стратегиях ? (•) игрока Е. Выбрав подходящим образом ?>0, можно обеспечить выполнение неравенства
К (х, у; и'е (•), ? (•))< V (х, у, Т)+е<1.
Последнее означает, что стратегия и\ игрока Р гарантирует ему /-встречу с игроком Е из начальных состояний х, у за время Т. В результате получаем следующее уточнение теоремы п. 4.5.
Теорема. Для любого фиксированного Т>0 все пространство делится на три неперескающиеся области А, В, С, обладающие следующими свойствами:
1) при любых х, уеА игрок Р обладает стратегией и*, (•), которая гарантирует 1-встречу с игроком Е на отрезке [О, Г] независимо от действий последнего;
2) для х, уеВ игрок Е обладает стратегией ю* (¦), которая гарантирует избежание 1-встречи с игроком Р на отрезке [0, 7] независимо от действий последнего;
3) если х, уеС и е>0, то игрок Р обладает стратегией и*, (•), гарантирующей (/+г)-встречу с игроком Е за время Т независимо от действий последнего.
§ 5. НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ СУЩЕСТВОВАНИЯ ОПТИМАЛЬНОЙ ПРОГРАММНОЙ СТРАТЕГИИ УБЕГАЮЩЕГО
5.1. Важным подклассом игр преследования являются игры, в которых оптимальная стратегия убегающего игрока является только функцией времени (так называемый регулярный случай).
Ограничимся рассмотрением игры преследования с предписанной продолжительностью, хотя все результаты могут быть перенесены и на игры преследования по быстродействию. Пусть СТР (х) (Се (у)) — множество достижимости игрока Р (Е) из начального состояния х (у) к моменту времени Т, т. е. множество тех позиций, в которые может попасть игрок Р (Е) из начального состояния х (у) в момент Т, используя всевозможные измеримые программные управления и (t), (? (/)), /е[0, 7] при условии, что движение происходит в соответствии с системой x—f(x, и) (y=g(y, ?)). Введем в рассмотрение величину
(5.1)
Рт (*о, Уо)= max min р (х, у),
называемую иногда (см. [7, 39, 40]) гипотетическим рассогласованием множеств Се (уо) и СР (х0) (см. пример 8 п. 2.6 гл. II).
Функция рт (х0, Уо) обладает следующими свойствами:
1°. Рт (*о, Уо)>0, рт (х0, У о) 1т-о= Р (*о, уо);
2°. Рт (х0, у0)=0, если СТР (х0) => СТЕ (у0);
3°. Если V (х0, уо, Т) — значение игры Г (х0, у0, Т) с предписанной продолжительностью и терминальным выигрышем р (х (7), У (Т)), то
V (х0, уо, Т)>рт (х0, уо).
Действительно, свойство 1° следует из неотрицательности функции р (х, у). Пусть Ср (х0) => СЕ (уо)- Тогда для любого у'еСЕ (уо) существует такое х'еСр (х0), что р (х\ у')=0, (х^у1), откуда получаем 2°. Свойство 3° следует из того, что игрок Е, выбирая направление движения на точку МеСЕ (у0), для которой
Рт (*о, Уо)= min р (х, М),
хеСЦх0)
всегда гарантирует получение выигрыша рт (*о, Уо)- Точка М называется центром преследования.
5.2. Пусть Г4 (jc0, уо, Т) —дискретная игра преследования с шагом 8 (S = tk+\ — tk), предписанной продолжительностью Т, дискриминацией игрока Е и начальными состояниями х0, у0. Тогда справедлива следующая теорема.
Теорема. Для того чтобы для любых х0, y0eRn и Т=8 к, fc= 1, 2, ..., выполнялось равенство
Рт (*о, Уо)=?аі Г4 (х0, у0, Т), (5.2)
необходимо и достаточно, чтобы для всех xQ, у0еR", 8>0 и Т=5 к, к= 1, 2, ..., имело место соотношение
Рт(хо,Уо)= max min рТ-і (х, у) (5.3)
J’eC'Ofl) дсбС'(*о)
(?аі Г4 (х0, уо, Т) — значение игры Г4 (х0, у0, Т)).
Доказательство теоремы опирается на следующий результат.
Лемма. Для любых jc0> у0 еRn, T^S выполняется неравенство
Рт(хо, Уо)< max min pT_s (х, у).
J’eC^O’o) xec‘f (*о)
Доказательство. По определению функции рт имеем
max min pT_s (jc, y)=
yeC‘t(yo) xec‘r(x o)
= max min max min p (3c, y).
УеС‘е<У0) хьС'г (хо) УеС1~‘ O’) (*)
Для всех хе Сp (x0) имеет место включение Cp~s (х) с: С р (х0). Следовательно, для любых хеСр (х0), уеСЕ~г (у)
min р (х, у) ^ min р (Зс, у).
хеС*1 (jc) хеСтт(хй)
Тогда для всех хеСр (х0), уеСЕ (у0)
max min р (Зс, у)^ max min р (Зс, >)
уеСт-‘ O’) ис;-'(х) уеСт-‘(у) хеСЦхо)
min max min р (Зс, у)> max min р (Зс, у).
хеС'г(хо) peC'-'W ІеС;-‘(дс) jeCj-'OO іеС*(діо)
Таким образом,
max min pT-i (л, у)^ max max min p (3c, y)—
J’eC^O’o) JteC‘(*o) yeC‘E(y0) yeCT~‘ O’) ~xeCTf(xQ)
= max min p (x, y)=pT(x0, y0);
yeC* Ob) xeC*{xo)
— лемма доказана.
Перейдем к доказательству теоремы.
Необходимость. Пусть выполняется условие (5.2) и не выполняется условие (5.3). Тогда согласно лемме существуют такие <5>0,
х0, УоеRn, Т0 = 8к0, ?0>1, что
(5.4)
Рто (хо, у0)< max min pTos (*, у).
>бС^О>о) *еС'(*о)
Пусть u° (¦) — оптимальная стратегия игрока Р в игре Га (х0, у„, Го) и на 1-м шаге игры игрок Е выбирает точку у* е С1 (у0), для которой
min рГо_а (х, у*)= max min pTo-S (х, у). (5.5)
хеС‘г(х0) >6С‘(ТО) ДС6С‘(ДЮ)
Пусть х° (8) — состояние, в которое переходит Р на 1-м шаге при использовании стратегии «° (¦), а ?° (¦) — оптимальная стратегия Е в игре Г4 (х° (<5), у*, Тй—8). Рассмотрим следующую стратегию ? (•) игрока Е в игре Г4 (х0, у0, Т0): в момент /=0 он выбирает
точку у*, а начиная с момента t=8, игрок Е использует стратегию ?° О- 0 0
Обозначим через и (•) сужение стратегии м° (•) на отрезке [й, Г0].
Из (5.2), (5.4), (5.5) (согласно формуле (5.2) рт (х0, Уо) — значение игры Г4 (х0, уо, Т) находим
Рг0 (*о, Уо)^К (и0 ('), ? (•); хо, У а, Тй)—
= К(й° (•), *° О; *° (8),у*,Т0-8) =
=Pt0-s (х° (8), у*)2* min ptq—s (х, у*) =
*6 С'(до)
= max min pTo_g (х, у)>р? (*о, Уо)-
>бС^0о) ДбС^(до)
Полученное противоречие доказывает необходимость условия (5.3).
Достаточность. Заметим, что условие (5.3) совместно с условием рт (х0, Уо)І7’-о=Р (-*0, Уо) показывает, что функция рт (х0, Уо)
удовлетворяет функциональному уравнению для функции значения игры Г4 (х0, уо, Г). Как следует из доказательства теоремы п. 2.2, это
условие является достаточным для того, чтобы рт (х0, уо) было
значением игры Г4 (х0, у0, Г).
5.3. Лемма. Для того чтобы в игре Г (хо, уо, Г) существовала
оптимальная программная стратегия игрока Е (т. е. стратегия, являющаяся функцией только времени), необходимо и достаточно, чтобы
?аі Г (х0, уо, Т) = рТ (х0, уо). (5.6)
Доказательство. Достаточность. Пусть ?* (і), fe[0, Г] — допустимое управление игрока Е, переводящее точку у0 в некоторую
точку М такую, что
Рт (ха, уа) = min р (х, М).
хбс;(х0)
Обозначим ?* (•) = {<т, ?* (/)}, где разбиение а отрезка [0, 7] состоит из двух точек /0=0, t\ = T. Очевидно, ?* (-)еЕ. Согласно теореме и.
3.4 гл. I I/* ()еЕ— оптимальная стратегия игрока Е в игре Г (*о, >>о5 Т), если
?аі Г (х0, Уо, Т)= inf К (и (•), і7* (¦); *о, Уо, Т).
К()6Р
Но это равенство следует из (5.6), поскольку
inf К (и (¦), і7* (•); х0, Уо, Т)=рт (х0, уо).
«ОеР
Необходимость. Пусть в игре Г (х0, у0, Т) существует оптимальная программная стратегия игрока Е, тогда
?аі Г (х0, уо, Т)= sup inf К (и (¦), і7 (•); х0, у0, Т)=
»()бЕ и ()еР
= max inf р (х (Г), у)=рт (х0, jy0).
и()еР
Лемма доказана.
Теорема. Для того чтобы при любых х0, УоеіС, Т>0 в игре Г С*о> Уо, Т) игрок Е имел оптимальную программную стратегию,
необходимо и достаточно, чтобы для любых 8>0, х0, Уо е R", Т^8 выполнялось равенство
Рт(х0,уо)= max min pTs(x,y). (5.7)
>6С^(У0) *SC‘(XQ)
Доказательство. Достаточность. Из условия (5.7) согласно теореме п. 5.2 следует соотношение (5.2), из которого предельным переходом (см. теорему п. 3.7) получим
Рт (Хо, А) = ?а1 Г (Ко, _у0, Г).
Отсюда согласно лемме п. 5.3 следует существование оптимальной программной стратегии игрока Е.
Необходимость условия (5.7) следует из теоремы п. 5.2, поскольку существование оптимальной программной стратегии игрока Е в игре Г (х0, уп, Т) влечет существование таковой во всех играх
Гг (х0, Уо, Т), T=8k, 1, и справедливость соотношения (5.3).
§ 6. ОСНОВНОЕ УРАВНЕНИЕ
В данном параграфе будет показано, что при определенных условиях функция значения дифференциальной игры удовлетворяет уравнению в частных производных, которое называется основным. Впервые в монографической литературе оно было рассмотрено Р. Айзексом [1] и его часто называют уравнением Айзекса—Веллмана.
6.1. Используя теорему п.5.3, выведем уравнение в частных производных для функции значения дифференциальной игры. Будем предполагать, что для игры Г (х, у, Т) выполнены условия теоремы п. 5.3. Тогда функция рт (х, >0 представляет собой значение игры
Г (х, у, Т) продолжительностью Т из начальных состояний х, у.
Пусть в некоторой области ft пространства R" xRn х [0, оо) функция рт (х, >>) имеет непрерывные частные производные по
всем переменным. Покажем, что в этом случае функция рт (х,
>0 в области ft удовлетворяет дифференциально-экстремальному уравнению
зр
--max
ат ?еу
^ gi O', «о—min ? ~-f (x, u)=0,
3yi ueU Зхі
(6.1)
Іш 1
где функции f (x, u), gt (у, v), i= 1, ..., n, определяют закон движения
игроков в игре Г (см. (3.1), (3.2)).
Предположим, что (6.1) не выполняется в некоторой точке (х, у, Г) eft. Пусть, для определенности,
ар
---max
ат ?6у
^ gi (у, «)—max ? ^ f (х, ы)<0.
ОУі ие? дх,
I
і-1
Пусть ?е? таково, что в рассматриваемой точке (х, у, Г)eft выполнено соотношение
^ зр - ар
L Т Si (у. ?)=тах ^ — gi ІУ, ?).
І_1 8Уі .6V Зуі
Тогда при любом ueU в точке (х, у, 7)eft имеет место неравенство:
(6.2)
|
dp дТ | 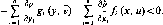 |
х (т)
/(х (о, и (0) dt, у (т)
g (у (t), V (0) dt
— траектории систем (3.1J, (3.2), отвечающие некоторому допустимому управлению и (і) и ? (t) = ? соответственно и начальным условиям х (0) = х, у (0)=у. Определим функцию
f
;_1 дУі І(* (г), > (г). Т-і)
(т)= — .
8Т |(х (Г), у (т), Т-і)
gi O' 0), v)-
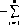 | dxt |(х (t), у (і), т-і) |
f (х (т), и (т)), те[0,
Функция G (т) непрерывна по т, поэтому найдется число с<0 такое, что G (т)^с при те[0, <5]. Отсюда имеем
s
J С? (т) dx^cS. (6.3)
о
Нетрудно убедиться в том, что
G( т)=-
dp
l(* 6), у W, Т-і)
Из (6.3) получаем
Рт (Х, у) — рт-і (х (8), у (8))^с8. Отсюда в силу произвольности и (t) следует
Рт(х, у)< max min рТ-»(х',уО»
у'еС‘?(у) *'еС‘(х)
что противоречит (5.7).
Таким образом, мы показали, что в том случае, когда у игрока
Е в игре Г (х, у, Т) при любых х, yeR", Т> 0 существует оптимальная программная стратегия, значение игры V (х, у, Т) (оно совпадает с рт (х, у) согласно лемме п. 5.3) в области пространства
Rn xRn х [0, оо), где существуют непрерывные частные производные у этой функции, удовлетворяет уравнению
(6.4)
д? ? , ч, • Л
—=тах 2, — gi (У, ?)+тт ? —// (*. «)
°т ?б? Оу, иЕ0 j=I OXj
при начальном условии V (х, у, Т) \т-а=р (х, у)- Предположим, что
каким-то образом удается определить и, ?, доставляющие шах и min
д? д?
в (6.4) как функции от х, у и —, —, т. е.
дх ду
(6.5)
(6.6)
(6-7)
д?
дТ
д?\ _ _ / д?'
U = U[X,-i V = vU-
Подставляя выражения (6.5) в (6.4), получаем
К44ЭИД44Д))-
при условииV (х, у, Т)\т„о=Р (X. у).
Таким образом, для определения V (х, у, Т) имеем задачу Коши для уравнения в частных производных первого порядка (6.6) при начальном условии (6.7).
Замечание. При выводе функциональных уравнений (6.4), (6.6) и доказательстве теоремы п. 5.3 мы не использовали конкретный вид функции выигрыша, поэтому теорема остается справедливой для любого непрерывного терминального выигрыша Я (х (Г), у (Т)). Однако в этом случае вместо величины рт (х, у) необходимо
рассмотреть величину
Нт(х,у)= max min Н(х',у').
Уравнение (6,4) также справедливо для значения дифференциальной игры с предписанной продолжительностью и любым терминальным выигрышем, т. е. если в дифференциальной игре с предписанной продолжительностью Г (х, у, Т) и терминальным выигрышем Я (х (Т), у (Т)) у игрока Е существует оптимальная программная стратегия, то значение игры V (х, у, Т) в области пространства і?" х Дл х [0, оо), где существуют непрерывные частные производные, удовлетворяет уравнению (6.4) при начальном условии V (х, у, Т)\т^о=Н (х, у) или уравнению (6.6) с тем же начальным условием.
6.2. Рассмотрим теперь игры преследования, в которых функция выигрыша равна времени до момента встречи. Предположим, для определенности, что терминальное многообразие F является сферой Р (х- У)—^> />0. Будем предполагать, что множества С \ (х) и С‘Е (у) непрерывны по t в нуле равномерно относительно хи у.
Пусть имеет смысл величина
? (х, у, /)=тах min t'„ (х, у; и (/), ? (/)),
«(О и (О
где t'„ (х, у; и (/), ? (/)) — время сближения на / — расстояние игроков Р и Е, движущихся из начальных точек х, у при использовании измеримых программных управлений и (t) и v (t) соответственно. Предположим также, что функция ? (х, у, I) непрерывна по совокупности аргументов.
Игру на быстродействие будем обозначать через Г (х0, >0)- Так
же как это было сделано в § 4, 5, можно вывести необходимые и достаточные условия существования оптимальной программной стратегии игрока Е в игре преследования на быстродействие. Справедлива следующая теорема.
Теорема. Для того чтобы игрок Е при любых х0, Уо^Р." в игре Г (х0, уо) имел оптимальную программную стратегию, необходимо
и достаточно, чтобы при любом 5 > 0 и любых Хо, е PC выполнялось равенство
? (хо, уо,І)=6+ max min ? (х\ у', I).
У'е С' Со) х'еС'ад
Для игры преследования по быстродействию уравнение (6.4) принимает вид
(6.8)
п д? и з?
maxE Т & (у. «)+min ? —f (х, u)= -1,
?еУ ,т 1 ЗУ, ueU
при начальном условии
?(х,у, [)lb,y)-,=0. (6.9)
Здесь предполагается существование непрерывных частных производных первого порядка функции ? (х, у, I) по х, у. Полагая, что каким-то образом можно определить и, ?, доставляющие max и min
„ , дв дв - - ( м\ -
в (6.8) как функции от х, у, —, —, т. е. м = н|х, — }, ? =
дх ду \ dxj
—v (^’ ^ перепишем уравнение (6.8) в виде
(6.10)
(6.11)
при условии
о (х, у, 1)\р(х.у)-І=0.
Вывод уравнения (6.8) аналогичен выводу уравнения (6.4) для игры преследования с предписанной продолжительностью.
Обе задачи Коши (6.4), (6.7) и (6.8), (6.9) являются нелинейными относительно частных производных, поэтому при их решении возникают значительные трудности.
6.3. Перейдем теперь к выводу уравнений характеристик для (6.4). Предположим, что функция V (х, у, Т) имеет непрерывные вторые смешанные производные на
всем пространстве, функции g, (у, к), /((х, и) и функции й=й^х, ~~J>
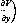
имеют непрерывные первые производные по всем переменным, а множества U, V имеют вид параллелепипедов <^,^ит^6т, m= 1, ..., к и cq^vq^dq, 9=1, ..., /, где u=(ui, ..., uk)eU, »=(»i,.... vj)e V. Обозначим
д?
дх,
п д?
/ (*. и)- ? — ft {у.
.-1 дУ‘
д? * В (х. у, Т)ш— - ?
»)•
дТ
і-і
Функция В (х, у, 7)=0, поэтому беря частные производные по х\.....x„, получим
дВ _ дг? " д*? • д? д/
Зхк дТдхк дх,дхк ' , dxt Зхк
" д2?
- I г-г-
Зуідхк
у JL(y
--1 Эит\,_1Вх/‘) Вхк
(6.12)
' д / ” д? \ ай, —
- I — (I т-«.)т-=0.
»_і \-1 дУ> ) дхк
Для каждой фиксированной точки (х,_у, T)eR хR х[0, оо) максимизирующее значение й и минимизирующее значение й в (6.4) лежат либо внутри, либо на границе интервала ограничений. Если это внутренняя точка, то
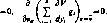
д ( " д? \
г- 1-Л -
oum дх, /ч-и
Если же й (5) лежит на границе, то здесь могут представиться два случая. Исследуем
их подробно для одной из компонент um ( х, вектора и. Исследование остальных
д?\
“m (х
іктора »(*'. У
. . ( , д?(х', у', Т)\
и"=илх’—*—nm-
компонент вектора й и компонент вектора ? проводится аналогично. Для простоты предположим, что в некоторой точке (х', у', г)
Случай 1. Существует шар в пространстве R с центром в точке х', для всех точек х которого выполняется равенство
_ ( д? (х, у', Г)\
'=“"Т’-аі Га”
д? (х, у', Г)\
ит ~
Функция Щп на этом шаре принимает постоянное значение, поэтому в точке х' имеем
дЦт, п . ,
—=0, і=1, и.
дХі
Случай 2. Такого шара не существует. Тогда найдется последовательность хг,
Ііш хг=х' такая, что
Г-ЮО
З?(хг,у',
-to-Г*"
Отсюда
8 ( " З?
дит \,_1 дхі
_)=°.
• «)/
А . ./ эк(х. у, m
функции u=u I х,-) следу-
\ дх )
(хг. У. n
5К Э/,
Из непрерывности производных —, — и
дх{ 8ит
ет, что предыдущее равенство выполняется и в точке (х', у', Т).
Таким образом, два последних слагаемых в (6.12) равны нулю, и при всех
(х, у, T)eR xR х [0, оо) выполняется равенство
дВ д2? ” д2? _
— ---I -/,(х, и)-
дхк 8Т8хк .“ 8xt8xk
” д? 8ft * д2? __
і_ 1 Зх{ дхк дуідхк
Пусть х (0, у (0. * е[0, Т] — решение системы
. J -( З?(х, у, T-t)\\ . ( _( 8? (х, у, T-t)\\
’"¦'г “с—*—J) '-‘И*—?—))
с начальным условием х (0)=xq, у (0)=уо- Вдоль решения х (0, У (0 имеем
---17^Гй(),-г)=0> fc=l,2,..., п.
32r (5 (0, у (О, Г-0 " д2?(і (О, у (О, Г-0,,_/ч ., чч -т-- I--—,-Л (х (0. “ (0)-
8Т8хк ,_1 dxjdxk
_ у 8? (х у «)’ Г-0 3/, (х (О, С(0)
Зх, Зх*
? 3JF(i(0, Г-0 .......... ,
- L-—-Si (у (0.«(0)=о. fc=i..... я,
Зу,дхк
где
зк(і(0, у (О, г-о\ --—),
... . ас См, И», г-і>\
•«-¦г*—*—}
Однако,
d /8 Л\
8?$ (0, у (0. г-о\ * з2У(х (0, у (0. г-0
Л (5 (0, й (0)+
Зхк3хі
Зхк
" 3JF(i(0, у«> Г-О
з2к(х(р, У (0, г-О
дхк8Т
, fc=l, л.
+ L
і-1
gt G (<). ® (0)-
(6.14)
менять
Зхкдуі
Заметим, что у дважды непрерывно дифференцируемой функции можно порядок дифференцирования. Перепишем (6.13) с учетом (6.14) в виде
d (8V (х (0, у (О, Г-0
)-і
' і-і
З? (х (t), у (t), г-0 3f (х (0, й(0)
ч
*\
Зхк
Зх*
.[ Зх/
*=1.....л-
Аналогичным образом получим уравнения
З? (х (0, у (0> Г-0 3gy(y (О, 5(0)
/ЗК(х(0, у(р, Г-О' Л \ дуі
' j-1
Зу/
Зуі
j=l, ..., л.
Так как при Г и [О, Г]
F (5 (о, у (О, Т-0=Н (х (7), у (Г)),
то
/?F_(i (О, У (0, г-о
dt \
8Т
Введем следующие обозначения:
„ А З?(х (О, у (О, Г-О
к (0=---,
Зхі
„ ,чд 8VGW, у(0. т-t) . ,
Ууі (0--:-. '=1.....я.
дуі
У,М-{?,,0)Ь
ИгМ
дан* (О, у (О, г-/)
дТ '
В результате получим следующую систему обыкновенных дифференциальных уравнений для функций х (/), у (/), ?х (/), ?у (/), ?т (/):
Xi=f (x, и (x, Vx)), yf=gi (у, V (y, Vy)),
„ ад(*. «(*. ^)) tV ? „ 8gl(y,Z(y, Vy))
Vx‘ Я, • --h ?Уі , •
Bxk j_i °Ук
-I
(6.15)
i-1
и, кроме того, согласно (6.6) имеем
Ут= I ?„а (У. ? (У, ?,))+? vXifi (X, й (х, ?х)).
Для решения системы нелинейных уравнений (6.15) относительно функций х (/), у (/), УХ)с (О, ?ук (0, TV (0 необходимо определить начальные условия. Для функции
V (х (/), у (/), T—t) они заданы в момент времени /= Т, поэтому введем переменную т = Г— / и запишем уравнение характеристик в регрессивной форме. Введем обозначения х = — х, у= —у. Уравнения характеристик принимают следующий вид:
*<=-/<(*.“), Уіш —gi (у, v),
(6.16)
ад (*¦ ц)
*' Зх* ’
? т, О. «)
L ?у, я >
і. 1 ' ал
Уг=0.
При задании начальных условий для системы (6.16) используется соотношение V (х. у, Т) \т-о=Н (х, у). Пусть х |t_0=J, У |т-о=*'- Тогда
дН
Уху*-—
1 дхі
дН
ду,
х—і, у—s'. Уу. It—0 —
(6.17)
х—г, у—У.
Кгіт-о- Z У у, Іт-0 ft (s'. v (S'. Vy |t-o))+ Z Vx lt-0 f (s. U (s. Vx |T_o)).
i-i j-i
Подробные исследования возможных путей решения системы (6.16)—(6.17) см. в[1].
Аналогичным образом, используя уравнение (6.8), можно записать уравнение характеристик для задачи преследования на быстродействие.
§ 7. МЕТОДЫ ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ ДЛЯ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ ИГР ПРЕСЛЕДОВАНИЯ
7.1. Пусть Гг (х, у, Т) — дискретная форма дифференциальной
игры Г (х, у, Т) продолжительностью Т> 0 с фиксированным шагом разбиения S и дискриминацией игрока Е на время <5>0 вперед. Обозначим через Vs (х, у, Т) значение игры Гг (х, у, Т)*. Тогда
lim Vs (х, у, Т)=? (х, у, Т)
«-.о
и оптимальные стратегии в игре Гг (х, у, Т) при достаточно малых
8 могут быть эффективно использованы для построения ситуаций Е равновесия в игре Г (х, у, Т).
7.2. Идея численного метода состоит в построении алгоритма нахождения решения игры Гг (х, у, Т). Перейдем непосредственно
к изложению метода.
Нулевое приближение. За нулевое приближение функции значения игры Vs (х, у, Т) принимаем функцию
?° (х, у, Т)= max min р (?, щ), (7.1)
necjoo f ec;w
где Ср (х), Се (у) — множества достижимости игроков Р и Е из
начальных состояний х, у еР" к моменту времени Т.
Выбор функции V°s (х, у, Т) в качестве начального приближения оправдан тем, что в достаточно широком классе игр (так называемый регулярный случай) она оказывается значением игры Г (х, у, Т). Следующие приближения строятся по правилу:
Vs(x, у, Т)= max min ?° (?, щ, Т-8),
чеС'ОО feC* (х)
?\ (^. У, Т)= max min ?\ й, q, Т-8),
ЧбС^ОО feC* (х)
?\ (х, у, Т)= max min ?\ ((, т), Т-8) (7.2)
ЧбС'Ог) f еС‘(х)
при Т>8 и Vq (х, у, Т)= ?° (х, у, Т) при Т^8, к^ 1.
Как видно из формул (7.2), операция max min берется по множествам достижимости Се (у), Ср (х) за время 8, т. е. за один шаг дискретной игры Гг (х, у, Т).
•Вопросы, связанные с обобщениями и приложениями теоремы Хелли, подробно изложены в книге: Данцер Л., Грюнбаум Б., Кли В. Теорема Хелли. М., 1968.
7.3. Теорема. При фиксированных х, у, Т, 8 числовая последовательность [?к (х, у, 7)] не убывает с ростом к.
Доказательство. Докажем сначала неравенство
?\{х, у, T)>V°s(x, У, Т).
_ Для всех ?еСр (х) справедливо: Cp~s (О с Ср (х). Для любых tje Сe~s (ц), ? е С ^ (х) имеем
min р (I, ц)> min р (?, rj).
UCTr(x)
Отсюда
V\ (х, у, Т)— max min max min p(?,i})^
(jeC^W {eC* (jc) SeCj-'di) {6C;-'(f)
^ max max min p (?, tj)=
<ieC‘W ieCp' fa) (eC*(x)
= max min p (?, tj)= V°s (x, у, T).
<16 СЦу) (еСЦх)
Предположим теперь, что для І^к справедливо неравенство
?\(х.у. T)>V'f'{x,y,T) (7.3)
и докажем его для l=k+1. Из соотношений (7.2) и (7.3) следует, что
Vg+1 (х, у, Т)= max min ?к (?, tj, Т-8)>
,eC'W {6С‘М
> max min Vks 1 (?, r\, T-8)=Vkg (x, у, T).
„еС^Ы {6 С‘(х)
Таким образом, в случае 7><5 по индукции утверждение теоремы доказано. В случае 7<<5 утверждение теоремы очевидно.
И-
7.4. Теорема. Последовательность {Vg(x, у, Т)} сходится за
конечное число шагов N, при этом имеет место оценка N<
где квадратные скобки означают целую часть.
Доказательство. Пусть N=[T/5\ + l. Покажем, что
?Пх,у,Т)=?$+1(х,у,Т). (7.4)
Равенство (7.4) легко получить из построения последовательности [Vg (х, у, 7)]. Действительно,
Vg (х, у, Т)= max min V?~l (f1, tj1, Т-8) =
tlleС* (у) {*еС’(х)
= max min max ...
(,‘eC'M {‘бс;м ч'бС^Ц1)
min V't(ZH-l,tiN-l,T-(N-l)8).
... max
n"-'eC't(n" ’)
Аналогично имеем
«'-'ее; «*-»)
Vg + l(x,y,T)= max min max ...
lf»eCjOO {‘бС*(х) чабС* (Ч1)
... max min n~\ T-(N-l) 8).
n'-'ec;!,'-1) i'-'ec;n
Однако T—(N— 1) <5 = a<5, поэтому
,лг-і
лЛ
V > *)» откуда и следует равенство (7.4).
Совпадение членов последовательности ?к при k^N выводится из (7.4) индукцией. Теорема доказана.
7.5. Теорема. Предел последовательности {?к (х, у, Т)} совпадает со значением игры Гг (х, у, Г).
Доказательство. Данная теорема является, по существу, следствием теоремы п. 7.4. Действительно, обозначим
?г (х, у, Г) = 1іт Vks (х, у, Г).
к-* аa
Сходимость происходит за конечное число шагов, не превосходящее 'N=[T/5] +1, поэтому в рекуррентном уравнении (7.2) можно перейти к пределу при к-*со. Предельная функция ?6 (х, у, Т) удовлетворяет уравнению
?ь (х, у, Т)= max min Vs (?, ц, Т-8) (7.5)
1,еС»О0 {еС‘(х)
при начальном условии
?ь (х, у. Т) |о<г<г= max min р (<!;, t\), (7.6)
кес^оо {ес;(х)
что и является достаточным условием для того, чтобы функция ?ь (jc, у, Т) была значением игры Г« (х, у, Т).
1.6. Зная функцию ?г (jc, у, Г), можно, используя уравнение (7.5),
построить оптимальные кусочно-программные стратегии в игре Гг (х, у, Т). С помощью стратегий, оптимальных в игре Г г (jc, у, Т),
строятся е-оптимальные стратегии в основной игре Г (jc, у, Т).
Как следует из (7.4), совпадение двух последовательных приближений на шагах к и k+ 1 означает, что соответствующее приближение уже является значением игры Гг (х, у, Т), поскольку в этом
случае все последующие приближения совпадают с к-м приближением. Такое совпадение и является критерием прекращения вычислений. Имеются достаточные основания полагать, что в широком классе задач сходимость происходит гораздо быстрее, чем за время, указанное в теореме п. 7.4, в частности в «регулярном случае» вычисления прекращаются на 1-м шаге после вычисления функции Vі (х, у, Т) (это в то же время является критерием «регулярности»).
7.7. Приведем модификацию метода последовательных приближений, изложенного выше.
_ В качестве начального приближения возьмем функцию ?% (х, у, Т)=?\ (х, у, Г), где ?\ (х, у, Т) определена равенством (7.1). Следующие приближения строим по правилу:
?к+1 (•*» У. Т)= max max min Рк (?, r\, T—iS)
іе[1:Л1 ЧеС“С) feС“ (дс)
при Т>8, где N=[T/5\, и V$+1 (х, у, Т)= ?% (х, у, Т) при Т^8.
Для последовательности функций {?к(х, у, Т7)} так же, как и для последовательности функций \?к (х, у, Т7)}, справедливы утверждения теорем п. 7.3—7.5.
Доказательство этих утверждений для последовательности функций {?к (х, у, Т)} почти дословно повторяет аналогичные рассуждения для последовательности функций {?к(х, у, Т)}. Функциональное уравнение для функции значения игры Гг (дс, у, Т) принимает в области {(дс, у, Т) \ Т> 5} вид
Vs (дс, у, Т)= max max min Vs (?, г/, T-iS), (7.7)
/е[1:М чеС“С) (еСЦх)
где N=[T/8), а начальное условие остается прежним, т. е. имеет вид
(7.6).
7.8. Докажем эквивалентность уравнений (7.5) и (7.7).
Теорема. Уравнения (7.5) и (7.7) с начальным условием (7.6)
являются эквивалентными.
Доказательство. Пусть функция ?ъ(х, у, Т) удовлетворяет
уравнению (7.5) и начальному условию (7.6). Покажем, что она удовлетворяет уравнению (7.7) в области {(дс, у, Т)\Т>8}. Действительно, справедливы следующие соотношения:
?ь (де, у, Т)= max min Vf (?, q, T-8) =
чеС'С) {6 C‘r(x)
= max min max min Vs (?, rj, T—28)>
,6 C‘(y) іеС^іх) чеС^(ч)
| ^ max max | min | min Vs (J, rj, T— |
| ЧчС^ (у) ібС‘г(і() | {бС'(х) | |
| = max | min | Vs{L if, T-2S)>... |
| хеС“(у) | {бС“(х) | |
| ...^ max | min | Vs(t, if, T-iS)>.... |
| чеС“(у) | (еС‘(х) |
Vs (х, у, Т) — max min Vs (?, r\, Т-5),
че С'С) {еС‘(х)
поэтому справедливо равенство
Vg (х, у, 7)=max max min ?} (?,, r\, Т—і5),
І6[1:Л(| 4eCj(y) feC“(x)
где N=[T/5\, что и доказывает требуемое утверждение.
Пусть теперь функция Vs(x, у, Т) в области {(*, у, Т)\Т>5}
удовлетворяет уравнению (7.7) и начальному условию (7.6). Покажем, что она удовлетворяет также уравнению (7.5). Предположим противное. Тогда в области {(jc, у, Т)\Т>5} должно иметь место неравенство
?{ (х, у, Т)> max min Vs (?, t], Т-5).
чеС>'(у)
Однако
max min Vs (?, r\, T—5) =
че&іу) feC‘(x)
| = max |
min teC‘r(x) |
max 2e[l: ЛГ—1] | max |
min ?6С'( о | П(?, if, Г-(і+1)<5)> |
|
> max че&Ы |
max іе[1:ЛГ-1] | max |
min {eC‘(x) |
min ?eCj( 0 | if, r-(i+l)5) = |
|
= max /е[1:ЛГ-1] |
max xeC'OO | max |
min fsc'w |
min 0 | if, Г-(і+1)й) = |
іе[2:Л0 чеС*(у) feC«(x)
Полученное противоречие доказывает теорему.
§ 8. ПРИМЕРЫ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ ИГР ПРЕСЛЕДОВАНИЯ
8.1. Пример 4. (Простое движение). Рассмотрим дифференциальную игру Г (хо, уч, Т), в которой движение игроков Р и Е происходит в евклидовом пространстве Л* согласно следующим уравнениям:
для Р\х = аи (t), ||м (OKI, х (0) = х0,
для Е:у = р? (0, ||» (OK*, у (0)=^0, (8.1)
где а, Р — константы а>/?>0, х, у, и, veR".
Выигрыш игрока Е равен
Н(х(Т),у(Т))=\\х(Т)-у (Г)||.
Пусть Гg(x, у, Т) — дискретная форма дифференциальной игры
Г (х, у, Т) с шагом разбиения <5>0 и дискриминацией игрока Е. Игра (х, у, Т) протекает в N шагов, где N= Tjb. Согласно
результатам § 2 (см. пример п. 2.3) игра Гг (х, у, Т) имеет значение
Vs (х, у, Г)=тах {0, \\x-y\\-N-5-(<x-p)} =
=max {0, \\х-у\\-Т(а-р)},
а оптимальное движение игроков происходит по прямой, соединяющей начальные состояния х, у.
Согласно результатам § 3 значение исходной дифференциальной игры
?(х,у, Г)=1іт Vs(x,y, Г)=тах{0, \\х-у\\-Т (<х-Р)}. (8.2)
а-о
Можно убедиться, что
?(х,у,Т)= max min \\х'-у'\\=рт(х, у),
y'eCTt(y) x'eCj(x)
где Се (y) = S (у, РТ) — шар в R" радиуса РТ с центром в точке у, аналогично С> (x) = S (х, аТ). Тем самым согласно лемме п. 5.3 у игрока Е в игре Г (х0, Уо, Т) существует оптимальная программная
стратегия ?* (t), fe[0, Т], которая приводит траекторию игрока Е в точку у*еСІ(Уо), для которой
Рт(х0,Уо)= min ||x'-j>*||.
х'еСтг(хо)
Очевидно,
Уо-хр
ІЛ>-*оІ
При Уо^Хо,
при —Xq9
где в е R" — произвольный вектор такой, что ||?|| = 1. Из результатов § 6 следует, что в области
где существуют непрерывные частные производные
| д={(*. у. Т):\\х-у\\-Т(а-Р)>0}, |
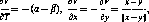 |
| функция V (х, у, Т) удовлетворяет уравнению (6.4): |
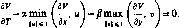 |
В уравнении (8.3) минимум и максимум достигаются при управле' ниях
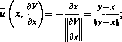
(8.4)
| д? |
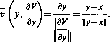 |
Стратегии (8.4), (8.5) являются оптимальными в дифференциальной игре (8.1). Стратегию й {х, у), определяемую соотношением (8.4), называют «погонной стратегией», так как в каждый момент времени вектор скорости игрока Р при использовании этой стратегии нацелен на преследуемого игрока Е.
8.2. Пример 5. (Игра преследования при наличии сил трения). Преследование происходит на плоскости. Уравнения движения имеют следующий вид:
для игрока Р:
для игрока Е:
ri=sh
(8.7)
st^Pvt-k&t, i=l, 2, ||ю||<1;
Чі (0) = ??, р, (0)=Ри г, (0) = г°, si (0)=s°, і= 1, 2; а, Р, кЕ, кр>0. (8.8)
Здесь ч=(чі, qi) и r=(ru r2) — местоположение на плоскости игроков 1 и 2 соответственно; р = (рь р2) и j=(ji, ^г) — их импульсы;
— некоторые константы, интерпретируемые как коэффициенты трения.
Выигрыш игрока Е полагается равным
Н (ч (Т), г (Т))= \\q (Т)—г (Г)!! =
=?[?. (Т)-Гі (T)]2 + [q2 (Т)—г2 (Г)]2.
В плоскости q=(qi, q2) множество достижимости СЕ (q°, р°)
игрока Р из начальных состояний р (0)=р°, q (Q)=q° за время Т представляет собой круг (см. упр. 18) радиуса
RP{T)=^{e-k>T+kpT-\)
с центром в точке к>
—к Т
a(q°,p0, T) = q°+P0
кр
Аналогично, множество СТЕ (г°, s°) представляет собой круг радиуса
КЕ(Т)=Іг(с-к^+кЕТ-1)
*Е
с центром в точке
l-e"t?r
Ь(г°, 5°, Т) = г°+— -j°.
кЕ
Для величины pr{q°, Р°> r°> s°), определяемой соотношением (5.1), в данной дифференциальной игре выполняется равенство
Pr(q°> Р°> r°> s°)~ max min ||?—г||.
Г6С^(Л*°) />°)
Отсюда (см. формулу (2.10)) имеем
Рт (q, Р> г, я)=тах {0, ||а (q, р, Т)-Ь (г, 5, T)\\-(R„ (T)-RE(T))} =
-квГу S )
~k„T
=max
--Si
kD kE
+kET-1'
~kgT
e kpT+kBT-1
(8.9)
Jr2 KE
(x ft
В частности, условий <x>/?, — >— достаточно, чтобы для любых
кр кЕ
начальных состояний q, р, г, s нашлось отвечающее им Т, при котором pT(q, р, г, s)=0.
Функция рт (q, р, г, s) удовлетворяет дифференциально-экстремальному уравнению (6.1) в области П = {(?, р, г, s, T)\pT{q, р,
г, j)>0}. Действительно, в области ?2 существуют непрерывные частные производные
др др др др др
(8.10)
. /=1,2.
дТ* dq’i др, dr, Bs,
Уравнение (6.1) принимает вид
др ? (др др др др \
о ?1 др • др
—рmax 2, — «i-amm 2. ~ к,=0. МО і-1 dsi МО /> 1 др,
(8.11)
Здесь экстремумы достигаются на управлениях й, ?, определяемых следующими формулами:
др
др,
(8.12)
«,= —
І(др?+(дру
S\dpJ \dpj
др
dsj
(8.13)
/=1,2.
?,-
?\й*і/ \ds2J
Подставляя эти управления в (8.11), получим нелинейное уравнение в частных производных первого порядка
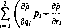 | Si |
|
др дТ дР , др д кррі д &еЗі ] dpi dsi |
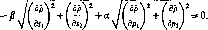 |
Вычисляя частные производные (8.10), убеждаемся, что функция Рт ІЯ> Р> r> s) в области П удовлетворяет уравнению (8.14).
Отметим, что величина рт (q°, р°, г°, s°) является значением
дифференциальной игры (8.6)—(8.8), а управления, определяемые соотношениями (8.12), (8.13),' оптимальные в области П.
Из формул (8.12), (8.13), (8.9) находим
-Pt-
-Pi
fi—qi+Sj
Ur
=, Vt-ut, і—1,2. (8.15)
L (гі-Чі+*-
В ситуации и, ? направление действия силы каждого из игроков параллельно линии, соединяющей центры кругов достижимости (как это следует из формулы (8.15)), и остается постоянным, поскольку в этой ситуации центры кругов достижимости перемещаются вдоль прямой линии.
§ 9. ИГРЫ ПРЕСЛЕДОВАНИЯ С ЗАДЕРЖКОЙ ИНФОРМАЦИИ У ПРЕСЛЕДОВАТЕЛЯ
9.1. Ранее в этой главе рассматривались конфликтные управляемые процессы, в которых каждый из участников (игроков) имел полную информацию, т. е. в каждый текущий момент игры Р (Е) знал свое состояние х (/) \у (/)] и состояние противника у (/) [х (/)]. Были получены теоремы о существовании ситуаций е-равновесия в чистых стратегиях в таких играх и проиллюстрированы различные методы построения движения. Это оказалось возможным, поскольку дифференциальные игры с полной информацией представляют собой предельный случай многошаговых игр с полной информацией, когда промежуток времени между двумя последовательными ходами стремится к нулю. Иначе обстоит дело с дифференциальными играми с неполной информацией, где применение смешанных стратегий играет существенную роль. Не останавливаясь на анализе всей проблемы, рассмотрим только случай игры преследования с предписанной продолжительностью, терминальным выигрышем и задержкой поступления информации игроку Р о фазовом состоянии игрока Е на время />0.
9.2. Пусть задано некоторое число /> 0, называемое временем задержки информации. При 0^/^/ преследователь Р в каждый момент времени t знает свое состояние х (/), время t и начальное местоположение у0 убегающего Е. При l^t^T игрок Р в каждый
момент t знает свое состояние х (/), время t и состояние у (t — l) игрока Е в момент t — l. Игрок Е в каждый момент времени t знает свое состояние у (/), состояние противника х (і) и время t. Его выигрыш равен расстоянию между игроками в момент времени Т, выигрыш игрока Р равен выигрышу Е с обратным знаком (игра антагонистическая). Обозначим эту игру Г (х0, уо, Т).
Определение. Под кусочно-программной чистой стратегией ? ( ) игрока Е будем понимать пару {т, Ь), где т —разбиение отрезка времени [0, 7] конечным числом точек 0^tl<...<tk=T и b — отображение, которое каждому состоянию х (tj), у (/,) /,• ставит в соответствие отрезок измеримого программного управления ? (t) игрока Епри te[th /,+ 1).
Определение. Под кусочно-программной чистой стратегией и (•) игрока Р будем понимать пару {о, а}, где а — произвольное разбиение отрезка времени [0, 7] конечным числом точек
D^t\<t^< ...<t,= T, а — отображение, которое каждому состоянию х (/j), у (t\—l), t \ при l^t'j ставит в соответствие отрезок измеримого программного управления и (/) игрока Р при t е [7 „ t -+1). Для t',^1 отображение а каждому состоянию х (/',), у0, t\ ставит
в соответствие отрезок измеримого управления и (і) игрока Р при Ыі)-
Множества всех кусочно-программных чистых стратегий игроков Р и Е будем обозначать соответственно через Р и Е.
Уравнения движения имеют вид
x=f (х, и), ие U a Ft, хеЯ",
y=g (у,?), ?е?с Я9, уеЯ”. (9.1)
Полагаем выполненными все условия, обеспечивающие существование и единственность решения системы (9.1) для любой пары измеримых программных управлений и (/), ? (/) при заданных начальных условиях Хо, уо. Это гарантирует существование единственного решения системы (9.1) в случае использования игроками Р и Е кусочно-программных стратегий ’и QeP, ? ()еЕ при заданных начальных условиях х0, Уо- Таким образом, в любой ситуации (и (¦), ? (¦))
при заданных начальных условиях х0, уй функция выигрыша игрока
Е определяется однозначно
К (хо, уо; и (•), « ( )) = Р (х (Т), у (7)), (9.2)
где х (0, у (0 — решение системы (9.1) при начальных условиях х0, Уо в ситуации (и (•), ? (¦)), а р — евклидово расстояние.
9.3. Можно на простейших примерах показать, что в рассматриваемой игре Г (х0, Уй, Т) ситуации е-равновесия существуют не для
всех чисел б>0. Поэтому для построения ситуаций равновесия воспользуемся подходом, предложенным Ф. Нейманом и О. Мор-генштерном для конечных позиционных игр с неполной информацией [47]. Расширим пространства стратегий игроков Р и Е до так называемых смешанных кусочно-программных стратегий поведения (СКПСП), которые предполагают возможность случайного выбора управления на каждом шаге.
Пример б. Уравнения движения имеют вид
для Р:х=ы, ||и||<а,
дляЕ:у=?, NKjS, (9.3)
a>j8>0, x.yeR1, u.veR2.
Выигрыш игрока E равен p (jc (7), у (T)), где х (/), у (/) — решение системы (9.3) при начальных условиях х (t0)=x0, у (to)=yo- Игрок Р в течение игры знает лишь начальное состояние _у0 противника, а игрок Е имеет полную информацию о состоянии игрока Р(1=Т). _
Пусть ? (х, у, t) — некоторая кусочно-программная стратегия игрока Е. Для каждой стратегии ? существует стратегия и (х, t) игрока Р, использующая только информацию о начальном положении игрока Е, своем текущем положении и времени, прошедшем с момента начала игры, гарантирующая выигрыш р (х (Т), у (7))<е для 7>р (х0, уо)/(а—Р). Действительно, пусть и* (х, у, t) — стратегия игрока Р в игре с полной информацией, имеющая следующую структуру: до момента встречи t„ осуществляется погонное преследование игрока Е, а при t„^t^T точка х (/) сохраняется в некоторой
е-окрестности убегающей точки. Такая стратегия в игре с полной информацией может быть легко описана аналитически (см. пример 4 п. 8.1). Построим траектории х (/), у (/) движения игроков в ситуации (и* (х, у, І), ? (х, у, t)) из начальных состояний х0, Уо> Для этого
достаточно проинтегрировать систему
х=и* (х, у, t), X (t0)=x0,
у=? (х, у, t), у Оо)=Уо- (9.4)
По построению р (х (Т), у (Т))^е. Пусть теперь й (t) = u* (jc (t), у (t), t), и хотя стратегия и* (jc, у, t), использующая для выработки управления информацию о положении Е, недопустима, стратегия й (t) является допустимой, поскольку использует лишь информацию о времени, прошедшем с момента начала игры и о начальном состоянии игрока Е. Очевидно, что в ситуациях (й (/), ? (х, у, і)) и (и* (jc, y,J), ? (х, у, і)) траектории игроков совпадают, поскольку стратегия ? (х, у, t) одинаково реагирует как на стратегию и* (jc, у, /), так и на стратегию и (t) выбором управления ? (х (/), у (t),Jt))-
Таким образом, мы показали, что для каждой стратегии v (jc, у, t) существует программное управление й (/), являющееся допустимой стратегией в игре_ с неполной информацией, и такое, что р (* (ТЪ у (Г))^?, где х (/), у (t) — соответствующие траектории. Выбор ? (jc, у, і) произволен, поэтому отсюда следует, что
sup inf р (х (7), У (7)) = 0, (9.5)
где sup inf берется по множествам стратегии игроков в игре с неполной информацией.
Вместе с тем для любой стратегии и (х, /) игрока Р можно построить такую стратегию ? (х, у, /) игрока Е, что в ситуации (и (jc, t), ? (х, у, /)) выигрыш р игрока Е превзойдет РТ. Действительно, пусть и (jc, /) — некоторая стратегия игрока Р. Так как его движение не зависит от у (t), то траектория движения игрока Р может быть получена интегрированием системы
х=й(х, І), х (t0)=x0 (9.6)
независимо от движения игрока Е. Пусть jc (/) — траектория, получившаяся в результате интегрирования системы (9.6). Соединим точки х (Т) и уо и направим движение игрока Е по прямой [jc (7), Л]
в направлении от точки х (Т) с максимальной скоростью. Очевидно, что такое движение игрока Е обеспечивает расстояние между ним и точкой х (Т) большее или равное РТ. Обозначим построенную таким образом стратегию игрока Е через ? (і). Тогда получим, что в ситуации (и (jc, t), v (t)) выигрыш игрока Е больше или равен величине РТ. Отсюда следует, что
infsupp(x(T),y(T))>PT, (9.7)
где inf sup берется по множествам стратегий игроков в игре с неполной информацией.
Из (9.5) и (9.7) следует, что значение игры в классе чистых стратегий в рассматриваемой игре не существует.
9.4. Определение. Под смешанной кусочно-программной стратегией поведения (СКПСП) игрока Р будем понимать пару р ( ) = {т, </}, где т — произвольное разбиение отрезка времени [О, Т\ конечным числом точек 0=ti<t2<...<tk=T и d-отображение, ставящее в соответствие состоянию х (/,), у (/, — /), t, при tt>l и состоянию х (/,), у0) ti при t,^l вероятностное распределение р, (•), сосредоточенное на конечном числе измеримых программных управлений и (t) при t е [th
Аналогично под СКПСП игрока Е будем понимать пару ? ()={<х, с}, где а — произвольное разбиение отрезка времени [О, Т\ конечным числом точек 0 = t\ <t2~- <ts= Ти с-отображение, ставящее в соответствие состоянию х (/,), у (/’), t \ вероятностное распределение ? , (•), сосредоточенное на конечном числе измеримых программных управлений v (t) при t е [/,, f/+!). СКПСП игроков р и Е будем обозначать соответственно через Р и Ё (ср. со «стратегиями поведения» п. 8.3 гл. IV).
Каждая пара СКПСП р (•), ? (•) индуцирует распределение вероятностей на пространстве траекторий х (/), х (0)=хо; у (/), у (0)=у0-
Поэтому под выигрышем R (х0, у0; р (.), ? (•)) в СКПСП будем
понимать математическое ожидание выигрыша К (х0, уй\ и (•), ? (¦)),
усредненное по распределениям на пространствах траекторий, которые индуцируются СКПСП р (•), ? (•). Определив пространства стратегий Р, Ё и выигрыш R, мы определили смешанное расширение Г (х0, Уа, Т) игры Г (х0, Уа, Т).
9.5. Обозначим через СЕ (х) и С / (у) соответственно множества достижимости игроков Р и Е из начальных состояний х и у в момент времени Т, а через СЕ(у)— выпуклую оболочку множества Ср (у). Предположим, что множества достижимости компактны, и введем в рассмотрение величину
у (у, Т)= min max р (<!;, ц).
feCJOO пеС'ОО
Пусть у (у, Т)=р(у, у), где уеСЦу), уеСтЕ(у). Из определения точки у следует, что она является центром минимальной сферы, содержащей множество СЕ (у). Отсюда получаем, что эта точка единственна. В то же время существуют по крайней мере две точки касания множества СЕ (у) с минимальной содержащей его сферой, которые совпадают с точками у.
Пусть у (/) — некоторая траектория (у (0)=у0) игрока Е при
O^t^T. При перемещении игрока Е вдоль этой траектории величина у (у (/), Т—і) изменяется, меняется также и точка у. Пусть у (/) — траектория точки у, соответствующая траектории у (/). Назовем точку МвСЕ~' (уд) центром преследования, если
у (М, 0= max у (у\ [).
>'е CJ-' (уо)
9.6. Рассмотрим вспомогательную одновременную антагонистическую игру преследования на выпуклой оболочке множества Се (у). Преследователь выбирает некоторую точку ?еС? (у), а убегающий — точку JjeСе (у). Выбор совершается одновременно, и игрок Р при выборе точки ? не знает выбора т\ игрока Е, и наоборот. Игрок Е получает выигрыш р (?, т\). Обозначим значение этой игры через V (у, Т), чтобы подчеркнуть зависимость значения игры от параметров у и Т, которые определяют множества стратегий Се (у) и Се (у) игроков Р и Е. Игру в нормальной форме запишем следующим образом:
Г(у,7) = <С5(у), СЦу),р(у', у")>.
Множество стратегий минимизирующего игрока Р выпукло, функция р (у', у") также выпукла по своим аргументам и непрерывна. Для таких игр мы можем применить теорему п. 5.5 гл. П. Поэтому в игре Г (у, Т) существует ситуация равновесия в смешанных стратегиях. Оптимальная стратегия игрока Р чистая, а оптимальная стратегия игрока Е предписывает положительную вероятность не более чем (л+1) точке из множества С| (у), причем V (у, Т) = у (у, Т). Оптимальная стратегия игрока Р в игре Г (у, Т) заключается в выборе центра минимальной сферы у, содержащей множество Се (у)- Оптимальная стратегия игрока Е предписывает положительные вероятности не более чем (л+1) точке из точек касания указанной сферы с множеством С Б (у) (здесь л — размерность пространства х, у). Значение игры равно радиусу этой сферы (см. пример 11п. 5.5 гл. II).
9.7. Рассмотрим одновременную игру Г (Л/, /), где М — центр преследования. Обозначим через уі (М),..., уя+1 (М) точки из множества С‘Б(М), которые входят в спектр оптимальной смешанной стратегии игрока Е в игре Г (М, I), а через у (М) — оптимальную стратегию игрока Р в этой игре.
Определение. Траектория у* (/) называется условно-оптимальной, если у* (0)=уо, у* (Т—[)=М, у* (7)=у, (М) для некоторого
і из чисел 1, ..., л + 1.
Для каждого і может существовать несколько условно-оптимальных траекторий игрока Е.
Теорема. Пусть Т^І и для любого числа е>0 игрок Р к моменту времени Т может гарантировать е-встречу с центром у (Т) минимальной сферы, содержащей множество С‘Б(у Тогда
игра Г (х0, Уо, Т) имеет значение у (М, [), е-оптимальная стратегия
игрока Р чистая и совпадает с любой его стратегией, гарантирующей еІ2-встречу с точкой у (Т). Оптимальная стратегия игрока Е смешанная: в течение времени O^t^T—l он должен перемещаться в точку М по любой условно-оптимальной траектории у* (/) и далее с вероятностямири ...,рп+1 (оптимальная стратегия игрока Е в игре
Г (Л/, [)) выбрать одну из условно-оптимальных траекторий, переводящих точку у* (Т—І)=М в точки у, (М), /= 1, и+1, входящие
в спектр оптимальной смешанной стратегии игрока Е в игре Г (М, I).
Доказательство. Обозначим через и, (•) ?, (•) указанные в теореме стратегии, оптимальность которых требуется доказать. Для доказательства теоремы достаточно убедиться в справедливости следующих соотношений:
R (х0, У6І Ц (•), ?, (.)) + е^К (х0, ул и, (¦), ?, (•))>
> R (х0, у0; и, (•), V (•)) - Е, р (¦) g Р, V О е Е; (9.8)
lim R (х0, Уь и. (•), ?. ( )) = у (М, I). (9.9)
в~*0
Левая часть неравенства (9.8) следует из определения стратегии и, (•), в силу которого для любой кусочно-программной стратегии
и (•) е Р выполняется неравенство
R (хо, у0; и (•), ?, ( ))+e^R (хо, у0; и, (•), ?, (•)).
Обозначим через х* (/) траекторию преследователя в ситуации (и. О, ?, (•)). Тогда
R (*о, Уо, и. О, ?. (•))= ? Рір (х* (Т), у, (М)). (9.10)
і-і
Пусть R — радиус минимальной сферы, содержащей множество С'Е(М), т. е. R=y (М, I). Тогда R-e/l^p (х* (Г), у.- (M))^R+e/2
для всех /= 1, ... , и + 1, поскольку точка х* (Т) принадлежит
л+1
е/2-окрестности точки у (М). Так как ? pt= 1, 0, то из формулы
(9.10) получаем 1-1
R-e/2^R (хо, у0; и. (•), V, (-))<Л+е/2, (9.11)
что доказывает (9.9).
Пусть состояния х (7), у (Т—І) реализовались в ситуации (и, (•),
? (•)) и Q О — вероятностная мера, индуцированная на множестве С'е(у(Т—Г)). Из оптимальности смешанной стратегии р=ір\, ...,
рп+і) в игре Г (М, /) имеем
R= X Pip O' (АО. Уі ІМ))>У (у (Т-1), і)=
=?а1Г (у (Т—І), l)^ J p(y\y(T-l)],y)dQ, (9.12)
c't(y(T-Q)
где у [у (Т— /)] — центр минимальной сферы, содержащей множество С‘Е(у(Т-Г>).
Однако р (.х (Т), у [у (Т— /)])^е/2, поэтому при уеС‘Е(у (Т-1)) имеем
Р (* (Т), у)^е/2 + р (у \у (Т— I)], y)^R + е/2. (9.13)
Из неравенства (9.11)—(9.13) вытекает, что
?(*о, Ж и. О, ?, (•))> f р (х (Т), у) dQ-e, (9.14) с'г(у{т-п
однако
J Р (х (Т), у) dQ = R (хо, уо, и. (•), ? (•)). (9.15)
с'^іт-О)
Из формул (9.14) и (9.15) получаем правую часть неравенства (9.8). Теорема доказана.
При Т<1 решение игры существенно не отличается от случая Т^І и теорема сохраняет силу, если вместо С‘Е (у0), СЕ (у0) У Щ, I),
у (Т—1) рассматривать соответственно СЕ (у0), СЕ (у0), у (М, Т), у0.
При /—*0 диаметр множества СЕ(М) стремится к нулю, что, в свою очередь, вызывает стремление к нулю значения вспомогательной игры Г (М, [). Однако значение этой вспомогательной игры равно значению V, (х0, Уо, Т) игры преследования с задержкой
информации Г (х0, Уо, Т) (здесь индекс / означает время задержки
информации). Смешанная оптимальная стратегия игрока Е в Г (М, I), сосредоточивающая свою массу на не более чем л+1 точке из С‘Е (М), в пределе сосредоточивает всю массу в одной точке М, т. е. превращается в чистую стратегию. Это вполне согласуется с тем, что при /—*0 игра Г (х0, Уо, Т) превращается в игру с полной
информацией.
Пример 7. Уравнения движения имеют вид
х=и, ||м||г*а; у=?, |M|«$/J, а>/1, x.yeR2.
Пусть время Т удовлетворяет условию Т>р(х0, у0)/(а — /?) + /. Множество достижимости С‘Е (уо) = С1Е (уо) и совпадает с кругом радиуса f)l с центром у0. Значение игры Г (у, I) равно радиусу круга С‘Е(у), т. е. ?(у,!) = рІ.
Так как величина V (у, I) в данном случае не зависит от у, то любая точка множества СЕ~‘ (у0) может быть центром преследования М. Оптимальная стратегия игрока Р в игре Г (у, I) заключается в выборе точки у, а оптимальная стратегия игрока Е — смешанная и заключается в выборе двух любых диаметрально противоположных точек круга С1Е(у) с вероятностями (1/2, 1/2). В соответствии
с этим оптимальная стратегия преследователя в игре Г (х0, у0, Т)
заключается в погонном преследовании точки у (t — l) при l^t^T (при точки уо) до встречи с этой точкой, кроме того, до
момента Т следует оставаться в е/2-окрестности этой точки. Оптимальная стратегия игрока Е — смешанная кусочно-программная стратегия поведения — и заключается в переходе из точки у0 в произвольную точку МеСт?1 (уо) в течение времени Т—1, далее в равновероятном выборе направления на одну из двух диаметрально противоположных точек круга С‘Е(М). При этом ?аіГ(х0, Уо,
Т)=Р1.
Упражнения н задачи
1. Построить множество достижимости в игре «простое движение» для игрока Р и игрока Е.
2. Пусть игрок Е перемещается из точки Уо=(у°? yj) с постоянной по величине
и направлению скоростью /?. Показать, что для каждого такого движения существует единственное движение игрока Р из точки xq=(х х%) с постоянной скоростью
a (<*>/?), которое осуществляет встречу (/-встречу) с игроком Е за минимальное время. Такое движение игрока Р будем называть быстродействием в точку встречи.
3. Пусть игрок Е перемещается из точки Уо=(У°, yj) с постоянной по величине
и направлению скоростью /?, а игрок Р осуществляет быстродействие в точку встречи из точки xq=(х ° xj). Для каждой такой пары движений игроков Е и Р построить
точку встречи. Показать, что полученное геометрическое место точек встречи игроков Е и Р представляет собой окружность Апполония, и написать ее уравнение.
4. В условиях предыдущего упражнения построить множество точек /-встречи игроков Ей Р.
5. Обозначим через А (х<ь уо) множество точек встречи относительно начальных состояний хо, уо игроков Р и Е (окружность Апполония). Пусть до некоторого
момента т (т меньше времени до момента встречи) игроки Е и Р перемещаются прямолинейно с максимальными скоростями в точку встречи М. Построим новое множество точек встречи А (х (т), у (г)) относительно состояний х (г), у (т) как начальных в момент времени т. Эго некоторая новая окружность Апполония. Показать, что окружности А (хо, уо) и А (х (г), у (т)) касаются в точке М, следовательно, А (х (т), у (г)) содержатся в круге А (х0, у0), ограниченном окружностью А (х0, Уо)-
6. Пусть игрок Е перемещается из точки уо вдоль некоторой гладкой кривой у (()
с максимальной скоростью /?. Игрок Р движется с максимальной скоростью з, в каждый момент времени т зная местоположение у (г) игрока Е и направление вектора скорости «>(т)={уі (г), ?2 (т)} {dJ (t)+i>j (x)=fr}. Построим П-стратегию
игрока Р. Согласно этой стратегии он выбирает направление вектора скорости на точку встречи М в предположении, что игрок Е будет на отрезке времени [т, со) придерживаться постоянного направления движения {») (х), ?2 (т)} (перемещаться вдоль луча с постоянной скоростью Р).
Показать, что если игрок Р использует П-стратегию, то отрезок [х (т), у (т)], соединяющий текущие местоположения игроков, останется до момента встречи параллельным отрезку [х0, Уо]-
7. Пусть игрок Е перемещается из уо вдоль некоторой гладкой кривой у (х) с максимальной скоростью /?. Написать аналитическое выражение для П-стратегии игрока Р.
8. Показать, что при использовании П-стратегии игроком Р точка встречи всегда содержится во множестве А (х0, у0), ограниченном окружностью Апполония А (х0, Уо).
Указание. Доказательство провести сначала для движений игрока Е вдоль к — вершинных ломаных, используя утверждение упр. 5, а затем совершить предельный переход.
9. (Игра «шофер-убийца»). Чтобы записать уравнения движения игроков в этой игре, достаточно задать пять фазовых координат: по две координаты для обозначения местоположения игроков Р (автомобиль) и Е (пешеход) и еще одну для обозначения направления движения преследователя. Обозначим их через хь х2, Уи у2, ? (рис.
29). Задание этих фазовых координат полностью и однозначно определяет состояние игры в каждый момент.
Управление для игрока Е выглядит просто. Для описания направления его движения достаточно задать угол ф (см. рис. 29).
Теперь выберем управление для игрока Р. Проведем через точку Р прямую СС (|С'Р| = |.РС|=Я), перпендикулярную вектору скорости преследования. По своему желанию игрок Р выбирает мгновенный центр кривизны своей траектории в любой точке, например в точке С\, лежащей на этой прямой вне интервала С'С.
Управление и будем считать равным по абсолютной величине R/\PC\\, положительным для точек С], лежащих слева от Р, и отрицательным — справа от Р; таким образом, — 1 1. Доказать, что уравнения движения имеют следующий вид:
дгі=о)і sin ?, дг2 = 0)i cos ?,
Уі = о)2sin <р, у2 = о)2 cos(р, ?=а>і/Е и.
10. (Игра «шофер-убийца». Понижение размерности.) Предположим, что на плоскости выбрана подвижная система координат, связанная с автомобилем Р. Координаты пешехода у и у2 можно рассматривать в этой системе как составляющие единственного переменного вектора х; ось х2 будем считать всегда направленной
| вдоль вектора скорости автомобиля. |
 |
его скорости получаются умножением модуля соответственно на —x^d
и (*і-Rl<p)ld).
Показать, что уравнения движения имеют вид:
а>і а>і
іі == ——X2W+a>2sm^, -*2=—х\и—а>і+а)2Со$ф,
R R
— 1<и< + 1, 0<^г<2я.
11. Пусть аяЬ—такие числа, что p=>Ja2+b2>0. Показать, что max (асовф+
*
+b sin ф) достигается на таком ф, что cos ф=а/р, sin ft/р и этот максимум равен р.
12. Пусть выигрыш терминальный и уравнения движения имеют вид
jCi—eF+CBSinM, І2“— 1+0)COSM,
2я, -1<К< + 1,
где а и to — гладкие положительные функции от xt и хі-
Записать уравнение для значения игры в форме (5.64) и (5.66) и показать, что уравнение в форме (5.69) имеет вид
а«хі Р-оір-?х2=0,
где _
Px*Jvll + vl2> PeSgn®xi, »х/р. COSU= —Vylp.
Указание. Использовать упр. 11.
13. (Игра «шофер-убийца».) Записать основное уравнение в форме (6.8) и (6.10) для уравнений движения в естественном пространстве (упр. 9) и в редуцированном пространстве (упр. 10). Для ?х, ?у, ? в первом случае ввести обозначения vj, «2, из, щ,
vj, где индексы относятся к соответствующим фазовым координатам в том порядке,
в каком они появляются в уравнениях движения.
14. Найти уравнение характеристик в регрессивной форме в естественном пространстве для игры «шофер-убийца». Здесь основное уравнение (6.10) имеет вид
<о\ .
<Ві (»iSinfl+»2cos®) + a>2/,'l--»5М + 1=0,
R
где
p=-*JvJ+trJ, й= — Sgnej, йаф=?$/р, СОй<р=щ/р.
15. С помощью решения упр. 14 показать, что решение в малом игры «шофер-убийца» состоит для игрока Р из возможно более резких поворотов вправо-влево, а для игрока Е — в движении по прямой.
16. Записать и проиллюстрировать уравнение (6.6) для игры на «перетягивание»
хі =u+p, Х2=и+?, Н</>, дг(0)=дго
с терминальным выигрышем р (х (Т), А), где А — некоторая точка, AeR2, лежащая вне множества достижимости системы к моменту времени Т из начального состояния ха.
17. Записать явные выражения для оптимальных стратегий в игре упр. 16 и для ее модификации, когда продолжительность игры не фиксируется заранее, а выигрыш игрока Е полагается равным времени попадания в начало координат.
18. Доказать, что множество достижимости управляемой системы
9і=Л. Рі=<и*і~ЬРь
9((0)=9?. Р/(0)=Р?, uf+uJsSl, /-1,2 в пространстве геометрических координат {q\, qi) — круг с центром в точке
q=q°+p° (1 —е *Г)/? и радиусом Л=а (е kT+kT—l)/k2.
19. Доказать, что функция рт (q, р, г, s) удовлетворяет уравнению (6.6), записанному для данного случая.
20. Преследование происходит в плоскости, уравнения движения имеют следующий вид: для Р
qi=Pt. Рі=Щ-крРі. М«1, /=1, 2,
для Е
Уі=Р»і> Н<1, *=1. 2.
Здесь q и у — местоположения игроков Р и Е соответственно, р — импульс игрока Р. Таким образом, в рассмотренном случае игрок Е двигается согласно «простому движению», а игрок Р, представляющий собой материальную точку единичной массы, перемещается под действием силы трения а.
Выигрыш игрока определим как расстояние между геометрическими местоположениями игроков в момент окончания игры Т:
Н (9 (Г), у (Г))=р (9 (I), у (7)) = / ? (9, {Т)-у, (!T)f.
У і-1
Вычислитъ величину рт (q, у).
21. Вывести уравнение (6.6) для задачи из упр. 20.
22. Рассмотреть игру «простое преследование» с предписанной продолжительностью Т в полуплоскости F, т. е. при дополнительном предположении, что игроки в процессе преследования не могут покинуть множество F. Построить области достижимости игроков. ^
23. Вычислить величину рт (х, у) для игры «простое преследование» на полуплоскости с предписанной продолжительностью.
24. Рассмотреть антагонистическую игру «простое преследование» с предписанной продолжительностью между двумя преследователями Р={Р\, Р^, действующими как один игрок, и преследуемым игроком Е. Уравнения движения имеют следу-
ЮЩЕШ ВИД!
х‘“«Л /?<тіп{а, а2},
х2=и2, И<а2, х? х2, yeR2, у=?, М</?, и1, и2, veR2, х1 (0)=Jcj, х2 (0)=xj, у (0) =у0.
Выигрыш игрока Е равен min р{х (7), у{Т)), т. е. игрок Е заинтересован в мак-
і-1,2
симизации расстояния до ближайшего из преследователей к моменту окончания игры.
Построить множества достижимости игроков и геометрически определить мак-симинное расстояние рт(х\, х\, у) между этими множествами.
25. Обобщить теорему п. 9.7 на случай, когда в преследовании участвует несколько преследователей Рх, .... Рт, действующих как один игрок, и один
убегающий игрок Е.
Основная
а) учебники
1. Айзекс Р. Дифференциальные игры. — М.: Мир, 1967.
2. Воробьев Н. Н. Теория игр для экономистов кибернетиков. — М.: Наука, 1985.
3. Давыдов Э. Г. Методы н модели теории антагонистических игр. — М.: Изд-во МГУ, 1978.
4. Дрешер М. Стратегические игры. Теория и приложения. — М.: Сов. радио, 1964.
5. Дюбин Г. Н., Суздаль В. Г. Введение в прикладную теорию игр.— М.: Наука, 1981.
6. Карлин С. Математические методы в теории игр, программировании и экономике. — М.: Мир, 1964.
7. Красовский Н. Н. Управление динамической системой. Задача о минимуме гарантированного результата — М.: Наука, 1985.
8. Крушевский А. В. Теория игр. — Киев: Вища школа, 1977.
9. Мак-Кинси Дж. Введение в теорию игр. — М.: Физматтиз, 1960.
10. Мулен Э. Теория игр. С примерами из математической экономики. — М.: Мир, 1985.
И. Оуэн Г. Теория игр. — М.: Мир, 1971.
12. Петросян Л. А. Дифференциальные игры преследования. — Л.: Изд-во ЛГУ, 1977.
б) сборники задач
13. Коваленко А. А. Сборник задач по теории игр. — Львов: Вшца школа, 1974.
14. Морозов В. В., Сухарев А. Г., Федоров В. В. Исследование операций в задачах и упражнениях. — М.: Высшая школа, 1986.
Дополнительная
в) монографии и учебные пособия
15. Ауман Р., Шепли Л. Значение для неатомических игр. — М.: Мир, 1977.
16. Ашманов С. А. Линейное программирование. — М.: Наука. 1981.
17. Берж К. Общая теория игр нескольких лиц. — М.: Физматтиз, 1961.
18. Беленький В. 3., Волконский В. А., Иванков С. А., Поманский А. Б., Шапиро А. Д. Итеративные методы в теории игр и программировании. — М.: Наука, 1974.
19. Блекуэлл Д., Гиршик М. Теория игр и статистических решений. — М.: ИЛ, 1958.
20. Бондарева О. Н. О теоретико-игровых моделях в экономике. — Л.: Изд-во ЛГУ, 1974.
21. Вайсборд Э. М., Жуковский В. И. Введение в дифференциальные игры нескольких лиц и их приложения. — М.: Сов. радио, 1980.
22. Вилкас Э. Й., Майминас Е. 3. Решение: теория, информация, моделирование. — М.: Радио и связь, 1981.
23. Воробьев Н. Н. Основы теории игр. Бескоалиционные игры. — М.: Наука, 1984.
24. Гаврилов В. М. Оптимальные процессы в конфликтных ситуациях. — М.: Сов. радио, 1969.
25. Гейл Д. Теория линейных экономических моделей. — М.: ИЛ, 1963.
26. Гермейер Ю. Б. Игры с непротивоположными интересами. — М.: Наука, 1976.
27. Горелик В. Д., Кононенко А. Ф. Теоретико-игровые модели принятия решений в эколого-экономических системах. — М.: Наука, 1982.
28. Григоренко Н. Л. Дифференциальные игры преследования несколькими объектами. — М.: Изд-во МГУ, 1983.
29. Данилов Н. Н. Игровые модели принятия решений. — Кемерово: Изд-во КГУ, 1981.
30. Данскин Дж. Теория максимина. — М.: Сов. радио, 1970.
31. Демьянов В. Ф., Малоземов В. Н. Введение в минимакс. — М.: Наука, 1972.
32. Жуковский В. И., Тынянский Н. Т. Равновесные управления многокритериальных динамических систем. — М.: Изд-во МГУ, 1984.
33. Зубов В. И. Динамика управляемых систем. — М., 1982.
34. Зубов В. И., Петросян Л. А. Математические методы в планировании. — Л.: Изд-во ЛГУ, 1982.
35. Карлин С. Сведение некоторых классов игр к интегральным уравнениям/Сб. ст. [СЗ].
36. Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа. — М.: Наука, 1981.
37. Кондратьев А. И. Теоретико-игровые модели в задачах распознавания. — М.: Наука, 1986.
38. Кононенко А. Ф. О равновесных позиционных стратегиях в неантагонистических дифференциальных играх//ДАН СССР. 1976. 231 № 2. С. 285 — 288.
39. Красовский Н. Н. Игровые задачи о встрече движений. — М.: Наука, 1970.
40. Красовский Н. Н., Субботин А. И. Позиционные дифференциальные игры. — М.: Наука, 1974.
41. Куржанский А. Б. Управление и наблюдение в условиях неопределенности. — М.: Наука, 1977.
42. Кукушкин Н. Н., Морозов В. В. Теория неантагонистических игр. — М.: Изд-во МГУ, 1977.
43. Лагунов В. Н. Введение и дифференциальные игры. Вильнюс. 1979.
44. Льюис Р. и Райфа X. Игры и решения. Введение и критический обзор.— М.: ИЛ, 1961.
45. Малафеев О. А. О существовании ситуации равновесия в дифференциальных
бескоалиционных играх двух лиц с независимыми движениями //Вестник ЛГУ 1980. № 7. С. 12 - 16. ’ ’
46. Моисеев Н. Н. Математические задачи системного анализа. М., 1981.
47. Фон Нейман Дж., Моргенштейн О. Теория игр и экономическое поведение.— М.: Наука. 1970.
48. Никольский М. С. Первый пряьДй метод Л. С. Понтрягина в дифференциальных играх.— М.: Изд-во МГУ, 1984.
49. Партхасаратхи Т., Рагхаван Т. Некоторые вопросы теории игр двух лиц.— М.: Мир, 1974.
50. Пек Дж., Э. Л. Далмидж А. Л. Игры на компактном множестве/Сб. ст. fC. 3].
51. Петросян Л. А., Данилов Н. Н. Кооперативные дифференциальные игры и их приложения.— Томск: Изд-во ТГУ, 1985.
52. Петросян Л. А., Захаров В. В. Введение в математическую экологию.— Л.: Изд-во ЛГУ, 1986.
53. Петросян Л. А., Зенкевич Н. А. Оптимальный поиск в условиях конфликта.— Л.; Изд-во ЛГУ, 1987.
54. Петросян Л. А., Томский Г. В. Динамические игры и их приложения.— Л.: Изд-во ЛГУ, 1982.
55. Петросян Л. А., Томский Г. В. Геометрия простого преследования. — Новосибирск.: Наука, сиб. отд., 1983.
56. Подиновский В. В., Ногин В. Д. — Парето-оптимальные решения многокритериальных задач. — М.: Наука, 1982.
57. Понтрягин Л. С., Болтянский В. Г., Гамкрелидзе Р. В., Мищенко Е. Ф. Математическая теория оптимальных процессов. — М.: Наука, 1976.
58. Понтрягин Л. С. К теории дифференциальных игр//Успехи математических наук, 1966. Т. 21. Вып. 4. С. 219 — 274.
59. Понтрягин Л. С. Линейная дифференциальная игра убегания//Труды МИАН СССР, 1971. Т. 112. С. 30 — 63.
60. Понтрягин Л. С. Линейные дифференциальные игры преследования. Математический сборник. Новая серия, 1980. Т. 112. Вып. 3. С. 307 — 330.
61. Пшеничный Б. Н. Выпуклый анализ и экстремальные задачи. — М.: Наука, 1980.
62. Розенмюллер Н. Кооперативные игры и рынки. — М.: Мир, 1974.
63. Рокафеллар Р. Выпуклый анализ. — М.: Мир, 1973.
64. Робинсон Дж. Итеративный метод решения игр/Сб. ст. [С 1, С. НО — 118].
65. Садовский А. Л. Монотонный итеративный алгоритм решения матричных игр//ДАН СССР, 1978. Т. 238. № 3, С. 538 — 540.
66. Сайон М. Некоторые общие теоремы о минимаксах/Сб. ст. [С. 3. С. 40 — 46].
67. Сайон М., Вульф Ф. Об игре, не обладающей значением/Сб. ст. [С. 4. С. 290 — 300].
68. Сансоне Дж. Обыкновенные дифференциальные уравнения. — М.: ИЛ, 1954. Т. 2.
69. Субботин А. И., Ченцов А. Г. Оптимизация гарантии в задачах управления. — М.: Наука, 1981.
70. Смольяков Э. Р. Равновесные модели при несовпадающих интересах участников. — М.: Наука, 1986.
71. Суздаль В. Г. Теория игр для флота. — М.: Воениздат, 1976.
72. Феллер В. Введение в теорию вероятностей и ее приложения. Т. 1,2. — М.: Мир, 1984.
73. Ху Т. Целочисленное программирование и потоки в сетях. — М.: Мир, 1974.
74. Черноусысо Ф. Л., Меликян А. А. Игровые задачи управления и поиска. — М.: Наука, 1978.
75. Яновская Е. Б. О существовании значения антагонистических игр с полунепрерывными функциями выигрыша//Изв. АН СССР. Техн. киберн., 1973. № 6. С. 56 — 60.
76. Зенкевич Н. А., Еськова В. А. Конечные антагонистические игры. Кемерово, Изд-во Кемеровского ГУ, 1989.
77. Зенкевич Н. А., Ширяев В. Д. Игры со многими участниками. Саранск, Изд-во Мордовского ГУ, 1989.
78. Данилов Н. Н., Зенкевич Н. А. Неантагонистические игры двух лиц. Кемеро-вов, Изд-во Кемеровского ГУ, 1990. — 99 с.
79. Петросян Л. А., Гарнаев А. Ю. Игры поиска. СПБ.: Изд-во Санкт-Петербургского ун-та, 1992.
80. Arunabha Bagchi. Stackelberg Diflerentai Games in Economic Models. — Springerg — Veriag, 1984.
81. Basar T., Olsder I. Dynamic Noncooperative Game Theory. — London, Acad. Press, 1982.
82. Friedman A. Differential Games. — N. Y., John Wiley, 1971.
83. Owen G. Game Theory. Second Edition. Acad. Press, 1982.
84. Bierman N. S., Fernandez L. Game theory nith economic applications. Addison — Wesley Publishing Company, INC, USA, 1993.
85. Brams S. J. Theory of Moves. Cambridge University Press, 1994.
86. Fudenberg D., Tirole J. Game theory. MIT Press, Cambridge, Massachusetts, London, England. 1992.
87. Giblons R. Game theory for applied economists. Princeton University Press, Princeton, New gersey, 1992.
88. Harsanyi J. C., Selten R. A. General Theory of Eguilibrium Selection in Games. The MIT Press, Cambridge, Massachusetts, London, England. 1989.
89. Myerson R. B. Game Theory. Analysis of Conflict. Harvard University Press. Cambridge, Massachusetts, London, England, 1991.
90. Petrosjan L. A. Differential Games of Pursuit. World Scientific Publishing Co. Pte Ltd. London, Singapore, 1993.
91. Van Damme, EES. Stability and Perfection of Nash Eguilibria. Springer — Verbag, Berlin, №. 9. 1991.
92. Weibull J. W. Evolutionary Game Theory. MIT Press, Cambridge, Massachusetts, London, England. 1995.
Специальная
г) справочники и обзоры
93. Теория игр. Аннотированный указатель публикаций по 1968 г. — Л.: Наука, 1976.
94. Теория игр. Аннотированный указатель публикаций отечественной и зарубежной литературы за 1969 — 1974 гг. — Л.: Наука, 1980.
298
95. Воробьев Н. Н. Современное состояние теории игр//Успехи мат. наук, 1970. 25. № 2. С. 81 — 140.
96. Воробьев Н. Н. Бескоалиционные игры/В кн.: Проблемы кибернетики. Выл.
33. М., 1978. С. 69 — 90.
97. Петросян Л. А., Томский Г. В. Динамические игры//Изв. АН СССР. Техн. киберн. № 2. 1983. С. 33 — 50.
98. Прохоров Ю. В., Рязанов Ю. А. Теория вероятностей. Основные понятия. Предельные теоремы. Случайные процессы. — М.: Наука, 1967.
99. Соболев А. И. Кооперативные игры. — Проблемы кибернетики. Выл. 39. М., 1982. С. 201 — 222.
100. Тынянский Н. Т, Жуковский В. И. Дифференциальные игры с ненулевой суммой (бескоалиционный вариант)/ В кн.: Итоги науки и техники: Математический анализ. — М.: ВИНИТИ, 1977. Т. 15. С. 199 — 266.
101. Тынянский Н. Г., Жуковский В. И. Дифференциальные игры с ненулевой суммой (кооперативный вариант)/В кн.: Итоги науки и техники: Математический анализ. — М.: ВИНИТИ, 1979. Т. 17. С. 3 — 112.
102. Яновская Е. Б. Бесконечные антагонистические игры/В кн: Теория вероятностей. Математическая статистика. Математическая кибернетика. Т. 10. М., 1972. С. 75 — 106.
103. Яновская Е. Б. Антагонистические игры/В кн.: Проблемы кибернетики. Вып.
34. — М.: Наука, 1978. С. 221 — 246.
104. Дифференциальные игры: Указатель русской и иностранной литературы за 1968 — 1974 гг. Свердловск: Уральск, научи центр, 1978.
105. Дифференциальные игры со многими участниками: Указатель литературы за 1968 — 1983 гг. — Русе: НРБ, 1985.
д) сборники статей
С1. Матричные игры/Ред. Н. Н. Воробьев. — М.: Физматгиз, 1961.
С2. Применение теории игр в военном деле/Ред. В. О. Ашкенази. — М.: Сов. радио, 1961.
СЗ. Бесконечные антагонистические игры/Ред. Н. Н. Воробьев. — М.: Физматгиз, 1963.
С4. Позиционные игры/Ред. Н. Н. Воробьев и Н. Н. Врублевская. — М.: Наука, 1967.
С5. Теория игр. Доклады на 1 Всесоюзной конференции по теории игр. Ереван, 1968/Ред. Н. Н. Воробьев. — Ереван: Изд-во АН Арм ССР, 1973.
С6. Успехи теории игр. Труды 11 Всесоюзной конференции по теории игр. Вильнюс, 1971/Ред. Э. Вилкас. — Вильнюс: Минтис, 1971.
С7. Теоретико-игровые вопросы принятия решений: Сб. статей. Ин-т сод-эк. проблем АН СССР/Ред. Н. Н. Воробьев. — Л.: Наука, 1978.
С8. The Shapley value: essays in honor of Lloyd S. Shapley/edited by Alvin E. Roth. Cambridge University Press. — 1988.
C9. Game Theory and Applications: vol. 1/edited by Petrosjan L. A., Mazalov V. V. Nova Science Publishers, Inc.; №.9. — 1995.
CIO. Game Theory and Applications: vol. 2/edited by Petrosjan L. A., Mazalov V. V. Nova Science Pyblishers, Inc.; №.9. — 1996.
Использованная литература
1. Айзекс Р. Дифференциальные игры. М., 1967.
2. Воробьев Н. Н. Теория игр для экономистов-кибернетиков. М., 1985.
3. Дюбин Г. Н., Суздаль В. Г. Введение в прикладную теорию игр. М., 1981.
4. Карлин С. Математические методы в теории игр, программировании и экономике. М., 1964.
5. Мак-Кинси Дж. Введение в теорию игр. М., 1960.
6. Мулен Э. Теория игр. М., 1985.
7. Оуэн Г. Теория игр. М., 1971.
8. Петросян JI. А. Дифференциальные игры преследования. Л., 1977.
9. Коваленко А. А. Сборник задач по теории игр. Львов, 1974.
10. Морозов В. В., Сухарев А. Г., Федоров В. В. Исследование операций в задачах н упражнениях. М., 1986.
11. Ашманов С. А. Линейное программирование. М., 1981.
12. Воробьев Н. Н. Основы теории игр. Бескоалиционные игры. М., 1984.
13. Гейл Д. Теория линейных экономических моделей. М., 1963.
14. Льюис Р., Райфа X. Игры и решения. М., 1961.
15. Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа. М., 1981.
16. Партхасаратхи Т., Рагхаван Т. Некоторые вопросы теории игр двух лиц. М., 1974.
17. Петросян Л. А., Данилов Н. Н. Кооперативные дифференциальные игры и их приложения. Томск, 1985.
18. Петросян Л. А., Захаров В. В. Введение в математическую экологию. Л., 1986.
19. Петросян Л. А., Зенкевич Н. А. Оптимальный поиск в условиях конфликта. Л., 1987.
20. Петросян Л. А., Томский Г. В. Геометрия простого преследования.
21. Рокафеллар Р. Выпуклый анализ. — М.: Мир. 1973.
22. Садовский А. Л. Монотонный итеративный алгоритм решения матричных игр//ДАН СССР,1978. 238. № з. С. 538—540.
23. Сансоне Дж. Обыкновенные дифференциальные уравнения. М., 1954.
24. Феллер В. Введение в теорию вероятностей и ее приложения. Т. 1, 2. М., 1984.
25. Ху Т. Целочисленное программирование и потоки в сетях. М., 1974.
26. Owen G. Game Theory. Second Edition. Acad, Press, 1982.
Учебное издание
Петросян Леон Аганесович, Зенкевич Николай Анатольевич, Семина Елена Александровна
ТЕОРИЯ ИГР
Редактор Яковлева Ж. И.
Художественный редактор Иванова Ю. Э.
Художник Орлова М. О.
Технический редактор Романова В. М.
Корректор Кожуткина В. В.
Оператор Новоселова В. Н.
ЛР № 010146 or 25Л2.96 ЛР № 065329 от 06.08.97
Изд. № ФМ-960 Сдано в набор 09.02.93. Поди, в печать 28 10.97 Формат 60х90'/|6- Бумаіа офс. № 1. Гарниіура Литературная Печать офсетная. Объем 18,62 уел печ. л , 18,87 уел. кр -отт., 17,34. уч.-изд. л. Тираж 10000 экз. Заказ № 1699
Издательство «Высшая школа», 101430, Москва, ГСП-4, Неглинная ул., д. 29/14 Набрано на персональном компьютере издательства
ООО «Книжным дом «Университет», 117234, Москва, Воробьевы юры, ГЗ МГУ, Сектор Д, коми. 4 Тел.' 938-21-84, 939-45-81
Отпечатано в тииоірафии издательства «Дом печати 432601, і. Ульяновск, ул. Гончарова, 14
Воробъев Н. Н. Философская энциклопедия. Т. 5. М., 1970. С. 208—210.
См., например: Сантало Л. А. Интегральная геометрия и геометрические вероятности. М., 1983.
Речь идет о «золотых рублях».
 Экономика: Знания - Циклы - Макроэкономика
Экономика: Знания - Циклы - Макроэкономика
- Введение в экономику
- Виды экономик
- Экология в экономике
- Экономическая теория
- Экономическая география
- Экономические знания
- Экономика России
- Циклы в экономике
- Макроэкономика
- Макроэкономика в России