Математика опционов

Рынок опционов считается чрезвычайно “темным” и запутанным сегментом фондового рынка даже среди профессиональных трейдеров, не говоря уже об индивидуальных инвесторах, не имеющих значительного опыта ведения торгов. Однако на самом деле эта наука не так сложна, как кажется, и многие рядовые инвесторы извлекают немалые прибыли из повседневной торговли опционами.
Опцион (option) является производным финансовым инструментом, или деривативом. Это означает, что его стоимость является производной от стоимости другого финансового инструмента, лежащего в его основе. В качестве инструмента, лежащего в основе опциона, могут выступать акции, облигации, валюта, ставки процента, биржевые индексы, фьючерсные контракты (далее будем рассматривать преимущественно опционы на акции). Торговля опционами на акции началась в 1973 г. на Чикагской бирже опционов (Chicago Board Options Exchange, CBOE), и сейчас они являются наиболее распространенными опционными контрактами. В самой общей форме опцион представляет собой контракт между двумя сторонами – продавцом (seller, writer) и покупателем (buyer, holder), дающий за определенную премию право (но не налагающий обязательства) купить или продать определенный финансовый инструмент, лежащий в основе данного контракта, по фиксированной цене в течение заранее установленного срока.

При характеристике опционов используются пять основных показателей:
1. Вид опциона (“call” или “put”)
2. Активы, лежащие в основе опциона
3. Цена исполнения
4. Дата истечения срока опциона
5. Опционная премия

Торгуемые на рынке опционы можно покупать или продавать по цене, представляющей долю от стоимости финансовых инструментов, лежащих в их основе. При этом продаются и покупаются не сами финансовые инструменты, а только возможность купить или продать их по определенной цене, представляющей собой цену исполнения опциона. Следует отметить, что опционы существуют не на все акции, т.е., другими словами, не все акции являются опционными.

"Производные" А-опционов

На основе введенных A-опционов можно строить многие другие инструменты, определяемые произвольными платежными функциями, зависящими от траектории движения цены базового актива. При этом, вообще говоря, вовсе не обязательно для каждого EÎR_n требовать присутствия на рынке всех 2ⁿ A-опционов. Как и в однопериодном случае, достаточно, чтобы множество страйков, для которых определен хотя бы один тип A-опциона, совпадало с R_n. Это позволяет отказаться от присутствия на рынке A-опционов, являющихся аналогом выигрышных опционов для однопериодного рынка, когда, например, вектора E и a таковы, что функция a, определяемая равенством (8), принимает положительные значения с близкой к 1 вероятностью.
Как и для однопериодных опционов колл и пут, можно рассмотреть "первые и вторые производные" A-опционов A(E; a) для многопериодного случая. Их мы будем обозначать A'(E; a) и A"(E; a) соответственно. Однако следует иметь в виду, что такие обозначения условны. На самом деле здесь речь идет о производных A(E; a) порядка n и 2n по всем страйкам (по каждому страйку – первого и второго порядка) соответственно, т.е. под этими обозначениями понимаются соответственно

.

Аналогичное соглашение действует и для обозначения стоимости "производных" A-опционов и платежных функций этих "производных".
Нетрудно проверить, что каждой "первой производной" по страйку E от A-опциона с некоторым вектором a в точке E отвечает платежная функция (по x)


Аналогично для получения "вторых производных" следует брать смешанные производные по всем страйкам, но уже по каждому – вторую. Нетрудно видеть, что платежные функции "вторых производных" всех типов A-опционов с одинаковым векторным страйком E совпадают между собой и являются n-мерными дельта-функциями относительно E, т.е. для любого вектора a инструмент "дельта-функция" определяется равенством



Отметим, что именно совпадение "вторых производных" всех типов A-опционов между собой делает необязательным их одновременное присутствие на теоретическом рынке для любого E.
С помощью "дельта-функции" D(E₁, E₂,…, E_n) формальное представление инструмента G{g(x)} с произвольной платежной функцией n переменных g(x) = g(x₁, x₂,…, x_n) можно задать в виде



Очевидно, что обычный n-периодный опцион может быть рассмотрен как частный случай зависящего от пути n-периодного опциона и потому получен из A-опционов (например, использованием формулы (12)). Менее очевидна связь опционов с разными сроками действия. Имеет смысл сопоставить зависящие от пути n-периодные опционы с зависящими от пути k-периодными опционами, k < n, и, в частности, с обычными k-периодными опционами, для которых платежная функция определяется лишь ценой актива в момент времени t = k.
Отметим следующее. Для репликации k-периодных опционов с помощью n-периодных зависящих от пути опционов можно, исходя из платежных функций n-периодных зависящих от пути опционов, построить функции n переменных, фактически зависящие лишь от первых k переменных. Это всегда можно сделать, используя введенные "производные" от базисных n-периодных A-опционов. Поэтому может показаться, что эти функции могут служить платежными функциями k-периодных опционов и что, следовательно, задача реализации k-периодных опционов из n-периодных опционов, в принципе, разрешима.
Однако это не совсем так. Различие, и неустранимое, все же остается. Оно состоит в сроках расчета по опционам. По k-периодным опционам расчет производится в момент k, а по n-периодным – в момент n. Можно сказать, что зависящий от пути n-периодный опцион с платежной функцией, определяемой ценами актива в моменты времени t £ k, идентичен некоторому зависящему от пути (или обычному) опциону с k-периодным сроком действия, но с задержкой расчетов до окончания процесса инвестирования (t = n), и потому требует учета накопленных процентов.
Тем не менее, когда на рынке присутствуют зависящие от пути (или обычные) опционы с разными сроками действия, их стоимости должны быть некоторым образом согласованы – иначе возможен временной арбитраж! Далее эта согласованность будет уточнена.

Ценообразование А-опционов и их "производных" на нейтральном к риску рынке

Если предполагать рынок нейтральным к риску, то аналогично однопериодному случаю можно предложить формулу ценообразования A-опционов. Так, для варианта A-опциона с вектором a°, все компоненты которого равны +1, естественно положить


Г
де r – относительный доход от инвестиции за весь горизонт инвестирования.
Дифференцируя по всем переменным x_i однократно и двукратно, получим стоимости "первой производной" и "второй производной" этого A-опциона соответственно (еще раз подчеркнем, что фактически речь идет о смешанных производных n-го и 2n-го порядков соответственно):


и


Из равенства (13) нетрудно получить соотношение, обобщающее формулу (2) из [1], задающую стоимость опциона пут через функцию распределения цены актива. Если обозначить через R_n(E) квадрант {x x_i £ E_i, i Î T} n-мерного евклидова пространства R_n, то равенство (13) можно записать в виде

Наведенная совместная плотность вероятности и наведенные безрисковые ставки

Остается вспомнить, что в силу обоснованно предполагаемой согласованности цен A-опционов (в случае, если области существования котировок разных A-опционов перекрываются) и функция f_m(x), и параметр



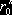
в сочетании с формулой (12) дает соотношение


означающее, что нормировочный коэффициент
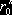
Далее, зависящие от пути опционы со сроками действия меньше n, которые также могут присутствовать на рынке (и такую возможность мы будем предполагать), определяют свои наведенную рынком совместную плотность вероятности f_m(x), x = (x₁, x₂,…, x_k), k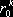, но они ничего не говорят о распределении наращивания этого дохода по периодам. Поэтому для полноты n-периодного рынка следовало бы потребовать, чтобы на нем котировались A-опционы всех сроков действия k £ n.
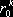
По совокупности наведенных рыночных спотовых безрисковых относительных доходов 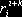за интервал длительности k периодов через i периодов от начального момента времени t = 0 (т.е. отсчитывая интервал от момента t = i) составит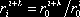




Отметим, что наведенные совместные плотности вероятности, соответствующие различным временным горизонтам, должны быть согласованы между собой. Именно из условия невозможности арбитража вытекает, что должно быть выполнено рекуррентное по k < n соотношение



Действительно, как следует из соотношения (16), обе наведенные плотности, входящие в эту формулу, означают стоимость инструмента D(E₁, E₂,…, E_k), помноженную на 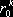₁, E₂,…, E_k+1), помноженную на 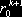_k+1 дает стоимость первого инструмента, но с отсрочкой платежа по нему на один период. Условие недопущения арбитража требует, чтобы эти стоимости различались множителем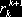 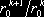. Последнее обстоятельство и подтверждает справедливость предположения (18).
Соотношение (18) означает, что система наведенных совместных плотностей вероятности обладает свойством согласованности, присущим системам обычных совместных плотностей. Кроме того, оно же говорит о том, что в n-периодных зависящих от пути опционах содержится почти вся информация относительно распределения вероятностей для последовательности цен базового актива длины n, за исключением лишь информации о последовательности безрисковых относительных доходов за отдельные периоды всего интервала инвестирования. Кстати, очевидно также, что для полноты рынка вовсе не нужно требовать наличия на рынке зависящих от пути опционов сроков действия меньше n – достаточно обычных k-периодных опционов для всех k Безопасность жизнедеятельности

Оптимальное поведение инвестора со своим взглядом на свойства рынка

Теперь нам надлежит обратиться к предпочтениям инвестора. Как и в случае однопериодного рынка, будем предполагать, что инвестор имеет свой взгляд на распределение вероятностей движения цены базового актива. Считаем, что это распределение имеет совместную n-мерную плотность, равную f_t(x). Как и ранее, вводим отношения правдоподобия (теперь уже многомерные)





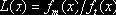
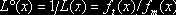
Средний доход инвестора принимает наибольшее значение при векторном страйке E_max, доставляющем наибольшее значение функции правдоподобия L°. Через E_min обозначается векторный страйк, доставляющий L° минимум (или L – максимум). Инструментом, обеспечивающим решение этой задачи, служит инструмент D(E_max). И снова использование короткой позиции по инструменту D(E_min) может неограниченно увеличить средний доход инвестора.
Решение задачи нахождения условного максимума ищется применением многомерной процедуры Неймана-Пирсона аналогично одномерному случаю.

О многопериодных опционах американского типа

До сих пор речь шла исключительно об опционах европейского типа, т.е. таких, исполнение которых могло происходить только при истечении срока – последний момент рассматриваемого горизонта времени (в момент n для n-периодных опционов). Интересно было бы распространить предлагаемую методику на опционы и американского типа, исполнение которых допускается в произвольный момент в течение жизни опциона по желанию его владельца. Однако на этом пути возникают трудности. Поясним это некоторыми рассуждениями.
В случае опционов американского типа инструмент D (d-функция) следует задавать не одной, а n платежными функциями, размерности которых последовательно возрастают – {d_k}_k=1,…,n. При этом возможны разновидности этого инструмента в зависимости от вариантов платежных функций. Рассмотрим сначала разновидность инструмента, когда эти функции фактически зависят лишь от последнего аргумента. Тогда d_k(x₁, x₂,…, x_k) = d(x_k–E_k) (одномерная d-функция), и для любого k имеет место



Действительно, при n=2 мы имеем дело с набором (x₀, x₁, x₂), образованным последовательными ценами базового актива. Обозначим через t момент исполнения опциона. Очевидно, что исполнение опциона произойдет в момент t = 1, если выполнится условие d(x₁–E₁) > D(E₂x₁)/r₂ = f(E₂x₁)/r₂, т.е. если x₁ = E₁, иначе t = 2. (Здесь под D(E₂x₁) следует понимать инструмент, который можно назвать "условной d-функцией"; его платежная функция строится очевидным образом.) Поэтому доход в момент t = 1 будет равен max{d(x₁–E₁), f(E₂x₁)/r₂}. И, следовательно, в момент t = 0 стоимость рассматриваемого инструмента определяется равенством



Для проверки выполнимости (19) для произвольного n применяется индукция.
Теперь рассмотрим другую разновидность инструмента "d-функция" (за ним сохраним прежнее обозначение), когда k-мерные платежные функции существенно зависят от всех переменных. В этом случае функции {d_k}_k=1,…,n задаются равенствами d_k(x₁, x₂,…, x_k) = d(x₁–E₁)d(x₂–E₂)…d(x_k–E_k). Аналогично предыдущему случаю можно показать, что



Далее, можно рассмотреть и вопросы ценообразования для инструментов типа колл и пут. Однако проблема в том, что цены этих инструментов не удается выразить через стоимости инструментов типа "d-функций" – в случае опционов американского типа нарушается свойство аддитивности цен. Так, для первой разновидности инструментов D, когда справедливы соотношения (19), а не (20), инструмент C (колл) должен будет задаваться системой функций c_k(x₁, x₂,…, x_k) = (x_k–E_k)⁺ = max(x_k–E_k, 0) для всех k = 1, 2,…, n.


Для такого опциона ценообразование при n = 2 проводится на основе следующего рассуждения. В момент t = 1 доход от опциона равен max{(x₁–E₁)⁺, C(E₂x₁)/r₂}. Поэтому исполнение опциона произойдет в момент t = 1, если максимален первый аргумент, и в момент t = 2, если – второй. Критическое (пограничное) значение x^* находится из условия равенства обоих аргументов, т.е. из соотношения x^*–E₁ = C(E₂x^*)/r₂. Окончательно, в момент t = 0 стоимость инструмента C равна




Очевидно, эту процедуру можно продолжить для нахождения стоимости колла для произвольного n. Кроме того, аналогичную процедуру можно применить и для определения стоимости пута. Но также очевидно и то, что эти стоимости (в отличие от случая опционов европейского типа) нельзя получить подходящим взвешенным интегрированием стоимостей "d-функций". Потому для опционов американского типа и не удается построить процедуру нахождения "оптимального" портфеля инвестора методом, аналогичным рассмотренному в данной работе. И в этом смысле вопрос остается открытым.
В заключение отметим, что, используя цены "d-функций", можно восстанавливать вероятностные распределения для цен базового актива. Однако если на рынке торгуются "d-функции", удовлетворяющие соотношению (19), то восстанавливаются лишь маргинальные плотности вероятности. При этом



Если же на рынке присутствуют "d-функции", цены которых определяются равенствами (20), то можно восстановить и совместные плотности вероятности по формуле

Нейтральный к риску рынок опционов

Рассматривается однопериодный рынок опционов, на котором обращаются традиционные инструменты, такие как опционы колл C(E) и пут P(E) со страйком E и ценами C(E) и P(E), сложившимися на рынке на начало периода соответственно: C(E) = C(E), P(E) = P(E) (для цены произвольного инструмента G используется обозначение G). Считаем, что страйк E, для которого задаются эти инструменты, в теоретической конструкции пробегает множество всех вещественных чисел. В работах [1,2] было показано, что на нейтральном к риску рынке при условии, что функция распределения F(x) при x ® ±¥ достаточно быстро стремится к своим предельным значениям (при наличии у функции распределения будущей цены актива абсолютного первого момента), справедливы соотношения




где r – безрисковый относительный доход.
Наряду с ними рассматриваются и производные инструменты, такие как "первые производные" и "вторые производные" колла и пута по страйку – C'(E), C"(E), P'(E) и P"(E). Операционные издержки не учитываются. Поэтому естественно, что стоимость линейной комбинации (также бесконечной) опционов равна соответствующей линейной комбинации стоимостей составляющих комбинацию опционов.


Следовательно, имеют место соотношения

,
.

при этом




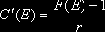
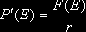
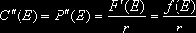
(1)
Последнее соотношение означает, что при r = 1 вторая производная стоимости опционов колл и пут по страйку совпадает с плотностью вероятности будущей цены актива. Также используются обозначения D(E) и I(X) для инструментов, платежными функциями которых служат дельта-функция относительно точки E и характеристическая функция (индикатор) множества X соответственно. При этом "единичный" безрисковый инструмент U = I(R). Кроме того, очевидно, что D(E) = C"(E) = P"(E).
Эти соотношения в работе [1] используются для построения процедуры нахождения оптимального поведения инвестора на однопериодном рынке опционов.

Наведенная рынком плотность вероятности будущей цены актива

Далее мы будем считать, что введенные в предыдущем разделе вероятностные характеристики будущей цены базового актива нам неизвестны. Если оставаться в условиях нейтрального к риску рынка, то по формуле (1) можно было бы восстанавливать плотность вероятности f(x) (с одновременным определением и параметра r). Но теперь мы желаем отказаться от предположения нейтральности к риску рынка. Тем самым мы признаем, что формулы предыдущего раздела не выполняются (во всяком случае, они не дают точного значения стоимости опционов) и восстановить по ним точно f(x) невозможно.
Поэтому далее для решения проблем инвестора мы оставляем в стороне вопросы ценообразования опционов. Оказывается, что для целей нахождения оптимального портфеля инвестора нет необходимости знать работу механизма ценообразования. Достаточно просто знать сами цены опционов. Однако подчеркнем еще раз, что для решения задачи в ее теоретической полноте потребуется предположение о наличии на рынке опционов со страйками из множества всех вещественных чисел (эти страйки будут многомерными в случае многопериодных опционов).
Итак, сложившиеся на начало периода цены опционов будем воспринимать как данность. Конечно, они должны удовлетворять определенным свойствам, вытекающим из общего финансового принципа недопустимости арбитража.
Из формулы (1) следует, что



Хотя инструменты C"(E) и P"(E) получены различными способами, естественно считать, что их стоимости совпадают, так как в противном случае был бы возможен арбитраж. Итак, имеем



Поскольку инструменту D(E) отвечает неотрицательная платежная функция, то его стоимость не может быть отрицательной, т.е.



Следовательно, цены колла и пута как функции страйка – выпуклы.


Вводится нормировочный множитель r равенством



Тогда функция



неотрицательна и интеграл от нее по всей вещественной прямой равен 1, т.е. ее можно рассматривать как плотность вероятности. Эту плотность естественно называть наведенной рынком плотностью вероятности цены базового актива. Индекс m подчеркивает рыночное происхождение этой плотности вероятности. При этом параметр r можно считать аналогом относительного дохода за период, т.е. r – наведенный относительный доход за период, а r–1 – наведенная доходность.
Следует подчеркнуть, что хотя мы в данном и предыдущем разделах используем одно и то же обозначение для относительного дохода r, он несет теперь иную смысловую нагрузку. В предыдущем разделе этот параметр задается экзогенно, в то время как в настоящем разделе он получен по ценам рынка.
Стоимость "индикатора" множества X



и потому



Таким образом, стоимость безрискового актива равна 1/r, и параметр r совпадает с безрисковым относительным доходом (а r–1 – с безрисковой доходностью).
Концепция обеспечения безопасности информации в системе организации

Задачи инвестора опционного рынка и способы их решения

Будем предполагать, что инвестор имеет собственное представление относительно распределения вероятностей будущей цены базового актива S. Оно может не совпадать ни с истинным распределением (не известным ему), ни с наведенным распределением. Плотность вероятности этого распределения обозначим f_t(x). Что касается рынка в целом, то его представление о распределении вероятностей цены базового актива (если о таковом можно говорить) проявляется исключительно в ценах опционов на начало периода и оно отражается в наведенной плотности вероятности f_m(x).
Сопоставляя свое прогнозное распределение вероятностей цены актива с ценами опционов, инвестор может пытаться обнаруживать какие-либо расхождения в этих описаниях и использовать их к своей выгоде. В зависимости от своих рисковых предпочтений он может формулировать различные задачи и в соответствии с этими задачами находить оптимальные портфели опционов, которые эти задачи решают.
В работах [1,2] рассматривался ряд последовательно усложняющихся задач и были приведены их решения в условиях нейтрального к риску рынка. Те же способы решения годятся и для случая рынка, не нейтрального к риску, если просто заменить "истинную" плотность вероятности наведенной плотностью. Кратко сформулируем результаты для однопериодного случая.
Простейшей задачей инвестора можно считать безусловную максимизацию среднего дохода от инвестиции заданного размера. Более сложной является простейшая задача условной максимизации среднего дохода, когда средний доход максимизируется при выполнении одного вероятностного ограничения на случайный доход инвестора (традиционный критерий VaR). Наконец, основным результатом работ [1,2] служит распространение метода условной оптимизации на случай континуального множества вероятностных ограничений на доход инвестора (континуальный критерий VaR).

Безусловная максимизация среднего дохода инвестора

Задача безусловной максимизации среднего дохода инвестора состоит в том, чтобы для заданной инвестиционной суммы A подобрать в качестве объекта инвестирования некоторый инструмент G с платежной функцией g(x), удовлетворяющий равенству G = A и доставляющий максимум M_tB.
Разумеется, такая задача представляет интерес лишь для нейтрального к риску инвестора. Если рассматривать случай, когда инвестор использует лишь инструменты, которые не могут приносить ему отрицательные доходы, т.е. используются лишь инструменты с неотрицательными платежными функциями, то оказывается, что решение задачи доставляют инструменты из класса D(E). При этом условие неотрицательности доходов инвестора означает, что по этим инструментам он фактически может использовать лишь длинные позиции. Для таких инструментов имеет место



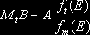
Для обоснования этого вводятся функции правдоподобия




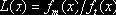
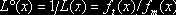
составляющие основу применяемого в статистике критерия Неймана-Пирсона (см., например, [4]).
Процедура Неймана-Пирсона позволяет утверждать, что средний доход инвестора принимает наибольшее значение при страйке E_max, доставляющем наибольшее значение функции правдоподобия L°. Любая другая платежная функция приносит меньший средний доход.
Задача безусловной максимизации среднего дохода не учитывает рисковых предпочтений инвестора. К тому же, очевидно, что предоставляемое инструментом D(E_max) решение не удовлетворительно: доход инвестора равен нулю с вероятностью 1 и бесконечности – с вероятностью нуль, т.е. случайный доход вырожден. Если же говорить о практической реализации этого решения, то речь идет о том, что максимизация среднего дохода инвестора достигается за счет получения весьма больших случайных доходов с незначительной вероятностью и нулевых доходов со значительной вероятностью.
Использование коротких позиций по инструменту D(E_min), где E_min обозначает страйк, доставляющий L° минимум (или же L – максимум), позволяет сколь угодно повысить доходность инвестиции.

Условная максимизация среднего дохода инвестора (стандартный метод VaR)

Качество решения задачи безусловной максимизации можно улучшить с помощью дополнительных ограничений, накладываемых критерием Value at Risk (VaR). В своей стандартной форме он предполагает максимизацию среднего дохода инвестора при выполнении условия



для некоторых значений критического уровня дохода B_cr и вероятности e (обычно небольшой), выбираемых инвестором.
Решение такой задачи также основано на критерии Неймана-Пирсона. Строится однопараметрическое семейство множеств {Z(c), c>0} по правилу



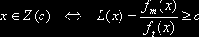
Для заданного e находится множество X(e) из семейства {Z(c)} с вероятностной мерой инвестора, равной e, т.е.


При этом наведенная рыночная вероятность множества X(e), равная , равная



минимальна. Решение задачи существует, если




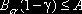
В этом случае инструмент _cr обеспечивает выполнение ограничения (2), а остаток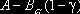


направляется на максимизацию среднего дохода, т.е. на приобретение инструмента D(E_max).

Средний доход от такой инвестиции составляет



а дисперсия –



Использование коротких позиций по инструменту D(E_min) и в этом случае позволяет сколь угодно повысить доходность инвестиции.
Недостатки этого метода несколько смягчены, но аналогичны случаю безусловной максимизации: с вероятностью 1 доход инвестора принимает значения, не превышающие B_cr, и равен бесконечности с вероятностью нуль, т.е. случайный доход вновь носит вырожденный характер.

Континуальный метод VaR

Недостатков можно избежать, используя континуальную версию критерия VaR. Интересы инвестора при этом описываются неубывающей функцией критических доходов B_cr(e), eÎ[0,1]. Эта функция может принимать и отрицательные значения. Более того, она может быть неограниченной в обоих концах отрезка [0,1]. Требуется построить стратегию инвестора, в соответствии с которой его доход B от инвестиции в размере A окажется не ниже B_cr(e) с вероятностью не меньше 1 – e для каждого eÎ[0,1], т.е.

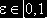. (1)

Если такая задача может быть решена полностью, то остающаяся после ее решения сумма направляется на максимизацию среднего дохода, т.е. инвестируется в инструмент D(E_max) с возможным использованием короткой позиции по инструменту D(E_min).
Каждому уровню вероятности eÎ[0,1] соответствует критическое множество X(e) вероятностной меры инвестора e и его рыночная вероятность g(e). X(e) – неубывающее по параметру e семейство множеств, g(e) – непрерывная и неубывающая функция e, g(e) > e для всех eÎ(0,1), g(0) = 0, g(1) = 1. Решение задачи дается следующей процедурой.
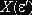
Рассматривается непрерывный процесс инвестирования суммы A по мере возрастания параметра e от 0 до 1. Через A(e) обозначим инвестиционную сумму, необходимую для реализации (6) до произвольной фиксированной точки e включительно (т.е. обеспечения доходов B_cr(e') на множествах 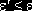). Тогда справедлива формула (имеющая смысл при B_cr(0) > –¥)




После интегрирования по частям получаем соотношение общего вида, не требующее конечности B_cr(0),


При



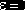
причем средняя часть этого двойного равенства снова имеет смысл лишь при B_cr(0) > –¥. Процесс достигает точки e, если A(e) £ A.
Если это неравенство нарушается в некоторой точке отрезка [0,1], процесс прекращается. Если же процесс не обрывается вплоть до точки

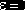
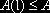
то это значит, что ограничения (6) выполняются для всех eÎ[0,1], и тогда сумма A – A(1) направляется на максимизацию среднего дохода, т.е. вкладывается в инструмент D(E_max).
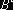
Случайный доход инвестора B может быть представлен как сумма двух случайных величин 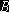, первая из которых фактически является вырожденной случайной величиной, принимающей бесконечно большое значение с бесконечно малой вероятностью и равной нулю с вероятностью 1, а вторая – случайная величина, отвечающая исключительно за выполнение ограничений метода VaR. При этом из неравенства (6) следует, что функция распределения случайной величины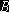



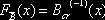
правую часть которого образует обратная к B_cr(e) функция.



Средний доход инвестора составляет


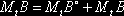
Где




В этих соотношениях не используются короткие позиции по инструменту D(E_min), однако при желании их можно легко учесть.
Инвестор может вообще отказаться от использования вырожденной компоненты дохода. В этом случае ему свои предпочтения удобнее задавать параметрическим семейством функций B_cr(e,b), а параметр b (вообще говоря, векторный) выбирать из условия выполнения равенства в (7). Тогда весь инвестиционный ресурс направляется на выполнение ограничений (6), а вырожденная компонента дохода отсутствует.

Многопериодный рынок опционов и поведение инвестора

Предложенная выше методика допускает обобщение на случай многопериодного рынка опционов. Такой рынок можно рассматривать уже как модель непрерывного по времени рынка. Если учесть, что каждый участник опционного рынка сообразует свои действия не только с общей для всех информацией, но и со своими оценками будущего развития событий, то становится ясно, что определение оптимального для каждого инвестора портфеля опционов – весьма важная задача (см. например, [5]).
Итак, мы полагаем, что временной горизонт рынка опционов охватывает n периодов времени. Дискретное время t пробегает множество значений T È {0}, где t = 0 – начальный момент времени, а T = {1, 2,…, n}. В начальный момент времени инвестор располагает некоторой суммой A, которую он инвестирует в опционы. На многопериодном рынке опционов, вообще говоря, котируются опционы всевозможных сроков действия – от одного до n периодов. Доход от инвестиции в k-периодный опцион, т.е. опцион с истечением срока через k периодов, k £ n, инвестор получает в момент t = k. (Оптимальный портфель строится лишь для опционов европейского типа, исполнение которых допускается только при истечении срока).
К сожалению, одни только эти опционы не в состоянии отразить все нюансы вероятностных характеристик движения цены актива на рынке и предпочтений инвестора. Дело в том, что, как и в однопериодном случае, цены обычных k-периодных опционов для всевозможных страйков, назначаемых на момент времени t = k, определяют безусловное распределение (точнее, наведенное безусловное распределение) вероятностей цены актива на данный момент. Поэтому без дополнительных предположений относительно движения цены актива в разные периоды (например, независимости приращений цены за разные периоды времени) они не могут определять совместных (а также условных) распределений.

    Производные ценные бумаги: Опционы - Фьючерсы - Расчеты

• Опционы
  
• Оценка опционов
  
• Торговля опционами
  
• Российские опционы
  
• Виды опционов
  
  
• Фьючерсы
  
• Анализ фьючерсов
  
• Торговля Фьючерсами
  
• Расчет фьючерса
  
• Фьючерсные риски
  
  
• Фьючерсы на товары
  
• Российские фьючерсы